Proposal for the Application of Fractional Operators in Polynomial Regression Models to Enhance the Determination Coefficient R² on Unseen Data

Abstract

Since polynomial regression models are generally quite reliable for data that can be handled using a linear system, it is important to note that in some cases, they may suffer from overfitting during the training phase. This can lead to negative values of the coefficient of determination $R^2$ when applied to unseen data. To address this issue, this work proposes the partial implementation of fractional operators in polynomial regression models to construct a fractional regression model. The aim of this approach is to mitigate overfitting, which could potentially improve the $R^2$ value for unseen data compared to the conventional polynomial model, under the assumption that this could lead to predictive models with better performance. The methodology for constructing these fractional regression models is presented along with examples applicable to both Riemann–Liouville and Caputo fractional operators, where some results show that regions with initially negative or near-zero $R^2$ values exhibit remarkable improvements after the application of the fractional operator, with absolute relative increases exceeding $800\%$ on unseen data. Finally, the importance of employing sets in the construction of the fractional regression model within this methodological framework is emphasized, since from a theoretical standpoint, one could construct an uncountable family of fractional operators derived from the Riemann–Liouville and Caputo definitions that, although differing in their formulation, would yield the same regression results as those shown in the examples presented in this work.

1. Introduction

Fractional calculus represents an extension of classical calculus, dealing with derivatives and integrals of arbitrary (non-integer) order. This mathematical framework emerged concurrently with traditional calculus, spurred by Leibniz’s notation for integer-order derivatives:

$$\begin{array}{c}\hfill {\displaystyle \frac{d^n}{d{x}^n}}.\end{array}$$

This symbolic formulation allowed L’Hôpital to pose an intriguing question to Leibniz in their correspondence, inquiring about the meaning of taking $n={\displaystyle \frac{1}{2}}$ as the order of a derivative. Although Leibniz was unable to provide a geometric or physical interpretation at the time, he responded insightfully, stating in a letter that it “… is an apparent paradox from which, one day, useful consequences will be drawn” [1]. Furthermore, in one of his correspondence with Johann Bernoulli, Leibniz explicitly mentioned derivatives of “general order” [2], indicating that he had already considered the concept of non-integer derivatives prior to formally proposing it as a mathematical notion, even though he did not fully understand its implications. The term fractional calculus originates from a historical context, as this branch of mathematical analysis studies derivatives and integrals of order $\alpha$, where $\alpha \in \mathbb{R}$.

At present, there exists no universally accepted definition of a fractional derivative. Consequently, when the specific form is not required, the general notation employed is

$$\begin{array}{c}\hfill {\displaystyle \frac{d^{\alpha }}{d{x}^{\alpha }}}.\end{array}$$

Fractional operators admit various formulations, with a key property being their consistency with classical calculus in the limit when $\alpha \to n$, where n is an integer. For instance, let $f:\Omega \subset \mathbb{R}\to \mathbb{R}$ be a function such that $f\in L_{loc}^1(a,b)$, where $L_{loc}^1(a,b)$ denotes the space of locally integrable functions on the open interval $(a,b)\subset \Omega$. One of the fundamental constructs in this theory is the Riemann–Liouville fractional integral, defined as [3,4]

$$\begin{array}{c}\hfill {}_{a}I_x^{\alpha }f\left(x\right):={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_a^x{(x-t)}^{\alpha -1}f\left(t\right)dt,\end{array}$$

(1)

where $\Gamma$ denotes the Gamma function. This operator serves as a foundational element for defining the Riemann–Liouville fractional derivative, expressed as [3,5]

$$\begin{array}{c}\hfill \begin{array}{c}{}_{a}D_x^{\alpha }f\left(x\right):=\left\{\begin{array}{cc}{\displaystyle {}_{a}I_x^{-\alpha }f\left(x\right),}& \mathrm{if} \alpha <0\\ {\displaystyle {\displaystyle \frac{d^n}{d{x}^n}}\left({}_{a}I_x^{n-\alpha }f\left(x\right)\right),}& \mathrm{if} \alpha \ge 0\end{array}\right.\end{array},\end{array}$$

(2)

where $n=\lceil \alpha \rceil$ and ${}_{a}I_x^{0}f\left(x\right):=f\left(x\right)$.

Moreover, if $f:\Omega \subset \mathbb{R}\to \mathbb{R}$ is n-times differentiable with $f,f^{\left(n\right)}\in L_{loc}^1(a,b)$, the Caputo fractional derivative can also be defined via the Riemann–Liouville integral [3,5]:

$$\begin{array}{c}\hfill \begin{array}{c}{}_a{}^{C}D_x^{\alpha }f\left(x\right):=\left\{\begin{array}{cc}{\displaystyle {}_{a}I_x^{-\alpha }f\left(x\right),}& \mathrm{if} \alpha <0\\ {\displaystyle {}_{a}I_x^{n-\alpha }{f}^{\left(n\right)}\left(x\right),}& \mathrm{if} \alpha \ge 0\end{array}\right.\end{array},\end{array}$$

(3)

where $n=\lceil \alpha \rceil$ and ${}_{a}I_x^0{f}^{\left(n\right)}\left(x\right):=f^{\left(n\right)}\left(x\right)$. Importantly, if the function f satisfies the condition $f^{\left(k\right)}\left(a\right)=0$ for all $k\in \left\{0,1,\dots ,n-1\right\}$, then the Riemann–Liouville and Caputo derivatives are equivalent:

$$\begin{array}{c}\hfill {}_{a}D_x^{\alpha }f\left(x\right)={}_a{}^{C}D_x^{\alpha }f\left(x\right).\end{array}$$

(4)

Applying operator (2) to the monomial $x^{\mu }$, with $a=0$ and $\mu >-1$, the following result is obtained:

$$\begin{array}{c}\hfill {}_{0}D_x^{\alpha }{x}^{\mu }={\displaystyle \frac{\Gamma \left(\mu +1\right)}{\Gamma \left(\mu -\alpha +1\right)}}{x}^{\mu -\alpha },\alpha \in \mathbb{R}\setminus \mathbb{Z},\end{array}$$

(5)

and when $1\le \lceil \alpha \rceil \le \mu$, it holds that ${}_{0}D_x^{\alpha }{x}^{\mu }={}_0{}^{C}D_x^{\alpha }{x}^{\mu }$. To illustrate the diversity in the formalism of fractional operators, it is advisable to review key articles such as the article “A Review of Definitions for Fractional Derivatives and Integral” by Capelas de Oliveira and Tenreiro Machado (2014), which provides a comprehensive analysis of the main definitions of fractional derivatives and integrals in mathematics, physics, and engineering, establishing a systematic classification of the most commonly used operators [6]. Subsequently, the article “A Review of Definitions of Fractional Derivatives and Other Operators” by Teodoro et al. (2019) extends this review by incorporating operators that are not strictly fractional but are relevant within the broader context of fractional calculus, highlighting their applications and practical limitations in both computational and physical domains [7]. More recently, the article “How Many Fractional Derivatives Are There?” by Valério et al. (2022) proposes a unified framework for fractional derivatives based on two fundamental parameters—order and asymmetry—through which many existing formulations can be derived while also addressing misconceptions and inaccurate definitions found in the literature [8]. Collectively, these studies offer a thorough and structured overview of the conceptual and formal evolution of fractional operators, which is essential for their rigorous application across various scientific and technological disciplines.

Before proceeding, it is important to highlight the broad applicability of fractional operators across diverse scientific domains. These include finance [9]; economics [10,11]; number theory through the Riemann zeta function [12]; engineering, particularly in the development of hybrid solar receivers [13]; and physics and mathematics, where they are employed to address systems of nonlinear algebraic equations [14,15]. Such problems involve finding the set of zeros of a function $f:\Omega \subset {\mathbb{R}}^n\to {\mathbb{R}}^n$, i.e.,

$$\begin{array}{c}\hfill \left\{\xi \in \Omega :∥f\left(\xi \right)∥=0\right\},\end{array}$$

where $∥·∥:{\mathbb{R}}^n\to \mathbb{R}$ denotes a given norm, or equivalently,

$$\begin{array}{c}\hfill \left\{\xi \in \Omega :{\left[f\right]}_k\left(\xi \right)=0\forall k\ge 1\right\},\end{array}$$

with ${\left[f\right]}_k:{\mathbb{R}}^n\to \mathbb{R}$ representing the k-th component of the vector-valued function f.

2. Sets of Fractional Operators

Prior to advancing, it is crucial to emphasize that the extensive variety of fractional operators reported in the literature can be appreciated by considering seminal contributions: Osler (1970) generalizes the classical Leibniz rule to fractional derivatives and demonstrates its applicability to infinite series expansions [16]; Almeida (2017) introduces a Caputo-type fractional derivative with respect to another function and explores its properties and applications in modeling phenomena such as population growth [17]; Fu et al. (2021) derive a generalized fractional Fokker–Planck equation on fractal media through continuous-time random walks, establishing a link between stochastic processes and fractional dynamics [18]; Fan, Wu and Fu (2022) analyze the function spaces and boundedness conditions of these generalized fractional integrals in the context of continuous-time random walks [19]; Abu-Shady and Kaabar (2021) propose yet another generalized fractional derivative, demonstrating its flexibility across various fractional frameworks [20]; Saad (2020) develops a new nonsingular-kernel fractional derivative and applies it to a Legendre spectral collocation method, enhancing numerical stability [21]; Rahmat (2019) defines a conformable fractional derivative on arbitrary time scales, thereby unifying discrete and continuous fractional calculus [22]; Sousa and De Oliveira (2018) introduce the $\psi$-Hilfer derivative, extending Hilfer’s operator by incorporating a nonconstant kernel function $\psi$ [23]; Jarad et al. (2017) present a novel class of fractional operators that generalizes and unifies several existing definitions [24]; Atangana and Gómez-Aguilar (2017) propose a fractional derivative with a normal-distribution kernel and discuss its theoretical foundations and applications [25]; Yavuz and Özdemir (2020) compare new fractional derivatives featuring exponential and Mittag-Leffler kernels, offering a systematic assessment of their merits and limitations [26]; Liu et al. (2020) introduce a fractional derivative with a sigmoid-function kernel and develop related modeling frameworks [27]; Yang and Machado (2017) develop a variable-order fractional operator and apply it to anomalous diffusion problems, highlighting its enhanced modeling capabilities [28]; Atangana (2016) applies a novel fractional derivative to the nonlinear Fisher reaction–diffusion equation, illustrating its impact on pattern formation in complex systems [29]; He, Li and Wang (2016) employ a new fractional derivative to explain thermophysical properties of polar bear hairs, demonstrating cross-disciplinary applicability [30]; and finally, Sene (2020) formulates a fractional diffusion equation driven by a newly proposed fractional operator, providing fresh insights into anomalous transport phenomena [31]. Collectively, these contributions illustrate the remarkable diversity of fractional derivatives and motivate a set-theoretical framework for their unified characterization. This perspective underpins the methodology known as the fractional calculus of sets [32,33,34,35].

Let $h:{\mathbb{R}}^m\to \mathbb{R}$ be a scalar function, and denote by ${\left\{{\widehat{e}}_k\right\}}_{k\ge 1}$ the canonical basis of ${\mathbb{R}}^m$. Applying Einstein’s summation convention, it is possible to define a fractional operator of order $\alpha$ as follows:

$$o_x^{\alpha }h\left(x\right):={\widehat{e}}_k{o}_k^{\alpha }h\left(x\right).$$

(6)

Define ${\partial }_k^n$ as the partial derivative of order n with respect to the k-th coordinate of x. Utilizing the aforementioned operator, we introduce the following family of fractional operators:

$$O_{x,\alpha }^n\left(h\right):=\left\{o_x^{\alpha }:\exists o_k^{\alpha }h\left(x\right)\mathrm{and}\underset{\alpha \to n}{lim}{o}_k^{\alpha }h\left(x\right)={\partial }_k^{n}h\left(x\right),\forall k\ge 1\right\},$$

(7)

which is nonempty as it contains, for instance, the subset

$$O_{0,x,\alpha }^n\left(h\right):=\left\{o_x^{\alpha }:\exists o_k^{\alpha }h\left(x\right)=\left({\partial }_k^n+\mu \left(\alpha \right){\partial }_k^{\alpha }\right)h\left(x\right),\mathrm{with}\underset{\alpha \to n}{lim}\mu \left(\alpha \right){\partial }_k^{\alpha }h\left(x\right)=0,\forall k\ge 1\right\}.$$

(8)

As a consequence, the following property is satisfied:

$$\mathrm{If}{o}_{i,x}^{\alpha },o_{j,x}^{\alpha }\in O_{x,\alpha }^n\left(h\right)\mathrm{and}i\ne j,\Rightarrow \exists o_{k,x}^{\alpha }={\displaystyle \frac{1}{2}}\left(o_{i,x}^{\alpha }+o_{j,x}^{\alpha }\right)\in O_{x,\alpha }^n\left(h\right),$$

(9)

moreover, the complement of the set (7) is defined by

$$O_{x,\alpha }^{n,c}\left(h\right):=\left\{o_x^{\alpha }:\exists o_k^{\alpha }h\left(x\right)\forall k\ge 1,\mathrm{and}\underset{\alpha \to n}{lim}{o}_k^{\alpha }h\left(x\right)\ne {\partial }_k^{n}h\left(x\right)\mathrm{for}\mathrm{at}\mathrm{least}\mathrm{one}k\right\},$$

(10)

and from this definition, the following assertion follows:

$$\mathrm{If}{o}_{i,x}^{\alpha }={\widehat{e}}_k{o}_{i,k}^{\alpha }\in O_{x,\alpha }^n\left(h\right),\Rightarrow \exists o_{j,x}^{\alpha }={\widehat{e}}_k{o}_{i,{\sigma }_j\left(k\right)}^{\alpha }\in O_{x,\alpha }^{n,c}\left(h\right),$$

(11)

where ${\sigma }_j:\{1,2,\dots ,m\}\to \{1,2,\dots ,m\}$ is a permutation different from the identity permutation.

The set (7) allows the extension of certain classical calculus elements. For instance, for $\gamma \in {\mathbb{N}}_0^m$ and $x\in {\mathbb{R}}^m$, the following multi-index notation can be defined:

$$\left\{\begin{array}{c}\begin{array}{ccc}{\displaystyle \gamma !:=\prod _{k=1}^m{\left[\gamma \right]}_k!,}& {\displaystyle \left|\gamma \right|:=\sum _{k=1}^m{\left[\gamma \right]}_k,}& {\displaystyle x^{\gamma }:=\prod _{k=1}^m{\left[x\right]}_k^{{\left[\gamma \right]}_k}}\end{array}\\ {\displaystyle \frac{{\partial }^{\gamma }}{\partial x^{\gamma }}}:={\displaystyle \frac{{\partial }^{{\left[\gamma \right]}_1}}{\partial {\left[x\right]}_1^{{\left[\gamma \right]}_1}}}{\displaystyle \frac{{\partial }^{{\left[\gamma \right]}_2}}{\partial {\left[x\right]}_2^{{\left[\gamma \right]}_2}}}\dots {\displaystyle \frac{{\partial }^{{\left[\gamma \right]}_m}}{\partial {\left[x\right]}_m^{{\left[\gamma \right]}_m}}}\end{array}\right..$$

(12)

So, given a function $h:\Omega \subset {\mathbb{R}}^m\to \mathbb{R}$, the following fractional operator can be defined:

$$s_x^{\alpha \gamma }\left(o_x^{\alpha }\right):=o_1^{\alpha {\left[\gamma \right]}_1}{o}_2^{\alpha {\left[\gamma \right]}_2}\dots o_m^{\alpha {\left[\gamma \right]}_m},$$

(13)

which leads to the definition of the following set:

$$S_{x,\alpha }^{n,\gamma }\left(h\right):=\left\{s_x^{\alpha \gamma }=s_x^{\alpha \gamma }\left(o_x^{\alpha }\right):\exists s_x^{\alpha \gamma }h\left(x\right)\mathrm{with}{o}_x^{\alpha }\in O_{x,\alpha }^s\left(h\right)\forall s\le n^2,\mathrm{and}\underset{\alpha \to k}{lim}{s}_x^{\alpha \gamma }h\left(x\right)={\displaystyle \frac{{\partial }^{k\gamma }}{\partial x^{k\gamma }}}h\left(x\right),\forall \alpha ,\left|\gamma \right|\le n\right\},$$

(14)

for which the following properties are valid:

$$\mathrm{If}{s}_x^{\alpha \gamma }\in S_{x,\alpha }^{n,\gamma }\left(h\right),\Rightarrow \left\{\begin{array}{c}{\displaystyle \underset{\alpha \to 0}{lim}{s}_x^{\alpha \gamma }h\left(x\right)=o_1^0{o}_2^0\dots o_m^{0}h\left(x\right)=h\left(x\right),}\hfill \\ {\displaystyle \underset{\alpha \to 1}{lim}{s}_x^{\alpha \gamma }h\left(x\right)=o_1^{{\left[\gamma \right]}_1}{o}_2^{{\left[\gamma \right]}_2}\dots o_m^{{\left[\gamma \right]}_m}h\left(x\right)={\displaystyle \frac{{\partial }^{\gamma }}{\partial x^{\gamma }}}h\left(x\right),\forall \left|\gamma \right|\le n,}\hfill \\ {\displaystyle \underset{\alpha \to q}{lim}{s}_x^{\alpha \gamma }h\left(x\right)=o_1^{q{\left[\gamma \right]}_1}{o}_2^{q{\left[\gamma \right]}_2}\dots o_m^{q{\left[\gamma \right]}_m}h\left(x\right)={\displaystyle \frac{{\partial }^{q\gamma }}{\partial x^{q\gamma }}}h\left(x\right),\forall q\left|\gamma \right|\le qn,}\hfill \\ {\displaystyle \underset{\alpha \to n}{lim}{s}_x^{\alpha \gamma }h\left(x\right)=o_1^{n{\left[\gamma \right]}_1}{o}_2^{n{\left[\gamma \right]}_2}\dots o_m^{n{\left[\gamma \right]}_m}h\left(x\right)={\displaystyle \frac{{\partial }^{n\gamma }}{\partial x^{n\gamma }}}h\left(x\right),\forall n\left|\gamma \right|\le n^2.}\hfill \end{array}\right.$$

(15)

Employing the little-o notation and denoting by $B(a;\delta )$ a ball centered at $a\in {\mathbb{R}}^m$ with radius $\delta$, it is possible to derive the following result:

$$\mathrm{If}x\in B(a;\delta ),\Rightarrow \underset{x\to a}{lim}{\displaystyle \frac{o\left({(x-a)}^{\gamma }\right)}{{(x-a)}^{\gamma }}}=0,\forall \left|\gamma \right|\ge 1.$$

(16)

This motivates the introduction of the following set of functions:

$$R_{\alpha \gamma }^n\left(a\right):=\left\{r_{\alpha \gamma }^n:\underset{x\to a}{lim}\parallel r_{\alpha \gamma }^n\left(x\right)\parallel =0,\forall \left|\gamma \right|\ge n,\mathrm{and}\parallel r_{\alpha \gamma }^n{\left(x\right)\parallel \le o(\parallel x-a\parallel }^n),\forall x\in B(a;\delta )\right\}.$$

(17)

Subsequently, considering the following sets of fractional operators,

$$T_{x,\alpha ,p}^{n,q,\gamma }(a,h):=\left\{t_x^{\alpha ,p}=t_x^{\alpha ,p}\left(s_x^{\alpha \gamma }\right):s_x^{\alpha \gamma }\in S_{x,\alpha }^{M,\gamma }\left(h\right),t_x^{\alpha ,p}h\left(x\right):=\sum _{\left|\gamma \right|=0}^p{\displaystyle \frac{1}{\gamma !}}{s}_x^{\alpha \gamma }h\left(a\right){(x-a)}^{\gamma }+r_{\alpha \gamma }^p\left(x\right),\forall \alpha \le n,\forall p\le q\right\},$$

(18)

$$T_{x,\alpha }^{\infty ,\gamma }(a,h):=\left\{t_x^{\alpha ,\infty }=t_x^{\alpha ,\infty }\left(s_x^{\alpha \gamma }\right):s_x^{\alpha \gamma }\in S_{x,\alpha }^{\infty ,\gamma }\left(h\right),t_x^{\alpha ,\infty }h\left(x\right):=\sum _{\left|\gamma \right|=0}^{\infty }{\displaystyle \frac{1}{\gamma !}}{s}_x^{\alpha \gamma }h\left(a\right){(x-a)}^{\gamma }\right\},$$

(19)

it is possible to extend the classical Taylor expansion of scalar functions using multi-index notation, where $M=max\{n,q\}$. Consequently, the following results emerge:

$$\mathrm{If}{t}_x^{\alpha ,p}\in T_{x,\alpha ,p}^{1,q,\gamma }(a,h)\mathrm{and}\alpha \to 1,\Rightarrow t_x^{1,p}h\left(x\right)=h\left(a\right)+\sum _{\left|\gamma \right|=1}^p{\displaystyle \frac{1}{\gamma !}}{\displaystyle \frac{{\partial }^{\gamma }}{\partial x^{\gamma }}}h\left(a\right){(x-a)}^{\gamma }+r_{\gamma }^p\left(x\right).$$

(20)

$$\mathrm{If}{t}_x^{\alpha ,p}\in T_{x,\alpha ,p}^{n,1,\gamma }(a,h)\mathrm{and}p\to 1,\Rightarrow t_x^{\alpha ,1}h\left(x\right)=h\left(a\right)+\sum _{k=1}^m{o}_k^{\alpha }h\left(a\right){\left[(x-a)\right]}_k+r_{\alpha \gamma }^1\left(x\right).$$

(21)

Lastly, the set in (7) can be regarded as a generator of fractional tensor operators. For instance, given $\alpha ,n\in {\mathbb{R}}^d$ with $\alpha ={\widehat{e}}_k{\left[\alpha \right]}_k$ and $n={\widehat{e}}_k{\left[n\right]}_k$, it is feasible to define the following set:

$$O_{x,\alpha }^n\left(h\right):=\left\{o_x^{\alpha }:\exists o_x^{\alpha }h\left(x\right)\mathrm{and}{o}_x^{\alpha }\in O_{x,{\left[\alpha \right]}_1}^{{\left[n\right]}_1}\left(h\right)\times O_{x,{\left[\alpha \right]}_2}^{{\left[n\right]}_2}\left(h\right)\times \dots \times O_{x,{\left[\alpha \right]}_d}^{{\left[n\right]}_d}\left(h\right)\right\}.$$

(22)

3. Groups of Fractional Operators

Consider a function $h:\Omega \subset {\mathbb{R}}^m\to {\mathbb{R}}^m$. We introduce the following sets of fractional operators associated with a vector function:

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m\mathrm{O}_{x,\alpha }^n\left(h\right):=\left\{o_x^{\alpha }:o_x^{\alpha }\in O_{x,\alpha }^n\left({\left[h\right]}_k\right)\mathrm{for}\mathrm{all}k\le m\right\},}\end{array}\end{array}$$

(23)

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m\mathrm{O}_{x,\alpha }^{n,c}\left(h\right):=\left\{o_x^{\alpha }:o_x^{\alpha }\in O_{x,\alpha }^{n,c}\left({\left[h\right]}_k\right)\mathrm{for}\mathrm{all}k\le m\right\},}\end{array}\end{array}$$

(24)

$$\begin{array}{c}{}_m\mathrm{O}_{x,\alpha }^{n,u}\left(h\right):={}_m\mathrm{O}_{x,\alpha }^n\left(h\right)\cup {}_m\mathrm{O}_{x,\alpha }^{n,c}\left(h\right),\end{array}$$

(25)

where ${\left[h\right]}_k:\Omega \subset {\mathbb{R}}^m\to \mathbb{R}$ denotes the k-th component of h. Utilizing these sets, we define the following family of fractional operators:

$${}_m\mathrm{MO}_{x,\alpha }^{\infty ,u}\left(h\right):=\bigcap _{k\in \mathbb{Z}}{}_m\mathrm{O}_{x,\alpha }^{k,u}\left(h\right).$$

(26)

It is noteworthy that this family adheres to the identity property relative to the classical Hadamard product:

$$o_x^0\circ h\left(x\right):=h\left(x\right)\forall o_x^{\alpha }\in {}_m\mathrm{MO}_{x,\alpha }^{\infty ,u}\left(h\right).$$

(27)

So, for every operator $o_x^{\alpha }\in {}_m\mathrm{MO}_{x,\alpha }^{\infty ,u}\left(h\right)$, the corresponding fractional matrix operator is defined:

$$A_{\alpha }\left(o_x^{\alpha }\right):=\left({\left[A_{\alpha }\left(o_x^{\alpha }\right)\right]}_{jk}\right):=\left(o_k^{\alpha }\right).$$

(28)

Subsequently, for each $o_x^{\alpha }\in {}_m\mathrm{MO}_{x,\alpha }^{\infty ,u}\left(h\right)$, the following a modified Hadamard product is introduced [32]:

$$o_{i,x}^{p\alpha }\circ o_{j,x}^{q\alpha }:=\left\{\begin{array}{cc}{o}_{i,x}^{p\alpha }\circ o_{j,x}^{q\alpha },\hfill & \mathrm{if}i\ne j(\mathrm{horizontal}\mathrm{Hadamard}\mathrm{product})\hfill \\ o_{i,x}^{(p+q)\alpha },\hfill & \mathrm{if}i=j(\mathrm{vertical}\mathrm{Hadamard}\mathrm{product})\hfill \end{array}\right..$$

(29)

Then, it is feasible, using the aforementioned definitions, to construct an Abelian group of fractional operators which is isomorphic to the additive group of integers, as stated in the following theorem [33]:

Theorem 1. 

Let $o_x^{\alpha }\in {}_m\mathrm{MO}_{x,\alpha }^{\infty ,u}\left(h\right)$ be a fractional operator, and consider the group of integers under addition $(\mathbb{Z},+)$. Then, employing the modified Hadamard product (29), the set of fractional matrix operators

$${}_m\mathrm{G}\left(A_{\alpha }\left(o_x^{\alpha }\right)\right):=\left\{A_{\alpha }^{\circ r}=A_{\alpha }\left(o_x^{r\alpha }\right):r\in \mathbb{Z}\right\}$$

(30)

constitutes an Abelian group generated by $A_{\alpha }\left(o_x^{\alpha }\right)$ that is isomorphic to $(\mathbb{Z},+)$:

$${}_m\mathrm{G}\left(A_{\alpha }\left(o_x^{\alpha }\right)\right)\cong (\mathbb{Z},+).$$

(31)

From this theorem, the following corollary naturally follows:

Corollary 1. 

Given $o_x^{\alpha }\in {}_m\mathrm{MO}_{x,\alpha }^{\infty ,u}\left(h\right)$, the group of integers $(\mathbb{Z},+)$, and any subgroup $\mathbb{H}\subseteq \mathbb{Z}$, one can define the subset of fractional matrix operators:

$${}_m\mathrm{G}(A_{\alpha }\left(o_x^{\alpha }\right),\mathbb{H}):=\left\{A_{\alpha }^{\circ r}=A_{\alpha }\left(o_x^{r\alpha }\right):r\in \mathbb{H}\right\},$$

(32)

which forms a subgroup of ${}_m\mathrm{G}\left(A_{\alpha }\left(o_x^{\alpha }\right)\right)$:

$${}_m\mathrm{G}(A_{\alpha }\left(o_x^{\alpha }\right),\mathbb{H})\le {}_m\mathrm{G}\left(A_{\alpha }\left(o_x^{\alpha }\right)\right).$$

(33)

Example 1. 

Let ${\mathbb{Z}}_n$ be the residue class ring modulo the positive integer n. So, for a fractional operator $o_x^{\alpha }\in {}_m\mathrm{MO}_{x,\alpha }^{\infty ,u}\left(h\right)$ and ${\mathbb{Z}}_{14}$, it is feasible to define the following Abelian group of fractional matrix operators under the modified Hadamard product (29):

$${}_m\mathrm{G}(A_{\alpha }\left(o_x^{\alpha }\right),{\mathbb{Z}}_{14})=\left\{A_{\alpha }^{\circ 0},A_{\alpha }^{\circ 1},A_{\alpha }^{\circ 2},\dots ,A_{\alpha }^{\circ 13}\right\}.$$

(34)

Moreover, Corollary 1 facilitates the generation of groups of fractional operators under alternative operations. For instance, considering the operation

$$A_{\alpha }^{\circ r}\ast A_{\alpha }^{\circ s}=A_{\alpha }^{\circ \left(rs\right)},$$

(35)

the following corollaries can be obtained:

Corollary 2. 

Let ${\mathbb{M}}_n$ be the multiplicative group of positive residue classes coprime to n. So, for each fractional operator $o_x^{\alpha }\in {}_m\mathrm{MO}_{x,\alpha }^{\infty ,u}\left(h\right)$, it is feasible to define the following set:

$${}_m\mathrm{G}^{\ast }\left(A_{\alpha }\left(o_x^{\alpha }\right),{\mathbb{M}}_n\right):=\left\{A_{\alpha }^{\circ r}=A_{\alpha }\left(o_x^{r\alpha }\right):r\in {\mathbb{M}}_n\right\}$$

(36)

which forms an Abelian group under the operation (35).

Corollary 3. 

Let ${\mathbb{Z}}_p^{+}$ be the multiplicative group of positive residue classes modulo a prime p. So, for each fractional operator $o_x^{\alpha }\in {}_m\mathrm{MO}_{x,\alpha }^{\infty ,u}\left(h\right)$, it is feasible to define the following set:

$${}_m\mathrm{G}^{\ast }\left(A_{\alpha }\left(o_x^{\alpha }\right),{\mathbb{Z}}_p^{+}\right):=\left\{A_{\alpha }^{\circ r}=A_{\alpha }\left(o_x^{r\alpha }\right):r\in {\mathbb{Z}}_p^{+}\right\}$$

(37)

which forms an Abelian group under the operation (35).

Finally, it is important to note that when n is prime, the following equality holds:

$${}_m\mathrm{G}^{\ast }\left(A_{\alpha }\left(o_x^{\alpha }\right),{\mathbb{M}}_n\right)={}_m\mathrm{G}^{\ast }\left(A_{\alpha }\left(o_x^{\alpha }\right),{\mathbb{Z}}_n^{+}\right).$$

(38)

4. Polynomial Regression Model

Polynomial regression constitutes an extension of linear regression that captures the relationship between the independent variable x and the dependent variable y through a polynomial function of degree n. Unlike simple linear regression, which assumes a purely linear association between x and y, polynomial regression introduces curvature by incorporating terms of higher powers of x. The general expression of a polynomial regression model is formulated as

$$\begin{array}{c}\hfill y={\beta }_0+{\beta }_{1}x+{\beta }_2{x}^2+\dots +{\beta }_n{x}^n.\end{array}$$

Here, the parameter ${\beta }_0$ denotes the intercept, corresponding to the expected value of y when $x=0$. The coefficients ${\beta }_1,{\beta }_2,\dots ,{\beta }_n$ quantify the influence of each power of x on the predicted outcome.

Incorporating polynomial terms enables the model to accommodate nonlinear tendencies while retaining linearity in terms of the parameters. The model’s adaptability increases with the polynomial degree n, thus permitting it to approximate complex data patterns more effectively.

The polynomial regression model can also be represented in matrix form, which simplifies the estimation of the coefficients. Using matrix notation, the model is expressed as

$$\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]=\left[\begin{array}{ccccc}1& x_1& x_1^2& \dots & x_1^n\\ 1& x_2& x_2^2& \dots & x_2^n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_m& x_m^2& \dots & x_m^n\end{array}\right]\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_n\end{array}\right]\Rightarrow \mathbf{y}=\mathbf{X}\mathit{\beta },$$

where:

• $\mathbf{y}$ represents the vector of observed responses;
• $\mathbf{X}$ is the design matrix, with each row corresponding to an observation and each column representing a specific power of x;
• $\mathit{\beta }$ denotes the vector of regression coefficients.

The parameter vector $\mathit{\beta }$ is commonly estimated via the least squares criterion, which minimizes the sum of squared residuals between observed and predicted values. The estimator for $\mathit{\beta }$ is given by

$$\begin{array}{c}\hfill \mathit{\beta }={\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}^T\mathbf{y}.\end{array}$$

This formula is fundamental in polynomial regression as it facilitates the identification of coefficients that optimally fit the data.

Each coefficient in the polynomial regression equation carries a distinct interpretation with respect to the shape of the regression curve:

• The intercept ${\beta }_0$ indicates the predicted value of y at $x=0$.
• The coefficient ${\beta }_1$ pertains to the linear term x, governing the slope of the regression line near $x=0$.
• The coefficient ${\beta }_2$ relates to the quadratic term $x^2$, influencing the curvature of the fit.
• Higher-order coefficients, such as ${\beta }_3$ for $x^3$, ${\beta }_4$ for $x^4$, etc., introduce additional degrees of flexibility, enabling the model to capture more intricate patterns.

Selecting the polynomial degree n is a critical modeling decision. A polynomial of insufficient degree may fail to capture essential trends in the data, whereas a polynomial of excessively high degree risks overfitting and producing unwarranted oscillations. Common strategies for selecting the degree include cross-validation techniques and incorporating prior knowledge of the data domain.

Polynomial regression has proven to be a valuable analytical tool across a wide range of disciplines, providing nuanced modeling of nonlinear relationships frequently encountered in empirical data. For example, in economics, polynomial regression has been employed to model the Laffer Curve, which posits a nonlinear relationship between tax rates and government revenue; Trabandt and Uhlig (2011) [36] applied this methodology to data from the United States and Europe, identifying optimal taxation thresholds that maximize revenue. In physics, polynomial models are utilized to capture deviations from ideal projectile motion caused by factors such as air resistance, yielding more accurate trajectory estimations beyond simple quadratic fits (Serway and Jewett, 2018) [37]. Similarly, in engineering—particularly within materials science—higher-degree polynomial regression is used to model the stress–strain behavior of materials during plastic deformation, enabling precise characterization of mechanical properties under varying loads (Callister and Rethwisch, 2020) [38].

By enabling the modeling of nonlinear associations while maintaining a simple and interpretable parametric form, polynomial regression significantly extends the applicability of classical regression frameworks.

5. Seen and Unseen Data in Regression Models

In regression modeling, distinguishing between “seen” and “unseen” data is essential for assessing a model’s performance and its capacity to generalize. This differentiation directly impacts how effectively the model can adapt to novel data and produce trustworthy predictions in practical applications.

Seen data, often called training data, refers to the dataset utilized during the model’s learning phase. Throughout this process, the model identifies the inherent patterns and dependencies between the independent variables (features) and the dependent variable (target). By tuning parameters such as coefficients, the model aims to minimize the discrepancy between predicted outputs and actual observations within the training dataset. The accuracy and volume of training data critically influence the model’s ability to accurately represent the relationships among variables.

The primary goal of training on seen data is to derive a function that characterizes the association between input features and output targets. Nonetheless, the model must not only achieve a good fit on the training data but also extend its learned structure to unseen, future data. This capacity for generalization is vital, as it determines the model’s effectiveness when applied to new datasets or real-world problems.

Unseen data, alternatively known as test data, comprises observations that the model has not encountered during training. This dataset serves as a benchmark to evaluate the model’s predictive capabilities on novel information. The chief purpose of employing unseen data is to measure the model’s accuracy and verify that it has identified genuine patterns instead of merely memorizing the training examples.

A model’s aptitude to generalize well to unseen data is a key indicator of its robustness. A well-generalized model can leverage its learned parameters to produce reliable predictions on new inputs. High performance on both training and test datasets implies that the model has effectively captured the fundamental relationships in the data rather than fitting noise or peculiarities present in the training set. Conversely, suboptimal results on unseen data may signal poor generalization, often caused by either overfitting or underfitting.

• Overfitting: This occurs when a model excessively adapts to the specific details and noise within the training data, thereby impairing its ability to perform accurately on unseen data. Overfitting is usually linked to models that are overly complex relative to the size or variability of the training set. Consequently, the model becomes too specialized in the training data, losing generalization capacity on new samples.
• Underfitting: This situation arises when the model is overly simplistic and fails to capture the genuine patterns in the data, resulting in poor predictive performance on both the training and test datasets. Underfitting generally happens when the model’s parameterization is insufficient or too rigid to reflect the underlying relationships, causing inaccurate predictions and low overall efficacy.

6. The Coefficient of Determination ${\mathbf{R}}^{\mathbf{2}}$

A fundamental metric for assessing the efficacy of regression models is the coefficient of determination, denoted by $R^2$. This statistic quantifies the proportion of variance in the dependent variable that can be accounted for by the independent variables. Formally, $R^2$ is expressed as

$$\begin{array}{c}\hfill R^2=1-\left(\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2\right){\left(\sum _{i=1}^n{(y_i-\overline{y})}^2\right)}^{-1},\end{array}$$

(39)

where $y_i$ indicates the observed values, ${\widehat{y}}_i$ denotes the predicted values, and $\overline{y}$ represents the mean of the observed data. The numerator corresponds to the residual sum of squares (RSS), reflecting the prediction errors, while the denominator represents the total sum of squares (TSS), measuring the overall variance in the data. An $R^2$ value approaching 1 signifies that the model explains a large fraction of the variance in the target variable.

The coefficient $R^2$ typically ranges from 0 to 1, although it can assume negative values in some cases, especially when the model is improperly specified or overfits the data. The interpretation of $R^2$ values is as follows:

• $R^2=1$: This indicates a perfect fit where the model explains all variance in the dependent variable. The predicted values coincide exactly with the actual values, implying zero prediction error. However, such a result is uncommon in practical contexts and often suggests overfitting.
• $0<R^2<1$: Values within this interval imply that the model accounts for a portion of the variance. The closer $R^2$ is to 1, the better the fit and the more variance explained. For instance, $R^2=0.8$ indicates that 80% of the variance is captured by the model.
• $R^2=0$: This value suggests that the model does not explain any variance beyond the mean of the dependent variable. Predictions are no better than simply using the average outcome, indicating no meaningful relationship is captured.
• Negative $R^2$: Though rare, negative $R^2$ values may occur when the model performs worse than a naive mean predictor. This signals poor model fit and often results from overfitting or incorrect model formulation.

Generally, a higher $R^2$ reflects superior model performance and greater explanatory power. Nonetheless, relying solely on $R^2$ is inadequate for model evaluation, as it does not penalize overfitting or consider model complexity. Complementary metrics and validation methods, such as cross-validation, are recommended to ensure model robustness.

A high $R^2$ on the training dataset indicates good fit, yet it is even more critical to obtain a strong $R^2$ on unseen test data. A robust $R^2$ on new data demonstrates the model’s ability to generalize true underlying patterns rather than overfit training noise. This confers several benefits:

• Enhanced generalization: Models with elevated $R^2$ on unseen data provide reliable predictions for novel observations, increasing practical utility.
• Mitigated overfitting: Sustained high $R^2$ on test sets suggests the model has learned substantive patterns rather than memorizing training instances.
• Improved decision support: In domains such as finance, healthcare, and engineering, dependable predictions based on high test $R^2$ facilitate better informed decisions.
• Robust model selection: Comparing $R^2$ values across models aids in identifying the optimal balance between complexity and predictive accuracy without overfitting.

Therefore, ensuring that a model maintains a consistently high $R^2$ across both training and unseen datasets is crucial for building reliable, interpretable regression frameworks.

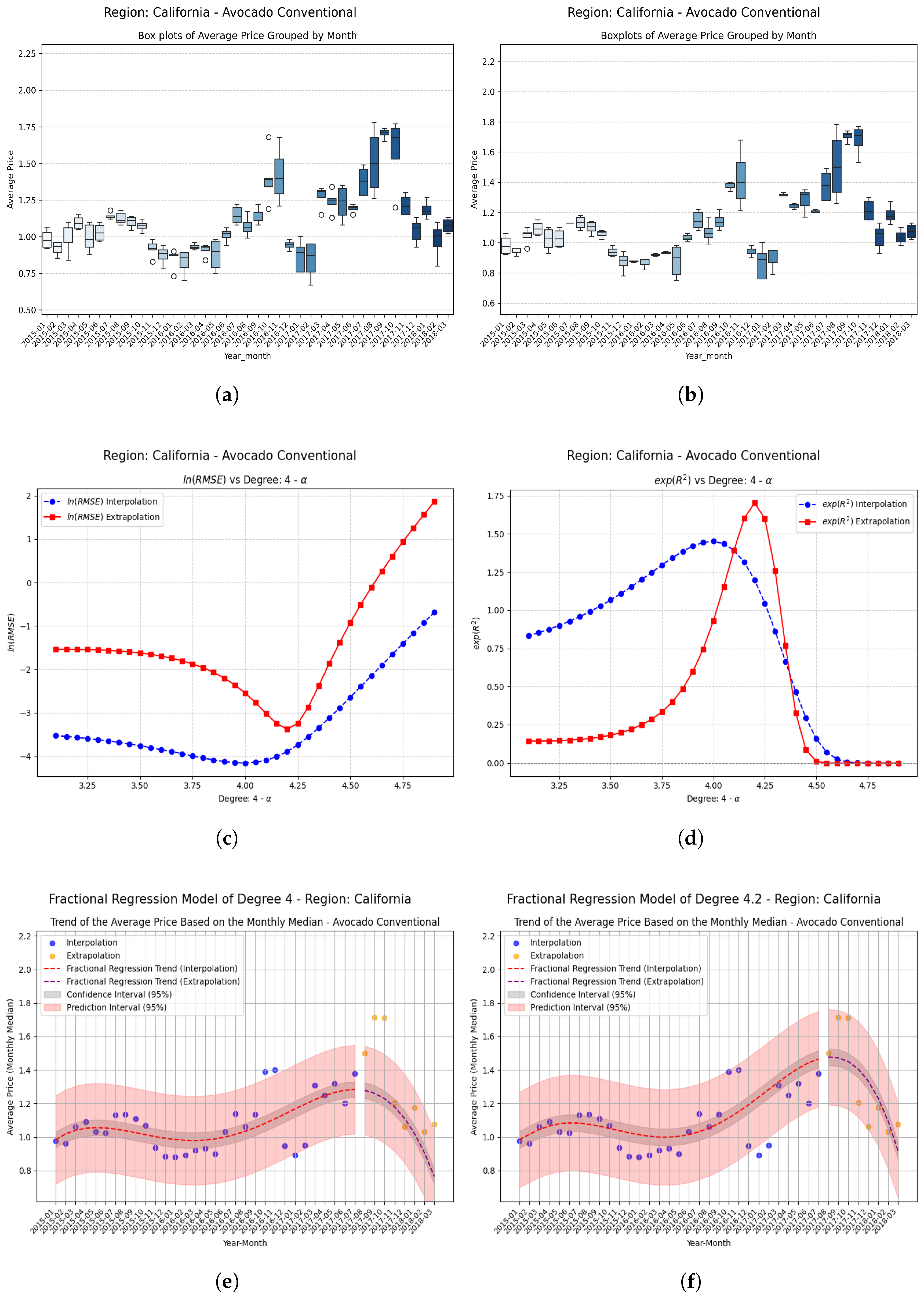
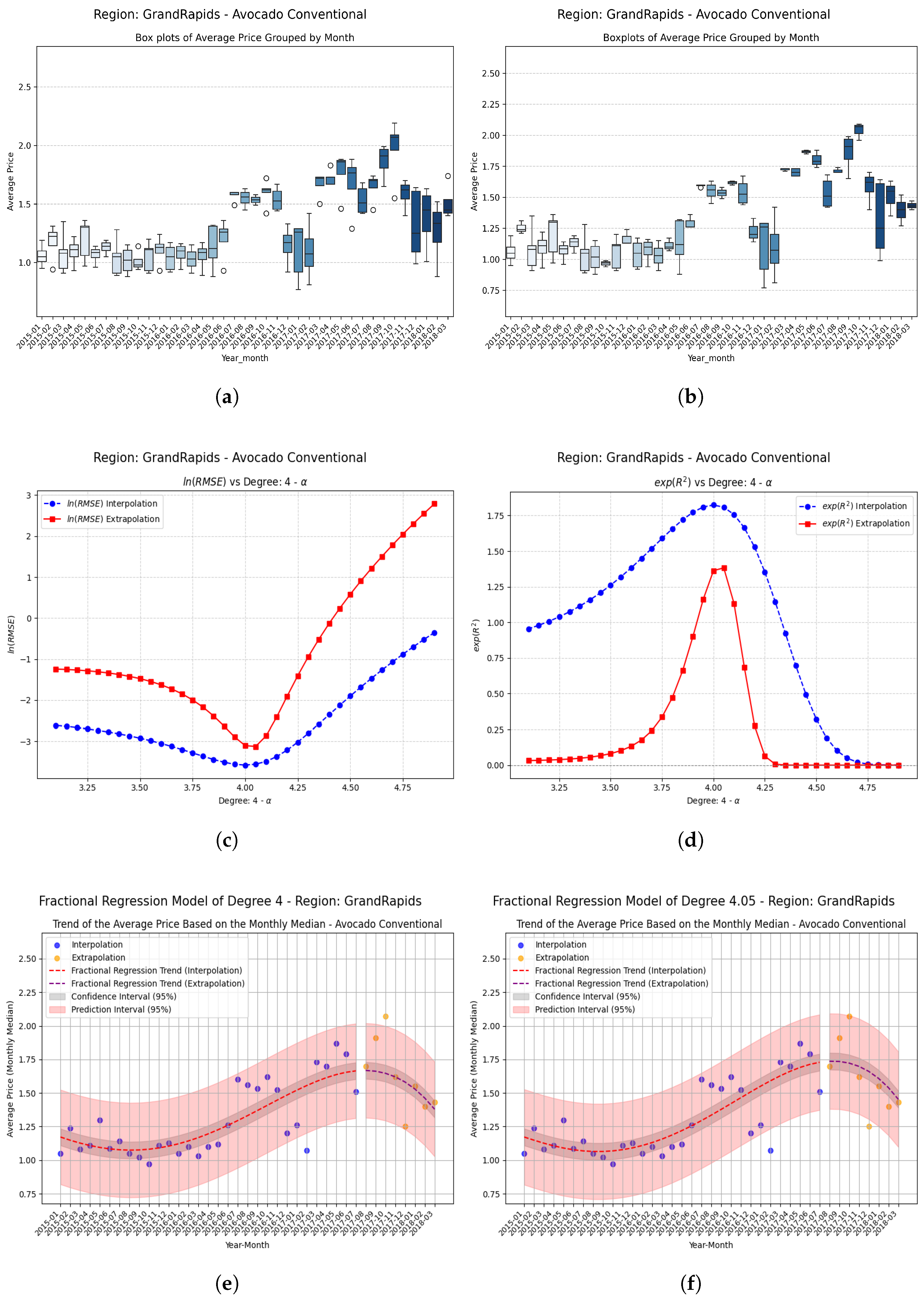
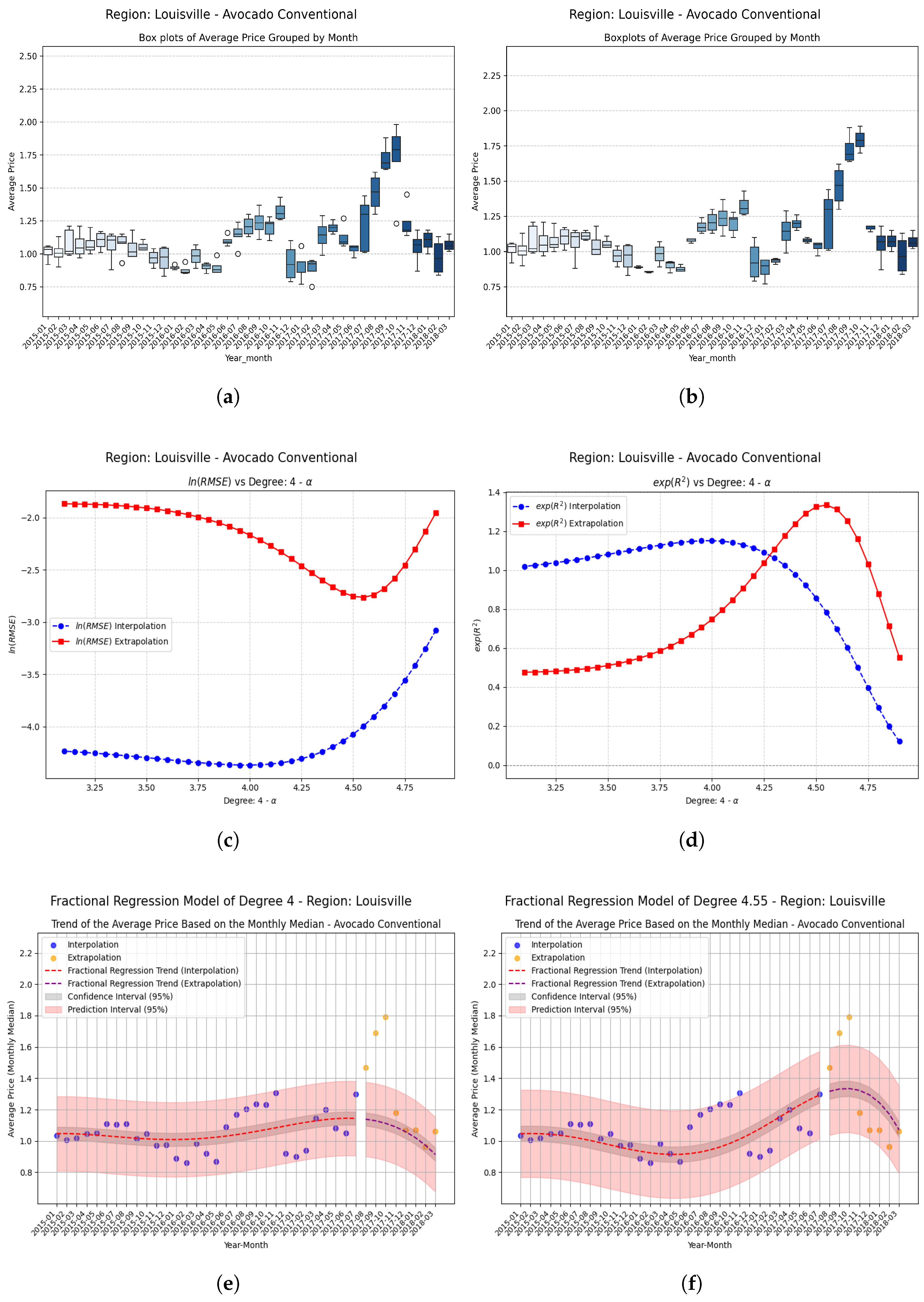
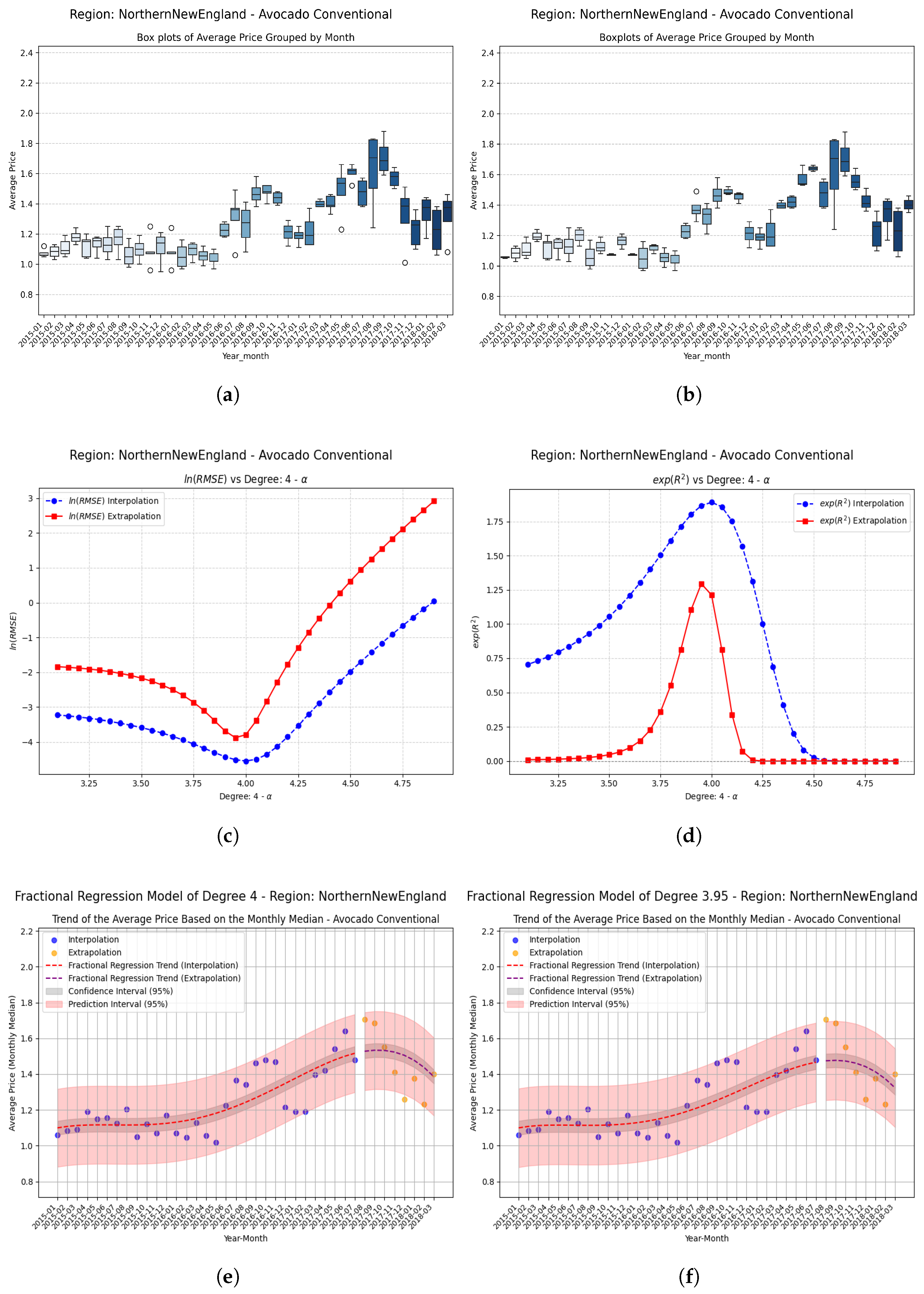
7. Fractional Regression Model

In the construction of predictive models based on time series data, it is standard practice to partition the dataset into two principal segments. The first, commonly referred to as the interpolation segment, comprises the training data used for model calibration. The second segment, associated with extrapolation, consists of data near or beyond the boundaries of the observed sample and serves to evaluate the predictive capability of the model once training and testing have been completed.

Within the framework of polynomial regression, the selection of the polynomial degree m plays a crucial role. Small variations in m—even by a single unit—can result in pronounced fluctuations in model performance, particularly during the validation phase. Such instability frequently necessitates a reevaluation of traditional modeling strategies. In response to this challenge, the present study explores a partial integration of fractional derivatives into regression models. This approach is inspired by recent developments in the literature, notably in [39,40], and aims to enhance model robustness in both interpolation and extrapolation contexts.

To examine the viability of this methodology, polynomial regression models are constructed using a dataset comprising average monthly prices of conventional and organic avocados from 2015 to 2018. This dataset is publicly accessible at the following GitHub repository: https://github.com/UOC-curso/curso/blob/main/proyectos/proyecto-1-regresion/avocado.csv (accessed on 18 April 2025).

A standard polynomial regression model of order m is given by

$$\begin{array}{c}\hfill y\left(x\right)=\sum _{i=0}^m{\beta }_i{x}^i,\end{array}$$

(40)

where the coefficients ${\left\{{\beta }_i\right\}}_{i=0}^m$ are to be estimated from the data, generally using an interpolation segment. Considering this structure, it is feasible to define the following set:

$$\begin{array}{c}\hfill {MO}_{x,\alpha }^m\left(y-{\beta }_0\right):=\bigcap _{k=-m}^m{O}_{x,\alpha }^k\left(y-{\beta }_0\right),\end{array}$$

(41)

which enables the construction of a fractional regression model for any operator $o_x^{\alpha }\in {MO}_{x,\alpha }^1\left(y-{\beta }_0\right)$ as follows:

$$\begin{array}{c}\hfill \sigma (\alpha ,x):={\beta }_0+\sum _{i=1}^m{\beta }_i{o}_x^{\alpha }{x}^i,\alpha \in (-1,1).\end{array}$$

(42)

It is worth mentioning that preserving the intercept term ${\beta }_0$ is essential to ensure that the regression model retains its original value at $x=0$. This formulation can be naturally extended to a multidimensional setting using a logistic function f, resulting in a fractional logistic regression model:

$$\begin{array}{c}\hfill \sigma (\alpha ,x):=f\left({\beta }_0+\sum _{i=1}^m{\beta }_i{o}_{x_i}^{\alpha }{x}_i\right),\alpha \in (-1,1).\end{array}$$

(43)

This generalized structure may be interpreted as a fractional activation function, thereby laying the foundation for developing fractional neural networks, provided that all features $x_i$ are non-negative. To satisfy this prerequisite, preprocessing methods such as normalization can be employed to scale all inputs to the interval $[0,1]$.

It is important to emphasize that the concept of fractional regression is not novel in the literature. Seminal contributions in this domain include the study “Regression Using Fractional Polynomials of Continuous Covariates” by Royston and Altman (1994) [41] and, more recently, “Regression Coefficient Derivation via Fractional Calculus Framework” by Awadalla et al. (2022) [42]. These works, although differing in methodology, share the objective of enhancing the flexibility and performance of regression models with a structure different from that of classical polynomial regression.

Royston and Altman propose the use of fractional polynomials, which enrich traditional polynomial regression by incorporating real-valued exponents in covariate transformations. This method provides an effective balance between model complexity and interpretability, capturing nonlinear trends while maintaining a parametric form consistent with conventional practices.

On the other hand, Awadalla et al. introduce a fundamentally different framework grounded in fractional calculus, particularly employing Caputo derivatives. Their approach modifies the classical least squares estimation technique to incorporate fractional differentiation, thereby expanding the model class. Traditional models are recovered when the fractional order $\alpha =1$. The practical applicability of this methodology has been demonstrated in diverse contexts, including wage analysis and demographic modeling, showing improvements in predictive accuracy.

While Royston and Altman introduce flexibility within the structure of the regression function itself, Awadalla and collaborators redefine the process by which regression coefficients are derived. Despite their methodological divergence, both frameworks contribute significantly to the advancement of regression modeling.

Nevertheless, a notable limitation of the approach by Awadalla et al. lies in its vulnerability to overfitting, particularly when employing a least squares criterion. This issue may result in negative values of the coefficient of determination $R^2$ on unseen data from the extrapolation segment, a drawback also observed in classical polynomial models.

The methodology proposed in this study aims to overcome the aforementioned limitations through a two-stage modeling framework. In the initial phase, model coefficients are estimated using conventional approaches—such as the least squares method, fixed-point algorithms, or backpropagation in the case of neural networks—applied exclusively to the interpolation segment. Overfitting risks are temporarily ignored during this stage. Subsequently, in the second phase, a fractional operator is introduced, transforming the classical model into its fractional counterpart. The parametric nature of this operator induces a controlled mismatch within the interpolation region in the fractional regression model, thereby enhancing its predictive performance in the extrapolation domain.

This effect is illustrated in Figure 1, where adjustments to the fractional order $\alpha$ produce a decline in interpolation $R^2$ values while simultaneously increasing the extrapolation $R^2$. In some cases, this transformation yields a positive extrapolation $R^2$ from an initially negative one, thereby significantly improving predictive reliability on unseen data.

It is pertinent to underscore a constraint inherent to the proposed fractional regression methods: they are applicable exclusively to non-negative features. This restriction arises from the potential emergence of outputs within the domain of complex numbers when fractional operators are applied to negative inputs. However, this issue can be effectively mitigated through preprocessing or encoding techniques such as Label Encoding, Ordinal Encoding, or One-Hot Encoding, which ensure that all input variables remain within the non-negative domain. Moreover, the proposed method can be considered a low-cost mismatch approach in computational terms, as it operates using the coefficients previously calculated in classical regression models, incurring only the computational cost associated with varying the parameter $\alpha$ in the fractional operator used. Consequently, this approach can improve the coefficient of determination $R^2$ performance on unseen data, in some cases transforming a negative $R^2$ value into a positive one.

Finally, the adoption of a fractional-operator-set-based framework introduces an additional layer of flexibility and provides a foundation for broader generalization. In contrast to conventional approaches—which typically rely on a single fractional operator and have led to a proliferation of studies in the field of fractional calculus that differ only in the choice of operator while often yielding equivalent results—the present methodology supports the integration of multiple operators. This facilitates the development of diverse families of models or equations. Consequently, it opens new avenues for both theoretical research and practical applications, enabling the incorporation of novel operators as they are introduced and offering the potential for more accurate modeling of complex real-world phenomena.

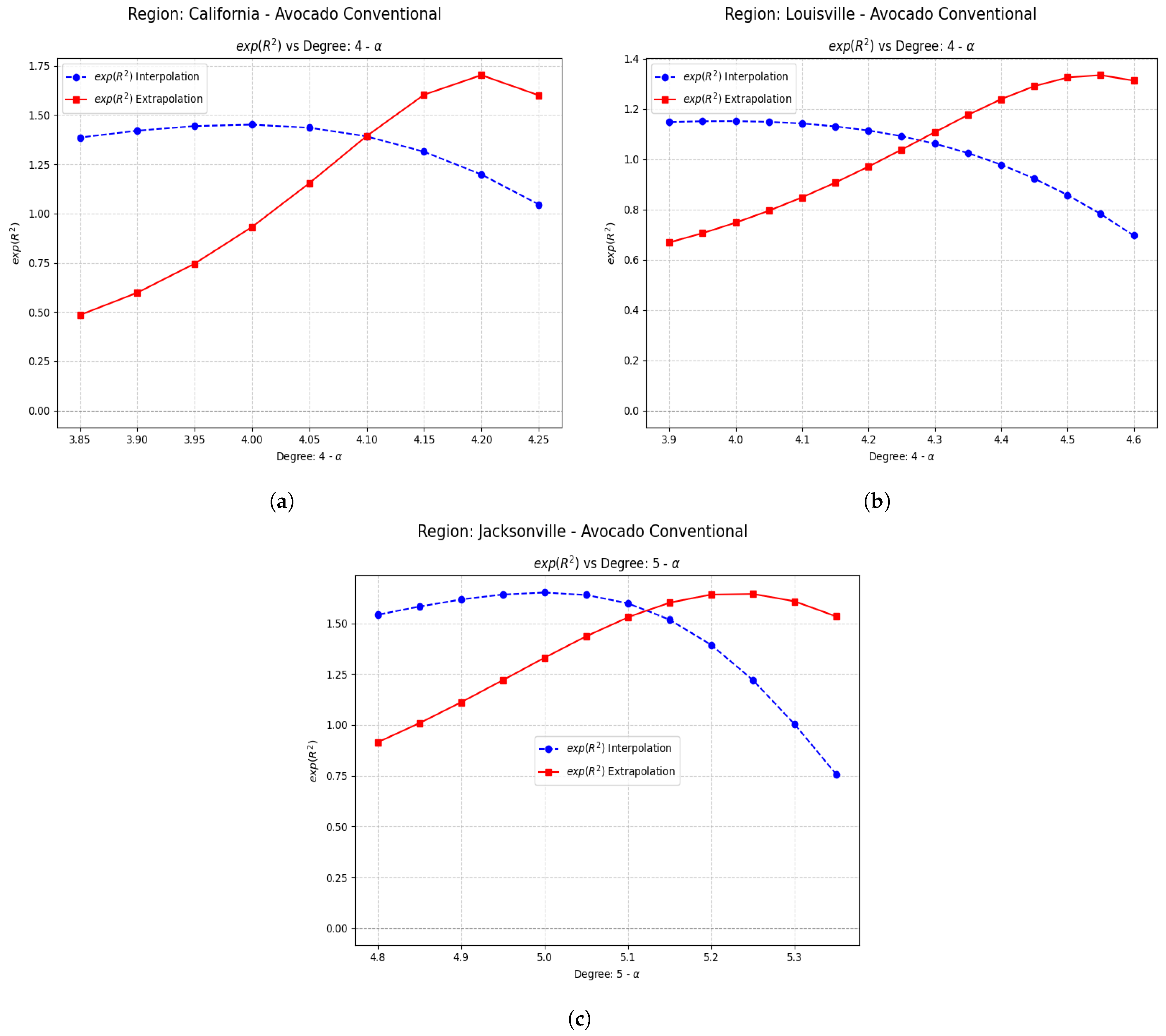
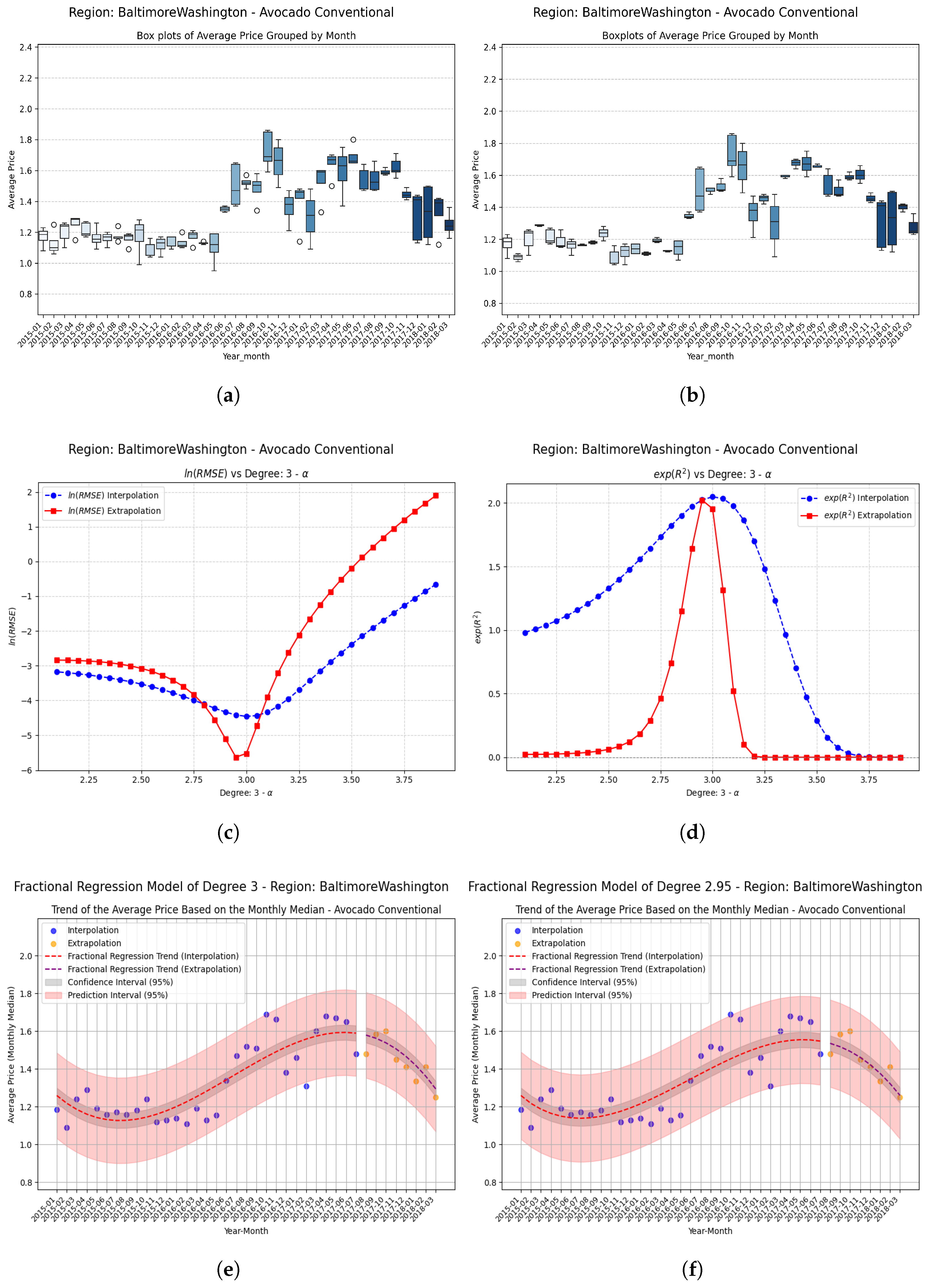
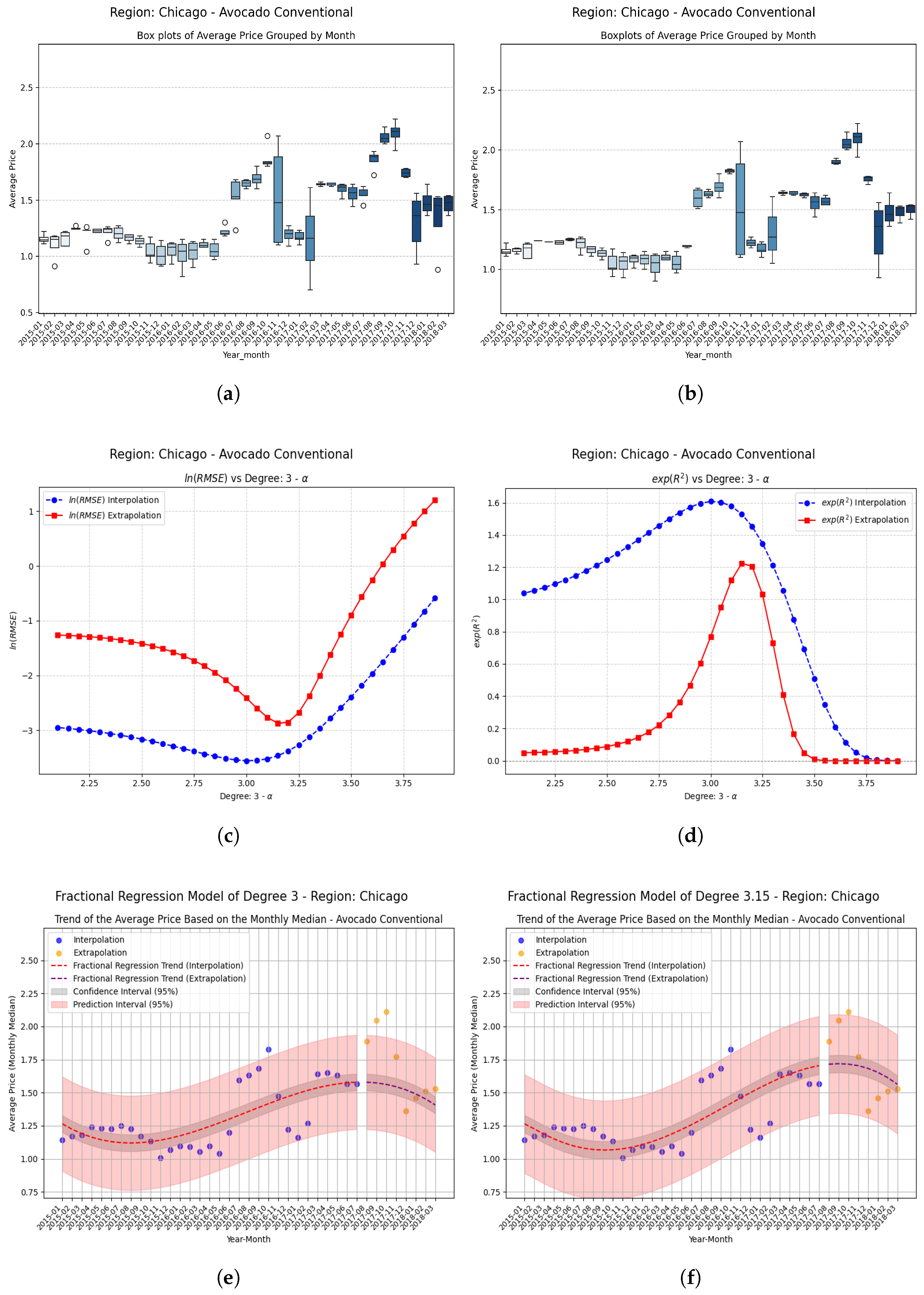
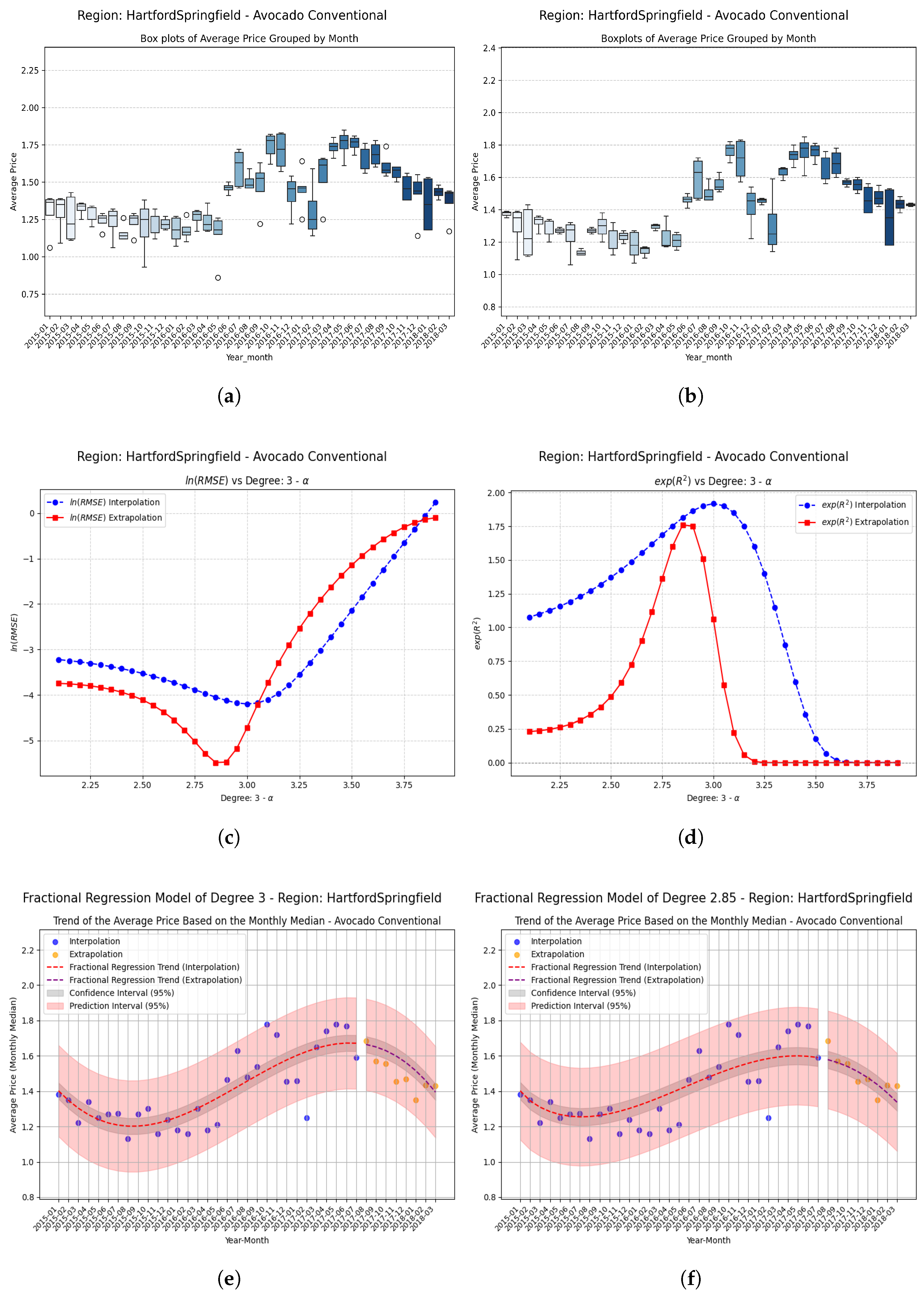
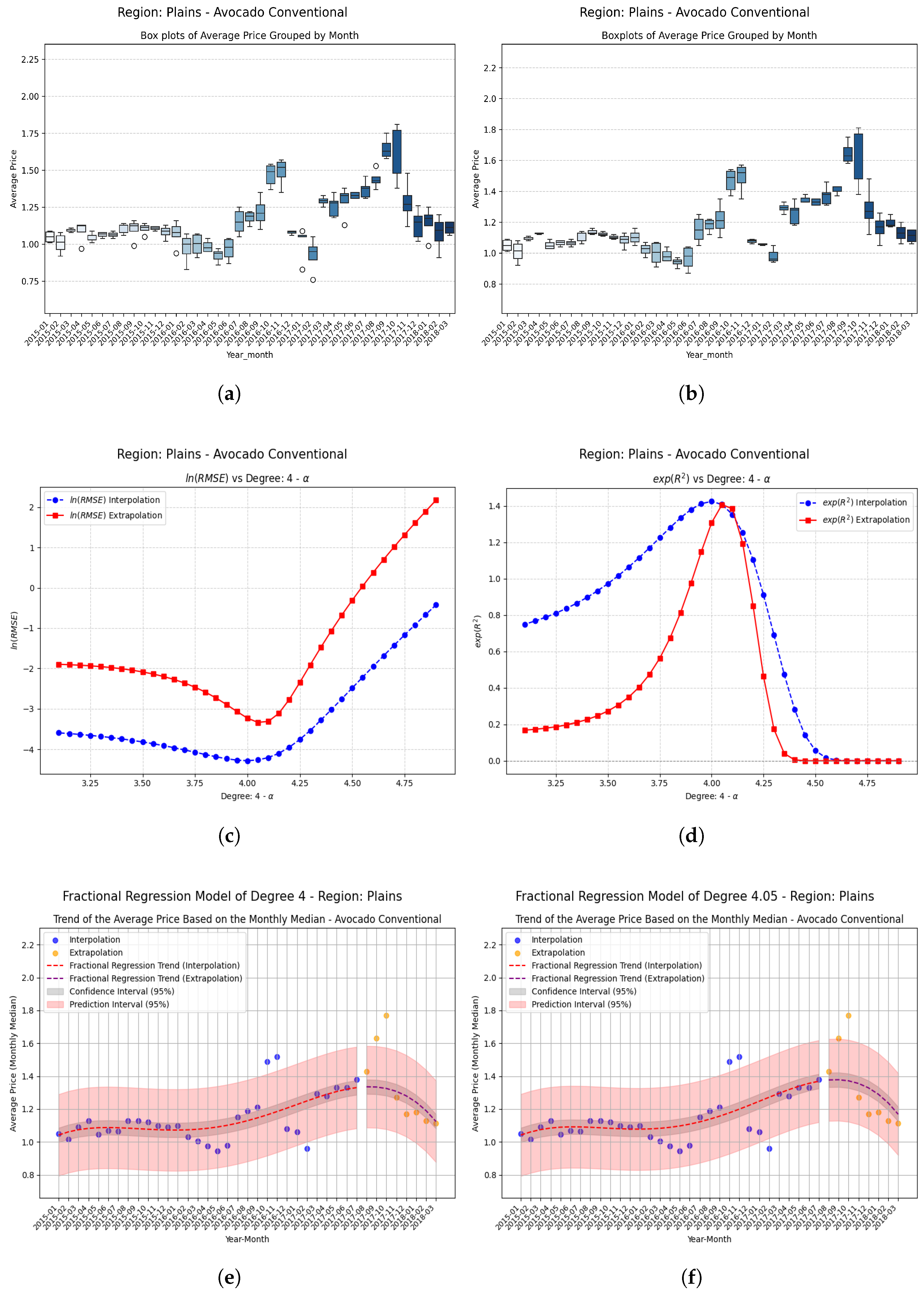
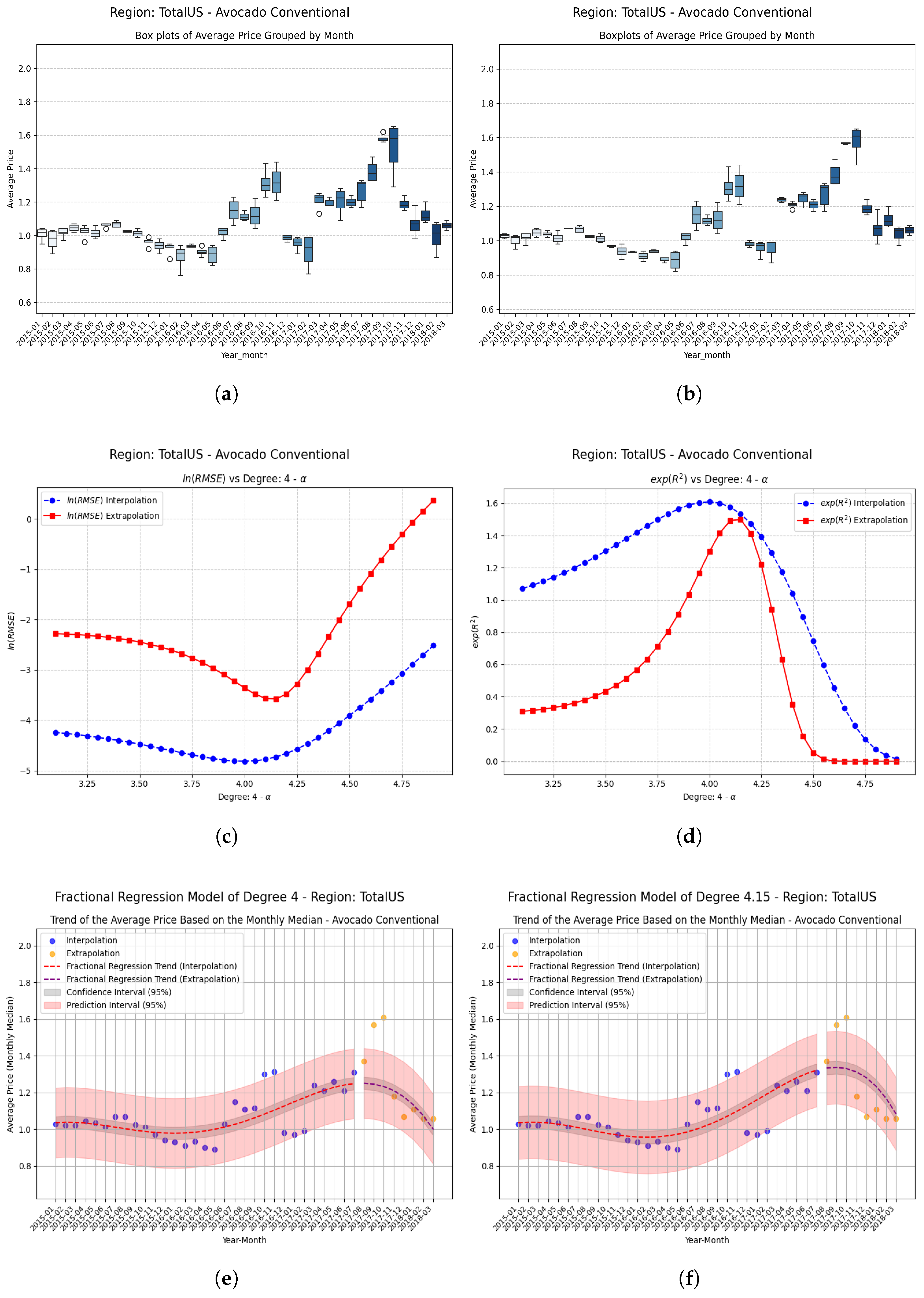
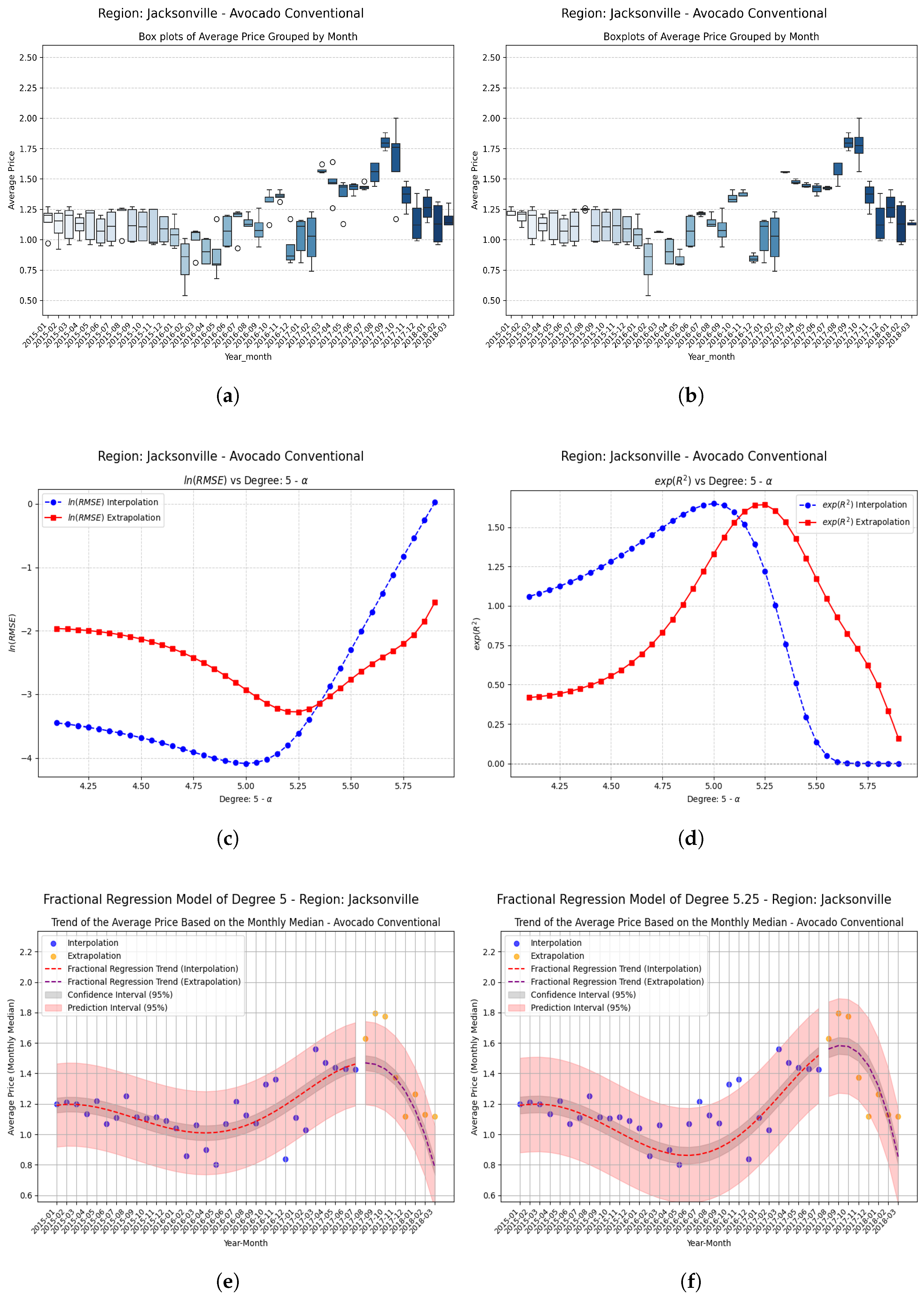
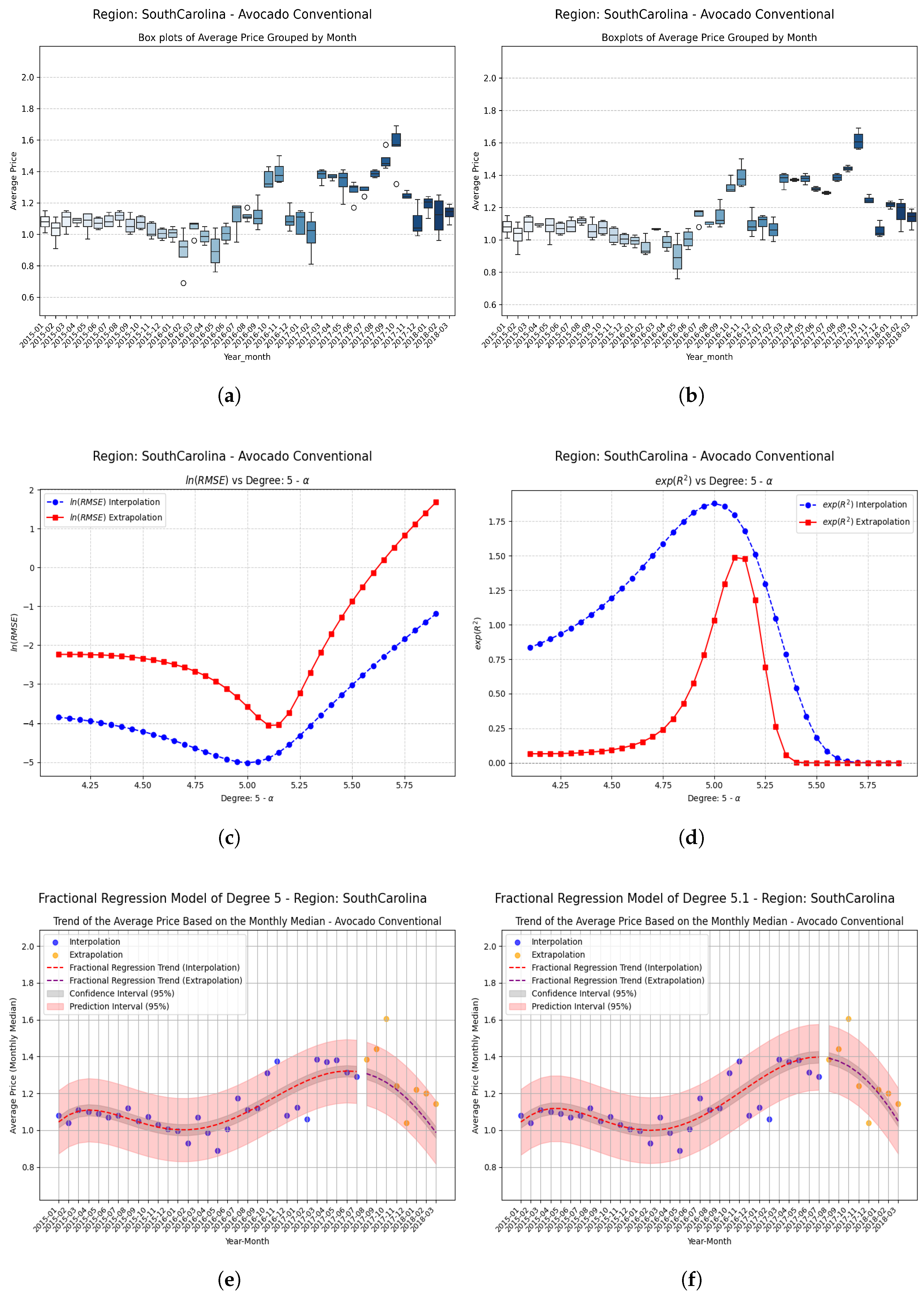
Examples Using Fractional Regression Model

Consider a polynomial regression function y of degree m and a fractional order parameter $\alpha \in (-1,1)$. The Riemann–Liouville and Caputo fractional operators, defined in Equations (2) and (3), belong to the set ${MO}_{x,\alpha }^1\left(y-{\beta }_0\right)$ and satisfy Equation (4). Consequently, both operators can be employed as described by Equation (5) within the fractional regression framework. To emphasize the relevance of using sets in the construction of the fractional regression model within this methodological framework, it is important to note that, from a theoretical perspective, one could construct an uncountably infinite family of fractional operators derived from the Riemann–Liouville and Caputo definitions. These operators, although differing in their formulation, would yield the same regression results as those shown in the subsequent examples and can be defined as follows:

$$\begin{array}{c}\hfill \left\{o_x^{\alpha }:o_x^{\alpha }=r{}_{0}D_x^{\alpha }+(1-r){}_0{}^{C}D_x^{\alpha },r\in [0,1]\right\}\subset {MO}_{x,\alpha }^1\left(y-{\beta }_0\right).\end{array}$$

(44)

So, to illustrate the proposed method, the average monthly prices of conventional avocados are extracted from the dataset. Due to notable dispersion within some groups, the monthly median is utilized instead of the mean, as it reduces sensitivity to outliers and extreme values. The dataset is partitioned into the following:

• Interpolation set: Comprises 80% of the data.
• Extrapolation set: Comprises the remaining 20%.

This division is performed using the following Python 3.10.12 command:

$$\begin{array}{c}\hfill \mathtt{train}\_\mathtt{test}\_\mathtt{split}(X,\mathtt{y}\_\mathtt{price},\mathtt{test}\_\mathtt{size}=0.2,\mathtt{random}\_\mathtt{state}=42,\mathtt{shuffle}=\mathtt{False})\end{array}$$

Here, train_test_split from sklearn.model_selection separates the data into training (interpolation) and testing (extrapolation) subsets as follows:

• X: Input features (time or date values).
• y_price: Average price of conventional avocados.
• test_size = 0.2: Proportion allocated for extrapolation.
• random_state = 42: Seed for reproducibility.
• shuffle = False: Maintains temporal order by avoiding data shuffling.

This methodology enables the generation of datasets suitable for evaluating polynomial models and subsequently constructing fractional regression models to analyze avocado price dynamics by region, as illustrated in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14.

In the forthcoming regression examples, the Student’s t-distribution is employed to construct both confidence and prediction intervals. This distribution is particularly advantageous for small sample sizes with unknown population variance. Its shape resembles that of the normal distribution but with heavier tails, reflecting the increased uncertainty inherent in the estimation process.

The t-statistic is defined as

$$t={\displaystyle \frac{\overline{x}-\mu }{s/\sqrt{n}}},$$

(45)

where $\overline{x}$ is the sample mean, $\mu$ is the population mean, s is the sample standard deviation, and n is the sample size. As n increases, the t-distribution converges to the normal distribution. Accordingly, a confidence interval for the population mean is given by

$$CI=\widehat{y}\pm t_{\alpha /2,n-1}\times {\displaystyle \frac{s}{\sqrt{n}}},$$

(46)

where $t_{\alpha /2,n-1}$ denotes the critical value from the t-distribution with $n-1$ degrees of freedom and confidence level $1-\alpha$. This interval estimates the range within which the true population parameter is expected to lie with the specified confidence (e.g., 95%).

Conversely, the prediction interval, which accounts for both data variability and prediction uncertainty, is expressed as

$$PI=\widehat{y}\pm t_{\alpha /2,n-1}\times \sqrt{s^2\left(1+{\displaystyle \frac{1}{n}}\right)},$$

(47)

where $\widehat{y}$ is the predicted value, $s^2$ is the residual variance, and n is the number of observations. Unlike the confidence interval, the prediction interval is wider, encompassing both the variability of future observations and the uncertainty in estimation.

8. Conclusions

This work has explored an innovative methodology aimed at improving polynomial regression models through the incorporation of fractional operators. This approach seeks to overcome classical limitations related to overfitting and predictive performance, particularly on unseen data, thereby enhancing the performance of time series forecasting.

The dataset was divided into two main segments: an interpolation segment used for model calibration and an extrapolation segment designed to evaluate the model’s predictive capacity on unseen or boundary-adjacent regions of the sample domain. This scheme is fundamental for assessing model robustness and generalization beyond the training sample.

Fractional operators parametrized by the order $\alpha \in (-1,1)$ have proven to be an effective tool for inducing a controlled mismatch in the interpolation segment, which translates into significant improvements in the extrapolation segment. This phenomenon, which can be referred to as the fractional mismatch effect, helps mitigate the classical overfitting commonly observed in traditional polynomial models—particularly when high polynomial degrees are used or when the dataset is limited.

It is important to emphasize the role of employing sets in the construction of the fractional regression model within this methodological framework. From a theoretical perspective, one can construct an uncountably infinite family of fractional operators derived from the Riemann–Liouville and Caputo definitions. Although these operators differ in their formulation, they yield equivalent regression results to those demonstrated in the examples presented in this study. This highlights the generality and robustness of the proposed approach regardless of the specific fractional operator chosen.

For a quantitative analysis of the results shown in the previously presented examples, the metric of absolute relative increase in the coefficient of determination $R^2$ can be used to measure the improvement in the extrapolation segments after the partial application of a chosen fractional operator to the classical regression model. This metric is defined as follows:

$$\mathrm{Absolute}\mathrm{Relative}\mathrm{Increase}={\displaystyle \frac{\left|R_{\mathrm{final}}^2-R_{\mathrm{initial}}^2\right|}{\left|R_{\mathrm{initial}}^2\right|}}$$

(48)

This indicator allows for the evaluation of improvement regardless of the initial coefficient’s sign or magnitude, facilitating a robust interpretation even in cases with negative or near-zero values, as shown in

Table 1. Differences in the $\alpha$ values of the fractional operators employed and the corresponding relative improvements in the coefficient of determination $R^2$ in the extrapolation segments across the considered regions.

Region	$\mathbf{\Delta }\mathit{\alpha }$	${\mathit{R}}_{\mathbf{Extrapolation}\mathbf{Initial}}^2$	${\mathit{R}}_{\mathbf{Extrapolation}\mathbf{Final}}^2$	Absolute Difference	Absolute Relative Increase
BaltimoreWashington	+0.05	0.670462	0.704112	0.033650	0.0502 (5.02%)
Chicago	−0.15	−0.263375	0.202223	0.465598	1.767 (176.7%)
HartfordSpringfield	+0.15	0.060748	0.565226	0.504478	8.31 (831%)
Midsouth	−0.10	0.291076	0.333769	0.042693	0.1467 (14.7%)
California	−0.20	−0.070536	0.532053	0.602589	8.54 (854%)
GrandRapids	−0.05	0.309643	0.324153	0.01451	0.0469 (4.69%)
Louisville	−0.55	−0.290752	0.288720	0.579472	1.993 (199.3%)
NorthernNewEngland	+0.05	0.192293	0.258411	0.066118	0.3439 (34.4%)
Plains	−0.05	0.268231	0.341435	0.073204	0.2729 (27.3%)
TotalUS	−0.15	0.261490	0.405492	0.144002	0.5509 (55.1%)
Boise	−0.10	0.119390	0.274019	0.154629	1.2947 (129.5%)
Jacksonville	−0.25	0.285206	0.496305	0.211099	0.7404 (74.0%)
SouthCarolina	−0.10	0.032100	0.397166	0.365066	11.371 (1137%)

.

Lastly, based on the analysis of the results presented in the above table, the following conclusions can be drawn:

• Regions with initial $R^2$ values that are negative or close to zero exhibit extraordinary improvements after applying the fractional operator. Notable cases include South Carolina, Hartford Springfield, and California, where absolute relative increases exceed $800\%$ on unseen data.
• Regions that start with relatively high and positive $R^2$ coefficients show more modest but consistent improvements, confirming that the technique adds value even where the base model already performs reasonably well.
• Small changes in the parameter $\alpha$ can produce large relative improvements, especially in regions with poor initial performance, highlighting the sensitivity and fine-tuning potential of fractional models.
• These results suggest that the proposed approach contributes to overcoming the classical limitations of polynomial models, mainly by increasing the coefficient of determination $R^2$ in unseen data and allowing the generalization of the methods through the implementation of fractional operators, thereby reinforcing the practical applicability of the methodology in predictive analyses based on time series.

In summary, the partial incorporation of fractional operators into polynomial regression models presents a promising approach to improve predictive accuracy and robustness, especially in extrapolation contexts. The flexibility introduced by the fractional parameter $\alpha$ allows effective control over the trade-off between mismatch and generalization, mitigating typical overfitting issues associated with classical regression methods.