Dynamic Mechanical Characteristics and Fracture Size Effect of Coal Sandstone Under High-Temperature and High-Strain Rate Coupling Action
Abstract
1. Introduction
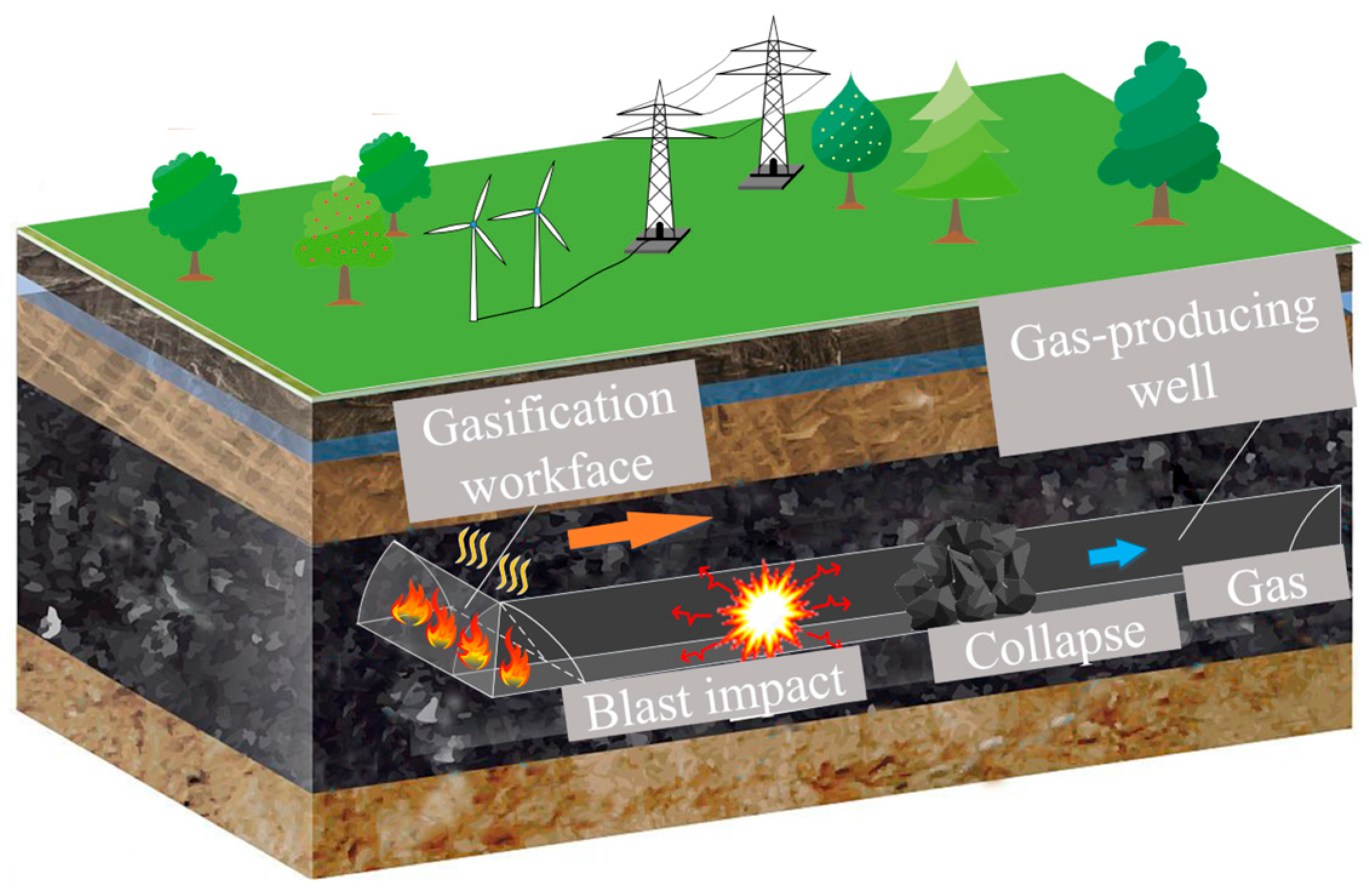
2. Specimen Preparation and Test Methods
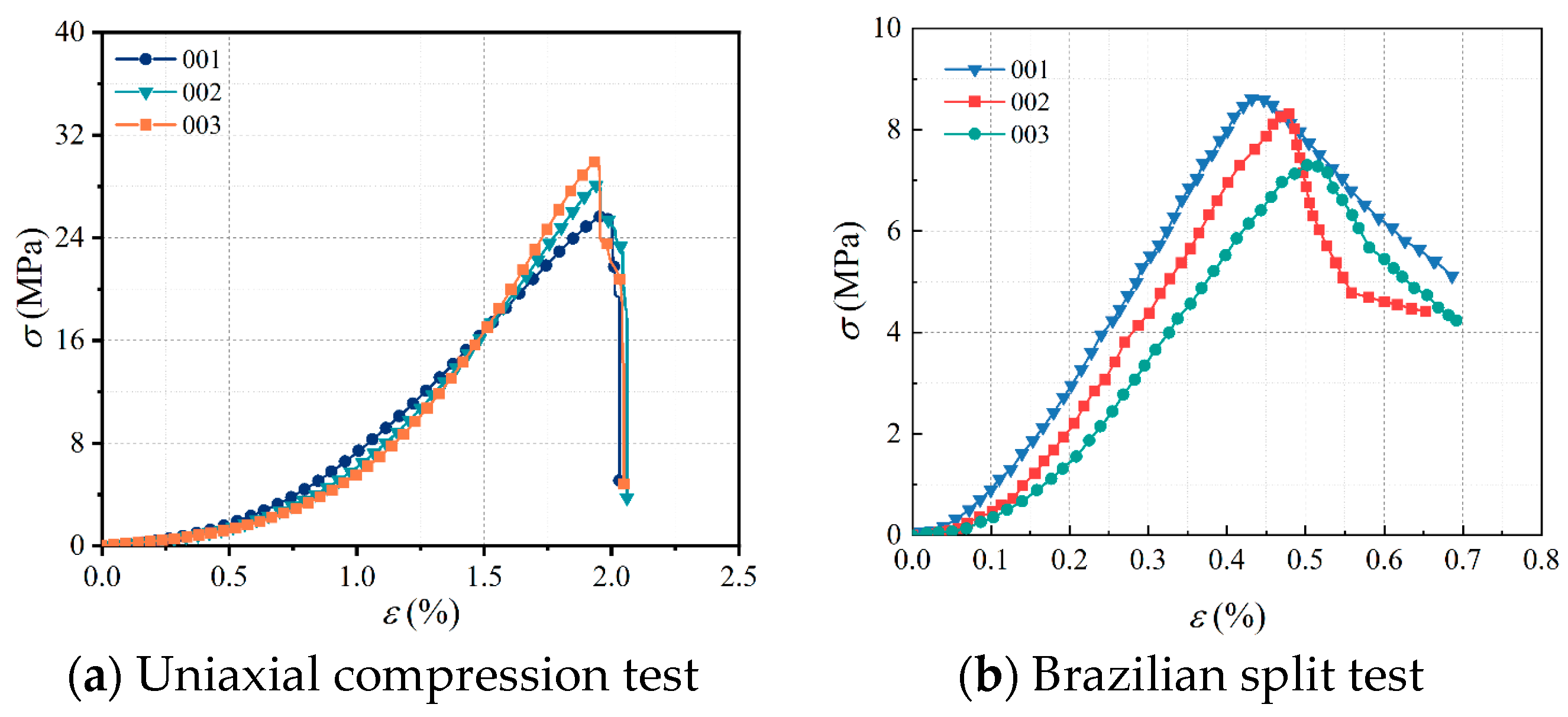
2.1. Standard Specimen Preparation of Coal Sandstone
2.2. Real-Time High-Temperature Loading Equipment and Test Methods
- (1)
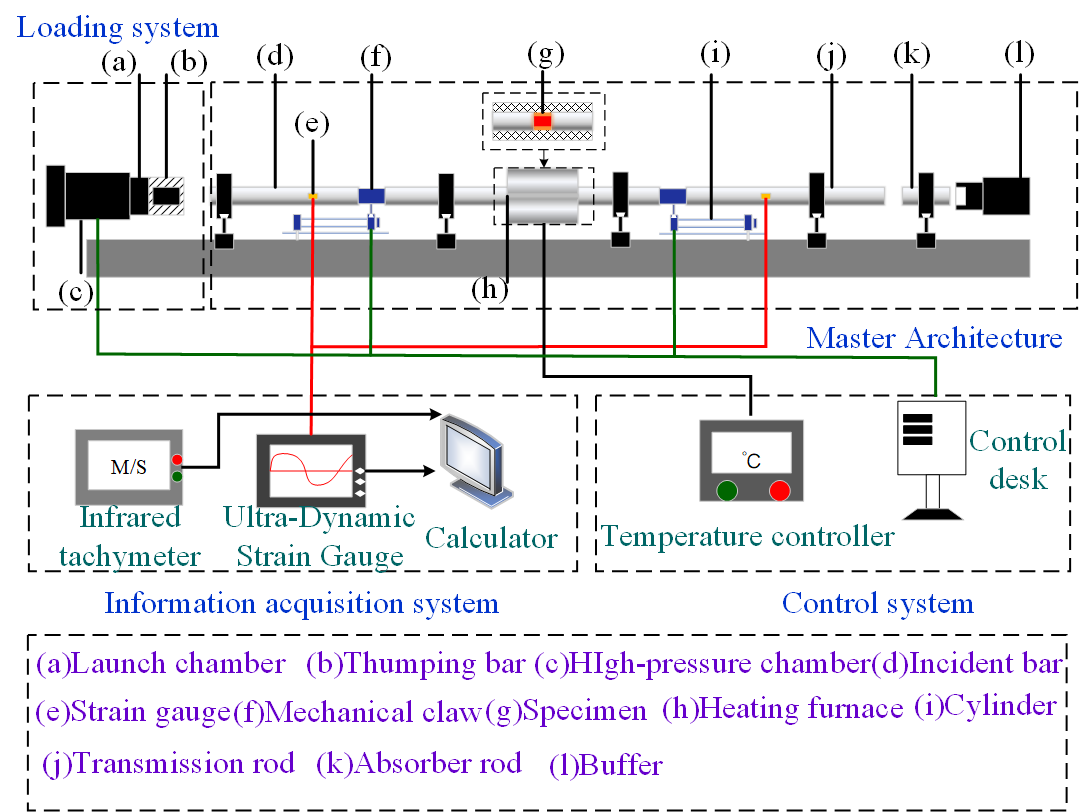
- Real-time high-temperature loading test equipment
- (2)
- High-temperature- and high-strain rate-coupled loading test program
3. Dynamic Mechanical Characteristics of Coal Sandstone Under High-Temperature and High-Strain Rate Action
3.1. Characteristics of Loading Test Waveform and Stress–Strain Curve
- (1)
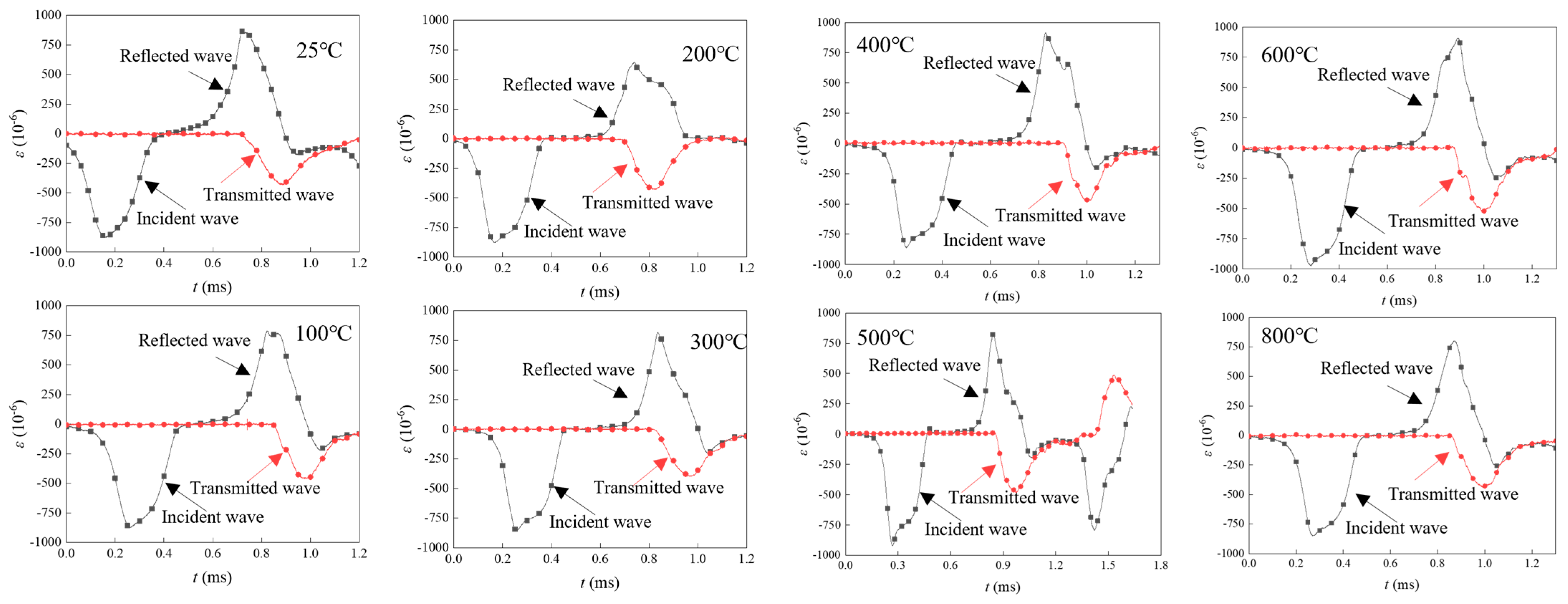
- Characteristics of test curves
- (2)
- Variation characteristics of strain rate () with loading temperature (T)
- (3)
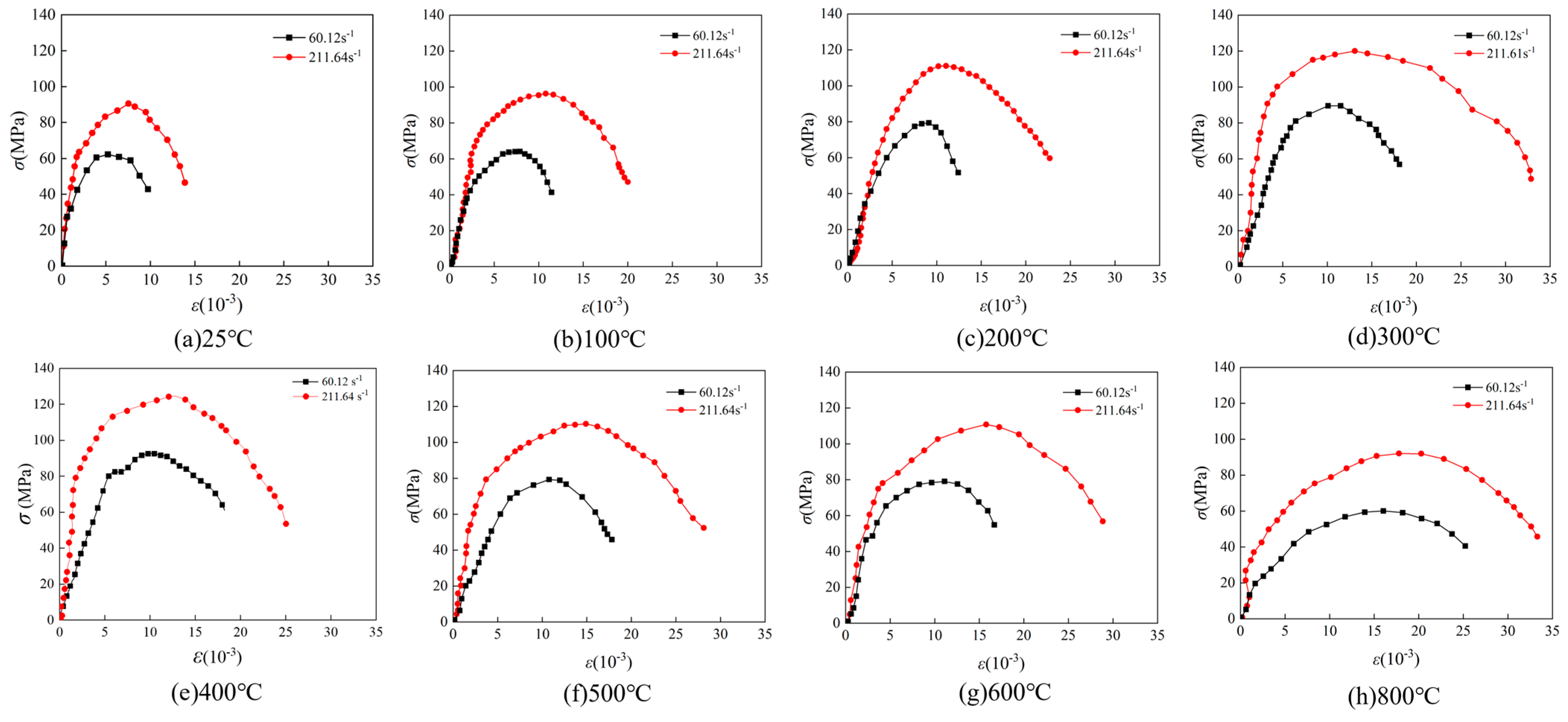
- Variation characteristics of dynamic stress–strain curves
3.2. Dynamic Mechanical Properties of Coal Sandstone Specimens
3.2.1. Characterization of Changes in Dynamic Modulus of Elasticity
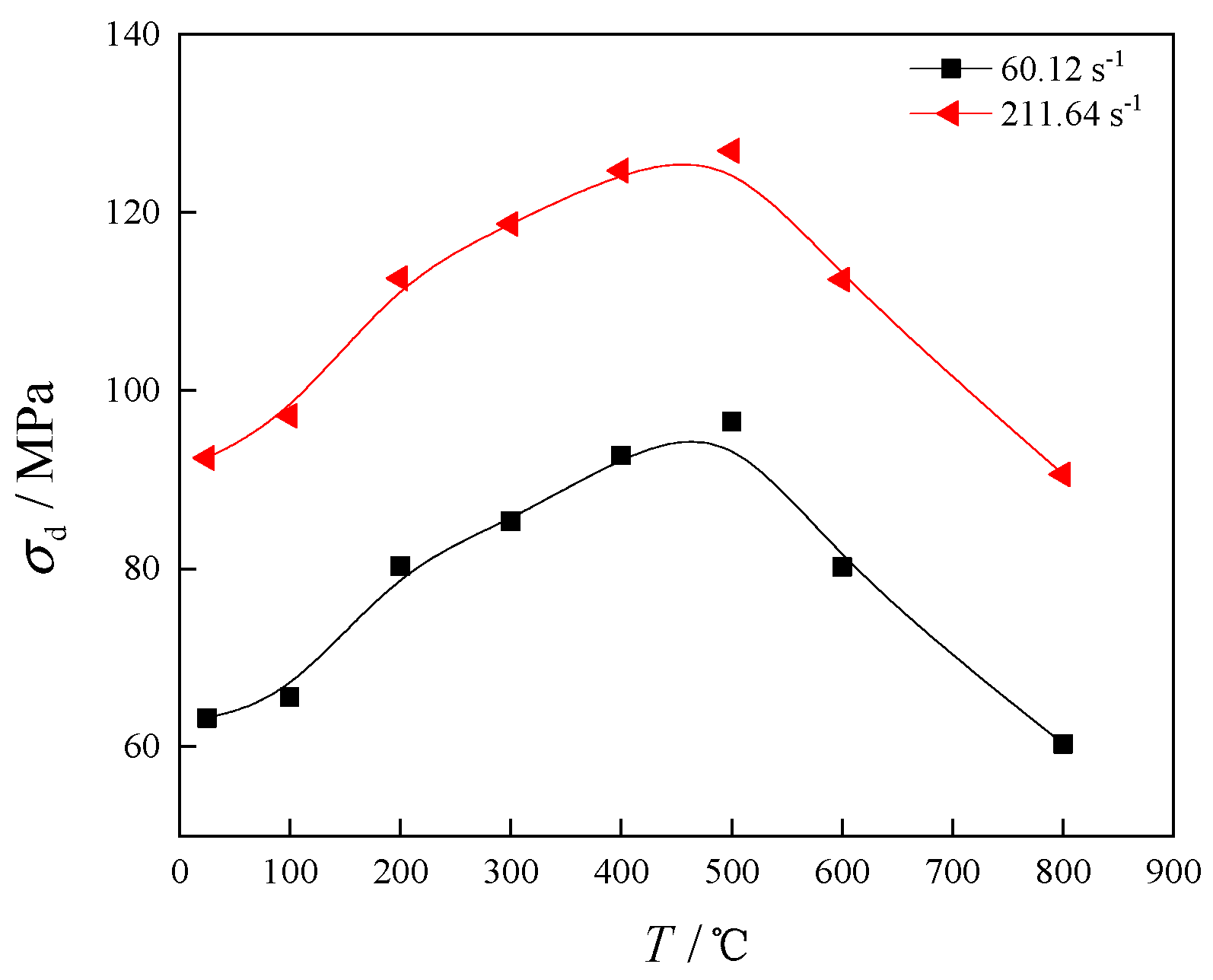
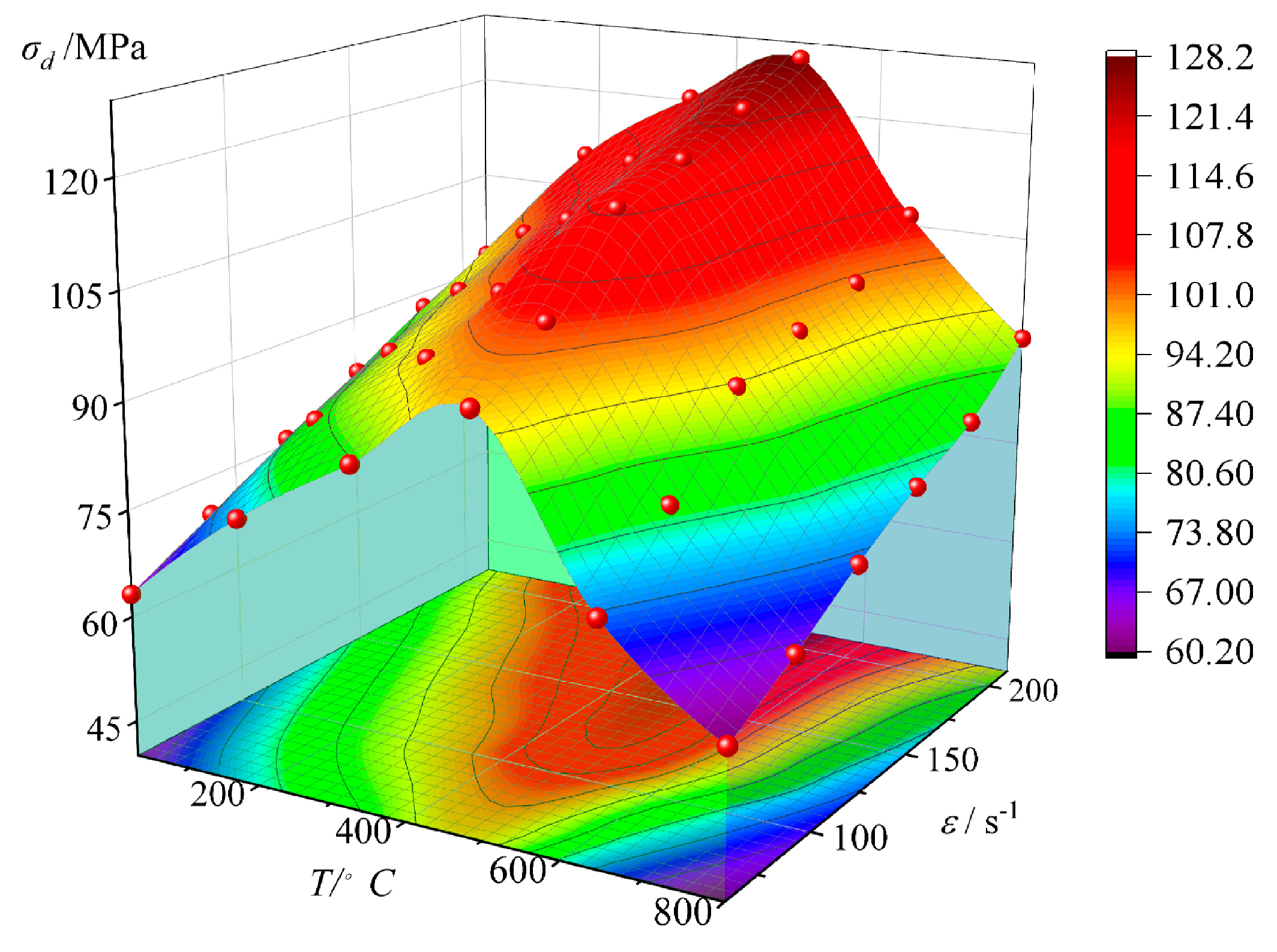
3.2.2. Characterization of Changes in Dynamic Compressive Strength
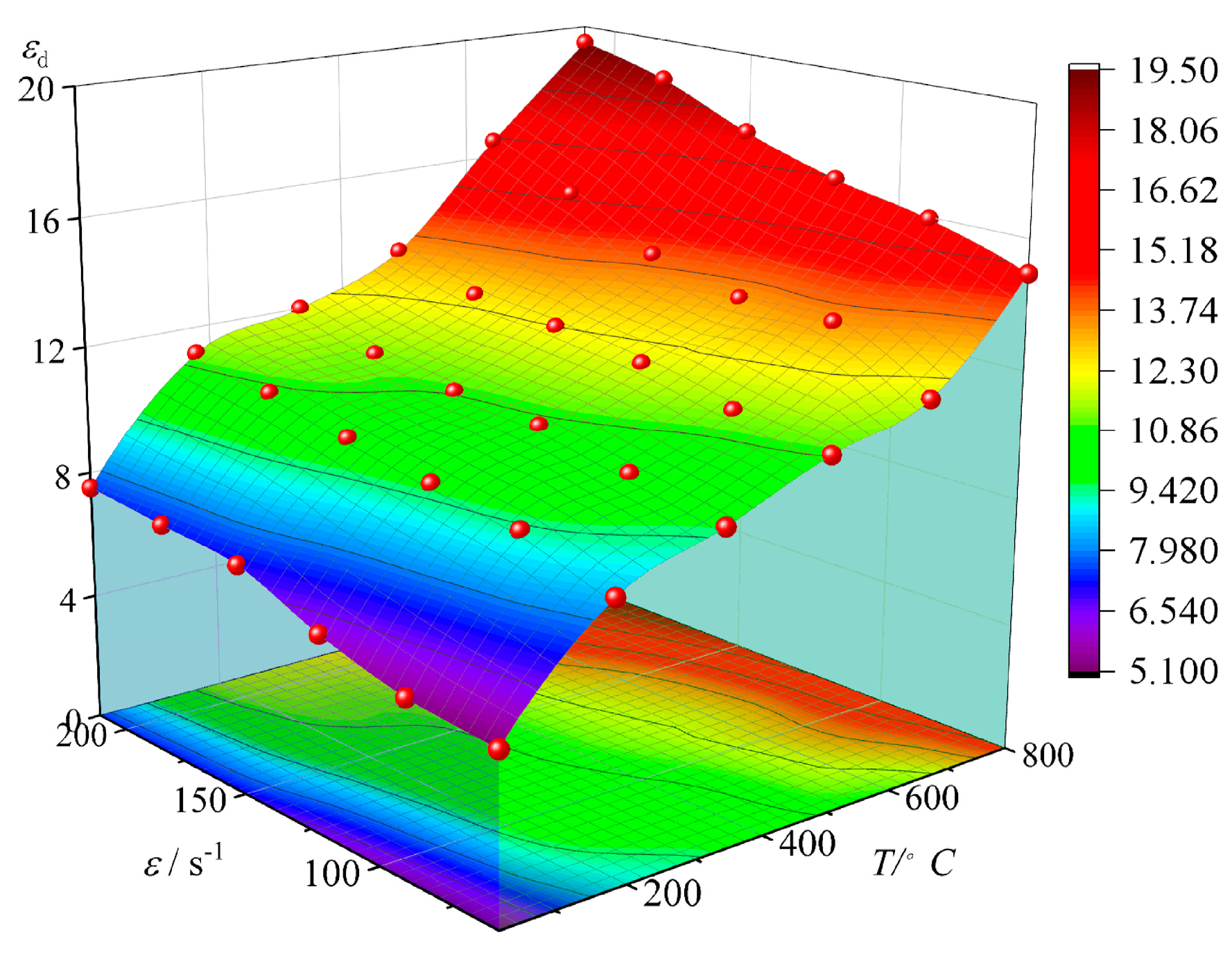
3.2.3. Characterization of Changes in Dynamic Peak Strain
4. Characteristics of Fracture Fractal and Energy Dissipation Mechanism Under High-Temperature and High-Strain Rate Coupling Effect
4.1. Characteristics of Fracture Fractalization of Coal Sandstone Samples
- (1)
- Characterization of the crushing degree of specimen damage
- (2)
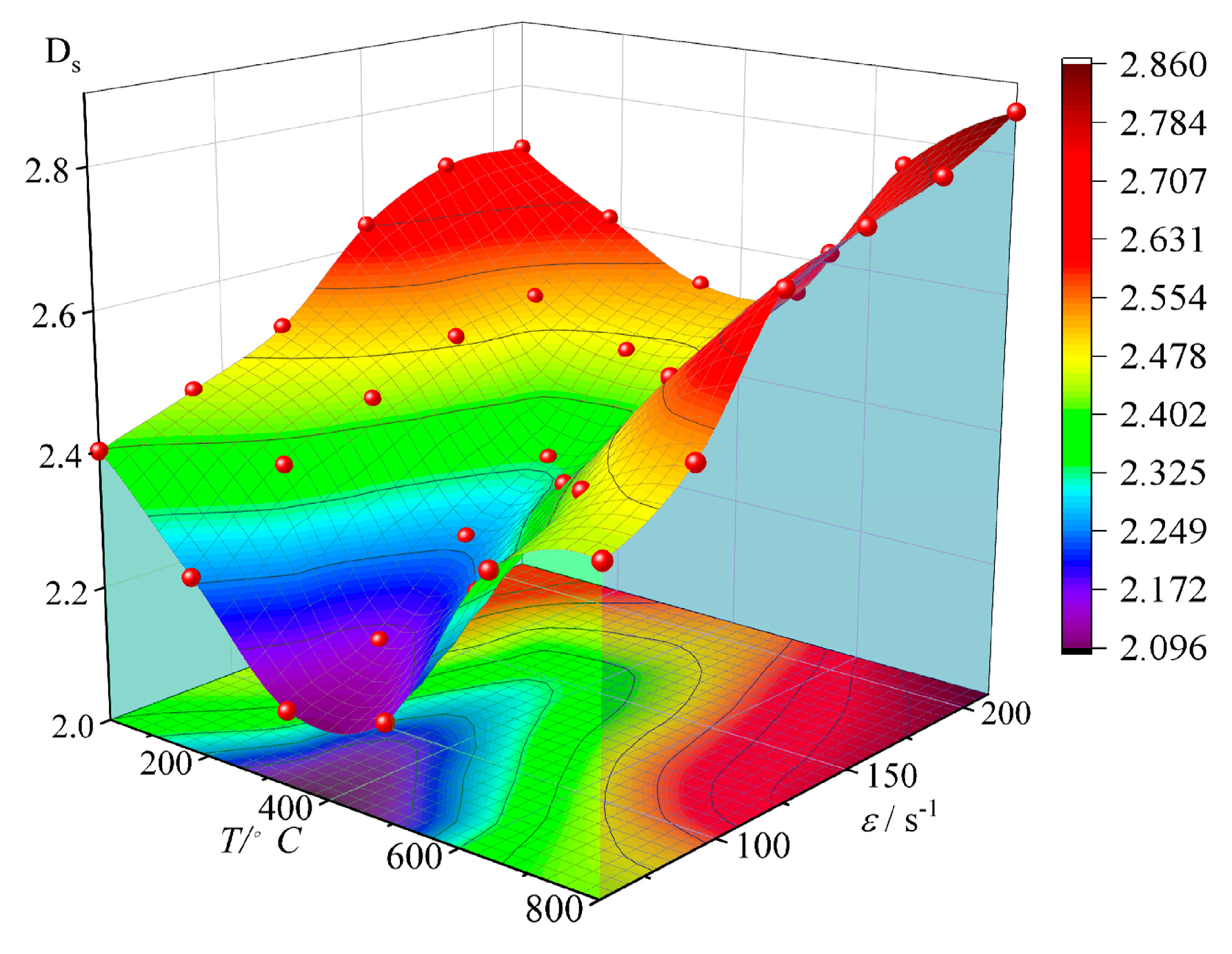
- Subdimensional characterization of the degree of specimen fragmentation
4.2. Influence of Temperature on the Microscopic Fracture Morphology of Coal-Measure Sandstone
- (1)
- Microscopic fracture morphology at ambient temperature (25 °C)
- (2)
- Microscopic fracture morphology of coal-measure sandstone at 400 °C
- (3)
- Microscopic fracture morphology of coal-measure sandstone at 800 °C
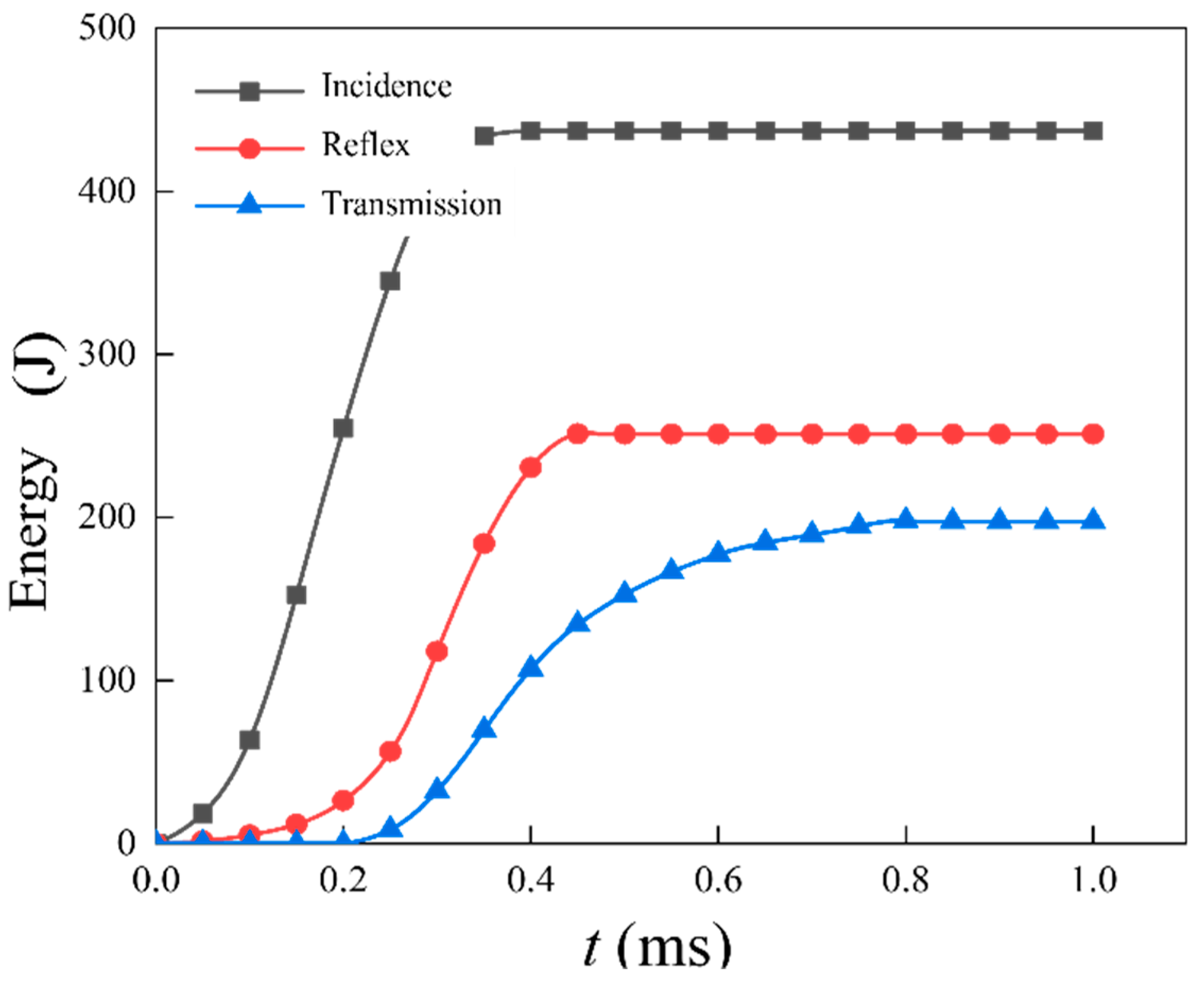
4.3. Dynamic Energy Dissipation Law of Coal Sandstone Specimens
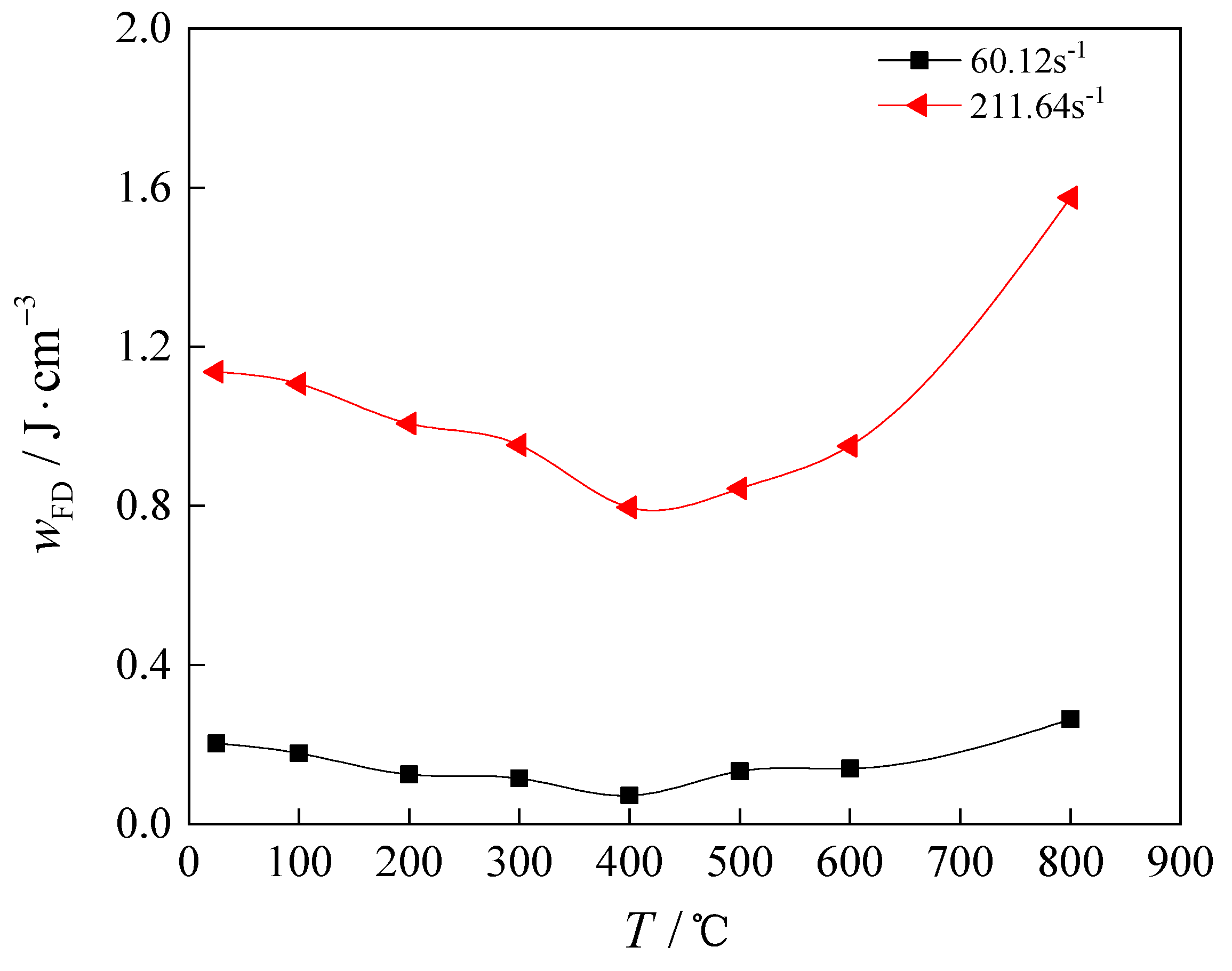
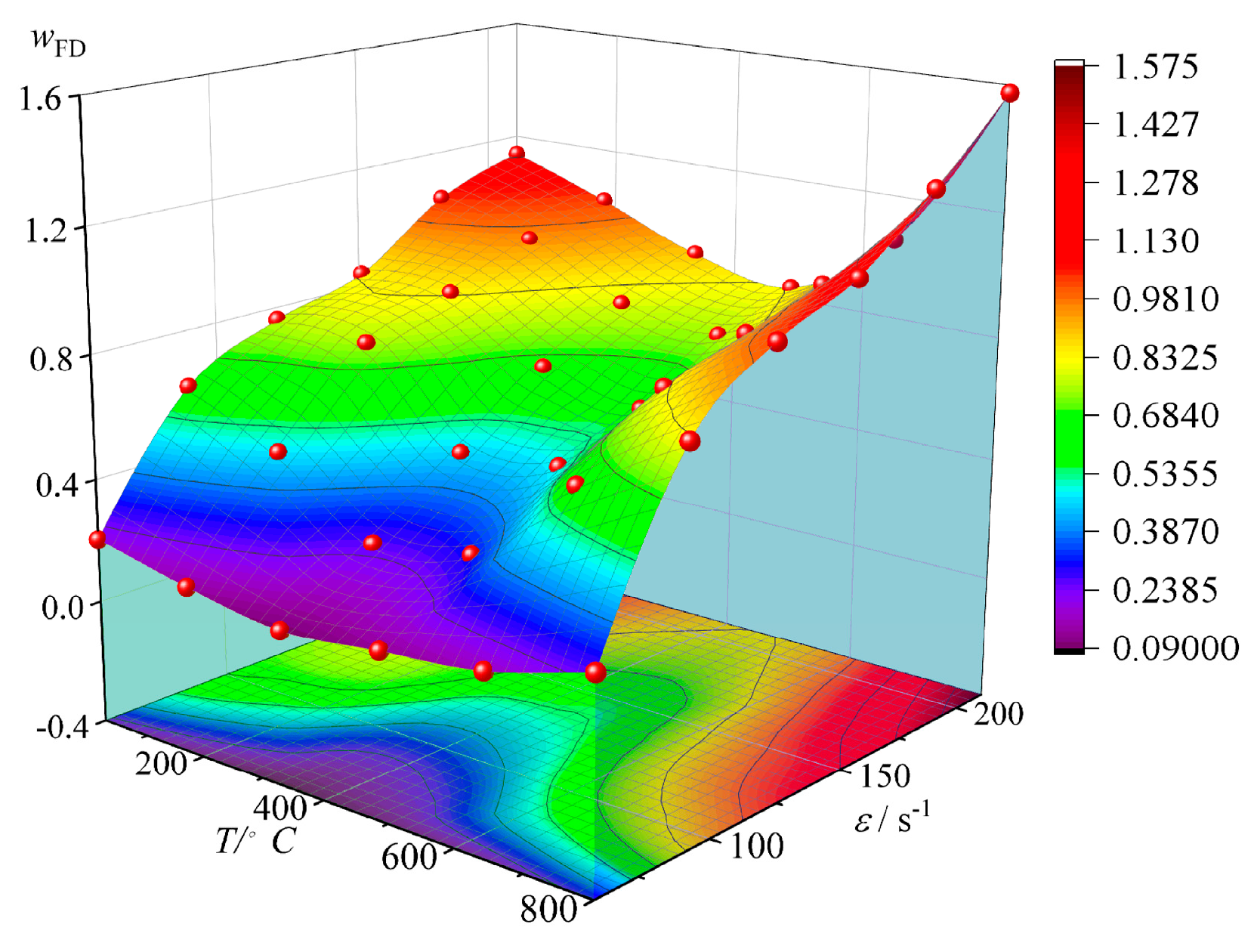
4.3.1. Characterization of Changes in Energy Dissipation Density
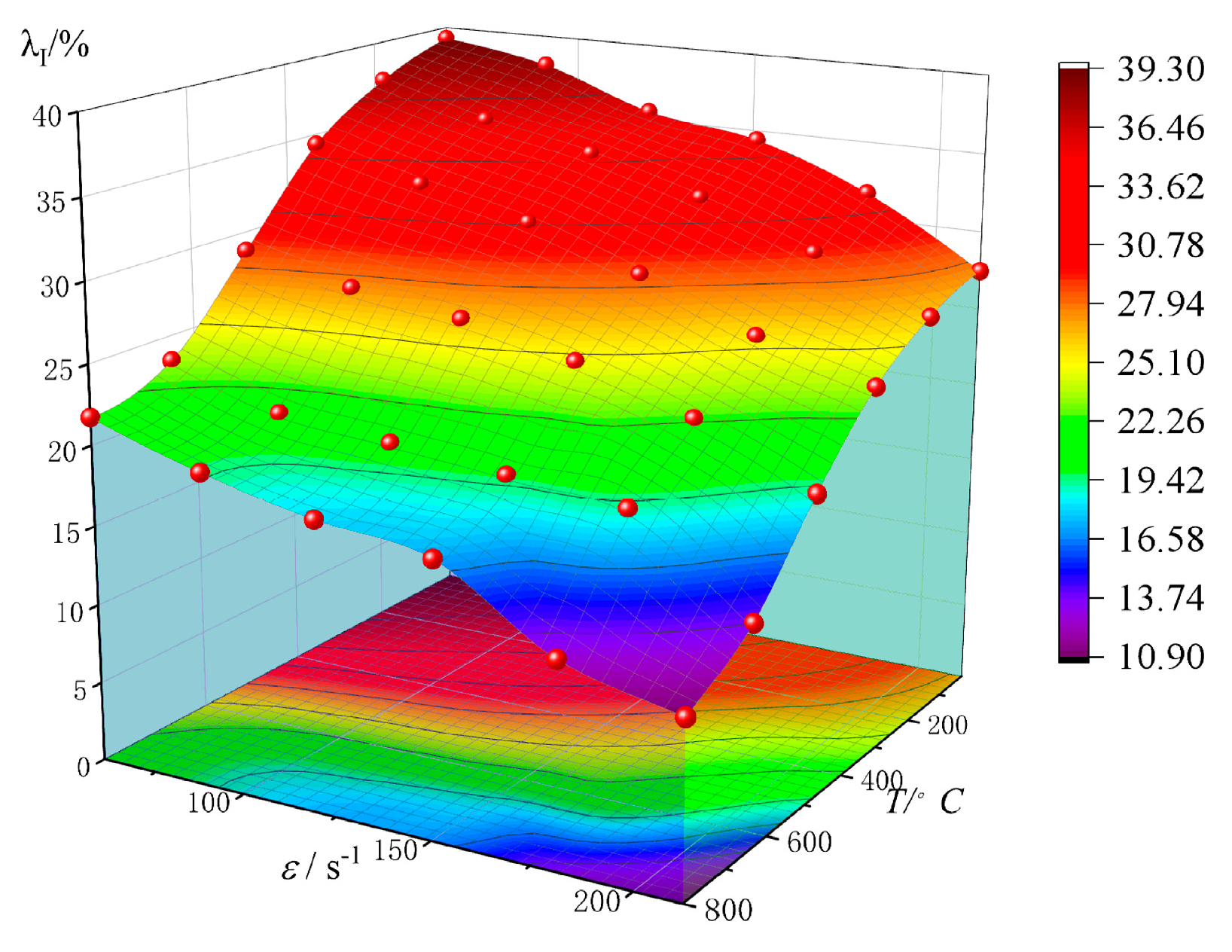
4.3.2. Characterization of Energy Consumption Rate of Rock Samples
4.4. Analysis of the Coupled Effect of High Temperature and Strain Rate in Coal Sandstone
4.4.1. Dynamic Mechanical Properties and Crushing Fractionation Laws
- 1.
- Characteristics of changes in dynamic modulus of elasticity
- 2.
- Characteristics of changes in dynamic compressive strength
- 3.
- Characteristics of changes in dynamic peak strain
- 4.
- Characteristics of the variation in fractal dimension of clasts
4.4.2. Dynamic Energy Dissipation Laws
- (1)
- Characteristics of changes in energy dissipation density
- (2)
- Characteristics of variation in energy consumption rates of rock samples
5. Conclusions
- (1)
- At a strain rate () of 211.64 s−1, the dynamic elastic modulus (Ed) decreases linearly from 33.38 GPa to 9.80 GPa as the temperature (T) increases, showing a decrease of 70.64%, which is 3.80% smaller than that at lower strain rates. The dynamic compressive strength (σd) increases initially and then decreases with temperature (T). From 25 °C to 500 °C, the dynamic compressive strength (σd) increases from 92.39 MPa to 126.88 MPa, showing an increase of 37.33%. However, as the temperature increases from 500 °C to 800 °C, it decreases from 126.88 MPa to 90.56 MPa, with a reduction of 28.63%. Both the increase and decrease are smaller at higher strain rates compared with lower ones. The dynamic peak strain (εd) of coal-bearing sandstone increases linearly from 0.00751 to 0.0195 as the temperature (T) rises, with an increase of 159.00%, which is 31.48% lower than at lower strain rates.
- (2)
- At a strain rate () of 211.64 s−1, rock samples visibly darken due to the real-time temperature effect between 100 °C and 800 °C. The coal-bearing sandstone samples show severe fracturing at different temperatures, with many fragments exhibiting a wedge-like shape and a higher proportion of powdery fragments. The fractal dimension (Ds) decreases initially and then increases with temperature (T). As the temperature rises from 25 °C to 400 °C, the fractal dimension (Ds) decreases from 2.70 to 2.52, a reduction of 6.67%. However, from 400 °C to 800 °C, it increases from 2.52 to 2.86, an increase of 13.49%. Both the increase and decrease are lower compared with lower strain rates.
- (3)
- At a strain rate () of 211.64 s−1, the energy dissipation density (wFD) of coal-bearing sandstone decreases initially and then increases with temperature (T). From 25 °C to 400 °C, the energy dissipation density (wFD) decreases from 1.137 to 0.796, a decrease of 29.99%, and from 400 °C to 800 °C, it increases from 0.796 to 1.575, showing an increase of 97.86%. Both the decrease and increase are smaller compared with lower strain rates. The energy consumption rate (λI) decreases linearly from 27.45% to 10.91% as temperature (T) increases, showing a decrease of 60.26%, which is 15.63% larger than at lower strain rates.
- (4)
- The dynamic elastic modulus (Ed) of coal-bearing sandstone increases with strain rate () but decreases with increasing temperature (T). The dynamic elastic modulus (σd) increases with strain rate () and initially rises with temperature (T) before decreasing, with an inflection point at T = 400 °C. The dynamic peak strain (εd) increases with both strain rate () and temperature (T). The fractal dimension (Ds) of coal-bearing sandstone fragment distribution increases with strain rate (), but with temperature (T), it initially decreases and then increases, with an inflection point at T = 400 °C. The energy dissipation density (wFD) increases with strain rate () and initially rises with temperature (T) before decreasing, with an inflection point at T = 400 °C. The energy consumption rate (λI) decreases with increasing strain rate () and temperature (T).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Konovsek, D.; Nadveznik, J.; Medved, M. An Overview of World History of Underground Coal Gasification. In Proceedings of the 22nd International Meeting of Thermophysics 2017 and 4th Meeting of EnRe 2017 (Thermophysics 2017), Terchova, Slovakia, 12–14 September 2017; Volume 1866, p. 5. [Google Scholar] [CrossRef]
- Liu, S.Q.; Liu, J.H.; Yu, L. Environmental benefits of underground coal gasification. J. Environ. Sci. 2002, 14, 284–288. [Google Scholar]
- Green, M. Recent developments and current position of underground coal gasification. Proc. Inst. Mech. Eng. Part a-J. Power Energy 2018, 232, 39–46. [Google Scholar] [CrossRef]
- Li, H.; Guo, G.; Zha, J.; Yuan, Y.; Zhao, B. Research on the surface movement rules and prediction method of underground coal gasification. Bull. Eng. Geol. Environ. 2016, 75, 1133–1142. [Google Scholar] [CrossRef]
- Wulandari, W.; Sasongko, D.; Rizkiana, J.; Anggayana, K.; Widayat, A.H.; Zahra, A.C.A.; Azhari, M.A. Non-isothermal Kinetics Analysis of Various Indonesian Coal Thermal Characteristics for Underground Coal Gasification Purposes. In Proceedings of the 11th Regional Conference On Chemical Engineering (RCChE 2018), Yogyakarta, Indonesia, 7–8 November 2018; Volume 2085, p. 9. [Google Scholar] [CrossRef]
- Liu, H.; Yao, H.; Yao, K.; Chen, F.; Luo, G. Characteristics of “Three zones” during Underground Coal Gasification. Nat. Resour. Sustain. Dev. II Pts 1-4 2012, 524–527, 56. [Google Scholar] [CrossRef]
- Yang, L.H.; Zhang, X.; Liu, S. Characteristics of Temperature Field during the Oxygen-enriched Underground Coal Gasification in Steep Seams. Energy Sources Part a-Recovery Util. Environ. Eff. 2010, 32, 384–393. [Google Scholar] [CrossRef]
- Zha, X.; Wang, H.; Cheng, S. Finite element analysis of the subsidence of cap rocks during underground coal gasification process. Adv. Res. Civ. Eng. Mater. Eng. Appl. Technol. 2014, 859, 91–94. [Google Scholar] [CrossRef]
- Pekpak, E.; Yoncaci, S.; Kilic, M.G. An overview of underground coal gasification and its applicability for Turkish lignite. In Proceedings of the 12th International Symposium On Environmental Issues and Waste Management in Energy and Mineral Production—SWEMP 2010, Prague, Czech Republic, 24–26 May 2010; pp. 398–407. [Google Scholar]
- Perkins, G.; Vairakannu, P. Considerations for oxidant and gasifying medium selection in underground coal gasification. Fuel Process. Technol. 2017, 165, 145–154. [Google Scholar] [CrossRef]
- Saulov, D.N.; Plumb, O.A.; Klimenko, A.Y. Flame propagation in a gasification channel. Energy 2010, 35, 1264–1273. [Google Scholar] [CrossRef]
- Wang, G.; Tan, J.; Li, C. Analysis of rock cracking characteristics during pyrolysis drilling. Therm. Sci. 2021, 25, 3377–3397. [Google Scholar] [CrossRef]
- Gautam, P.K.; Verma, A.K.; Jha, M.K.; Sharma, P.; Singh, T.N. Effect of high temperature on physical and mechanical properties of Jalore granite. J. Appl. Geophys. 2018, 159, 460–474. [Google Scholar] [CrossRef]
- Ma, X.; Wang, G.; Hu, D.; Liu, Y.; Zhou, H.; Liu, F. Mechanical properties of granite under real-time high temperature and three-dimensional stress. Int. J. Rock Mech. Min. Sci. 2020, 136, 8. [Google Scholar] [CrossRef]
- Salman, H.; Copeland, L. Effect of repeated heating and cooling cycles on the pasting properties of starch. J. Cereal Sci. 2010, 51, 105–109. [Google Scholar] [CrossRef]
- Weinbrandt, R.M.; Ramey, H.J., Jr.; Casse, F.J. Effect of temperature on relative and absolute permeability of sandstones. Soc. Pet. Eng. J. 1975, 15, 376–384. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, Q.; Hao, S.; Geng, J.; Lv, C. Experimental study on the variation of physical and mechanical properties of rock after high temperature treatment. Appl. Therm. Eng. 2016, 98, 1297–1304. [Google Scholar] [CrossRef]
- Porada, S.; Czerski, G.; Dziok, T.; Grzywacz, P.; Makowska, D. Kinetics of steam gasification of bituminous coals in terms of their use for underground coal gasification. Fuel Process. Technol. 2015, 130, 282–291. [Google Scholar] [CrossRef]
- Perkins, G. Underground coal gasification—Part II: Fundamental phenomena and modeling. Prog. Energy Combust. Sci. 2018, 67, 234–274. [Google Scholar] [CrossRef]
- Laciak, M.; Kacur, J.; Durdan, M.; Skvarekova, E.; Wittenberger, G. Underground coal gasification in laboratory conditions. In Proceedings of the 11th International Multidisciplinary Scientific Geoconference (SGEM 2011), Albena, Bulgaria, 20–25 June 2011; Volume III, p. 123. [Google Scholar]
- Li, M.; Yu, H.; Zhang, J.; Lin, G.; Zhu, F.; Mao, Y.; Zhang, L.; Chen, Y. Dynamic tensile mechanical properties of thermally damaged sandstone under impact loads and the influence mechanism of composition. Eng. Fract. Mech. 2023, 289, 19. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, F.; Hu, L.; Jiang, F.; Huang, G. Experimental investigation on the mechanical behavior and fracture mechanism of sandstone after heat treatment. Bull. Eng. Geol. Environ. 2024, 83, 18. [Google Scholar] [CrossRef]
- Wen, D.; Jiang, N.; Liu, C.; Lv, Z. Study of the Influence of Temperature Rise on the Microstructure of Frozen Soil Based on SEM and MIP. J. Mater. Civ. Eng. 2023, 35, 8. [Google Scholar] [CrossRef]
- Jing, S.; Wen, Z.; Jiang, Y.; Wen, J.; Du, W. Mechanical behaviors and failure characteristics of coal-rock combination under quasi-static and dynamic disturbance loading: A case based on a new equipment. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 16. [Google Scholar] [CrossRef]
- Yin, T.B.; Wang, P.; Li, X.B.; Shu, R.H.; Ye, Z.Y. Effects of thermal treatment on physical and mechanical characteristics of coal rock. J. Cent. South Univ. 2016, 23, 2336–2345. [Google Scholar] [CrossRef]
- Zhou, C.; He, X.; Song, D.; Li, Z.; Yang, H.; Liu, Y.; Guo, L. Study on signal characteristics of burst tendency coal under different loading rates. Int. J. Coal Sci. Technol. 2024, 11, 9. [Google Scholar] [CrossRef]
- Wang, X.; Shen, R.; Wang, X.; Gu, Z.; Zhang, L.; Tan, E.; Yan, S.; Wang, E.; Zhao, E. Study on the mechanical behavior and energy evolution mechanism of coal samples with water content under dynamic load: Field and experimental tests. Phys. Fluids 2024, 36, 23. [Google Scholar] [CrossRef]
- GB/T50266-2013; Standard for Test Methods of Engineering Rock Mass. Beijing China Planning Publishing House: Beijing, China, 2013.
- Xie, B.J.; Ai, D.H.; Yang, Y. Crack Detection and Evolution Law for Rock Mass under SHPB Impact Tests. Shock Vib. 2019, 2019, 12. [Google Scholar] [CrossRef]
- Mishra, S.; Khetwal, A.; Chakraborty, T.; Basu, D. Effect of loading characteristics and specimen size in split Hopkinson pressure bar test on high-rate behavior of phyllite. Arch. Civ. Mech. Eng. 2022, 22, 20. [Google Scholar] [CrossRef]
- Sun, B.; Chen, R.; Ping, Y.; Zhu, Z.; Wu, N.; Shi, Z. Research on Dynamic Strength and Inertia Effect of Concrete Materials Based on Large-Diameter Split Hopkinson Pressure Bar Test. Materials 2022, 15, 15. [Google Scholar] [CrossRef]
- Huang, H.; Sun, Q.; Guo, C.; Xue, S.; Zhou, S. Investigating the evolution of pore space and magnetization rate of rocks under the effect of coal fire burning. Environ. Earth Sci. 2024, 83, 14. [Google Scholar] [CrossRef]
- Meng, T.; Guangwu, X.; Jiwei, M.; Yang, Y.; Liu, W.; Zhang, J.; Bosen, J.; Fang, S.; Ren, G. Mixed mode fracture tests and inversion of FPZ at crack tip of overlying strata in underground coal gasification combustion cavity under real-time high temperature condition. Eng. Fract. Mech. 2020, 239, 23. [Google Scholar] [CrossRef]
- Wang, S.; Wang, L.; Ren, B.; Ding, K.; Jiang, C.; Guo, J. Study of the mechanical characteristics of coal-serial sandstone after high temperature treatment under true triaxial loading. Sci. Rep. 2023, 13, 15. [Google Scholar] [CrossRef]
- Chen, S.; Huang, C.; Wang, C.; Duan, Z. Mechanical properties and constitutive relationships of 30CrMnSiA steel heated at high rate. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2008, 483–484, 105–108. [Google Scholar] [CrossRef]
- Huang, R.; Li, S.; Meng, L.; Jiang, D.; Li, P. Coupled Effect of Temperature and Strain Rate on Mechanical Properties of Steel Fiber-Reinforced Concrete. Int. J. Concr. Struct. Mater. 2020, 14, 15. [Google Scholar] [CrossRef]
- Gao, C.Y.; Zhang, L.C.; Guo, W.G.; Li, Y.L.; Lu, W.R.; Ke, Y.L. Dynamic plasticity of AZ31 magnesium alloy: Experimental investigation and constitutive modeling. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2014, 613, 379–389. [Google Scholar] [CrossRef]
- Ruan, Z.; Chen, L.; Fang, Q. Numerical investigation into dynamic responses of RC columns subjected for fire and blast. J. Loss Prev. Process Ind. 2015, 34, 10–21. [Google Scholar] [CrossRef]
- Xie, Q.; Chen, Y.; Lyu, H.; Gu, J.; Chen, Y.; Cui, H.; Wu, P. Dynamic mechanical properties and energy dissipation analysis of frozen sandstone with initial damage. Front. Earth Sci. 2023, 11, 10. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Z.; Sun, Q.; Zhang, W. Effect of Temperature and Strain Rate on the Brittleness of China Sandstone. Geofluids 2021, 2021, 10. [Google Scholar] [CrossRef]
- Ping, Q.; Diao, Q.; Qi, D.; Wang, C.; Zhang, C. Influence of Two Cooling Methods on Dynamic Mechanical Properties of High Temperature Sandstone. Shock Vib. 2021, 2021, 12. [Google Scholar] [CrossRef]
- Li, J.; Tang, S.; Zhang, S.; Li, L.; Wei, J.; Xi, Z.; Sun, K. Characterization of unconventional reservoirs and continuous accumulations of natural gas in the Carboniferous-Permian strata, mid-eastern Qinshui basin, China. J. Nat. Gas Sci. Eng. 2018, 49, 298–316. [Google Scholar] [CrossRef]
- Shi, S.; Wei, J.; Xie, D.; Yin, H.; Zhang, W.; Li, L. An attribute recognition model to predict the groundwater potential of sandstone aquifers in coal mines. J. Earth Syst. Sci. 2019, 128, 12. [Google Scholar] [CrossRef]
- Yang, S.; Ranjith, P.G.; Jing, H.; Tian, W.; Ju, Y. An experimental investigation on thermal damage and failure mechanical behavior of granite after exposure to different high temperature treatments. Geothermics 2017, 65, 180–197. [Google Scholar] [CrossRef]
- Ma, C.; Zhu, C.; Zhou, J.; Ren, J.; Yu, Q. Dynamic response and failure characteristics of combined rocks under confining pressure. Sci. Rep. 2022, 12, 17. [Google Scholar] [CrossRef] [PubMed]
- Sygala, A.; Bukowska, M. Identification of temperature effect on post-critical geomechanical properties of loaded sandstones. Arab. J. Geosci. 2019, 12, 10. [Google Scholar] [CrossRef]
- Pinetown, K.L.; Ward, C.R.; van der Westhuizen, W.A. Quantitative evaluation of minerals in coal deposits in the Witbank and Highveld Coalfields, and the potential impact on acid mine drainage. Int. J. Coal Geol. 2007, 70, 166–183. [Google Scholar] [CrossRef]
- Jiang, B.; Ye, W.; Zhao, Y. Nanopore structure and fractal characteristics of sandstone after high-temperature action. Environ. Earth Sci. 2024, 83, 19. [Google Scholar] [CrossRef]
- Yu, H.; Li, M.; Pu, H.; Zhang, L.; Chen, Y.; Shi, X.; Yue, Z. Direct tensile mechanical properties and damage fracture mechanisms of thermally damaged coal measures sandstone under high strain rate loading. J. Mater. Res. Technol.-JMRT 2023, 26, 6356–6374. [Google Scholar] [CrossRef]
- Li, M.; Mao, X.; Cao, L.; Pu, H.; Mao, R.; Lu, A. Effects of Thermal Treatment on the Dynamic Mechanical Properties of Coal Measures Sandstone. Rock Mech. Rock Eng. 2016, 49, 3525–3539. [Google Scholar] [CrossRef]
- Yin, T.; Wang, P.; Yang, J.; Li, X. Mechanical Behaviors and Damage Constitutive Model of Thermally Treated Sandstone Under Impact Loading. IEEE Access 2018, 6, 72047–72062. [Google Scholar] [CrossRef]











| Number | P/MPa | T/°C | /s−1 | Arithmetic Mean | |
|---|---|---|---|---|---|
| W-1-1 | 0.30 | 25 | 5.41 | 50.45 | 60.12 |
| W-1-2 | 100 | 5.60 | 51.72 | ||
| W-1-3 | 200 | 5.50 | 58.65 | ||
| W-1-4 | 300 | 5.46 | 61.69 | ||
| W-1-5 | 400 | 5.87 | 61.90 | ||
| W-1-6 | 500 | 5.38 | 62.12 | ||
| W-1-7 | 600 | 5.85 | 64.53 | ||
| W-1-8 | 800 | 5.73 | 69.90 | ||
| W-6-1 | 0.80 | 25 | 10.65 | 210.87 | 211.64 |
| W-6-2 | 100 | 10.56 | 210.9 | ||
| W-6-3 | 200 | 10.51 | 211.39 | ||
| W-6-4 | 300 | 10.55 | 211.85 | ||
| W-6-5 | 400 | 10.72 | 212.02 | ||
| W-6-6 | 500 | 10.55 | 212.09 | ||
| W-6-7 | 600 | 10.66 | 213.00 | ||
| W-6-8 | 800 | 10.60 | 213.20 |
| (s−1) | T (°C) | |||||||
|---|---|---|---|---|---|---|---|---|
| R = 6 | R = 8.5 | R = 11 | R = 13 | R = 15 | ||||
| 60.12 | 25 | 0.13 | 0.16 | 0.18 | 0.20 | 0.28 | 0.60 | 2.40 |
| 100 | 0.41 | 0.51 | 0.60 | 0.69 | 0.73 | 0.64 | 2.36 | |
| 200 | 0.26 | 0.37 | 0.43 | 0.48 | 0.54 | 0.77 | 2.23 | |
| 300 | 0.12 | 0.17 | 0.19 | 0.21 | 0.29 | 0.84 | 2.16 | |
| 400 | 0.21 | 0.28 | 0.33 | 0.44 | 0.52 | 0.96 | 2.04 | |
| 500 | 0.23 | 0.27 | 0.36 | 0.41 | 0.48 | 0.84 | 2.16 | |
| 600 | 0.24 | 0.28 | 0.35 | 0.38 | 0.43 | 0.66 | 2.34 | |
| 800 | 0.33 | 0.40 | 0.51 | 0.52 | 0.65 | 0.56 | 2.44 | |
| 211.64 | 25 | 0.61 | 0.66 | 0.71 | 0.77 | 0.79 | 0.30 | 2.70 |
| 100 | 0.54 | 0.59 | 0.65 | 0.71 | 0.74 | 0.35 | 2.65 | |
| 200 | 0.27 | 0.30 | 0.35 | 0.40 | 0.44 | 0.40 | 2.60 | |
| 300 | 0.54 | 0.59 | 0.65 | 0.76 | 0.79 | 0.45 | 2.55 | |
| 400 | 0.51 | 0.56 | 0.62 | 0.68 | 0.71 | 0.48 | 2.52 | |
| 500 | 0.53 | 0.58 | 0.68 | 0.74 | 0.77 | 0.44 | 2.56 | |
| 600 | 0.73 | 0.79 | 0.89 | 0.90 | 0.94 | 0.29 | 2.71 | |
| 800 | 0.84 | 0.94 | 0.94 | 0.96 | 0.96 | 0.14 | 2.86 | |
| Ed/GPa | ||||||||
|---|---|---|---|---|---|---|---|---|
| 25 °C | 100 °C | 200 °C | 300 °C | 400 °C | 500 °C | 600 °C | 800 °C | |
| 60.12 | 25.51 | 21.05 | 17.23 | 15.13 | 13.45 | 10.87 | 9.25 | 6.52 |
| 81.52 | 26.87 | 22.18 | 18.35 | 16.73 | 14.99 | 11.72 | 10.17 | 7.29 |
| 112.60 | 28.26 | 24.58 | 19.95 | 17.47 | 16.58 | 12.45 | 11.01 | 7.63 |
| 153.22 | 30.24 | 26.60 | 20.24 | 19.15 | 17.15 | 13.46 | 12.09 | 8.48 |
| 187.85 | 31.92 | 27.13 | 21.21 | 19.38 | 17.86 | 14.28 | 12.79 | 8.80 |
| 211.64 | 33.38 | 28.49 | 23.56 | 21.84 | 18.04 | 16.16 | 13.12 | 9.80 |
| 25 °C | 100 °C | 200 °C | 300 °C | 400 °C | 500 °C | 600 °C | 800 °C | |
|---|---|---|---|---|---|---|---|---|
| 60.12 | 63.22 | 65.55 | 80.29 | 85.29 | 92.70 | 96.5 | 80.18 | 60.31 |
| 81.52 | 67.58 | 66.72 | 87.09 | 92.91 | 99.97 | 100.05 | 85.34 | 64.23 |
| 112.60 | 74.16 | 74.82 | 93.21 | 97.33 | 108.22 | 112.54 | 98.23 | 70.79 |
| 153.22 | 82.03 | 81.12 | 99.55 | 105.53 | 115.71 | 118.49 | 104.70 | 78.45 |
| 187.85 | 88.88 | 91.57 | 105.16 | 112.84 | 118.45 | 123.57 | 108.08 | 83.94 |
| 211.64 | 92.39 | 97.15 | 112.61 | 118.69 | 124.66 | 126.88 | 112.45 | 90.56 |
| 25 °C | 100 °C | 200 °C | 300 °C | 400 °C | 500 °C | 600 °C | 800 °C | |
|---|---|---|---|---|---|---|---|---|
| 60.12 | 5.145 | 7.158 | 8.648 | 9.248 | 10.403 | 10.913 | 11.222 | 14.945 |
| 81.52 | 5.301 | 7.512 | 9.217 | 9.617 | 10.550 | 11.244 | 12.520 | 15.708 |
| 112.60 | 5.822 | 8.932 | 9.567 | 10.367 | 10.976 | 11.890 | 12.750 | 16.366 |
| 153.22 | 7.127 | 9.783 | 10.223 | 10.699 | 11.400 | 12.398 | 13.311 | 17.580 |
| 187.85 | 7.308 | 9.840 | 10.889 | 11.258 | 11.644 | 12.815 | 14.651 | 18.919 |
| 211.64 | 7.512 | 10.650 | 11.160 | 11.729 | 12.545 | 13.456 | 15.565 | 19.456 |
| Ds | ||||||||
|---|---|---|---|---|---|---|---|---|
| 25 °C | 100 °C | 200 °C | 300 °C | 400 °C | 500 °C | 600 °C | 800 °C | |
| 60.12 | 2.40 | 2.36 | 2.23 | 2.16 | 2.04 | 2.16 | 2.34 | 2.44 |
| 81.52 | 2.44 | 2.41 | 2.33 | 2.18 | 2.10 | 2.25 | 2.38 | 2.47 |
| 112.60 | 2.48 | 2.45 | 2.39 | 2.27 | 2.24 | 2.37 | 2.49 | 2.67 |
| 153.22 | 2.64 | 2.57 | 2.47 | 2.36 | 2.35 | 2.44 | 2.56 | 2.76 |
| 187.85 | 2.70 | 2.59 | 2.52 | 2.50 | 2.48 | 2.52 | 2.63 | 2.81 |
| 211.64 | 2.70 | 2.65 | 2.60 | 2.55 | 2.52 | 2.56 | 2.71 | 2.86 |
| 25 °C | 100 °C | 200 °C | 300 °C | 400 °C | 500 °C | 600 °C | 800 °C | |
|---|---|---|---|---|---|---|---|---|
| 60.12 | 0.203 | 0.178 | 0.125 | 0.115 | 0.072 | 0.133 | 0.140 | 0.264 |
| 81.52 | 0.525 | 0.479 | 0.355 | 0.234 | 0.213 | 0.267 | 0.438 | 0.699 |
| 112.60 | 0.737 | 0.716 | 0.685 | 0.454 | 0.348 | 0.479 | 0.692 | 0.989 |
| 153.22 | 0.851 | 0.825 | 0.838 | 0.746 | 0.551 | 0.616 | 0.83 | 1.143 |
| 187.85 | 1.076 | 1.01 | 0.962 | 0.871 | 0.749 | 0.792 | 0.922 | 1.390 |
| 211.64 | 1.137 | 1.107 | 1.007 | 0.953 | 0.796 | 0.844 | 0.951 | 1.575 |
| λI | ||||||||
|---|---|---|---|---|---|---|---|---|
| 25 °C | 100 °C | 200 °C | 300 °C | 400 °C | 500 °C | 600 °C | 800 °C | |
| 60.12 | 39.26 | 38.56 | 37.12 | 35.46 | 31.72 | 28.43 | 24.76 | 21.74 |
| 81.52 | 38.70 | 37.47 | 35.71 | 34.02 | 31.05 | 27.25 | 22.89 | 20.24 |
| 112.60 | 36.04 | 35.26 | 34.15 | 32.15 | 29.50 | 26.38 | 22.16 | 18.23 |
| 153.22 | 34.27 | 33.04 | 31.52 | 29.87 | 25.46 | 24.41 | 20.76 | 16.87 |
| 187.85 | 30.85 | 29.27 | 28.43 | 26.16 | 23.79 | 21.51 | 19.63 | 11.89 |
| 211.64 | 27.45 | 26.79 | 25.90 | 24.46 | 21.59 | 18.81 | 15.15 | 10.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zhu, F.; Mao, Y.; Fan, F.; Wu, B.; Deng, J. Dynamic Mechanical Characteristics and Fracture Size Effect of Coal Sandstone Under High-Temperature and High-Strain Rate Coupling Action. Fractal Fract. 2025, 9, 381. https://doi.org/10.3390/fractalfract9060381
Li M, Zhu F, Mao Y, Fan F, Wu B, Deng J. Dynamic Mechanical Characteristics and Fracture Size Effect of Coal Sandstone Under High-Temperature and High-Strain Rate Coupling Action. Fractal and Fractional. 2025; 9(6):381. https://doi.org/10.3390/fractalfract9060381
Chicago/Turabian StyleLi, Ming, Fuqiang Zhu, Yiwen Mao, Fangwei Fan, Boyuan Wu, and Jishuo Deng. 2025. "Dynamic Mechanical Characteristics and Fracture Size Effect of Coal Sandstone Under High-Temperature and High-Strain Rate Coupling Action" Fractal and Fractional 9, no. 6: 381. https://doi.org/10.3390/fractalfract9060381
APA StyleLi, M., Zhu, F., Mao, Y., Fan, F., Wu, B., & Deng, J. (2025). Dynamic Mechanical Characteristics and Fracture Size Effect of Coal Sandstone Under High-Temperature and High-Strain Rate Coupling Action. Fractal and Fractional, 9(6), 381. https://doi.org/10.3390/fractalfract9060381






