Analytical Characterization of Self-Similarity in k-Cullen Sequences Through Generating Functions and Fibonacci Scaling

Abstract

In this study, we define the $k$-Cullen, $k$-Cullen–Lucas, and Modified $k$-Cullen sequences, and certain terms in these sequences are given. Then, we obtain the Binet formulas, generating functions, summation formulas, etc. In addition, we examine the relations among the terms of the $k$-Cullen, $k$-Cullen–Lucas, Modified $k$-Cullen, Cullen, Cullen–Lucas, Modified Cullen, $k$-Woodall, $k$-Woodall–Lucas, Modified $k$-Woodall, Woodall, Woodall–Lucas, and Modified Woodall sequences. The generating functions were derived and analyzed, especially for cases where Fibonacci numbers were assigned to parameter $k.$ Graphical representations of the generating functions and their logarithmic transformations revealed interesting growth trends and convergence behavior. Further, by multiplying the generating functions with exponential expressions such as $e^k$, we explored the self-similar nature and mirrored dynamics among the sequences. Specifically, it was observed that the Modified Cullen sequence exhibited a symmetric and inverse-like resemblance to the Cullen and Cullen–Lucas sequences, suggesting the presence of deeper structural dualities. Additionally, indefinite integrals of the generating functions were computed and visualized over a range of Fibonacci-indexed k values. These integral-based graphs further reinforced the phenomenon of symmetry and self-similarity, particularly in the Modified Cullen sequence. A key insight of this study is the discovery of a structural duality between the Modified Cullen and standard Cullen-type sequences, supported both algebraically and graphically. This duality suggests new avenues for analyzing generalized recursive sequences through generating function transformations. This observation provides new insight into the structural behavior of generalized Cullen-type sequences.

1. Introduction

In mathematics, sequences play a crucial role in understanding a problem that arises under specific conditions more clearly. One of the most famous of these problems is the Rabbit Problem from Leonardo Fibonacci’s renowned book Liber Abaci. Based on the outcomes of the rabbit problem, the Fibonacci sequence is defined, and the relationships between consecutive terms of this sequence are derived.

The Fibonacci sequence has long been recognized not only for its mathematical elegance but also for its relevance in modeling natural fractal structures, such as the spiral arrangement of leaves, pinecones, and sunflower seeds. While Zhang et al. [1] propose a Fibonacci-based fractal superstructure, the theoretical underpinnings of such multi-scale models are more rigorously defined by the two-scale fractal dimension framework [2,3,4], which provides a robust mathematical and physical basis.

The most famous number sequences are the Fibonacci and Lucas sequences. These sequences have attracted the attention of scientists for centuries. Fibonacci sequences have been applied in various fields such as engineering [5], chemistry [6], group theory [7], graph theory [8], phylotaxis [9], cryptology [10], biomathematics [11], etc. Scientists have conducted many studies on the generalization of the Fibonacci sequence. Examples of studies carried out are Bronze Fibonacci [12], Leonardo [13], Copper Fibonacci [14], Gaussian Fibonacci numbers [15], Fermat [16], Perrin [17], Narayana [18], $k$-Oresme [19], Padovan [20], Bronze Leonardo [21], Mersenne [22], Bernoulli–Euler polynomials [23], Hyperharmonic Fibonacci [24], $q$-Narayana [25], Pell and Pell–Lucas polynomials [26], Complex-type $k$-Fibonacci [27], $r$-Fibonacci [28], Bell [29], Jacobsthal–Padovan [30], Francois [31] sequences, etc.

For $n\in \mathbb{N}$, Fibonacci numbers $F_n$ and Lucas numbers $L_n$ are defined by the recurrence relations, respectively:

$$F_{n+2}=F_{n+1}+F_n,\mathrm{with}{F}_0=0\mathrm{and}{F}_1=1,$$

$$L_{n+2}=L_{n+1}+L_n,\mathrm{with}{L}_0=2\mathrm{and}{L}_1=1.$$

Binet formulas for $F_n$ and $L_n$ are given by the following relations, respectively:

$$F_n={\displaystyle \frac{{\phi }^n-{\sigma }^n}{\alpha -\beta }}\mathrm{and}{L}_n={\phi }^n+{\sigma }^n$$

where $\phi ={\displaystyle \frac{1+\sqrt{5}}{2}}$ and $\sigma ={\displaystyle \frac{1-\sqrt{5}}{2}}$ are the roots of the characteristic equation $r^2-r-1=0$. Here, the number$\phi$ is the known golden ratio.

In mathematics, Cullen numbers are a special class of numbers defined by the following formula. This class of numbers was defined by an Irish priest and mathematician named James Cullen in 1905. These numbers are helpful in many areas of number theory, such as computer-aided prime number searches and prime number tests. In addition, these numbers are special cases of Proth numbers.

Furthermore, for $n\in \mathbb{N}$, the Woodall numbers $R_n$, Woodall–Lucas numbers $D_n$, Modified Woodall numbers $W_n$, Cullen numbers $C_n$, Cullen–Lucas numbers $E_n$, and Modified Cullen–Lucas numbers $H_n$ are defined by the recurrence relations, respectively:

$$R_{n+2}={4R}_{n+1}-4R_n-1,\mathrm{with}{R}_0=-1\mathrm{and}{R}_1=1,$$

$$D_{n+2}={4D}_{n+1}-4D_n-1,\mathrm{with}{D}_0=1\mathrm{and}{D}_1=4,$$

$$W_{n+2}={4W}_{n+1}-{4W}_n+1,\mathrm{with}{W}_0=0\mathrm{and}{W}_1=1,$$

$$C_{n+2}={4C}_{n+1}-4C_n+1,\mathrm{with}{C}_0=1\mathrm{and}{C}_1=3,$$

$$E_{n+2}={4E}_{n+1}-4E_n+1,\mathrm{with}{E}_0=1\mathrm{and}{E}_1=4,$$

$$H_{n+2}={4H}_{n+1}-4H_n-1,\mathrm{with}{H}_0=-1\mathrm{and}{H}_1=2.$$

For $R_n$, $D_n$, $W_n$, $C_n$, $E_n$, and $H_n$, the Binet formulas are given by the following relations, respectively:

$$R_n=n{2}^n-1,D_n=(4+n)2^{n-1}-1,W_n=\left(n-1\right)2^n+1,$$

$$C_n=n{2}^n+1,E_n=3n{2}^{n-1}+1,\mathrm{and}{H}_n=3n{2}^{n-1}-1.$$

The authors found many properties of these sequences and made many applications related to these sequences (for details, see [32,33,34,35]).

Using the recurrence relation of the classical Fibonacci sequence as a foundation, the $k$-Fibonacci and $k$-Lucas sequences were developed, both of which play a significant role in number theory. In [36], Falcon and Plaza introduced the concept of the $k$-Fibonacci sequence and explored numerous properties associated with it. Furthermore, in [37], Falcon extended this study by defining the $k$-Lucas sequences. In addition, Akkuş and Özkan defined a new generalization of $k$-Woodall sequences and found many properties of these sequences [38].

For $k\in {\mathbb{R}}^{+}$ and $n\in \mathbb{N}$, the $k$-Woodall ${\mathcal{O}}_{k,n}$, $k$-Woodall–Lucas${\mathcal{S}}_{k,n}$, and Modified $k$-Woodall ${\mathcal{B}}_{k,n}$ are defined, respectively, by

$${\mathcal{O}}_{k,n+3}=5{\mathcal{O}}_{k,n+2}-8{\mathcal{O}}_{k,n+1}+{4\mathcal{O}}_{k,n},\mathrm{with}{\mathcal{O}}_{k,0}=-1,{\mathcal{O}}_{k,1}=1,\mathrm{and}{\mathcal{O}}_{k,2}=8-k,$$

$${\mathcal{S}}_{k,n+3}=5{\mathcal{S}}_{k,n+2}-8{\mathcal{S}}_{k,n+1}+4{\mathcal{S}}_{k,n},\mathrm{with}{\mathcal{S}}_{k,0}=1,{\mathcal{S}}_{k,1}=4,\mathrm{and}{\mathcal{S}}_{k,2}=12-k,$$

$${\mathcal{B}}_{k,n+3}=5{\mathcal{B}}_{k,n+2}-8{\mathcal{B}}_{k,n+1}+4{\mathcal{B}}_{k,n},\mathrm{with}{\mathcal{B}}_{k,0}=0,{\mathcal{B}}_{k,1}=1,\mathrm{and}{\mathcal{B}}_{k,2}=k+4.$$

For ${\mathcal{O}}_{k,n}$, ${\mathcal{S}}_{k,n}$, and ${\mathcal{B}}_{k,n}$, the Binet formulas are given by the following relations, respectively:

$${\mathcal{O}}_{k,n}=\left(k-1+{\displaystyle \frac{3-k}{2}}n\right)2^n-k,{\mathcal{S}}_{k,n}=\left(k+1+{\displaystyle \frac{2-k}{2}}n\right)2^n-k,$$

$${\mathcal{B}}_{k,n}=\left(-k+{\displaystyle \frac{k+1}{2}}n\right)2^n+k.$$

As seen above, many generalizations of Fibonacci and Lucas sequences have been given so far. In this study, we give new generalizations inspired by the $k$-Fibonacci and Cullen sequences. We call these sequences the $k$-Cullen, $k$-Cullen–Lucas, and Modified $k$-Cullen sequences and denote them as $U_{k,n}$, $N_{k,n}$, and $M_{k,n}$, respectively.

Self-similarity is a fundamental concept in mathematics and complexity science, describing structures or patterns that are invariant under scaling transformations. A self-similar object appears “the same” at different levels of magnification, a property commonly found in fractals, recursive functions, and dynamic systems. According to Mandelbrot [39], self-similarity encapsulates the idea of infinite complexity emerging from simple iterative rules and is thus pivotal in modeling both natural phenomena and algorithmic processes. In mathematics, it plays a central role in the analysis of fractal dimensions, automata, wavelets, and recursive sequences [40].

Recent studies have extended the scope of self-similarity into discrete mathematics and number theory, especially through sequences that exhibit repeated growth patterns governed by recurrence relations [41]. Fibonacci-related sequences, due to their recursive and proportional structure, are natural candidates for revealing self-similar dynamics. Furthermore, generating functions and their analytic transformations, such as integration and exponentiation, provide deeper insights into the scale-invariant behaviors embedded within such sequences.

The aim of this study is to explore the emergence of self-similar patterns within the Cullen, Cullen–Lucas, and Modified Cullen sequences by analyzing their generating functions, logarithmic profiles, exponential transformations, and indefinite integrals, particularly when the recursion parameter $k$ is taken from the Fibonacci sequence. Through graphical and analytical evaluations, we demonstrate how self-similarity and symmetry emerge, providing potential applications in areas ranging from complexity theory to financial modeling and medical image analysis.

We separate the article into four parts.

In Section 2, we introduce the $k$-Cullen, $k$-Cullen–Lucas, and Modified $k$-Cullen sequences. We derive their characteristic equations and present the corresponding Binet formulas along with several of their fundamental properties. In addition, we construct the generating functions for these sequences and explore various special summation identities related to them.

In Section 3, we examine the relations between the terms of the $k$-Cullen, $k$-Cullen–Lucas, Modified $k$-Cullen, Cullen, Cullen–Lucas, and Modified Cullen sequences. Then, we associate the $k$-Cullen, $k$-Cullen–Lucas, and Modified $k$-Cullen sequences with special number sequences. Furthermore, we represent the terms of these sequences using matrix formulations.

In Section 4, we examine a graphical review: Self-Similarity behavior of Generator Functions for Logarithmic Scale, Exponential Scale, and through Integration of Generating Functions.

2. k-Cullen, $\mathit{k}$-Cullen–Lucas, and Modified $\mathit{k}$-Cullen Sequences

In this section, we explore a new generalization of Cullen sequences. Then we obtain many properties of this generalization such as special summation formulas, Binet formulas, and generating functions.

For $k\in {\mathbb{R}}^{+}$ and $n\in \mathbb{N}$, the $k$-Cullen $U_{k,n}$, $k$-Cullen–Lucas$N_{k,n}$, and Modified $k$-Cullen $M_{k,n}$ are defined, respectively, by

$$U_{k,n+2}={4U}_{k,n+1}-{4U}_{k,n}+k,\mathrm{with}{U}_{k,0}=1\mathrm{and}{U}_{k,1}=3,$$

$$N_{k,n+2}={4N}_{k,n+1}-4N_{k,n}+k,\mathrm{with}{N}_{k,0}=1\mathrm{and}{N}_{k,1}=4,$$

$$M_{k,n+2}={4M}_{k,n+1}-{4M}_{k,n}-k,\mathrm{with}{M}_{k,0}=-1\mathrm{and}{M}_{k,1}=2.$$

Also, the third-order recurrence relations of the sequences $U_{k,n}$, $N_{k,n}$, and $M_{k,n}$ are respectively, as follows:

$$U_{k,n+3}=5U_{k,n+2}-8U_{k,n+1}+{4U}_{k,n},\mathrm{with}{U}_{k,0}=1,U_{k,1}=3,\mathrm{and}{U}_{k,2}=k+8,$$

$$N_{k,n+3}=5N_{k,n+2}-8N_{k,n+1}+4N_{k,n},\mathrm{with}{N}_{k,0}=1,N_{k,1}=4,\mathrm{and}{N}_{k,2}=k+12,$$

$$M_{k,n+3}=5M_{k,n+2}-8M_{k,n+1}+4M_{k,n},\mathrm{with}{M}_{k,0}=-1,M_{k,1}=2,\mathrm{and}{M}_{k,2}=12-k.$$

Next, we provide an overview of the equations associated with these sequences.

The characteristic equation of the $k$-Cullen, $k$-Cullen–Lucas, and Modified $k$-Cullen sequences is

$$r^3-5r^2+8r-4=\left(r^2-4r+4\right)\left(r-1\right)=0.$$

The roots of this equation are

$$r_1{=r}_2=2,\mathrm{and}{r}_3=1.$$

The relationship between these roots is given below:

$$r_1+r_2+r_3=5,r_1{r}_2+r_1{r}_3+r_2{r}_3=8,\mathrm{and}{r}_1{r}_2{r}_3=4.$$

The$U_{k,n}$, $N_{k,n}$, and $M_{k,n}$ values for the first four $n$ natural numbers are given below:

$$U_{k,0}=1,N_{k,0}=1,M_{k,0}=-1,$$

$$U_{k,1}=3,N_{k,1}=4,M_{k,1}=2,$$

$$U_{k,2}=k+8,N_{k,2}=k+12,M_{k,2}=12-k,$$

$$U_{k,3}=5k+20,N_{k,3}=5k+32,M_{k,3}=40-5k.$$

Next, the values of these sequences for some k values are related to the sequences in the Electronic Encyclopedia of Integer Sequences (OEIS):

• $U_{1,n}=\left\{1,3,9,25,\dots \right\}$: A002064,
• $U_{2,n}=\left\{1,3,10,30,\dots \right\}$: A001700,
• $N_{4,n}=\left\{1,4,16,32,\dots \right\}$: A107767,
• $N_{6,n}=\left\{1,4,18,62,\dots \right\}$: A057414,
• $M_{5,n}=\left\{2,7,15,26,\dots \right\}$: A005449,
• $M_{6,n}=\left\{2,6,10,14,\dots \right\}$: A016825.

Next, the Binet formulas of the $k$-Cullen $U_{k,n}$, $k$-Cullen–Lucas$N_{k,n}$, and Modified $k$-Cullen $M_{k,n}$ sequences are expressed.

Theorem 1.

Let  $k\in {\mathbb{R}}^{+}$  and  $n\in \mathbb{N}$.  We obtain

i. 

$U_{k,n}=\left(1-k+{\displaystyle \frac{k+1}{2}}n\right)2^n+k$

ii. 

$N_{k,n}=\left(1-k+{\displaystyle \frac{k+2}{2}}n\right)2^n+k$,

iii. 

$M_{k,n}=\left(k-1+{\displaystyle \frac{4-k}{2}}n\right)2^n-k$.

Proof. i.

The Binet form of a sequence is as follows (two distinct root cases where $r_1=r_2=2$ and $r_3=1$):

$$U_{k,n}=(x+yn){r_1}^n+z{r_3}^n.$$

For these $n$ values, we obtain

$$U_{k,0}=x+z,$$

$$U_{k,1}=(x+y)r_1+z{r}_3,$$

$$U_{k,2}=(x+2y){r_1}^2+z{r_3}^2.$$

We find

$$x=1-k,y={\displaystyle \frac{k+1}{2}}\mathrm{and}z=k.$$

The other proofs follow a similar approach. $\square$

Theorem 2.

he generating functions for  $k$-Cullen  $U_{k,n}$, $k$-Cullen–Lucas  $N_{k,n}$, and Modified  $k$-Cullen  $M_{k,n}$  sequences are given, respectively, as follows:

i. 

$u\left(t\right)=\sum _{n=0}^{\infty }{U}_{k,n}{t}^n={\displaystyle \frac{1-2t+(k+1)t^2}{{-4t}^3+8t^2-5t+1}}$,

ii. 

$n\left(t\right)=\sum _{n=0}^{\infty }{N}_{k,n}{t}^n={\displaystyle \frac{1-t+k{t}^2}{{-4t}^3+8t^2-5t+1}}$,

iii. 

$m(t)=\sum _{n=0}^{\infty }{M}_{k,n}{t}^n={\displaystyle \frac{-1+2t+(7-k)t^2}{{-4t}^3+8t^2-5t+1}}$.

Proof. i.

For the $k$-Woodall sequence, we get

$$\begin{array}{c}u\left(t\right)=\sum _{n=0}^{\infty }{U}_{k,n}{t}^n=1+3t+(k+8)t^2+\sum _{n=3}^{\infty }{U}_{k,n}{t}^n\hfill \\ =1+3t+(k+8)t^2+5\sum _{n=3}^{\infty }{U}_{k,n-1}{t}^n-8\sum _{n=3}^{\infty }{U}_{k,n-2}{t}^n+4\sum _{n=3}^{\infty }{U}_{k,n-3}{t}^n\hfill \\ =1+3t+(k+8)t^2+5t\sum _{n=2}^{\infty }{U}_{k,n}{t}^n-8t^2\sum _{n=1}^{\infty }{U}_{k,n}{t}^n+4t^3\sum _{n=0}^{\infty }{U}_{k,n}{t}^n\hfill \\ ={\displaystyle \frac{1-2t+(k+1)t^2}{{-4t}^3+8t^2-5t+1}}.\hfill \end{array}$$

The other proofs follow a similar approach. $\square$

In the following theorems, we give special sum formulas of the $k$-Cullen $U_{k,n}$, $k$-Cullen–Lucas$N_{k,n}$, and Modified $k$-Cullen $M_{k,n}$ sequences.

Theorem 3.

Let  $k\in {\mathbb{R}}^{+}$  and  $n\in \mathbb{N}$. We find

i. 

$\sum _{s=0}^n{U}_{k,n}=4U_{k,n-1}+\left(n-1\right)k$,

ii. 

$\sum _{s=0}^n{N}_{k,s}=4N_{k,n-1}+\left(n-1\right)k-1$,

iii. 

$\sum _{s=0}^n{M}_{k,n}=4M_{k,n-1}-\left(n-1\right)k+5.$

Proof. ii.

From the definition of the$k$-Cullen–Lucas sequence, we obtain

$$\begin{array}{c}{N}_{k,2}={4N}_{k,1}{-4N}_{k,0}+k,\\ N_{k,3}={4N}_{k,2}-4N_{k,1}+k,\\ ⋮\\ N_{k,n}={4N}_{k,n-1}-{4N}_{k,n-2}+k.\end{array}$$

So, we have

$$\begin{array}{c}-5+\sum _{s=0}^n{N}_{k,s}=4\sum _{s=1}^{n-1}{N}_{k,s}-4\sum _{s=0}^{n-2}{N}_{k,s}+(n-1)k,\\ -5+\sum _{s=0}^n{N}_{k,s}=4\left(-N_{k,n}-N_{k,0}+\sum _{s=0}^n{N}_{k,s}\right)-4\left(-N_{k,n}-N_{k,n-1}+\sum _{s=0}^n{N}_{k,s}\right)\\ +(n-1)k.\end{array}$$

Thus, we obtain

$${\sum }_{s=0}^n{N}_{k,s}=4N_{k,n-1}+\left(n-1\right)k-1.$$

The other proofs follow a similar approach. $\square$

Theorem 4.

Let  $k\in {\mathbb{R}}^{+}$  and  $n\in \mathbb{N}$. We obtain

i. 

$\sum _{s=0}^n{U}_{k,2s}={\displaystyle \frac{20U_{k,2n}-4U_{k,2n+1}+9nk+1}{9}}$,

ii. 

$\sum _{s=0}^n{U}_{k,2s+1}={\displaystyle \frac{16U_{k,2n}+4U_{k,2n+1}+9nk-1}{9}}$,

iii. 

$\sum _{s=0}^n{N}_{k,2s}={\displaystyle \frac{20N_{k,2n}-4N_{k,2n+1}+9nk+5}{9}}$,

iv. 

$\sum _{s=0}^n{N}_{k,2s+1}={\displaystyle \frac{16N_{k,2n}+4N_{k,2n+1}+9nk+4}{9}}$,

v. 

$\sum _{s=0}^n{M}_{k,2s}={\displaystyle \frac{20M_{k,2n}-4M_{k,2n+1}-9nk+19}{9}}$,

vi. 

$\sum _{s=0}^n{M}_{k,2s+1}={\displaystyle \frac{16M_{k,2n}+4M_{k,2n+1}-9nk+26}{9}}$.

Proof. i. and ii.

From the definition of the$k$-Cullen sequence, we obtain

$$\begin{array}{c}{U}_{k,2}={4U}_{k,1}{-4U}_{k,0}+k,U_{k,3}={4U}_{k,2}{-4U}_{k,1}+k,\\ U_{k,4}={4U}_{k,3}-4U_{k,2}+k,U_{k,5}={4U}_{k,4}-4U_{k,3}+k,\\ ⋮⋮\\ U_{k,2n}={4U}_{k,2n-1}-{4U}_{k,2n-2}+k,U_{k,2n+1}={4U}_{k,2n}-{4U}_{k,2n-1}+k.\end{array}$$

So,

$$-3+{\sum }_{s=0}^n{U}_{k,2s+1}=4\left(-U_{k,2n+1}+{\sum }_{s=0}^n{U}_{k,2s+1}\right)-4\left(-U_{k,2n}+{\sum }_{s=0}^n{U}_{k,2s}\right)+nk$$

(1)

And

$$-1+{\sum }_{s=0}^n{U}_{k,2s}=4\left(-1+{\sum }_{s=0}^n{U}_{k,2s}\right)-4\left(-U_{k,2n+1}+{\sum }_{s=0}^n{U}_{k,2s+1}\right)+nk$$

(2)

If Equations (1) and (2) are solved jointly, we find

$${\sum }_{s=0}^n{U}_{k,2s}={\displaystyle \frac{20U_{k,2n}-4U_{k,2n+1}+9nk+1}{9}},\mathrm{and}{\sum }_{s=0}^n{U}_{k,2s+1}={\displaystyle \frac{16U_{k,2n}+4U_{k,2n+1}+9nk-1}{9}}.$$

The other proofs follow a similar approach. $\square$

3. Exploring Relations in Special Sequences

In this chapter, we examine the relationships among the $k$-Cullen, $k$-Cullen–Lucas, Modified $k$-Cullen, Cullen, Cullen–Lucas, Modified Cullen, Woodall, Woodall–Lucas, Modified Woodall, $k$-Woodall, $k$-Woodall–Lucas, and Modified $k$-Woodall sequences. In addition, we represent the terms of these sequences using matrix formulations.

Next, we examine the relations among the $k$-Cullen $U_{k,n}$, $k$-Cullen–Lucas$N_{k,n}$, Modified $k$-Cullen $M_{k,n}$, Cullen $C_n$, Cullen–Lucas $E_n$, Modified Cullen $H_n$, $k$-Woodall ${\mathcal{O}}_{k,n}$, $k$-Woodall–Lucas${\mathcal{S}}_{k,n}$, and Modified $k$-Woodall sequences.

Theorem 5.

Let  $k\in {\mathbb{R}}^{+}$  and  $n\in \mathbb{N}$. The following relations are found between the  $k$-Cullen sequence and other sequences:

i. 

$U_{k,n}={\displaystyle \frac{3}{k^2+4k+4}}{N}_{k,n+2}-{\displaystyle \frac{k+11}{k^2+4k+4}}{N}_{k,n+1}+{\displaystyle \frac{k^2+5k+12}{k^2+4k+4}}{N}_{k,n}$,

ii. 

$U_{k,n}=-{\displaystyle \frac{15}{k^2-8k+16}}{M}_{k,n+2}+{\displaystyle \frac{-5k+65}{k^2-8k+16}}{M}_{k,n+1}+{\displaystyle \frac{{-k}^2+13k-66}{k^2-8k+16}}{M}_{k,n}$,

iii. 

$U_{k,n}={\displaystyle \frac{-k+1}{2}}{C}_{n+1}+{\displaystyle \frac{3k-1}{2}}{C}_n$,

iv. 

$U_{k,n}={\displaystyle \frac{k}{3}}{E}_{n+2}+{\displaystyle \frac{-5k+1}{3}}{E}_{n+1}+{\displaystyle \frac{7k-1}{3}}{E}_n$,

v. 

$U_{k,n}=-{\displaystyle \frac{5k}{3}}{H}_{n+2}+{\displaystyle \frac{19k+1}{3}}{H}_{n+1}-{{\displaystyle \frac{17k+1}{3}}H}_n$,

vi. 

$U_{k,n}=-{\displaystyle \frac{8}{k^2-6k+9}}{\mathcal{O}}_{k,n+2}-{\displaystyle \frac{4k-36}{k^2-6k+9}}{\mathcal{O}}_{k,n+1}-{\displaystyle \frac{k^2-10k+37}{k^2-6k+9}}{\mathcal{O}}_{k,n}$,

vii. 

$U_{k,n}=-{\displaystyle \frac{2k+5}{k^2-4k+4}}{S}_{k,n+2}+{\displaystyle \frac{3k+21}{k^2-4k+4}}{S}_{k,n+1}+{\displaystyle \frac{-k^2+3k-20}{k^2-4k+4}}{S}_{k,n}$,

viii. 

$U_{k,n}={\displaystyle \frac{k^2+k}{k^3+2k^2+33k+48}}{\mathcal{B}}_{k,n+2}+{\displaystyle \frac{-3k^2+29k+48}{k^3+2k^2+33k+48}}{\mathcal{B}}_{k,n+1}+{\displaystyle \frac{k^3-28k^2-77k-48}{k^3+2k^2+33k+48}}{\mathcal{B}}_{k,n}$.

Proof. i.

To carry out the proofs, we utilize the following relation:

$$U_{k,n}=a\times N_{k,n+2}+b\times N_{k,n+1}+c\times N_{k,n}.$$

For these $n$ values, we obtain

$$U_{k,0}=a\times N_{k,2}+b\times N_{k,1}+c\times N_{k,0},$$

$$U_{k,1}=a\times N_{k,3}+b\times N_{k,2}+c\times N_{k,1},$$

$$U_{k,2}=a\times N_{k,4}+b\times N_{k,3}+c\times N_{k,2}.$$

We find

$$a={\displaystyle \frac{3}{k^2+4k+4}},b=-{\displaystyle \frac{k+11}{k^2+4k+4}},\mathrm{and}c={\displaystyle \frac{k^2+5k+12}{k^2+4k+4}}.$$

Thus, we have

$$U_{k,n}={\displaystyle \frac{3}{k^2+4k+4}}{N}_{k,n+2}-{\displaystyle \frac{k+11}{k^2+4k+4}}{N}_{k,n+1}+{\displaystyle \frac{k^2+5k+12}{k^2+4k+4}}{N}_{k,n}.$$

The other proofs follow a similar approach. $\square$

Theorem 6.

Let  $k\in {\mathbb{R}}^{+}$  and  $n\in \mathbb{N}$. The following relations are found between the  $k$-Cullen–Lucas sequence and other sequences: 

i. 

$N_{k,n}=-{\displaystyle \frac{2}{k^2+2k+1}}{U}_{k,n+2}+{\displaystyle \frac{k+7}{k^2+2k+1}}{U}_{k,n+1}+{\displaystyle \frac{k^2+k-4}{k^2+2k+1}}{U}_{k,n}$,

ii. 

$N_{k,n}=-{\displaystyle \frac{18}{k^2-8k+16}}{M}_{k,n+2}+{\displaystyle \frac{-6k+78}{k^2-8k+16}}{M}_{k,n+1}+{\displaystyle \frac{{-k}^2+14k-76}{k^2-8k+16}}{M}_{k,n}$,

iii. 

$N_{k,n}=-{\displaystyle \frac{1}{2}}{C}_{n+2}+{\displaystyle \frac{-k+5}{2}}{C}_{n+1}+{\displaystyle \frac{3k-4}{2}}{C}_n$,

iv. 

$N_{k,n}={\displaystyle \frac{k-1}{3}}{E}_{n+2}+{\displaystyle \frac{-5k+5}{3}}{E}_{n+1}+{\displaystyle \frac{7k-4}{3}}{E}_n$,

v. 

$N_{k,n}=-{\displaystyle \frac{5k+1}{3}}{H}_{n+2}+{\displaystyle \frac{19k+5}{3}}{H}_{n+1}-{\displaystyle \frac{17k+4}{3}}{H}_n$,

vi. 

$N_{k,n}=-{\displaystyle \frac{10}{k^2-6k+9}}{\mathcal{O}}_{k,n+2}-{\displaystyle \frac{5k-45}{k^2-6k+9}}{\mathcal{O}}_{k,n+1}-{\displaystyle \frac{k^2-11k+44}{k^2-6k+9}}{\mathcal{O}}_{k,n}$,

vii. 

$N_{k,n}=-{\displaystyle \frac{2k+8}{k^2-4k+4}}{S}_{k,n+2}+{\displaystyle \frac{2k+32}{k^2-4k+4}}{S}_{k,n+1}+{\displaystyle \frac{-k^2+4k-28}{k^2-4k+4}}{S}_{k,n}$,

viii. 

$N_{k,n}={\displaystyle \frac{k^2}{k^3+2k^2+33k+48}}{\mathcal{B}}_{k,n+2}+{\displaystyle \frac{-2k^2+33k+48}{k^3+2k^2+33k+48}}{\mathcal{B}}_{k,n+1}+{\displaystyle \frac{k^3-29k^2-48k}{k^3+2k^2+33k+48}}{\mathcal{B}}_{k,n}$.

Proof. iii.

By applying the Binet formulas in the proofs, we obtain the following result:

$$\begin{array}{c}-{\displaystyle \frac{1}{2}}{C}_{n+2}+{\displaystyle \frac{-k+5}{2}}{C}_{n+1}{+{\displaystyle \frac{3k-4}{2}}C}_n=-{\displaystyle \frac{1}{2}}\left((n+2)2^{n+2}+1\right)+{\displaystyle \frac{-k+5}{2}}\left((n+1)2^{n+1}+1\right)\hfill \\ +{\displaystyle \frac{3k-4}{2}}\left(n{2}^n+1\right)\left(1-k+{\displaystyle \frac{k+2}{2}}n\right)2^n+k\hfill \\ =\left(1-k+{\displaystyle \frac{k+2}{2}}n\right)2^n+k\hfill \\ =N_{k,n}.\hfill \end{array}$$

The other proofs follow a similar approach. $\square$

Theorem 7.

Let $k\in {\mathbb{R}}^{+}$  and  $n\in \mathbb{N}$ . The following relations are found between the Modified  $k$-Cullen sequence and other sequences:

i. 

$M_{k,n}=-{\displaystyle \frac{10}{k^2+2k+1}}{U}_{k,n+2}+{\displaystyle \frac{5k+35}{k^2+2k+1}}{U}_{k,n+1}-{\displaystyle \frac{k^2+7k+26}{k^2+2k+1}}{U}_{k,n}$,

ii 

$M_{k,n}=-{\displaystyle \frac{18}{k^2+4k+4}}{N}_{k,n+2}+{\displaystyle \frac{6k+66}{k^2+4k+4}}{N}_{k,n+1}-{\displaystyle \frac{k^2+10k+52}{k^2+4k+4}}{N}_{k,n}$,

iii. 

$M_{k,n}=-{\displaystyle \frac{5}{2}}{C}_{n+2}+{\displaystyle \frac{k+19}{2}}{C}_{n+1}-{\displaystyle \frac{3k+14}{2}}{C}_n$,

iv. 

$M_{k,n}=-{\displaystyle \frac{k+5}{3}}{E}_{n+2}+{\displaystyle \frac{5k+19}{3}}{E}_{n+1}-{\displaystyle \frac{7k+14}{3}}{E}_n$,

v. 

$M_{k,n}={\displaystyle \frac{5k-5}{3}}{H}_{n+2}+{\displaystyle \frac{-19k+19}{3}}{H}_{n+1}+{\displaystyle \frac{17k-14}{3}}{H}_n$,

vi. 

$M_{k,n}=-{\displaystyle \frac{2}{k^2-6k+9}}{\mathcal{O}}_{k,n+2}+{\displaystyle \frac{-k+9}{k^2-6k+9}}{\mathcal{O}}_{k,n+1}+{\displaystyle \frac{k^2-5k+2}{k^2-6k+9}}{\mathcal{O}}_{k,n}$,

vii. 

$M_{k,n}={\displaystyle \frac{2k-10}{k^2-4k+4}}{S}_{k,n+2}+{\displaystyle \frac{-8k+34}{k^2-4k+4}}{S}_{k,n+1}+{\displaystyle \frac{k^2+2k-20}{k^2-4k+4}}{S}_{k,n}$,

viii. 

$M_{k,n}={\displaystyle \frac{k^2+8}{k^3+2k^2+33k+48}}{\mathcal{B}}_{k,n+2}+{\displaystyle \frac{-2k^2+25k+16}{k^3+2k^2+33k+48}}{\mathcal{B}}_{k,n+1}-{\displaystyle \frac{k^3+25k^2+90k+64}{k^3+2k^2+33k+48}}{\mathcal{B}}_{k,n}$.

Proof. 

The proofs are carried out in a manner similar to that of Theorem 5. $\square$

Theorem 8.

Let  $k\in {\mathbb{R}}^{+}$  and  $n\in \mathbb{N}$. The following equations are true:

i. 

Cullen sequences are associated with the  $k$-Cullen,  $k$-Cullen–Lucas, and Modified $k$-Cullen sequences:

• $C_n={\displaystyle \frac{k^2-2k+1}{k^3+2k^2+k}}{U}_{k,n+2}+{\displaystyle \frac{-2k^2+6k-4}{k^3+2k^2+k}}{U}_{k,n+1}+{\displaystyle \frac{2k^2-2k+4}{k^3+2k^2+k}}{U}_{k,n}$,
• $C_n={\displaystyle \frac{k^2-2k+4}{k^3+4k^2+4k}}{N}_{k,n+2}+{\displaystyle \frac{-2k^2+6k-16}{k^3+4k^2+4k}}{N}_{k,n+1}+{\displaystyle \frac{2k^2+16}{k^3+4k^2+4k}}{N}_{k,n}$,
• $C_n={\displaystyle \frac{-k^2+2k-16}{k^3+2k^2-144k}}{M}_{k,n+2}+{\displaystyle \frac{2k^2-56k+64}{k^3+2k^2-144k}}{M}_{k,n+1}+{\displaystyle \frac{-12k^2+72k-64}{k^3+2k^2-144k}}{M}_{k,n}$,

ii. 

Cullen–Lucas sequences are associated with the $k$-Cullen,  $k$-Cullen–Lucas, and Modified  $k$-Cullen sequences:

• $E_n={\displaystyle \frac{k^2-4k+1}{k^3+2k^2+k}}{U}_{k,n+2}+{\displaystyle \frac{-k^2+13k-4}{k^3+2k^2+k}}{U}_{k,n+1}+{\displaystyle \frac{k^2-7k+4}{k^3+2k^2+k}}{U}_{k,n}$,
• $E_n={\displaystyle \frac{k^2-5k+4}{k^3+4k^2+4k}}{N}_{k,n+2}+{\displaystyle \frac{{-k}^2+17k-16}{k^3+4k^2+4k}}{N}_{k,n+1}+{\displaystyle \frac{k^2-8k+16}{k^3+4k^2+4k}}{N}_{k,n}$,
• $E_n=-{\displaystyle \frac{k^2+k+16}{k^3+2k^2-144k}}{M}_{k,n+2}+{\displaystyle \frac{k^2-53k+64}{k^3+2k^2-144k}}{M}_{k,n+1}+{\displaystyle \frac{-11k^2+42k-64}{k^3+2k^2-144k}}{M}_{k,n}$.

iii. 

Modified Cullen sequences are associated with the $k$-Cullen,  $k$-Cullen–Lucas, and Modified  $k$-Cullen sequences:

• $H_n=-{\displaystyle \frac{k^2+8k+1}{k^3+2k^2+k}}{U}_{k,n+2}+{\displaystyle \frac{7k^2+29k+4}{k^3+2k^2+k}}{U}_{k,n+1}-{\displaystyle \frac{7k^2+23k+4}{k^3+2k^2+k}}{U}_{k,n}$,
• $H_n=-{\displaystyle \frac{k^2+13k+4}{k^3+4k^2+4k}}{N}_{k,n+2}+{\displaystyle \frac{{7k}^2+49k+16}{k^3+4k^2+4k}}{N}_{k,n+1}-{\displaystyle \frac{7k^2+40k+16}{k^3+4k^2+4k}}{N}_{k,n}$,
• $H_n={\displaystyle \frac{k^2-17k+16}{k^3+2k^2-144k}}{M}_{k,n+2}+{\displaystyle \frac{{-7k}^2+71k-64}{k^3+2k^2-144k}}{M}_{k,n+1}+{\displaystyle \frac{17k^2-222k+64}{k^3+2k^2-144k}}{M}_{k,n}$.

Proof. 

The proofs are carried out in a manner similar to that of Theorem 6. $\square$

In the following theorem, we examine the relationships between the $k$-Cullen, $k$-Cullen–Lucas, Modified $k$-Cullen sequences, and special number sequences.

Theorem 9.

Let  $k\in {\mathbb{R}}^{+}$  and  $n\in \mathbb{N}$. The relationships of the  $k$-Cullen  $U_{k,n}$,  $k$-Cullen–Lucas  $N_{k,n}$, and Modified  $k$-Cullen  $M_{k,n}$  sequences with the Woodall sequence  $R_n$, Woodall–Lucas sequence  $D_n$, and Modified Woodall sequence  $W_n$  are as follows:

i. 

For the  $k$-Cullen sequence,

• $U_{k,n}=-2k{R}_{n+2}+{\displaystyle \frac{15k+1}{2}}{R}_{n+1}-{\displaystyle \frac{13k+1}{2}}{R}_n$,
• $U_{k,n}={-(5k+2)D}_{n+2}+(17k+7)D_{n+1}-(13k+5)D_n$,
• $U_{k,n}={\displaystyle \frac{k+1}{4}}{W}_{n+2}-{\displaystyle \frac{5k+1}{4}}{W}_{n+1}+2k{W}_n$,
• $R_n={\displaystyle \frac{1}{k^3+2k^2+k}}(-\left(k^2+6k+1\right)U_{k,n+2}+\left(6k^2+22k+4\right)U_{k,n+1}$
      $-(6k^2+18k+4)U_{k,n})$,
• $D_n={\displaystyle \frac{1}{k^3+2k^2+k}}(\left(k^2-2k-1\right)U_{k,n+2}+\left(-k^2+9k+4\right)U_{k,n+1}-(k^2+9k+4)U_{k,n})$,
• $W_n={\displaystyle \frac{1}{k^3+2k^2+k}}(\left(-3k+1\right)U_{k,n+2}+\left(k^2+9k-4\right)U_{k,n+1}+(-4k+4)U_{k,n})$.

ii. 

For the  $k$-Cullen–Lucas sequence, 

• $N_{k,n}=-{\displaystyle \frac{4k+1}{2}}{R}_{n+2}+{\displaystyle \frac{15k+5}{2}}{R}_{n+1}-{\displaystyle \frac{13k+4}{2}}{R}_n$,
• $N_{k,n}=-\left(5k+5\right)D_{n+2}+(17k+17)D_{n+1}-(13k+12)D_n$,
• $N_{k,n}={\displaystyle \frac{k}{4}}{W}_{n+2}+{\displaystyle \frac{-5k+4}{4}}{W}_{n+1}+(2k-1)W_n$,
• $R_n={\displaystyle \frac{1}{{k^3+4k}^2+4k}}(-\left(k^2+10k+4\right)N_{k,n+2}+\left({6k}^2+38k+16\right)N_{k,n+1}$
      $-({6k}^2+32k+16)N_{k,n})$,
• $D_n={\displaystyle \frac{1}{{k^3+4k}^2+4k}}(\left(k^2-3k-4\right)N_{k,n+2}+\left(-k^2+15k+16\right)N_{k,n+1}$
      $-(k^2+16k+16)N_{k,n})$
• $W_n={\displaystyle \frac{1}{{k^3+4k}^2+4k}}({\left(-4k+4\right)N}_{k,n+2}+\left(k^2+12k-16\right)N_{k,n+1}+(-4k+16)N_{k,n})$.

iii. 

For the Modified  $k$-Cullen sequence, 

• $M_{k,n}={\displaystyle \frac{4k-5}{2}}{R}_{n+2}+{\displaystyle \frac{-15k+19}{2}}{R}_{n+1}+{\displaystyle \frac{13k-14}{2}}{R}_n$,
• $M_{k,n}={(5k-13)D}_{n+2}+(-17k+43)D_{n+1}+(13k-30)D_n$,
• $M_{k,n}=-{\displaystyle \frac{k+6}{4}}{W}_{n+2}+{\displaystyle \frac{5k+26}{4}}{W}_{n+1}-(2k+5)W_n$,
• $R_n={\displaystyle \frac{1}{{k^3-8k}^2+16k}}(\left(k^2-14k+16\right)M_{k,n+2}+\left(-6k^2+58k-64\right)M_{k,n+1}$
      $+(6k^2-52k+64)M_{k,n})$,
• $D_n={\displaystyle \frac{1}{{k^3-8k}^2+16k}}(\left(-k^2-3k+16\right)M_{k,n+2}+\left(k^2+21k-64\right)M_{k,n+1}$
      $+(k^2-26k+64)M_{k,n})$,
• $W_n={\displaystyle \frac{1}{{k^3-8k}^2+16k}}(-\left(2k+16\right)M_{k,n+2}+\left(-k^2+16k+64\right)M_{k,n+1}+(4k-64)M_{k,n})$.

Proof. i.

By applying the Binet formulas in the proofs, we obtain the following result:

$-2k{R}_{n+2}+{\displaystyle \frac{15k+1}{2}}{R}_{n+1}-{\displaystyle \frac{13k+1}{2}}{R}_n$

$=-2k(\left(n+2\right)2^{n+2}-1)+{\displaystyle \frac{15k+1}{2}}(\left(n+1\right)2^{n+1}-1)-{\displaystyle \frac{13k+1}{2}}(n{2}^n-1)$

$=\left(1-k+{\displaystyle \frac{k+1}{2}}n\right)2^n+k$

$=U_{k,n}$.

The other proofs follow a similar approach. $\square$

In the following theorem, we associate the terms of the $k$-Cullen $U_{k,n}$, $k$-Cullen–Lucas $N_{k,n}$, and Modified $k$-Cullen $M_{k,n}$ sequences with matrices. In addition, we calculate the Simson formulas of these sequences.

Theorem 10.

Let  $k\in {\mathbb{R}}^{+}$  and  $n\in \mathbb{N}$  . We observe that the following equations hold true:

i. 

For the  $k$-Cullen sequence, 

1. 

$\left[\begin{array}{c}{U}_{k,n+2}\\ U_{k,n+1}\\ U_{k,n}\end{array}\right]={\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]}^n\left[\begin{array}{c}k+8\\ 3\\ 1\end{array}\right]$,

2. 

$\left[\begin{array}{c}{U}_{k,n+2}\\ U_{k,n+1}\\ U_{k,n}\end{array}\right]=\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]\left[\begin{array}{c}{U}_{k,n+1}\\ U_{k,n}\\ U_{k,n-1}\end{array}\right]$,

3. 

$\left[\begin{array}{c}{U}_{k,n}\\ U_{k,n+1}\\ U_{k,n+2}\end{array}\right]={\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 5& -8& 4\end{array}\right]}^n\left[\begin{array}{c}1\\ 3\\ k+8\end{array}\right]$

ii. 

For the  $k$-Cullen–Lucas sequence, 

1. 

$\left[\begin{array}{c}{N}_{k,n+2}\\ N_{k,n+1}\\ N_{k,n}\end{array}\right]={\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]}^n\left[\begin{array}{c}k+12\\ 4\\ 1\end{array}\right]$,

2. 

$\left[\begin{array}{c}{N}_{k,n+2}\\ N_{k,n+1}\\ N_{k,n}\end{array}\right]=\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]\left[\begin{array}{c}{N}_{k,n+1}\\ N_{k,n}\\ N_{k,n-1}\end{array}\right]$,

3. 

$\left[\begin{array}{c}{N}_{k,n}\\ N_{k,n+1}\\ N_{k,n+2}\end{array}\right]={\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 5& -8& 4\end{array}\right]}^n\left[\begin{array}{c}1\\ 4\\ k+12\end{array}\right]$.

iii. 

For the Modified  $k$-Cullen sequence, 

1. 

$\left[\begin{array}{c}{M}_{k,n+2}\\ M_{k,n+1}\\ M_{k,n}\end{array}\right]={\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]}^n\left[\begin{array}{c}12-k\\ 2\\ -1\end{array}\right]$,

2. 

$\left[\begin{array}{c}{M}_{k,n+2}\\ M_{k,n+1}\\ M_{k,n}\end{array}\right]=\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]\left[\begin{array}{c}{M}_{k,n+1}\\ M_{k,n}\\ M_{k,n-1}\end{array}\right]$,

3. 

$\left[\begin{array}{c}{M}_{k,n}\\ M_{k,n+1}\\ M_{k,n+2}\end{array}\right]={\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 5& -8& 4\end{array}\right]}^n\left[\begin{array}{c}-1\\ 2\\ 12-k\end{array}\right]$.

Proof. i. 1.

We will prove the statement by induction on $n$. For $n=1$, the equality holds. We assume the equality is true for $n-1$. We obtain

$$\begin{array}{c}{\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]}^n\left[\begin{array}{c}k+12\\ 4\\ 1\end{array}\right]=\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]{\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]}^{n-1}\left[\begin{array}{c}k+8\\ 3\\ 1\end{array}\right]\\ =\left[\begin{array}{ccc}5& -8& 4\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]\left[\begin{array}{c}{U}_{k,n+1}\\ U_{k,n}\\ U_{k,n-1}\end{array}\right]\\ =\left[\begin{array}{c}{U}_{k,n+2}\\ U_{k,n+1}\\ U_{k,n}.\end{array}\right]\end{array}$$

It follows from the last equation that the equality holds for $n$.

The other proofs follow a similar approach. $\square$

Theorem 11.

(Simson Formulas) Let  $k\in {\mathbb{R}}^{+}$  and  $t\in \mathbb{N}$. The following equations are satisfied:

i. 

$det\left[\begin{array}{ccc}{U}_{k,t+2}& U_{k,t+1}& U_{k,t}\\ U_{k,t+1}& U_{k,t}& U_{k,t-1}\\ U_{k,t}& U_{k,t-1}& U_{k,t-2}\end{array}\right]=-4^{t-2}k{(k+1)}^2$,

ii. 

$det\left[\begin{array}{ccc}{N}_{k,t+2}& N_{k,t+1}& N_{k,t}\\ N_{k,t+1}& N_{k,t}& N_{k,t-1}\\ N_{k,t}& N_{k,t-1}& N_{k,t-2}\end{array}\right]=-4^{t-2}k{(k+2)}^2$,

iii. 

$det\left[\begin{array}{ccc}{M}_{k,t+2}& M_{k,t+1}& M_{k,t}\\ M_{k,t+1}& M_{k,t}& M_{k,t-1}\\ M_{k,t}& M_{k,t-1}& M_{k,t-2}\end{array}\right]=4^{t-2}k{(k-4)}^2$.

Proof. 

The proofs are shown by the induction method using the definition and determinant properties. $\square$

4. Graphical Review: Self-Similarity Behavior of Generator Functions

In this section, we conduct a comprehensive graphical investigation of the $k$-Cullen, $k$-Cullen–Lucas, and Modified $k$-Cullen sequences by utilizing their generating functions under varying Fibonacci-based parameters. The aim is to visualize and interpret the inherent self-similarity structures embedded in these sequences. Starting with the direct plots of the generating functions, we progressively extend the analysis by applying exponential transformations to amplify scaling behaviors, followed by logarithmic projections to reveal growth tendencies in a compressed scale. Finally, we incorporate the indefinite integrals of the generating functions to further explore the analytical geometry of the sequences. This multi-layered graphical approach allows for the detection of self-similar patterns, including mirror symmetry and convergence behaviors, particularly highlighting the distinct fractal-like symmetry exhibited by the Modified Cullen sequence as the Fibonacci parameter increases. The resulting graphical framework provides a deeper insight into the complex dynamics of these integer sequences and establishes a visual foundation for understanding their recursive and scale-invariant characteristics.

Also, it is aimed to find suitable application areas in other sub-branches of mathematics by performing graphical analyses with Fibonacci numbers given as the variable $k$ belonging to the number sequences.

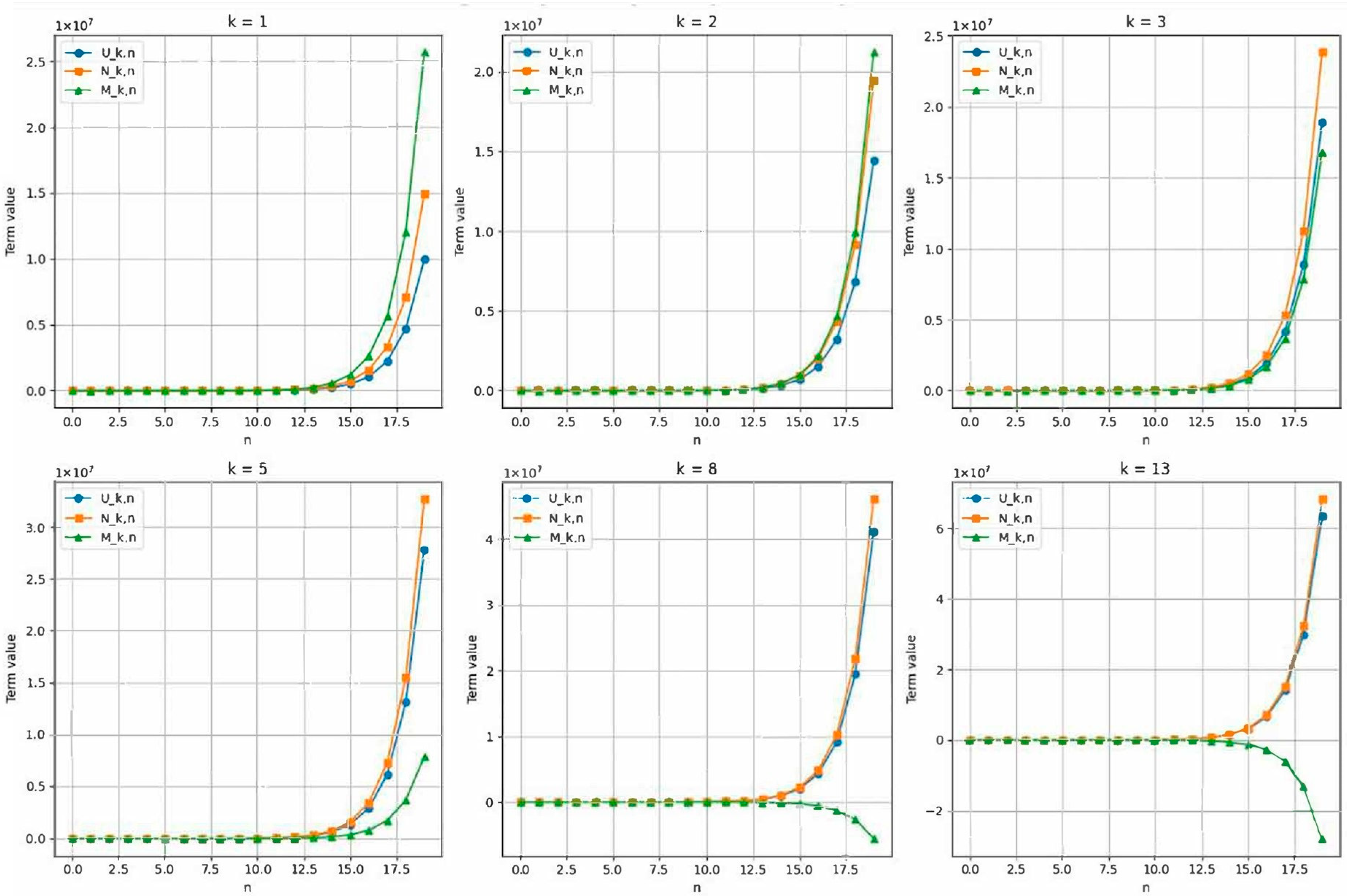
4.1. Parametric Analysis: k = Fibonacci Numbers

In the graphical analysis (Figure 1), the following Fibonacci number values were taken as parameters: $k\in \left\{\mathrm{1,2},\mathrm{3,5},\mathrm{8,13}\right\}$. Using these numbers, the first 20 terms of all three series were calculated, and the resulting series were visualized with $n$ on the horizontal axis and the term value on the vertical axis. Fibonacci numbers were chosen as the specific values for k because the Fibonacci sequence naturally models proportional and self-similar growth patterns frequently observed in nature. Its intrinsic connection to the golden ratio provides a mathematical foundation that aligns well with the analysis of scale-invariant and fractal-like behaviors in the graphical representation of the sequences. Both growth trends and comparative behavior between the sequences were examined.

The generating functions for $k$-Cullen $U_{k,n}$, $k$-Cullen–Lucas$N_{k,n}$, and Modified $k$-Cullen $M_{k,n}$ sequences are given, respectively, as follows:

$$u\left(t\right)={\displaystyle \frac{1-2t+(k+1)t^2}{{-4t}^3+8t^2-5t+1}},n\left(t\right)={\displaystyle \frac{1-t+k{t}^2}{{-4t}^3+8t^2-5t+1}},m(t)={\displaystyle \frac{-1+2t+(7-k)t^2}{{-4t}^3+8t^2-5t+1}}.$$

The coefficient sequences derived from the Taylor expansions of these generating functions, evaluated for various Fibonacci values of the parameter $k$, reveal distinct growth patterns. Then we can make the following observations in order:

$k$-Cullen Sequence $U_{k,n}$:

As the value of $k$ increases, the terms of the sequence grow more rapidly. The presence of the term $(k+1)t^2$ in the numerator directly accelerates this growth. For a large $n$, the sequence exhibits behavior that is influenced predominantly by the degree and roots of the denominator polynomial.

$k$-Cullen–Lucas Sequence $N_{k,n}$:

This sequence grows in a similarly structured fashion but at a slightly slower and more stable rate. The numerator includes the term $k{t}^2$, but with a smaller linear coefficient, contributing to a smoother progression.

Modified $k$-Cullen Sequence $M_{k,n}$:

The behavior of this sequence is more volatile, due to the term $(7-k)t^2$, which becomes negative for larger $k$ values. Initially, the sequence may diverge from the others, but as n increases, all three sequences exhibit convergence in their growth trends due to the shared characteristic denominator.

Summary of Growth Trends:

All three sequences demonstrate faster growth as $k$ increases $(\mathrm{e}.\mathrm{g}.,k=\mathrm{8,13,21,34,55,89})$, and particularly when $k$ is a Fibonacci number, the growth follows a structured and recursive pattern.

Although the Modified $k$-Cullen sequence deviates in early terms, it converges asymptotically towards the others, indicating a dominant influence of the denominator polynomial for large $n$.

In this study, we examine three distinct number sequences, namely the classical $k$-Cullen $U_{k,n}$, $k$-Cullen–Lucas $N_{k,}$, and Modified $k$-Cullen $M_{k,n}$ via their respective generating functions, in which the parameter $k$ is assigned values from the Fibonacci sequence. Our analysis reveals that, beginning with $k=F_7=13$, the behavior of the Cullen and Cullen–Lucas sequences converges graphically, exhibiting nearly identical patterns. In contrast, the Modified $k$-Cullen sequence, while retaining equivalent magnitude, begins to diverge in an inversely self-similar manner. This indicates a structural self-similarity among these sequences, where symmetry and inversion coexist within the same generative framework.

Self-similarity plays a critical role in the mathematical interpretation of complex systems, particularly when exponential generating functions are involved. It provides a means to observe infinite complexity within finite bounds, facilitating the analysis of size, scale, and recursive pattern formation. This property is not only foundational in theoretical studies but has also been proven to be invaluable in practical domains.

In financial time series analysis, for instance, the presence of self-similar structures enables the modeling of market dynamics and the identification of repeating patterns across multiple temporal scales. Such insights are instrumental in risk assessment and the development of predictive strategies (details, see [42,43,44]). Similarly, in the field of medical imaging, fractal analysis based on self-similarity has been employed to detect anomalies and pathological features that may assist in diagnosis and personalized treatment planning [45].

Ultimately, the self-similarity observed in our constructed sequences underscores their broader applicability. It simplifies the modeling of complex phenomena, enhances predictive modeling, and leverages the recursive and scalable properties of self-similar systems to foster efficient design and analysis across disciplines.

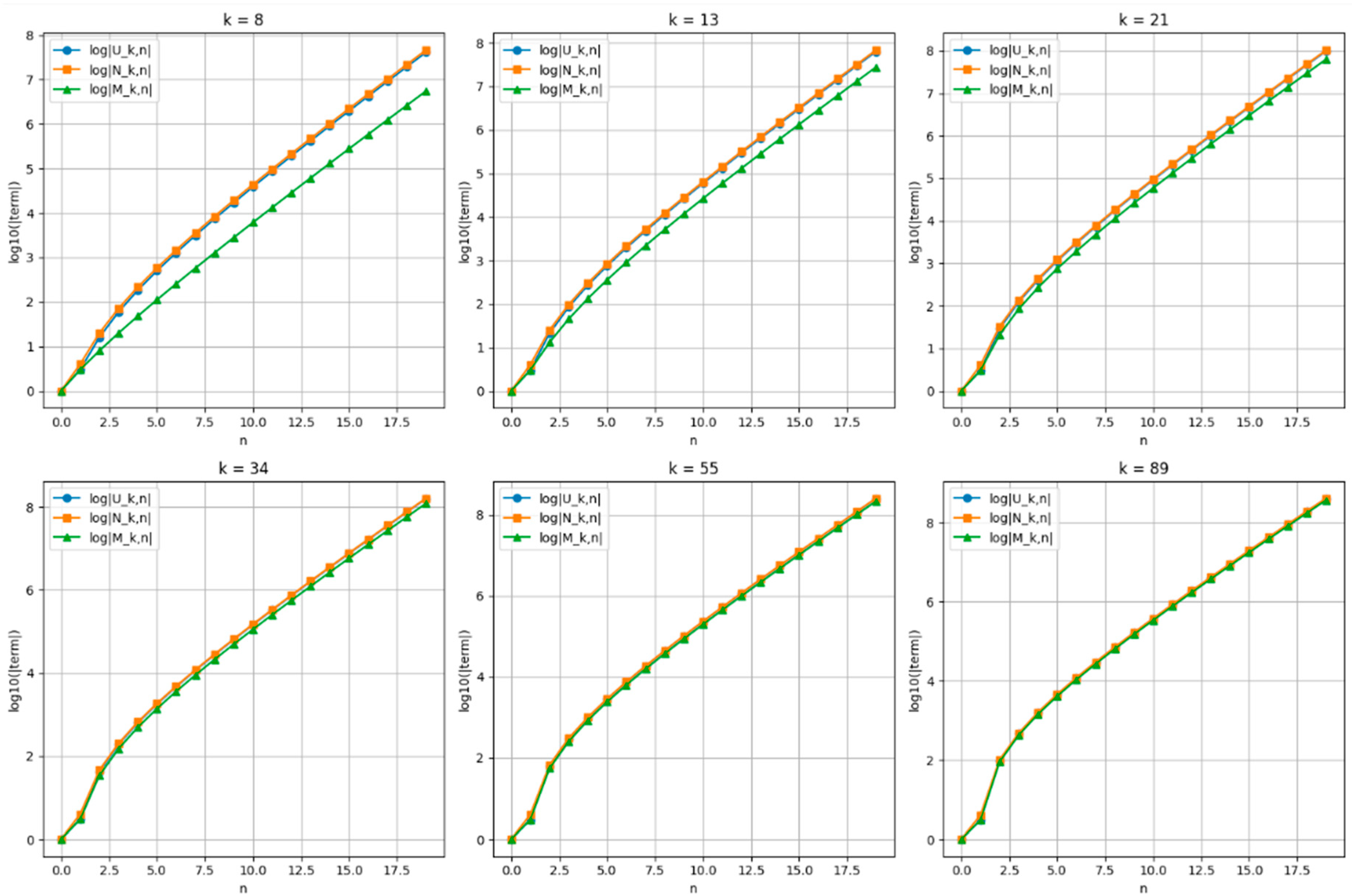
4.2. Behavior of Series on Logarithmic Scale

In this section, the growth trends are observed more clearly by drawing graphs of the $\mathrm{l}\mathrm{o}\mathrm{g}(U_{k,n})$, $\mathrm{l}\mathrm{o}\mathrm{g}(N_{k,n})$, and $\mathrm{l}\mathrm{o}\mathrm{g}(M_{k,n})$ terms for all three sequences (Figure 2). The logarithmic transformation is especially helpful in comparing the growth in higher terms and determining possible asymptotic trends.

In the logarithmic graphs for ${\log }_{10}\left|U_{k,n}\right|$, each sequence’s growth is visualized on a compressive scale that highlights relative differences. Key observations include the following:

• The Modified $k$-Cullen sequence $M_{k,n}$, while initially lower in magnitude for large $k$, eventually grows and aligns closely with the other sequences.
• This indicates that although the initial behavior depends strongly on the structure of the numerator, the long-term growth is governed more significantly by the common denominator.
• The logarithmic representation confirms that all sequences are of comparable order in asymptotic growth, despite differences in early terms.

Potential Applications:

(i)

Coding Theory and Data Transmission:

Generating functions provide a powerful tool for constructing recurrence-based sequences with predictable growth.

Such sequences may be applied in the design of error-correcting codes and data compression schemes, particularly where redundancy or pattern structure is advantageous.

(ii)

Signal Processing and Time Series Modeling:

The structure of the sequences, especially when visualized on a logarithmic scale, reflects properties similar to those found in signal magnitudes and energy distributions.

Sequences with initial divergence followed by convergence may model transient behavior in systems or act as basis functions in filtering and prediction models.

(iii)

Cryptography and Pseudorandomness:

The dependence on a tunable parameter $k$, especially when drawn from structured sets like Fibonacci numbers, allows for the design of key-dependent recurrence systems.

Modular applications of these sequences, along with their generating function properties, can inspire novel cryptographic primitives.

(iv)

Mathematical Modeling and Growth Dynamics:

The observed convergence in the logarithmic domain suggests applicability to biological models, financial systems, or algorithmic complexity analysis, where different systems eventually align in behavior.

The connection between the characteristic roots and the sequences’ asymptotic behavior provides insights into stability analysis in both discrete systems and continuous models.

In summary, the graphical and analytical investigations of the $U_{k,n}$, $N_{k,n}$, and$M_{k,n}$ sequences both in standard and logarithmic scales reveal that while the numerator structure controls the short-term dynamics, the shared denominator structure ultimately governs long-term behavior. These findings suggest that the designed sequences are not only theoretically rich but also practically versatile for applications across multiple domains of science and engineering.

In addition to the standard graphical representations, we examined the generating functions of the $k$-Cullen $U_{k,n}$, $k$-Cullen–Lucas $N_{k,n}$, and Modified $k$-Cullen $M_{k,n}$ sequences on a logarithmic scale. As the parameter k, chosen from Fibonacci numbers, increases, the resulting curves for all three sequences gradually converge and exhibit striking visual similarity. Despite originating from distinct recurrence relations and possessing different analytical forms, the logarithmic representations reveal a unifying growth behavior at larger values of $k$, suggesting a form of asymptotic equivalence in their exponential dynamics.

However, unlike the graphical observations in linear scale where clear self-similarity patterns were detectable, the logarithmic plots do not yield consistent or measurable self-similarity indices. This suggests that while exponential scaling dominates their global behavior, the finer recursive structures that support self-similarity become less distinguishable in logarithmic space. The fractal-like traits seen in the linear plots are smoothed out due to the logarithmic compression, thereby obscuring local oscillatory characteristics.

From a real-world perspective, the convergence of such sequence behaviors under logarithmic scaling can have several implications:

• Computational Complexity Estimation: If different generating systems yield similar logarithmic growth, this can inform algorithmic optimization by identifying which processes are equivalent in time or space complexity for large-scale input values [46].
• Model Unification in Physics or Biology: Many biological and physical systems grow exponentially but are interpreted via log transformations (e.g., in population dynamics, signal processing, or allometric scaling). Observing convergence among structurally different models can aid in developing unified models for predicting long-term behavior [47].
• Robustness in Signal Processing: When different signal representations converge in log scales, it points to redundancy or robustness in encoding, suggesting that slight variations in sequence construction may not impact large-scale information patterns, which is useful in noise-resistant communication systems [48].

These observations reinforce the idea that structural differences in mathematical sequences can diminish under exponential transformation, while still preserving valuable insights at the macro level. Although precise self-similarity metrics are not extractable from logarithmic plots, the convergence behavior itself serves as a heuristic for identifying long-term stability, redundancy, or equivalence across diverse systems.

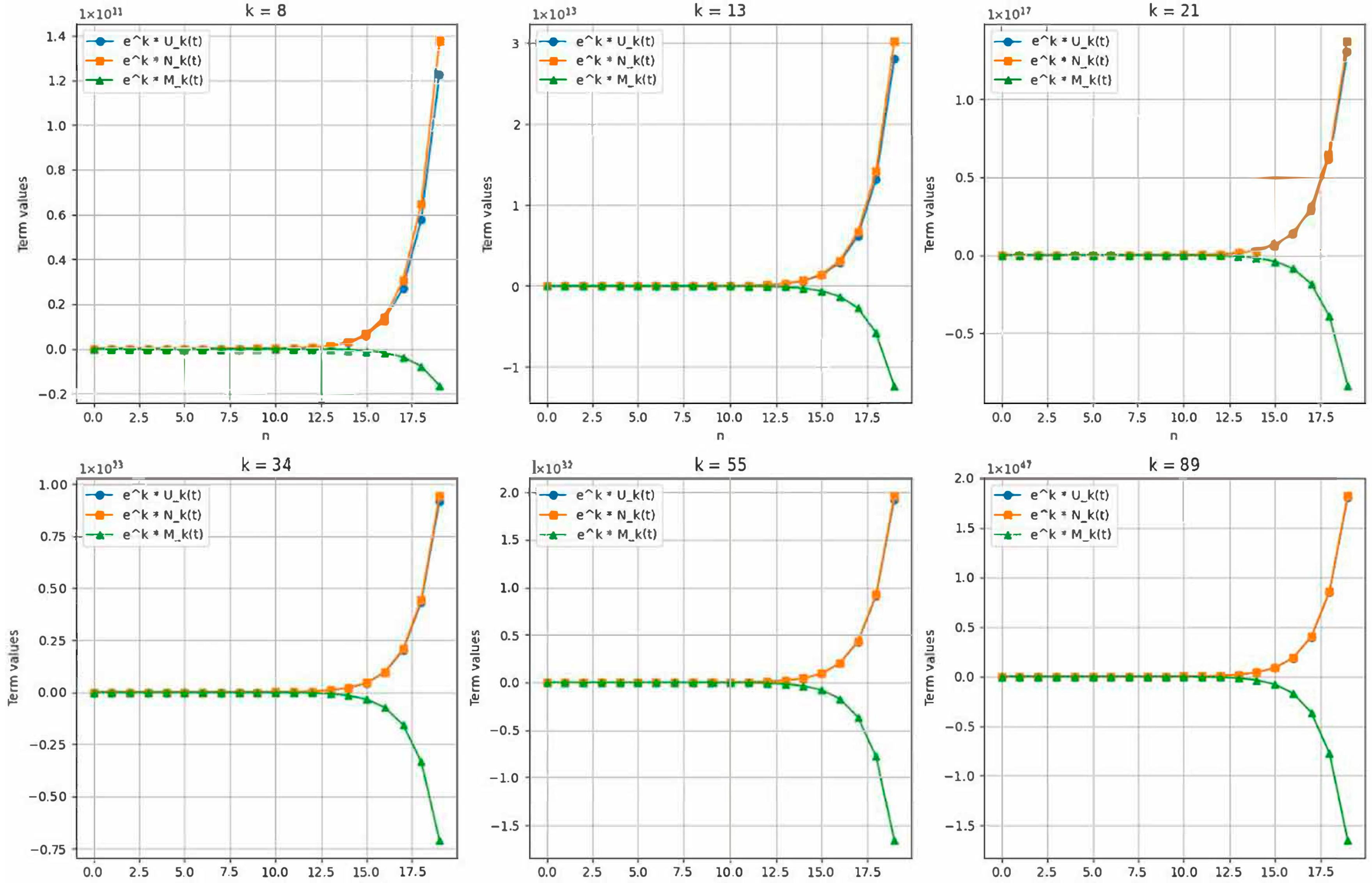
4.3. Behavior of Sequences on Exponential Scale

In this section, we explore the combined effect of exponential functions with the generating functions of the $k$-Cullen-type sequences, namely the $k$-Cullen sequence $U_{k,n}$, the $k$-Cullen–Lucas sequence $N_{k,n}$, and the Modified $k$-Cullen sequence $M_{k,n}$. By graphing the expressions $e^{k}G(t)$, where $G(t)$ denotes the respective generating function of each sequence, we uncover deeper structural properties, especially those related to self-similarity and scale invariance (Figure 3).

• Mathematical Observation

Let $GU(t),GN(t),GM(t)$ denote the generating functions of $U_{k,n},N_{k,n}$, and $M_{k,n}$ respectively. Then we consider the modified functions:

$$F_U\left(t\right)=e^k{G}_U\left(t\right),F_N\left(t\right)=e^k{G}_N\left(t\right),F_M\left(t\right)=e^k{G}_M\left(t\right)$$

These expressions are visualized for varying Fibonacci values of, $e.g.,k=\mathrm{8,13,21},\dots )$, and plotted over their respective domains. The graphical behavior reveals the following:

• Similarity: The sequences $U_{k,n}$ and $N_{k,n}$ show parallel curvature and converging growth patterns under exponential scaling.
• Mirror Symmetry: The Modified $k$-Cullen $M_{k,n}$ sequence, in contrast, demonstrates a reflected curve, suggesting a form of negative-directional self-similarity in opposition to the other two sequences.
• Interpretation in Terms of Self-Similarity

The mirrored behavior of $M_{k,n}$, compared to $U_{k,n}$, and $N_{k,n}$ under exponential transformation provides a compelling case of negative self-similarity. This can be interpreted as a structural invariant that persists under exponential scaling but in an opposing direction:

“Self-similarity is the property of an object or process where parts of it resemble the whole. Here, modified self-similarity emerges in the altered growth dynamics of $M_{k,n}$, relative to the other Cullen-type sequences”.

• Applications Across Domains
  This observed self-similarity has wide-reaching applications:
  • Mathematics and Complexity: As in fractal theory, self-similarity over finite bounds implies infinite complexity. This helps in understanding recursive behaviors in number theory and generating recursive or fractal structures algorithmically.
  • Finance: Time series data, such as stock prices or economic indices, exhibit patterns that repeat at various scales. The self-similarity in our sequences could be utilized in predictive modeling, enhancing strategic risk assessments and long-term financial planning.
  • Medical Imaging: Fractal analysis of diagnostic images (MRIs and CT scans) relies on identifying repeated patterns. Self-similar structures, as indicated by our model, could support early anomaly detection and classification of pathological features.
  • Further Remarks

The use of Fibonacci values for $k$ enhances the universality of these patterns, as Fibonacci sequences themselves are inherently tied to natural growth processes and recursive definitions. As a result, the interaction between Fibonacci-based parameters and generating functions not only yields aesthetically pleasing mathematical patterns but also enriches the modeling capabilities across diverse scientific disciplines.

In conclusion, analyzing $e^{k}G(t)$ offers a bridge between discrete sequence generation and continuous scaling behavior, and self-similarity acts as the unifying theme that provides insight into both mathematical structure and real-world phenomena.

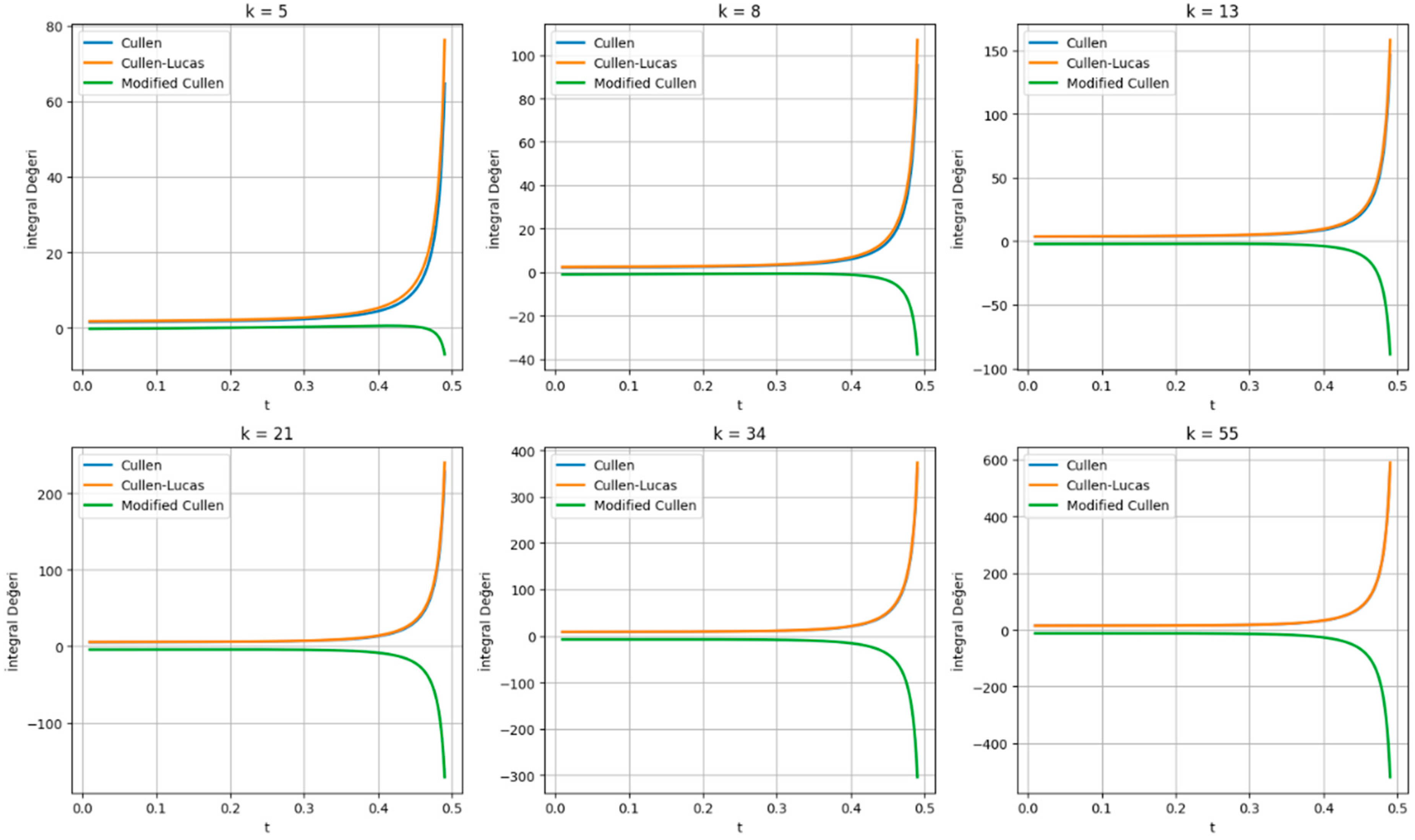
4.4. Analysis of Self-Similarity Through Integration of Generating Functions

In this section, we deepen our investigation of the self-similar structures observed in the Cullen, Cullen–Lucas, and Modified Cullen sequences by integrating their respective generating functions. By analyzing the indefinite integrals of these generating functions for various Fibonacci-indexed values of the parameter $k$, we aim to uncover the underlying mathematical symmetries and growth patterns across the sequences (Figure 4).

The generating functions previously defined for each sequence are integrated with respect to the variable $t$. The symbolic indefinite integrals yield logarithmic and rational terms, highlighting asymptotic behavior as $t\to 0.5$ and $t\to 1$.

We generalize these results to symbolic expressions in $k$ as follows:

• $k$-Cullen:

  $$\begin{array}{c}\int u_k\left(t\right)dt=\int {\displaystyle \frac{1-2t+(k+1)t^2}{{-4t}^3+8t^2-5t+1}}dt\hfill \\ ={\displaystyle \frac{-1-k}{4(1+2(-1+t))}}+{\displaystyle \frac{-1+3k}{4}}\log \left(1+2\left(-1+t\right)\right)-k\log (-1+t)\hfill \end{array}$$
• $k$-Cullen–Lucas:

  $$\begin{array}{c}\int n_k\left(t\right)dt=\int {\displaystyle \frac{1-t+k{t}^2}{{-4t}^3+8t^2-5t+1}}dt\hfill \\ ={\displaystyle \frac{2+k}{4(1-2t)}}-k\log \left(-1+t\right)+{\displaystyle \frac{3k}{4}}\log (-1+2t)\hfill \end{array}$$
• Modified $k$-Cullen:

  $$\begin{array}{c}\int m_k\left(t\right)dt=\int {\displaystyle \frac{-1+2t+(7-k)t^2}{{-4t}^3+8t^2-5t+1}}dt\hfill \\ ={\displaystyle \frac{-4+k}{4(-1+2t)}}+(k-3)\log \left(-1+t\right)+{\displaystyle \frac{8-3k}{4}}\log (-1+2t)\hfill \end{array}$$

These expressions will serve as the basis for subsequent visual and structural analysis.

To examine the behavior of the integrated generating functions, we plotted the corresponding expressions for several Fibonacci-indexed values of $k:k=5,8,13,21,34,55$. The visualization reveals key findings:

• As $k$ increases, the $k$-Cullen and $k$-Cullen–Lucas sequences converge towards nearly identical curves, reinforcing their shared structural traits.
• In contrast, the Modified $k$-Cullen sequence exhibits a perfectly symmetric trend relative to the other two, representing a form of negative-direction self-similarity.

This emergent symmetry is not merely aesthetic but represents a deep mathematical property: self-similarity under sign inversion. As $k$ grows, the curves scale proportionally, maintaining their shape while diverging in opposite directions, which is particularly evident in the Modified Cullen sequence.

The combined effect of rational and logarithmic terms in the integrals yields piecewise smooth functions with asymptotic edges. Such behavior closely mimics the characteristics of fractal systems. This offers valuable insight into how finite systems can exhibit infinite complexity through self-replication at different scales.

Applications of this analysis include the following:

• Fractal Dimension Analysis: The smooth yet singular structure of these curves can be used in estimating local fractal dimensions in data.
• Financial Modeling: The similarity between Modified Cullen and inverse versions of Cullen–Lucas curves may model mirrored price behaviors in bullish vs. bearish market conditions.
• Medical Imaging: Fractal and symmetric analysis of these expressions may aid in identifying repeated structures in biological tissues.

In summary, in this study, the generating functions of the $k$-Cullen, $k$-Cullen–Lucas, and Modified $k$-Cullen sequences were examined by assigning Fibonacci numbers to the parameter k. On linear-scale plots, $U_{k,n}$ and $N_{k,n}$ began to show nearly identical behavior after a certain k, while $M_{k,n}$ exhibited a mirrored but self-similar structure. On logarithmic-scale graphs, all three sequences appeared to converge in shape as $k$ increased, despite their differing recursions. This graphical behavior suggests a deeper structural connection and emphasizes how scale impacts the perception of self-similarity and growth dynamics.

Although some conclusions in this study are based on graphical observations, the underlying behavior is consistent with the known asymptotic properties of Fibonacci-based recurrence structures. Where applicable, additional justification and clarification have now been provided to support the claims, particularly regarding the convergence and self-similar patterns observed in the generated sequences [49].

4.5. Discussion of Self-Similarity Results

To further investigate the self-similarity behavior observed in generating functions of Cullen, Cullen Lucas and Modified Cullen sequences, we employed a quantitative two-scale fractal dimension analysis. Although the Cullen and Cullen–Lucas generating function exhibit similar visual progression in standard and log–log scales, the Modified Cullen function initially appeared to diverge from this behavior. To resolve this discrepancy and obtain meaningful scaling information, we applied an absolute value transformation to all three generating functions before performing the two-scale fractal dimension analysis.

Using two different box sizes, the estimated two-scale fractal dimensions were found to be approximately

$${\mathit{D}}_{{\mathit{U}}_{\mathit{k}}}\approx 1.01$$

$${\mathit{D}}_{{\mathit{N}}_{\mathit{k}}}\approx 1.00$$

$${\mathit{D}}_{{\mathit{M}}_{\mathit{k}}}\approx 1.03$$

This indicates a high degree of self-similarity of all three sequences. Notably, the Modified Cullen sequence, though initially visually inverted, shares a quantitatively similar scaling behavior with the other two sequences when its absolute values are considered.

In Figure 5, log–log plots show the absolute values of the generating functions for Cullen, Cullen–Lucas, and Modified Cullen sequences with $\mathit{k}=13.$ The use of absolute values allows the Modified Cullen function to be analyzed alongside the others in a two-scale fractal dimension framework. All three graphs show power-law-like behavior, indicating structural suitability for fractal analysis [50]. All three plots exhibit power-law-like behavior, meaning the output scales have inputs in a consistent ratio. This is a key indicator of self-similarity, making fractal dimension analysis meaningful.

5. Conclusions

The comparative analysis of the $k$-Cullen, $k$-Cullen–Lucas, and Modified $k$-Cullen sequences through their generating functions and integrals reveals rich self-similar patterns that scale with Fibonacci-indexed parameters. The Modified Cullen sequence, in particular, demonstrates near-perfect symmetrical behavior relative to the other two sequences, indicating a form of mathematical reflection or inverse self-similarity.

This property has broad implications across scientific domains. In finance, self-similar patterns can support multi-scale forecasting and risk modeling. In medical imaging, fractal characteristics derived from these sequences may aid in identifying repeating patterns that correlate with pathological anomalies. The ability to derive such behaviors directly from generating function analysis underscores the utility of integrative mathematical techniques in revealing deep, recursive structures within seemingly linear systems.

Future directions may include extending these results to multidimensional generalizations, exploring entropy-based complexity analysis, or applying these constructs to encryption systems and symbolic dynamics.

Finally, when the article is examined, research can be conducted on topics such as applications to multidimensional difference equations [51], linear thermoelasticity [52], and the elasticity of porous micropolar bodies [53].