Quasi-Mittag-Leffler Projective Synchronization of Delayed Chaotic Fractional Order Neural Network with Mismatched Parameters
Abstract
1. Introduction
- (1)
- Incorporation of time delays and mismatched parameters between the driven and response systems, enhancing generality;
- (2)
- Design of both static and adaptive controllers to achieve synchronization in the DFONNs;
- (3)
- Estimation of synchronization error bounds and explicit characterization of the convergence rate.
2. Preliminaries and Problem Formulation
2.1. Preliminaries of Fractional Order Calculus
2.2. System Model and Problem Formulation
3. Main Results
3.1. Static Controllers
3.2. Adaptive Controllers
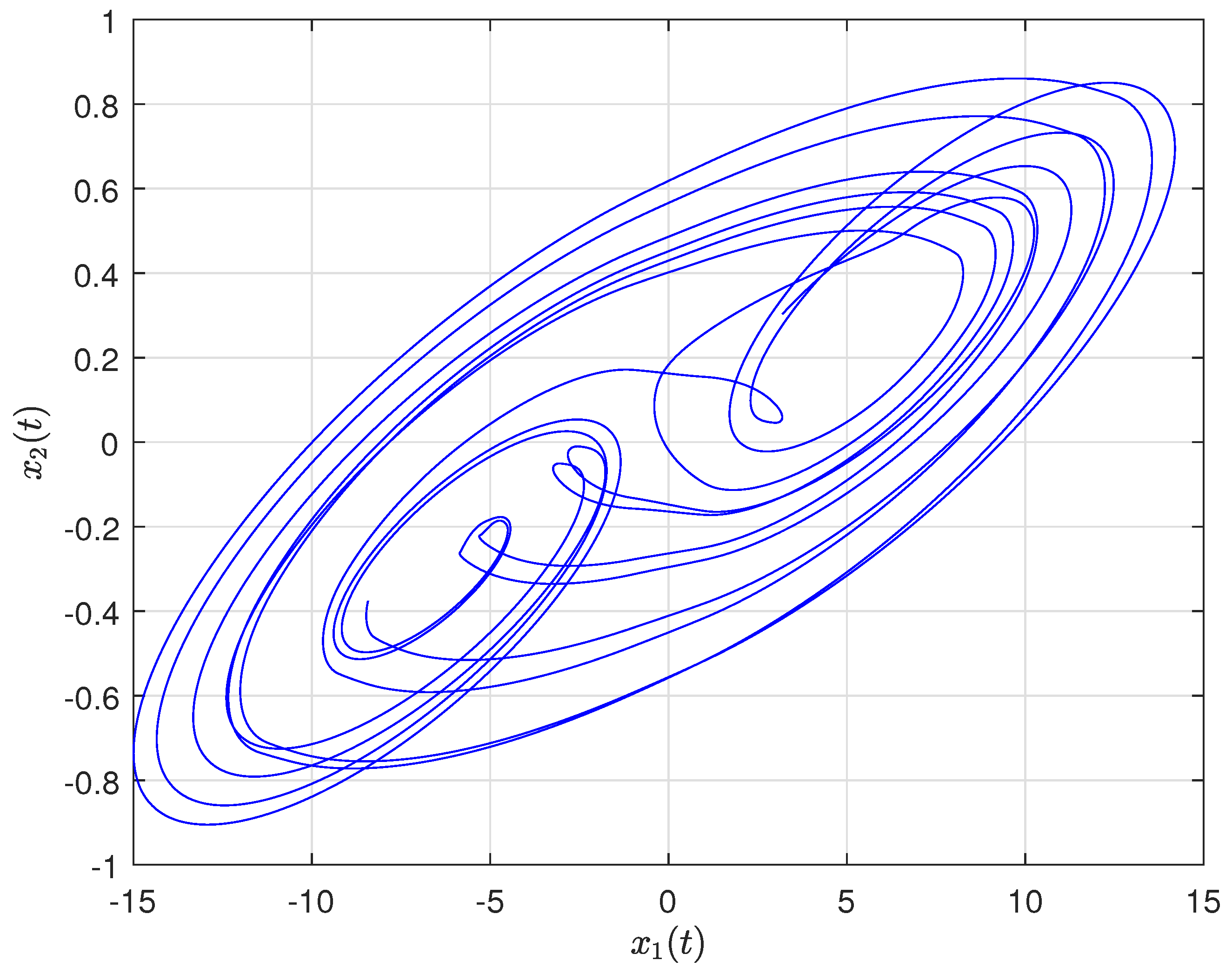
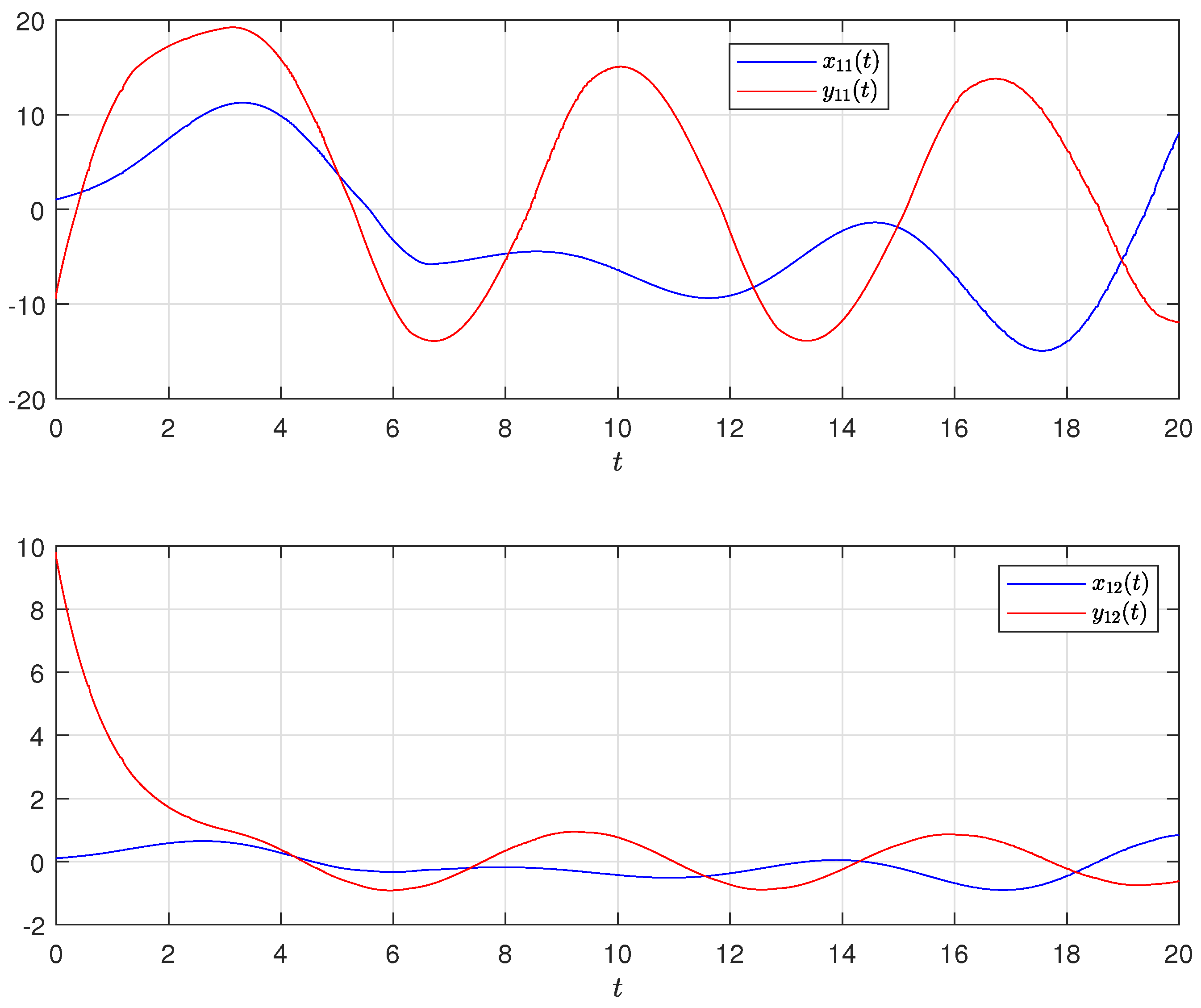
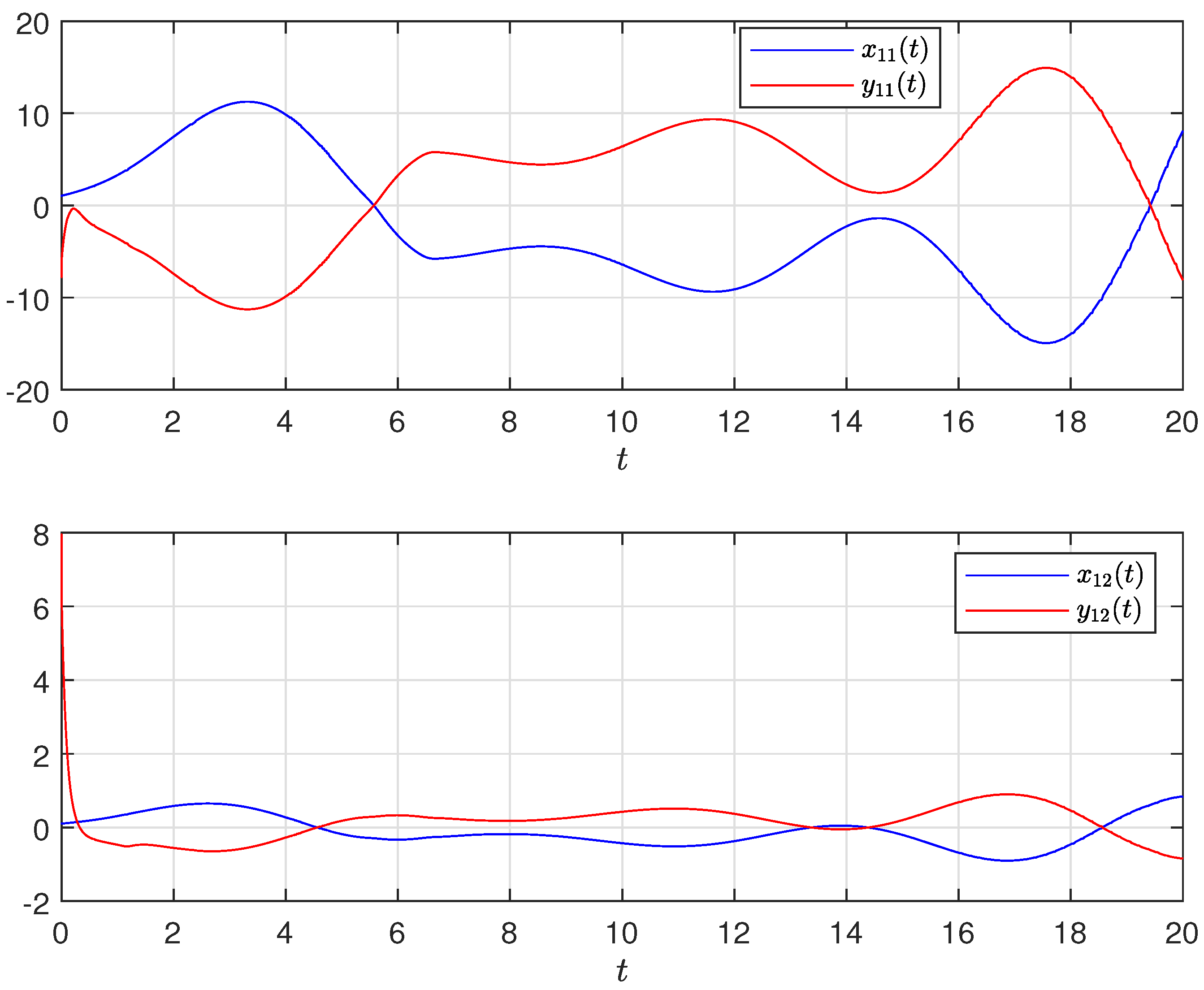
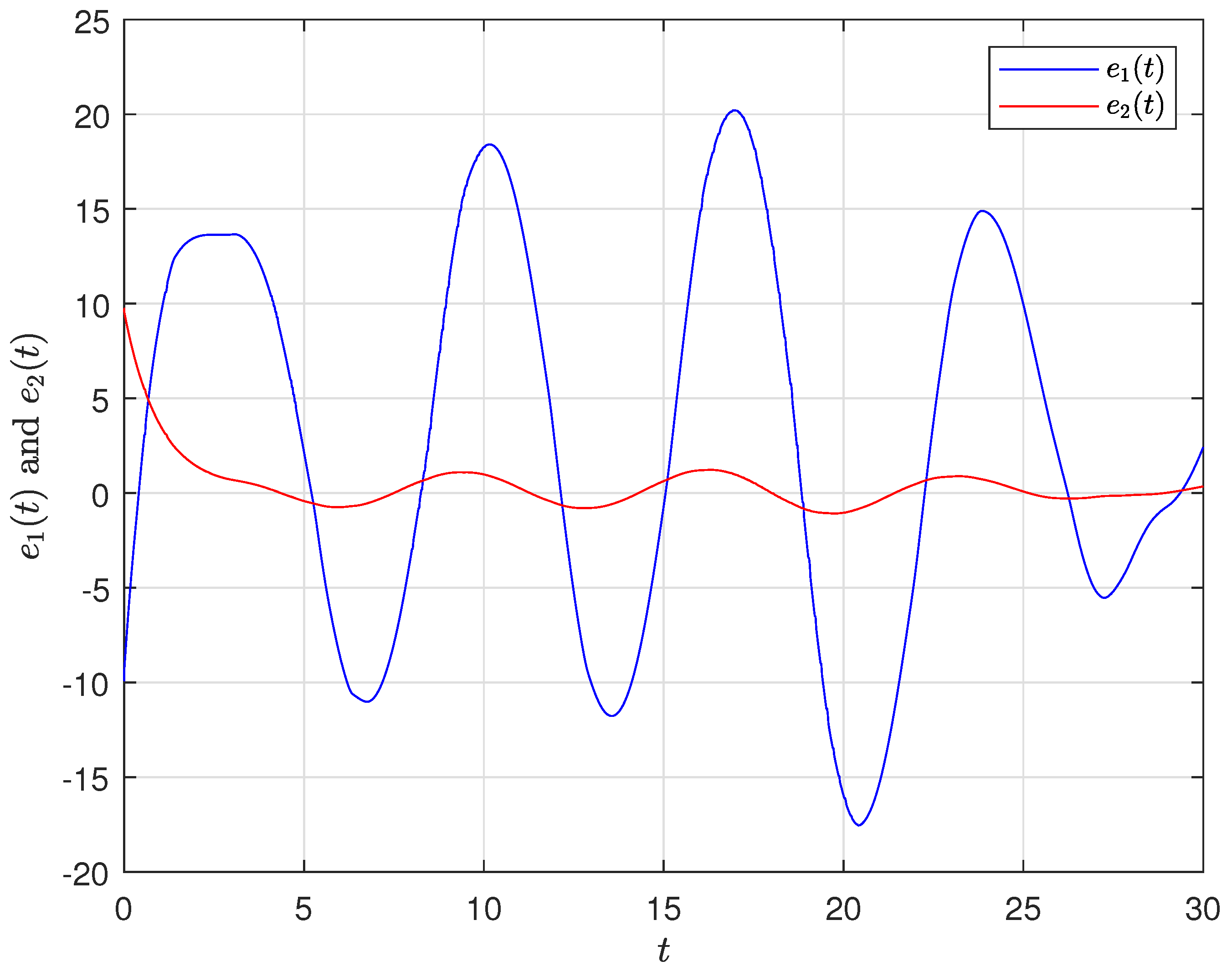
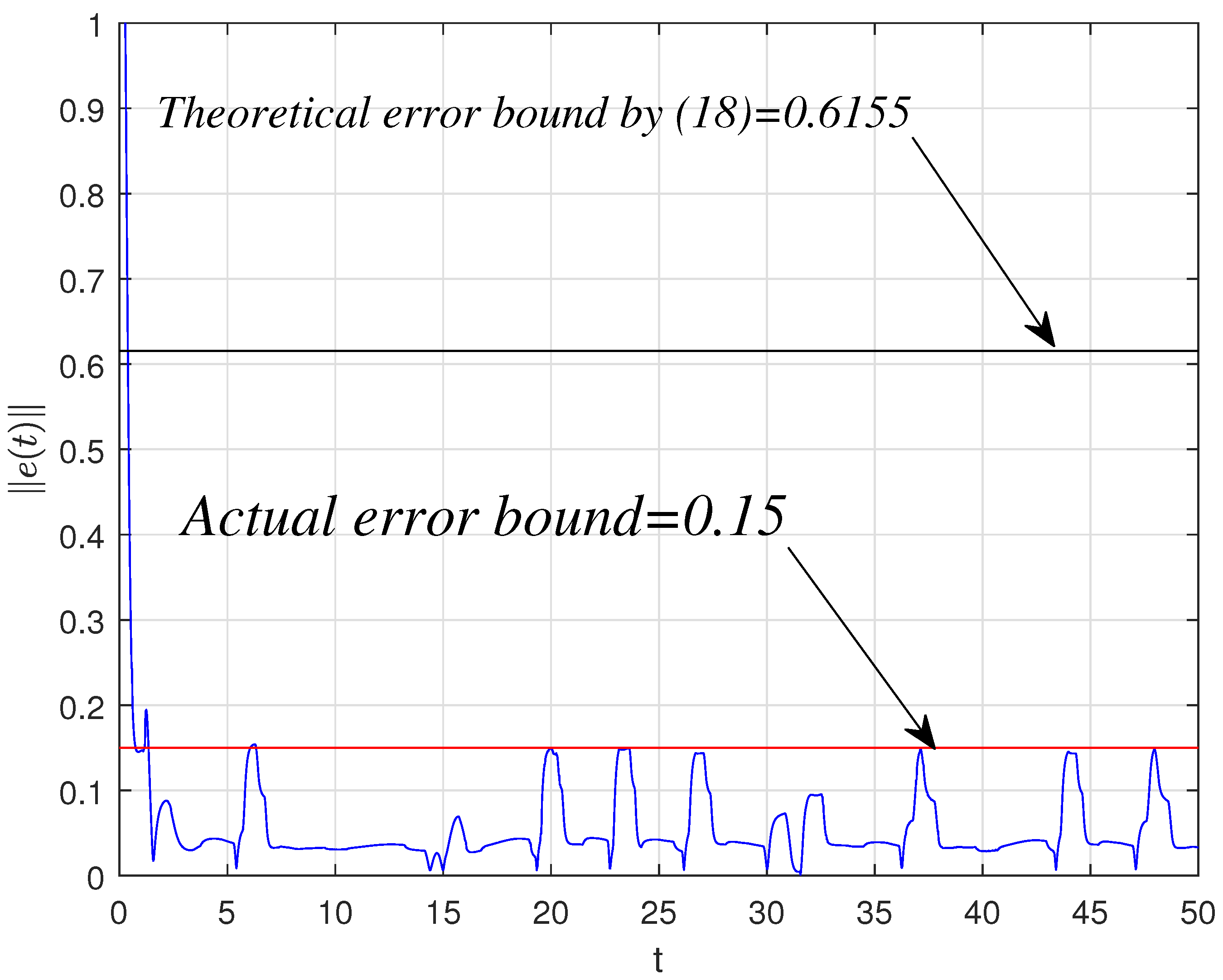
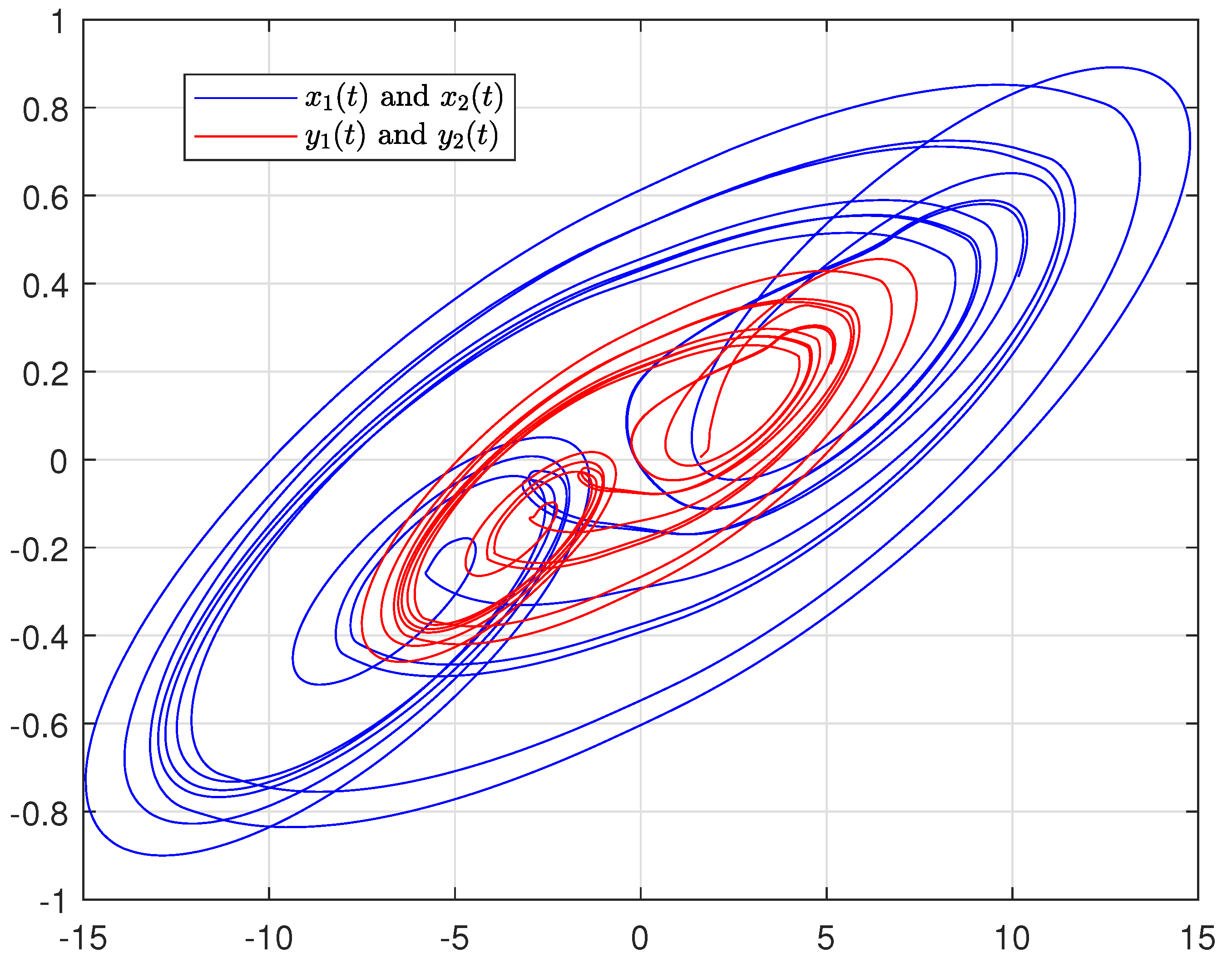
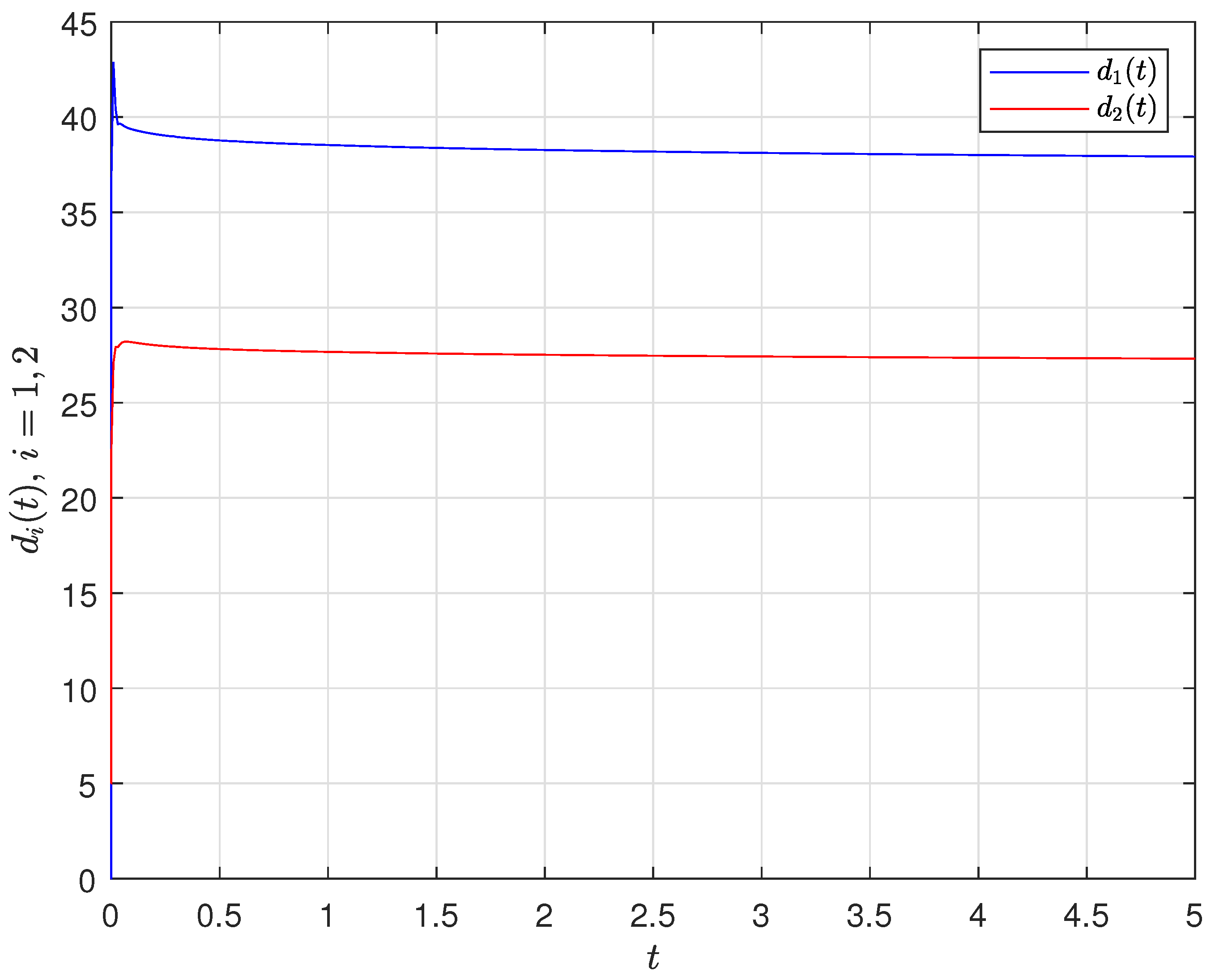
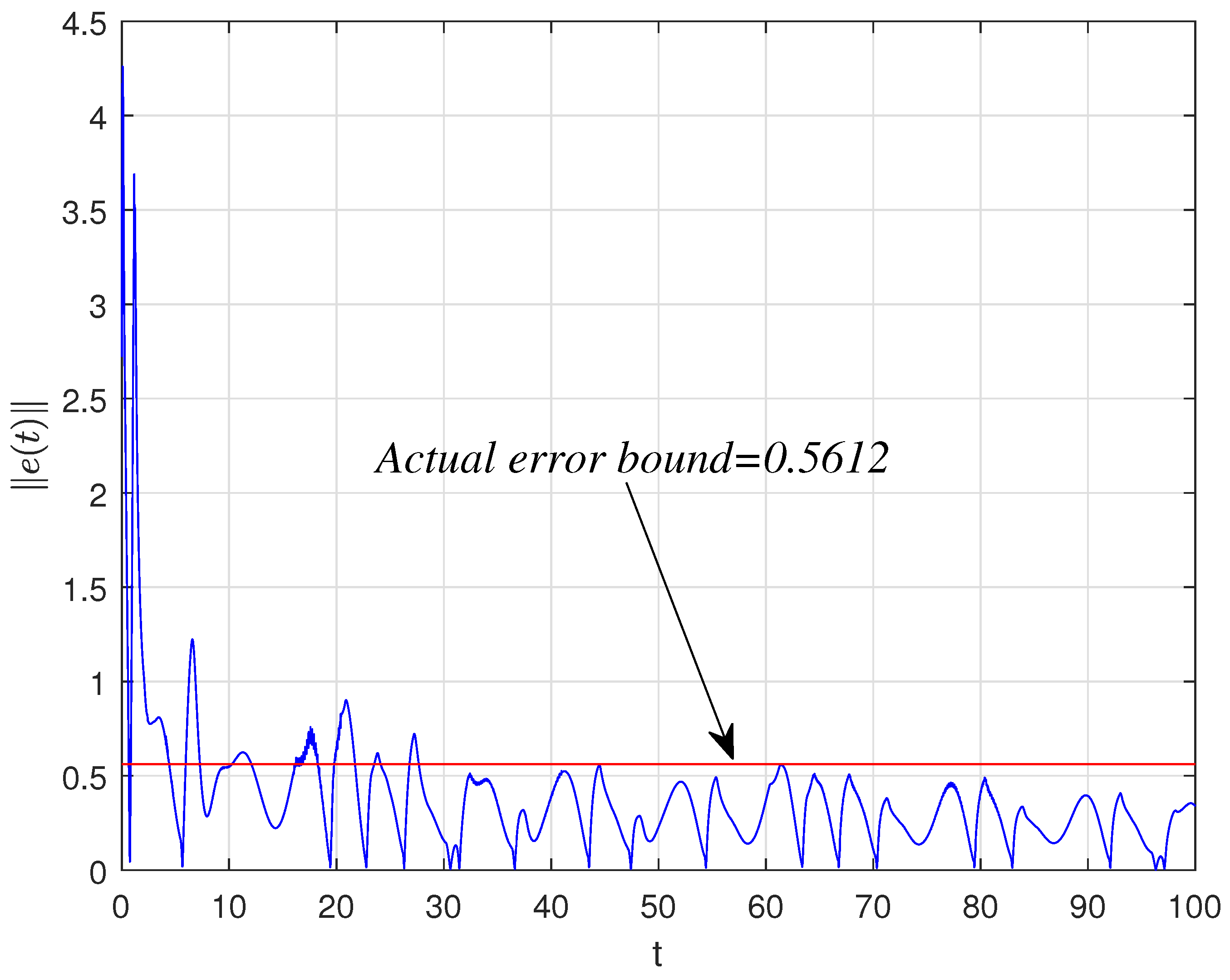
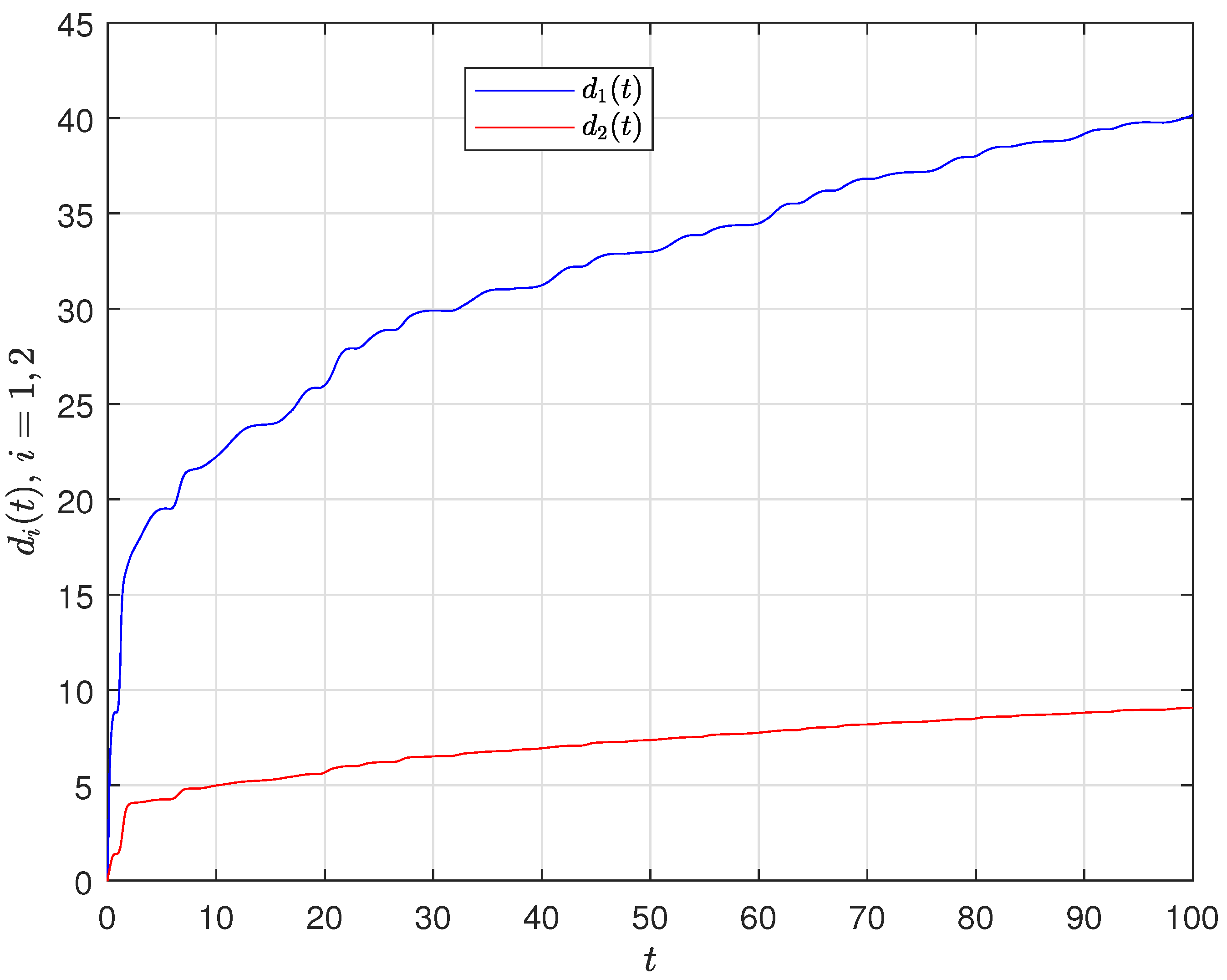
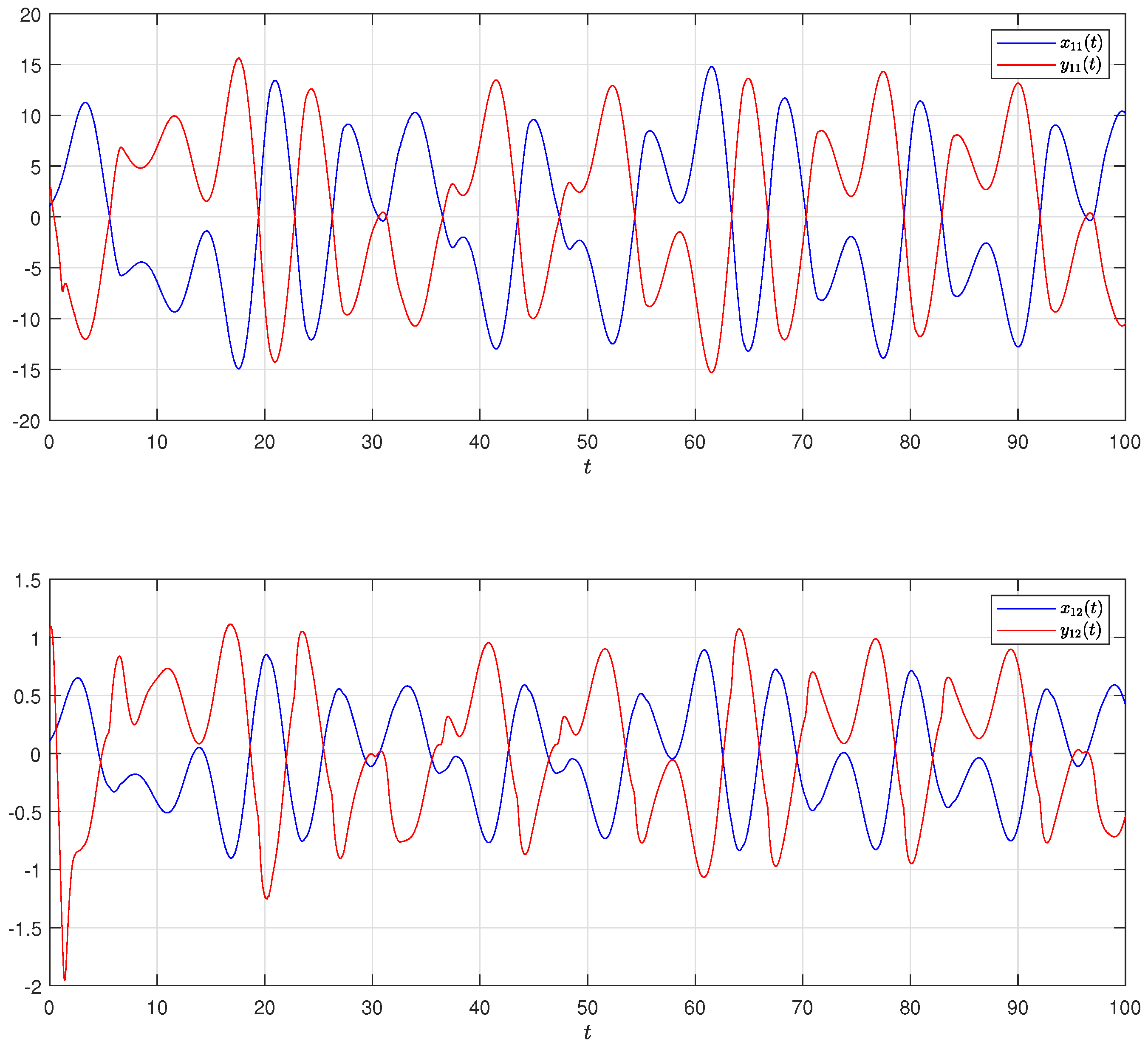
4. Numerical Simulation
4.1. Synchronization Behaviors with Matched Parameters
4.2. Synchronization Behaviors with Mismatched Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, T. A survey of chaotic secure communication systems. Int. J. Comput. Cogn. 2004, 2, 81–130. [Google Scholar]
- Liu, J.; Zhang, J.; Wang, Y. Secure communication via chaotic synchronization based on reservoir computing. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 285–299. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef] [PubMed]
- Arecchi, F.T. Chaotic neuron dynamics, synchronization and feature binding. Phys. A Stat. Mech. Its Appl. 2004, 338, 218–237. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Deng, Q.; Xu, C.; Deng, Z.; Zhou, C. Review on chaotic dynamics of memristive neuron and neural network. Nonlinear Dyn. 2021, 106, 959–973. [Google Scholar] [CrossRef]
- Mainieri, R.; Rehacek, J. Projective synchronization in three-dimensional chaotic systems. Phys. Rev. Lett. 1999, 82, 3042. [Google Scholar] [CrossRef]
- Sun, J.; Zang, M.; Wang, Z.; Wang, Y. Coupling projection synchronization of three chaotic systems and its multilevel secure communication via DNA CRNs. IEEE Internet Things J. 2023, 10, 17282–17292. [Google Scholar] [CrossRef]
- Li, Z.; Tang, Y.; Xu, F.; Zhang, Y. Full states pseudo-random projective synchronization of hyperchaotic system and corresponding secure communication algorithm. Multimed. Tools Appl. 2024, 84, 3527–3568. [Google Scholar] [CrossRef]
- Bharti, J.K.; Balasubramaniam, P.; Murugesan, K. Image encryption algorithm based on matrix projective combination-combination synchronization of an 11-dimensional time delayed hyperchaotic system. Phys. Scr. 2024, 99, 125008. [Google Scholar] [CrossRef]
- He, J.; Wu, Y.; Yang, C. Function matrix projective synchronization for disturbed fractional laser chaotic systems and image encryption. Chin. J. Phys. 2025, 95, 1078–1095. [Google Scholar] [CrossRef]
- Kothari, K.; Mehta, U.V.; Prasad, R. Fractional-order system modeling and its applications. J. Eng. Sci. Technol. Rev. 2019, 12, 1–10. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, F.; Yu, Q.; Li, T. Review of fractional epidemic models. Appl. Math. Model. 2021, 97, 281–307. [Google Scholar] [CrossRef] [PubMed]
- Ding, D.; Niu, Y.; Yang, Z.; Wang, J.; Wang, W.; Wang, M.; Jin, F. Extreme multi-stability and microchaos of fractional-order memristive Rulkov neuron model considering magnetic induction and its digital watermarking application. Nonlinear Dyn. 2024, 112, 15523–15545. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, X.; Duan, L.; Gong, Q.; Wang, Y.; Ao, X. A novel method for state of health estimation of lithium-ion batteries based on fractional-order differential voltage-capacity curve. Appl. Energy 2025, 377, 124404. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 2012, 32, 245–256. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Yang, Y.; Hu, M. Asymptotic stability of delayed fractional-order neural networks with impulsive effects. Neurocomputing 2015, 154, 239–244. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, T.; Wu, Q.; Zeng, Z. Multistability of delayed fractional-order competitive neural networks. Neural Netw. 2021, 140, 325–335. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, T.; Wu, A.; Zeng, Z. Mittag-Leffler stability and application of delayed fractional-order competitive neural networks. Neural Netw. 2024, 179, 106501. [Google Scholar] [CrossRef]
- Wang, C.; Yang, Q.; Zhuo, Y.; Li, R. Synchronization analysis of a fractional-order non-autonomous neural network with time delay. Phys. A Stat. Mech. Its Appl. 2020, 549, 124176. [Google Scholar] [CrossRef]
- Roohi, M.; Zhang, C.; Taheri, M.; Basse-O’Connor, A. Synchronization of fractional-order delayed neural networks using dynamic-free adaptive sliding mode control. Fractal Fract. 2023, 7, 682. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Y.; Chang, Q. Synchronization of fractional-order delayed neural networks with reaction–diffusion terms: Distributed delayed impulsive control. Commun. Nonlinear Sci. Numer. Simul. 2023, 124, 107303. [Google Scholar] [CrossRef]
- Fan, H.; Chen, X.; Shi, K.; Liang, Y.; Wang, Y.; Wen, H. Mittag-Leffler synchronization in finite time for uncertain fractional-order multi-delayed memristive neural networks with time-varying perturbations via information feedback. Fractal Fract. 2024, 8, 422. [Google Scholar] [CrossRef]
- Yu, J.; Hu, C.; Jiang, H.; Fan, X. Projective synchronization for fractional neural networks. Neural Netw. 2014, 49, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Kong, M.; Zeng, Z. Projective synchronization analysis of fractional-order neural networks with mixed time delays. IEEE Trans. Cybern. 2020, 52, 6798–6808. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Yu, Y.; Wang, H. Projective synchronization for fractional-order memristor-based neural networks with time delays. Neural Comput. Appl. 2019, 31, 6039–6054. [Google Scholar] [CrossRef]
- Zhang, X.L.; Li, H.L.; Yu, Y.; Zhang, L.; Jiang, H. Quasi-projective and complete synchronization of discrete-time fractional-order delayed neural networks. Neural Netw. 2023, 164, 497–507. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.; Ye, R.; Stamova, I.; Cao, J. Quasi-projective synchronization analysis of discrete-time FOCVNNs via delay-feedback control. Chaos Solitons Fractals 2023, 173, 113629. [Google Scholar] [CrossRef]
- Li, D.D.; Li, H.L.; Hu, C.; Jiang, H.; Cao, J. Projective synchronization of discrete-time variable-order fractional neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 9313–9325. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, H.; Zhang, W.; Zhang, H. Quasi-projective synchronization for Caputo type fractional-order complex-valued neural networks with mixed delays. Int. J. Control. Autom. Syst. 2022, 20, 1723–1734. [Google Scholar] [CrossRef]
- Yan, H.; Qiao, Y.; Duan, L.; Miao, J. New results of quasi-projective synchronization for fractional-order complex-valued neural networks with leakage and discrete delays. Chaos Solitons Fractals 2022, 159, 112121. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, G.; Wang, L. Quasi-projective and finite-time synchronization of fractional-order memristive complex-valued delay neural networks via hybrid control. AIMS Math. 2024, 9, 7627–7644. [Google Scholar] [CrossRef]
- Pu, Y.F.; Yi, Z.; Zhou, J.L. Fractional Hopfield neural networks: Fractional dynamic associative recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2319–2333. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Zhang, J.; Zhou, Y.; Wang, H. Adaptive hybrid projective synchronization of two coupled fractional-order complex networks with different sizes. Neurocomputing 2015, 164, 182–189. [Google Scholar] [CrossRef]
- Wang, D.; Zou, J. Dissipativity and contractivity analysis for fractional functional differential equations and their numerical approximations. SIAM J. Numer. Anal. 2019, 57, 1445–1470. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar, V. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calc. Appl. 2011, 1, 1–9. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, X.; Yang, Y. Quasi-Mittag-Leffler Projective Synchronization of Delayed Chaotic Fractional Order Neural Network with Mismatched Parameters. Fractal Fract. 2025, 9, 379. https://doi.org/10.3390/fractalfract9060379
Sui X, Yang Y. Quasi-Mittag-Leffler Projective Synchronization of Delayed Chaotic Fractional Order Neural Network with Mismatched Parameters. Fractal and Fractional. 2025; 9(6):379. https://doi.org/10.3390/fractalfract9060379
Chicago/Turabian StyleSui, Xin, and Yongqing Yang. 2025. "Quasi-Mittag-Leffler Projective Synchronization of Delayed Chaotic Fractional Order Neural Network with Mismatched Parameters" Fractal and Fractional 9, no. 6: 379. https://doi.org/10.3390/fractalfract9060379
APA StyleSui, X., & Yang, Y. (2025). Quasi-Mittag-Leffler Projective Synchronization of Delayed Chaotic Fractional Order Neural Network with Mismatched Parameters. Fractal and Fractional, 9(6), 379. https://doi.org/10.3390/fractalfract9060379




