On Polynomial φ-Contractions with Applications to Fractional Logistic Growth Equations
Abstract
1. Introduction
2. Mathematical Preliminaries
- for each ,
- ,
- φ is continuous at 0.
- (i)
- The mapping T is continuous;
- (ii)
- For some , the coefficient function is uniformly bounded below by a positive constant (i.e., ).
- (i)
- The mapping T is Picard-continuous;
- (ii)
- For some , the coefficient function is uniformly bounded below by a positive constant (i.e., ).
3. Main Results
3.1. The Family of Polynomial -Contractions
- (a)
- By setting and , we deduce polynomial contractions.
- (b)
- By choosing , , and , we obtain φ-contractions.
- (c)
- Taking , , , , and , we obtain Banach contractions.
- They control the type of nonlinearity (e.g., quadratic, cubic).
- They determine convergence rates and stability conditions.
- Their flexibility allows the framework to unify classical and modern contraction theories.
- (i)
- The mapping T is continuous;
- (ii)
- For some , the coefficient function is uniformly bounded below by a positive constant (i.e., ).
- Monotonicity of φ: The assumption that is monotonically increasing ensures that smaller values are mapped to smaller values under iteration. This property supports the preservation of a generalized contraction behavior.
- Convergence Requirement (): The condition ensures that the iterates decay to zero sufficiently fast for all and any . This guarantees the convergence of the Cauchy sequence and the stability of fixed point iterations, as the series’ convergence implies faster than any polynomial in n.
- (i)
- for all ;
- (ii)
- For each , the coefficient function is uniformly bounded above by a positive constant (i.e., );
- (iii)
- For some , the coefficient function is uniformly bounded below by a positive constant (i.e., ).
- (i)
- for all ;
- (ii)
- are continuous at ;
- (iii)
- For some , the coefficient function is uniformly bounded below by a positive constant (i.e., ).
- (i)
- The mapping T is Picard-continuous;
- (ii)
- For some , the coefficient function is uniformly bounded below by a positive constant (i.e., ).
- Case 1: For ,
- Case 2: For and ,
- Case 3: For ,
3.2. Convergence Rate and Numerical Verification
- (i)
- A priori error estimatewhere
- ,
- ,
- and with .
- (ii)
- A posteriori error estimate
- (i)
- A priori error estimate: From the contractive condition (Equation (1)) with , , we getFor , the triangle inequality yieldsTaking , we obtain the priori error estimate
- (ii)
- A Posteriori Error Estimate: Again, from (1) with , , we haveLet . The above inequality becomeswhich inductively yieldsFor , applying the triangle inequality yieldTaking , we derive the a posteriori error estimate.where This completes the proof.
- (i)
- A priori error estimate
- (ii)
- A posteriori error estimate
- (iii)
- Convergence rate
- (i)
- A priori error estimate
- (ii)
- A posteriori error estimate
- (iii)
- Convergence ratewhere s is a partial sum function of the series .
4. Application to Fractional Logistic Equation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fund. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Jleli, M.; Samet, B. A new generalization of the Banach contraction principle. J. Inequal. Appl. 2014, 2014, 38. [Google Scholar] [CrossRef]
- Suzuki, T. A generalized Banach contraction principle that characterizes metric completeness. Proc. Am. Math. Soc. 2008, 136, 1861–1869. [Google Scholar] [CrossRef]
- Wardowski, D. Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 2012, 94. [Google Scholar] [CrossRef]
- Khojasteh, F.; Shukla, S.; Radenović, S. A new approach to the study of fixed point theory for simulation functions. Filomat 2015, 29, 1189–1194. [Google Scholar] [CrossRef]
- Berinde, V. Approximating fixed points of weak contractions using the Picard iteration. Nonlinear Anal. Forum 2004, 9, 43–54. [Google Scholar]
- Jleli, M.; Păcurar, C.; Samet, B. New directions in fixed point theory in G-metric spaces and applications to mappings contracting perimeters to triangles. arXiv 2024. [Google Scholar] [CrossRef]
- Rakotch, E. A note on contractive mappings. Proc. Am. Math. Soc. 1962, 13, 459–465. [Google Scholar] [CrossRef]
- Browder, F.E. On the convergence of successive approximations for nonlinear functional equations. Ned. Akad. Wet. Proc. Ser. A Indag. Math. 1968, 71, 27–35. [Google Scholar] [CrossRef]
- Boyd, D.W.; Wong, J.S. On nonlinear contractions. Proc. Am. Math. Soc. 1969, 20, 458–464. [Google Scholar] [CrossRef]
- Matkowski, J. Integrable solutions of functional equations. Dissertationes Math. Rozpr. Mat. 1975, 127, 1–68. [Google Scholar]
- Jachymski, J.; Jóźwik, I. Nonlinear contractive conditions: A comparison and related problems. Banach Cent. Publ. 2007, 77, 123–146. [Google Scholar]
- Berinde, V. Approximating fixed points of weak φ-contractions using the Picard iteration. Fixed Point Theory 2003, 4, 131–142. [Google Scholar]
- Berinde, V. Iterative Approximation of Fixed Points, 2nd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Jachymski, J. Around Browder’s fixed point theorem for contractions. J. Fixed Point Theory Appl. 2009, 5, 47–61. [Google Scholar] [CrossRef]
- Jachymski, J. Remarks on contractive conditions of integral type. Nonlinear Anal. Theory Methods Appl. 2009, 71, 1073–1081. [Google Scholar] [CrossRef]
- Jachymski, J. On iterative equivalence of some classes of mappings. Ann. Math. Silesianae 1999, 13, 149–165. [Google Scholar]
- Jleli, M.; Păcurar, C.; Samet, B. Fixed point results for contractions of polynomial type. Demonstr. Math. 2025, 58, 20250098. [Google Scholar] [CrossRef]
- Saber, H.; Almalaiah, M.; Albala, H.; Aldowah, K.; Alsulami, A.; Shah, K.; Moumen, A. Investigating a nonlinear fractional evolution model using W-piecewise hybrid derivatives: An application of a breast cancer model. Fractal Fract. 2024, 8, 735. [Google Scholar] [CrossRef]
- Saber, H.; Ali, A.; Aldowah, K.; Alraqad, T.; Moumen, A.; Alsulami, A.; Eljenaid, N. Exploring impulsive and delay differential systems using piecewise fractional derivatives. Fractal Fract. 2025, 9, 105. [Google Scholar] [CrossRef]
- Saber, H.; Albala, T.; Aljaaidi, T.; Jawarneh, J.; Moumen, A.; Aldowah, K. Fractional order modeling of prostate cancer with pulsed treatment and the impact of effector cell killing and cell competition. Sci. Rep. 2025, 15, 12580. [Google Scholar] [CrossRef]
- Almalaiah, M.; Saber, H.; Moumen, A.; Ali, E.E.; Aldowah, K.; Hassan, M. Application of proven fixed point on modified cubic coupled model of impulsive equations in high-fractional order. Fractals 2025, 33, 1–21. [Google Scholar]
- Hamza, A.E.; Osman, A.; Ali, A.; Alsulami, A.; Aldowah, K.; Mustafa, H.; Saber, H. Fractal–fractional-order modeling of liver fibrosis disease and its mathematical results with subinterval transitions. Fractal Fract. 2024, 8, 638. [Google Scholar] [CrossRef]
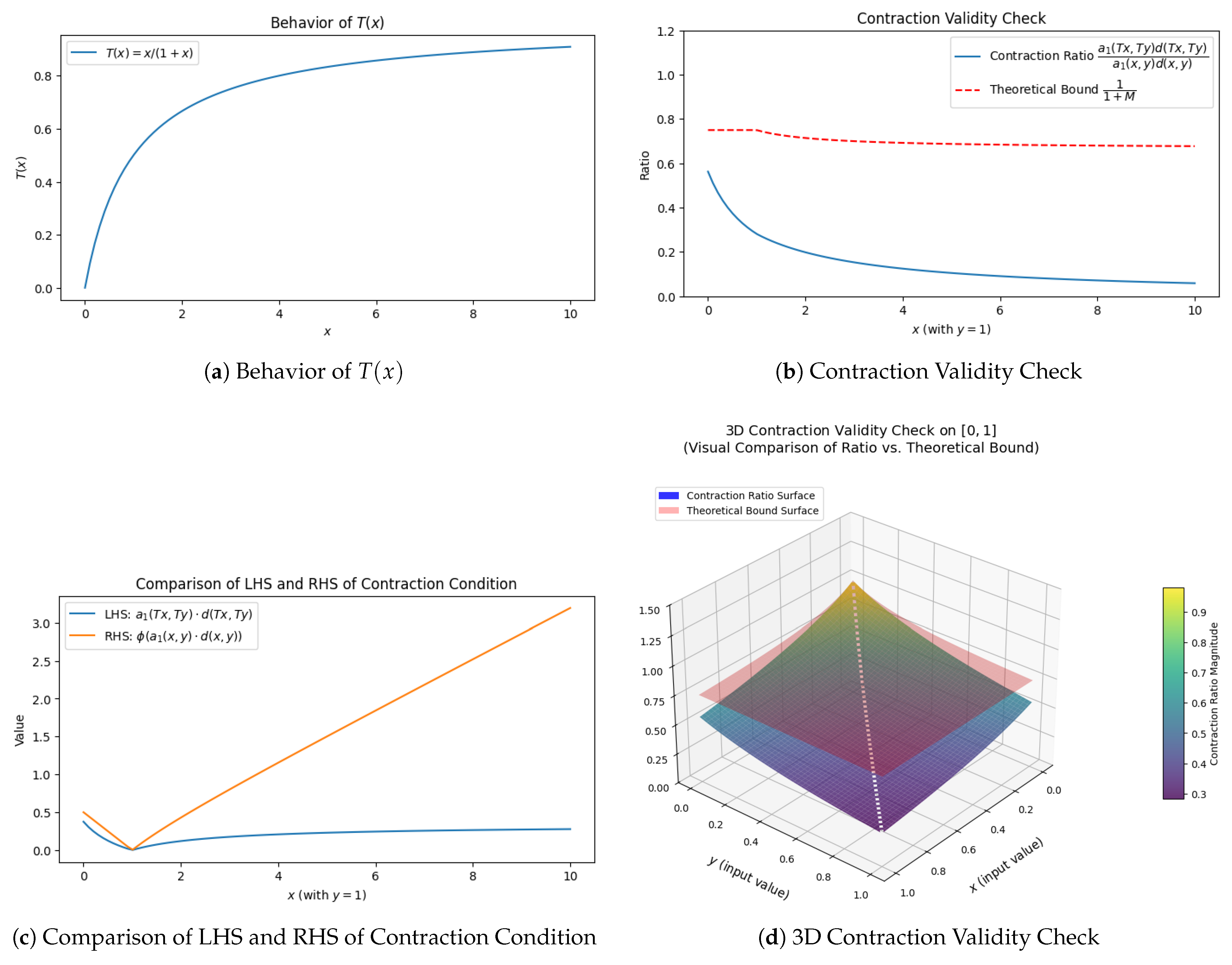
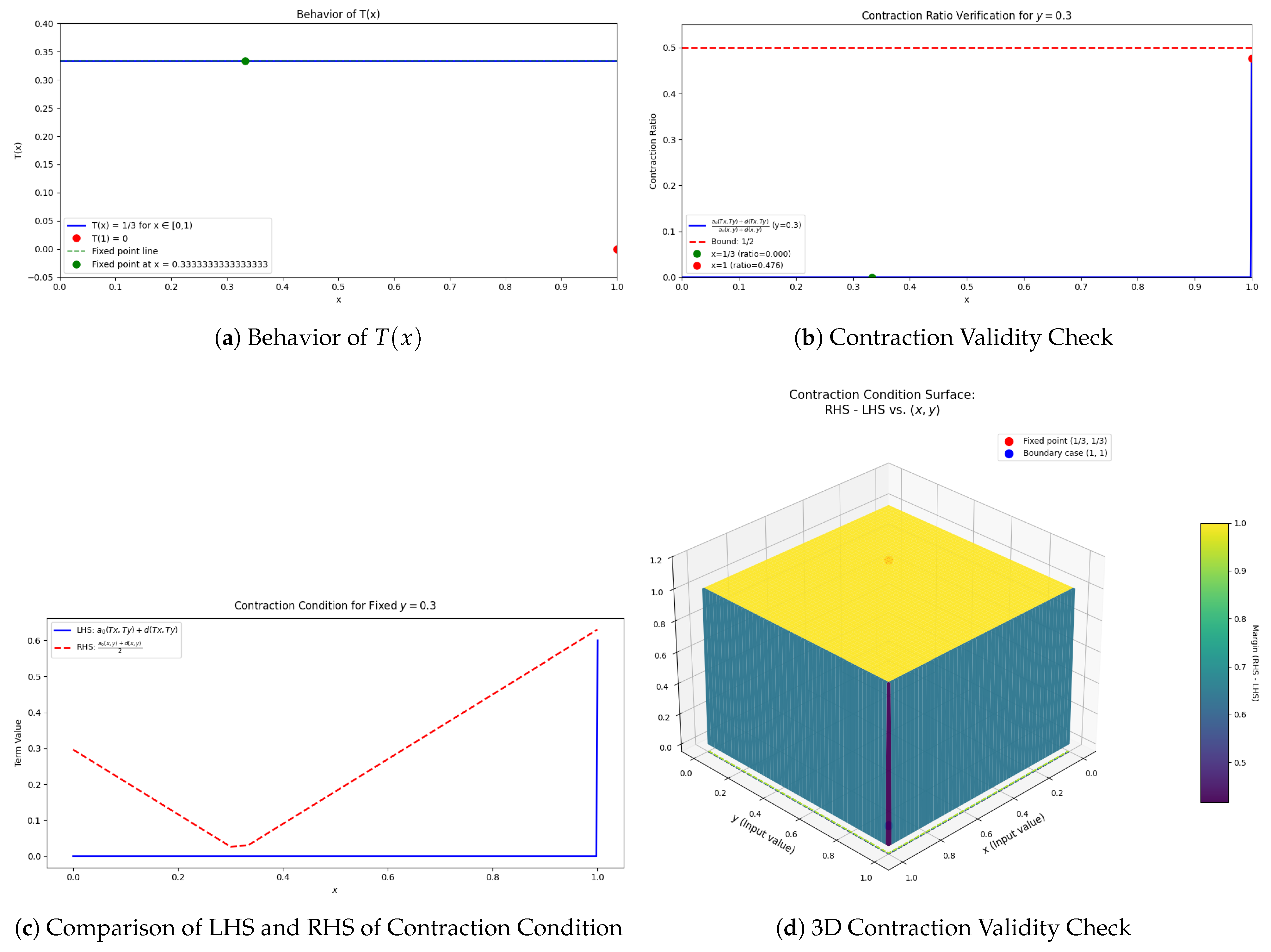
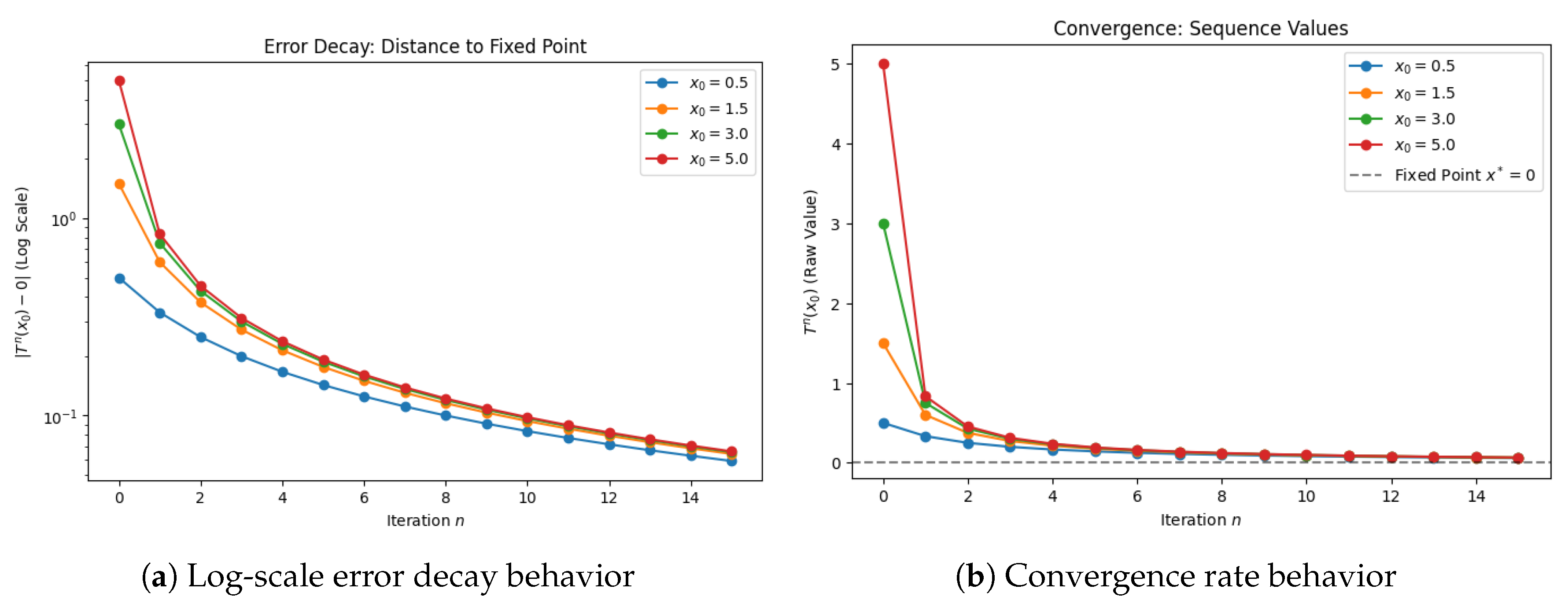
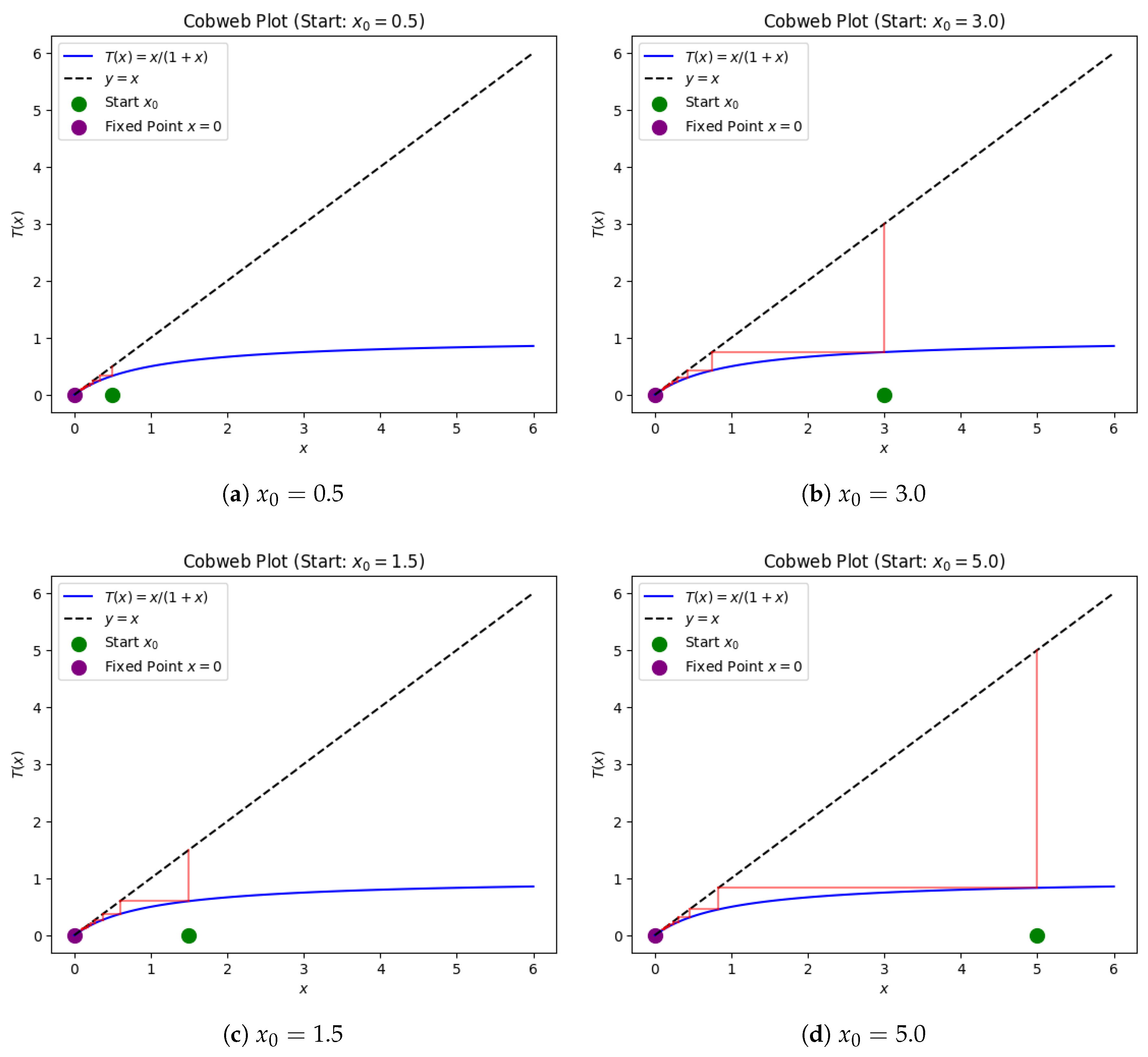
| Iteration | ||||
|---|---|---|---|---|
| 0 | 1.000000 | 5.000000 | 10.000000 | 20.000000 |
| 1 | 0.500000 | 0.833333 | 0.909091 | 0.952381 |
| 2 | 0.333333 | 0.454545 | 0.476190 | 0.487805 |
| 3 | 0.250000 | 0.312500 | 0.322581 | 0.327869 |
| 4 | 0.200000 | 0.238095 | 0.243902 | 0.246914 |
| 5 | 0.166667 | 0.192308 | 0.196078 | 0.198020 |
| 6 | 0.142857 | 0.161290 | 0.163934 | 0.165289 |
| 7 | 0.125000 | 0.138889 | 0.140845 | 0.141844 |
| 8 | 0.111111 | 0.121951 | 0.123457 | 0.124224 |
| 9 | 0.100000 | 0.108696 | 0.109890 | 0.110497 |
| 10 | 0.090909 | 0.098039 | 0.099010 | 0.099502 |
| 11 | 0.083333 | 0.089286 | 0.090090 | 0.090498 |
| 12 | 0.076923 | 0.081967 | 0.082645 | 0.082988 |
| 13 | 0.071429 | 0.075758 | 0.076336 | 0.076628 |
| 14 | 0.066667 | 0.070423 | 0.070922 | 0.071174 |
| 15 | 0.062500 | 0.065789 | 0.066225 | 0.066445 |
| Iteration n | Classical Contraction | Polynomial -Contraction |
|---|---|---|
| 0 | 1.0000 | 1.0000 |
| 1 | 0.5000 | 0.5000 |
| 2 | 0.2500 | 0.2500 |
| 3 | 0.1250 | 0.1250 |
| 4 | 0.0625 | 0.0625 |
| 5 | 0.0313 | 0.0313 |
| 6 | 0.0156 | 0.0156 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moumen, A.; Saleh, H.N.; Albala, H.; Aldwoah, K.; Saber, H.; Hassan, E.I.; Hassan, T.S. On Polynomial φ-Contractions with Applications to Fractional Logistic Growth Equations. Fractal Fract. 2025, 9, 366. https://doi.org/10.3390/fractalfract9060366
Moumen A, Saleh HN, Albala H, Aldwoah K, Saber H, Hassan EI, Hassan TS. On Polynomial φ-Contractions with Applications to Fractional Logistic Growth Equations. Fractal and Fractional. 2025; 9(6):366. https://doi.org/10.3390/fractalfract9060366
Chicago/Turabian StyleMoumen, Abdelkader, Hayel N. Saleh, Hussien Albala, Khaled Aldwoah, Hicham Saber, E. I. Hassan, and Taher S. Hassan. 2025. "On Polynomial φ-Contractions with Applications to Fractional Logistic Growth Equations" Fractal and Fractional 9, no. 6: 366. https://doi.org/10.3390/fractalfract9060366
APA StyleMoumen, A., Saleh, H. N., Albala, H., Aldwoah, K., Saber, H., Hassan, E. I., & Hassan, T. S. (2025). On Polynomial φ-Contractions with Applications to Fractional Logistic Growth Equations. Fractal and Fractional, 9(6), 366. https://doi.org/10.3390/fractalfract9060366









