AI-Based Deep Learning of the Water Cycle System and Its Effects on Climate Change
Abstract
1. Introduction
1.1. Fractional-Order Modeling of Dynamical Systems
1.2. AI Applications in Science
2. FF Modeling of the Water Cycle System
- represents global temperature in Kelvin;
- represents precipitation of atmospheric water and is measured in mm;
- is the water availability, recorded in mm.
- Importance of the Model
- To analyze the role of changing climate parameters on temperature and precipitation over time;
- To study the impacts of the greenhouse effect, water availability, and runoff on climate systems;
- The analyze the sensitivity of global temperature to changes in solar radiation, water cycles, and precipitation patterns.
- Model Predictions
- Projecting future climate scenarios;
- Guiding policy decisions related to climate mitigation and adaptation;
- Informing strategies to manage water resources in response to climate change.
- Model Validity
- Significance of the Model
- Evaluating the effectiveness of climate policies;
- Understanding the long-term impacts of different emission scenarios;
- Designing climate adaptation strategies, especially in regions vulnerable to changes in water availability.
3. Mathematical Analysis of the Model
- : The continuous functions , , and , , all belong to to the extent that , , and for ,, and constants.
- : Assume that there exist and such that
4. Numerical Scheme
Tabular Data with Illustration
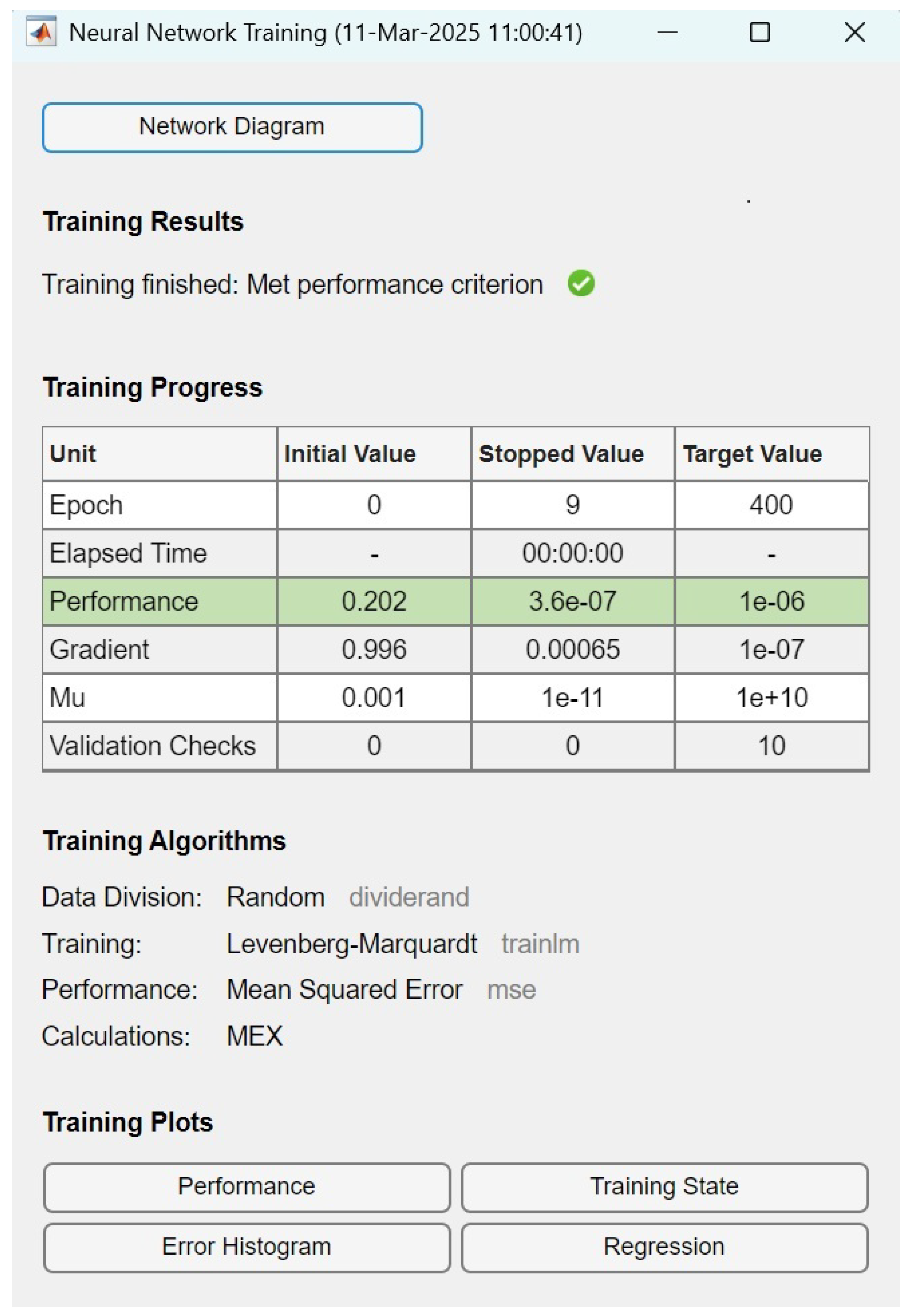
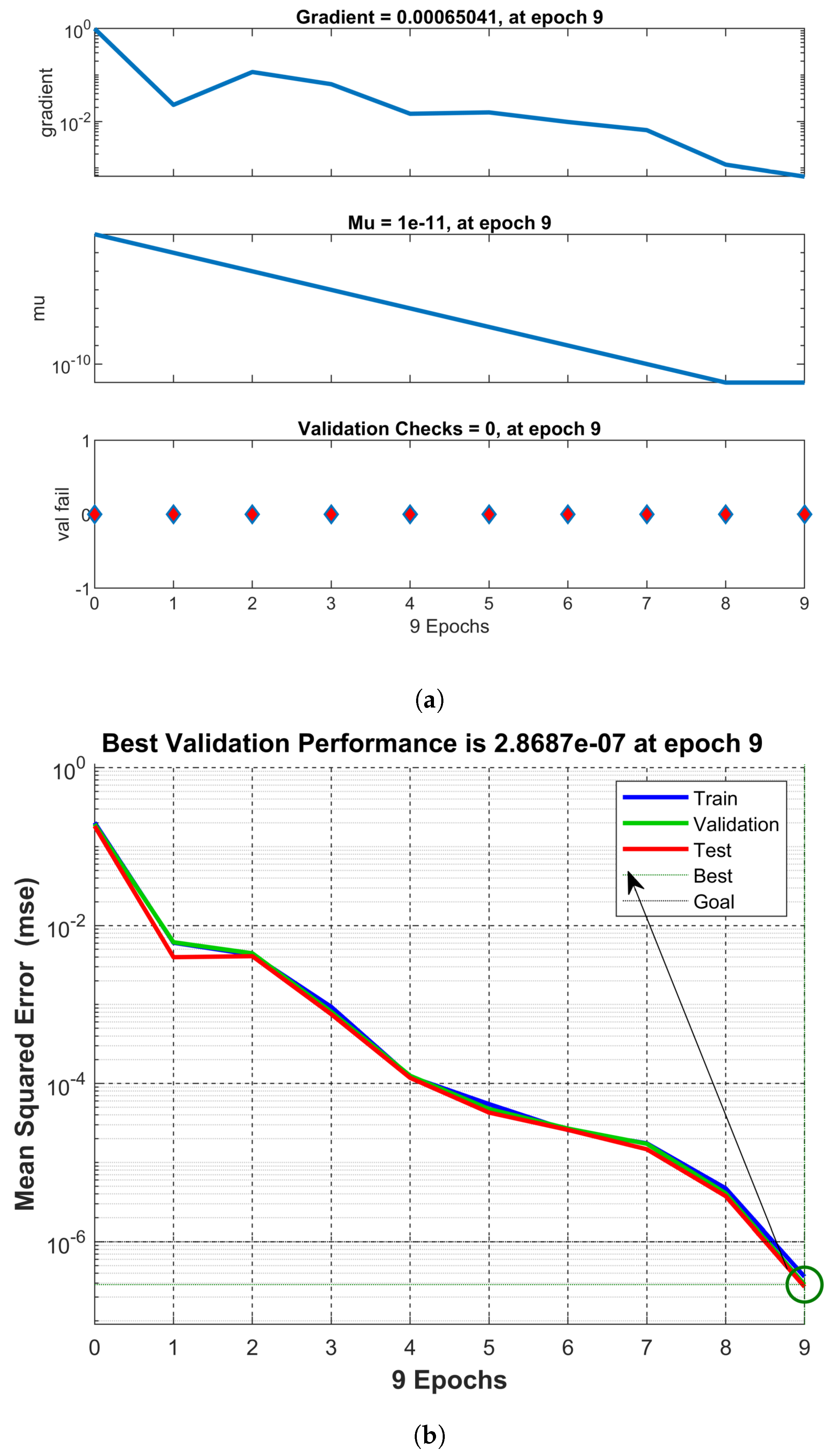
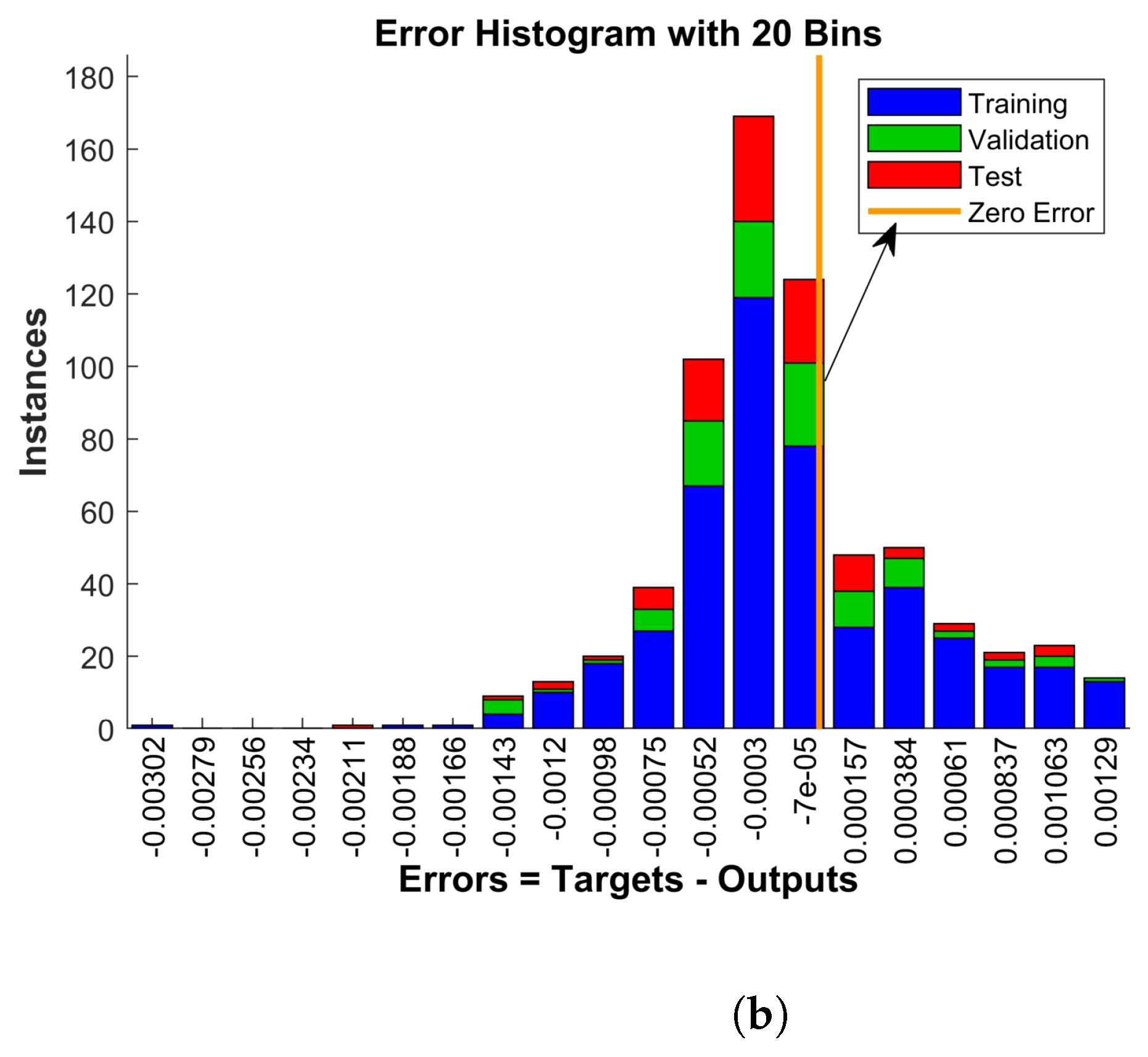
5. Deep Learning Analysis of Water Cycle Complex Neural Dynamical Mechanism
5.1. Mean Square Error
5.2. Regression of the Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Trenberth, K.E. Water cycles and climate change. Glob. Environ. Chang. 2014, 2014, 31–37. [Google Scholar]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.; Tang, W.; Chen, Y. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Glob. Planet. Chang. 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Gallant, A.L. Predicting impacts of increased CO2 and climate change on the water cycle and water quality in the semiarid James River Basin of the Midwestern USA. Sci. Total Environ. 2012, 430, 150–160. [Google Scholar] [CrossRef]
- Nan, Y.; Men, B.; Lin, C.-K. Impact analysis of climate change on water resources. Procedia Eng. 2011, 24, 643–648. [Google Scholar] [CrossRef]
- Barry, S.M.; Davies, G.R.; Forton, J.; Williams, S.; Thomas, R.; Paxton, P.; Moore, G.; Davies, C.R. Trends in low global warming potential inhaler prescribing: A UK-wide cohort comparison from 2018–2024. NPJ Prim. Care Respir. Med. 2025, 35, 9. [Google Scholar] [CrossRef] [PubMed]
- An, R.; Ji, M.; Zhang, S. Global warming and obesity: A systematic review. Obes. Rev. 2018, 19, 150–163. [Google Scholar] [CrossRef]
- Cao, M.; Wang, F.; Ma, S.; Geng, H.; Sun, K. Recent advances on greenhouse gas emissions from wetlands: Mechanism, global warming potential, and environmental drivers. Environ. Pollut. 2024, 355, 124204. [Google Scholar] [CrossRef]
- Amnuaylojaroen, T. Perspective on the era of global boiling: A future beyond global warming. Adv. Meteorol. 2023, 2023, 5580606. [Google Scholar] [CrossRef]
- Janni, M.; Maestri, E.; Gullì, M.; Marmiroli, M.; Marmiroli, N. Plant responses to climate change, how global warming may impact on food security: A critical review. Front. Plant Sci. 2024, 14, 1297569. [Google Scholar] [CrossRef]
- Ripple, W.J.; Wolf, C.; Gregg, J.W.; Rockström, J.; Mann, M.E.; Oreskes, N.; Lenton, T.M.; Rahmstorf, S.; Newsome, T.M.; Xu, C.; et al. The 2024 state of the climate report: Perilous times on planet Earth. BioScience 2024, 74, 812–824. [Google Scholar] [CrossRef]
- Van Daalen, K.R.; Tonne, C.; Semenza, J.C.; Rocklöv, J.; Markandya, A.; Dasandi, N.; Jankin, S.; Achebak, H.; Ballester, J.; Bechara, H.; et al. The 2024 Europe report of the Lancet Countdown on health and climate change: Unprecedented warming demands unprecedented action. Lancet Public Health 2024, 9, e495–e522. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Zhang, C.; Zhang, S.; Bai, Y.; Callaghan, M.; Chang, N.; Chen, B.; Chen, H.; Cheng, L.; Dai, H.; et al. The 2024 China report of the Lancet Countdown on health and climate change: Launching a new low-carbon, healthy journey. Lancet Public Health 2024, 9, e1070–e1088. [Google Scholar] [CrossRef]
- Su, Y.; Ullah, K. Exploring the correlation between rising temperature and household electricity consumption: An empirical analysis in China. Heliyon 2024, 10, e30130. [Google Scholar] [CrossRef] [PubMed]
- Yaseen, R.M.; Ali, N.F.; Mohsen, A.A.; Khan, A.; Abdeljawad, T. The modeling and mathematical analysis of the fractional-order of Cholera disease: Dynamical and Simulation. Partial Differ. Equ. Appl. Math. 2024, 12, 100978. [Google Scholar] [CrossRef]
- Alsaadi, A. Advancing water quality management: A synergistic approach using fractional differential equations and neural networks. AIMS Math. 2025, 10, 5332–5352. [Google Scholar] [CrossRef]
- Bedi, P.; Kumar, A.; Deora, G.; Khan, A.; Abdeljawad, T. An investigation into the controllability of multivalued stochastic fractional differential inclusions. Chaos Solitons Fractals X 2024, 12, 100107. [Google Scholar] [CrossRef]
- Nordhaus, W.D.; Boyer, J. Warming the World: Economic Models of Global Warming; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Nobre, P.; Malagutti, M.; Urbano, D.F.; de Almeida, R.A.; Giarolla, E. Amazon deforestation and climate change in a coupled model simulation. J. Climate 2009, 22, 5686–5697. [Google Scholar] [CrossRef]
- Henderson-Sellers, A.; Dickinson, R.E.; Wilson, M.F. Tropical deforestation: Important processes for climate models. Clim. Chang. 1988, 13, 43–67. [Google Scholar] [CrossRef]
- Sabatier, J.A.; Agrawal, O.P.; Machado, J.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2011. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Bas, E.; Acay, B.; Ozarslan, R. Fractional models with singular and non-singular kernels for energy efficient buildings. Chaos 2019, 29, 023110. [Google Scholar] [CrossRef]
- Khan, A.; Abdeljawad, T.; Abdel-Aty, M.; Almutairi, D.K. Digital analysis of discrete fractional order cancer model by artificial intelligence. Alex. Eng. J. 2025, 118, 115–124. [Google Scholar] [CrossRef]
- Khan, A.; Abdeljawad, T.; Alkhawar, H.M. Digital analysis of discrete fractional order worms transmission in wireless sensor systems: Performance validation by artificial intelligence. Model. Earth Syst. Environ. 2025, 11, 25. [Google Scholar] [CrossRef]
- Ahmad, I.; Bakar, A.A.; Ahmad, H.; Khan, A.; Abdeljawad, T. Investigating virus spread analysis in computer networks with Atangana–Baleanu fractional derivative models. Fractals 2024, 2440043, 17. [Google Scholar] [CrossRef]
- Atangana, A. Fractal–fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Atangana, A.; Qureshi, S. Modeling attractors of chaotic dynamical systems with fractal–fractional operators. Chaos Solitons Fractals 2019, 123, 320–337. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. Atangana–Seda numerical scheme for Labyrinth attractor with new differential and integral operators. Fractals 2020, 28, 2040044. [Google Scholar] [CrossRef]
- Sekerci, Y. Climate change effects on fractional order prey-predator model. Chaos Solitons Fractals 2020, 134, 109690. [Google Scholar] [CrossRef]
- Khan, H.; Aslam, M.; Rajpar, A.H.; Chu, Y.M.; Etemad, S.; Rezapour, S.; Ahmad, H. A new fractal-fractional hybrid model for studying climate change on coastal ecosystems from the mathematical point of view. Fractals. 2024, 32, 2440015. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Banerjee, R.; Yavuz, M.; Govindaraj, V. Fractional modeling of plankton-oxygen dynamics under climate change by the application of a recent numerical algorithm. Phys. Scr. 2021, 96, 124044. [Google Scholar] [CrossRef]
- Kumar, V.R.; Mani, N. The application of artificial intelligence techniques for intelligent control of dynamical physical systems. Int. J. Adapt. Control Signal Process. 1994, 8, 379–392. [Google Scholar] [CrossRef]
- Böttcher, L.; Antulov-Fantulin, N.; Asikis, T. AI Pontryagin or how artificial neural networks learn to control dynamical systems. Nat. Commun. 2022, 13, 333. [Google Scholar] [CrossRef] [PubMed]
- Yuksel, G. Dynamical Systems and Artificial Intelligence. In Artificial Intelligence; CRC Press: Boca Raton, FL, USA, 2024; pp. 75–83. [Google Scholar]
- Sharma, P.; Khan, J.S.; Radhika, K.; Thatipudi, J.G.; Sridevi, K.; Upadhyay, S. Evolutionary Intelligence: A Hybrid Neural Framework for Dynamic System Innovation. In Proceedings of the 2025 International Conference on Electronics and Renewable Systems (ICEARS), Thoothukudi, India, 1–13 February 2025; pp. 1743–1749. [Google Scholar]
- Khan, H.; Alzabut, J.; Almutairi, D.K.; Alqurashi, W.K. The Use of Artificial Intelligence in Data Analysis with Error Recognitions in Liver Transplantation in HIV-AIDS Patients Using Modified ABC Fractional Order Operators. Fractal Fract. 2025, 9, 16. [Google Scholar] [CrossRef]
- Khan, H.; Alzabut, J.; Tounsi, M.; Almutairi, D.K. AI-Based Data Analysis of Contaminant Transportation with Regression of Oxygen and Nutrients Measurement. Fractal Fract. 2025, 9, 125. [Google Scholar] [CrossRef]
- Khan, A.; Shah, K.; Abdeljawad, T.; Alqudah, M.A. Existence of results and computational analysis of a fractional order two strain epidemic model. Results Phys. 2022, 39, 105649. [Google Scholar] [CrossRef]
- Wan-Arfah, N.; Muzaimi, M.; Naing, N.N.; Subramaniyan, V.; Wong, L.S.; Selvaraj, S. Prognostic factors of first-ever stroke patients in suburban Malaysia by comparing regression models. Electron. J. Gen. Med. 2023, 20, em545. [Google Scholar] [CrossRef]


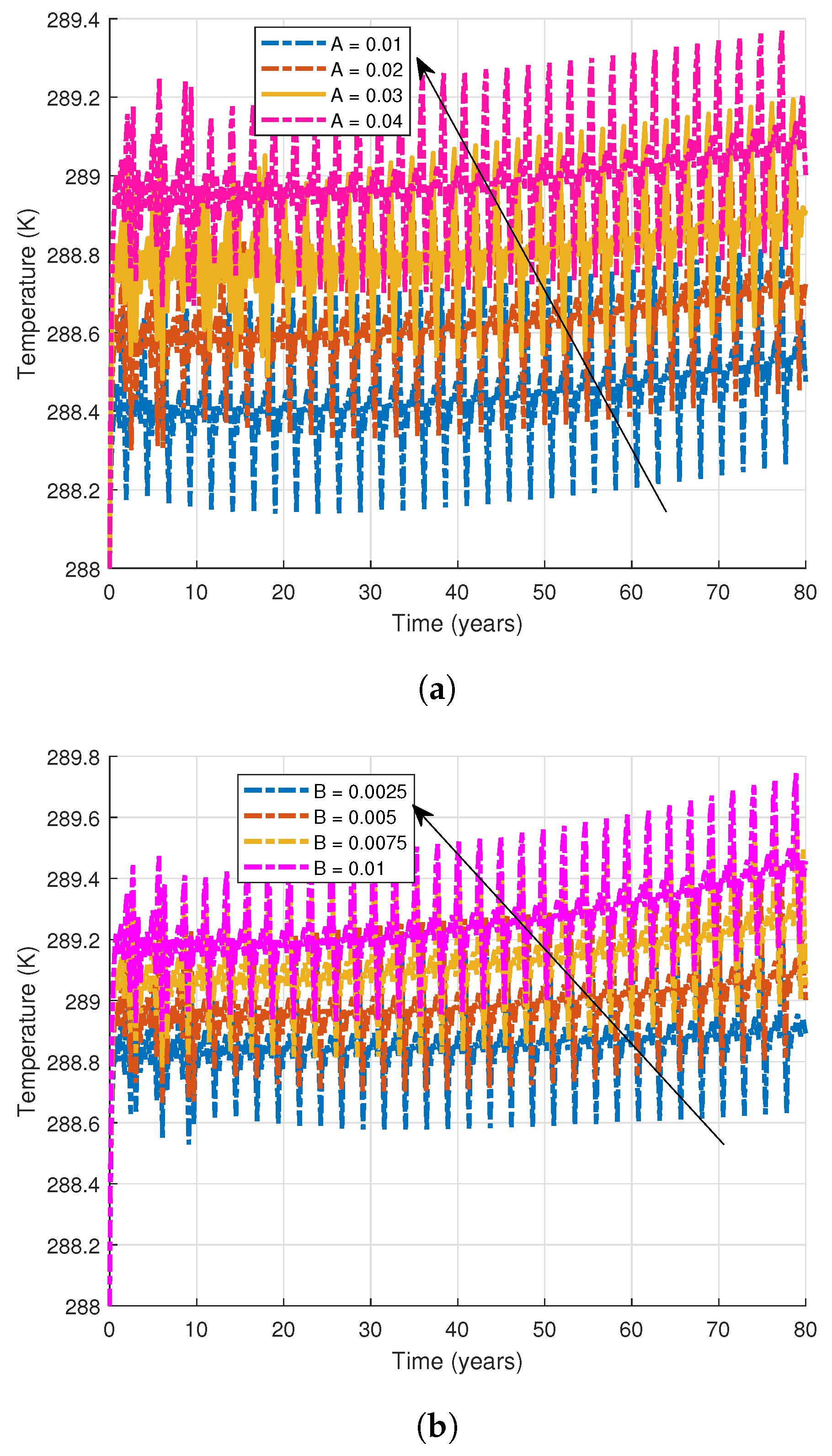
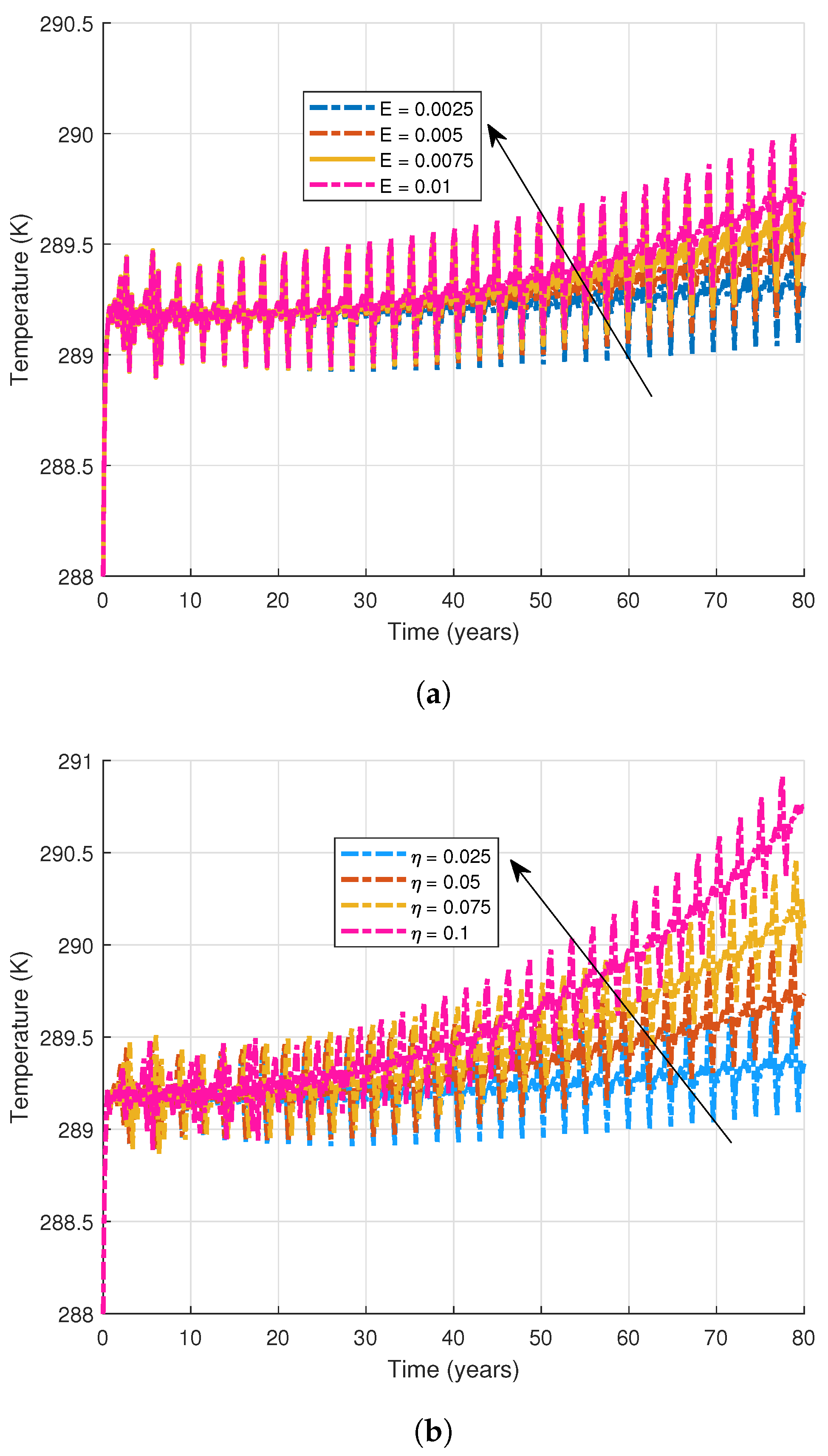


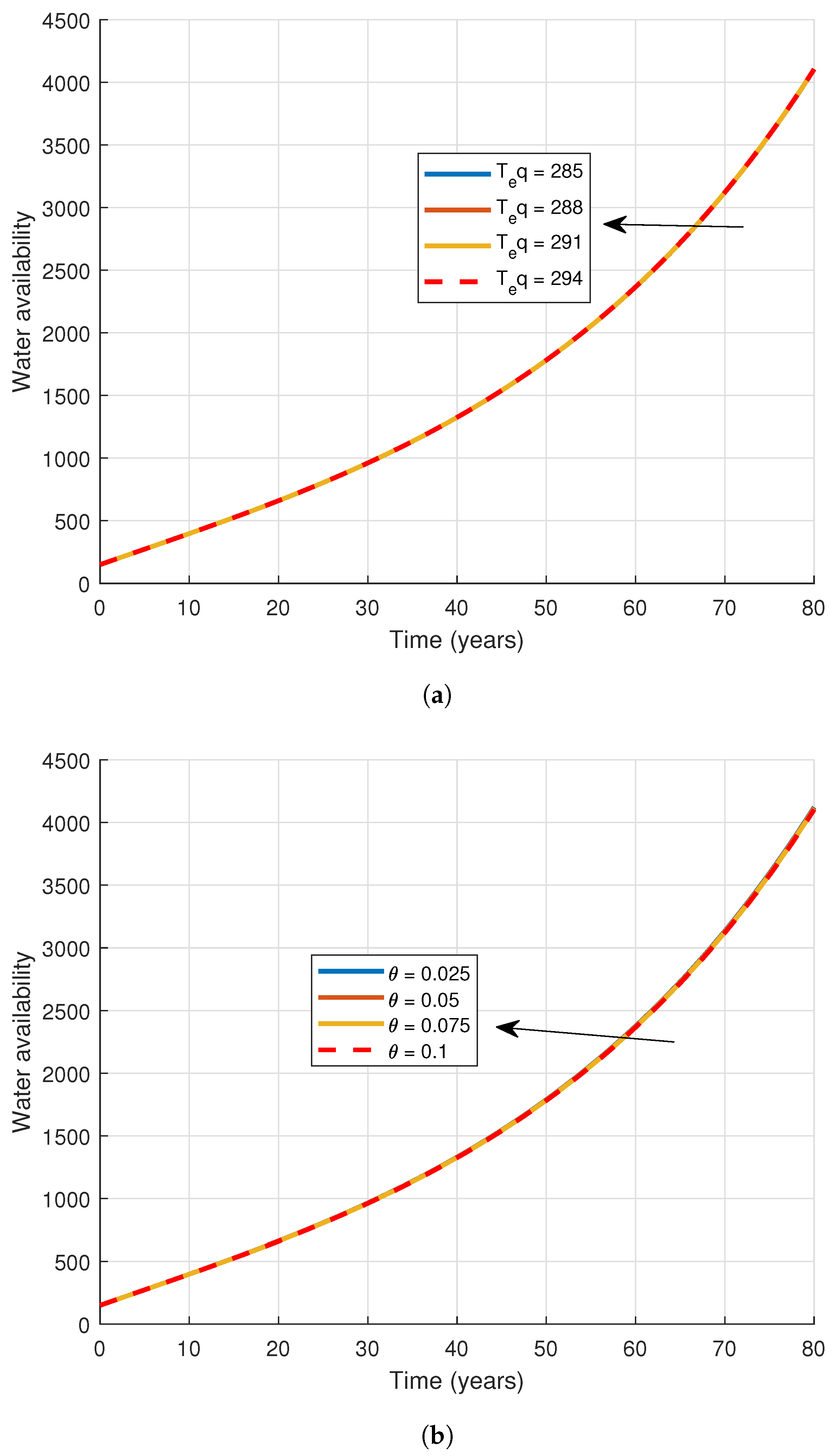

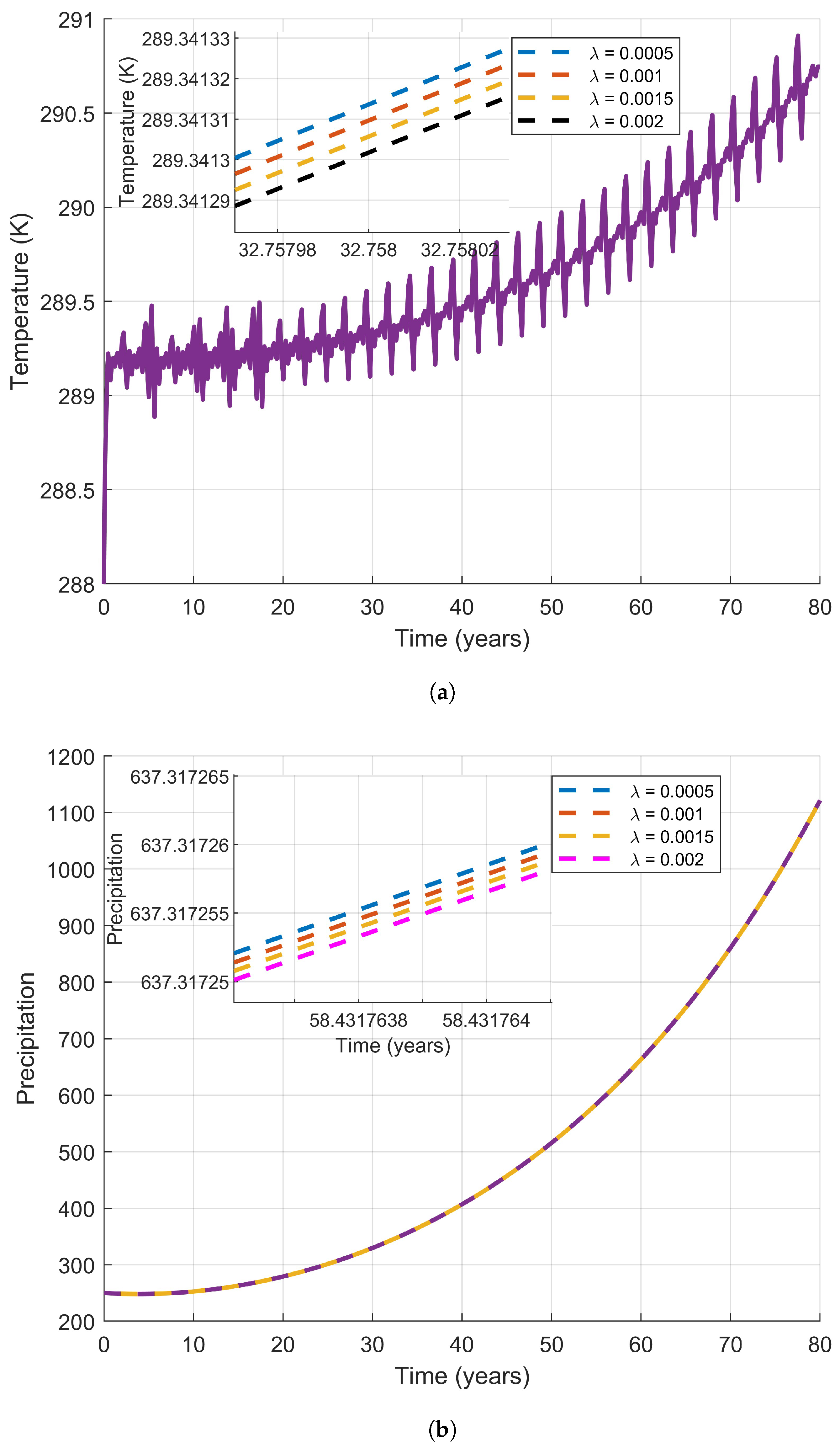


| Parameter | Description | Value |
|---|---|---|
| Solar constant: incoming solar radiation | 340 W/m2 | |
| Stefan–Boltzmann constant: governs Earth’s radiation balance | 5.67 W/m2K4 | |
| Response of temperature to solar radiation | 0.02 K·m2/W | |
| Effect of precipitation on temperature | 0.0050 K/mm | |
| Impact of evaporation on temperature | 0.0050 K/mm | |
| Response of precipitation to temperature | 0.0050 mm/K | |
| Effect of water availability on precipitation | 0.0050 1/time | |
| Runoff factor | 0.0050 1/time | |
| Response of water availability to precipitation | 0.050 1/time | |
| Feedback effect of water availability on temperature | 0.050 1/time | |
| Greenhouse effect coefficient (models impact of greenhouse effect on T) | 0.0010 K/time | |
| Equilibrium temperature: baseline temperature for the climate model | 288 K |
| Parameter | Value | Temperature (K) | Precipitation (mm) | Water |
|---|---|---|---|---|
| 0.03 | 288.91 | 406.99 | 1327.3 | |
| 0.0075 | 289.05 | 406.95 | 1326.7 | |
| 0.0075 | 289.05 | 406.95 | 1326.7 | |
| 0.0075 | 289.05 | 407.15 | 1327.1 | |
| 0.0075 | 289.13 | 483.48 | 1413.5 | |
| 0.0075 | 289.13 | 483.50 | 1413.5 |
| Parameter | Value | Temperature (K) | Precipitation (mm) | Water |
|---|---|---|---|---|
| 0.075 | 289.38 | 664.40 | 2371.8 | |
| 0.075 | 289.38 | 663.77 | 2368.6 | |
| 0.0015 | 289.38 | 663.77 | 2368.6 | |
| 432 | 432.42 | 662.70 | 2363.3 | |
| 0.045 | 432.51 | 662.60 | 2362.7 | |
| 0.01125 | 432.63 | 662.53 | 2362.1 |
| Parameter | Value | Temperature (K) | Precipitation (mm) | Water |
|---|---|---|---|---|
| 0.01125 | 432.63 | 662.53 | 2362.1 | |
| 0.01125 | 432.63 | 662.63 | 2362.3 | |
| 0.01125 | 432.74 | 885.26 | 2727.6 | |
| 0.01125 | 432.74 | 885.60 | 2728.4 | |
| 0.1125 | 432.91 | 1463.1 | 5381.0 | |
| 0.1125 | 432.91 | 1462.9 | 5379.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.; Alfwzan, W.F.; Latif, R.; Alzabut, J.; Thinakaran, R. AI-Based Deep Learning of the Water Cycle System and Its Effects on Climate Change. Fractal Fract. 2025, 9, 361. https://doi.org/10.3390/fractalfract9060361
Khan H, Alfwzan WF, Latif R, Alzabut J, Thinakaran R. AI-Based Deep Learning of the Water Cycle System and Its Effects on Climate Change. Fractal and Fractional. 2025; 9(6):361. https://doi.org/10.3390/fractalfract9060361
Chicago/Turabian StyleKhan, Hasib, Wafa F. Alfwzan, Rabia Latif, Jehad Alzabut, and Rajermani Thinakaran. 2025. "AI-Based Deep Learning of the Water Cycle System and Its Effects on Climate Change" Fractal and Fractional 9, no. 6: 361. https://doi.org/10.3390/fractalfract9060361
APA StyleKhan, H., Alfwzan, W. F., Latif, R., Alzabut, J., & Thinakaran, R. (2025). AI-Based Deep Learning of the Water Cycle System and Its Effects on Climate Change. Fractal and Fractional, 9(6), 361. https://doi.org/10.3390/fractalfract9060361







