Multifractal Analysis of Tight Sandstone Using Micro-CT Methods: A Case from the Lower Cretaceous Quantou Formation, Southern Songliao Basin, NE China
Abstract
1. Introduction
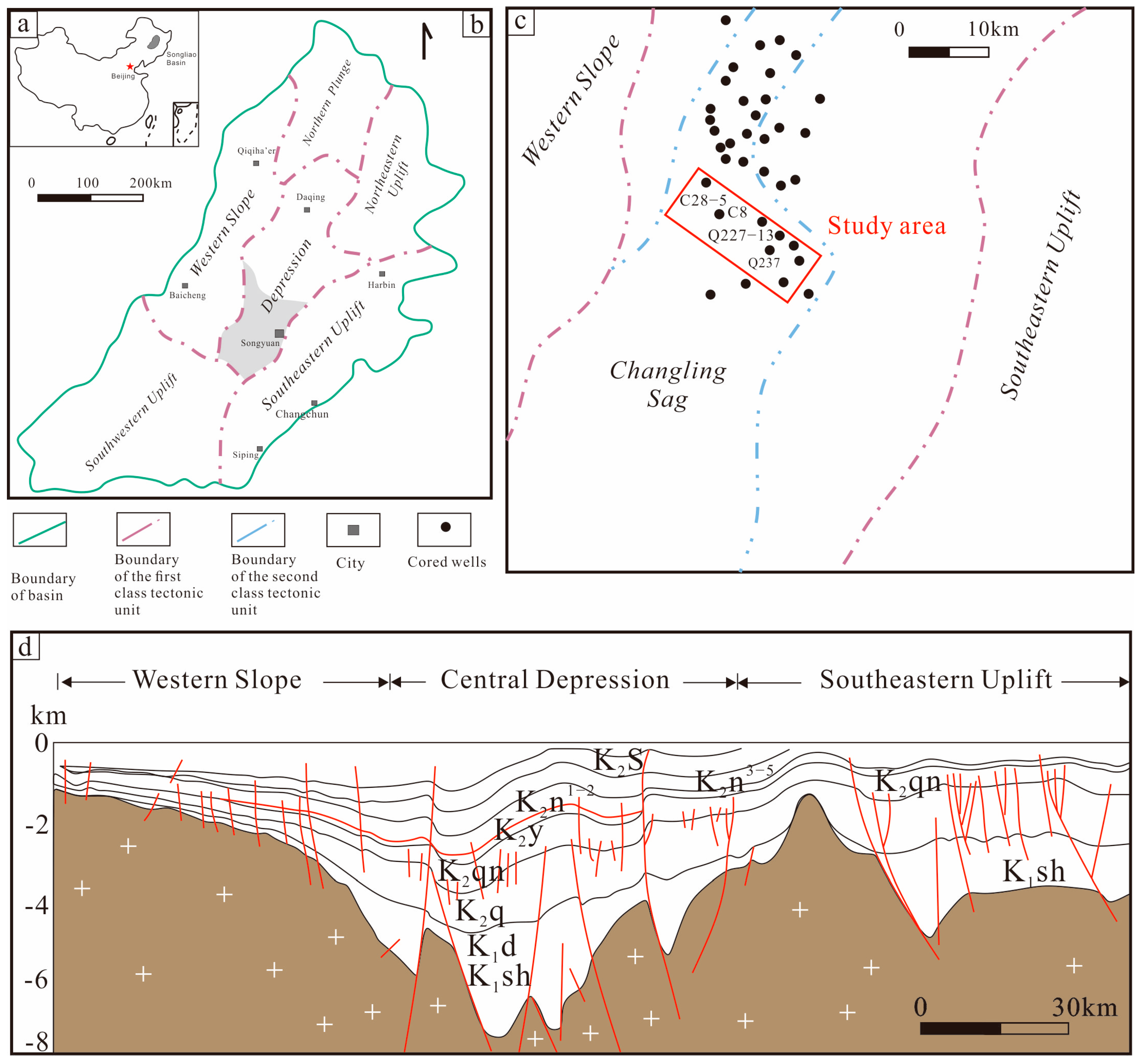
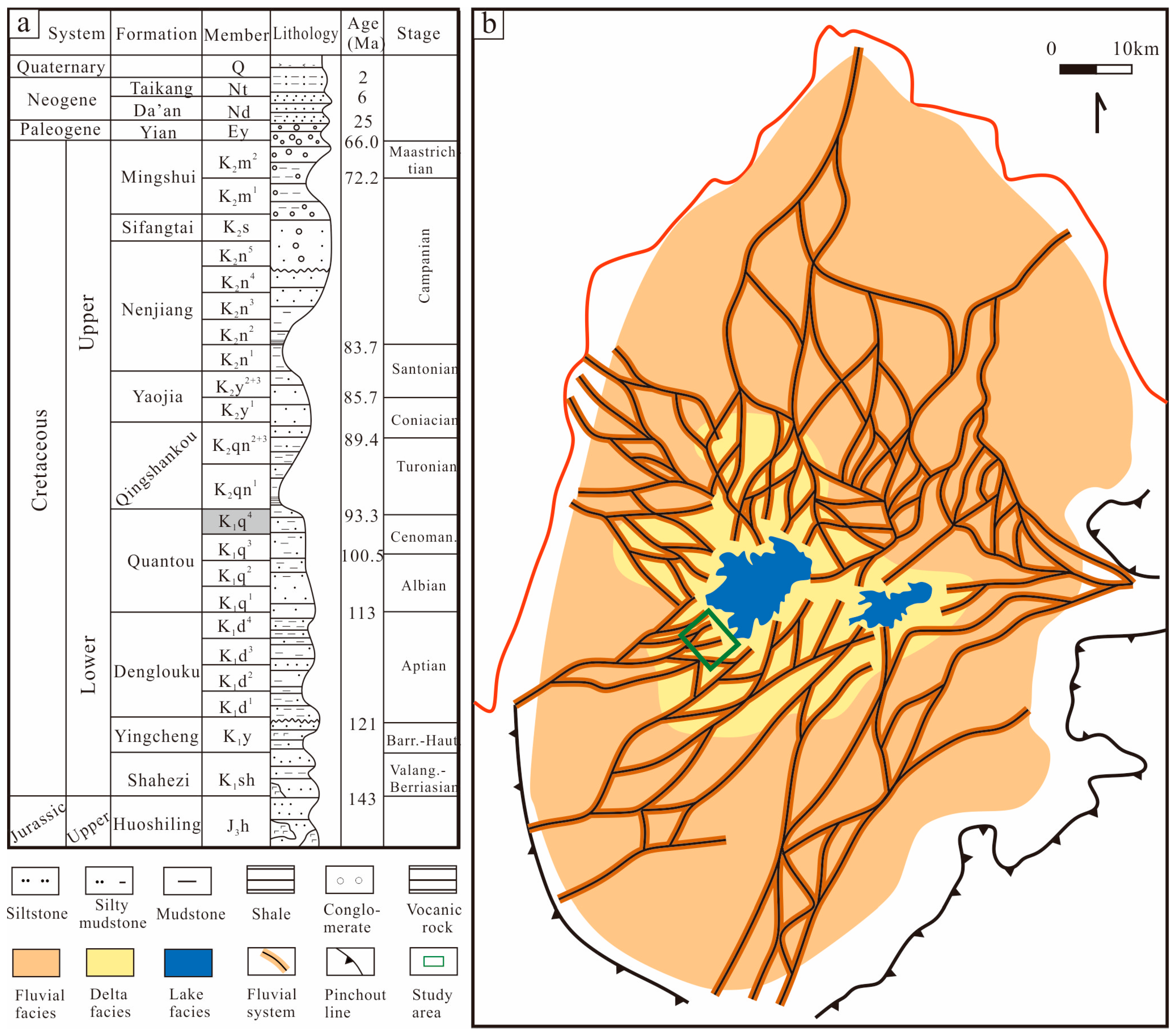
2. Geological Setting
3. The Experimental Work and Multifractal Theory
3.1. Sample Preparation and Experiments
3.1.1. XRD
3.1.2. Thin Sections and SEM
3.1.3. HPMI
3.1.4. Micro-CT
3.2. Multifractal Theory
4. Results
4.1. Mineralogical Compositions
4.2. Pore Morphology
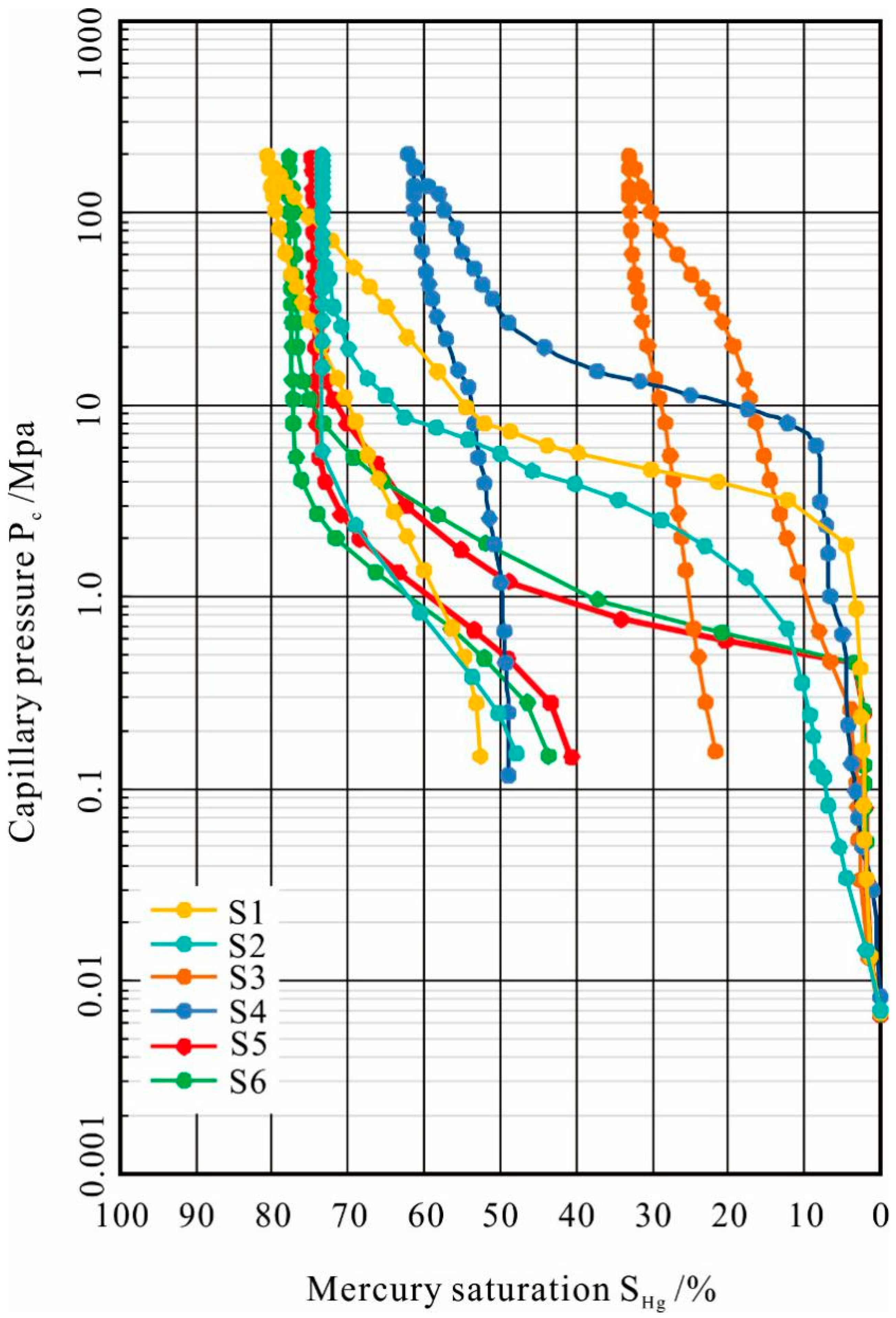
4.3. Mercury Intrusion Curves
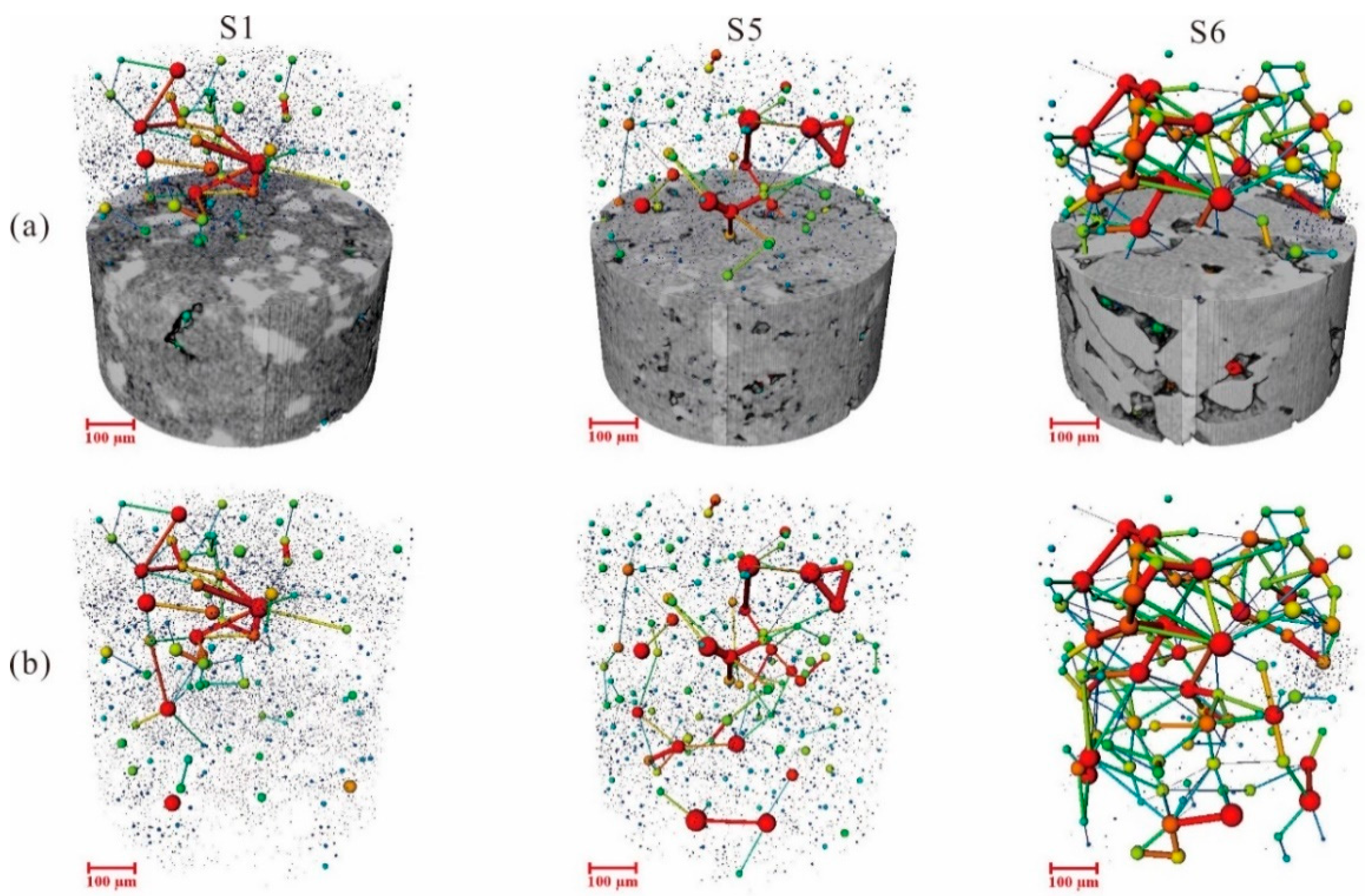
4.4. Three-Dimensional Micro-CT Models
5. Discussion
5.1. Pore System Characteristics of Tight Sandstone Reservoirs
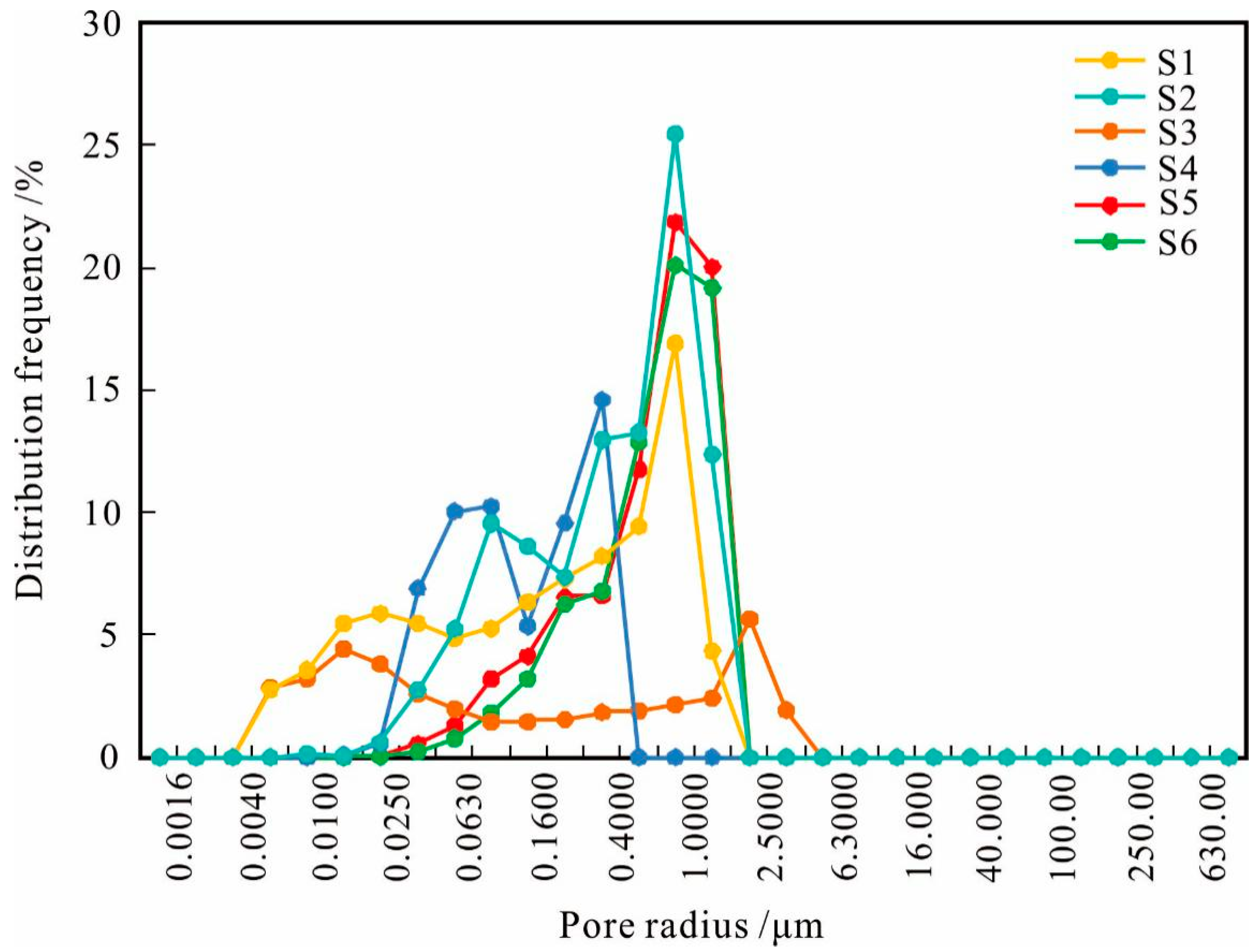
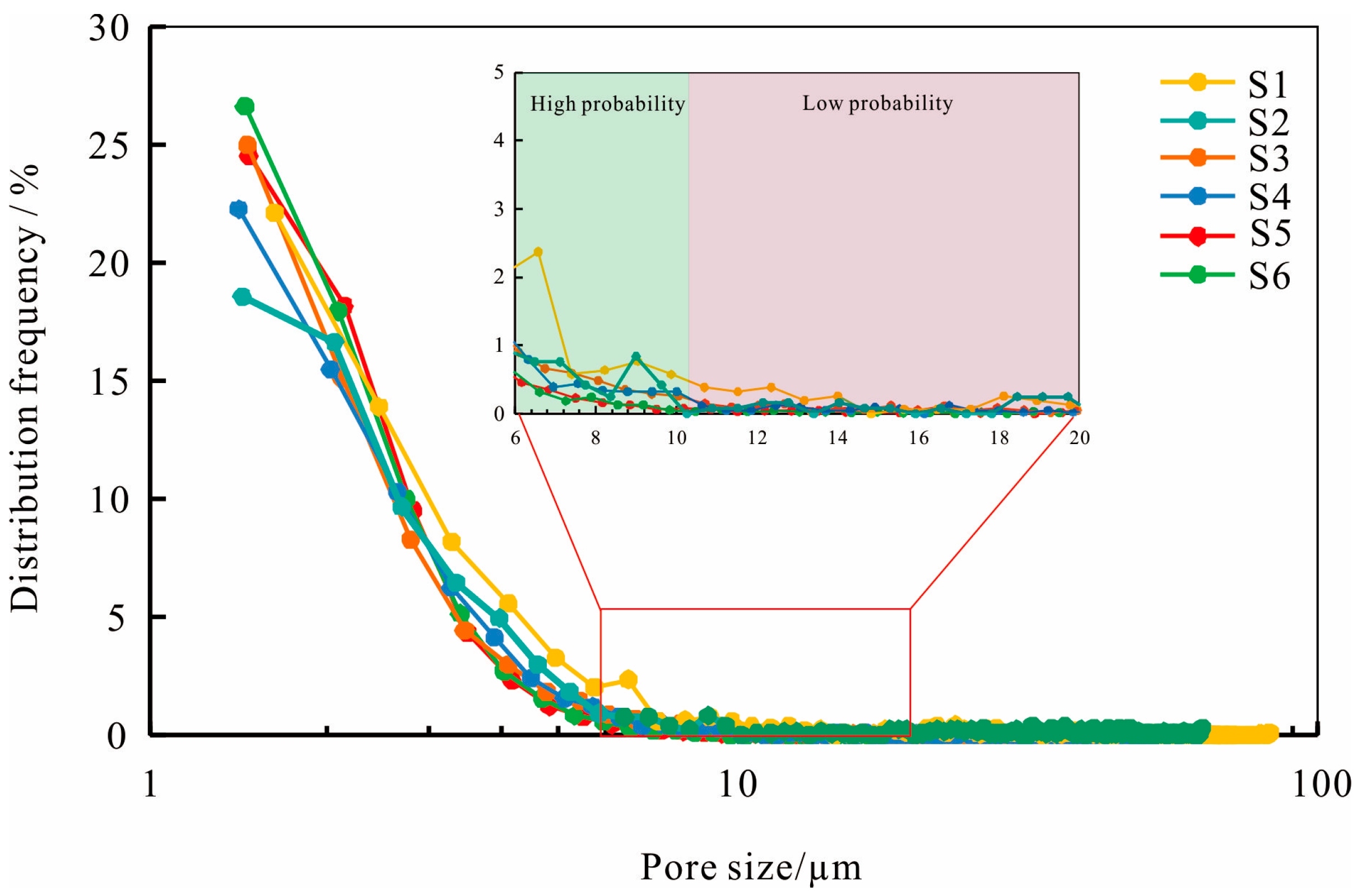
5.1.1. Pore Size Distribution
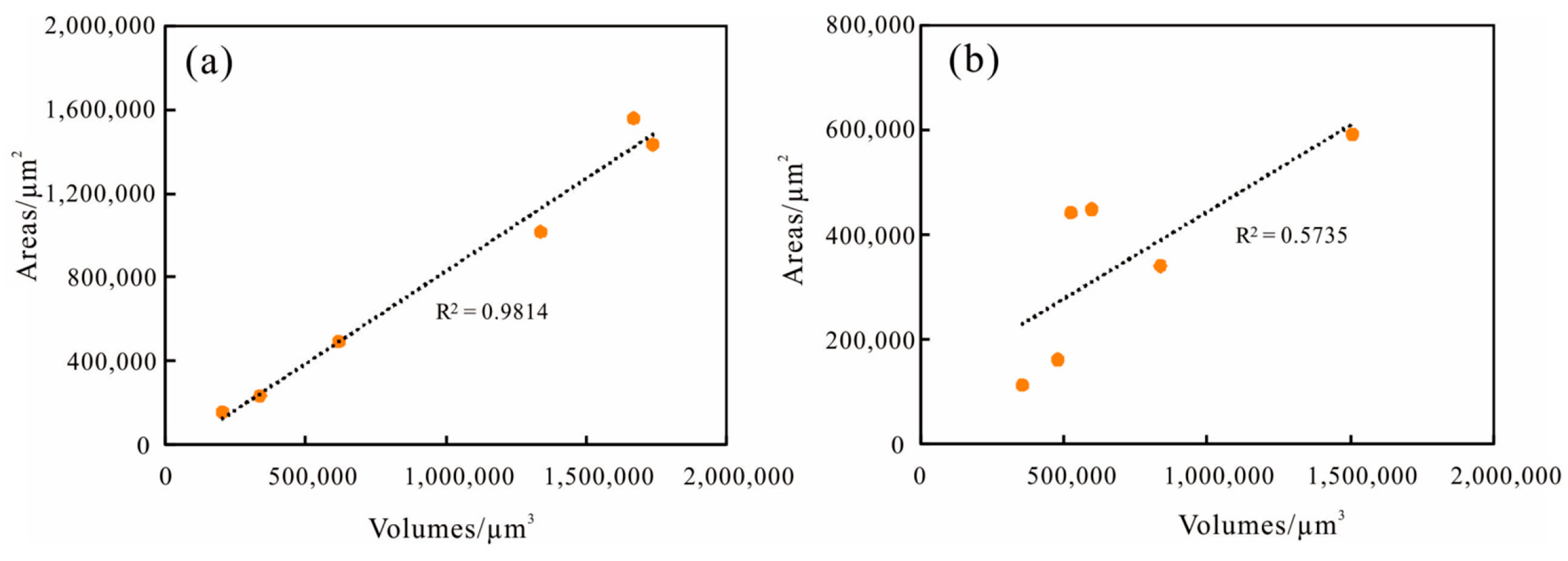
5.1.2. Pore Connectivity
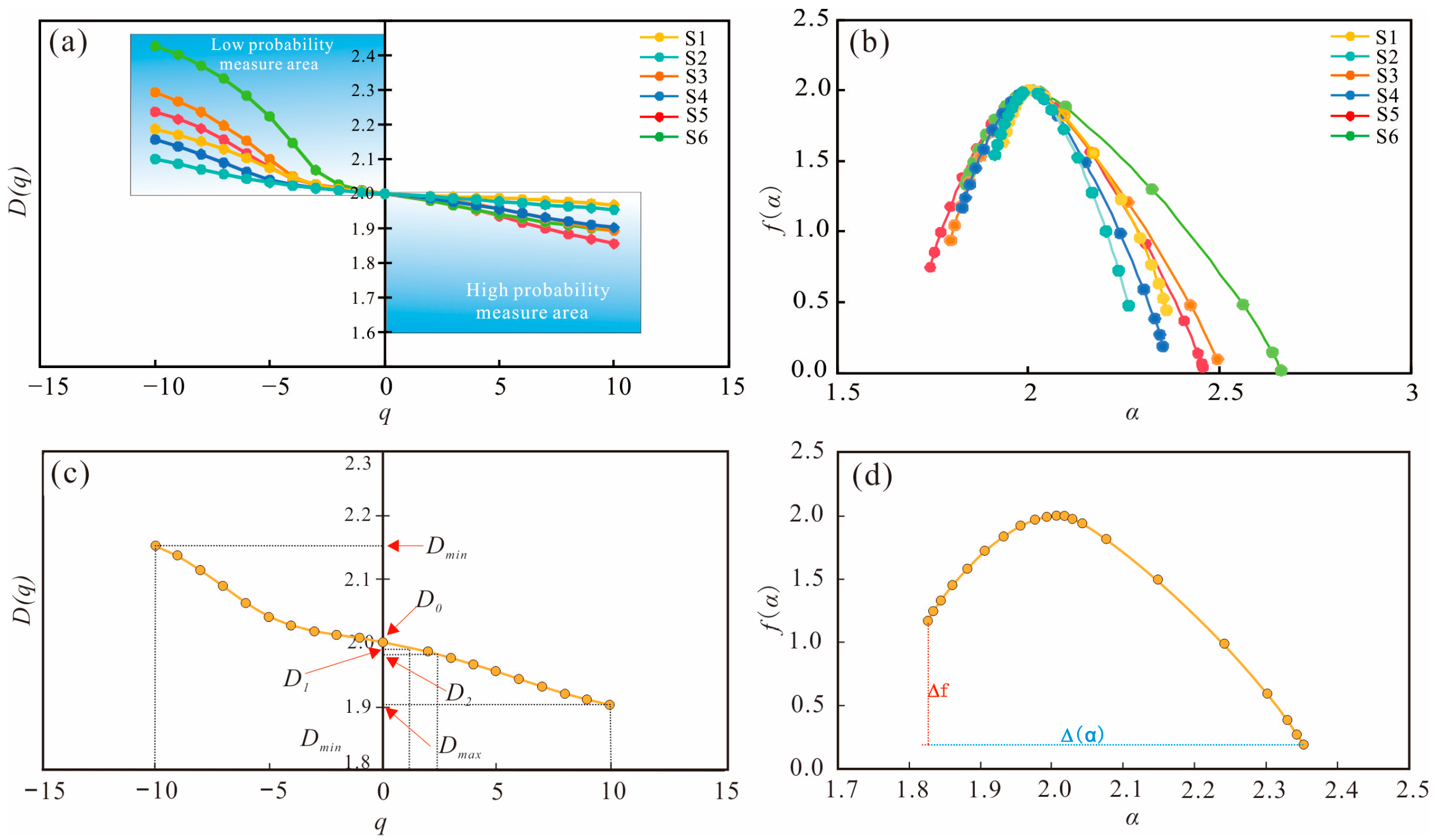
5.2. Multifractal Analyses of Tight Sandstone Reservoirs
5.2.1. Multiscale Pore Structure Determination
5.2.2. Multifractal Analyses for Multiscale Pore Structure
5.3. The Research Significance of Characterizing Pore Structure Based on Multi-Fractal Dimension
5.3.1. The Relationship Between Multifractal Characteristics and Rock Physical Properties
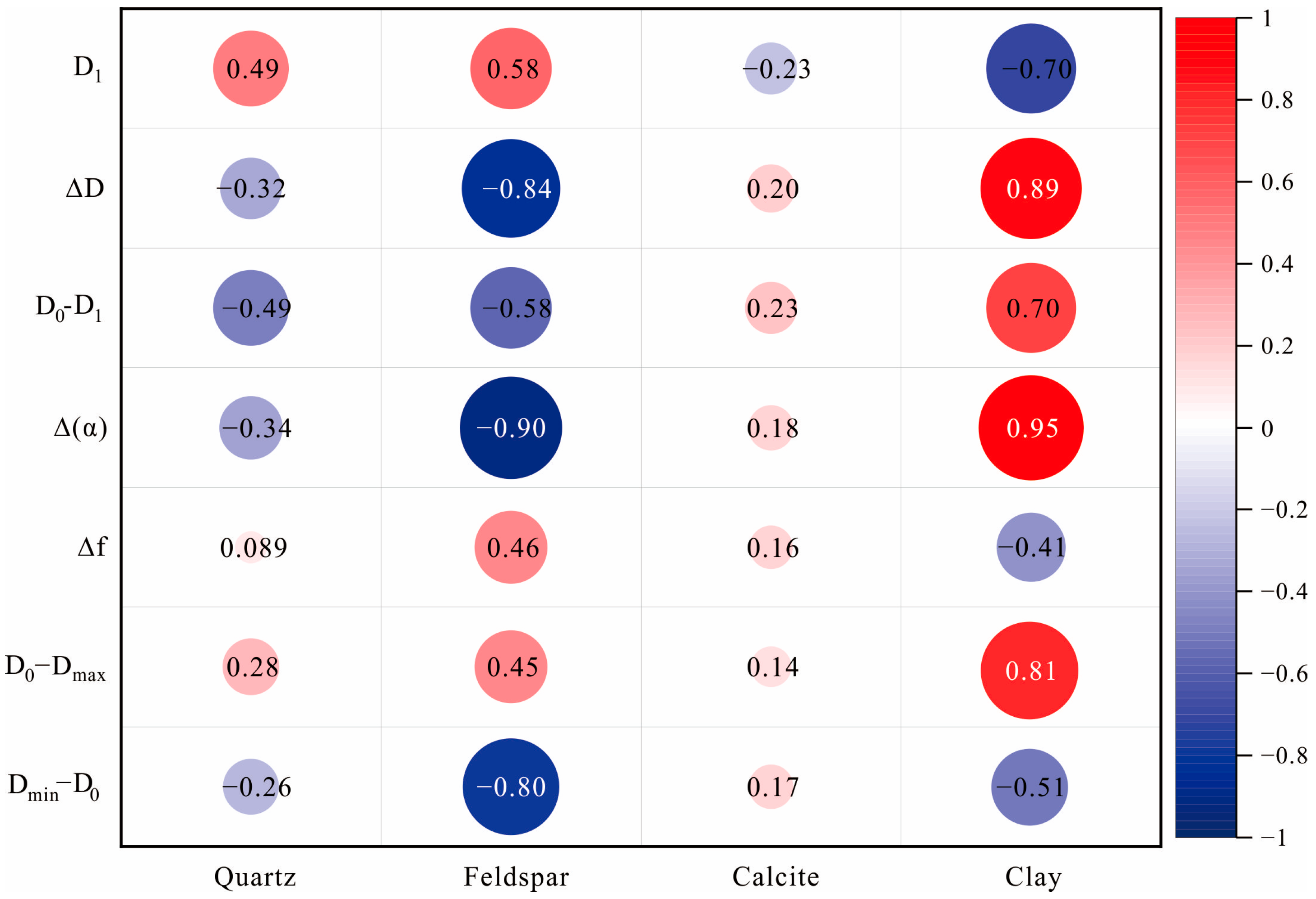
5.3.2. The Relationship Between Multifractal Parameters and Mineral Composition
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman: New York, NY, USA, 1982. [Google Scholar]
- Broseta, D.; Barré, L.; Vizika, O.; Shahidzadeh, N.; Guilbaud, J.; Lyonnard, S. Capillary condensation in a fractal porous medium. Phys. Rev. Lett. 2001, 86, 5313. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, Z.; Pan, Z.; Niu, X.; Yu, Y.; Meng, S. Pore structure and its fractal dimensions of transitional shale: A cross-section from east margin of the Ordos Basin, China. Fuel 2019, 241, 417–431. [Google Scholar] [CrossRef]
- Xin, Y.; Wang, G.; Liu, B.; Ai, Y.; Cai, D.; Yang, S.; Liu, H.; Xie, Y.; Chen, K. Pore structure evaluation in ultra-deep tight sandstones using NMR measurements and fractal analysis. J. Pet. Sci. Eng. 2022, 211, 110180. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, C.; Ouyang, S.; Luo, B.; Zhao, D.; Sun, W.; Awan, R.S.; Lu, Z.; Li, G.; Zang, Q. Investigation of pore-throat structure and fractal characteristics of tight sandstones using HPMI, CRMI, and NMR methods: A case study of the lower Shihezi Formation in the Sulige area, Ordos Basin. J. Pet. Sci. Eng. 2022, 210, 110053. [Google Scholar] [CrossRef]
- Anovitz, L.M.; Cole, D.R.; Jackson, A.J.; Rother, G.; Littrell, K.C.; Allard, L.F.; Pollington, A.D.; Wesolowski, D.J. Effect of quartz overgrowth precipitation on the multiscale porosity of sandstone: A (U) SANS and imaging analysis. Geochim. Cosmochim. Acta 2015, 158, 199–222. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Xiao, X.; Chen, Y.N.; Han, D. Pore Structure and Fractal Characteristics of Inter-Layer Sandstone in Marine–Continental Transitional Shale: A Case Study of the Upper Permian Longtan Formation in Southern Sichuan Basin, South China. Fractal Fract. 2024, 9, 11. [Google Scholar] [CrossRef]
- Shanley, K.W.; Cluff, R.M. The evolution of pore-scale fluid-saturation in low-permeability sandstone reservoirs. AAPG Bull. 2015, 99, 1957–1990. [Google Scholar] [CrossRef]
- Wang, W.; Lin, C.; Zhang, X. Fractal Characteristics of Pore Throat and Throat of Tight Sandstone Sweet Spot: A Case Study in the East China Sea Basin. Fractal Fract. 2024, 8, 684. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, Y.; Meng, X.; Li, Z.; Xie, Z.; Li, M. Characterization of micro-nano pore networks in shale oil reservoirs of Paleogene Shahejie Formation in Dongying Sag of Bohai Bay Basin, East China. Pet. Explor. Dev. 2017, 44, 720–730. [Google Scholar] [CrossRef]
- Liu, P.; Nie, B.; Zhao, Z.; Li, J.; Yang, H.; Qin, C. Permeability of micro-scale structure in coal: Insights from μ-CT image and pore network modelling. Gas Sci. Eng. 2023, 111, 204931. [Google Scholar] [CrossRef]
- Yang, R.; He, S.; Yi, J.; Hu, Q. Nano-scale pore structure and fractal dimension of organic-rich Wufeng-Longmaxi shale from Jiaoshiba area, Sichuan Basin: Investigations using FE-SEM, gas adsorption and helium pycnometry. Mar. Pet. Geol. 2016, 70, 27–45. [Google Scholar] [CrossRef]
- Sun, M.; Zhao, J.; Pan, Z.; Hu, Q.; Yu, B.; Tan, Y.; Sun, L.; Bai, L.; Wu, C.; Blach, T.P. Pore characterization of shales: A review of small angle scattering technique. J. Nat. Gas Sci. Eng. 2020, 78, 103294. [Google Scholar] [CrossRef]
- Liu, P.; Nie, B.; Zhao, Z.; Zhao, Y.; Li, Q. Characterization of ultrasonic induced damage on multi-scale pore/fracture in coal using gas sorption and μ-CT 3D reconstruction. Fuel 2023, 332, 126178. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, D.; Cai, Y.; Yao, Y.; Li, Z. 3D characterization and quantitative evaluation of pore-fracture networks of two Chinese coals using FIB-SEM tomography. Int. J. Coal Geol. 2017, 174, 41–54. [Google Scholar] [CrossRef]
- Soto-Gomez, D.; Perez-Rodriguez, P.; Juiz, L.V.; Paradelo, M.; Lopez-Periago, J.E. 3D multifractal characterization of computed tomography images of soils under different tillage management: Linking multifractal parameters to physical properties. Geoderma 2020, 363, 114129. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, M.; Sun, X.; Liu, B.; Ostadhassan, M.; Huang, W.; Chen, X.; Pan, Z. Pore network characterization of shale reservoirs through state-of-the-art X-ray computed tomography: A review. Gas Sci. Eng. 2023, 113, 204967. [Google Scholar] [CrossRef]
- Zhu, H.; Huang, C.; Ju, Y.; Bu, H.; Li, X.; Yang, M.; Chu, Q.; Feng, H.; Qiao, P.; Qi, Y. Multi-scale multi-dimensional characterization of clay-hosted pore networks of shale using FIBSEM, TEM, and X-ray micro-tomography: Implications for methane storage and migration. Appl. Clay Sci. 2021, 213, 106239. [Google Scholar] [CrossRef]
- Alyafei, N.; Mckay, T.J.; Solling, T.I. Characterization of petrophysical properties using pore-network and lattice-Boltzmann modelling: Choice of method and image sub-volume size. J. Pet. Sci. Eng. 2016, 145, 256–265. [Google Scholar] [CrossRef]
- Zhang, L.; Bao, Z.; Dou, L.; Xu, Q. Diagenetic alterations related to sedimentary architecture of deltaic distributary channels in red beds of the Cretaceous Yaojia Formation, Songliao Basin. J. Pet. Sci. Eng. 2021, 203, 108564. [Google Scholar] [CrossRef]
- Peng, H.; Jiao, Y.; Fu, X.; Wu, L.; Guo, X.; Wang, Q.; Liu, C. Provenance and uranium source tracing for uranium-bearing series in the south of Songliao Basin: Evidence from zircon UPb chronology and lithogeochemistry. J. Geochem. Explor. 2025, 272, 107703. [Google Scholar] [CrossRef]
- Feng, Z.; Jia, C.; Xie, X.; Zhang, S.; Feng, Z.; Cross, T.A. Tectonostratigraphic units and stratigraphic sequences of the nonmarine Songliao basin, northeast China. Basin Res. 2010, 22, 79–95. [Google Scholar]
- Li, L.; Bao, Z.; Li, L.; Li, Z.; Ban, S.; Li, Z.; Wang, T.; Li, Y.; Zheng, N.; Zhao, C. The source and preservation of lacustrine shale organic matter: Insights from the Qingshankou Formation in the Changling Sag, Southern Songliao Basin, China. Sediment. Geol. 2024, 466, 106649. [Google Scholar] [CrossRef]
- Xi, K.; Cao, Y.; Jahren, J.; Zhu, R.; Bjørlykke, K.; Zhang, X.; Cai, L.; Hellevang, H. Quartz cement and its origin in tight sandstone reservoirs of the Cretaceous Quantou formation in the southern Songliao basin, China. Mar. Pet. Geol. 2015, 66, 748–763. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, X.; Radwan, A.E.; Wang, B.; Wang, K.; Tian, H.; Yin, S. Diagenesis of continental tight sandstone and its control on reservoir quality: A case study of the Quan 3 member of the cretaceous Quantou Formation, Fuxin uplift, Songliao Basin. Mar. Pet. Geol. 2022, 145, 105883. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, S.; Feng, Z. Discovery of “Enveloping surface of oil and gas overpressure migration” in the Songliao Basin and its bearings on hydrocarbon migration and accumulation mechanisms. Sci. China Earth Sci. 2012, 55, 2005–2017. [Google Scholar] [CrossRef]
- Liu, B.; Wang, H.; Fu, X.; Bai, Y.; Bai, L.; Jia, M.; He, B. Lithofacies and depositional setting of a highly prospective lacustrine shale oil succession from the Upper Cretaceous Qingshankou Formation in the Gulong sag, northern Songliao Basin, northeast China. AAPG Bull. 2019, 103, 405–432. [Google Scholar] [CrossRef]
- Bish, D.L.; Howard, S.A. Quantitative phase analysis using the Rietveld method. Appl. Crystallogr. 1988, 21, 86–91. [Google Scholar] [CrossRef]
- Środoń, J.; Drits, V.A.; McCarty, D.K.; Hsieh, J.C.; Eberl, D.D. Quantitative X-ray diffraction analysis of clay-bearing rocks from random preparations. Clays Clay Miner. 2001, 49, 514–528. [Google Scholar] [CrossRef]
- Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; Jarvie, D.M. Morphology, genesis, and distribution of nanometer-scale pores in siliceous mudstones of the Mississippian Barnett Shale. J. Sediment. Res. 2009, 79, 848–861. [Google Scholar] [CrossRef]
- Milliken, K.L.; Rudnicki, M.; Awwiller, D.N.; Zhang, T. Organic matter–hosted pore system, Marcellus formation (Devonian), Pennsylvania. AAPG Bull. 2013, 97, 177–200. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, Z.; Sun, W.; Li, Y.; Zhang, X.; Zhu, L.; Wen, M. A multiscale comprehensive study on pore structure of tight sandstone reservoir realized by nuclear magnetic resonance, high pressure mercury injection and constant-rate mercury injection penetration test. Mar. Pet. Geol. 2019, 109, 208–222. [Google Scholar] [CrossRef]
- Klaver, J.; Desbois, G.; Littke, R.; Urai, J.L. BIB-SEM characterization of pore space morphology and distribution in postmature to overmature samples from the Haynesville and Bossier Shales. Mar. Pet. Geol. 2015, 59, 451–466. [Google Scholar] [CrossRef]
- Ramkumar, M.; Nagarajan, R.; Santosh, M. Advances in sediment geochemistry and chemostratigraphy for reservoir characterization. Energy Geosci. 2021, 2, 308–326. [Google Scholar] [CrossRef]
- Soleimani, M.; Jodeiri Shokri, B. 3D static reservoir modeling by geostatistical techniques used for reservoir characterization and data integration. Environ. Earth Sci. 2015, 74, 1403–1414. [Google Scholar] [CrossRef]
- Peyton, R.L.; Gantzer, C.J.; Anderson, S.H.; Haeffner, B.A.; Pfeifer, P. Fractal dimension to describe soil macropore structure using X ray computed tomography. Water Resour. Res. 1994, 30, 691–700. [Google Scholar] [CrossRef]
- Zeleke, T.B.; Si, B.C. Characterizing scale-dependent spatial relationships between soil properties using multifractal techniques. Geoderma 2006, 134, 440–452. [Google Scholar] [CrossRef]
- Li, R.; Hou, X.; Chen, L.; Fang, H.; Zheng, C. Multifractal investigation on multi-scale pore structure heterogeneity of high rank coal reservoirs. Nat. Resour. Res. 2022, 31, 1665–1685. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141. [Google Scholar] [CrossRef]
- Taud, H.; Martinez-Angeles, R.; Parrot, J.F.; Hernandez-Escobedo, L. Porosity estimation method by X-ray computed tomography. J. Pet. Sci. Eng. 2005, 47, 209–217. [Google Scholar] [CrossRef]
- Cao, Z.; Lin, C.; Dong, C.; Ren, L.; Han, S.; Dai, J.; Xu, X.; Qin, M.; Zhu, P. Impact of sequence stratigraphy, depositional facies, diagenesis and CO2 charge on reservoir quality of the lower cretaceous Quantou Formation, Southern Songliao Basin, China. Mar. Pet. Geol. 2018, 93, 497–519. [Google Scholar] [CrossRef]
- Zhou, N.; Wang, M.; Lu, S.; Dodd, T.J.; Liu, W.; Guan, Y. Evolution of fractal pore structure in sedimentary rocks. Earth Space Sci. 2022, 9, e2021E–e2167E. [Google Scholar] [CrossRef]
- Zhang, P.; Misch, D.; Meng, Q.; Sachsenhofer, R.F.; Liu, Z.; Jia, J.; Gao, F.; Bechtel, A.; Hu, F. Lateral changes of organic matter preservation in the lacustrine Qingshankou Formation (Cretaceous Songliao Basin, NE China): Evidence for basin segmentation. Int. J. Coal Geol. 2022, 254, 103984. [Google Scholar] [CrossRef]
- Giffin, S.; Littke, R.; Klaver, J.; Urai, J.L. Application of BIB–SEM technology to characterize macropore morphology in coal. Int. J. Coal Geol. 2013, 114, 85–95. [Google Scholar] [CrossRef]
- Wang, F.; Yang, K.; Zai, Y. Multifractal characteristics of shale and tight sandstone pore structures with nitrogen adsorption and nuclear magnetic resonance. Pet. Sci. 2020, 17, 1209–1220. [Google Scholar] [CrossRef]
- Ramandi, H.L.; Mostaghimi, P.; Armstrong, R.T.; Saadatfar, M.; Pinczewski, W.V. Porosity and permeability characterization of coal: A micro-computed tomography study. Int. J. Coal Geol. 2016, 154, 57–68. [Google Scholar] [CrossRef]







| No. | Well | Depth/m | Lithology | Porosity/% | Permeability/×10−3 μm2 |
|---|---|---|---|---|---|
| S1 | C8 | 2390.01–2390.21 | siltstone | 4.34 | 0.19 |
| S2 | C8 | 2391.53–2391.73 | siltstone | 7.82 | 0.12 |
| S3 | C28-5 | 2221.67–2221.77 | siltstone | 7.29 | 0.25 |
| S4 | Q227-13 | 1678.69–1678.78 | fine sandstone | 9.84 | 0.69 |
| S5 | Q237 | 1665.12–1665.20 | fine sandstone | 12.65 | 0.71 |
| S6 | Q237 | 1684.47–1684.57 | fine sandstone | 6.91 | 0.29 |
| No. | Quartz (%) | Feldspar (%) | Calcite (%) | Ankerite (%) | Dolomite (%) | Siderite (%) | Pyrite (%) | Clay (%) |
|---|---|---|---|---|---|---|---|---|
| S1 | 26.2 | 10.5 | 5.20 | 3.20 | 0.00 | 1.40 | 2.40 | 51.10 |
| S2 | 30.6 | 12.1 | 4.30 | 0.00 | 0.00 | 2.90 | 2.30 | 47.80 |
| S3 | 35.8 | 6.7 | 2.40 | 3.90 | 0.00 | 1.40 | 2.40 | 47.40 |
| S4 | 36.2 | 21.5 | 3.20 | 0.00 | 6.20 | 1.10 | 0.60 | 31.20 |
| S5 | 30.4 | 32.8 | 6.70 | 0.00 | 9.10 | 1.60 | 0.30 | 19.10 |
| S6 | 34.4 | 30.2 | 1.20 | 0.00 | 13.20 | 0.60 | 0.30 | 20.10 |
| No. | Pore Size (μm) | Total Pores | Closed Pores | Connected Pores | Connected Pores Proportion | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Voxels Count | Volumes /μm3 | Areas /μm2 | Voxels Count | Volumes /μm3 | Areas /μm2 | Voxels Count | Volumes /μm3 | Areas /μm2 | Volumes | Areas | ||
| S5 | 1–2 | 8335 | 117,782.36 | 205,770.12 | 8193 | 116,116.53 | 202,759.29 | 142 | 1665.83 | 3010.83 | 1.41% | 1.46% |
| 2–3 | 4662 | 289,852.33 | 369,030.20 | 4535 | 281,931.05 | 358,951.09 | 127 | 7921.28 | 10,079.11 | 2.73% | 2.73% | |
| 3–4 | 1731 | 289,523.89 | 295,763.68 | 1651 | 276,190.81 | 282,052.21 | 80 | 13,333.08 | 13,711.46 | 4.61% | 4.64% | |
| 4–5 | 621 | 227,435.22 | 201,123.33 | 585 | 213,758.66 | 188,666.16 | 36 | 13,676.55 | 12,457.17 | 6.01% | 6.19% | |
| 5–6 | 256 | 173,501.81 | 136,826.30 | 237 | 160,439.21 | 126,410.63 | 19 | 13,062.60 | 10,415.67 | 7.53% | 7.61% | |
| 6–7 | 128 | 143,411.68 | 103,184.85 | 116 | 129,808.11 | 93,018.01 | 12 | 13,603.57 | 10,166.85 | 9.49% | 9.85% | |
| 7–8 | 76 | 131,031.73 | 82,624.81 | 70 | 120,922.97 | 76,200.67 | 6 | 10,108.76 | 6424.14 | 7.71% | 7.78% | |
| 8–9 | 44 | 113,469.66 | 67,596.48 | 38 | 98,022.09 | 58,972.12 | 6 | 15,447.57 | 8624.35 | 13.61% | 12.76% | |
| 9–10 | 22 | 78,972.38 | 39,991.28 | 18 | 64,495.11 | 32,562.76 | 4 | 14,477.27 | 7428.52 | 18.33% | 18.58% | |
| 10–11 | 21 | 102,918.69 | 55,810.80 | 15 | 74,569.52 | 39,265.61 | 6 | 28,349.17 | 16,545.19 | 27.55% | 29.65% | |
| 11–12 | 13 | 82,716.21 | 43,245.58 | 9 | 57,368.11 | 29,691.39 | 4 | 25,348.10 | 13,554.19 | 30.64% | 31.34% | |
| 12–13 | 10 | 79,822.47 | 37,244.55 | 8 | 64,188.14 | 29,090.07 | 2 | 15,634.33 | 8154.48 | 19.59% | 21.89% | |
| 13–14 | 13 | 134,382.71 | 58,804.19 | 12 | 124,591.66 | 55,514.33 | 1 | 9791.05 | 3289.85 | 7.29% | 5.59% | |
| 14–15 | 7 | 85,880.42 | 29,111.20 | 5 | 60,229.64 | 19,677.14 | 2 | 25,650.78 | 9434.06 | 29.87% | 32.41% | |
| 15–16 | 5 | 79,281.50 | 29,440.52 | 4 | 64,731.25 | 22,970.98 | 1 | 14,550.26 | 6469.53 | 18.35% | 21.97% | |
| 16–17 | 5 | 79,281.50 | 32,192.50 | 4 | 73,305.12 | 25,505.38 | 1 | 5976.38 | 6687.11 | 7.54% | 20.77% | |
| 17–18 | 5 | 110,734.78 | 48,231.80 | 4 | 86,852.87 | 40,792.45 | 1 | 23,881.91 | 7439.35 | 21.57% | 15.42% | |
| 18–19 | 3 | 77,233.56 | 31,460.01 | 1 | 25,977.08 | 13,003.42 | 2 | 51,256.48 | 18,456.59 | 66.37% | 58.67% | |
| 19–20 | 3 | 96,251.07 | 30,294.76 | 2 | 63,301.55 | 19,643.88 | 1 | 32,949.52 | 10,650.89 | 34.23% | 35.16% | |
| S6 | 1–2 | 548 | 7715.20 | 13,412.42 | 501 | 7073.34 | 12,290.67 | 47 | 641.86 | 1121.76 | 8.32% | 8.36% |
| 2–3 | 350 | 22,557.41 | 28,044.51 | 328 | 21,275.83 | 26,429.65 | 22 | 1281.57 | 1614.86 | 5.68% | 5.76% | |
| 3–4 | 161 | 28,366.35 | 26,974.31 | 142 | 24,648.28 | 23,549.24 | 19 | 3718.07 | 3425.07 | 13.11% | 12.70% | |
| 4–5 | 103 | 39,196.39 | 30,939.30 | 93 | 35,370.99 | 28,101.40 | 10 | 3825.40 | 2837.90 | 9.76% | 9.17% | |
| 5–6 | 61 | 42,482.98 | 29,813.39 | 54 | 37,728.06 | 26,450.01 | 7 | 4754.92 | 3363.38 | 11.19% | 11.28% | |
| 6–7 | 39 | 45,776.00 | 28,830.38 | 35 | 41,293.71 | 25,896.72 | 4 | 4482.29 | 2933.66 | 9.79% | 10.18% | |
| 7–8 | 21 | 34,198.90 | 19,555.06 | 19 | 31,135.58 | 18,046.79 | 2 | 3063.33 | 1508.27 | 8.96% | 7.71% | |
| 8–9 | 13 | 33,909.10 | 16,717.22 | 10 | 26,870.11 | 13,151.42 | 3 | 7038.99 | 3565.79 | 20.76% | 21.33% | |
| 9–10 | 14 | 49,959.89 | 24,831.22 | 11 | 40,140.94 | 19,198.60 | 3 | 9818.96 | 5632.62 | 19.65% | 22.68% | |
| 10–11 | 7 | 32,807.85 | 16,136.72 | 5 | 22,892.29 | 10,930.56 | 2 | 9915.56 | 5206.16 | 30.22% | 32.26% | |
| 11–12 | 10 | 62,120.89 | 27,582.33 | 6 | 37,652.92 | 16,740.58 | 4 | 24,467.96 | 10,841.75 | 39.39% | 39.31% | |
| 12–13 | 6 | 49,818.21 | 22,236.36 | 4 | 33,864.02 | 14,596.28 | 2 | 15,954.19 | 7640.08 | 32.02% | 34.36% | |
| 13–14 | 4 | 42,510.88 | 15,965.30 | 3 | 33,026.81 | 12,520.39 | 1 | 9484.07 | 3444.91 | 22.31% | 21.58% | |
| 14–15 | 3 | 38,249.70 | 12,594.01 | 2 | 25,036.83 | 8389.07 | 1 | 13,212.87 | 4204.94 | 34.54% | 33.39% | |
| 15–16 | 1 | 79,281.50 | 6463.29 | 0 | 0.00 | 0.00 | 1 | 15,632.19 | 6463.29 | 100.00% | 100.00% | |
| 16–17 | 1 | 15,632.19 | 4761.29 | 0 | 0.00 | 0.00 | 1 | 15,632.19 | 4761.29 | 100.00% | 100.00% | |
| 17–18 | 1 | 21,649.36 | 5884.28 | 0 | 0.00 | 0.00 | 1 | 21,649.36 | 5884.28 | 100.00% | 100.00% | |
| 18–19 | 4 | 106,563.79 | 26,574.31 | 1 | 27,666.53 | 6533.34 | 3 | 78,897.26 | 20,040.97 | 74.04% | 75.41% | |
| 19–20 | 4 | 123,655.73 | 39,967.66 | 1 | 30,877.98 | 9860.40 | 3 | 92,777.75 | 30,107.26 | 75.03% | 75.33% | |
| No. | D1 | D0 − D1 | ∆(α) | ∆f | D0 − Dmax | Dmin − D0 | |
|---|---|---|---|---|---|---|---|
| S1 | 1.9875 | 0.3820 | 0.0125 | 0.7127 | 0.7080 | 0.0323 | 0.2366 |
| S2 | 1.9887 | 0.5341 | 0.0113 | 0.8242 | 1.3173 | 0.1066 | 0.3275 |
| S3 | 1.9977 | 0.4003 | 0.0023 | 0.6980 | 0.8391 | 0.1078 | 0.2925 |
| S4 | 1.9913 | 0.2543 | 0.0087 | 0.5243 | 0.9802 | 0.0668 | 0.1556 |
| S5 | 1.9994 | 0.2197 | 0.0006 | 0.4276 | 1.1887 | 0.1454 | 0.1874 |
| S6 | 1.9988 | 0.1471 | 0.0012 | 0.3505 | 1.0669 | 0.0988 | 0.1402 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Li, Z.; Han, H.; Liu, C.; Li, Y.; Zhao, W.; Wang, J.; Bao, Z. Multifractal Analysis of Tight Sandstone Using Micro-CT Methods: A Case from the Lower Cretaceous Quantou Formation, Southern Songliao Basin, NE China. Fractal Fract. 2025, 9, 336. https://doi.org/10.3390/fractalfract9060336
Li L, Li Z, Han H, Liu C, Li Y, Zhao W, Wang J, Bao Z. Multifractal Analysis of Tight Sandstone Using Micro-CT Methods: A Case from the Lower Cretaceous Quantou Formation, Southern Songliao Basin, NE China. Fractal and Fractional. 2025; 9(6):336. https://doi.org/10.3390/fractalfract9060336
Chicago/Turabian StyleLi, Lei, Zhongcheng Li, Haotian Han, Chao Liu, Yilin Li, Wanchun Zhao, Jianyi Wang, and Zhidong Bao. 2025. "Multifractal Analysis of Tight Sandstone Using Micro-CT Methods: A Case from the Lower Cretaceous Quantou Formation, Southern Songliao Basin, NE China" Fractal and Fractional 9, no. 6: 336. https://doi.org/10.3390/fractalfract9060336
APA StyleLi, L., Li, Z., Han, H., Liu, C., Li, Y., Zhao, W., Wang, J., & Bao, Z. (2025). Multifractal Analysis of Tight Sandstone Using Micro-CT Methods: A Case from the Lower Cretaceous Quantou Formation, Southern Songliao Basin, NE China. Fractal and Fractional, 9(6), 336. https://doi.org/10.3390/fractalfract9060336










