Multifractal Cross-Correlation Analysis of Carbon Emission Markets Between the European Union and China: A Study Based on the Multifractal Detrended Cross-Correlation Analysis and Empirical Mode Decomposition Multifractal Detrended Cross-Correlation Analysis Methods
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1.
3.2. MF-DCCA
3.3. EMD-MF-DCCA
4. Data
5. Empirical Analysis
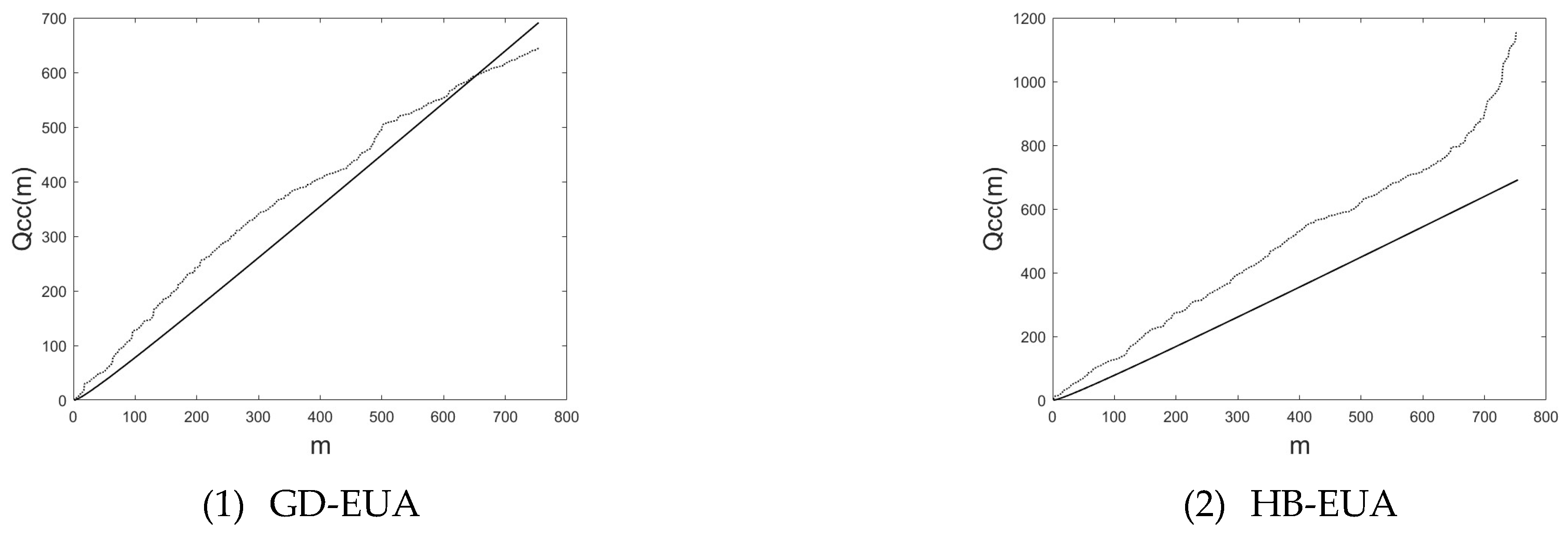
5.1. Cross-Correlation Test
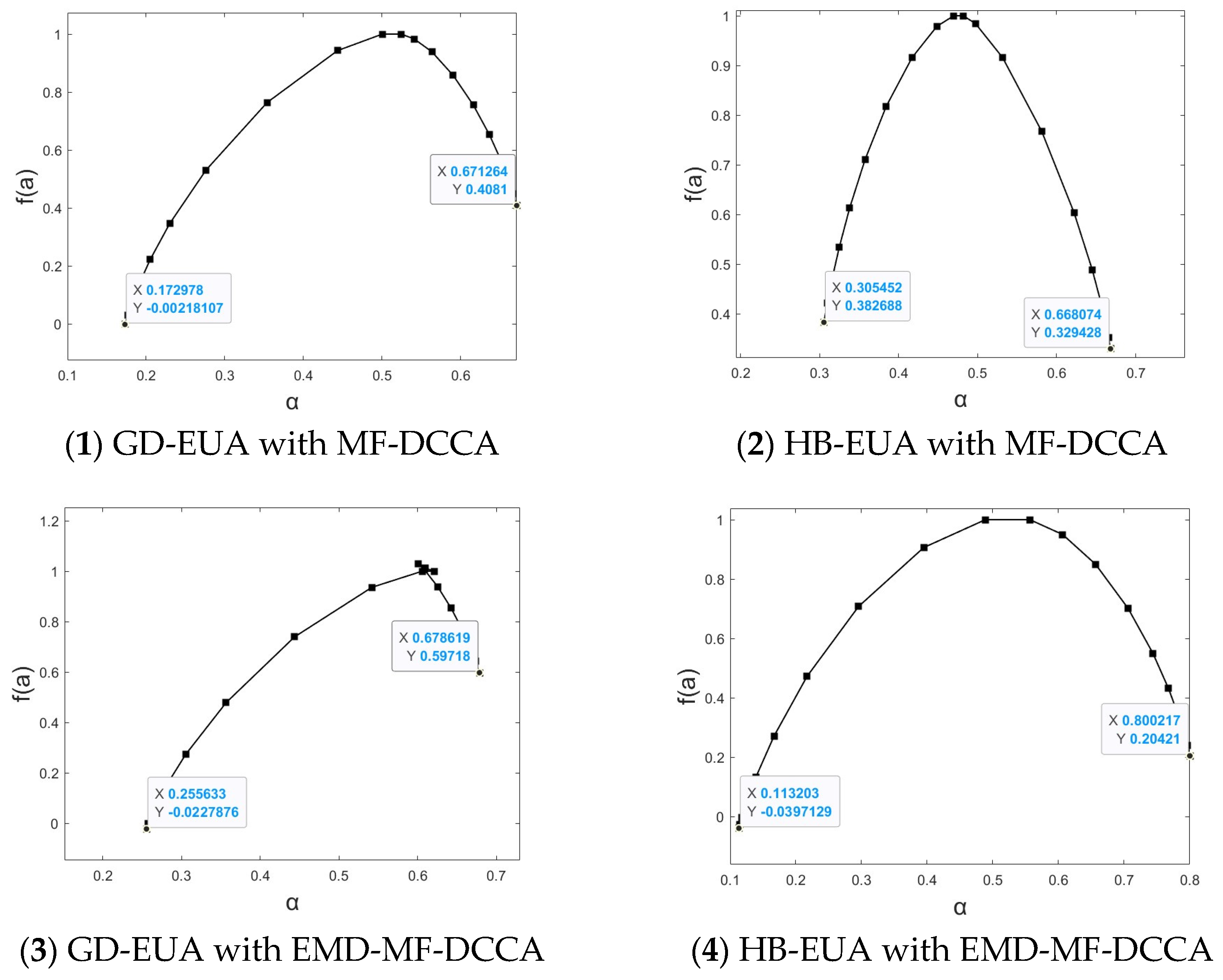
5.2. Cross-Correlation of Multiple Fractal Features
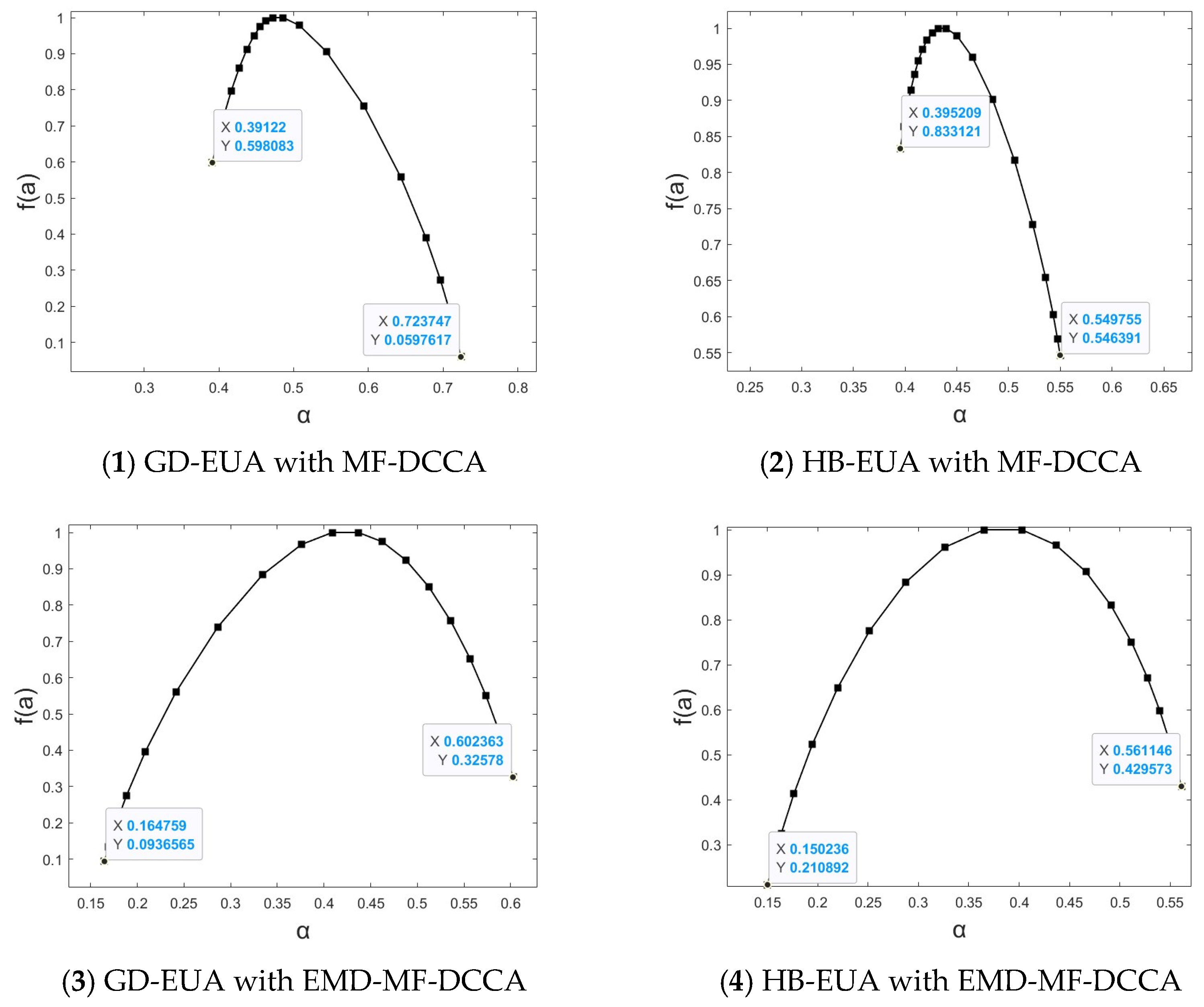
6. Multiple Fractal Source Analysis
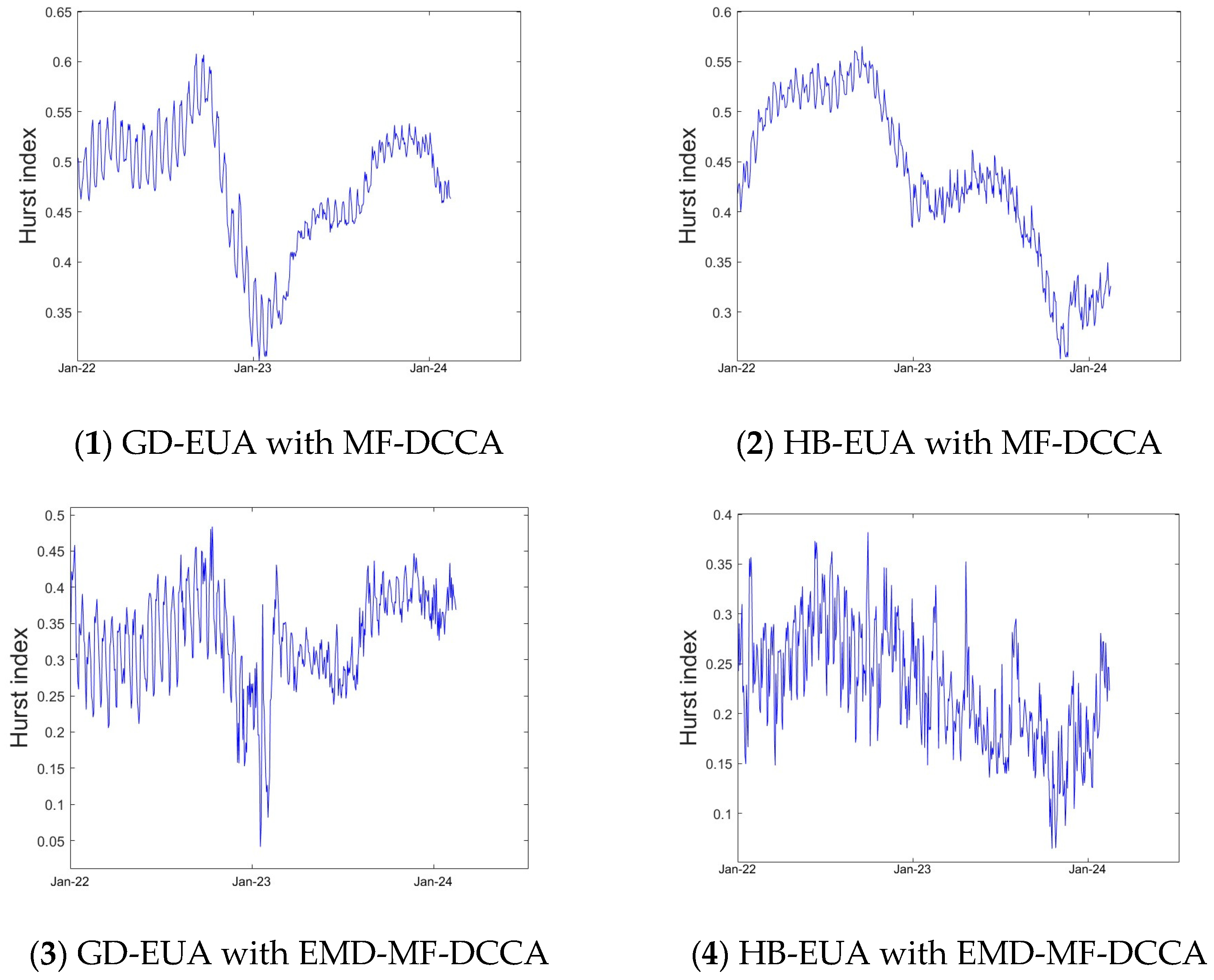
7. Sliding Window Analysis
8. Conclusions and Recommendations
8.1. Conclusions
8.2. Recommendations
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, L.; Xiang, M.; Shen, Q. A comparative study on the volatility of EU and China’s carbon emission permits trading markets. Phys. A Stat. Mech. Appl. 2020, 560, 125037. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, C.; Pan, D.; Hu, S. Multifractal cross-correlation analysis between carbon spot and futures markets considering asymmetric conduction effect. Fractals 2021, 29, 2150176. [Google Scholar] [CrossRef]
- Meng, J.; Hu, S.; Mo, B. Dynamic tail dependence on China’s carbon market and EU carbon market. Data Sci. Financ. Econ. 2021, 1, 393–407. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, Z. Time-varying risk aversion and dynamic dependence between crude oil futures and European Union allowance futures markets. Front. Environ. Sci. 2023, 11, 1152761. [Google Scholar] [CrossRef]
- Benz, E.; Trück, S. Modeling the price dynamics of CO2 emission allowances. Energy Econ. 2009, 31, 4–15. [Google Scholar] [CrossRef]
- Yu, J.; Mallory, M.L. Carbon price interaction between allocated permits and generated offsets. Oper. Res. 2020, 20, 671–700. [Google Scholar] [CrossRef]
- Zhu, B.; Han, D.; Wang, P.; Wu, Z.; Zhang, T.; Wei, Y.M. Forecasting carbon price using empirical mode decomposition and evolutionary least squares support vector regression. Appl. Energy 2019, 191, 521–530. [Google Scholar] [CrossRef]
- Yu, L.; Li, C.; Wang, J.; Sun, H. A hybrid model for predicting the carbon price in Beijing: A pilot low-carbon city in China. Front. Phys. 2024, 12, 1427794. [Google Scholar] [CrossRef]
- Qi, S.; Cheng, S.; Tan, X.; Feng, S.; Zhou, Q. Predicting China’s carbon price based on a multi-scale integrated model. Appl. Energy 2022, 324, 119784. [Google Scholar] [CrossRef]
- Sun, W.; Huang, C. A carbon price prediction model based on secondary decomposition algorithm and optimized back propagation neural network. J. Clean. Prod. 2020, 243, 118671. [Google Scholar] [CrossRef]
- Zhou, W. Multifractal detrended cross-correlation analysis for two nonstationary signals. Phys. Rev. E 2008, 77, 066211. [Google Scholar] [CrossRef] [PubMed]
- Zou, S.; Zhang, T. Multifractal Detrended Cross-Correlation Analysis of Electricity and Carbon Markets in China. Math. Probl. Eng. 2019, 1, 13. [Google Scholar] [CrossRef]
- An, Y.; Jiang, K.; Song, J. Does a Cross-Correlation of Economic Policy Uncertainty with China’s Carbon Market Really Exist? A Perspective on Fractal Market Hypothesis. Sustainability 2023, 15, 10818. [Google Scholar] [CrossRef]
- Fan, X.; Lv, X.; Yin, J.; Tian, L.; Liang, J. Multifractality and market efficiency of carbon emission trading market: Analysis using the multifractal detrended fluctuation technique. Appl. Energy 2019, 251, 113333. [Google Scholar] [CrossRef]
- Podobnik, B.; Stanley, H.E. Detrended cross-correlation analysis: A new method for analyzing two nonstationary time series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [PubMed]
- Podobnik, B.; Grosse, I.; Horvatić, D.; Ilic, S.; Ivanov, P.C.; Stanley, H.E. Quantifying cross-correlations using local and global detrending approaches. Eur. Phys. J. B 2009, 71, 243–250. [Google Scholar] [CrossRef]
- Shadkhoo, S.; Jafari, G.R. Multifractal detrended cross-correlation analysis of temporal and spatial seismic data. Eur. Phys. J. B 2009, 72, 679–683. [Google Scholar] [CrossRef]
- Kantelhardt, J.; Zschiegner, S.; Bunde, E.K.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]




| Mean | Std. Dev. | Min | Median | Max | Skewness | Kurtosis | J-B | |
|---|---|---|---|---|---|---|---|---|
| EUA | 72.681 | 15.47 | 32.81 | 77.975 | 97.58 | −0.696 | 2.428 | 71.327 |
| HB | 42.903 | 6.457 | 27.22 | 45.005 | 61.48 | −0.809 | 2.619 | 87.105 |
| GD | 64.749 | 17.116 | 30.64 | 72.95 | 95.26 | −0.632 | 1.851 | 91.946 |
| q | MF-DCCA Method | EMD-MF-DCCA Method | ||
|---|---|---|---|---|
| GD-EUA | HB-EUA | GD-EUA | HB-EUA | |
| −10 | 0.612074238 | 0.601016823 | 0.638336613 | 0.720637866 |
| −9 | 0.605497572 | 0.593566022 | 0.633860841 | 0.711795760 |
| −8 | 0.597841228 | 0.58456948 | 0.628923317 | 0.701234052 |
| −7 | 0.588923627 | 0.573513491 | 0.623601284 | 0.688469500 |
| −6 | 0.578635205 | 0.559742604 | 0.618164641 | 0.672903769 |
| −5 | 0.567089634 | 0.542690056 | 0.613266044 | 0.653938745 |
| −4 | 0.554843097 | 0.52284656 | 0.610167946 | 0.631427177 |
| −3 | 0.542985368 | 0.50347946 | 0.610641367 | 0.606519114 |
| −2 | 0.532719171 | 0.48943375 | 0.615530332 | 0.581468008 |
| −1 | 0.524290483 | 0.481618116 | 0.621611513 | 0.556460242 |
| 0 | 0.511469118 | 0.475065391 | 0.612970200 | 0.518683102 |
| 1 | 0.500321768 | 0.469733574 | 0.606105505 | 0.488778941 |
| 2 | 0.471852482 | 0.459096756 | 0.574131289 | 0.441791954 |
| 3 | 0.432547122 | 0.445100073 | 0.530703222 | 0.393065725 |
| 4 | 0.393425024 | 0.429932075 | 0.487237611 | 0.349072761 |
| 5 | 0.360752264 | 0.415461571 | 0.450914220 | 0.312618647 |
| 6 | 0.334839748 | 0.402587316 | 0.422529583 | 0.283651923 |
| 7 | 0.314296833 | 0.391501845 | 0.400508118 | 0.260919736 |
| 8 | 0.297792746 | 0.382067176 | 0.383178602 | 0.243007416 |
| 9 | 0.284331564 | 0.374042206 | 0.369276187 | 0.228726195 |
| 10 | 0.273196219 | 0.367183185 | 0.357911881 | 0.217173829 |
| Δh | 0.338878019 | 0.233833638 | 0.280424732 | 0.503464037 |
| MF-DCCA | EMD-MF-DCCA | |||||||
|---|---|---|---|---|---|---|---|---|
| GD-EUA | HB-EUA | GD-EUA | HB-EUA | |||||
| ΔH | Δα | ΔH | Δα | ΔH | Δα | ΔH | Δα | |
| Original | 0.338878019 | 0.362622 | 0.233833638 | 0.498286 | 0.280424732 | 0.422986 | 0.503464037 | 0.687014 |
| Shuffled | 0.224481172 | 0.366747 | 0.09249771 | 0.441052 | 0.258676593 | 0.39247 | 0.419479703 | 0.579661 |
| Surrogate | 0.198311338 | 0.332527 | 0.274066896 | 0.154546 | 0.27954758 | 0.437604 | 0.274956401 | 0.41091 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, X.; Wang, Z.; Tong, H. Multifractal Cross-Correlation Analysis of Carbon Emission Markets Between the European Union and China: A Study Based on the Multifractal Detrended Cross-Correlation Analysis and Empirical Mode Decomposition Multifractal Detrended Cross-Correlation Analysis Methods. Fractal Fract. 2025, 9, 326. https://doi.org/10.3390/fractalfract9050326
Liao X, Wang Z, Tong H. Multifractal Cross-Correlation Analysis of Carbon Emission Markets Between the European Union and China: A Study Based on the Multifractal Detrended Cross-Correlation Analysis and Empirical Mode Decomposition Multifractal Detrended Cross-Correlation Analysis Methods. Fractal and Fractional. 2025; 9(5):326. https://doi.org/10.3390/fractalfract9050326
Chicago/Turabian StyleLiao, Xin, Zheyu Wang, and Huimin Tong. 2025. "Multifractal Cross-Correlation Analysis of Carbon Emission Markets Between the European Union and China: A Study Based on the Multifractal Detrended Cross-Correlation Analysis and Empirical Mode Decomposition Multifractal Detrended Cross-Correlation Analysis Methods" Fractal and Fractional 9, no. 5: 326. https://doi.org/10.3390/fractalfract9050326
APA StyleLiao, X., Wang, Z., & Tong, H. (2025). Multifractal Cross-Correlation Analysis of Carbon Emission Markets Between the European Union and China: A Study Based on the Multifractal Detrended Cross-Correlation Analysis and Empirical Mode Decomposition Multifractal Detrended Cross-Correlation Analysis Methods. Fractal and Fractional, 9(5), 326. https://doi.org/10.3390/fractalfract9050326






