Abstract
This article considers a class of Caputo fractional-order fuzzy cellular neural networks (CFOFCNNs) with transmission delays and uncertain perturbations. In particular, nonlinear activations and fuzzy operators AND and OR are investigated in the drive-response neural networks (NNs). To achieve practical finite-time (PFT) synchronization and finite-time (FT) synchronization of the studied systems, we design new nonlinear controllers including four feedback terms in this paper, and each carries a different role in the control process. Integrating different comparison principles and nonlinear feedback schemes, straightforward synchronization criteria of the CFOFCNNs are derived. Unlike existing works, a significant finding is that adjusting the feedback coefficients and parameters can enable synchronization switching. Namely, changing one of the feedback terms from positive to negative can cause PFT synchronization to switch to FT synchronization via adjusted control parameters, making our control methods applicable to different scenarios. The settling time depends explicitly on feedback coefficients, initial conditions, and fractional order.
1. Introduction
Recently, with the development of computer performance and artificial intelligence technology, varieties of NNs have received widespread attention from scholars and have been applied to different fields, including information encryption [1,2], optimal control [3,4], system stability [5,6,7,8], and signal sampling [9,10]. To better utilize NNs, researchers have focused on their fundamental dynamic properties and behaviors [11,12,13]. Synchronization in NNs means that different neurons adjust their behaviors to achieve a consistent state [14]. As an important property of NNs, synchronization shows the dynamic aggregation behavior of neurons. In reality, synchronization phenomena are prevalent, such as fireflies glowing, starlings migrating in flocks, neurons firing synchronously, crickets chirping synchronously, and pacemaker cells contracting.
1.1. Synchronization Principles and Applications
For two NNs, the drive network is the leader, and the response network is the follower. With the evolution of time, under the self-evolution of the network structure or the intervention of external control inputs, the evolution trajectories of the neurons in the response network remain consistent with the evolution trajectory of the neurons in the drive network, which is the generalized principle of synchronization. Neural synchronization plays a crucial role in cognitive functions of the human brain, including attention, memory, perception, and motor control.
Indeed, the ability of a neural network to achieve synchronization depends on the topological connectivity, the strength of the external control, and environmental factors. The study of synchronization phenomena helps to understand the evolution of NNs and their value in practical applications. For example, in image processing, neural network synchronization results can be used for image segmentation and secure image communication. In bioinformatics research, applying neuron synchronization mechanisms to DNA computing can develop molecular-level parallel processors. To date, there exist various synchronization modes, such as projection synchronization [15], Mittag-Leffler synchronization [16], master–slave synchronization [17], FT synchronization [18], and PFT synchronization [19,20].
1.2. Related Works
Partial NNs can achieve a state of self-organized synchronization through coupling strength and network structure adjustments. For the vast majority of networks, external control forces must intervene to enable neurons to achieve synchronization behavior [21]. For instance, Liu et al. [22] discussed the bipartite synchronization of coupled NNs through the external input of error information to part of the pinning neurons. In [23], Zhang et al. studied the global synchronization of coupled networks with impulsive perturbation via external impulse sampling control schemes. In [24], the research paid attention to a dynamic self-triggering mechanism to optimize the sampling frequency and synchronized memristive NNs by inputting error information only at special moments. Based on a simple linear controller and system solution method, Hua and Wang et al. [25] conducted exponential synchronization analysis on multilayer cellular NNs. By output-based adaptive schemes, Alsaedi and Cao et al. [26] devoted themselves to exploring the system synchronization of master-slave memristive NNs.
The above neural network synchronization models mainly rely on integer order calculus operators. Fractional calculus adds a degree that includes information from the initial instant to the current moment [27]. Different from integer calculus, fractional-order operators have non-locality and long-term memorization [28,29]. Hence, fractional-order NNs break through the localization and Markovian limitations of integer-order models through differential-order degrees of freedom and are particularly suitable for describing complex biophysical phenomena, such as memory dependence, fractal structure, multi-scale dynamics, and heat transport [30,31]. With the exploration of fractional order properties, researchers have begun to discuss the synchronization of fractional-order NNs. Based on the matrix and inequality analysis, Yang et al. [32] investigated the existence of equilibrium points in the fractional-order NNs and derived the Mittag-Leffler synchronization criteria for drive-response models. By the fractional nature of Caputo, Bao et al. [33] studied the projection synchronization problem for fractional-order NNs with discontinuous sides via a hybrid controller. In [34], the authors addressed the synchronization of fractional delayed NNs by combining adaptive laws and error feedback control. To better describe real systems, Yan et al. [35] established nonintegral order associative memory NNs with parameter perturbations and explored the master-slave synchronization problem in networks using the properties of fractional calculus and the Barbalat Lemma.
NNs are susceptible to external perturbations, metric inaccuracies, and environmental influences in the real world [36]. Especially for nonlinear NNs, it is common that partial parameters cannot be precisely measured [37,38]. For example, in [39], Yang et al. evaluated the asymptotic synchronization of complex-valued NNs with uncertain parameters via feedback control strategies. In [40], Peng et al. dealt with the FT synchronization of fractional multiplex networks with uncertain couplings. In [41], Du et al. acquired the FT synchronization conditions for nonintegral order cellular NNs with uncertain links with the aid of information feedback methods. On the other hand, network modeling and inference approaches are generally fuzzy or imprecise [42]. Fuzzy operators can be used as an efficacious assessment implement to model various complex systems and NNs [43]. In [44], Zhao et al. discussed the FT synchronization of fuzzy systems via feedback and adaptive control schemes. In [45], Du et al. explored the FT synchronization of fractional delayed NNs with fuzzy operators by the Laplace transform. In [19], the authors analyzed the PFT synchronization for fractional delayed fuzzy NNs via nonlinear control methods.
1.3. Research Motivation and Highlights
The above analysis shows that there have been many synchronization results on fractional-order NNs. However, few studies have considered the problems of PFT and FT synchronization of fractional-order fuzzy cellular NNs with transmission delays and uncertain perturbations through nonlinear information feedback, especially the switching problem between the two synchronization modes. How to design the relevant controllers and tune the parameters for synchronization mode switching is the main motivation and challenge of this paper. Inspired by the above findings, this paper explores the PFT and FT synchronization issues for CFOFCNNs with transmission delays and uncertainties by applying nonlinear information feedback schemes. In particular, the feedback links and templates contemplate uncertain perturbations, and all activations can be nonlinear. The major innovations of our work are enumerated in two aspects. First, new nonlinear feedback controllers are proposed to ensure the PFT and FT synchronization for CFOFCNNs based on stability principles and matrix analytical techniques. We provide a quantitative estimation of the synchronization settling time, which depends on the feedback coefficients, the initial conditions, and the fractional order. Second, theoretical analysis and experiments show that adjusting the feedback coefficients and control parameters can enable synchronization mode switching. Unlike the existing results [31,41,45], when one of four feedback terms in the controller is positive, PFT synchronization but not FT synchronization can be achieved by designing appropriate control parameters. Moreover, if all the feedback terms are negative, suitable parameters can be selected to achieve network FT synchronization, making our control strategies more widely applicable.
2. Background Knowledge and Cellular Neural Networks
This subsection gives background knowledge about fractional operators, including definitions, assumptions, and stability principles. Then, the transmission delays and multiple fuzzy operators are introduced into the fractional-order master-slave cellular NNs.
Definition 1
([27]). The -order Caputo derivative of is
where . More specifically, if , then .
Definition 2
([27]). The fractional integral of is
where , and .
Consider a class of CFOFCNNs with transmission delays and uncertain perturbations as follows:
where , and . is the state variable of neuron u. and represent the activation functions of NNs. is the positive delay signal. represents the self-feedback coefficient. and denote the uncertain perturbations, which satisfy and . and denote the input and bias. Two operational symbols ⋀ and ⋁ represent the fuzzy AND and OR. and stand for elements of the feedback and feed-forward templates. and characterize elements of the feedback MIN and MAX templates. Likewise, and characterize the feed-forward MIN and MAX templates.
Considering cellular networks (3) as the drive network system, the response network system can be given by
where , and . characterizes the state variable of the response system. denotes the nonlinear information feedback controller. denotes the starting value of neuron u. The remaining parameters possess similar meanings as drive cellular networks (3).
Let the error signal be . Combining cellular NNs (3) and (4), we can acquire the following error system
where , and . Then, the information feedback control schemes for delayed drive-response networks with uncertainties are shown in Figure 1.
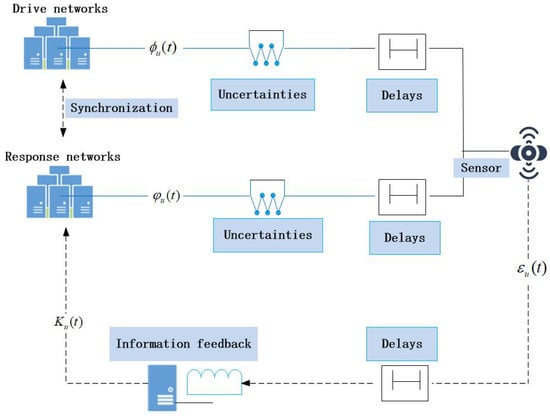
Figure 1.
Information feedback control mechanisms for drive communication networks and response communication networks with uncertainties and delays.
Remark 1.
Fractional-order operators are more advantageous than integer-order operators for describing biophysical phenomena. For the propagation dynamics of biological viruses, the fractional-order modeling approach can more accurately simulate the propagation process of viruses because the fractional-order derivatives can reflect the effect of the historical state on the current state, whereas the integer-order model cannot reflect this memory property. In the study of cancer tumor growth, the fractional-order model can better capture the growth pattern of tumor cells and the delayed effect of drug action by introducing the fractional derivative, thus avoiding the problem of neglecting cell interactions and memory effects in the traditional integer-order model. In modeling physically viscoelastic materials, the fractional-order model can more accurately describe the relaxation and creep behavior of the material, but with the integer-order model, it is difficult to achieve the same accuracy.
Remark 2.
Traditional calculus has been widely utilized to model network dynamical systems and study synchronous behaviors. In [22], the bipartite synchronization of integer-order NNs was discussed. In [24], the authors investigated a self-triggering mechanism for synchronizing integer-order memristive NNs. Based on integer-order calculus, the exponential synchronization on multilayer cellular NNs [25] and the system synchronization of NNs [26] were considered by a linear control method and adaptive control scheme, respectively. However, these control protocols and inequality techniques cannot be extended to fractional-order systems directly because the Caputo cellular NNs studied in this paper have non-locality and long-term memory.
Remark 3.
Compared with memristor-based NNs in [33,34,35,46], the cellular delayed NNs discussed in this paper take into account not only nonlinear activation functions but also uncertainties and different fuzzy operators, making our system suitable for modeling complex environmental networks. Although fuzzy operators and nonlinear activation behaviors have been discussed in the literature [45], the effects of uncertainties for feedback coefficients and templates were ignored.
Definition 3
Definition 4
Assumption 1.
For , there exist constants and satisfying
and
where .
Lemma 2.
For a differentiable function , one can derive [47]
where and sign(·) denote the mathematical symbol function.
Lemma 3.
Consider the following -order differential system [19]
If there are constants and a function satisfying
then there exists a positive T such that
and T can be calculated by
where satisfies the condition .
Lemma 4.
Assume that is differentiable and meets [41]
where , and . Then, we get and , and satisfies
3. New PFT and FT Synchronization Results of CFOFCNNs
To finish the PFT synchronization assignment between drive-response CFOFCNNs (3) and (4), a nonlinear controller including negative feedback and positive feedback terms is devised as
where , and represent positive control parameters.
3.1. PFT Synchronization Results
Theorem 1.
Proof.
Consider an auxiliary function
In virtue of Lemmas 1 and 2, Assumption 1, and error system (5), one can obtain
For , one can obtain
Based on inequality (26), one can future derive
According to Lemma 3, there exists a positive constant T such that
and T can be calculated by
where satisfies the condition . □
Remark 4.
The FT synchronization problems of NNs based on information feedback schemes have been widely studied, such as in [41,45]. Existing controllers use only negative feedback terms. Different from these existing feedback control methods, the mixed nonlinear controller (19) devised in this article considers both negative feedback and positive feedback terms. The positive feedback term ensures that the fractional derivative of the auxiliary function in (28) includes a positive result , which lays the foundation for utilizing the comparison principle in Lemma 3.
In particular, if uncertain perturbations are not considered, then fuzzy cellular NNs (3) and (4) can be simplified as
and
where , and . Based on the nonlinear feedback controller (19), utilizing the same analysis of Theorem 1, one can obtain a noteworthy synchronization corollary as below.
Corollary 1.
3.2. FT Synchronization Results
Theorem 2.
Proof.
Consider an auxiliary function
In virtue of Lemmas 1 and 2, Assumption 1, and error system (5), one can obtain
Based on the FT synchronization results in Theorem 2, one derives the below meaningful corollary.
Corollary 2.
Remark 5.
The theoretical results derived in this paper are suitable for the case . That is to say, the nonlinear information feedback schemes can be utilized for the PFT synchronization and FT synchronization issues of integer-order cellular NNs with uncertain perturbations.
3.3. Design Principle Analysis of Nonlinear Feedback Controllers
In the PFT and PF synchronization study of fractional-order NNs in this paper, the core of the design of the nonlinear error feedback controller lies in the transformation of the drive-response synchronization problem into a stability problem of the error system by solving the effects of nonlinear dynamics, time-delayed effects, and parameter uncertainties.
To finish the FT synchronization of the system, the controller contains two cases, i.e., and . We apply error information feedback to the network only in case and design a discontinuous controller that includes four feedback terms. Specifically, the first term can overcome the effect of time delays on system stability. The second term can eliminate quasi-linear growth errors. The last two terms can reduce the error between the master-slave systems and achieve the synchronization target. The controller for the PFT synchronization has similar design principles.
Remark 6.
In [2], the authors considered a state estimation feedback controller for the synchronization of uncertain NNs with disturbances. In [4], a fuzzy event-triggered control scheme was utilized for the synchronization of T-S fuzzy NNs. In [17], a memory-state feedback controller was considered to synchronize delayed NNs. Unlike these control protocols for non-fractional networks, this paper utilizes a hybrid information feedback scheme.
Remark 7
Remark 8.
Comparing feedback controllers (19) and (37), the key difference is that the positive feedback term in (19) has been changed to a negative feedback term in (37). In addition, the range of the parameters in the two controllers has changed because the synchronization conditions between Theorem 1 and Theorem 2 are different.
Remark 9.
Inequality (44) shows that the settling time of network synchronization can be effectively estimated. The settling time depends on not only the fractional order ρ, neuron size n, and initial value , but also the feedback intensities , and δ.
4. Simulation Experiments
To demonstrate the applicability of the derived synchronization theorems, simulation examples are provided in this section.
Example 1. Consider 2-dimensional CFOFCNNs with transmission delays and uncertain perturbations as below:
where , , , , , , , , , , and . Giving activation functions , one can verify that Assumption 1 holds and and .
Based on the above drive networks with fractional order, one can consider the following NNs as the response networks:
where the system parameters have the same values with (47), and the control parameters are set individually according to different synchronization patterns.
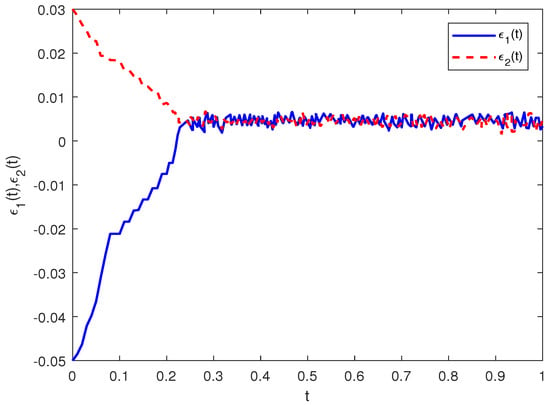
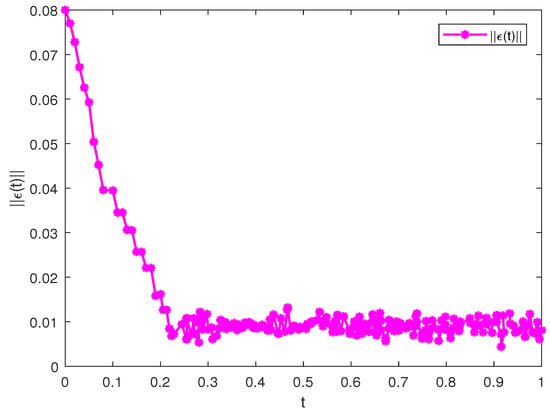
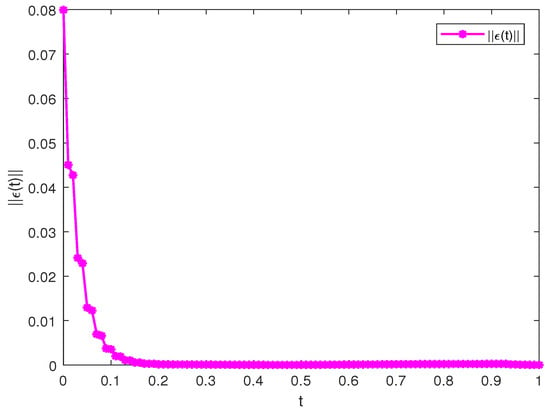
Let control parameters and . Through straightforward computations, one can derive that , and , , and the setting time can be evaluated by . Hence, the computation results show that the synchronization conditions in Theorem 1 can be satisfied. By predictor-corrector methods, CFOFCNNs (3) and (4) can achieve the PFT synchronization via control schemes (19), including hybrid negative and positive feedback terms, as depicted in Figure 2. Moreover, the time evolution of the error norm is given in Figure 3, which indicates the fact for . It verifies the validity of the control schemes (19) and the correctness of Theorem 1.
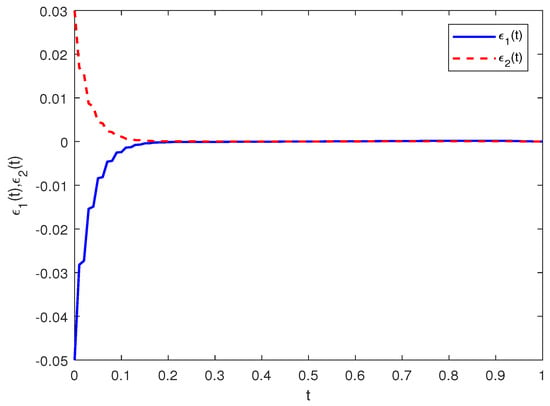
Select control parameters . By simple computations, one can derive that , and , and the evaluated setting time . As shown in Figure 4, both the red and blue curves converge to zero over time, which shows that CFOFCNNs (3) and (4) can achieve the PF synchronization through control methods (37) with four negative feedback terms. Figure 5 shows that the error norm between the drive and response systems equals zero at the end of the setting time. The above experimental results indicate that the PFT synchronization switches to FT synchronization when the controller changes from hybrid feedback to negative feedback, which provides a new perspective for us to design the feedback control schemes.
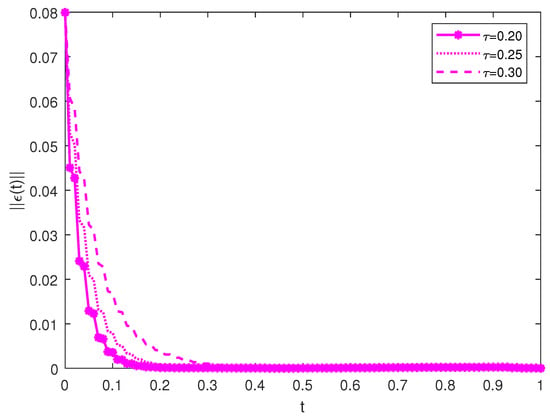
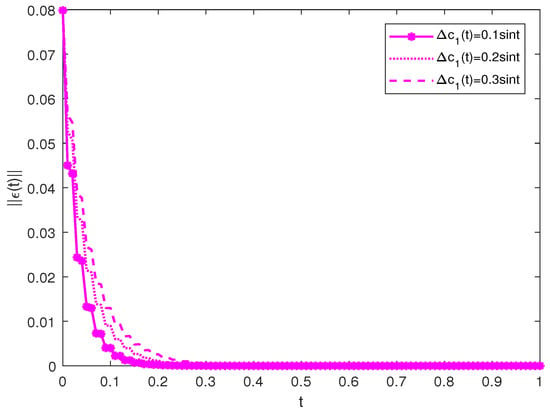
To investigate the influence of parameter variation on the FT synchronization process, we focus on the variation in time delays and uncertain perturbations. First, the time delays are set to 0.20, 0.25, and 0.30. In Figure 6, the control time required for the drive-response systems to reach finite time synchronization gradually increases as the time delays increase. This is mainly because extensive delays have a greater impact on the stability of the system and increase the difficulty of control. Second, the bound of perturbation coefficients is adjusted from 0.1 to 0.3 with step 0.1. As shown in Figure 7, we can observe that as the magnitude of the perturbation increases, it takes a longer time for the networks to reach synchronization. Overall, as long as the adjusted parameters satisfy the conditions in the theorem, the studied delayed NNs can be synchronized under the action of the controller regardless of the variation of the system parameters.
Remark 10.
Based on the long-term memory properties of fractional NNs, the Adams–Bashforth–Moulton method [29] can be applied in simulation experiments to resolve delayed differential equations by Matlab R2020b. The solution process includes two prominent steps: prediction and correction. First, a uniform grid approach is utilized to divide time intervals. To better assess the prediction item, a product rectangle rule is utilized. Then, a product trapezoidal quadrature rule can be applied to derive the correction item. By combining the above rules, one can finish the simulation experiments easily.
5. Conclusions
This paper investigated the PFT synchronization and FT synchronization of generalized drive-response CFOFCNNs. With the help of nonlinear controllers and comparison principles, important criteria have been derived to ensure the two synchronization patterns of CFOFCNNs. Unlike the existing results [31,41,45], these control strategies only considered the effect of negative feedback on network synchronization. The results of the experiment showed that the FT synchronization can be achieved only by using negative feedback. A main finding is that when one of the four feedback terms in the controller is positive, PFT synchronization instead of FT synchronization can be achieved by designing appropriate control parameters.
Fractional-order fuzzy cellular NNs have good application value in medical imaging lesion segmentation and image encryption. The memory property of fractional-order calculus can capture the historical evolution characteristics of image lesions in the time sequence, and then dynamically adjust the segmentation threshold based on the fuzzy affiliation function. The chaotic property of fractional-order fuzzy cellular NNs and the robustness of fuzzy logic make it significantly better than the traditional methods regarding the key space of image encryption and anti-attack ability. Future work should investigate the intermittent feedback control and automatic event-triggering mechanisms to address the PFT and FT synchronization for higher-order stochastic NNs, which will help resolve control costs and secure communication issues of systems.
Author Contributions
Conceptualization, K.S., H.F., and H.W.; methodology, K.S., and H.W.; software, H.F., and A.Z.; writing—original draft, H.F., K.S., and A.Z.; writing—review and editing, H.F., K.S., and H.W. All authors have read and agreed to the published version of the manuscript.
Funding
The first author was partially supported by the Engineering Research Center for Big Data Application in Private Health Medicine of Fujian Universities, Putian University under Grant (MKF202401), and the APC was funded by (MKF202401). The second author was partially supported by the Ministry of Education’s Industry-University Cooperation Collaborative Education Project under grant (231102311285117), the Putian Science and Technology Project under grants (2024NJJ009, 2023GJGZ003), and the Fujian Province Natural Science Foundation Project under grants (2022J011179, 2023J011015). The third author was partially supported by the Key R&D Projects of Sichuan Provincial Department of Science and Technology under Grant (2023YFG0287), and the Sichuan Science and Technology Program (25NSFSC2581, 2024NSFSC2056).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, H.; Yang, X.S.; Xiang, Z.R.; Tang, R.Q.; Ning, Q. Synchronization of switched neural networks via attacked mode-dependent event-triggered control and its application in image encryption. IEEE Trans. Cybern. 2023, 53, 5994–6003. [Google Scholar] [CrossRef] [PubMed]
- Li, M.Y.; Li, X.D. Synchronization of neural networks involving unmeasurable states and impulsive disturbances by observer and feedback control. Commun. Nonlinear Sci. Numer. Simul. 2023, 31, 107396. [Google Scholar] [CrossRef]
- Ding, D.; Tang, Z.; Park, J.H.; Ji, Z.C. Quasi-bipartite synchronization of derivatively coupled complex dynamic networks: Memory-based self-triggered approach. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1611–1621. [Google Scholar] [CrossRef]
- Zhang, J.J.; Li, Z.H.; Cao, J.D.; Abdel-Aty, M.; Meng, X.F. Dynamic self-triggered impulsive synchronization of complex networks with mismatched parameters and distributed delay. Chaos Solitons Fractals 2025, 196, 116403. [Google Scholar] [CrossRef]
- Luo, R.F.; Ren, J.J.; Shi, K.B. Stability analysis of delayed T-S fuzzy power system via a cubic function negative determination lemma. Nonlinear Dyn. 2025, 113, 5439–5456. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, Q.X.; Li, S.B. Stabilization of discrete-time hidden semi-Markov jump linear systems with partly unknown emission probability matrix. IEEE Trans. Autom. Control 2024, 69, 1952–1959. [Google Scholar] [CrossRef]
- Zhu, Q.X. Event-triggered sampling problem for exponential stability of stochastic nonlinear delay systems driven by levy processes. IEEE Trans. Autom. Control 2025, 70, 1176–1183. [Google Scholar] [CrossRef]
- Yang, X.T.; Zhu, Q.X.; Wang, H. Exponential stabilization of stochastic systems via novel event-triggered switching controls. IEEE Trans. Autom. Control 2024, 69, 7948–7955. [Google Scholar] [CrossRef]
- Fan, H.G.; Chen, X.J.; Shi, K.B.; Wen, H. Distributed delayed impulsive control for μ-synchronization of multi-link structure networks with bounded uncertainties and time-varying delays of unmeasured bounds: A novel Halanay impulsive inequality approach. Chaos Solitons Fractals 2024, 186, 115226. [Google Scholar] [CrossRef]
- Cai, J.Y.; Yi, C.B.; Luo, X.; Xiao, C.R. Output feedback tracking consensus of switched stochastic uncertain multiagent systems via event-triggered control. IEEE Syst. J. 2025, 19, 130–141. [Google Scholar] [CrossRef]
- Han, T.Y.; Liang, Y.; Fan, W.J. Dynamics and soliton solutions of the perturbed Schrodinger-Hirota equation with cubic-quintic-septic nonlinearity in dispersive media. AIMS Math. 2025, 10, 754–776. [Google Scholar] [CrossRef]
- Ding, K.; Zhu, Q.X. A note on sampled-data synchronization of memristor networks subject to actuator failures and two different activations. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2097–2101. [Google Scholar] [CrossRef]
- Yi, C.B.; Cai, J.Y.; Guo, R. Synchronization of a class of nonlinear multiple neural networks with delays via a dynamic event-triggered impulsive control strategy. Electron. Res. Arch. 2024, 32, 4581–4603. [Google Scholar] [CrossRef]
- Yao, W.; Wang, C.H.; Sun, Y.C.; Gong, S.Q.; Lin, H.R. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Netw. 2023, 164, 67–80. [Google Scholar] [CrossRef]
- Fu, Q.H.; Zhong, S.M.; Jiang, W.B.; Xie, W.Q. Projective synchronization of fuzzy memristive neural networks with pinning impulsive control. J. Frankl. Inst. 2020, 357, 10387–10409. [Google Scholar] [CrossRef]
- Fan, H.G.; Chen, X.J.; Shi, K.B.; Liang, Y.H.; Wang, Y.; Wen, H. Mittag-Leffler synchronization in finite time for uncertain fractional-order multi-delayed memristive neural networks with time-varying perturbations via information feedback. Fractal Fract. 2024, 8, 422. [Google Scholar] [CrossRef]
- Wang, Z.K.; Zhuang, G.M.; Xie, X.P.; Xia, J.W. H∞ master–slave synchronization for delayed impulsive implicit hybrid neural networks based on memory-state feedback control. Neural Netw. 2023, 165, 540–552. [Google Scholar] [CrossRef]
- Li, X.F.; Zhang, W.B.; Fang, J.A.; Li, H.Y. Finite-time synchronization of memristive neural networks with discontinuous activation functions and mixed time-varying delays. Neurocomputing 2019, 340, 99–109. [Google Scholar] [CrossRef]
- Du, F.F.; Lu, J.G.; Zhang, Q.H. Practical finite-time synchronization of delayed fuzzy cellular neural networks with fractional-order. Inf. Sci. 2024, 667, 120457. [Google Scholar] [CrossRef]
- Louodop, P.; Kountchou, M.; Fotsin, H.; Bowong, S. Practical finite-time synchronization of jerk systems: Theory and experiment. Nonlinear Dyn. 2014, 78, 597–607. [Google Scholar] [CrossRef]
- Huan, M.C.; Li, C.D. Synchronization of reaction-diffusion neural networks with sampled-data control via a new two-sided looped-functional. Chaos Solitons Fractals 2023, 167, 113059. [Google Scholar] [CrossRef]
- Liu, F.; Song, Q.; Wen, G.H.; Cao, J.D.; Yang, X.S. Bipartite synchronization in coupled delayed neural networks under pinning control. Neural Netw. 2018, 108, 146–154. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Y.; Li, C.D.; Li, H.F.; Cao, Z.R. Synchronization of uncertain coupled neural networks with time-varying delay of unknown bound via distributed delayed impulsive control. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 3624–3635. [Google Scholar] [CrossRef]
- Ding, D.; Tang, Z.; Wen, C.B.; Ji, Z.C. Bipartite synchronization for coupled memristive neural networks: Memory-based dynamic updating law. Knowl.-Based Syst. 2024, 299, 112102. [Google Scholar] [CrossRef]
- Hua, W.T.; Wang, Y.T.; Liu, C.Y. New method for global exponential synchronization of multi-link memristive neural networks with three kinds of time-varying delays. Appl. Math. Comput. 2024, 471, 128593. [Google Scholar] [CrossRef]
- Alsaedi, A.; Cao, J.D.; Ahmad, B.; Alshehri, A.; Tan, X.G. Synchronization of master-slave memristive neural networks via fuzzy output-based adaptive strategy. Chaos Solitons Fractals 2022, 158, 112095. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Fan, H.G.; Shi, K.B.; Guo, Z.Z.; Zhou, A.R. Finite-time synchronization criteria for Caputo fractional-order uncertain memristive neural networks with fuzzy operators and transmission delay under communication feedback. Fractal Fract. 2024, 8, 619. [Google Scholar] [CrossRef]
- Bhalekar, S.; Gejji, V. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calc. Appl. 2011, 1, 1–9. [Google Scholar]
- Wang, F.; Zheng, Z.W.; Yang, Y.Q. Quasi-synchronization of heterogenous fractional-order dynamical networks with time-varying delay via distributed impulsive control. Chaos Solitons Fractals 2021, 142, 110465. [Google Scholar] [CrossRef]
- Duan, L.; Wei, H.; Huang, L.H. Finite-time synchronization of delayed fuzzy cellular neural networks with discontinuous activations. Fuzzy Sets Syst. 2019, 361, 56–70. [Google Scholar] [CrossRef]
- Yang, X.J.; Li, C.D.; Song, Q.K.; Chen, J.Y.; Huang, J.J. Global Mittag-Leffler stability and synchronization analysis of fractional-order quaternion-valued neural networks with linear threshold neurons. Neural Netw. 2018, 105, 88–103. [Google Scholar] [CrossRef]
- Bao, H.B.; Cao, J.D. Projective synchronization of fractional-order memristor-based neural networks. Neural Netw. 2015, 63, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.B.; Park, J.H.; Cao, J.D. Adaptive synchronization of fractional-order memristor-based neural networks with time delay. Nonlinear Dyn. 2015, 82, 1343–1354. [Google Scholar] [CrossRef]
- Yan, H.Y.; Qiao, Y.H.; Ren, Z.H.; Duan, L.J.; Miao, J. Master-slave synchronization of fractional-order memristive MAM neural networks with parameter disturbances and mixed delays. Commun. Nonlinear Sci. Numer. Simul. 2023, 120, 107152. [Google Scholar] [CrossRef]
- Gu, Y.J.; Wang, H.; Yu, Y.G. Synchronization for commensurate Riemann-Liouville fractional-order memristor-based neural networks with unknown parameters. J. Frankl. Inst. 2020, 357, 8870–8898. [Google Scholar] [CrossRef]
- Liu, S.X.; Yu, Y.G.; Zhang, S. Robust synchronization of memristor-based fractional-order Hopfield neural networks with parameter uncertainties. Neural Comput. Appl. 2019, 31, 3533–3542. [Google Scholar] [CrossRef]
- Zhao, J.H.; Lin, Y.L.; Liu, T.; Liu, P.; Sun, J.W. Cluster output synchronization analysis of coupled fractional-order uncertain neural networks. Inf. Sci. 2025, 705, 121993. [Google Scholar] [CrossRef]
- Yang, X.J.; Li, C.D.; Huang, T.W.; Song, Q.K.; Huang, J.J. Synchronization of fractional-order memristor-based complex-valued neural networks with uncertain parameters and time delays. Chaos Solitons Fractals 2018, 110, 105–123. [Google Scholar] [CrossRef]
- Peng, Q.; Lin, S.M.; Tan, M.C. Quantized hybrid impulsive control for finite-time synchronization of fractional-order uncertain multiplex networks with multiple time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2025, 142, 108540. [Google Scholar] [CrossRef]
- Du, F.F.; Luo, J.G. Finite-time synchronization of fractional-order delayed fuzzy cellar neural networks with parameter uncertainties. IEEE Trans. Fuzzy Syst. 2023, 31, 1769–1779. [Google Scholar] [CrossRef]
- Li, H.L.; Cao, J.D.; Hu, C.; Jiang, H.J.; Alsaedi, A. Synchronization analysis of nabla fractional-order fuzzy neural networks with time delays via nonlinear feedback control. Fuzzy Sets Syst. 2024, 475, 108750. [Google Scholar] [CrossRef]
- Li, H.L.; Cao, J.D.; Hu, C.; Zhang, L.; Jiang, H.J. Adaptive control-based synchronization of discrete-time fractional-order fuzzy neural networks with time-varying delays. Neural Netw. 2023, 168, 59–73. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Jian, J.G.; Wang, B.X. Finite-time synchronization of fractional-order delayed memristive fuzzy neural networks. Fuzzy Sets Syst. 2023, 467, 108578. [Google Scholar] [CrossRef]
- Du, F.F.; Lu, J.G. Adaptive finite-time synchronization of fractional-order delayed fuzzy cellular neural networks. Fuzzy Sets Syst. 2023, 466, 108480. [Google Scholar] [CrossRef]
- Yang, S.Y.; Tang, H.A.; Hu, X.F.; Xia, Q.L.; Wang, L.D.; Duan, S.K. Adaptive finite-time passivity and synchronization of coupled fractional-order memristive neural networks with multi-state couplings. Neurocomputing 2024, 579, 127380. [Google Scholar] [CrossRef]
- Chen, B.S.; Chen, J.J. Global asymptotical ω-periodicity of a fractional-order non-autonomous neural networks. Neural Netw. 2015, 68, 78–88. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).