Finite-Time Synchronization and Practical Synchronization for Caputo Fractional-Order Fuzzy Cellular Neural Networks with Transmission Delays and Uncertainties via Information Feedback
Abstract
1. Introduction
1.1. Synchronization Principles and Applications
1.2. Related Works
1.3. Research Motivation and Highlights
2. Background Knowledge and Cellular Neural Networks
3. New PFT and FT Synchronization Results of CFOFCNNs
3.1. PFT Synchronization Results
3.2. FT Synchronization Results
3.3. Design Principle Analysis of Nonlinear Feedback Controllers
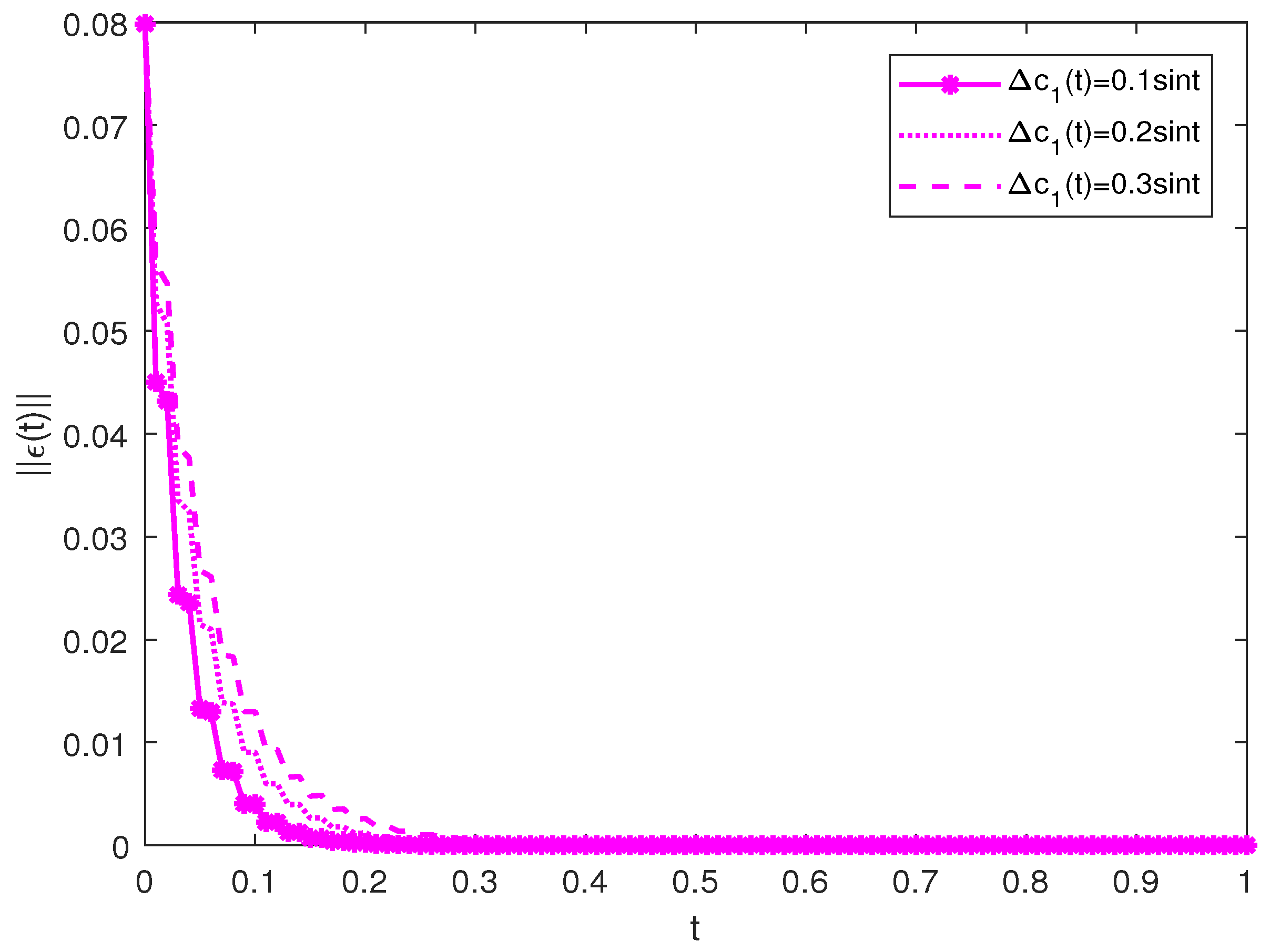
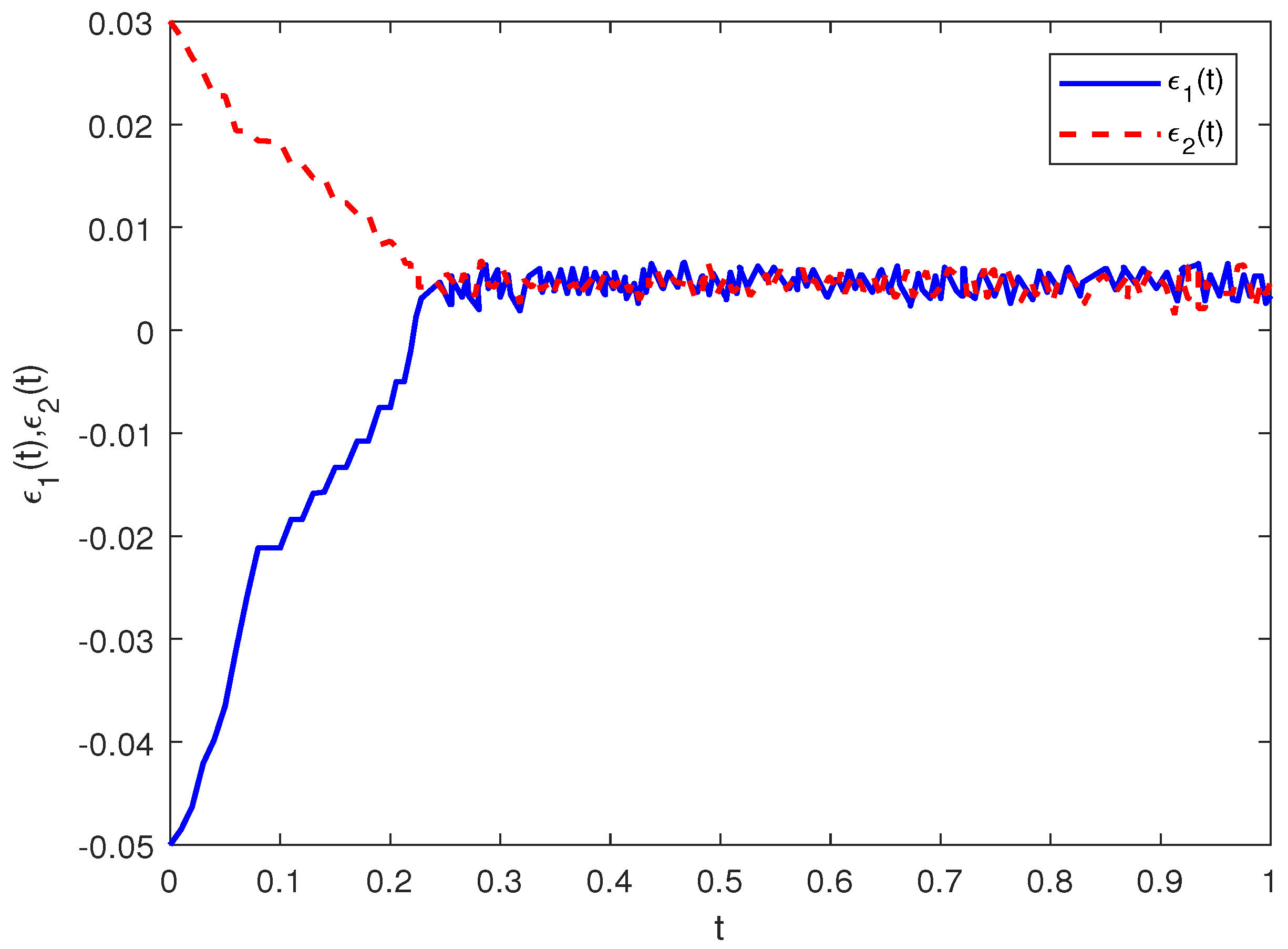
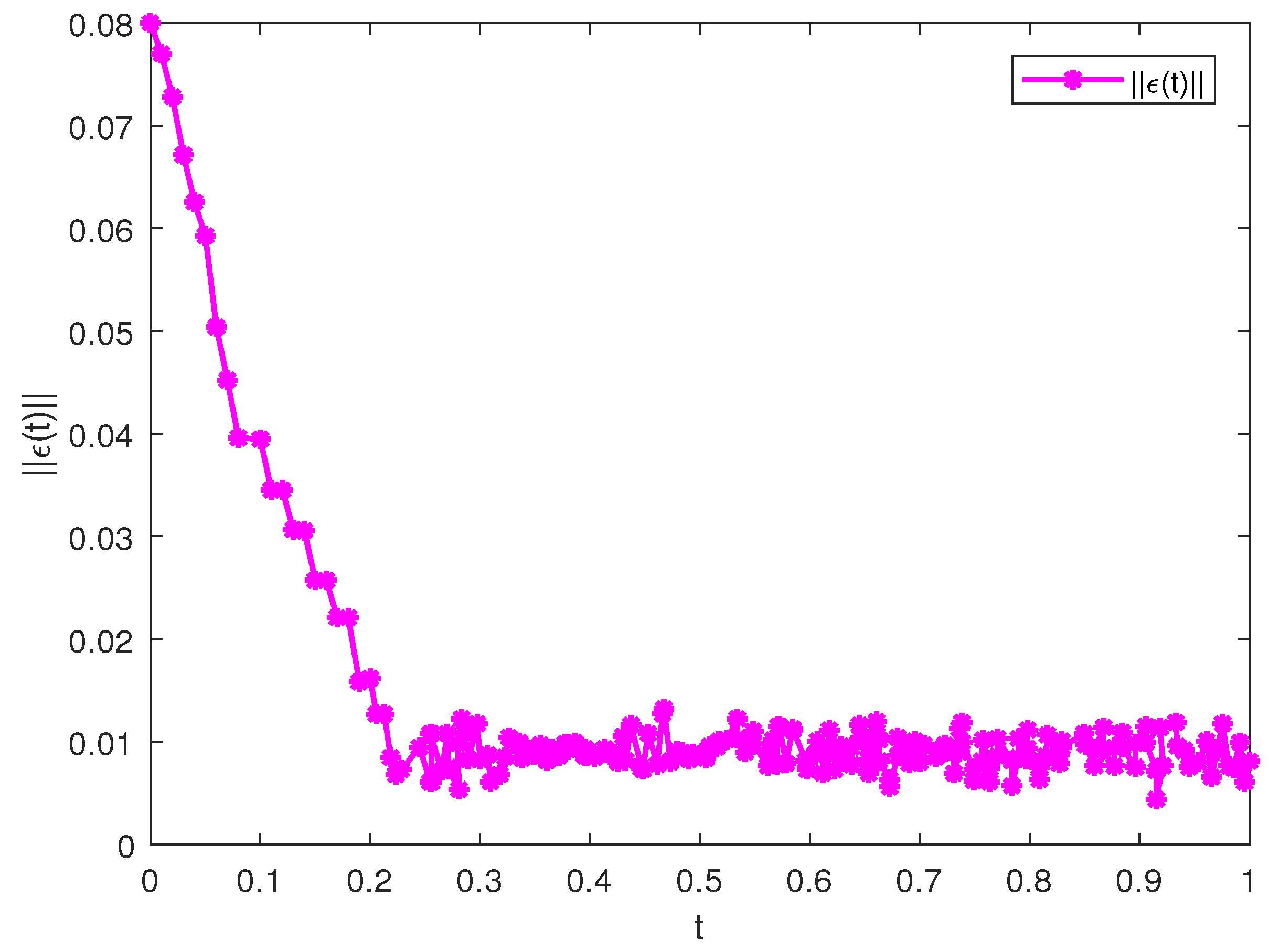
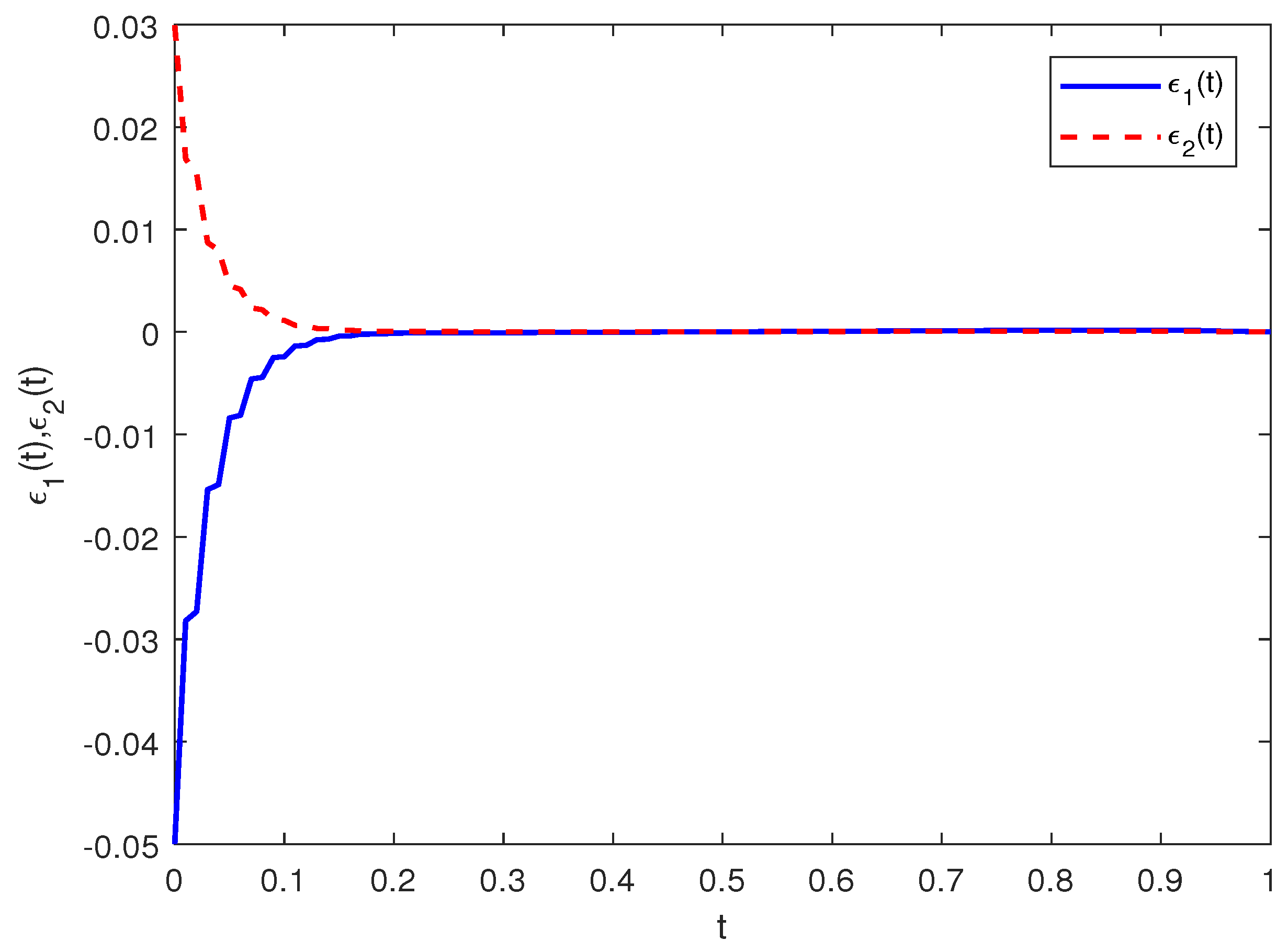
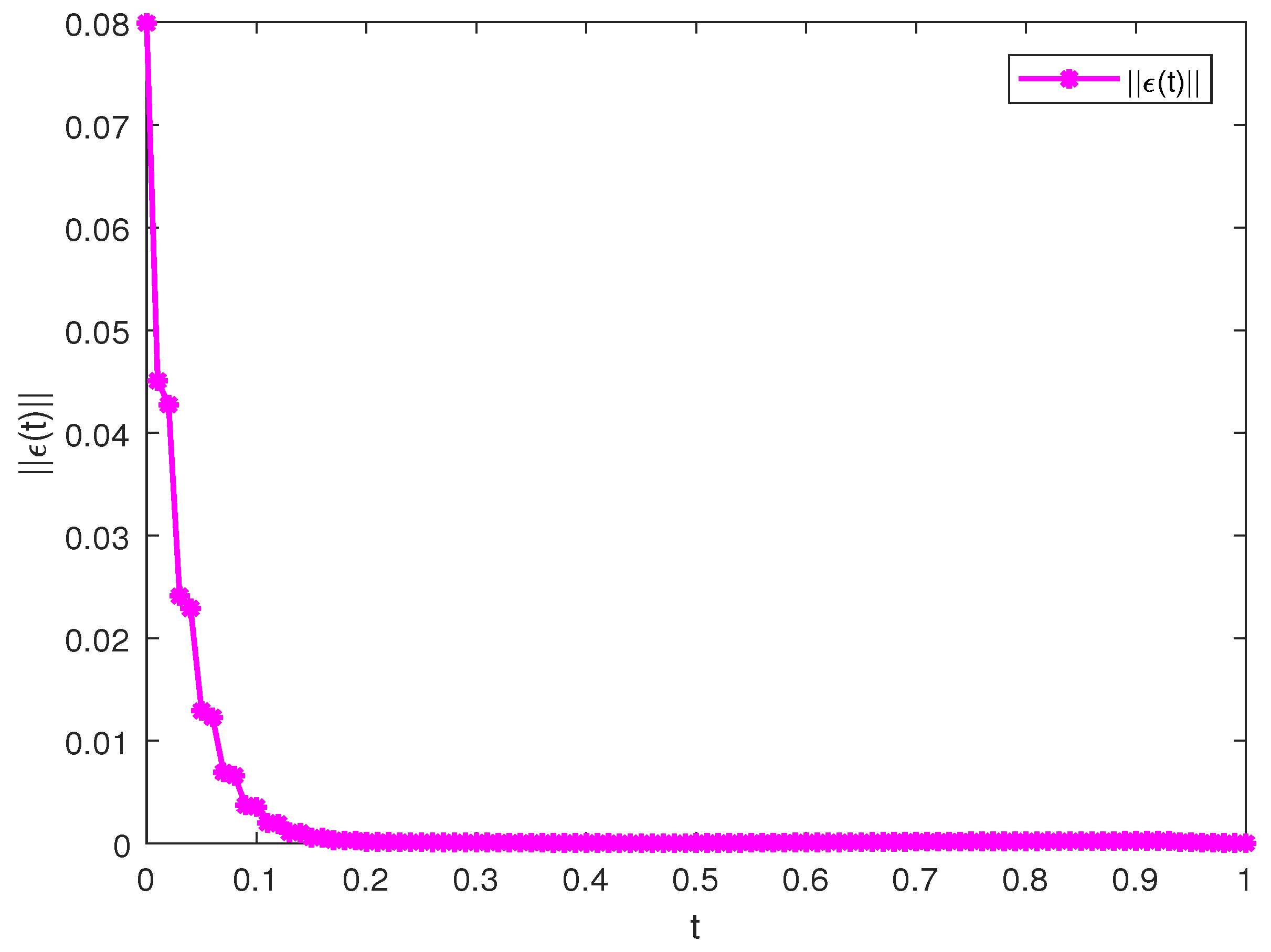
4. Simulation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Yang, X.S.; Xiang, Z.R.; Tang, R.Q.; Ning, Q. Synchronization of switched neural networks via attacked mode-dependent event-triggered control and its application in image encryption. IEEE Trans. Cybern. 2023, 53, 5994–6003. [Google Scholar] [CrossRef] [PubMed]
- Li, M.Y.; Li, X.D. Synchronization of neural networks involving unmeasurable states and impulsive disturbances by observer and feedback control. Commun. Nonlinear Sci. Numer. Simul. 2023, 31, 107396. [Google Scholar] [CrossRef]
- Ding, D.; Tang, Z.; Park, J.H.; Ji, Z.C. Quasi-bipartite synchronization of derivatively coupled complex dynamic networks: Memory-based self-triggered approach. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1611–1621. [Google Scholar] [CrossRef]
- Zhang, J.J.; Li, Z.H.; Cao, J.D.; Abdel-Aty, M.; Meng, X.F. Dynamic self-triggered impulsive synchronization of complex networks with mismatched parameters and distributed delay. Chaos Solitons Fractals 2025, 196, 116403. [Google Scholar] [CrossRef]
- Luo, R.F.; Ren, J.J.; Shi, K.B. Stability analysis of delayed T-S fuzzy power system via a cubic function negative determination lemma. Nonlinear Dyn. 2025, 113, 5439–5456. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, Q.X.; Li, S.B. Stabilization of discrete-time hidden semi-Markov jump linear systems with partly unknown emission probability matrix. IEEE Trans. Autom. Control 2024, 69, 1952–1959. [Google Scholar] [CrossRef]
- Zhu, Q.X. Event-triggered sampling problem for exponential stability of stochastic nonlinear delay systems driven by levy processes. IEEE Trans. Autom. Control 2025, 70, 1176–1183. [Google Scholar] [CrossRef]
- Yang, X.T.; Zhu, Q.X.; Wang, H. Exponential stabilization of stochastic systems via novel event-triggered switching controls. IEEE Trans. Autom. Control 2024, 69, 7948–7955. [Google Scholar] [CrossRef]
- Fan, H.G.; Chen, X.J.; Shi, K.B.; Wen, H. Distributed delayed impulsive control for μ-synchronization of multi-link structure networks with bounded uncertainties and time-varying delays of unmeasured bounds: A novel Halanay impulsive inequality approach. Chaos Solitons Fractals 2024, 186, 115226. [Google Scholar] [CrossRef]
- Cai, J.Y.; Yi, C.B.; Luo, X.; Xiao, C.R. Output feedback tracking consensus of switched stochastic uncertain multiagent systems via event-triggered control. IEEE Syst. J. 2025, 19, 130–141. [Google Scholar] [CrossRef]
- Han, T.Y.; Liang, Y.; Fan, W.J. Dynamics and soliton solutions of the perturbed Schrodinger-Hirota equation with cubic-quintic-septic nonlinearity in dispersive media. AIMS Math. 2025, 10, 754–776. [Google Scholar] [CrossRef]
- Ding, K.; Zhu, Q.X. A note on sampled-data synchronization of memristor networks subject to actuator failures and two different activations. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2097–2101. [Google Scholar] [CrossRef]
- Yi, C.B.; Cai, J.Y.; Guo, R. Synchronization of a class of nonlinear multiple neural networks with delays via a dynamic event-triggered impulsive control strategy. Electron. Res. Arch. 2024, 32, 4581–4603. [Google Scholar] [CrossRef]
- Yao, W.; Wang, C.H.; Sun, Y.C.; Gong, S.Q.; Lin, H.R. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Netw. 2023, 164, 67–80. [Google Scholar] [CrossRef]
- Fu, Q.H.; Zhong, S.M.; Jiang, W.B.; Xie, W.Q. Projective synchronization of fuzzy memristive neural networks with pinning impulsive control. J. Frankl. Inst. 2020, 357, 10387–10409. [Google Scholar] [CrossRef]
- Fan, H.G.; Chen, X.J.; Shi, K.B.; Liang, Y.H.; Wang, Y.; Wen, H. Mittag-Leffler synchronization in finite time for uncertain fractional-order multi-delayed memristive neural networks with time-varying perturbations via information feedback. Fractal Fract. 2024, 8, 422. [Google Scholar] [CrossRef]
- Wang, Z.K.; Zhuang, G.M.; Xie, X.P.; Xia, J.W. H∞ master–slave synchronization for delayed impulsive implicit hybrid neural networks based on memory-state feedback control. Neural Netw. 2023, 165, 540–552. [Google Scholar] [CrossRef]
- Li, X.F.; Zhang, W.B.; Fang, J.A.; Li, H.Y. Finite-time synchronization of memristive neural networks with discontinuous activation functions and mixed time-varying delays. Neurocomputing 2019, 340, 99–109. [Google Scholar] [CrossRef]
- Du, F.F.; Lu, J.G.; Zhang, Q.H. Practical finite-time synchronization of delayed fuzzy cellular neural networks with fractional-order. Inf. Sci. 2024, 667, 120457. [Google Scholar] [CrossRef]
- Louodop, P.; Kountchou, M.; Fotsin, H.; Bowong, S. Practical finite-time synchronization of jerk systems: Theory and experiment. Nonlinear Dyn. 2014, 78, 597–607. [Google Scholar] [CrossRef]
- Huan, M.C.; Li, C.D. Synchronization of reaction-diffusion neural networks with sampled-data control via a new two-sided looped-functional. Chaos Solitons Fractals 2023, 167, 113059. [Google Scholar] [CrossRef]
- Liu, F.; Song, Q.; Wen, G.H.; Cao, J.D.; Yang, X.S. Bipartite synchronization in coupled delayed neural networks under pinning control. Neural Netw. 2018, 108, 146–154. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Y.; Li, C.D.; Li, H.F.; Cao, Z.R. Synchronization of uncertain coupled neural networks with time-varying delay of unknown bound via distributed delayed impulsive control. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 3624–3635. [Google Scholar] [CrossRef]
- Ding, D.; Tang, Z.; Wen, C.B.; Ji, Z.C. Bipartite synchronization for coupled memristive neural networks: Memory-based dynamic updating law. Knowl.-Based Syst. 2024, 299, 112102. [Google Scholar] [CrossRef]
- Hua, W.T.; Wang, Y.T.; Liu, C.Y. New method for global exponential synchronization of multi-link memristive neural networks with three kinds of time-varying delays. Appl. Math. Comput. 2024, 471, 128593. [Google Scholar] [CrossRef]
- Alsaedi, A.; Cao, J.D.; Ahmad, B.; Alshehri, A.; Tan, X.G. Synchronization of master-slave memristive neural networks via fuzzy output-based adaptive strategy. Chaos Solitons Fractals 2022, 158, 112095. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Fan, H.G.; Shi, K.B.; Guo, Z.Z.; Zhou, A.R. Finite-time synchronization criteria for Caputo fractional-order uncertain memristive neural networks with fuzzy operators and transmission delay under communication feedback. Fractal Fract. 2024, 8, 619. [Google Scholar] [CrossRef]
- Bhalekar, S.; Gejji, V. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calc. Appl. 2011, 1, 1–9. [Google Scholar]
- Wang, F.; Zheng, Z.W.; Yang, Y.Q. Quasi-synchronization of heterogenous fractional-order dynamical networks with time-varying delay via distributed impulsive control. Chaos Solitons Fractals 2021, 142, 110465. [Google Scholar] [CrossRef]
- Duan, L.; Wei, H.; Huang, L.H. Finite-time synchronization of delayed fuzzy cellular neural networks with discontinuous activations. Fuzzy Sets Syst. 2019, 361, 56–70. [Google Scholar] [CrossRef]
- Yang, X.J.; Li, C.D.; Song, Q.K.; Chen, J.Y.; Huang, J.J. Global Mittag-Leffler stability and synchronization analysis of fractional-order quaternion-valued neural networks with linear threshold neurons. Neural Netw. 2018, 105, 88–103. [Google Scholar] [CrossRef]
- Bao, H.B.; Cao, J.D. Projective synchronization of fractional-order memristor-based neural networks. Neural Netw. 2015, 63, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.B.; Park, J.H.; Cao, J.D. Adaptive synchronization of fractional-order memristor-based neural networks with time delay. Nonlinear Dyn. 2015, 82, 1343–1354. [Google Scholar] [CrossRef]
- Yan, H.Y.; Qiao, Y.H.; Ren, Z.H.; Duan, L.J.; Miao, J. Master-slave synchronization of fractional-order memristive MAM neural networks with parameter disturbances and mixed delays. Commun. Nonlinear Sci. Numer. Simul. 2023, 120, 107152. [Google Scholar] [CrossRef]
- Gu, Y.J.; Wang, H.; Yu, Y.G. Synchronization for commensurate Riemann-Liouville fractional-order memristor-based neural networks with unknown parameters. J. Frankl. Inst. 2020, 357, 8870–8898. [Google Scholar] [CrossRef]
- Liu, S.X.; Yu, Y.G.; Zhang, S. Robust synchronization of memristor-based fractional-order Hopfield neural networks with parameter uncertainties. Neural Comput. Appl. 2019, 31, 3533–3542. [Google Scholar] [CrossRef]
- Zhao, J.H.; Lin, Y.L.; Liu, T.; Liu, P.; Sun, J.W. Cluster output synchronization analysis of coupled fractional-order uncertain neural networks. Inf. Sci. 2025, 705, 121993. [Google Scholar] [CrossRef]
- Yang, X.J.; Li, C.D.; Huang, T.W.; Song, Q.K.; Huang, J.J. Synchronization of fractional-order memristor-based complex-valued neural networks with uncertain parameters and time delays. Chaos Solitons Fractals 2018, 110, 105–123. [Google Scholar] [CrossRef]
- Peng, Q.; Lin, S.M.; Tan, M.C. Quantized hybrid impulsive control for finite-time synchronization of fractional-order uncertain multiplex networks with multiple time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2025, 142, 108540. [Google Scholar] [CrossRef]
- Du, F.F.; Luo, J.G. Finite-time synchronization of fractional-order delayed fuzzy cellar neural networks with parameter uncertainties. IEEE Trans. Fuzzy Syst. 2023, 31, 1769–1779. [Google Scholar] [CrossRef]
- Li, H.L.; Cao, J.D.; Hu, C.; Jiang, H.J.; Alsaedi, A. Synchronization analysis of nabla fractional-order fuzzy neural networks with time delays via nonlinear feedback control. Fuzzy Sets Syst. 2024, 475, 108750. [Google Scholar] [CrossRef]
- Li, H.L.; Cao, J.D.; Hu, C.; Zhang, L.; Jiang, H.J. Adaptive control-based synchronization of discrete-time fractional-order fuzzy neural networks with time-varying delays. Neural Netw. 2023, 168, 59–73. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Jian, J.G.; Wang, B.X. Finite-time synchronization of fractional-order delayed memristive fuzzy neural networks. Fuzzy Sets Syst. 2023, 467, 108578. [Google Scholar] [CrossRef]
- Du, F.F.; Lu, J.G. Adaptive finite-time synchronization of fractional-order delayed fuzzy cellular neural networks. Fuzzy Sets Syst. 2023, 466, 108480. [Google Scholar] [CrossRef]
- Yang, S.Y.; Tang, H.A.; Hu, X.F.; Xia, Q.L.; Wang, L.D.; Duan, S.K. Adaptive finite-time passivity and synchronization of coupled fractional-order memristive neural networks with multi-state couplings. Neurocomputing 2024, 579, 127380. [Google Scholar] [CrossRef]
- Chen, B.S.; Chen, J.J. Global asymptotical ω-periodicity of a fractional-order non-autonomous neural networks. Neural Netw. 2015, 68, 78–88. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, H.; Wen, H.; Shi, K.; Zhou, A. Finite-Time Synchronization and Practical Synchronization for Caputo Fractional-Order Fuzzy Cellular Neural Networks with Transmission Delays and Uncertainties via Information Feedback. Fractal Fract. 2025, 9, 297. https://doi.org/10.3390/fractalfract9050297
Fan H, Wen H, Shi K, Zhou A. Finite-Time Synchronization and Practical Synchronization for Caputo Fractional-Order Fuzzy Cellular Neural Networks with Transmission Delays and Uncertainties via Information Feedback. Fractal and Fractional. 2025; 9(5):297. https://doi.org/10.3390/fractalfract9050297
Chicago/Turabian StyleFan, Hongguang, Hui Wen, Kaibo Shi, and Anran Zhou. 2025. "Finite-Time Synchronization and Practical Synchronization for Caputo Fractional-Order Fuzzy Cellular Neural Networks with Transmission Delays and Uncertainties via Information Feedback" Fractal and Fractional 9, no. 5: 297. https://doi.org/10.3390/fractalfract9050297
APA StyleFan, H., Wen, H., Shi, K., & Zhou, A. (2025). Finite-Time Synchronization and Practical Synchronization for Caputo Fractional-Order Fuzzy Cellular Neural Networks with Transmission Delays and Uncertainties via Information Feedback. Fractal and Fractional, 9(5), 297. https://doi.org/10.3390/fractalfract9050297