Qualitative Analysis and Traveling Wave Solutions of a (3 + 1)- Dimensional Generalized Nonlinear Konopelchenko-Dubrovsky-Kaup-Kupershmidt System
Abstract
1. Introduction
- , .
- , .
- .
2. Mathematical Derivation
3. Qualitative Analysis
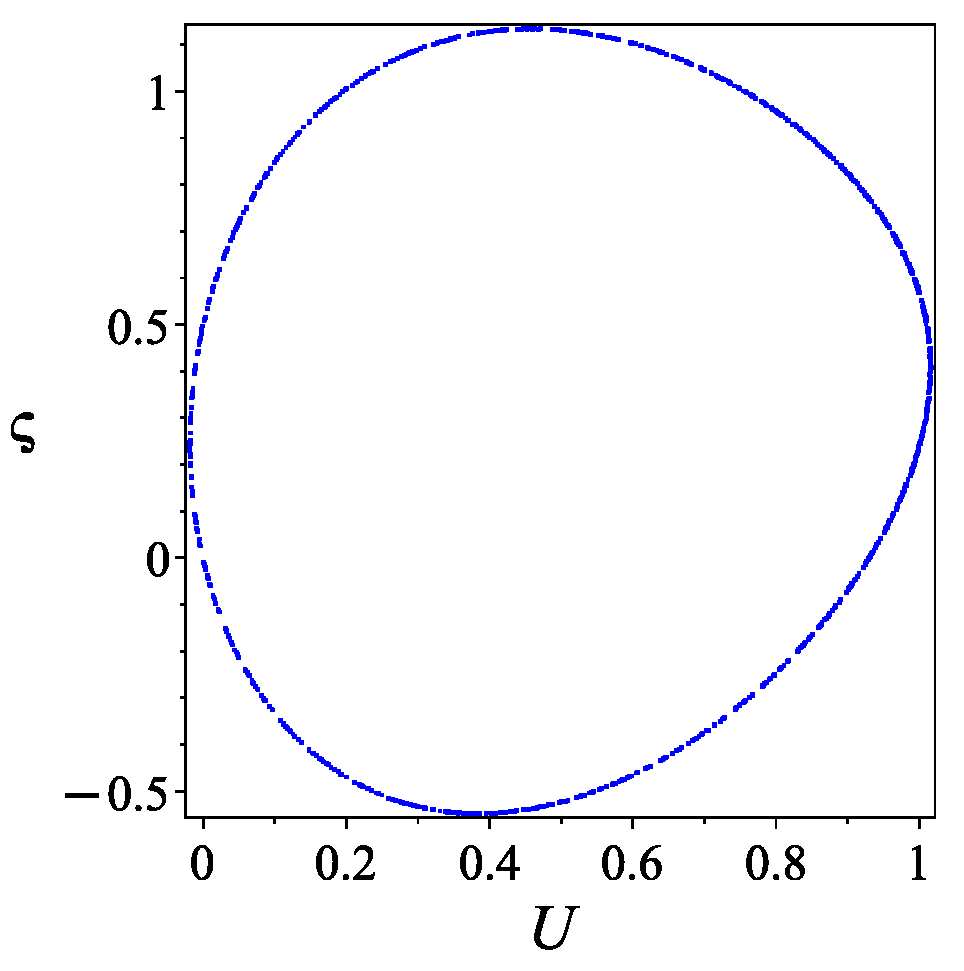
- When , has two different roots recorded as and , is a saddle point and is center point (see Figure 1a,b), where .
- When , has only one root recorded as , and is a degenerate saddle point (see Figure 1c,d).

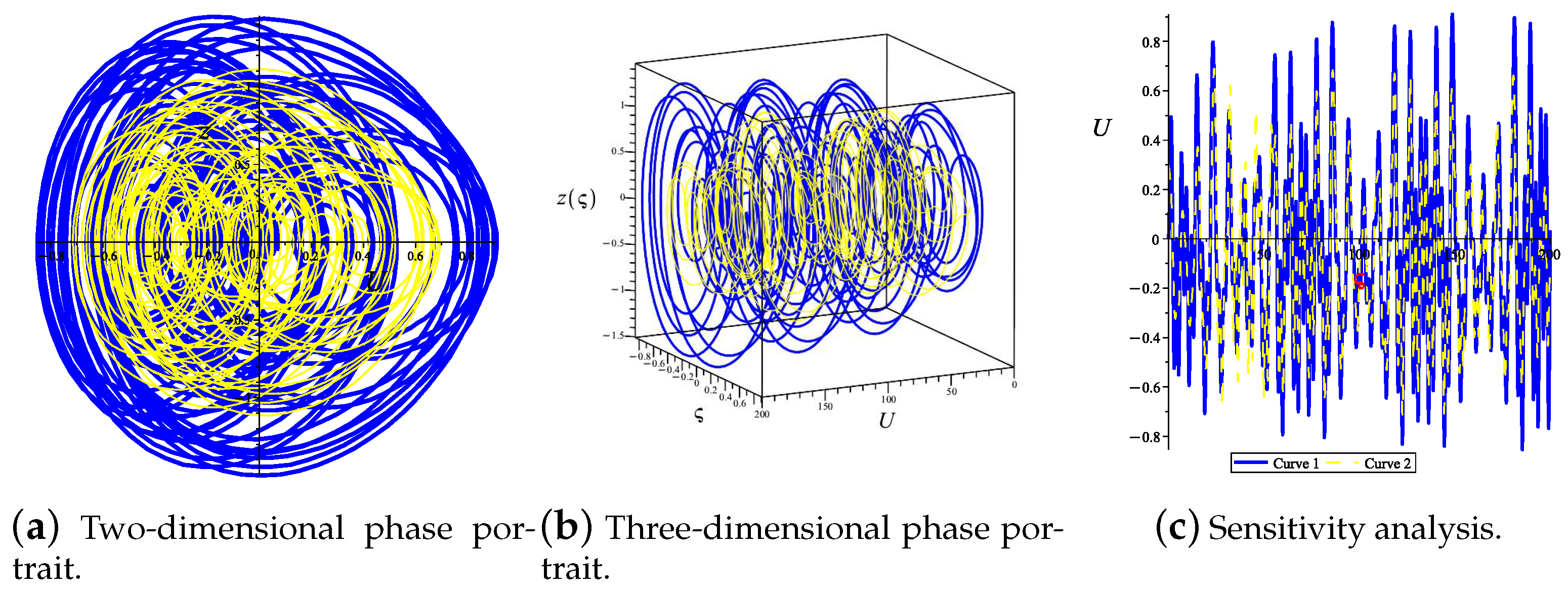
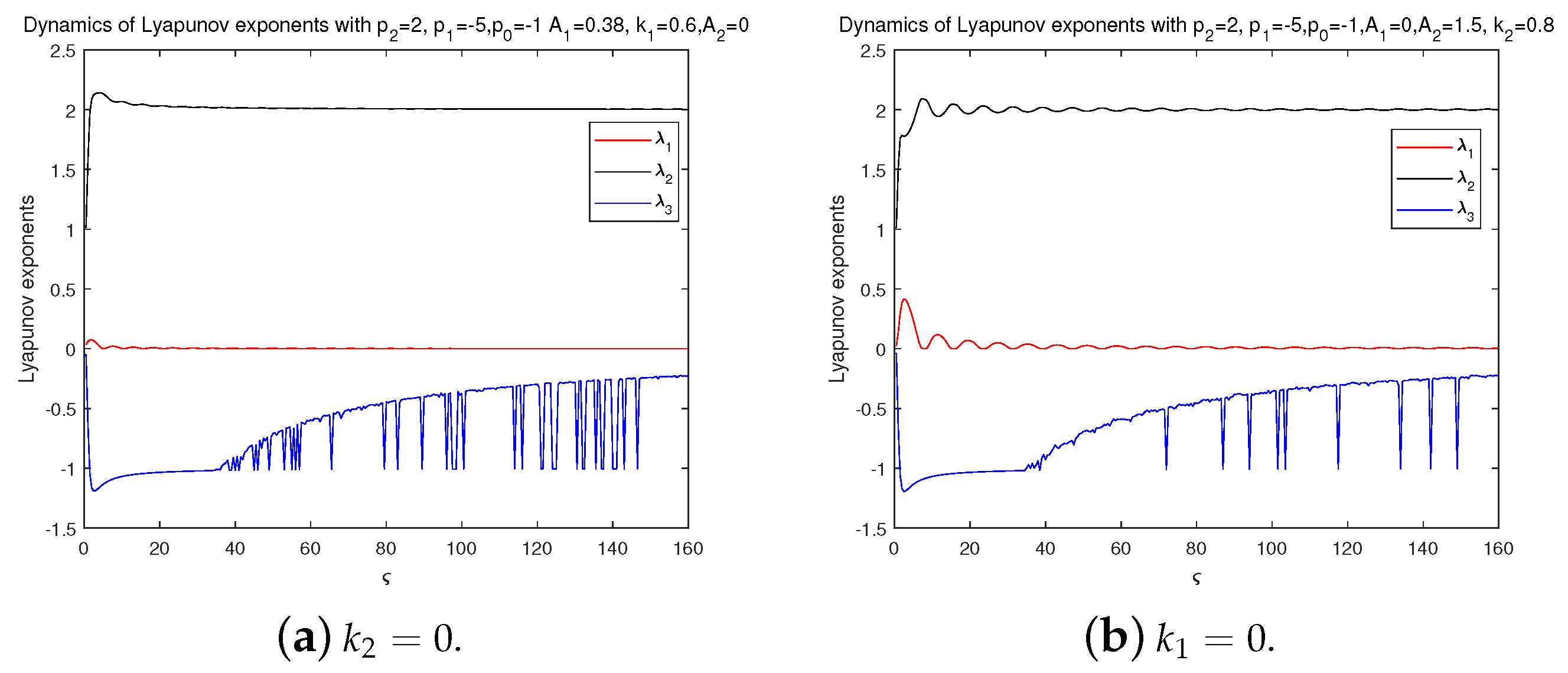
- When , , , , , , and , we plot a two-dimensional phase portrait, three-dimensional phase portrait, and sensitivity analysis diagram, as shown in Figure 2. In Figure 2, the blue and yellow curves represent the phase diagram and sensitivity of the system (13) under different initial conditions, respectively. Obviously, under the parameters of the characteristics, the system exhibits chaotic behavior, and for different initial values, the system (13) is not the same.
4. Traveling Wave Solutions of Equation (1)
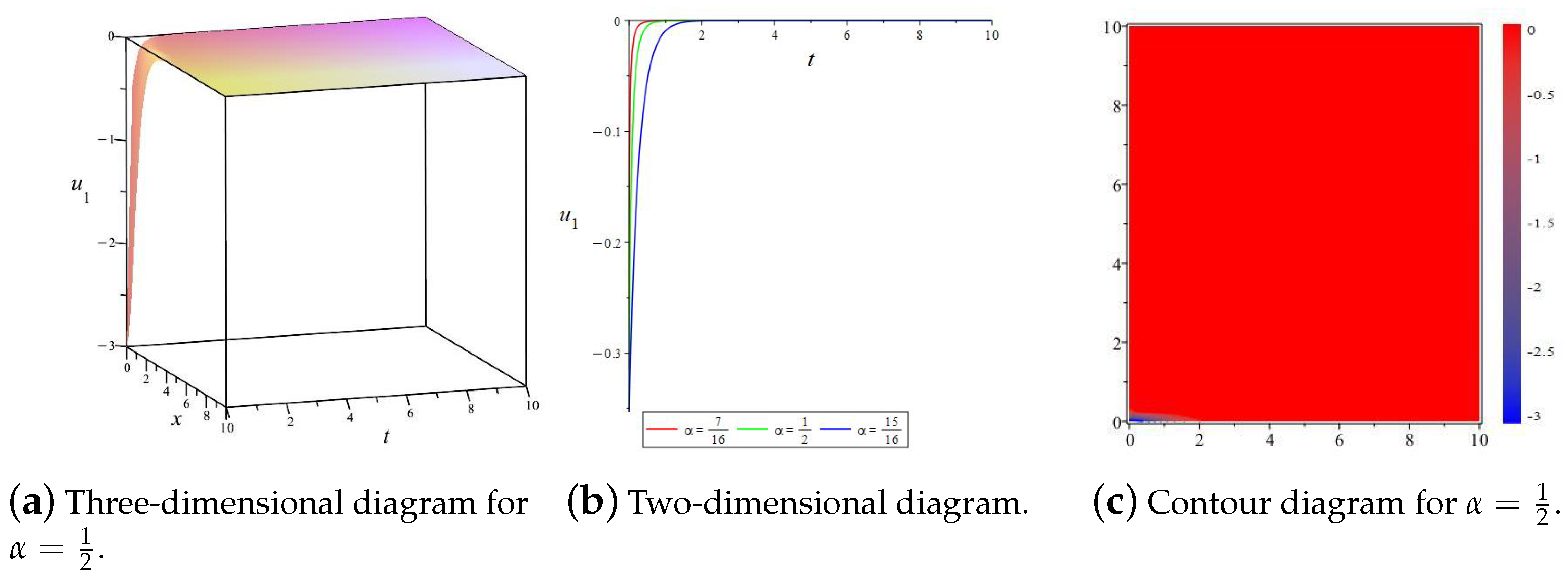
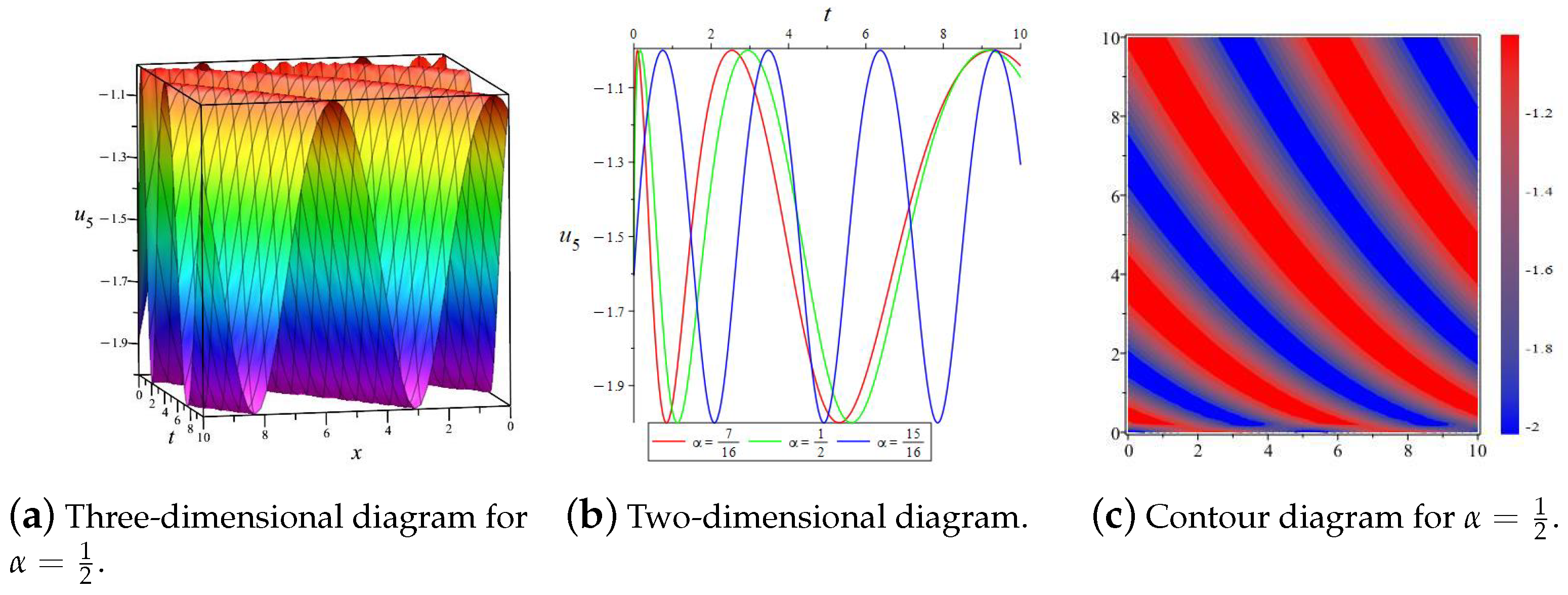
5. Numerical Simulation
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, D.; Shi, D.; Chen, F. Qualitative analysis and new traveling wave solutions for the stochastic Biswas-Milovic equation. AIMS Math. 2025, 10, 4092–4119. [Google Scholar] [CrossRef]
- Zhang, K.; Cao, J.P.; Lyu, J.J. Dynamic behavior and modulation instability for a generalized nonlinear Schrödinger equation with nonlocal nonlinearity. Phys. Scr. 2025, 100, 015262. [Google Scholar] [CrossRef]
- Sawangtong, P.; Taghipour, M.; Najafi, A. An efficient computational method for solving the fractional form of the European option price PDE with transaction cost under the fractional Heston model. Eng. Anal. Bound. Elem. 2024, 169, 105972. [Google Scholar] [CrossRef]
- Zhang, K.; Cao, J.P. Dynamic behavior and modulation instability of the generalized coupled fractional nonlinear Helmholtz equation with cubic-quintic term. Open Phys. 2025, 23, 20250144. [Google Scholar] [CrossRef]
- Qayyum, M.; Ahmad, E.; Tawfiq, F.M.; Salleh, S.; Saeed, S.T.; Inc, M. Series form solutions of time-space fractional Black-Scholes model via extended He-Aboodh algorithm. Alex. Eng. J. 2024, 109, 83–88. [Google Scholar] [CrossRef]
- Merad, H.; Merghadi, F.; Merad, A. Solution of Sakata-Taketani Equation via the Caputo and Riemann-Liouville fractional derivatives. Rep. Math. Phys. 2022, 89, 359–370. [Google Scholar] [CrossRef]
- Ishibashi, K. Riccati technique and nonoscillation of damped linear dynamic equations with the conformable derivative on time scales. Results Appl. Math. 2025, 25, 100553. [Google Scholar] [CrossRef]
- Sadek, L.; Ldris, S.A.; Jarad, F. The general Caputo-Katugampola fractional derivative and numerical approach for solving the fractional differential equations. Alex. Eng. J. 2025, 121, 539–557. [Google Scholar] [CrossRef]
- Yao, Z.C.; Yang, Z.W.; Gao, J.F. Unconditional stability analysis of Grünwald Letnikov method for fractional-order delay differential equations. Chaos Solitons Fract. 2023, 177, 114193. [Google Scholar] [CrossRef]
- Zhang, Q.; Liang, Y.S. The Weyl-Marchaud fractional derivative of a type of self-affine functions. Appl. Math. Comput. 2012, 218, 8695–8701. [Google Scholar] [CrossRef]
- Liu, X.Y.; Cai, M. Spectral deferred correction method for fractional initial value problem with Caputo-Hadamard derivative. Math. Comput. Simul. 2024, 226, 323–337. [Google Scholar] [CrossRef]
- Odibat, Z.; Odibat, Z. On a New Modification of the Erdélyi-Kober Fractional Derivative. Fractal Fract. 2021, 5, 121. [Google Scholar] [CrossRef]
- Li, C.Y. Zero-r law on the analyticity and the uniform continuity of fractional resolvent families. Integral Equ. Oper. Theory 2024, 96, 34. [Google Scholar]
- Li, C.Y. The Hautus-type inequality for abstract fractional cauchy problems and its observability. J. Math. 2024, 2024, 6179980. [Google Scholar]
- Patel, Y.F.; Izadi, M. An analytical investigation of nonlinear time-fractional Schrödinger and coupled Schrödinger-KdV equations. Results Phys. 2025, 70, 108317. [Google Scholar] [CrossRef]
- Chen, S.Q.; Liu, Y.; Wei, L.X.; Guan, B. Exact solutions to fractional Drinfel’d-Sokolov-Wilson equations. Chin. J. Phys. 2018, 56, 708–720. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z. A dynamical analysis and new traveling wave solution of the fractional coupled Konopelchenko-Dubrovsky model. Fractal Fract. 2024, 8, 341. [Google Scholar] [CrossRef]
- Shi, D.; Liu, C.Y.; Li, Z. New optical soliton solutions to the coupled fractional Lakshmanan-Porsezian-Daniel equations with Kerr law of nonlinearity. Results Phys. 2023, 51, 106625. [Google Scholar] [CrossRef]
- Rahman, M.U.; AL-Essa, L.A. Explorating the solition solutions of fractional Chen-Lee-Liu equation with birefringent fibers arising in optics and their sensitive analysis. Opt. Quant. Electron. 2024, 56, 1041. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C. Bifurcation, phase portrait and traveling wave solution of time-fractional thin-film ferroelectric material equation with beta fractional derivative. Phys. Lett. A 2023, 484, 129080. [Google Scholar] [CrossRef]
- Qi, J.M.; Li, X.W.; Bai, L.Q.; Sun, Y.Q. The exact solutions of the variable-order fractional stochastic Ginzburg-Landau equation along with analysis of bifurcation and chaotic behaviors. Chaos Solitons Fract. 2023, 175, 113946. [Google Scholar] [CrossRef]
- Tuan, N.M.; Meesad, P. A bilinear neural network method for solving a generalized fractional (2+1)-dimensional Konopelchenko-Dubrovsky-Kaup-Kupershmidt equation. Int. J. Theor. Phys. 2025, 64, 17. [Google Scholar] [CrossRef]
- Khater, M.M.A. Pfaffian solutions and nonlinear dynamics of surface waves in two horizontal and one vertical directions with dispersion, dissipation and nonlinearity effects. Alex. Eng. J. 2024, 108, 232–243. [Google Scholar] [CrossRef]
- Raza, N. Exact periodic and explicit solutions the conformable time fractional Ginzburg-Landau equation. Opt. Quantum Electron. 2018, 50, 154–170. [Google Scholar] [CrossRef]
- Liu, C.S. Applications of complete discrimination system for polynomial for classifications of traveling wave solutions to nonlinear differential equations. Comput. Phys. Commun. 2010, 181, 317–324. [Google Scholar] [CrossRef]
- Liu, C.Y. The traveling wave solution and dynamics analysis of the fractional order generalized Pochhammer-Chree equation. AIMS Math. 2024, 9, 33956–33972. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Hussain, E. Qualitative Analysis and Traveling Wave Solutions of a (3 + 1)- Dimensional Generalized Nonlinear Konopelchenko-Dubrovsky-Kaup-Kupershmidt System. Fractal Fract. 2025, 9, 285. https://doi.org/10.3390/fractalfract9050285
Li Z, Hussain E. Qualitative Analysis and Traveling Wave Solutions of a (3 + 1)- Dimensional Generalized Nonlinear Konopelchenko-Dubrovsky-Kaup-Kupershmidt System. Fractal and Fractional. 2025; 9(5):285. https://doi.org/10.3390/fractalfract9050285
Chicago/Turabian StyleLi, Zhao, and Ejaz Hussain. 2025. "Qualitative Analysis and Traveling Wave Solutions of a (3 + 1)- Dimensional Generalized Nonlinear Konopelchenko-Dubrovsky-Kaup-Kupershmidt System" Fractal and Fractional 9, no. 5: 285. https://doi.org/10.3390/fractalfract9050285
APA StyleLi, Z., & Hussain, E. (2025). Qualitative Analysis and Traveling Wave Solutions of a (3 + 1)- Dimensional Generalized Nonlinear Konopelchenko-Dubrovsky-Kaup-Kupershmidt System. Fractal and Fractional, 9(5), 285. https://doi.org/10.3390/fractalfract9050285






