Discrete Memristive Hindmarsh-Rose Neural Model with Fractional-Order Differences
Abstract
1. Introduction
2. The Model
2.1. Discrete mHR Model
2.2. Basic Definitions of Fractional Difference
- The definition of the forward difference operator is as follows:
- For the function , where , , the discrete fractional integral is obtained aswith the order and being the Gamma function as follows:Also, , and is defined as the falling factorial as
- The Caputo-like delta difference of the function u for is defined aswhere .
2.3. Fractional-Order mHR Model
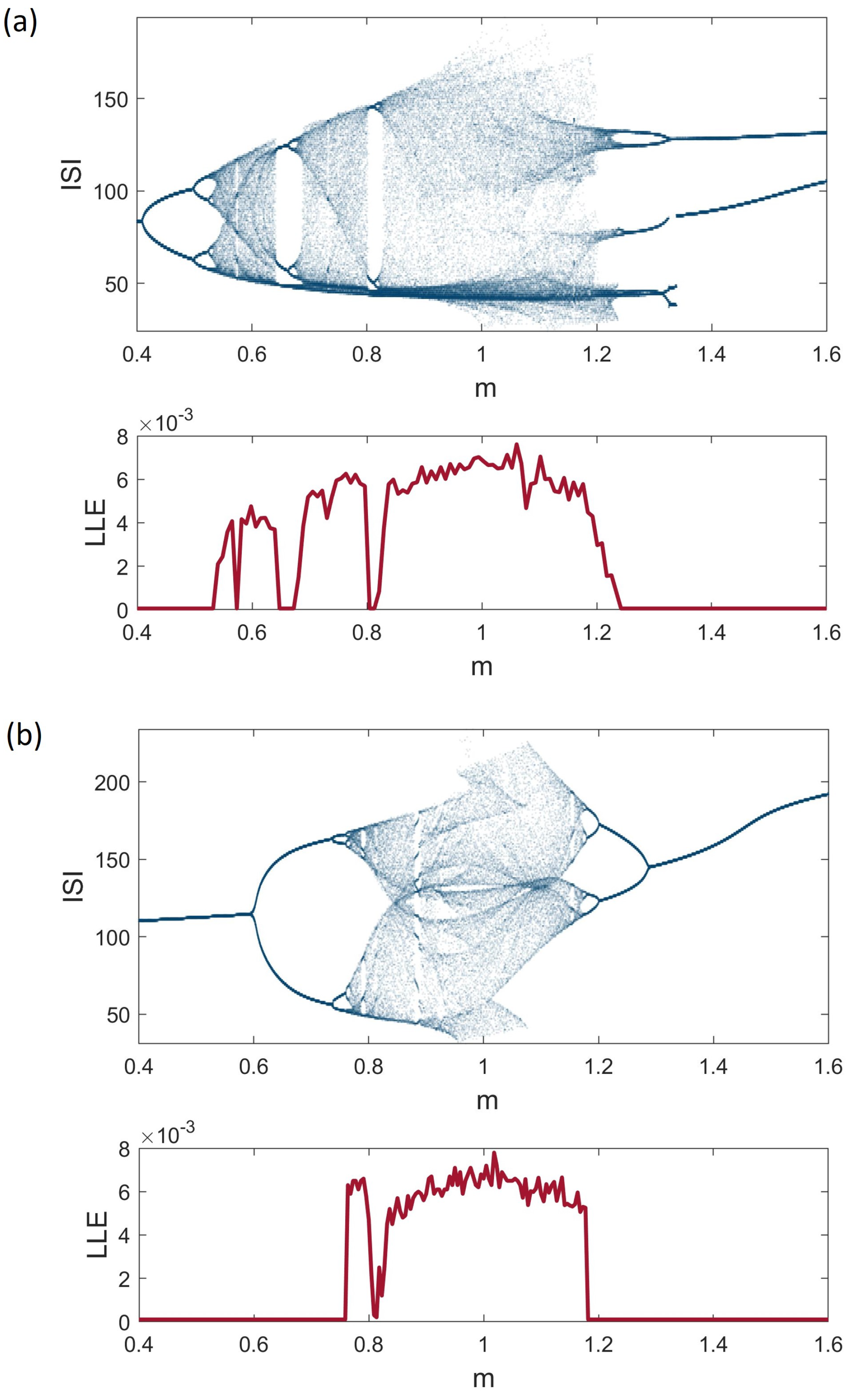
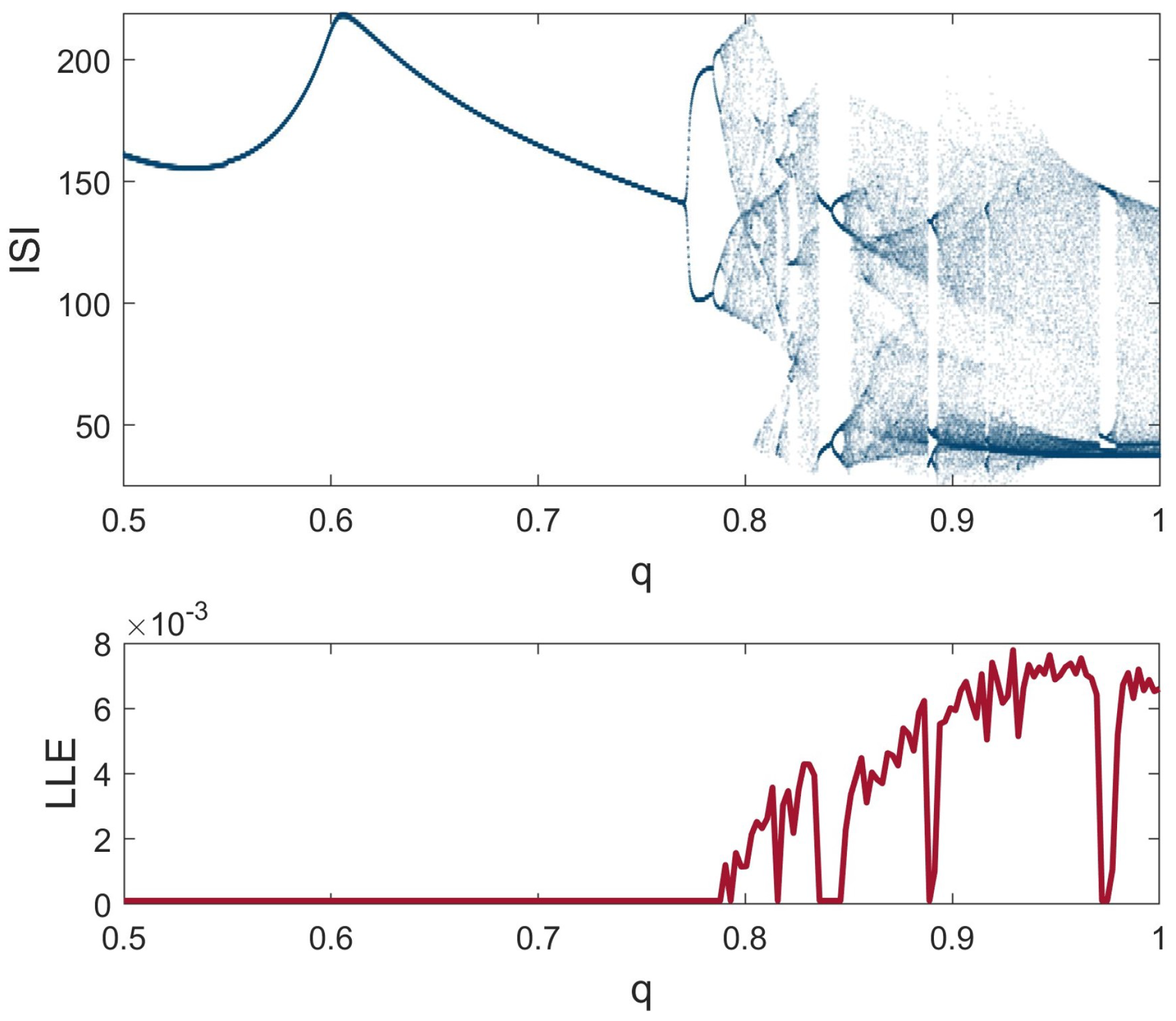
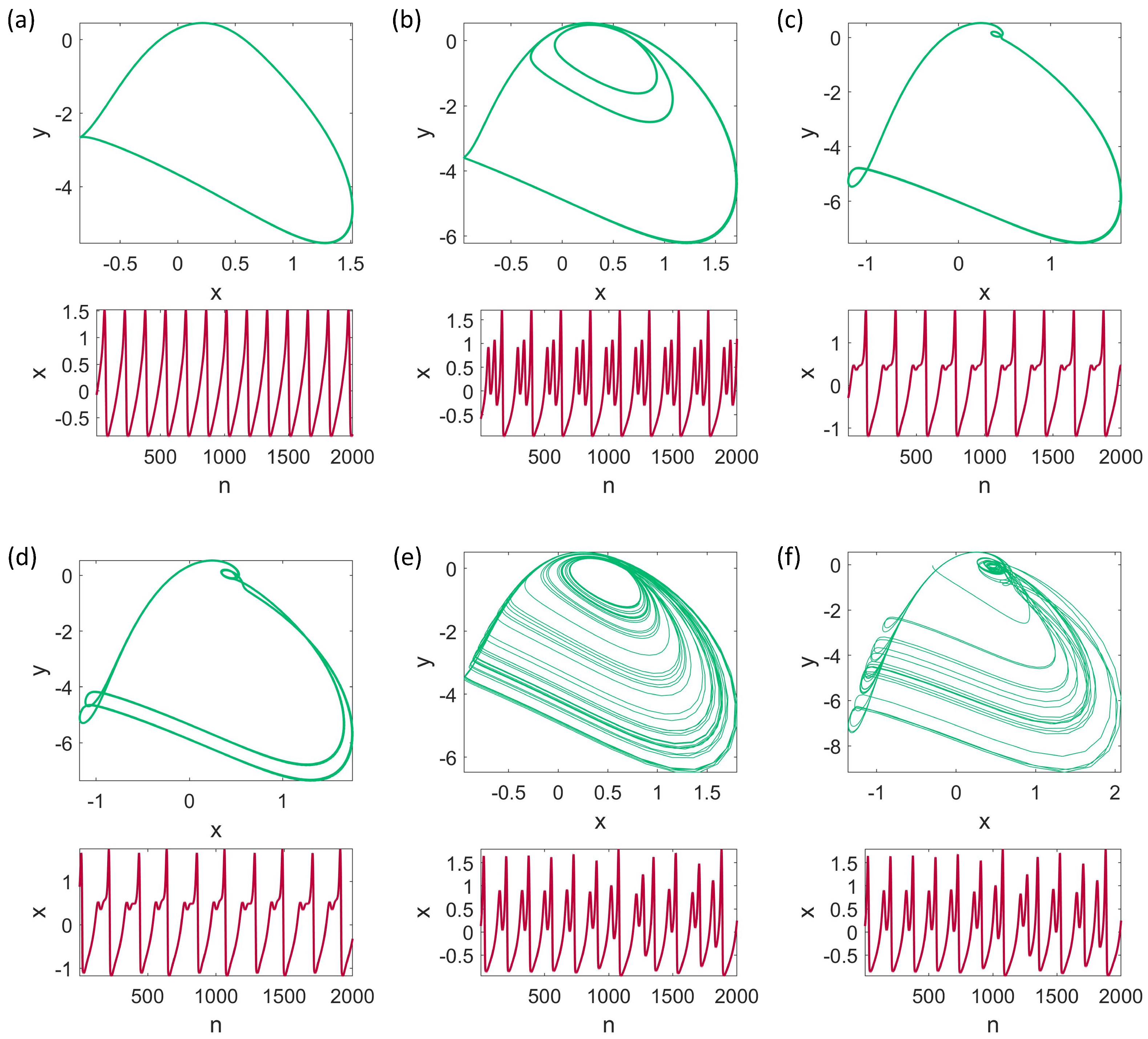
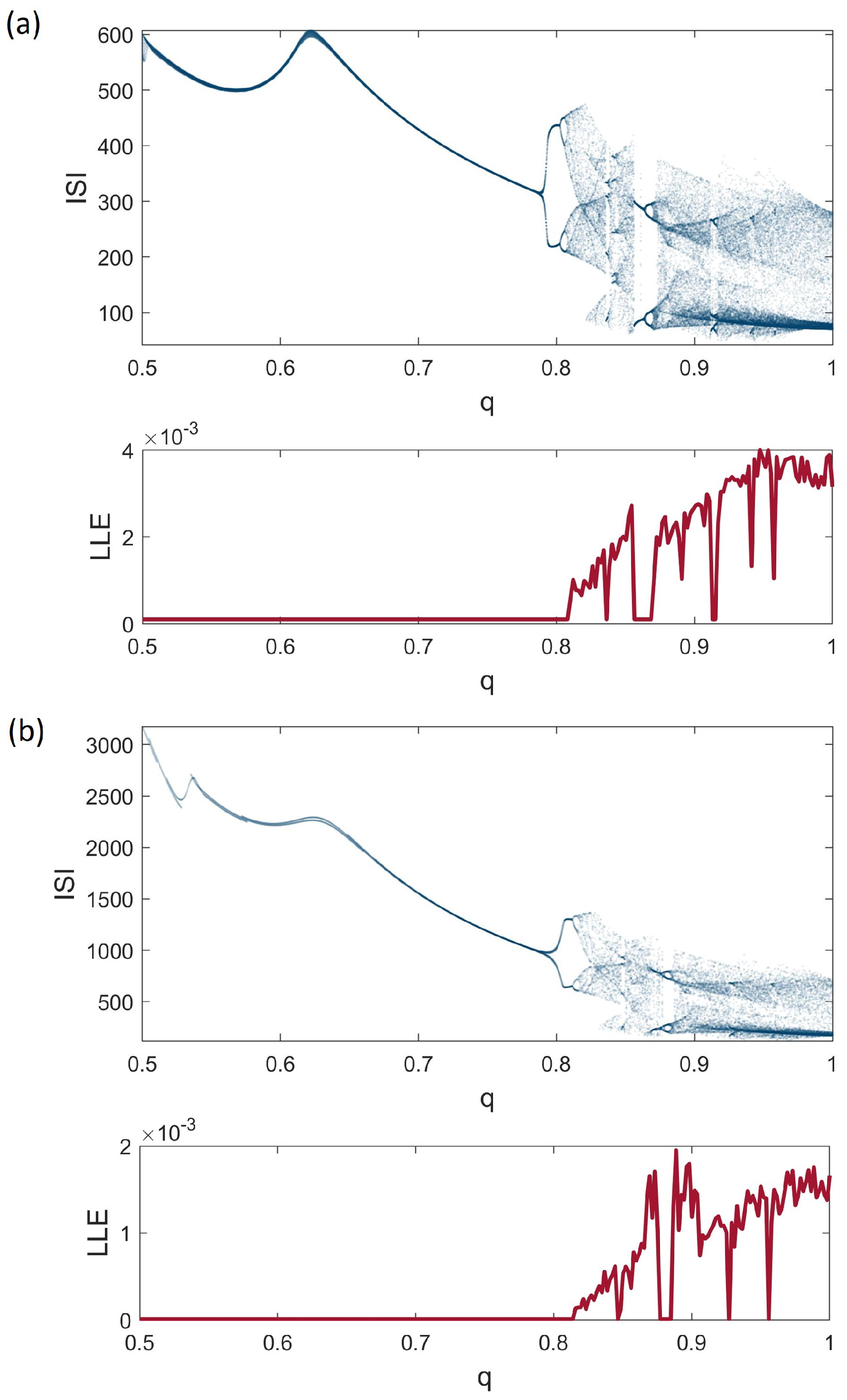
3. Dynamical Analysis
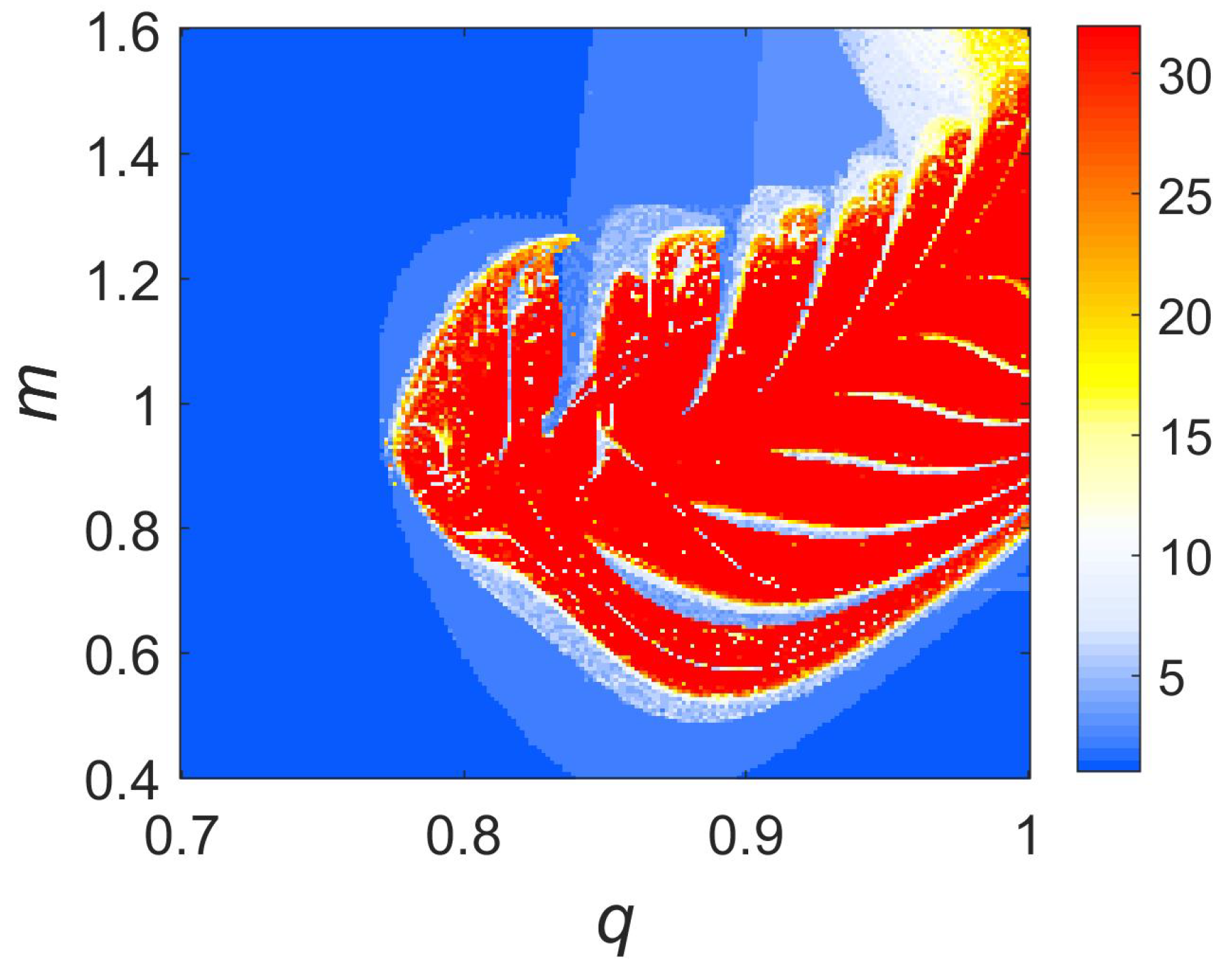
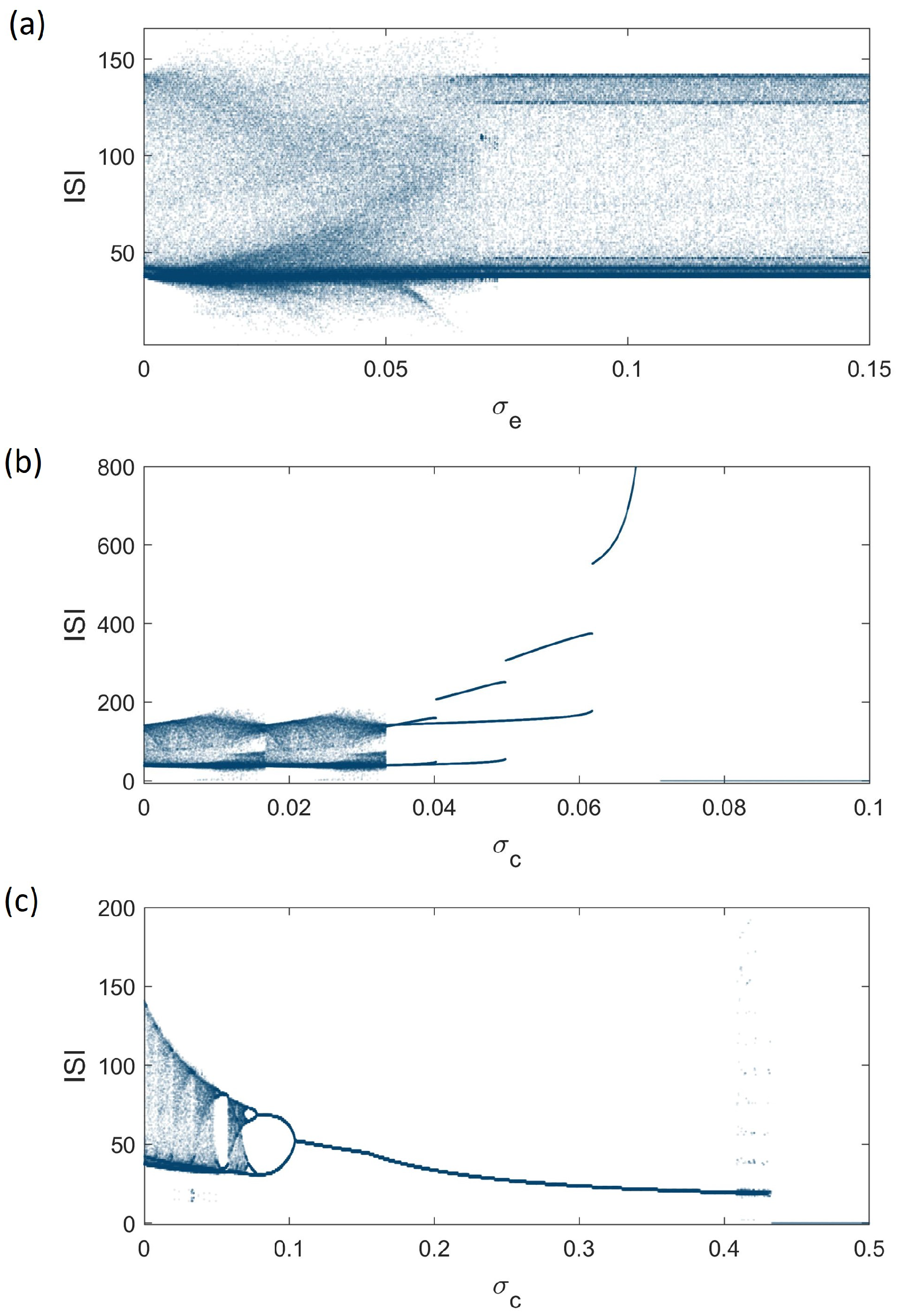
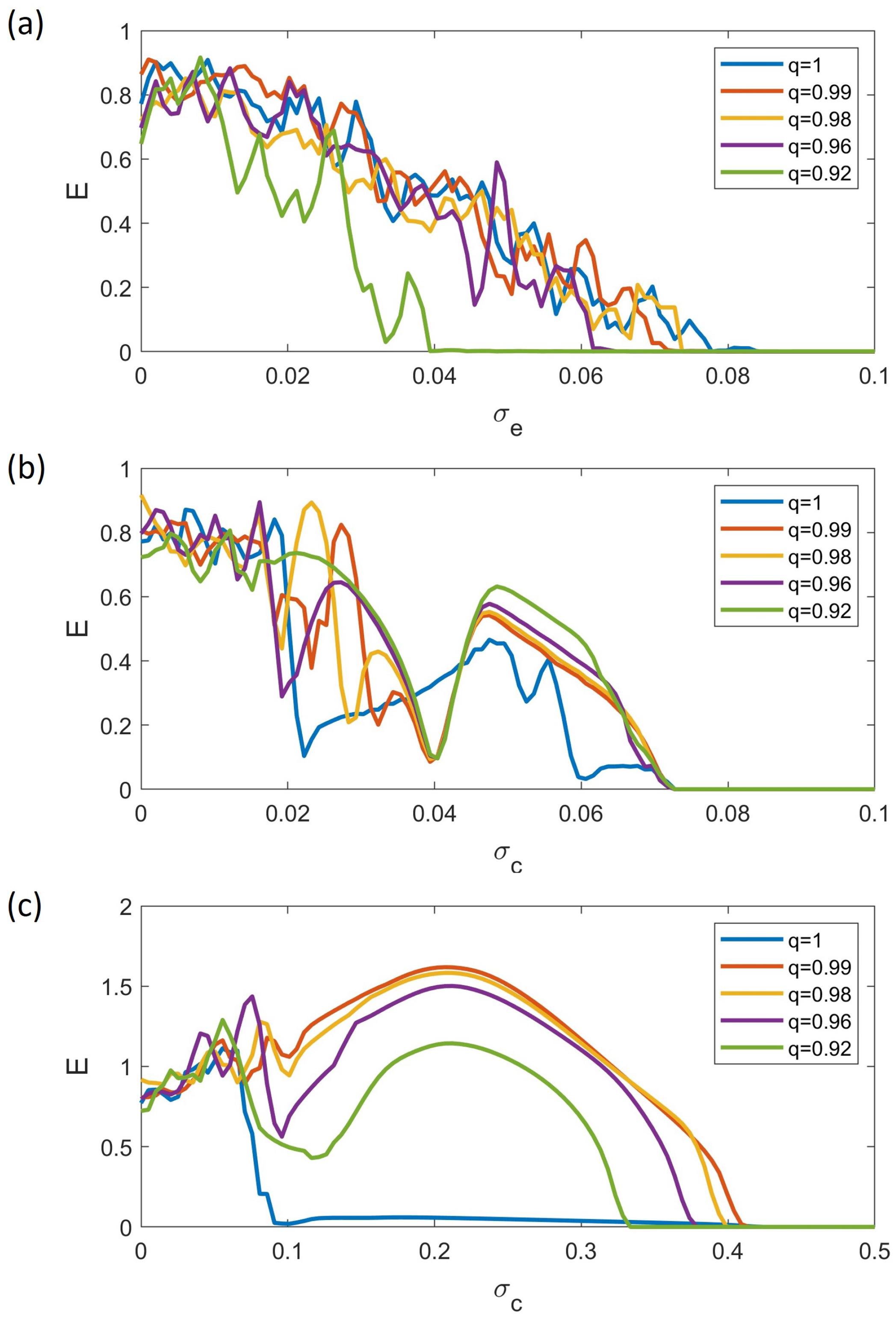
4. Synchronization Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Fortuna, L.; Buscarino, A. Spiking neuron mathematical models: A compact overview. Bioengineering 2023, 10, 174. [Google Scholar] [CrossRef] [PubMed]
- Oliveri, H.; Goriely, A. Mathematical models of neuronal growth. Biomech. Model. Mechanobiol. 2022, 21, 89–118. [Google Scholar] [CrossRef] [PubMed]
- FitzHugh, R. Mathematical models of threshold phenomena in the nerve membrane. Bull. Math. Biophys. 1955, 17, 257–278. [Google Scholar] [CrossRef]
- Hindmarsh, J.L.; Rose, R. A model of neuronal bursting using three coupled first order differential equations. Proc. R. Soc. B 1984, 221, 87–102. [Google Scholar]
- Rulkov, N.F. Modeling of spiking-bursting neural behavior using two-dimensional map. Phys. Rev. E 2002, 65, 041922. [Google Scholar] [CrossRef]
- Chialvo, D.R. Generic excitable dynamics on a two-dimensional map. Chaos Solitons Fractals 1995, 5, 461–479. [Google Scholar] [CrossRef]
- Li, B.; He, Z. Bifurcations and chaos in a two-dimensional discrete Hindmarsh–Rose model. Nonlinear Dyn. 2014, 76, 697–715. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, K.; Shan, Y.; Wu, H.; Chen, M.; Wang, N. Dynamical effects of memristive electromagnetic induction on a 2D Wilson neuron model. Cognit. Neurodyn. 2024, 18, 645–657. [Google Scholar] [CrossRef]
- Xu, Q.; Huang, L.; Wang, N.; Bao, H.; Wu, H.; Chen, M. Initial-offset-boosted coexisting hyperchaos in a 2D memristive Chialvo neuron map and its application in image encryption. Nonlinear Dyn. 2023, 111, 20447–20463. [Google Scholar] [CrossRef]
- Caravelli, F.; Sheldon, F.C.; Traversa, F.L. Global minimization via classical tunneling assisted by collective force field formation. Sci. Adv. 2021, 7, eabh1542. [Google Scholar] [CrossRef]
- Barrows, F.; Lin, J.; Caravelli, F.; Chialvo, D.R. Uncontrolled Learning: Codesign of Neuromorphic Hardware Topology for Neuromorphic Algorithms. Adv. Intell. Syst. 2024; early view. [Google Scholar] [CrossRef]
- Wu, F.; Ma, J.; Zhang, G. A new neuron model under electromagnetic field. Appl. Math. Comput. 2019, 347, 590–599. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Yao, Z.; Ma, J. A feasible neuron for estimating the magnetic field effect. Nonlinear Dyn. 2020, 102, 1849–1867. [Google Scholar] [CrossRef]
- Ge, M.; Jia, Y.; Xu, Y.; Yang, L. Mode transition in electrical activities of neuron driven by high and low frequency stimulus in the presence of electromagnetic induction and radiation. Nonlinear Dyn. 2018, 91, 515–523. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Wang, C.; Li, Y. Dynamic analysis and FPGA implementation of a new, simple 5D memristive hyperchaotic Sprott-C system. Mathematics 2023, 11, 701. [Google Scholar] [CrossRef]
- Ding, X.; Feng, C.; Wang, N.; Liu, A.; Xu, Q. Fast-slow dynamics in a memristive ion channel-based bionic circuit. Cognit. Neurodyn. 2024, 18, 3901–3913. [Google Scholar] [CrossRef]
- Wu, F.; Hu, X.; Ma, J. Estimation of the effect of magnetic field on a memristive neuron. Appl. Math. Comput. 2022, 432, 127366. [Google Scholar] [CrossRef]
- Xie, Y.; Ye, Z.; Li, X.; Wang, X.; Jia, Y. A novel memristive neuron model and its energy characteristics. Cognit. Neurodyn. 2024, 18, 1989–2001. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Liu, W.; Bao, B. Discrete memristive neuron model and its interspike interval-encoded application in image encryption. Sci. China Technol. Sci. 2021, 64, 2281–2291. [Google Scholar] [CrossRef]
- Tang, D.; Wang, C.; Lin, H.; Yu, F. Dynamics analysis and hardware implementation of multi-scroll hyperchaotic hidden attractors based on locally active memristive Hopfield neural network. Nonlinear Dyn. 2024, 112, 1511–1527. [Google Scholar] [CrossRef]
- Wang, C.; Tang, D.; Lin, H.; Yu, F.; Sun, Y. High-dimensional memristive neural network and its application in commercial data encryption communication. Expert Syst. Appl. 2024, 242, 122513. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F.; Hong, Q.; Xu, C.; Sun, Y. A triple-memristor Hopfield neural network with space multistructure attractors and space initial-offset behaviors. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2023, 42, 4948–4958. [Google Scholar] [CrossRef]
- Etémé, A.S.; Tabi, C.B.; Mohamadou, A. Firing and synchronization modes in neural network under magnetic stimulation. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 432–440. [Google Scholar] [CrossRef]
- Etémé, A.S.; Tabi, C.B.; Beyala Ateba, J.F.; Ekobena Fouda, H.P.; Mohamadou, A.; Crépin Kofané, T. Chaos break and synchrony enrichment within Hindmarsh-Rose-type memristive neural models. Nonlinear Dyn. 2021, 105, 785–795. [Google Scholar] [CrossRef]
- Gutiérrez, R.E.; Rosário, J.M.; Tenreiro Machado, J. Fractional order calculus: Basic concepts and engineering applications. Math. Probl. Eng. 2010, 2010. [Google Scholar] [CrossRef]
- Dalir, M.; Bashour, M. Applications of fractional calculus. Appl. Math. Sci. 2010, 4, 1021–1032. [Google Scholar]
- Danca, M.F.; Chen, G. Bifurcation and Chaos in Fractional-Order Systems; MDPI: Basel, Switzerland, 2021. [Google Scholar]
- Rahimy, M. Applications of fractional differential equations. Appl. Math. Sci. 2010, 4, 2453–2461. [Google Scholar]
- He, S.; Wang, H.; Sun, K. Solutions and memory effect of fractional-order chaotic system: A review. Chin. Phys. B 2022, 31, 060501. [Google Scholar] [CrossRef]
- Jin, T.; Xia, H.; Deng, W.; Li, Y.; Chen, H. Uncertain fractional-order multi-objective optimization based on reliability analysis and application to fractional-order circuit with caputo type. Circuits Syst. Signal Process. 2021, 40, 5955–5982. [Google Scholar] [CrossRef]
- Jin, T.; Sun, Y.; Zhu, Y. Time integral about solution of an uncertain fractional order differential equation and application to zero-coupon bond model. Appl. Math. Comput. 2020, 372, 124991. [Google Scholar] [CrossRef]
- Liu, W.; Dai, G. Multiple solutions for a fractional nonlinear Schrödinger equation with local potential. Commun. Pure Appl. Anal. 2017, 16. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Wang, C.; Li, Y. Dynamic analysis and field-programmable gate array implementation of a 5D fractional-order memristive hyperchaotic system with multiple coexisting attractors. Fractal Fract. 2024, 8, 271. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M.; Olsson, P. On the fractional order model of viscoelasticity. Mech. Time-Depend. Mater. 2005, 9, 15–34. [Google Scholar] [CrossRef]
- Sierociuk, D.; Skovranek, T.; Macias, M.; Podlubny, I.; Petras, I.; Dzielinski, A.; Ziubinski, P. Diffusion process modeling by using fractional-order models. Appl. Math. Comput. 2015, 257, 2–11. [Google Scholar] [CrossRef]
- Wu, G.C.; Luo, M.; Huang, L.L.; Banerjee, S. Short memory fractional differential equations for new memristor and neural network design. Nonlinear Dyn. 2020, 100, 3611–3623. [Google Scholar] [CrossRef]
- Song, C.; Cao, J. Dynamics in fractional-order neural networks. Neurocomputing 2014, 142, 494–498. [Google Scholar] [CrossRef]
- Yan, B.; Parastesh, F.; He, S.; Rajagopal, K.; Jafari, S.; Perc, M. Interlayer and intralayer synchronization in multiplex fractional-order neuronal networks. Fractals 2022, 30, 2240194. [Google Scholar] [CrossRef]
- Rajagopal, K.; Parastesh, F.; Abdolmohammadi, H.R.; Jafari, S.; Perc, M.; Klemenčič, E. Effects of coupling on extremely multistable fractional-order systems. Chin. J. Phys. 2024, 87, 246–255. [Google Scholar] [CrossRef]
- Brandibur, O.; Kaslik, E. Stability properties of a two-dimensional system involving one Caputo derivative and applications to the investigation of a fractional-order Morris–Lecar neuronal model. Nonlinear Dyn. 2017, 90, 2371–2386. [Google Scholar] [CrossRef]
- Jun, D.; Guang-Jun, Z.; Yong, X.; Hong, Y.; Jue, W. Dynamic behavior analysis of fractional-order Hindmarsh–Rose neuronal model. Cognit. Neurodyn. 2014, 8, 167–175. [Google Scholar] [CrossRef]
- Mondal, A.; Sharma, S.K.; Upadhyay, R.K.; Mondal, A. Firing activities of a fractional-order FitzHugh-Rinzel bursting neuron model and its coupled dynamics. Sci. Rep. 2019, 9, 15721. [Google Scholar] [CrossRef] [PubMed]
- Shi, M.; Wang, Z. Abundant bursting patterns of a fractional-order Morris–Lecar neuron model. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1956–1969. [Google Scholar] [CrossRef]
- Yao, Z.; Sun, K.; He, S. Firing patterns in a fractional-order FithzHugh–Nagumo neuron model. Nonlinear Dyn. 2022, 110, 1807–1822. [Google Scholar] [CrossRef]
- Yu, Y.; Shi, M.; Kang, H.; Chen, M.; Bao, B. Hidden dynamics in a fractional-order memristive Hindmarsh–Rose model. Nonlinear Dyn. 2020, 100, 891–906. [Google Scholar] [CrossRef]
- Atıcı, F.M.; Şengül, S. Modeling with fractional difference equations. J. Math. Anal. Appl. 2010, 369, 1–9. [Google Scholar] [CrossRef]
- Danca, M.F. Symmetry-breaking and bifurcation diagrams of fractional-order maps. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106760. [Google Scholar] [CrossRef]
- Danca, M.F. Fractional order logistic map: Numerical approach. Chaos Solitons Fractals 2022, 157, 111851. [Google Scholar] [CrossRef]
- Al-Khedhairi, A.; Elsadany, A.A.; Elsonbaty, A. On the Dynamics of a Discrete Fractional-Order Cournot–Bertrand Competition Duopoly Game. Math. Prob. Eng. 2022, 2022, 8249215. [Google Scholar] [CrossRef]
- Ji, Y.; Lai, L.; Zhong, S.; Zhang, L. Bifurcation and chaos of a new discrete fractional-order logistic map. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 352–358. [Google Scholar] [CrossRef]
- Al-Qurashi, M.; Asif, Q.U.A.; Chu, Y.M.; Rashid, S.; Elagan, S. Complexity analysis and discrete fractional difference implementation of the Hindmarsh–Rose neuron system. Results Phys. 2023, 51, 106627. [Google Scholar] [CrossRef]
- Bao, H.; Hu, A.; Liu, W.; Bao, B. Hidden bursting firings and bifurcation mechanisms in memristive neuron model with threshold electromagnetic induction. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 502–511. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Chen, Y. Existence of solutions to anti-periodic boundary value problem for nonlinear fractional differential equations with impulses. Adv. Differ. Equations 2011, 2011, 915689. [Google Scholar] [CrossRef]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.; Zhou, C. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parastesh, F.; Rajagopal, K.; Jafari, S.; Perc, M. Discrete Memristive Hindmarsh-Rose Neural Model with Fractional-Order Differences. Fractal Fract. 2025, 9, 276. https://doi.org/10.3390/fractalfract9050276
Parastesh F, Rajagopal K, Jafari S, Perc M. Discrete Memristive Hindmarsh-Rose Neural Model with Fractional-Order Differences. Fractal and Fractional. 2025; 9(5):276. https://doi.org/10.3390/fractalfract9050276
Chicago/Turabian StyleParastesh, Fatemeh, Karthikeyan Rajagopal, Sajad Jafari, and Matjaž Perc. 2025. "Discrete Memristive Hindmarsh-Rose Neural Model with Fractional-Order Differences" Fractal and Fractional 9, no. 5: 276. https://doi.org/10.3390/fractalfract9050276
APA StyleParastesh, F., Rajagopal, K., Jafari, S., & Perc, M. (2025). Discrete Memristive Hindmarsh-Rose Neural Model with Fractional-Order Differences. Fractal and Fractional, 9(5), 276. https://doi.org/10.3390/fractalfract9050276








