Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions
Abstract
1. Introduction
2. ADR and the Derivation of vcRfgNLS Equation
3. IST and Analytical Solutions for the vcRfgNLS Equation
4. Explicit Form of the vcRfgNLS Equation
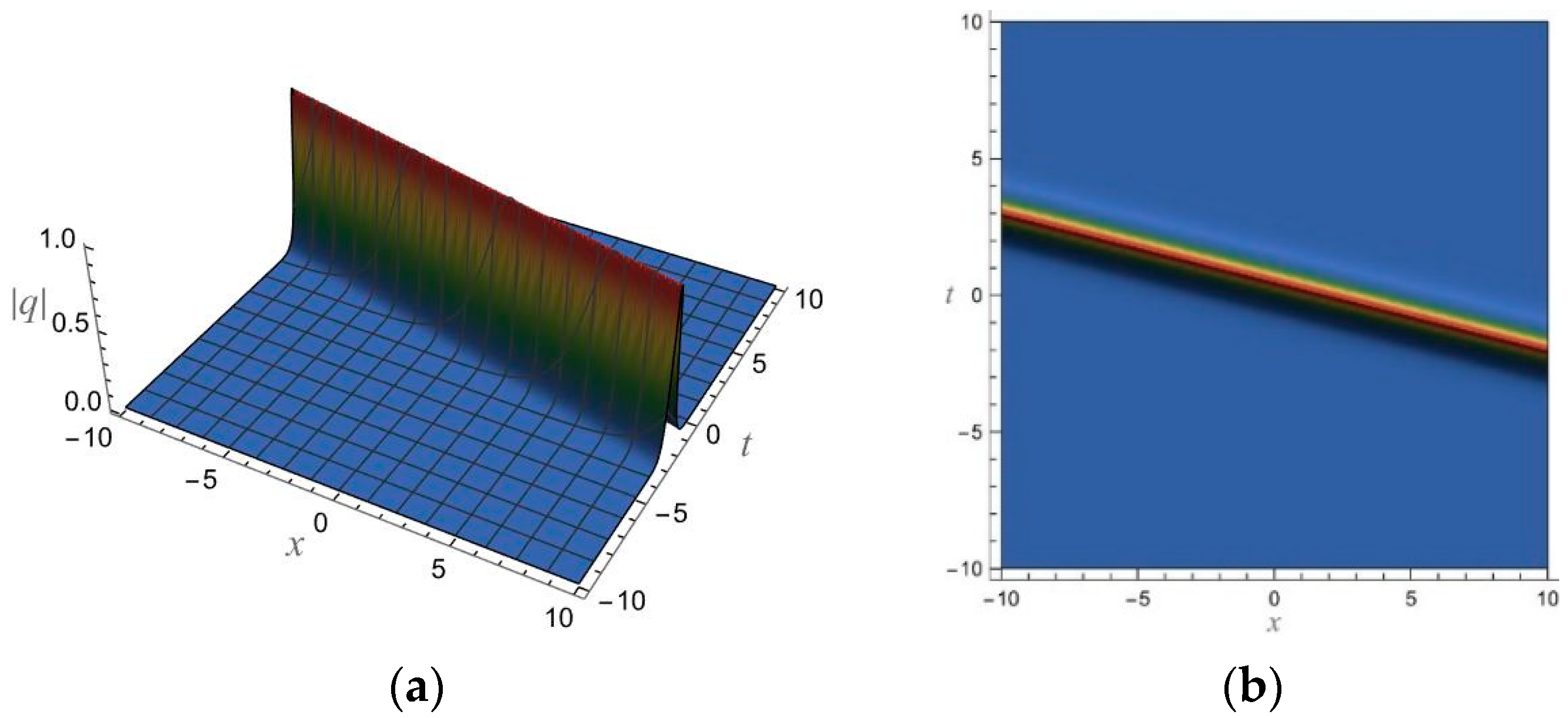
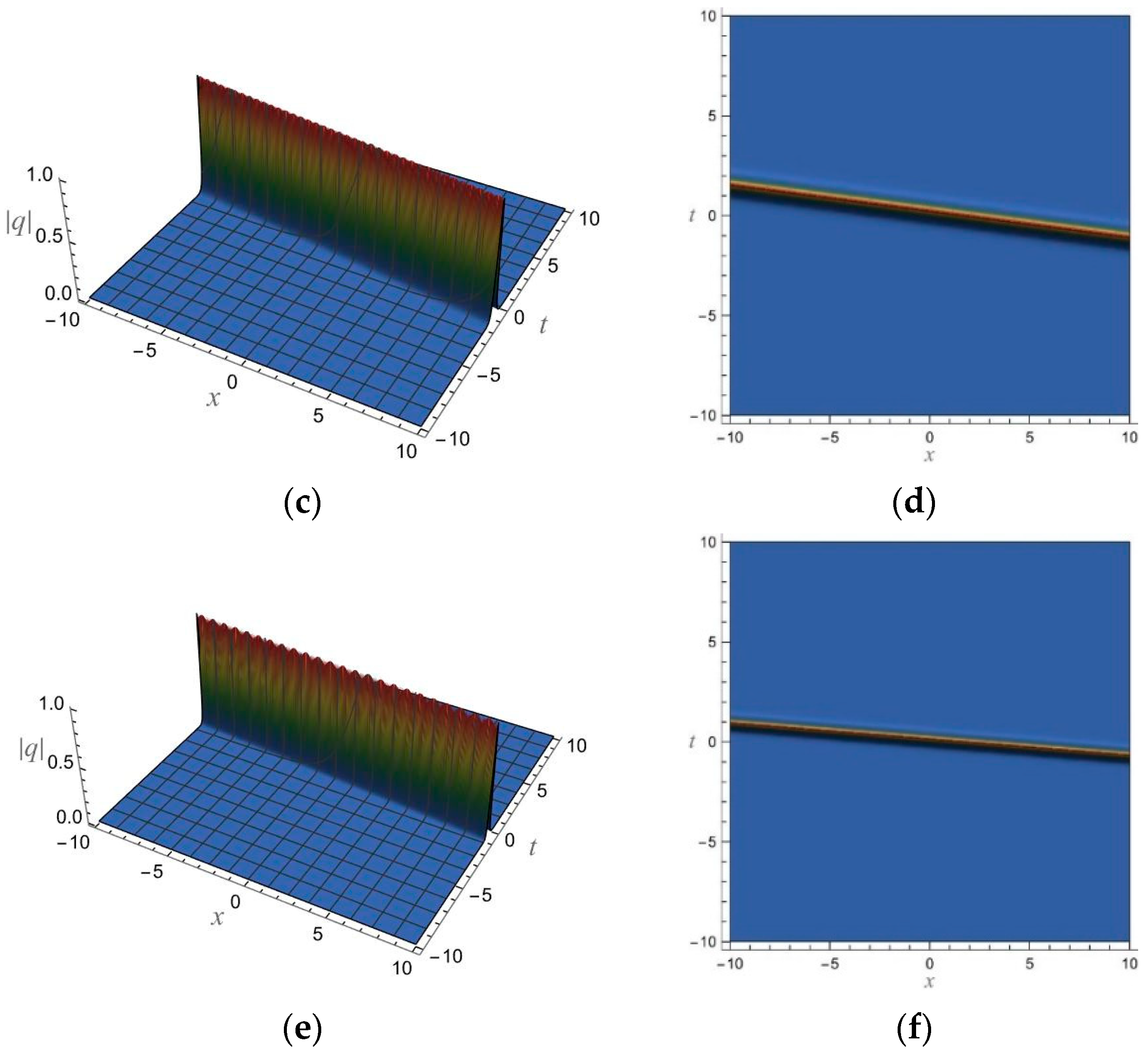
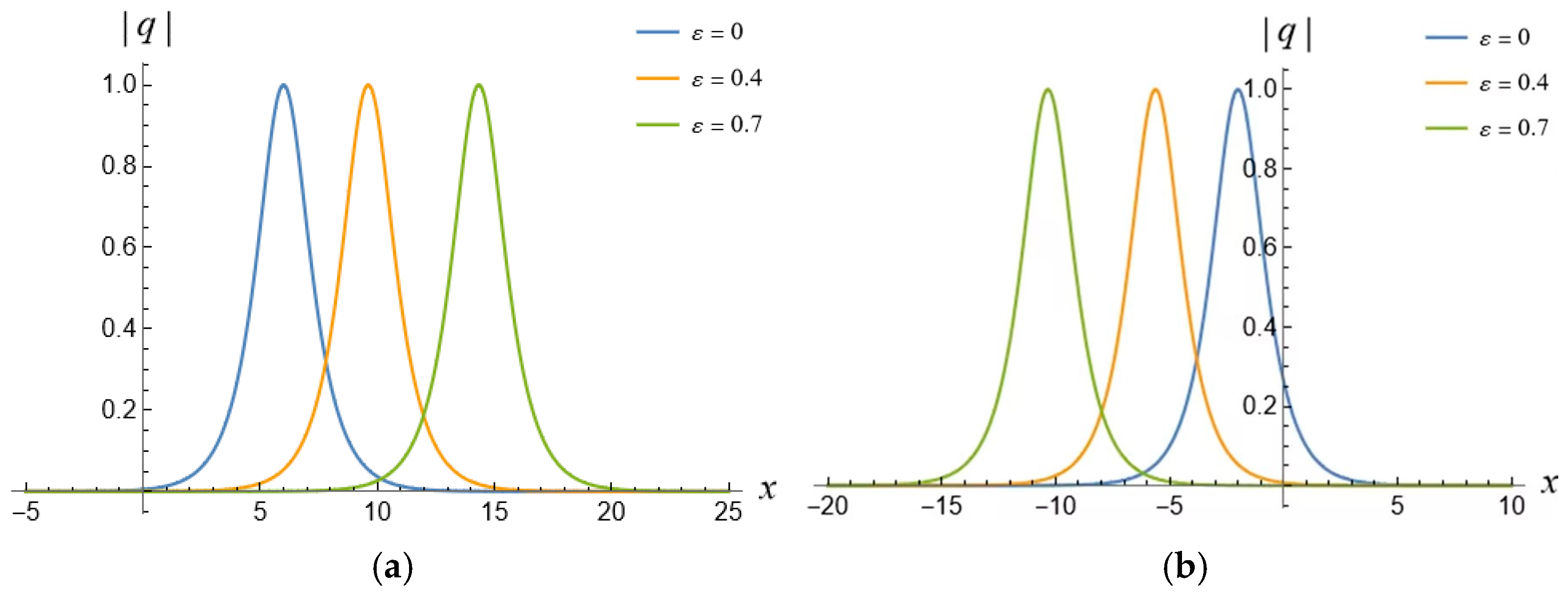
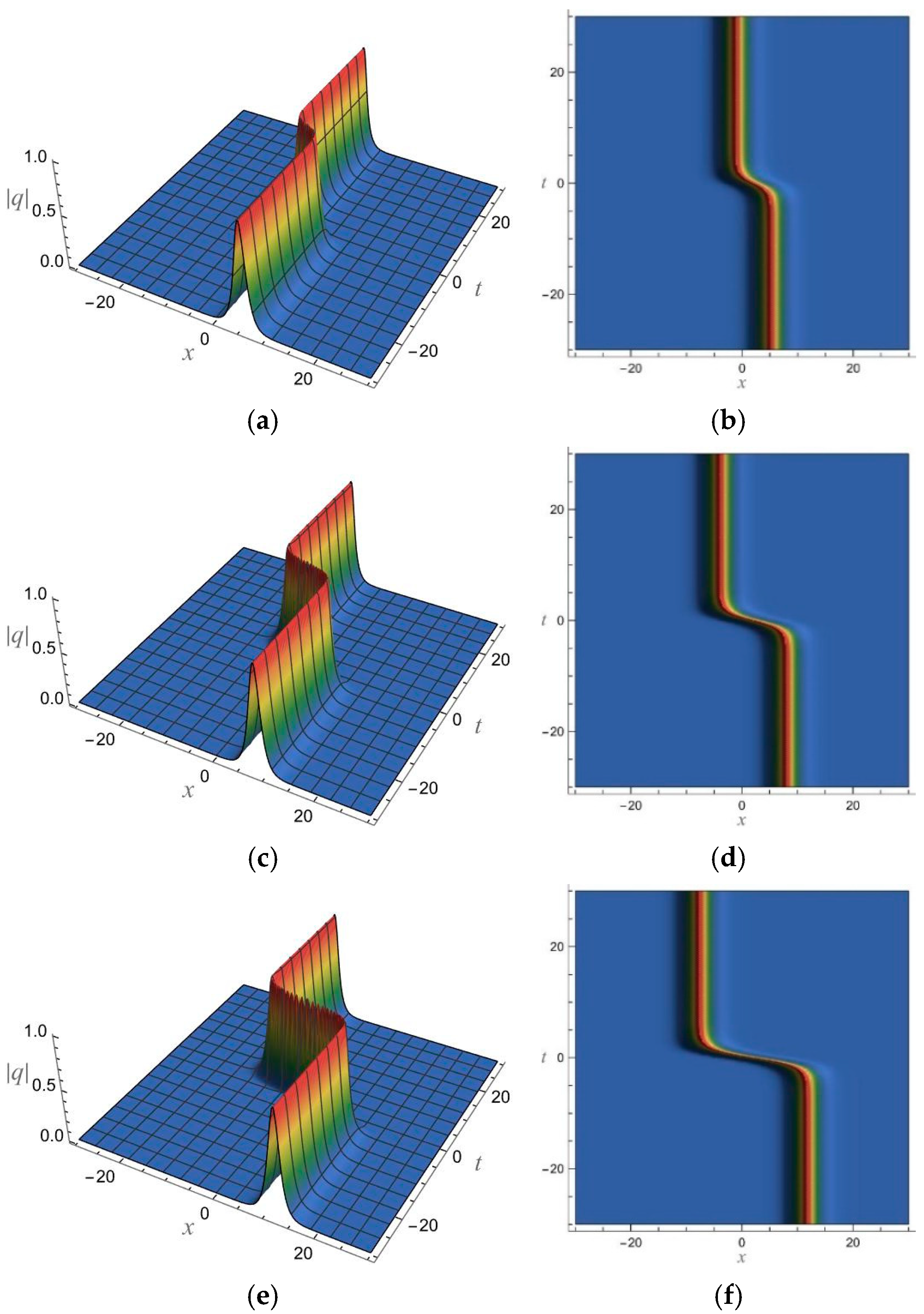
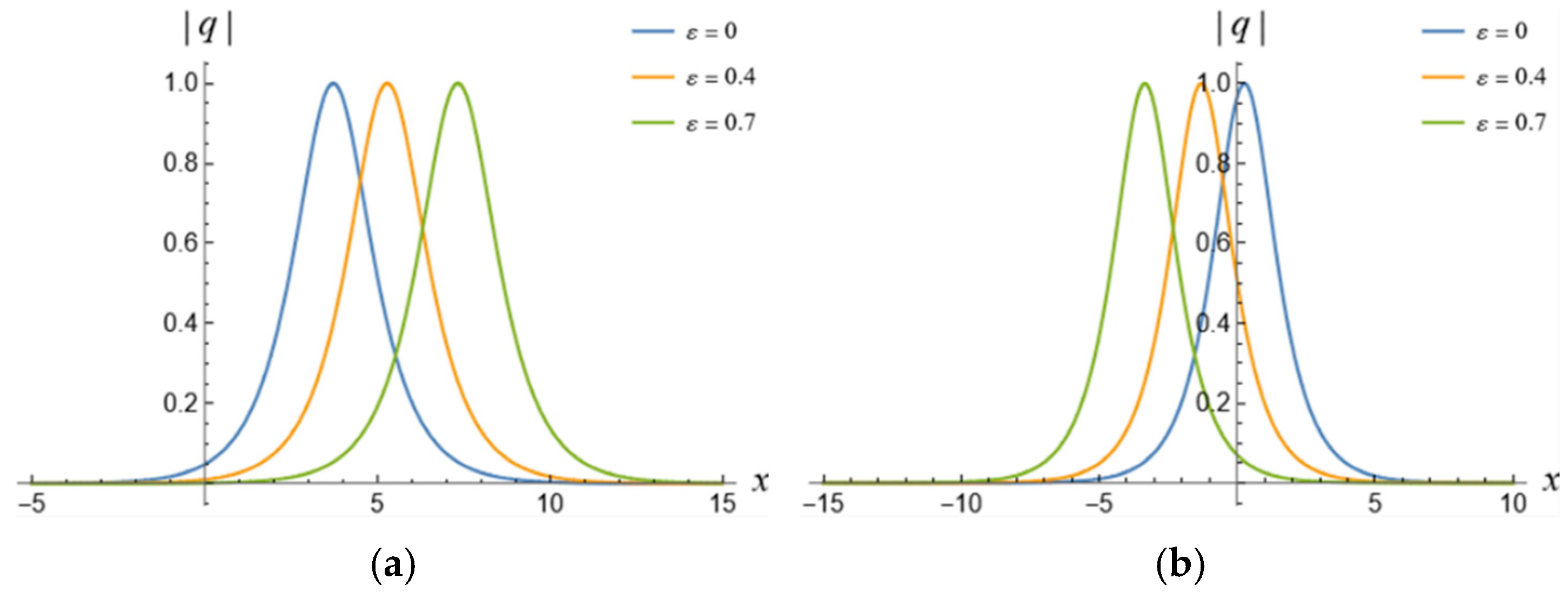
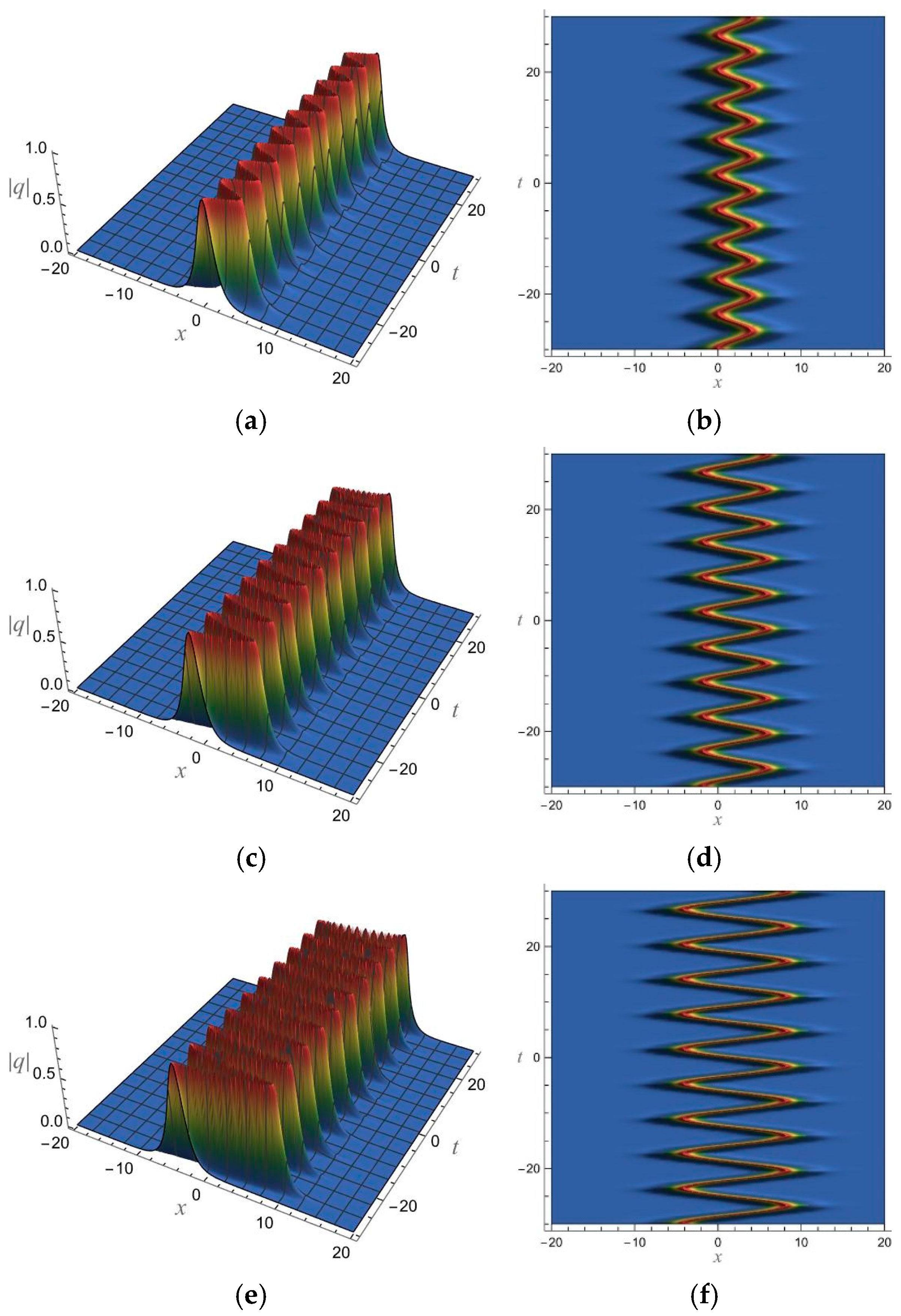
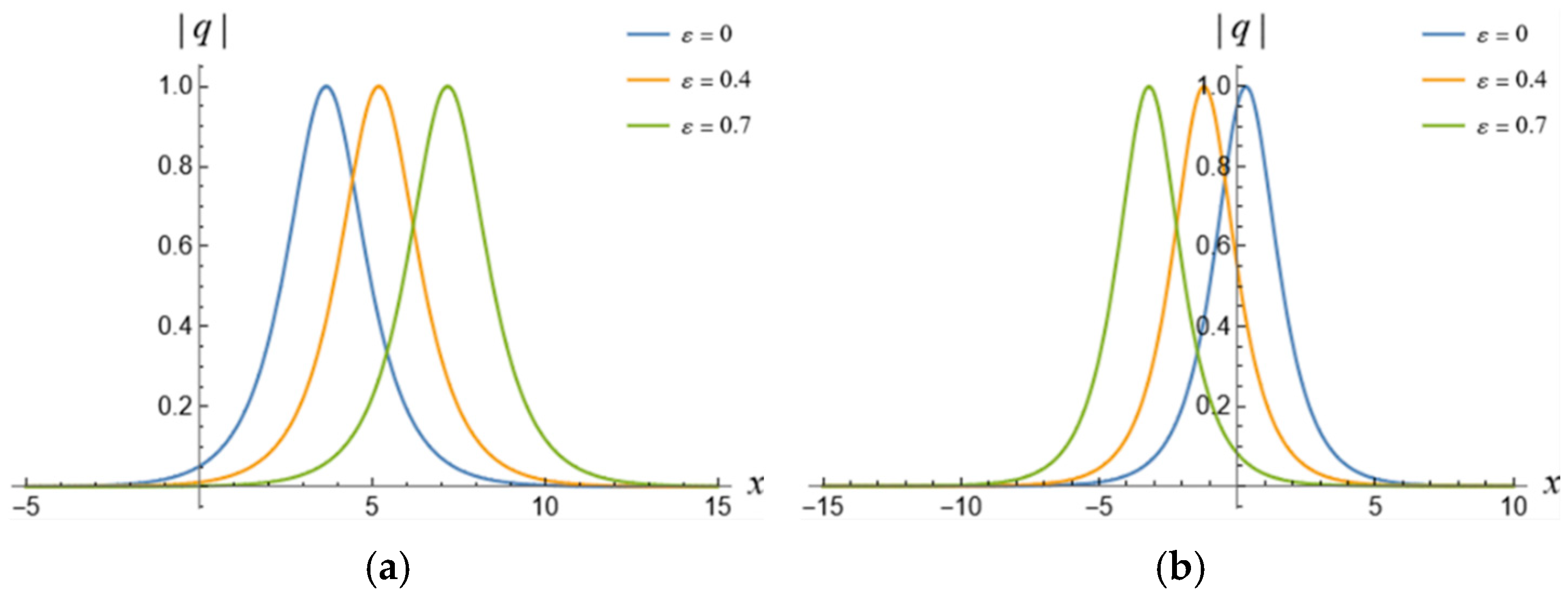
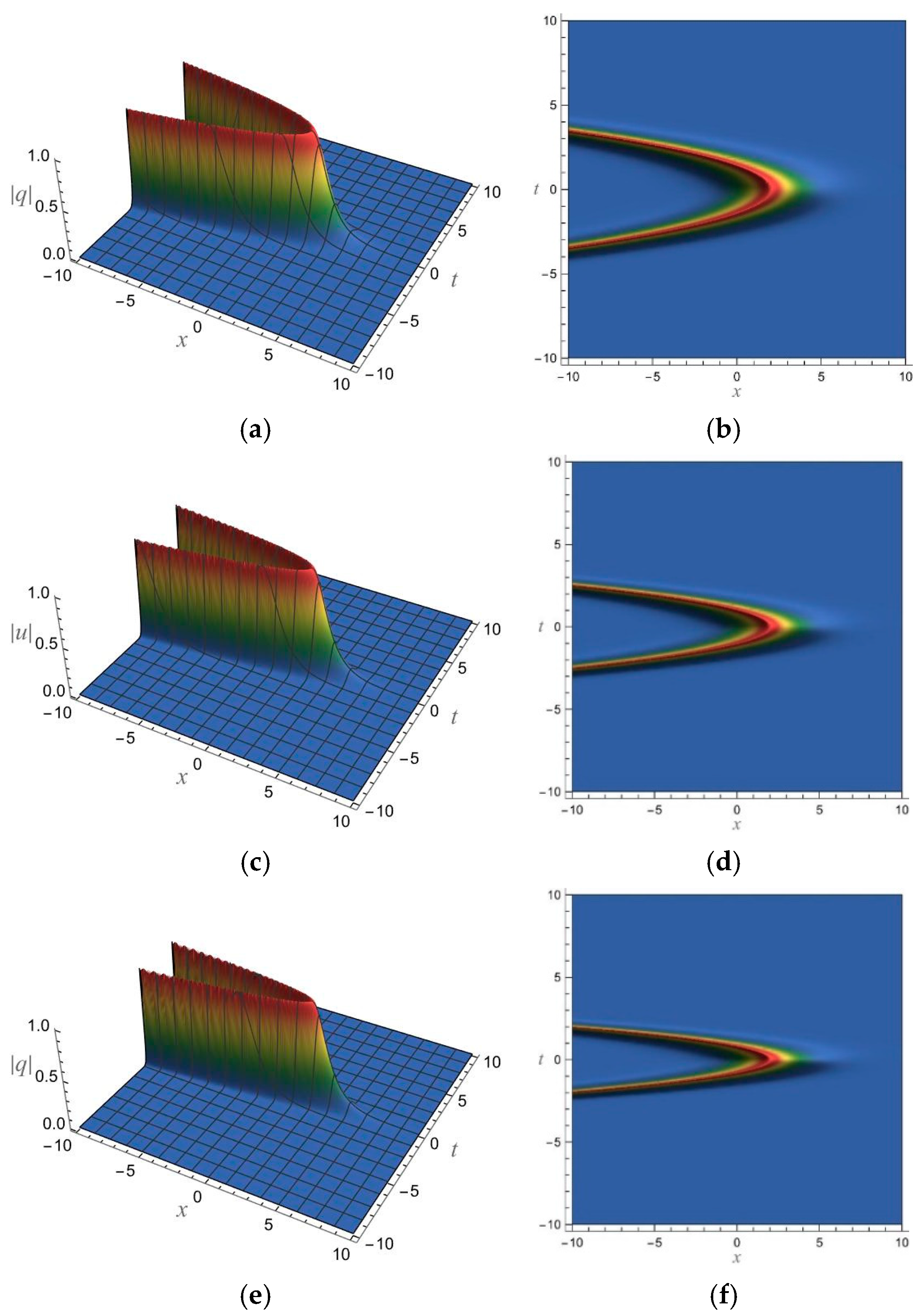
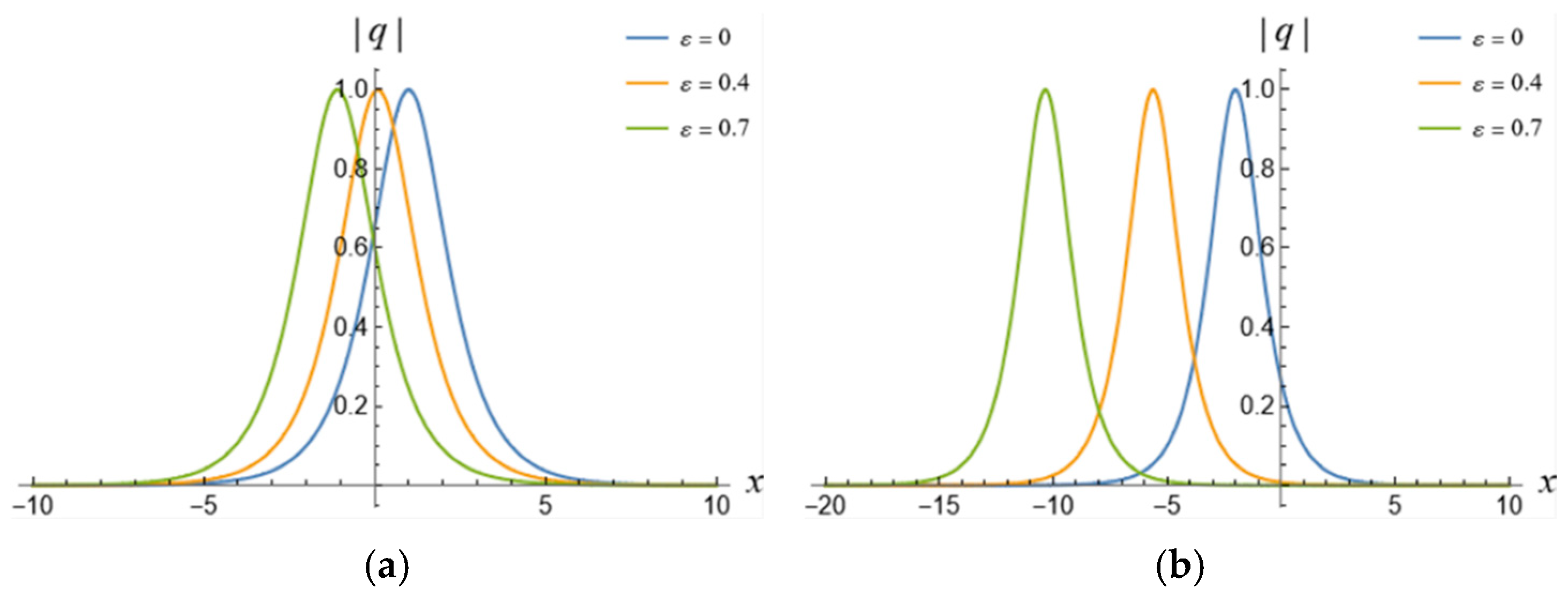
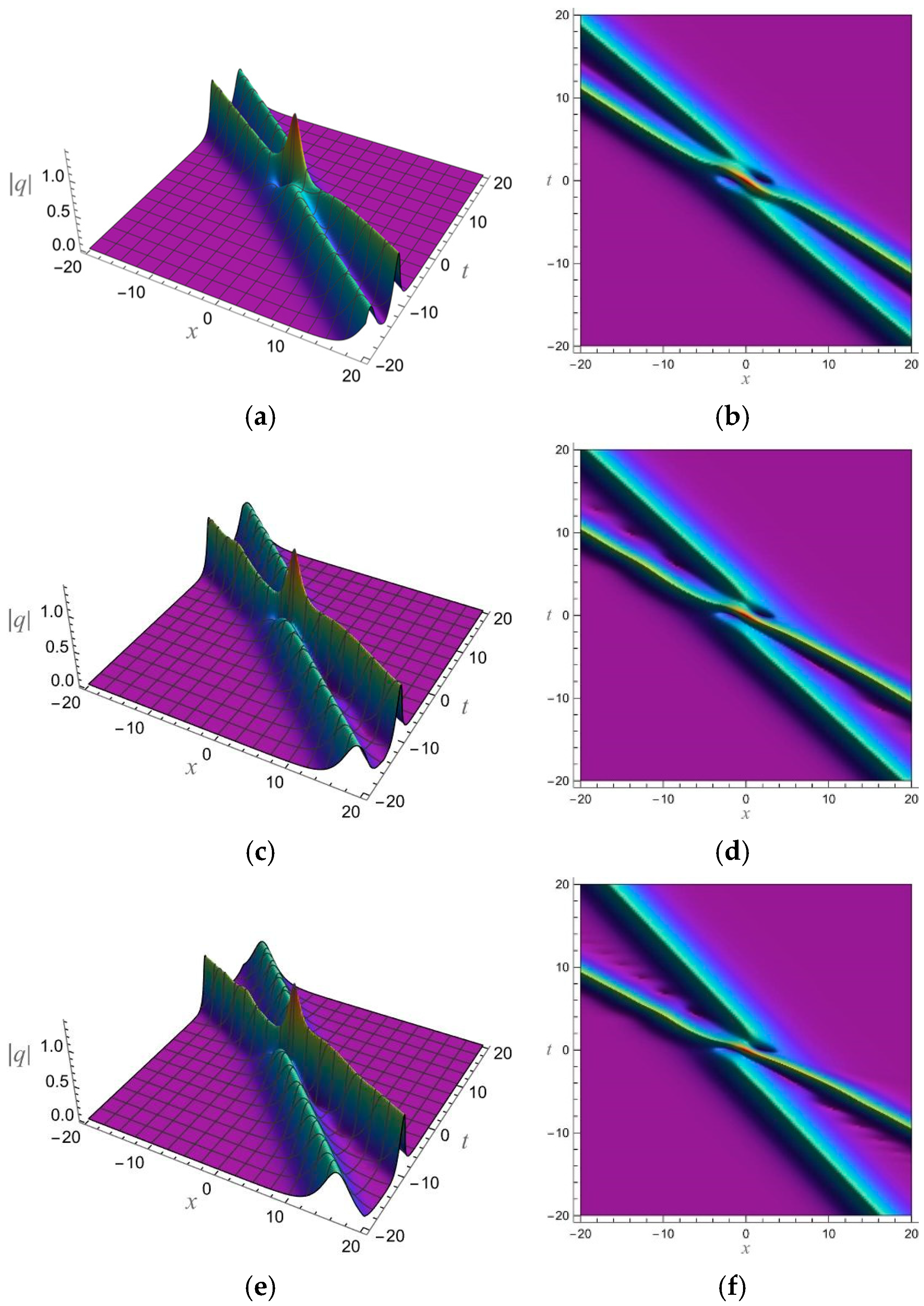
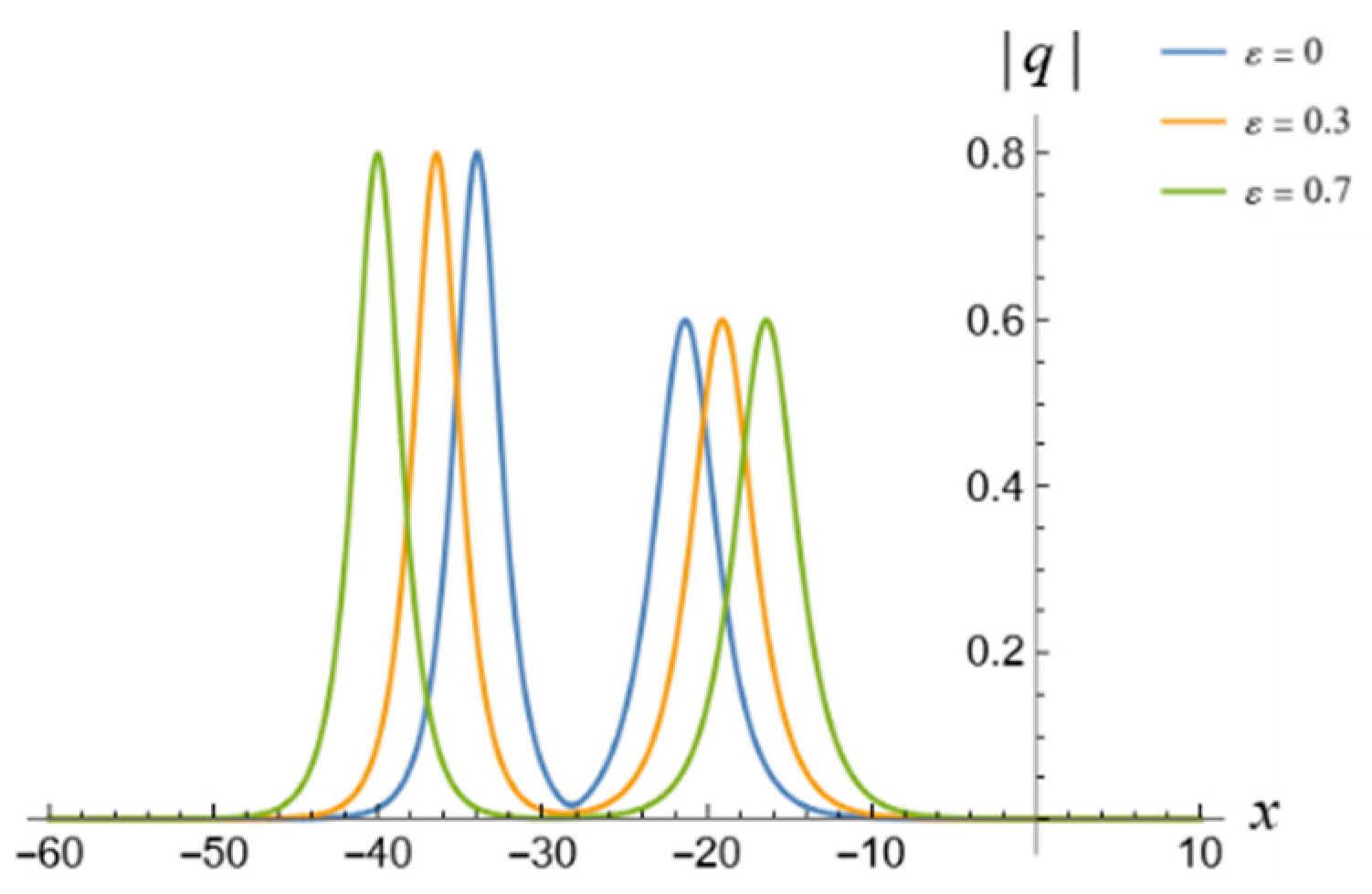
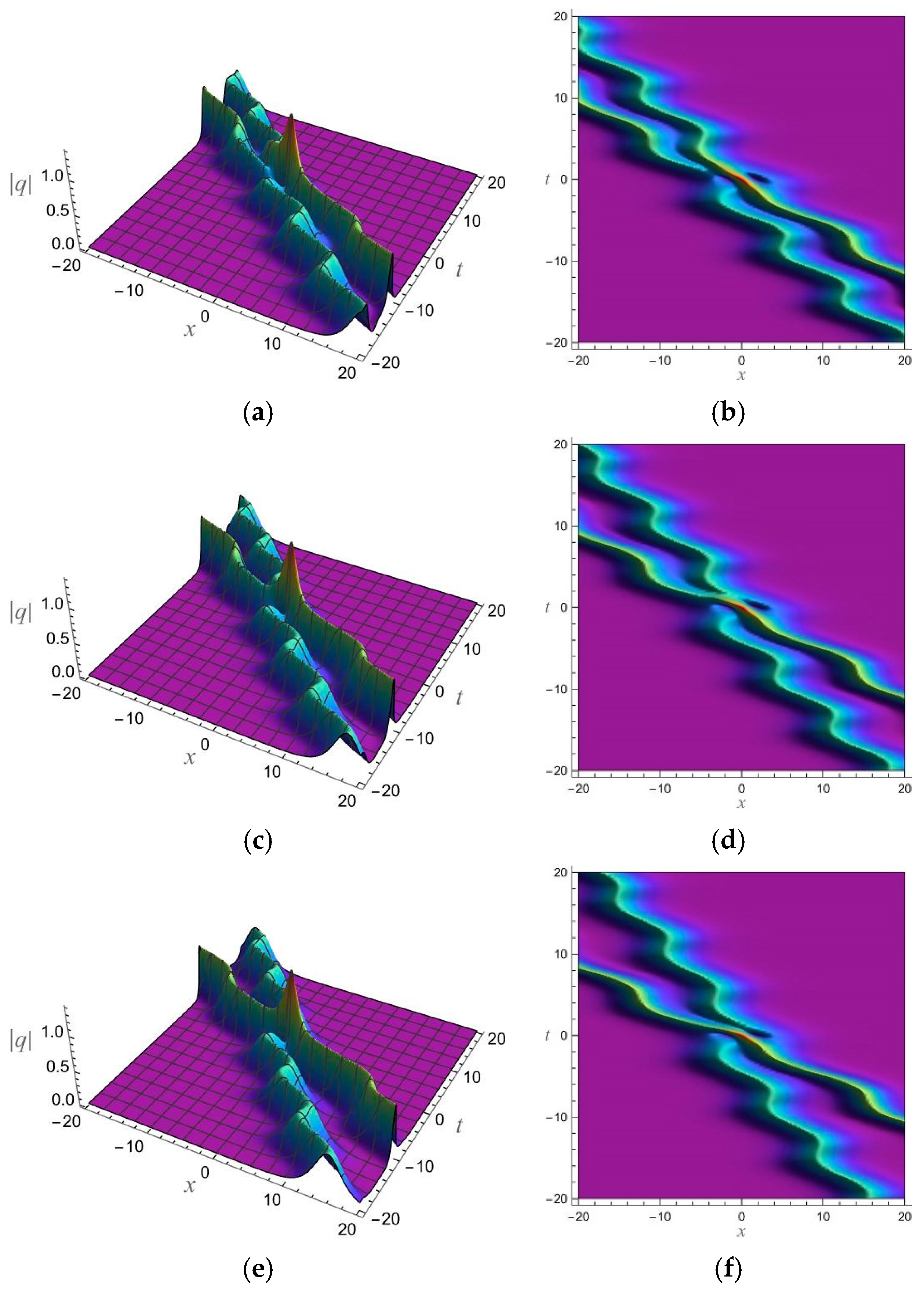
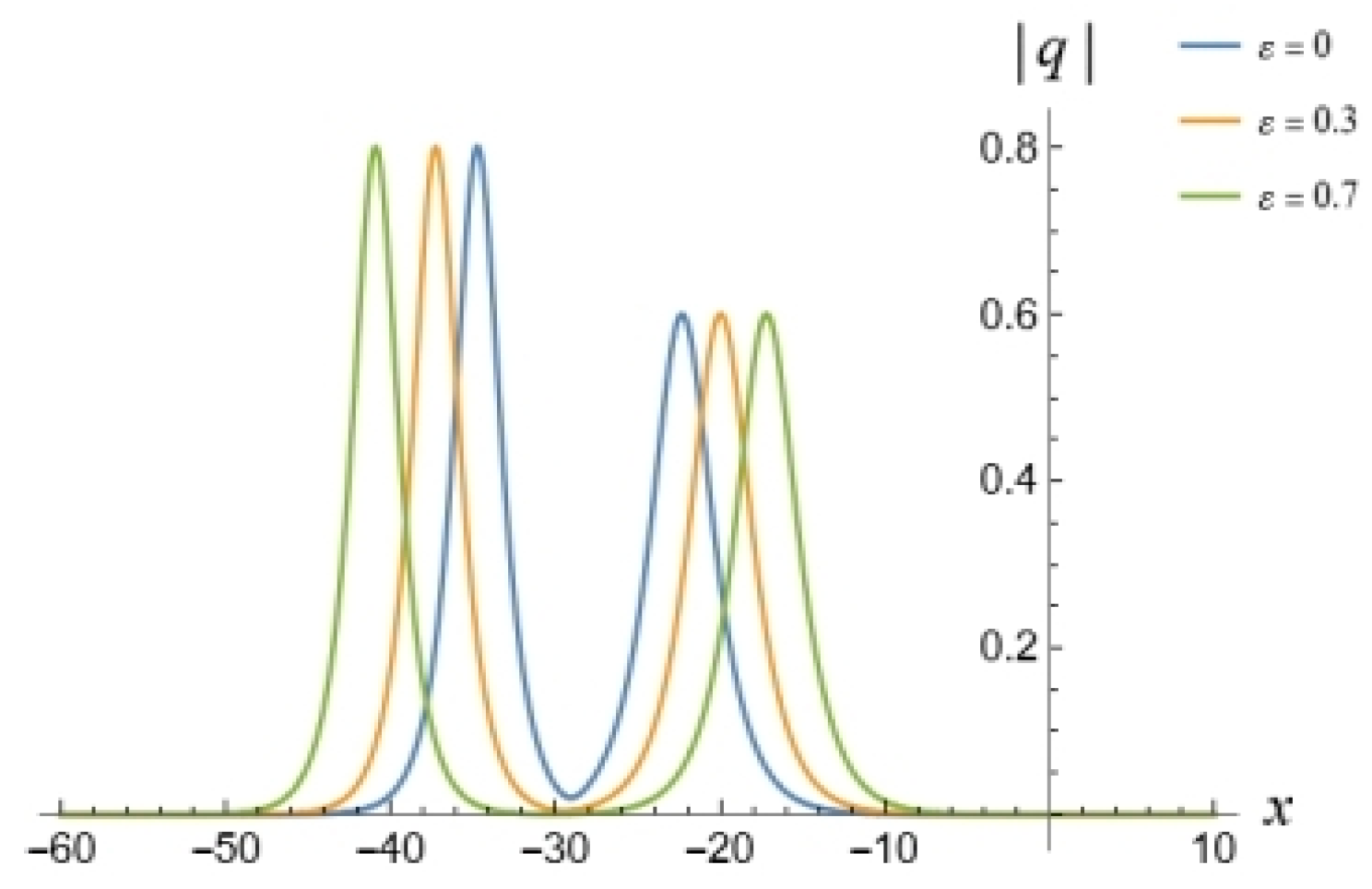
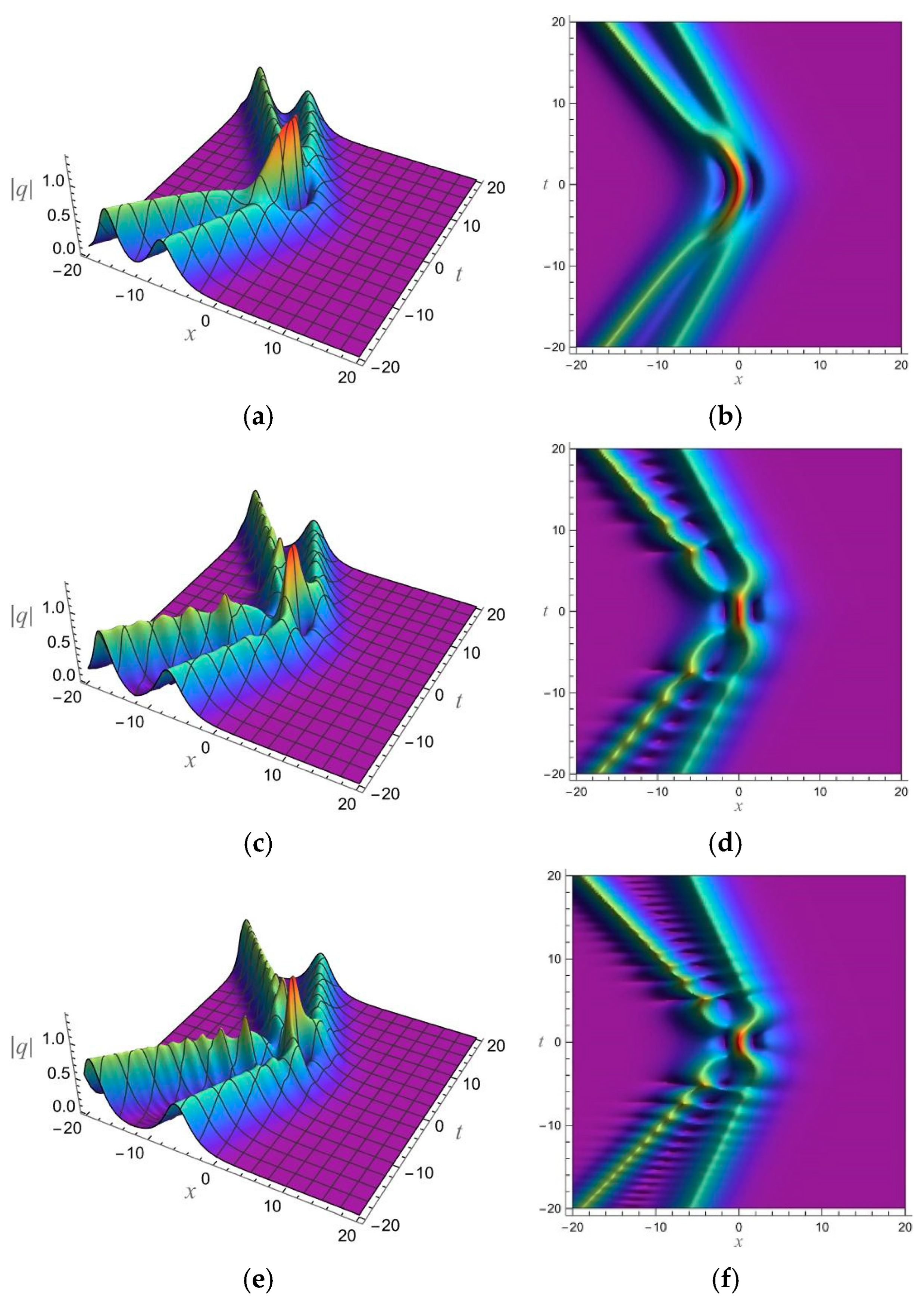
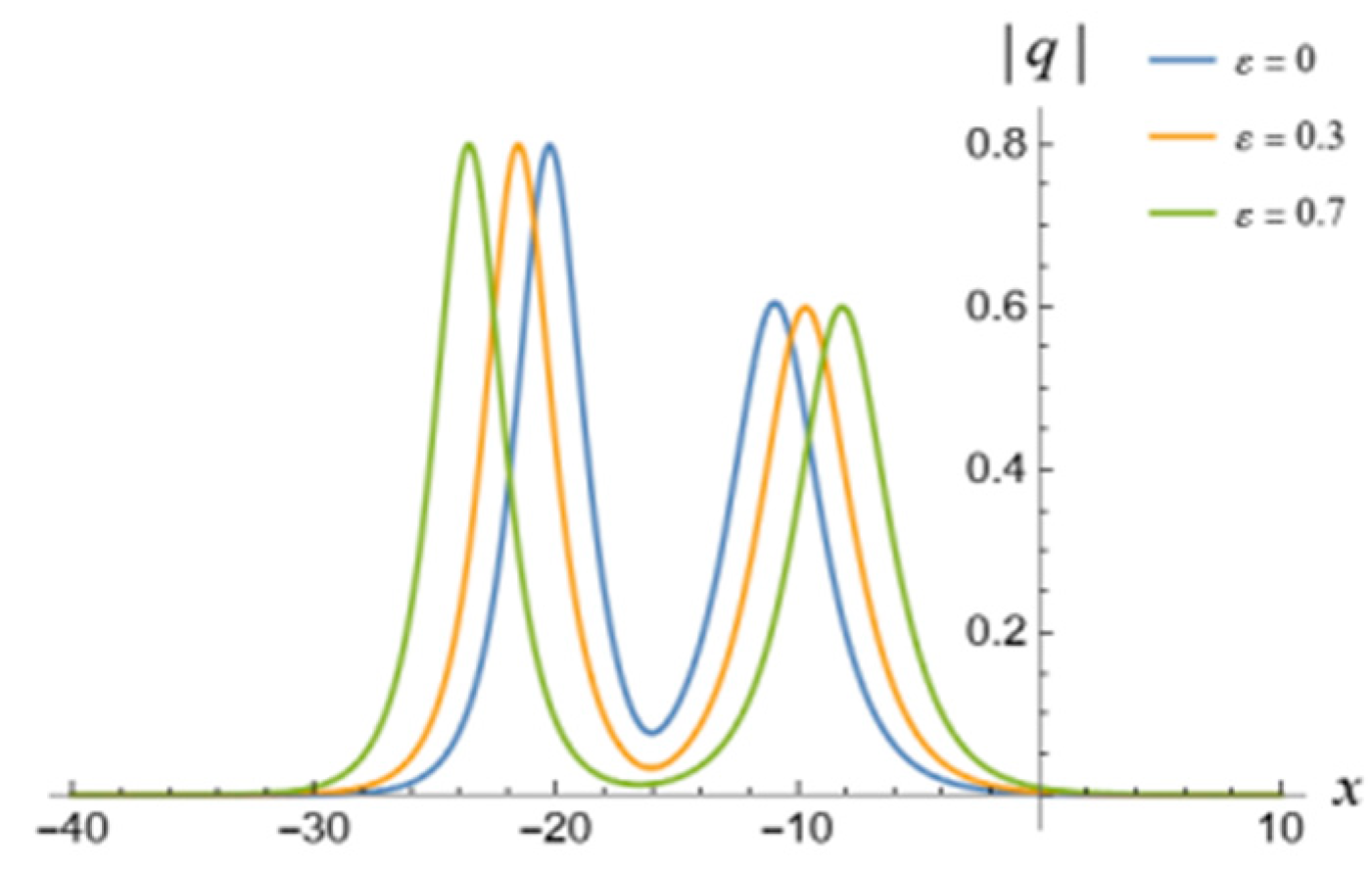
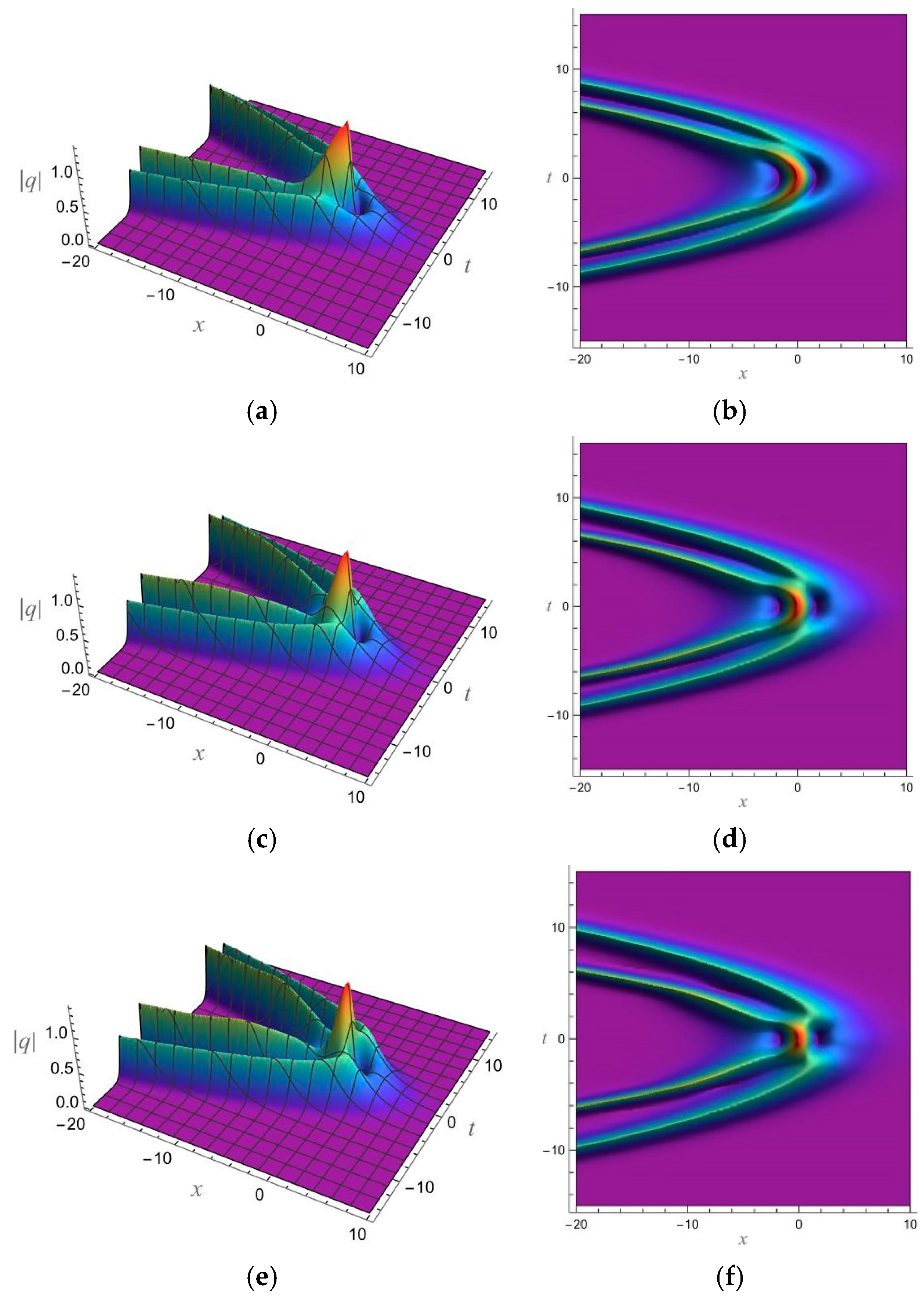
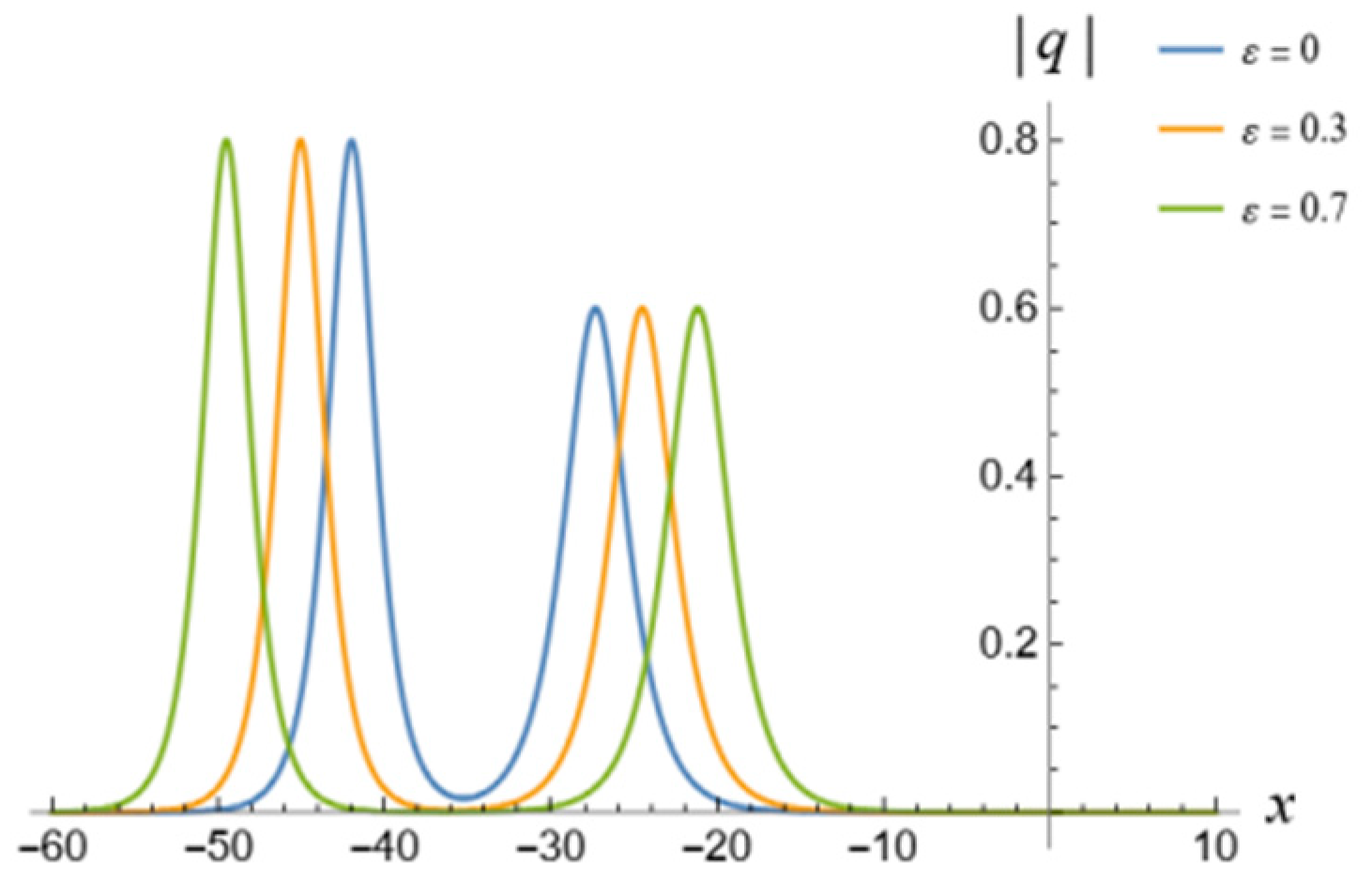
5. 1-Soliton Solution and 2-Soliton Solution of the vcRfgNLS Equation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Carrillo, J.A.; Manresa, M.D.P.; Figalli, A.; Mingione, G. Nonlocal and Nonlinear Diffusions and Interactions: New Methods and Directions; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Bronski, J.C.; Carr, L.D.; Deconinck, B.; Kutz, J.N. Bose-einstein condensates in standing waves: The cubic nonlinear Schrödinger equation with a periodic potential. Phys. Rev. Lett. 2001, 86, 1402–1405. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focusing and one dimensional self-modulation of waves in nonlinear media. J. Exp. Theor. Phys. 1972, 34, 62–69. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- West, B.J. Colloquium: Fractional calculus view of complexity: A tutorial. Rev. Mod. Phys. 2014, 86, 1169–1186. [Google Scholar] [CrossRef]
- Zhong, W.P.; Belić, M.R.; Malomed, B.A.; Zhang, Y.Q.; Huang, T.W. Spatiotemporal accessible solitons in fractional dimensions. Phys. Rev. E 2016, 94, 012216. [Google Scholar]
- Metzler, R.; Joseph, K. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar]
- Lischke, A.; Pang, G.F.; Gulan, M.; Song, F.Y.; Glusa, C.; Zheng, X.N.; Mao, Z.P.; Cai, W.; Meerschaertd, M.M.; Ainswortha, M.; et al. What is the fractional Laplacian? A comparative review with new results. J. Comput. Phys. 2020, 404, 109009. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Sikorskii, A. Stochastic Models for Fractional Calculus; Walter de Gruyter GmbH & Co KG: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar]
- Khawaja, U.A.; Al-Refai, M.; Carr, L.D. High-accuracy power series solutions with arbitrarily large radius of convergence for the fractional nonlinear Schrödinger-type equations. J. Phys. A Math. Theor. 2018, 51, 235201. [Google Scholar] [CrossRef]
- Li, P.F.; Malomed, B.A.; Mihalache, D. Vortex solitons in fractional nonlinear Schrödinger equation with the cubic-quintic nonlinearity. Chaos Solitons Fractals 2020, 137, 109783. [Google Scholar] [CrossRef]
- Qiu, Y.; Malomed, B.A.; Mihalache, D.; Zhu, X.; Peng, X.; He, Y. Stabilization of single-and multi-peak solitons in the fractional nonlinear Schrödinger equation with a trapping potential. Chaos Solitons Fractals 2020, 140, 110222. [Google Scholar] [CrossRef]
- Li, P.F.; Malomed, B.A.; Mihalache, D. Symmetry-breaking bifurcations and ghost states in the fractional nonlinear Schrödinger equation with a PT-symmetric potential. Opt. Lett. 2021, 46, 3267–3270. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Been, J.B.; Carr, L.D. Fractional integrable nonlinear soliton equation. Phys. Rev. Lett. 2022, 128, 184101. [Google Scholar] [CrossRef] [PubMed]
- Ablowitz, M.J.; Been, J.B.; Carr, L.D. Integrable fractional modified Korteweg–de Vries, sine-Gordon, and sinh-Gordon equations. J. Phys. A Math. Theor. 2022, 55, 384010. [Google Scholar] [CrossRef]
- Riesz, M. L’intégrale de Riemann-Liouville et le problème de Cauchy. Acta Math. 1949, 81, 1–222. [Google Scholar] [CrossRef]
- Cai, M.; Li, C.P. On Riesz derivative. Fract. Calc. Appl. Anal. 2019, 22, 287–301. [Google Scholar] [CrossRef]
- Weng, W.F.; Zhang, M.H.; Zhang, G.Q.; Yan, Z.Y. Dynamics of fractional N-soliton solutions with anomalous dispersions of integrable fractional higher-order nonlinear Schrödinger equations. Chaos 2022, 32, 123110. [Google Scholar] [CrossRef]
- Mou, D.S.; Dai, C.Q.; Wang, Y.Y. Integrable fractional n-component coupled nonlinear Schrödinger model and fractional n-soliton dynamics. Chaos Solitons Fractals 2023, 171, 113451. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Been, J.B.; Carr, L.D. Fractional integrable and related discrete nonlinear Schrodinger equations. Phys. Lett. A 2022, 452, 12845. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Peacock, A.C.; Harvey, J.D. Exact self-similar solutions of the generalized nonlinear Schrödinger equation with distributed coefficients. Phys. Rev. Lett. 2003, 90, 113902. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, S. Analytical method for generalized nonlinear Schrödinger equation with time-varying coefficients: Lax representation, Riemann–Hilbert problem solutions. Mathematics 2022, 10, 1043. [Google Scholar] [CrossRef]
- Serkin, V.N.; Hasegawa, A. Novel soliton solutions of the nonlinear Schrödinger equation model. Phys. Rev. Lett. 2000, 85, 4502–4505. [Google Scholar] [CrossRef]
- Li, Y.S. Solitons and Integrable Systems; Shanghai Science and Technology Education Press: Shanghai, China, 1999. [Google Scholar]
- Chen, D.Y. Introduction of Soliton; Science Press: Beijing, China, 2006. [Google Scholar]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. The inverse scattering transform—Fourier analysis for nonlinear problems. Stud. Appl. Math. 1974, 53, 249–315. [Google Scholar] [CrossRef]
- Kaup, D. Closure of the squared Zakharov–Shabat eigenstates. J. Math. Anal. Appl. 1975, 54, 849–864. [Google Scholar] [CrossRef]
- Zeng, L.W.; Shi, J.C.; Lu, X.W.; Cai, Y.; Zhu, Q.F.; Chen, H.Y.; Long, H.; Li, J.Z. Stable and oscillating solitons of PT-symmetric couplers with gain and loss in fractional dimension. Nonlinear Dyn. 2021, 103, 1831–1840. [Google Scholar] [CrossRef]
- Wu, G.Z.; Dai, C.Q. Nonautonomous soliton solutions of variable-coefficient fractional nonlinear Schrödinger equation. Appl. Math. Lett. 2020, 106, 106365. [Google Scholar] [CrossRef]
- Heydari, M.H.; Atangana, A. A cardinal approach for nonlinear variable-order time fractional Schrodinger equation defined by Atangana-Baleanu-Caputo derivative. Chaos Soliton. Fract. 2019, 128, 339–348. [Google Scholar] [CrossRef]
- Hong, B.J. Exact solutions for the conformable fractional coupled nonlinear Schrödinger equations with variable coefficients. J. Low Freq. Noise Vib. Act. Control. 2023, 42, 628–641. [Google Scholar] [CrossRef]
- Tian, F.Z.; Wang, Y.L.; Li, Z.Y. Numerical simulation of soliton propagation behavior for the fractional-in-space NLSE with variable coefficients on unbounded domain. Fractal Fract. 2024, 8, 163. [Google Scholar] [CrossRef]
- Liu, M.W.; Wang, H.T.; Yang, H.J.; Liu, W.J. Study on propagation properties of fractional soliton in the inhomogeneous fiber with higher-order effects. Nonlinear Dyn. 2024, 112, 1327–1337. [Google Scholar] [CrossRef]
- Tang, W.F.; Wang, Y.L.; Li, Z.Y. Numerical simulation of fractal wave propagation of a multi-dimensional nonlinear fractional-in-space Schrödinger equation. Phys. Scr. 2023, 98, 045205. [Google Scholar] [CrossRef]
- García-Ferrero, M.A.; Rüland, A. Strong unique continuation for the higher order fractional Laplacian. Math. Eng. 2019, 1, 715–774. [Google Scholar]
- Wang, H.M.; Chen, H.J.; Li, T. Numerical simulation for the wave of the variable coefficient nonlinear Schrödinger equation based on the lattice Boltzmann method. Mathematics 2024, 12, 3807. [Google Scholar] [CrossRef]
- Yu, F.J.; Li, L.; Zhang, J.F.; Yan, J.W. Fractional-order effect on soliton wave conversion and stability for the two-Levy-index fractional nonlinear Schrödinger equation with PT-symmetric potential. Phys. D 2024, 460, 134089. [Google Scholar] [CrossRef]
| Time | Velocity and Amplitude with | Velocity and Amplitude with | Velocity and Amplitude with |
|---|---|---|---|
| −100 | −1.48803 × 10−43; 1 | −2.83269 × 10−43; 1 | −4.59083 × 10−43; 1 |
| −10 | −1.816 × 10−4; 1 | −3.45703 × 10−4; 1 | −5.60266 × 10−4; 1 |
| −1 | −1.29611; 1 | −2.46734; 1 | −3.99871; 1 |
| 0 | −2; 1 | −3.80731; 1 | −6.17034; 1 |
| 5 | −2.69506 × 10−2; 1 | −5.13045 × 10−2; 1 | −8.31471 × 10−2; 1 |
| 200 | −5.53559 × 10−87; 1 | −1.05378 × 10−86; 1 | −1.70782 × 10−86; 1 |
| 1000 | −2.0030383559 × 10−424; 1 | −3.8614765923 × 10−424; 1 | −6.2640077051 × 10−424; 1 |
| Height and Time | Width with | Width with | Width with |
|---|---|---|---|
| 0.1; −5 | 5.98642 | 5.98644 | 5.98643 |
| 0.1; 0 | 5.986443 | 5.986443 | 5.986443 |
| 0.1; 10 | 5.98644 | 5.986443 | 5.98644 |
| 0.2; −5 | 4.58486 | 4.58483 | 4.58484 |
| 0.2; 0 | 4.584862 | 4.584862 | 4.584862 |
| 0.2; 10 | 4.58486 | 4.58486 | 4.58487 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, S.; Xu, B. Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions. Fractal Fract. 2025, 9, 228. https://doi.org/10.3390/fractalfract9040228
Li H, Zhang S, Xu B. Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions. Fractal and Fractional. 2025; 9(4):228. https://doi.org/10.3390/fractalfract9040228
Chicago/Turabian StyleLi, Hongwei, Sheng Zhang, and Bo Xu. 2025. "Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions" Fractal and Fractional 9, no. 4: 228. https://doi.org/10.3390/fractalfract9040228
APA StyleLi, H., Zhang, S., & Xu, B. (2025). Integrable Riesz Fractional-Order Generalized NLS Equation with Variable Coefficients: Inverse Scattering Transform and Analytical Solutions. Fractal and Fractional, 9(4), 228. https://doi.org/10.3390/fractalfract9040228






