A Certain Numerical Algorithm for Solving a Fractional Partial Model with a Neumann Constraint in a Hilbert Space
Abstract
1. Introduction
2. Appropriate Hilbert Spaces
3. Numerical Solution and Convergence
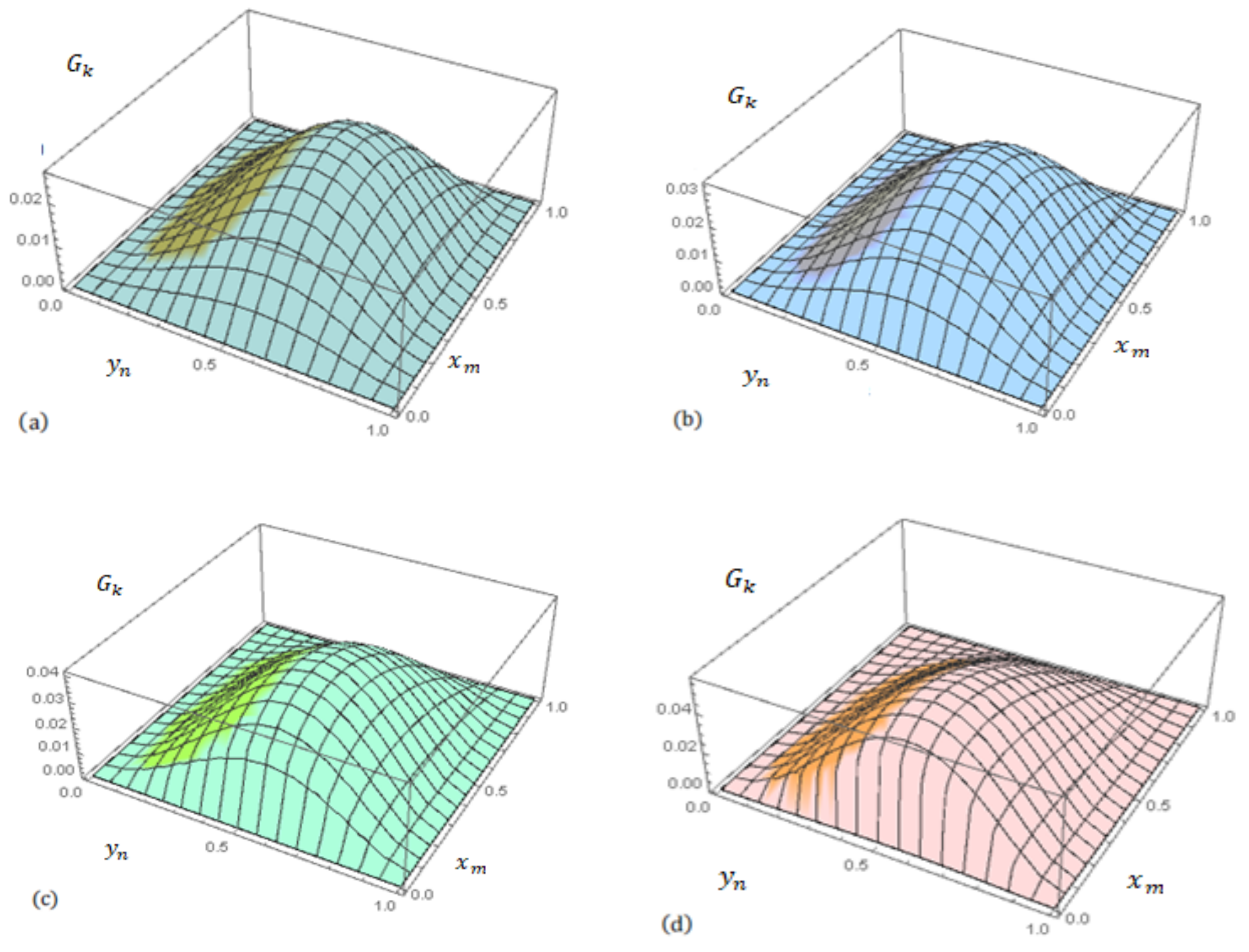
4. Algorithms and Application
| Algorithm 1. Steps of the orthogonal systems |
|
| Algorithm 2. Steps of the RHA |
|
5. Concluding Notes
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Daftardar-Gejji, V. Fractional Calculus and Fractional Differential Equations; Birkhäuser: Basel, Switzerland, 2019. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Zaslavsky, G.M. Hamiltonian Chaos and Fractional Dynamics; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives Theory and Applications; Gordon and Breach: Philadelphia, PA, USA, 1993. [Google Scholar]
- Atangana, A. Fractional Operators with Constant and Variable Order with Application to Geo-Hydrology; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Jafari, H.; Ganji, R.M.; Sayevand, K.; Baleanu, D. A numerical approach for solving fractional optimal control problems with mittag-leffler kernel. J. Vib. Control 2021, 28, 2596–2606. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.T. An efficient local meshless approach for solving nonlinear time-fractional fourth-order diffusion model. J. King Saud Univ.-Sci. 2021, 33, 101243. [Google Scholar] [CrossRef]
- Nikan, O.; Machado, J.T.; Golbabai, A. Numerical solution of time-fractional fourth-order reaction-diffusion model arising in composite environments. Appl. Math. Model. 2021, 89, 819–836. [Google Scholar] [CrossRef]
- Gao, X.; Jiang, X.; Chen, S. The numerical method for the moving boundary problem with space-fractional derivative in drug release devices. Appl. Math. Model. 2015, 39, 2385–2391. [Google Scholar] [CrossRef]
- Alaroud, M.; Al-Smadi, M.; Rozita Ahmad, R.; Salma Din, U.K. An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations. Symmetry 2019, 11, 205. [Google Scholar] [CrossRef]
- Saadeh, R.; Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Salma Din, U.K. Application of Fractional Residual Power Series Algorithm to Solve Newell-Whitehead-Segel Equation of Fractional Order. Symmetry 2019, 11, 1431. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, F.; Turner, I.; Anh, V.; Gu, Y.T. A RBF meshless approach for modeling a fractal mobile/immobile transport model. Appl. Math. Comput. 2014, 226, 336–347. [Google Scholar] [CrossRef]
- Schumer, R.; Benson, D.A.; Meerschaert, M.M.; Baeumer, B. Fractal mobile/immobile solute transport. Water Resour. Res. 2003, 39, 1296–1307. [Google Scholar] [CrossRef]
- Hansen, S.K. Effective ADE models for first-order mobile–immobile solute transport: Limits on validity and modeling implications. Adv. Water Resour. 2015, 86, 184–192. [Google Scholar] [CrossRef]
- Ma, H.; Yang, Y. Jacobi Spectral Collocation Method for the Time Variable-Order Fractional Mobile-Immobile Advection-Dispersion Solute Transport Model. East Asian J. Appl. Math. 2016, 6, 337–352. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Zaky, M.A.; Bhrawy, A.H.; Baleanu, D. Numerical Simulation of Time Variable Fractional Order Mobile-Immobile Advection-Dispersion Model. Rom. Rep. Phys. 2015, 67, 773–791. [Google Scholar]
- Modanli, M.; Karadag, K.; Abdulazeez, S.T. Solutions of the mobile-immobile advection-dispersion model based on the fractional operators using the Crank-Nicholson difference scheme. Chaos Solit. Fractals 2023, 167, 113114. [Google Scholar] [CrossRef]
- Aghdam, Y.E.; Farnam, B. A numerical process the mobile-immobile advection-dispersion model arising in solute transport. Math. Comput. Sci. 2022, 3, 1–10. [Google Scholar]
- Gupta, R.; Kumar, S. Chebyshev spectral method for the variable-order fractional mobile-immobile advection-dispersion equation arising from solute transport in heterogeneous media. J. Eng. Math. 2023, 142, 1. [Google Scholar] [CrossRef]
- Jafari, H.; Aghdam, Y.E.; Farnam, B.; Nguyen, V.T.; Masetshaba, M.T. A convergence analysis of the mobile–immobile advection–dispersion model of temporal fractional order arising in watershed catchments and rivers. Fractals 2023, 31, 2340068. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Phanikumar, M.S.; Meerschaert, M.M. A novel numerical method for the time variable fractional order mobile-immobile advection-dispersion model. Comput. Math. Appl. 2013, 66, 693–701. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, N. A numerical method for solving the time variable fractional order mobile-immobile advection-dispersion model. Appl. Numer. Math. 2017, 119, 18–32. [Google Scholar] [CrossRef]
- Sadri, K.; Aminikhah, H. An efficient numerical method for solving a class of variable-order fractional mobile-immobile advection-dispersion equations and its convergence analysis. Chaos Solit. Fractals 2021, 146, 110896. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, X.; Liu, F. Error analysis of nonlinear time fractional mobile/immobile advection-diffusion equation with weakly singular solutions. Fract. Calc. Appl. Anal. 2021, 24, 202–224. [Google Scholar] [CrossRef]
- Almeida, R.M.P.; Duque, J.C.M.; Ferreira, J.; Robalo, R.J. The Crank–Nicolson–Galerkin finite element method for a nonlocal parabolic equation with moving boundaries. Numer. Methods Partial. Differ. Equ. 2015, 31, 1515–1533. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O.; Gaith, M. Numerical simulation of telegraph and Cattaneo fractional-type models using adaptive reproducing kernel framework. Math. Methods Appl. Sci. 2021, 44, 8472–8489. [Google Scholar] [CrossRef]
- Zolfaghari, R.; Shidfar, A. Solving a parabolic PDE with nonlocal boundary conditions using the Sinc method. Numer. Algorithms 2013, 62, 411–427. [Google Scholar] [CrossRef]
- Cui, M.; Lin, Y. Nonlinear Numerical Analysis in the Reproducing Kernel Space; Nova Science: Hauppauge, NY, USA, 2009. [Google Scholar]
- Arqub, O.A. Fitted reproducing kernel Hilbert space method for the solutions of some certain classes of time-fractional partial differential equations subject to initial and Neumann boundary conditions. Comput. Math. Appl. 2017, 73, 1243–1261. [Google Scholar] [CrossRef]
- Gumah, G.; Naser, M.F.M.; Al-Smadi, M.; Al-Omari, S.K.Q.; Baleanu, D. Numerical solutions of hybrid fuzzy differential equations in a Hilbert space. Appl. Numer. Math. 2020, 151, 402–412. [Google Scholar] [CrossRef]
- Berlinet, A.; Agnan, C.T. Reproducing Kernel Hilbert Space in Probability and Statistics; Kluwer Academic Publishers: Norwell, MA, USA, 2004. [Google Scholar]
- Daniel, A. Reproducing Kernel Spaces and Applications; Springer: Basel, Switzerland, 2003. [Google Scholar]
- Hasan, S.; Al-Smadi, M.; Freihet, A.; Momani, S. Two computational approaches for solving a fractional obstacle system in Hilbert space. Adv. Differ. Equ. 2019, 2019, 55. [Google Scholar] [CrossRef]
- Jiang, W.; Chen, Z. A collocation method based on reproducing kernel for a modified anomalous subdiffusion equation. Numer. Methods Partial. Differ. Equ. 2014, 30, 289–300. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Deiakeh, R.; Al-Omari, S.; Al kenany, A.; Al-Smadi, M. A Certain Numerical Algorithm for Solving a Fractional Partial Model with a Neumann Constraint in a Hilbert Space. Fractal Fract. 2025, 9, 243. https://doi.org/10.3390/fractalfract9040243
Al-Deiakeh R, Al-Omari S, Al kenany A, Al-Smadi M. A Certain Numerical Algorithm for Solving a Fractional Partial Model with a Neumann Constraint in a Hilbert Space. Fractal and Fractional. 2025; 9(4):243. https://doi.org/10.3390/fractalfract9040243
Chicago/Turabian StyleAl-Deiakeh, Rawya, Shrideh Al-Omari, Amra Al kenany, and Mohammed Al-Smadi. 2025. "A Certain Numerical Algorithm for Solving a Fractional Partial Model with a Neumann Constraint in a Hilbert Space" Fractal and Fractional 9, no. 4: 243. https://doi.org/10.3390/fractalfract9040243
APA StyleAl-Deiakeh, R., Al-Omari, S., Al kenany, A., & Al-Smadi, M. (2025). A Certain Numerical Algorithm for Solving a Fractional Partial Model with a Neumann Constraint in a Hilbert Space. Fractal and Fractional, 9(4), 243. https://doi.org/10.3390/fractalfract9040243





