Fixed-Time Adaptive Synchronization of Fractional-Order Memristive Fuzzy Neural Networks with Time-Varying Leakage and Transmission Delays
Abstract
1. Introduction
2. Preliminaries
3. Main Results
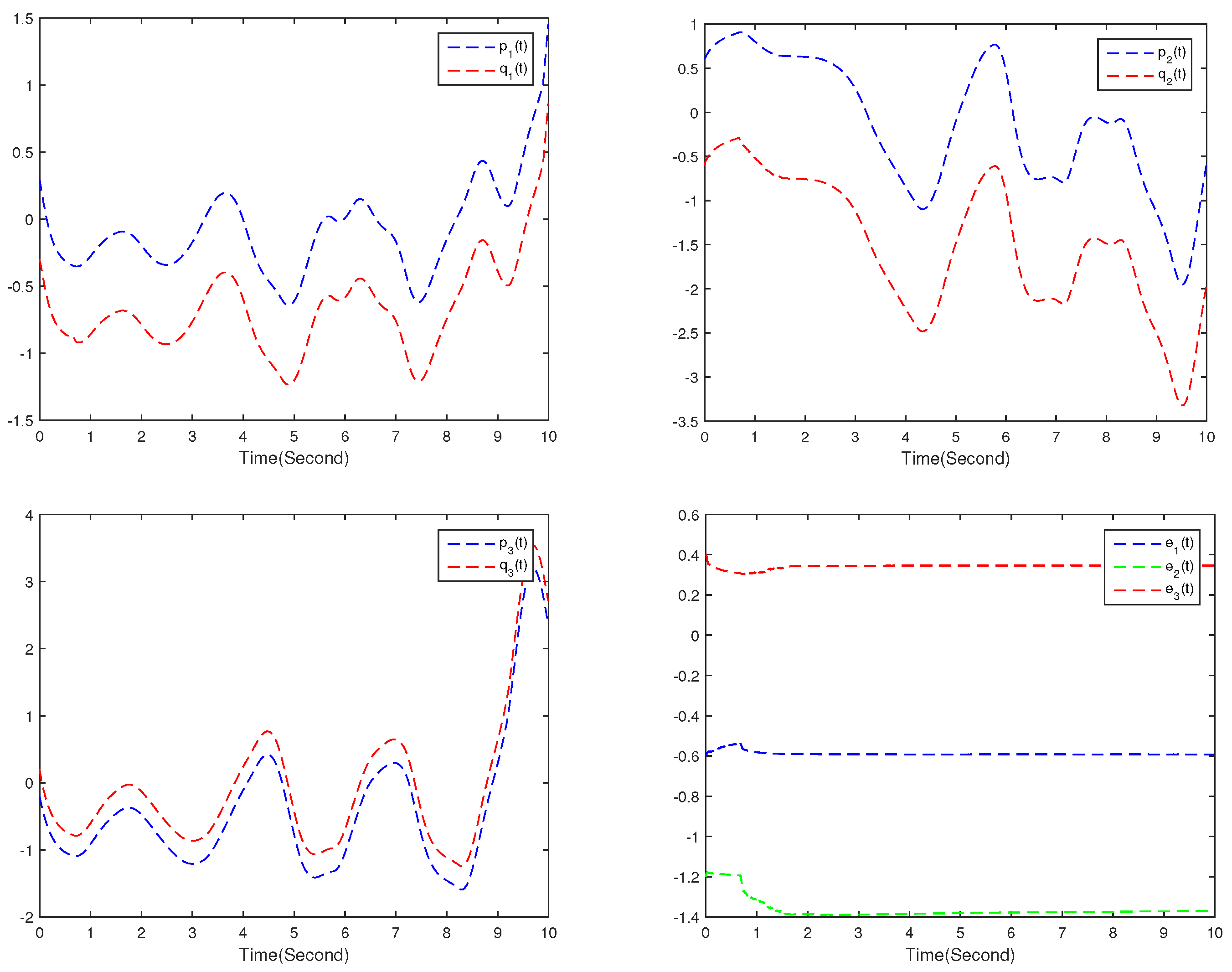
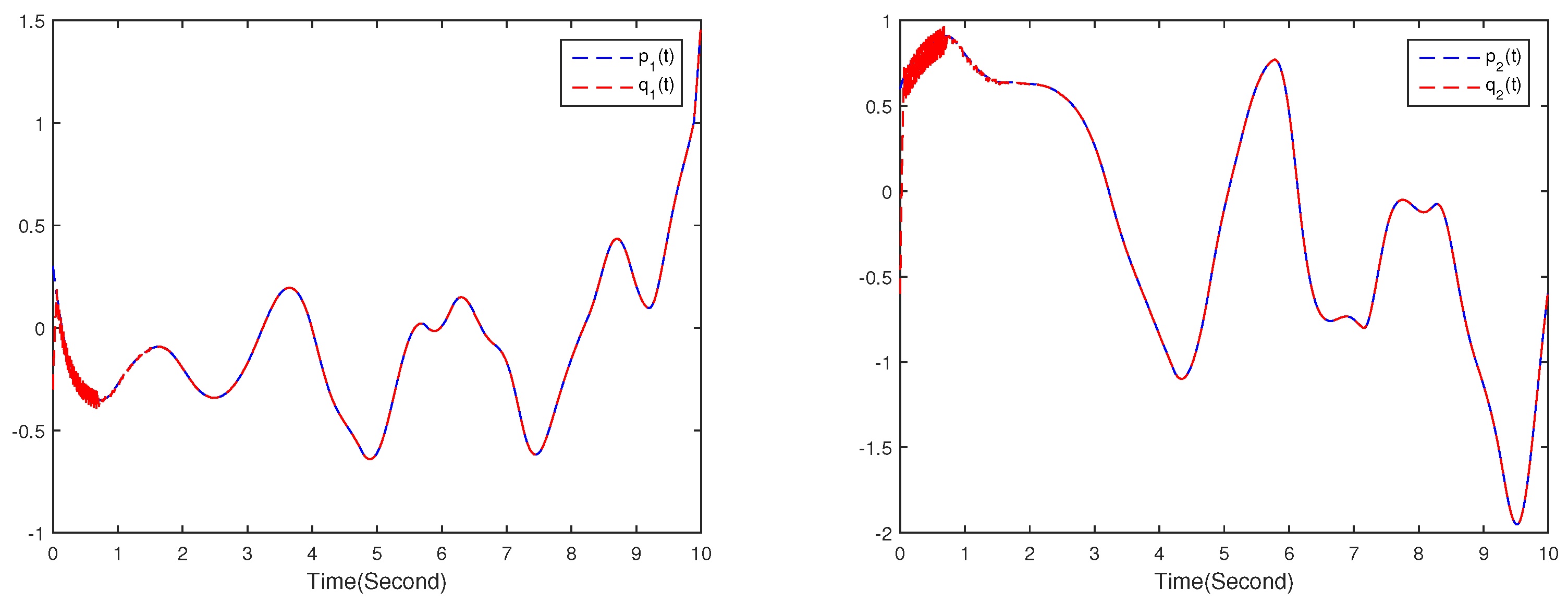
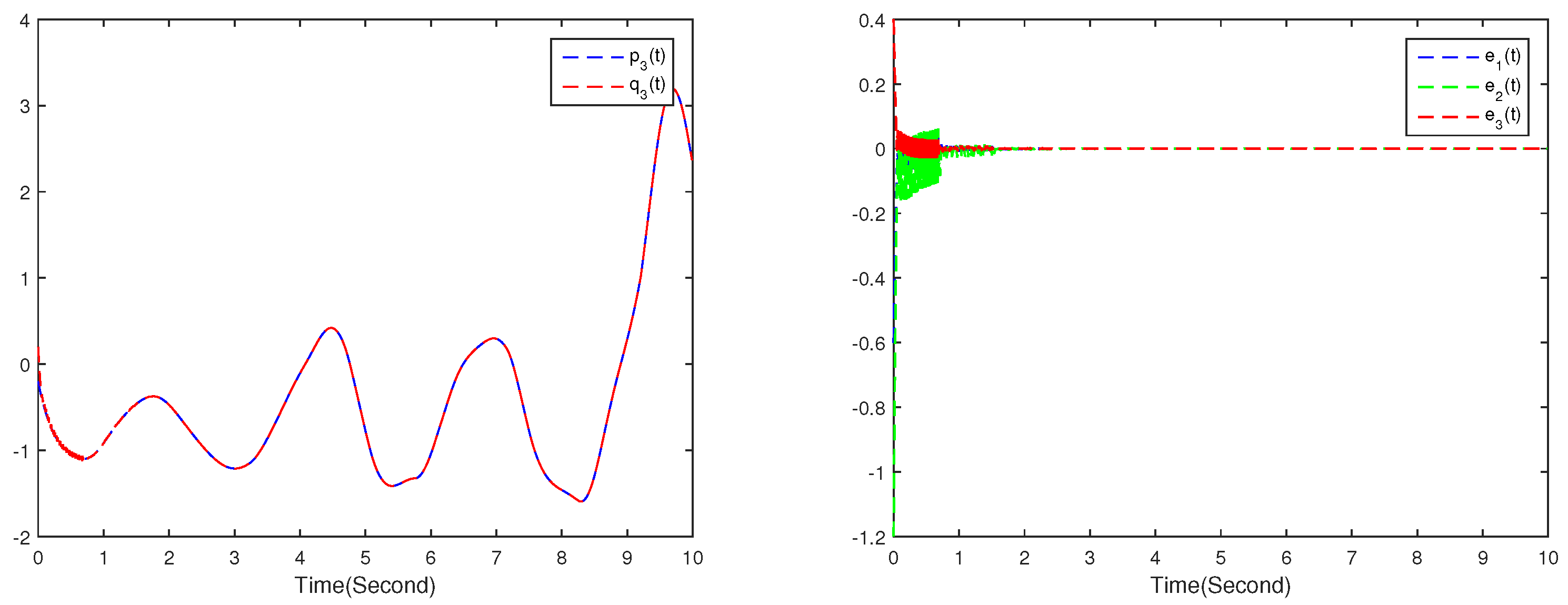
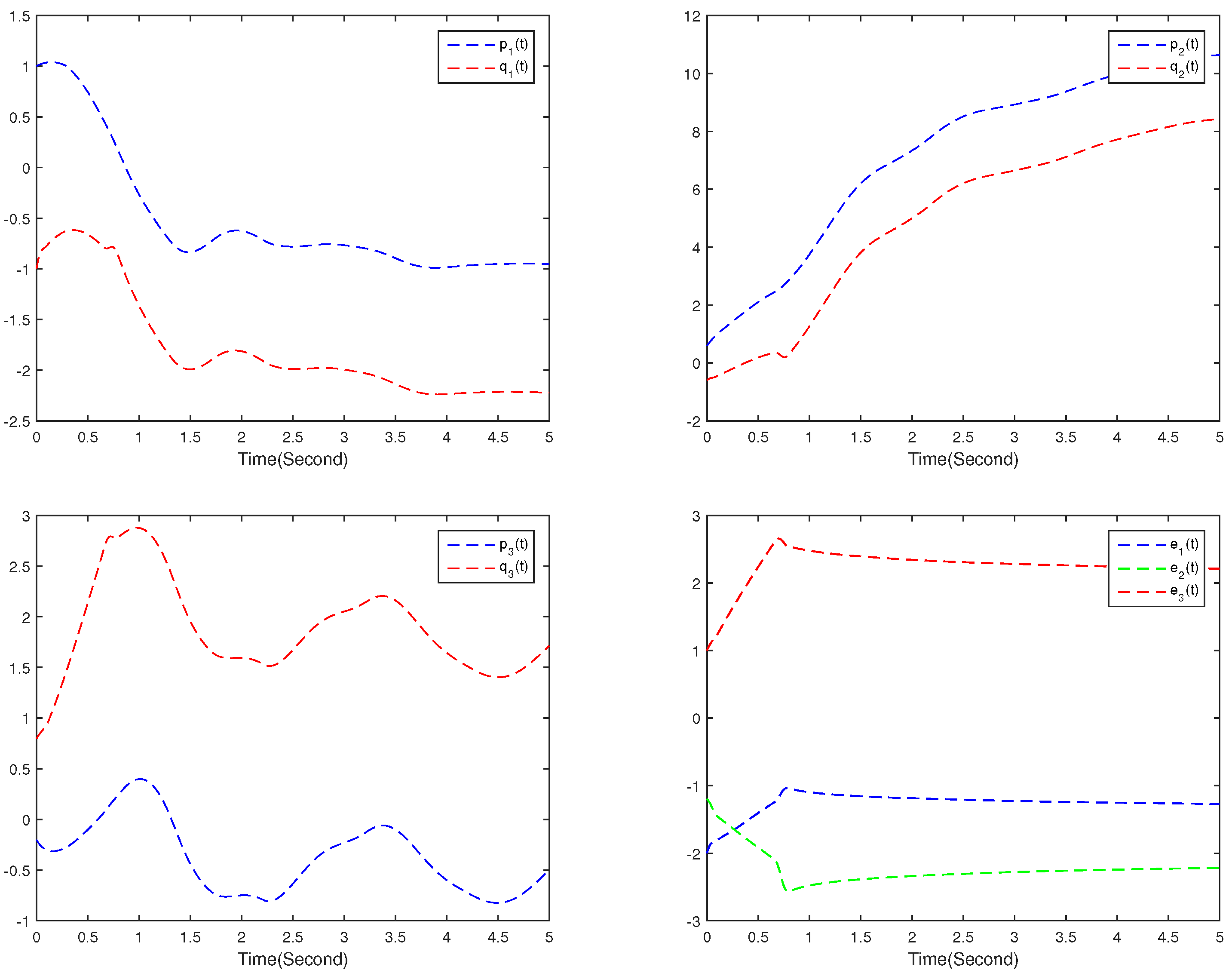
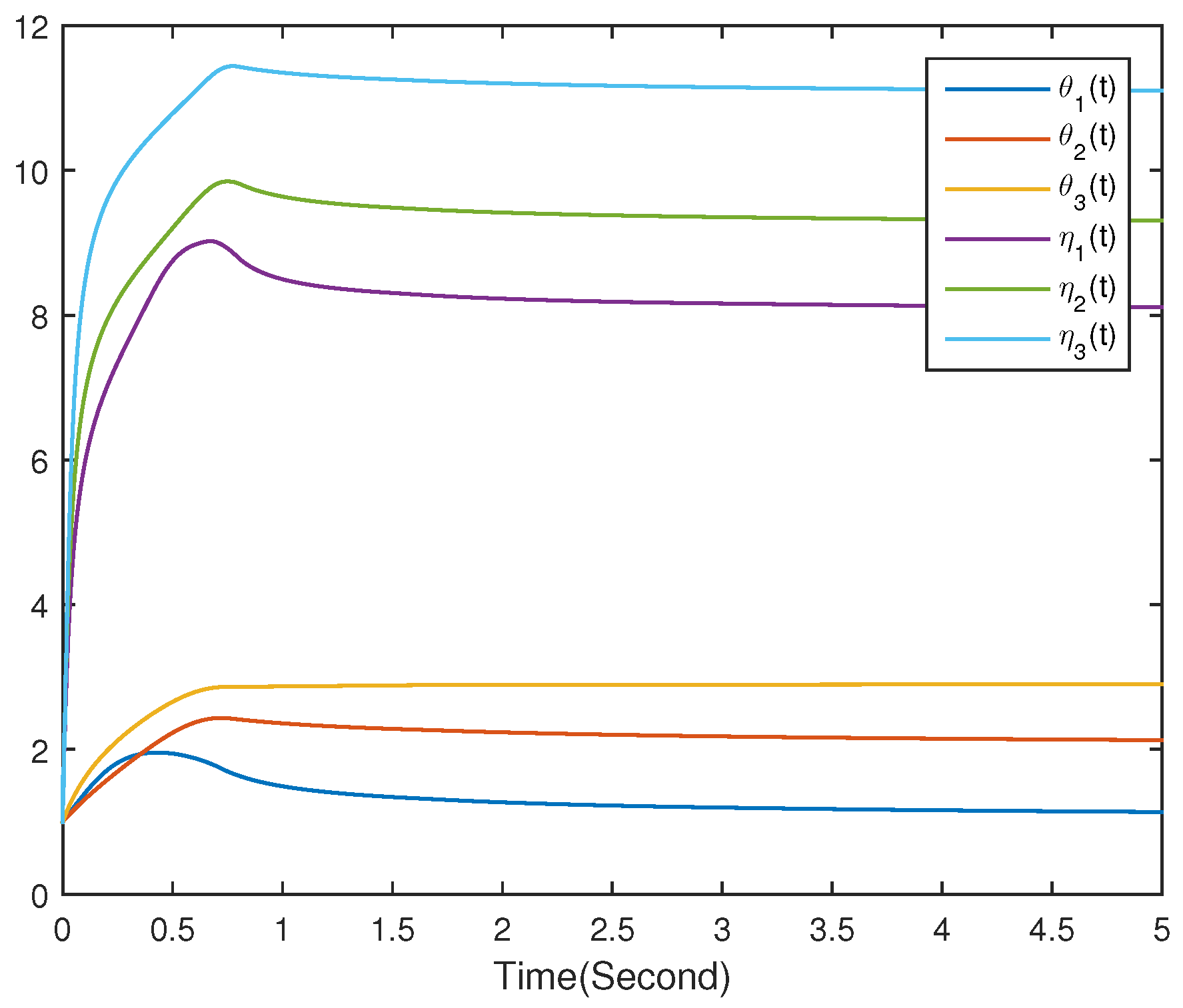
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Struko, D.; Snider, G.; Stewart, D. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zeng, Z.; Jiang, P. Global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 2014, 51, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Lu, J.; Jin, X.; Yang, X.Y. Novel results on asymptotic stability and synchronization of fractional-order memristive neural networks with time delays: The 0 < δ ≤ 1 case. Neural Netw. 2023, 167, 680–691. [Google Scholar]
- Yao, X.; Liu, X.; Zhong, S. Exponential stability and synchronization of Memristor-based fractional-order fuzzy cellular neural networks with multiple delays. Neurocomputing 2021, 419, 239–250. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, C.; Wen, S.; Li, S.; Wang, L. Lag projective synchronization of nonidentical fractional delayed memristive neural networks. Neurocomputing 2022, 469, 138–150. [Google Scholar] [CrossRef]
- Li, H.; Cao, J.; Hu, C.; Zhang, L.; Jiang, H. Adaptive control-based synchronization of discrete-time fractional-order fuzzy neural networks with time-varying delays. Neural Netw. 2023, 168, 59–73. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y. Finite time impulsive synchronization of fractional order memristive BAM neural networks. Neurocomputing 2020, 384, 213–224. [Google Scholar] [CrossRef]
- Du, F.; Lu, J. New criterion for finite-time synchronization of fractional order memristor-based neural networks with time delay. Appl. Math. Comput. 2021, 389, 125616. [Google Scholar] [CrossRef]
- Anbalagan, P.; Ramachandran, R.; Alzabut, J.; Hincal, E.; Niezabitowski, M. Improved results on finite-time passivity and synchronization problem for fractional-order memristor-based competitive neural networks: Interval matrix approach. Fractal Fract. 2022, 6, 36. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Liu, L. Asymptotic and finite-time synchronization of fractional-order memristor-based inertial neural networks with time-varying delay. Fractal Fract. 2022, 6, 350. [Google Scholar] [CrossRef]
- Wei, R.; Cao, J.; Alsaedi, A. Fixed-time synchronization of memristive Cohen-Grossberg neural networks with impulsive effects. Int. J. Control Autom. Syst. 2018, 16, 2214–2224. [Google Scholar] [CrossRef]
- Ren, H.; Peng, Z.; Gu, Y. Fixed-time synchronization of stochastic memristor-based neural networks with adaptive control. Neural Netw. 2020, 130, 165–175. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Ren, S.; Kurths, J. Finite-time and fixed-time synchronization for a class of memristor-based competitive neural networks with different time scales. Chaos Solitons Fractals 2021, 148, 111033. [Google Scholar] [CrossRef]
- Wei, R.; Cao, J.; Gorbachev, S. Fixed-time control for memristor-based quaternion-valued neural networks with discontinuous activation functions. Cogn. Comput. 2023, 15, 50–60. [Google Scholar] [CrossRef]
- Jia, T.; Chen, X.; Yao, X.; Zhao, F.; Qiu, J. Adaptive fixed-time synchronization of delayed memristor-based neural networks with discontinuous activations. CMES-Comput. Model. Eng. Sci. 2023, 134, 221–239. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Liu, L. Fixed-time synchronization for fractional-order cellular inertial fuzzy neural networks with mixed time-varying delays. Fractal Fract. 2024, 8, 97. [Google Scholar] [CrossRef]
- Zhao, F.; Jian, J.; Wang, B. Finite-time synchronization of fractional-order delayed memristive fuzzy neural networks. Fuzzy Sets Syst. 2023, 467, 108578. [Google Scholar] [CrossRef]
- Du, F.; Lu, J. Adaptive finite-time synchronization of fractional-order delayed fuzzy cellular neural networks. Fuzzy Sets Syst. 2023, 466, 108480. [Google Scholar] [CrossRef]
- Jian, J.; Duan, L. Finite-time synchronization for fuzzy neutral-type inertial neural networks with time-varying coefficients and proportional delays. Fuzzy Sets Syst. 2020, 381, 51–67. [Google Scholar] [CrossRef]
- Gopalsamy, K. Leakage delays in BAM. J. Math. Anal. Appl. 2007, 325, 1117–1132. [Google Scholar] [CrossRef]
- Alia, M.; Narayanana, G.; Sarohab, S.; Priya, B.; Thakur, G.K. Finite-time stability analysis of fractional-order memristive fuzzy cellular neural networks with time delay and leakage term. Math. Comput. Simul. 2021, 185, 468–485. [Google Scholar]
- Yan, H.; Qiao, Y.; Duan, L.; Miao, J. New results of quasi-projective synchronization for fractional-order complex-valued neural networks with leakage and discrete delays. Chaos Solitons Fractals 2022, 159, 112121. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, B.; Wu, Y. Stability and Hopf bifurcation for a quaternion-valued three-neuron neural network with leakage delay and communication delay. J. Frankl. Inst. 2023, 360, 12969–12989. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, Y.; Zhang, X. Global exponential synchronization of switching neural networks with leakage time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2024, 133, 107979. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, J.; Zhang, H.; Zhang, W.; Cao, J. Quasi-uniform synchronization of Caputo type fractional neural networks with leakage and discrete delays. Chaos Solitons Fractals 2021, 152, 11432. [Google Scholar] [CrossRef]
- Kao, Y.; Li, Y.; Park, J.; Chen, X. Mittag-Leffler synchronization of delayed fractional memristor neural networks via adaptive control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2279–2284. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yu, J.; Hu, C.; Jiang, H. Finite-time synchronization of memristive neural networks with fractional-order. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3739–3750. [Google Scholar] [CrossRef]
- Filippov, A. Differential Equations with Discontinuous Righthand Sides; Kluwer Academic Publishers: Boston, MA, USA, 1988. [Google Scholar]
- Li, C.; Deng, W. Remarks on fractional derivatives. Aied Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, Y.; Wang, H. Mittag-Leffler stability of fractional-order hopfield neural networks. Nonlinear Anal. Hybrid Syst. 2015, 16, 104–121. [Google Scholar] [CrossRef]
- Zheng, M.; Li, L.; Peng, H.; Xiao, J.; Yang, Y.; Zhang, Y.; Zhao, H. Fixed-time synchronization of memristor-based fuzzy cellular neural network with time-varying delay. J. Frankl. Inst. 2018, 355, 6780–6809. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y. Fixed-time synchronization of delayed fractional-order memristor-based fuzzy cellular neural networks. IEEE Access 2020, 8, 165951–165962. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Liu, Y.; Liu, L. Fixed-Time Adaptive Synchronization of Fractional-Order Memristive Fuzzy Neural Networks with Time-Varying Leakage and Transmission Delays. Fractal Fract. 2025, 9, 241. https://doi.org/10.3390/fractalfract9040241
Sun Y, Liu Y, Liu L. Fixed-Time Adaptive Synchronization of Fractional-Order Memristive Fuzzy Neural Networks with Time-Varying Leakage and Transmission Delays. Fractal and Fractional. 2025; 9(4):241. https://doi.org/10.3390/fractalfract9040241
Chicago/Turabian StyleSun, Yeguo, Yihong Liu, and Lei Liu. 2025. "Fixed-Time Adaptive Synchronization of Fractional-Order Memristive Fuzzy Neural Networks with Time-Varying Leakage and Transmission Delays" Fractal and Fractional 9, no. 4: 241. https://doi.org/10.3390/fractalfract9040241
APA StyleSun, Y., Liu, Y., & Liu, L. (2025). Fixed-Time Adaptive Synchronization of Fractional-Order Memristive Fuzzy Neural Networks with Time-Varying Leakage and Transmission Delays. Fractal and Fractional, 9(4), 241. https://doi.org/10.3390/fractalfract9040241




