Mega-Instability: Order Effect on the Fractional Order of Periodically Forced Oscillators
Abstract
1. Introduction
2. Mega-Stability of Non-Autonomous Systems: General Case
- 1.
- The attractors of system (2) are countable infinity nested.
- 2.
- At least one of the attractors is strange with chaotic behavior.
3. Simple 4D Mega-Stable Oscillator
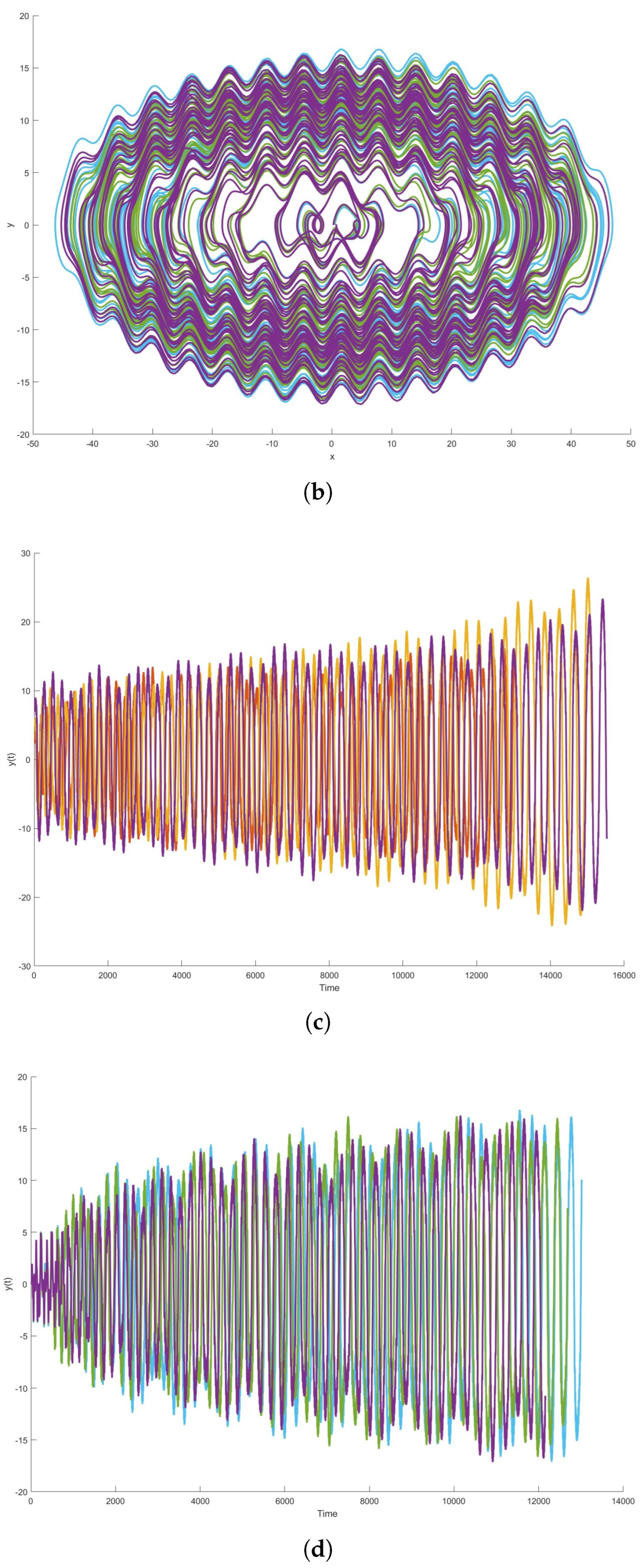
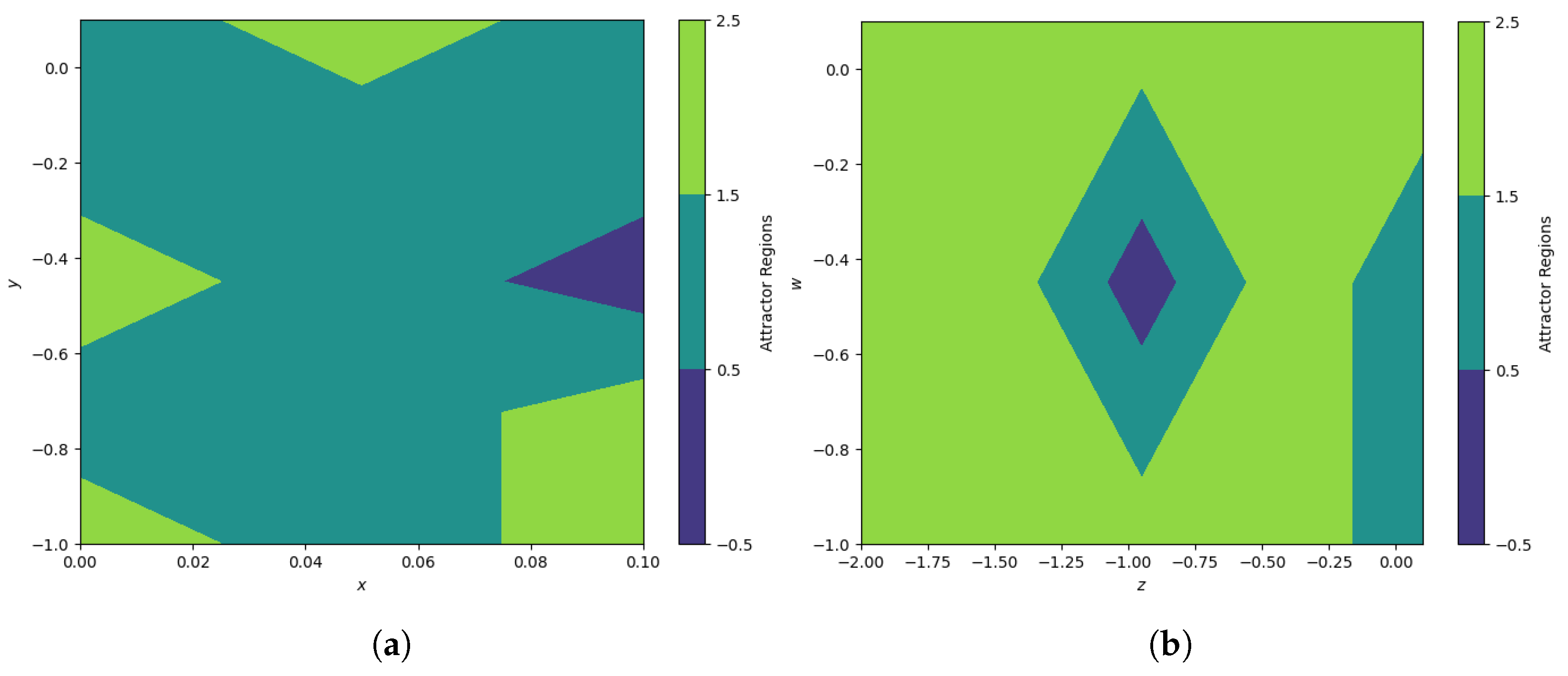
Mega-Stability of Oscillator (8)
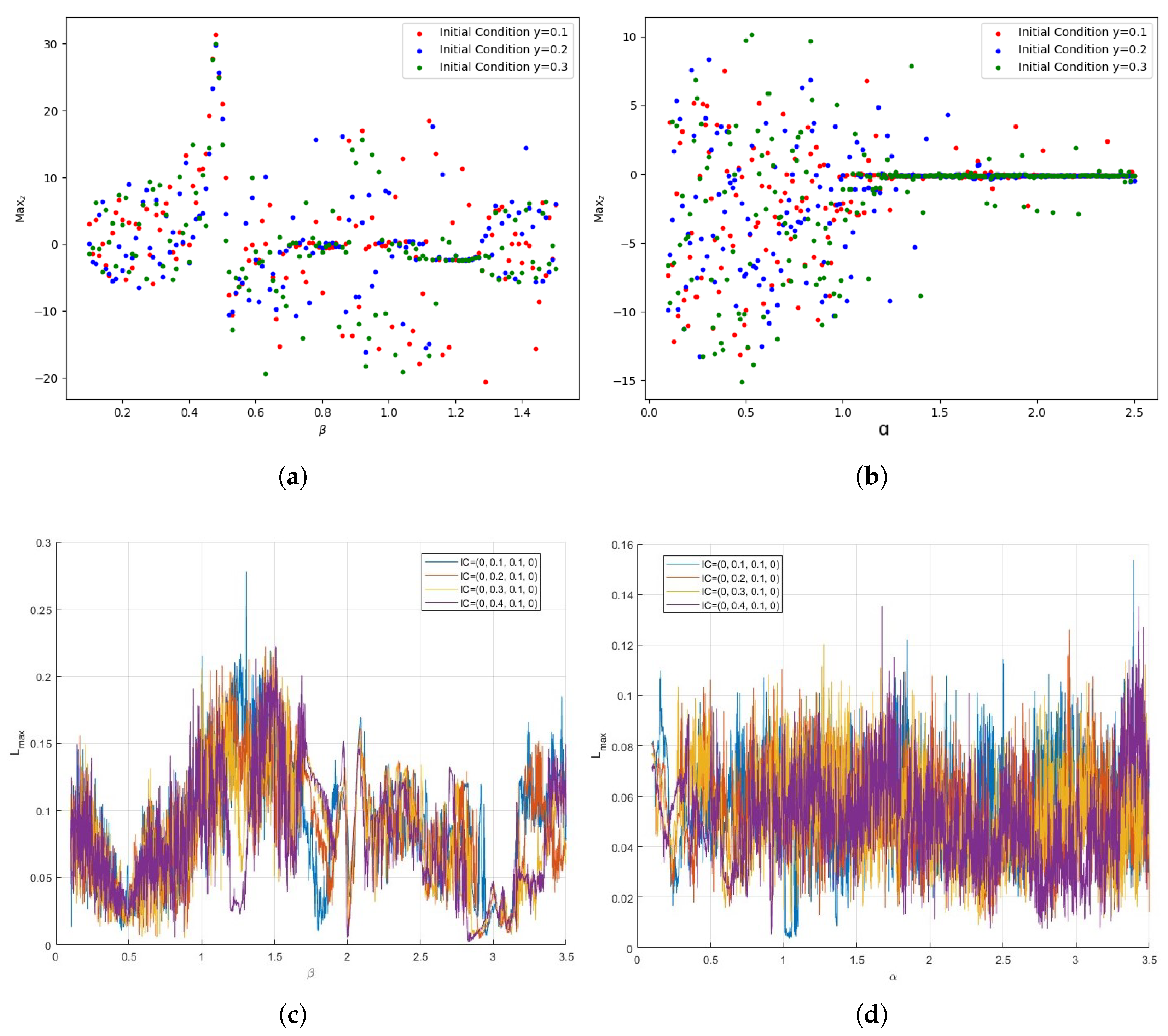
4. Complexity of and
5. Fractional-Order Mega-Stable Systems
Stability Analysis
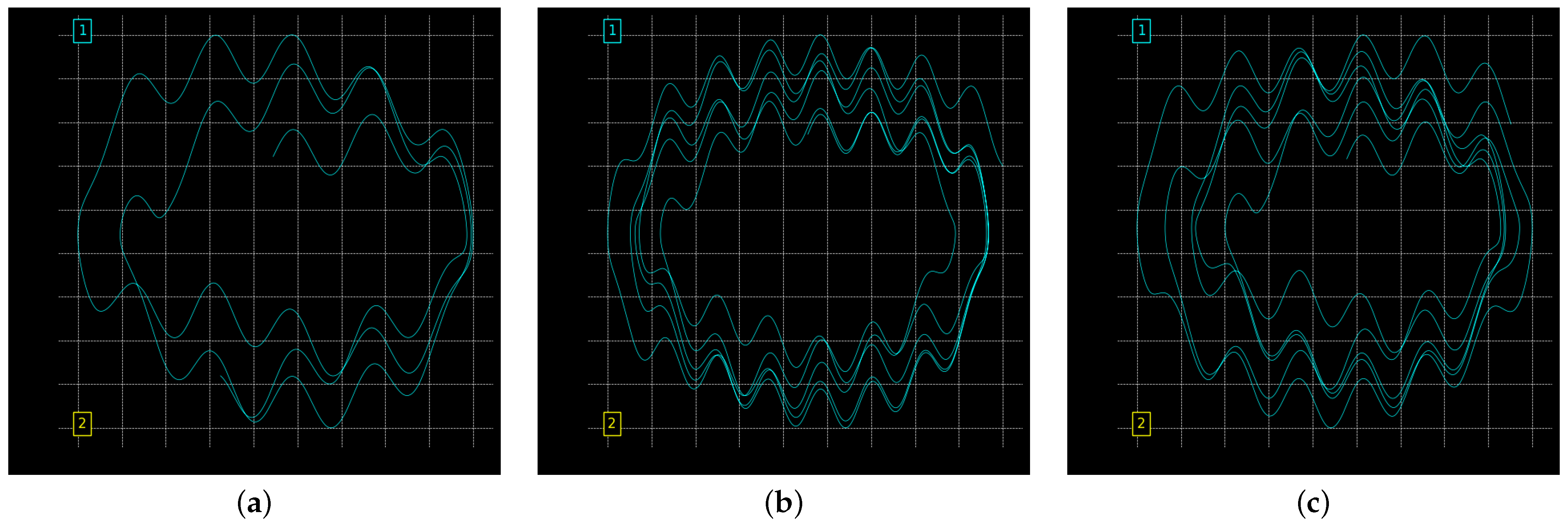
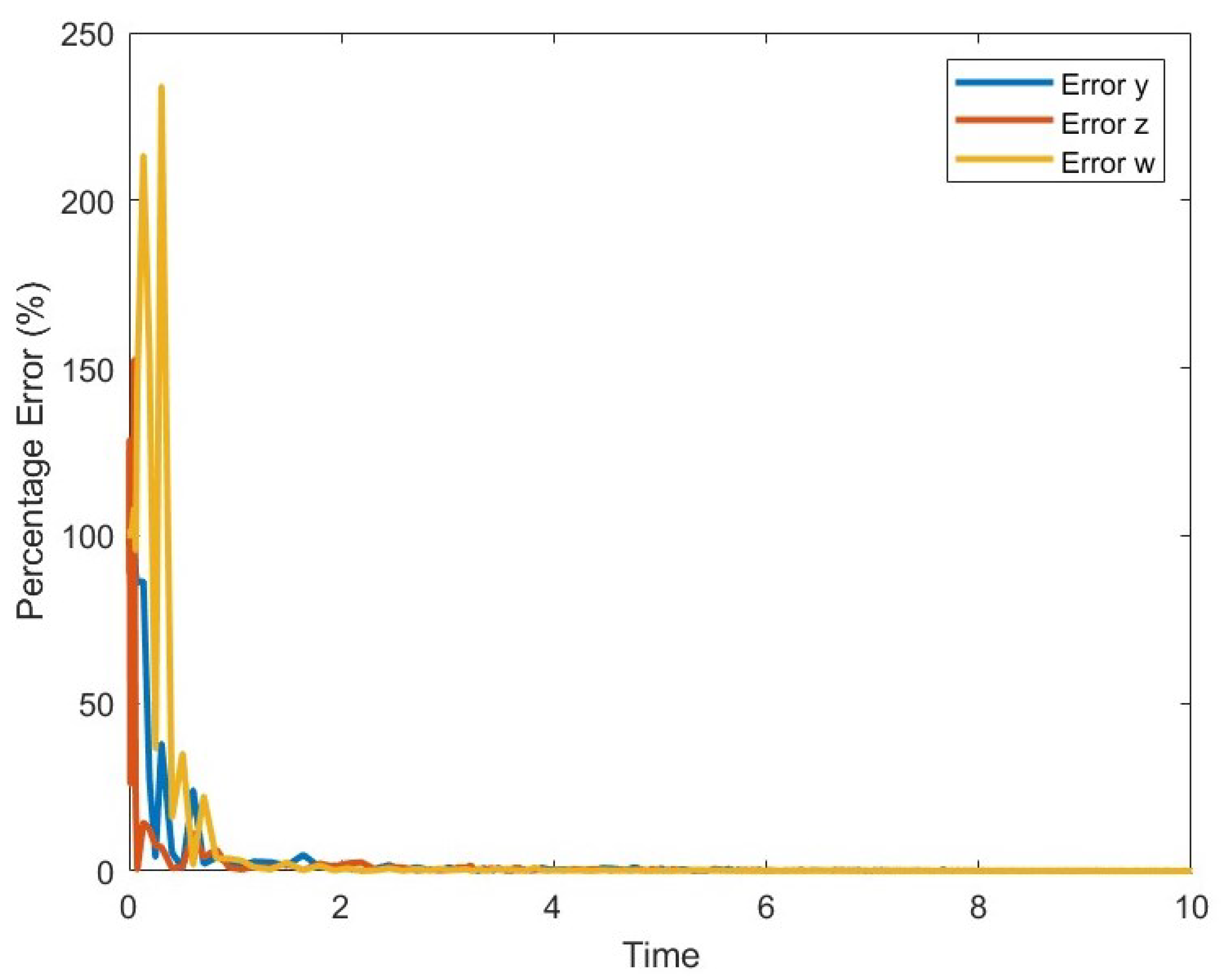
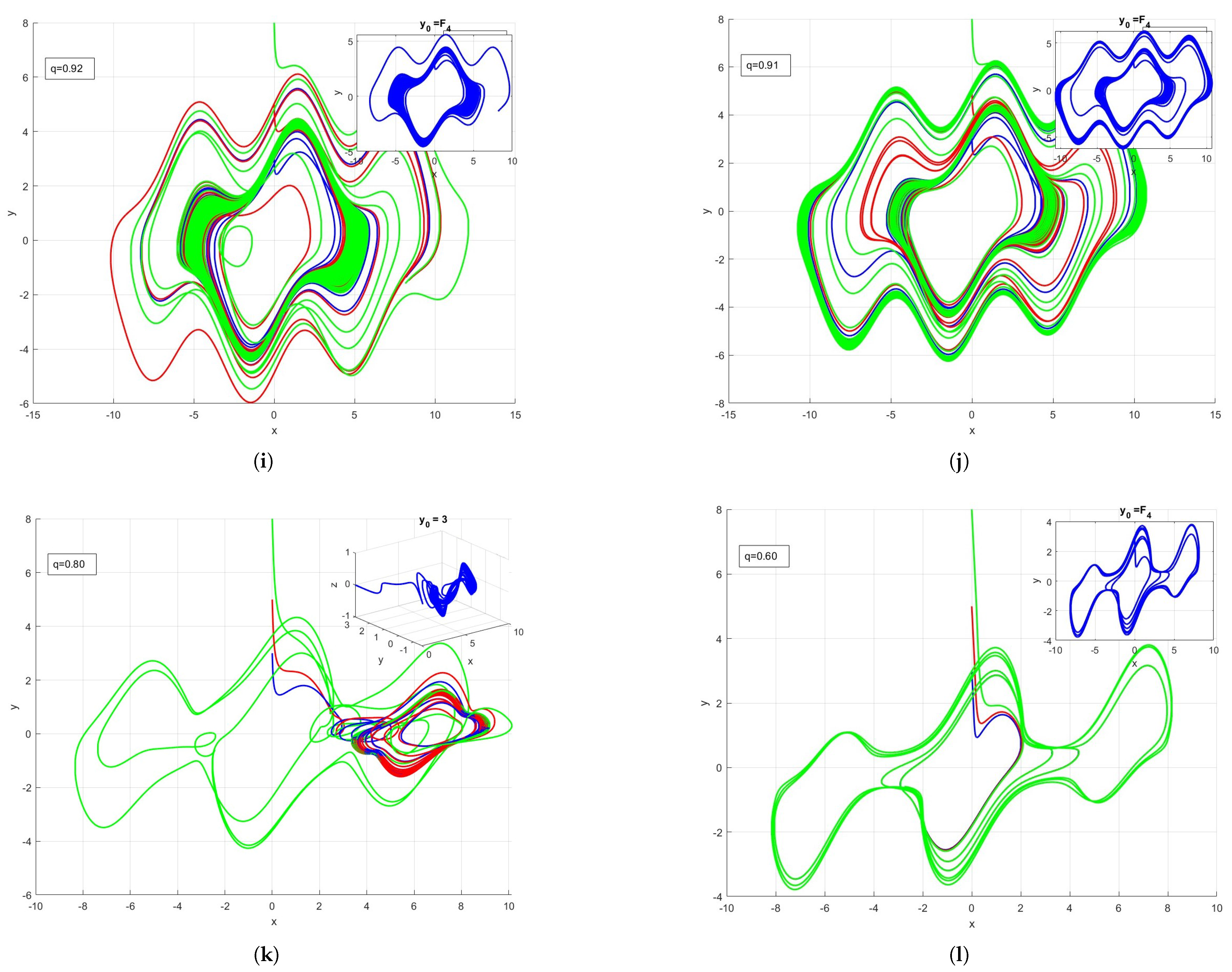
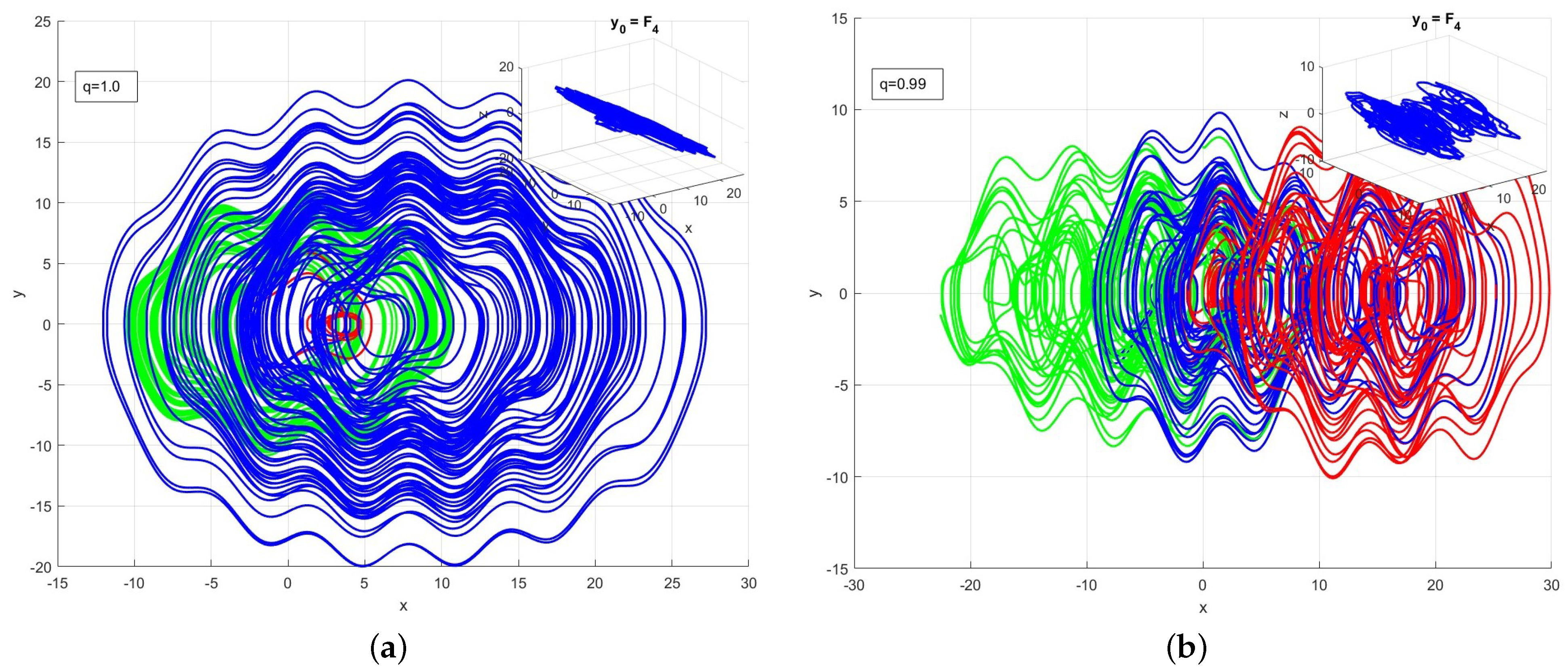
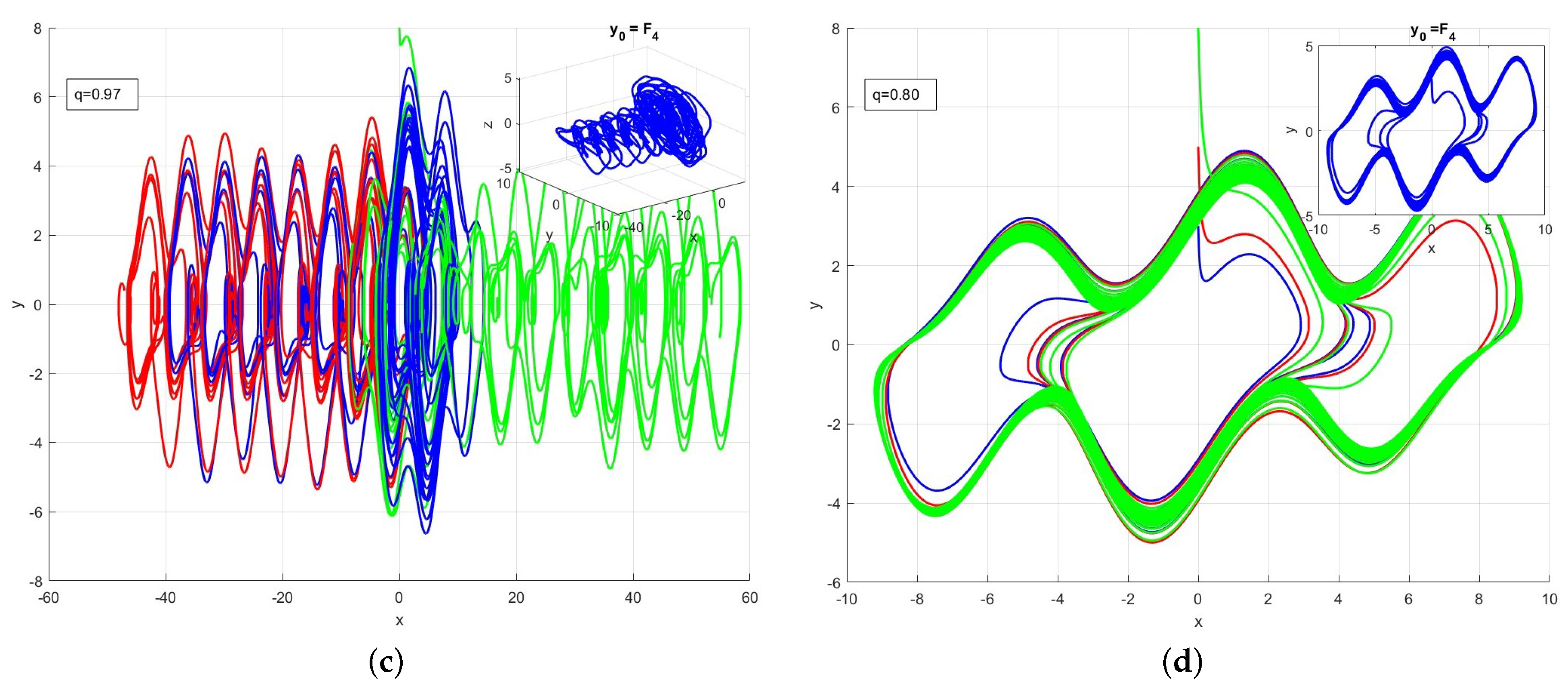
6. Order Effect
7. Microcontroller Implementation
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E. Deterministic nonperiodic flow. J. Atmos. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics Biology Chemistry and Engineering; Chapman and Hall/CRC: Boulder, CO, USA, 2000. [Google Scholar]
- Minati, L. Simulation versus experiment in non-linear dynamical systems. Chaos Solitons Fractals 2021, 144, 110656. [Google Scholar] [CrossRef]
- Fatemeh, P.; Karthikeyan, R.; Anitha, K.; Ahmed, A.; Tasawar, H.; Viet-Thanh, P. Complex dynamics of a neuron model with discontinuous magnetic induction and exposed to external radiation. Cogn. Neurodyn. 2018, 12, 607–614. [Google Scholar]
- Yang, Y.; Ma, J.; Xu, Y.; Jia, Y. Energy dependence on discharge mode of izhikevich neuron driven by external stimulus under electromagnetic induction. Cogn. Neurodyn. 2021, 15, 265–277. [Google Scholar] [CrossRef]
- Quan, X.; Yiteng, W.; Bei, C.; Ze, L.; Ning, W. Firing pattern in a memristive hodgkin-huxley circuit: Numerical simulation and analog circuit validation. Chaos Solitons Fractals 2023, 172, 113627. [Google Scholar]
- Jafari, S.; Sprott, J.; Mohammad, S. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 2013, 377, 699–702. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G.; Chen, A. chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1264–1272. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84.100. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Srinivasan, A. Bifurcation and chaos in time delayed fractional order chaotic oscillator and its sliding mode synchronization with uncertainties. Chaos Solitons Fractals 2017, 103, 347–356. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Kuznetsov, N.; Bao, H. Hidden attractors and multistability in a modified Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105494. [Google Scholar]
- Bao, B.; Bao, H.; Wang, N.; Chen, M.; Xu, Q. Hidden extreme multistability in memristive hyperchaotic system. Chaos Solitons Fractals 2017, 94, 102–111. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Diethelm, K.; Ford, N.J. The Analysis of Fractional Differential Equations; Lecture notes in mathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Vastarouchas, C.; Psychalinos, C.; Elwakil, S. Fractional-order model of a commercial ear simulator. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), IEEE Xplore, Florence, Italy, 27–30 May 2018; pp. 1–4. [Google Scholar]
- Santanu, R.; Abdon, A.; Oukouomi, S.; Muhammet, K.; Necdet, B.; Adem, K. Fractional calculus and its applications in applied mathematics and other sciences. Math. Probl. Eng. 2014, 2014, 849395. [Google Scholar]
- Rihan, A. Numerical modeling of fractional-order biological systems. Abstr. Appl. Anal. 2013, 1, 816803. [Google Scholar]
- Rajagopal, K.; Laarem, G.; Karthikeyan, A.; Srinivasan, A. FPGA implementation of adaptive sliding mode control and genetically optimized PID control for fractional-order induction motor system with uncertain load. Adv. Differ. Equ. 2017, 1, 273. [Google Scholar] [CrossRef]
- Vasily, E. Mathematical economics: Application of fractional calculus. Mathematics 2020, 8, 660. [Google Scholar] [CrossRef]
- Rahman, Z.; Jasim, B.; Al-Yasir, Y.; Abd-Alhameed, R.; Bilal, N. A new no equilibrium fractional order chaotic system, dynamical investigation, synchronization. and its digital implementation. Inventions 2021, 6, 49. [Google Scholar] [CrossRef]
- Echenausía-Monroy, J.; Quezada-Tellez, L.; Gilardi-Velázquez, H.; Fernando Ruíz-Martinez, O.; Carmen Heras-Sanchez, M.; Lozano-Rizk, J.; Cuesta-Garcia, J.; Marquez-Martinez, L.; Rivera-Rodriguez, R.; Pena Ramirez, J.; et al. Beyond Chaos in Fractional-Order Systems: Keen Insight in the Dynamic Effects. Fractal Fract. 2025, 9, 22. [Google Scholar] [CrossRef]
- Wang, Z.; Hamarash, I.; Shabestari, P.; Jafari, S. A new megastable oscillator with rational and irrational parameters. Int. J. Bifurc. Chaos 2019, 13, 1950176. [Google Scholar]
- Jafari, S.; Rajagopal, K.; Hayat, T.; Alsaedi, A.; Pham, V. Simplest megastable chaotic oscillator. Int. J. Bifurc. Chaos 2019, 13, 1950187. [Google Scholar] [CrossRef]
- Leutcho, G.; Fozin, T.; Negou, A.; Njitacke, Z.; Pham, V.; Engne, J.; Jafari, S. A novel megastable Hamiltonian system with infinite hyperbolic and nonhyperbolic equilibria. Complexity 2020, 2020, 9260823. [Google Scholar] [CrossRef]
- Lu, H.; Rajagopal, K.; Nazarimehr, F.; Jafari, S. A new multiscroll megastable oscillator based on the sign function. Int. J. Bifurc. Chaos 2021, 8, 2150140. [Google Scholar] [CrossRef]
- Ramakrishnan, B.; Natiq, H.; Rajagopal, K.; Jafari, S.; Nazarimehr, F. A novel megastable system: Cloud, kite, and arrow-like attractors and their dynamics. Int. J. Bifurcation Chaos 2022, 10, 2250152. [Google Scholar] [CrossRef]
- Ahmadi, A.; Vijayan, V.; Natiq, H.; Pchelintsev, A.; Rajagopal, K.; Jafari, S. A novel megastable chaotic system with hidden attractors and its parameter estimation using the sparrow search algorithm. Computation 2023, 12, 245. [Google Scholar] [CrossRef]
- Gervais, D.; Jafari, S.; Hamarash, I.; Kengne, J.; Njitacke, Z.; Hussain, I. A new megastable nonlinear oscillator with infinite attractors. Chaos Solitons Fractals 2020, 134, 109703. [Google Scholar]
- Sprott, J.; Jafari, S.; Khalaf, A.; Kapitaniak, T. Megastability: Coexistence of110 a countable infinity of nested attractors in a periodically-forced oscillator with spatially-periodic damping. Eur. Phys. J. Spec. Top. 2017, 226, 1979–1985. [Google Scholar] [CrossRef]
- Daletskii, Y.; Krein, M. Ustoichivost’ reshenii differentsial’nykh uravnenii vs. banakhovom prostranstve (Stability of Solutions of Differential Equations in a Banach Space); Nauka: Moscow, Russia, 1970. [Google Scholar]
- Nikolay, K.; Volker, R. Attractor Dimension Estimates for Dynamical Systems: Theory and Computation; Springer: Cham, German, 2020. [Google Scholar]
- Doering, C.; Gibbon, J. On the shape and dimension of the Lorenz attractor. Dyn. Stab. Syst. 1995, 10, 255–268. [Google Scholar] [CrossRef]
- Gronwall, T. Note on the Derivatives with Respect to a Parameter of the Solutions of a System of Differential Equations. Ann. Math. 1919, 4, 292–296. [Google Scholar] [CrossRef]
- Rossler, O. An equation for hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar] [CrossRef]
- Shukur, A.; Viet-Thanh, P.; Kamdoum, V.; Giuseppe, G. Hyperchaotic Oscillator with Line and Spherical Equilibria: Stability. Entropy, and Implementation for Random Number Generation. Symmetry 2024, 10, 1341. [Google Scholar] [CrossRef]
- Shukur, A.; MAlFallooji Viet-Thanh, P. Asymmetrical novel hyperchaotic system with two exponential functions and an application to image encryption. Nonlinear Eng. 2024, 13, 20220362. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J. An infinite 3-d quasiperiodic lattice of chaotic attractors. Phys. Lett. 2018, 382, 581–587. [Google Scholar] [CrossRef]
- Ahmadi, A.; Parthasarathy, S.; Natiq, H.; Jafari, S.; Franovi, I.; Rajagopal, K. Rajagopal, A non-autonomous mega-extreme multistable chaotic system. Chaos Solitons Fractals 2023, 174120, 113765. [Google Scholar] [CrossRef]
- Rajagopal, K.; Cimen, M.; Jafari, S.; Singhd, J.; Roy, B.; Akmese, O.; Akgul, A. A family of circulant megastable chaotic oscillators. its application for the detection of a feeble signal and PID controller for time-delay systems by using chaotic sca algorithm. Chaos Solitons Fractals 2021, 148, 110992. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.; Swinney, H.; Vastano, J. Determining Lyapunov exponents from a time series. Physica D 2023, 12, 285–317. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, M.; Juan, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Burton, T. Two direct Tustin discretization methods for fractional order differentiator integrator. Acta Phys. Sin. 2013, 24, 62. [Google Scholar]
- Jpetráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Matignon, D. Stability Results for Fractional Differential Equations with Applications to Control Processing. Comput. Eng. Syst. Appl. 1996, 2, 963. [Google Scholar]
- Li, H.; Shen, Y.; Han, Y.; Dong, J. Determining Lyapunov exponents of fractional-order systems: A general method based on memory principle. Chaos Solitons Fractals 2023, 168, 113167. [Google Scholar]



| Refs | Dim. | Term | Autonomous | Nonlin. Count Except Forcing Term |
|---|---|---|---|---|
| [29] | 2D | 4 | No | 1 |
| [37] | 3D | 6 | Yes | 6 |
| [28] | 2D | 4 | Yes | 3 |
| [38] | 3D | 5 | No | 2 |
| [27] | 2D | 4 | Aut/No | 3 |
| [39] | 4D | 8 | Yes | 8 |
| System (8) | 4D | 7 | No | 2 |
| n | Attractor Class. | |||||
|---|---|---|---|---|---|---|
| 1 | 0.101340 | 0.022871 | 0 | −0.221613 | 3.554 | Hyperchaotic |
| 2 | 0.141520 | 0.029890 | 0 | −0.184635 | 3.829 | Hyperchaotic |
| 3 | 0.089957 | 0.020787 | 0 | −0.213151 | 3.213 | Hyperchaotic |
| 4 | 0.167079 | 0 | −0.035889 | −0.178175 | 3.737 | Chaotic |
| Fractional Order | n | LEs | Attractor Class. | |
|---|---|---|---|---|
| 1 | 3 | (0.1066, 0, −0.6683) | 2.2605 | Strange attractors |
| 5 | (0.0169, 0, −0.7997) | 2.2100 | Strange attractors | |
| 8 | (0.1095, 0, −0.9054) | 2.2302 | Strange attractors | |
| 0.99 | 3 | (0.0236, −0.4387, −0.0014) | 2.1412 | Strange attractors |
| 5 | (0.0256, −0.7081, −0.0014) | 2.1205 | Strange attractors | |
| 8 | (0.0424, −0.9036, −0.0014) | 2.1307 | Strange attractors | |
| 0.98 | 3 | (0.0601, −0.7521, −0.0029) | 2.0928 | Strange attractors |
| 5 | (0.0591, −0.8213, −0.0029) | 2.0805 | Strange attractors | |
| 8 | (0.0691, −0.9932, −0.0029) | 2.0857 | Strange attractors | |
| 0.97 | 3 | (0.0323, −0.6090, −0.0047) | 2.1444 | Strange attractors |
| 5 | (0.0260, −0.6205, −0.0047) | 2.1302 | Strange attractors | |
| 8 | (0.0454, −0.9128, −0.0047) | 2.1384 | Strange attractors | |
| 0.96 | 3 | (0.0174, −0.5381, −0.0067) | 2.0834 | Strange attractors |
| 5 | (0.0247, −0.5633, −0.0067) | 2.0725 | Strange attractors | |
| 8 | (0.0376, −0.6902, −0.0067) | 2.0775 | Strange attractors | |
| 0.95 | 3 | (0, −0.8030, −0.0090) | Limit cycle | |
| 5 | (0, −0.7133, −0.0090) | Limit cycle | ||
| 8 | (0, −0.8186, −0.0090) | Limit cycle | ||
| 0.94 | 3 | (0, −0.5565, −0.0117) | Limit cycle | |
| 5 | (0, −0.9130, −0.0117) | Limit cycle | ||
| 8 | (0, −0.6169, −0.0117) | Limit cycle | ||
| 0.93 | 3 | (0, −0.5473, −0.0146) | Limit cycle | |
| 5 | (0, −0.8067, −0.0146) | Limit cycle | ||
| 8 | (0, −0.8307, −0.0146) | Limit cycle | ||
| 0.92 | 3 | (0, −0.6295, −0.0180) | Limit cycle | |
| 5 | (0, −0.7152, −0.0180) | Limit cycle | ||
| 8 | (0, −0.7772, −0.0180) | Limit cycle | ||
| 0.91 | 3 | (0, −0.7660, −0.0218) | Limit cycle | |
| 5 | (0, −0.9177, −0.0218) | Limit cycle | ||
| 8 | (0, −0.8605, −0.0218) | Limit cycle | ||
| 0.90 | 3 | (0, −0.9419, −0.0262) | Limit cycle | |
| 5 | (0, −1.0126, −0.0262) | Limit cycle | ||
| 8 | (0 −1.0294, −1.0294, −0.0262) | Limit cycle |
| Fractional Order | IC | LEs | Attractor Class. | |
|---|---|---|---|---|
| 1 | 1 | (0.1119, 0.0575, 0, −0.1140) | 2.2605 | Hyperchaotic |
| 2 | (0.1320, 0.0439, 0, −0.1191) | 2.2100 | Hyperchaotic | |
| 3 | (0.1281, 0.0816, 0, −0.1211) | 2.2302 | Hyperchaotic | |
| 0.99 | 1 | (0.0239, 0, −0.0304, −0.0456) | 2.1412 | Chaotic |
| 2 | (0.0350, 0, −0.0235, −0.0611) | 2.1205 | Chaotic | |
| 3 | (0.0297,0, −0.0288, −0.0550) | 2.1307 | Chaotic | |
| 0.97 | 1 | (0.0392, 0 −0.0221, −0.2845) | 2.0928 | Chaotic |
| 2 | (0.0387, 0, −0.0246, −0.2579) | 2.0805 | Chaotic | |
| 3 | (0.0391, 0, −0.0217, −0.2699) | 2.0857 | Chaotic | |
| 0.80 | 1 | (0, −0.3733, −0.9666, −0.9752) | Limit cycle | |
| 2 | (0, −0.3718, −0.9651, −0.9742) | Limit cycle | ||
| 3 | (0, −0.3611, −0.9585, −0.9675) | Limit cycle |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ridha, Z.D.; Shukur, A.A. Mega-Instability: Order Effect on the Fractional Order of Periodically Forced Oscillators. Fractal Fract. 2025, 9, 238. https://doi.org/10.3390/fractalfract9040238
Ridha ZD, Shukur AA. Mega-Instability: Order Effect on the Fractional Order of Periodically Forced Oscillators. Fractal and Fractional. 2025; 9(4):238. https://doi.org/10.3390/fractalfract9040238
Chicago/Turabian StyleRidha, Zainab Dheyaa, and Ali A. Shukur. 2025. "Mega-Instability: Order Effect on the Fractional Order of Periodically Forced Oscillators" Fractal and Fractional 9, no. 4: 238. https://doi.org/10.3390/fractalfract9040238
APA StyleRidha, Z. D., & Shukur, A. A. (2025). Mega-Instability: Order Effect on the Fractional Order of Periodically Forced Oscillators. Fractal and Fractional, 9(4), 238. https://doi.org/10.3390/fractalfract9040238