1. Introduction
The global tanker freight market plays a crucial role in the shipping industry and has long been a focus for both academicians and industry practitioners [
1,
2,
3]. This market exhibits complex behaviors driven by geopolitical events [
4,
5,
6], economic conditions [
7], technological innovations, and environmental policies [
8]. Its inherent volatility and multi-scale temporal correlations further complicate the study of market dynamics [
9,
10]. Understanding these trends is essential for stakeholders seeking to navigate market shifts and leverage technological advancements [
11,
12,
13,
14,
15,
16,
17,
18].
Despite growing interest in this field, several key gaps remain. There is a need for a deeper understanding of how multifractal dynamics in the tanker freight market interact with external influences, such as geopolitical tensions, economic cycles, and environmental policies [
4,
9]. Additionally, more interdisciplinary research is required, integrating insights from complexity economics, financial engineering, and operations research to develop more advanced methodologies for analyzing and managing risks in this evolving market [
19,
20,
21].
Complexity economics provides an interdisciplinary framework that integrates economics, information science, physics, and operations research [
22,
23,
24]. It recognizes agent heterogeneity, imperfect information, and dynamic system behavior, offering valuable insights into energy and tanker freight markets [
4,
12,
25,
26,
27,
28]. Fractals, characterized by self-similarity and fragmented geometric structures, have become an effective tool in complexity economics [
29,
30]. Early methodologies, such as Hurst’s rescaled range analysis, struggled to assess long-range dependencies in nonstationary series [
31]. To address this, Castro et al. introduced a novel approach for multi-affine fractal exponents and correlation coefficients [
32], while Peng et al. developed a detrended fluctuation analysis (DFA) to quantify long-term correlations [
33]. However, DFA was limited in capturing multi-scale and fractal structures, necessitating the development of multifractal detrended fluctuation analysis (MF-DFA) by Kantelhardt et al. [
34], which has since become a standard tool for multifractal characterization [
35,
36]. In parallel, the detrending moving average (DMA) technique emerged as an effective method for analyzing long memory in nonstationary time series [
37,
38,
39]. By refining the moving average function, DMA excels in detecting scaling properties [
40], with MF-DMA extending its application to higher dimensions. This method helps distinguish true multifractality—arising from nonlinear correlations—from spurious effects caused by fat-tailed probability distributions [
41,
42]. Kwapien et al. further confirmed that true multifractality in time series originates from temporal correlations using both analytical and numerical evidence [
43].
To provide a clearer understanding of the methods used in this study, we present a comparative chart outlining the key differences between the MF-DFA, MF-DMA, and conventional methods. As shown in
Table 1, this comparison highlights the core principles, advantages, limitations, and applicability of each method in analyzing multifractal behavior in the tanker freight market.
Research on tanker freight rate volatility is a key area in maritime economics, influencing the broader global economy. These studies explore the interplay of factors such as crude oil prices, charter rates, fleet size, and policy changes [
13,
14,
15,
16,
17,
18,
19,
44]. Multifractal analysis has gained traction in this field for its ability to capture asymmetric market risks, revealing varying responses to upward and downward trends and identifying distinct scaling behaviors [
45]. Unlike traditional methods, multifractality recognizes that freight rates exhibit a spectrum of fractal characteristics rather than a single fluctuation pattern [
46,
47,
48,
49]. It accounts for both small and large market movements, offering a nuanced perspective on data correlations, particularly during turbulent periods, such as the 2008 financial crisis and the COVID-19 pandemic [
4,
12,
46]. This study aims to analyze the market’s evolving complexity, providing insights into its long-term dynamics and informing strategies to mitigate the impact of unpredictable market changes and crises. This study tries to comprehend the intricate, multifaceted nature of the market to provide a comprehensive understanding of the market’s complexity and its evolution over time and design strategies that buffer the fallout from unpredictable market shifts or crises.
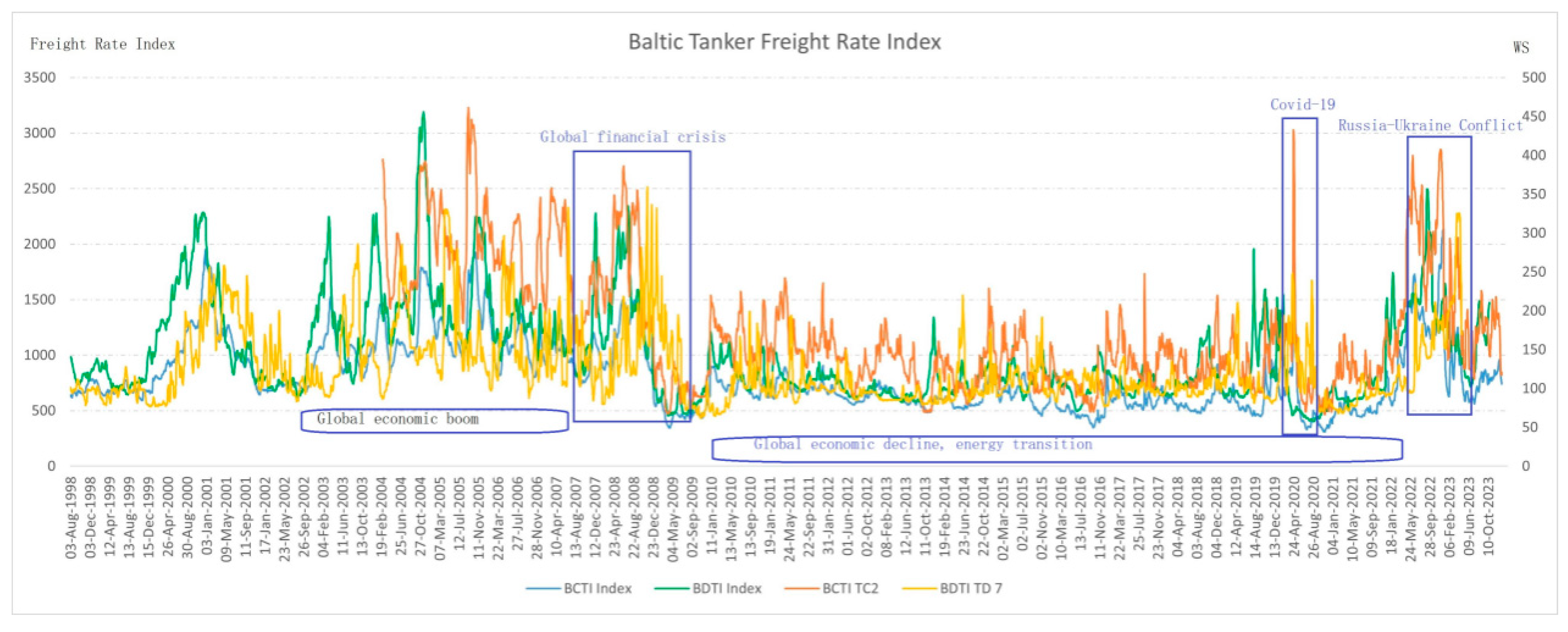
The research is driven by the following key questions: (a) How has the multifractal nature of the tanker freight market evolved across two distinct periods—1998–2010 and 2010–2024—and what insights does this evolution provide regarding market behavior and systemic risks? (b) What role do temporal correlations and inherent volatility play in shaping the complex structure of the market, and how do these factors contribute to the observed multifractal dynamics? (c) How do external factors shape the complexity and multifractal characteristics of the tanker freight market, particularly through financial crises, supply chain disruptions, regulatory interventions, technological advancements in energy efficiency, and carbon emission policies? (d) Can tanker freight rates, specifically the Baltic Dirty Tanker Index (BDTI, a vital benchmark that assesses the cost of shipping dirty petroleum products, including crude oil, on selected routes within the Baltic region), be used to predict Brent oil prices during periods of heightened market complexity, and how do multifractal features enhance the predictive power of such models?
This study investigates the complexity and multifractal characteristics of the Baltic Clean and Dirty Tankers markets from 1998 to 2023. Using MF-DFA, we analyze clean and dirty tanker freight rates, specifically the TC2 and TD7 routes, from 28 January 1998, to 12 January 2024. To examine market patterns following major fluctuations, we compare Period I (1998–2010) and Period II (2010–2024). Additionally, to better understand the multifractality of Baltic Dirty Tanker Index (BCTI, a widely recognized benchmark that tracks freight rates for large capesize vessels and reflects global shipping market conditions), we employ MF-DMA to quantify three key components: linear correlation, nonlinear correlation, and fat-tailed probability distribution.
Building on this foundational analysis, we further extend the scope of our research to explore the predictive potential of freight rates in forecasting Brent oil prices, particularly during periods of heightened market volatility and complexity. Traditionally, most studies have focused on forecasting freight rates based on oil price movements, reflecting the conventional economic logic that oil prices drive downstream costs, including shipping. Numerous studies support this view, emphasizing the dominant role of oil prices in shaping the freight market. For instance, Alizadeh and Nomikos (2004) examined the cost-of-carry relationship between oil futures and freight markets, but found no significant link that would allow freight rates to predict oil price movements [
50]. Similarly, Gavriilidis et al. (2018) utilized GARCH-X models and demonstrated that oil price shocks, particularly demand and precautionary demand shocks, significantly affect freight rate volatility, yet their findings did not establish freight rates as an effective predictor of oil price fluctuations [
14]. Shi et al. (2022) further explored the dynamic dependence between these markets through a copula-MIDAS-X model, concluding that oil price non-supply shocks played a crucial role in shaping freight rate behavior, while freight rates themselves lacked substantial feedback effects on oil prices [
51]. Furthermore, Siddiqui and Basu (2020), by decomposing cyclical components of oil prices and freight rates, reaffirmed the prevailing view that oil prices generally lead freight rate movements over medium- to long-term cycles, underscoring the asymmetric influence of oil prices over the shipping sector [
18]. However, freight rates, due to their responsiveness to supply–demand dynamics, vessel utilization rates, and macroeconomic shifts, may serve as valuable leading indicators for oil prices. This study, therefore, adopts an innovative perspective by investigating whether BDTI can predict Brent oil prices and how multifractal features contribute to the accuracy of such predictions.
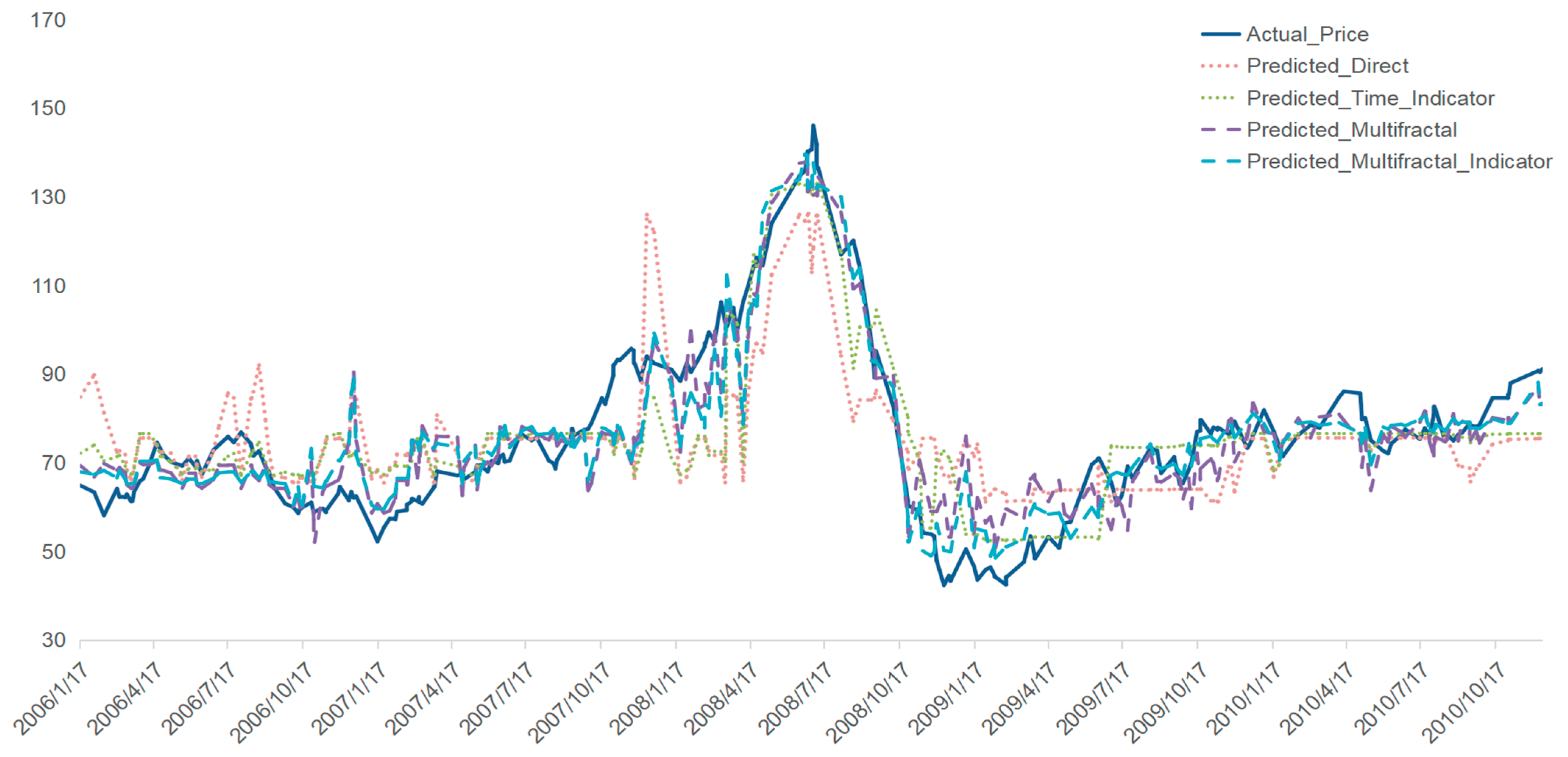
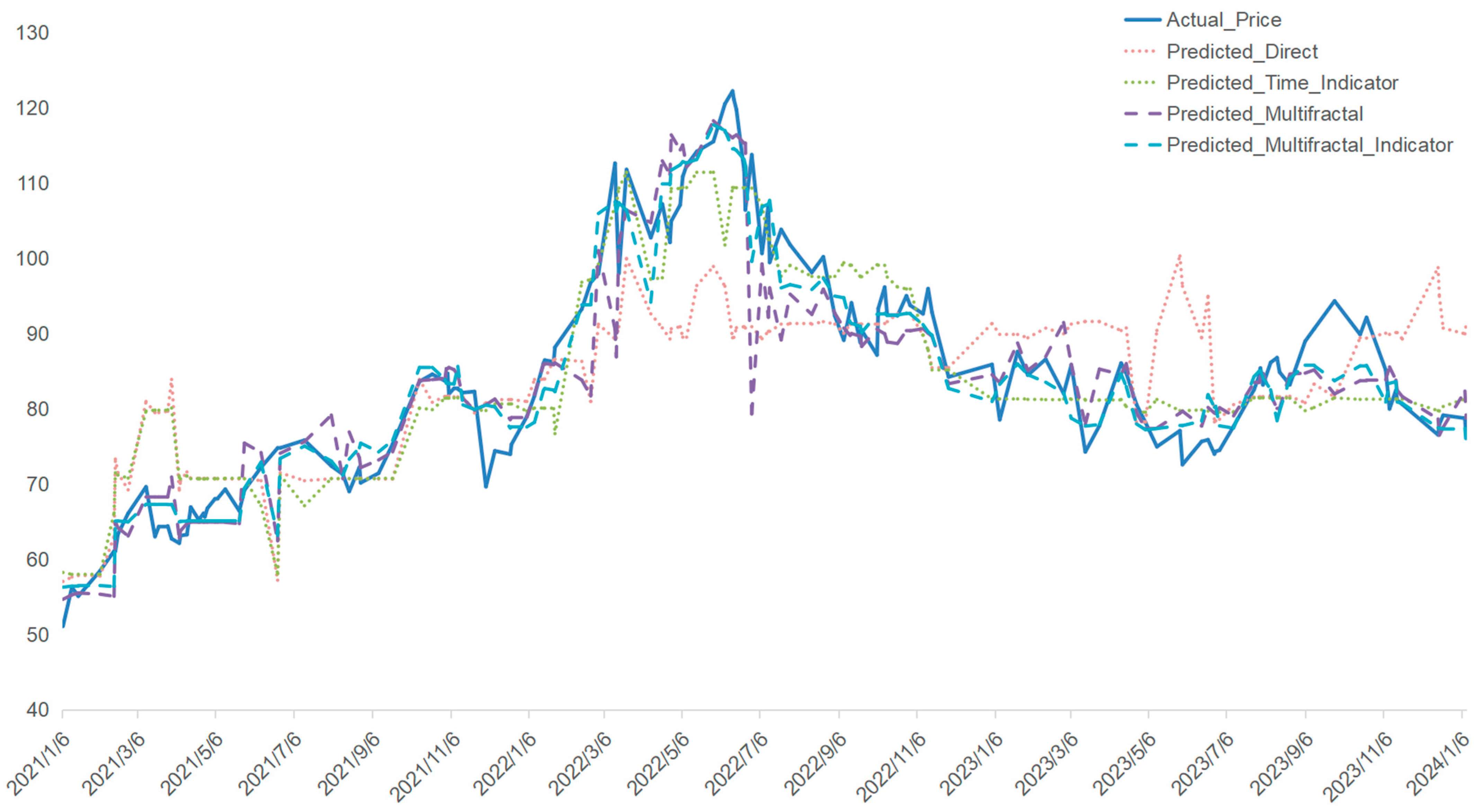
To address this question, we examine four distinct periods characterized by major global events that significantly influenced market dynamics: (1) 2006–2010: marked by the 2008 global financial crisis, which caused widespread disruptions in financial and commodity markets; (2) 2013–2016: defined by the 2014 Shale Oil Revolution, which reshaped global energy supply dynamics; (3) 2019–2021: dominated by the COVID-19 pandemic, leading to unprecedented supply chain disruptions; and (4) 2021–2024: influenced by the Russia–Ukraine conflict, introducing severe geopolitical uncertainties and energy market volatility.
For each period, we develop predictive models using BDTI data as the primary feature, incorporating multifractal characteristics extracted via MF-DFA, such as the Hurst exponent and multifractal spectrum. To capture market dynamics during global events, these models are further enhanced with crisis period indicators. To improve prediction robustness, we employ stacking regression, integrating XGBoost, LightGBM, and CatBoost as base learners [
52,
53,
54]. XGBoost, known for its scalability and efficiency, delivers state-of-the-art performance across various machine learning tasks [
55]. Ridge Regression serves as the meta-learner, refining the final predictions. By structuring these powerful algorithms systematically, we enhance the accuracy and stability of our models, ensuring more reliable and insightful outcomes [
56].
The major contribution of this study is summarized as follows. The methodology evaluates the individual and combined effects of multifractal features and crisis indicators on predictive accuracy. This comprehensive framework not only assesses the predictive capacity of freight rates for oil prices but also provides deeper insights into how economic and geopolitical crises influence market dynamics. In addition, this study offers valuable insights for investors, energy companies, and policymakers. For investors, the enhanced predictive models enable better risk management and informed decision-making, especially during periods of market volatility. Companies can optimize trading strategies and hedge against price fluctuations by leveraging the predictive power of the Baltic Dirty Tanker Index (BDTI) and multifractal features. Policymakers can develop more effective regulations to promote market stability and mitigate systemic risks by understanding the multifractal nature of tanker freight markets. Overall, this research provides a robust framework for stakeholders to explore market complexities and enhance resilience in the face of global uncertainties. The integration of multifractal analysis with predictive modeling demonstrates the potential for advanced analytics to effectively navigate the complexities of modern financial markets.
The paper structure is as follows:
Section 2 introduces the MF-DFA and MF-DMA methods, and
Section 3 describes the Baltic Clean and Dirty Tanker Indexes and the data used in the analysis.
Section 4 presents the empirical results, including the multifractal characteristics of freight rate returns, the impact of structural breaks across different periods, and the predictive performance of the proposed framework under varying market conditions.
Section 5 discusses the implications of the findings for market participants, including investors, energy companies, and policymakers, and suggests potential directions for future research.
Section 6 concludes the study with key insights and future research directions.
2. Methods
2.1. The Multifractal Detrended Fluctuation Analysis Method
The following introduction of the MF-DFA method is based on the work by Kantelhardt et al. (2002) [
34].
Here are the general steps of the MF-DFA method on the series , where and is the length of the series. stands for the average value of series .
Assuming that
are increments of a random walk process around the mean
, the “trajectory” or “profile”, by the signal integration, could be expressed as
Segment Division: We divide the integrated series into , non-overlapping segments of equal length . Generally, the length of the series is not a multiple of the considered time scale , and a short part may remain at the end of the profile . Not to disregard this remaining part, this procedure is repeated in reverse, starting from the end. So, segments are obtained.
Detrending: The local trend for each of the
segments could be calculated by a least-square fit of the series. Then, the variance is determined by
For each segment
,
and
for
. Here,
is the fitting line in segment
.
Fluctuation Function
: All segments are averaged to obtain the
-th order fluctuation function by
where the index variable
can generally take any real value except zero.
Scaling Exponent
: Repeating the above steps for several time scales
,
will increase as
increases. The scaling behavior of the fluctuation functions could be analyzed using log–log plots
versus
for each value of
. A power-law between
and
exists, as shown in Equation (5), when the series
exhibits a long-range power-law correlation.
However, because of the diverging exponent, the averaging procedure of Equation (4) could not be applied directly to calculate the value
, which corresponds to the limit
as
. Instead, we must employ a logarithmic averaging procedure using Equation (6).
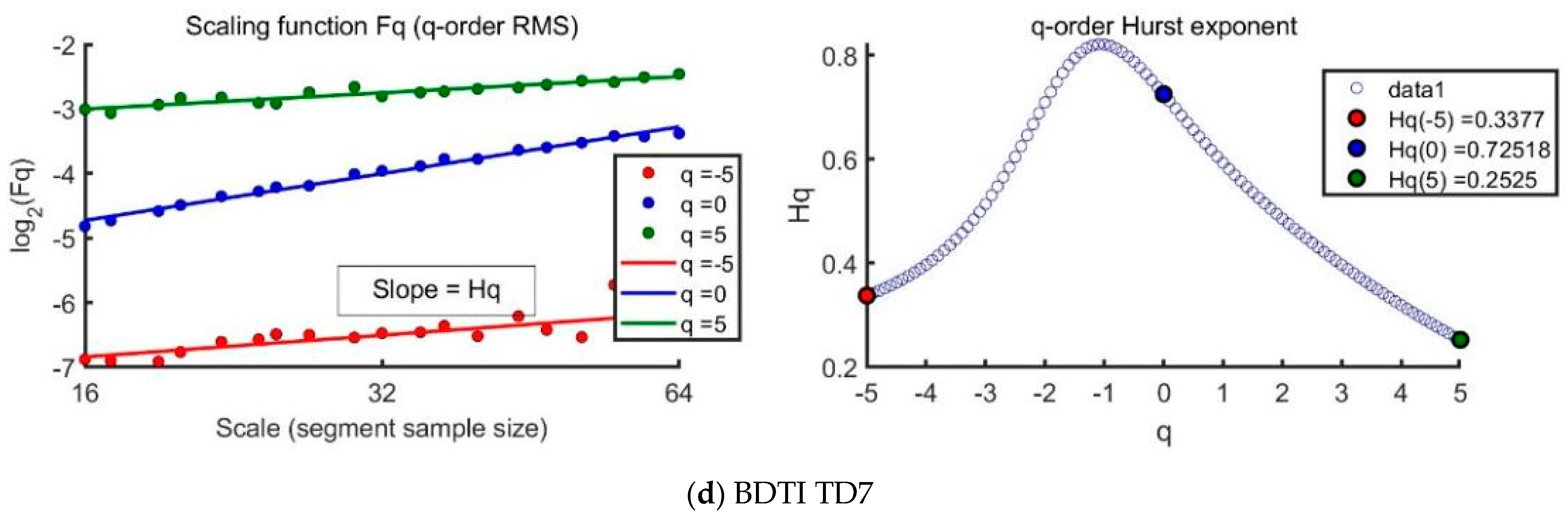
The exponent generally depends on . For the stationary series, is the well-defined Hurst exponent . Therefore, is called the generalized Hurst exponent. In a special case, when is independent of , it is defined as a monofractal series. The distinct scaling patterns exhibited by small and large fluctuations have a substantial impact on the relationship between the -th-order Hurst exponent and the scaling parameter . In the case of positive , segments characterized by a significant deviation from the expected trend, i.e., those with large variances, will exert a dominant influence on the average -order Hurst exponent . Consequently, a positive captures the scaling behavior of the segments with notable fluctuations, which typically correspond to smaller scaling exponents in multifractal time series. Conversely, for negative values, the segments with smaller variances take precedence in determining the average -order Hurst exponent . Hence, a negative describes the scaling behavior of segments with minor fluctuations, which generally exhibit larger scaling exponents in multifractal time series. This intricate interplay between , the scaling behavior of different segments , and the corresponding fluctuations provides valuable insights into the multifractal nature of the time series, shedding light on how various levels of variance impact the overall scaling exponents.
Let us take a simple example using a small synthetic time series of length :
Step 1: Calculate the profile by subtracting the mean and performing the cumulative sum:
Step 2: Divide the profile into segments of size , resulting in 10 segments.
Step 3: Perform local detrending for each segment by fitting a linear polynomial (least-squares fit) and subtracting the fit from the data.
Step 4: Calculate the fluctuation function for different values of q, e.g., q = 1, 2, −1.
Step 5: Analyze the scaling of with and estimate the generalized Hurst exponent .
This procedure allows you to assess the multifractal characteristics of the time series, as the scaling behavior reveals information about the correlation and variance of the series across different scales.
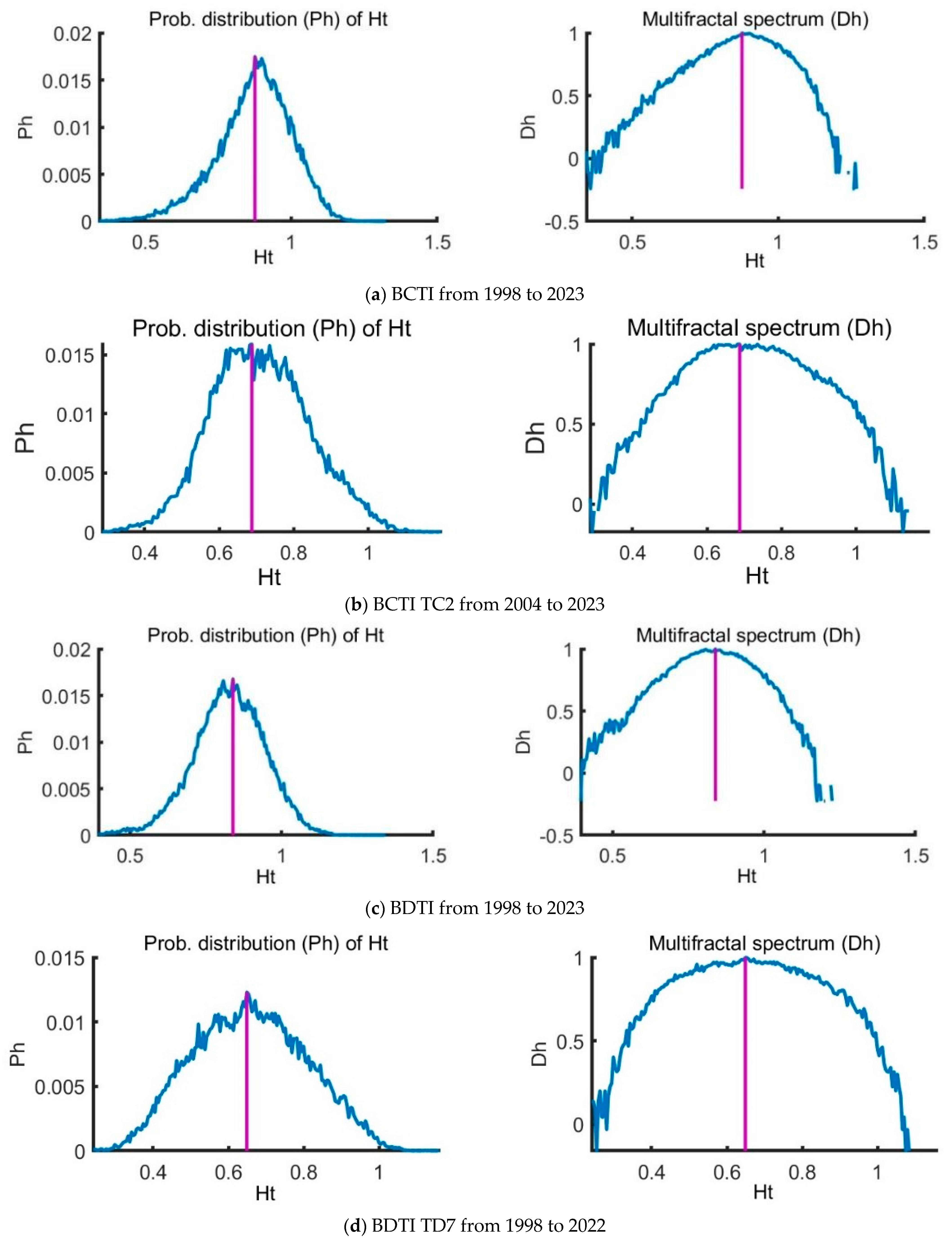
The multifractal spectrum
is another tool to characterize multifractality in a series.
can be obtained by Equation (7):
and then the Legendre transform
where
is the Holder exponent value, which indicates the strength of singularity. When
is broader, it indicates a stronger multifractality or complexity.
The width of the spectrum could be
where
and
indicate the maximum and minimum values, respectively.
We name MF-DFA1, MF-DFA2, and MF-DFA3 separately with polynomial order . Here, we apply MF-DFA1 and MF-DFA2 to investigate the BCTI, BDTI, and specific routes of TC2 and TD7.
2.2. The Multifractal Detrending Moving Average Method
The following brief introduction of the MF-DMA method is based on the works of Gu and Zhou (2010) [
41].
Assuming time series
,
, and
is the length of the series. We construct a new series:
In the next step,
indicates the moving average function. To calculate the sequence of cumulative totals, we slide a window of fixed size across the sequence:
where
is the size of window,
is the largest integer but not greater than
,
is the smallest integer but not smaller than
, and
is the position parameter, varying from 0 to 1. Here
is calculated over
data points from the preceding period but
data points from the subsequent period. We must notice three special cases with different
values. The backward-moving average, where
and
, is calculated using all the past data points.
efers to the centered moving average, where
is calculated over half past and half future data points.
represents the forward-moving average, where
is based on the trend of future data points. In this context, we utilize the selected case
, as it has demonstrated superior performance compared to the other two alternatives, based on the evidence presented in references [
37,
41,
43].
Subsequently, we eliminate the moving average component
from the series
to eliminate any underlying trend, resulting in a residual sequence
:
where
.
Then, the residual series
is divided into
(
) non-overlapping segments, each of equal length
. These segments can be represented as
for
, where
. We can obtain the root-mean-square function
using Equation (14).
Additionally, the
-th-order overall fluctuation function
is expressed as
When the values of
varies, we can get the power-law relation between
and
in Equation (17):
Finally, the multifractal scaling exponent and multifractal spectrum could be defined similarly to that of the above MF-DFA.
2.3. The Effective Multifractality
According to the references [
57,
58], the total multifractal spectrum could be intricately divided into three parts: the nonlinear (NL) and linear correlation (LM), and the probability density function (PDF). This decomposition is captured by Equation (18):
It is important to emphasize that both the linear correlation component
and the nonlinear correlation component
represent temporal correlations [
2,
5]. Specifically, the linear correlation component is attributed to finite-size effects [
52,
58]. Furthermore, it is noteworthy that
, indicating the linear correlation component, can be computed using semi-analytical formulas of an explicit form, offering a comprehensive quantitative characterization of this phenomenon [
39]. A type of computational deviation stemming from the sample number constraints is defined as the finite-size effect in reference [
26]. In essence, smaller time series sizes lead to greater computation deviations. To mitigate the impact of sample size limitations, especially for small sample sizes <10,000, it is necessary to calculate and exclude the linear correlation component from the true multifractality. Consequently, the true multifractality, denoted as
, which encompasses the nonlinearity component
and the PDF component
, is determined [
40,
57,
59].
To depict the spectrum of multifractality, it is important to conduct an analysis that involves both the elimination of the linear correlation component stemming from the sample size limitations (sample size < 10,000 points) and the decomposition of the remaining two effective parts [
57,
59,
60]. This quantitative analysis can be achieved through the creation of two new series: the shuffled and the surrogate time series. The shuffled time series is generated through the shuffled original series. During this process, the temporal correlations are disrupted, while the probability distribution remains unaltered [
43,
59].
The creation of surrogate data is accomplished through a two-stage procedure. Initially, the process ensures that the surrogate data match the original volatility time series in terms of probability distribution, which is executed through a transformation technique described in reference [
48]. Subsequently, the surrogate time series is manipulated to include linear correlations by applying an improved version of the amplitude-adjusted Fourier transform (IAAFT), as detailed in reference [
57]. To gain a thorough grasp of the surrogate time series construction process, it is recommended that readers refer to the comprehensive explanation in the reference [
26].
2.4. Machine Learning: Three Learners
After careful consideration of various machine learning models, we selected XGBoost, LightGBM, and CatBoost for their superior performance in handling structured data and regression tasks. Below is the justification for choosing these models over others:
These models have demonstrated strong predictive capabilities in numerous benchmarks and real-world applications, consistently outperforming other models such as Random Forest or Support Vector Machines in our preliminary experiments. XGBoost includes built-in regularization mechanisms (L1 and L2), which effectively mitigate the risk of overfitting, thereby maintaining good generalization, even with complex datasets. LightGBM utilizes a histogram-based algorithm, significantly improving training speed and memory efficiency when dealing with large datasets. This made it a suitable choice for the large-scale data scenarios in our study. CatBoost’s ability to handle categorical variables natively, without extensive pre-processing or encoding, reduces the risk of manual errors and improves overall model performance. This feature was particularly advantageous given the nature of the data we worked with.
Overall, we selected and combined three learners (XGBoost, LightBGM, and CatBoost) from machine learning to form our stacking regression model. Therefore, the introduction of machine learning is based on three studies conducted, respectively, by Chen T and Guestrin C [
52]; Ke G, Meng Q, and Finley T [
53]; and Prokhorenkova L, Gusev G, and Vorobev A [
54].
XGBoost is a scalable tree boosting system, which first uses tree boosting in a nutshell to regularize the learning objective:
where
,
is the loss function,
is the predicted value,
is the target value,
and
are the regularization parameters,
is the number of trees,
represents the square of the output score on each tree’s leaf nodes (equivalent to L2 regularization), and
represents the index of the tree.
Then, the system adds ft to minimize the objective and uses second-order approximation to quickly optimize the objective in the general setting. The corresponding optimal is
In the final stage, it is necessary to scale the newly added weights and perform column sampling to prevent overfitting (similar to random forests). XGBoost also includes a split finding algorithm, where the basic greedy algorithm enumerates all possible splits, calculates the gain for each split, and then selects the split with the maximum gain. The approximate algorithm, on the other hand, proposes candidate split points by mapping continuous features into bins and then aggregating statistics to find the optimal solution. In summary, XGBoost introduces a new sparse-aware algorithm and weighted quantile sketch, where caching access patterns, data compression, and partitioning are key, thus enabling the solution of real-world scale problems with minimal resources.
LightGBM is an efficient Gradient Boosting Decision Tree (GBDT) algorithm proposed by Ke et al. at the NIPS conference in 2017. It addresses the efficiency and scalability issues associated with high-dimensional features and large datasets by introducing two innovative techniques: gradient-based one-side sampling (GOSS) and exclusive feature bundling (EFB). The GOSS technique excludes data instances with small gradients, using only the remaining instances to estimate the information gain, thereby significantly reducing the amount of data processed while maintaining the accuracy of information gain estimation. The EFB technique reduces the number of features by bundling mutually exclusive features that rarely take non-zero values simultaneously, such as one-hot encoded features in text mining. LightGBM safely bundles these exclusive features together, constructing the same feature histograms from feature bundles as from individual features through a carefully designed feature scanning algorithm, thus reducing the complexity of histogram construction from O(#data×#feature) to O(#data×#bundle), where #bundle is much smaller than #feature, significantly accelerating the training of GBDT. Experimental results show that LightGBM is over 20 times faster in training on multiple public datasets, while achieving nearly the same accuracy as traditional GBDT. These achievements not only demonstrate the superior performance of LightGBM in handling large-scale datasets but also provide new directions for the optimization of GBDT algorithms.
CatBoost introduced two algorithmic improvements: ordered boosting and an innovative algorithm for handling categorical features, corresponding to the Ordered mode and Plain mode (built-in ordered TS standard GBDT algorithm). For the Plain mode, multiple random permutations are first used to calculate gradients and TS, evaluate candidate splits, update the support model to construct decision trees, and then perform a complexity comparison and analysis with the standard GBDT algorithm, culminating in the greedy construction of high-order feature combinations. CatBoost identified and analyzed the problem of prediction shift, proposing ordered boosting and ordered TS as solutions, and demonstrated superior performance in multiple benchmark tests.
2.5. Predictive Methodology Overview
To investigate how freight rates can help predict Brent oil prices in different periods, we employed the following methodology across four distinct periods (Periods I–IV). In
Table 2, each of these periods corresponds to a significant global event that profoundly affected both freight rates and oil prices.
We used a segmented (or “dummy variable”) regression approach to identify these structural breaks in the overall time series. For each suspected break period, the following regression model was estimated:
where time_num is the continuous time variable, dummy is a binary indicator that equals 1 during the period under investigation (the suspected structural break period) and 0 otherwise, time_dummy is the interaction term (time_num × dummy),
(constant) is the baseline level of the BDTI_Index during non-break periods,
the general time trend (slope) during non-break periods,
(level effect) is the coefficient on the dummy variable, which captures any abrupt shift (jump) in the level of the BDTI_Index during the break period, and
(trend change) is the coefficient of the interaction term, indicating a change in the time trend (slope) during the break period. The overall trend during the break period becomes
.
We perform
t-tests on
and
. A statistically significant
(with
p < 0.05) indicates a significant level shift during the break period. A statistically significant
(with
p < 0.05) indicates that the time trend during the break period is significantly different from that of the non-break periods. If both coefficients are statistically significant, this provides strong evidence of a structural break—meaning that the time series exhibits a significant change in both its level and trend in the period under study.
Table 3 below summarizes the key statistics from the regression models for the four time periods. All coefficients are statistically significant (
p < 0.001), reinforcing the conclusion that each of these periods represents a structural break. By incorporating dummy variables and their interactions with time, our regression models reveal that each of the four time periods exhibits statistically significant changes in both the level and trend of the BDTI_Index. This dual change is strong evidence of structural breaks. The summary table provides the essential statistics to support this claim, making it clear to reviewers that the changes observed are not random fluctuations but rather systematic shifts in the time series.
For each of these periods, we employed the same predictive approach to understand the effect of multifractal features on forecasting oil prices. Specifically, freight rates (BDTI) were utilized alongside different feature sets to predict Brent oil prices, with the following principles:
Direct Prediction Using BDTI: As a baseline, we predicted Brent prices using only BDTI data.
Addition of Crisis Period Indicator: An indicator variable was introduced to capture the effect of significant events—for instance, the 2020 COVID-19 pandemic, particularly between December 2019 and June 2020. This indicator took the value of 1 during the crisis and 0 otherwise to help the model account for the dramatic market shifts.
Addition of Multifractal Features: Multifractal features extracted using multifractal detrended fluctuation analysis (MFDFA) were included to capture complex market behaviors. We computed the Hurst exponent for various q-values (ranging from −5 to 5) to quantify the complexity and self-similarity within the time series.
Combination of Crisis Indicators and Multifractal Features: Both crisis indicators and multifractal features were included to examine their combined effect on prediction accuracy.
To optimize the performance of the machine learning models, we conducted a systematic hyperparameter tuning process for each base learner. Hyperparameter tuning was performed using a grid search combined with K-fold cross-validation to identify the best combination of parameters that minimized overfitting and maximized model performance. For each model, we defined a search space for key parameters, such as n_estimators, learning_rate, max_depth, and regularization terms, and evaluated different combinations using cross-validation. This process helped ensure that the selected hyperparameters were optimal for achieving robust and accurate predictions.
To combine these features for predicting Brent oil prices, we employed a stacking regression model consisting of the following base learners:
XGBoost: Capable of handling high-dimensional feature spaces and mitigating overfitting, XGBoost was used with 300 estimators, a learning rate of 0.01, and a maximum depth of 3.
LightGBM: Known for its efficient handling of large datasets, LightGBM was configured similarly to XGBoost to provide complementary strengths in feature learning.
CatBoost: Particularly effective in dealing with categorical features and reducing pre-processing requirements, CatBoost was employed with 300 iterations and a learning rate of 0.01.
The predictions from these base learners were then integrated using a Ridge Regression model as the meta-learner. This stacking approach allows the model to capture a diverse range of data patterns and interactions, thereby improving the robustness of predictions.
To provide a measure of uncertainty in the predictions, we calculated 95% confidence intervals for the predicted Brent oil prices. These intervals were derived using bootstrap resampling, offering a range within which the true values are likely to fall with 95% certainty.
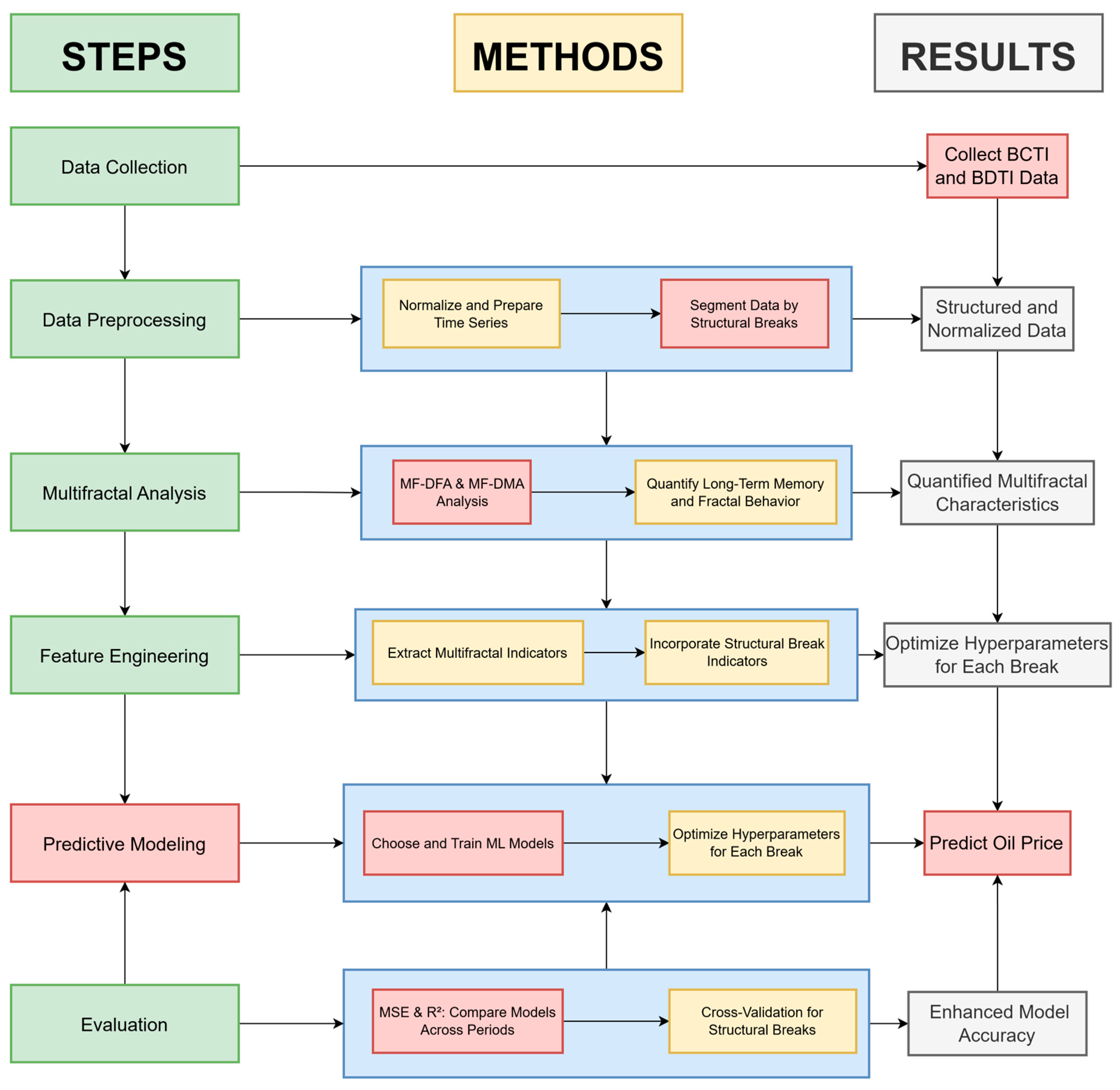
To provide a clear visual representation of the methodology, the following flowchart in
Figure 1 outlines the framework for multifractal analysis and predictive modeling, which uses the Baltic Dirty Tanker Index (BDTI) and its application to Brent crude oil price prediction.
5. Discussion of Results
From the discussion, one may conclude that this study successfully unravels the multifaceted complexity of the Baltic Tanker Freight market using multifractal analysis techniques and advanced machine learning models. By integrating the Baltic Dirty Tanker Index (BDTI) as a leading indicator, we demonstrate that freight rates can effectively predict Brent oil prices, particularly during heightened market volatility caused by global crises, such as the 2008 financial crisis, the 2014 Shale Oil Revolution, the COVID-19 pandemic, and the Russia–Ukraine conflict. The findings reveal that multifractal characteristics, such as the generalized Hurst exponent and multifractal spectrum, significantly enhance the predictive accuracy of the models, outperforming traditional approaches that rely solely on linear or unidirectional relationships [
7,
8,
9]. Moreover, the stacking regression framework combining XGBoost, LightGBM, CatBoost, and Ridge Regression validates the robustness of the proposed methodology, aligning closely with contemporary machine learning advancements [
26,
58,
60]. These results provide actionable insights for policymakers, energy companies, and investors, emphasizing the utility of multifractal analysis in managing systemic risks and navigating energy market volatility [
4,
5,
6].
5.1. Resolution and Discussion of Key Research Questions
The results indicate that the multifractal complexity of the tanker freight market intensified over time, particularly after 2010. The expansion of the multifractal spectrum width suggests a shift from crisis-driven volatility to a market increasingly shaped by regulatory changes, technological advancements, and macroeconomic dynamics. Beyond these general factors, our findings reveal that major external shocks—such as the 2008 global financial crisis, the 2014 Shale Oil Revolution, the COVID-19 pandemic, and the Russia–Ukraine conflict—each introduced distinct structural changes in market behavior, further reinforcing the role of multifractal analysis in capturing such transformations. The increasing multifractality implies that systemic risks have grown, as heightened market complexity makes price movements more sensitive to external shocks. These findings highlight the evolving nature of the freight market and underscore the necessity of adaptive risk management strategies to mitigate the effects of rising uncertainty.
Furthermore, temporal correlations and volatility play a significant role in shaping market dynamics. The MF-DFA and MF-DMA analyses show that long-range dependencies and nonlinear patterns are evident in the freight rate time series, influencing both short-term fluctuations and long-term trends. The Hurst exponent confirms that persistent correlations are present, suggesting that freight rate changes are not purely random but follow structured patterns across different time scales. Additionally, decomposing multifractal properties reveal that both nonlinear dependencies and heavy-tailed distributions contribute to market complexity. These results reinforce the importance of incorporating multifractal analysis alongside traditional econometric models to improve market forecasting and risk assessment.
The role of external shocks and structural shifts is also evident in the analysis. Significant global events, such as the 2008 financial crisis, the 2014 Shale Oil Revolution, the COVID-19 pandemic, and the Russia–Ukraine conflict, have introduced structural breaks and heightened multifractal behavior. For instance, the financial crisis caused abrupt market contractions, while the Shale Oil Revolution led to fundamental shifts in supply–demand balances. The COVID-19 pandemic resulted in extreme volatility due to unprecedented supply chain disruptions, and the Russia–Ukraine conflict further exacerbated oil price instability. These findings suggest that external shocks not only increase short-term volatility but also contribute to long-term changes in market complexity, highlighting the need for more adaptive analytical techniques.
The predictive utility of the Baltic Dirty Tanker Index (BDTI) in forecasting Brent oil prices is particularly evident during periods of heightened market uncertainty. While traditional models often assume that oil prices drive freight rates, the results suggest that freight rates, influenced by supply chain dynamics and macroeconomic conditions, can serve as leading indicators of oil price movements [
17,
18]. The inclusion of multifractal characteristics, such as the Hurst exponent and multifractal spectrum, significantly improves forecast accuracy, especially during market turbulence. This highlights the advantages of integrating multifractal features into predictive models to better capture the nonlinearity and evolving structure of global energy markets.
5.2. Guiding Energy Market Decisions Through Predictive Insights
The findings of this study provide actionable insights for investors, energy companies, and policymakers, particularly in managing risks and making strategic decisions during periods of economic and geopolitical instability. Investors can use the predictive framework to anticipate oil price fluctuations, adjust portfolios, and optimize trading strategies. For example, during market disruptions, such as the 2008 financial crisis or the 2022 Russia–Ukraine conflict, early signals from freight rate trends could help investors mitigate exposure to volatile price swings. Energy companies can integrate these insights into hedging strategies, contract negotiations, and operational planning. By leveraging freight rate-based predictions, firms can proactively adjust chartering and fuel procurement strategies to minimize cost fluctuations and supply chain risks.
Policymakers can utilize these findings to enhance market stability by incorporating freight rate indicators into early warning systems. Predictive insights can help regulators anticipate disruptions in the energy supply chain and implement timely interventions, such as adjusting strategic petroleum reserves or introducing temporary regulatory measures. By demonstrating the predictive value of freight indices and the power of multifractal analysis, this study offers a practical framework for industry stakeholders to navigate the complexities of the global energy market with greater confidence and strategic foresight.
5.3. Additional Considerations and Future Directions
While the proposed framework demonstrates strong predictive capability, an important question remains: To what extent can the model generalize beyond the Baltic Dirty Tanker Index (BDTI)? The BDTI serves as a key indicator within the tanker freight market, yet future research should assess whether similar multifractal properties extend to other freight indices, such as the Baltic Clean Tanker Index (BCTI) or liquefied natural gas (LNG) freight rates. If these indices exhibit similar complexity patterns, it would reinforce the broader applicability of the methodology across various maritime and energy markets. Additionally, expanding the dataset to include diverse market indicators, such as global trade volumes, bunker fuel prices, and macroeconomic indicators, may further enhance predictive robustness and applicability.
Furthermore, while our model effectively captures major macroeconomic and geopolitical disruptions, regulatory and policy changes represent an additional dimension of uncertainty that warrants further exploration. The implementation of environmental regulations, such as the IMO 2020 sulfur cap, has introduced significant cost adjustments in the shipping industry, altering freight rate structures. Similarly, carbon pricing policies and regional emission trading schemes could further influence market behavior. Future research could incorporate such policy-driven variables into predictive modeling frameworks, enabling more comprehensive assessments of regulatory impacts on energy and freight markets.
In addition, an important consideration in financial and energy market forecasting is how to further enhance the predictive power of multifractal analysis. While this study successfully integrates machine learning models, deeper insights may be gained by leveraging advanced deep learning techniques that can dynamically adapt to the multifractal characteristics of the tanker freight market. Long short-term memory (LSTM) networks and transformer-based architectures, which have shown exceptional ability in capturing long-range dependencies, could be tailored to incorporate multifractal features such as the generalized Hurst exponent and multifractal spectrum. By embedding these features within attention mechanisms or hierarchical temporal modeling, deep learning methods could potentially refine the detection of structural shifts and volatility patterns in freight markets. Future studies could explore hybrid approaches that integrate deep learning techniques with multifractal feature engineering, allowing for a more adaptive and robust forecasting framework that better captures the evolving complexity of global energy markets.
While our predictive framework demonstrates strong forecasting accuracy, several challenges may arise in real-world trading applications. First, the model’s reliance on historical freight rate data means that sudden, unprecedented market disruptions—such as geopolitical crises or extreme weather events—may introduce unaccounted volatility, requiring adaptive recalibration. Second, integrating multifractal features into trading algorithms demands computational efficiency, as real-time market conditions require fast decision-making. Third, liquidity constraints in the tanker freight and oil futures markets may affect the practical execution of trading strategies based on model predictions, particularly during periods of high volatility. Addressing these challenges through adaptive learning techniques, real-time data integration, and further testing under different market conditions would enhance the robustness and practical applicability of the proposed approach.
Despite these contributions, it is important to acknowledge the inherent limitations of our approach. While the predictive models exhibit high accuracy, they remain reliant on historical data patterns, which may not always generalize to unprecedented market conditions. The emergence of unforeseen economic or geopolitical shocks could introduce structural changes that require continuous model adaptation. Future research should explore adaptive forecasting techniques that integrate real-time data streams, such as satellite-based vessel tracking or high-frequency trading data, to enhance responsiveness to rapid market shifts.
In conclusion, this study demonstrates the significant potential of multifractal analysis and machine learning in accurately forecasting energy prices during periods of high volatility. The findings not only advance the theoretical understanding of tanker freight markets, but also provide practical tools for stakeholders to manage uncertainty and enhance decision-making. By successfully integrating multifractal features and advanced predictive models, this study offers a robust framework that can serve as a foundation for future research. Moving forward, further refinements and broader applications of the proposed methodology may uncover additional insights into the intricate relationships shaping global energy markets, paving the way for more resilient and adaptive forecasting strategies.
6. Conclusions
This study employs MF-DMA to analyze the Baltic tanker freight market. The findings reveal a strong multifractal structure, with total multifractality reaching 0.90 in the clean tanker market, driven by a fat-tailed probability distribution (0.48) and nonlinear correlations (0.29). Analysis of the TC2 route (37,000 ton) confirms its multifractal nature, though reduced after shuffling and surrogating, highlighting the role of temporal structure. The clean tanker market reflects a tight supply–demand balance, with freight rates responding sharply to external factors.
For dirty tankers, the study identifies moderate complexity, with multifractality at 0.58, decreasing under surrogate and shuffled conditions. In the TD7 route (80,000 ton), multifractality peaks at 1.03 but declines when temporal and structural correlations are removed, confirming the impact of chronological sequencing.
The comparison of multifractal dynamics between 1998–2010 and 2010–2024 reveals notable differences in market behavior, reflecting the influence of technological, regulatory, and environmental factors.
Based on these findings, this study establishes a predictive framework integrating BDTI, multifractal features, and crisis indicators to forecast Brent oil prices. Analysis of four major global events—the 2008 financial crisis, the 2014 Shale Oil Revolution, COVID-19, and the Russia–Ukraine conflict—demonstrates how external factors shape market dynamics. Using stacking regression (XGBoost, LightGBM, CatBoost, and Ridge Regression) enhances predictive accuracy, reinforcing the role of freight rates as leading indicators in energy markets.
This study provides strong empirical evidence that tanker freight rates, particularly the Baltic Dirty Tanker Index (BDTI), can serve as leading indicators for Brent oil prices. While conventional economic models often assume that oil prices drive freight rates, our results indicate that freight rates, shaped by supply chain dynamics and macroeconomic shifts, contain valuable predictive signals for oil prices. By leveraging the multifractal properties of freight indices, the proposed model significantly improves prediction accuracy, particularly during periods of heightened market uncertainty. The findings highlight the potential of incorporating maritime freight market signals into broader energy market forecasting models.
Multifractal analysis enhances machine learning-based forecasting methods by providing a more refined understanding of market dynamics, particularly in capturing nonlinear patterns and structural shifts. By incorporating multifractal features such as the Hurst exponent and multifractal spectrum, the predictive framework improves the ability to recognize variations in market complexity over different time periods. This approach complements traditional forecasting models by offering deeper insights into the evolving nature of financial time series, especially in the tanker freight and oil markets. The results indicate that integrating multifractal characteristics helps refine model predictions, improving stability and reducing errors, particularly during periods of heightened volatility and structural transitions.
In conclusion, this study combines multifractal analysis and predictive modeling to provide a comprehensive framework for understanding and navigating the complexities of the Baltic tanker freight market. By revealing the evolving multifractal dynamics and demonstrating the predictive power of freight rates, the research underscores the importance of integrating multifractal characteristics into forecasting models. The findings offer practical implications for strategic decision-making, operational resilience, and risk management in the shipping and energy industries. Subsequent research endeavors should expand upon this foundational framework by integrating additional datasets, optimizing predictive algorithms, and investigating the interactions between multifractal properties and other market indicators to further enhance prediction accuracy and application scope.