G-Metric Spaces via Fixed Point Techniques for Ψ-Contraction with Applications

Abstract

The primary aim of this manuscript is to establish unique fixed point results for a class of $\Psi$-contraction operators in complete G-metric spaces. By combining and extending various fixed point theorems in the context of $\Psi$-contraction operators, we introduce a novel function, denoted as $\psi$, and explore its properties. Our work presents new theoretical results, supported by examples and applications, that enrich the study of G-metric spaces. These results not only generalize and unify a broad range of existing findings in the literature but also expand their use to boundary value problems, Fredholm-type integral equations, and nonlinear Caputo fractional differential equations. In doing so, we offer a more comprehensive understanding of fixed point theory in the G-metric space framework and broaden its scope in applied mathematics. We also offer a numerical spectral approach for solving fractional initial value problems, utilizing shifted Chebyshev polynomials to construct a semi-analytic solution that inherently satisfies the given homogeneous initial conditions.

1. Mathematical Introduction

Let $\mathfrak{F}$ be a self-operator on a set $\mathfrak{X}$. A fixed point ($\mathbb{FP}$) in $\mathfrak{X}$ is defined as an element q such that $\mathfrak{F}q=q$, where $\mathfrak{F}$ is an operator on $\mathfrak{X}$. The $\mathbb{FP}$ Theorem argues that under specific conditions (on the operator $\mathfrak{F}$ and the space $\mathfrak{X}$), an operator $\mathfrak{F}$ of $\mathfrak{X}$ into itself admits one or more $\mathbb{FP}$. There are many results on different cases of the $\mathbb{FP}$ Theorem. The basic foundations upon which $\mathbb{FP}$ theory studies are built include the Banach contraction principle ($\mathbb{BCP}$) [1], Brouwer’s $\mathbb{FP}$ theorem [2], Schauder’s $\mathbb{FP}$ theorem [3], and the contraction operators theorem.

The $\mathbb{FP}$ theorem, commonly recognized as the Banach contraction principle, first appeared in definitive form in Banach’s thesis in 1922 [1], where it was used to establish the existence of a solution to an integral equation ($\mathbb{IE}$). Since then, its simplicity and usefulness have made it become a widely used tool for solving problems in many mathematical analysis branches. This principle remarks that if $(\mathfrak{X},\delta )$ is a complete metric space and $\mathfrak{F}:\mathfrak{X}\to \mathfrak{X}$ is a contraction operator (i.e., $\delta (\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \lambda \delta (\varpi ,\varrho )$ for all $\varpi ,w\in \mathfrak{X}$, where $\lambda \in (0,1)$ is a constant), then $\mathfrak{F}$ has a $\mathbb{FP}$.

The $\mathbb{BCP}$ has been generalized in various ways over the years. Some generalizations, such as those in [4,5] and others, relax the contractive conditions of the operator, while others, including [6,7] and others, weaken the topological assumptions. In [8], Nadler extended the Banach $\mathbb{FP}$ theorem from single-valued operators to set-valued contractive operators. Additional $\mathbb{FP}$ results for set-valued operators can be found in [9] and the references therein.

Mustafa [10] introduced an extension of metric spaces known as generalized metric spaces (or G-metric spaces) and established $\mathbb{FP}$ results for Banach-type contraction operators within this framework. This concept was further explored by Mustafa and Sims [11]. Subsequently, Mustafa et al. [12] established $\mathbb{FP}$ results for Lipschitzian-type operators in G-metric spaces, which garnered significant interest from researchers in $\mathbb{FP}$ theory. However, Jleli and Samet [13] and Samet et al. [14] later pointed out that many $\mathbb{FP}$ results in G-metric spaces are essentially direct consequences of corresponding results in metric spaces. Specifically, Jleli and Samet [13] observed that if a G-metric can be reduced to a quasi-metric, the associated $\mathbb{FP}$ results align with known results in quasi-metric spaces. Numerous $\mathbb{FP}$ results in such spaces have subsequently appeared (see, for example, [15,16]).

Integral equations ($\mathbb{IE}s$) appear in a wide range of applications [17]. Depending on the field, one may encounter Fredholm integro-differential equations ($\mathbb{FIDE}s$) [18], Volterra integral equations ($\mathbb{VIE}s$) [19], or Fredholm integral equations ($\mathbb{FIE}s$) [20]. The latter can be further divided into linear and nonlinear $\mathbb{FIE}s$ of the first or second kind. Although they have become a recent research focus, linear $\mathbb{FIE}s$ of the first kind are less commonly known due to their frequent ill-posedness. They are typically studied only within a finite interval [21].

Furthermore, most $\mathbb{IE}s$ that are closely related to differential equations are $\mathbb{FIE}s$ [22]. These equations are typically derived from boundary value problems ($\mathbb{BVP}s$) for differential equations and are often solved using various simplified methods. Fredholm’s work on these equations was driven by a strong motivation to explore and understand this class of equations. Consequently, they were named $\mathbb{FIE}s$ in his honor. This discovery marked a significant step forward in overcoming key challenges that had hindered the progress of mathematics [23]. It is also worth noting that $\mathbb{FIE}s$ can appear in both linear and nonlinear forms, including homogeneous and non-homogeneous types [24].

Fractional calculus has almost three centuries of history. L’Hospital is credited with introducing the idea of the fractional derivative when he posed the query regarding the derivative of order $1/2$. Because fractional derivatives have so many uses in biology, economics, science, and engineering, academics have recently focused more on them [25,26,27].

There are now definitions of fractional derivatives that are both local and nonlocal. The history of the function is crucial for many of these applications, hence nonlocal derivatives are more interesting. Singular kernels are used to define some fractional derivatives, including the Riemann–Liouville, Grünwald, and Caputo definitions [28], as well as numerous others found in the literature [29,30]. Caputo–Fabrizio and Atangana–Baleanu fractional derivatives are two examples of more recent formulations of fractional derivatives that are based on nonsingular kernels [31,32].

Because some models of dissipative processes cannot be sufficiently characterized by standard fractional derivatives, fractional derivatives with nonsingular kernels are important. The Hadamard fractional integral and derivative is one of the additional definitions of fractional integrals and derivatives that are available. The Riemann–Liouville or Caputo integral and the Hadamard integral differ primarily in the type of kernel that is employed. Hadamard [33] introduced the Hadamard integral, which incorporates a logarithmic function, whereas the Riemann–Liouville integral utilizes a power function.

Thus, mathematical models based on the Caputo fractional derivative ($\mathbb{CFD}$) extend those relying on classical derivatives, offering improved descriptions of certain real-world phenomena. Specifically, $\mathbb{BVP}s$ for systems of differential equations with $\mathbb{CFD}$ can model the behavior of a damping system in mechanics [34], pollution levels in lakes connected by rivers [35], the spread of COVID-19 [36], global population growth, and tape counter readings at a specific time [37], among others.

The study of G-metric space is considered an extension and generalization of the classical concept of metric space. G-metric space has been presented for analyzing distance and convergence in many mathematical structures. Metric space measures the distance between two points but G-metric space measures the distance between three points that provides us a wide framework for reading and studying geometry of spaces. Also, G-metric space focuses on the notions of compactness, sequence convergence, and completeness. The main motivations for studying G-metric space are its applications in many branches of analysis and applied mathematics such as topology, functional analysis, fixed point theory, differential equations, $\mathbb{FDE}s$, and $\mathbb{IE}s$.

We present a fixed point solution for $\Psi$-contraction operators in complete G-metric spaces. By generalizing and extending existing fixed point theorems, we establish a new function, denoted as $\psi$, and investigate its unique features. Our findings not only consolidate and build on prior discoveries, but also offer novel applications to boundary value problems, Fredholm-type integral equations, and nonlinear Caputo fractional differential equations. Furthermore, we describe a numerical spectral method to fractional initial value problems that employ shifted Chebyshev polynomials, providing an efficient semi-analytic solution that is inherently homogeneous under initial conditions.

Now, we can summarize the content of this manuscript as follows:

Section 1 introduces the definitions and basic concepts that lay the foundation for understanding general metric spaces. Section 2 presents several theorems that generalize the theorems given in [10,38], which prove the existence and uniqueness of $\mathbb{FP}$s. Section 3 explores the unique solutions of $\mathbb{BVP}s$. Section 4 considers applications for boundary value problems. Section 5 focuses on methods for finding solutions to the $\mathbb{FIE}s$ in G-metric spaces, and Section 6 discusses the existence and uniqueness of solutions for $\mathbb{FDE}s$ in G-metric spaces. Finally, in Section 7, we present a numerical solution for fractional initial value problems using the spectral Chebyshev method, proposing a basis that inherently satisfies the homogeneous initial conditions.

2. Basic Facts

This section introduces the fundamental concepts necessary to achieve our objectives. We present the key definitions and results related to G-metric spaces, which will form the basis for the subsequent sections of the paper.

Definition 1

([11]). Suppose that $\mathfrak{X}$ is a nonempty set. Let $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}\to {\mathbb{R}}_{+}$ be a function satisfying the following conditions:

(1) 

$G(\varpi ,\varrho ,\kappa )=0$ if and only if $\varpi =\varrho =\kappa$;

(2) 

$G(\varpi ,\varpi ,\varrho )\le G(\varpi ,\varrho ,\kappa )$ for all $\varpi ,\varrho ,\kappa \in \mathfrak{X}$ with $\varrho \ne \kappa$;

(3) 

$G(\varpi ,\varrho ,\kappa )=G(\varpi ,\kappa ,\varrho )=G(\varrho ,\kappa ,\varpi )=\cdots$ (symmetry in all three variables);

(4) 

$G(\varpi ,\varrho ,\kappa )\le G(\varpi ,a,a)+G(a,\varrho ,\kappa )$, for all $\varpi ,\varrho ,\kappa ,a\in \mathfrak{X}$.

Then G is called a G-metric on $\mathfrak{X}$ and $(\mathfrak{X},G)$ is called a G-metric space.

Geometric understanding of $G(\varpi ,\varrho ,\kappa )$: (See Figure 1) Instead of requesting information on the distance between two points as in a conventional metric space, a G-metric requests information on the ’triangle like interaction’ among three points at once. You can think of this as a measure of how ‘spread out’ three points are in the space.

•

If $G(\varpi ,\varrho ,\kappa )$ is small, then $\varpi ,\varrho$, and $\kappa$ are close.

•

If $G(\varpi ,\varrho ,\kappa )$ is large, then at least one of the points is far from the others.

•

The function $G(\varpi ,\varpi ,\varrho )$ can be seen as a replacement for the usual metric $d(\varpi ,\varrho )$, but the value depends on an additional reference point.

Envisioning G-Metric Geometry

•

Triangle Representation: $G(\varpi ,\varrho ,\kappa )$ can be viewed as a measurement that establishes the “spread” of a triangle in space since it depends on three points at a time.

•

Deformation of Distances: Because G-metric spaces depend on a third point, they provide flexibility in measuring distances, unlike Euclidean spaces, where the distances between two points are fixed.

•

Curvature-Like Behavior: According to some interpretations, the G-metrics can capture curvature-like phenomena, in which the placement of extra points affects distances.

Figure 1. Geometric meaning of G-metric space.

Figure 1. Geometric meaning of G-metric space.

Example 1.

Let $\mathfrak{X}=[0,+\infty )$ and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$ such that $G(\varpi ,\kappa ,\varrho )=sup\{\varpi ,\kappa ,\varrho \}$ for all $\varpi ,\kappa ,\varrho \in \mathfrak{X}$. Then, $(\mathfrak{X},G)$ is a G-metric space.

Example 2.

Let $\mathfrak{X}=[0,+\infty )$ and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$ such that $G(\varpi ,\kappa ,\varrho )=sup\left\{d\right(\varpi ,\kappa ),d(\kappa ,\varrho ),d(\varrho ,\varpi \left)\right\}$ for all $\varpi ,\kappa ,\varrho \in \mathfrak{X}$, where d is a standard metric on $\mathfrak{X}$. Then, $(\mathfrak{X},G)$ is a G-metric space.

Definition 2

([11]). A G-metric space $(\mathfrak{X},G)$ is said to be symmetric if $G(\varpi ,\varrho ,\varrho )=G(\varrho ,\varpi ,\varpi )$ for all $\varpi ,\varrho \in \mathfrak{X}$.

The simplest example of a nonsymmetric G-metric, which also happens to be one that does not originate from any metric in the methods mentioned above, is shown in the example that follows.

Example 3

([11]). Suppose that $\mathfrak{X}=\{\varpi ,\varrho \}$. Assume $G(\varpi ,\varpi ,\varpi )=G(\varrho ,\varrho ,\varrho )=0$, $G(\varpi ,\varpi ,\varrho )=1,$ and $G(\varpi ,\varrho ,\varrho )=2$ and extend G to all of $\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}$ using the symmetry in the variables. Then, it is easily verified that G is G-metric, but $G(\varpi ,\varrho ,\varrho )\ne G(\varpi ,\varpi ,\varrho )$.

Example 4

([39]). Assume that $\mathfrak{X}=[a,b]\subset \mathbb{R}$, where $1<a<b$, and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}\to {\mathbb{R}}_{+}$ is given by the following:

$$G(\varpi ,\varrho ,\kappa )=sup\{\mid \varpi -\varrho \mid ,\mid \varrho -\kappa \mid ,\mid \kappa -\varpi \mid \}.$$

Then, $(\mathfrak{X},G)$ is G-metric space.

Proposition 1

([11]). Suppose that $(\mathfrak{X},G)$ is a G-metric space; then, for any $\varpi ,\varrho ,\kappa ,a\in \mathfrak{X}$ it follows that

(1) 

if $G(\varpi ,\varrho ,\kappa )=0$, then $\varpi =\varrho =\kappa$,

(2) 

$G(\varpi ,\varrho ,\kappa )\le G(\varpi ,\varpi ,\varrho )+G(\varpi ,\varpi ,\kappa )$,

(3) 

$G(\varpi ,\varrho ,\kappa )\le G(\varpi ,a,\kappa )+G(a,\varrho ,\kappa )$.

Definition 3

([11]). Suppose that $(\mathfrak{X},G)$ is a G-metric space, and let $\left\{{\varpi }_n\right\}$ be a sequence of points of $\mathfrak{X}$. We say that $\left\{{\varpi }_n\right\}$ is

(1) 

a G-Cauchy sequence if, for any $\epsilon >0$, there is $N\in \mathbb{N}$ such that for all $n,m,l\ge N$, $G({\varpi }_n,{\varpi }_m,{\varpi }_l)<\epsilon$;

(2) 

a G-convergent sequence to $\varpi \in \mathfrak{X}$ if, for any $\epsilon >0$, there is $N\in \mathbb{N}$ such that for all $n,m\ge N$, $G(\varpi ,{\varpi }_n,{\varpi }_m)<\epsilon$.

Definition 4

([11]). Suppose that $(\mathfrak{X},G)$ and $({\mathfrak{X}}^{*},G^{*})$ are G-metric spaces. Then, a function $f:\mathfrak{X}⟶{\mathfrak{X}}^{*}$ is G-continuous at a point $\varpi \in \mathfrak{X}$ if and only if it is G-sequentially continuous at ϖ; that is, whenever a sequence $\left\{{\varpi }_n\right\}$ is G-convergent to ϖ, we have that $\left\{f\left({\varpi }_n\right)\right\}$ is G-convergent to $f\left(\varpi \right)$.

Definition 5

([11]). A G-metric space $(\mathfrak{X},G)$ is said to be G-complete if every G-Cauchy sequence in $\mathfrak{X}$ is G-convergent in $\mathfrak{X}$.

Proposition 2

([11]). Let $(\mathfrak{X},G)$ be a G-metric space. Define on $\mathfrak{X}$ the metric ${\delta }_G$ with ${\delta }_G(\varpi ,\varrho )=G(\varpi ,\varrho ,\varrho )+G(\varrho ,\varpi ,\varpi ),$ for all $\varpi ,\varrho \in \mathfrak{X}$. Then, for a sequence $\left\{{\varpi }_n\right\}\subset \mathfrak{X}$, the following are equivalent:

(1) 

$\left\{{\varpi }_n\right\}$ is G-convergent to ϖ;

(2) 

$G({\varpi }_n,{\varpi }_n,\varpi )\to 0$ as $n\to +\infty$;

(3) 

${\delta }_G({\varpi }_n,\varpi )=0$;

(4) 

$G({\varpi }_n,\varpi ,\varpi )\to 0$ as $n\to +\infty$;

(5) 

$G({\varpi }_n,{\varpi }_m,\varpi )\to 0$ as $n,m\to +\infty$.

Proposition 3

([11]). Let $(\mathfrak{X},G)$ be a G-metric space. Then, the following are equivalent:

(1) 

the sequence $\left\{{\varpi }_n\right\}$ is G-Cauchy;

(2) 

$G({\varpi }_n,{\varpi }_m,{\varpi }_m)\to 0$ as $n,m\to +\infty$.

Proposition 4

([11]). A G-metric space $(\mathfrak{X},G)$ is G-complete if and only if $(\mathfrak{X},{\delta }_G)$ is complete metric space.

Definition 6.

Assume that Ψ is the family of all functions $\psi :[0,+\infty )\to [0,+\infty )$ fulfilling the conditions below:

(1) 

$\psi \left(0\right)=0$;

(2) 

${lim}_{n\to +\infty }{\psi }^n\left(\varpi \right)=0$ for $\varpi >0$, where ${\psi }^n$ stands for the n-th iterate of ψ;

(3) 

$\psi (\varpi +\varrho )\le \psi \left(\varpi \right)+\psi \left(\varrho \right)$;

(4) 

$\psi \left(\varpi \varrho \right)\le \psi \left(\varpi \right)\psi \left(\varrho \right)$.

The following example supports Definition 6:

Example 5.

Let $\psi :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ be defined by $\psi \left(\varpi \right)=\varpi exp(-\varpi )$, which satisfies the four conditions in the family Ψ. Let us check each condition one by one.

(1) 

If $\varpi =0$, then we have $\psi \left(0\right)=0·exp\left(0\right)=0.$ Thus, $\psi \left(0\right)=0$, so condition (1) is satisfied.

(2) 

$\underset{n\to +\infty }{lim}{\psi }^n\left(\varpi \right)=\underset{n\to +\infty }{lim}{\displaystyle \frac{{\varpi }^n}{exp\left(n\varpi \right)}}=0$. Thus, condition (2) is satisfied.

(3) 

For every $\varpi ,\varrho \in {\mathbb{R}}_{+}$ and $n\in \mathbb{N}$, we have

$$\begin{array}{ccc}\hfill \psi (\varpi +\varrho )& =& (\varpi +\varrho )exp(-(\varpi +\varrho \left)\right)\hfill \\ & =& \varpi exp(-(\varpi +\varrho \left)\right)+\varrho exp(-(\varpi +\varrho \left)\right)\hfill \\ & \le & \varpi exp(-\varpi )+\varrho exp(-\varrho )\hfill \\ & =& \psi \left(\varpi \right)+\psi \left(\varrho \right).\hfill \end{array}$$

Thus, condition (3) is satisfied.

(4) 

For every $\varpi ,\varrho \in {\mathbb{R}}_{+}$, we have

$$\begin{array}{ccc}\hfill \psi \left(\varpi \varrho \right)=\left(\varpi \varrho \right)exp(-(\varpi \varrho \left)\right)& =& \left(\varpi exp(-(\varpi \varrho \left)\right)\right)\left(\varrho exp(-(\varpi \varrho \left)\right)\right)exp\left(\varpi \varrho \right)\hfill \\ & \le & \left(\varpi exp(-\varpi )\right)\left(\varrho exp(-\varrho )\right)\hfill \\ & =& \psi \left(\varpi \right)\psi \left(\varrho \right).\hfill \end{array}$$

Thus, condition (4) is satisfied.

Lemma 1.

Let $\psi <\mathfrak{I},$ where $\mathfrak{I}$ is the identity, then $(\mathfrak{I}-\psi )$ has an inverse where

$${(\mathfrak{I}-\psi )}^{-1}=\sum _{n=0}^{+\infty }{\psi }^n.$$

Proof. 

Suppose that the function $\psi :[0,+\infty )\to [0,+\infty )$ satisfies $\psi <\mathfrak{I}$. We want to show that

$${\left(\mathfrak{I}-\psi \right)}^{-1}=\sum _{n=0}^{+\infty }{\psi }^n.$$

The partial sum $S_M$ is as follows:

$$S_M=\sum _{n=0}^M{\psi }^n.$$

Using $S_M$, we determine the product

$$\left(\mathfrak{I}-\psi \right)S_M=\left(\mathfrak{I}-\psi \right)\left(\sum _{n=0}^M{\psi }^n\right)=\sum _{n=0}^M{\psi }^n-\sum _{n=0}^M{\psi }^{n+1}.$$

Note that

$$\sum _{n=0}^M{\psi }^n-\sum _{n=0}^M{\psi }^{n+1}={\psi }^0-{\psi }^{M+1}=\mathfrak{I}-{\psi }^{M+1}.$$

Condition (2) in Definition 6 states that for each $\varpi >0$, we have

$$\underset{M\to +\infty }{lim}{\psi }^{M+1}\left(\varpi \right)=0.$$

Consequently, if we take $M\to +\infty$, we obtain

$$\left(\mathfrak{I}-\psi \right)\left(\sum _{n=0}^{+\infty }{\psi }^n\right)=\mathfrak{I}.$$

Hence, ${\sum }_{n=0}^{+\infty }{\psi }^n$ operates as a right-inverse of $\mathfrak{I}-\psi$ and converges (in the pointwise sense on $[0,+\infty )$). Similarly, one can confirm that

$$\left(\sum _{n=0}^{+\infty }{\psi }^n\right)(\mathfrak{I}-\psi )=\mathfrak{I},$$

Thus, $\mathfrak{I}-\psi$ is the two-sided inverse of the series. Therefore, $(\mathfrak{I}-\psi )$ is invertible and

$${\left(\mathfrak{I}-\psi \right)}^{-1}=\sum _{n=0}^{+\infty }{\psi }^n.$$

□

Lemma 2.

For the following $\mathbb{BVP}$

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2\varpi }{d{t}^2}}=\lambda (t,\varpi \left(t\right)),t\in [0,1],\varpi \in {\mathbb{R}}_{+},\hfill \\ \\ \varpi \left(0\right)=\varpi \left(1\right)=0,\hfill \end{array}\right.$$

(1)

the solution can be expressed as follows:

$$\varpi \left(t\right)=-\underset{0}{\overset{1}{\int }}\Omega (t,s)\lambda (s,\varpi \left(s\right))ds,$$

where $\lambda :[0,1]\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ is a continuous function and $\Omega (t,s)$ is a Green function defined by

$$\Omega (t,s)=\left\{\begin{array}{cc}t(1-s),\hfill & \mathrm{if}0\le t\le s\le 1,\hfill \\ s(1-t),\hfill & \mathrm{if}0\le s\le t\le 1.\hfill \end{array}\right.$$

Proof. 

Integrating Equation (1) with respect to t from 0 to t two times yields

$${\varpi }^{\prime }\left(r\right)-{\varpi }^{\prime }\left(0\right)=\underset{0}{\overset{r}{\int }}{\varpi }^{″}\left(s\right)ds=\underset{0}{\overset{r}{\int }}\lambda (s,\varpi \left(s\right))ds,$$

and

$$\begin{array}{c}\hfill \underset{0}{\overset{t}{\int }}\left[{\varpi }^{\prime }\left(r\right)-{\varpi }^{\prime }\left(0\right)\right]dr=\underset{0}{\overset{t}{\int }}{\varpi }^{\prime }\left(r\right)dr-\underset{0}{\overset{t}{\int }}{\varpi }^{\prime }\left(0\right)dr=\varpi \left(t\right)-\varpi \left(0\right)-t{\varpi }^{\prime }\left(0\right),\end{array}$$

Then,

$$\begin{array}{ccc}\hfill \varpi \left(t\right)& =& \varpi \left(0\right)+t{\varpi }^{\prime }\left(0\right)+\underset{0}{\overset{t}{\int }}\underset{0}{\overset{r}{\int }}\lambda (s,\varpi \left(s\right))dsdr\hfill \\ & =& 0+t{\varpi }^{\prime }\left(0\right)+\underset{0}{\overset{t}{\int }}\lambda (s,\varpi \left(s\right))\left(\underset{s}{\overset{t}{\int }}dr\right)ds\hfill \\ & =& t{\varpi }^{\prime }\left(0\right)+\underset{0}{\overset{t}{\int }}\lambda (s,\varpi \left(s\right))(t-s)ds\hfill \\ & =& t{\varpi }^{\prime }\left(0\right)+\underset{0}{\overset{t}{\int }}(t-s)\lambda (s,\varpi \left(s\right))ds.\hfill \end{array}$$

(2)

To determine ${\varpi }^{\prime }\left(0\right)$, we use the condition at $t=1$, $\varpi \left(1\right)=0$,

$$\varpi \left(1\right)=0={\varpi }^{\prime }\left(0\right)+\underset{0}{\overset{1}{\int }}(1-s)\lambda (s,\varpi \left(s\right))ds.$$

Therefore,

$${\varpi }^{\prime }\left(0\right)=-\underset{0}{\overset{1}{\int }}(1-s)\lambda (s,\varpi \left(s\right))ds.$$

Thus, Equation (2) can be written as

$$\begin{array}{ccc}\hfill \varpi \left(t\right)& =& -t\underset{0}{\overset{1}{\int }}(1-s)\lambda (s,\varpi \left(s\right))ds+\underset{0}{\overset{t}{\int }}(t-s)\lambda (s,\varpi \left(s\right))ds\hfill \\ & =& \underset{0}{\overset{t}{\int }}\left[(t-s)-t(1-s)\right]\lambda (s,\varpi \left(s\right))ds-\underset{t}{\overset{1}{\int }}t(1-s)\lambda (s,\varpi \left(s\right))ds\hfill \\ & =& \underset{0}{\overset{t}{\int }}\left[t-s-t+ts)\right]\lambda (s,\varpi \left(s\right))ds-\underset{t}{\overset{1}{\int }}t(1-s)\lambda (s,\varpi \left(s\right))ds\hfill \\ & =& \underset{0}{\overset{t}{\int }}-\left[-ts+s)\right]\lambda (s,\varpi \left(s\right))ds-\underset{t}{\overset{1}{\int }}t(1-s)\lambda (s,\varpi \left(s\right))ds\hfill \\ & =& -\underset{0}{\overset{t}{\int }}s\left(1-t\right)\lambda (s,\varpi \left(s\right))ds-\underset{t}{\overset{1}{\int }}t(1-s)\lambda (s,\varpi \left(s\right))ds\hfill \\ & =& -\underset{0}{\overset{1}{\int }}\Omega (t,s)\lambda (s,\varpi \left(s\right))ds,\hfill \end{array}$$

in which the kernel is given by

$$\Omega (t,s)=\left\{\begin{array}{cc}t(1-s),\hfill & \mathrm{if}0\le t\le s\le 1,\hfill \\ s(1-t),\hfill & \mathrm{if}0\le s\le t\le 1.\hfill \end{array}\right.$$

□

Definition 7

([30]). Let $[a,b]$ ($-\infty <a<b<+\infty$) be a finite interval on the real axis $\mathbb{R}$. The Riemann–Liouville fractional integrals $I_{a^{+}}^{\alpha }f$ and $I_{b^{-}}^{\alpha }$ of order $\alpha \in \mathbb{C}$ ($\mathfrak{R}\left(\alpha \right)>0$) are defined by

$$\begin{array}{c}\hfill \left(I_{a^{+}}^{\alpha }f\right)\left(s\right):={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{a}{\overset{s}{\int }}{\displaystyle \frac{f\left(t\right)dt}{{(s-t)}^{1-\alpha }}}\left(s>a;\mathfrak{R}\left(\alpha \right)>0\right),\end{array}$$

(3)

and

$$\begin{array}{c}\hfill \left(I_{b^{-}}^{\alpha }f\right)\left(s\right):={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}\underset{s}{\overset{b}{\int }}{\displaystyle \frac{f\left(t\right)dt}{{(t-s)}^{1-\alpha }}}\left(s<b;\mathfrak{R}\left(\alpha \right)>0\right),\end{array}$$

(4)

respectively. Here, $\Gamma \left(\alpha \right)$ is the Gamma function. These integrals are called the left-sided and the right-sided fractional integrals. When $\alpha =n\in \mathbb{N}$, the definitions (3) and (4) coincide with the nth integrals of the form

$$\begin{array}{ccc}\hfill \left(I_{a^{+}}^{n}f\right)\left(s\right)& =& \underset{a}{\overset{s}{\int }}d{t}_1\underset{a}{\overset{t_1}{\int }}d{t}_2\cdots \underset{a}{\overset{t_{n-1}}{\int }}f\left(t_n\right)d{t}_n\hfill \\ & =& {\displaystyle \frac{1}{(n-1)!}}\underset{a}{\overset{s}{\int }}{(s-t)}^{n-1}f\left(t\right)dt(n\in \mathbb{N}),\hfill \end{array}$$

(5)

and

$$\begin{array}{ccc}\hfill \left(I_{b^{-}}^{n}f\right)\left(s\right)& =& \underset{s}{\overset{b}{\int }}d{t}_1\underset{t_1}{\overset{b}{\int }}d{t}_2\cdots \underset{t_{n-1}}{\overset{b}{\int }}f\left(t_n\right)d{t}_n\hfill \\ & =& {\displaystyle \frac{1}{(n-1)!}}\underset{s}{\overset{b}{\int }}{(t-s)}^{n-1}f\left(t\right)dt(n\in \mathbb{N}).\hfill \end{array}$$

(6)

The Riemann–Liouville fractional derivatives $D_{a^{+}}^{\alpha }\varpi$ and $D_{b^{-}}^{\alpha }\varpi$ of order $\alpha \in \mathbb{C}$ ($\mathfrak{R}\left(\alpha \right)\geqq 0$) are defined by

$$\begin{array}{ccc}\hfill \left(D_{a^{+}}^{\alpha }\varpi \right)& :=& {\left({\displaystyle \frac{d}{ds}}\right)}^n\left(I_{a^{+}}^{n-\alpha }\varpi \right)\left(s\right)\hfill \\ & =& {\displaystyle \frac{1}{\Gamma (n-\alpha )}}{\left({\displaystyle \frac{d}{ds}}\right)}^n\underset{a}{\overset{s}{\int }}{\displaystyle \frac{\varpi \left(t\right)dt}{{(s-t)}^{\alpha -n+1}}}\left(n=\left[\mathfrak{R}\right(\alpha \left)\right]+1;s>a\right),\hfill \end{array}$$

(7)

and

$$\begin{array}{ccc}\hfill \left(D_{b^{-}}^{\alpha }\varpi \right)& :=& {\left({\displaystyle \frac{-d}{ds}}\right)}^n\left(I_{b^{-}}^{n-\alpha }\varpi \right)\left(s\right)\hfill \\ & =& {\displaystyle \frac{1}{\Gamma (n-\alpha )}}{\left({\displaystyle \frac{-d}{ds}}\right)}^n\underset{s}{\overset{b}{\int }}{\displaystyle \frac{\varpi \left(t\right)dt}{{(t-s)}^{\alpha -n+1}}}\left(n=\left[\mathfrak{R}\right(\alpha \left)\right]+1;s<b\right),\hfill \end{array}$$

(8)

respectively, where $\left[\mathfrak{R}\right(\alpha \left)\right]$ means the integral part of $\mathfrak{R}\left(\alpha \right)$.

Definition 8

([30]). Suppose that $[a,b]$ is a finite interval of the real line $\mathbb{R}$, and let $D_{a^{+}}^{\alpha }\left[\varpi \left(t\right)\right]\left(s\right)\equiv \left(D_{a^{+}}^{\alpha }\varpi \right)\left(s\right)$ and $D_{b^{-}}^{\alpha }\left[\varpi \left(t\right)\right]\left(s\right)\equiv \left(D_{b^{-}}^{\alpha }\varpi \right)\left(s\right)$ is the Riemann–Liouville fractional derivatives of order $\alpha \in \mathbb{C}$ ($\mathfrak{R}\left(\alpha \right)\geqq 0$ ) defined by (7) and (8), respectively. The fractional derivatives ${(}^C{D}_{a^{+}}^{\alpha }\varpi )\left(s\right)$ and ${(}^C{D}_{b^{-}}^{\alpha }\varpi )\left(s\right)$ of order $\alpha \in \mathbb{C}$ ($\mathfrak{R}\left(\alpha \right)\geqq 0$) on $[a,b]$ are defined via the above Riemann–Liouville fractional derivatives by

$$\begin{array}{c}\hfill \left({}^{C}D_{a^{+}}^{\alpha }\varpi \right)\left(s\right):=\left(D_{a^{+}}^{\alpha }\left[\varpi \left(t\right)-\sum _{k=0}^{n-1}{\displaystyle \frac{{\varpi }^{\left(k\right)}\left(a\right)}{k!}}{(t-a)}^k\right]\right)\left(s\right),\end{array}$$

and

$$\begin{array}{c}\hfill \left({}^{C}D_{b^{-}}^{\alpha }\varpi \right)\left(s\right):=\left(D_{b^{-}}^{\alpha }\left[\varpi \left(t\right)-\sum _{k=0}^{n-1}{\displaystyle \frac{{\varpi }^{\left(k\right)}\left(b\right)}{k!}}{(b-t)}^k\right]\right)\left(s\right),\end{array}$$

respectively, where

$$\begin{array}{c}\hfill n=\left[\mathfrak{R}\left(\alpha \right)\right]+1for\alpha \notin {\mathbb{N}}_0;n=\alpha for\alpha \in {\mathbb{N}}_0.\end{array}$$

These derivatives are called the left-sided and right-sided Caputo fractional derivatives of order α.

Lemma 3.

The following nonlinear fractional differential equation ($\mathbb{FDE}$) of Caputo type

$${}^{C}D_{0^{+}}^{\mu }\varpi \left(t\right)=\left\{\begin{array}{c}f(t,\varpi (t\left)\right),t\in (0,1),1<\mu \le 2,\hfill \\ \\ \varpi \left(0\right)=0,\varpi \left(1\right)=\underset{0}{\overset{m}{\int }}\varpi \left(s\right)ds,0<m<1,\hfill \end{array}\right.$$

where ${}^{C}D_{0^{+}}^{\mu }$ represents the ( $\mathbb{CFD}$) of order μ and $f:[0,1]\times \mathbb{R}⟶\mathbb{R}$ is a continuous function. This nonlinear $\mathbb{FDE}$ can also be represented as follows:

$$\begin{array}{ccc}\hfill \varpi \left(t\right)& =& {\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & -& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & +& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}f(\tau ,\varpi \left(\tau \right))d\tau \right]ds.\hfill \end{array}$$

(9)

A function $\varpi \left(t\right)$ is a solution of the defined nonlinear $\mathbb{FDE}$ whenever it is the solution of the $\mathbb{FDE}$ (9) and vice-versa.

Proof. 

Applying the R-L fractional integral $I_{0^{+}}^{\mu }$ to both sides to the equation ${}^{C}D_{0^{+}}^{\mu }\varpi \left(t\right)=f(t,\varpi \left(t\right))$, we have

$$\varpi \left(t\right)={\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}f(s,\varpi \left(s\right))ds+C_{1}t+C_0,$$

(10)

where $C_0$, $C_1$ are arbitrary constants. From the condition $\varpi \left(0\right)=0$ we find $C_0=0$.

Then, in view of the condition $\varpi \left(1\right)=\underset{0}{\overset{\mu }{\int }}\varpi \left(s\right)ds$, we have

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}f(s,\varpi \left(s\right))ds+C_1\hfill \\ & =& {\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}f(\tau ,\varpi \left(\tau \right))d\tau ds+C_1\underset{0}{\overset{m}{\int }}sds\hfill \\ & \Rightarrow & C_1-C_1{\displaystyle \frac{m^2}{2}}={\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}f(\tau ,\varpi \left(\tau \right))d\tau ds\hfill \\ & & -{\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & \Rightarrow & C_1\left(1-{\displaystyle \frac{m^2}{2}}\right)={\displaystyle \frac{-1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & & +{\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}f(\tau ,\varpi \left(\tau \right))d\tau \right]ds\hfill \\ & \Rightarrow & C_1={\displaystyle \frac{2}{(2-m^2)}}[{\displaystyle \frac{-1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & & +{\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}f(\tau ,\varpi \left(\tau \right))d\tau \right]ds]\hfill \end{array}$$

substituting the value of $C_1$ in (10), we have

$$\begin{array}{ccc}\hfill \varpi \left(t\right)& =& {\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & -& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & +& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}f(\tau ,\varpi \left(\tau \right))d\tau \right]ds.\hfill \end{array}$$

□

Example 6.

(numerical example) Let the following be true:

• $f(t,\varpi (t\left)\right)=t\varpi \left(t\right)+sin\left(t\right)$,
• $\mu =1.5$ (order of the fractional derivative, $1<\mu \le 2$),
• $m=0.5$ (satisfying $0<m<1$).

Using the representation in Equation (10), the solution is expressed as follows:

$$\begin{array}{ccc}\hfill \varpi \left(t\right)& =& {\displaystyle \frac{1}{\Gamma \left(1.5\right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{0.5}[s\varpi \left(s\right)+sin\left(s\right)]ds\hfill \\ & & -{\displaystyle \frac{2t}{(2-0.5^2)\Gamma \left(1.5\right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{0.5}[s\varpi \left(s\right)+sin\left(s\right)]ds\hfill \\ & & +{\displaystyle \frac{2t}{(2-0.5^2)\Gamma \left(1.5\right)}}\underset{0}{\overset{0.5}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{0.5}[\tau \varpi \left(\tau \right)+sin\left(\tau \right)]d\tau \right]ds.\hfill \end{array}$$

Here,

$$\Gamma \left(1.5\right)={\displaystyle \frac{\sqrt{\pi }}{2}}.$$

In [10], Mustafa described the well-known Banach contraction operator principle within the framework of G-metric spaces as follows:

Theorem 1

([10]). Suppose that $(\mathfrak{X},G)$ is a complete G-metric space. Let $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ be an operator satisfying the following condition for all $\varpi ,\varrho ,\kappa \in \mathfrak{X}$:

$$\begin{array}{c}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varrho ,\mathfrak{F}\kappa )\le \sigma G(\varpi ,\varrho ,\kappa ),\end{array}$$

where $\sigma \in [0,1)$. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$.

Theorem 2

([10]). Suppose that $(\mathfrak{X},G)$ is a G-metric space. Let $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ be an operator satisfying the following condition for all $\varpi ,\varrho \in \mathfrak{X}$:

$$\begin{array}{c}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )\le \sigma G(\varpi ,\varrho ,\varrho ),\end{array}$$

where $\sigma \in [0,1)$. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$.

Theorem 3

([38]). Suppose that $(\mathfrak{X},G)$ is a complete G-metric space. Let $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ be an operator satisfying the following condition for all $\varpi ,\varrho ,\kappa \in \mathfrak{X}$:

$$\begin{array}{c}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )\le \sigma \left[G(\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varpi )+G(\varrho ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )+G(\kappa ,\mathfrak{F}\kappa ,\mathfrak{F}\kappa )\right],\end{array}$$

where $\sigma \in [0,{\displaystyle \frac{1}{3}})$. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$.

3. Main Results

This section consists of an overview of fundamental principles that play a role in achieving our main objectives. Now, we generalize, unify, and extend Mustafa’s [10] results.

Theorem 4.

Suppose that $(\mathfrak{X},G)$ is a G-complete G-metric space. Let $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$ be operators satisfying

$$G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \psi \left(G(\varpi ,\varpi ,\varrho )\right),forall\varpi ,\varrho \in \mathfrak{X},$$

where $\psi \in \Psi$ and $\psi <\mathfrak{I}$. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$ in $\mathfrak{X}$.

Proof. 

Let ${\varpi }_0$ be an arbitrary element in $\mathfrak{X}$. Define a sequence $\left\{{\varpi }_n\right\}$ by ${\mathfrak{F}}^{2n+1}{\varpi }_0=\mathfrak{F}{\varpi }_{2n}={\varpi }_{2n+1},n\ge 1$, then we obtain

$$\begin{array}{ccc}\hfill G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})& =& G(\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n})\hfill \\ & \le & \psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right)\hfill \\ & =& \psi \left(G(\mathfrak{F}{\varpi }_{2n},\mathfrak{F}{\varpi }_{2n},\mathfrak{F}{\varpi }_{2n-1})\right)\hfill \\ & \le & {\psi }^2\left(G({\varpi }_{2n},{\varpi }_{2n},{\varpi }_{2n-1})\right)\hfill \\ & ⋮& \\ & \le & {\psi }^{2n+1}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right).\hfill \end{array}$$

Then, for $m,n\in \mathbb{N}$ with $n>m$, we find that

$$\begin{array}{ccc}& & G({\varpi }_n,{\varpi }_n,{\varpi }_m)\hfill \\ & \le & G({\varpi }_n,{\varpi }_n,{\varpi }_{n-1})+G({\varpi }_{n-1},{\varpi }_{n-1},{\varpi }_{n-2})+\cdots +G({\varpi }_{m+1},{\varpi }_{m+1},{\varpi }_m)\hfill \\ & \le & {\psi }^{n-1}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)+{\psi }^{n-2}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)+\cdots +{\psi }^m\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)\hfill \\ & \le & \sum _{k=m}^{n-1}{\psi }^k\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)⟶0,\mathrm{for}\mathrm{all}G({\varpi }_1,{\varpi }_1,{\varpi }_0)>0,n,m⟶+\infty .\hfill \end{array}$$

Hence, $\left\{{\varpi }_n\right\}$ is a G-Cauchyness in $\mathfrak{X}$. Based on G-completeness of $\mathfrak{X}$, there exists ${\varpi }^{*}\in \mathfrak{X}$ such that $\underset{n\to +\infty }{lim}{\varpi }_n={\varpi }^{*}$. Therefore, one has

$$\begin{array}{ccc}\hfill 0\le G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})& \le & G({\varpi }^{*},\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)+G(\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\hfill \\ & \le & G({\varpi }^{*},{\varpi }_{n+1},{\varpi }_{n+1})+\psi \left(G({\varpi }_n,{\varpi }^{*},{\varpi }^{*})\right).\hfill \end{array}$$

It follows that

$$\begin{array}{ccc}\hfill 0\le G({\varpi }^{*},{\varpi }^{*},\mathfrak{F}{\varpi }^{*})& \le & G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})+\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})\right)\hfill \\ & \le & 0+\psi \left(0\right).\hfill \end{array}$$

Thus, $G({\varpi }^{*},{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\le 0$, which is a contradiction. Then, $G({\varpi }^{*},{\varpi }^{*},\mathfrak{F}{\varpi }^{*})=0$, i.e., ${\varpi }^{*}=\mathfrak{F}{\varpi }^{*}$ is a $\mathbb{FP}$ of $\mathfrak{F}$. Now, if ${\varrho }^{*}\ne {\varpi }^{*}$ is another $\mathbb{FP}$ of the operator $\mathfrak{F}$, then

$$\begin{array}{ccc}\hfill 0\le G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})& =& G(\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varrho }^{*})\hfill \\ & \le & \psi \left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right),\hfill \end{array}$$

that is,

$$(\mathfrak{I}-\psi )\left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right)\le 0.$$

Since $(\mathfrak{I}-\psi )$ is invertible, then

$$\begin{array}{ccc}\hfill {(\mathfrak{I}-\psi )}^{-1}(\mathfrak{I}-\psi )\left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right)& \le & {(\mathfrak{I}-\psi )}^{-1}\left(0\right)\hfill \\ \hfill ⟺\mathfrak{I}\left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right)& \le & \sum _{n=0}^{+\infty }{\psi }^n\left(0\right)\hfill \\ \hfill ⟺G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\le 0.\end{array}$$

Again, we obtain a contradiction. Therefore,

$$G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})=0⟹{\varpi }^{*}={\varrho }^{*}.$$

This implies that the $\mathbb{FP}$ is unique. □

The following example affirms Theorem 4:

Example 7.

Let $\mathfrak{X}=\mathbb{R}$ and the metric $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$be defined by

$$G(\varpi ,\varrho ,\kappa ):=sup\{\mid \varpi -\varrho \mid ,\mid \varrho -\kappa \mid ,\mid \kappa -\varpi \mid \}.$$

Then, $(\mathfrak{X},G)$ is a G-complete G-metric space.

To verify that the given function $G(\varpi ,\varrho ,\kappa )$ is a valid G-metric, we need to check that it satisfies the four conditions required for a G-metric.

(1) 

⇒: If $\varpi =\varrho =\kappa$, then $|\varpi -\varrho |=|\varrho -\kappa |=|\kappa -\varpi |=0$. Therefore, $G(\varpi ,\varrho ,\kappa )=sup\{0,0,0\}=0$.

⇐: If $G(\varpi ,\varrho ,\kappa )=0$, then $sup\left\{\right|\varpi -\varrho |,|\varrho -\kappa |,|\kappa -\varpi \left|\right\}=0$, which implies that $|\varpi -\varrho |=|\varrho -\kappa |=|\kappa -\varpi |=0$. Hence, $\varpi =\varrho =\kappa$.

(2) 

Since $G(\varpi ,\varpi ,\varrho )=|\varpi -\varrho |$ and $G(\varpi ,\varrho ,\kappa )=sup\left\{\right|\varpi -\varrho |,|\varrho -\kappa |,|\kappa -\varpi \left|\right\}$.

Clearly, $|\varpi -\varrho |\le sup\left\{\right|\varpi -\varrho |,|\varrho -\kappa |,|\kappa -\varpi \left|\right\}=G(\varpi ,\varrho ,\kappa )$.

(3) 

The function $G(\varpi ,\varrho ,\kappa )=sup\left\{\right|\varpi -\varrho |,|\varrho -\kappa |,|\kappa -\varpi \left|\right\}$ is clearly symmetric because the supremum is taken over all the pairwise differences and reordering these differences does not change the result.

(4) 

We need to check if the inequality holds for the given function:

$$\begin{array}{c}\hfill G(\varpi ,\varrho ,\kappa )=sup\left\{\right|\varpi -\varrho |,|\varrho -\kappa |,|\kappa -\varpi \left|\right\},\end{array}$$

and

$$\begin{array}{c}\hfill G(\varpi ,a,a)=sup\left\{\right|\varpi -a|,|a-a|,|a-\varpi \left|\right\}=|\varpi -a|,\end{array}$$

$$\begin{array}{c}\hfill G(a,\varrho ,\kappa )=sup\left\{\right|a-\varrho |,|\varrho -\kappa |,|\kappa -a\left|\right\}.\end{array}$$

Now,

$$\begin{array}{c}\hfill G(\varpi ,\varrho ,\kappa )\le G(\varpi ,a,a)+G(a,\varrho ,\kappa ),\end{array}$$

translates to

$$\begin{array}{c}\hfill sup\left\{\right|\varpi -\varrho |,|\varrho -\kappa |,|\kappa -\varpi \left|\right\}\le |\varpi -a|+sup\left\{\right|a-\varrho |,|\varrho -\kappa |,|\kappa -a\left|\right\}.\end{array}$$

Since the supremum represents the largest of the distances between the points, and the triangle inequality holds in $\mathbb{R}$, this inequality is valid.

To prove that the G-metric space $(\mathfrak{X},G)$ is G-complete,we need to show that every G-Cauchy sequence in this space is G-convergent to some point in$\mathbb{R}$.

Let $\left\{{\varpi }_n\right\}$ be a G-Cauchy sequence in the given G-metric space. Then for every $\epsilon >0$ there exists an integer $N\in \mathbb{N}$ such that for all $n,m,l\ge N$,

$$G({\varpi }_n,{\varpi }_m,{\varpi }_l)<\epsilon .$$

That is

$$G({\varpi }_n,{\varpi }_m,{\varpi }_l)=sup\left\{\right|{\varpi }_n-{\varpi }_m|,|{\varpi }_m-{\varpi }_l|,|{\varpi }_l-{\varpi }_n\left|\right\}<\epsilon .$$

In particular,

$$|{\varpi }_n-{\varpi }_m|<\epsilon \mathrm{and}|{\varpi }_m-{\varpi }_l|<\epsilon \mathrm{and}|{\varpi }_l-{\varpi }_n|<\epsilon .$$

Therefore, for all $n,m\ge N$, we have $|{\varpi }_n-{\varpi }_m|<\epsilon$. This shows that a G-Cauchy sequence in the G-metric space is also a Cauchy sequence in the usual sense of the real numbers. Since $\mathbb{R}$ with the usual metric is a complete metric space, every Cauchy sequence in $\mathbb{R}$ converges to some limit in $\mathbb{R}$. Therefore, the sequence $\left\{{\varpi }_n\right\}$ converges to some point $\varpi \in \mathbb{R}$ in the usual metric, i.e., for every $\epsilon >0$, there exists $N\in \mathbb{N}$ such that for all $n\ge N$,

$$|{\varpi }_n-\varpi |<\epsilon .$$

Next, we show that the sequence $\left\{{\varpi }_n\right\}$ also G-converges to ϖ in the G-metric sense. That is, for every $\epsilon >0$, there exists $N\in \mathbb{N}$ such that for all $n,m\ge N$,

$$G(\varpi ,{\varpi }_n,{\varpi }_m)<\epsilon .$$

Using the definition of the G-metric, we need to show that

$$G(\varpi ,{\varpi }_n,{\varpi }_m)=sup\left\{\right|\varpi -{\varpi }_n|,|{\varpi }_n-{\varpi }_m|,|{\varpi }_m-\varpi \left|\right\}<\epsilon .$$

Since $\left\{{\varpi }_n\right\}$ converges to ϖ in the usual sense, for any $\epsilon >0$, there exists $N\in \mathbb{N}$ such that for all $n\ge N$, $|{\varpi }_n-\varpi |<{\displaystyle \frac{\epsilon }{2}}$. Therefore, for all $n,m\ge N$,

$$|\varpi -{\varpi }_n|<{\displaystyle \frac{\epsilon }{2}},|{\varpi }_n-{\varpi }_m|<{\displaystyle \frac{\epsilon }{2}},|{\varpi }_m-\varpi |<{\displaystyle \frac{\epsilon }{2}}.$$

Thus, for all $n,m\ge N$,

$$G(\varpi ,{\varpi }_n,{\varpi }_m)=sup\left\{\right|\varpi -{\varpi }_n|,|{\varpi }_n-{\varpi }_m|,|{\varpi }_m-\varpi \left|\right\}<sup\left\{{\displaystyle \frac{\epsilon }{2}},{\displaystyle \frac{\epsilon }{2}},{\displaystyle \frac{\epsilon }{2}}\right\}={\displaystyle \frac{\epsilon }{2}}<\epsilon .$$

Therefore, $G(\varpi ,{\varpi }_n,{\varpi }_m)<\epsilon$, proving that $\left\{{\varpi }_n\right\}$ is G-convergent to ϖ in the G-metric space. Since every G-Cauchy sequence in $(\mathfrak{X},G)$ is also G-convergent to some point in $\mathfrak{X}$, the space $(\mathfrak{X},G)$ is G-complete.

Now, define the operator $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ by

$$\mathfrak{F}\varpi :={\displaystyle \frac{\varpi }{4}},$$

and $\psi :{\mathbb{R}}_{+}⟶{\mathbb{R}}_{+}$ by

$$\psi \left(t\right):=texpt.$$

Then, we obtain

$$\begin{array}{ccc}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varrho ,\mathfrak{F}\kappa )& =& sup\{\mid \mathfrak{F}\varpi -\mathfrak{F}\varrho \mid ,\mid \mathfrak{F}\varrho -\mathfrak{F}\kappa \mid ,\mid \mathfrak{F}\kappa -\mathfrak{F}\varpi \mid \}\hfill \\ & =& {\displaystyle \frac{1}{4}}\left(sup\{\mid \varpi -\varrho \mid ,\mid \varrho -\kappa \mid ,\mid \kappa -\varpi \mid \}\right)\hfill \\ & =& {\displaystyle \frac{1}{4}}G(\varpi ,\varrho ,\kappa )\hfill \\ & \le & G(\varpi ,\varrho ,\kappa )expG(\varpi ,\varrho ,\kappa )\hfill \\ & =& \psi \left(G(\varpi ,\varrho ,\kappa )\right).\hfill \end{array}$$

Therefore, all hypotheses of Theorem 4 are satisfied and $0$ is a unique $\mathbb{FP}$ of $\mathfrak{F}$.

Theorem 5.

Let $(\mathfrak{X},G)$ be a G-complete G-metric space. Assume that $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$ are operators satisfying

$$G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \psi \left(G(\varpi ,\varpi ,\varrho )+G(\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varpi )+G(\varrho ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )\right),forall\varpi ,\varrho \in \mathfrak{X},$$

where $\psi \in \Psi$ and $\psi <\mathfrak{I}$. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$ in $\mathfrak{X}$.

Proof. 

Let ${\varpi }_0$ be an arbitrary element in $\mathfrak{X}$. Define a sequence $\left\{{\varpi }_n\right\}$ by ${\mathfrak{F}}^{2n+2}{\varpi }_0=\mathfrak{F}{\varpi }_{2n+1}={\varpi }_{2n+2},n\ge 1$.

$$\begin{array}{ccc}& & G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})\hfill \\ & =& G(\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n})\hfill \\ & \le & \psi (G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})+G({\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n+1})\hfill \\ & & +G({\varpi }_{2n},\mathfrak{F}{\varpi }_{2n},\mathfrak{F}{\varpi }_{2n}))\hfill \\ & =& \psi (G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})+G({\varpi }_{2n+1},{\varpi }_{2n+2},{\varpi }_{2n+2})\hfill \\ & & +G({\varpi }_{2n},{\varpi }_{2n+1},{\varpi }_{2n+1}))\hfill \\ & \le & \psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right)+\psi \left(G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})\right)\hfill \\ & & +\psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right).\hfill \end{array}$$

It follows that

$$\begin{array}{ccc}\hfill (\mathfrak{I}-\psi )G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})& \le & 2\psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right).\hfill \end{array}$$

By multiplying ${(\mathfrak{I}-\psi )}^{-1}$, we have

$$\begin{array}{ccc}\hfill G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})& \le & 2{(\mathfrak{I}-\psi )}^{-1}\psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right)\hfill \\ & ⋮& \\ & \le & {\left[2{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^{2n+1}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right).\hfill \end{array}$$

Thus, for $n,m\in \mathbb{N}$ with $n>m$, we obtain

$$\begin{array}{ccc}& & G({\varpi }_n,{\varpi }_n,{\varpi }_m)\hfill \\ & \le & G({\varpi }_n,{\varpi }_n,{\varpi }_{n-1})+G({\varpi }_{n-1},{\varpi }_{n-1},{\varpi }_{n-2})+\cdots +G({\varpi }_{m+1},{\varpi }_{m+1},{\varpi }_m)\hfill \\ & \le & {\left[2{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^{n-1}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)+{\left[2{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^{n-2}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)\hfill \\ & & +\cdots +{\left[2{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^m\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)\hfill \\ & \le & \sum _{k=m}^{n-1}{\left[2{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^k\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)⟶0,\hfill \\ & & \mathrm{for}\mathrm{all}G({\varpi }_1,{\varpi }_1,{\varpi }_0)>0,n,m⟶+\infty .\hfill \end{array}$$

Hence, $\left\{{\varpi }_n\right\}$ is a G-Cauchyness in $\mathfrak{X}$. Based on G-completeness of $\mathfrak{X}$, there exists ${\varpi }^{*}\in \mathfrak{X}$ such that $\underset{n\to +\infty }{lim}{\varpi }_n={\varpi }^{*}$. Therefore, we obtain

$$\begin{array}{ccc}\hfill 0\le G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})& \le & G({\varpi }^{*},\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)+G(\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\hfill \\ & =& G({\varpi }^{*},\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)+G(\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }_n)\hfill \\ & \le & G({\varpi }^{*},\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)+\psi (G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)\hfill \\ & & +G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})+G({\varpi }_n,\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n))\hfill \\ & \le & G({\varpi }^{*},\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)+\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)\right)\hfill \\ & & +\psi \left(G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\right)+\psi \left(G({\varpi }_n,\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)\right)\hfill \\ & =& G({\varpi }^{*},{\varpi }_{n+1},{\varpi }_{n+1})+\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)\right)\hfill \\ & & +\psi \left(G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\right)+\psi \left(G({\varpi }_n,{\varpi }_{n+1},{\varpi }_{n+1})\right).\hfill \end{array}$$

Taking $n\to +\infty$, we obtain

$$\begin{array}{ccc}\hfill G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})& \le & G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})+\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})\right)\hfill \\ & & +\psi \left(G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\right)+\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})\right)\hfill \\ & \le & 0+0+\psi \left(G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\right)+0,\hfill \end{array}$$

that is,

$$(\mathfrak{I}-\psi )\left(G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\right)\le 0.$$

Since $(\mathfrak{I}-\psi )$ is invertible, then

$${(\mathfrak{I}-\psi )}^{-1}(\mathfrak{I}-\psi )\left(G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\right)\le {(\mathfrak{I}-\psi )}^{-1}\left(0\right).$$

Thus, $G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\le 0$, which is a contradiction. Then, $G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})=0$, i.e., ${\varpi }^{*}=\mathfrak{F}{\varpi }^{*}$ is a $\mathbb{FP}$ of $\mathfrak{F}$. Now, if ${\varrho }^{*}\ne {\varpi }^{*}$ is another $\mathbb{FP}$ of the operator $\mathfrak{F}$, then

$$\begin{array}{ccc}\hfill 0& \le & G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\hfill \\ & =& G(\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varrho }^{*})\hfill \\ & \le & \psi \left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})+G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})+G({\varrho }^{*},\mathfrak{F}{\varrho }^{*},\mathfrak{F}{\varrho }^{*})\right)\hfill \\ & \le & \psi \left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right)+\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})\right)+\psi \left(G({\varrho }^{*},{\varrho }^{*},{\varrho }^{*})\right),\hfill \end{array}$$

that is,

$$(\mathfrak{I}-\psi )\left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right)\le 0.$$

Since $\psi \left(\varpi \right)=0$ if and only if $\varpi =0$ and $\mathfrak{I}\left(\varpi \right)\ne \psi \left(\varpi \right)$. Then

$$G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})=0⟹{\varpi }^{*}={\varrho }^{*}.$$

This implies that the $\mathbb{FP}$ is unique. □

Corollary 1.

Let $(\mathfrak{X},G)$ be a G-complete G-metric space, $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$ be operators satisfying

$$G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \psi \left(G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\varpi )+G(\mathfrak{F}\varrho ,\mathfrak{F}\varrho ,\varrho )\right),\mathrm{for}\mathrm{all}\varpi ,\varrho \in \mathfrak{X},$$

where $\psi \in \Psi$ and $\psi <\mathfrak{I}$. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$ in $\mathfrak{X}$.

The following example affirms Corollary 1:

Example 8.

Consider all hypotheses of Example 7 are true, we conclude that

$$\begin{array}{ccc}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\varpi )+G(\mathfrak{F}\varrho ,\mathfrak{F}\varrho ,\varrho )& =& sup\{\mid \mathfrak{F}\varpi -\mathfrak{F}\varpi \mid ,\mid \mathfrak{F}\varpi -\varpi \mid ,\mid \varpi -\mathfrak{F}\varpi \mid \}\hfill \\ & & +sup\{\mid \mathfrak{F}\varrho -\mathfrak{F}\varrho \mid ,\mid \mathfrak{F}\varrho -\varrho \mid ,\mid \varrho -\mathfrak{F}\varrho \mid \}\hfill \\ & =& {\displaystyle \frac{3}{4}}\left(\left|\varpi \right|\right)+{\displaystyle \frac{3}{4}}\left(\left|\varrho \right|\right)\hfill \\ & =& {\displaystyle \frac{3}{4}}\left(\left|\varpi \right|+\left|\varrho \right|\right)\hfill \\ & \ge & {\displaystyle \frac{3}{4}}\left(\left|\varpi -\varrho \right|\right)\hfill \\ & =& 3\left(\left|{\displaystyle \frac{\varpi }{4}}-{\displaystyle \frac{\varrho }{4}}\right|\right)\hfill \\ & =& 3\left(\left|\mathfrak{F}\varpi -\mathfrak{F}\varrho \right|\right)\hfill \\ & =& 3sup\{\mid \mathfrak{F}\varpi -\mathfrak{F}\varpi \mid ,\mid \mathfrak{F}\varpi -\mathfrak{F}\varrho \mid ,\mid \mathfrak{F}\varrho -\mathfrak{F}\varpi \mid \}\hfill \\ & =& 3G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho ),\hfill \end{array}$$

which yields,

$$\begin{array}{ccc}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )& \le & {\displaystyle \frac{1}{3}}\left(G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\varpi )+G(\mathfrak{F}\varrho ,\mathfrak{F}\varrho ,\varrho )\right)\hfill \\ & \le & \left(G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\varpi )+G(\mathfrak{F}\varrho ,\mathfrak{F}\varrho ,\varrho )\right)expG(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\varpi )+G(\mathfrak{F}\varrho ,\mathfrak{F}\varrho ,\varrho ).\hfill \end{array}$$

It follows that

$$G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \psi \left(G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\varpi )+G(\mathfrak{F}\varrho ,\mathfrak{F}\varrho ,\varrho )\right).$$

Therefore, all conditions of Corollary 1 are verified and $0$ is a unique $\mathbb{FP}$ of $\mathfrak{F}$.

The example below supports Theorem 5:

Example 9.

Considering that all hypotheses of Example 7 are true, we conclude that

$$\begin{array}{ccc}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )& =& sup\{\mid \mathfrak{F}\varpi -\mathfrak{F}\varpi \mid ,\mid \mathfrak{F}\varpi -\mathfrak{F}\varrho \mid ,\mid \mathfrak{F}\varrho -\mathfrak{F}\varpi \mid \}\hfill \\ & =& {\displaystyle \frac{1}{4}}\left(\left|\varpi -\varrho \right|\right)\hfill \\ & =& {\displaystyle \frac{1}{4}}\left(\left|\varpi -\mathfrak{F}\varpi +\mathfrak{F}\varpi -\varrho \right|\right)\hfill \\ & \le & {\displaystyle \frac{1}{4}}\left(\left|\varpi -\mathfrak{F}\varpi \right|+\left|\mathfrak{F}\varpi -\varrho \right|\right)\hfill \\ & =& {\displaystyle \frac{1}{4}}\left|\varpi -\mathfrak{F}\varpi \right|+{\displaystyle \frac{1}{4}}\left|\mathfrak{F}\varpi -\varrho \right|\hfill \\ & =& {\displaystyle \frac{1}{4}}\left|\varpi -\mathfrak{F}\varpi \right|+{\displaystyle \frac{1}{4}}\left(\left|\mathfrak{F}\varpi -\mathfrak{F}\varrho +\mathfrak{F}\varrho -\varrho \right|\right)\hfill \\ & \le & {\displaystyle \frac{1}{4}}\left|\varpi -\mathfrak{F}\varpi \right|+{\displaystyle \frac{1}{4}}\left|\mathfrak{F}\varpi -\mathfrak{F}\varrho \right|+{\displaystyle \frac{1}{4}}\left|\mathfrak{F}\varrho -\varrho \right|\hfill \\ & =& {\displaystyle \frac{1}{4}}sup\{\mid \varpi -\mathfrak{F}\varpi \mid ,\mid \mathfrak{F}\varpi -\mathfrak{F}\varpi \mid ,\mid \mathfrak{F}\varpi -\varpi \mid \}\hfill \\ & & +{\displaystyle \frac{1}{4}}sup\{\mid \mathfrak{F}\varpi -\mathfrak{F}\varpi \mid ,\mid \mathfrak{F}\varpi -\mathfrak{F}\varrho \mid ,\mid \mathfrak{F}\varrho -\mathfrak{F}\varpi \mid \}\hfill \\ & & +{\displaystyle \frac{1}{4}}sup\{\mid \varrho -\mathfrak{F}\varrho \mid ,\mid \mathfrak{F}\varrho -\mathfrak{F}\varrho \mid ,\mid \mathfrak{F}\varrho -\varrho \mid \}\hfill \\ & =& {\displaystyle \frac{1}{4}}\left[G(\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varpi )+G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )+G(\varrho ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )\right]\hfill \\ & \le & \left(G(\varpi ,\varpi ,\varrho )+G(\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varpi )+G(\varrho ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )\right)exp\left(G(\varpi ,\varpi ,\varrho )+G(\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varpi )+G(\varrho ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )\right).\hfill \end{array}$$

Then,

$$G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \psi \left(G(\varpi ,\varpi ,\varrho )+G(\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varpi )+G(\varrho ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )\right).$$

Therefore, all conditions of Theorem 5 are verified and $0$ is a unique $\mathbb{FP}$ of $\mathfrak{F}$.

Theorem 6.

Let $(\mathfrak{X},G)$ be a G-complete G-metric space. Assume that $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$ are operators verifying

$$G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \psi \left(G(\varpi ,\varpi ,\varrho )+{\displaystyle \frac{G(\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varpi ).G(\varrho ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )}{1+G(\varpi ,\varpi ,\varrho )}}\right),\mathrm{for}\mathrm{all}\varpi ,\varrho \in \mathfrak{X},$$

where $\psi \in \Psi$ and $\psi <\mathfrak{I}$. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$ in $\mathfrak{X}$.

Proof. 

Let ${\varpi }_0$ be an arbitrary element in $\mathfrak{X}$. Define a sequence $\left\{{\varpi }_n\right\}$ by

$${\mathfrak{F}}^{2n+2}{\varpi }_0=\mathfrak{F}{\varpi }_{2n+1}={\varpi }_{2n+2},\forall n\ge 1;$$

then, we have

$$\begin{array}{ccc}\hfill G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})& =& G(\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n})\hfill \\ & \le & \psi \left(G\right({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\hfill \\ & & +{\displaystyle \frac{G({\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n+1}).G({\varpi }_{2n},\mathfrak{F}{\varpi }_{2n},\mathfrak{F}{\varpi }_{2n})}{1+G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})}})\hfill \\ & =& \psi \left(G\right({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\hfill \\ & & +{\displaystyle \frac{G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})}{1+G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})}})\hfill \\ & \le & \psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})+G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})\right)\hfill \\ & \le & \psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right)+\psi \left(G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})\right).\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill (\mathfrak{I}-\psi )G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})& \le & \psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right).\hfill \end{array}$$

By multiplying ${(\mathfrak{I}-\psi )}^{-1}$, we have

$$\begin{array}{ccc}\hfill G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})& \le & \left[{(\mathfrak{I}-\psi )}^{-1}\psi \right]\left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right)\hfill \\ & ⋮& \\ & \le & {\left[{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^n\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right).\hfill \end{array}$$

Thus, for $n,m\in \mathbb{N}$ with $n>m$, we obtain

$$\begin{array}{ccc}\hfill G({\varpi }_n,{\varpi }_n,{\varpi }_m)& \le & G({\varpi }_n,{\varpi }_n,{\varpi }_{n-1})+G({\varpi }_{n-1},{\varpi }_{n-1},{\varpi }_{n-2})+\cdots +G({\varpi }_{m+1},{\varpi }_{m+1},{\varpi }_m)\hfill \\ & \le & {\left[{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^{n-1}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)+{\left[{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^{n-2}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)\hfill \\ & & +\cdots +{\left[{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^m\left(G({\varpi }_1,{\varpi }_1{\varpi }_0)\right)\hfill \\ & \le & \sum _{k=m}^{n-1}{\left[{(\mathfrak{I}-\psi )}^{-1}\psi \right]}^k\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)⟶0,\forall G({\varpi }_1,{\varpi }_1,{\varpi }_0)>0,n,m⟶+\infty .\hfill \end{array}$$

Hence, $\left\{{\varpi }_n\right\}$ is a G-Cauchyness in $\mathfrak{X}$. Based on G-completeness of $\mathfrak{X}$, there exists ${\varpi }^{*}\in \mathfrak{X}$ such that $\underset{n\to +\infty }{lim}{\varpi }_n={\varpi }^{*}$. Therefore, one has

$$\begin{array}{ccc}\hfill 0\le G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})& \le & G({\varpi }^{*},\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)+G(\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\hfill \\ & \le & G({\varpi }^{*},{\varpi }_{n+1},{\varpi }_{n+1})+\psi (G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)\hfill \\ & & +{\displaystyle \frac{G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*}).G({\varpi }_n,\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)}{1+G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)}})\hfill \\ & =& G({\varpi }^{*},{\varpi }_{n+1},{\varpi }_{n+1})+\psi (G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)\hfill \\ & & +{\displaystyle \frac{G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*}).G({\varpi }_n,{\varpi }_{n+1},{\varpi }_{n+1})}{1+G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)}}).\hfill \end{array}$$

Taking $n\to +\infty$, we obtain

$$\begin{array}{ccc}\hfill G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})& \le & G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})+\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})+{\displaystyle \frac{G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*}).G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})}{1+G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})}}\right).\hfill \end{array}$$

Thus, $G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\le 0$, which is a contradiction. Then, $G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})=0$, i.e., ${\varpi }^{*}=\mathfrak{F}{\varpi }^{*}$ is an $\mathbb{FP}$ of $\mathfrak{F}$. Now, if ${\varrho }^{*}\ne {\varpi }^{*}$ is another $\mathbb{FP}$ of the operator $\mathfrak{F}$, then

$$\begin{array}{ccc}\hfill 0\le G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})& =& G(\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varrho }^{*})\hfill \\ & \le & \psi \left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})+{\displaystyle \frac{G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*}).G({\varrho }^{*},\mathfrak{F}{\varrho }^{*},\mathfrak{F}{\varrho }^{*})}{1+G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})}}\right)\hfill \\ & =& \psi \left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right),\hfill \end{array}$$

that is,

$$(\mathfrak{I}-\psi )\left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right)\le 0.$$

Since $(\mathfrak{I}-\psi )$ is invertible, then

$${(\mathfrak{I}-\psi )}^{-1}(\mathfrak{I}-\psi )\left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right)\le {(\mathfrak{I}-\psi )}^{-1}\left(0\right).$$

Then,

$$G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})=0⟹{\varpi }^{*}={\varrho }^{*}.$$

This implies that the $\mathbb{FP}$ is unique. □

In Theorem 6, if $\psi =\lambda \mathfrak{I}$ then we obtain the result below:

Corollary 2.

Let $(\mathfrak{X},G)$ be a G-complete G-metric space. Suppose that $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$ are operators satisfying

$$G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \lambda \left(G(\varpi ,\varpi ,\varrho )+{\displaystyle \frac{G(\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varpi ).G(\varrho ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )}{1+G(\varpi ,\varpi ,\varrho )}}\right),forall\varpi ,\varrho \in \mathfrak{X},$$

where $0\le \lambda <1$ is a constant. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$ in $\mathfrak{X}$.

Theorem 7.

Let $(\mathfrak{X},G)$ be a G-complete G-metric space. Assume that $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$ are operators satisfying

$$G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \psi \left(G(\varpi ,\varpi ,\varrho )+{\displaystyle \frac{G(w,\mathfrak{F}\varpi ,\mathfrak{F}\varpi ).G(\varpi ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )}{1+G(\varpi ,\varrho ,\varrho )}}\right),forall\varpi ,\varrho \in \mathfrak{X},$$

where $\psi \in \Psi$ and $\psi <\mathfrak{I}$. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$ in $\mathfrak{X}$.

Proof. 

Let ${\varpi }_0$ be an arbitrary element in $\mathfrak{X}$. Define a sequence $\left\{{\varpi }_n\right\}$ by ${\mathfrak{F}}^{2n+2}{\varpi }_0=\mathfrak{F}{\varpi }_{2n+1}={\varpi }_{2n+2},n\ge 1$ then, we have

$$\begin{array}{ccc}\hfill G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})& =& G(\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n})\hfill \\ & \le & \psi \left(G\right({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\hfill \\ & & +{\displaystyle \frac{G({\varpi }_{2n},\mathfrak{F}{\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n+1}).G({\varpi }_{2n+1},\mathfrak{F}{\varpi }_{2n},\mathfrak{F}{\varpi }_{2n})}{1+G({\varpi }_{2n+1},{\varpi }_{2n},{\varpi }_{2n})}})\hfill \\ & =& \psi \left(G\right({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\hfill \\ & & +{\displaystyle \frac{G({\varpi }_{2n},{\varpi }_{2n+2},{\varpi }_{2n+2}).G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n+1})}{1+G({\varpi }_{2n+1},{\varpi }_{2n},{\varpi }_{2n})}})\hfill \\ & \le & \psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right).\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill G({\varpi }_{2n+2},{\varpi }_{2n+2},{\varpi }_{2n+1})& \le & \psi \left(G({\varpi }_{2n+1},{\varpi }_{2n+1},{\varpi }_{2n})\right)\hfill \\ & ⋮& \\ & \le & {\psi }^{2n+1}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right).\hfill \end{array}$$

Thus, for $m,n\in \mathbb{N}$ with $n>m$, we find

$$\begin{array}{ccc}\hfill G({\varpi }_n,{\varpi }_n,{\varpi }_m)& \le & G({\varpi }_n,{\varpi }_n,{\varpi }_{n-1})+G({\varpi }_{n-1},{\varpi }_{n-1},{\varpi }_{n-2})+\cdots +G({\varpi }_{m+1},{\varpi }_{m+1},{\varpi }_m)\hfill \\ & \le & {\psi }^{n-1}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)+{\psi }^{n-2}\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)+\cdots +{\psi }^m\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)\hfill \\ & \le & \sum _{k=m}^{n-1}{\psi }^k\left(G({\varpi }_1,{\varpi }_1,{\varpi }_0)\right)⟶0,\mathrm{for}\mathrm{all}G({\varpi }_1,{\varpi }_1,{\varpi }_0)>0,n,m⟶+\infty .\hfill \end{array}$$

Hence, $\left\{{\varpi }_n\right\}$ is a G-Cauchyness in $\mathfrak{X}$. Based on G-completeness of $\mathfrak{X}$, there exists ${\varpi }^{*}\in \mathfrak{X}$ such that $\underset{n\to +\infty }{lim}{\varpi }_n={\varpi }^{*}$. Therefore, one has

$$\begin{array}{ccc}\hfill 0\le G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})& \le & G({\varpi }^{*},\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)+G(\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }_n)\hfill \\ & \le & G({\varpi }^{*},{\varpi }_{n+1},{\varpi }_{n+1})+\psi (G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)\hfill \\ & & +{\displaystyle \frac{G({\varpi }_n,\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*}).G({\varpi }^{*},\mathfrak{F}{\varpi }_n,\mathfrak{F}{\varpi }_n)}{1+G({\varpi }^{*},{\varpi }_n,{\varpi }_n)}})\hfill \\ & \le & G({\varpi }^{*},{\varpi }_{n+1},{\varpi }_{n+1})+\psi (G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)\hfill \\ & & +{\displaystyle \frac{G({\varpi }_n,\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*}).G({\varpi }^{*},{\varpi }_{n+1},{\varpi }_{n+1})}{1+G({\varpi }^{*},{\varpi }_n,{\varpi }_n)}})\hfill \\ & \le & G({\varpi }^{*},{\varpi }_{n+1},{\varpi }_{n+1})+\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varpi }_n)\right)\hfill \\ & & +\psi \left({\displaystyle \frac{G({\varpi }_n,\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*}).G({\varpi }^{*},{\varpi }_{n+1},{\varpi }_{n+1})}{1+G({\varpi }^{*},{\varpi }_n,{\varpi }_n)}}\right).\hfill \end{array}$$

Taking $n\to +\infty$, we obtain

$$\begin{array}{ccc}\hfill G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})& \le & G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})+\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})\right)\hfill \\ & & +\psi \left({\displaystyle \frac{G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*}).G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})}{1+G({\varpi }^{*},{\varpi }^{*},{\varpi }^{*})}}\right)\hfill \\ & =& 0+\psi \left(0\right)+\psi \left(0\right)=0.\hfill \end{array}$$

Thus, $G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})\le 0$, that is a contradiction. Then, $G({\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*})=0$, i.e., ${\varpi }^{*}=\mathfrak{F}{\varpi }^{*}$ is a $\mathbb{FP}$ of $\mathfrak{F}$. Now, if ${\varrho }^{*}\ne {\varpi }^{*}$ is another $\mathbb{FP}$ of the operator $\mathfrak{F}$, then

$$\begin{array}{ccc}\hfill 0\le G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})& =& G(\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varrho }^{*})\hfill \\ & \le & \psi \left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})+{\displaystyle \frac{G({\varrho }^{*},\mathfrak{F}{\varpi }^{*},\mathfrak{F}{\varpi }^{*}).G({\varpi }^{*},\mathfrak{F}{\varrho }^{*},\mathfrak{F}{\varrho }^{*})}{1+G({\varpi }^{*},{\varrho }^{*},{\varrho }^{*})}}\right)\hfill \\ & \le & \psi \left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})+{\displaystyle \frac{G({\varrho }^{*},{\varpi }^{*},{\varpi }^{*}).G({\varpi }^{*},{\varrho }^{*},{\varrho }^{*})}{1+G({\varpi }^{*},{\varrho }^{*},{\varrho }^{*})}}\right)\hfill \\ & \le & 2\psi \left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right),\hfill \end{array}$$

that is,

$$(\mathfrak{I}-2\psi )\left(G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})\right)\le 0.$$

Since $\psi \left(\varpi \right)=0$ if $\varpi =0$ and $\mathfrak{I}\left(\varpi \right)\ne 2\psi \left(\varpi \right)$. Then,

$$G({\varpi }^{*},{\varpi }^{*},{\varrho }^{*})=0⟹{\varpi }^{*}={\varrho }^{*}.$$

This implies that the $\mathbb{FP}$ is unique. □

In Theorem 7, if $\psi =\lambda \mathfrak{I}$ then we have the result below:

Corollary 3.

Let $(\mathfrak{X},G)$ be a G-complete G-metric space. Assume that $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ and $G:\mathfrak{X}\times \mathfrak{X}\times \mathfrak{X}⟶{\mathbb{R}}_{+}$ are operators satisfying

$$G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \lambda \left(G(\varpi ,\varpi ,\varrho )+{\displaystyle \frac{G(w,\mathfrak{F}\varpi ,\mathfrak{F}\varpi ).G(\varpi ,\mathfrak{F}\varrho ,\mathfrak{F}\varrho )}{1+G(\varpi ,\varrho ,\varrho )}}\right),forall\varpi ,\varrho \in \mathfrak{X},$$

where $0\le \lambda <1$ is a constant. Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$ in $\mathfrak{X}$.

4. Applications to Boundary Value Problems

In this section, we use Theorem 4 to establish the conditions under which the solution to $\mathbb{BVP}$ can be expressed

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2\varpi }{d{t}^2}}=\lambda (t,\varpi \left(t\right)),t\in [0,1],\varpi \in {\mathbb{R}}_{+},\hfill \\ \\ \varpi \left(0\right)=\varpi \left(1\right)=0,\hfill \end{array}\right.$$

(11)

where $\lambda :[0,1]\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ is a continuous function. The ideas presented in this section are inspired by [40,41,42,43].

Note that (11) corresponds to the $\mathbb{IE}$

$$\varpi \left(t\right)=-\underset{0}{\overset{1}{\int }}\Omega (t,s)\lambda (s,\varpi \left(s\right))ds,t\in [0,1],$$

where $\Omega (t,s)$ is called Green function, defined by

$$\Omega (t,s)=\left\{\begin{array}{cc}t(1-s)\hfill & \mathrm{if}0\le t<s\le 1,\hfill \\ s(1-t)\hfill & \mathrm{if}0\le s<t\le 1.\hfill \end{array}\right.$$

Let $\mathfrak{X}=C([0,1],{\mathbb{R}}_{+})$ denote the set of all continuous real-valued functions defined on the interval $[0,1]$. We equip $\mathfrak{X}$ with an operator defined for all $\varpi ,\varrho ,\kappa \in \mathfrak{X}$ as follows:

$$\begin{array}{c}\hfill G(\varpi ,\varrho ,\kappa )=\underset{t\in [0,1]}{sup}\left(\mid \varpi \left(t\right)-\varrho \left(t\right)\mid +\mid \varpi \left(t\right)-\kappa \left(t\right)\mid +\mid \varrho \left(t\right)-\kappa \left(t\right)\mid \right).\end{array}$$

(12)

Then, $(\mathfrak{X},G)$ is a G-complete G-metric space. Consider the self-operator $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ be defined as

$$\mathfrak{F}\varpi \left(t\right)=-\underset{0}{\overset{1}{\int }}\Omega (t,s)\lambda (s,\varpi \left(s\right))ds,t\in [0,1].$$

(13)

Then, any solution ${\varpi }^{*}$ to (11) is a $\mathbb{FP}$ of $\mathfrak{F}$ and conversely.

The physical meaning of boundary value problem (11) is as follows:

A vibrating beam with fixed ends $\varpi \left(0\right)=\varpi \left(1\right)=0$, that mean the ends are fixed at zero.

The displacement of an elastic beam under force, where

(a)

$\varpi \left(t\right)$ indicates the displacement at position t,

(b)

$\lambda (t,\varpi (t\left)\right)$ indicates the applied force, which depend on both displacement and position,

(c)

the boundary conditions $\varpi \left(0\right)=\varpi \left(1\right)=0$ indicate the beam is fixed at both ends.

Now, we examine the conditions for the existence of solutions to the $\mathbb{BVP}$ (11) under the following assumptions.

Theorem 8.

Assume that $\psi \in \Psi$ and $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ is a self-operator on $\mathfrak{X}$. Assume that the conditions below are satisfied:

• (C₁) there exists $t\in [0,1]$ and for all $\varpi ,\varrho ,\kappa \in \mathbb{R}$, we have

  $$\begin{array}{cc}\hfill & \mid \lambda (t,\varpi )-\lambda (t,\varrho )\mid +\mid \lambda (t,\varpi )-\lambda (t,\kappa )\mid +\mid \lambda (t,\varrho )-\lambda (t,\kappa )\mid \hfill \\ \hfill & \le \psi \left(\mid \varpi -\varrho \mid +\mid \varpi -\kappa \mid +\mid \varrho -\kappa \mid \right);\hfill \end{array}$$
• (C₂) $\underset{0}{\overset{1}{\int }}\Omega (t,s)ds\le 1$.

Then, the boundary value problem (11) has a solution in $\mathfrak{X}$.

Proof. 

Taking (12) and (13) into account, and for all $\varpi ,\varrho \in \mathfrak{X}$ with $t\in [0,1]$, we have

$$\begin{array}{ccc}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )& =& \underset{t\in [0,1]}{sup}\left[\mid \mathfrak{F}\varpi \left(t\right)-\mathfrak{F}\varpi \left(t\right)\mid +\mid \mathfrak{F}\varpi \left(t\right)-\mathfrak{F}\varrho \left(t\right)\mid +\mid \mathfrak{F}\varpi \left(t\right)-\mathfrak{F}\varrho \left(t\right)\mid \right]\hfill \\ & \le & \underset{t\in [0,1]}{sup}\underset{0}{\overset{1}{\int }}\Omega (t,s)[\mid \lambda (s,\varpi \left(s\right))-\lambda (s,\varpi \left(s\right))\mid +\mid \lambda (s,\varpi \left(s\right))-\lambda (s,\varrho \left(s\right))\mid \hfill \\ & & +\mid \lambda (s,\varpi (s\left)\right)-\lambda (s,\varrho (s\left)\right)\mid ]ds\hfill \\ & \le & \underset{t\in [0,1]}{sup}\underset{0}{\overset{1}{\int }}\Omega (t,s)\left[\psi \left(\mid \varpi \left(s\right)-\varpi \left(s\right)\mid +\mid \varpi \left(s\right)-\varrho \left(s\right)\mid +\mid \varpi \left(s\right)-\varrho \left(s\right)\mid \right)\right]ds\hfill \\ & \le & \underset{0}{\overset{1}{\int }}\Omega (t,s)\left[\psi \left[\underset{t\in [0,1]}{sup}\left(\mid \varpi \left(s\right)-\varpi \left(s\right)\mid +\mid \varpi \left(s\right)-\varrho \left(s\right)\mid +\mid \varpi \left(s\right)-\varrho \left(s\right)\mid \right)\right]\right]ds\hfill \\ & \le & \psi \left(G(\varpi ,\varpi ,\varrho )\right)\underset{0}{\overset{1}{\int }}\Omega (t,s)ds\hfill \\ & \le & \psi \left(G(\varpi ,\varpi ,\varrho )\right).\hfill \end{array}$$

We see that $\mathfrak{F}$ verifies all hypotheses of Theorem 4. It follows that $\mathfrak{F}$ has a $\mathbb{FP}$${\varpi }^{*}$ in $\mathfrak{X}$, which corresponds to solution of the $\mathbb{BVP}$. □

5. Application to Fredholm-Type Integral Equations

In this part, we let $\mathfrak{X}=C\left(\right[t,r],\mathbb{R})$, represent the set of all continuous real-valued functions defined on the interval $[t,r]$, where $t,r\in \mathbb{R}$. We use Theorem 4 to derive a result guaranteeing a unique solution for nonlinear Fredholm-type integral equations:

$$\varpi \left(\alpha \right)=\gamma \underset{t}{\overset{r}{\int }}\mathcal{K}\left(\alpha ,\eta ,\varpi \left(\eta \right)\right)d\eta ,$$

(14)

where $\mathcal{K}:[t,r]\times [t,r]\times \mathbb{R}⟶\mathbb{R}$ is a given continuous function, $\gamma$ is constant and $\varpi \in C\left(\right[t,r],\mathbb{R})$.

The physical meaning of each operator in the Fredholm-type integral equation is: please confirm

(a)

$\varpi \left(\alpha \right)$ represents the temperature distribution at point $\alpha$ in a heat conduction problem,

(b)

$\gamma$ indicates the thermal conductivity coefficient of the material,

(c)

the kernel function $\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)$ represents the heat transfer kernel that describes how heat at point $\eta$ affects the temperature at point $\alpha$,

(d)

the integral from t to r indicates the total accumulation of heat effects over the entire physical domain from point t to r,

(e)

the interval $[t,r]$ represents the physical length of the conducting material.

Theorem 9.

Assume that the kernel function $\mathcal{K}$ satisfies the following condition:

$$\begin{array}{ccc}\hfill \left|\mathcal{K}\right(\alpha ,\eta ,\varpi \left(\eta \right))-\mathcal{K}(\alpha ,\eta ,\varrho \left(\eta \right)\left)\right|& +& \left|\left(\mathcal{K}(\alpha ,\eta ,\varrho (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\kappa (\eta )\right)\right|\hfill \\ & +& \left|\right(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\kappa (\eta \left)\right)|\hfill \\ & \le & \psi \left(\left|\varpi \right(\eta )-\varrho (\eta \left)\right|+\left|\varrho \right(\eta )-\kappa (\eta \left)\right|+\left|\varpi \right(\eta )-\kappa (\eta \left)\right|\right),\hfill \end{array}$$

and consider the nonlinear $\mathbb{IE}$ problem (14). Then, for some constant $0<\gamma \le {\displaystyle \frac{1}{r-t}}$ the Equation (14) has a unique solution $\varpi \in C\left(\right[t,r],\mathbb{R})$.

Proof. 

Let $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ be defined as

$$\mathfrak{F}\varpi \left(\alpha \right)=\gamma \underset{t}{\overset{r}{\int }}\mathcal{K}\left(\alpha ,\eta ,\varpi \left(\eta \right)\right)d\eta ,\mathrm{for}\mathrm{all}\varpi \in \mathfrak{X},$$

where $\mathfrak{X}=C\left(\right[t,r],\mathbb{R})$. Assume for all $\varpi ,\varrho ,\kappa \in \mathfrak{X}$

$$\begin{array}{c}\hfill G(\varpi ,\varrho ,\kappa )=\underset{\eta \in [t,r]}{sup}\left(\left|\varpi \right(\eta )-\varrho (\eta \left)\right|+\left|\varpi \right(\eta )-\kappa (\eta \left)\right|+\left|\varrho \right(\eta )-\kappa (\eta \left)\right|\right).\end{array}$$

It is clear that $(\mathfrak{X},G)$ form a G-complete G-metric space.

$$\begin{array}{ccc}\hfill G\left(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho \right)& =& \underset{\eta \in [t,r]}{sup}\left[\mid \mathfrak{F}\varpi \left(\eta \right)-\mathfrak{F}\varpi \left(\eta \right)\mid +\mid \mathfrak{F}\varpi \left(\eta \right)-\mathfrak{F}\varrho \left(\eta \right)\mid +\mid \mathfrak{F}\varpi \left(\eta \right)-\mathfrak{F}\varrho \left(\eta \right)\mid \right]\hfill \\ & \le & \underset{\eta \in [t,r]}{sup}\mid \gamma \mid \left[\right|\underset{t}{\overset{r}{\int }}\left(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)\right)d\eta |\hfill \\ & & +\left|\underset{t}{\overset{r}{\int }}\left(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\varrho (\eta \left)\right)\right)d\eta \right|\hfill \\ & & +\left|\underset{t}{\overset{r}{\int }}\left(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\varrho (\eta \left)\right)\right)d\eta \right|]\hfill \\ & \le & \underset{\eta \in [t,r]}{sup}\mid \gamma \mid \left[\underset{t}{\overset{r}{\int }}\right|\left(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)\right)|d\eta \hfill \\ & & +\underset{t}{\overset{r}{\int }}\left|\left(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\varrho (\eta \left)\right)\right)\right|d\eta \hfill \\ & & +\underset{t}{\overset{r}{\int }}\left|\left(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\varrho (\eta \left)\right)\right)\right|d\eta ]\hfill \end{array}$$

$$\begin{array}{ccc}& \le & \underset{\eta \in [t,r]}{sup}\mid \gamma \mid \underset{t}{\overset{r}{\int }}\left[\right|\left(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)\right)|\hfill \\ & & +\left|\left(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\varrho (\eta \left)\right)\right)\right|\hfill \\ & & +\left|\left(\mathcal{K}(\alpha ,\eta ,\varpi (\eta \left)\right)-\mathcal{K}(\alpha ,\eta ,\varrho (\eta \left)\right)\right)\right|]d\eta \hfill \\ & \le & \underset{\eta \in [t,r]}{sup}\mid \gamma \mid \underset{t}{\overset{r}{\int }}\left[\psi \left(\left|\varpi \right(\eta )-\varpi (\eta \left)\right|+\left|\varpi \right(\eta )-\varrho (\eta \left)\right|+\left|\varpi \right(\eta )-\varrho (\eta \left)\right|\right)\right]d\eta \hfill \\ & \le & \mid \gamma \mid \psi \left(\underset{\eta \in [t,r]}{sup}\left(\left|\varpi \right(\eta )-\varpi (\eta \left)\right|+\left|\varpi \right(\eta )-\varrho (\eta \left)\right|+\left|\varpi \right(\eta )-\varrho (\eta \left)\right|\right)\right)\underset{t}{\overset{r}{\int }}d\eta \hfill \\ & \le & \psi \left(G(\varpi ,\varpi ,\varrho )\right)\gamma (r-t)\hfill \\ & \le & \psi \left(G(\varpi ,\varpi ,\varrho )\right).\hfill \end{array}$$

Therefore, the nonlinear $\mathbb{FIE}$ (14) has a unique solution. □

6. Application of Nonlinear Fractional Differential Equation

The aim of this part is to introduce an application of Theorem 4 to obtain a common solution of the nonlinear fractional differential equation ($\mathbb{FDE}$) of Caputo type for a pair of generalized $\Psi$-contraction of the operator in G-metric space. The Caputo nonlinear fractional differential equation proposed by Kilbas [30] is given as follows:

$${}^{C}D_{0^{+}}^{\mu }\varpi \left(t\right)=\left\{\begin{array}{c}f(t,\varpi (t\left)\right),t\in (0,1),1<\mu \le 2,\hfill \\ \\ \varpi \left(0\right)=0,\varpi \left(1\right)=\underset{0}{\overset{m}{\int }}\varpi \left(s\right)ds,0<m<1,\hfill \end{array}\right.$$

where ${}^{C}D_{0^{+}}^{\mu }$ represents the ($\mathbb{CFD}$) of order $\mu$ and $f:[0,1]\times \mathbb{R}⟶\mathbb{R}$ is a continuous function. This nonlinear $\mathbb{FDE}$ can also be represented in the form as follows:

$$\begin{array}{ccc}\hfill \varpi \left(t\right)& =& {\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & -& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & +& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}f(\tau ,\varpi \left(\tau \right))d\tau \right]ds.\hfill \end{array}$$

(15)

A function $\varpi \left(t\right)$ is a solution of the defined nonlinear $\mathbb{FDE}$ whenever it is the solution of the $\mathbb{FDE}$ (15) and vice versa.

The physical meaning of function f is:

It indicates the forcing function in the system and describes how the system responds to both time t and the current state $\varpi \left(t\right)$.

Theorem 10.

Consider the space of all continuous functions $\mathfrak{X}=C\left(\right[0,1],\mathbb{R})$ constructed on closed interval $[0,1]$, equipped with a binary relation $\mathfrak{B}=\left(C[0,1]\times C[0,1]\right)$. Let $C\left([0,1],\mathbb{R}\right)$ be the Banach space of all continuous functions from $[0,1]$ into $\mathbb{R}$ with norm $\parallel \varpi \parallel ={sup}_{t\in [0,1]}\mid \varpi \left(t\right)\mid$; for all $\varpi \left(t\right)\in C[0,1]$. This space defines the metric as follows:

$$\begin{array}{c}\hfill G(\varpi ,\varrho ,\kappa )=\underset{t\in [0,1]}{sup}\left(\mid \varpi \left(t\right)-\varrho \left(t\right)\mid +\mid \varpi \left(t\right)-\kappa \left(t\right)\mid +\mid \varrho \left(t\right)-\kappa \left(t\right)\mid \right),forall\varpi ,\varrho ,s\in \mathfrak{X}.\end{array}$$

Now, if we construct self-operator $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ as

$$\begin{array}{ccc}\hfill \mathfrak{F}\varpi \left(t\right)& =& {\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & -& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}f(s,\varpi \left(s\right))ds\hfill \\ & +& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}f(\tau ,\varpi \left(\tau \right))d\tau \right]ds.\hfill \end{array}$$

Then, $\mathfrak{F}$ has a unique $\mathbb{FP}$ if we have the following assumptions:

(1) 

there exists a continuous function $f:[0,1]\times \mathbb{R}⟶\mathbb{R}$ satisfying that

$$\begin{array}{cc}\hfill & \left|f\right(s,\varpi \left(s\right))-f(s,\varpi \left(s\right)\left)\right|+\left|f\right(s,\varpi \left(s\right))-f(s,\varrho \left(s\right)\left)\right|+\left|f\right(s,\varpi \left(s\right))-f(s,\varrho \left(s\right)\left)\right|\hfill \\ & \le \psi \left(\left|\varpi \right(s)-\varpi (s\left)\right|+\left|\varpi \right(s)-\varrho (s\left)\right|+\left|\varpi \right(s)-\varrho (s\left)\right|\right),\hfill \end{array}$$

(2) 

$$\begin{array}{c}\hfill {\displaystyle \frac{t^{\mu }(2-m^2)(\mu +1)+2t(m^{\mu +1}-\mu -1)}{(2-m^2)(\mu +1)}}\le 1.\end{array}$$

Proof. 

Obviously, $C\left([0,1],\mathbb{R}\right)$ is a complete metric space.

(a)

Since $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ is a self operator, and $\mathfrak{B}=\{\mathfrak{X}\times \mathfrak{X}\}$, then for any ${\varpi }_0\in \mathfrak{B}$ we have $\mathfrak{F}{\varpi }_0\in \mathfrak{B}$. Thus, $\left({\varpi }_0,\mathfrak{F}{\varpi }_0\right)\in \mathfrak{B}$, and hence $\mathfrak{B}$ is nonempty.

(b)

For any arbitrary element ${\varpi }_0\in \mathfrak{X}$, the sequence ${\left\{{\mathfrak{F}}^n{\varpi }_0\right\}}_{n\in \mathbb{N}}\subset \mathfrak{X}$, where $\mathfrak{F}:\mathfrak{X}⟶\mathfrak{X}$ is a self-operator. Therefore, $\{{({\mathfrak{F}}^{n-1}\left({\varpi }_0\right),{\mathfrak{F}}^n\left({\varpi }_0\right)\}}_{n\in \mathbb{N}}\subset \mathfrak{B}$, where ${\mathfrak{F}}^0=\mathfrak{I}$, and hence $\mathfrak{B}$ is $\mathfrak{F}$-closed.

(c)

It is only required to prove that $\mathfrak{F}$ is a generalized $\Psi$-contractive operator.

$$\begin{array}{ccc}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )& =& \underset{t\in [0,1]}{sup}\left(\mid \mathfrak{F}\varpi \left(t\right)-\mathfrak{F}\varpi \left(t\right)\mid +\mid \mathfrak{F}\varpi \left(t\right)-\mathfrak{F}\varrho \left(t\right)\mid +\mid \mathfrak{F}\varrho \left(t\right)-\mathfrak{F}\varpi \left(t\right)\mid \right)\hfill \\ & =& \underset{t\in [0,1]}{sup}\left|{\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}\right(\left[f(s,\varpi (s\left)\right)-f(s,\varpi (s\left)\right)\right]\hfill \\ & & +\left[f(s,\varpi (s\left)\right)-f(s,\varrho (s\left)\right)\right]+\left[f(s,\varpi (s\left)\right)-f(s,\varrho (s\left)\right)\right])\hfill \\ & & -{\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}(\left[f(s,\varpi (s\left)\right)-f(s,\varpi (s\left)\right)\right]\hfill \\ & & +\left[f(s,\varpi (s\left)\right)-f(s,\varrho (s\left)\right)\right]+\left[f(s,\varpi (s\left)\right)-f(s,\varrho (s\left)\right)\right])ds\hfill \\ & & +{\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}\right(\left[f(\tau ,\varpi (\tau \left)\right)-f(\tau ,\varpi (\tau \left)\right)\right]\hfill \\ & & +\left[f(\tau ,\varpi (\tau \left)\right)-f(\tau ,\varrho (\tau \left)\right)\right]+\left[f(\tau ,\varpi (\tau \left)\right)-f(\tau ,\varrho (\tau \left)\right)\right]\left)d\tau \right]ds|\hfill \\ & =& \underset{t\in [0,1]}{sup}\left[{\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}\right(|f(s,\varpi \left(s\right))-f(s,\varpi \left(s\right))|\hfill \\ & & +\left|f\right(s,\varpi \left(s\right))-f(s,\varrho \left(s\right)\left)\right|+\left|f\right(s,\varpi \left(s\right))-f(s,\varrho \left(s\right)\left)\right|)ds\hfill \\ & & -{\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}\left(\right|f(s,\varpi \left(s\right))-f(s,\varpi \left(s\right))|\hfill \\ & & +\left|f\right(s,\varpi \left(s\right))-f(s,\varrho \left(s\right)\left)\right|+\left|f\right(s,\varpi \left(s\right))-f(s,\varrho \left(s\right)\left)\right|)ds\hfill \\ & +& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}\right(|f(\tau ,\varpi \left(\tau \right))-f(\tau ,\varpi \left(\tau \right))|\hfill \\ & & +\left|f\right(\tau ,\varpi \left(\tau \right))-f(\tau ,\varrho \left(\tau \right)\left)\right|+\left|f\right(\tau ,\varpi \left(\tau \right))-f(\tau ,\varrho \left(\tau \right)\left)\right|\left)d\tau \right]ds]\hfill \\ & \le & \underset{t\in [0,1]}{sup}[{\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}\psi \left(\right|\varpi \left(s\right)-\varpi \left(s\right)|+|\varpi \left(s\right)-\varrho \left(s\right)|\hfill \\ & & +|\varpi \left(s\right)-\varrho \left(s\right)|)ds-{\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}\psi (|\varpi \left(s\right)-\varpi \left(s\right)|\hfill \\ & & +|\varpi \left(s\right)-\varrho \left(s\right)|+|\varpi \left(s\right)-\varrho \left(s\right)|)ds+{\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\hfill \\ & & \underset{0}{\overset{m}{\int }}[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}\psi \left(\right|\varpi \left(\tau \right)-\varpi \left(\tau \right)|+|\varpi \left(\tau \right)-\varrho \left(\tau \right)|\hfill \\ & & +\left|\varpi \right(\tau )-\varrho (\tau \left)\right|\left)d\tau \right]]ds\hfill \end{array}$$

$$\begin{array}{ccc}& =& {\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}\psi \left(\underset{t\in [0,1]}{sup}\left(\left|\varpi \right(s)-\varpi (s\left)\right|+\left|\varpi \right(s)-\varrho (s\left)\right|+\left|\varpi \right(s)-\varrho (s\left)\right|\right)\right)ds\hfill \\ & -& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}\psi \left(\underset{t\in [0,1]}{sup}\right(|\varpi \left(s\right)-\varpi \left(s\right)|\hfill \\ & & +\left|\varpi \right(s)-\varrho (s\left)\right|+\left|\varpi \right(s)-\varrho (s\left)\right|\left)\right)ds\hfill \\ & +& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}\psi \right(\underset{t\in [0,1]}{sup}(|\varpi \left(\tau \right)-\varpi \left(\tau \right)|\hfill \\ & & +\left|\varpi \right(\tau )-\varrho (\tau \left)\right|+\left|\varpi \right(\tau )-\varrho (\tau \left)\right|\left)\right)d\tau ]ds\hfill \\ & =& {\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}\psi \left(G(\varpi ,\varpi ,\varrho )\right)\hfill \\ & -& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}\psi \left(G(\varpi ,\varpi ,\varrho )\right)ds\hfill \\ & +& {\displaystyle \frac{2t}{(2-m^2)\Gamma \left(\mu \right)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}\psi \left(G(\varpi ,\varpi ,\varrho )\right)d\tau \right]ds.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}& & G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\hfill \\ & \le & {\displaystyle \frac{\psi \left(G(\varpi ,\varpi ,\varrho )\right)}{\Gamma \left(\mu \right)}}[\underset{0}{\overset{t}{\int }}{(t-s)}^{\mu -1}ds-{\displaystyle \frac{2t}{(2-m^2)}}\underset{0}{\overset{1}{\int }}{(1-s)}^{\mu -1}ds\hfill \\ & & +{\displaystyle \frac{2t}{(2-m^2)}}\underset{0}{\overset{m}{\int }}\left[\underset{0}{\overset{s}{\int }}{(s-\tau )}^{\mu -1}d\tau \right]ds]\hfill \\ & =& {\displaystyle \frac{\psi \left(G(\varpi ,\varpi ,\varrho )\right)}{\mu \Gamma \left(\mu \right)}}\left[t^{\mu }-{\displaystyle \frac{2t}{(2-m^2)}}+{\displaystyle \frac{2t}{(2-m^2)}}\times {\displaystyle \frac{m^{\mu +1}}{(\mu +1)}}\right]\hfill \\ & =& {\displaystyle \frac{\psi \left(G(\varpi ,\varpi ,\varrho )\right)}{\mu \Gamma \left(\mu \right)}}\left[{\displaystyle \frac{t^{\mu }(2-m^2)(\mu +1)+2t(m^{\mu +1}-\mu -1)}{(2-m^2)(\mu +1)}}\right].\hfill \end{array}$$

By using given condition $\left(3\right)$, we obtain

$$\begin{array}{c}\hfill G(\mathfrak{F}\varpi ,\mathfrak{F}\varpi ,\mathfrak{F}\varrho )\le \psi \left(G(\varpi ,\varpi ,\varrho )\right).\end{array}$$

Therefore, all the hypothesis of Theorem 4 are satisfied; hence, $\mathfrak{F}$ has a unique $\mathbb{FP}$. □

Numerical Solution of Fractional Initial Value Problems

In this section, we present a numerical spectral approach to obtain a semi-analytic solution for the following fractional initial value problem:

$${}^{C}D_{0^{+}}^{\mu }\varpi \left(t\right)=f\left(t,\varpi \left(t\right)\right),t\in (0,1),1<\mu \le 2,$$

(16)

subject to the following homogeneous initial conditions:

$$\varpi \left(0\right)={\varpi }^{\prime }\left(0\right)=0.$$

(17)

We assume the following approximate solution:

$$\varpi \left(t\right)\approx {\varpi }_n\left(t\right)=\sum _{i=0}^n{u}_i{t}^2{C}_i\left(t\right),$$

where $C_i\left(t\right)=cos\left(i{cos}^{-1}(2t-1)\right)$ represents the shifted Chebyshev polynomials of the first kind [44]. This choice ensures that the approximate solution inherently satisfies the homogeneous initial conditions in (17).

Note 1.

If the initial value problem (16) satisfies nonhomogeneous initial conditions, such as the following:

$$y\left(0\right)=y_0,y^{\prime }\left(0\right)=y_1,$$

we can apply the following transformation:

$$y\left(t\right)=u\left(t\right)+y_0+y_{1}t.$$

With this substitution, $u\left(t\right)$ satisfies the homogeneous initial conditions given in (17).

Lemma 1.

The following power series representation of the shifted Chebyshev polynomials holds [45]:

$$C_{\ell }\left(t\right)=\ell \sum _{k=0}^{\ell }{\displaystyle \frac{{(-1)}^{\ell -k}{2}^{2k}(\ell +k-1)!}{(\ell -k)!\left(2k\right)!}}{t}^k,\ell >0.$$

(18)

Theorem 11.

The following fractional derivative formula holds:

$${}^{C}D_{0^{+}}^{\mu }\left[t^2{C}_i\left(t\right)\right]={\displaystyle \frac{2{(-1)}^i}{\Gamma (3-\mu )}}{t}^{2-\mu }{}_{3}F_2\left(3,-i,i;{\displaystyle \frac{1}{2}},3-\mu ;t\right).$$

Proof. 

Using Lemma 1, we express the following:

$$t^2{C}_i\left(t\right)=i\sum _{k=0}^i{\displaystyle \frac{{(-1)}^{i-k}{2}^{2k}(i+k-1)!}{(i-k)!\left(2k\right)!}}{t}^{k+2}.$$

Applying the fractional derivative ${}^{C}D_{0^{+}}^{\mu }$, we obtain the following:

$${}^{C}D_{0^{+}}^{\mu }\left[t^2{C}_i\left(t\right)\right]=\sum _{k=0}^i{\displaystyle \frac{i{4}^k{(-1)}^{i-k}\Gamma (k+3)\Gamma (i+k)}{\left(2k\right)!(i-k)!\Gamma (k-\mu +3)}}{t}^{k+2-\mu },$$

and simplifying the right-hand side yields the desired result. □

The residual of (16) is given by the following:

$$R\left(t\right){=}^C{D}_{0^{+}}^{\mu }{\varpi }_n\left(t\right)-f\left(t,{\varpi }_n\left(t\right)\right).$$

Using Theorem 1, we express the simplified residual as follows:

$$\tilde{R}\left(t\right)=t^{\mu }R\left(t\right)=t^2\sum _{i=0}^n{u}_i{\displaystyle \frac{2{(-1)}^i}{\Gamma (3-\mu )}}{}_{3}F_2\left(3,-i,i;{\displaystyle \frac{1}{2}},3-\mu ;t\right)-t^{\mu }f\left(t,t^2\sum _{i=0}^n{u}_i{C}_i\left(t\right)\right).$$

Applying the collocation method at the first roots of $C_{n+1}\left(t\right)$, denoted by $t_i$ for $i=1\left(1\right)n+1$, we obtain the following:

$$\tilde{R}\left(t_i\right)=0,i=1,2,...,n+1.$$

(19)

Newton’s iterative method with a vanishing initial guess is employed to solve the resulting system of $(n+1)$ nonlinear algebraic equations, yielding the unknown expansion coefficients $u_i$.

Example 10.

Consider the following fractional initial value problem [46]:

$${}^{C}D_{0^{+}}^{\alpha }y\left(x\right)={\displaystyle \frac{40320}{\Gamma (9-\alpha )}}{x}^{8-\alpha }-3{\displaystyle \frac{\Gamma (5+\alpha /2)}{\Gamma (5-\alpha /2)}}{x}^{4-\alpha /2}+{\displaystyle \frac{9}{4}}\Gamma (\alpha +1)+{\left({\displaystyle \frac{3}{2}}{x}^{\alpha /2}-x^4\right)}^3-{\left[y\left(x\right)\right]}^{3/2}.$$

The initial conditions are homogeneous: $y\left(0\right)=0$, $y^{\prime }\left(0\right)=0$. The exact solution is as follows:

$$y\left(x\right)=x^8-3x^{4+\alpha /2}+{\displaystyle \frac{9}{4}}{x}^{\alpha }.$$

We apply the proposed Chebyshev collocation method.

Table 1. Absolute Errors of Example 10 for $\alpha ={\displaystyle \frac{5}{4}}$.

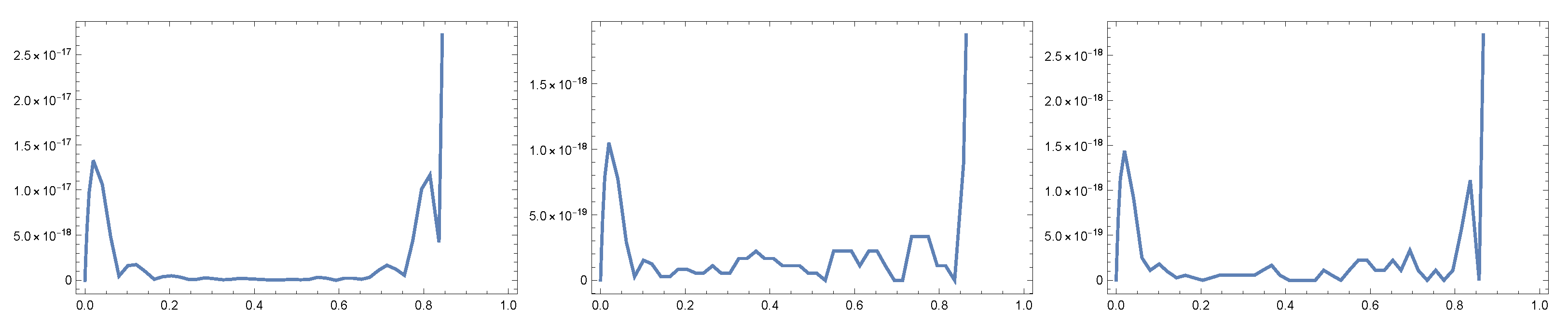
n	4	6	8	10
Absolute Error	$2.3\times {10}^{-5}$	$3.7\times {10}^{-10}$	$5.2\times {10}^{-16}$	$2.2\times {10}^{-16}$

lists the absolute errors for different values of n, while

Table 2. Comparison between best errors of Example 10 for $\alpha ={\displaystyle \frac{5}{4}}$.

Present Method $\mathit{n}=10$	Predictor-Corrector Method [46]
$2.2\times {10}^{-16}$	$3.25\times {10}^{-11}$

compares our best error with that reported in [46].

Example 11.

Consider the fractional oscillator problem arising in physics [47]:

$$D^{\mu }u\left(t\right)+u\left(t\right)=0,u\left(0\right)=1,u^{\prime }\left(0\right)=0,t\in (0,L),$$

where $1<\mu \le 2$. The exact solution is given by the following:

$$u\left(t\right)=\sum _{k=0}^{+\infty }{\displaystyle \frac{{(-t^{\mu })}^k}{\Gamma (k\mu +1)}}=E_{\mu }(-t^{\mu }),$$

where $E_{\mu }\left(t\right)$ denotes the well-known Mittag–Leffler function.

Table 3. Maximum pointwise error of Example 11 ($n=16$).

$\mathit{\mu }$	1.95	1.9	1.85	1.8	1.75
[47]	$3.47\times {10}^{-14}$	$2.52\times {10}^{-13}$	$5.78\times {10}^{-12}$	$2.71\times {10}^{-11}$	$3.25\times {10}^{-11}$
Our Method	$5.72\times {10}^{-15}$	$2.78\times {10}^{-15}$	$2.51\times {10}^{-14}$	$7.64\times {10}^{-14}$	$2.22\times {10}^{-14}$

compares our method with the fifth-kind Chebyshev method proposed in [47], using the following truncated series:

$$u\left(t\right)=\sum _{k=0}^{10}{\displaystyle \frac{{(-t^{\mu })}^k}{\Gamma (k\mu +1)}}=E_{\mu }(-t^{\mu }).$$

In Table 3, we compare our method and the fifth-kind Chebyshev method offered in [47], we compare the numerical solutions with the following solution,

$$u\left(t\right)=\sum _{k=0}^{10}{\displaystyle \frac{{\left(-t^{\mu }\right)}^k}{\Gamma (k\mu +1)}}=E_{\mu }\left(-t^{\mu }\right).$$

Example 12.

Consider the following fractional nonlinear Bratu’s initial value problem appears in physics [48]:

$${}^{C}D_{0^{+}}^{\alpha }y\left(x\right)=2e^{y\left(x\right)}.$$

The initial conditions are homogeneous: $y\left(0\right)=0$, $y^{\prime }\left(0\right)=0$. The exact solution is available only when $\alpha =2$:

$$y\left(x\right)=-2ln(cos(x\left)\right).$$

We apply the proposed Chebyshev collocation method.

Table 4. Maximum residual errors of Example 12 for different values of $\alpha$.

n	3	7	11	15
$\alpha =1.9$	$3.4\times {10}^{-4}$	$7.2\times {10}^{-9}$	$2.6\times {10}^{-14}$	$2.2\times {10}^{-17}$
$\alpha =1.8$	$5.3\times {10}^{-4}$	$8.1\times {10}^{-9}$	$3.8\times {10}^{-14}$	$2.2\times {10}^{-17}$
$\alpha =1.7$	$2.7\times {10}^{-4}$	$6.3\times {10}^{-9}$	$4.7\times {10}^{-14}$	$2.2\times {10}^{-17}$

lists the maximum residual errors for different values of n, where the residual error is defined by

$$re{s}_n\left(x\right)={|}^C{D}_{0^{+}}^{\alpha }{y}_n\left(x\right)-2e^{y_n\left(x\right)}|.$$

In Figure 2, we depict the residual errors for different values of α, when $n=15$, these results show the exponential convergence.

From the results presented in Table 1, Table 2, Table 3 and Table 4, we confirm that our proposed method demonstrates superior accuracy compared to the approach presented in recent literature. This highlights the effectiveness and superiority of our method over other contemporary techniques published in reputable journals.

7. Conclusions and Future Work

This manuscript contributes significantly to the field of mathematical analysis by introducing new results within the framework of G-metric spaces. The research expands upon existing findings, providing a deeper understanding of $\mathbb{FP}$ theorems for single and paired operators in G-metric spaces. The application of these theorems to establish the existence of unique solutions for boundary value problems, Fredholm-type integral equations, and Caputo fractional differential equations in G-metric spaces not only confirms the theoretical outcomes but also underscores their practical importance. Looking forward, several promising directions for future research in $C^{*}$-metric spaces present themselves. Extending the results obtained in G-metric spaces to modular metric space and modular G-metric space and investigating the application of these $\mathbb{FP}$ theorems in solving more complex differential and integral equations within such spaces could be particularly valuable. We also discuss the numerical solution of fractional initial value problems using the spectral collocation method to provide a comprehensive study.