Applying a Gain Scheduled Fractional Order Proportional Integral and Derivative Controller to a Quadratic Buck Converter
Abstract
1. Introduction
- •
- To present a fractional order Proportional Integral and Derivative controller with adaptation characteristics;
- •
- To apply a fractional order PID to control the voltage of a DC–DC buck quadratic converter (QBC);
- •
- To simulate the system with different output voltages and different loads.
2. Quadratic Buck Switched Converter Model
2.1. ON–OFF Equations
2.2. Quadratic Buck Switched Model
2.3. Quadratic Buck Average Model
3. Description of the Controllers
3.1. Classical PID
3.2. Gain Scheduling PID
3.3. Fractional Order Controllers
3.3.1. Fractional Order PID
3.3.2. Gain Scheduling Fractional Order PID
3.4. Stability of the Sytem
4. Analysis of System Response Under the Controllers
4.1. Analysis of the System
4.2. Tuning PID Controllers
Fractional Order Tuning
4.3. Closed-Loop System Response
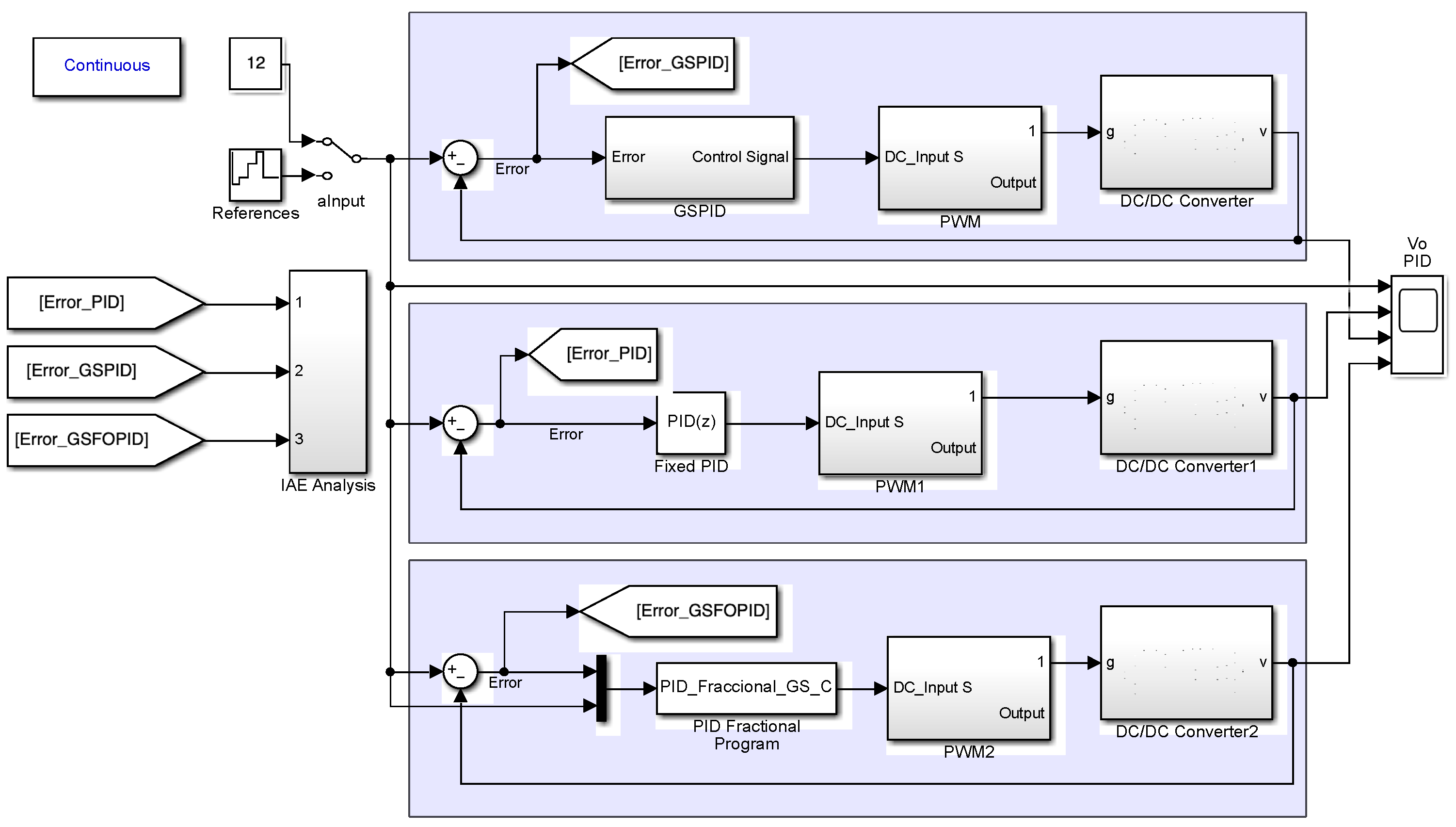
4.3.1. Simulation Overview
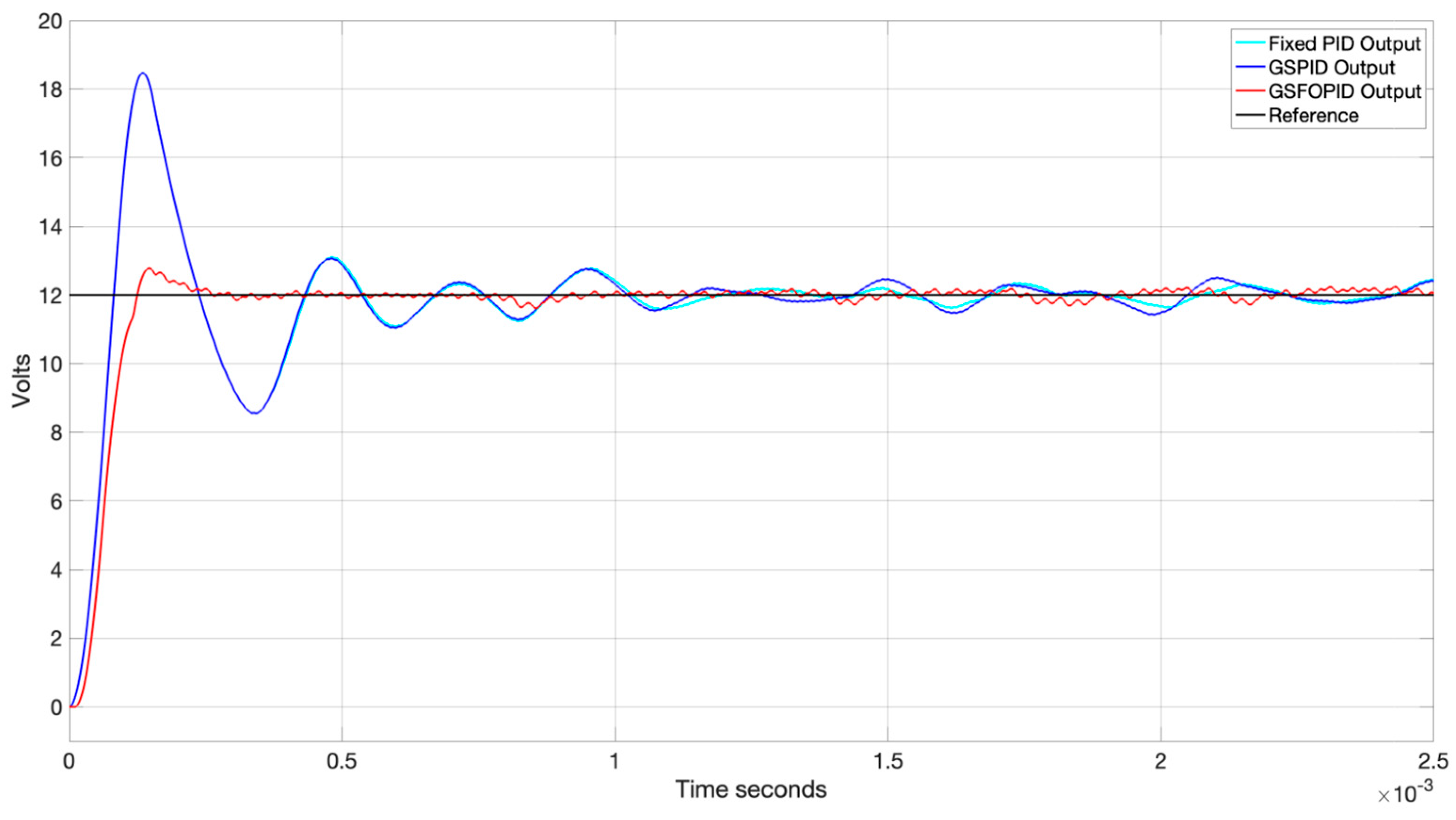
4.3.2. Scenario 1: Reference Voltage Change
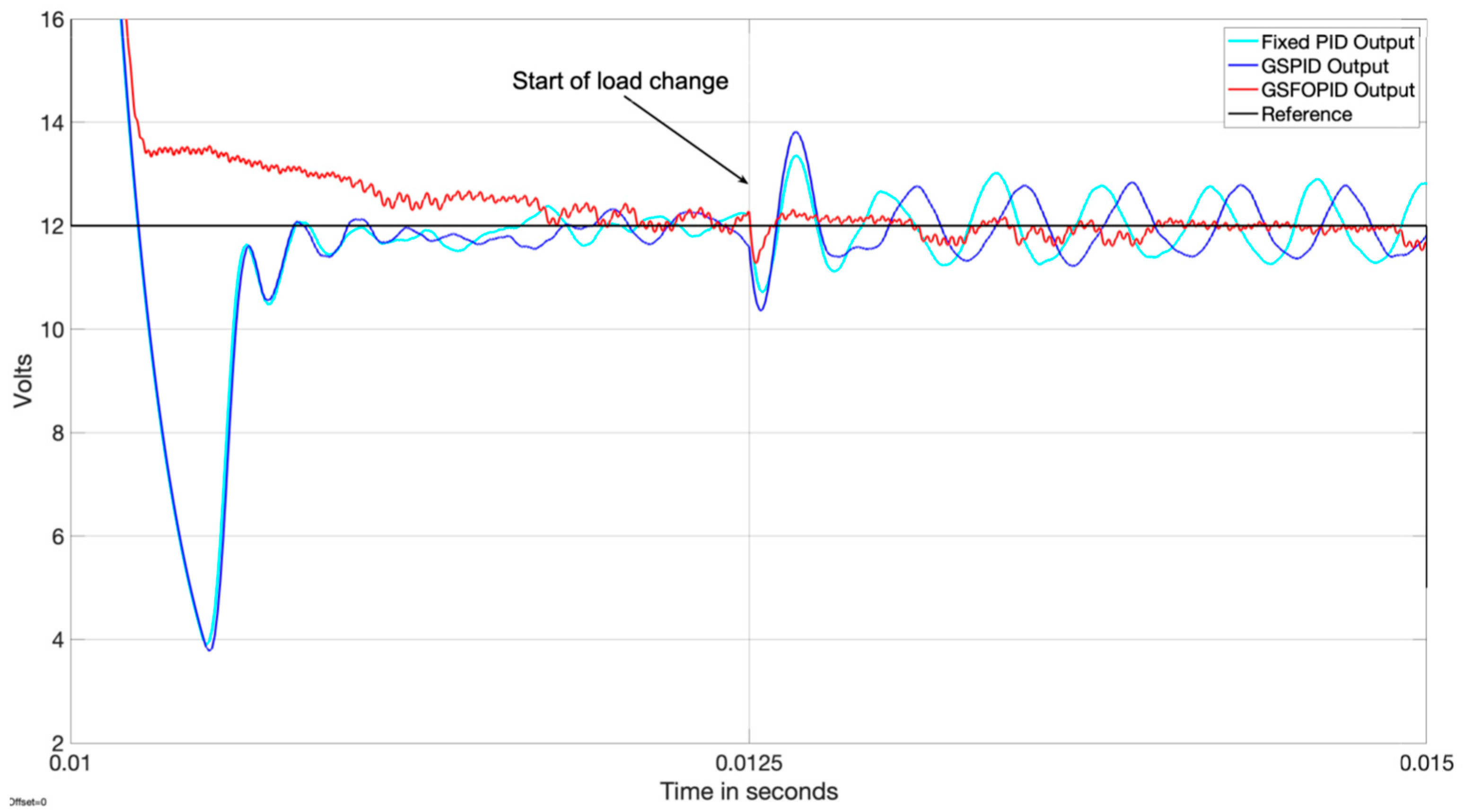
4.3.3. Scenario 2: Load Change
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Okati, M.; Eslami, M.; Shahbaz, M.J. A New Transformerless DC/DC Converter with Dual Operating Modes and Continuous Input Current Port. IET Gener. Transm. Distrib. 2023, 17, 1553–1567. [Google Scholar] [CrossRef]
- Okati, M.; Eslami, M.; Shahbazzadeh, M.J. A Non-Isolated DC-DC Converter with Dual Working Modes and Positive Output Voltage. Electr. Power Compon. Syst. 2021, 49, 1143–1157. [Google Scholar] [CrossRef]
- Okati, M.; Eslami, M.M.; Jafari Shahbazzadeh, M.; Shareef, H. A New Transformerless Quadratic Buck-Boost Converter with High Voltage Gain Ratio and Continuous Input/Output Current Port. IET Power Electron. 2022, 15, 1280–1294. [Google Scholar] [CrossRef]
- Damodaran, R.V.; Shareef, H.; Errouissi, R.; Eslami, M. A Common Ground Four Quadrant Buck Converter for DC-AC Conversion. IEEE Access 2022, 10, 44855–44868. [Google Scholar] [CrossRef]
- Pandey, K.; Kumar, M.; Kumari, A.; Kumar, J. Control of Quadratic Buck Converter Using Non-Linear Controller. In Proceedings of the IEEE 17th India Council International Conference (INDICON), New Delhi, India, 11–13 December 2020. [Google Scholar] [CrossRef]
- Arteaga-Orozco, M.I. Nonlinear Control of Switched DC/DC Converters: Performance Analysis and Experimental Verification. Ph.D. Thesis, UPC, Institut d’Organització i Control de Sistemes Industrials, Barcelona, Spain, 2007. [Google Scholar] [CrossRef]
- Ali, M.S.; Soliman, M.; Hussein, A.M. Robust Controller of Buck Converter Feeding Constant Power Load. J. Control Autom. Electr. Syst. 2021, 32, 153–164. [Google Scholar] [CrossRef]
- Trakuldit, S.; Tattiwong, K.; Bunlaksananusorn, C. Design and evaluation of a Quadratic Buck Converter. In Proceedings of the 8th International Conference on Power and Energy Systems Engineering (CPESE 2021), Fukuoka, Japan, 10–12 September 2021. [Google Scholar]
- Carbajal-Gutierrez, E.E.; Morales-Saldana, J.A.; Leyva-Ramos, J. Modeling of a Single-Switch Quadratic Buck Converter. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1451–1457. [Google Scholar] [CrossRef]
- Ortiz-Lopez, M.; Leyva-Ramos, J.; Carbajal-Gutierrez, E.E.; Morales-Saldana, J.A. Modelling and analysis of switch-mode cascade converters with a single active switch. IET Power Electron. 2008, 1, 478–487. [Google Scholar] [CrossRef]
- Ayachit, A.; Kazimierczuk, M.K. Steady-state analysis of PWM quadratic buck converter in CCM. In Proceedings of the IEEE 56th International Midwest Symposium on Circuits and Systems (MWSCAS), Columbus, OH, USA, 4–7 August 2013. [Google Scholar]
- Mostaan, A.; Gorji, S.A.; Soltani, M.; Ektesabi, M. A novel quadratic buck-boost DC-DC converter without floating gate-driver. In Proceedings of the 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016. [Google Scholar] [CrossRef]
- Bonela, A.K.; Sarkar, M.K.; Kumar, K. Robust non-fragile control of DC–DC buck converter. Electr. Eng. 2024, 106, 983–991. [Google Scholar] [CrossRef]
- Montano-Saavedra, A.C.; Barra-Junior, W.; de Medeiros, R.L.P.; Roozembergh-Junior, C.; Sovano-Gomes, A. Experimental Evaluation of the Robust Controllers Applied on a Single Inductor Multiple Output DC-DC Buck Converter to Minimize Cross Regulation Considering Parametric Uncertainties and CPL Power Variations. Energies 2024, 17, 3359. [Google Scholar] [CrossRef]
- Kumari, S.; Rayguru, M.M.; Upadhyaya, S. Analysis of Model Predictive Controller versus Linear Quadratic Regulator for DC-DC Buck Converter Systems. In Proceedings of the IEEE International Conference on Intelligent Computing and Control Systems, Madurai, India, 17–19 May 2023. [Google Scholar]
- Raza, M.M.; Rayguru, M.M.; Kaushik, G. Robust Model Predictive Control of a Buck Converter with Constraints. In Proceedings of the International Conference on Computational Intelligence and Sustainable Engineering Solutions (CISES), New Delhi, India, 28–30 April 2023. [Google Scholar]
- Fetene, Y.; Ayenew, E.; Feleke, S. Full state observer-based pole placement controller for pulse width modulation switched mode voltage-controlled buck Converter. Heliyon 2024, 10, e30662. [Google Scholar] [CrossRef] [PubMed]
- Nanyan, N.F.; Ahmad, M.A.; Hekimoglu, B. Optimal PID controller for the DC-DC buck converter using the improved sine cosine algorithm. Results Control. Optim. 2024, 14, 100352. [Google Scholar] [CrossRef]
- Bui, V.-H.; Mohammadi, S.; Das, S.; Hussain, A.; Hollweg, G.V.; Su, W. A critical review of safe reinforcement learning strategies in power and energy systems. Eng. Appl. Artif. Intell. 2025, 143, 110091. [Google Scholar] [CrossRef]
- Lopez-Santos, O.; Flores-Bahamonde, F.; Torres-Pinzon, C.A.; Haroun, R.; Valderrama-Blavi, H.; Garriga, J.A.; Martınez-Salamero, L. Multi-loop Sliding-Mode Control for a Battery Charger Using a Quadratic Buck Converter. In Proceedings of the IEEE 8th Southern Power Electronics Conference (SPEC), Florianopolis, Brazil, 4–6 December 2023. [Google Scholar]
- Pop, G.M.; Pop-Calimanu, I.M.; Lascu, D. Fourth-Order Quadratic Buck Converter Controller Design. Sensors 2024, 24, 557. [Google Scholar] [CrossRef] [PubMed]
- Acosta-Rodriguez, R.A.; Martinez-Sarmiento, F.H.; Munoz-Hernandez, G.A.; Portilla-Flores, E.A.; Salcedo-Parra, O.J. Validation of Passivity-Based Control and Array PID in High-Power Quadratic Buck Converter Through Rapid Prototyping. IEEE Access 2024, 12, 58288–58316. [Google Scholar] [CrossRef]
- Karaket, K.; Bunlaksananusorn, C. Modeling of a Quadratic Buck Converter. In Proceedings of the 8th Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI), Khon Kaen, Thailand, 17–19 May 2011. [Google Scholar]
- Ogata, K. Ingeniería de Control Moderna, 5th ed.; Pearson Education: Madrid, Spain, 2010. (In Spanish) [Google Scholar]
- Orelind, G.; Wozniak, L.; Medanic, J.; Whitemore, T. Optimal PID gain schedule for Hydrogenerators-Design and application. IEEE Trans. Energy Convers. 1989, 4, 300–307. [Google Scholar] [CrossRef]
- Petras, I. Fractional Calculus and Applied Analyisis. Int. J. Theory Appl. 2012, 15, 282–303. [Google Scholar]
- Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent -I. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional Order Systems and Controls: Fundamentals and Applications; Johnson, Ed.; Springer-Verlag: London, UK, 2010; p. 414. [Google Scholar]
- Podlubny, I.; Dorcak, L.; Kostial, I. On Fractional Derivatives, Fractional-Order Dynamic Systems and PIlDu Controllers. In Proceedings of the Conference on Decision and Control, San Diego, CA, USA, 10–12 December 1997. [Google Scholar]
- Podlubny, I. Fractional-Order Systems and PILDu-Controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Podlubny, I.; Dorcak, L.; Feliu, V. On Fractional PID Controllers: A Frequency Domain Aproach. In Proceedings of the IFAC Digital Control: Past, Present and Future of PID Control, Terrassa, Spain, 5–7 April 2000. [Google Scholar]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y.Q. On Auto-Tuning of Fractional Order PIlDu Controllers. In Proceedings of the 2nd IFAB Workshop on Fractional Differentiation and its Applications, Porto, Portugal, 19–21 July 2006. [Google Scholar]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y.Q. Tuning and auto-tuning of fractional order controllers for industry applications. Control. Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef]
- Petras, I. Tuning and implementation methods for fractional-order controllers. Fract. Calc. Appl. Anal. 2012, 15, 282–303. [Google Scholar] [CrossRef]
- Milanesi, M.; Padula, F.; Visioli, A. On the implementation of gain scheduling in FOPID controllers. IFAC Pap. Online 2024, 58, 330–335. [Google Scholar] [CrossRef]
- Ayere-Junior, F.A.C.; Bessa, I.; Batista-Pereira, V.M.; Da Silva-Farias, N.J.; de Menezes, A.R.; de Medeiros, R.L.P.; Chavez-Filho, J.E.; Lenzi, M.K.; Da Costa-Junior, C.T. Fractional Order Pole Placement for a buck converter based on commensurable transfer function. ISA Trans. 2020, 107, 370–384. [Google Scholar]
- Wu, Z.; Li, D.; Xue, Y.; He, T.; Zheng, S. Tuning for Fractional Order PID Controller based on Probabilistic Robustness. IFAC Pap. Online 2018, 51, 675–680. [Google Scholar] [CrossRef]
- Awouda, A.E.A.; Mamat, R.B. Refine PID tuning rule using ITAE criteria. In Proceedings of the 2010 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010. [Google Scholar]
- Chen, Y.Q.; Petras, I.; Xue, D. Fractional Order Control—A Tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar]
- Choudhary, S.K. Stability and Performance Analysis of Fractional Order Control Systems. WSEAS Trans. Syst. Control 2014, 9, 438–444. [Google Scholar]
- Dewangan, P.D.; Singh, V.P.; Sinha, S.L. Design of FOPID controller for higher order continuous interval system using improved approximation ensuring stability. SN Appl. Sci. 2021, 3, 493. [Google Scholar] [CrossRef]
- Rhouma, A.; Hafsi, S.; Laabidi, K. Stabilizing and Robust Fractional PID Controller Synthesis for Uncertain First-Order plus Time-Delay Systems. Math. Probl. Eng. Hindawi 2021, 2021, 9940634. [Google Scholar] [CrossRef]
- Matignon, D. Generalized Fractional Differential and Difference Equations: Stability Properties and Modelling Issues. In Proceedings of the Mathematical Theory of Networks and Systems Symposium, Padova, Italy, 6–10 July 1998. [Google Scholar]
- Astrom, K.J.; Wittenmark, B. Adaptive Control; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Sangeetha, S.; Revathi, B.S.; Balamurugan, K.; Suresh, G. Performance analysis of buck converter with fractional PID controller using hybrid technique. Robot. Auton. Syst. 2023, 169, 104515. [Google Scholar] [CrossRef]





| Voltage | K | Ki | Kd |
|---|---|---|---|
| 5 V | 0.44437 | 5347.5 | 8.715 × 10−6 |
| 12 V | 0.44377 | 5309.2 | 8.76 × 10−6 |
| 24 V | 0.4431 | 5250 | 8.8275 × 10−6 |
| 36 V | 0.44325 | 5194.5 | 8.94 × 10−6 |
| Voltage | K | Ki | Kd |
|---|---|---|---|
| 5 V | 34.82 | 9.69 × 105 | 2.495 × 10−4 |
| 12 V | 48.88 | 1.3 × 105 | 3.877 × 10−4 |
| 24 V | 2.769 | 3.012 × 103 | 5.549 × 10−4 |
| 36 V | 62.36 | 7.101 × 105 | 1.195 × 10−4 |
| Voltage | λ | δ |
|---|---|---|
| 5 V | 1.25 | 1.15 |
| 12 V | 1.25 | 1.15 |
| 24 V | 1.14 | 0.875 |
| 36 V | 1.7 | 0.95 |
| Voltage | Fixed PID | GS-PID | GS-FO-PID |
|---|---|---|---|
| 5 V | 50% | 50% | 20% |
| 12 V | 50% | 50% | 0% |
| 24 V | 65% | 68% | 0% |
| 36 V | 70% | 50% | 1% |
| Voltage | Fixed PID | GS-PID | GS-FO-PID |
|---|---|---|---|
| 5 V | 0.8673 × 10−3 | 0.8686 × 10−3 | 0.5886 × 10−3 |
| 12 V | 1.356 × 10−3 | 1.448 × 10−3 | 0.7999 × 10−3 |
| 24 V | 2.895 × 10−3 | 2.972 × 10−3 | 2.059 × 10−3 |
| 36 V | 3.056 × 10−3 | 2.484 × 10−3 | 2.207 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munoz Hernandez, G.A.; Guerrero-Castellanos, J.F.; Acosta-Rodriguez, R.A. Applying a Gain Scheduled Fractional Order Proportional Integral and Derivative Controller to a Quadratic Buck Converter. Fractal Fract. 2025, 9, 160. https://doi.org/10.3390/fractalfract9030160
Munoz Hernandez GA, Guerrero-Castellanos JF, Acosta-Rodriguez RA. Applying a Gain Scheduled Fractional Order Proportional Integral and Derivative Controller to a Quadratic Buck Converter. Fractal and Fractional. 2025; 9(3):160. https://doi.org/10.3390/fractalfract9030160
Chicago/Turabian StyleMunoz Hernandez, German Ardul, Jose Fermi Guerrero-Castellanos, and Rafael Antonio Acosta-Rodriguez. 2025. "Applying a Gain Scheduled Fractional Order Proportional Integral and Derivative Controller to a Quadratic Buck Converter" Fractal and Fractional 9, no. 3: 160. https://doi.org/10.3390/fractalfract9030160
APA StyleMunoz Hernandez, G. A., Guerrero-Castellanos, J. F., & Acosta-Rodriguez, R. A. (2025). Applying a Gain Scheduled Fractional Order Proportional Integral and Derivative Controller to a Quadratic Buck Converter. Fractal and Fractional, 9(3), 160. https://doi.org/10.3390/fractalfract9030160








