A Compact Difference-Galerkin Spectral Method of the Fourth-Order Equation with a Time-Fractional Derivative
Abstract
1. Introduction
2. Algebraic Equation and Preliminaries
2.1. Variational Equations for the Fourth-Order Equation
2.2. Galerkin–Legendre Scheme
2.3. Algebraic Equation of Weak Form with the Boundary Conditions
2.4. Preliminary Lemmas
3. Some Lemmas
4. Main Results
5. Numerical Experiments
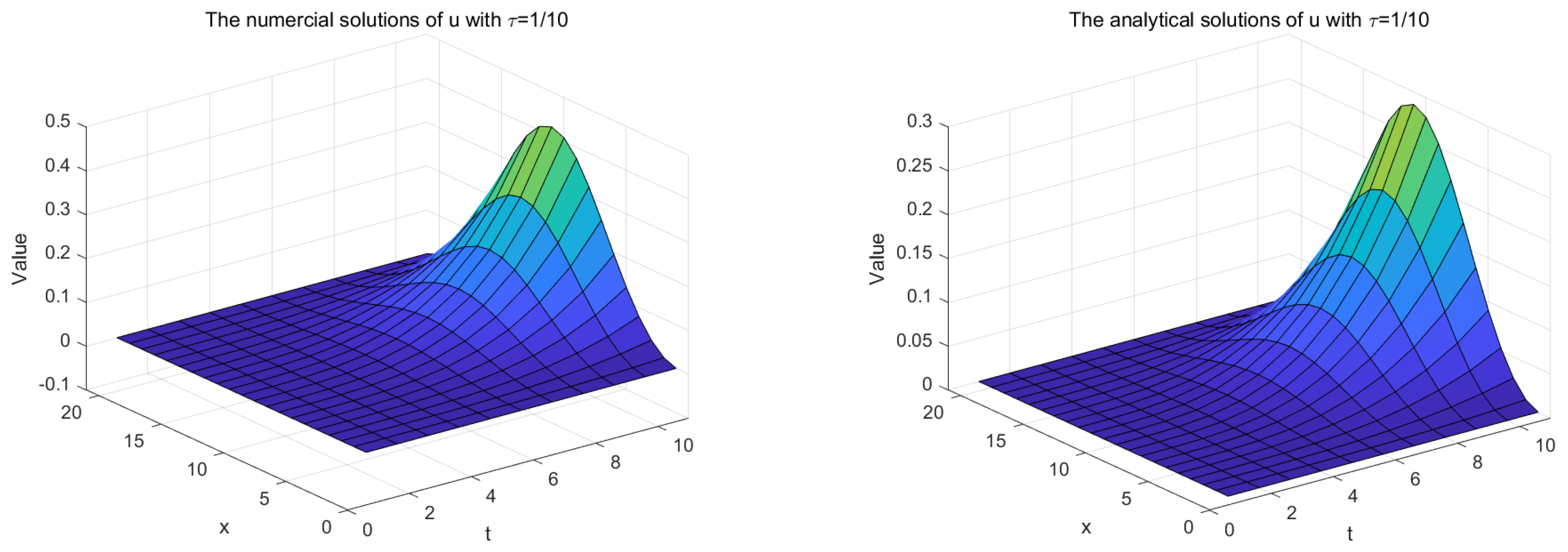
5.1. One-Dimensional Time-Fractional Fourth-Order System
5.2. Two-Dimensional Time-Fractional Fourth-Order System
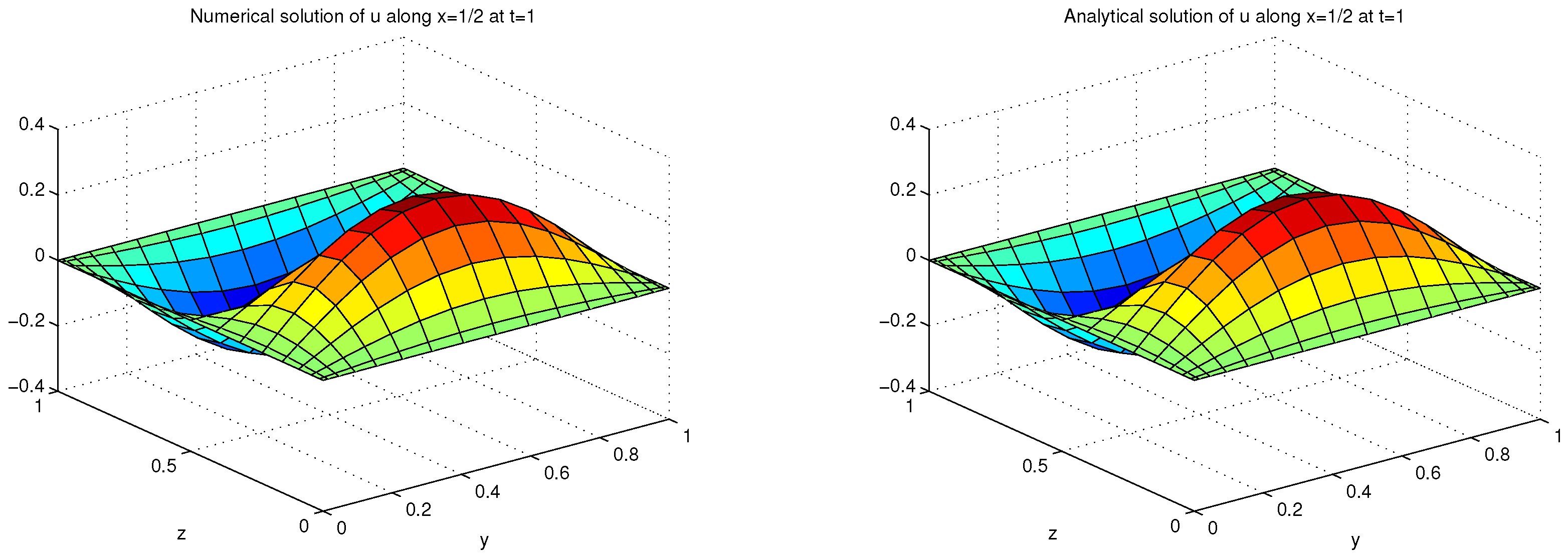
5.3. Three-Dimensional Time-Fractional Fourth-Order System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory Applications; Gordon and Breach Science: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland: New York, NY, USA, 2006. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods; Series on Complexity, Nonlinearity and Chaos; World Scientific: Singapore, 2012. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Li, X.; Xu, C. A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 2009, 47, 2108–2131. [Google Scholar] [CrossRef]
- Zhao, J.; Xiao, J.; Xu, Y. Stability and convergence of an effective finite element method for multiterm fractional partial differential equations. Abstr. Appl. Anal. 2013, 2013, 857205. [Google Scholar] [CrossRef]
- Zhuang, P.; Gu, Y.T.; Liu, F.; Turner, I.; Yarlagadda, P.K.D.V. Time-dependent fractional advection-diffusion equations by an implicit MLS meshless method. Int. J. Numer. Methods Eng. 2011, 88, 1346–1362. [Google Scholar] [CrossRef]
- Gu, X.M.; Sun, H.W.; Zhao, Y.L.; Zheng, X. An implicit difference scheme for time-fractional diffusion equations with a time-invariant type variable order. Appl. Math. Lett. 2021, 120, 107270. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Caputo, M. Elasticitàe Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Caputo, M.; Mainardi, F. Linear models of dissipation in an elastic solids. Riv. Nuevo Clmento (Ser. II) 1971, 1, 161–198. [Google Scholar]
- Bagley, R. Applications of Generalized Derivatives of Viscoelasticity. Ph.D. Thesis, Air Force Institute of Technology, Wright-Patterson AFB, OH, USA, 1979. [Google Scholar]
- Golbabai, A.; Sayevand, K. Fractional calculus—A new approach to the analysis of generalized fourth-order diffusion-wave equations. Comput. Math. Appl. 2011, 67, 2227–2231. [Google Scholar] [CrossRef]
- Jafari, H.; Dehghan, M.; Sayevand, K. Solving a fourth-order fractional diffusion wave equation in a bounded domain by decomposition method. Numer. Methods Partial. Differ. Equ. 2008, 24, 1115–1126. [Google Scholar] [CrossRef]
- Agrawal, O.P. A general solution for a fourth-order fractional diffusion-wave equation defined in a bounded domain. Comput. Struct. 2001, 79, 1497–1501. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Vong, S.; Wang, Z. Compact finite difference scheme for the fourth-order fractional subdiffusion system. Adv. Appl. Math. Mech. 2014, 6, 419–435. [Google Scholar] [CrossRef]
- Hu, X.L.; Zhang, L.M. On finite difference methods for fourth-order fractional diffusion-wave and subdiffusion systems. Appl. Math. Comput. 2012, 218, 5019–5034. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.W.; Li, H.; Li, J.C.; He, S. A two-grid mixed finite element method for a nonlinear fourth-order reaction diffusion problem with time-fractional derivative. Comput. Math. Appl. 2015, 70, 2474–2492. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.W.; Li, H.; He, S.; Gao, W. Finite difference/finite element method for a nonlinear time-fractional fourth-order reaction-diffusion problem. Comput. Math. Appl. 2015, 70, 573–593. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. The solution of the linear fractional partial differential equations using the homotopy analysis method. Z. Naturforschung-A 2010, 65, 935–949. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial. Differ. Equ. 2010, 26, 448–479. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Phanikumar, M.S.; Meerschaert, M.M. A novel numerical method for the time variable fractional order mobile-immobile advection–dispersion model. Comput. Math. Appl. 2013, 66, 693–701. [Google Scholar] [CrossRef]
- Parvizi, M.; Eslahchi, M.R.; Dehghan, M. Numerical solution of fractional advection-diffusion equation with a nonlinear source term. Numer. Algorithms 2015, 68, 601–629. [Google Scholar] [CrossRef]
- Tang, T.; Jie, S. Spectral and High-Order Methods with Applications; Science Press: Alexandria, NSW, Australia, 2006. [Google Scholar]
- Yi, S.C.; Yao, L.Q. A steady barycentric lagrange interpolation method for the 2d higher order time-fractional telegraph equation with nonlocal boundary condition with error analysis. Numer. Methods Partial. Differ. Equ. 2019, 35, 1694–1716. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Wu, X.N. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]

| 5 | 7 | 9 | 11 | 13 | Exact Solution | |
|---|---|---|---|---|---|---|
| 0.1046 | 0.1044 | 0.1044 | 0.1044 | 0.1044 | 0.1044 | |
| 0.2863 | 0.2857 | 0.2857 | 0.2857 | 0.2857 | 0.2857 |
| 1/10 | 1/20 | 1/40 | 1/80 | 1/160 | 1/320 | Value | |
|---|---|---|---|---|---|---|---|
| 7.1808 × 10−3 | 2.9680 × 10−3 | 1.2150 × 10−3 | 4.9515 × 10−4 | 2.0139 × 10−4 | 8.1845 × 10−5 | ||
| Order | 1.2746 | 1.2886 | 1.2950 | 1.2979 | 1.2991 | 1.3000 |
| Order | Order | Order | ||||||
|---|---|---|---|---|---|---|---|---|
| 1/10 | 5.6317 × 10−3 | 2.6130 × 10−3 | 1.1484 × 10−3 | |||||
| 1/20 | 2.1551 × 10−3 | 1.3858 | 9.3348 × 10−4 | 1.4850 | 3.6085 × 10−4 | 1.6701 | ||
| 1/40 | 8.4851 × 10−4 | 1.3448 | 3.3230 × 10−4 | 1.4901 | 1.1222 × 10−4 | 1.6851 | ||
| 1/80 | 3.3976 × 10−4 | 1.3204 | 1.1790 × 10−4 | 1.4949 | 3.4712 × 10−5 | 1.6928 | ||
| 1/160 | 1.3716 × 10−4 | 1.3086 | 4.1762 × 10−5 | 1.4973 | 1.0711 × 10−5 | 1.6964 | ||
| 1/320 | 5.5570 × 10−5 | 1.3035 | 1.4781 × 10−5 | 1.4985 | 3.3012 × 10−6 | 1.6980 | ||
| 1/640 | 2.2547 × 10−5 | 1.3015 | 5.2290 × 10−6 | 1.4991 | 1.0169 × 10−6 | 1.6988 | ||
| 1/1280 | 9.1538 × 10−6 | 1.3005 | 1.8495 × 10−6 | 1.4994 | 3.1317 × 10−7 | 1.6992 | ||
| 1/2560 | 3.7172 × 10−6 | 1.3002 | 6.5406 × 10−7 | 1.4996 | 9.6428 × 10−8 | 1.6994 | ||
| Theoretical value | 1.3000 | 1.5000 | 1.7000 | |||||
| Order | Order | Order | ||||||
|---|---|---|---|---|---|---|---|---|
| 1/10 | 2.1249 × 10−4 | 4.9392 × 10−3 | 9.7883 × 10−3 | |||||
| 1/20 | 6.6285 × 10−4 | 1.6806 | 1.7756 × 10−4 | 1.4760 | 3.9602 × 10−3 | 1.3055 | ||
| 1/40 | 2.0573 × 10−5 | 1.6979 | 6.3224 × 10−5 | 1.4897 | 1.6177 × 10−4 | 1.2916 | ||
| 1/80 | 6.3850 × 10−5 | 1.6880 | 2.2444 × 10−5 | 1.4942 | 6.6040 × 10−5 | 1.2925 | ||
| 1/160 | 1.9992 × 10−6 | 1.6752 | 7.9736 × 10−6 | 1.4930 | 2.6878 × 10−5 | 1.2946 | ||
| 1/320 | 6.4637 × 10−7 | 1.6291 | 2.8493 × 10−6 | 1.4846 | 1.0932 × 10−5 | 1.2945 | ||
| Theoretical value | 1.7000 | 1.5000 | 1.3000 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yi, S. A Compact Difference-Galerkin Spectral Method of the Fourth-Order Equation with a Time-Fractional Derivative. Fractal Fract. 2025, 9, 155. https://doi.org/10.3390/fractalfract9030155
Wang Y, Yi S. A Compact Difference-Galerkin Spectral Method of the Fourth-Order Equation with a Time-Fractional Derivative. Fractal and Fractional. 2025; 9(3):155. https://doi.org/10.3390/fractalfract9030155
Chicago/Turabian StyleWang, Yujie, and Shichao Yi. 2025. "A Compact Difference-Galerkin Spectral Method of the Fourth-Order Equation with a Time-Fractional Derivative" Fractal and Fractional 9, no. 3: 155. https://doi.org/10.3390/fractalfract9030155
APA StyleWang, Y., & Yi, S. (2025). A Compact Difference-Galerkin Spectral Method of the Fourth-Order Equation with a Time-Fractional Derivative. Fractal and Fractional, 9(3), 155. https://doi.org/10.3390/fractalfract9030155









