Fractional-Calculus Analysis of the Dynamics of a Vector-Borne Infection with Preventive Measures

Abstract

Vector-borne infections pose serious public health challenges due to the complex interplay of biological, environmental, and social factors. Therefore, comprehensive approaches are essential to mitigate the burden of vector-borne infections and minimize their impact on public health. In this research, an epidemic model for the vector-borne disease malaria is structured with a saturated incidence rate via fractional calculus and preventive measures. The essential results and concepts are introduced to examine the proposed model. The solution of the system is examined for some necessary results, and the threshold parameter of the model, indicated by ${\mathcal{R}}_0$, is calculated. In this paper, the proposed malaria model is analyzed both quantitatively and qualitatively. The fixed-point theorems of Banach and Schaefer are utilized to examine the uniqueness and existence of the solution dynamics. Furthermore, the necessary conditions for the stability of the model have been determined. A numerical approach is offered to visualize the solution pathways of the system and identify its key factors. Through the results, the most influential factors for the control and management of the disease are highlighted.

1. Introduction

Vector-borne diseases impose a significant burden on global public health, affecting millions of people in the world each year. Malaria, a health issue of considerable global significance, remains a persistent challenge, with Plasmodium parasites being the causative agents transmitted by the bites of infected mosquitoes, as indicated in [1]. The complex life cycle of the parasites and their interaction with Anopheles mosquitoes contribute to the persistence of this disease. Upon infection, the parasites initially target the liver, undergoing a phase of maturation before entering the bloodstream and infecting red blood cells. A frequent occurrence of flu, chills, and fever-like symptoms that are typical of malaria are caused by this cyclical pattern. The burden of malaria extends beyond individual health impacts, exerting substantial socio-economic effects [2]. Areas with high malaria prevalence often face challenges in economic development, as malaria can contribute to absenteeism, decreased productivity, and increased healthcare expenditures. Policies to address malaria encompass a comprehensive approach, incorporating various elements, including vector control measures and the use of antimalarial medications for both treatment and prevention [3,4]. Furthermore, ongoing research aims to develop more effective vaccines and therapies to further reduce the global incidence of malaria and alleviate its profound public health implications.

Sir Ronald Ross, in his pioneering work, laid the foundation for mathematical epidemiology by developing the first compartmental models to describe the transmission dynamics of malaria, revolutionizing the understanding of infectious disease spread [5]. It is evident that modeling contributes significantly to studying the transmission dynamics of vector-borne infections and to efficiently exploring disease dynamics to guide control interventions [6,7]. By utilizing mathematical analysis, it is possible to identify the main aspects of the transmission process associated with various infections [8,9]. In the literature, numerous researchers have developed models for the management and prevention of malaria, each with different assumptions [10,11,12]. Researchers looked at how drug resistance and treatment interventions affected malaria dynamics in endemic areas [13]. The study used mathematical modeling to assess how treatment strategies and drug resistance influence the dynamics of the infection. Their results offered valuable insights into the factors affecting disease prevalence and suggested potential strategies for effective control in endemic areas. In another study, researchers explored the dynamics of both drug-resistant and drug-sensitive malaria strains within human populations through a mathematical model [14]. They also applied optimal control theory to assess the potential impact of new preventive policies on the spread of the disease. In the literature, the dynamics of malaria have also been examined in relation to the effects of treatment and vaccination. By applying optimal control methods, they evaluated the effectiveness of treatment and vaccination in reducing the spread of the infection [15].

The dynamics of Aedes aegypti with a seasonal population through a mathematical framework have been studied [16]. In this model, the effectiveness of insecticide has been evaluated, and insecticide resistance has been assessed. In [17], the researchers introduced and examined a model to understand temephos resistance within Aedes aegypti populations. The issue of insecticide resistance was further explored in [18,19], where the authors introduced new assumptions to examine broader contexts of resistance development. A significant challenge in disease control is the issue of population migration. The movement of infected vectors or hosts from infected areas to non-infected areas can increase the risk of infection. This has been compounded by the rise in resistance to both insecticides and antimalarial drugs [20]. In response to migration-related challenges, scholars have utilized multi-patch models, as demonstrated in [21,22], to explore the dynamics of disease spread across geographically distinct areas. The dynamics of epidemic spread facilitated by carriers have been investigated in the literature [23]. The challenges related to migration, particularly in the context of malaria and general epidemic models, have been explored in [24,25]. To address the aforementioned challenges, it is essential to examine the impact of resistance to antimalarial drugs, insecticides, and population movement as key factors influencing malaria control, especially in the context of a saturated incidence rate.

The associative learning mechanism and early stages of vector-borne disease transmission have been shown to occur [26]. Mosquitoes utilize prior knowledge of a host’s location, blood type, appearance, and defensive behaviors to select their feeding targets. Meanwhile, host populations employ memory-based awareness, which can reduce the interaction rate between vectors and hosts [27]. Such behaviors are effectively represented in the mathematical modeling of infectious diseases using a fractional-order system. Therefore, we choose to present the dynamics of malaria through fractional derivatives to demonstrate the impact of memory on infection control and prevention. The concept of the Ulam–Hyers stability is crucial as it provides a mathematical framework that ensures the robustness and reliability of model solutions [28,29]. This stability guarantees that, even with fluctuations in parameters or external conditions, the core insights and predictions of the model remain valid and dependable [30]. It is particularly important for accurately predicting disease dynamics, designing effective control strategies, and evaluating policy interventions. This work aims to establish the Ulam–Hyers stability in a fractional model of malaria, thereby advancing our ability to predict and control malaria transmission.

The current research is ordered as follows: the essential concepts and ideas of fractional theory are delineated in Section 2. An epidemic model is constructed to conceptualize the transmission dynamics of malaria with a saturated incidence rate in Section 3. Section 4 undertakes an in-depth analysis of the model, while Section 5 provides the requisite conditions for the Ulam–Hyers stability. Moreover, we present a computational technique to depict the solutions of the system. Finally, the conclusion of the work is presented in Section 6.

2. Essential Concepts and Theory

Here, we will provide a comprehensive overview of the fundamental concepts and terminology associated with fractional calculus theory. These concepts and theories will be used in the investigation of the malaria model. The essential results are outlined below:

Definition 1

([31]). Assume $g\left(t\right)$ in a way that $g\left(t\right)\in {\mathrm{L}}^1([b,c],R)$, and let ν be the order of the fractional operator; then, the fractional integral is

$${}_{ }{}^{\nu }I_{b^{+}}^{b}g\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\nu \right)}}{\mathit{\int }}_0^t{(t-s)}^{\nu -1}g\left(s\right)ds,0<\nu \le 1.$$

(1)

Definition 2

([31]). In case that $g\left(t\right)\in C^n[b,c]$, then the Caputo operator is

$${}_{ }{}^{LC}D_{0^{+}}^{\nu }g\left(t\right)={\displaystyle \frac{1}{\Gamma (n-\nu )}}{\int }_0^t{(t-s)}^{n-\nu -1}{g}^{\left(n\right)}\left(s\right)ds.$$

(2)

Lemma 1

([31]). Take the below system for a function $g\left(t\right)$:

$$\left\{\begin{array}{cc}\hfill {}_{ }{}^{LC}D_{0+}^{\nu }g\left(t\right)=& w\left(t\right),t\in [0,\tau ],\\ \hfill g\left(0\right)=& w_0,n-1<\nu <n,\end{array}\right.$$

(3)

in which $w\left(t\right)\in C\left(\right[0,\tau \left]\right)$ and

$$b\left(t\right)=\sum _{i=0}^{n-1}{d}_i{t}^i$$

for $i=0,1,\cdots ,n-1$ and $d_i\in R$.

Definition 3

([32]). The Laplace transformation for the Caputo operator is given by the following:

$$\pounds {[}^{LC}{D}_{0^{+}}^{\nu }g\left(t\right)]=s^{\nu }g\left(s\right)-\sum _{k=0}^{n-1}{s}^{\nu -k-1}{g}^{\left(k\right)}\left(0\right),$$

(4)

in which $n-1<ħ<n$.

Theorem 1

([33]). Let $G:\mathcal{X}\to \mathcal{X}$ be continuous and compact, where $\mathcal{X}$ is the Banach space. If the following is bounded,

$$\mathcal{E}=\{g\in \mathcal{X}:b=\lambda G,\lambda \in (0,1\left)\right\};$$

(5)

then, G has a fixed point.

3. Evaluation of the Fractional Dynamics

Here, we develop an epidemic model of malaria, categorizing the host strength ${\mathcal{N}}_h$ into susceptible (${\mathcal{S}}_h$), infected (${\mathcal{I}}_h$), and recovered (${\mathcal{R}}_h$) classes. Simultaneously, the mosquito’s strength ${\mathcal{N}}_v$ is classified into susceptible (${\mathcal{S}}_v$) and infectious (${\mathcal{I}}_v$) categories. The recruitment of hosts and vectors is denoted by ${\Xi }_h$ and ${\Xi }_v$ within this formulation. We represent the natural death rate for the host as ${\mu }_h$ and for the mosquitoes as ${\mu }_v$. Let ${\beta }_{h}b{\displaystyle \frac{{\mathcal{I}}_v}{1+{\alpha }_1{\mathcal{I}}_v}}$ and ${\beta }_{v}b{\displaystyle \frac{{\mathcal{I}}_h}{1+{\alpha }_2{\mathcal{I}}_h}}$ indicate the force of infection from hosts and vectors. A constant rate of ${ϵ}_1{\theta }_1$ is applied to the population of infected persons, where ${ϵ}_1$ indicates the drug’s effectiveness and ${\tau }_1$ indicates the drug-induced recovery. Furthermore, ${ϵ}_1{\tau }_1{p}_1{\mathcal{I}}_h$ represents the proportion of ${\mathcal{I}}_h$ that exhibits drug resistance, whereas $p_1$ ranges from 0 to 1 to represent the ratio of resistance acquisition to the drug. Therefore, the proportion of susceptible people impacted by the medicine is shown by the formula ${ϵ}_1{\tau }_1(1-p_1){\mathcal{I}}_h$. In addition to this, a part of the ${\mathcal{I}}_h$ dies from the infection at a rate of $\rho$, and another part recovers spontaneously at a rate of $\delta$.

The population of vectors undergoes a reduction through natural mortality at a rate of $d_v$ and is further impacted by the application of insecticides at a rate of ${ϵ}_2{\tau }_2$. Here, ${ϵ}_2$ denotes the effectiveness of the insecticide, and ${\tau }_2$ signifies the mortality of mosquitoes resulting from the insecticide application. The quantity of mosquitoes exhibiting resistance to insecticides is denoted as ${ϵ}_2{\tau }_2{p}_2$, where $p_2\in [0,1]$ signifies the ratio of acquiring resistance to insecticides. Consequently, the term ${ϵ}_2{\tau }_2(1-p_2)$ expresses the fraction of mosquitoes that remain sensitive to insecticides. The system of ODEs with the above-mentioned assumptions can be expressed as follows:

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{d{\mathcal{S}}_h}{dt}}& =& \Xi -{\beta }_{h}b{\displaystyle \frac{{\mathcal{I}}_v}{1+{\alpha }_1{\mathcal{I}}_v}}{\mathcal{S}}_h+\omega {\mathcal{R}}_h-d_h{\mathcal{S}}_h,\hfill \\ \hfill {\displaystyle \frac{d{\mathcal{I}}_h}{dt}}& =& {\beta }_{h}b{\displaystyle \frac{{\mathcal{I}}_v}{1+{\alpha }_1{\mathcal{I}}_v}}{\mathcal{S}}_h-{ϵ}_1{\tau }_1(1-p_1){\mathcal{I}}_h-(\delta +\rho +d_h){\mathcal{I}}_h,\hfill \\ \hfill {\displaystyle \frac{d{\mathcal{R}}_h}{dt}}& =& {ϵ}_1{\tau }_1(1-p_1){\mathcal{I}}_h+\delta {\mathcal{I}}_h-(\omega +d_1){\mathcal{R}}_h,\hfill \\ \hfill {\displaystyle \frac{d{\mathcal{S}}_v}{dt}}& =& \Xi -{\beta }_{v}b{\displaystyle \frac{{\mathcal{I}}_h}{1+{\alpha }_2{\mathcal{I}}_h}}{\mathcal{S}}_v-{ϵ}_2{\tau }_2(1-p_2){\mathcal{S}}_v-d_v{\mathcal{S}}_v,\hfill \\ \hfill {\displaystyle \frac{d{\mathcal{I}}_v}{dt}}& =& {\beta }_{v}b{\displaystyle \frac{{\mathcal{I}}_h}{1+{\alpha }_2{\mathcal{I}}_h}}{\mathcal{S}}_v-{ϵ}_2{\tau }_2(1-p_2){\mathcal{I}}_v-d_v{\mathcal{I}}_v,\hfill \end{array}\right.$$

(6)

where

$${\mathcal{S}}_h\left(0\right)\ge 0,{\mathcal{I}}_h\left(0\right)\ge 0,{\mathcal{R}}_h\left(0\right)\ge 0,{\mathcal{S}}_v\left(0\right)\ge 0,and{\mathcal{I}}_v\left(0\right)\ge 0.$$

Additionally, the vector size is

$${\mathcal{N}}_v={\mathcal{S}}_v+{\mathcal{I}}_v;$$

similarly, the size of the host population is

$${\mathcal{N}}_h={\mathcal{S}}_h+{\mathcal{I}}_h+{\mathcal{R}}_h.$$

Fractional models provide a more comprehensive framework for vector-borne infection modeling, enhancing our ability to understand and control diseases transmitted by vectors. They capture essential features, making them invaluable tools for researchers and public health practitioners working on vector-borne diseases. For more accurate representation, our model in a fractional framework can be expressed as follows:

$$\left\{\begin{array}{ccc}\hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{S}}_h& =& \Xi -{\beta }_{h}b{\displaystyle \frac{{\mathcal{I}}_v}{1+{\alpha }_1{\mathcal{I}}_v}}{\mathcal{S}}_h+\omega {\mathcal{R}}_h-d_h{\mathcal{S}}_h,\hfill \\ \hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{I}}_h& =& {\beta }_{h}b{\displaystyle \frac{{\mathcal{I}}_v}{1+{\alpha }_1{\mathcal{I}}_v}}{\mathcal{S}}_h-{ϵ}_1{\tau }_1(1-p_1){\mathcal{I}}_h-(\delta +\rho +d_h){\mathcal{I}}_h,\hfill \\ \hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{R}}_h& =& {ϵ}_1{\tau }_1(1-p_1){\mathcal{I}}_h+\delta {\mathcal{I}}_h-(\omega +d_1){\mathcal{R}}_h,\hfill \\ \hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{S}}_v& =& \Xi -{\beta }_{v}b{\displaystyle \frac{{\mathcal{I}}_h}{1+{\alpha }_2{\mathcal{I}}_h}}{\mathcal{S}}_v-{ϵ}_2{\tau }_2(1-p_2){\mathcal{S}}_v-d_v{\mathcal{S}}_v,\hfill \\ \hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{I}}_v& =& {\beta }_{v}b{\displaystyle \frac{{\mathcal{I}}_h}{1+{\alpha }_2{\mathcal{I}}_h}}{\mathcal{S}}_v-{ϵ}_2{\tau }_2(1-p_2){\mathcal{I}}_v-d_v{\mathcal{I}}_v,\hfill \end{array}\right.$$

(7)

where ${}_{0 }{}^{LC}D_t^{\vartheta }$ denotes the Liouville–Caputo’s operator, and $\vartheta$ is the tfractional order. It has been acknowledged that the findings of fractional systems are more reliable and precise for biological phenomena. In the next step, we will examine the solution of the proposed model of malaria.

Theorem 2.

The solutions $({\mathcal{S}}_h,{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)$ of the proposed model (7) of malaria infection are non-negative and bounded.

Proof. 

For the proof, we proceed as follows:

$$\left\{\begin{array}{ccc}\hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{S}}_h{\mid }_{{\mathcal{S}}_h=0}& =& {\Xi }_h\ge 0,\hfill \\ \hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{I}}_h{\mid }_{{\mathcal{I}}_h=0}& =& {\beta }_{h}b{\mathcal{I}}_v\ge 0,\hfill \\ \hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{R}}_h{\mid }_{{\mathcal{R}}_h=0}& =& {ϵ}_1{\tau }_1(1-p_1){\mathcal{I}}_h+\delta {\mathcal{I}}_h\ge 0,\hfill \\ \hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{S}}_v{\mid }_{{\mathcal{S}}_v=0}& =& {\Xi }_v\ge 0,\hfill \\ \hfill {}_{0 }{}^{LC}D_t^{\vartheta }{\mathcal{I}}_v{\mid }_{{\mathcal{I}}_v=0}& =& {\beta }_{v}b{\mathcal{I}}_h\ge 0.\hfill \end{array}\right.$$

(8)

Thus, the solutions of the fractional dynamics (7) are non-negative. To prove the boundedness, the first three equations of the model imply the following:

$$\begin{array}{ccc}\hfill {}_{0 }{}^{LC}D_t^{\vartheta }({\mathcal{S}}_h+{\mathcal{I}}_h+{\mathcal{R}}_h)& \le & {\Xi }_h-d_h({\mathcal{S}}_h+{\mathcal{I}}_h+{\mathcal{R}}_h).\hfill \end{array}$$

(9)

Through further simplification, we have

$$\left(({\mathcal{S}}_h+{\mathcal{I}}_h+{\mathcal{R}}_h)\right)\le \left({\mathcal{S}}_h\left(0\right)+{\mathcal{I}}_h\left(0\right)+{\mathcal{R}}_h\left(0\right)-{\displaystyle \frac{{\Xi }_h}{d_h}}\right)E_{\vartheta }(-d_h{t}^{\vartheta })+{\displaystyle \frac{{\Xi }_h}{d_h}}.$$

Applying the concept of the work [31], the below is obtained:

$$\left({\mathcal{S}}_h+{\mathcal{I}}_h+{\mathcal{R}}_h)\right)\le {\displaystyle \frac{\Xi }{d_h}}\cong {\mathcal{M}}_1.$$

Similarly, the compartments of vector population imply that ${\mathcal{S}}_v+{\mathcal{I}}_v\le {\mathcal{M}}_2$, in which ${\mathcal{M}}_2={\displaystyle \frac{{\Xi }_v}{d_v}}$. As a result, the solutions of the recommended model are bounded and non-negative. Let the infection-free equilibrium of (7) be symbolized by ${\mathcal{E}}_0({\mathcal{S}}_h^0,{\mathcal{I}}_h^0,{\mathcal{R}}_h^0,{\mathcal{S}}_v^0,{\mathcal{I}}_v^0)$, given by

$$\left({\displaystyle \frac{\Xi }{d_h}},0,0,{\displaystyle \frac{{\Xi }_v}{{ϵ}_2{\tau }_2(1-p_2)+d_v}},0\right).$$

The fundamental reproduction number, commonly symbolized as ${\mathcal{R}}_0$, stands as a crucial parameter in the field of epidemiology. It signifies the average count of secondary infections produced by an individual who is infected, assuming an entirely susceptible population. It is an important parameter for assessing the potential for an epidemic to spread. We will use the next-generation matrix approach to calculate the ${\mathcal{R}}_0$ of the proposed system as follows:

$$F=\left[\begin{array}{cc}0& {\beta }_{h}b{\mathcal{S}}_h^0\\ {\beta }_{v}b{\mathcal{S}}_v^0& 0\end{array}\right] andV=\left[\begin{array}{cc}{ϵ}_1{\tau }_1(1-p_1)+\delta +\rho +d_h& 0\\ 0& {ϵ}_2{\tau }_2(1-p_2)+{\mu }_v\end{array}\right],$$

which implies that

$$F=\left[\begin{array}{cc}0& {\beta }_{h}b{\mathcal{S}}_h^0\\ {\beta }_{v}b{\mathcal{S}}_v^0& 0\end{array}\right] andV=\left[\begin{array}{cc}{\displaystyle \frac{1}{{ϵ}_1{\tau }_1(1-p_1)+\delta +\rho +d_h}}& 0\\ 0& {\displaystyle \frac{1}{{ϵ}_2{\tau }_2(1-p_2)+{\mu }_v}}\end{array}\right].$$

Further, we have

$$F{V}^{-1}=\left[\begin{array}{cc}0& {\displaystyle \frac{{\beta }_{h}b{\mathcal{S}}_h^0}{{ϵ}_1{\tau }_1(1-p_1)+\delta +\rho +d_h}}\\ {\displaystyle \frac{{\beta }_{v}b{\mathcal{S}}_v^0}{{ϵ}_2{\tau }_2(1-p_2)+{\mu }_v}}& 0\end{array}\right].$$

Then, the ${\mathcal{R}}_0$ of the recommended model (7) of malaria is calculated as follows:

$$\rho \left(F{V}^{-1}\right)=\sqrt{{\displaystyle \frac{{\beta }_{h}b{\mathcal{S}}_h^0}{({ϵ}_1{\tau }_1(1-p_1)+\delta +\rho +d_h)}}{\displaystyle \frac{{\beta }_{v}b{\mathcal{S}}_v^0}{({ϵ}_2{\tau }_2(1-p_2)+{\mu }_v)}}},$$

which gives

$${\mathcal{R}}_0=\sqrt{{\displaystyle \frac{{\beta }_{h}b{\mathcal{S}}_h^0}{({ϵ}_1{\tau }_1(1-p_1)+\delta +\rho +d_h)}}{\displaystyle \frac{{\beta }_{v}b{\mathcal{S}}_v^0}{({ϵ}_2{\tau }_2(1-p_2)+{\mu }_v)}}}.$$

□

Theorem 3.

If ${\mathcal{R}}_0<1$, the infection-free equilibrium in the proposed malaria model exhibits local asymptotic stability; otherwise, it is unstable.

Proof of Theorem 3. 

To achieve the desired outcomes, we used the approach of the Jacobian matrix at the DFE, as given below:

$$J\left(E_0\right)=\left[\begin{array}{ccccc}-d_h& 0& \omega & 0& -{\beta }_{h}b{\mathcal{S}}_h^0\\ 0& -({ϵ}_1{\tau }_1(1-p_1)+\delta +\rho +d_h)& 0& 0& {\beta }_{h}b{\mathcal{S}}_h^0\\ 0& ({ϵ}_1{\tau }_1(1-p_1)+\delta )& -(\omega +d_h)& 0& 0\\ 0& -{\beta }_{v}b{\mathcal{S}}_v^0& 0& -({ϵ}_2{\tau }_2(1-p_2)+d_v)& 0\\ 0& {\beta }_{v}b{\mathcal{S}}_v^0& 0& 0& -({ϵ}_2{\tau }_2(1-p_2)+d_v)\end{array}\right].$$

Here, the first and second eigenvalues are $-d_h$ and $-(\omega +d_h)$, and the below is as follows:

$$J_1\left(E_0\right)=\left[\begin{array}{ccc}-({ϵ}_1{\tau }_1(1-p_1)+\delta +\rho +d_h)& 0& {\beta }_{h}b{\mathcal{S}}_h^0\\ -{\beta }_{v}b{\mathcal{S}}_v^0& -({ϵ}_2{\tau }_2(1-p_2)+d_v)& 0\\ {\beta }_{v}b{\mathcal{S}}_v^0& 0& -({ϵ}_2{\tau }_2(1-p_2)+d_v)\end{array}\right],$$

where the third eigenvalue is given by $-({ϵ}_2{\tau }_2(1-p_2)+d_v)$. Further, we have

$$J_2\left(E_0\right)=\left[\begin{array}{cc}-({ϵ}_1{\tau }_1(1-p_1)+\delta +\rho +d_h)& {\beta }_{h}b{\mathcal{S}}_h^0\\ {\beta }_{v}b{\mathcal{S}}_v^0& -({ϵ}_2{\tau }_2(1-p_2)+d_v)\end{array}\right].$$

Here, the LAS of the disease-free steady state of the suggested model depends on the eigenvalues of matrix $J_2$. To establish the necessary result, we will prove that $Det\left(J_2\right)>0$ and $Trc\left(J_2\right)<0$ for ${\mathcal{R}}_0<1$. Clearly, both these conditions are satisfied for ${\mathcal{R}}_0<1$. Hence, the Jacobian matrix of our system has negative eigenvalues for ${\mathcal{R}}_0<1$. Thus, the DFE of the proposed model (7) of the disease is LAS for ${\mathcal{R}}_0<1$ and is unstable otherwise. □

4. Existence Theory

In this part of the research, we will probe the qualitative aspects of the model (7) of malaria using the framework of existence theory. We proceed as follows:

$$\left\{\begin{array}{ccc}\hfill {\mathcal{C}}_1(t,{\mathcal{S}}_h,{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)& =& \Xi -{\beta }_{h}b{\displaystyle \frac{{\mathcal{I}}_v}{1+{\alpha }_1{\mathcal{I}}_v}}{\mathcal{S}}_h+\omega {\mathcal{R}}_h-d_h{\mathcal{S}}_h,\hfill \\ \hfill {\mathcal{C}}_2(t,{\mathcal{S}}_h,{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)& =& {\beta }_{h}b{\displaystyle \frac{{\mathcal{I}}_v}{1+{\alpha }_1{\mathcal{I}}_v}}{\mathcal{S}}_h-{ϵ}_1{\tau }_1(1-p_1){\mathcal{I}}_h-(\delta +\rho +d_h){\mathcal{I}}_h,\hfill \\ \hfill {\mathcal{C}}_3(t,{\mathcal{S}}_h,{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)& =& {ϵ}_1{\tau }_1(1-p_1){\mathcal{I}}_h+\delta {\mathcal{I}}_h-(\omega +d_1){\mathcal{R}}_h,\hfill \\ \hfill {\mathcal{C}}_4(t,{\mathcal{S}}_h,{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)& =& \Xi -{\beta }_{v}b{\displaystyle \frac{{\mathcal{I}}_h}{1+{\alpha }_2{\mathcal{I}}_h}}{\mathcal{S}}_v-{ϵ}_2{\tau }_2(1-p_2){\mathcal{S}}_v-d_v{\mathcal{S}}_v,\hfill \\ \hfill {\mathcal{C}}_5(t,{\mathcal{S}}_h,{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)& =& {\beta }_{v}b{\displaystyle \frac{{\mathcal{I}}_h}{1+{\alpha }_2{\mathcal{I}}_h}}{\mathcal{S}}_v-{ϵ}_2{\tau }_2(1-p_2){\mathcal{I}}_v-d_v{\mathcal{I}}_v.\hfill \end{array}\right.$$

(10)

Here, we can generalized the system (10) as given below:

$$\left\{\begin{array}{cc}\hfill {}_{ }{}^{LC}D_{0^{+}}^{\vartheta }\mathcal{C}\left(t\right)=& \mathcal{H}(t,\mathcal{C}(t\left)\right),t\in [0,\tau ],\\ \hfill \mathcal{C}\left(0\right)=& {\mathcal{C}}_0,0<\vartheta \le 1,\end{array}\right.$$

(11)

with

$$\left\{\begin{array}{cc}\hfill \mathcal{C}\left(t\right)=& {\mathcal{S}}_h\left(t\right),\\ & {\mathcal{I}}_h\left(t\right),\\ & {\mathcal{R}}_h\left(t\right),\\ & {\mathcal{S}}_v\left(t\right),\\ & {\mathcal{I}}_v\left(t\right).\end{array}\right.\left\{\begin{array}{cc}\hfill {\mathcal{C}}_0\left(t\right)=& {\mathcal{S}}_{h0},\\ & {\mathcal{I}}_{h0},\\ & {\mathcal{R}}_{h0},\\ & {\mathcal{S}}_{v0},\\ & {\mathcal{I}}_{v0}.\end{array}\right.\left\{\begin{array}{c}\hfill \mathcal{H}(t,\mathcal{C}\left(t\right))={\mathcal{C}}_1(t,{\mathcal{S}}_{h1},{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)\\ \hfill {\mathcal{C}}_2(t,{\mathcal{S}}_{h1},{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)\\ \hfill {\mathcal{C}}_3(t,{\mathcal{S}}_{h1},{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)\\ \hfill {\mathcal{C}}_4(t,{\mathcal{S}}_{h1},{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)\\ \hfill {\mathcal{C}}_5(t,{\mathcal{S}}_{h1},{\mathcal{I}}_h,{\mathcal{R}}_h,{\mathcal{S}}_v,{\mathcal{I}}_v)\end{array}\right.$$

(12)

The above system (11) can be expressed in the following way through Lemma 1:

$$\mathcal{C}\left(t\right)={\mathcal{C}}_0\left(t\right)+{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^t{(t-s)}^{\vartheta -1}\mathcal{H}(s,\mathcal{C}\left(s\right))ds.$$

(13)

We utilize Lipschitz-condition-based criteria to evaluate the suggested dynamics:

(P1) 

For q in $[0,1)$, one can find ${\mathcal{U}}_{\mathcal{H}}$ and ${\mathcal{V}}_{\mathcal{H}}$ in a manner such that the following holds.

$$\left|\mathcal{H}(t,\mathcal{C}\left(t\right))\right|\le {\mathcal{U}}_{\mathcal{C}}{\left|\mathcal{C}\right|}^q+{\mathcal{V}}_{\mathcal{H}}.$$

(14)

(P2) 

One can find $M_{\mathcal{H}}>0$ for all $\mathcal{C}$ and $\overline{\mathcal{C}}$ in $\mathcal{X}$ associated with the following condition:

$$|\mathcal{H}(t,\mathcal{C})-\mathcal{H}(t,\overline{\mathcal{C}})|\le M_{\mathcal{H}}\left[\right|\mathcal{C}-\overline{\mathcal{C}}\left|\right].$$

(15)

In set $\mathcal{X}$, define mapping $\mathcal{B}$ as follows:

$$\mathcal{B}\mathcal{C}\left(t\right)={\mathcal{C}}_0\left(t\right)+{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^t{(t-s)}^{\vartheta -1}\mathcal{H}(s,\mathcal{C}\left(s\right))ds.$$

(16)

If $\mathbf{P}\mathbf{1}$ and $\mathbf{P}\mathbf{2}$ are satisfied, then there is a solution to (11). We take the following actions to investigate the offered model’s solution:

Theorem 4.

As long as $\mathbf{P}\mathbf{1}$ and $\mathbf{P}\mathbf{2}$ are met, there is at least one solution for the system (7) of malaria infection.

Proof. 

To establish the necessary findings, we first use Schaefer’s fixed point theorem. The following method is used to illustrate this theorem by outlining four distinct stages:

(C1): 

First, we will validate the continuity of operator $\mathcal{B}$. Assuming ${\mathcal{C}}_i$ is continuous for $i=1,2,\dots ,5$, this implies that $\mathcal{H}(t,\mathcal{C}(t\left)\right)$ is continuous. After that, considering ${\mathcal{C}}_j$, $\mathcal{C}\in \mathcal{X}$ in a manner that ${\mathcal{C}}_j\to \mathcal{C}$, we have $\mathcal{B}{\mathcal{C}}_j\to \mathcal{B}\mathcal{C}$.

Furthermore, let us take

$$\begin{array}{cc}\hfill \left|\right|\mathcal{B}{\mathcal{C}}_j-\mathcal{B}\mathcal{C}\left|\right|& =\underset{t\in [0,\tau ]}{max}|{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^t{(t-r)}^{\vartheta -1}{Q}_j(r,{\mathcal{C}}_j\left(r\right))dr-{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^t{(t-r)}^{\vartheta -1}\mathcal{H}(r,\mathcal{C}\left(r\right))ds|\hfill \\ & \le \underset{t\in [0,\tau ]}{max}{\int }_0^t\left|{\displaystyle \frac{{(t-r)}^{\vartheta -1}}{\Gamma \left(\vartheta \right)}}\right||{\mathcal{H}}_j(r,{\mathcal{C}}_j\left(r\right))-\mathcal{H}(r,\mathcal{C}\left(r\right))|dr\hfill \\ & \le {\displaystyle \frac{{\tau }^{\vartheta }{M}_{\mathcal{H}}}{\Gamma (\vartheta +1)}}\left|\right|{\mathcal{C}}_j-\mathcal{C}\left|\right|\to 0asj\to \infty .\hfill \end{array}$$

(17)

Thus, the continuity of $\mathcal{B}{\mathcal{C}}_j\to \mathcal{B}\mathcal{C}$ is ensured from the continuity of $\mathcal{H}$, which implies that $\mathcal{B}$ is continuous.

(C2): 

Now, we will verify the bounded nature of $\mathcal{B}$. Let the following conditions be satisfied by operator $\mathcal{B}$ for every $\mathcal{C}\in \mathrm{X}$:

$$\begin{array}{cc}\hfill \left|\right|\mathcal{B}\mathcal{C}\left|\right|& =\underset{t\in [0,\tau ]}{max}|{\mathcal{C}}_o\left(t\right)+{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^t{(t-s)}^{\vartheta -1}\mathcal{H}(s,\mathcal{C}\left(s\right))ds|\hfill \\ & \le |{\mathcal{C}}_0|\underset{t\in [0,\tau ]}{max}{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^t{|(t-s)}^{\vartheta -1}\left|\right|\mathcal{H}(s,\mathcal{C}\left(s\right))|ds\hfill \\ & \le |{\mathcal{C}}_0|+{\displaystyle \frac{{\tau }^{\vartheta }}{\Gamma (\vartheta +1)}}\{U_Z{\left|\right|\mathcal{C}\left|\right|}^q+V_{\mathcal{H}}\}.\hfill \end{array}$$

(18)

Subsequently, we demonstrate the boundedness of $\mathcal{B}\left(T\right)$ in subset T of $\mathcal{X}$, where T is bounded. Given $\mathcal{C}\in T$, one may determine a non-negative value U in the following way due to the bounded nature of S:

$$\left|\right|\mathcal{C}\left|\right|\le U,\forall \mathcal{C}\in T.$$

(19)

Accordingly, the outcome for any $\mathcal{C}$ within the set T is derived from the above expression as follows:

$$\left|\right|\mathcal{B}W\left|\right|\le |{\mathcal{C}}_0|+{\displaystyle \frac{{\tau }^{\vartheta }}{\Gamma (\vartheta +1)}}[U_{\mathcal{H}}{\left|\right|\mathcal{C}\left|\right|}^q+V_{\mathcal{H}}]\le |{\mathcal{C}}_0|+{\displaystyle \frac{{\tau }^{\vartheta }}{\Gamma (\vartheta +1)}}[U_{\mathcal{H}}{U}^q+V_{\mathcal{H}}].$$

(20)

This implies that $\mathcal{B}\left(T\right)$ is a bounded operator.

(C3): 

For equi-continuity, take $t_1$ and $t_2$ in $[0,\tau ]$, in which $t_1\ge t_2$. Subsequently, we obtain the following:

$$\begin{array}{cc}\hfill |\mathcal{B}\mathcal{C}\left(t_1\right)-\mathcal{B}\mathcal{C}\left(t_1\right)|& =|{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^{t_1}|{(t_1-s)}^{\vartheta -1}||\mathcal{H}(s,\mathcal{C}\left(s\right))|dr\hfill \\ & -{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^{t_2}|{(t_2-s)}^{\vartheta -1}||\mathcal{H}(s,\mathcal{C}\left(s\right))|dr|\hfill \\ & \le |{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^{t_1}|{(t_1-s)}^{\vartheta -1}|-{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^{t_2}|{(t_2-s)}^{\vartheta -1}|||\mathcal{H}(s,\mathcal{C}\left(r\right))|dr\hfill \\ & \le {\displaystyle \frac{{\tau }^{\vartheta }}{\Gamma (\vartheta +1)}}[U_{\mathcal{H}}{\left|\right|\mathcal{C}\left|\right|}^q+V_{\mathcal{H}}][t_1^{\vartheta }-t_2^{\vartheta }]\to 0when{t}_1\to t_2.\hfill \end{array}$$

(21)

This uses the Arzelà–Ascoli theorem to guarantee the relative compactness of $\mathcal{B}\left(T\right)$.

(C4): 

For the final stage, take the below set:

$$\mathcal{E}=\{\mathcal{C}\in \mathcal{X}:\mathcal{C}=\lambda B\mathcal{C},\lambda \in (0,1\left)\right\}.$$

(22)

To determine the boundedness of $\mathcal{E}$, we assume that $\mathcal{C}$ is a member of $\mathcal{E}$. All t in $[0,\tau ]$ satisfy the below:

$$||\mathcal{C}||=\lambda ||B\mathcal{C}||\le \lambda \left[|{\mathcal{C}}_0|{\displaystyle \frac{{\tau }^{\vartheta }}{\Gamma (\vartheta +1)}}[U_{\mathcal{H}}{||\mathcal{C}||}^q+V_{\mathcal{H}}]\right].$$

(23)

Consequently, the set $\mathcal{E}$ is bounded. The operator B has a fixed point that can be found using Schaefer’s theorem. Therefore, the malaria model (11) has at least one solution.

□

Remark 1.

If the condition $C1$ holds true for $q=1$, then it is possible to demonstrate Theorem 4 for ${\displaystyle \frac{{\tau }^{\vartheta }{U}_Z}{\Gamma (\vartheta +1)}}<1$.

Theorem 5.

The system (11) of malaria fever possesses a unique solution when the condition ${\displaystyle \frac{{\tau }^{\vartheta }{U}_Z}{\Gamma (\vartheta +1)}}<1$ is fulfilled.

Proof. 

To achieve this, use Banach’s contraction theorem, assuming that $\mathcal{C}$ and $\overline{\mathcal{C}}\in \mathcal{X}$:

$$\begin{array}{cc}\hfill \left|\right|B\mathcal{C}-B\overline{\mathcal{C}}\left|\right|& \le \underset{t\in [0,\tau ]}{max}{\displaystyle \frac{1}{\Gamma \left(\vartheta \right)}}{\int }_0^t{|(t-s)}^{\vartheta -1}\left|\right|\mathcal{H}(s,\mathcal{C}\left(s\right))-\mathcal{H}(s,\overline{\mathcal{C}}\left(s\right))|ds\hfill \\ & \le {\displaystyle \frac{{\tau }^{\vartheta }{U}_{\mathcal{H}}}{\Gamma (\vartheta +1)}}\left|\right|\mathcal{C}-\overline{\mathcal{C}}\left|\right|.\hfill \end{array}$$

(24)

Thus, there exists a fixed point for B, which implies that model (11) of malaria has a unique solution. □

5. Stability Analysis

In this section of the paper, the Ulam–Hyers stability (UHS) of the system will be examined. This is a foundational concept for ensuring that systems and equations are resilient to small errors, providing both theoretical insight and practical assurance in the analysis of dynamic and functional equations.

Take $\mathcal{Z}:\mathcal{X}\to \mathcal{X}$ in such a manner that

$$\mathcal{Z}\mathcal{P}=\mathcal{P}for\mathcal{P}\in \mathcal{X}.$$

(25)

Definition 4.

The above (25) is UHS if $\zeta >0$, and for any solution $\mathcal{C}$ in $\mathcal{X}$, the below fulfills

$$\left|\right|\mathcal{P}-\mathcal{ZP}\left|\right|\le \zeta ,\forall t\in [0,\tau ].$$

(26)

In addition to this, let $\overline{\mathcal{C}}$ be a unique solution for the above (25) in a manner that ${\mathcal{C}}_q>0$, and the below holds true as follows:

$$\left|\right|\overline{\mathcal{P}}-\mathcal{P}\left|\right|\le {\mathcal{C}}_q\zeta ,\forall t\in [0,\tau ].$$

(27)

Definition 5.

Let $\mathcal{C}$ and $\overline{\mathcal{C}}$ be solutions of (25); then, the solution of (25) is generalized UHS if

$$\left|\right|\overline{\mathcal{P}}-\mathcal{P}\left|\right|\le \mathcal{H}\left(\zeta \right),$$

(28)

in which $\mathcal{H}\in C(R,R)$, and zero is the image of zero.

Remark 2.

Let the solution $\overline{\mathcal{C}}$ belonging to $\mathcal{X}$ fulfill Equation (27), and the below condition is satisfied:

(a) 

$\left|ħ\right(t\left)\right|\le \zeta ,$ in which $ħ\in C\left(\right[0,\tau ];R)$

(b) 

$\mathcal{K}\overline{\mathcal{P}}\left(T\right)=\overline{\mathcal{P}}+ħ\left(T\right),\forall t\in [0,\tau ].$

After perturbation, the system (11) can be expressed as follows:

$$\left\{\begin{array}{cc}\hfill {}_{ }{}^{C}D_{0^{+}}^{\vartheta }\mathcal{P}\left(t\right)=& \mathcal{C}(t,\mathcal{P}(t\left)\right)+ħ\left(t\right),\\ \hfill \mathcal{P}\left(0\right)={\mathcal{P}}_0.\end{array}\right.$$

(29)

Lemma 2.

The system (29) fulfills the following:

$$|\mathcal{P}\left(t\right)-T\mathcal{P}\left(t\right)|\le a\zeta ,inwhicha={\displaystyle \frac{{\tau }^{\vartheta }}{\Gamma (\vartheta +1)}}.$$

(30)

This can be easily proved through Remark 2 and Lemma 1.

Theorem 6.

If ${\displaystyle \frac{{\tau }^{\vartheta }{L}_{\mathcal{C}}}{\Gamma (\vartheta +1)}}<1$ satisfies Lemma (2), system (11) has a UHS and generalized UHS solution.

Proof. 

For the proof, we assume solutions $\mathcal{P}\in X$ and $\overline{\mathcal{P}}\in X$ of the system (11) and take the following:

$$\begin{array}{cc}\hfill |\mathcal{P}\left(t\right)-\overline{\mathcal{P}}\left(t\right)|& =|\mathcal{P}\left(t\right)-\overline{\mathcal{P}}\left(t\right)|\hfill \\ & \le |\mathcal{P}\left(t\right)-T\overline{\mathcal{P}}\left(t\right)|\hfill \\ & \le |\mathcal{P}\left(t\right)-T\overline{\mathcal{P}}\left(t\right)|\hfill \\ & \le a\zeta +{\displaystyle \frac{{\tau }^{\xi }{L}_{\mathcal{U}}}{\Gamma (\xi +1)}}|\mathcal{P}\left(t\right)-\overline{\mathcal{P}}\left(t\right)|\hfill \\ & \le {\displaystyle \frac{a\zeta }{1-\frac{{\tau }^{\xi }{L}_{\mathcal{U}}}{\Gamma (\xi +1)}}}.\hfill \end{array}$$

(31)

As a result, the solution of the recommended dynamics (11) of malaria infection is UHS and generalized UHS. □

Definition 6.

For any $\mathcal{P}\in \mathcal{X}$, the solution of (25) is the Ulam–Hyers–Rassias stability (UHS) if the below holds true:

$$\left|\right|\mathcal{P}-\mathcal{KV}\left|\right|\le \Omega \left(t\right)\zeta$$

(32)

for all $t\in [0,\tau ]$. If $0<{\mathcal{C}}_q$, one can find a unique solution $\overline{\mathcal{P}}$ of (25), satisfying

$$\left|\right|\overline{\mathcal{P}}-\mathcal{P}\left|\right|\le {\mathcal{C}}_q\Omega \left(t\right)\zeta ,\forall t\in [0,\tau ].$$

(33)

Definition 7.

Assume a unique solution $\overline{\mathcal{C}}$, and suppose $\mathcal{C}$ is any other solution to the Equation (25). If

$$\left|\right|\overline{\mathcal{P}}-\mathcal{P}\left|\right|\le C_{q,\Omega }\Omega \left(t\right)\zeta ,fort\in [0,\tau ],$$

(34)

in which $\zeta >0$ and $\Omega \in D\left[\right[0,\tau ],R]$ such that $C_{q,\Omega }$. Then, the solution to (25) is generalized UHS.

Remark 3.

Assume $\overline{\mathcal{P}}\in X$, which fulfills (27) and satisfies the following:

(a) 

$\left|ħ\right(t\left)\right|\le \zeta \Omega \left(t\right),$ in which $ħ\left(t\right)\in \mathcal{C}\left(\right[0,\tau ];R)$

(b) 

$\mathcal{Z}\overline{\mathcal{P}}\left(t\right)=\overline{\mathcal{P}}+ħ\left(t\right).$

Lemma 3.

The perturbed system in (2) satisfies the subsequent conditions:

$$|\mathcal{P}\left(t\right)-T\mathcal{P}\left(T\right)|\le a\Omega \left(t\right)\zeta ,wherea={\displaystyle \frac{{\tau }^{\vartheta }}{\Gamma (\vartheta +1)}}.$$

(35)

It is easy to show this using Lemma 1 and Remark 3.

Theorem 7.

If ${\displaystyle \frac{{\tau }^{\vartheta }{L}_{\mathcal{U}}}{\Gamma (\vartheta +1)}}<1$ holds true with Lemma 3, then (11) has a UHS and generalized UHS solution.

Proof. 

Let $\mathcal{P}\in \mathcal{X}$ be any solution of (11) and $\overline{\mathcal{P}}\in \mathcal{X}$ be a unique solution; then, the following fulfills

$$\begin{array}{cc}\hfill |\mathcal{P}\left(t\right)-\overline{\mathcal{P}}\left(t\right)|& =|\mathcal{P}\left(t\right)-\overline{\mathcal{P}}\left(t\right)|\hfill \\ & \le |\mathcal{P}\left(t\right)-T\overline{\mathcal{P}}\left(t\right)|\hfill \\ & \le |\mathcal{P}\left(t\right)-T\overline{\mathcal{P}}\left(t\right)|\hfill \\ & \le a\Omega \left(t\right)\zeta +{\displaystyle \frac{{\tau }^{\vartheta }{L}_{\mathcal{C}}}{\Gamma (\vartheta +1)}}|\mathcal{P}\left(t\right)-\overline{\mathcal{P}}\left(t\right)|\hfill \\ & \le {\displaystyle \frac{a\Omega \left(t\right)\zeta }{1-\frac{{\tau }^{\vartheta }{L}_{\mathcal{C}}}{\Gamma (\vartheta +1)}}}.\hfill \end{array}$$

(36)

Thus, system (11) has a UHS and generalized UHS solution. □

These stability results ensure that the model remains reliable and resilient to fluctuations in parameters or external conditions, preserving the validity of its predictions. In this study, we established existing results and stability analysis; however, comparative analysis with existing work and data fitting will be performed in our future work.

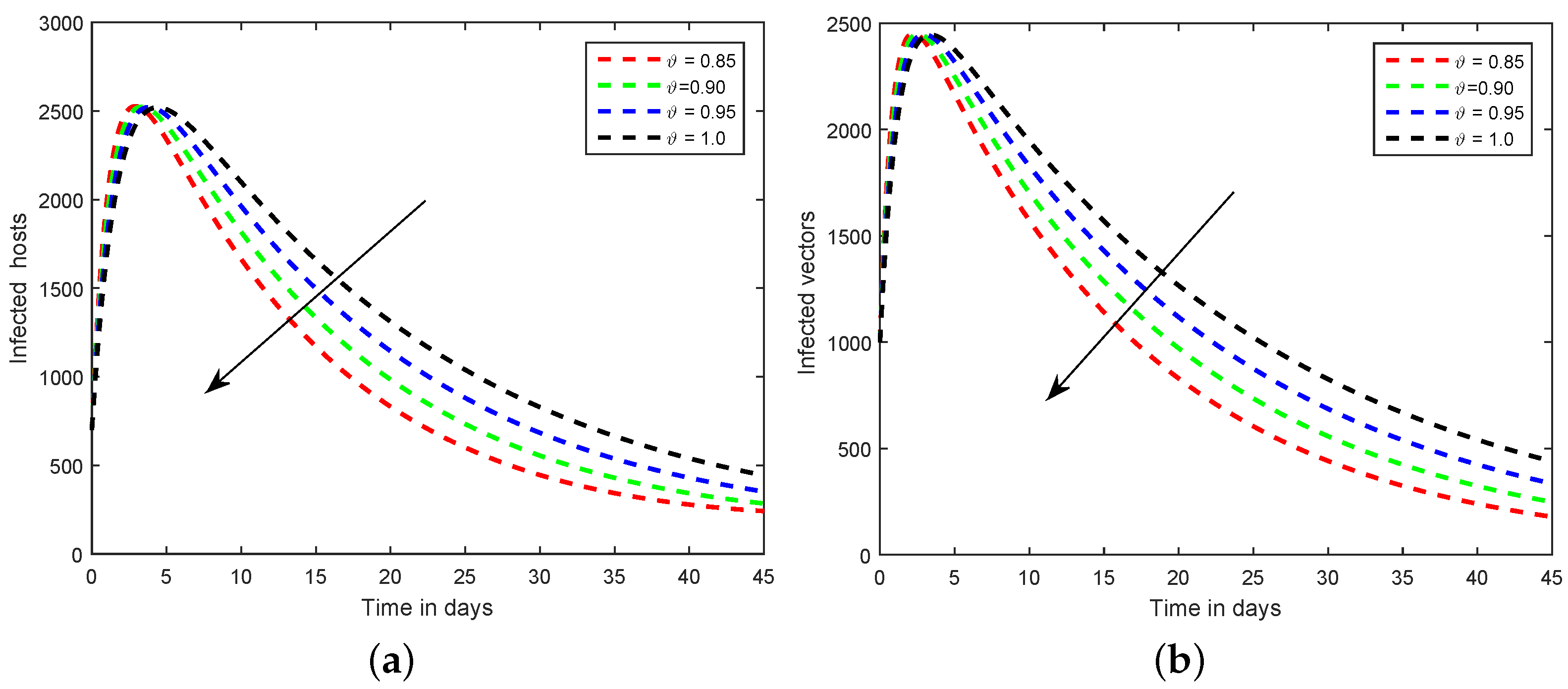
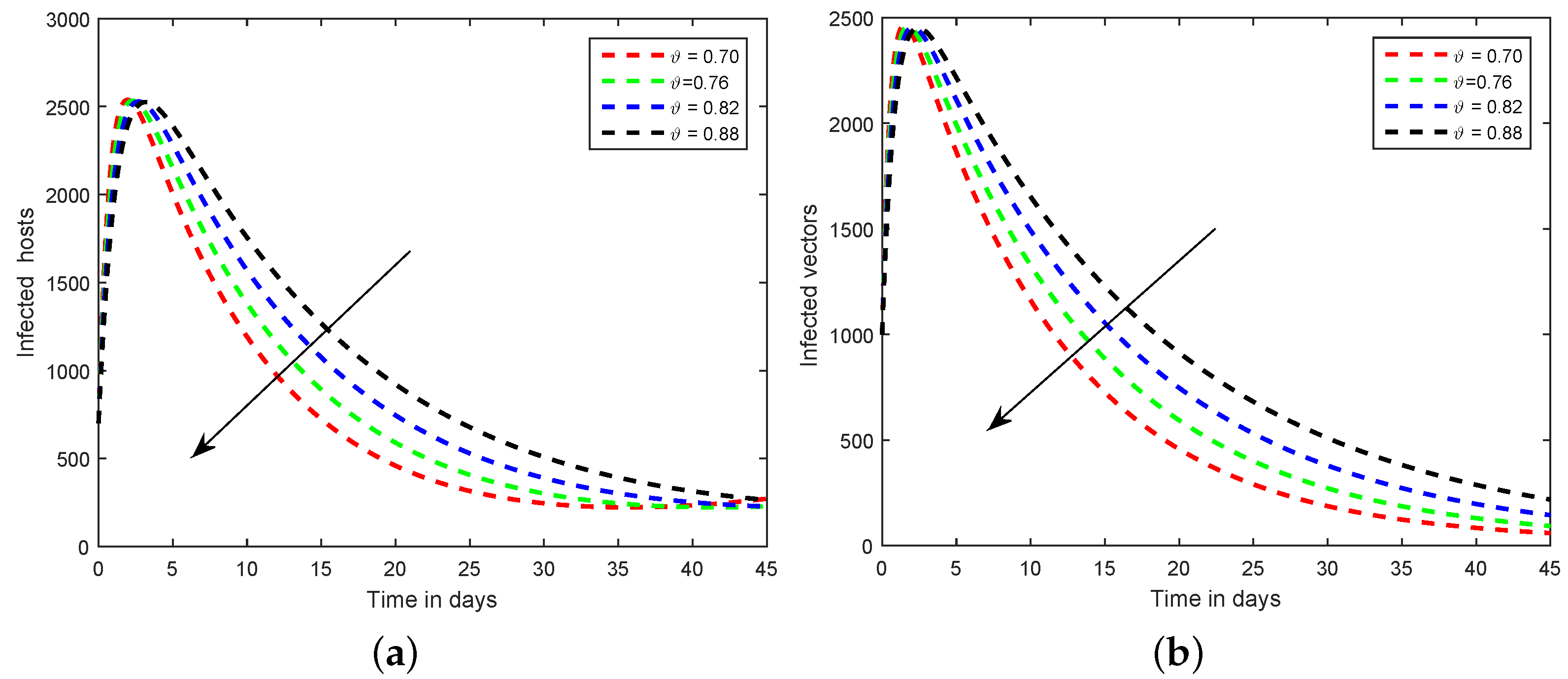
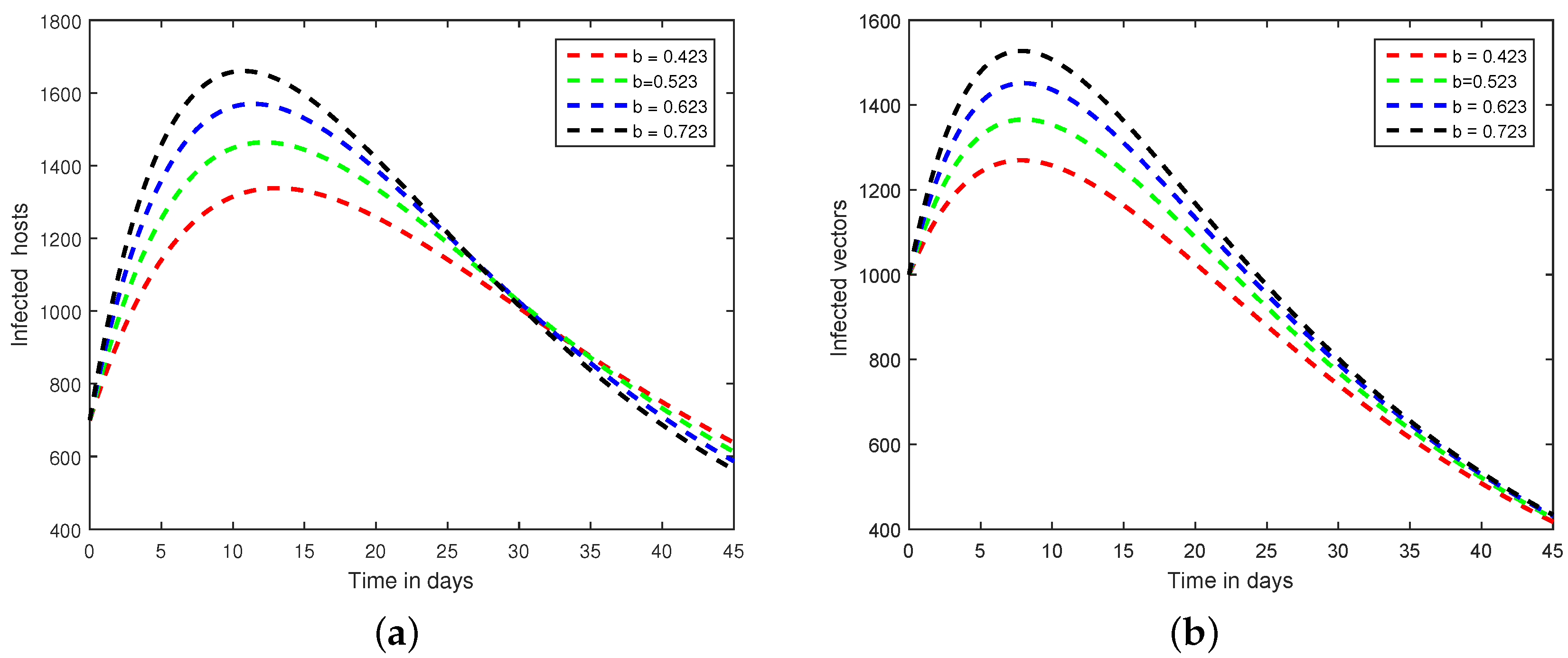
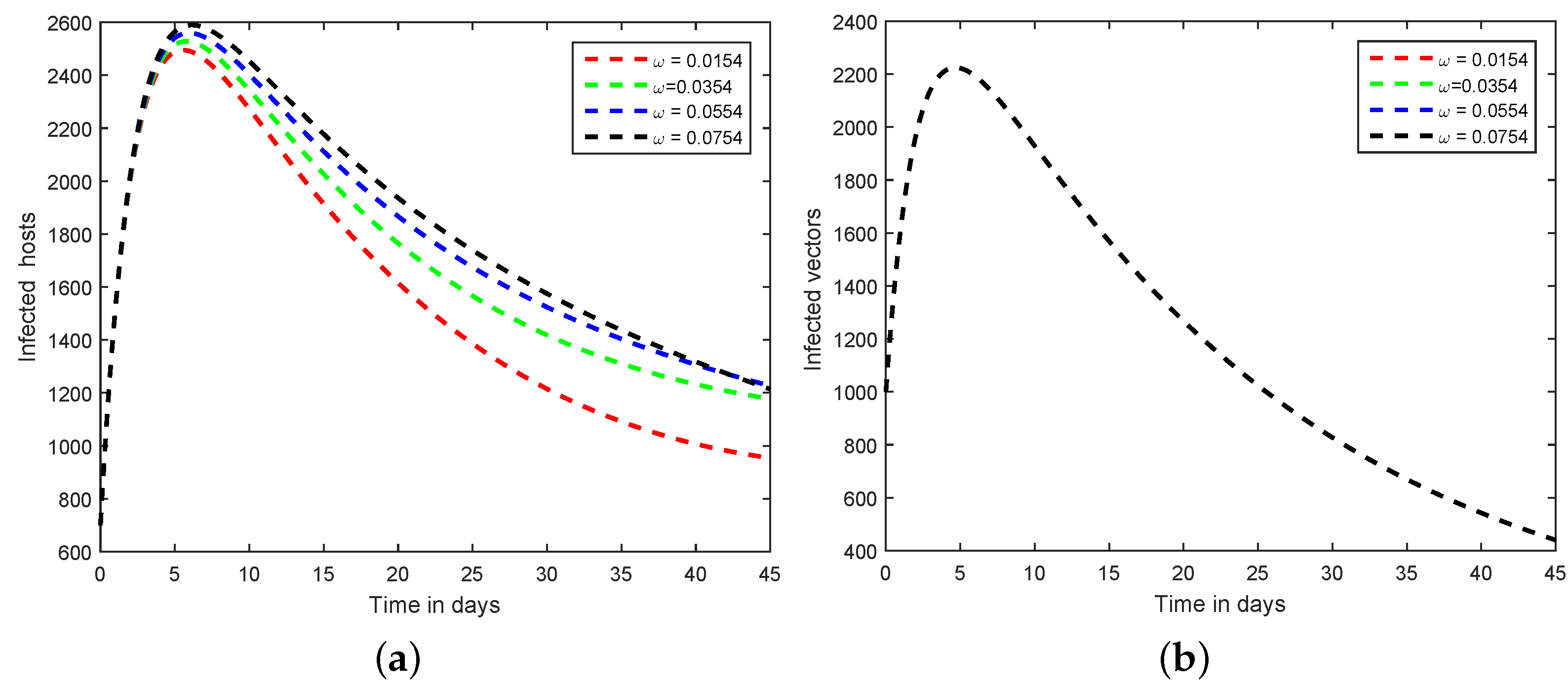
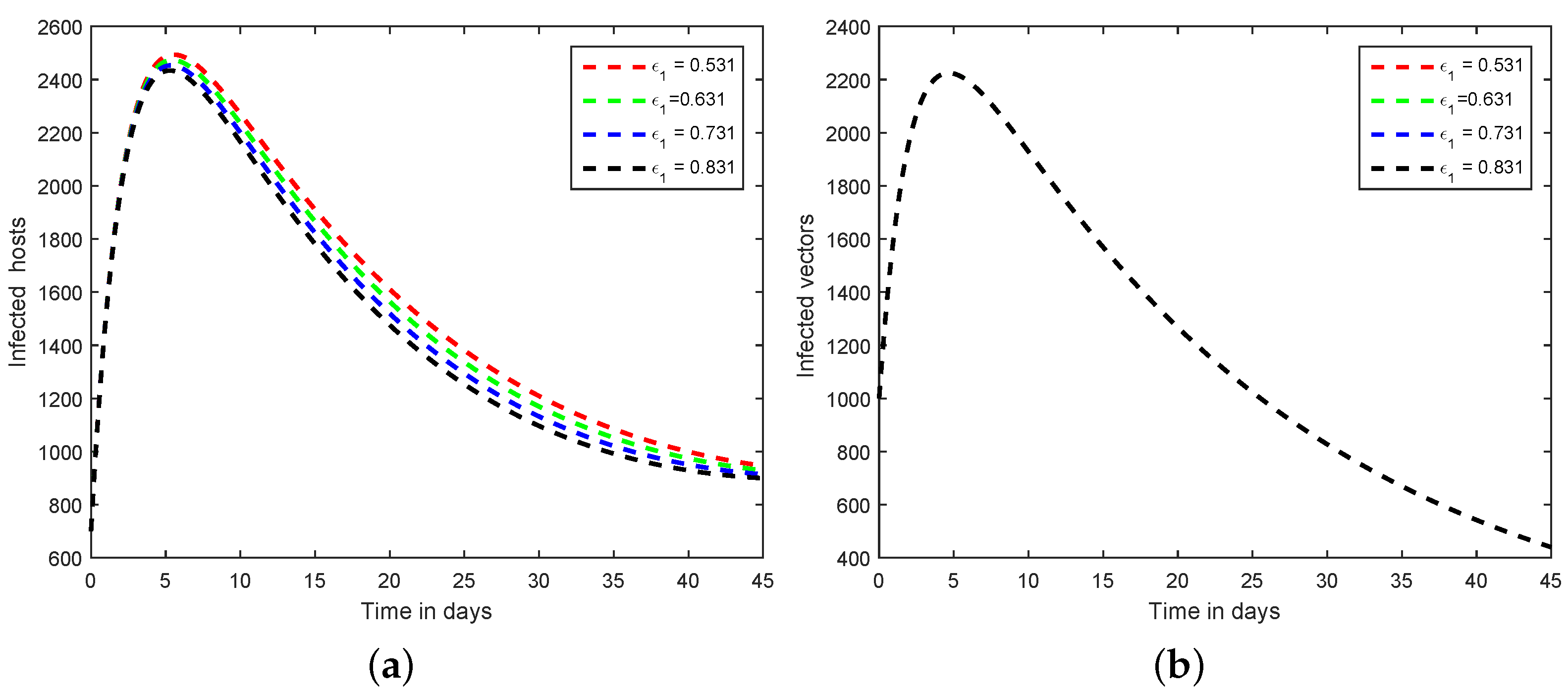
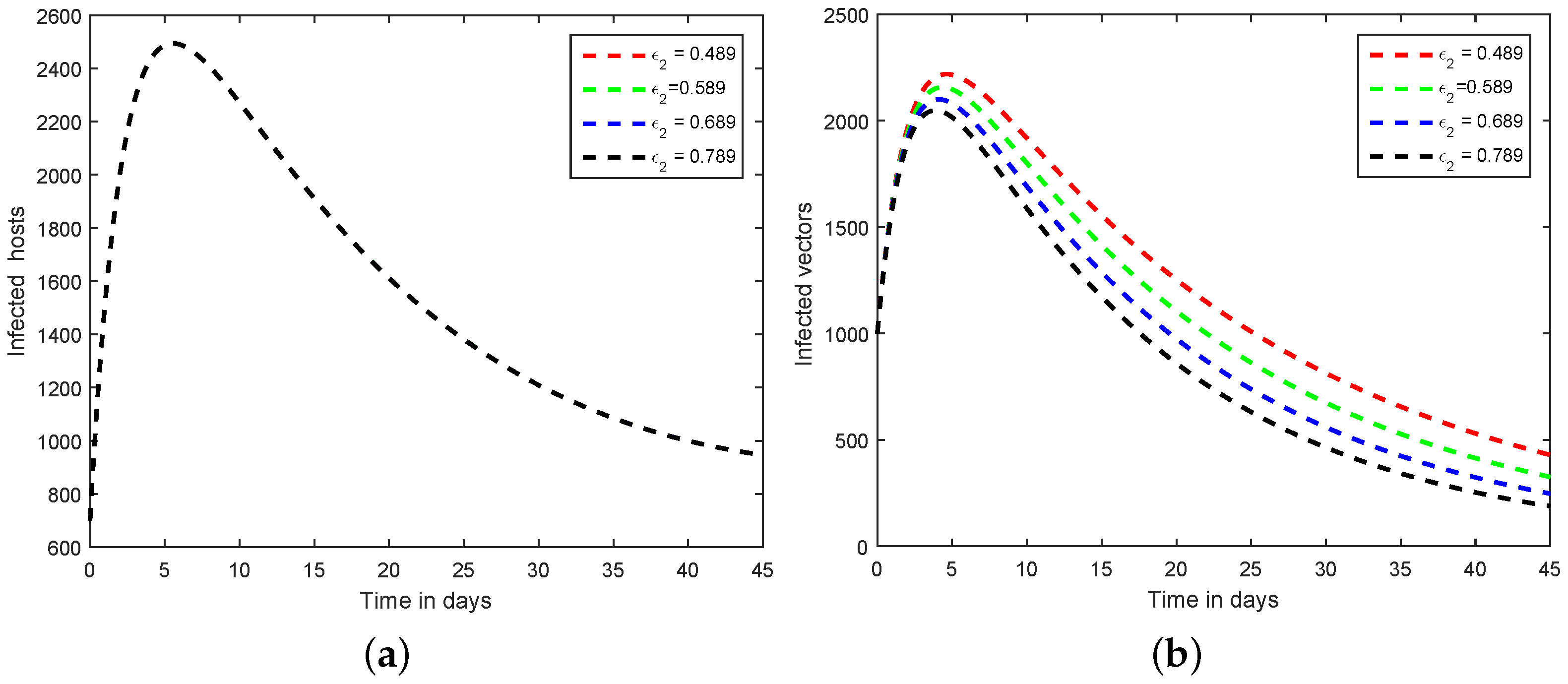
6. Numerical Scheme for the Dynamics

Here, an iterative approach is presented to illustrate the dynamical behavior of malaria infection. The scheme is based on the methodology proposed in [34] for fractional model and is described as follows:

$$\begin{array}{c}\hfill {}_{0 }{}^{C}D_t^{\alpha }k\left(t\right)=f(t,k\left(t\right)),\end{array}$$

(37)

which can be expressed as

$$\begin{array}{c}\hfill k\left(t\right)-k\left(0\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t}f(\eta ,k\left(\eta \right)){(t-\eta )}^{\alpha -1}d\eta ;\end{array}$$

(38)

therefore, at time $t=t_{n+1}$, $n=0,1,\dots$, we have

$$\begin{array}{c}\hfill k\left(t_{n+1}\right)-k\left(0\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t_{n+1}}{(t_{n+1}-t)}^{\alpha -1}f(t,k\left(t\right))dt\end{array}$$

(39)

and

$$\begin{array}{c}\hfill f\left(t_n\right)-f\left(0\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t_n}{(t_n-t)}^{\alpha -1}f(t,k\left(t\right))dt.\end{array}$$

(40)

From (40) and (39), one can get the following:

$$\begin{array}{ccc}\hfill k\left(t_{n+1}\right)& =\hfill & k\left(t_n\right)+\underset{{\mathcal{A}}_{\alpha ,1}}{\underbrace{{\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t_{n+1}}{(t_{n+1}-t)}^{\alpha -1}f(t,k\left(t\right))dt}}\hfill \\ & & -\underset{{\mathcal{A}}_{\alpha ,2}}{\underbrace{{\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t_n}{(t_n-t)}^{\alpha -1}f(t,k\left(t\right))dt}}.\hfill \end{array}$$

(41)

where

$$\begin{array}{c}\hfill {\mathcal{A}}_{\alpha ,1}={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t_{n+1}}{(t_{n+1}-t)}^{\alpha -1}f(t,k\left(t\right))dt\end{array}$$

(42)

and

$$\begin{array}{c}\hfill {\mathcal{A}}_{\alpha ,2}={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t_n}{(t_n-t)}^{\alpha -1}f(t,k\left(t\right))dt.\end{array}$$

(43)

Here, the approximation of Lagrange implies

$$\begin{array}{cc}\hfill \mathbf{P}\left(t\right)& \simeq {\displaystyle \frac{t-t_{n-1}}{t_n-t_{n-1}}}f(t_n,k_n)+{\displaystyle \frac{t-t_n}{t_{n-1}-t_n}}f(t_{n-1},k_{n-1})\hfill \\ & ={\displaystyle \frac{f(t_n,k_n)}{h}}(t-t_{n-1})-{\displaystyle \frac{f(t_{n-1},k_{n-1})}{h}}(t-t_n).\hfill \end{array}$$

(44)

The above yields the following:

$$\begin{array}{ccc}\hfill {\mathcal{A}}_{\alpha ,1}& =\hfill & {\displaystyle \frac{f(t_n,k_n)}{h\Gamma \left(\alpha \right)}}{\int }_0^{t_{n+1}}{(t_{n+1}-t)}^{\alpha -1}(t-t_{n-1})dt\hfill \\ & & -{\displaystyle \frac{f(t_{n-1},k_{n-1})}{h\Gamma \left(\alpha \right)}}{\int }_0^{t_{n+1}}{(t_{n+1}-t)}^{\alpha -1}(t-t_n)dt.\hfill \end{array}$$

(45)

After additional simplification,

$$\begin{array}{ccc}\hfill {\mathcal{A}}_{\alpha ,1}& =\hfill & {\displaystyle \frac{f(t_n,k_n)}{h\Gamma \left(\alpha \right)}}\left[{\displaystyle \frac{2h}{\alpha }}{t}_{n+1}^{\alpha }-{\displaystyle \frac{t_{n+1}^{\alpha +1}}{\alpha +1}}\right]\hfill \\ & & -{\displaystyle \frac{f(t_{n-1},k_{n-1})}{h\Gamma \left(\alpha \right)}}\left[{\displaystyle \frac{h}{\alpha }}{t}_{n+1}^{\alpha }-{\displaystyle \frac{1}{\alpha +1}}{t}_{n+1}^{\alpha +1}\right].\hfill \end{array}$$

(46)

Similarly,

$$\begin{array}{ccc}\hfill {\mathcal{A}}_{\alpha ,2}& =\hfill & {\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t_n}{(t_n-t)}^{\alpha -1}[{\displaystyle \frac{f(t_n,k_n)}{h}}(t-t_{n-1})\hfill \\ & & -{\displaystyle \frac{f(t_{n-1},k_{n-1})}{h}}(t-t_n)]dt.\hfill \end{array}$$

(47)

The below is obtained through simplification:

$$\begin{array}{ccc}\hfill {\mathcal{A}}_{\alpha ,2}& =\hfill & {\displaystyle \frac{f(t_n,k_n)}{h\Gamma \left(\alpha \right)}}\left[{\displaystyle \frac{h}{\alpha }}{t}_n^{\alpha }-{\displaystyle \frac{t_n^{\alpha +1}}{\alpha +1}}\right]\hfill \\ & & +{\displaystyle \frac{f(t_{n-1},k_{n-1})}{h\Gamma \left(\alpha \right)}}\left[{\displaystyle \frac{1}{\alpha +1}}{t}_n^{\alpha +1}\right].\hfill \end{array}$$

(48)

Putting (47) and (48) into (41), we have

$$\begin{array}{ccc}\hfill k\left(t_{n+1}\right)& =\hfill & k\left(t_n\right)+{\displaystyle \frac{f(t_n,k_n)}{h\Gamma \left(\alpha \right)}}\left[{\displaystyle \frac{2h{t}_{n+1}^{\alpha }}{\alpha }}-{\displaystyle \frac{t_{n+1}^{\alpha +1}}{\alpha +1}}+{\displaystyle \frac{h}{\alpha }}{t}_n^{\alpha }-{\displaystyle \frac{t_{n+1}^{\alpha +1}}{\alpha +1}}\right]\hfill \\ & & +{\displaystyle \frac{f(t_{n-1},k_{n-1})}{h\Gamma \left(\alpha \right)}}\left[-{\displaystyle \frac{h}{\alpha }}{t}_{n+1}^{\alpha }+{\displaystyle \frac{t_{n+1}^{\alpha +1}}{\alpha +1}}+{\displaystyle \frac{t_n^{\alpha +1}}{\alpha +1}}\right].\hfill \end{array}$$

(49)

We examined the time series of our system (7) of malaria using the numerical scheme outlined above. It is important to investigate the dynamical behavior of epidemic models to illustrate the impact of the scenario on the models. We performed several simulations to analyze our model of malaria infection.

We illustrated how the fractional order in the suggested malaria model affects the population of infected people in the first scenario shown in Figure 1 and Figure 2. With a comparison study to the standard system, we assumed different values of $\vartheta$ in these figures. The $\vartheta$ values in Figure 1 are $\vartheta =0.85$, $0.90$, $0.95$, and $1.00$. This simulation illustrates the impact of both fractional and classical derivatives, demonstrating the flexibility of fractional systems and the ability to evaluate several values instead of just one. The values of $\vartheta$ in Figure 2 are taken to be $\vartheta =0.70$, $0.76$, $0.82$, and $0.88$. We found that the dynamics of infected persons are significantly and attractively impacted by the index of memory. Moreover, a drop in this system parameter may result in a drop in the prevalence of infections in the community. The memory index can be used to manage the infection level. Policymakers are therefore urged to take the memory index into account as a practical means of managing and mitigating illness.

The influence of the biting rate b on the infection level is depicted in Figure 3. In the second simulation, we assumed that b had the following values: $b=0.423$, $0.523$, $0.623$, and $0.723$. Evidently, this element is risky and increases the likelihood of infection in the community. In order to stop the virus from spreading across the population, we thus support controlling the bite rate as a preventative approach. The impact of the immunity loss rate on malaria transmission dynamics is depicted in Figure 4. $\omega$ was supposed to be 0.0154, 0.0354, 0.0554, and 0.0754. We can observe from this simulation that this input factor raises the risk of infected hosts. We have illustrated the impact of treatment effectiveness on malaria dynamics in Figure 5. This element has a beneficial effect on the system and lowers the level of infection. The impact of pesticide effectiveness on malaria dynamics is depicted in Figure 6. In this simulation, it is assumed that the pesticide efficacy values are 0.531, 0.631, 0.731, and 0.831. This variable lowers the levels of infection by having a positive impact on the system.

In this study, our primary focus was on these factors to show their impact on the transmission pathways. Our outcomes emphasize that the index of memory can effectively control the infection level, providing valuable insights for policymakers. We propose that the control of malaria can be significantly enhanced through the implementation of vaccination and treatment. Furthermore, effective infection control measures can be achieved by utilizing bed nets, insecticide spraying, and regulating the memory index.

7. Concluding Remarks

In our work, we structured an epidemic model for the transmission dynamics of malaria with a saturated incidence rate through a fractional framework. We modeled the impact of drug resistance and insecticide on the dynamics of malaria infection. It has been shown that the solutions of the proposed system are non-negative and bounded. The endemic indicator of the system is denoted by ${\mathcal{R}}_0$ and is determined through the next-generation matrix approach. For the existence and uniqueness of solutions, we applied the Banach and Schaefer frameworks through the fixed-point theorem. We also derived sufficient conditions to guarantee the Ulam–Hyers stability of the model. A numerical method was employed to explore the dynamics of infection, revealing the influence of various input factors on its behavior. Our numerical results identified the most sensitive factors for the effective prevention and management of malaria within the community. Our study highlights the crucial role of memory effects in shaping the complex dynamics of malaria, suggesting its potential as a modifiable control parameter for the management of the infection. Moving forward, our future research will focus on examining the impact of variables such as maturation and incubation delays on malaria dynamics. In future studies, we will investigate the effects of maturation and incubation delay on the dynamics of malaria. Additionally, the impact of pulse vaccination will be analyzed and visualized.