A Novel Approach for Solving Fractional Differential Equations via a Multistage Telescoping Decomposition Method
Abstract
1. Introduction and Mathematical Preliminaries
2. Fundamental Definitions
2.1. Fractional Calculus
2.2. Properties and Definition of Elzaki Transform
2.3. Algorithm of Telescoping Decomposition Method
Multistage Telescoping Decomposition Method
3. Multistage Telescoping Decomposition Elzaki Method
3.1. Solving the Nonlinear Fractional Differential Equations
3.2. Solving the Nonlinear Fractional Partial Differential Equations
4. Program of the MFTDM
| Algorithm 1: Programme of the novel algorithm. |
| Programme: ; endproc: Warning, ’g’ is implicitly declared local to procedure ’abc’ >for k from 2 to n do ; end; >for i from 1 to do >for k from 2 to n do ; print end; |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adomian, G. Solution of physical problems by decomposition. Comp. Math. Appl. 1994, 27, 145–154. [Google Scholar] [CrossRef]
- Momani, S.; Shawagfeh, N. Decomposition method for solving fractional Riccati differential equations. Asian J. Math. Comput. 2016, 13, 203–214. [Google Scholar] [CrossRef]
- Elzaki, T.M.; Chamekh, M. Solving nonlinear fractional differential equations using a new decomposition method. Univ. J. Appl. Math. Comput. 2018, 6, 27–35. [Google Scholar]
- Ziane, D.; Belghaba, K.; Cherif, M.H. Fractional homotopy perturbation transform method for solving the time-fractional KdV, k(2,2) and Burgers equations. Int. J. Open Prob. Comput. Sci. Math. 2015, 8, 63–75. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of homotoping technique and perturbation technique for nonlinear problems. Int. J. Nonlinear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- Hilall, E.; Elzaki, M.T. Solution of nonlinear partial differential equations by new Laplace variational iteration method. J. Funct. Spaces 2014, 2014, 790714. [Google Scholar] [CrossRef]
- Afshan, K.; Tauseef, M.S. Coupling of Laplace transform and correction functional for wave equations. Word J. Mod. Simul. 2013, 9, 173–180. [Google Scholar]
- Elzaki, T.M.; Elzaki, S.M. On the connections between Laplace and Elzaki transforms. Adv. Theor. Appl. Math. 2014, 6, 1–10. [Google Scholar]
- Abel-Rady, A.S.; Rida, S.Z.; Arafa, A.A.M.; Abedi-Rahim, H.R. Variational iteration Sumudu transform method for solving fractional nonlinear gaz dynamics equation. Int. J. Res. Stud. Sci. Eng. Technol. 2014, 1, 82–90. [Google Scholar]
- Kumar, D.; Singh, J.; Rathore, S. Sumudu decomposition method for nonlinear equations. Int. Math. Forum 2012, 7, 515–521. [Google Scholar]
- Singh, J.; Kumar, D.; Sushila. Homotopy perturbation Sumudu transform method for nonlinear equations. Adv. Theor. Appl. Mach. 2011, 4, 165–175. [Google Scholar]
- Rathore, S.; Kumar, D.; Singh, J.; Gupta, S. Homotopy analysis Sumudu transform method for nonlinear equations. Int. J. Ind. Math. 2012, 4, 301–314. [Google Scholar]
- Elzaki, T.M. The new integral transform Elzaki transform. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Elzaki, T.M.; Hilal, E.M.A. Homotopy perturbation and Elzaki transform for solving nonlinear partial differential equations. Math. Theor. Mod. 2012, 2, 33–42. [Google Scholar]
- Elzaki, T.M.; Elzaki, S.M.; Elnour, E.A. On the new integral transform “Elzaki Transform” fundamental properties investigations and applications. Glob. J. Math. Sci. 2012, 2, 1–13. [Google Scholar]
- Elzaki, T.M. On the Elzaki transform and ordinary differential equation with variable coefficients. Adv. Theor. Appl. Math. 2011, 6, 13–18. [Google Scholar]
- Elzaki, T.M.; Biazar, J. Homotopy perturbation method and Elzaki transform for solving system of nonlinear partial differential equatios. World Appl. Sci. 2013, 24, 944–948. [Google Scholar]
- Riabi, L.; Belghaba, K.; Cherif, M.H.; Ziane, D. Homotopy perturbation method combined with ZZ transform to solve some nonlinear fractional differential equations. Int. J. Anal. Appl. 2019, 17, 406–419. [Google Scholar]
- Al-Refai, M.; Abu-Dalu, M.; Al-Rawashde, A. Telescoping decomposition method for solving first order nonlinear differential equations. In Proceedings of the International Multi-Conference of Engineers and Computer Scientists, (IMECS 2008), Kowloon, Hong Kong, 19–21 March 2008. [Google Scholar]
- Khalid, M.; Sultana, M.; Zaidi, F.; Arshad, U. An Elzaki transform decomposition algorithm applied to a class of non-linear differential equations. J. Nat. Sci. Res. 2015, 5, 48–55. [Google Scholar]
- Nibron, M.; Mishra, A.K.; Kabala, D. Telescoping decomposition method for solving second order nonlinear differential equations. Int. J. Eng. Res. Technol. 2014, 3, 590–595. [Google Scholar]
- Ige, O.E.; Heilio, M.; Oderinu, R.A.; Elzaki, T.M. Adomian polynomial and Elzaki transform method of solving third order Korteweg-De Vries equatios. Glob. J. Pure Appl. Math. 2019, 15, 261–277. [Google Scholar]
- Ige, O.E.; Oderinu, R.A.; Elzaki, T.M. Adomian polynomial and Elzaki transform method for solving Klein Gordon equations. Int. J. Appl. Math. 2019, 32, 451–468. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Burqan, A. A new integral transform: ARA transform and its properties and applications. Symmetry 2020, 12, 925. [Google Scholar] [CrossRef]
- Zafar, Z.U.A. ZZ transform method. Int. J. Adv. Eng. Glob. Technol. 2016, 4, 1605–1611. [Google Scholar]
- Zafar, Z.U.A. Application of ZZ transform method on some fractional differential equation. Int. J. Adv. Eng. Glob. Technol. 2016, 4, 1355–1363. [Google Scholar]
- Ziane, D. The combined of Homotopy analysis method with new transform for nonlinear partial differential equations. Malaya J. Math. 2018, 6, 34–40. [Google Scholar] [CrossRef]
- Raghavendar, K.; Pavani, K.; Aruna, K.; Okposo, N.I.; Inc, M. Application of Natural Transform Decomposition Method for Solution of Fractional Richards Equation. Contemp. Math. 2024, 5, 5881. [Google Scholar] [CrossRef]
- Kharrat, B.N. New Double Kharrat-Toma Transform and its Application in Partials Differential Equations. World Appl. Sci. J. 2024, 42, 30–36. [Google Scholar]
- Bouhassoun, A. Multistage telescoping decomposition method for solving fractional differential equations. Int. J. Appl. Math. 2013, 43, 1–7. [Google Scholar]
- Chita, F.; Belghaba, K. Solving systems of nonlinear fractional differential equations using multistage telescoping decomposition method. Asian J. Math. Comput. 2016, 13, 203–214. [Google Scholar]
- Diethelm, K. The Analysis Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
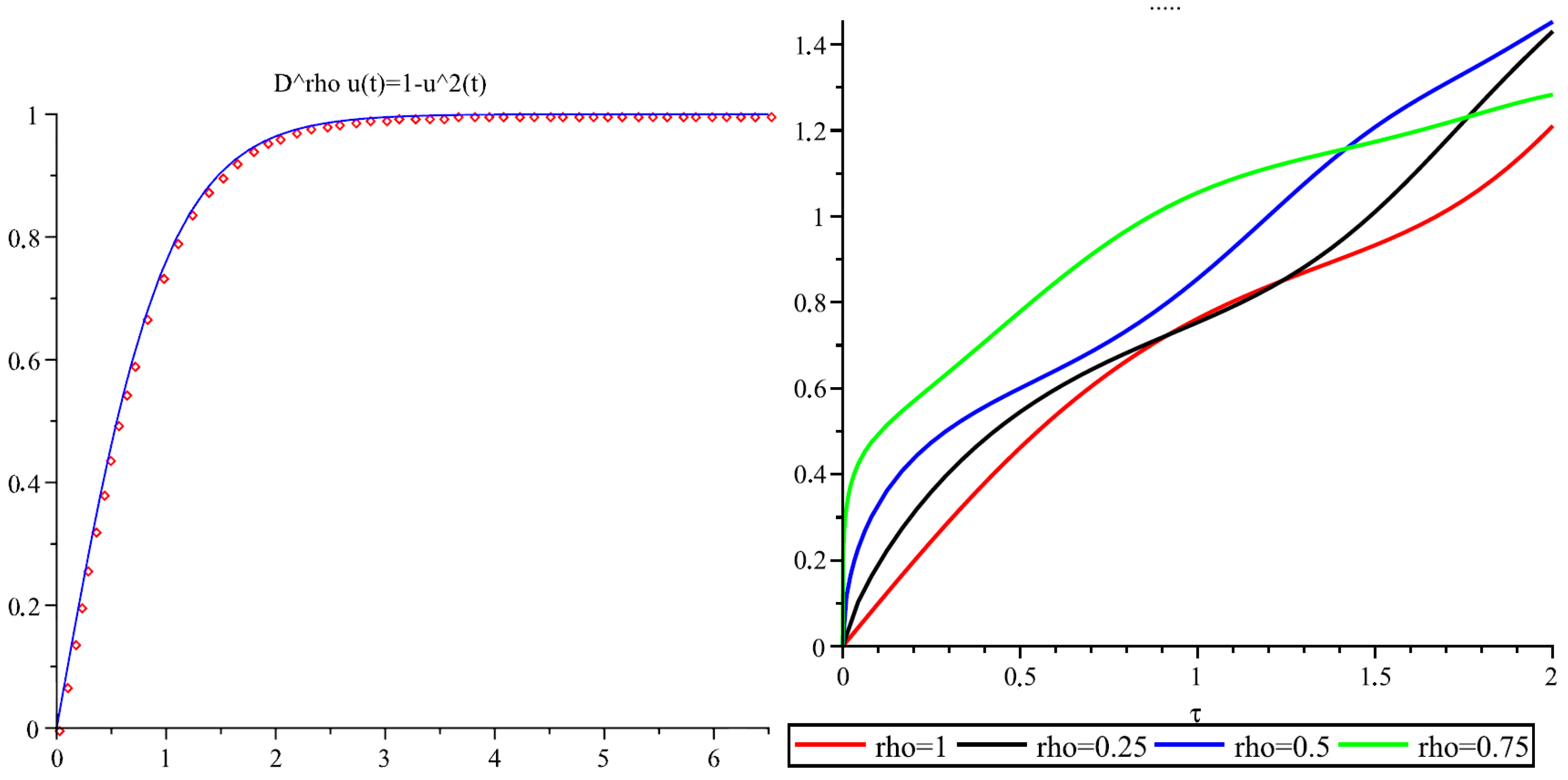
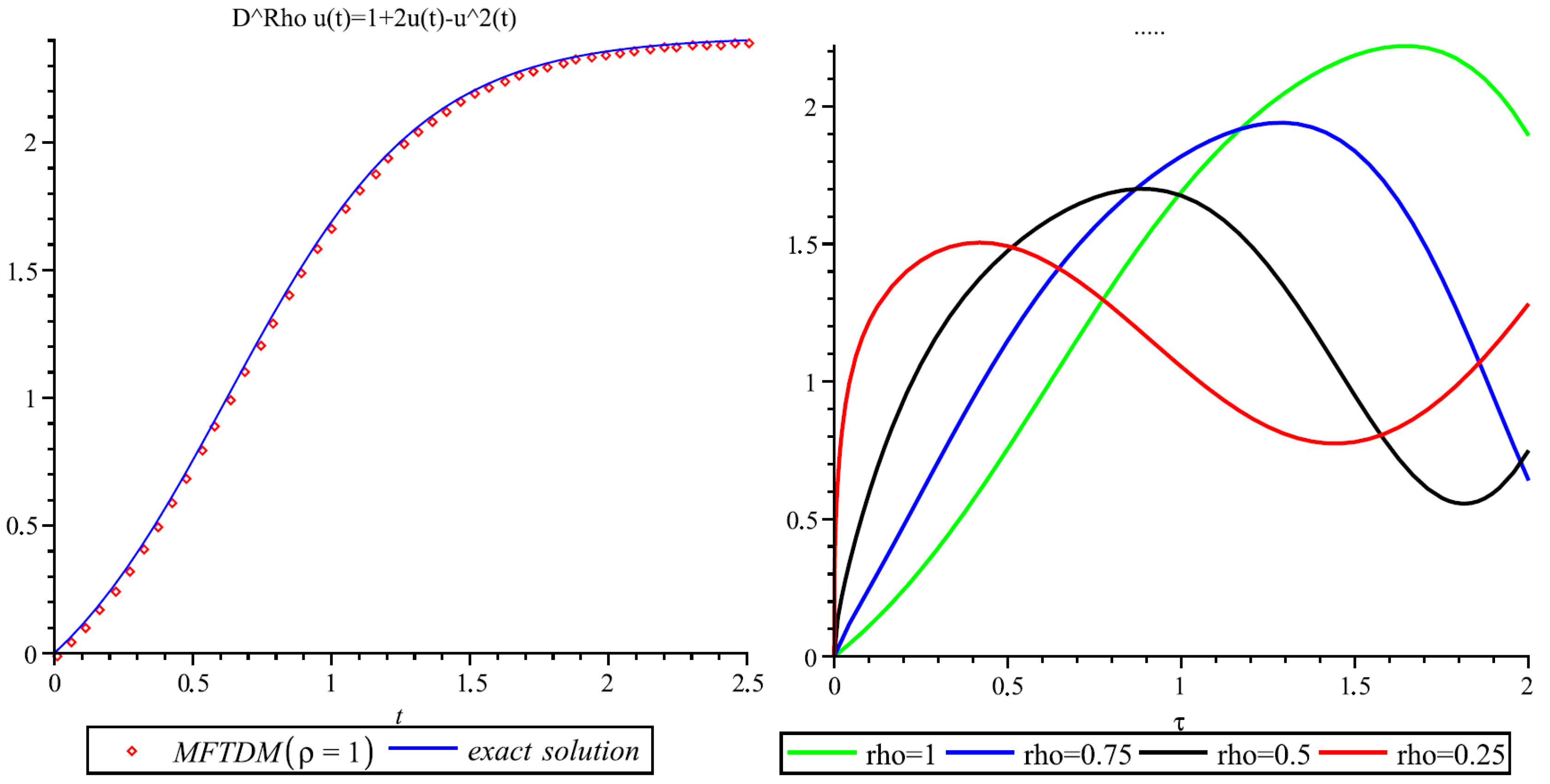
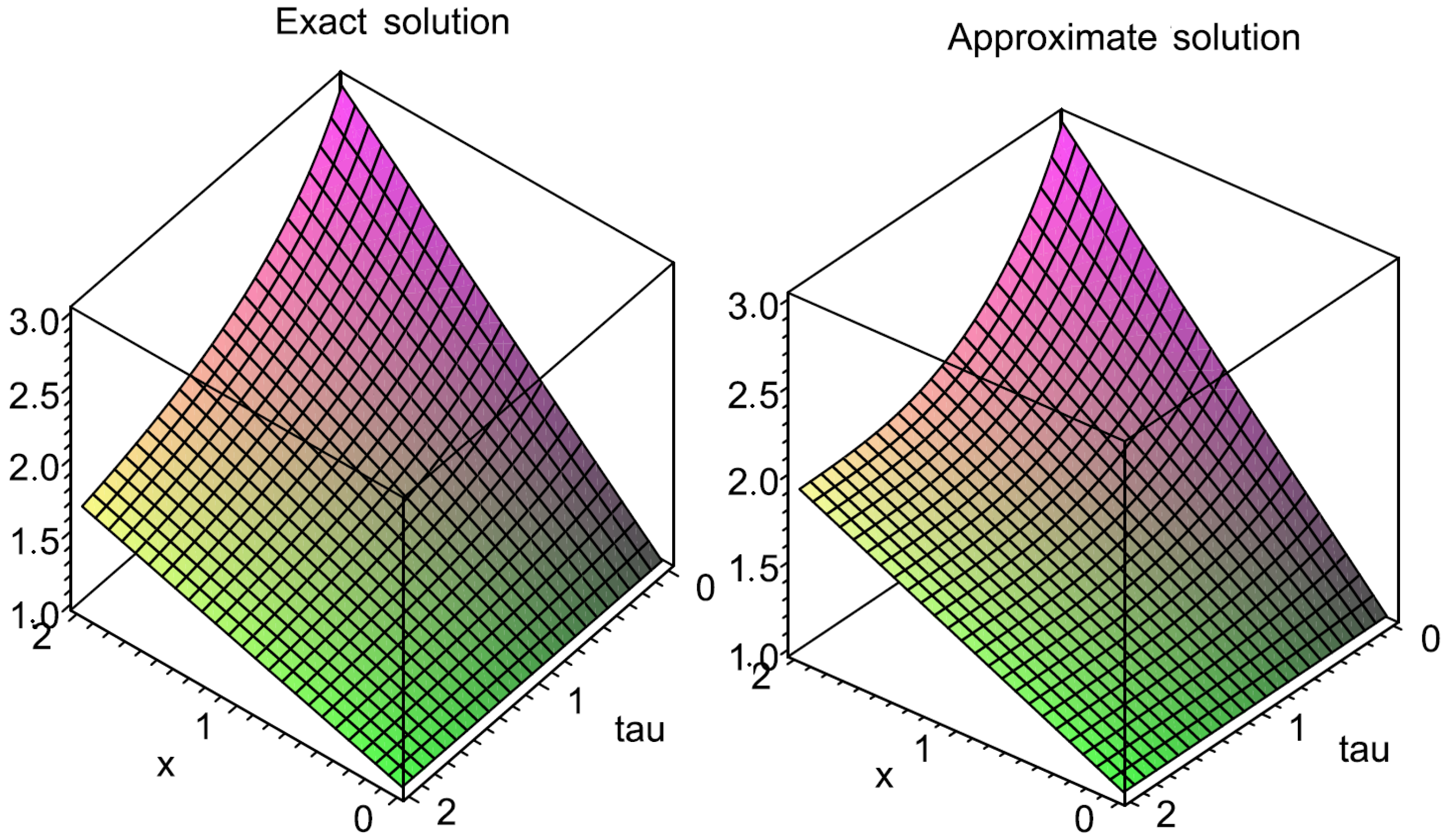

| 1 | |||
| ADM Error | FTDM Error | MFTDEM 1 Error | MFTDEM 2 | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0.0000527183 | 0.0000138244 | 0.000258833 | 0.000014334 |
| 1 | 4.11264 | 0.0044278890 | 0.00392701 | 0.000198 |
| 1.5 | 10323.1 | 0.09144481177 | 0.0062466 | 0.00023656 |
| 2 | 0.5723355101 | 0.00493943 | 0.00021433 | |
| 2.5 | 1.075212598 | 0.00285709 | 0.00060915 | |
| 3 | 7.413059554 | 0.00141436 | 0.000064128 | |
| 3.5 | 304.3789789 | 0.00524319 | 0.00019047 | |
| 4 | 4250.670072 | 0.0213869 | 0.0022778 | |
| 4.5 | 35669.87361 | 0.0587671 | 0.0099358 | |
| 5 | 861.079 | 0.126514 | 0.027505 | |
| 5.5 | 1796.48 | 0.23312 | 0.059500 | |
| 6 | 3473.63 | 0.385885 | 0.11034 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chita, F.; Ayadi, S.; Erden Ege, M.; Ege, O.; Ramaswamy, R. A Novel Approach for Solving Fractional Differential Equations via a Multistage Telescoping Decomposition Method. Fractal Fract. 2025, 9, 65. https://doi.org/10.3390/fractalfract9020065
Chita F, Ayadi S, Erden Ege M, Ege O, Ramaswamy R. A Novel Approach for Solving Fractional Differential Equations via a Multistage Telescoping Decomposition Method. Fractal and Fractional. 2025; 9(2):65. https://doi.org/10.3390/fractalfract9020065
Chicago/Turabian StyleChita, Fouzia, Souad Ayadi, Meltem Erden Ege, Ozgur Ege, and Rajagopalan Ramaswamy. 2025. "A Novel Approach for Solving Fractional Differential Equations via a Multistage Telescoping Decomposition Method" Fractal and Fractional 9, no. 2: 65. https://doi.org/10.3390/fractalfract9020065
APA StyleChita, F., Ayadi, S., Erden Ege, M., Ege, O., & Ramaswamy, R. (2025). A Novel Approach for Solving Fractional Differential Equations via a Multistage Telescoping Decomposition Method. Fractal and Fractional, 9(2), 65. https://doi.org/10.3390/fractalfract9020065








