Application of the φ,ψ-Double Integral Transform to Particular φ,ψ-Fractional Differential Equations

Abstract

In this work, we propose a simple analytical/semi-analytical approach to solve various φ,ψ-fractional partial differential equations (φ,ψ-FPDEs) using initial and boundary conditions (ICs, BCs) depending on the φ,ψ-Double Elzaki transform (φ,ψ-DET) method. The suggested approach takes advantage of a DPET modification that works well with φ,ψ-fractional operators. The proposed method not only solves the φ,ψ-FPDEs but also reduces them to a more straightforward algebraic recurrence issue. This simple yet powerful idea can be used to solve φ,ψ-FPDEs in science and engineering. We contrast the outcomes of the stated computational examples with exact solutions in order to verify the exactness and efficacy of this methodology.

1. Introduction

Fractional derivatives have a long history in mathematics, although scientific domains did not employ them for a very long period. The fact that a fractional derivative has numerous non-equivalent definitions may contribute to its unpopularity [1]. One area of mathematics that was long considered arcane was fractional calculus. Fractional calculus is generally defined as an extension of classical differentiation and integration to any order. It has been developed by numerous academics and mathematicians since its inception. Liouville, Riemann, Leibniz, Weyl, Abel, Grünwald, Letnikov, Caputo, Riesz, Hadamard, and Feller are among the mathematicians that spring to mind.

For derivatives and integrals of non-integer orders, fractional calculus is a subfield of classical calculus. More than three centuries have passed since the idea was initially put forward, and it has had a substantial influence on a number of fields, including anomalous diffusion, control theory, and viscoelasticity.

To find the classical derivatives of fractional order, a variety of techniques have been employed, such as Riemann–Liouville, Caputo, Grünwald–Letnikov, and others. Despite the multiplicity of these concepts, researchers have gone ahead and developed certain generalized conceptions that place these fractional derivatives into a more generic concept. This might be the main motivation behind the creation of the Ψ-fractional derivative. The concept of the fractional derivative with regard to another function has existed since Érdlyi first introduced this generalized derivative in [2] in 1964. Olser then provided a precise definition of the ψ-fractional derivative in 1970 [3].

Since then, several scholars have developed this concept, with examples offered by Almeida [4,5], Sousa, and Oliveira [6]. But there was more to these concepts than merely mathematics. However, more recent studies show that the efficiency of particular models varies according to the type of ψ-FDEs. For example, modeling that considers the relaxation and/or the law of deformation of certain substances is based on this type of generalized fractional equations Yang [7]. Xin Li, Weiyuan Ma, Xionggai Bao, study Generalized fractional calculus on time scales based on the generalized Laplace transform [8]. Using the ET, Singh et al. in [9] developed the Hilfer-Prabhakar fractional derivative to investigate the free electron laser equation. In this article, inspired by these physical applications, we propose to handle some equations with fractional derivatives while maintaining another function. However, the issues involving the Ψ-fractional derivative are challenging to solve. Given their obvious popularity, we propose a new technique, the ψ-ET, which is based on Elzaki’s ET, that can improve the investigation of approximation solutions. In Lemnaouar, M.R. et al. [10] study the double Laplace transform with respect to another function.

The classic transforms of Laplace, Sumudu, and Elzaki were originally created for conventional (integer-order) differential equations, and each offers unique benefits for specific problem types. To apply these transforms within fractional calculus, adjustments are needed to accommodate fractional integrals and derivatives. Initial methods frequently utilized the straightforward power law kernel linked to the Riemann–Liouville and Caputo derivatives. This aligns with recent findings in fractional calculus, where the exploration of generalized kernels, commonly known as φ and ψ functions or kernels, is a vibrant area of research aimed at broadening the use and adaptability of integral transforms such as the Laplace, Sumudu, and Elzaki transforms. The φ,ψ-DET fractional derivative serves as a broad operator that encompasses and enhances several current fractional derivatives, such as the Hilfer, Caputo, Riemann–Liouville, Caputo–Fabrizio, and Atangana–Baleanu derivatives. By choosing specific functions for ϕ and ψ along with certain kernels, this generalized version can be simplified to match these different established operators.

This paper aims to solve φ,ψ-FPDEs using a novel technique known as the φ,ψ-DET approach. Initial value difficulties are addressed by φ,ψ-DET and its variants. Some instances of the issues described are addressed in the general explanation of the suggested approach. Analytically solving φ,ψ-FPDEs using ICs and BCs is a challenging task. A comparatively easy and direct method is used in this work to obtain the analytical solutions of ψ,φ-FPDEs, which results in closed-form solutions. This approach works well for solving φ,ψ-FPDEs that arise from the mathematical modeling of different processes.

The aim of expanding the DET to the two-parameter (φ,ψ)-framework is to create a broader and stronger mathematical instrument that can tackle a more diverse array of intricate physical and engineering challenges, especially those related to fractional calculus and changing coefficients.

2. Elzaki Transform (ET)

These fundamental explanations are given below for the ET of the function $y(t)$.

$$E[y](r)=r{\displaystyle \underset{0}{\overset{\infty }{\int }}y(t)e^{-\frac{t}{r}}dt},t>0,$$

(1)

where r is a complex value.

Elzaki et al. showed in [10] how to apply the ET, to PDEs, ODEs, systems of ODEs and PDEs, and integral equations. When Sumudu and Laplace transforms are unable to solve DEs with variable coefficients, ET may be effectively employed. ET was used to study a few engineering and biological issues and showed high efficacy in locating precise answers.

Theorem 1

([2]). The following is how ET transforms the partial derivatives:

$$\begin{array}{l}(a)\hspace{0.17em}\hspace{0.17em}E\left[y^{\prime }(t)\right]\hspace{0.17em}=\hspace{0.17em}{\displaystyle \frac{E\left[y(t)\right]}{r}}\hspace{0.17em}-ry(0)\\ \left(b\right)\hspace{0.17em}\hspace{0.17em}E\left[y^{(n)}(t)\right]={\displaystyle \frac{E\left[y(t)\right]}{r^n}}-{\displaystyle \sum _{k=0}^{n-1}{r}^{2-n+k}}{y}^{\left(k\right)}\left(0\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n\ge 1.\end{array}$$

ET of some functions:

$y(t)$	$E[y(t)]=Y(r)$
$1$	$r^2$
$t$	$r^3$
$t^n$	$n!r^{n+2}$
$e^{at}$	${\displaystyle \frac{r^2}{1-ar}}$
$\sin at$	${\displaystyle \frac{a{r}^3}{1+a^2{r}^2}}$
$\cos at$	${\displaystyle \frac{r^2}{1+a^2{r}^2}}$

Let us now demonstrate several lemmas that may be utilized to infer the function from its ET.

Definition 1

([11]). A real function  $y(t),$  $y>0$ is said to be in the space  $C_{\eta }, \eta \in \Re$ if there exists a real number  $\gamma >\eta ,$ such that:  $y(t)=t^{\eta }{y}_1(t)$, where  $y_1(t)\in C(0,\infty )$, and it is said to be in the space  $C_{\eta }^n$ if and only if  $y^n\in C_{\eta }, n\in N$.

Definition 2

([12]). The Riemann–Liouville (R-L) fractional integral operator, of the order  $\alpha >0,$ of  $y\in C_{\eta }, \eta \ge -1,$ is defined as,

$$J^{\alpha }y(t)={\displaystyle \frac{1}{\Gamma (\alpha )}}{\displaystyle \underset{0}{\overset{t}{\int }}{(t-v)}^{\alpha -1}y(v)dv, \alpha >0.}{J}^{0}y(t)=y(t)$$

Lemma 1.

For R-L fractional operator for  $\alpha >0$, then:

$$E[J^{\alpha }y(t)]=r^{\alpha }Y(r)$$

Proof. 

Using ET on R-L fractional operator for $\alpha >0$ to obtain:

$$E[J^{\alpha }y(t)]=E\left[{\displaystyle \frac{1}{\Gamma (\alpha )}}{\displaystyle \underset{0}{\overset{A}{\int }}{(t-\alpha )}^{\alpha -1}}y(v)dv\right]={\displaystyle \frac{1}{\Gamma (\alpha )}}{\displaystyle \frac{1}{r}}Y(r)G(r)=r^{\alpha }Y(r)$$

where $G(r)=E[t^{\alpha -1}]=r^{\alpha +1}\Gamma (\alpha )$.

The generalized Mittag-Leffler function is:

$${\in }_{\alpha ,\beta }(t)={\displaystyle \sum _{n=0}^{\infty }\frac{t^n}{\Gamma (n\alpha +\beta )}}. \mathrm{Especially} \mathrm{for}, {\in }_{\alpha }(t)={\in }_{\alpha ,1}(t).$$

□

Lemma 2.

If,  $\alpha ,\beta >0$, $a\in C$ and  ${\displaystyle \frac{1}{r^{\alpha }}}>\left|a\right|$, the inverse ET is:

$$E^{-1}\left[{\displaystyle \frac{r^{\beta +1}}{1+a{r}^{\alpha }}}\right]=t^{\beta -1}{\in }_{\alpha ,\beta }(-a{t}^{\alpha })$$

Proof. 

$${\displaystyle \frac{r^{\beta +1}}{1+b{r}^{\alpha }}}=r^{\beta +1}{\displaystyle \frac{1}{1+b{r}^{\alpha }}}=r^{\beta +1}{\displaystyle \sum _{j=0}^{\infty }{(-b)}^j{(r^{\alpha })}^j}={\displaystyle \sum _{j=0}^{\infty }{(-b)}^j}{r}^{j\alpha +\beta +1},$$

Then:

$$E^{-1}\left[{\displaystyle \frac{r^{\beta +1}}{1+b{r}^{\alpha }}}\right]=E^{-1}\left[{\displaystyle \sum _{j=0}^{\infty }{(-b)}^j{r}^{j\alpha +\beta +1}}\right]={\displaystyle \sum _{j=0}^{\infty }\frac{{(-b)}^j{t}^{j\alpha +\beta -1}}{\Gamma (j\alpha +\beta )}}=t^{\beta -1}{\displaystyle \sum _{j=0}^{\infty }\frac{{(-b{t}^{\alpha })}^j}{\Gamma (j\alpha +\beta )}=t^{\beta -1}{\in }_{\alpha ,\beta }(-b{t}^{\alpha })}$$

□

3. Preliminary

We go over certain definitions and conclusions in this section; for more details on these explanations and the proofs of the features, see [3,9].

Definition 3

([13]). Let  $y$ an integrable function on  $\left[{\tau }_1,{\tau }_2\right]\to ℝ$, $\left(\alpha ,r\right)\in ℝ\times \mathbb{N}$ and  $\psi \in C^r\left(\left[{\tau }_1,{\tau }_2\right]\right)$ such that  ${\psi }^{\prime }\left(t\right)>0$ the definitions listed below are applicable:

−

The right ψ-Riemann–Liouville fractional integral of order  $\alpha >0$ is:

$$I_{{\tau }_1^{+}}^{\alpha ,\psi }y(t)={\displaystyle \frac{1}{\Gamma (\alpha )}}{\displaystyle \underset{{\tau }_1}{\overset{t}{\int }}{\psi }^{\prime }(r)y(r)(}\psi (t)-\psi (r){)}^{\alpha -1}dr.$$

−

For  $\alpha >0,$  $n-1<\alpha \le n$, the ψ-Reimann-Liouville fractional derivatives on the left and right are shown as follows:

$$D_{{\tau }^{\pm }}^{n-\alpha ,\psi }y(t)={\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(t\right)}}{\displaystyle \frac{d}{dt}}\right)}^n{I}_{{\tau }^{\pm }}^{\alpha ,\psi }y(t). \mathrm{For} n-1<\alpha \le n,$$

The ψ-Caputo fractional derivatives of order  $\alpha$ on the left and right are defined as follows:

$${}^{C}D_{{\tau }^{\pm }}^{\alpha ,\psi }y(t)=I_{{\tau }^{\pm }}^{\alpha ,\psi }{y}_{\psi }^{⌈n⌉}(t) \mathrm{with}, y_{\psi }^{\left[n\right]}(t)={\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(t\right)}}{\displaystyle \frac{d}{dt}}\right)}^{n}y(t).$$

Along with the ψ-Riemann–Liouville and -Caputo fractional derivatives, this is the subsequent fractional derivative of ψ-Hilfer.

Definition 4

([13]). If  $\psi \in C^1\left(\left[{\tau }_1,{\tau }_2\right],ℝ\right)$ increasing function such that  ${\psi }^{\prime }(t)\ne 0$ and  $y$ an integrable function defined on  $\left[{\tau }_1,{\tau }_2\right]$, for all  $t\in \left[{\tau }_1,{\tau }_2\right]$ then: the right-sided ψ-Hilfer fractional derivative of order  $\zeta >0, \sigma =⌈\zeta ⌉$ and type  $0\le \alpha \le 1$ is described as:

$${}^{H}D_{{\tau }_1^{+}}^{\alpha ,\psi }y(t)=I_{{\tau }_1^{+}}^{\alpha \left(n-\zeta \right),\psi }{\left({\displaystyle \frac{1}{{\psi }^{\prime }(t)}}{\displaystyle \frac{d}{dt}}\right)}^n{I}_{{\tau }_1^{+}}^{(1-\alpha )\left(n-\zeta \right),\psi }y(t).$$

Property 1

([13]). If  $y(t)={\left(\psi \left(t\right)-\psi \left({\tau }_1\right)\right)}^{\sigma }$ where  $\sigma >n$ and  $\alpha >0$ then,

(i) 

${}^{C}D_{{\tau }_1}^{\alpha ,\psi }y(t)={\displaystyle \frac{\Gamma \left(\sigma +1\right)}{\Gamma \left(\sigma -\alpha +1\right)}}{\left(\psi (t)-\psi ({\tau }_1)\right)}^{\sigma -\alpha },\hspace{0.17em}$

(ii) 

$I_{{\tau }_1}^{\alpha ,\psi }y(t)={\displaystyle \frac{\Gamma \left(\sigma +1\right)}{\Gamma \left(\sigma +\alpha +1\right)}}{\left(\psi (t)-\psi ({\tau }_1)\right)}^{\sigma +\alpha },$

(iii) 

${}^{C}D_{{\tau }_1}^{\alpha ,\psi }{I}_{{\tau }_1}^{\alpha ,\psi }y(t)=y(t),\hspace{0.17em}$

(iv) 

$I_{{\tau }_1}^{n,\psi }{y}_{\psi }^{\left[n\right]}=y(t)-{\displaystyle \sum _{k=0}^{n-1}\frac{y_{\psi }^{\left[n\right]}\left({\tau }_1\right)}{k!}}{\left(\psi (t)-\psi ({\tau }_1)\right)}^k,$

(v) 

$I_{{\tau }_1}^{\alpha ,\psi }{}^{C}D_{{\tau }_1}^{\alpha ,\psi }y(t)=y(t)-{\displaystyle \sum _{k=0}^{n-1}\frac{y_{\psi }^{\left[n\right]}\left({\tau }_1\right)}{k!}}{\left(\psi (t)-\psi ({\tau }_1)\right)}^k.$

4. ψ-Elzaki Transform

Integral transforms types of methods that have been and still are useful for solving certain DEs, are covered in this section. This method has the advantage of being able to simplify a complicated issue. In addition to being obvious, integral transforms have helped create a number of fractional calculus formulae.

Demonstrating the usefulness and efficiency of this new transform in solving certain φ,ψ-FPDEs is the aim of this study. We will look at the following revised definition of the generalized integral transform:

Definition 5

([13]). Let  $y$ on  $\left[0,\infty \right).$ with respect to  $t$, and ψ is an increasing function such that  $\psi \left(0\right)=0$ and let  $r_1,r_2>0,$ if it exists  $M>0$ such that exp  $\left({\displaystyle \frac{\left|t\right|}{r_j}}\right)$ for  $t\in {\left(-1\right)}^j\times \left[0,\infty \right)$, then the ET of  $y$ with respect to ψ is:

$$U_{\psi }(r)=E_{\psi }\left[y(t)\right](r)=r{\displaystyle {\int }_0^{\infty }{\psi }^{\prime }}(t)y(t)\exp \left(-{\displaystyle \frac{\psi (t)}{r}}\right)dt.$$

(2)

where  $r$ is a complex number,  $t>0$ and  $\left|r\right|\in \left[r_1,r_2\right]$.

The suggested ψ-ET is distinct from the traditional ET as it includes a generalized function ψ(t) in its formulation, enabling it to address a wider variety of FDEs that utilize a general ψ-fractional operator.

We can easily verify the duality between the ψ-ET and ψ-Laplace transforms since we have duality’s ownership between the ET and LT. The duality relation is provided by the relations mentioned as:

$$E_{\psi }\left[y(t)\right](r)=r{L}_{\psi }\left[y(t)\right]\left({\displaystyle \frac{1}{r}}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{L}_{\psi }\left[y(t)\right]\left(r\right)=r{E}_{\psi }\left[y(t)\right]\left({\displaystyle \frac{1}{r}}\right).$$

These dualities can be employed for transforming some of the results for the ψ-LT in [6] into ψ-ET.

Remark 1.

We obtain the result immediately if

$$E_{\psi }\left[y(t)\right]\left(r\right)=Y(r) \mathrm{Then}: E_{\psi }\left[y(\psi (t))\right]\left(r\right)=Y(r)$$

i.e., we have  $E_{\psi }\left(r\right)=Y(r)$.

The following properties may also be easily obtained with the aid of Remark 1, the duality propriety of ψ-ET and ψ-LT, and the results shown in [3]:

Property 2.

1. 

$E_{\psi }\left[1\right]={\displaystyle \frac{1}{r}}, r>0$.

2. 

$E_{\psi }\left[\exp \hspace{0.17em}a\left(\psi (t)-\psi (0)\right)\right]=\frac{r^2}{1-ar}.$

3. 

$E_{\psi }\left[{\left(\psi (t)-\psi (0)\right)}^{\alpha }\right]=\Gamma (\alpha +1)r^{\alpha +2}, \mathrm{Re}(\alpha )>0, r>0$.

4. 

$E_{\psi }\left[\sin \hspace{0.17em}a\left(\psi (t)-\psi (0)\right)\right]=\frac{a{r}^3}{1+a^2{r}^2}.$

5. 

$E_{\psi }\left[\cos \hspace{0.17em}a\left(\psi (t)-\psi (0)\right)\right]=\frac{r^2}{1+a^2{r}^2}.$

6. 

$E_{\psi }\left[\sinh \hspace{0.17em}a\left(\psi (t)-\psi (0)\right)\right]=\frac{a{r}^3}{1-a^2{r}^2}.\hspace{0.17em}$

7. 

$E_{\psi }\left[\cosh \hspace{0.17em}a\left(\psi (t)-\psi (0)\right)\right]=\frac{r^2}{1-a^2{r}^2}.$

8. 

$E_{\psi }\left[{\in }_{\alpha }{\left(a\left(\psi (t)-\psi (0)\right)\right)}^{\alpha }\right]={\displaystyle \frac{r^2}{1-a{r}^{\alpha }}}.$

9. 

$E_{\Psi }\left[{\left(\psi (t)-\psi (0)\right)}^{\alpha -1}{\in }_{\upsilon ,\alpha }{\left(a\left(\psi (t)-\psi (0)\right)\right)}^{\upsilon }\right]={\displaystyle \frac{r^{\alpha +1}}{1-a{r}^{\upsilon }}}.\hspace{0.17em}$

4.1. Convergence of ψ-ET

Theorem 2.

Let ψ an increasing function with  $\psi \left(0\right)=0\in ℝ$ and  $y$ is continuous on  $\left[0,+\infty \right)$ and a ψ-exponentially function bounded order  ${\displaystyle \frac{1}{h}}>0$ (i.e.,  ${‖y‖}_{\infty }\le Q\exp (\frac{{\psi }_t}{h})$ with  $Q$ a positive constant). Then, the ψ-ET of  $y$ exists for  $r>h.$ ($r,\hspace{0.17em}h$ are constants).

Proof. 

We have:

$$\begin{array}{l}\left|E_{\Psi }\left[y(t)\right]\right|=\left|r{\displaystyle {\int }_0^{\infty }{\psi }^{\prime }}(t)y(t)\exp \left(-{\displaystyle \frac{\psi (t)}{r}}\right)dt\right|\le r{\displaystyle {\int }_0^{\infty }{\psi }^{\prime }}(t)y(t)\exp \left(-{\displaystyle \frac{\psi (t)}{r}}\right){‖y‖}_{\infty }dt\\ =rQ{\displaystyle {\int }_0^{\infty }{\psi }^{\prime }}(t)\exp \left(-{\displaystyle \frac{\psi (t)}{r}}+{\displaystyle \frac{\psi (t)}{d}}\right)dt\end{array}$$

Due to $r>h$ the simple limit canceling for infinity, we may utilize this data to obtain:

$$\left|E_{\psi }\left[y(t)\right]\right|\le {\displaystyle \frac{r^{2}Qh}{r-h}}$$

After that, the ψ-ET converges.

The inverse of ψ-ET is as follows:

$$E_{\psi }^{-1}\left[Y(r)\right]\left(t\right)={\displaystyle \frac{1}{2\pi i}}{\displaystyle \underset{a-i\hspace{0.17em}\infty }{\overset{a+i\hspace{0.17em}\infty }{\int }}Y\left(\frac{1}{r}\right)\exp \left(-\frac{\psi (t)}{r}\right)rdr.}$$

(3)

where $Y\left({\displaystyle \frac{1}{r}}\right)$ must be an analytic function in a region of the complex plane containing the path of integration. □

4.2. ψ-ET and ψ-Fractional Operators

This section will discuss the results of ψ-ET that may be used to solve fractional equations of the ψ-Caputo type. However, the same results may also be used to equations like ψ-Hilfer or ψ-Riemann Liouville fractional equations that are based on ψ-fractional differential operators.

Property  3

([13]). If  $\alpha \in \left[n-1.n\right],n\in \mathbb{N}$ then

$$\begin{array}{l}(i)\hspace{0.17em}{E}_{\psi }\left[{}^{RL}I_0^{\alpha ,\psi }y(t)\right]=r^{\alpha }{E}_{\psi }\left[y(t)\right]\\ (ii)\hspace{0.17em}{E}_{\psi }\left[{}^{RL}D_0^{\alpha ,\psi }y(t)\right]={\displaystyle \frac{E_{\psi }\left[y(t)\right]}{r^{\alpha }}}-{\displaystyle \sum _{k=0}^{n-1}{r}^{2-n+k}{}^{RL}I_0^{n-k-\alpha ,\psi }y(0)}\\ (iii)\hspace{0.17em}{E}_{\psi }\left[{}^{C}D_0^{\alpha ,\psi }y(t)\right]={\displaystyle \frac{E_{\psi }\left[y(t)\right]}{r^{\alpha }}}-{\displaystyle \sum _{k=0}^{n-1}{r}^{2-n+k}{}^{RL}D_0^{k,\psi }y(0)}\\ (iv)\hspace{0.17em}{E}_{\psi }\left[{}^{H}D_0^{\mu ,\alpha ,\psi }y(t)\right]={\displaystyle \frac{E_{\psi }\left[y(t)\right]}{r^{\mu }}}-{\displaystyle \sum _{k=0}^{n-1}{r}^{2-n\left(1-\alpha \right)+k}{I}_0^{\left(1-\alpha \right)\left(n-\mu \right)-k,\psi }y(0)}\end{array}$$

In specifically, the ψ-FDE will be solved using the following relationships:

$$\begin{array}{l}(i)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<\alpha \le 1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{E}_{\psi }\left[{}^{C}D_0^{\alpha ,\psi }y(t)\right]={\displaystyle \frac{E_{\psi }\left[y(t)\right]}{r^{\alpha }}}-r^{2-\alpha }y(0),\\ (ii)\hspace{0.17em}\hspace{0.17em}1<\alpha \le 2\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{E}_{\psi }\left[{}^{C}D_0^{\alpha ,\psi }y(t)\right]={\displaystyle \frac{E_{\psi }\left[y(t)\right]}{r^{\alpha }}}-r^{2-\alpha }y(0)-r^{3-\alpha }{y}^{\prime }(0).\end{array}$$

(4)

4.3. Properties of the φ,ψ-DET

We will first give some definitions and lemmas pertaining to the classical DET that are used throughout the rest of the study before going on to introduce the φ,ψ -DET and explain its basic characteristics.

We assume for the rest of our study that: $(\phi (x),\psi (t))\in \hspace{0.17em}{C}^n[a,\infty )\times C^n[b,\infty )$ such that ${\phi }^{\prime }(x), {\psi }^{\prime }(t)>0 and \phi (x), \psi (t)\ge 0\forall (x,t)\in [a,\infty )\times [b,\infty ).$ The set of functions that are n-times absolutely continuous on $[a,H]$ is represented by $A{C}^n[a,H]$, while the space of functions that are n-times continuously differentiable on $[a,\infty )$ is represented by $C^n[a,\infty )$.

Definition 6.

Let,  $w(x,t), t, x\in R^{+}$, be a function which can be expressed as a convergent infinite series, then, its DET given by:

$$E_2\left[w(x,t)\right]\left(s,r\right)=T(s,r)=sr{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}w(x,t)\hspace{0.17em}{e}^{-\left(\frac{x}{s}+\frac{t}{r}\right)}}}\hspace{0.17em}dxdt,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x,t>0$$

(5)

where  $s,r$ are complex values.

Definition 7.

Let,  $w(x,t), t, x\in R^{+}$, be a continuous function in  $[a,\infty )\times [b,\infty )$. The φ,ψ-DET is defined by:

$$T_{\phi ,\psi }\left(s,r\right)=E_{\phi ,\psi }\left[w(x,t)\right](s,r)=sr{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}w(x,t)\hspace{0.17em}{e}^{-\left(\frac{\left(\phi (x)-\phi (0)\right)}{s}+\frac{\left(\psi (t)-\psi (0)\right)}{p}\right)}}}\hspace{0.17em}{\phi }^{\prime }(x){\psi }^{\prime }(t)dxdt,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x,t>0,$$

(6)

Using Equation (3), the inverse of φ,ψ-DET is:

$$w(x,t)=E_{\phi ,\psi }^{-1}\left[T_{\phi ,\psi }\left(s,r\right)\right]={\displaystyle \frac{1}{{\left(2\pi i\right)}^2}}{\displaystyle \underset{c-i\hspace{0.17em}\infty }{\overset{c+i\hspace{0.17em}\infty }{\int }}{\displaystyle \underset{d-i\hspace{0.17em}\infty }{\overset{d+i\hspace{0.17em}\infty }{\int }}sr\hspace{0.17em}\hspace{0.17em}{e}^{-\left(\frac{\left(\phi (x)-\phi (0)\right)}{s}+\frac{\left(\psi (t)-\psi (0)\right)}{r}\right)}}}\hspace{0.17em}{T}_{\phi ,\psi }\left({\displaystyle \frac{1}{s}},{\displaystyle \frac{1}{r}}\right)dsdr,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}c\ge a,\hspace{0.17em}d\ge b.$$

Theorem 3.

If  $w(x,t)=g(x)h(t), x>a\hspace{0.17em}\wedge \hspace{0.17em}t>b$, then:

$$E_{\phi \psi }\left[w(x,t)\right](s,r)=E_{\phi }\left[g(x)\right](s)E_{\psi }\left[h(t)\right](r).$$

Proof. 

We have,

$$\begin{array}{c}{E}_{\phi ,\psi }\left[w(x,t)\right](s,r)=sr{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}g(x)h(t)\hspace{0.17em}{e}^{-\left(\frac{\left(\phi (x)-\phi (0)\right)}{s}+\frac{\left(\psi (t)-\psi (0)\right)}{r}\right)}}}\hspace{0.17em}{\phi }^{\prime }(x){\psi }^{\prime }(t)dxdt,\\ ={\displaystyle \underset{0}{\overset{\infty }{\int }}sg(x)\hspace{0.17em}{e}^{-\left(\frac{\left(\phi (x)-\phi (0)\right)}{s}\right)}{\phi }^{\prime }(x)dx}{\displaystyle \underset{0}{\overset{\infty }{\int }}rh(t)\hspace{0.17em}{e}^{-\left(\frac{\left(\psi (t)-\psi (0)\right)}{r}\right)}{\psi }^{\prime }(t)dt}\\ =E_{\phi }\left(g(x)\right)(s)E_{\psi }\left(h(t)\right)(r).\end{array}$$

□

Theorem 4.

These properties are verified by the φ,ψ-DET:

$$\begin{array}{l}1.\hspace{0.17em}{E}_{\phi ,\psi }\left[1\right]=s^2{r}^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{Re}(s)>0,\hspace{0.17em}\hspace{0.17em}\mathrm{Re}(r)>0.\\ 2.\hspace{0.17em}{E}_{\phi ,\psi }\left[{\left(\phi (x)-\phi (0)\right)}^{{\alpha }_1}{\left(\psi (t)-\psi (0)\right)}^{{\alpha }_2}\right]=\Gamma ({\alpha }_1+1)\Gamma ({\alpha }_2+1)s^{{\alpha }_1+2}{r}^{{\alpha }_2+2},\\ {\alpha }_1,{\alpha }_2>-1,\hspace{0.17em}\mathrm{Re}(s)>0,\hspace{0.17em}\hspace{0.17em}\mathrm{Re}(r)>0.\\ 3.\hspace{0.17em}{E}_{\phi ,\psi }\left\{\exp \left[c_1\left(\phi (x)-\phi (0)\right)+c_2\left(\psi (t)-\psi (0)\right)\hspace{0.17em}\right]\right\}={\displaystyle \frac{s^2{r}^2}{\left(1-c_{1}s\right)\left(1-c_{2}r\right)}},\\ \mathrm{Re}(s)>c_1,\hspace{0.17em}\hspace{0.17em}\mathrm{Re}(r)>c_2.\\ 4.\hspace{0.17em}{E}_{\phi ,\psi }\left\{\sin \left[c_1\left(\phi (x)-\phi (0)\right)+c_2\left(\psi (t)-\psi (0)\right)\hspace{0.17em}\right]\right\}={\displaystyle \frac{s^2{r}^2\left(c_{1}s+c_{2}r\right)}{\left(1+c_1^2{s}^2\right)\left(1+c_2^2{r}^2\right)}}\hspace{0.17em},\\ \mathrm{Re}(s)>0,\hspace{0.17em}\hspace{0.17em}\mathrm{Re}(r)>0.\\ 5.\hspace{0.17em}{E}_{\phi ,\psi }\left\{\cos \left[c_1\left(\phi (x)-\phi (0)\right)+c_2\left(\psi (t)-\psi (0)\right)\hspace{0.17em}\right]\right\}={\displaystyle \frac{s^2{r}^2\left(1-c_1{c}_{2}sr\right)}{\left(1+c_1^2{s}^2\right)\left(1+c_2^2{r}^2\right)}}\hspace{0.17em},\\ \mathrm{Re}(s)>0,\hspace{0.17em}\hspace{0.17em}\mathrm{Re}(r)>0.\\ 6.\hspace{0.17em}{E}_{\phi ,\psi }\left\{\sinh \left[c_1\left(\phi (x)-\phi (0)\right)+c_2\left(\psi (t)-\psi (0)\right)\hspace{0.17em}\right]\right\}={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{s^2{r}^2}{\left(1-c_{1}s\right)\left(1-c_{2}r\right)}}-{\displaystyle \frac{s^2{r}^2}{\left(1-c_{1}s\right)\left(1-c_{2}r\right)}}\right]\hspace{0.17em},\\ \mathrm{Re}(s)>0,\hspace{0.17em}\hspace{0.17em}\mathrm{Re}(r)>0.\\ 7.\hspace{0.17em}{E}_{\phi ,\psi }\left\{\cosh \left[c_1\left(\phi (x)-\phi (0)\right)+c_2\left(\psi (t)-\psi (0)\right)\hspace{0.17em}\right]\right\}={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{s^2{r}^2}{\left(1-c_{1}s\right)\left(1-c_{2}r\right)}}+{\displaystyle \frac{s^2{r}^2}{\left(1-c_{1}s\right)\left(1-c_{2}r\right)}}\right]\hspace{0.17em},\\ \mathrm{Re}(s)>0,\hspace{0.17em}\hspace{0.17em}\mathrm{Re}(r)>0.\end{array}$$

Proof. 

Using Properties 2, it is easy to prove the above relationships. □

4.4. φ,ψ-DET of Fractional Derivatives

Assume that:

$$\begin{array}{l}{E}_{\phi ,\psi }(w(x,t))(s,r)=T_{\phi ,\psi }(s,r),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{E}_{\phi }\left\{{\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(t\right)}}{\displaystyle \frac{d}{dt}}\right)}^{i}w(x,b)\right\}(s)=T_{\phi ,i}(s),\\ E_{\psi }\left\{{\left({\displaystyle \frac{1}{{\phi }^{\prime }\left(x\right)}}{\displaystyle \frac{d}{dx}}\right)}^{i}w(a,t)\right\}(r)=T_{\psi ,i}(p),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=0,\hspace{0.17em}\dots ,\hspace{0.17em}n.\end{array}$$

The φ,ψ-DET for classical and φ,ψ-FPDEs will be derived in the following theorems under suitable assumptions about $w(x,t)$.

Theorem 5.

$$\begin{array}{l}1.\hspace{0.17em}{E}_{\phi ,\psi }\left\{{\displaystyle \frac{1}{{\phi }^{\prime }\left(x\right)}}{\displaystyle \frac{d}{dx}}w(x,t)\right\}(s,r)={\displaystyle \frac{1}{s}}{T}_{\phi ,\psi }(s,r)-T_{\psi }\left[w(0,t)\right](r),\\ 2.\hspace{0.17em}{E}_{\phi ,\psi }\left\{D^{\alpha ,\phi (x)}\hspace{0.17em}w(x,t)\right\}(s,r)={\displaystyle \frac{1}{s^{\alpha }}}{T}_{\phi ,\psi }(s,r)-{\displaystyle \sum _{k=0}^{n-1}{s}^{2+k-\alpha }{E}_{\psi }\left[D^{k,\psi }w(0,t)\right]}(r).\end{array}$$

Proof. 

$$\begin{array}{l}{E}_{\phi ,\psi }\left[w(x,t)\right](s,r)=sr{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}w(x,t)\hspace{0.17em}{e}^{-\left(\frac{\left(\phi (x)-\phi (0)\right)}{s}+\frac{\left(\psi (t)-\psi (0)\right)}{r}\right)}}}\hspace{0.17em}{\phi }^{\prime }(x){\psi }^{\prime }(t)dxdt,\\ ={\displaystyle \underset{0}{\overset{\infty }{\int }}r\hspace{0.17em}{\psi }^{\prime }(t)e^{-\left(\frac{\left(\psi (t)-\psi (0)\right)}{r}\right)}}\left({\displaystyle \underset{0}{\overset{\infty }{\int }}s\hspace{0.17em}w(x,t){\phi }^{\prime }(x)e^{-\left(\frac{\left(\phi (x)-\phi (0)\right)}{s}\right)}dx}\right)dt=E_{\psi }\left[E_{\phi }\left(w(x,t)\right)\right](s)=E_{\phi }\left[E_{\psi }\left(w(x,t)\right)\right](r).\end{array}$$

□

Theorem 6.

$$\begin{array}{l}1.\hspace{0.17em}{E}_{\phi ,\psi }\left\{{\displaystyle \frac{1}{{\psi }^{\prime }\left(t\right)}}{\displaystyle \frac{d}{dt}}w(x,t)\right\}(s,r)={\displaystyle \frac{1}{r}}{T}_{\phi ,\psi }(s,r)-T_{\phi }\left[w(x,0)\right](s),\\ 2.\hspace{0.17em}{E}_{\phi ,\psi }\left\{D^{\alpha ,\psi (x)}\hspace{0.17em}w(x,t)\right\}(s,r)={\displaystyle \frac{1}{r^{\alpha }}}{T}_{\phi ,\psi }(s,r)-{\displaystyle \sum _{k=0}^{n-1}{r}^{2+k-\alpha }{E}_{\phi }\left[D^{k,\phi }w(x,0)\right]}(s).\end{array}$$

Prove this theorem in the same way as prove Theorem 5.

If  $0<\alpha \le 1,$ then:

$$\begin{array}{l}1.\hspace{0.17em}{E}_{\phi ,\psi }\left\{D^{\alpha ,\phi (x)}\hspace{0.17em}w(x,t)\right\}(s,r)={\displaystyle \frac{1}{s^{\alpha }}}{T}_{\phi ,\psi }(s,r)-s^{2-\alpha }{E}_{\psi }\left[w(0,t)\right](r),\\ 2.\hspace{0.17em}{E}_{\phi ,\psi }\left\{D^{\alpha ,\psi (t)}\hspace{0.17em}w(x,t)\right\}(s,r)={\displaystyle \frac{1}{r^{\alpha }}}{T}_{\phi ,\psi }(s,r)-r^{2-\alpha }{E}_{\psi }\left[w(x,0)\right](s).\end{array}$$

(7)

If  $1<\alpha \le 2$, then:

$$\begin{array}{l}1.\hspace{0.17em}{E}_{\phi ,\psi }\left\{D^{\alpha ,\phi (x)}\hspace{0.17em}w(x,t)\right\}(s,r)={\displaystyle \frac{1}{s^{\alpha }}}{T}_{\phi ,\psi }(s,r)-s^{2-\alpha }{E}_{\psi }\left[w(0,t)\right](r)-s^{3-\alpha }{E}_{\psi }\left[{\displaystyle \frac{{\partial }^{\psi }w(0,t)}{\partial x}}\right](r),\\ 2.\hspace{0.17em}{E}_{\phi ,\psi }\left\{D^{\alpha ,\psi (x)}\hspace{0.17em}w(x,t)\right\}(s,r)={\displaystyle \frac{1}{r^{\alpha }}}{T}_{\phi ,\psi }(s,r)-r^{2-\alpha }{E}_{\phi }\left[w(x,0)\right](s)-r^{3-\alpha }{E}_{\phi }\left[{\displaystyle \frac{{\partial }^{\phi }w(x,0)}{\partial t}}\right](s).\end{array}$$

(8)

5. Solution of φ,ψ-FDEs

Despite decades of exploration of the proposal of a φ,ψ-fractional operator, the concept of φ,ψ-FDEs has just lately received a lot of attention. We propose discussing the solutions to these three types of equations in light of these considerations.

The φ,ψ-DET approach is noted for its ability to identify the precise solution more efficiently than alternative analytical or numerical techniques.

In this part of the article, we solve some φ,ψ-FDEs using the GDLT. Let $T(s,r)$, represent the φ,ψ-DET of the unknown function $w(x,t)$.

To keep things simple, we observe that:

$${\displaystyle \frac{{\partial }^{\phi }w(x,t)}{\partial x}}=\left({\displaystyle \frac{1}{{\phi }^{\prime }\left(x\right)}}{\displaystyle \frac{d}{dx}}\right)w(x,t),\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{{\partial }^{2\phi }w(x,t)}{\partial x^2}}={\left({\displaystyle \frac{1}{{\phi }^{\prime }\left(x\right)}}{\displaystyle \frac{d}{dx}}\right)}^{2}w(x,t)\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{{\partial }^{\psi }w(x,t)}{\partial t}}=\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(t\right)}}{\displaystyle \frac{d}{dt}}\right)w(x,t).$$

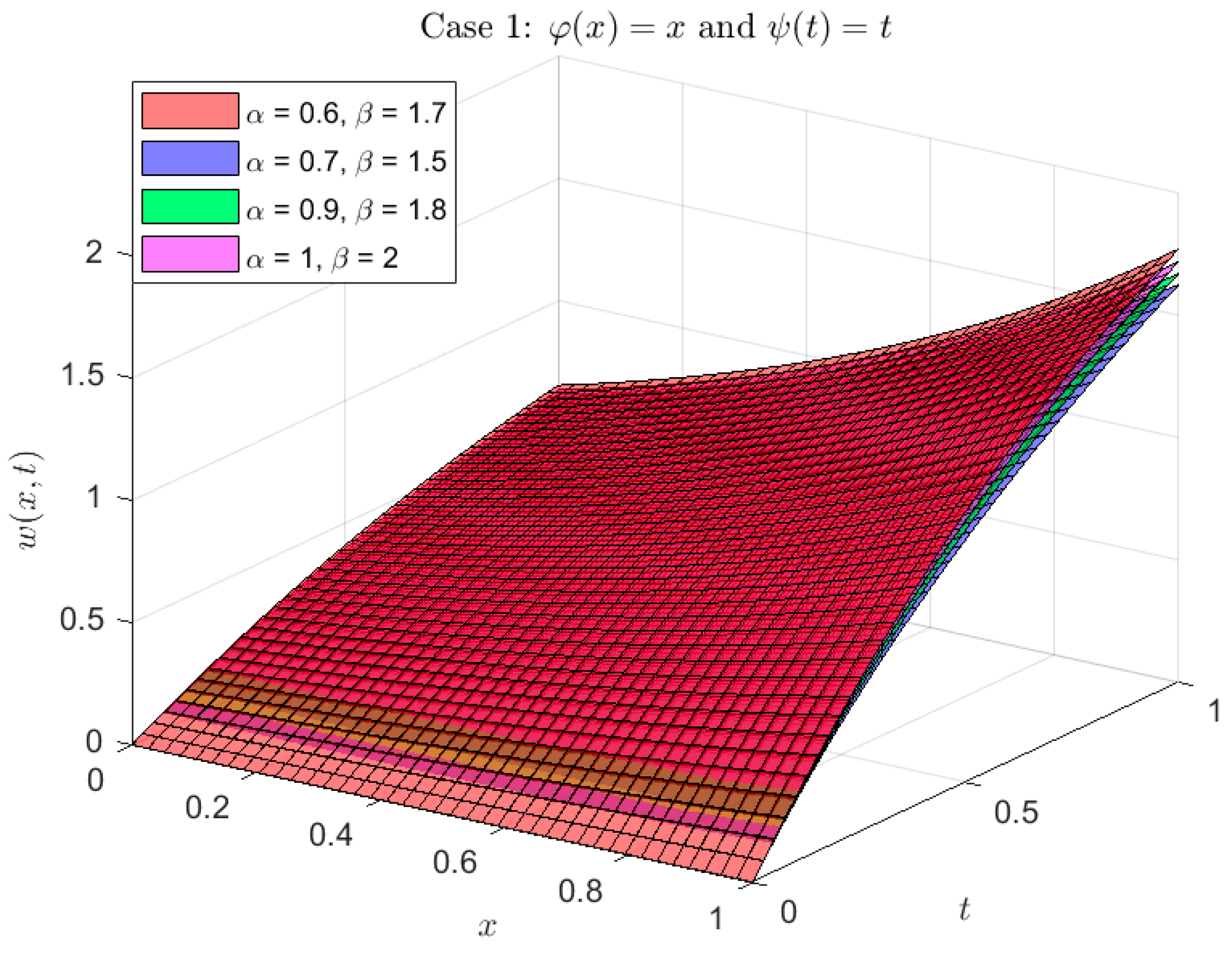
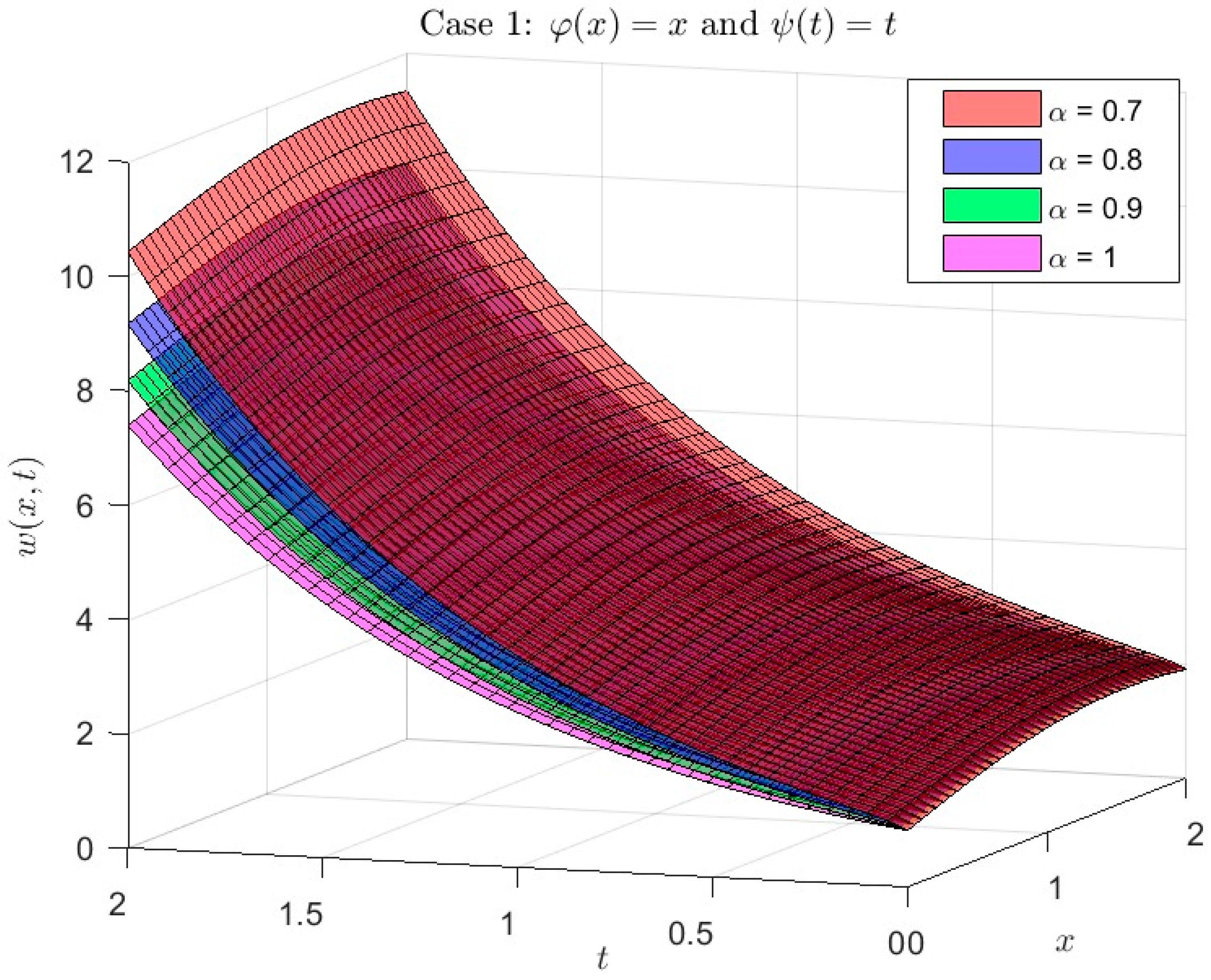
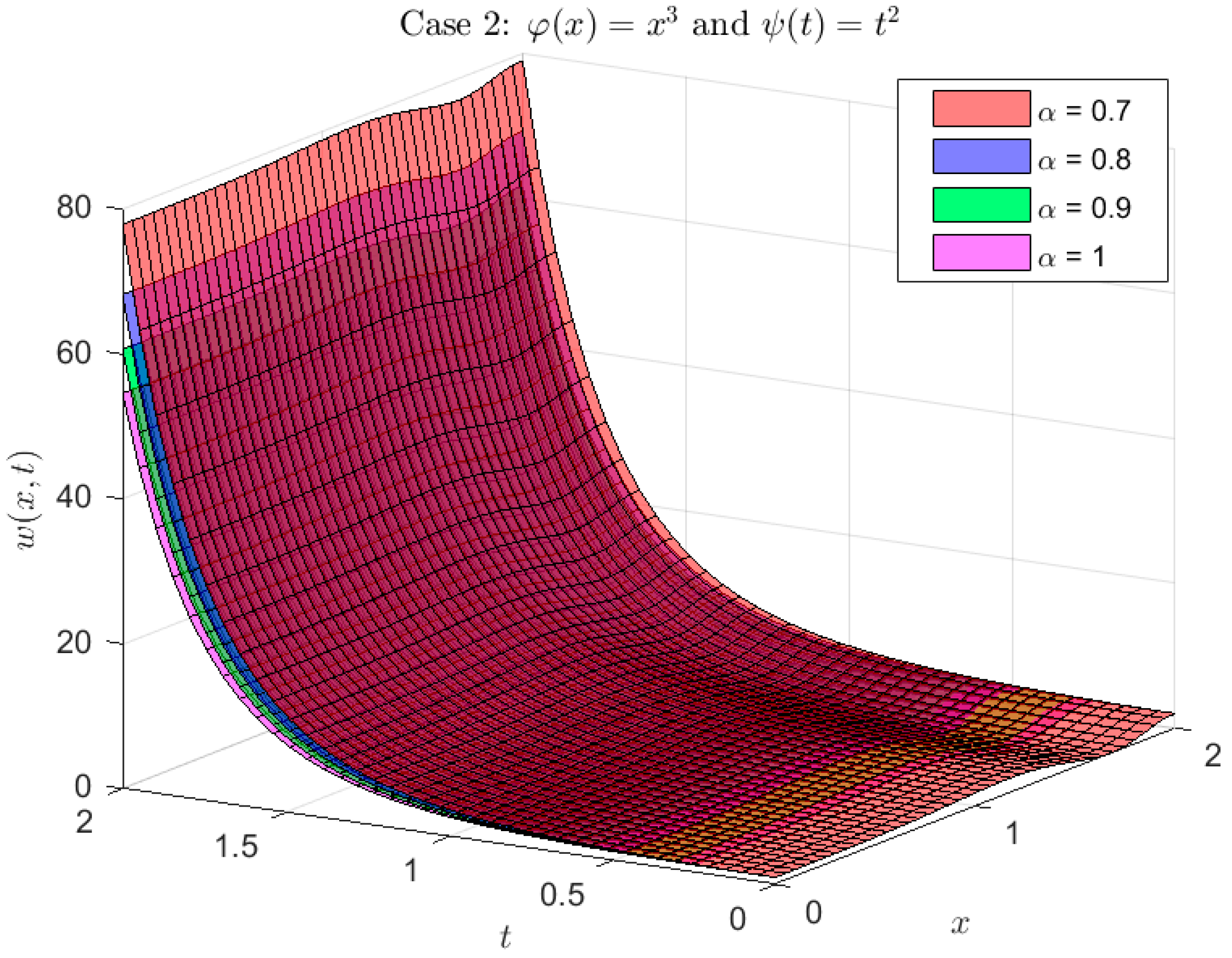
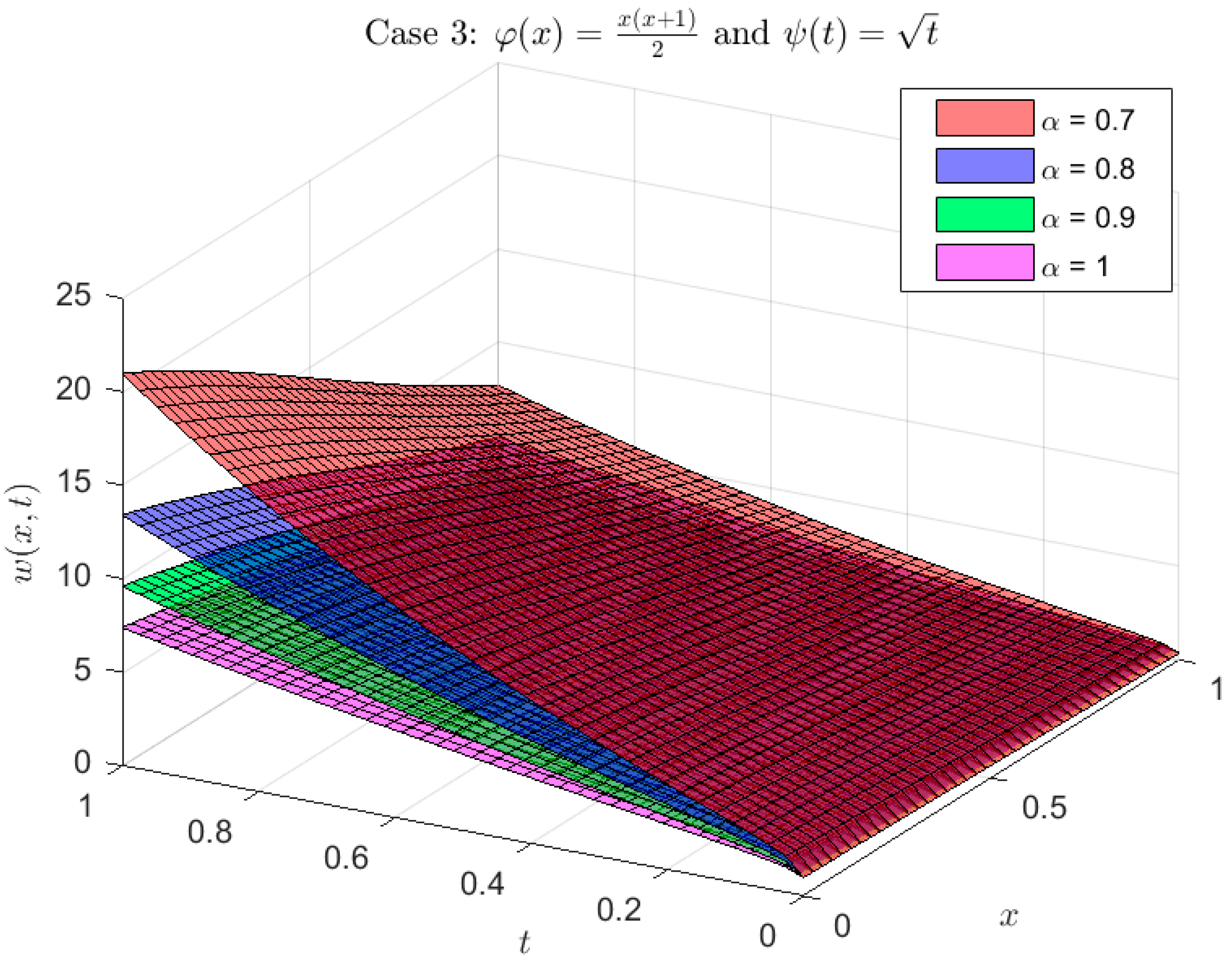
Example 1.

Take the φ,ψ-fractional telegraph equation as an example,

$$D_0^{\beta ,\psi }w(x,t)+D_0^{\alpha ,\psi }w(x,t)+w(x,t)={\displaystyle \frac{{\partial }^{2\phi }w(x,t)}{\partial x^2}},\hspace{0.17em}\hspace{0.17em}(x,t)\in \hspace{0.17em}{(0,\pm \hspace{0.17em}\infty )}^2,\hspace{0.17em}\hspace{0.17em}1<\beta \le 2,\hspace{0.17em}\hspace{0.17em}0<\alpha \le 1,$$

(9)

With ICs and BCs:

$$\begin{array}{l}w(x,0)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{{\partial }^{\psi }w(x,0)}{\partial t}}=e^{\left(\phi (x)-\phi (0)\right)},\\ w(0,t)=\hspace{0.17em}{\displaystyle \frac{{\partial }^{\phi }w(0,t)}{\partial x}}=\left(\psi (t)-\psi (0)\right){\in }_{\beta -\alpha ,2}\left(-{\left(\psi (t)-\psi (0)\right)}^{\beta -\alpha }\right).\end{array}$$

(10)

Using Equations (7) and (8) and the φ,ψ-DET, we obtain:

$$\begin{array}{l}{\displaystyle \frac{1}{r^{\beta }}}{T}_{\phi ,\psi }(s,r)-r^{2-\beta }{E}_{\phi }\left[w(x,0)\right](s)-r^{3-\beta }{E}_{\phi }\left[{\displaystyle \frac{{\partial }^{\phi }w(x,0)}{\partial t}}\right](s)+{\displaystyle \frac{1}{r^{\alpha }}}{T}_{\phi ,\psi }(s,r)-r^{2-\alpha }{E}_{\psi }\left[w(x,0)\right](s)\\ +T_{\phi ,\psi }(s,r)={\displaystyle \frac{1}{s^2}}{T}_{\phi ,\psi }(s,r)-E_{\psi }\left[w(0,t)\right](r)-s{E}_{\psi }\left[{\displaystyle \frac{{\partial }^{\psi }w(0,t)}{\partial x}}\right](r),\end{array}$$

We obtain the following after using properties 2 Equation (10) and algebraic operations:

$$\begin{array}{l}\left({\displaystyle \frac{1}{r^{\beta }}}+{\displaystyle \frac{1}{r^{\alpha }}}-{\displaystyle \frac{1}{s^2}}+1\right)T_{\phi ,\psi }(s,r)={\displaystyle \frac{s^2{r}^{3-\beta }}{\left(1-s\right)}}-{\displaystyle \frac{r^3+s{r}^3}{\left(1+r^{\beta -\alpha }\right)}}={\displaystyle \frac{s^2{r}^3\left(\frac{1}{r^{\beta }}+\frac{1}{r^{\alpha }}-\frac{1}{s^2}+1\right)}{\left(1-s\right)\left(1+r^{\beta -\alpha }\right)}},\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{T}_{\phi ,\psi }(s,r)={\displaystyle \frac{s^2{r}^3}{\left(1-s\right)\left(1+r^{\beta -\alpha }\right)}},\end{array}$$

Inverse φ,ψ-ET indicates that:

$$\hspace{0.17em}w(x,t)=e^{\left(\phi (x)-\phi (0)\right)}\left(\psi (t)-\psi (0)\right){\in }_{\beta -\alpha ,2}\left(-{\left(\psi (t)-\psi (0)\right)}^{\beta -\alpha }\right).$$

The calculated solution for the model using the following kernels  $\left(i\right)\hspace{0.17em}\phi (x)=x, \psi (t)=t\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(ii\right)\hspace{0.17em}\phi (x)=x^3, \psi (t)=t^2\hspace{0.17em}\hspace{0.17em}\left(iii\right)\hspace{0.17em}\phi (x)=x^2, \psi (t)=\log (t+1)$, is shown graphically in Figure 1, Figure 2 and Figure 3. As is well known, in case 1, the problem (9) simplified to the Caputo fractional derivative.

Actually, next solution scenarios are offered for specific situations that are crucial to the function  $\phi (x),\hspace{0.17em}\psi (t),\hspace{0.17em}\alpha ,\hspace{0.17em}\beta ,$ selection process.

Case 1.

$$\begin{array}{l}\left(i\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =1,\hspace{0.17em}\hspace{0.17em}\beta =2\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=t{e}^x{\in }_{1,2}\left(-t\right),\\ \left(ii\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =0.9,\hspace{0.17em}\hspace{0.17em}\beta =1.8\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=t{e}^x{\in }_{0.9,2}\left(-t^{0.9}\right),\\ \left(iii\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =0.7,\hspace{0.17em}\hspace{0.17em}\beta =1.5\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=t{e}^x{\in }_{0.8,2}\left(-t^{0.8}\right),\\ \left(iv\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =0.6,\hspace{0.17em}\hspace{0.17em}\beta =1.7\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=t{e}^x{\in }_{1.1,2}\left(-t^{1.1}\right).\end{array}$$

Case 2.

$$\begin{array}{l}\left(i\right)\hspace{0.17em}\phi (x)=x^3,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t^2,\hspace{0.17em}\alpha =1,\hspace{0.17em}\hspace{0.17em}\beta =2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=t^2{e}^{x^3}{\in }_{1,2}\left(-t^2\right),\\ \left(ii\right)\hspace{0.17em}\phi (x)=x^3,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t^2,\hspace{0.17em}\alpha =0.9,\hspace{0.17em}\hspace{0.17em}\beta =1.8\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=t^2{e}^{x^3}{\in }_{0.9,2}\left(-t^{1.8}\right),\\ \left(iii\right)\hspace{0.17em}\phi (x)=x^3,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t^2,\hspace{0.17em}\alpha =0.7,\hspace{0.17em}\hspace{0.17em}\beta =1.5\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=t^2{e}^{x^3}{\in }_{0.8,2}\left(-t^{1.6}\right),\\ \left(iv\right)\hspace{0.17em}\phi (x)=x^3,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t^2,\hspace{0.17em}\alpha =0.6,\hspace{0.17em}\hspace{0.17em}\beta =1.7\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=t^2{e}^{x^3}{\in }_{1.1,2}\left(-t^{1.21}\right).\end{array}$$

Case 3.

$$\begin{array}{l}\left(i\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\log (t+1),\hspace{0.17em}\alpha =1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\beta =2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\log (t+1)e^{x^2}{\in }_{1,2}\left(-\left(\log (t+1)\right)\right),\\ \left(ii\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\log (t+1),\hspace{0.17em}\alpha =0.9,\hspace{0.17em}\hspace{0.17em}\beta =1.8\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\log (t+1)e^{x^2}{\in }_{0.9,2}\left(-{\left(\log (t+1)\right)}^{0.9}\right),\\ \left(iii\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\log (t+1),\hspace{0.17em}\alpha =0.7,\hspace{0.17em}\hspace{0.17em}\beta =1.5\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\log (t+1)e^{x^2}{\in }_{0.8,2}\left(-{\left(\log (t+1)\right)}^{0.8}\right),\\ \left(iv\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\log (t+1),\hspace{0.17em}\alpha =0.6,\hspace{0.17em}\hspace{0.17em}\beta =1.7\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\log (t+1)e^{x^2}{\in }_{1.1,2}\left(-{\left(\log (t+1)\right)}^{1.1}\right).\end{array}$$

In Figure 2, the lengths of the x- and t-axes are not identical in order to obtain clearer spatial curves.

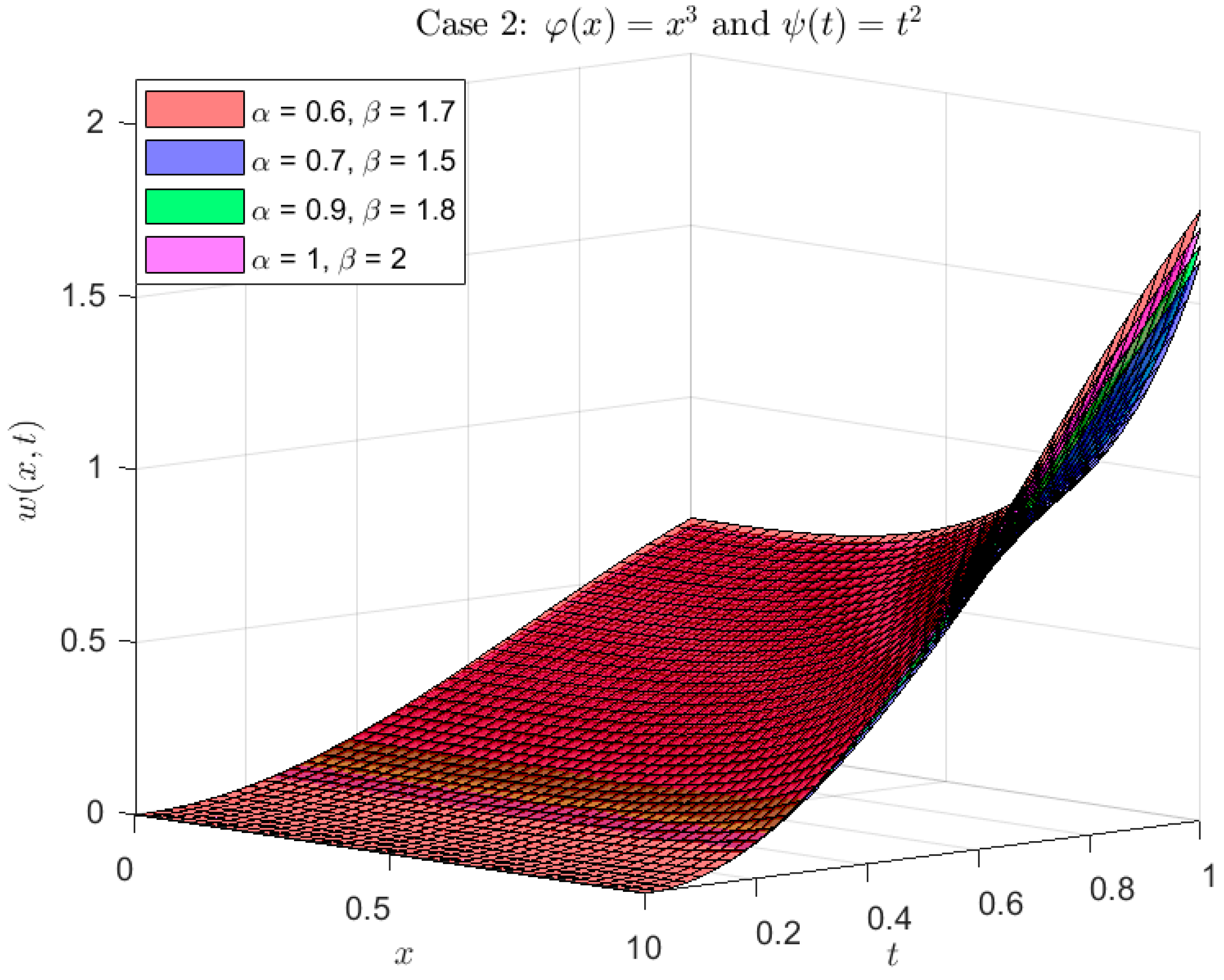
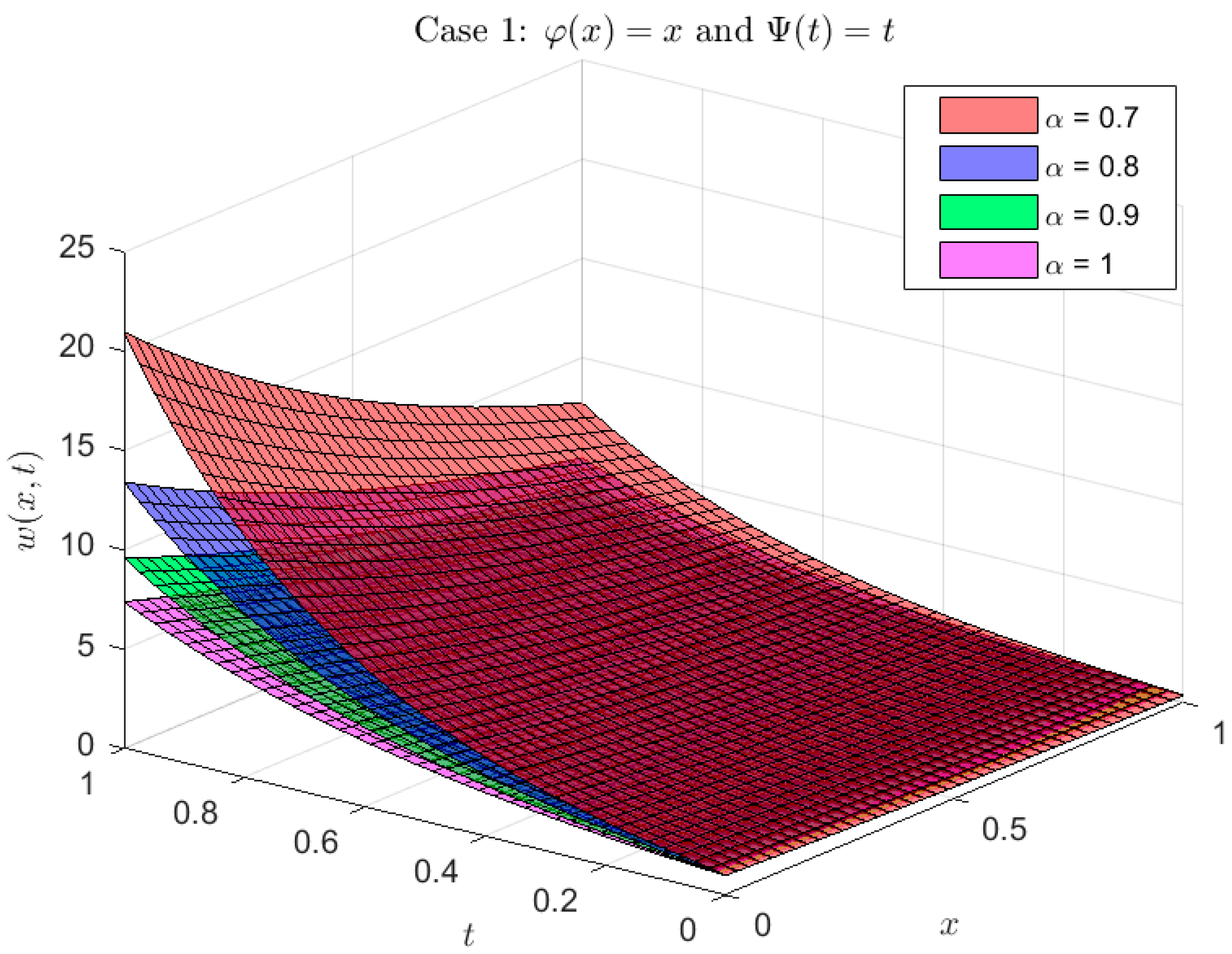
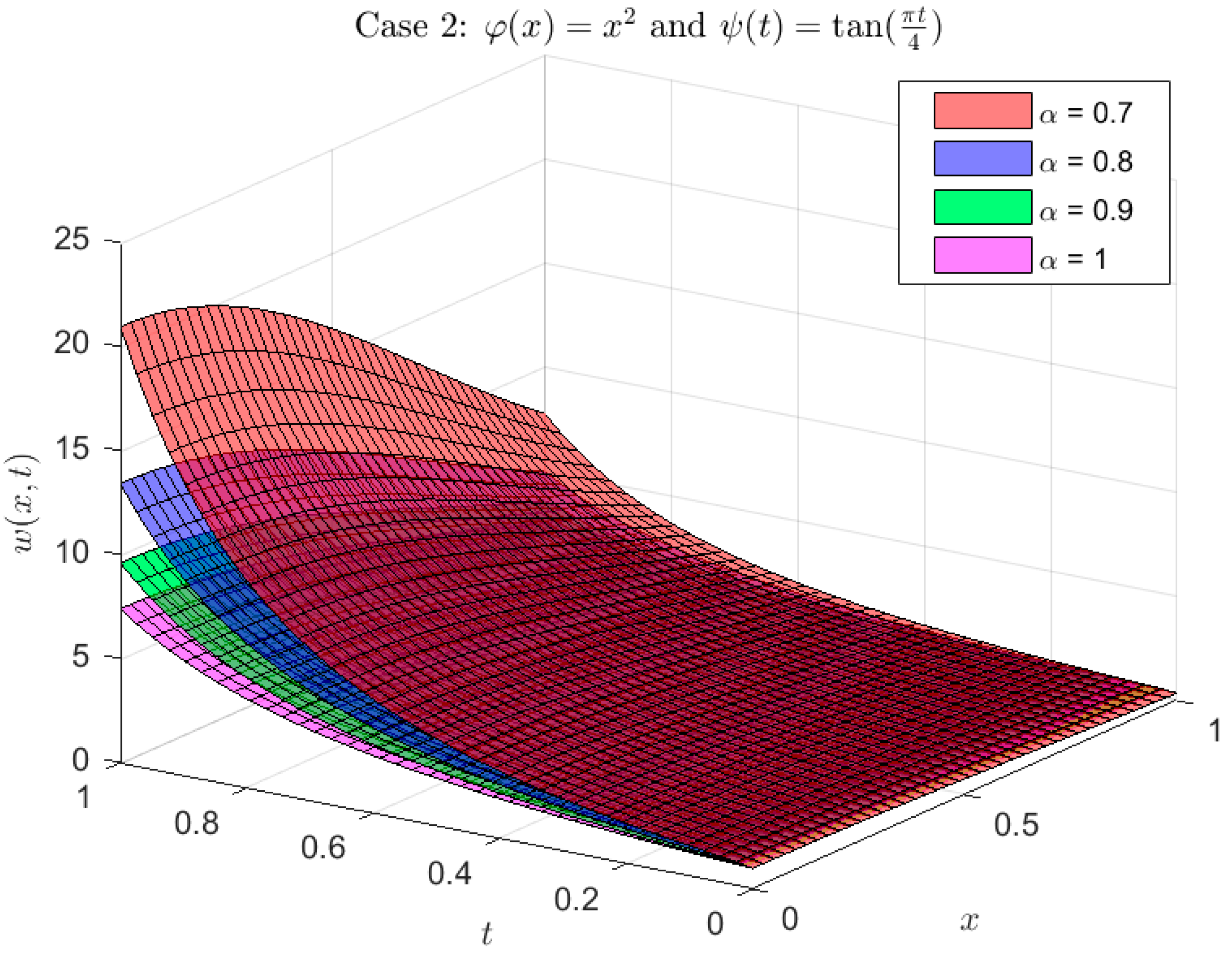
Example 2.

Examine the following φ,ψ-fractional Klein–Gordon problem,

$$D_0^{\alpha ,\psi }w(x,t)-{\displaystyle \frac{{\partial }^{2\phi }w(x,t)}{\partial x^2}}-w(x,t)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(x,t)\in \hspace{0.17em}{(0,\pm \hspace{0.17em}\infty )}^2,\hspace{0.17em}\hspace{0.17em}1<\alpha \le 2,$$

(11)

with ICs and BCs:

$$\begin{array}{l}w(x,0)=\sin \left(\phi (x)-\phi (0)\right)+1,\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{{\partial }^{\psi }w(x,0)}{\partial t}}=0,\\ w(0,t)=\hspace{0.17em}{\in }_{\alpha }\left({\left(\psi (t)-\psi (0)\right)}^{\alpha }\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{{\partial }^{\phi }w(0,t)}{\partial x}}=1.\end{array}$$

(12)

Using the φ,ψ-DET and Equations (7) and (8), Properties 2, Equation (12) and algebraic operations we obtain:

$$\begin{array}{l}\left({\displaystyle \frac{1}{r^{\alpha }}}-{\displaystyle \frac{1}{s^2}}-1\right)T_{\phi ,\psi }(s,r)={\displaystyle \frac{s^3{r}^2\left(\frac{1}{r^{\alpha }}-\frac{1}{s^2}-1\right)}{\left(1+s^2\right)}}+{\displaystyle \frac{s^2{r}^2\left(\frac{1}{r^{\alpha }}-\frac{1}{s^2}-1\right)}{\left(1-r^{\alpha }\right)}},\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{T}_{\phi ,\psi }(s,p)={\displaystyle \frac{s^3{r}^2}{\left(1+s^2\right)}}+{\displaystyle \frac{s^2{r}^2}{\left(1-r^{\alpha }\right)}},\end{array}$$

Inverse φ,ψ-ET indicates that:

$$\hspace{0.17em}w(x,t)=\sin \left(\phi (x)-\phi (0)\right)+{\in }_{\alpha }\left({\left(\psi (t)-\psi (0)\right)}^{\alpha }\right).$$

The calculated solution for the model using the following kernels  $\left(i\right)\hspace{0.17em}\phi (x)=x, \psi (t)=t\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(ii\right)\hspace{0.17em}\phi (x)=x^3, \psi (t)=t^2\hspace{0.17em}\hspace{0.17em}\left(iii\right)\hspace{0.17em}\phi (x)=x^2, \psi (t)=\log (t+1),$ is shown graphically in Figure 4, Figure 5 and Figure 6. As is well known, in case 1, the problem (11) simplified to the Caputo fractional derivative.

Actually, the solution scenarios listed below are provided for specific situations that are crucial for choosing the functions  $\phi (x), \psi (t), \alpha .$

Case 1.

$$\begin{array}{l}\left(i\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x\right)+{\in }_1\left(t\right),\hspace{0.17em}\\ \left(ii\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =0.9\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x\right)+{\in }_{0.9}\left(t^{0.9}\right),\\ \left(iii\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =0.8\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x\right)+{\in }_{0.8}\left(t^{0.8}\right),\\ \left(iv\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =0.7\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x\right)+{\in }_{0.7}\left(t^{0.7}\right).\end{array}$$

Case 2.

$$\begin{array}{l}\left(i\right)\hspace{0.17em}\phi (x)=x^3,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t^2,\hspace{0.17em}\alpha =1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x^3\right)+{\in }_1\left(t^2\right),\hspace{0.17em}\\ \left(ii\right)\hspace{0.17em}\phi (x)=x^3,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t^2,\hspace{0.17em}\alpha =0.9\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x^3\right)+{\in }_{0.9}\left(t^{1.8}\right),\\ \left(iii\right)\hspace{0.17em}\phi (x)=x^3,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t^2,\hspace{0.17em}\alpha =0.8\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x^3\right)+{\in }_{0.8}\left(t^{1.6}\right),\\ \left(iv\right)\hspace{0.17em}\phi (x)=x^3,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t^2,\hspace{0.17em}\alpha =0.7\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x^3\right)+{\in }_{0.7}\left(t^{1.4}\right).\end{array}$$

Case 3.

$$\begin{array}{l}\left(i\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\log (t+1),\hspace{0.17em}\alpha =1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x^2\right)+{\in }_1\left(\log (t+1)\right),\hspace{0.17em}\\ \left(ii\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\log (t+1),\hspace{0.17em}\alpha =0.9\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x^2\right)+{\in }_{0.9}\left({\left(\log (t+1)\right)}^{0.9}\right),\\ \left(iii\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\log (t+1),\hspace{0.17em}\alpha =0.8\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x^2\right)+{\in }_{0.8}\left({\left(\log (t+1)\right)}^{0.8}\right),\\ \left(iv\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\log (t+1),\hspace{0.17em}\alpha =0.7\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=\sin \left(x^2\right)+{\in }_{0.7}\left({\left(\log (t+1)\right)}^{0.7}\right).\end{array}$$

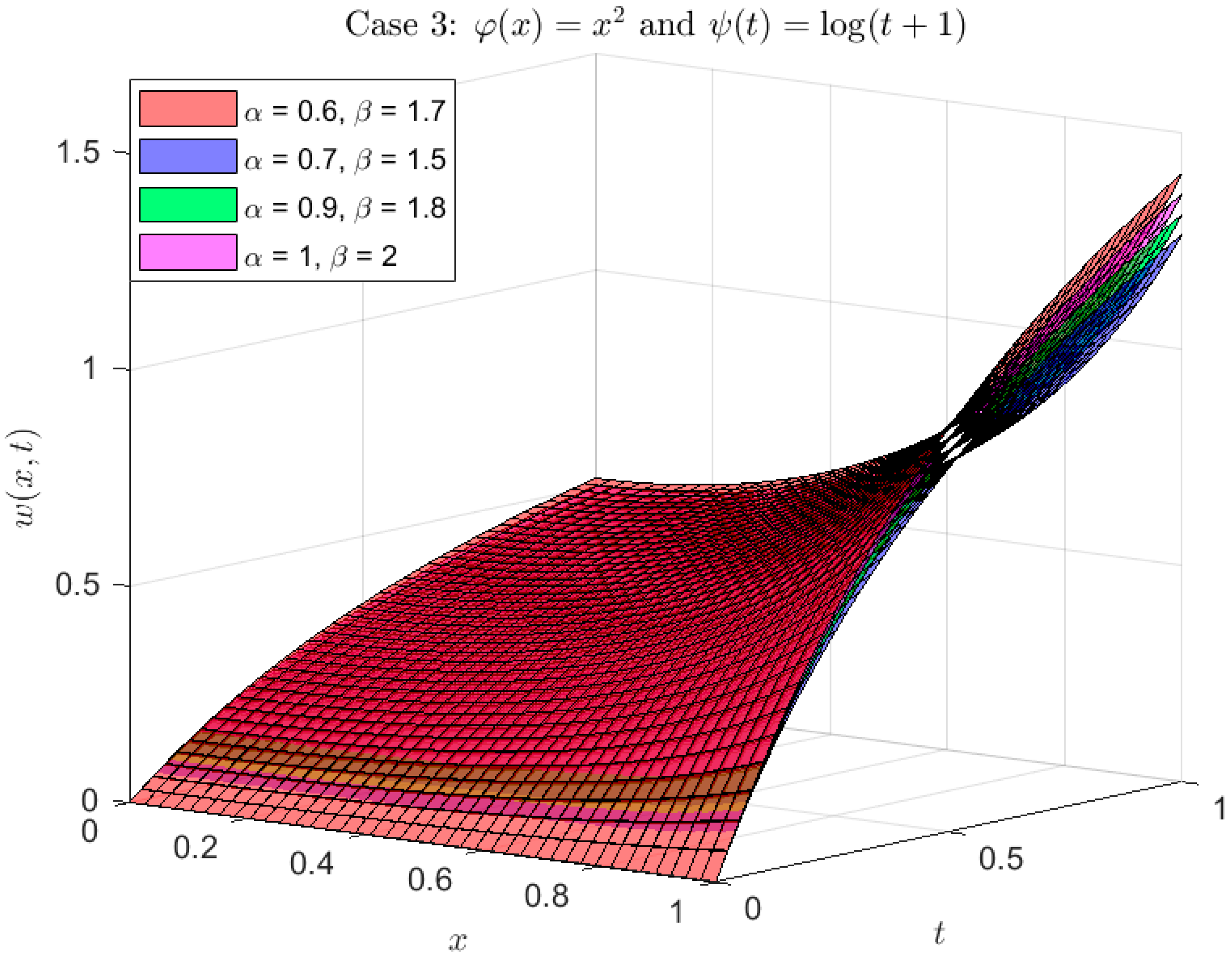
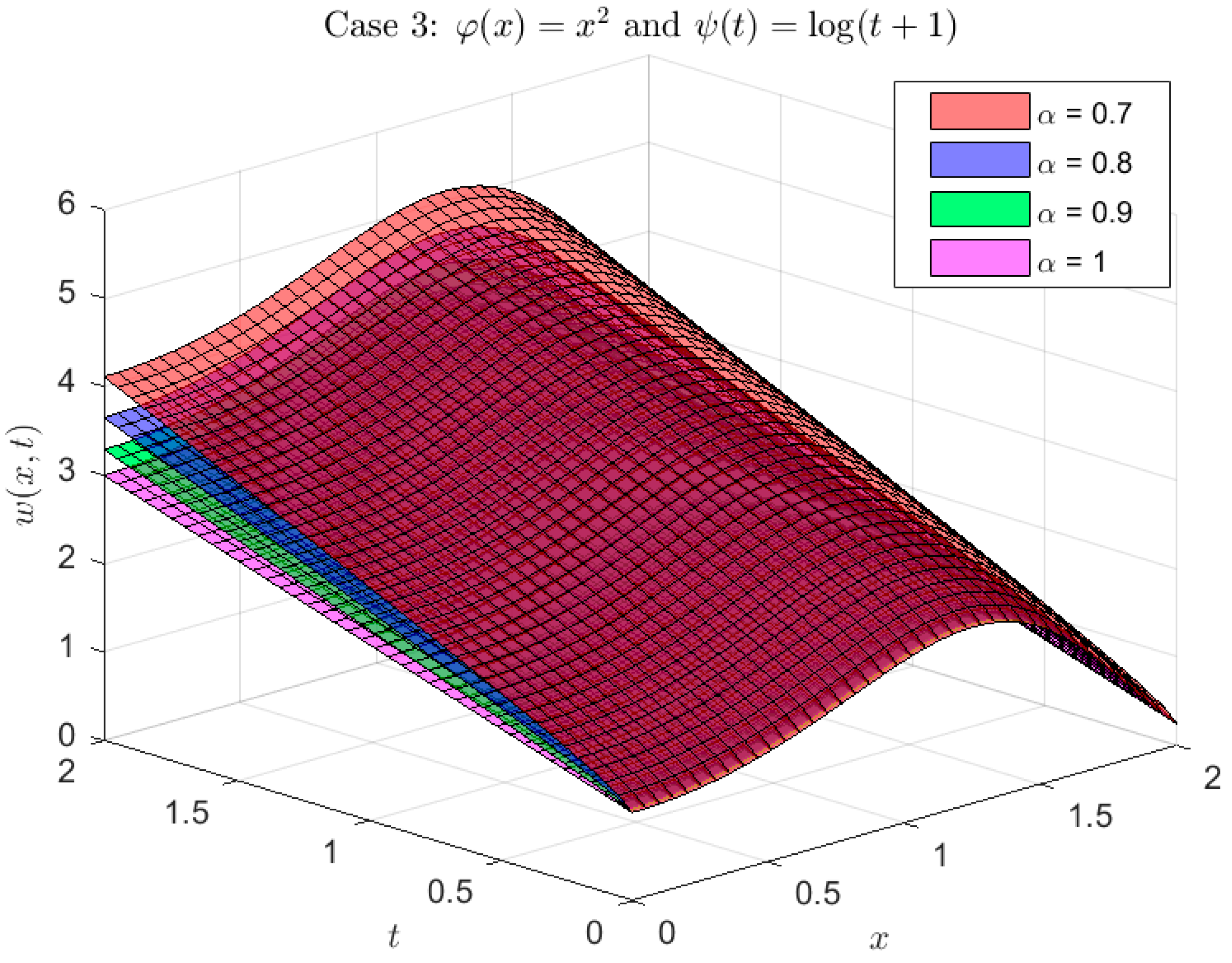
Example 3.

Consider the following φ,ψ-fractional Burgers problem,

$$D_0^{\alpha ,\psi }w(x,t)+{\displaystyle \frac{{\partial }^{\phi }w(x,t)}{\partial x}}={\displaystyle \frac{{\partial }^{2\phi }w(x,t)}{\partial x^2}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(x,t)\in \hspace{0.17em}{(0,\pm \hspace{0.17em}\infty )}^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}1<\alpha \le 1,$$

(13)

with ICs and BCs:

$$\begin{array}{l}w(x,0)=e^{-\left(\phi (x)-\phi (0)\right)},\\ w(0,t)=\hspace{0.17em}{\in }_{\alpha }\left(2{\left(\psi (t)-\psi (0)\right)}^{\alpha }\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{{\partial }^{\phi }w(0,t)}{\partial x}}=-{\in }_{\alpha }\left(2{\left(\psi (t)-\psi (0)\right)}^{\alpha }\right).\end{array}$$

(14)

Equations (7) and (8), Properties 2, Equation (14) and algebraic operations, along with the φ,ψ-DET, yield the following:

$$\left({\displaystyle \frac{1}{r^{\alpha }}}+{\displaystyle \frac{1}{s}}-{\displaystyle \frac{1}{s^2}}\right)T_{\phi ,\psi }(s,r)={\displaystyle \frac{s^2{r}^2\left(\frac{1}{r^{\alpha }}+\frac{1}{s}-\frac{1}{s^2}\right)}{\left(1+s\right)\left(1-r^{\alpha }\right)}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}\hspace{0.17em}{T}_{\phi ,\psi }(s,r)={\displaystyle \frac{s^2{r}^2}{\left(1+s\right)\left(1-r^{\alpha }\right)}}$$

Take the inverse φ,ψ-ET to obtain:

$$\hspace{0.17em}w(x,t)=e^{-\left(\phi (x)-\phi (0)\right)}{\in }_{\alpha }\left(2{\left(\psi (t)-\psi (0)\right)}^{\alpha }\right).$$

Figure 2 displays the model’s computed solution using the following kernels:

$$\left(i\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(ii\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\tan \left({\displaystyle \frac{\pi t}{4}}\right)\hspace{0.17em}\hspace{0.17em}\left(iii\right)\hspace{0.17em}\phi (x)={\displaystyle \frac{x}{2}}\left(x+1\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\sqrt{t},$$

graphically. The problem (13) was reduced to the Caputo fractional derivative in case 1, as is well known (see Figure 7, Figure 8 and Figure 9). Surprisingly, the solution scenarios listed below are provided for specific situations that are crucial to the functions  $\phi (x), \psi (t), \alpha$ function selection process.

Case 1.

$$\begin{array}{l}\left(i\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-x}{\in }_1\left(2t\right),\hspace{0.17em}\\ \left(ii\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =0.9\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-x}{\in }_{0.9}\left(2t^{0.9}\right),\\ \left(iii\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =0.8\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-x}{\in }_{0.8}\left(2t^{0.8}\right),\\ \left(iv\right)\hspace{0.17em}\phi (x)=x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=t,\hspace{0.17em}\alpha =0.7\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-x}{\in }_{0.7}\left(2t^{0.7}\right).\end{array}$$

Case 2.

$$\begin{array}{l}\left(i\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\tan \left({\displaystyle \frac{\pi t}{4}}\right),\hspace{0.17em}\alpha =1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-x^2}{\in }_1\left(2\tan \left({\displaystyle \frac{\pi t}{4}}\right)\right),\hspace{0.17em}\\ \left(ii\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\tan \left({\displaystyle \frac{\pi t}{4}}\right),\hspace{0.17em}\alpha =0.9\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-x^2}{\in }_{0.9\hspace{0.17em}}\left(2{\tan }^{0.9\hspace{0.17em}}\left({\displaystyle \frac{\pi t}{4}}\right)\right),\\ \left(iii\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\tan \left({\displaystyle \frac{\pi t}{4}}\right),\hspace{0.17em}\alpha =0.8\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-x^2}{\in }_{0.8}\left(2{\tan }^{0.8}\left({\displaystyle \frac{\pi t}{4}}\right)\right),\\ \left(iv\right)\hspace{0.17em}\phi (x)=x^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\tan \left({\displaystyle \frac{\pi t}{4}}\right),\hspace{0.17em}\alpha =0.7\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-x^2}{\in }_{0.7}\left(2{\tan }^{0.7}\left({\displaystyle \frac{\pi t}{4}}\right)\right).\end{array}$$

Case 3.

$$\begin{array}{l}\left(i\right)\hspace{0.17em}\phi (x)={\displaystyle \frac{x}{2}}\left(x+1\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\sqrt{t},\hspace{0.17em}\alpha =1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-{\displaystyle \frac{x}{2}}\left(x+1\right)}{\in }_1\left(2\sqrt{t}\right),\hspace{0.17em}\\ \left(ii\right)\hspace{0.17em}\phi (x)={\displaystyle \frac{x}{2}}\left(x+1\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\sqrt{t},\hspace{0.17em}\alpha =0.9\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-{\displaystyle \frac{x}{2}}\left(x+1\right)}{\in }_{0.9}\left(2{\left(\sqrt{t}\right)}^{0.9}\right),\\ \left(iii\right)\hspace{0.17em}\phi (x)={\displaystyle \frac{x}{2}}\left(x+1\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\sqrt{t},\hspace{0.17em}\alpha =0.8\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-{\displaystyle \frac{x}{2}}\left(x+1\right)}{\in }_{0.8}\left(2{\left(\sqrt{t}\right)}^{0.8}\right),\\ \left(iv\right)\hspace{0.17em}\phi (x)={\displaystyle \frac{x}{2}}\left(x+1\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\psi (t)=\sqrt{t},\hspace{0.17em}\alpha =0.7\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}w(x,t)=e^{-{\displaystyle \frac{x}{2}}\left(x+1\right)}{\in }_{0.7}\left(2{\left(\sqrt{t}\right)}^{0.7}\right).\end{array}$$

6. Conclusions

Considering the preliminary, the literature includes a lot of existing details concerning fractional calculus, including developments, φ,ψ-DET. In order to handle the fractional derivatives involving functions φ,ψ, the φ,ψ-DET was applied to the φ,ψ-fractional telegraph equation, φ,ψ-fractional Klein–Gordon problem and the φ,ψ-fractional Burgers problem as recommended in numerical testing. We concluded that this approach is effective for solving a particular type of linear φ,ψ-FPDEs. Therefore, the method proposed in this study and its numerical results might inspire more research on other fractional calculus operators.

Our findings demonstrate that the existing approach is effective for linear φ,ψ-FPDEs based on φ,ψ-DET, enabling its future application to other linear and non-linear φ,ψ-FPDEs. Furthermore, one of our main goals going forward is to develop a more complex application that can be used in a variety of applied disciplines by broadening the applicability of this approach or merging it with other numerical techniques or symbolic computing tools. Additionally, this technique can be advanced to effectively tackle nonlinear φ,ψ-FPDEs by integrating it with an Adomian method or other approximation techniques. In upcoming research, we will also focus on Chebyshev’s phantom constrained operators related to Fredholm-type integral equations [14], which could act as a beneficial numerical alternative to the ϕ,ψ-DET analytical method.

Furthermore, 3D graphs were used to show how the recommended strategy influenced the results. Figures show how the forms of the solutions found using the recommended approach resemble the exact solution with the same set of parameters. The suggested approach can also be expanded to address other φ,ψ-FPDEs that occur in applied research, depending on how easily it can be implemented.