Application of a Fractional Laplacian-Based Adaptive Progressive Denoising Method to Improve Ambient Noise Crosscorrelation Functions

Abstract

Extracting high-quality surface wave dispersion curves from crosscorrelation functions (CCFs) of ambient noise data is critical for seismic velocity inversion and subsurface structure interpretation. However, the non-uniform spatial distribution of noise sources may introduce spurious noise into CCFs, significantly reducing the signal-to-noise ratio (SNR) of empirical Green’s functions (EGFs) and degrading the accuracy of dispersion measurement and velocity inversion. To mitigate this issue, this study aims to develop an effective denoising approach that enhances the quality of CCFs and facilitates more reliable surface wave extraction. We propose a fractional Laplacian-based adaptive progressive denoising (FLAPD) method that leverages local gradient information and a fractional Laplacian mask to estimate noise variance and construct a fractional bilateral kernel for iterative noise removal. We applied the proposed method to the CCFs from 79 long-period seismic stations in Shandong, China. The results demonstrate that the denoising method enhanced the data quality substantially, increasing the number of reliable dispersion curves from 1094 to 2196, and allowing an increased number of temporal sampling points to be retrieved from previously low-SNR curves. This helps to expand the spatial coverage and results in a more accurate velocity inversion result than that without denoising. This study provides a robust denoising solution for ambient noise tomography in regions with complex noise source distributions.

1. Introduction

Ambient noise data contains implicit information about Earth’s internal structure [1]. Applying the crosscorrelation to continuously recorded ambient noise enables us to extract the empirical Green’s functions (EGFs) between station pairs [2]. This approach, referred to as seismic interferometry, removes the dependency on earthquakes and artificial sources in seismic imaging [3]. Since EGFs are predominantly composed of surface waves, which exhibit high sensitivity to S-wave velocity [4], this interferometry approach has been widely utilized for estimating subsurface S-wave velocity models [5,6,7,8].

Traditional seismic interferometry relies on the assumption of diffuse field, which posits that ambient noise sources must be homogeneously distributed in space [2]. However, observational studies demonstrate that the ambient noise sources in many regions are often spatially heterogeneous, with pronounced directional and temporal variability [9,10,11,12]. These biased sources result in the EGFs being contaminated by spurious noise, which significantly degrades the quality of EGFs and collectively renders inaccurate structural interpretation [13,14]. To address this issue, a couple of targeted data processing strategies have been developed for crosscorrelation functions (CCFs) [9,15]. One typical representation is the spectral normalization, which applies one-bit normalization, running absolute-mean normalization, and spectral whitening to reduce the effect of earthquake events. The directional source compensation is commonly used to reduce directional source asymmetry by averaging the positive and negative components of CCFs. In addition, the temporal stacking for long-duration recordings has been widely utilized to account for temporal variations in noise sources.

Based on the foundational work of Bensen et al. [15], subsequent studies have proposed some data processing methods to enhance the SNR of CCFs. For instance, Baig et al. developed enhanced stacking weights using a discrete orthogonal S transform in the time-frequency domain, which improved the arrival measurement precision of Rayleigh and Love waves at distant stations [16]. Seats et al. utilized Welch’s method to partition seismic time-series into overlapping segments, accelerating the conversion of CCFs to EGFs compared to non-overlapping approach [17]. In addition, Stehly et al. and Mao et al. have, respectively, implemented the wavelet and curvelet transform-based methods for de-noising CCFs [18,19]. Schimmel et al. proposed a phase-weighted stacking method that amplifies surface wave signals by leveraging instantaneous phase coherence, achieving a superior performance over traditional linear stacking [20]. To further enhance EGF quality, Shen et al. applied frequency-time normalization [21], whereas Cheng et al. developed SNR-weighted stacking for optimized stacking results [22]. Liu et al. introduced a probabilistic description of stacked cross-spectrum, enabling a selective exclusion for low-quality data segments generated by small earthquakes [23]. Li et al. systematically compared the efficacy of time- and frequency-domain inverse S transforms within these stacking workflows [24]. Olivier et al. designed a selective stacking method to amplify the phases from stationary phase zones [25], and Weaver and Yoritomo created a weighting scheme that approximates an isotropic intensity distribution during stacking [26]. Moreau et al. employed a singular value decomposition-based Wiener filter to improve the quality of EGFs [27]. Afonin et al. optimized the stacking weights through incremental SNR monitoring for extracting high-quality EGFs from high-frequency ambient noise [28]. Xie et al. proposed an RMS-ratio selection stacking method to enhance the quality of short-duration CCFs [29]. Qiu et al. developed a three-station interferometry method that amplifies high-frequency surface waves via coherent stacking of direct arrivals [30]. Yang et al. developed a quantitative method for assessing seismic wavefield diffuseness in the frequency domain, enabling the selection of EGFs with enhanced amplitude and phase reliability [31]. Luo et al. introduced a high-resolution Radon-transform-based mode separation method, which effectively suppresses near-zero time-lag noise while enhancing surface wave signals for ambient noise tomography [32]. Zhang et al. applied polarization analysis to improve CCF quality in complex noise environments [3].

The adaptive progressive seismic denoising (APSD) method has demonstrated effectiveness in enhancing weak reflection signals within exploration seismic data by employing a local noise variance field and a 3-D bilateral kernel [33]. Enhancing surface waves in CCFs is akin to denoising exploration seismic data, as both processes require suppressing non-stationary noise while preserving coherent signals. To better address the spurious noise in CCFs, we introduce a fractional Laplacian-based adaptive progressive denoising (FLAPD) method by enhancing the APSD framework. The proposed method leverages a fractional Laplacian mask to construct a spatially varying noise variance field, where the fractional order s provides tunable control over the spectral sensitivity for multi-scale noise characterization. It implements progressive denoising through adaptive iterations, during which the fractional range kernel expands geometrically to preserve weak signals, while the spatial kernel contracts linearly to sharpen local noise discrimination. The feasibility and effectiveness of the proposed method are validated through numerical experiments on real data in Section 3.

2. Data and Methods

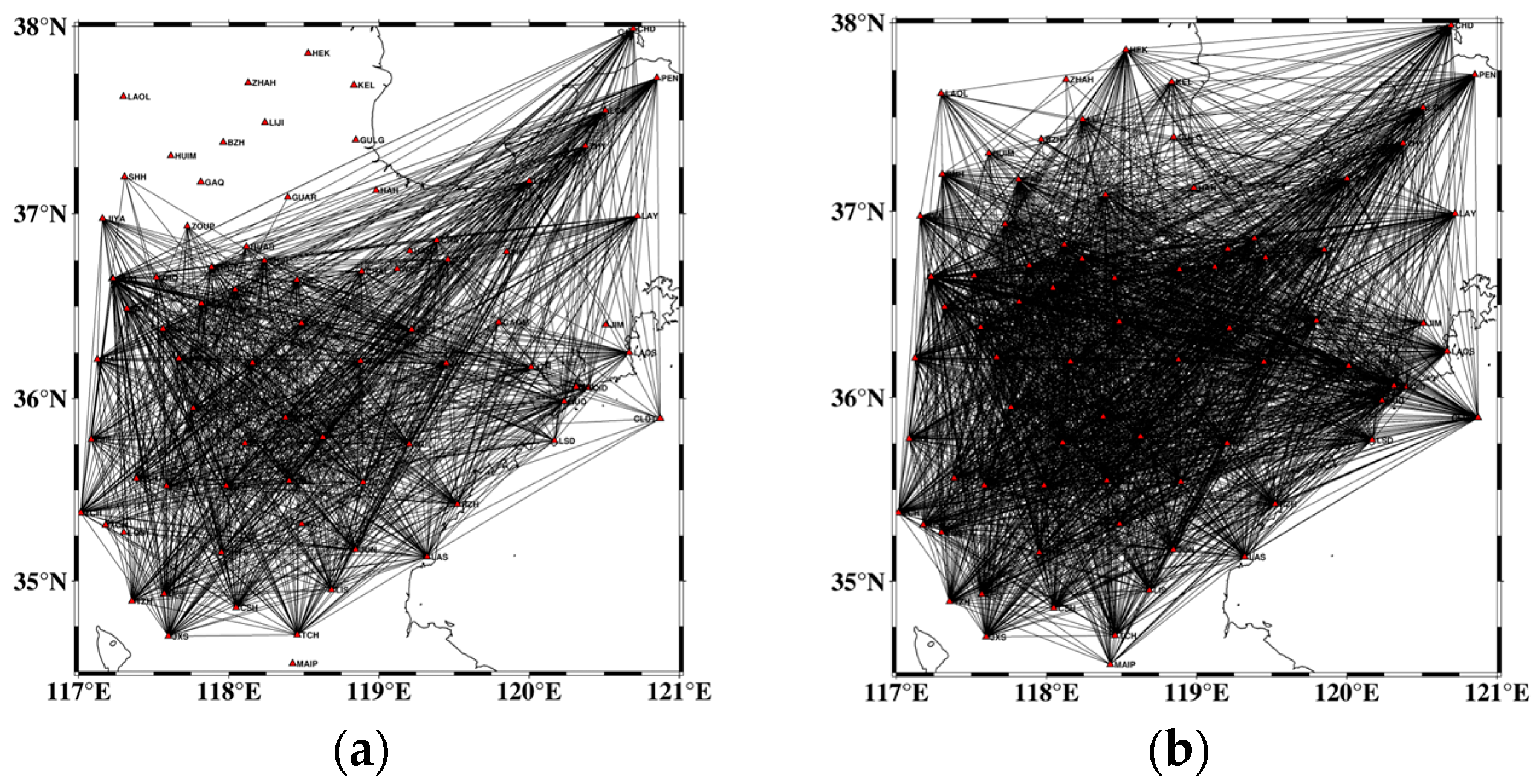
2.1. Study Area and Data

The Tanlu Fault Zone, a continental-scale sinistral strike-slip fault system in eastern China, extends approximately 2400 km along an NNE-trending structural belt developed within the convergent margin of the Eurasian Plate and the Paleo-Pacific subduction system. This fault system exhibits complex segmentation with alternating transtensional and transpressional regimes, characterized by distinct kinematic partitioning and multi-phase reactivation since the Mesozoic. Serving as the principal structural boundary separating the South China Block and North China Craton, it exerts primary control on strain partitioning during the Mesozoic-Cenozoic intracontinental deformation associated with the Dabie-Sulu ultrahigh-pressure metamorphic belt and lithospheric thinning beneath the Bohai Bay Basin. Since its initial characterization during systematic geological mapping campaigns, the Tanlu Fault Zone has remained a focal point for multidisciplinary research. Our study concentrates on the Yishu Fault Zone (34.5° N–38° N, 117° E–121° E), the central Tanlu segment in Shandong Province (Figure 1), where complex fault geometries create inhomogeneous ambient noise sources that complicate CCF noise suppression. We use continuous seismic noise data recorded in 2021 by 79 broadband stations deployed by the Shandong Earthquake Agency, forming a dense array covering the Yishu Fault Zone.

2.2. Method

2.2.1. Review of Seismic Interferometry

Ambient noise seismology establishes that under homogeneous source distribution conditions, the EGFs derived from ambient noise CCFs closely approximate the true Green’s functions when corrected for amplitude discrepancies [34,35]. This relationship emerges through the time derivative of CCFs, expressed as:

$$-{\displaystyle \frac{d}{dt}}\left[{\displaystyle \frac{C_{AB}\left(t\right)+C_{AB}\left(-t\right)}{2}}\right]={\widehat{G}}_{AB}\left(t\right)\approx G_{AB}\left(t\right),$$

(1)

where $C_{AB}\left(t\right)$ is the CCF between stations A and B, ${\widehat{G}}_{AB}(t)$ denotes the EGF, and $C_{AB}\left(t\right)$ represents the true Green’s function at B for an impulsive source at A.

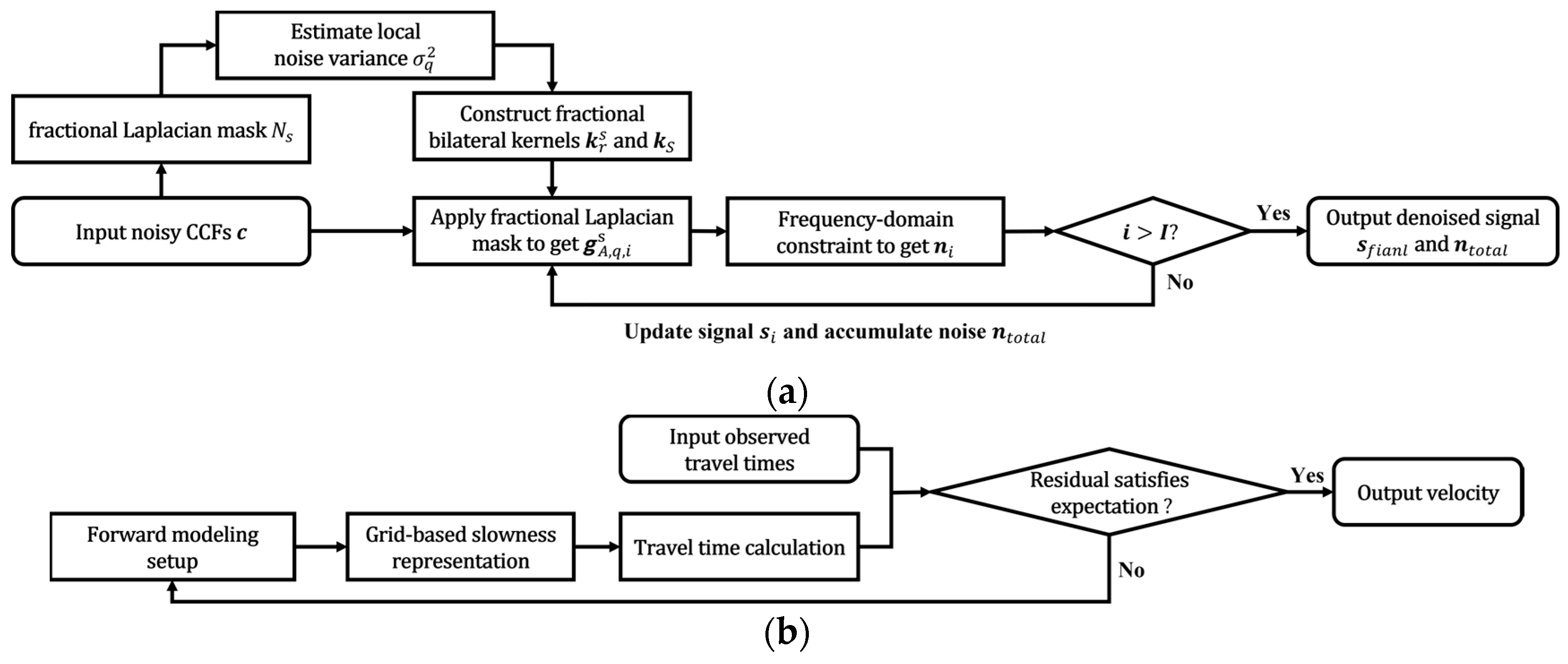
2.2.2. CCF Denoising with the FLAPD

Noise suppression in CCFs involves extracting surface waves $\mathit{s}$ from noise-contaminated dataset $\mathit{c}$. This process follows the observation model

$$\mathit{c}=\mathit{s}+\mathit{n},$$

(2)

where $\mathit{n}$ represents noise within CCFs. Accurately estimating $\mathit{n}$ requires distinguishing surface waves from noise. Exploiting surface wave correlation and sparsity in the frequency domain enables effective separation from noise in the frequency-wavenumber domain. For CCFs $\mathit{c}(x,y)$, we define a local data block A with a window radius r. The gradient at the center point q of a is then computed as follows:

$${\mathit{g}}_{A,q,i}={\mathit{c}}_{A,i}-{\mathit{c}}_{q,i},$$

(3)

where ${\mathsf{g}}_{A,q,i}$ represents the gradient of q within the local window A during the $i$th iteration. The local noise variance field ${\sigma }_q^2$ is calculated based on the gradient ${\mathsf{g}}_{A,q,i}$ at the local center point and a fractional Laplacian mask $N_s$ to allow more flexible spectral weighting of local gradients, thereby reflecting variations in the local gradient field. The ∗ denotes convolution.

$${\sigma }_q^2={\displaystyle \frac{1}{{‖N_s‖}_2^2{\left(r-2\right)}^2}}{\displaystyle \sum _A{\left({\mathit{g}}_{A,q,i}\ast N_s\right)}^2}.$$

(4)

The fractional Laplacian mask $N_s$ is constructed in the spectral domain using the discrete Fourier transform:

$$N_s\left(x,y\right)=F^{-1}\left({[4-2\cos (k_x\Delta x)-2\cos (k_y\Delta y)]}^s\right),$$

(5)

where $k_x$ and $k_y$ are the discrete spatial frequencies corresponding to the sampling intervals $∆x$ and $∆y$ in the x and y directions, respectively. Here $s>0$ denotes the fractional order, and $s=1$ restores the conventional Laplacian case. Under normalized spatial sampling ( $\Delta x=\Delta y=1$), the fractional Laplacian mask Ns modifies the spectral weighting of the local gradients according to the fractional order $s$. A smaller fractional order ( $s<1$) weakens the high-frequency components of $N_s$, resulting in smoother local variance estimation and stronger noise suppression. When $s>1$, the spectral response of $N_s$ enhances the high-frequency components, making the variance field more sensitive to fine-scale fluctuations and weak coherent signals. Therefore, the fractional order $s$ provides a tunable control over the balance between noise attenuation and detail preservation, allowing adaptive adjustment of the local noise variance estimation in different frequency regimes.

The local gradient is utilized to design the range kernel ${\mathit{k}}_r$ and the spatial kernel ${\mathit{k}}_S$. The range kernel ${\mathit{k}}_r$ features a smooth decay profile that effectively attenuates high-amplitude signals, while the spatial kernel ${\mathit{k}}_S$ reduces the influence of distant points in the time domain, preserving signal accuracy. Both kernels undergo Gaussian smoothing to minimize variations caused by spatial separation. Their specific forms are as follows:

$${\mathit{k}}_r={\displaystyle \frac{{\left|{\mathit{g}}_{A,q,i}\right|}^2}{{\sigma }^2{\gamma }_r{\alpha }^{-i}}}, {\mathit{k}}_S={\displaystyle \frac{{\left|\mathit{A}-\mathit{q}\right|}^2}{{\sigma }_S^2{\gamma }_S{\alpha }^{i/2}}},$$

(6)

where ${\alpha }^{-i}$ represents the decay rate of the range kernel ${\mathit{k}}_r$ at iteration $i$. ${\gamma }_r$ controls the range’s large initial scaling, whereas ${\gamma }_s$ governs the spatial kernel’s small initial scaling. ${\sigma }_s$ is the spatial kernel’s reference standard deviation. As iterations progress, spatial kernel ${\mathit{k}}_S$ diminishes while range kernel ${\mathit{k}}_r$ amplifies, progressively improving noise estimation accuracy. We introduce the fractional gradient and further develop the fractional bilateral kernel by integrating the fractional gradient into the kernel design framework. For the $i$th iteration, the fractional gradient at the center point $q$ of local window $A$ and the fractional range kernel are defined as:

$${\mathit{g}}_{A,q,i}^s={\mathit{g}}_{A,q,i}\ast N_s, {\mathit{k}}_r^s={\displaystyle \frac{{\left|{\mathit{g}}_{A,q,i}^s\right|}^2}{{\sigma }^2{\gamma }_r{\alpha }^{-i}}}.$$

(7)

Here, the range kernel ${\mathit{k}}_r^s$ operates on the local gradient amplitude and thus reflects the fractional-order characteristics of the gradient field, providing a frequency-dependent modulation of the amplitude weighting.

Ultimately, the bilateral kernel applied to gradient ${\mathsf{g}}_{\mathit{A},\mathit{q},\mathit{i}}^{\mathit{s}}$ yields spatial noise estimation $\tilde{n}$:

$${\tilde{\mathit{n}}}_{q,i}^s={\mathit{k}}_r^s\cdot {\mathit{k}}_S\cdot {\mathit{g}}_{A,q,i}^s.$$

(8)

Time–space results are transformed into the frequency domain for Fourier coefficient noise variance estimation. Just as in the time domain, the Fourier coefficients in the frequency domain are also constrained using the range and space kernels. The constraint operator is defined as follows:

$${\mathit{K}}_{f,i}^s(q)={\sigma }^2{{\displaystyle \sum _{\omega \in F_q}\left({\mathit{k}}_r^s\times {\mathit{k}}_S\right)}}^2,$$

(9)

where $F_q$ represents the Fourier domain of window A, and ${\mathit{K}}_{f,i}^s$ is the bilateral kernel operator applied to the Fourier coefficients. This operator is derived from the variance of the input noisy data and the bilateral kernel of the window. The procedure for constraining the Fourier coefficients is as follows:

$${\tilde{\mathit{n}}}_i^s\left(q\right)={\displaystyle \frac{1}{{\left(2r+1\right)}^2}}{\displaystyle \sum _{\omega \in F_q}{\mathit{N}}_{q,f,i}^s\cdot }{\displaystyle \frac{{\left|{\mathit{N}}_{q,f,i}^s\right|}^2}{{\mathit{K}}_i^s(q)}}.$$

(10)

where $N_{q,f,i}^s$ represents the Fourier coefficient of time–space noise estimation. The incorporation of the fractional Laplacian mask and the fractional range kernel significantly enhances the final noise estimation. Parameterized by the order $s$, the fractional Laplacian operator adaptively reweights the gradient field in the frequency domain, enabling multi-scale control over the noise variance estimation. Based on numerical experiments conducted in this study, the fractional order $s$ typically lies within the range of [0.5, 1.5]. A value of $s$ < 1 promotes smoother variance estimation, favoring stronger noise suppression, whereas $s$ > 1 enhances the sensitivity to fine-scale features, which is beneficial for preserving weak coherent signals.

In our application, the value of $s$ was selected based on the interstation distance. For station pairs with larger separations, which are more susceptible to spurious noise from heterogeneous sources and are sensitive to deeper structures, a smaller $s$ value was preferred to emphasize denoising. Conversely, for shorter paths that are crucial for retrieving high-frequency signals for shallow structural inversion, a larger $s$ value was adopted to prioritize signal fidelity. The fractional range kernel then utilizes this adaptively weighted gradient information to modulate the amplitude weighting in the bilateral filter, effectively distinguishing between noise and signal based on their fractional-order characteristics.

Regarding the other kernel parameters, we adopted the empirically optimized values from the APSD framework [33], which have been validated on both synthetic and field data. These parameters are fixed and require no user adjustment, ensuring reproducibility. While automated parameter optimization is a promising direction for future work, the empirical values used here demonstrated consistent effectiveness and stability across all station pairs in our dataset.

The application of frequency-domain constraints further improves the accuracy of noise estimation. Throughout this process, the kernel function remains robust and effectively preserves structural edges. Finally, the inverse Fourier transform is applied, and the Fourier slice theorem is used to compute the average of all Fourier coefficients, yielding the final noise estimate at point $q$ for CCF processing.

2.2.3. Data Processing and Dispersion Curve Measurement

We first converted raw seismic data from SEED to SAC format, merged discontinuous fragments into continuous waveforms, and downsampled to 10 Hz, producing daily files for each station. From these daily vertical-component records, we computed ambient noise CCFs [5]. Individual station waveforms underwent four preprocessing stages before CCF calculation: (1) detrending and demeaning, (2) instrument response removal via spectral division, (3) time-domain running absolute-mean normalization, and (4) frequency domain whitening. We then applied a fourth-order Butterworth bandpass filter (0.02–1 Hz) to attenuate signals outside the target frequency range. To mitigate the influence of earthquake events and instrument irregularities, we implemented a multiple-period normalization approach designed to produce a more even spectrum and amplify weak signals. Specifically, we applied the time-domain running absolute-mean normalization across four period bands: 1–5 s, 5–15 s, 15–30 s, and 30–50 s. Finally, daily CCFs from all station pairs were stacked, enhancing SNR through constructive interference of coherent signals. The processed CCFs from the aforementioned method are symmetrically averaged across positive and negative time-lagged signals to generate symmetric CCFs. While this processing demonstrates partial compensation for azimuthal source imbalance to some extent, its effectiveness remains constrained under pronounced source heterogeneity.

We next applied the FLAPD method to enhance surface wave coherence. This method operates through three key stages. First, we selected each station as a virtual source and extracted its corresponding CCFs to form a virtual source gather in the space-time domain. We then applied the FLAPD method to each gather to estimate and remove noise, generating a processed virtual source gather. This process was repeated for all virtual sources, resulting in two CCFs per station pair. Ideally, these CCFs should have been equivalent, but due to heterogeneous structures and non-uniform wavefields, complete equivalence was rarely achieved. Therefore, we averaged the two CCFs to enhance data consistency for further processing.

We obtained the EGFs by applying the Hilbert transform to the CCFs [5]. After computing the EGFs for each station pair, we applied three selection criteria before tomographic inversion. First, the interstation distance was required to exceed two wavelengths to satisfy the far-field approximation. Second, the SNR was required to be greater than 5 within the target period. We defined SNR as the ratio of the maximum envelope amplitude in the signal window to the mean envelope amplitude in a 150-s noise window immediately afterward. To further ensure data quality, a path cluster analysis was conducted on the dispersion data, assuming that station pairs with similar ray paths should have similar dispersion curves. Dispersion data that significantly deviated from the average was removed.

2.2.4. Direct Tomography for S-Wave Velocity

We derived the 3D Vs structure through direct surface wave tomography by inverting mixed-path Rayleigh wave dispersion data. The method accounts for curved ray paths caused by 3D structural heterogeneity using the fast-marching method and incorporates partial sensitivity kernels for Vp and density derived from empirical relationships, which enhance the efficiency of surface wave tomography [36]. For the detailed derivation, readers are referred to the Supplementary Materials. The flowcharts of denoising and inversion is shown in Figure 2.

Empirical relationships indicate that fundamental-mode Rayleigh wave phase velocities are predominantly sensitive to shear wave velocities at depths near one-third of their wavelengths. For a uniform Poisson solid half-space, we approximate the phase velocity (c) as 0.92 times Vs. Accordingly, we constructed the initial shear wave velocity model by scaling the average measured phase velocities by 1.1 (Vs ≈ 1.1c) at depths equivalent to one-third of the wavelength. Sensitivity analysis of 1D models demonstrates that dispersion data in the 1–25 s period exhibit high sensitivity to the velocity structure at 0–30 km depth. Empirically defining depth nodes at 0, 1, 2, 3.5, 5, 7, 9, 12, 15, 18, 22, 26, and 30 km, we adopted finer intervals for shallow layers and broader spacing for deeper structures, while configuring horizontal grids at 0.1° × 0.1° resolution.

3. Results

Following preprocessing of vertical noise components from seismic station recordings, we computed CCFs for all station pairs. In our study area, the azimuthal inhomogeneity of ambient noise sources, attributed to the complex fault system, introduced significant spurious components into the raw CCFs. As described earlier, we organized the CCFs into virtual source gathers based on stations and applied the FLAPD method for spurious components estimation and removal. For comparison, we also processed the same dataset using the Curvelet Transform method, a widely recognized multi-scale denoising technique. The results indicate that the FLAPD method exhibits stronger noise suppression capability while effectively preserving the V-shaped travel-time trajectories of surface wave signals. In contrast, the Curvelet Transform not only shows limited denoising performance but also introduces signal leakage in the noise profile (denoted by the red dashed border in Figure 3c), indicating unintended damage to the coherent surface wave components during denoising. These comparative outcomes demonstrate that the proposed FLAPD method achieves a better balance between noise removal and signal fidelity, offering superior performance in both denoising effectiveness and coherent energy preservation. Comparative analysis of CCF datasets before and after FLAPD processing demonstrates effective suppression of spurious components while preserving continuous surface wave signals (Figure 3). Figure 4 illustrates representative CCFs pre- and post-treatment, further confirming the method’s efficacy in enhancing surface wave components within the processed correlations.

During quality control of FLAPD-processed CCFs, we removed unreliable CCFs caused by abnormal ambient noise signals while retaining qualified CCFs for EGF extraction. Our comparative analysis demonstrated that EGFs derived from FLAPD-processed CCFs showed significantly higher SNR than those from raw data, calculated using the method detailed in Section 2.2.3 (Figure 5). Applying our quality criterion (SNR > 5 threshold for valid dispersion-point extraction), the SNR enhancement increased valid dispersion points per curve in the period domain, which consequently enriched usable dispersion data for shear-wave velocity inversion (Figure 6). Notably, 1987 original EGFs (64.5% of 3081) failed to meet the SNR threshold throughout all frequency bands, precluding effective dispersion extraction. With FLAPD-processed surface wave enhancement, we obtained 2196 qualified EGFs (1102 added), substantially expanding both the spatial coverage and density of retrievable dispersion data (Figure 7).

The checkerboard test serves as a standard method in seismic tomography to evaluate the resolution and recoverability of 3D velocity models. Our investigation employed two synthetic Vs models with distinct horizontal anomaly scales: 0.5° × 0.5° and 0.6° × 0.6°. These Vs anomalies exhibited ±8% amplitude variations relative to the initial 1D velocity model. We generated theoretical arrival times through forward modeling of these prescribed structures, which were subsequently superimposed with 1% Gaussian-distributed random errors to simulate observational uncertainties. During tomographic inversion, these synthetic datasets were processed as observed data. Resolution assessments demonstrated recoverable 0.5° × 0.5° anomalies within the shallow depth range (0–15 km) and 0.6° × 0.6° features at greater depths (0–30 km) (Figure 8). However, checkerboard analysis should be regarded as referential rather than indicative of true recoverability, as various other factors collectively influence model resolution.

Following the methodology in Section 2.2.4, we conducted 3D Vs tomography. Comparative analysis between velocity models derived from FLAPD-processed and raw CCF data reveals enhanced structural resolution (Figure 9 and Figure 10). The results demonstrate that enhanced dispersion information enables the velocity field to attain higher resolution, with improved delineation of velocity anomalies.

The traveltime residual, defined as the difference between the observed and model-predicted traveltimes, is a key metric for assessing the fit of the velocity model. Figure 11 compares the distributions of these residuals from inversions of raw and FLAPD-processed data. The distribution for the raw data (orange) shows a larger mean (μ = 0.099 s) and standard deviation (σ = 0.418 s), reflecting greater bias and uncertainty in the model fit. The distribution for the FLAPD-processed data (light blue), however, is characterized by a significantly smaller mean (μ = 0.014 s) and standard deviation (σ = 0.133 s). This superior result demonstrates that traveltime predictions are much closer to the observations, with residuals being more concentrated. 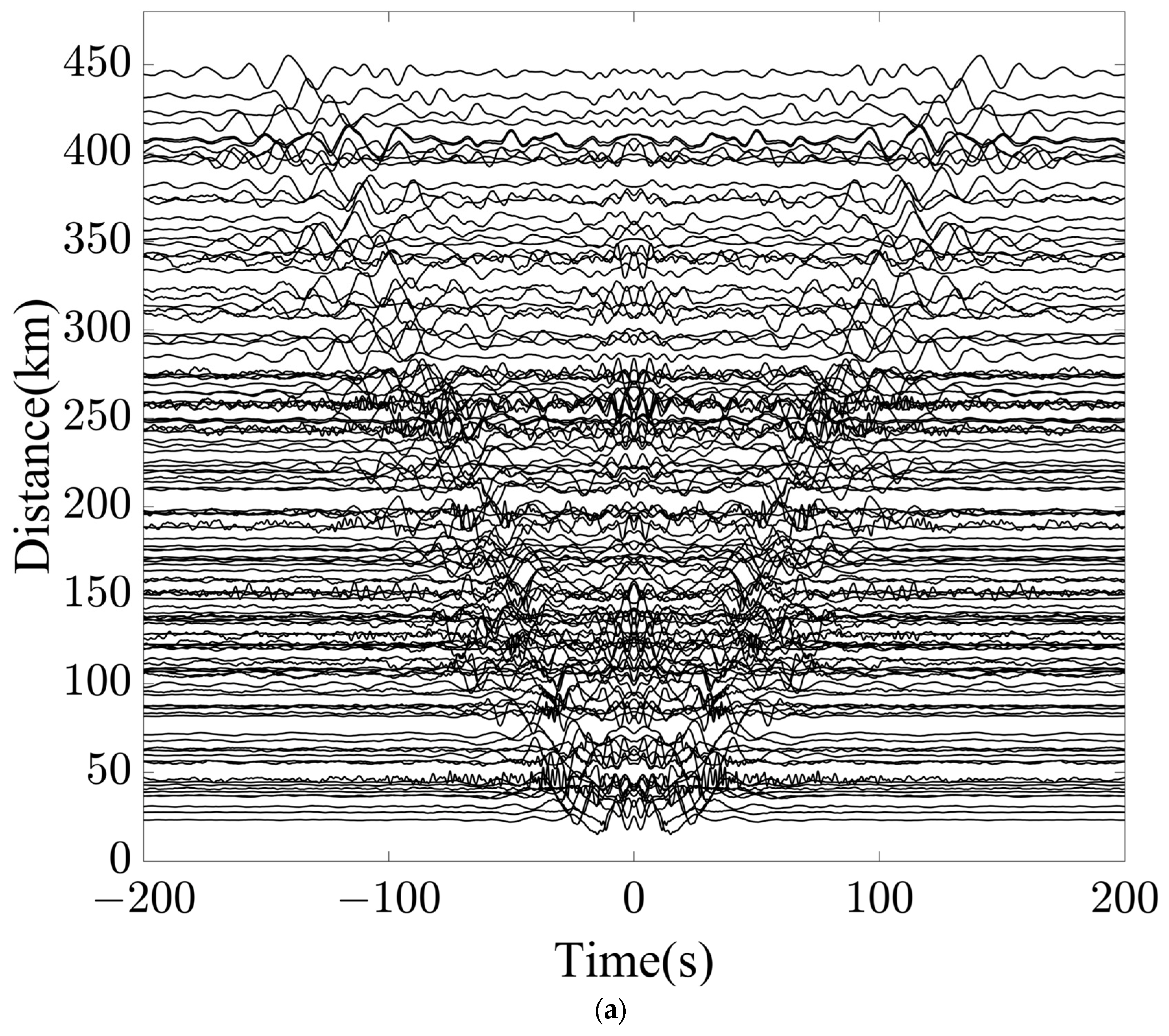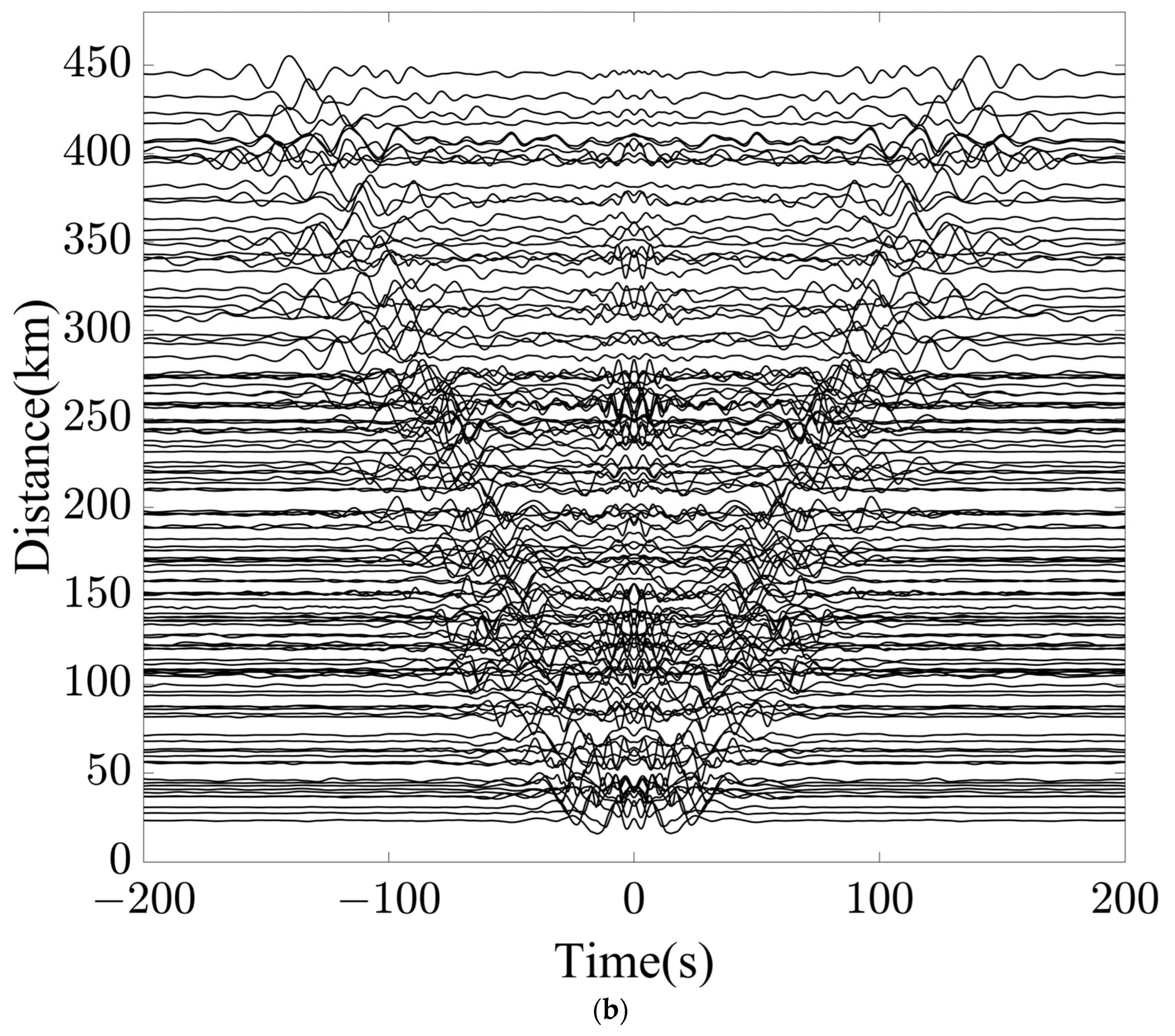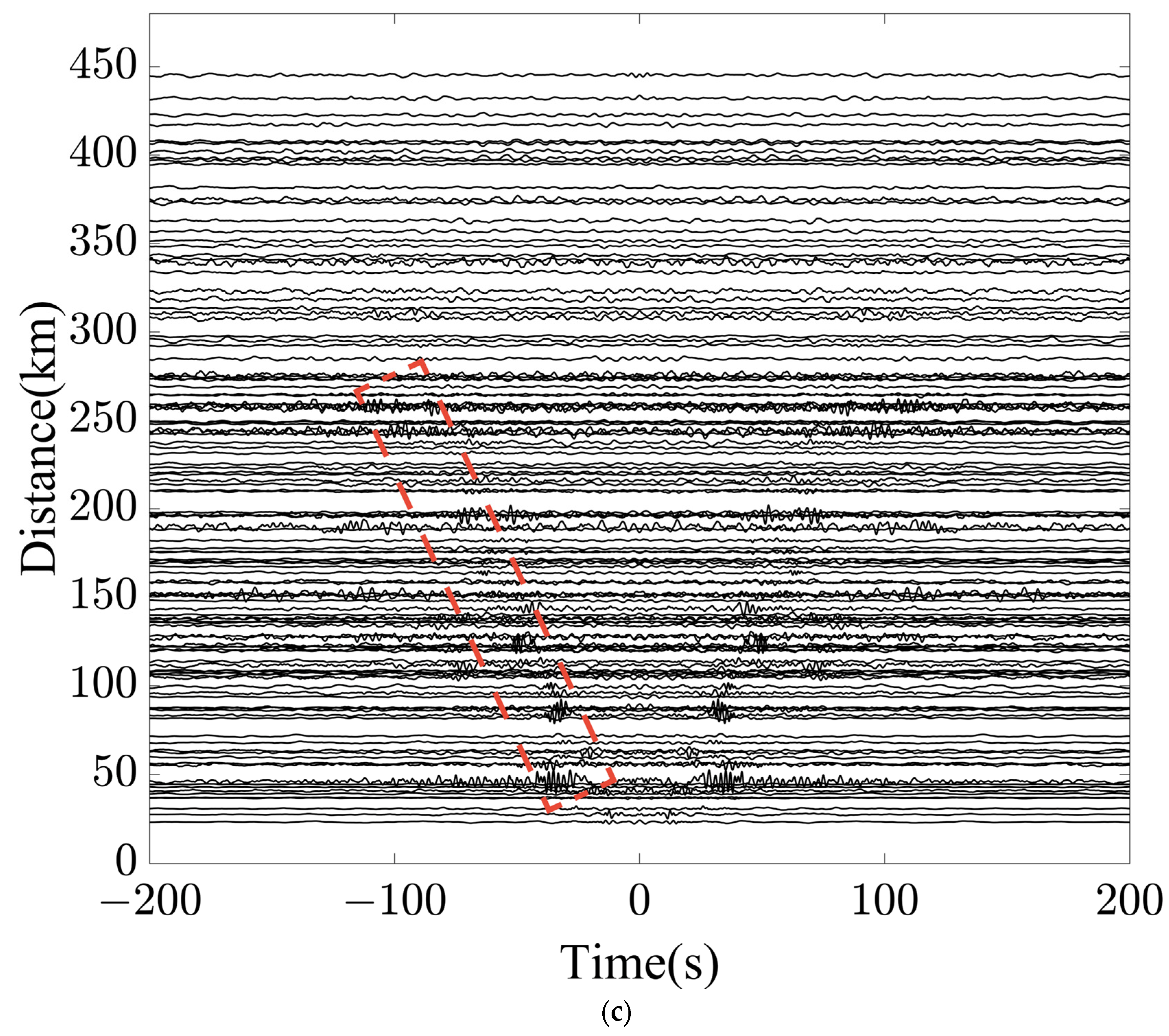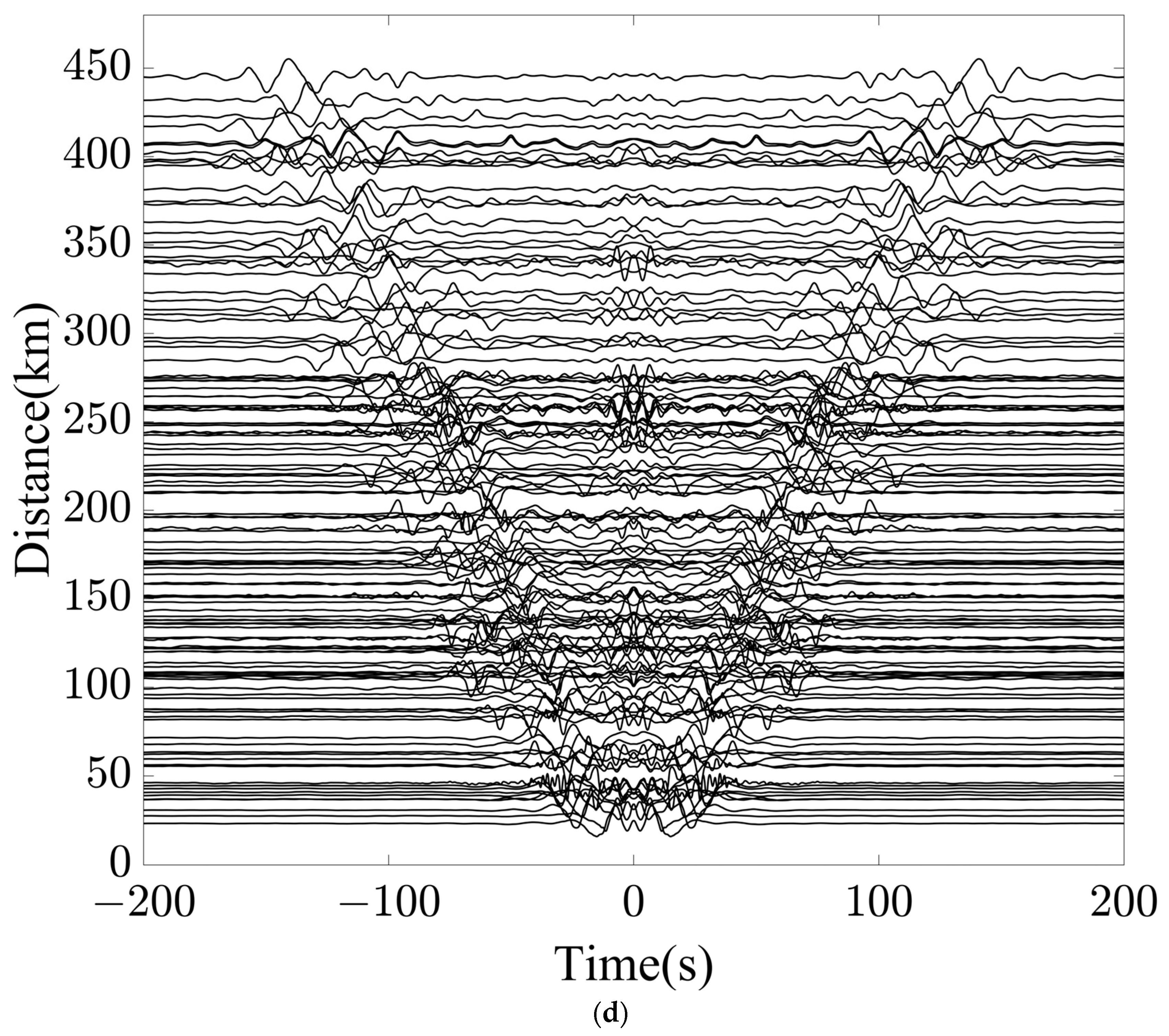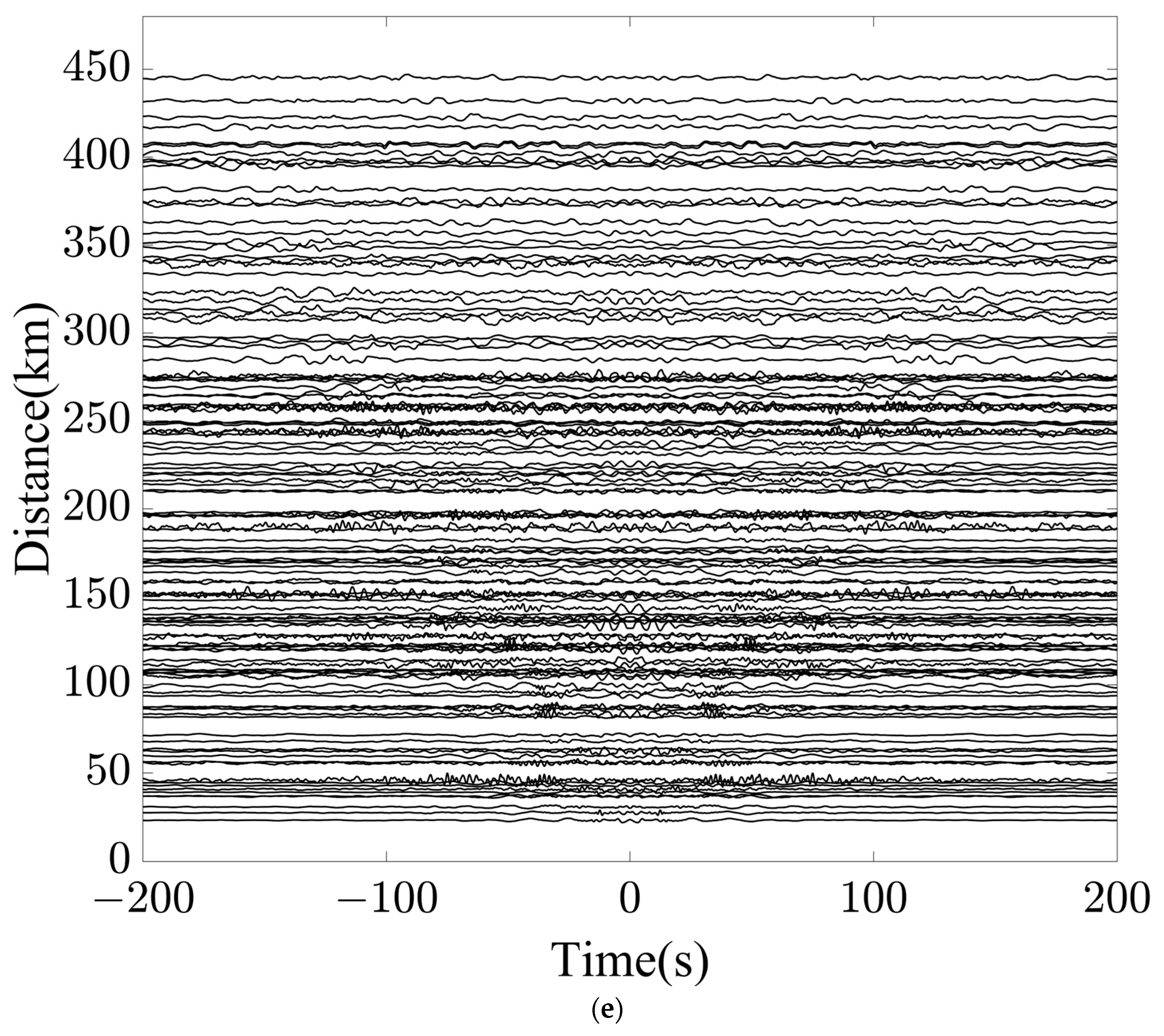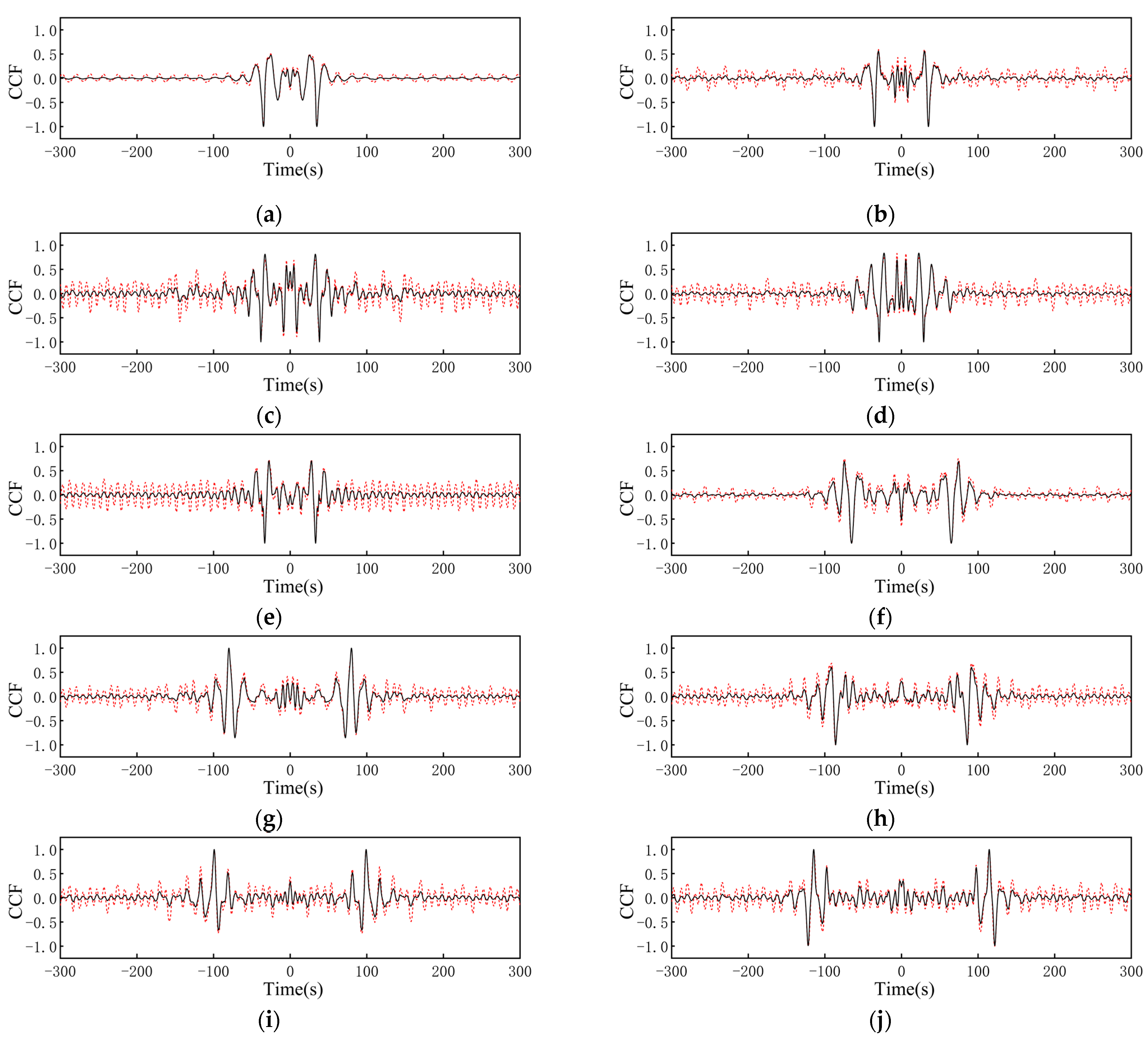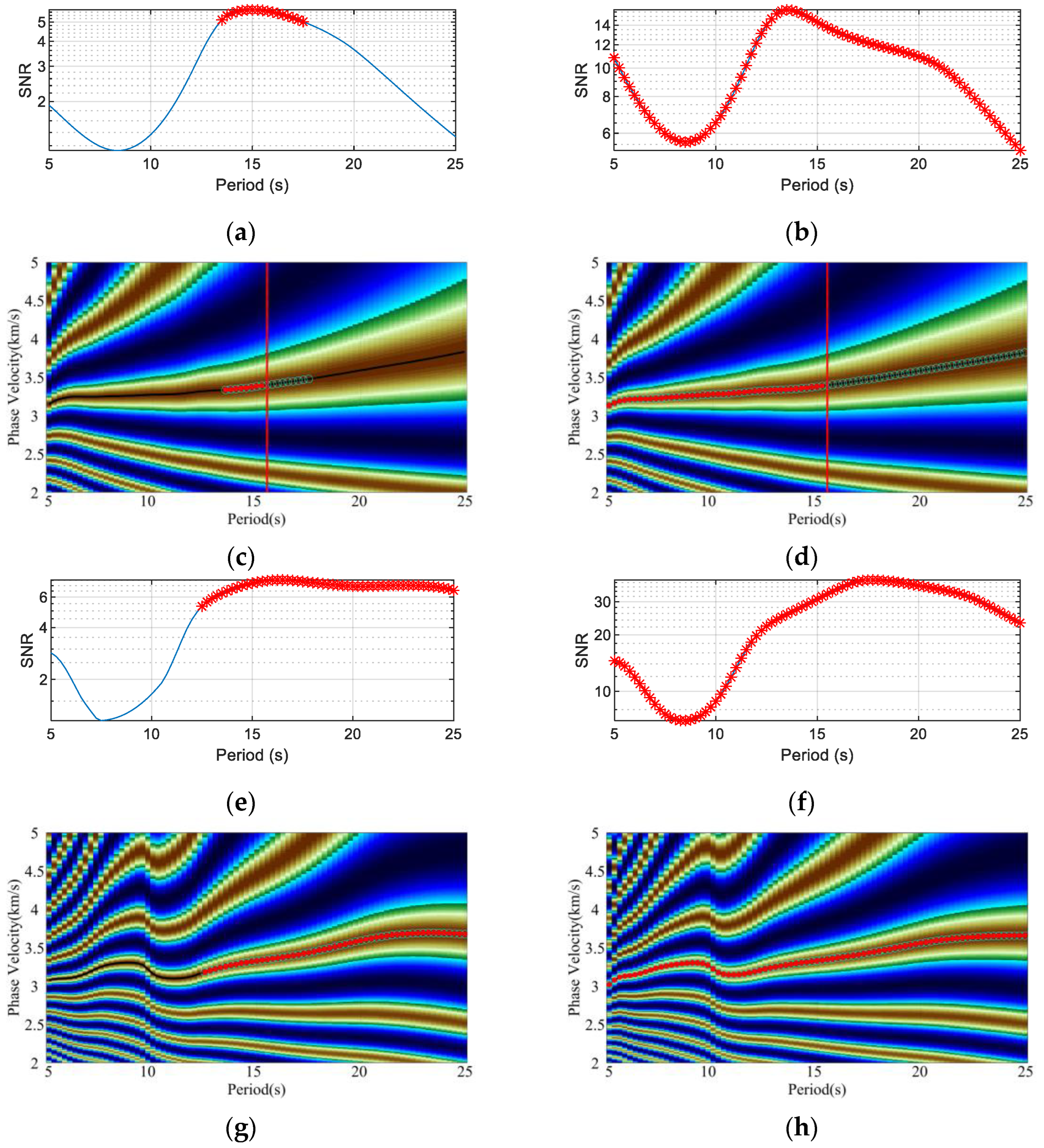These findings confirm the efficacy of the FLAPD method in improving data quality, thereby leading to more reliable and convergent velocity inversion results.

4. Discussion

4.1. Performance Advancement over Conventional Processing Workflows

A critical clarification is that the data termed as ‘raw’ in this study have already undergone the standard preprocessing sequence established by Bensen et al. [15], a benchmark in ambient noise tomography. Consequently, the enhancements from our FLAPD method are achieved as a supplementary step to this conventional foundation. As illustrated in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, FLAPD provides significant further improvement by effectively suppressing spurious components caused by source heterogeneity (Figure 3). This results in a marked enhancement of the coherent, V-shaped surface wave signals within the CCF gathers and directly translates to a higher SNR in the extracted EGFs (Figure 5). The impact on dispersion measurement is twofold: it increases not only the total number of usable dispersion curves but also the number of reliable phase-velocity picks per curve (Figure 6). This dual improvement substantially expands the quantity and quality of data for subsequent tomographic inversion, highlighting a key advantage over the conventional workflow alone.

4.2. Comparison with a Representative Multi-Scale Denoising Method

To further evaluate the performance of our method, we compare it with the Curvelet Transform, a typical multi-scale denoising technique. A visual comparison of the processed CCF gathers (Figure 3) indicates that FLAPD achieves more effective suppression of spurious noise while better preserving the integrity of the surface wave arrivals. In contrast, the Curvelet Transform shows limited denoising efficacy and, more critically, introduces apparent signal leakage in the noise profile (Figure 3c), suggesting unintended removal of coherent seismic energy. This visual assessment is corroborated by quantitative analysis. Specifically, we extracted 2103 valid dispersion curves from the Curvelet-denoised CCFs, a number lower than the 2196 curves obtained using FLAPD. Furthermore, a period-by-period comparison of reliable phase-velocity picks demonstrated that FLAPD yields a greater number of measurements across most of the period range, with the exception of the very shortest periods (1–5 s) (Supplementary Material Table S3). Together, these visual and quantitative results confirm that FLAPD provides a superior balance between noise attenuation and signal fidelity for processing ambient noise CCFs compared to the Curvelet Transform.

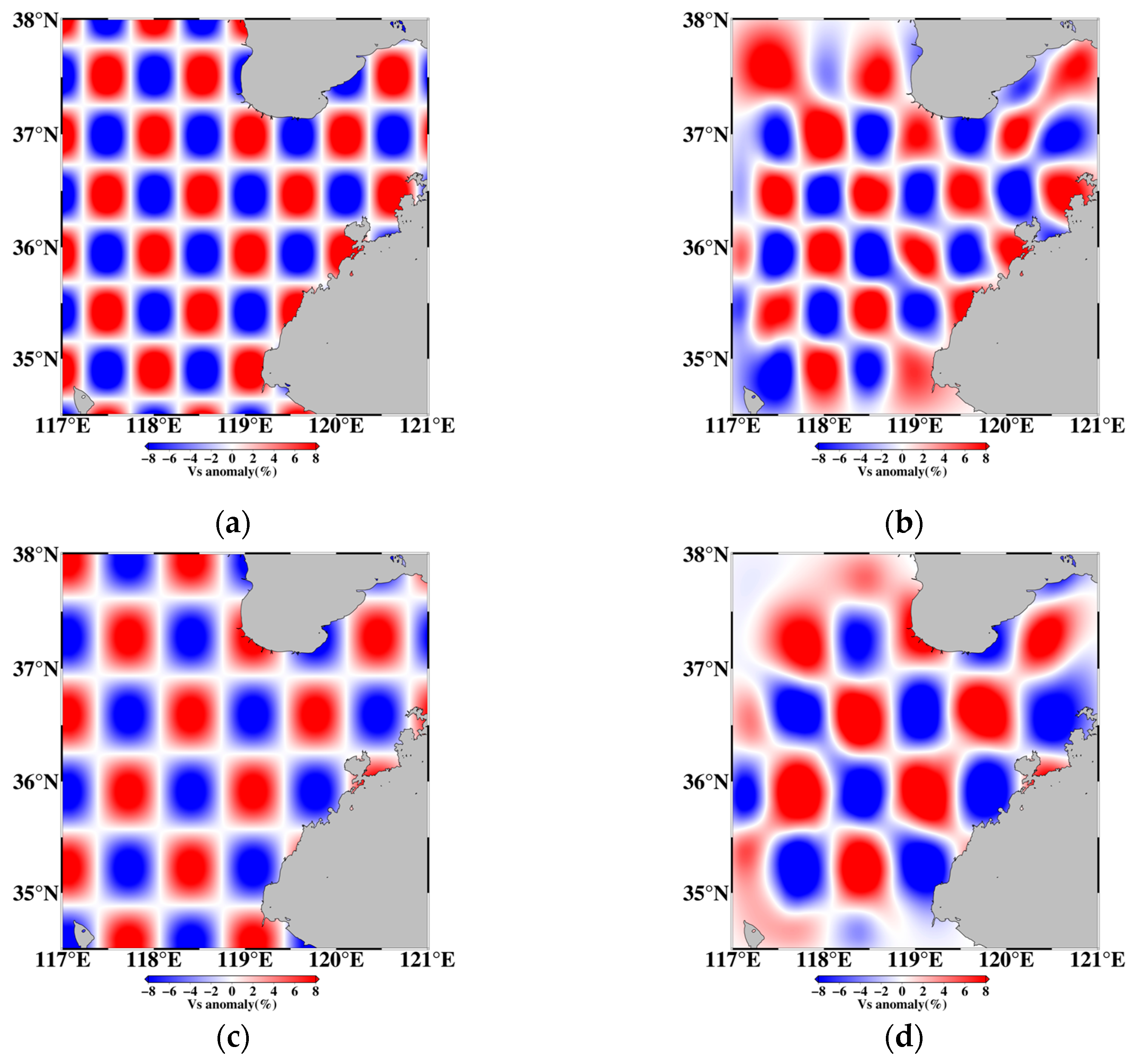
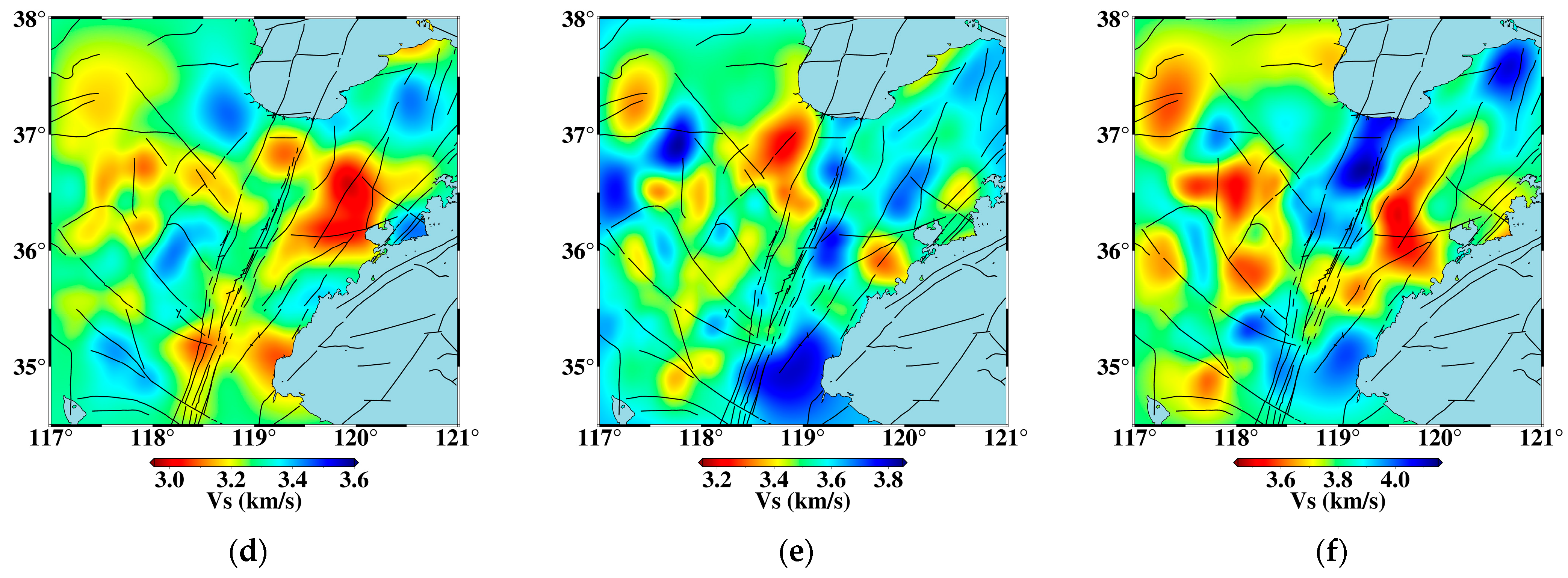
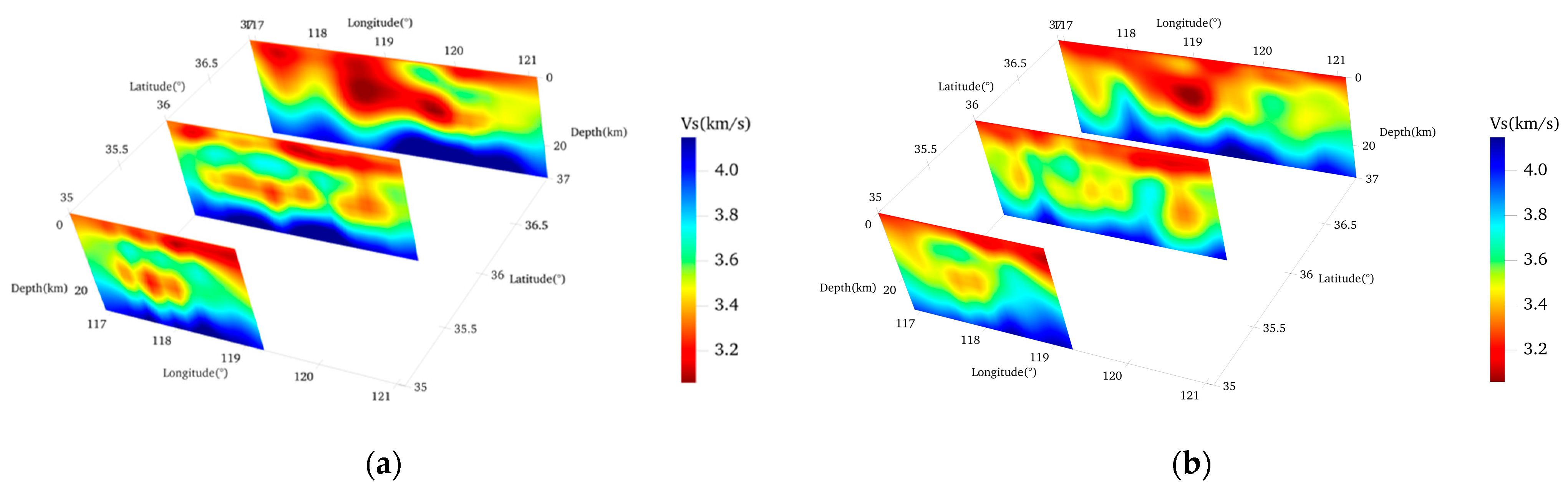
4.3. Comparative Analysis of Inversion Results Pre- and Post-FLAPD Processing

The ultimate validation of any denoising method in seismic imaging lies in the quality of the final inverted model. The improvements achieved by FLAPD during data preparation directly translate into superior inversion results. The Vs model derived from FLAPD-processed data exhibits enhanced structural resolution compared to the model from the raw data. As shown in the horizontal and vertical slices (Figure 9 and Figure 10), velocity anomalies, particularly those associated with the complex Yishu Fault Zone, appear more clearly defined and spatially continuous. The most compelling quantitative evidence comes from the analysis of traveltime residuals. The residual distribution from the FLAPD-based inversion is markedly tighter and more centered around zero, with the mean $\mathsf{\mu }$ reduced from 0.099 s to 0.014 s and the standard deviation $\mathsf{\sigma }$ from 0.418 s to 0.133 s (Figure 11). This significant reduction in both bias and variance unambiguously demonstrates that the phase-velocity measurements extracted from the denoised CCFs are more accurate and consistent. Consequently, the resulting velocity model provides a more reliable fit to the observed data.

4.4. Limitations of the Study

Despite its demonstrated effectiveness, the current implementation of the FLAPD method has certain limitations that present opportunities for future work. The primary consideration is computational efficiency. The iterative denoising process, which involves calculations with the fractional Laplacian mask and dual-domain (time–space and frequency) constraints, is more demanding than simpler, transform-based methods like the Curvelet Transform. Algorithmic optimizations and parallel computing strategies would be essential for large-scale applications or near-real-time processing. Secondly, this study relied solely on data from permanent stations. While the denoising process enriched the dataset from this network, the inherent limitations in spatial coverage remain. Deploying dense temporary arrays in key areas would complement the denoising effort and further improve the resolution of the inverted model.

5. Conclusions

In this study, we proposed a novel fractional Laplacian-based adaptive progressive denoising (FLAPD) method to address the challenge of spurious noise in ambient noise CCFs caused by spatially heterogeneous noise sources. Application to a dense seismic array in China’s Yishu Fault Zone supports the following key conclusions:

(1)

The FLAPD method substantially improves the signal-to-noise ratio of CCFs. By integrating a fractional Laplacian mask for multi-scale noise variance estimation and a fractional bilateral kernel for dual-domain iterative denoising, the method effectively suppresses spurious noise while ensuring the high-fidelity preservation of coherent surface wave signals. Comparative analysis verifies its superiority over the Curvelet Transform method in balancing noise attenuation and signal integrity.

(2)

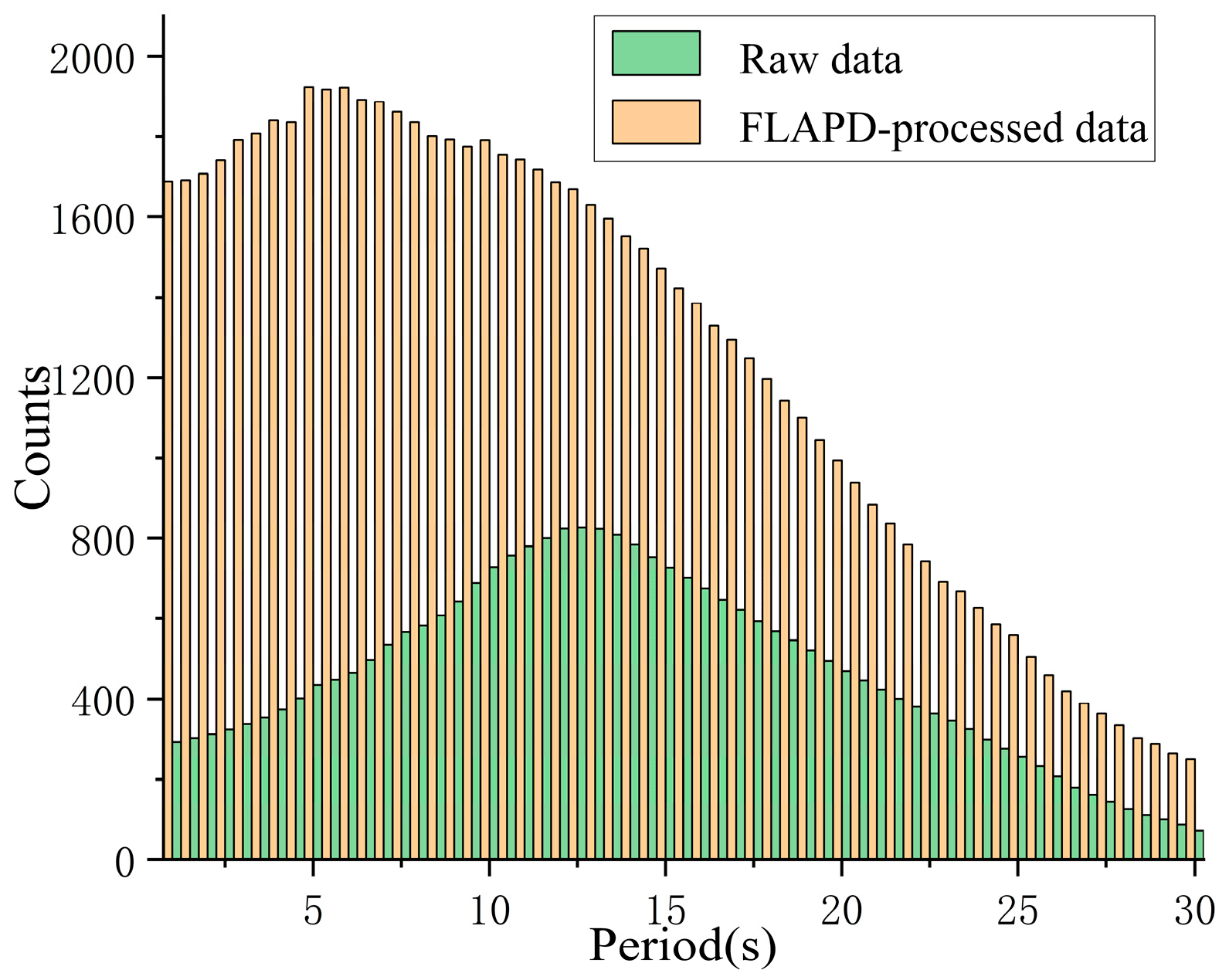
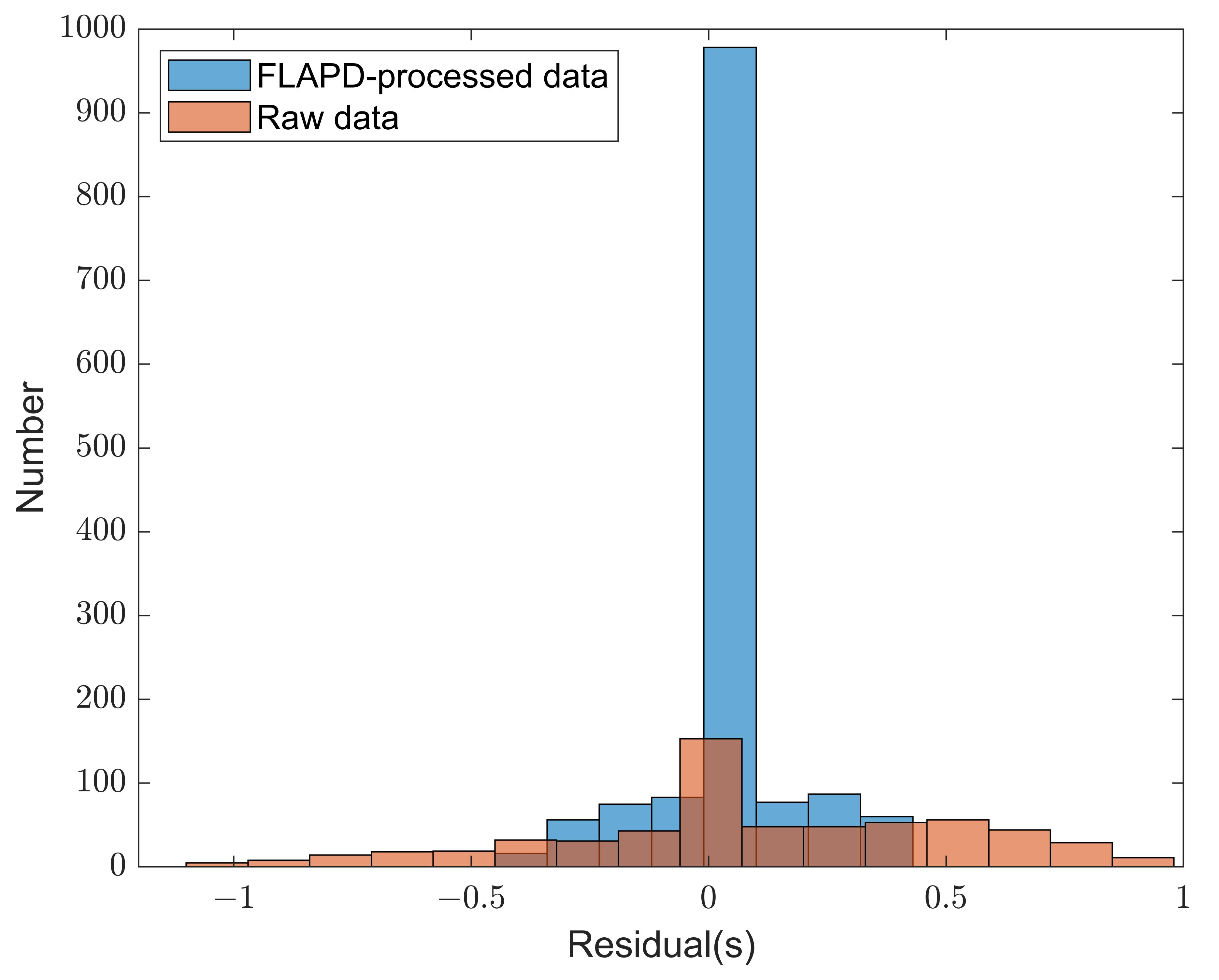
This denoising process greatly enhances the reliability of surface wave analysis. EGFs extracted from FLAPD-processed CCFs show a significantly higher SNR. Consequently, the number of usable dispersion measurements increased substantially, with an additional 1106 qualified EGFs, thereby expanding the spatial coverage and density of data available for tomographic inversion.

(3)

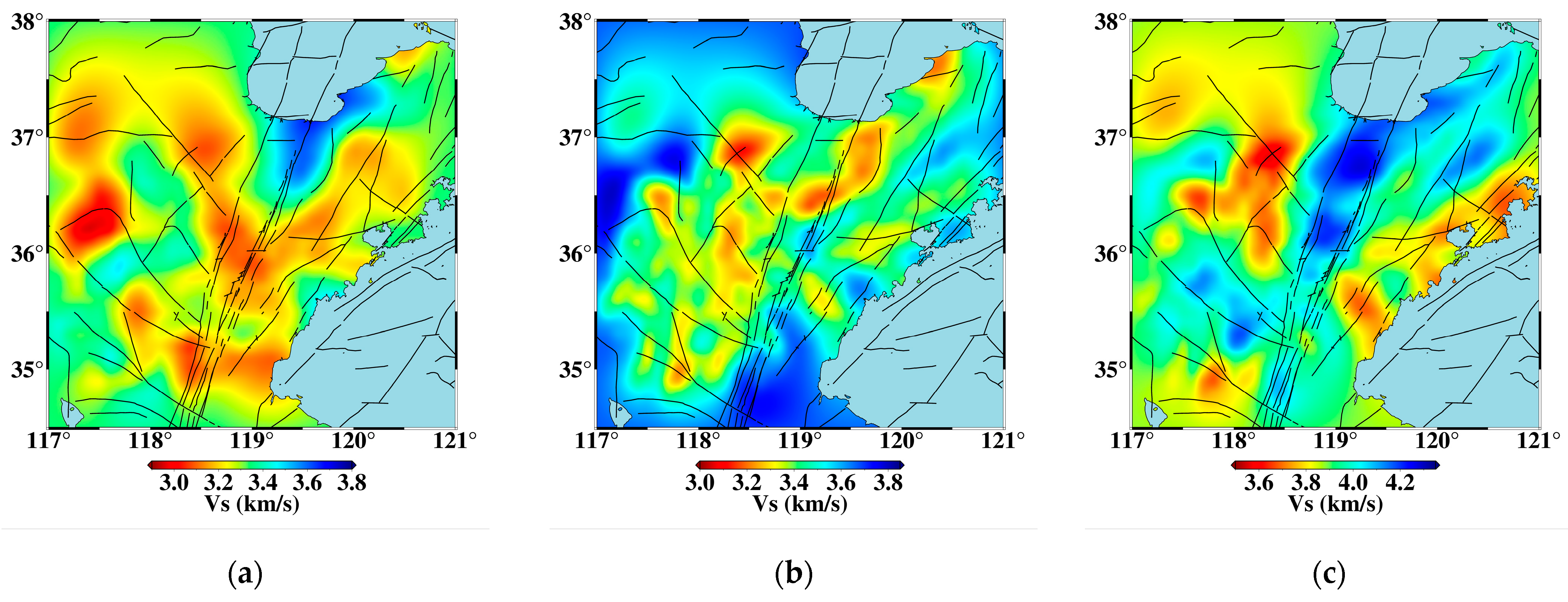
The enhancement in data quality enables the construction of a more reliable and higher-resolution 3D shear-wave velocity model. Tomographic inversion of the processed data yielded a Vs model with significantly reduced traveltime residuals. The resultant model reveals distinct velocity anomalies that correlate strongly with surface topography, fault structures, and seismicity patterns, providing new geophysical constraints on the differential tectonic processes within the Yishu Fault Zone.

In summary, the FLAPD method provides a robust solution for enhancing ambient noise CCFs. Its capability to improve both data quality and quantitative imaging outcomes renders it a valuable tool for passive seismic investigations, particularly in regions with complex noise source distributions.