Synchronization of Fractional-Order Reaction–Diffusion Neural Networks via ETILC

Abstract

This paper focuses on the synchronization of fractional-order reaction–diffusion neural networks (FORDNN) under sampling event-triggered iterative learning control. A ${\mathcal{D}}^{\alpha }$-type iterative learning protocol of complete synchronization is proposed, which combines the advantages of both event-triggered control and sampling iterative learning control. Using mathematical tools, sufficient conditions for synchronization are derived. A numerical simulation example is provided to confirm the effectiveness of the analysis.

1. Introduction

Neural networks (NNs) were first proposed in 1940 and an improved model was proposed by Hopfield in 1982 [1]. Numerous studies have demonstrated that NNs possess strong capabilities for nonlinear mapping, nonlinear learning, and parallel computation. Consequently, NNs have found applications in various fields. In recent years, the combination of factional calculus and NNs has received widespread attention.

Fractional derivatives have been proposed in many fields, such as fluid mechanics [2], biology [3], and others [4]. Due to the characteristics of fractional derivatives, fractional-order systems have certain advantages, particularly in terms of infinite memory. To study neuron dynamics, the concept of fractional order is introduced into the neural networks, forming the fractional-order neural networks (FONN). The importance of fractional-order calculus lies in two aspects. First, as [5,6] note, its integrals and derivatives can accurately describe neurons’ nonlinear responses and non-integer-order dynamics that integer-order calculus cannot fully capture. Second, as [7,8] confirm, adjusting the fractional order enables fine-grained characterization of neural networks’ dynamic behaviors (e.g., synchronization speed, stability).

As we have known, diffusion phenomenon of electrons in a nonuniform magnetic field cannot be neglected. Fractional differential operators possess memory and hereditary properties, enabling them to better describe non-local characteristics. As a result, fractional-order reaction–diffusion neural networks exhibit unique advantages. Since differential operators can more accurately capture the temporal dynamic characteristics between neurons, this allows FORDNNs to simulate the complex behaviors of biological neural systems. Some researchers have studied RDNN; Ref. [9] studied the exponential synchronization of fractional-order reaction–diffusion coupled neural networks. There are many different methods of synchronization, such as Mittag–Leffler synchronization [10,11], pinning synchronization [12], quasi-synchronization [9], and others [13,14,15].

In order to address synchronization issues, considering the high precision tracking characteristic of iterative learning, the method of iterative learning control is adopted to achieve the purpose of tracking synchronization. In Ref. [16] the D-type learning law was used to realize the RDNNs tracking synchronization. Ref. [17] studied the system parameters using neural networks and conducted research on iterative learning control. Ref. [18] studied a nonlinear unknown model, using neural networks as estimators to solve the system’s key parameters, and then applied an iterative learning control algorithm to achieve tracking objectives.

Event-triggered control (ETC), whose execution timing is entirely determined by the designed event-triggering conditions, can effectively reduce control resource consumption. It should be noted that although event-triggered control has broad application prospects, a major challenge in its design is avoiding the Zeno phenomenon. The Zeno phenomenon refers to the occurrence of an infinite number of events within an extremely short time, which prevents the system from effectively conserving network resources and may even lead to system collapse. Therefore, avoiding the Zeno phenomenon has become a primary principle in designing event-triggering conditions. Due to the advantage of event-triggered control in significantly reducing network resource consumption, the integration of event-triggered control into neural network research has attracted widespread attention from scholars. In Ref. [19], due to the bidirectional synchronization problem of multi-order fractional neural networks with time-varying delays, the authors proposed an event-triggered controller and analyzed its Zeno behavior. Ref. [20] studied the synchronization problem of neural networks with communication delays and introduced an event-triggering condition based on measurement errors and current sampled states. Ref. [21] explored the synchronization of coupled neural networks affected by cyber attacks, proposing an adaptive distributed dynamic event-triggered strategy with local random state information sampling. By introducing different dynamic variables for each node, this strategy dynamically adjusts the event-triggering threshold, effectively reducing data transmission load. Since iterative learning control (ILC) requires the use of computational data from previous iteration batches, event-triggered iterative learning control (ETILC) has also been extensively studied by many scholars [22,23,24,25]. Fractional-order differential operators have memory—they capture the continuous influence of past states on current dynamics (not just local instantaneous changes), enabling accurate modeling of non-local characteristics in real systems (e.g., neurotransmitter diffusion in brain neural circuits, chemical concentration propagation in industrial sensors). Adjusting the fractional order allows for finer description of complex dynamics (e.g., smaller orders for slow-response systems like furnace temperature control, larger orders for fast neuromorphic chip signal processing), and fractional calculus can simplify to integer-order in specific cases, expanding application flexibility. These advantages make FORDNN more suitable for simulating real neuronal time dynamics, driving scholarly research on its dynamics [26]. In this paper, a data sampling mechanism is employed to ensure that there exists a lower bound between two consecutive event-triggering instants, thereby avoiding the occurrence of the Zeno phenomenon.

The main novelties of this paper are highlighted as follows:

• Unlike the reference [16], conventional ILC for RDNN which updates controllers at all sampling points, our ETILC adds a sampling-based event-triggering condition only updating when error energy fails to decay, reducing controller updates while ensuring synchronization. ETILC precisely controls the update frequency of ILC inputs through triggering conditions, eliminating the need for additional redundant update operations. In essence, it shares the same design goal as ETC in that both achieve efficient saving of system resources and reduction in energy consumption by decreasing the amount of data transmission and the number of controller updates during the iteration process.
• This paper uses a fractional-order-type ILC, that is ${\mathcal{D}}^{\alpha }$-type iterative learning law, to achieve tracking synchronization for the FONNs with diffusion term model, in which different results exist [16,17].
• Different from [23] (ETILC for integer-order systems), our ETILC combines a Lyapunov-like function with the actuator–sensor network and integrates FORDNN’s fractional diffusion terms into an event-triggering condition, adapting to non-local spatial–temporal dynamics.

The remaining contents of this paper are as follows. In Section 2, the model description of FORDNN is introduced. In Section 3, the event-triggering condition is given and the convergence of tracking synchronization errors is analyzed. A numerical simulation example demonstrates the effectiveness of the analysis in Section 4.

Notation 1. 

$\mathbb{N}$ be the set of natural numbers. ${\mathbb{R}}^n$ and ${\mathbb{C}}^n$ represent the n-dimensional real vector space and n-dimensional complex vector space, respectively. Let $a=a^R+\iota a^I$, where ι represents the imaginary unit, i.e., ι=$\sqrt{-1}$$. \mathrm{\otimes }$ denotes the Kronecker product between two matrices. ’T’ is the superscript and represented the transposition of the matrix. If G is a real matrix, $\parallel G\parallel =\sqrt{{\lambda }_{\max }\left(G^{\mathrm{T}}G\right)}$, where ${\lambda }_{\max }(·)$ denotes the maximum eigenvalue. $I_N$ represent the $N\times N$ identity matrix. $\Omega =\{\zeta =({\zeta }_1,{\zeta }_2,\cdots ,{\zeta }_n)\in {\mathbb{R}}^n,|{\zeta }_k|<H,k=1,2,\cdots ,n\}$ is a bounded domain with a smooth boundary $\partial \Omega$. Suppose $G(\zeta ,t)={[G_1(\zeta ,t),G_2(\zeta ,t),\cdots ,G_n(\zeta ,t)]}^{\mathrm{T}}\in {\mathbb{R}}^n$, then the definition of $L^2$ norm is ${\parallel G(·,t)\parallel }_{L^2}^2={\int }_{\Omega }G{(\zeta ,t)}^{\mathrm{T}}G(\zeta ,t)\mathrm{d}\zeta$. And ($L^2,\lambda$) norm is defined as ${\parallel G\parallel }_{(L^2,\lambda )}^2=\underset{0⩽t⩽T}{sup}{\{\parallel G(·,t)\parallel }_{L_2}^2{e}^{-\lambda t}\}(\lambda >0)$. For discrete time t, ${\parallel G\parallel }_{(L^2,\lambda )}^2=\underset{0⩽t⩽N}{sup}{\{\parallel G(·,t)\parallel }_{L_2}^2{e}^{-\lambda t}\}(\lambda >0)$. 

2. Preliminaries

2.1. Fractional-Order Calculus

First, some useful definitions and lemmas are introduced as follows.

Definition 1 

([27]). The definition of fractional integral is described by

$${{}_{t_0}I}_t^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_{t_0}^t{(t-\tau )}^{\alpha -1}f\left(\tau \right)d\tau ,\alpha >0,$$

where the gamma function $\mathrm{\Gamma }\left(\alpha \right)={\int }_0^{+\infty }{(t-s)}^{\alpha -1}{e}^{-s}ds$.

Definition 2 

([27]). The Caputo fractional derivative with fractional-order α is defined as

$${{}_{t_0}{}^C\mathcal{D}}_t^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(k-\alpha )}}{\int }_{t_0}^t{(t-s)}^{k-\alpha -1}{f}^{\left(k\right)}\left(s\right)ds,$$

where $t⩾t_0,\alpha \in (k-1,k), k$ is a positive integer, especially, if $\alpha \in (0,1)$,

$${{}_{t_0}{}^C\mathcal{D}}_t^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\int }_{t_0}^t{(t-s)}^{-\alpha }{f}^{\prime }\left(s\right)ds.$$

Definition 3 

([27]). Define the two-parameter Mittag–Leffler function as

$$E_{i,j}\left(t\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{t^k}{\mathrm{\Gamma }(ik+j)}},i>0,j>0,$$

where t is a complex value; the Mittag–Leffler function is defined as

$$E_{i,1}\left(t\right)=E_i\left(t\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{t^k}{\mathrm{\Gamma }(ik+1)}},i>0.$$

Remark 1. 

Our study exclusively uses the Caputo fractional derivative. This choice is suitable. First, the Caputo derivative only requires integer-order initial conditions, which have clear biological engineering meaning; second, its time-decaying weight aligns with real neuronal memory—recent inputs exert stronger influence on current states than distant ones, matching the dynamic behavior of biological neurons.

Lemma 1 

([27]). According to the definition of Caputo fractional derivative, when $0<\alpha ⩽1$,

$${{}_{t_0}I}_t^{\alpha }{{}_{t_0}{}^C\mathcal{D}}_t^{\alpha }\left(A\left(t\right)\right)=A\left(t\right)-A\left(t_0\right).$$

Lemma 2 

([28]). For differentiable vector $A\left(t\right)\in {\mathbb{R}}^n$, when $t⩾t_0$ the following relation holds

$${{}_{t_0}{}^C\mathcal{D}}_t^{\alpha }\left(A{\left(t\right)}^{\mathrm{T}}PA\left(t\right)\right)⩽2A{\left(t\right)}^{\mathrm{T}}P{{}_{t_0}{}^C\mathrm{d}}_t^{\alpha }A\left(t\right).$$

Lemma 3 

([29]). For $0⩽t_0⩽t⩽T$, non-negative non-decreasing function $a\left(t\right)$, non-negative non-decreasing continuous function $g\left(t\right)$, non-negative integrable function $u\left(t\right)$ satisfy

$$\begin{array}{cc}\hfill u\left(t\right)& ⩽a\left(t\right)+g\left(t\right){\int }_{t_0}^t{(t-s)}^{\alpha -1}u\left(s\right)\mathrm{d}s\hfill \\ & ⩽a\left(t\right)E_{\alpha }\left(g\left(t\right)\mathrm{\Gamma }\left(\alpha \right)t^{\alpha }\right).\hfill \end{array}$$

2.2. Graph Theory

Let $\mathcal{G}=\{\mathcal{V},\mathcal{A},\mathcal{G}\}$ be a directed graph, wherein $\mathcal{V}=\{1,2,\dots ,N\}$ is the set of nodes, edge set $\mathcal{A}=\left\{\right(i,j):i,j\in \mathcal{V}\}\subseteq \mathcal{V}\times \mathcal{V}$ and $\mathcal{G}={\left[G_{i,j}\right]}_{N\times N}$ is the adjacent matrix which means that if exists $(i,j)\mathcal{A}$, then $G_{ij}=1$, otherwise $G_{ij}=0$; one thing to note is $G_{ii}$ is defined as 0. The Laplacian matrix $L={\left[l_{ij}\right]}_{N\times N}$ is defined as $l_{ij}=-G_{ij}(i\ne j)$ and $l_{ii}=-{\sum }_{j=1}^N{l}_{ij}$. If a graph has an initial node passing through a directed path to other nodes, then the graph is a spanning tree.

2.3. FORDNN Model

Consider a coupled network composed of N identical FORDNNs operating repeatedly, with its communication topology described by the Laplacian matrix L. After incorporating the control input and system output, the mathematical model of the system is expressed as

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}{z}_{i,k}(\zeta ,t)& =D{\displaystyle \frac{{\partial }^2}{\partial {\zeta }^2}}{z}_{i,k}(\zeta ,t)-A{z}_{i,k}(\zeta ,t)+Bf\left(z_{i,k}(\zeta ,t)\right)+c\sum _{j=1}^N{L}_{ij}\Phi z_{j,k}(\zeta ,t)\hfill \\ \hfill & +o(\zeta ;{\zeta }^a)u_{i,k}\left(t\right)+J,\hfill \\ \hfill y_{i,k}\left(t\right)& ={\int }_{\Omega }g(\zeta ;{\zeta }^s)z_{i,k}(\zeta ,t)\mathrm{d}\zeta .\hfill \end{array}\hfill \end{array}\right.$$

(1)

where i is the number of nodes in the network and $k\in \mathbb{N}$ represents the number of iterations. $\zeta ={({\zeta }_1,{\zeta }_2,\cdots ,{\zeta }_p)}^{\mathrm{T}}\in \Omega$ denotes the spatial variable, $\Omega$ is bounded smooth open set with boundary $\partial \Omega$. $z(\zeta ,t)={[z_1(\zeta ,t),z_2(\zeta ,t),\cdots ,z_n(\zeta ,t)]}^{\mathrm{T}}\in {\mathbb{R}}^n$ represent the state of the neurons on the i-th node. $t\in [0,T]$ is a fixed time interval. $D,A\in {\mathbb{R}}^{n\times n}$ are positive definite matrices representing the transmission diffusion matrix along the i-th node and self-feedback matrix, respectively. $B={\left(b_{ij}\right)}_{n\times n}\in {\mathbb{R}}^{n\times n}$ is the connect weight matrix of the j-th neuron on the i-th node. $L={\left(L_{ij}\right)}_{N\times N}$ denotes the Laplacian matrix. $\Phi \in {\mathbb{R}}^{n\times n}$ is a positive definite matrix, denotes the inner coupling matrix. $c>0$ is overall coupling strength. $J\in {\mathbb{R}}^n$ is an external input. $u\left(t\right)\in {\mathbb{R}}^n$ is the control input. $o(\zeta ,{\zeta }^a)$ is a spatial distribution function. $f(·)$ denote the activation function.

The boundary condition and initial condition of (1) are given as follows:

$$\begin{array}{cc}\hfill & z_{i,k}(\zeta ,t)=0,(\zeta ,t)\in \partial \Omega \times [0,T],\hfill \\ \hfill & z_{i,k}(\zeta ,0)=z_0\left(\zeta \right).\hfill \end{array}$$

where $z_0\left(\zeta \right)$ denotes the initial activity state of neurons at each spatial point.

Using the Kronecker product to extend the dimension of (1), one obtains

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}{z}_k(\zeta ,t)& =(I_N\otimes D){\displaystyle \frac{{\partial }^2}{\partial {\zeta }^2}}{z}_k(\zeta ,t)-(I_N\otimes A)z_k(\zeta ,t)+(I_N\otimes B)f\left(z_k(\zeta ,t)\right)\hfill \\ \hfill & +c(L\otimes \Phi )z_k(\zeta ,t)+(I_N\otimes o(\zeta ;{\zeta }^a)I_n)u_k\left(t\right)+1_N\otimes J,\hfill \\ \hfill y_k\left(t\right)& ={\int }_{\Omega }[I_N\otimes g(\zeta ;{\zeta }^s)I_n]z_k(\zeta ,t)\mathrm{d}\zeta .\hfill \end{array}\hfill \end{array}\right.$$

(2)

where $z_k(·,·)={[z_{1,k}^{\mathrm{T}},z_{2,k}^{\mathrm{T}},\cdots ,z_{N,k}^{\mathrm{T}}]}^{\mathrm{T}},u_k(·)={[u_{1,k}^{\mathrm{T}},u_{2,k}^{\mathrm{T}},\cdots ,u_{N,k}^{\mathrm{T}}]}^{\mathrm{T}}$, $y_k(·)={[y_{1,k}^{\mathrm{T}},y_{2,k}^{\mathrm{T}},\cdots ,y_{N,k}^{\mathrm{T}}]}^{\mathrm{T}}$.

Assumption 1. 

$f(·)$ satisfy the Lipschitz condition. For any $x_i\in {\mathbb{R}}^n$ exists a positive constant $l_f>0$ that satisfy $\parallel f\left(x_1\right)-f\left(x_2\right)\parallel ⩽l_f\parallel x_1-x_2\parallel$.

Assumption 2. 

The FORDNN is the ideal model without time delay.

2.4. Synchronization of FORDNN with Iteration

Assumption 3. 

The output vector $y_{i,k}\left(t\right)$ of the NNs model (1) is defined as (see [30])

$$y_{i,k}\left(t\right)={\int }_{\Omega }g(\zeta ;{\zeta }^s)z_{i,k}(\zeta ,t)d\zeta ,$$

(3)

where $g(\zeta ;{\zeta }^s)$ is a spatial distribution function. The spatial distributions of $o(\zeta ;{\zeta }^a)$ and $g(\zeta ;{\zeta }^s)$ satisfy

$$\begin{array}{cc}& o(\zeta ,{\zeta }^a)=\gamma ,\zeta \in [0,H],\hfill \\ & g(\zeta ,{\zeta }^s)=\beta ,\zeta \in [0,H],\hfill \end{array}$$

where $\gamma ,\beta >0$. H denotes the upper limit of the operating range for both the actuator and sensor.

Assumption 4. 

There exists a unique control input $u_d\left(t\right)$ and desired state $z_d(\zeta ,t)$ for the desired output $y_d\left(t\right)$, which satisfy the following:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}{z}_d(\zeta ,t)& =D{\displaystyle \frac{{\partial }^2}{\partial {\zeta }^2}}{z}_d(\zeta ,t)-A{z}_d(\zeta ,t)+Bf\left(z_d(\zeta ,t)\right)+c\sum _{j=1}^N{L}_{ij}\Phi z_d(\zeta ,t)\hfill \\ \hfill & +J+o(\zeta ,{\zeta }^a)u_d\left(t\right),\hfill \\ \hfill y_d\left(t\right)& ={\int }_{\Omega }g(\zeta ,{\zeta }^s)z_d(\zeta ,t)d\zeta .\hfill \end{array}\hfill \end{array}\right.$$

(4)

The control objective is to achieve tracking synchronization of fractional-order reaction–diffusion neural networks using an event-triggered sampled-data iterative learning control approach. First, Equation (4) is discretized in time with W sampling intervals, where the sampling period is h, and $t=nh$ denotes the n-th sampling instant. To achieve state synchronization at the sampling points, it is required that the synchronization error converge to zero as the iteration number k approaches infinity, i.e.,

$$\underset{k\to \infty }{lim}{\parallel z_{i,k}(·,t)-z_{j,k}(·,t)\parallel }_{L^2}^2=0,t=nh,n=0,1,2,\cdots ,N.$$

(5)

3. Main Result

3.1. Event-Triggering Condition

For the event-triggered sampling iterative learning control problem of the neural network system (1), this section designs the event-triggered strategy using a Lyapunov-like energy function approach. The proposed strategy ensures the decay property of the energy function along the iteration axis. At the sampling points, the following Lyapunov energy function is constructed:

$$V_{i,k}\left(nh\right)={\parallel e_{i,k}\left(nh\right)\parallel }^2,$$

(6)

where $e_k(·)=y_k(·)-yd(·)$. Due to the decay property of the Lyapunov energy function, a relaxation factor can be introduced to make the event-triggered frequency controllable. Based on the above description, the following event-triggering function is proposed.

$$E_{i,k}\left(nh\right)=V_{i,k}\left(nh\right)-ϵV_{i,k-1}\left(nh\right),ϵ\in [0,1].$$

(7)

It should be noted that when $ϵ=0$, due to the non-negativity of the norm, $E_k⩾0$ holds, causing the controller to update iteratively at all sampling points. This corresponds to the traditional iterative learning control method.

According to the event-triggering function (7), it can be observed that when $E_k⩾0$, the energy decay property is not satisfied. Consequently, at the occurrence of the $k+1$-th iteration, the control input at this sampling point will be updated. Conversely, when $E_k<0$, it indicates that the output error at the sampling point continues to decay even without updating the control input, making an update unnecessary. Based on the above analysis, the event-triggering sequence can be formally defined as follows:

$$k_{r+1}^v=inf\{k+1|k+1>k_r^v,E_{i,k}\left(vh\right)⩾0\}.$$

(8)

3.2. Controller Design

Combining the definition of the Caputo fractional derivative, this paper employs a $D^{\alpha }$-type iterative learning control algorithm, with the controller structure designed as follows:

$$u_{i,k+1}\left(nh\right)=u_{i,k}\left(nh\right)+\Lambda \sum _{j=1}^N[L_{ij}{\mathcal{D}}_t^{\alpha }(y_{j,k}\left(nh\right)-y_{i,k}\left(nh\right))+p_i{\mathcal{D}}_t^{\alpha }(y_{i,k}\left(nh\right)-y_d\left(nh\right))].$$

(9)

Conventional ILC for neural networks mostly uses P-type (proportional to error) or D-type (proportional to error derivative) laws, which are designed for full-space state feedback. However, our discrete finite-point actuator–sensor network cannot provide full-space state information—thus, we developed the iterative learning protocol (9) tailored to it. This protocol only relies on the discrete state signals collected by the sensor network and the control output of the discrete actuator network, realizing effective synchronization control while adapting to the discrete characteristics of the actuator–sensor network.

Due to the characteristics of sampling iterative learning control, the control input is held constant between sampling instants using a zero-order hold mechanism.

$$u_{i,k}\left(t\right)=u_{i,k}\left(nh\right),t\in [nh,(n+1)h).$$

(10)

Considering the characteristics of event-triggered sampled-data iterative learning control, the control input updates only when the event-triggering conditions are satisfied; otherwise, it maintains the control input from the last triggering instant. Based on this analysis and incorporating Equations (9) and (10), the controller can be designed as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill u_{i,k+1}\left(nh\right)& =u_{i,k}\left(nh\right)+\Lambda [\sum _{j=1}^N{L}_{ij}{\mathcal{D}}_t^{\alpha }(y_{j,k}\left(nh\right)-y_{i,k}\left(nh\right))\hfill \\ \hfill & +p_i{\mathcal{D}}_t^{\alpha }(y_{i,k}\left(nh\right)-y_d\left(nh\right))],k=k_r^n,\hfill \\ \hfill u_{i,k+1}\left(nh\right)& =u_{i,k}\left(nh\right),k\in (k_r^n,k_{r+1}^n),\hfill \\ \hfill u_{i,k}\left(t\right)& =u_{i,k}\left(nh\right),t\in [nh,(n+1)h),\hfill \end{array}\hfill \end{array}\right.$$

(11)

where $\Lambda$ is the gain matrix. The notation $k_{r+1}^n$ represents the $r+1$-th triggered iteration batch at the n-th sampling point, while $k\in (k_r^n,k_{r+1}^n)$ indicates the current iteration batch remains non-triggered.

3.3. Convergence Analysis

3.3.1. Initial State Fixed FORDNN Model

Theorem 1. 

For the FORDNN (1) if Assumptions 1–4 are satisfied and the iterative learning control algorithm (11) is applied. When the learning gain meets

$$(1+{\displaystyle \frac{1}{2\xi }}){\parallel I_{Nn}+(L+K)\otimes \Lambda \gamma \beta H\parallel }^2<1,$$

(12)

where constant $\xi >0$, then the synchronization error at the sampling points converges to zero in the sense of the $L^2$ norm as the iteration batch k tends to infinity.

Proof. 

Define

$$\begin{array}{cc}\hfill & \delta z_k(\zeta ,t)\triangleq z_k(\zeta ,t)-z_d(\zeta ,t),\delta u_k\left(t\right)\triangleq u_k\left(t\right)-u_d\left(t\right),\hfill \\ \hfill & e_k\left(t\right)\triangleq y_k\left(t\right)-y_d\left(t\right),f\left(\delta z_k(\zeta ,t)\right)\triangleq f\left(z_k(\zeta ,t)\right)-f\left(z_d(\zeta ,t)\right).\hfill \end{array}$$

(13)

For event-triggered batch $\left\{k_r\right\}$, arbitrary sampling interval $t\in \left[\right(n-1)h,nh)$ is considered. According to (2) and (13), one has

$$\begin{array}{cc}\hfill {\mathcal{D}}_t^{\alpha }\delta z_k(\zeta ,t)& =(I_N\otimes D){\displaystyle \frac{{\partial }^2}{\partial {\zeta }^2}}\delta z_k(\zeta ,t)-(I_N\otimes A)\delta z_k(\zeta ,t)+(I_N\otimes B)f\left(\delta z_k(\zeta ,t)\right)\hfill \\ \hfill & +c(L\otimes \Phi )\delta z_k(\zeta ,t)+(I_N\otimes o(\zeta ;{\zeta }^a)I_n)\delta u_k\left(t\right),\hfill \end{array}$$

(14)

According to Lemma 2, one obtains

$$\begin{array}{c}{{}_{t_0}{}^C\mathcal{D}}_t^{\alpha }\left(\delta {z_k}^{\mathrm{T}}(\zeta ,t)\delta z_k(\zeta ,t)\right)\hfill \\ ⩽2\delta {z_k}^{\mathrm{T}}(\zeta ,t)[(I_N\otimes D){\displaystyle \frac{{\partial }^2}{\partial {\zeta }^2}}\delta z_k(\zeta ,t)-(I_N\otimes A)\delta z_k(\zeta ,t)+(I_N\otimes B)f\left(\delta z_k(\zeta ,t)\right)\hfill \\ +c(L\otimes \Phi )\delta z_k(\zeta ,t)+(I_N\otimes o(\zeta ;{\zeta }^a)I_n)\delta u_k\left(t\right)].\hfill \end{array}$$

(15)

Based on the definition of $L^2$ norm, integrating about $\zeta$ in $\Omega$ on both sides (15),

$$\begin{array}{c}{{}_{t_0}{}^C\mathcal{D}}_t^{\alpha }{\parallel \delta z_k(·,t)\parallel }_{L^2}^2\hfill \\ ⩽2{\int }_{\Omega }\delta {z_k}^{\mathrm{T}}(\zeta ,t)[(I_N\otimes D){\displaystyle \frac{{\partial }^2}{\partial {\zeta }^2}}\delta z_k(\zeta ,t)-(I_N\otimes A)\delta z_k(\zeta ,t)+(I_N\otimes B)f\left(\delta z_k(\zeta ,t)\right)\hfill \\ +c(L\otimes \Phi )\delta z_k(\zeta ,t)+(I_N\otimes o(\zeta ;{\zeta }^a)I_n)\delta u_k\left(t\right)]\mathrm{d}\zeta \hfill \\ \triangleq Q_1+Q_2+Q_3+Q_4+Q_5.\hfill \end{array}$$

(16)

For $Q_1$, using Green’s formula and boundary condition, one gets

$$\begin{array}{cc}\hfill Q_1& ={\int }_{\Omega }\delta {z_k}^{\mathrm{T}}(\zeta ,t)(I_N\otimes D){\displaystyle \frac{{\partial }^2}{\partial {\zeta }^2}}{z}_k(\zeta ,t)\mathrm{d}\zeta \hfill \\ & ={\int }_{\partial \Omega }\delta {z_k}^{\mathrm{T}}(I_N\otimes D){\displaystyle \frac{\partial }{\partial \overrightarrow{v}}}{z}_k(\zeta ,t)\mathrm{d}S-{\int }_{\Omega }{\displaystyle \frac{\partial }{\partial \zeta }}\delta {z_k}^{\mathrm{T}}(\zeta ,t)(I_N\otimes D){\displaystyle \frac{\partial }{\partial \zeta }}\delta z_k(\zeta ,t)\mathrm{d}\zeta ⩽0.\hfill \end{array}$$

where $\overrightarrow{v}$ represents the outward normal vector on the boundary $\partial \Omega$, and $\mathrm{d}S$ denotes the infinitesimal surface element for integration over $\partial \Omega$. For $Q_5$, by applying the Cauchy–Schwarz inequality and fundamental inequalities, one obtains

$$\begin{array}{cc}\hfill Q_5& ={\int }_{\Omega }\delta {z_k}^{\mathrm{T}}(\zeta ,t)(I_N\otimes o(\zeta ,{\zeta }^a)I_n)\delta u_k\left(t\right)\mathrm{d}\zeta \hfill \\ & ⩽{\int }_{\Omega }{\delta z_k}^{\mathrm{T}}(\zeta ,t)\delta z_k(\zeta ,t)\mathrm{d}{\zeta }^{{\displaystyle \frac{1}{2}}}{\int }_{\Omega }{\left[(I_N\otimes o(\zeta ,{\zeta }^a)I_n)\delta u_k\left(t\right)\right]}^{\mathrm{T}}(I_N\otimes o(\zeta ,{\zeta }^a)I_n)\delta u_k\left(t\right)\mathrm{d}{\zeta }^{{\displaystyle \frac{1}{2}}}\hfill \\ & ⩽{\displaystyle \frac{1}{2}}{\int }_{\Omega }{\delta z_k}^{\mathrm{T}}(\zeta ,t)\delta z_k(\zeta ,t)\mathrm{d}\zeta +{\displaystyle \frac{1}{2}}{\beta }^{2}H\delta {u_k}^{\mathrm{T}}\left(t\right)\delta u_k\left(t\right)\hfill \\ & ⩽{\displaystyle \frac{1}{2}}\parallel \delta z_k{(·,t)\parallel }_{L^2}^2+{\displaystyle \frac{1}{2}}{\beta }^{2}H{\parallel \delta u_k\left(t\right)\parallel }^2.\hfill \end{array}$$

Using the same method for $Q_2,Q_3,Q_4$, from (16), we have

$$\begin{array}{cc}\hfill & {{}_{t_0}{}^C\mathcal{D}}_t^{\alpha }\parallel \delta z_k{(·,t)\parallel }_{L^2}^2⩽(\parallel I_N{\otimes A\parallel }^2+{\parallel I_N\otimes B\parallel }^2+l_f\hfill \\ \hfill & +{\parallel 2c(L\otimes \Phi )\parallel }^2+2)\parallel \delta z_k{(·,t)\parallel }_{L^2}^2+H{\beta }^2\parallel \delta u_k{\left(t\right)\parallel }^2\triangleq \nu (\parallel \delta z_k{(·,t)\parallel }_{L^2}^2)+\psi (\parallel \delta u_k\left(t\right){\parallel }^2),\hfill \end{array}$$

(17)

where $\nu =\parallel I_N{\otimes A\parallel }^2+\parallel I_N{\otimes B\parallel }^2+l_f+{\parallel 2c(L\otimes \Phi )\parallel }^2+2$, $\psi =H{\beta }^2$. With the definition of fractional order integrating, one gets

$$\begin{array}{cc}\hfill {{}_{(n-1)h}I}_{nh}^{\alpha }{\mathcal{D}}_t^{\alpha }(\parallel \delta z_k(·,t){\parallel }_{L^2}^2)& ⩽{\displaystyle \frac{\nu }{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_{(n-1)h}^{nh}{(nh-\tau )}^{\alpha -1}(\parallel \delta z_k(·,\tau ){\parallel }_{L^2}^2)\mathrm{d}\tau \hfill \\ \hfill & +{\displaystyle \frac{\psi }{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_{(n-1)h}^{nh}{(nh-\tau )}^{\alpha -1}{\parallel \delta u_k\left(\tau \right)\parallel }^2\mathrm{d}\tau .\hfill \end{array}$$

(18)

According to Lemma 3, one obtains

$$\begin{array}{cc}\hfill \parallel \delta z_k{(·,nh)\parallel }_{L^2}^2& ⩽\parallel \delta z_k{(·,(n-1)h)\parallel }_{L^2}^2+{\displaystyle \frac{\psi h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)\alpha }}(\parallel \delta u_k\left((n-1)h\right){\parallel }^2)\hfill \\ & +{\displaystyle \frac{\nu }{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_{(n-1)h}^{nh}{(nh-\tau )}^{\alpha -1}(\parallel \delta z_k(·,\tau ){\parallel }_{L^2}^2)\mathrm{d}\tau \hfill \\ \hfill & ⩽[\parallel \delta z_k{(·,(n-1)h)\parallel }_{L^2}^2+{\displaystyle \frac{\psi h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)\alpha }}(\parallel \delta u_k{\left((n-1)h\right)\parallel }^2\left)\right]E_{\alpha }({\displaystyle \frac{\nu }{\mathrm{\Gamma }\left(\alpha \right)}}\mathrm{\Gamma }\left(\alpha \right)t^{\alpha })\hfill \\ \hfill & \triangleq \kappa (\parallel \delta z_k{(·,(n-1)h)\parallel }_{L^2}^2)+\omega (\parallel \delta u_k\left((n-1)h\right){\parallel }^2),\hfill \end{array}$$

where $\kappa =E_{\alpha }\left(\nu t^{\alpha }\right),\omega =E_{\alpha }\left(\nu t^{\alpha }\right){\displaystyle \frac{\psi h^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)\alpha }}$, one has

$$\begin{array}{c}\hfill \parallel \delta z_k{(·,nh)\parallel }_{L^2}^2⩽{\kappa }^n(\parallel \delta z_k{(·,0)\parallel }_{L^2}^2+\omega \sum _{l=0}^{n-1}{\kappa }^{n-1-l}(\parallel \delta u_k\left(lh\right)).\end{array}$$

(19)

Noting the definition of $\delta u_{k+1}$ with Kronecker product at triggering time,

$$\delta u_{k+1}\left(nh\right)=\delta u_k\left(nh\right)+(L+K)\otimes \Lambda {\mathcal{D}}_t^{\alpha }{e}_k\left(nh\right).$$

(20)

When estimating the value of ${\mathcal{D}}_t^{\alpha }{e}_k\left(nh\right)$,

$$\begin{array}{cc}\hfill & {\mathcal{D}}_t^{\alpha }{e}_k\left(nh\right)\hfill \\ \hfill & ={\int }_{\Omega }g(\zeta ;{\zeta }^s){\mathcal{D}}_t^{\alpha }\delta z_k(\zeta ,nh)\mathrm{d}\zeta \hfill \\ \hfill & ={\int }_{\Omega }g(\zeta ;{\zeta }^s)[(I_N\otimes D){\displaystyle \frac{{\partial }^2}{\partial {\zeta }^2}}\delta z_k(\zeta ,nh)-(I_N\otimes A)\delta z_k(\zeta ,nh)+(I_N\otimes B)f\left(\delta z_k(\zeta ,nh)\right)\hfill \\ \hfill & +c(L\otimes \Phi )\delta z_k(\zeta ,nh)+(I_N\otimes o(\zeta ;{\zeta }^a)I_n)\delta u_k\left(nh\right)]\mathrm{d}\zeta .\hfill \end{array}$$

(21)

According boundary condition, one has

$${\int }_{\Omega }g(\zeta ;{\zeta }^s)(I_N\otimes D){\displaystyle \frac{{\partial }^2}{\partial {\zeta }^2}}\delta z_k\mathrm{d}\zeta =0.$$

Noting the definition of $g(\zeta ;{\zeta }^s)$ and $o(\zeta ;{\zeta }^a)$, we can obtain

$${\int }_{\Omega }(I_N\otimes g(\zeta ;{\zeta }^s)o(\zeta ;{\zeta }^a)I_n)\delta u_k\left(nh\right)\mathrm{d}\zeta =\gamma \beta H\delta u_k\left(nh\right).$$

Let ${\int }_{\Omega }g(\zeta ;{\zeta }^s)[-(I_N\otimes A)\delta z_k(\zeta ,nh)+(I_N\otimes B)f\left(\delta z_k(\zeta ,nh)\right)+c(L\otimes \Phi )\delta z_k(\zeta ,nh)]\mathrm{d}\zeta ={\tilde{e}}_k\left(nh\right)$; one gets

$$\begin{array}{c}\hfill \delta u_{k+1}\left(nh\right)=\delta u_k\left(nh\right)+(L+K)\otimes \Lambda \gamma \beta H\delta u_k\left(nh\right)+[(L+K)\otimes \Lambda {\tilde{e}}_k\left(nh\right)].\end{array}$$

Let $(L+K)\Lambda {\tilde{e}}_k\left(nh\right)={\widehat{z}}_k$, where based on Young’s inequality,

$$\begin{array}{c}\hfill \parallel \delta u_{k+1}{(nh)\parallel }^2⩽(1+{\displaystyle \frac{1}{2\xi }}){\parallel (I_{Nn}+(L+K)\otimes \Lambda \gamma \beta H)\delta u_k\left(nh\right)\parallel }^2+(1+{\displaystyle \frac{\xi }{2}}){\widehat{z}}_k^T{\widehat{z}}_k.\end{array}$$

(22)

Estimating ${\widehat{z}}_k^{\mathrm{T}}{\widehat{z}}_k$ using Jensen’s inequality,

$$\begin{array}{cc}\hfill {\widehat{z}}_k^{\mathrm{T}}{\widehat{z}}_k& ⩽3{\lambda }_{\Lambda }\{{[{\int }_{\Omega }g(\zeta ;{\zeta }^s)(I_N\otimes A)\delta z_k(\zeta ,nh)\mathrm{d}\zeta ]}^{\mathrm{T}}·[{\int }_{\Omega }g(\zeta ;{\zeta }^s)(I_N\otimes A)\delta z_k(\zeta ,nh)\mathrm{d}\zeta ]\hfill \\ & +{[{\int }_{\Omega }g(\zeta ;{\zeta }^s)(I_N\otimes B)f\left(\delta z_k(\zeta ,nh)\right)\mathrm{d}\zeta ]}^{\mathrm{T}}·[{\int }_{\Omega }g(\zeta ;{\zeta }^s)(I_N\otimes B)f\left(\delta z_k(\zeta ,nh)\right)\mathrm{d}\zeta ]\hfill \\ & +{[{\int }_{\Omega }g(\zeta ;{\zeta }^s)c(L\otimes \Phi )\delta z_k(\zeta ,nh)\mathrm{d}\zeta ]}^{\mathrm{T}}·[{\int }_{\Omega }g(\zeta ;{\zeta }^s)c(L\otimes \Phi )\delta z_k(\zeta ,nh)\mathrm{d}\zeta ]\}\hfill \\ & \triangleq X_1+X_2+X_3,\hfill \end{array}$$

where ${\lambda }_{\Lambda }={\parallel (L+K)\otimes \Lambda \parallel }^2$. When estimating $X_1$ by using Cauchy–Schwarz inequality,

$$\begin{array}{cc}& {\int }_{\Omega }{I}_{Nn}\otimes g(\zeta ;{\zeta }^s)A\delta z_k(\zeta ,nh)\mathrm{d}\zeta \hfill \\ & ⩽{\int }_{\Omega }{[I_{Nn}\otimes g(\zeta ;{\zeta }^s)A]}^{\mathrm{T}}[I_{Nn}\otimes g(\zeta ;{\zeta }^s)A]\mathrm{d}{\zeta }^{{\displaystyle \frac{1}{2}}}·{\int }_{\Omega }\delta {z_k}^{\mathrm{T}}(\zeta ,nh)\delta z_k(\zeta ,nh)\mathrm{d}{\zeta }^{{\displaystyle \frac{1}{2}}}\hfill \\ & ⩽H^{{\displaystyle \frac{1}{2}}}\parallel I_N\otimes \gamma A\parallel \parallel \delta z_k{(·,nh)\parallel }_{L^2}.\hfill \end{array}$$

Utilizing the same method for $X_2,X_3$, to obtain

$$\begin{array}{cc}\hfill {\widehat{z}}_k^{\mathrm{T}}{\widehat{z}}_k& ⩽3{\lambda }_{\Lambda }(H\parallel I_N{\otimes \gamma A\parallel }^2+H{l}_f\parallel I_N{\otimes \gamma B\parallel }^2{+H\parallel L\otimes c\Phi \parallel }^2)\parallel \delta z_k{(·,nh)\parallel }_{L^2}^2\hfill \\ \hfill & \triangleq \eta \parallel \delta z_k{(·,nh)\parallel }_{L^2}^2.\hfill \end{array}$$

(23)

Multiply both sides of (19) by ${\kappa }^{-\lambda n}$, according to the initial value condition and the definition of $\lambda$ norm, one obtains

$$\parallel \delta z_k{\parallel }_{(L^2,\lambda )}^2⩽\omega {\displaystyle \frac{{\kappa }^{(-\lambda -1)n}-1}{\kappa -{\kappa }^{\lambda }}}(\parallel \delta u_k{\parallel }_{\lambda }^2).$$

(24)

When substituting (24) into (23) and multiplying ${\kappa }^{-\lambda n}$ on both sides (22), one can obtain

$$\begin{array}{c}\hfill \parallel \delta u_{k+1}{\parallel }_{\lambda }^2⩽({\lambda }_{\Lambda }+\eta \omega {\displaystyle \frac{{\kappa }^{(-\lambda -1)n}-1}{\kappa -{\kappa }^{\lambda }}})(\parallel \delta u_k{\parallel }_{\lambda }^2),\end{array}$$

(25)

where ${\lambda }_{\Lambda }=(1+{\displaystyle \frac{1}{2\xi }}){\parallel I_{Nn}+(L+K)\otimes \Lambda \gamma \beta H\parallel }^2$. According to the properties of the Mittag–Leffler function, $\kappa >1$. When choosing a $\lambda$ that is sufficiently large, combining the conditions in Theorem 1 with the contraction-mapping principle, one has

$$\underset{k\to \infty }{lim}{\parallel \delta u_k\left(nh\right)\parallel }^2=0.$$

According to the relationship between $\delta u_k$ and $\delta z_k$ in (19),

$$\underset{k\to \infty }{lim}{\parallel \delta z_k(·,nh)\parallel }_{L^2}^2=0.$$

Noting the definition of synchronization error,

$$\begin{array}{cc}& \parallel z_{i,k}(·,nh)-z_{j,k}{(·,nh)\parallel }_{L^2}^2\hfill \\ & ⩽\parallel z_{i,k}(·,nh)-z_d(·,nh)-\delta z_{j,k}(·,nh)+z_d{(·,nh)\parallel }_{L^2}^2\hfill \\ & ⩽\parallel \delta z_{i,k}{(·,nh)\parallel }_{L^2}^2+{\parallel \delta z_{j,k}(·,nh)\parallel }_{L^2}^2=0.\hfill \end{array}$$

The proof of Theorem 1 is completed. □

3.3.2. Initial State Offset FORDNN Model

Theorem 1 proves the convergence of the synchronization error in FORDNN under fixed initial-state values. However, in many practical scenarios, the initial values of the system are not fixed. Therefore, this subsection considers the following iterative learning control algorithm with initial-state learning.

$$\left\{\begin{array}{c}{u}_{i,k+1}\left(nh\right)=u_{i,k}\left(nh\right)+\Lambda [\sum _{j\in \mathcal{V}}{L}_{ij}{\mathcal{D}}_t^{\alpha }(y_{j,k}\left(nh\right)-y_{i,k}\left(nh\right))+p_i{\mathcal{D}}_t^{\alpha }(y_{i,k}\left(nh\right)-y_{\mathrm{d}}\left(nh\right))],k=k_r^n,\hfill \\ u_{i,k+1}\left(nh\right)=u_{i,k}\left(nh\right),k\in (k_r^n,k_{r+1}^n),\hfill \\ u_{i,k}\left(t\right)=u_{i,k}\left(nh\right),t\in [nh,(n+1)h),\hfill \\ z_{i,k+1}(\zeta ,0)=z_{i,k}(\zeta ,0)+{\Lambda }_1{e}_{i,k}\left(0\right),\hfill \end{array}\right.$$

(26)

where ${\Lambda }_1$ is the initial-state learning gain. Different from (11), it increases the initial value learning.

Theorem 2. 

For the FORDNN (1) under Assumptions 1–4, the iterative learning control algorithm (27) is applied, if the learning gain meets

$$\left\{\begin{array}{c}\begin{array}{c}(1+{\displaystyle \frac{1}{2\xi }}){\parallel I_{Nn}+(L+K)\otimes \Lambda \gamma \beta H\parallel }^2<1,\hfill \\ \parallel I+\gamma H{\Lambda }_1{\parallel }^2<1.\hfill \end{array}\hfill \end{array}\right.$$

(27)

where constant $\xi >0$, ${\Lambda }_1$ is the initial value learning gain. Then, the synchronization error at the sampling points converges to zero in the sense of the $L^2$ norm as the iteration batch k tends to infinity.

Proof. 

When $t=0$, one has

$$y_{k+1}\left(0\right)-y_k\left(0\right)={\int }_{\Omega }g(\zeta ;{\zeta }^s)[z_{k+1}(\zeta ,0)-z_k(\zeta ,0)]\mathrm{d}\zeta .$$

Noting $y_{k+1}\left(0\right)-y_k\left(0\right)=e_{k+1}\left(0\right)-e_k\left(0\right)$, one has

$${\int }_{\Omega }g(\zeta ;{\zeta }^s)[z_{k+1}(\zeta ,0)-z_k(\zeta ,0)]\mathrm{d}\zeta =e_{k+1}\left(0\right)-e_k\left(0\right).$$

(28)

Substituting (26) into (28), one obtains

$$\begin{array}{cc}\hfill e_{k+1}\left(0\right)-e_k\left(0\right)=& {\int }_{\Omega }g(\zeta ;{\zeta }^s){\Lambda }_1{e}_k\left(0\right)\mathrm{d}\zeta \hfill \\ \hfill =& \gamma H{\Lambda }_1{e}_k\left(0\right)\hfill \\ \hfill e_{k+1}\left(0\right)=& (I+\gamma H{\Lambda }_1)e_k\left(0\right).\hfill \end{array}$$

(29)

Taking the norm on both sides of (29),

$$\begin{array}{cc}\hfill \parallel e_{k+1}{\left(0\right)\parallel }^2& =\parallel (I+\gamma H{\Lambda }_1)e_k\left(0\right){\parallel }^2\hfill \\ \hfill & ⩽\parallel I+\gamma H{\Lambda }_1{\parallel }^2{\parallel e_k\left(0\right)\parallel }^2.\hfill \end{array}$$

(30)

According to (27), one obtains $\underset{k\to \infty }{lim}{\parallel \delta z_k(·,0)\parallel }_{L^2}^2=0$. Similarly as Theorem 1, one has

$$\begin{array}{cc}\hfill \parallel \delta u_{k+1}{\parallel }_{\lambda }^2& ⩽({\lambda }_{\Lambda }+\eta \omega {\displaystyle \frac{{\kappa }^{(-\lambda -1)n}-1}{\kappa -{\kappa }^{\lambda }}})\parallel \delta u_k{\parallel }_{\lambda }^2+{\kappa }^{-\lambda n}{\kappa }^n{\parallel \delta z_k(·,0)\parallel }_{L^2}^2\hfill \\ \hfill & ⩽({\lambda }_{\Lambda }+\eta \omega {\displaystyle \frac{{\kappa }^{(-\lambda -1)n}-1}{\kappa -{\kappa }^{\lambda }}}){\parallel \delta u_k\parallel }_{\lambda }^2.\hfill \end{array}$$

(31)

Again, according to (27), we can obtain that

$$\underset{k\to \infty }{lim}{\parallel \delta u_k\left(nh\right)\parallel }^2=0.$$

Correspondingly,

$$\underset{k\to \infty }{lim}{\parallel \delta z_k(·,nh)\parallel }_{L^2}^2=0.$$

(32)

The proof of Theorem 2 is completed. □

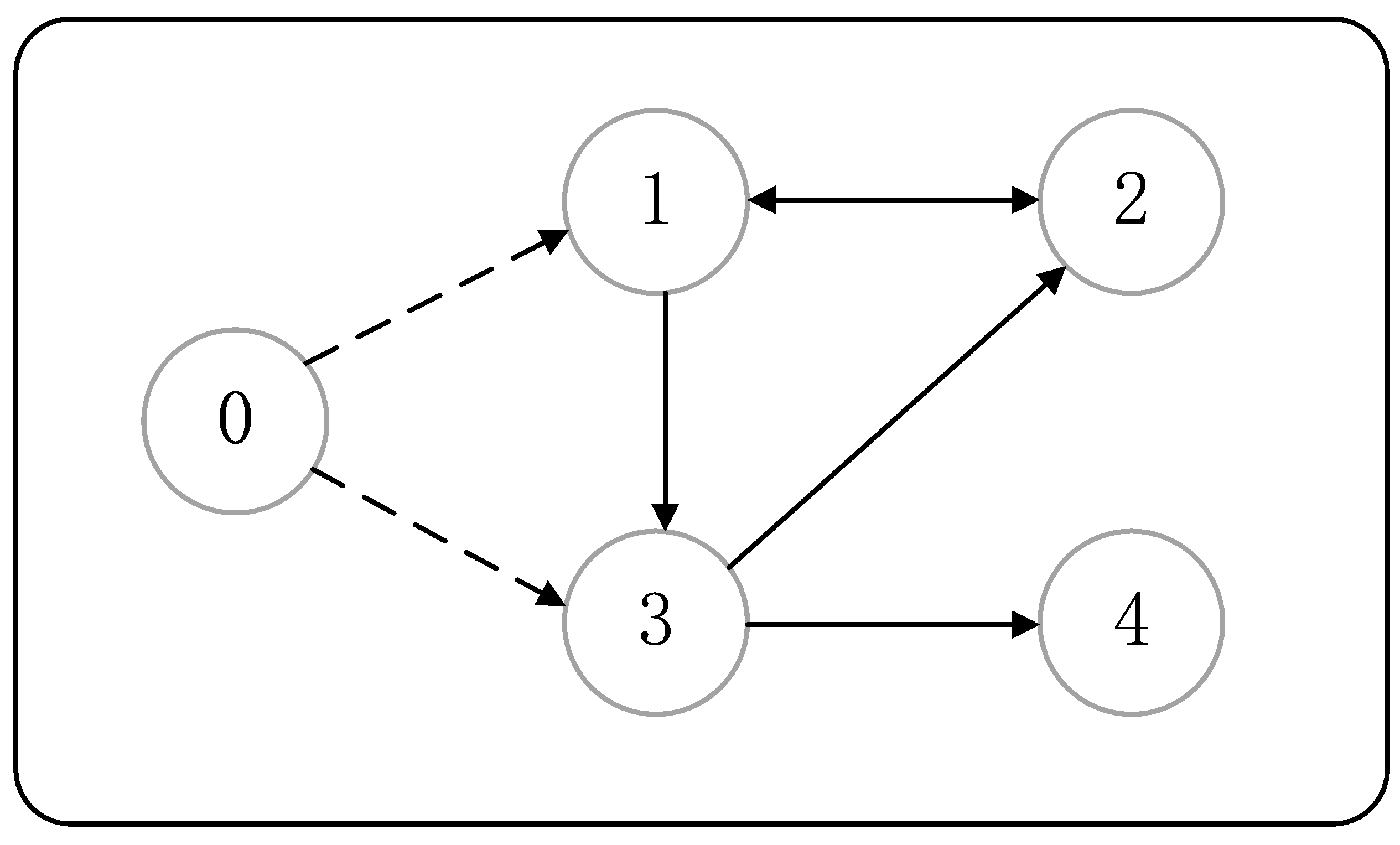
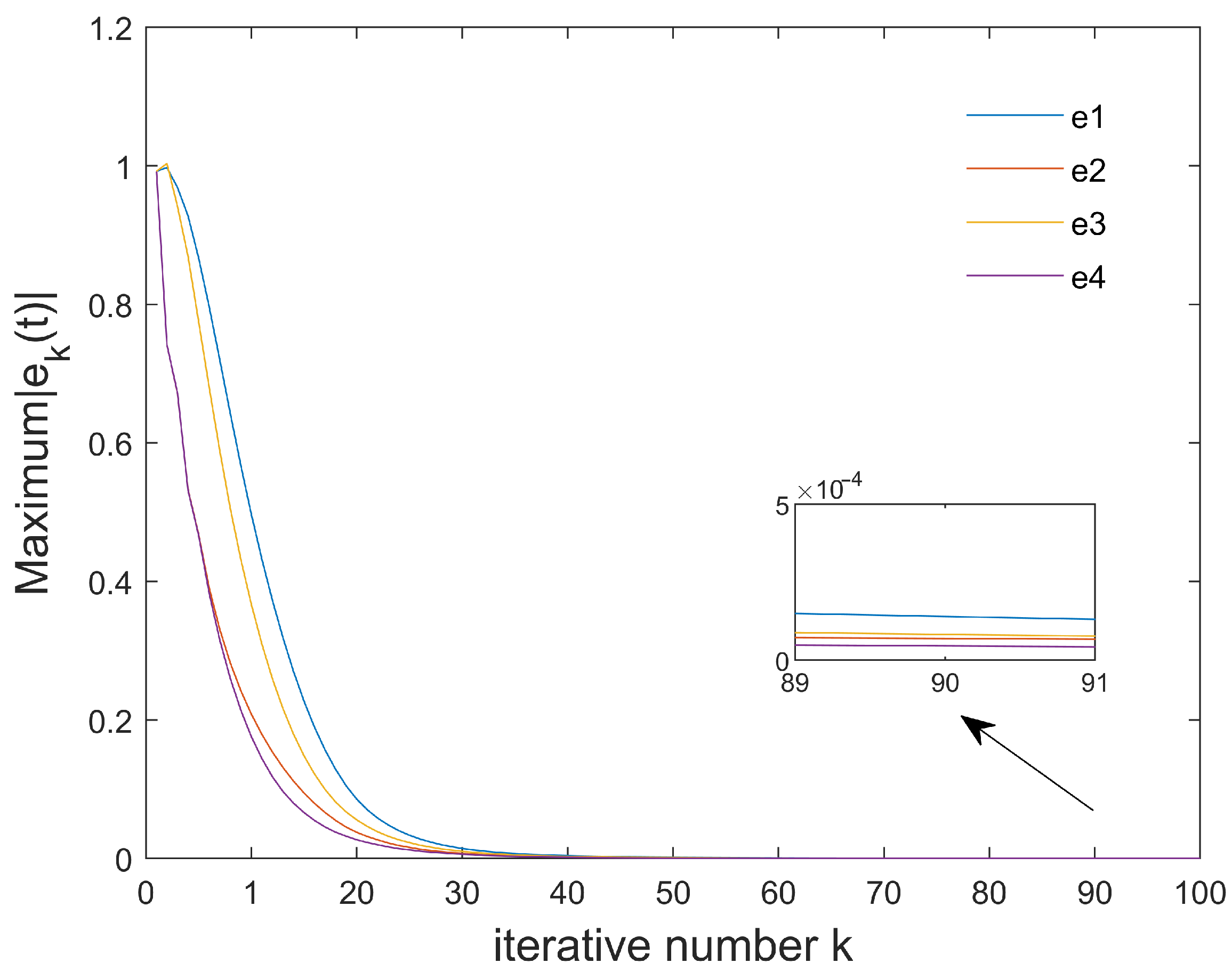
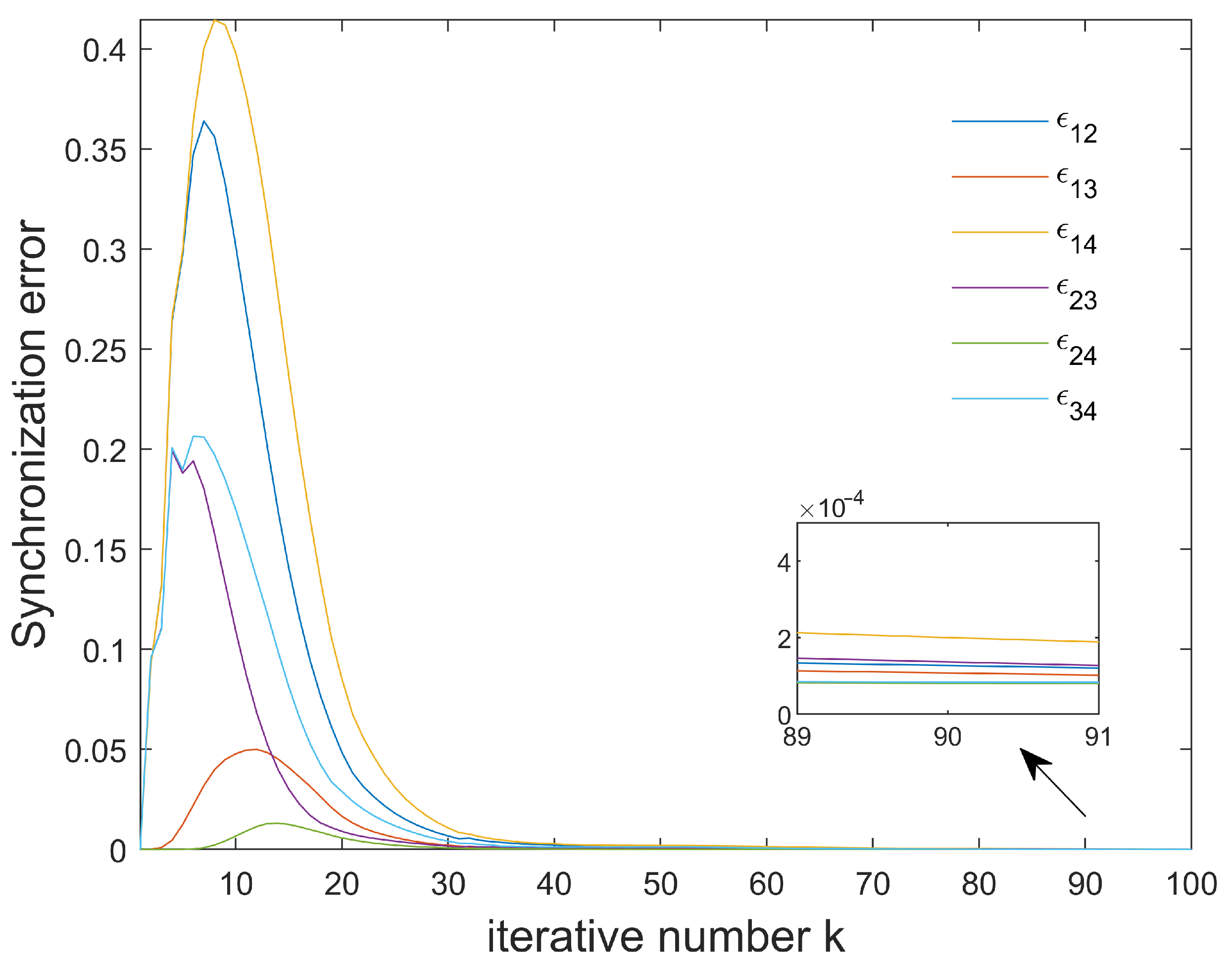
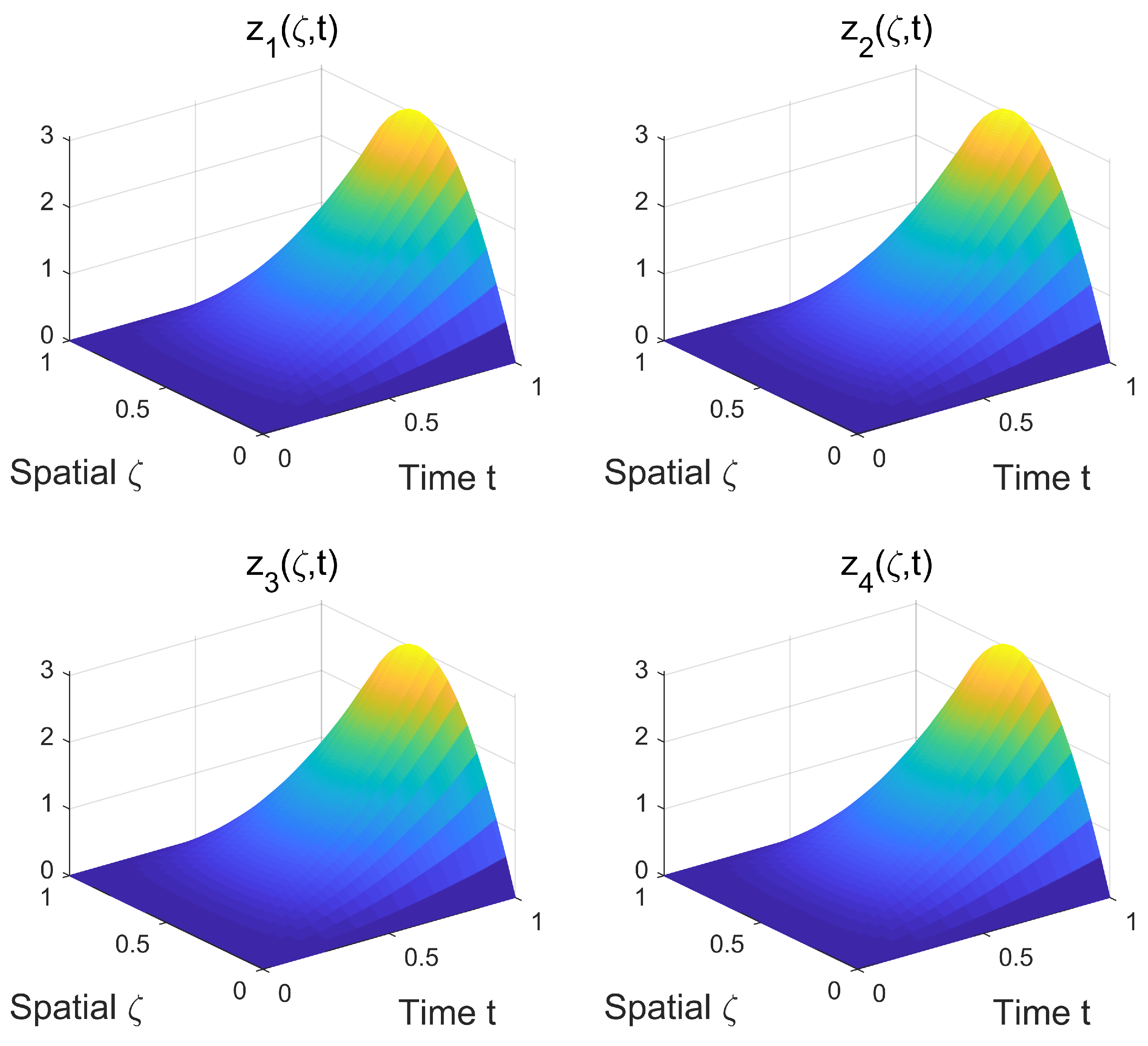
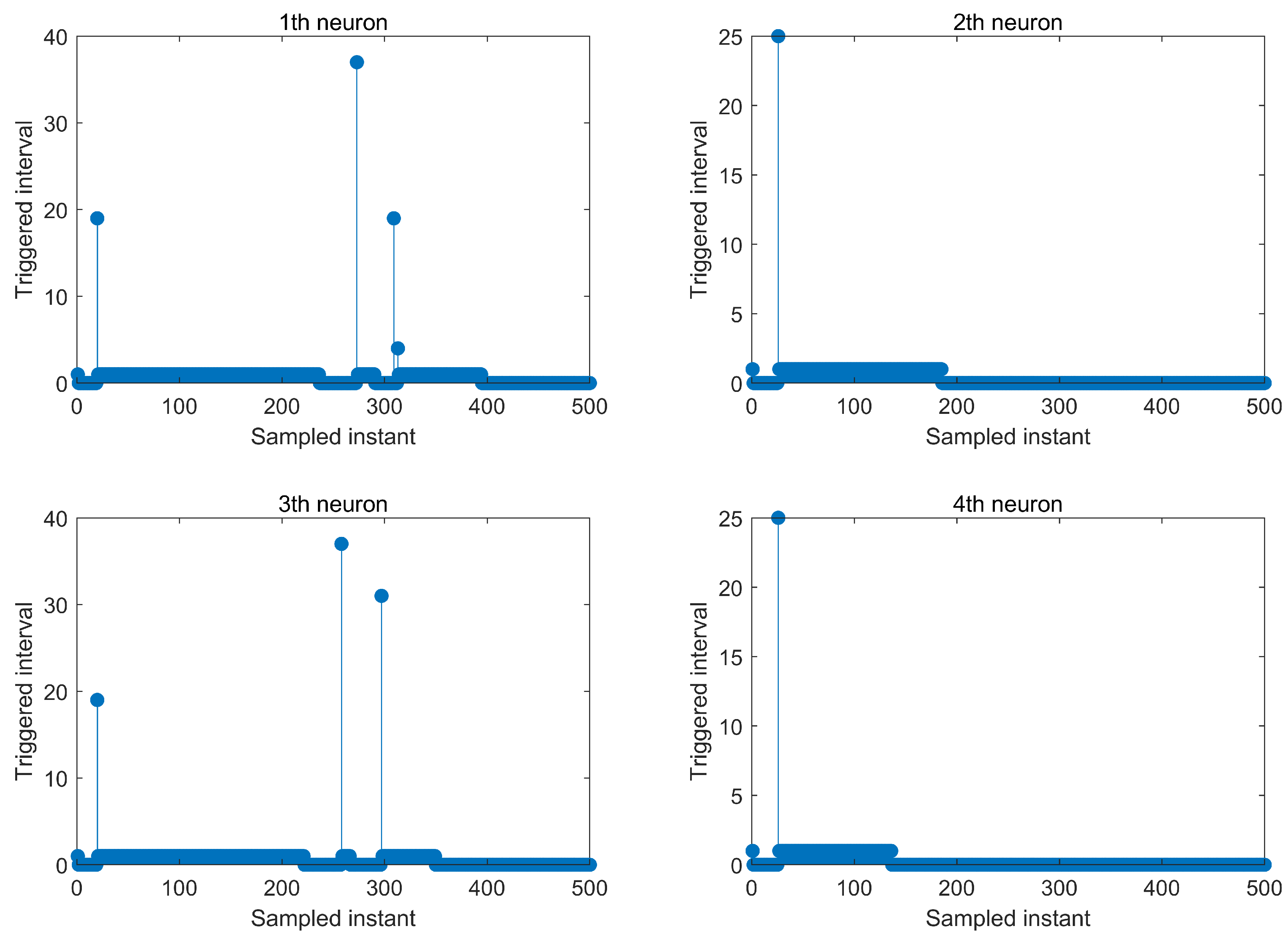
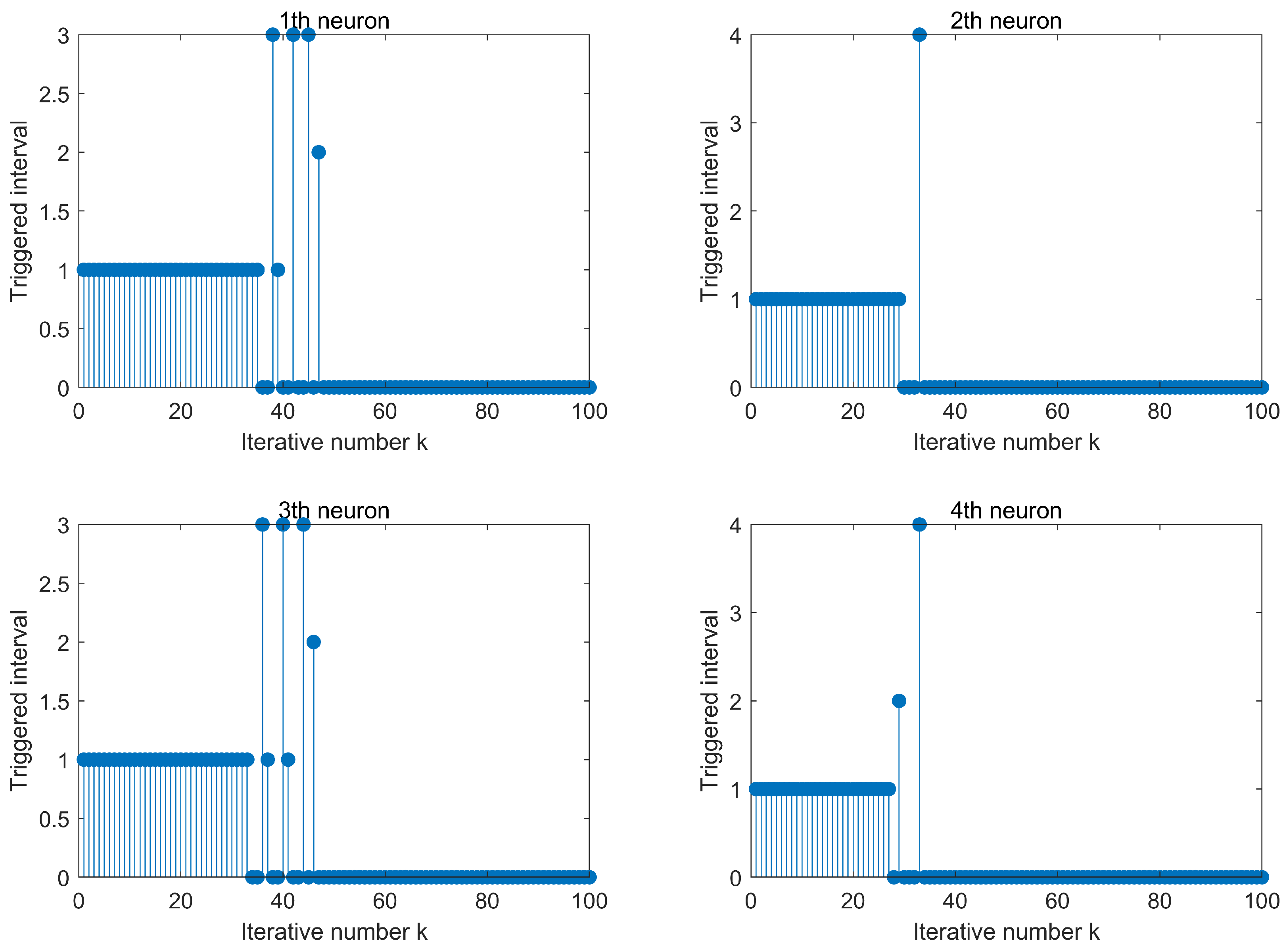
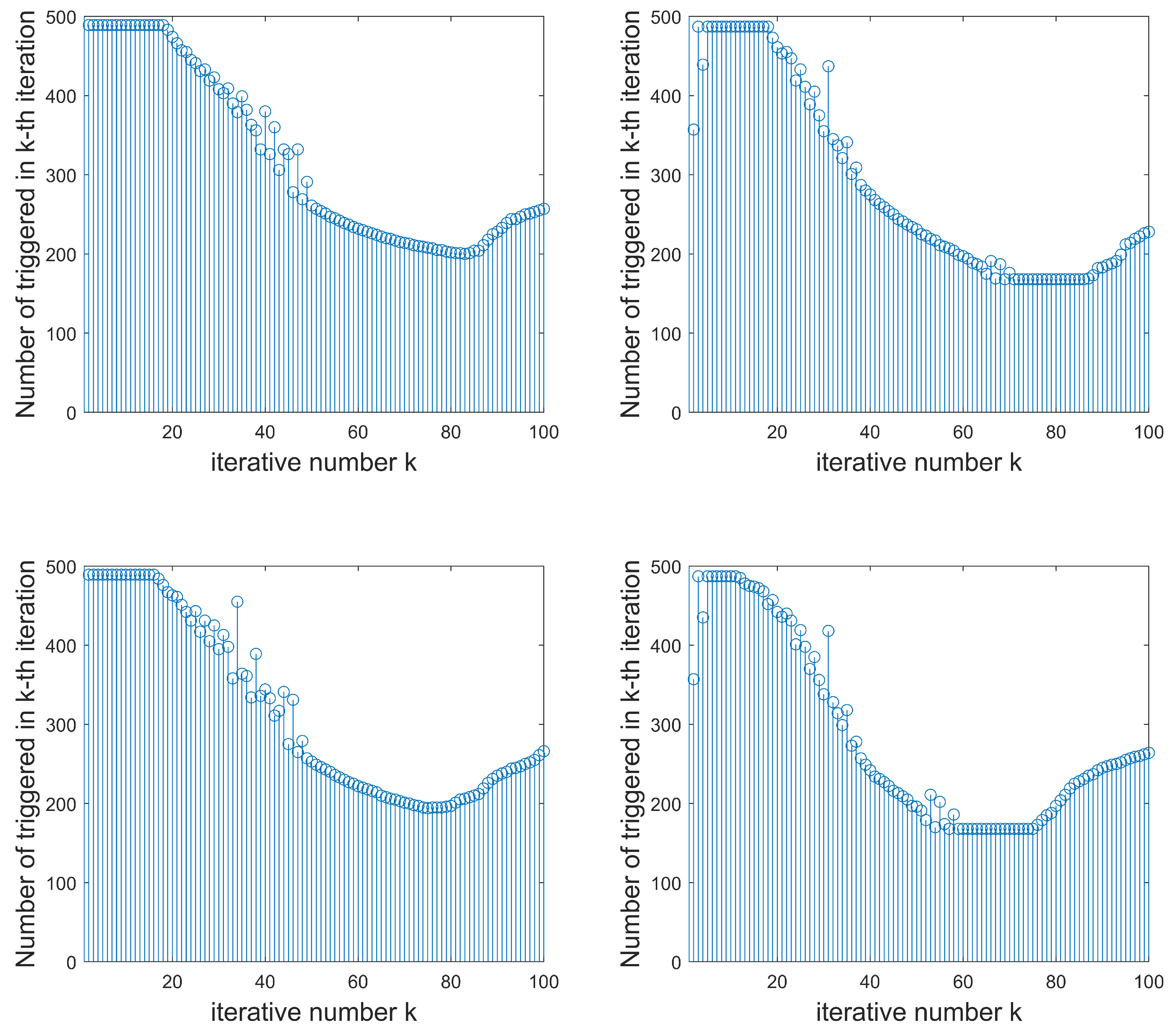
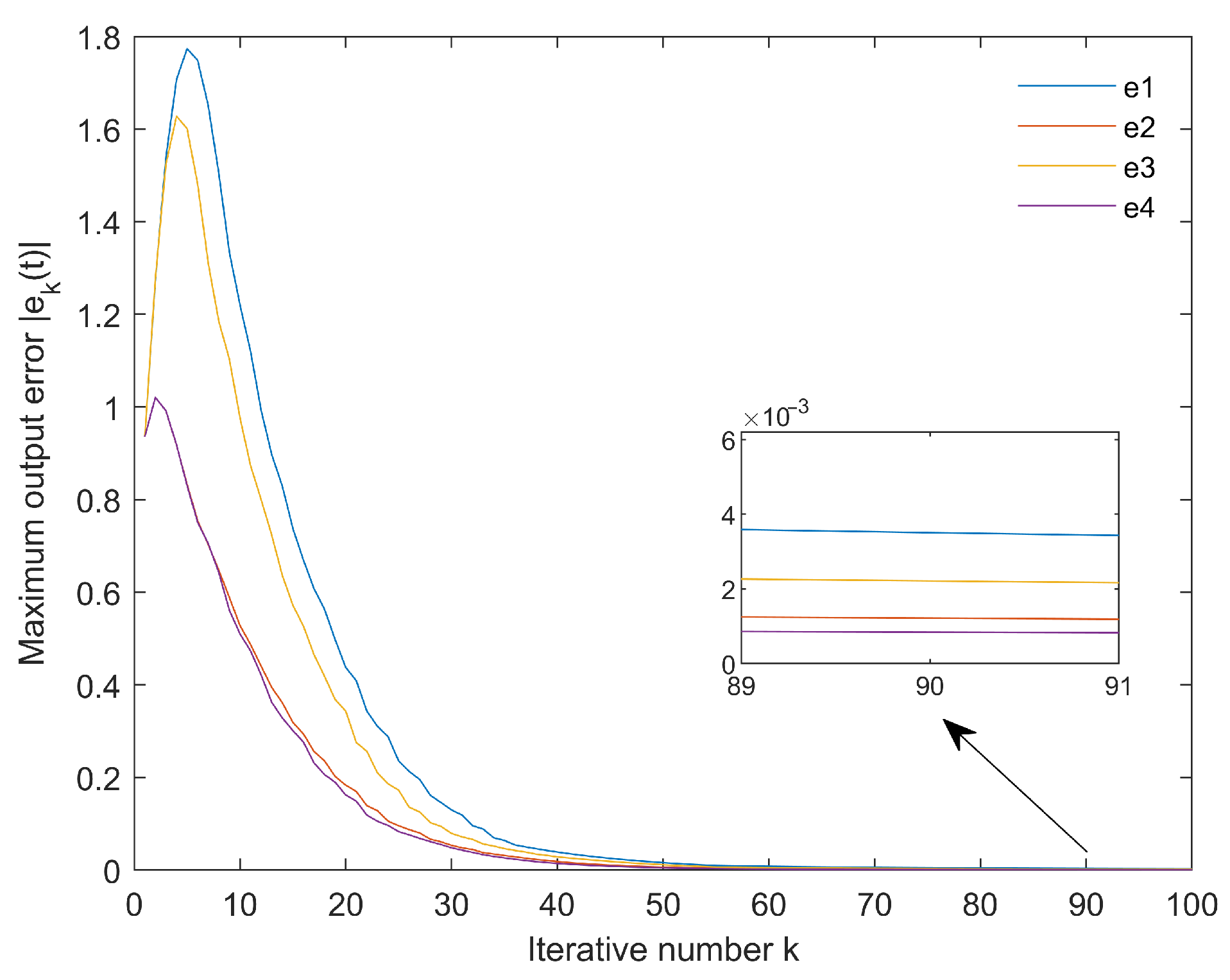
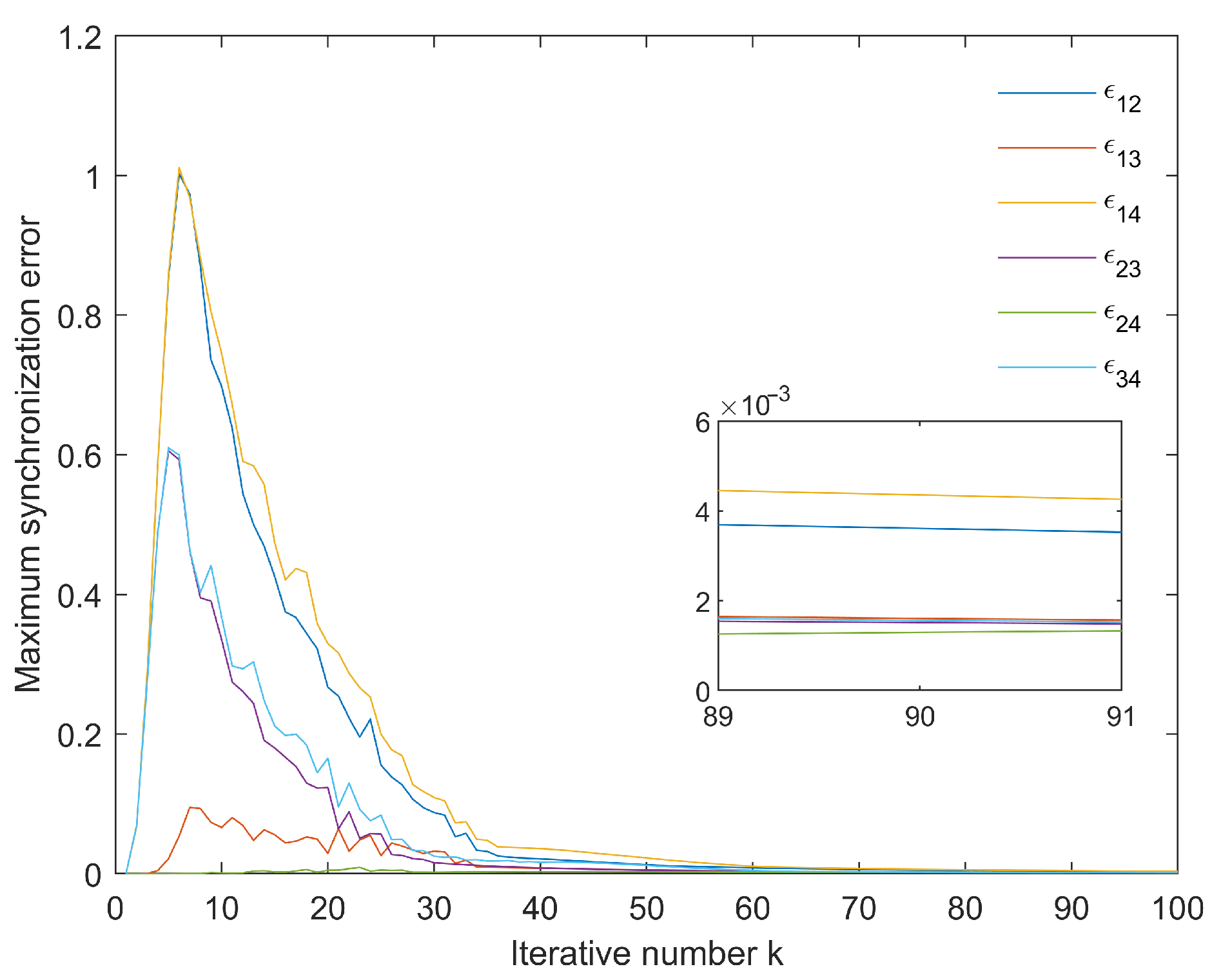
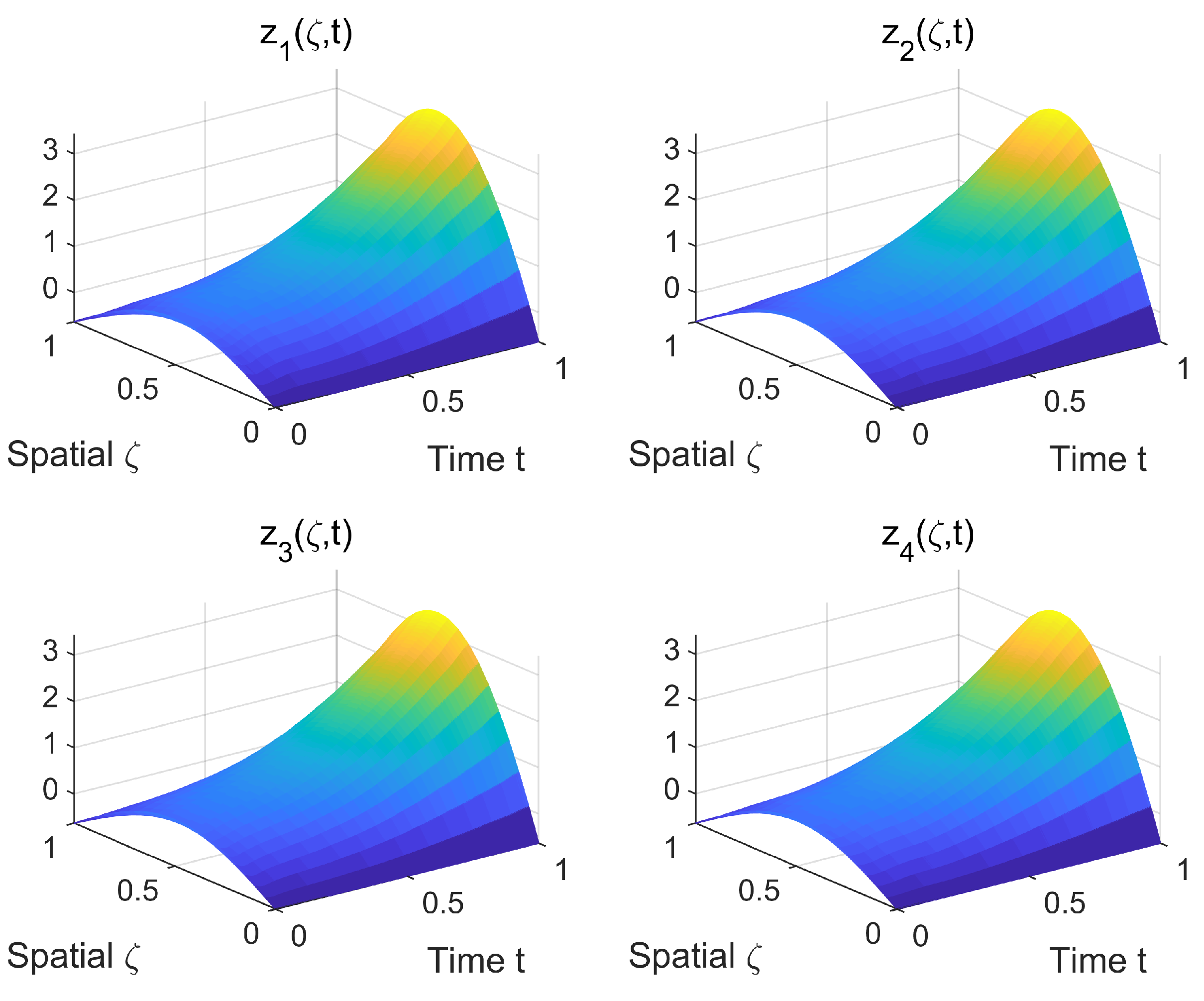
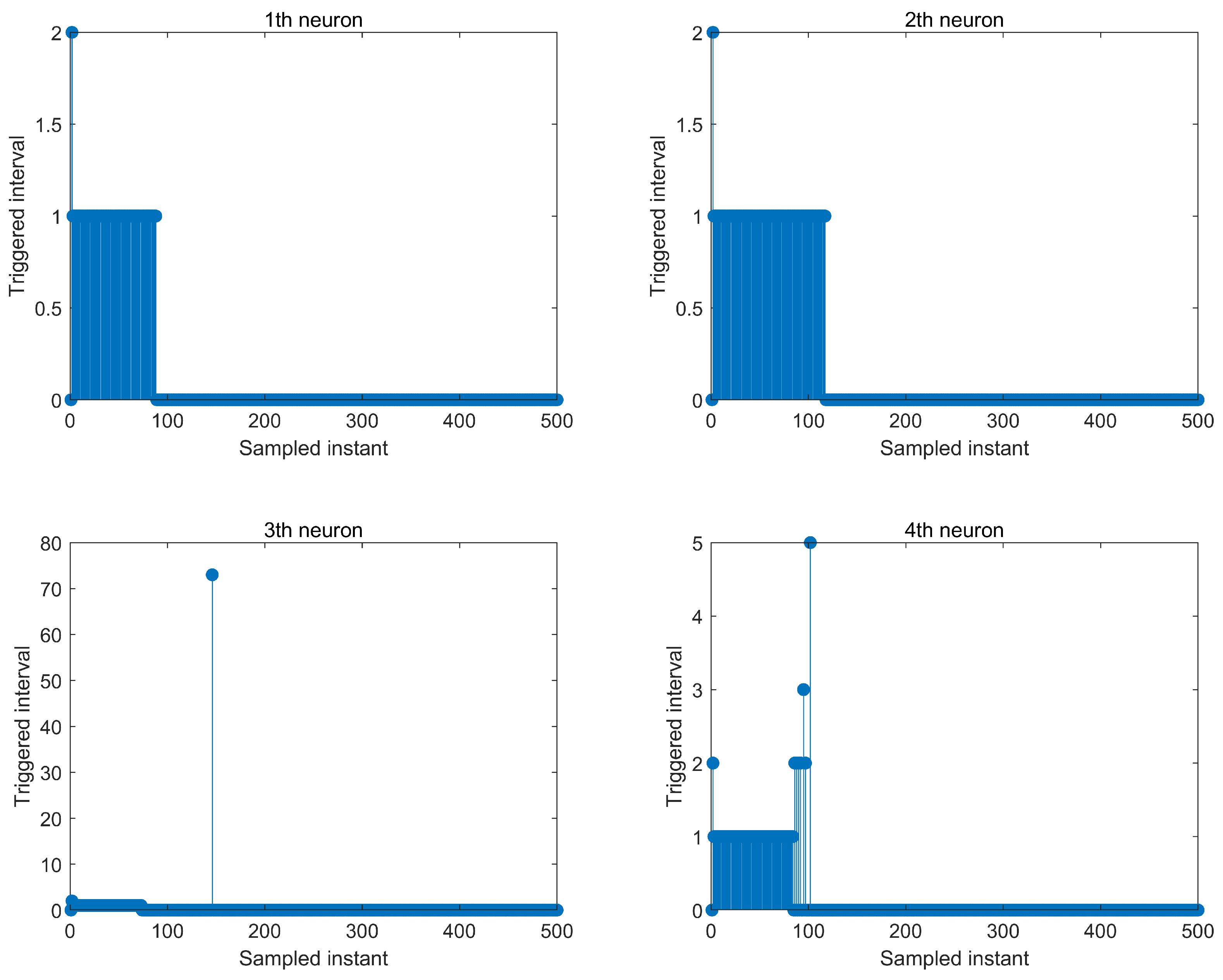
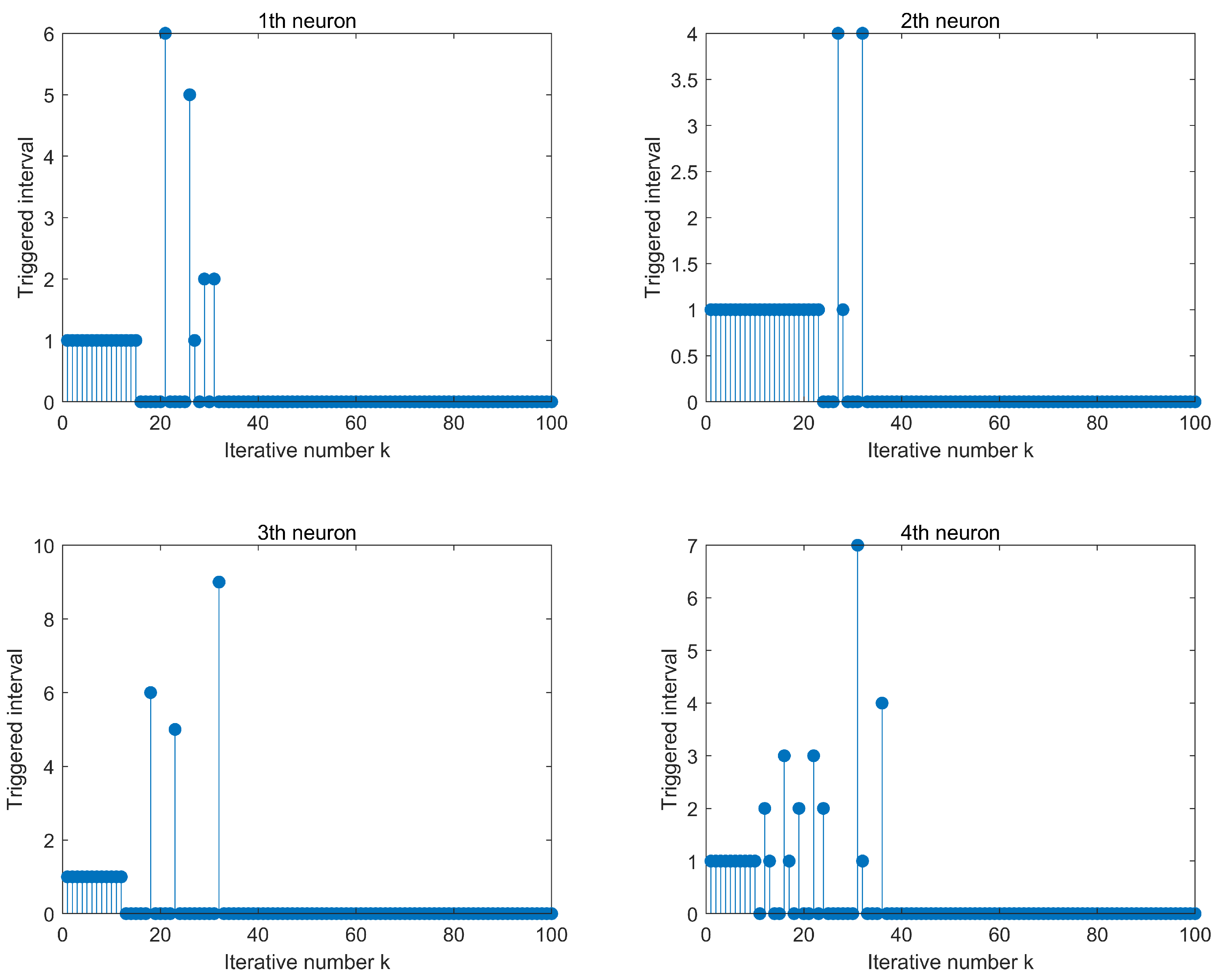
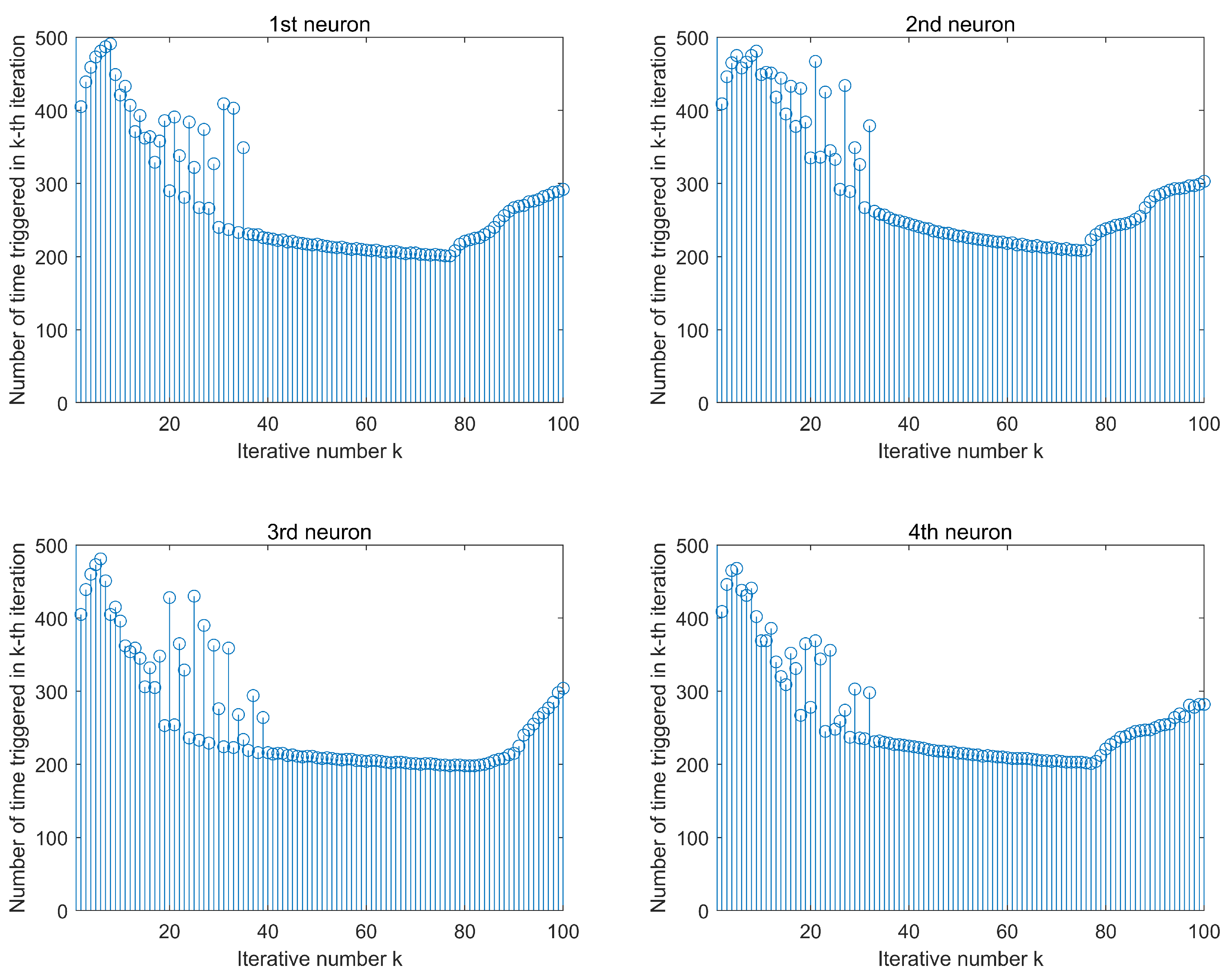
4. Simulations

Let $\zeta \in [0,1]$, $t\in [0,1]$, $c=0.1$, $J=0$, $\alpha =0.5,\gamma =0.4,\beta =0.5,H=1$. The remaining parameters are chosen as

$$\begin{array}{c}\hfill D=0.1,A=0.2,B=0.4,\Phi =0.2,\end{array}$$

where the gain matrix $\mathrm{\Gamma }=-0.7$. Substituting the parameters into Theorem 1, one has $0.8824<1$. The activation function is chosen as $f\left(x\right)=0.25\ast \left(\right|x+1|-|x-1\left|\right)$, which meets the Lipchitz condition. And the expected output trajectory is selected as

$$\begin{array}{c}\hfill y_d\left(t\right)=t^2.\end{array}$$

The initial values of the neuron states $z_k(\zeta ,0)$ and control input $u_k\left(0\right)$ are set as zero. The Laplacian matrix L and matrix K are

$$L=\left[\begin{array}{cccc}2& -1& -1& 0\\ -1& 1& 0& 0\\ 0& -1& 2& -1\\ 0& 0& -1& 1\end{array}\right]\mathrm{and}K=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right],$$

The corresponding communication topology is shown in Figure 1.

Case 1: Initial state fixed

Numerical simulation is conducted, yielding the following results.

Figure 2 and Figure 3 show the norm curves of the maximum output error and the maximum synchronization error, respectively. Both the output error and synchronization error exhibit a clear convergence trend, reaching the order of ${10}^{-4}$, thus accomplishing the tracking synchronization control objective.

Figure 4 illustrates the state surfaces of individual neurons at the 100th iteration, demonstrating that the neural states have achieved synchronization.

Figure 5 depicts the event-triggering intervals at the 40th iteration. Similarly, if no triggering occurs at a given sampling point, the interval is 0; otherwise, it is determined by the time elapsed since the previous trigger.

Figure 6 displays the event-triggering intervals at the 300th sampling point. If the sampling point does not satisfy the triggering condition in the current iteration, the interval is recorded as 0. If triggered, the interval is calculated based on the number of iterations since the last triggering event (e.g., if the last trigger occurred two iterations ago, the interval is 2).

Figure 7 presents the number of event triggers during the iterative learning process. From the perspective of triggering frequency, it can be concluded that the controller’s update frequency is reduced. Combined with the results in Figure 2 and Figure 3, the proposed event-triggered sampled-data iterative learning control algorithm not only ensures the convergence of synchronization errors but also effectively reduces the computational burden on the controller. In Figure 7, the higher number of triggers in the initial iterations is due to the complexity of the fractional-order reaction–diffusion neural network system. At this stage, the controller’s effectiveness is relatively weak, causing most sampling points to meet the event-triggering condition and thus increasing the triggering frequency. As the iteration progresses, the controller’s performance gradually improves, leading to a reduction in triggering events.

By analyzing Figure 5, Figure 6 and Figure 7 together, it is evident that the proposed event-triggering scheme effectively reduces the number of triggering events, confirming its efficiency.

Case 2: Initial state offset

The system parameters and iterative learning gains from the fixed initial condition (Case 1) are retained. With the initial learning gain set as ${\Lambda }_1=-0.5$, the following simulation results are obtained.

Figure 8 and Figure 9 depict the maximum output error curve and the $L^2$-norm curve of the maximum synchronization error, respectively. It can be observed that during initial-state learning, the error magnitude remains on the order of ${10}^{-3}$, which indicates lower control accuracy compared to the case with a fixed initial state.

Figure 10 illustrates the state surfaces of individual neurons at the 100th iteration, demonstrating that the neural states have achieved synchronization.

Figure 11, Figure 12 and Figure 13 represent the event-triggering intervals at the 40th iteration, the event-triggering intervals along the iteration axis at the 300th sampling point, and the number of event-triggered actions at per iteration, respectively.

Assuming 500 sampling points per iteration and 100 iterations, with four neurons (each having 50,000 potential triggering opportunities in the absence of event triggering), Figure 13 shows that the actual triggering rates of these four neurons are approximately 45%, 35%, 50%, and 45%, respectively. This means that each neuron avoided 55%, 65%, 50%, and 55% of unnecessary controller updates, thereby conserving resources for the event-triggering mechanism.

5. Conclusions

In this work, an algorithm for event-triggered sampling iterative learning control is proposed for FORDNN. The algorithm provides the event-triggering condition as well as sufficient conditions for synchronization. The scenario with initial-state offset is considered, where the Neumann boundary condition is applied in this case. Numerical simulations demonstrate that after a certain number of iterative learning iterations, the synchronization error converges and effectively saves network resources. Future work will extend the proposed ETILC algorithm to FORDNN with time-varying delays and external disturbances for more practical engineering scenarios, explore the synchronization of heterogeneous FORDNN (with non-identical node dynamics) under the event-triggered iterative learning framework, and investigate the optimal design of event-triggering thresholds and learning gains to enhance system convergence speed and resource-saving efficiency.