Elementary Fractal Geometry 7: An Algorithm Visualizing the Magnification Flow

Abstract

Self-similar sets are defined as compact attractors. Their interior structure, however, is revealed only by successive magnification. This requires the use of a computer. We describe a new and very simple algorithm which performs an unlimited magnification of self-similar sets. In the case of integer data, it works without numerical error propagation. In other words, the program visualizes the scenery flow introduced by Bedford and Fisher, and Hochman. An open-source MATLAB implementation of the program is provided as a starting point and invitation to computational work in fractals.

1. Introduction

Self-similar sets. A compact non-empty set A in Euclidean ${\mathbb{R}}^d$ is called self-similar if it is a finite union of pieces $A_j$ which are geometrically similar to A [1]. Using contractive similitudes $f_j$ with $A_j=f_j\left(A\right),$ Hutchinson (cf. [2,3,4,5]) has characterized these sets as unique solutions of the equation

$$A=\bigcup _{j=1}^m{f}_j\left(A\right).$$

(1)

The set $F=\{f_1,\dots ,f_m\}$ is called an iterated function system or IFS, and A is the attractor of $F.$ A contractive similitude from Euclidean ${\mathbb{R}}^d$ to itself fulfils $\left|f\right(x)-f(y\left)\right|=r|x-y|$ where the constant $r<1$ is called the factor of $f.$ We assume that all maps in F have the same factor $r.$ In that case, we can write $f_j=g^{-1}{h}_j$ where $g^{-1}$ is a contractive linear map and $h_j\left(x\right)=s_j\left(x\right)+v_j$ is an isometry of ${\mathbb{R}}^d.$ Here, $s_j$ denotes a linear map and $v_j$ a translation vector. With this notation, Equation (1) is turned into the so-called numeration from

$$g\left(A\right)=\bigcup _{j=1}^m{h}_j\left(A\right).$$

(2)

The maps $h_j$ and the matrix of g are often considered as the digits and base of a numeration system. For the decimal system, we have $g\left(x\right)=10x$ and $h_j\left(x\right)=x+j-1$ for $j=1,\dots ,10,$ and $A=[0,1].$ We can assume that $v_1=0.$ (Otherwise, replace $v_k$ by $\widetilde{v_k}=v_k-(g-s_k){(g-s_1)}^{-1}{v}_1$ and consider the translated attractor $\tilde{A}=\phi \left(A\right)$ with $\phi \left(x\right)=x-{(g-s_1)}^{-1}{v}_1,$ cf. ([6] Section VI.A).) That is, $f_1\left(0\right)=h_1\left(0\right)=0,$ so that zero is in A and can be taken as a ’control point’ of the attractor. The idea of control points goes back to Thurston [7] and plays an important part in this paper.  

Motivation. With these assumptions and additional properties, a comprehensive theory of the measure and dimension of self-similar fractals was established [2,4,5,8]. Nevertheless, there are few concrete examples of self-similar sets in the literature. Most of them, like the Sierpiński gasket, fractal squares, and post-critically finite fractals, have a fairly simple structure, or, like Barnsley’s fern [3], approximate natural phenomena with an unclear mathematical structure. The lack of examples has led to the widespread belief that magnifications of a self-similar set all look more or less the same.

This is not true. In the paper [6] with Mekhontsev in 2018, we have shown that even simple modifications of the Sierpiński gasket have a very rich interior structure which in the presence of a separation condition can be described by finite-state automata. Without a computer, this structure cannot be recognized. Mekhontsev [9] built the free IFStile package with excellent graphics which visualizes and classifies thousands of examples within minutes. It has not been generally used, however, since it is sophisticated and not open source. There is a definitive need for transparent software in fractal geometry.

Moreover, all traditional magnification algorithms for self-similar sets are limited by two constraints:

(i)

Bounded number of digits. Suppose the diameter of A is one, and we use floating-point numbers with 16 decimal digits. Then, the magnification of A by the factor ${10}^{17}$ is not possible, since ${10}^{-17}$ equals zero in the computer.

(ii)

Numerical error propagation. Each magnification step is expressed by certain operations, such as multiplication. If magnification steps are iterated, the inaccuracies of the operations will accumulate.

Main contribution. In this note, we introduce the principle of virtual magnification, which solves problem (i) and speeds up the magnification procedure. The basic idea is to calculate with control points and directions of pieces instead of all their points. The principle works for arbitrary self-similar sets without the assumption of a separation condition.

Moreover, our algorithm will magnify without numerical error propagation and thus also solve problem (ii) when we have integer data in (2). That is, g and the $s_j$ must be given by integer matrices, and the $v_j$ must have integer coordinates. The $s_j$ must belong to a finite group S of linear isometries such that $gS=Sg.$ The $v_j$ could be rational, since the multiplication of all $v_j$ by the common denominator would change the size but not the shape of $A.$ Most concrete examples in the literature fulfill these conditions.

The algorithm was implemented in MATLAB R2020b as an open-source program with 100 lines of code, which are appended as Supplementary Materials to this paper. The program was successfully tested with several other MATLAB versions as well as with Octave. It visualizes the interior structure of self-similar sets as a slow-motion film. For certain IFSs with integer data and open set condition, including most examples from the literature, you can run it almost as long as you want. Otherwise, a decisive constraint is the memory and speed of the computer. There is much room for improvement.

Exploration with our program shows that except for the most simple cases, self-similar attractors have a very rich local structure. An IFS does not just generate a compact set $A,$ it also generates a collection of photos of small places in $A.$ The theory of scenery flow and uniform scaling, discussed in Section 3, says that magnification at different spots will lead to the same infinite collection although in different order. Our program is a practical way to sample photos from an IFS, showing the importance of the scenery flow.

Contents of the paper. Our program is written for attractors A in the plane. Extensions are discussed in Section 7. The simplest examples come from $g=\left({\displaystyle \genfrac{}{}{0pt}{}{20}{02}}\right)$ and $s_j\in \{\pm 1,\pm s\}$ with $s=\left({\displaystyle \genfrac{}{}{0pt}{}{0-1}{10}}\right).$ While the program is based on matrix calculations, notation in the text will often use complex numbers, such as $g=2,s=i,$ and $v=x+iy$ instead of $v=\left({\displaystyle \genfrac{}{}{0pt}{}{x}{y}}\right).$ The IFS data for Figure 1 are

$$g\left(z\right)=2,h_1\left(z\right)=iz,h_2\left(z\right)=iz-1+3i,h_3\left(z\right)=z+3+2i.$$

(3)

For this example, the function of the program will be explained in the next section. In Section 3, we discuss the well-known concept of scenery flow and our discrete version for self-similar sets. We then formulate our principle of virtual magnification and operate with control points and neighbor maps. In Section 5, we explain the structure of the program. Our implementation puts transparency and simplicity over the efficiency and quality of figures. In the two final sections, we discuss the example data, possible extensions of the program, and open problems. We hope that readers will feel encouraged to conduct their own experiments. The study of fractal structures requires explorative computer work.

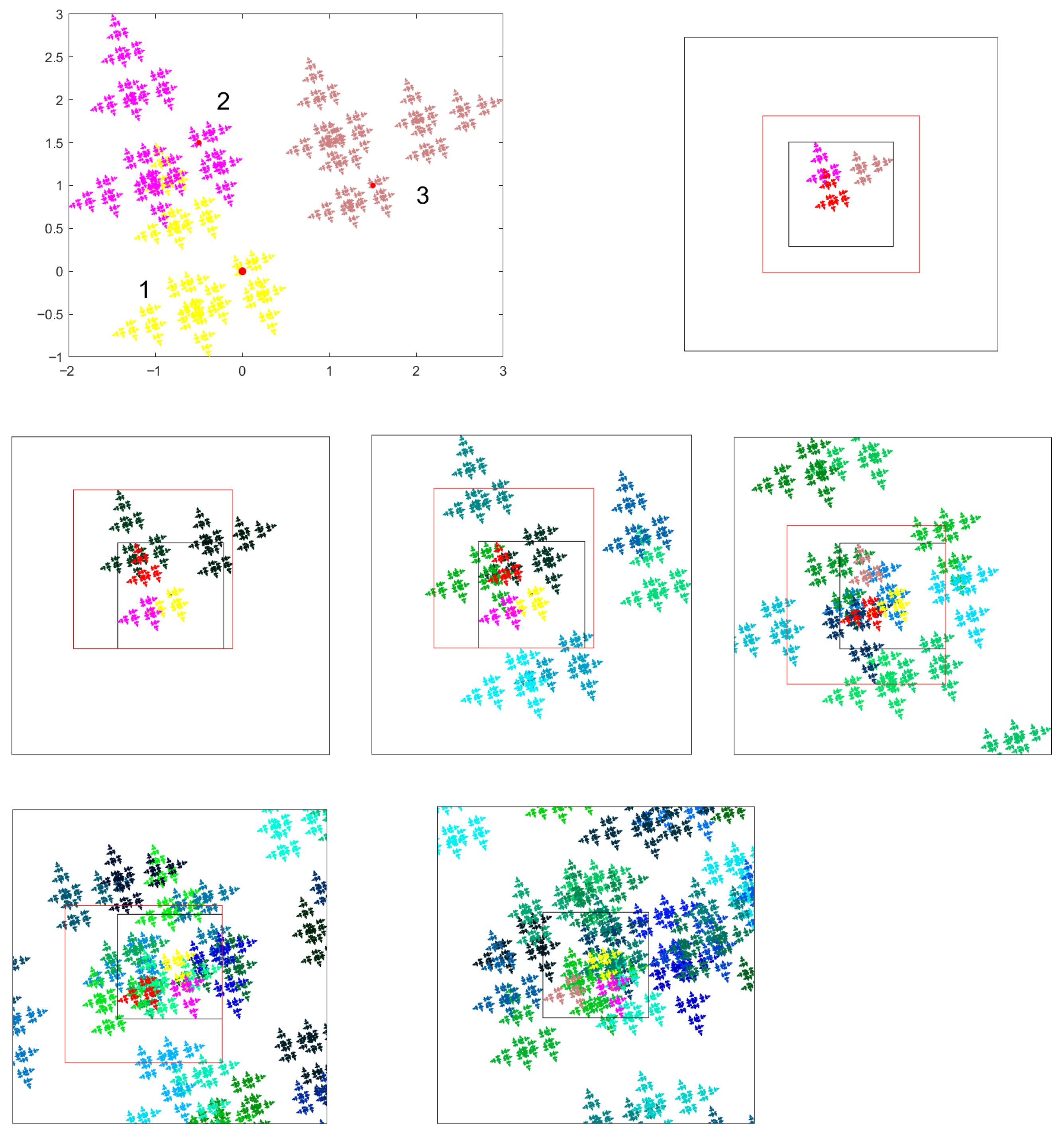
2. A Preview of the Program

Our MATLAB program scenery.m and a number of data files *.mat are the Supplementary Materials of this paper. If you have access to MATLAB or the non-commercial version Octave, you can start it from one of the data files that contain the IFS matrices g and $H.$ The example in Figure 1 is obtained from loading the file B1-figure1.mat and executing the command scenery(g,H,6,5,w(1,:)). Details will be given in Section 5.

First, the fractal A is shown in full scale in a coordinate system in the upper left of Figure 1. If there are three pieces, the first is yellow, the second pink, and the third brown. We also draw the control point 0 as a red spot. Since we assume $f_1\left(0\right)=0,$ the control point of $A_1$ agrees with that of $A,$ while the control points of $A_2,A_3$ are $f_2\left(0\right),f_3\left(0\right),$ respectively. In the figure, A looks like a Cantor set, but the pieces $A_1$ and $A_2$ do intersect, and this is a place where magnification gives more information.

Next, A is moved to the inner subsquare of a square screen in such a way that the control point of A coincides with the center of the square. One of the pieces is selected and colored red. On the upper right of Figure 1 is $A_1$, which was yellow before. The red subpiece is the central piece in the next magnification. The red square indicates the window of this magnification. On the left of the middle row, we have drawn $A_1$ as the central piece with three subpieces. The sets $A_2,A_3$ are now neighbor pieces with random shades of dark color. Note that the central piece has the same control point as A but another orientation. The brown subpiece of the central piece is already colored red in order to show that the third part $A_{13}$ of $A_1$ is the next central piece. The piece $A_{33}$ of the right neighbor is outside the red square and will not be seen in the next magnification.

In the picture in the middle, $A_{13}$ is the central reference piece, and its third subpiece $A_{133}$ is selected for the next step and colored red. The blue neighbors below the central piece are $A_{12}$ and $A_{11}.$ Only a small part of $A_{11}$ is in the red square and will be visible in the next magnification. The choice of piece 3 does not change the orientation of the central piece since $s_3\left(z\right)=z$ in (3). There is a slight shift in the picture since the focus goes from the control point of the piece to the control point of its subpiece.

In the next step, piece 2 is selected, which rotates the central piece. For the last magnification, we have again chosen piece 3. Thus, the central pieces in the last row are $A_{1332}$ and $A_{13323}.$ In the last picture, 45 neighbors intersect the screen, and it is not clear anymore whether we have a Cantor set. This view could not be anticipated from the global picture on the upper left. In the present case, however, subsequent magnification again simplifies the structure and indicates that it is indeed a Cantor set.

3. Continuous and Discrete Magnification Flow

Furstenberg’s concept of a photo. Now, let us treat the magnification process more formally. We first slightly modify Furstenberg’s notion of a miniset [10]. Suppose we have an object $A,$ a mapping $\phi :A\to X,$ and a subset $W\subset X.$ Then, $\phi \left(A\right)\cap W$ is called a photo of A on the screen $W.$

This is a very nice abstraction of the everyday concept of a photo. Usually, $X={\mathbb{R}}^2$ is the plane, although with 3D printing, we could have three-dimensional photos and in theory also n-dimensional ones [10]. In this paper, W is a square. The object A in our examples is part of the plane. It could also be in some higher-dimensional space. The mapping $\phi$ represents the properties of the camera. In our case, $\phi$ is a similitude. Usually, $A\cap {\phi }^{-1}\left(W\right)$ is a small part of A, which is shown in standard size as the photo $\phi \left(A\right)\cap W.$ So, $\phi$ will be an expanding similitude.  

The scenery flow. Let $B_{\epsilon }\left(c\right)$ denote the closed ball with center c and radius $\epsilon .$ For $c\in A,$ the photos generated by

$${\phi }_{\epsilon }:A\to B_1\left(0\right)\mathrm{with}{\phi }_{\epsilon }\left(z\right)=(z-c)/\epsilon \mathrm{for}\epsilon >0$$

(4)

have been considered by many authors [10,11,12,13,14,15,16,17,18,19]. The photo is ${\phi }_{\epsilon }(A\cap B_{\epsilon }\left(c\right)),$ a subset of the unit ball $B_1\left(0\right)$, which serves as a circular window. Some authors, in particular Furstenberg, take square windows. For a fixed c and variable $\epsilon$, which tends to 0, these photos form a film which is called the magnification flow or scenery flow of A at $c.$

It is appropriate to consider $\epsilon$ on a logarithmic scale, taking $\delta =-log\epsilon$ as the parameter. The values $\epsilon =r^k,k=1,2,\dots$ then go to equidistant values $\delta =klog{\displaystyle \frac{1}{r}}.$ For self-similar sets, it was observed that on this logarithmic scale, the collection of photos of the scenery flow is independent of c in a measure-theoretic sense [11,15,19]. If we change the center point $c,$ the magnification film will show the same pictures but in different order. This ’uniform scaling property’ requires a limit $\epsilon \to 0$ from Furstenberg minisets to Furstenberg microsets. It was recently proved for much more general measures and used to solve various problems in geometric measure theory [12,14,17,18]. Our interpretation from a somewhat applied viewpoint is that self-similar sets in the 1990s were seen as models of certain sets in nature, like a fern or a maple leaf [3], and now appear as models of scale-free texture given by a collection of photos which share certain characteristic features.

The discrete magnification flow. It is good to know that our magnification experiments are connected with contemporary fractal research. We need not go into detail, however, since computers do not allow indefinite magnification with $\epsilon \to 0$ and $\delta \to \infty .$ We consider a discrete version of the magnification flow. Instead of assuming a point c as the center for the magnification flow, we take a sequence $j_1,j_2,j_3,\dots$ of indices in $\{1,\dots ,m\}$ and the corresponding nested sequence

$$A_{j_1}\supset A_{j_1{j}_2}\supset A_{j_1{j}_2{j}_3}\supset \dots$$

of pieces of A of level 1, 2, 3, …, which in the limit would determine a unique point c of intersection. The center of magnification is slightly shifted at every step. When $A_{j_1{j}_2\dots j_k}=f_{j_1}{f}_{j_2}\cdots f_{j_k}\left(A\right)$ with control point $c_k=f_{j_1}{f}_{j_2}\cdots f_{j_k}\left(0\right)$ is taken as reference piece in our program, the corresponding photo is given by

$${\phi }^k:A\to W\mathrm{with}{\phi }^k\left(z\right)=(z-c_k)/r^k\mathrm{for}k=1,2,\dots$$

(5)

If we compare this with (4) for $\epsilon =r^k$ where ${\phi }_{r^k}\left(z\right)=(z-c)/r^k,$ only the reference point is different. Without loss of generality, we can assume that $A\subset B_1\left(0\right).$ Moreover, 0 is the control point and $c\in A.$ Then, the distance between 0 and c is at most one, and the distance between $c_k=f_{j_1}{f}_{j_2}\cdots f_{j_k}\left(0\right)$ and $c\in A_{j_1{j}_2\dots j_k}$ is at most $r^k.$ Consequently, the difference

$${\phi }^k\left(z\right)-{\phi }_{r^k}\left(z\right)=(c-c_k)/r^k\mathrm{is} \mathrm{the} \mathrm{same} \mathrm{vector} \mathrm{for} \mathrm{all}z\in A,\mathrm{with} \mathrm{lenght} \le 1.$$

Thus, corresponding photos of the continuous and the discrete scenery flow at c differ only by a translation of length at most one. In our implementation of the discrete flow illustrated in Figure 1, the translation vector is between two points in the small black square. By calculating our picture in the larger black square, we included the translated photo of the continuous scenery flow for the small square. In Figure 1, the ratio of the side lengths of the large and small squares is 3. It can be increased so that the translation vector appears even smaller. This requires additional computer time and memory.

To summarize, the photos of our discrete setting include the photos of the established scenery flow for $\epsilon =r^k,k=1,2,\dots .$ It is possible to interpolate our photos numerically on the continuous scale of all $\epsilon .$ Thus, our method is indeed a visualization of the scenery flow—not for all k up to infinity, only up to some $k_0$ depending on the IFS and the capacity of the computer. The use of magnification factors $1/r^k$ is motivated by our algorithm, which will now be presented. There is a mathematical benefit, too: for a finite type IFS with the open set condition, our discrete magnification flow is given by a finite number of photos repeated in random order [20].

4. The Principle of Virtual Magnification

Traditional algorithms of magnification calculate the fractal at smaller places and then magnify to the size of the screen. The key idea of the present paper is to represent the data at the small place by a much simpler data structure: the control points of the reference piece and its neighbors in the small place. The configuration of these control points is magnified to standard size. Then, around each standardized control point, we draw the corresponding piece. For this, we need only one numerical copy of $A,$ which is given as a cloud of N points.

Let us demonstrate this idea with Figure 1. The global point cloud on the upper left was calculated by a classical IFS algorithm [3]. It is then transformed to fit into the small black square W at the upper right with a control point at the center. This is our standard point cloud. No further IFS iteration is calculated. All pieces in subsequent magnifications are obtained as rotated and translated copies of the standard cloud.

The self-similarity of A allows the algorithm to determine the positions of the control points in a recursive way. We can forget the coordinates of the small place where we are. We only have to keep track of the relative positions of neighbor control points with respect to the control point of the reference piece. This requires much less work than the local calculation of small pieces of $A.$

When we have integer IFS data, the calculations of control points and corresponding directions involve fairly small integers. There will be no numerical errors. We may have numerical errors in the initial calculation of the standard point cloud, but these errors cannot accumulate. That is why we can magnify as long as the computer can handle the number of neighbors.

To formulate the principle of virtual magnification in technical terms, we need the concept of a neighbor map which has been used in various forms [6,7,21,22,23,24,25]. Suppose $u=u_1\dots u_k$ and $w=w_1\dots w_k$ are two words of length k from the alphabet $\{1,\dots ,m\}.$ Given the IFS $F=\{f_1,\dots ,f_m\},$ there are similitudes $f_u=f_{u_1}{f}_{u_2}\cdots f_{u_k}$ and $f_v=f_{v_1}{f}_{v_2}\cdots f_{v_k}$ which generate the k-th level pieces $A_u=f_u\left(A\right)$ and $A_v=f_v\left(A\right)$ of the attractor $A.$ The neighbor map from $A_u$ to $A_v$ then is

$$h(u,v)=f_u^{-1}{f}_v.$$

Note that $h(u,v)$ does not map $A_u$ to $A_v.$ This is accomplished by $k(u,v)=f_v{f}_u^{-1}.$ The neighbor map $h=h(u,v)$ maps the full-size attractor A to a neighboring set $h\left(A\right)$ of the same size such that the following diagram commutes.

$$\begin{array}{cccc}& A& \stackrel{h}{\to }& h\left(A\right)\\ f_u& \downarrow & & \downarrow f_u\\ & A_u& \stackrel{k}{\to }& A_V\end{array}$$

Thus, $h\left(A\right)$ has the same metric position with respect to A as $A_v$ has with respect to $A_u,$ up to similarity. The conjugating map is $f_u.$ The following basic equation allows the calculation of neighbor maps of level $k+1$ from those of level k. For $i,j\in \{1,\dots ,m\},$ the words $ui=u_1\dots u_{k}i$ and $vj$ have a length of $k+1.$

$$h(ui,vj)=f_{ui}^{-1}{f}_{vj}=f_i^{-1}{f}_u^{-1}{f}_v{f}_j=f_i^{-1}h(u,v)f_j.$$

(6)

Starting with the neighbor maps $f_i^{-1}{f}_j$ of the first level, we can now inductively determine all neighbor maps. This has been accomplished in other papers [6,21,26]. However, there are three differences.

(i)

In other papers, only proper neighbor maps have been considered—that is, neighbors $h\left(A\right)$ which intersect $A.$ The definition above includes all potential neighbors. Below, we choose as actual neighbor maps those $h\left(x\right)=sx+t$ for which $\left|t\right|<C$ where C is a constant depending on A and our window $W.$

(ii)

In other papers, it was assumed that the IFS fulfills the open set condition or weak separation condition in order to keep the number of proper neighbors finite. For visualization, this assumption is not needed. The computer can perform only finitely many steps, anyway.

(iii)

The standardization forced by $f_u^{-1}$ concerns size, position and direction. In our magnification flow, we change size and position but keep the direction of pieces. In the program, we work with neighbor maps and restore the direction afterwards.

We assumed that the $f_j$ values are given by integer data, $f_j\left(x\right)=g^{-1}(s_j\left(x\right)+v_j)$ where the matrices $g,s_j$ and the vectors $v_j$ have integer entries, and the $s_j$ belong to a finite group S of isometries with $gS=Sg.$ Then, a straightforward calculation of $f_i^{-1}{f}_j$ and of $h(ui,vj)$ from $h(u,v)$ by (6) shows that

Proposition 1.

For integer data, all neighbor maps have the form $h\left(x\right)=sx+t$ with some integer matrix $s\in S$ and some integer vector t, which is the control point of the neighbor $h\left(A\right).$

Since s describes the direction change from A to $h\left(A\right),$ a neighbor map describes what in geometry is called a flag: combined information on position and direction. The principle of virtual magnification says that instead of magnifying tens of thousands of points, we perform the calculation with tens of flags. Then, we transform one copy of our standard point cloud to each position and direction.

5. The Algorithm and Its Implementation

The algorithm uses only elementary matrix operations. Here are the main steps.

1.

Initialization. We calculate a global point cloud x representing A by a classical IFS algorithm. We draw x on the whole screen and in the small square. Initial values of parameters include the iteration number $it=1$ and the total number $nit$ of iterations. The word u and the list of neighbor maps $nb$ are empty. The reference piece is $A.$

2.

Choice of a subpiece. There are different options. The simplest is to take a random i uniformly from $\{1,\dots ,m\}.$ We replace the reference piece $A_u$ by its subpiece $A_{ui}$ by putting $u=ui,$ and we save the direction matrix D of the new reference piece.

3.

Calculation of neighbors. For all neighbor maps h in the list $nb,$ and $j=1,\dots ,m,$ we calculate the new neighbor map $h^{\prime }=f_i^{-1}h{f}_j$ as in (6) and add the neighbor maps $f_i^{-1}{f}_j$ with $j\ne i.$ Then, we remove the neighbor maps for which $h^{\prime }\left(A\right)$ cannot intersect the large square. This is our new list $nb.$

4.

Plotting the magnification. The cloud of the reference piece with its new direction is $Dx.$ The clouds of the reference pieces are $Dh\left(x\right)$ with h in $nb.$ If $it=nit,$ the job is completed. Otherwise, we increase $it$ by one and go to 2.

We now discuss the implementation of the steps in the appended MATLAB program scenery.m and verify the correctness of the algorithm.

The program is run by loading an IFS data file into the workspace and typing scenery(g,H,nit,np,3). Here, $nit$ is the total number of magnifications and $np$ is the length of pauses in seconds to study subsequent pictures. The last parameter determines the choice of subpieces in step 2. Various data files are provided. Each data file consists of an $2\times 2$ integer matrix g and an $2\times 3\times m$ integer array H which contains the digits $h_1,\dots ,h_m,$ as described in Section 1. The mapping $h_j\left(x\right)=s_{j}x+v_j$ with the $2\times 2$ matrix $s_j$ and $2\times 1$ vector $v_j$ is represented by $H(:,:,j)=\left[s_j{v}_j\right].$ It is very simple to edit these data and produce your own data files.

Step 1 starts with the calculation of the cloud x by the procedure globa.m. A minimum size of $N=\mathrm{30,000}$ points is prescribed. This parameter can be adapted to the size of the screen and the capacity of the computer. Attractors A with larger Hausdorff dimensions require greater N values for graphical accuracy. We determine the minimum level L with $mL>N$ and take the actual number as $N=mL.$ The point cloud x is the set of all $f_v\left(0\right)$ for words $v=v_1\dots v_L$ from our alphabet $\{1,\dots ,m\}$—that is, all control points of pieces of level $L.$ It is calculated by a double loop. See Barnsley [3] for related algorithms. As a matrix, x has dimension $2\times N.$

The system automatically determines maximal and minimal coordinates of x and plots the global point cloud in a corresponding rectangle. We prefer a quadratic window with the control point 0 of A in the center. The maximum length a of a vector in x is called the radius of $A.$ In other words, a is the root of ${max}_{n=1}^{N}x{(1,n)}^2+x{(2,n)}^2.$ The small square in the middle of our screen will be ${[-a,a]}^2.$ It will include the point cloud x describing A as well as any rotation of x around 0.

The big square representing the screen is $W={[-b,b]}^2$ where the ratio $rat=b/a$ is a parameter which can be changed. We put $rat=3.$ Moreover, we draw the red square which goes to the big square in the next step. Its radius is $b/R$ where $R=\sqrt{detg}$ denotes the expanding factor of our IFS. The center of the red square is the control point of the subpiece which will be chosen in step 3. To ensure the correctness of step 3, the red square must be contained in $W.$ Since the center of the red square is in the small black square, this condition is fulfilled if $b=rat·a\ge a+b/R$ or $rat\ge R/(R-1).$ So, $rat$ should be taken larger than $R/(R-1)$ but not too large because of the computational effort.

For step 2, the simplest choice of a random $i\in \{1,\dots ,m\}$ is uniform. This is realized by the command scenery(g,H,nit,np,0). Successive magnifications with uniform choice can be boringly repetitive, however. In particular, when the attractor contains islands as in Figure 1, smaller islands will be regularly visited. For that reason, we wrote the empirical procedure greedychoice which leads somewhat faster to interesting places with many neighbors. When the parameter w in the command scenery(g,H,nit,np,w) is larger than 0, subpieces with a greater number of neighbors will be favored. 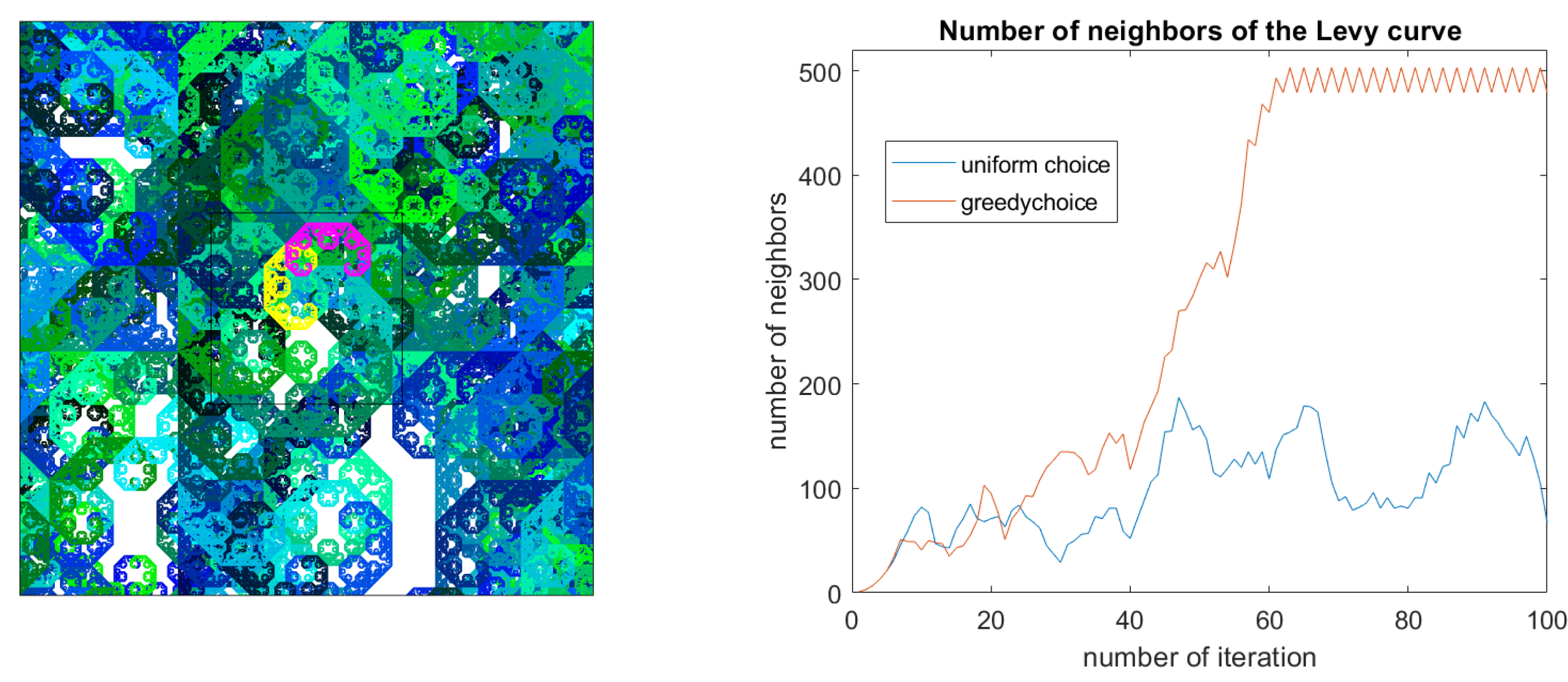The weights will be the numbers of neighbors to the power of $w.$ (The window for those neighbors is chosen smaller than the large square, however.) In our experiments, $w=3$ performed well, as shown in Figure 2. A deterministic choice of subpiece i is also possible, taking the vector $w=i_1{i}_2\dots i_n$ as an input parameter of scenery(g,H,nit,np,w). The program then produces n iterations, and in the case $nit>n$ continues with random choices according to $w=3.$ The vector of the actually chosen $i_1,i_2\dots i_{nit}$ is an output of the program scenery. Thus, an interesting magnification series can be repeated, extended and modified.

The direction matrix D of the reference piece is calculated recursively, starting with an initial unity matrix for $A.$ Suppose the actual piece $A_u=f_u\left(A\right)$ has direction D and the subpiece $A_{ui}=f_u\left(f_i\left(A\right)\right)$ was selected. Since $f_i=g^{-1}{h}_i,$ the new direction is $D{g}^{-1}{s}_i/R.$ Division by R is necessary to keep an isometry matrix. (For very large numbers of iterations, this calculation can be modified to minimize numerical errors.)

Step 3 is performed by the procedure nbmaps.m. We select the neighbor maps h for $A_u$ in such a way that they include all the sets which hit the screen $W.$ It is here that we move from potential neighbor sets to those whose control point is in the vicinity.

Proposition 2.

Suppose $A\subseteq B_{\kappa }\left(0\right)$ and $W\subseteq B_{\lambda }\left(0\right)$ and $h\left(x\right)=sx+t$ is a neighbor map with isometry matrix s and translation vector $t,$ and $\left|t\right|>\kappa +\lambda .$ Then, $h\left(A\right)\cap W=\varnothing .$

This is easy to see. Since $h\left(A\right)\subseteq B_{\kappa }\left(t\right),$ the existence of a point $y\in h\left(A\right)\cap W$ would contradict the triangle inequality for $0,y,$ and $t.$ To apply this to our squares, let $\kappa =\sqrt{2}a$ and $\lambda =\sqrt{2}b.$ Then, the assumptions of the proposition are fulfilled for our attractor A and our screen $W.$ Let t be the translation vector of a neighbor map $h.$

$$If\left|t\right|>\sqrt{2}(a+b)\mathrm{then}h\left(A\right)\mathrm{does} \mathrm{not} \mathrm{intersect} \mathrm{the} \mathrm{screen}W.$$

(7)

So, all neighbor maps with this condition are cancelled from our list in each step. In two dimensions, this works well, although some remaining neighbor maps miss the screen, too.

When $A_u$ is drawn as a central piece, the list of neighbor maps $h=f_u^{-1}{f}_v$ comprises all neighbor sets $A_v$ which intersect the screen $W.$ Now, we select a subpiece $A_{ui}$ and draw the red square which goes to W in the next step. Since the red square is contained in W by the choice of $rat,$ the neighbor sets of $A_{ui}$ must be of the form $A_{vj}$ where $A_v$ is a neighbor of $A_u.$ So, we obtain the list of neighbor maps for $A_{ui}$ by applying Equation (6) to all maps h in the list for $A_u$ and $j=1,\dots ,m.$ Again, we drop the neighbor maps which fulfill (7).

The number of remaining neighbors is saved in every step and is an output of the program. So, the full command is z=scenery(g,H,nit,np,w) where z is a $2\times nit$ matrix. The upper line contains the indices $i_1,i_2,\dots ,$ and the lower line contains the number of neighbors at each step. They give insight into the change of density of pieces during magnification and on the computational effort, as shown in Figure 2.

Step 4 of our algorithm needs no explanation. It involves matrix multiplications and graphics operations which in the presence of many neighbors require a lot of time. It is possible to skip this step and perform only the neighbor calculations. One may like to see only a few magnifications on screen and evaluate the other pictures statistically. In our version, step 4 is regularly performed. This allows us to correct the neighbor list and take only those neighbors for which the cloud includes points on our screen.

6. Remarks on the Program and the Data Files

A starting point for explorative work. MATLAB was designed 40 years ago as a toolbox for experiments with matrices with a very simple and intuitive language. This is exactly what we need here. The language has become a standard. Now, the system is slow, but it is still available at most universities, and there is a free version, Octave. Our procedures are small. You can easily change the data, the parameters or the whole procedure. If you prefer to program in another environment, like Julia, R, Python, C++, Maple etc., you can transfer our algorithm.

Instead of making the program fast and the graphics beautiful, we focused on simplicity, transparency, and accessibility. Our program contains no black box.

Six families of data. We recommend to proceed with the data in lexikographic order. The letter A marks simple examples for which the magnification process can be easily followed. They can be run with $nit=6$ and $np=5$ in order to gather some experience with the method. Later, you might prefer $np=0.$

The relatives of the Sierpiński gasket, mostly taken from [6] and including Figure 1, are distinguished by the letter B. They all have three maps, expanding factor $R=2$ and Hausdorff dimension ${\displaystyle \frac{logm}{logR}}={\displaystyle \frac{log3}{log2}}\approx 1.58.$ The IFS values from [6] were taken without change, and some of them have the control point 0 outside $A.$ This does not matter, however, as long as 0 and A and thus all $f_j\left(0\right)$ belong to the small black square. These examples perform well with large $nit$ values and can be easily modified.

The data files marked with the letter C use $g=2\pm i$ as an expanding map so that pieces are rotated by 26.6° in each magnification step. These IFSs contain four maps. Their Hausdorff dimension is ${\displaystyle \frac{log4}{log\sqrt{5}}}\approx 1.72.$ The symmetries are again 90° rotations. All IFSs designated by A, B, C are small integer data with the open set condition (OSC), permitting unlimited magnification. Since integer variables are not declared in our implementation, however, they are taken as floating-point numbers, which could result in significant error propagation for very large $nit$ values. We checked that $nit=1000$ causes no problems. When there is a number at the end of the file name, it denotes the number of proper neighbors and indicates in some way the complexity of the IFS.

The other examples show that the program works well even for non-integer data and IFSs without the open set condition. There are some restrictions, so $nit<30$ is recommended for the beginning. The family marked by D is related to the hexagonal lattice and rotations by multiples of 60°. D1 up to D3 have expanding map $g=(5\pm i\sqrt{3})/2$ with $R=\sqrt{7},$ and $m=6$ mappings, which yields the Hausdorff dimension ${\displaystyle \frac{logm}{logR}}\approx 1.95.$ They fulfill the OSC and provide very interesting, natural-looking patterns. D4 is a non-periodic tile with three pieces and $g=(3+i\sqrt{3})/2.$ In example D5, we have the same m and g but obviously not a tile. Here, two pieces of the second level coincide. To treat such ’exact overlaps’ efficiently, the program has to be modified so that it counts multiple occurences of the same neighbor piece only once. All these examples on the hexagonal lattice can be mapped into integer data by a linear coordinate transformation.

The three examples designated by the letter E come from a Pisot number of degree four and integer data projected from four-dimensional space, as explained in ([26] Section 4). They all have exact overlaps. The final group of examples with F are definitely not integer data. They have no exact overlaps and do probably not fulfill the OSC. For ’fatfireworks’, we replaced the factor $g=2$ of the ’fireworks’ example in family B by $g=\sqrt{3}.$ If this would fulfill the OSC, it must be a tile. Our program suggests that this is not the case. In F2 and F3, three incommensurable rotations were used together with both values of $g.$ In the ’fat’ case, we have no tile and thus no OSC. The ’slim’ case is hard to decide. In the final example, F4, we have replaced $g=2$ by the affine map $g\left(x\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{2.30}{02}}\right)x.$ The attractor is not self-similar, but the program calculates $R=\sqrt{2.3·2}.$ If there were no rotations, magnifications would show line fibers, since the contractions in horizontal and vertical directions differ. With 90^o rotations, the scenery flow shows patterns such as in the self-similar examples for many iterations. This observation was unexpected.

Simple and more complex cases. For integer data IFSs in two dimensions, the finite type condition holds ([26] Section 1). This means that there are only finitely many proper neighbor maps. We can use Proposition 1 and (7) to estimate directly the number of possible neighbor maps $h\left(x\right)=sx+t$ which intersect our window $W.$ According to (7), the integer vector t is in the circle with radius $\sqrt{2}(a+b)$ around 0, where a is the radius of A and $b=rat·a.$ For our value $rat=3,$ there are

$$\mathrm{at} \mathrm{most} 8{(a+b)}^2=128a^2\mathrm{translation} \mathrm{vectors}t\mathrm{and}\left|S\right|·128a^2\mathrm{neighbor} \mathrm{maps}.$$

(8)

Here, $\left|S\right|$ denotes the number of possible symmetries s, which is 4 for the data files with A, B, and C. So, we have 500 possible neighbor maps when the radius of A is 1 and 500 millions when the radius of A is 1000 (or when the radius is one, and the translations are not integers but decimals with three digits). The size of A matters a lot.

Although the upper bound in (8) need not coincide with the actual number of neighbor maps, it is a good rule that IFSs with small integers in the $v_j$ lead to a small radius of A and are tractable. Our data files A, B, and C belong to this class. It is possible to determine all neighbor maps and to organize them in the neighbor graph. From this automaton, topological properties of A can be derived, as we have shown in [6,26]. Sometimes, even a neighborhood graph can be established which collects the connections between all possible photos [20]. However, from n given neighbors, we can theoretically compose $2^n$ neighborhoods. So, the neighborhood automaton can be huge compared to our computer’s memory. If the radius of A is large, even the neighbor automaton may be too large. To evaluate such cases correctly, we probably have to apply statistical methods.

The open set condition (OSC) is fulfilled if and only if all neighbor maps are different from the identity [2,4,26]. Thus, it could be desirable to display a warning or stop the program if $h\left(x\right)=x$ for some neighbor map. This can easily be accomplished. However, there are examples without an OSC where it can take hours to find such h values. On the other hand, there are examples with an OSC where a proof of the OSC may take hours. Our experience indicates that the question ’OSC or not OSC?’ should be replaced by ’low or high complexity?’ with a gradual change from one to the other. There are various ways to measure complexity. For our setting, a measurable parameter is the maximum number of neighbors on a ’photo’.

7. How to Continue

Improvements of the program and the database. The graphics can be improved when we represent A as an image of $n_1\times n_2$ pixels and add image intensities on a matrix. This graphical representation is necessary to study IFSs of the form (1) where the $f_j$ values have different contraction factors or self-similar measures instead of self-similar sets. It is also desirable to have more interaction between users and the program. For larger examples, MATLAB has to be replaced by some faster system, like Julia.

Before you start programming, however, we urge you to test our simple package with your own IFS examples. Our data files are a tiny selection from a wide field. The command H(:,:,j)=[a b c; d e f]; will change the mapping $h_j$ in (2) to $h_j\left(x\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{ab}{de}}\right)x+\left({\displaystyle \genfrac{}{}{0pt}{}{c}{f}}\right)$ or define a new mapping for $j=m+1.$ Experiments will slow down mainly because of an abundance of neighbors. There is an emergency stop if the number of neighbors exceeds 1000. This command at the end of the program can be removed or changed. In the case of many neighbors, one pragmatic way to modify the IFS is by g=1.2*g, which increases the expansion factor and makes the attractor thinner. Feel free to find better solutions. It is not forbidden to perform numerical experiments with IFSs given by decimal numbers without regard to integers or separation conditions, or similarity maps with different contraction factors, or affine contractions.

A change in the program is needed for IFSs with exact overlaps. Either identical neighbor maps must be eliminated, or, in the case of work with image intensities, must be counted with multiplicity. If this is settled, any complex Pisot number g is a possible expansion for an IFS, and this can be considered as integer data, since g is represented by an integer matrix G in a d-dimensional space. The neighbor calculations are performed in the d-dimensional integer lattice and then projected to the two-dimensional eigenspace of G, which corresponds to the eigenvalue $g.$ The point cloud is drawn in this plane. This method, implemented in Mekhontsev’s IFStile package [9], is discussed in ([26] Section 3).

New classes of spaces. While two-dimensional self-similar sets have been investigated since 1990 by many authors, there are almost no studies of the three-dimensional case. On one hand, it is difficult to draw 3D fractals (see, however, ref. [9] and Mandelbrot-type fractal demonstrations on diverse web sites). On the other hand, there are very few integer-valued matrices of similitudes or isometries on ${\mathbb{R}}^3.$ Our program can easily be modified for the three-dimensional case. With $g\left(x\right)=2x$ and the symmetry group of the cube, we have a very rich family of examples. It is much more general than the Sierpiński relatives, since we can go from $m=3$ with dimension 1.58 up to $m=7$ with dimension 2.8. We expect new geometrical insight from such examples, even for Cantor sets. The problem is to visualize and analyze the 3D constructions. When we use our point cloud method, we need less than twice the memory for the plane for the same number of neighbors, and we will project the three dimensional point clouds to the observer’s plane. This is a first step. A good 3D representation must include light sources and ray tracing, and working with intensities instead of point clouds may require hardware beyond a PC.

A similar remark concerns the study of graph-directed IFSs. Concrete examples have been rarely studied, and their potential, in particular in 3D constructions, has not been exploited. They are implemented in [9]. We expect that in 3D, self-similar graph-directed constructions go much beyond ordinary IFSs. This question concerns mathematical exploration rather than computer programming.

Theoretical problems. So far, we have no rigorous method to decide whether a self-similar construction represents a Cantor set, although there are theoretical results [27]. This is an annoying situation especially in 3D where our eyesight can be helpless. An algorithm for disconnectedness probably has to use the neighbor graph and thus would be applicable only to relatively simple IFSs. However, one can also think about computational methods in case the set is given as a finite set of 3D pixels. If an attractor is neither connected nor a Cantor set, one would like to know the structure of its non-trivial connectivity components. In the case of self-similar sets, we conjecture that they are given by a graph-directed IFS.

In the family B of data files, there are four Cantor sets and four non-Cantor sets, which can be distinguished by magnification. We think the visualization can help understand Cantor sets and the structure of components.

All Cantor sets are homeomorphic by a classical theorem, but their metrical structure differs. By eyesight, we can distinguish the photos of different IFSs. So, it is a challenge to find rigorous methods to describe and classify Cantor sets with a fairly homogeneous structure from a metric viewpoint.

Other questions are related to our algorithm. As Figure 2 demonstrates, our empirical greedychoice procedure usually leads faster to dense patterns than the uniform choice of subpieces. Is there a rigorous method which in self-similar constructions finds the densest patterns? This is connected with the dynamical interior of $A,$ which is defined in [20] with the help of the neighborhood graph. In the case of tilings, it coincides with the topological interior. Lévy did search a long time for an interior point in his curve, which he found in 1937. As Figure 2 indicates, we needed more than 50 steps of random magnification to have the window completely filled with neighbor curves. What is the fastest algorithm to find an interior point in a complicated self-similar tile? Which methods can extract geometric information from the ’photos’? While colleagues from science have their specific methods to describe soil, smoke and snow, we should have some methodology to understand simple mathematical model sets.