A Novel Red-Billed Blue Magpie Optimizer Tuned Adaptive Fractional-Order for Hybrid PV-TEG Systems Green Energy Harvesting-Based MPPT Algorithms
Abstract
1. Introduction
- This research develops a PV-TEG hybrid system that synergistically enhances solar energy conversion by recycling waste heat, increasing output density, and extending PV module lifespan. A novel fractional-order controller with an optimized design is integrated to advance MPPT in PV-TEG systems, thereby improving energy harvesting efficiency and system reliability.
- A novel adaptive fractional-order controller (FOPID) based MPPT in PV-TEG hybrid mechanism systems, designed to exploit the advantages of fractional dynamics for faster and more robust tracking under fluctuating conditions. To ensure optimal performance, the controller’s gains are simultaneously tuned using the RBBMO, which efficiently searches the parameter space and overcomes the limitations of traditional element-by-element tuning. This integration enables improved convergence, reduced steady-state oscillations, and enhanced energy harvesting efficiency compared with conventional approaches.
- Five case studies are conducted under varying temperature, irradiance conditions, and partial shading to validate the proposed framework. A comprehensive evaluation approach is introduced, incorporating both technical performance and environmental considerations. Comparative analysis with several optimization algorithms is carried out, and statistical validation confirms the superior efficiency and robustness of the proposed RBBMO-based controller optimization.
- Compared with eight baselines, AOS (Atomic Orbital Search Optimization Algorithm), PSO (Particle Swarm Optimization), MFO (Moth–Flame Optimizer), SSA (Salp swarm algorithm), GHO (Grasshopper Optimization), RSA (Reptile Search Algorithm), AOA (Arithmetic Optimization Algorithm), and P&O, the proposed tracker is consistently the fastest and most energy-efficient: it reaches 95% of the MPP in 0.06 s, settles within 0.12 s (±1%), and harvests 1950 W·s at start-up (vs. 1910 W·s for AOS, 1880 W·s for PSO, and 200 W·s for P&O).
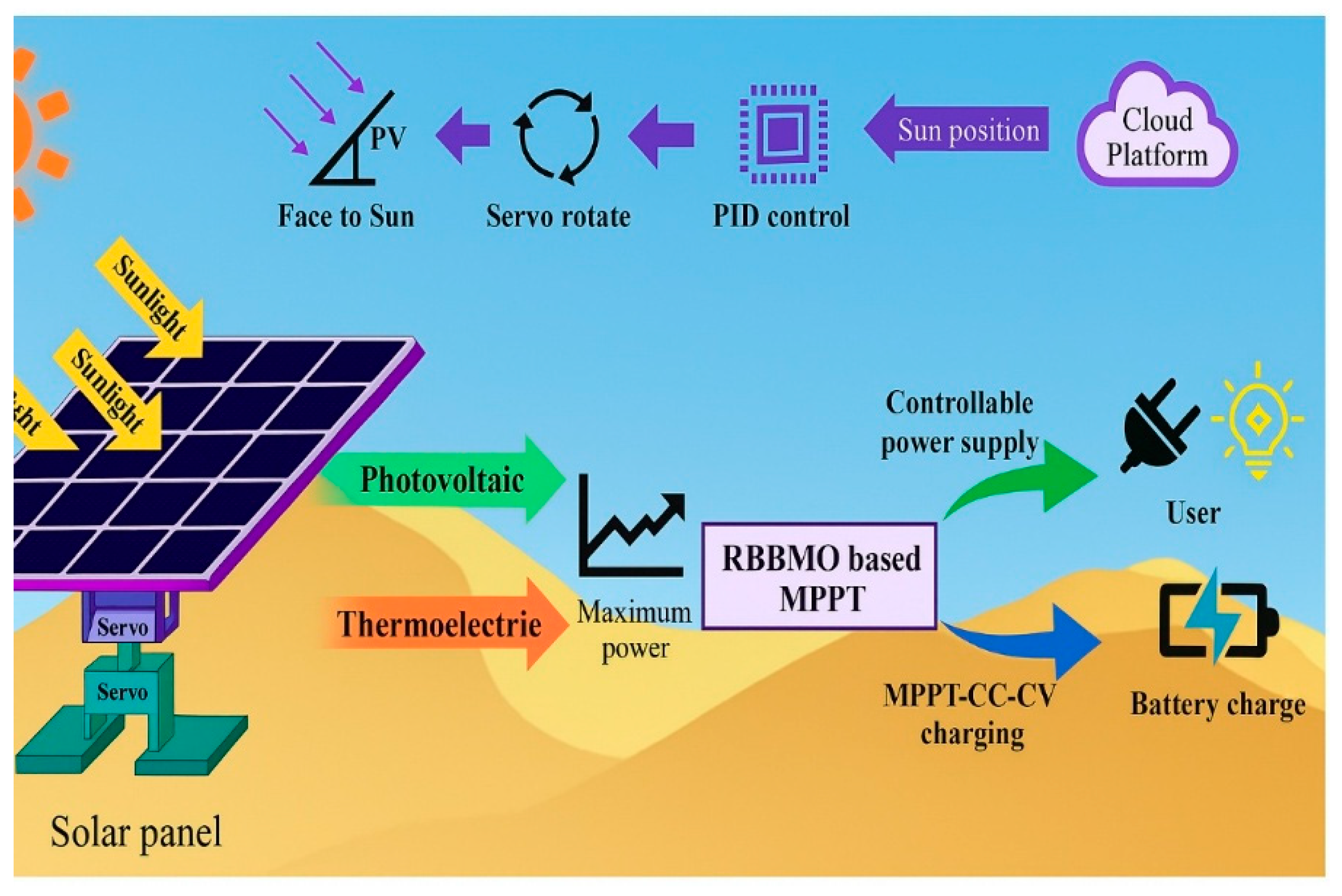
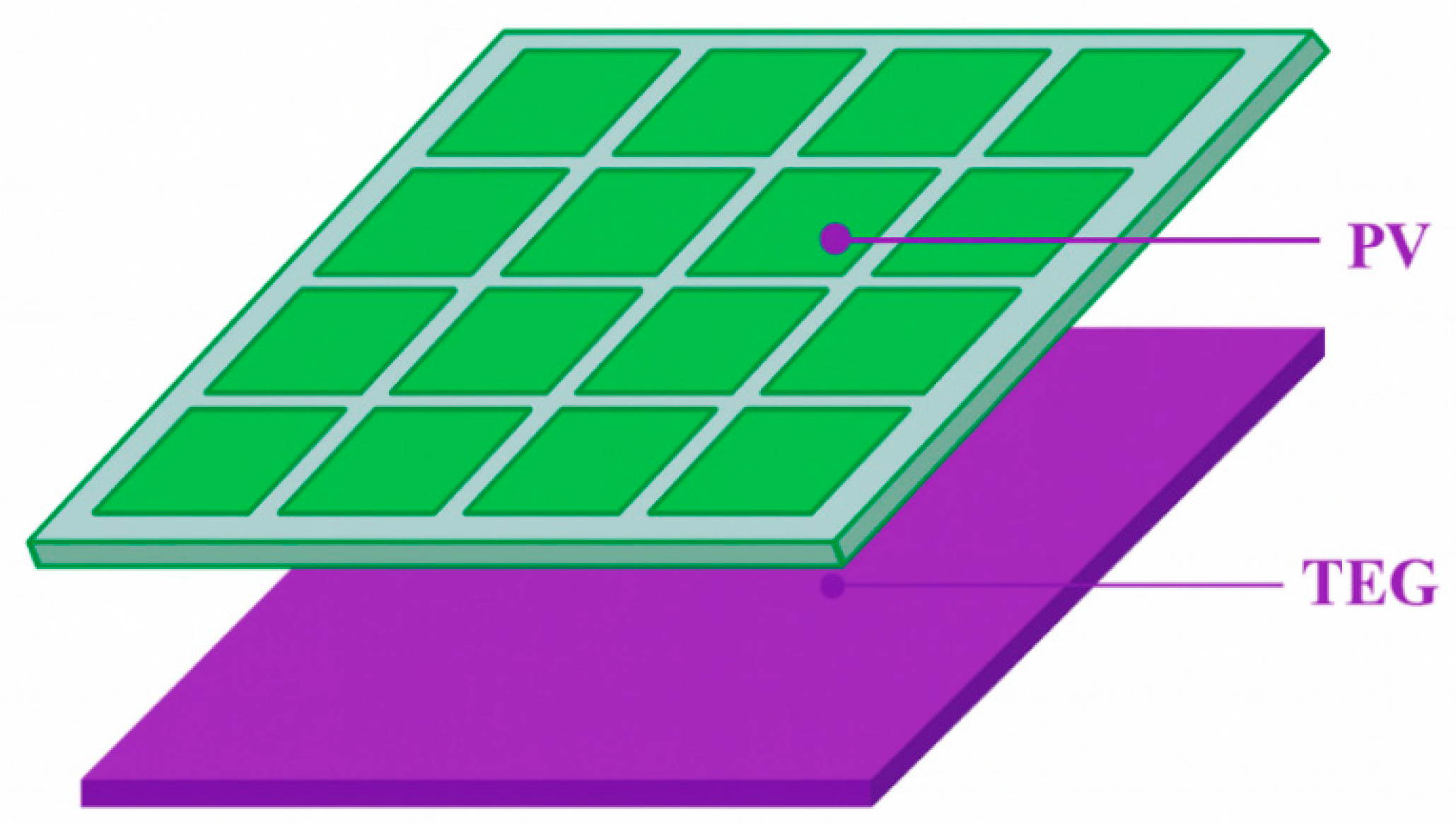
2. PV-TEG Hybrid System Modeling
2.1. PV Model
2.2. TEG Modeling
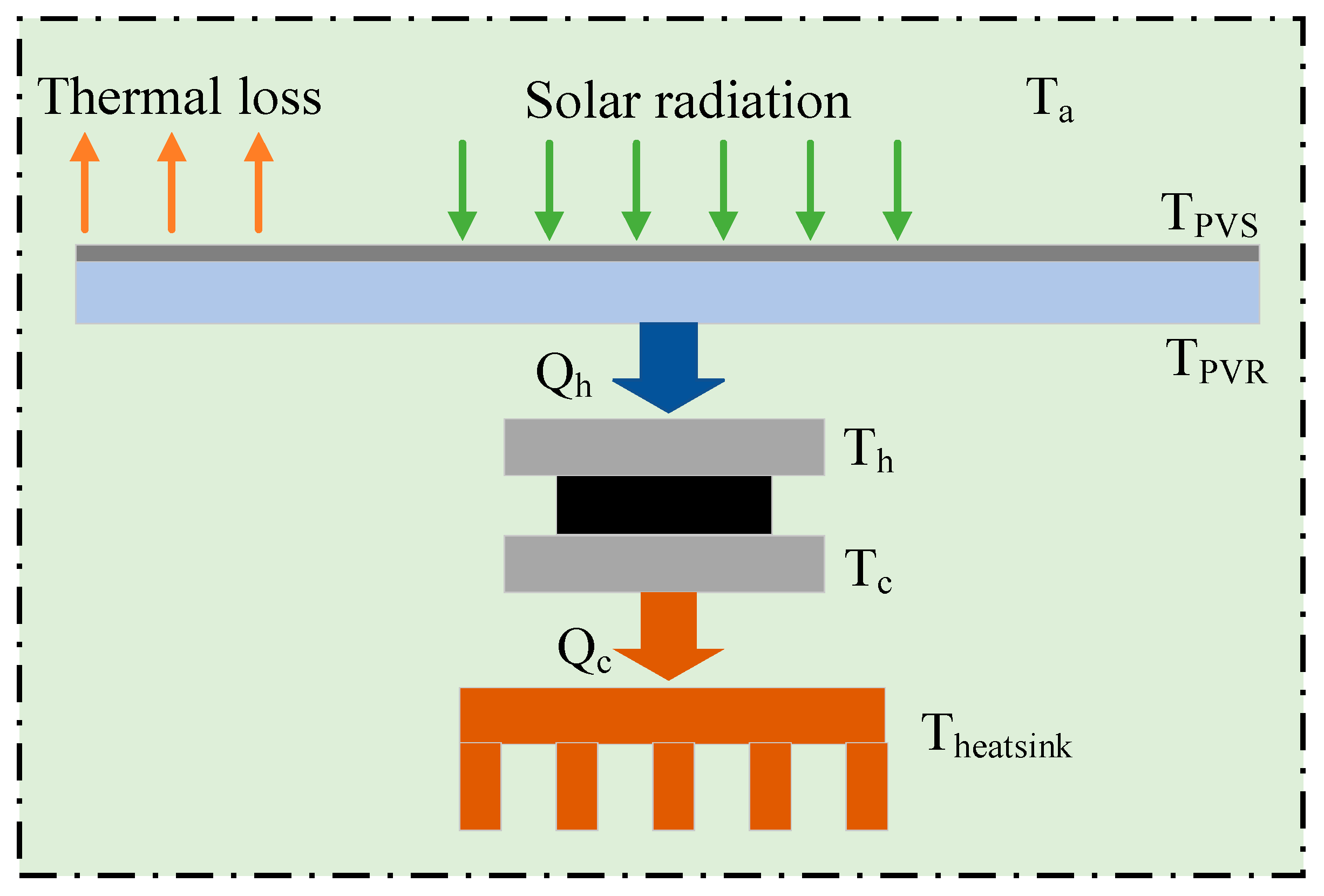
2.3. Hybrid PV-TEG Modeling
2.3.1. Thermal Decoupling and Safe Operating Limits
2.3.2. Compact Thermal Model and Implications
2.3.3. Energy Accounting and Units
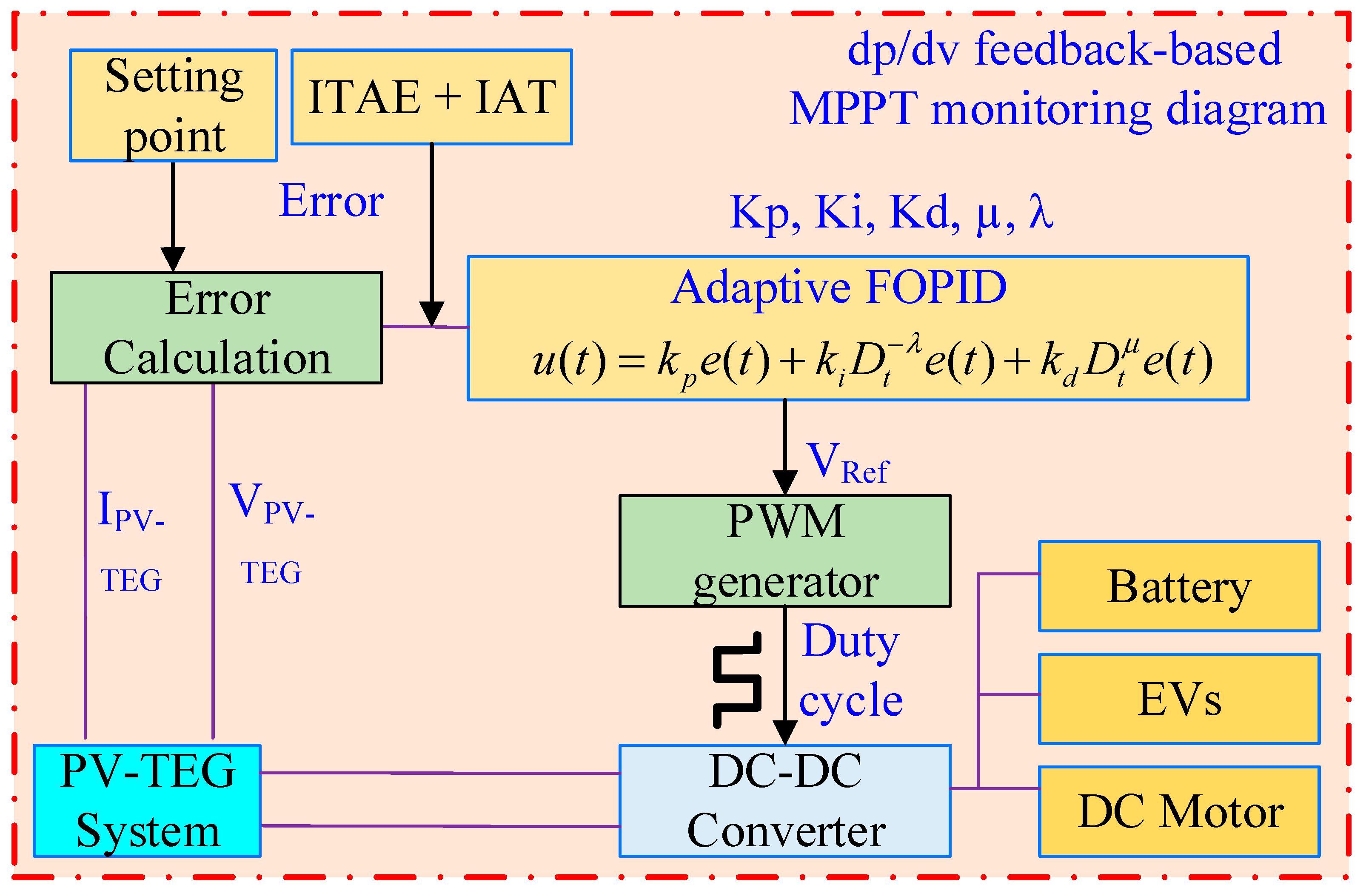
3. Development of Proposed FOPID Optimized by RBBMO-Based MPPT Method
3.1. Control System Based on the MPPT dp/dv Evaluation Mechanism
3.2. Fractional Calculus
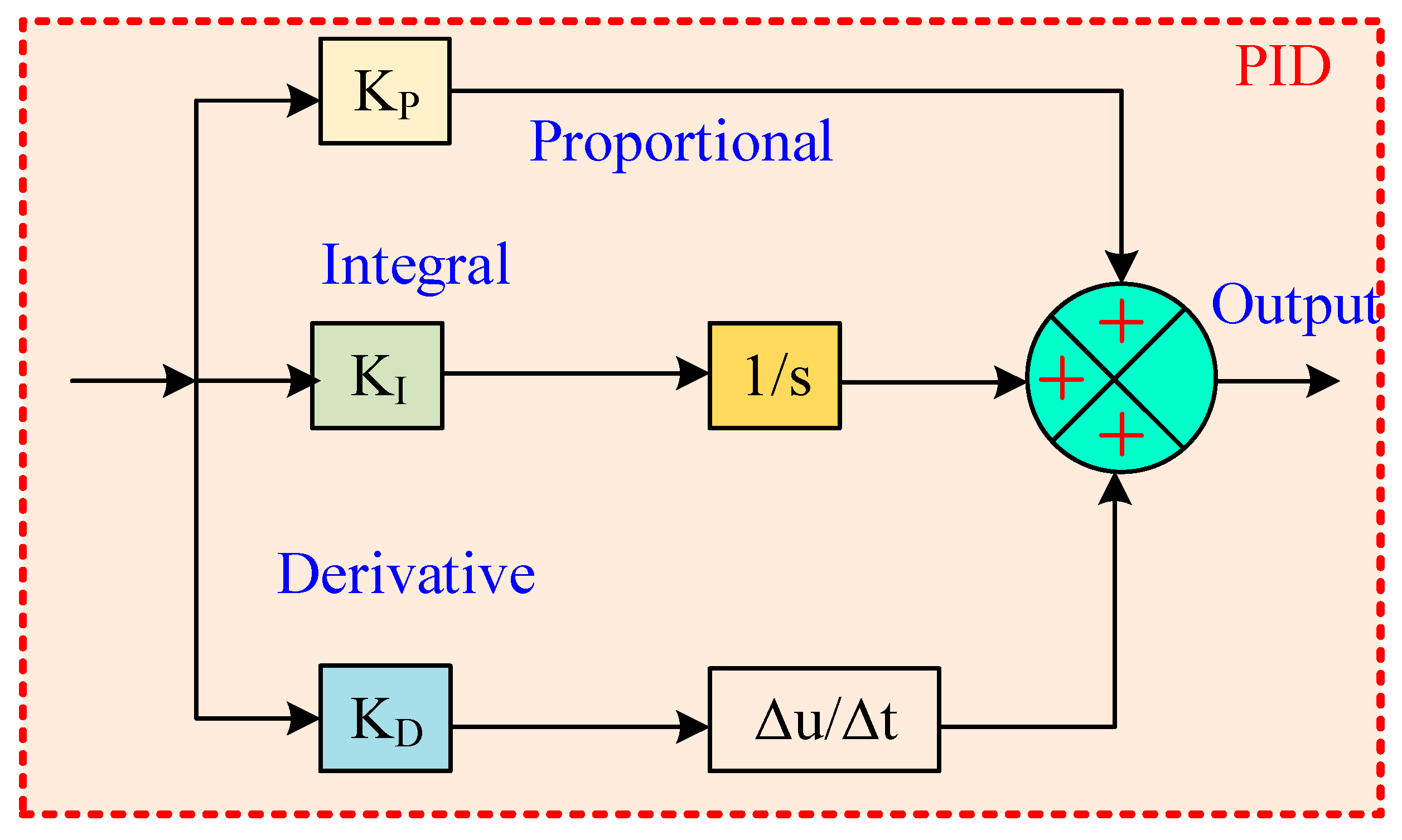
3.3. Classical PID Controller Description
3.4. Classical Fractional-Order PID Controller Description
3.5. Adaptive FOPID Tracker for PV-TEG System
3.6. RBBMO
3.6.1. Initialization
3.6.2. Seeking Food
3.6.3. Attacking Prey
3.6.4. Storing Food
3.7. RBBMO for Adaptive FOPID MPPT
3.8. Controller and Optimizer Reproducibility
3.9. Converter Topology, Timing, and Sizing
4. Results and Discussions
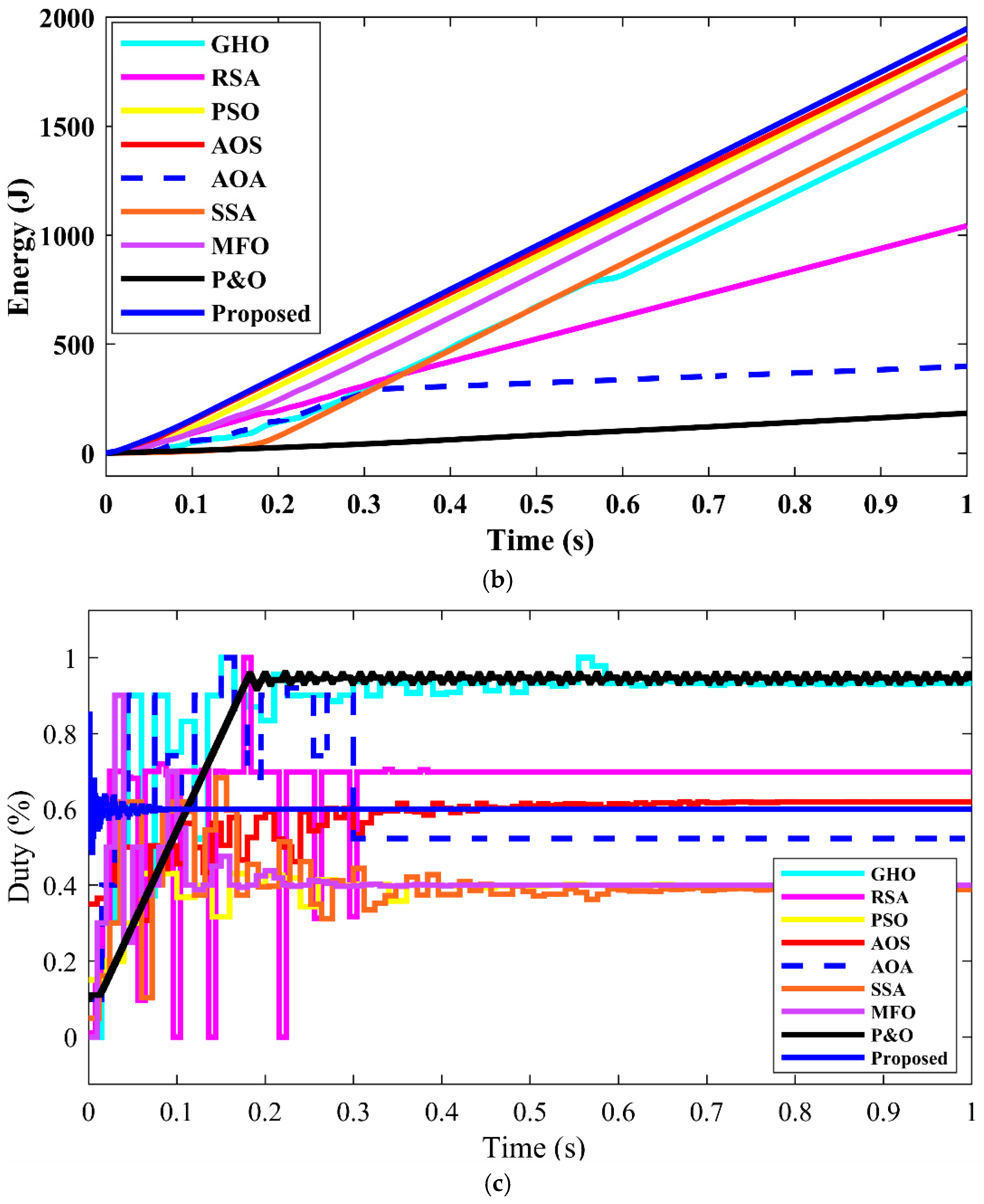
4.1. Start-Up/Phase Search Assessment
4.2. Stepwise Irradiance with Constant Temperature
4.3. Partially Shaded Conditions
4.4. Gradually Load Steps with Constant Conditions
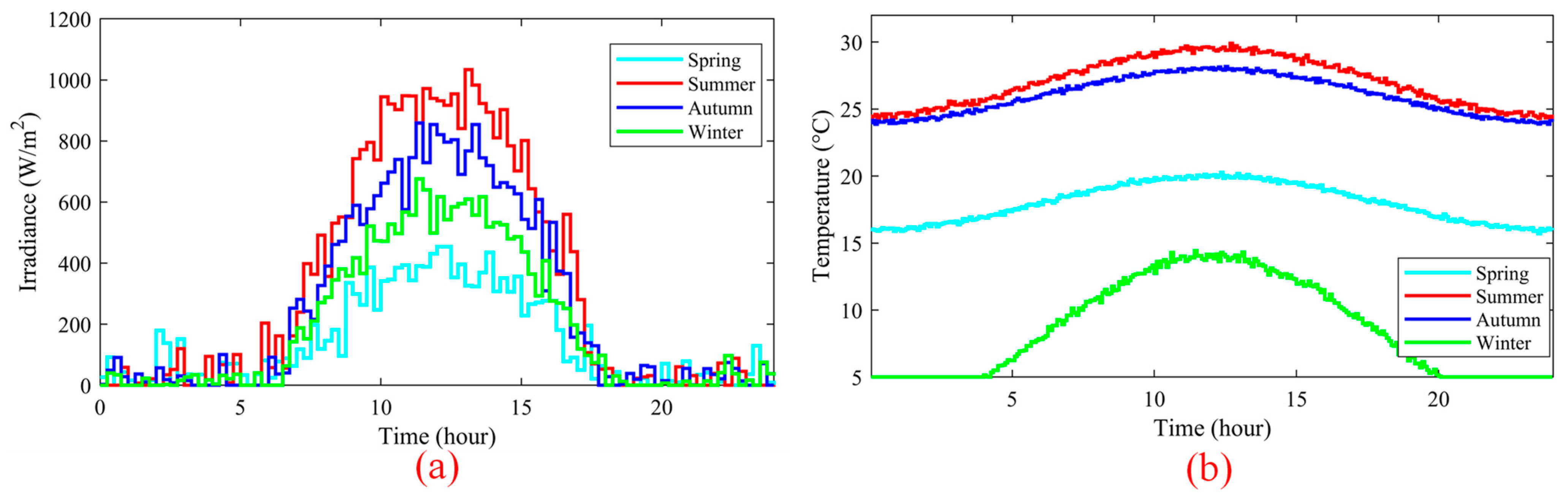
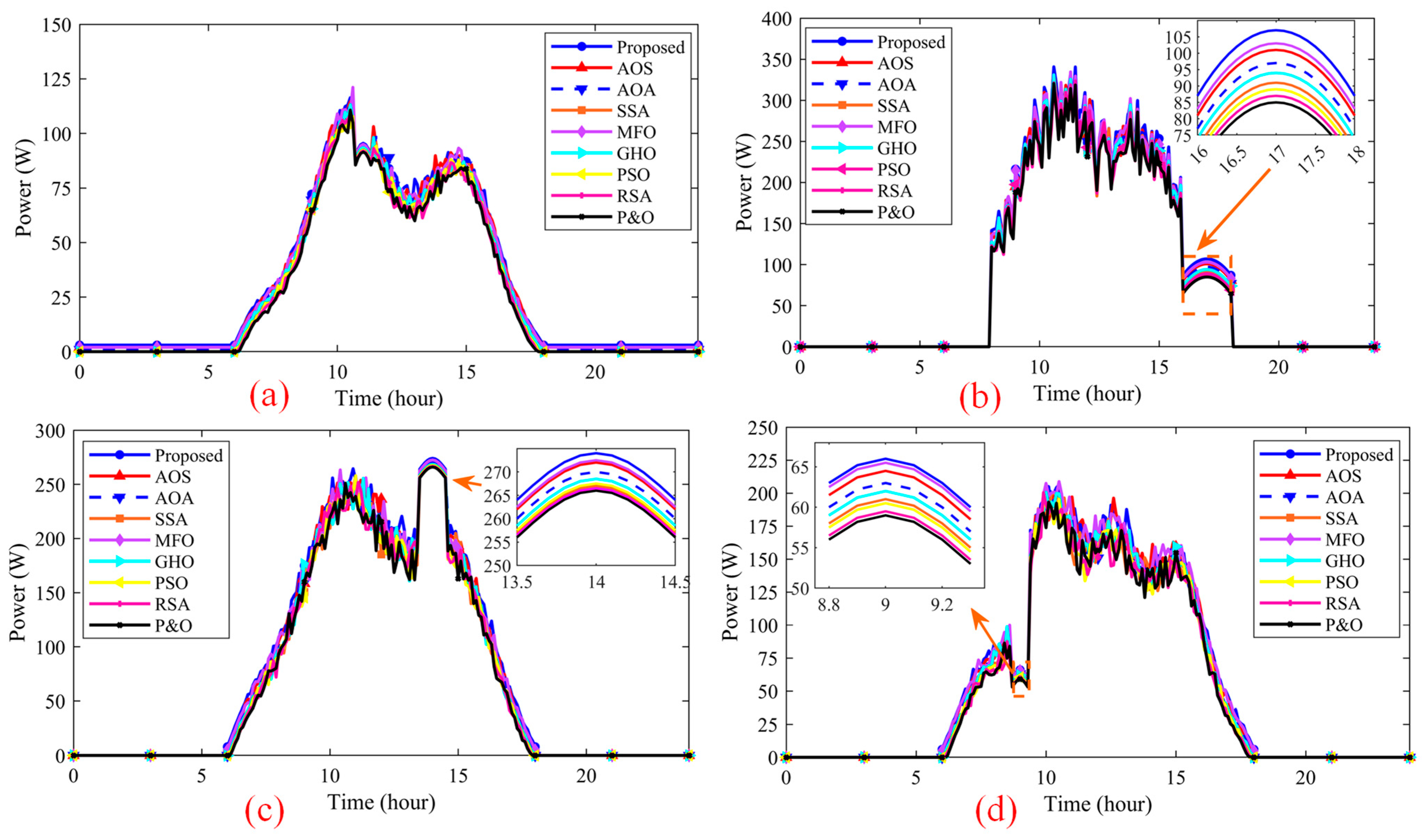
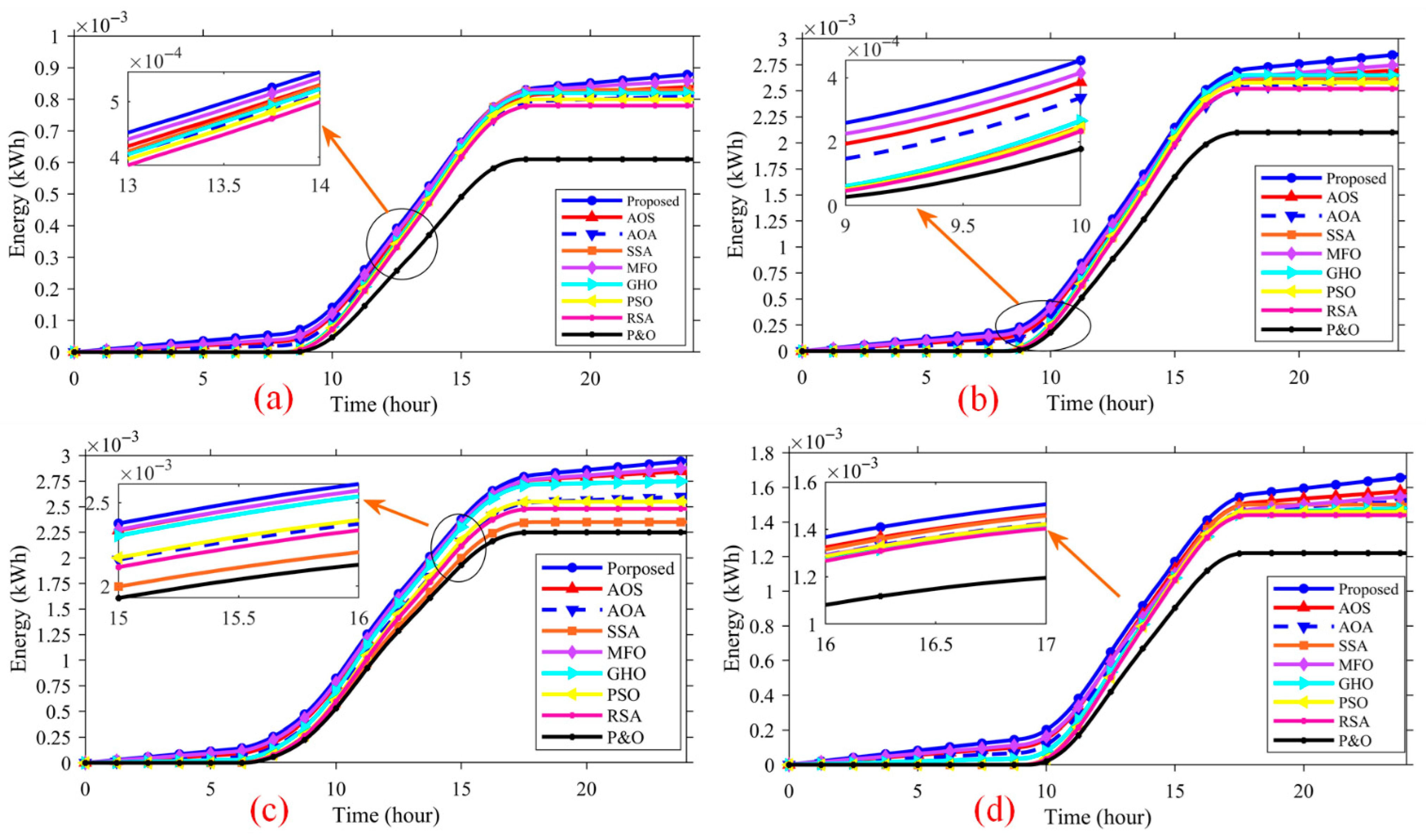
4.5. Field-Measured Irradiance and Temperature in Shanxi Province, and Seasonal MPPT Performance
- Spring (Figure 23a): proposed 0.88 × 10−3 kWh vs. AOS 0.85, AOA 0.83, PSO 0.82, RSA 0.80, P&O 0.72 → 3–8% better than the strongest baseline and 20% over P&O.
- Summer (Figure 23b): proposed 2.95 × 10−3 kWh vs. AOS 2.85, AOA 2.75, GHO/MFO/SSA 2.70–2.80, P&O 2.10 → 3–7% over the best competitor and 30% over P&O.
- Autumn (Figure 23c): proposed 2.90 × 10−3 kWh vs. AOS 2.80 and others 2.60–2.75 → 3–10% higher.
- Winter (Figure 23d): proposed 1.55 × 10−3 kWh vs. AOS/RSA 1.48–1.50 and P&O 1.20 → 3–5% over the best baseline and 25–30% over P&O.
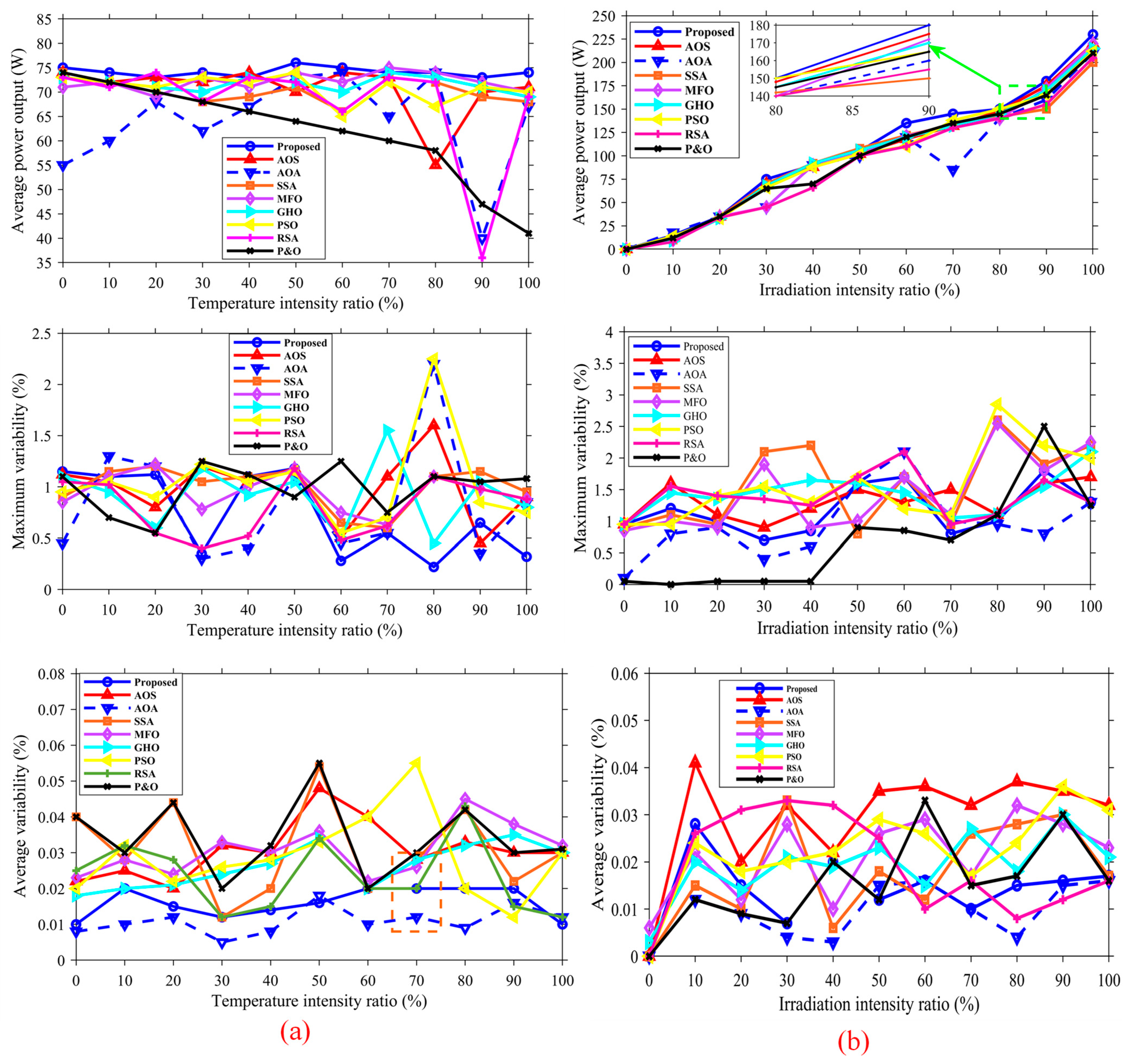
4.6. Robustness Evaluation Under Environmental Uncertainty
4.6.1. Temperature Variation Test
- Average power (Figure 24a). All methods show the expected downward trend with rising temperature, but the RBBMO-tuned adaptive FOPID sustains the highest power at every operating point and degrades the least: it drops only 2.74% (from 75.55 W to 73.48 W). In contrast, RSA falls from 74.17 W to 63.55 W (14.32%), and the deterministic P&O suffers the sharpest decline, from 68.89 W to 41.49 W (40%). Several meta-heuristics also exhibit temperature-sensitivity spikes (e.g., abrupt dips near 80–90% intensity), indicating susceptibility to thermally induced local optima.
- Maximum variability (Figure 24a). The proposed method maintains low and flat Δvmax across the sweep and levels off beyond 50% intensity, evidencing strong convergence stability at higher temperatures. Some competitors (e.g., AOA, GHO) show isolated spikes up to 2% around 70–80%. Notably, P&O appears near-zero in variability, but this reflects early stagnation near a suboptimal LMPP, not robustness, consistent with its low Pavgout.
- Average variability (Figure 24a). While AOA attains a relatively small Δvavg in mid-range temperatures, it does so with lower power levels than the proposed method. The RBBMO-FOPID achieves a similarly low variability band (0.01–0.03%) and maintains the highest average power, yielding the best overall stability, performance trade-off.
4.6.2. Irradiance Variation Test
- Figure 24b shows the expected monotonic rise of the average power output with irradiance for all methods; however, the RBBMO-tuned adaptive FOPID remains highest across the range and becomes the clear leader for irradiance ≥ 80%. At 100% irradiance, the proposed method delivers 230–235 W, exceeding AOS by 2–4%, GHO/MFO by 5–8%, PSO by 8–10%, and P&O by 15%. A pronounced dip around 70% is visible for AOA, suggesting a convergence slip toward a suboptimal operating point.
- The maximum variability results in Figure 24b indicate that the proposed controller maintains a low and smooth profile (generally ≤ 1–1.5%), whereas most meta-heuristics (e.g., AOA, RSA, AOS, SSA) exhibit spikes, especially in the low-irradiance zone (5–30%) where the MPP signal is weak and search becomes noise-sensitive. For example, RSA shows a sharp rise in variability from 0% to 10% irradiance (95% relative increase). Although P&O appears to have very low variability, this stems from early stagnation near a local optimum, consistent with its lower average power.
- Figure 24b (average variability) shows a similar story: the proposed method tracks with consistently low values (0.01–0.02%) and no abrupt excursions, while competitors exhibit multiple peaks up to 0.03–0.05%. AOA attains low variability in some intervals, but at the cost of lower power.
4.7. Techno-Environmental Assessment
- Start-up/search phase (1 s window). The RBBMO-tuned adaptive FOPID (Proposed) obtains the highest energy (1950 W·s), beating AOS (+2.1%), PSO (+3.7%), MFO (+9.6%), SSA (+18.2%), GHO (+21.9%), RSA (+85.7%), AOA (+364%), and P&O (+875%). It also exhibits the lowest fluctuations among meta-heuristics (Δvmax = 13.0%, Δvavg = 0.15%), roughly 50–75% lower than typical baselines (AOS 26%, PSO 32%, … AOA 58%). This indicates fast settling with minimal overshoot.
- Stepwise variations in irradiance. Energy after 1 s is 965 W·s for the proposed controller—higher than AOS (+7.2%), GHO (+9.7%), RSA (+16.3%), AOA (+22.2%), MFO (+30.4%), P&O (+39.9%), and far above PSO (+135%) and SSA (+69%). Stability is again superior (Δvmax = 20.3%, Δvavg = 0.32%), the smallest among meta-heuristics (others range Δvmax = 23.5–39% and Δvavg = 0.34–0.62%). The controller reacquires each new MPP quickly and limits oscillation losses.
- Partial shading. The proposed method consistently locks onto the global peak, delivering 1950–2000 W·s, exceeding AOS by ~1–3%, MFO/GHO by ~8–12%, and RSA/PSO by ≥15% (AOA and P&O trail further). Fluctuations remain the lowest class (Δvmax = 18.0%, Δvavg = 0.28%; others typically 25–38% and 0.40–0.60%). This confirms robust global MPP tracking and a stable, steady state.
- Field-measured irradiance and temperature (Shanxi Province, four representative days). Daily energy is the largest for the proposed in each season: Spring: 0.00088 kWh (3–10% above most baselines). Δvavg = 0.0254% (top-tier; only GHO is slightly lower at 0.0214%). Summer: 0.00295 kWh (3–9% above strong baselines). Δvavg = 0.0342% (within the low group). Autumn: 0.00290 kWh (4–9% advantage). Δvavg = 0.0269% (among the lowest). Winter: 0.00155 kWh (3–8% advantage). Δvavg = 0.0240% (lowest or co-lowest). Across seasons, the proposed controller pairs higher energy yield with small average fluctuations (≈0.024–0.034%), maintaining a favorable energy–stability trade-off under real weather variability.
5. Conclusions
- Start-up/search: t95 = 0.06 s and settling = 0.12 s with 1950 W·s energy (closest baseline AOS 1910 W·s).
- Stepwise irradiance: ≥95% reacquisition in 0.06–0.08 s, settling 0.12–0.15 s, and 0.95–0.98 kJ energy at 1 s; ripple ≈ ±1%, about 30% average stability improvement vs. SSA.
- Partial shading: reliable escape from local peaks and lock-in to the global peak with 1.95–2.00 kJ at 1 s (AOS 1.90–1.96 kJ; PSO ≈ 1.70 kJ); duty jitter ≈ ±1%.
- Load steps: fastest reacquisition at every step (0.06–0.08 s to 95%), smallest transient dips (≈5–8%), and tight duty control.
- Field data (Shanxi Province): daily energies of 0.88 × 10−3, 2.95 × 10−3, 2.90 × 10−3, 1.55 × 10−3 kWh in spring/summer/autumn/winter, exceeding the strongest baseline by 3–10% and P&O by 20–30%. Seasonal variability is low (e.g., Δvmax = 8.43–9.43% and Δvavg = 0.024–0.034% for the proposed tracker), whereas P&O’s apparently small variability stems from premature stagnation and low energy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Parameter | Value | Unit | Source/Note |
|---|---|---|---|---|
| α | Seebeck coefficient (module) | 215 | µV/K | Datasheet, 25 °C |
| Rint | Internal resistance | 4.2 | Ω | Measured (4-wire), 25 °C |
| K | Thermal conductance (hot–cold) | 1.8 | W/K | Datasheet |
| ZT | Figure of merit (avg) | 0.9 | – | Manufacturer typical |
| ATEG | TEG contact area | 40 × 40 | mm2 | Geometry |
| tTIM | TIM thickness | 100 | µm | Specified adhesive |
| Rth,c | Contact thermal resistance | 0.15 | K/W | Vendor app note |
| (kPV | PV backsheet conductivity | 0.2 | W·m−1·K−1 | Literature |
| tPV | PV backsheet thickness | 0.3 | mm | Literature |
| Rth,hs | Heat-sink thermal resistance | 3.0 | K/W | Heatsink datasheet |
| hback | Back-side convection coeff. | 10 | W·m−2·K−1 | No-wind assumption |
| G | Irradiance | 1000 | W·m−2 | Case study |
| T | Ambient temperature | 25 | °C | Case study |
| Δt | Simulation time step | 0.1 | s | Transient run |
References
- Ibrahim, A.-W.; Farh, H.M.H.; Al-Shamma’a, A.A. A Comprehensive Review of MPPT Strategies for Hybrid PV-TEG Systems: Advances, Challenges, and Future Directions. Mathematics 2025, 13, 2900. [Google Scholar] [CrossRef]
- Abbassi, R. Design of a Novel Chaotic Horse Herd Optimizer and Application to MPPT for Optimal Performance of Stand-Alone Solar PV Water Pumping Systems. Mathematics 2024, 12, 594. [Google Scholar] [CrossRef]
- Dong, F.; Li, Y.; Gao, Y.; Zhu, J.; Qin, C.; Zhang, X. Energy transition and carbon neutrality: Exploring the non-linear impact of renewable energy development on carbon emission efficiency in developed countries. Resour. Conserv. Recycl. 2022, 177, 106002. [Google Scholar] [CrossRef]
- Fan, S.; Wang, Y.; Cao, S.; Sun, T.; Liu, P. A novel method for analyzing the effect of dust accumulation on energy efficiency loss in photovoltaic (PV) system. Energy 2021, 234, 121112. [Google Scholar] [CrossRef]
- Zaky, A.A.; Ibrahim, M.N.; Taha, I.B.M.; Yousif, B.; Sergeant, P.; Hristoforou, E.; Falaras, P. Perovskite solar cells and thermoelectric generator hybrid array feeding a synchronous reluctance motor for an efficient water pumping system. Mathematics 2022, 10, 2417. [Google Scholar] [CrossRef]
- Amalu, E.H.; Fabunmi, O.A. Thermal control of crystalline silicon photovoltaic (c-Si PV) module using Docosane phase change material (PCM) for improved performance. Sol. Energy 2022, 234, 203–221. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, T.; Cai, J.; Fan, Y.; Shi, Z. Investigation on the operating characteristics of a directly-attached light crystalline silicon PV roof. Sol. Energy 2023, 262, 111849. [Google Scholar] [CrossRef]
- Jamali, E.; Nobakhti, M.H.; Ziapour, B.M.; Khayat, M. Performance analysis of a novel model of photovoltaic PV-TEGs system enhanced with flat plate mirror reflectors. Energy Convers. Manag. 2023, 279, 116766. [Google Scholar] [CrossRef]
- Eikeland, O.F.; Kelsall, C.C.; Buznitsky, K.; Verma, S.; Bianchi, F.M.; Chiesa, M.; Henry, A. Power availability of PV plus thermal batteries in real-world electric power grids. Appl. Energy 2023, 348, 121572. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, D.; Dai, Z.; Wang, C.; Zhu, L.; Zhang, J.; Xu, G.; Zhang, X. A passive evaporative cooling strategy to enhance the electricity production of hybrid PV-STEG system. Appl. Energy 2023, 349, 121689. [Google Scholar] [CrossRef]
- De Luca, D.; Strazzullo, P.; Di Gennaro, E.; Caldarelli, A.; Gaudino, E.; Musto, M.; Russo, R. High vacuum flat plate photovoltaic-thermal (HV PV-T) collectors: Efficiency analysis. Appl. Energy 2023, 352, 121895. [Google Scholar] [CrossRef]
- Tyagi, K.; Gahtori, B.; Kumar, S.; Dhakate, S.R. Advances in solar thermoelectric and photovoltaic-thermoelectric hybrid systems for power generation. Sol. Energy 2023, 254, 195–212. [Google Scholar] [CrossRef]
- Qasim, M.A.; Velkin, V.I.; Shcheklein, S.E. Experimental study on hybridization of a PV-TEG system for electrical performance enhancement using heat exchangers, energy, exergy and economic levelized cost of energy (LCOE) analysis. Clean Energy 2023, 7, 808–823. [Google Scholar] [CrossRef]
- Yang, B.; Zeng, C.; Li, D.; Guo, Z.; Chen, Y.; Shu, H.; Cao, P.; Li, Z. Improved immune genetic algorithm based TEG system reconfiguration under non-uniform temperature distribution. Appl. Energy 2022, 325, 119691. [Google Scholar] [CrossRef]
- Ibrahim, A.W.; Xu, J.; Hussein Farh, H.M.; Al-Shamma’a, A.A.; Yang, Y.; Shi, Z.; Zafar, M.H. An efficient linear-extrapolation catch-fish algorithm for maximizing the harvested power from thermoelectric generators sources. Appl. Therm. Eng. 2025, 268, 125916. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J.A. Operating temperature of photovoltaic modules: A survey of pertinent correlations. Renew. Energy 2009, 34, 23–29. [Google Scholar] [CrossRef]
- Yang, B.; Xie, R.; Wu, S.; Han, Y. Hybrid PV-TEG system maximum power point tracking based on an exponential distribution optimizer. Power Syst. Prot. Control 2024, 52, 12–25. [Google Scholar]
- Manna, S.; Akella, A.K.; Singh, D.K. Novel Lyapunov-based rapid and ripple-free MPPT using a robust model reference adaptive controller for solar PV system. Prot. Control Mod. Power Syst. 2023, 8, 1–25. [Google Scholar] [CrossRef]
- Zhang, X.; Tan, T.; Yang, B.; Wang, J.; Li, S.; He, T.; Yang, L.; Yu, T.; Sun, L. Greedy search based data-driven algorithm of centralized thermoelectric generation system under non-uniform temperature distribution. Appl. Energy 2020, 260, 114232. [Google Scholar] [CrossRef]
- Yang, B.; Li, Y.; Huang, J.; Li, M.; Zheng, R.; Duan, J.; Fan, T.; Zou, H.; Liu, T.; Wang, J. Modular reconfiguration of hybrid PV-TEG systems via artificial rabbit algorithm: Modelling, design and HIL validation. Appl. Energy 2023, 351, 121868. [Google Scholar] [CrossRef]
- Singh, S.; Saini, S.; Gupta, S.K.; Kumar, R. Solar-PV inverter for the overall stability of power systems with intelligent MPPT control of DC-link capacitor voltage. Prot. Control Mod. Power Syst. 2023, 8, 1–20. [Google Scholar] [CrossRef]
- Wang, J.; Wen, J.; Wu, S.; Yang, B.; Zeng, P.; Jiang, L. Optimal green energy harvesting for hybrid photovoltaic-thermoelectric generator system via chaotic RIME optimizer: A techno-environmental assessment. Prot. Control Mod. Power Syst. 2025, 10, 63–80. [Google Scholar] [CrossRef]
- Motahhir, S.; Chalh, A.; El Ghzizal, A.; Derouich, A. Development of a low-cost PV system using an improved INC algorithm and a PV panel Proteus model. J. Clean. Prod. 2018, 204, 355–365. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Member, S.; Ray, P.K. A Grey Wolf Assisted Perturb & Observe MPPT Algorithm for a PV System. IEEE Trans. Energy Convers. 2016, 32, 340–347. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, B.; Yu, T.; Jiang, L. Dynamic Surrogate Model based optimization for MPPT of centralized thermoelectric generation systems under heterogeneous temperature difference. IEEE Trans. Energy Convers. 2020, 35, 966–976. [Google Scholar] [CrossRef]
- Refaat, A.; Ali, Q.A.; Elsakka, M.M.; Elhenawy, Y.; Majozi, T.; Korovkin, N.V.; Elfar, M.H. Extraction of maximum power from PV system based on horse herd optimization MPPT technique under various weather conditions. Renew. Energy 2024, 220, 119718. [Google Scholar] [CrossRef]
- Salim, J.A.; Albaker, B.M.; Alwan, M.S.; Hasanuzzaman, M. Hybrid MPPT approach using Cuckoo Search and Grey Wolf Optimizer for PV systems under variant operating conditions. Glob. Energy Interconnect. 2022, 5, 627–644. [Google Scholar] [CrossRef]
- Sarvi, M.; Azadian, A. A comprehensive review and classified comparison of MPPT algorithms in PV systems. Energy Syst. 2022, 13, 281–320. [Google Scholar] [CrossRef]
- Khan, N.M.; Mansoor, M.; Mirza, A.F.; Moosavi, S.K.R.; Qadir, Z.; Zafar, M.H. Energy harvesting and stability analysis of centralized TEG system under non-uniform temperature distribution. Sustain. Energy Technol. Assess. 2022, 52, 102028. [Google Scholar] [CrossRef]
- Khan, M.K.; Zafar, M.H.; Mansoor, M.; Mirza, A.F.; Khan, U.A.; Khan, N.M. Green energy extraction for sustainable development: A novel MPPT technique for hybrid PV-TEG system. Sustain. Energy Technol. Assess. 2022, 53, 102388. [Google Scholar]
- Mirza, A.F.; Mansoor, M.; Zerbakht, K.; Javed, M.Y.; Zafar, M.H.; Khan, N.M. High-efficiency hybrid PV-TEG system with intelligent control to harvest maximum energy under various non-static operating conditions. J. Clean. Prod. 2021, 320, 128643. [Google Scholar] [CrossRef]
- Yang, B.; Wu, S.; Huang, J.; Guo, Z.; Wang, J.; Zhang, Z.; Xie, R.; Shu, H.; Jiang, L. Salp swarm optimization algorithm based MPPT design for PV-TEG hybrid system under partial shading conditions. Energy Convers. Manag. 2023, 292, 117410. [Google Scholar] [CrossRef]
- Liu, W.; Lu, M.; Bai, H.; Liu, Z.; Lv, S. All-day autonomous MPPT energy storage PV-TEG hybrid system based on dual axis solar tracker. Renew. Energy 2025, 256, 124094. [Google Scholar]
- Abdullah, A.M.; Rezk, H.; Elbloye, A.; Hassan, M.K.; Mohamed, A.F. Grey Wolf Optimizer-Based Fractional MPPT for Thermoelectric Generator. Intell. Autom. Soft Comput. 2021, 29, 730. [Google Scholar] [CrossRef]
- Al-Dhaifallah, M.; Saif, A.-W.A.; Elferik, S.; Elkhider, S.M.; Aldean, A.S. Combining Sliding Mode and Fractional-Order Theory for Maximum Power Point Tracking Enhancement of Variable-Speed Wind Energy Conversion. Fractal Fract. 2024, 8, 447. [Google Scholar]
- Rangi, S.; Jain, S.; Arya, Y. Utilization and performance comparison of several HESSs with cascade optimal-FOD controller for multi-area multi-source power system under deregulated environment. J. Energy Storage 2024, 94, 112469. [Google Scholar] [CrossRef]
- Ruiz, F.; Pichardo, E.; Aly, M.; Vazquez, E.; Avalos, J.G.; Sánchez, G. A high-performance fractional order controller based on chaotic manta-ray foraging and artificial ecosystem-based optimization algorithms applied to dual active bridge converter. Fractal Fract. 2024, 8, 332. [Google Scholar]
- Al-Dhaifallah, M.; Nassef, A.M.; Rezk, H.; Nisar, K.S. Optimal parameter design of fractional order control based INC-MPPT for PV system. Sol. Energy 2018, 159, 650–664. [Google Scholar] [CrossRef]
- Rezk, H.; Alhato, M.M.; Al-Dhaifallah, M.; Bouallègue, S. A sine cosine algorithm-based fractional mppt for thermoelectric generation system. Sustainability 2021, 13, 11650. [Google Scholar] [CrossRef]
- Aly, M.; Rezk, H. Optimum hybrid fractional order maximum power point tracker for thermoelectric generators. Energy Rep. 2025, 13, 5486–5500. [Google Scholar] [CrossRef]
- Mohamed, E.A.; Ahmed, E.M.; Elmelegi, A.; Aly, M.; Elbaksawi, O.; Mohamed, A.-A.A. An optimized hybrid fractional order controller for frequency regulation in multi-area power systems. IEEE Access 2020, 8, 213899–213915. [Google Scholar] [CrossRef]
- Mseddi, A.; Abid, A.; Naifar, O.; Rhaima, M.; Ben Makhlouf, A.; Mchiri, L. Investigation of the robust fractional order control approach associated with the online analytic unity magnitude shaper: The case of wind energy systems. Fractal Fract. 2024, 8, 187. [Google Scholar] [CrossRef]
- Verma, V.; Kane, A.; Singh, B. Complementary performance enhancement of PV energy system through thermoelectric generation. Renew. Sustain. Energy Rev. 2016, 58, 1017–1026. [Google Scholar] [CrossRef]
- Obaid, W.; Hamid, A.-K. Grid-connected hybrid solar/thermoelectric power system with hybrid INC/PSO/PO MPPT system in Sharjah, United Arab Emirates. In Proceedings of the 2022 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 21–24 February 2022; IEEE: New York, NY, USA, 2022; pp. 1–5. [Google Scholar]
- Qasim, M.A.; Alwan, N.T.; PraveenKumar, S.; Velkin, V.I.; Agyekum, E.B. A new maximum power point tracking technique for thermoelectric generator modules. Inventions 2021, 6, 88. [Google Scholar] [CrossRef]
- Olabi, A.G.; Rezk, H.; Sayed, E.T.; Awotwe, T.; Alshathri, S.I.; Abdelkareem, M.A. Optimal Parameter Identification of Single-Sensor Fractional Maximum Power Point Tracker for Thermoelectric Generator. Sustainability 2023, 15, 5054. [Google Scholar] [CrossRef]
- Yang, B.; Xie, R.; Shu, H.; Han, Y.; Zheng, C.; Lu, H.; Luo, E.; Ren, Y.; Jiang, L.; Sang, Y. Techno-economic-environmental optimization of hybrid photovoltaic-thermoelectric generator systems based on data-driven approach. Appl. Therm. Eng. 2024, 257, 124222. [Google Scholar] [CrossRef]
- Xie, R.; Wu, S.; Yang, B. MPPT Design for Hybrid PV-TEG System under Partial Shading Condition via Manta Ray Foraging Optimization. In Proceedings of the 2023 5th International Conference on Power and Energy Technology ICPET, Tianjin, China, 27–30 July 2023; pp. 765–770. [Google Scholar] [CrossRef]
- Ibrahim, A.; Al-shamma, A.A.; Xu, J.; Aboudrar, I.; Ameur, K.; Al, R.; Hussein, H.M.; Charles, G. An enhanced uncertainty and disturbance estimator based on Bi-LSTM-OTC-LADRC of grid-connected wind energy conversion system. Comput. Electr. Eng. 2025, 127, 110534. [Google Scholar] [CrossRef]
- Ibrahim, A.W.; Xu, J.; Al-Shamma’a, A.A.; Farh, H.M.H.; Aboudrar, I.; Oubail, Y.; Alaql, F.; Alfraidi, W. Optimized Energy Management Strategy for an Autonomous DC Microgrid Integrating PV/Wind/Battery/Diesel-Based Hybrid PSO-GA-LADRC Through SAPF. Technologies 2024, 12, 226. [Google Scholar] [CrossRef]
- Cotfas, P.A.; Cotfas, D.T. Comprehensive review of methods and instruments for photovoltaic–thermoelectric generator hybrid system characterization. Energies 2020, 13, 6045. [Google Scholar] [CrossRef]
- Lamba, R.; Kaushik, S.C. Modeling and performance analysis of a concentrated photovoltaic–thermoelectric hybrid power generation system. Energy Convers. Manag. 2016, 115, 288–298. [Google Scholar] [CrossRef]
- Zhu, W.; Deng, Y.; Wang, Y.; Shen, S.; Gulfam, R. High-performance photovoltaic-thermoelectric hybrid power generation system with optimized thermal management. Energy 2016, 100, 91–101. [Google Scholar] [CrossRef]
- Babu, C.; Ponnambalam, P. The theoretical performance evaluation of hybrid PV-TEG system. Energy Convers. Manag. 2018, 173, 450–460. [Google Scholar] [CrossRef]
- Hatzikraniotis, E.; Zorbas, K.T.; Samaras, I.; Kyratsi, T.; Paraskevopoulos, K.M. Efficiency study of a commercial thermoelectric power generator (TEG) under thermal cycling. J. Electron. Mater. 2010, 39, 2112–2116. [Google Scholar] [CrossRef]
- Barako, M.T.; Park, W.; Marconnet, A.M.; Asheghi, M.; Goodson, K.E. A reliability study with infrared imaging of thermoelectric modules under thermal cycling. In Proceedings of the 13th InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, San Diego, CA, USA, 30 May–1 June 2012; IEEE: New York, NY, USA, 2012; pp. 86–92. [Google Scholar]
- Tenorio, H.C.R.L.; Vieira, D.A.; de Souza, C.P.; de Macêdo, E.C.T.; Freire, R.C.S. A thermoelectric module thermal-cycling testing platform with automated measurement capabilities. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference Proceedings, San Diego, CA, USA, 30 May–1 June 2012; IEEE: New York, NY, USA, 2016; pp. 1–5. [Google Scholar]
- Williams, N.P.; Power, J.; Trimble, D.; O’Shaughnessy, S.M. An experimental evaluation of thermoelectric generator performance under cyclic heating regimes. Heat Mass Transf. 2024, 60, 1991–2003. [Google Scholar] [CrossRef]
- Castillo, E.E.; Hapenciuc, C.L.; Borca-Tasciuc, T. Thermoelectric characterization by transient Harman method under nonideal contact and boundary conditions. Rev. Sci. Instrum. 2010, 81, 044902. [Google Scholar] [CrossRef]
- Barako, M.T.; Park, W.; Marconnet, A.M.; Asheghi, M.; Goodson, K.E. Thermal cycling, mechanical degradation, and the effective figure of merit of a thermoelectric module. J. Electron. Mater. 2013, 42, 372–381. [Google Scholar] [CrossRef]
- Champier, D. Thermoelectric generators: A review of applications. Energy Convers. Manag. 2017, 140, 167–181. [Google Scholar] [CrossRef]
- Kanagaraj, N. Photovoltaic and thermoelectric generator combined hybrid energy system with an enhanced maximum power point tracking technique for higher energy conversion efficiency. Sustainability 2021, 13, 3144. [Google Scholar] [CrossRef]
- Khan, M.A.I.; Khan, M.I.; Kazim, A.H.; Shabir, A.; Riaz, F.; Mustafa, N.; Javed, H.; Raza, A.; Hussain, M.; Salman, C.A. An experimental and comparative performance evaluation of a hybrid photovoltaic-thermoelectric system. Front. Energy Res. 2021, 9, 722514. [Google Scholar] [CrossRef]
- Fathy, A.; Agwa, A.M. Red-Billed Blue Magpie Optimizer for Modeling and Estimating the State of Charge of Lithium-Ion Battery. Electrochem 2025, 6, 27. [Google Scholar] [CrossRef]
- Fu, S.; Li, K.; Huang, H.; Ma, C.; Fan, Q.; Zhu, Y. Red-billed blue magpie optimizer: A novel metaheuristic algorithm for 2D/3D UAV path planning and engineering design problems. Artif. Intell. Rev. 2024, 57, 134. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, M.; Hu, F.; Zhu, Z. Manuscript Title: Thermal-Electrical scheduling of Low-Carbon Industrial energy systems with rooftop PV: An improved Red-Billed blue magpie optimization approach. Therm. Sci. Eng. Prog. 2025, 61, 103599. [Google Scholar] [CrossRef]
- Sharma, A. Improved Red-Billed Blue Magpie Optimizer for Unmanned Aerial Vehicle Path Planning. In Proceedings of the 2024 International Conference on Computational Intelligence and Network Systems (CINS), Dubai, United Arab Emirates, 28–29 November 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Luo, Z.Z.; Chongwei, H.; Kai, S.; Qikai, H.; Jiayue, J.; Ziyi, Z. Trajectory Tracking Control for USVs Based on Red-billed Blue Magpie Optimized ADRC. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2024; Volume 2891, p. 112019. [Google Scholar]
- El-Fergany, A.A.; Agwa, A.M. Red-billed blue magpie optimizer for electrical characterization of fuel cells with prioritizing estimated parameters. Technologies 2024, 12, 156. [Google Scholar] [CrossRef]

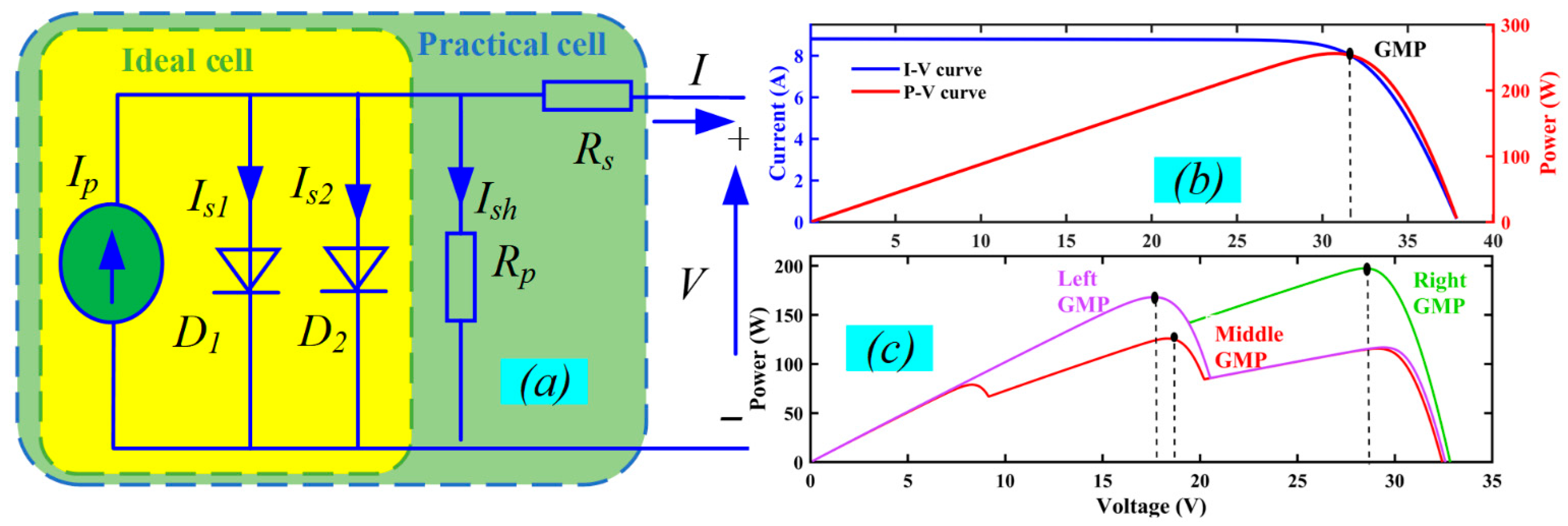
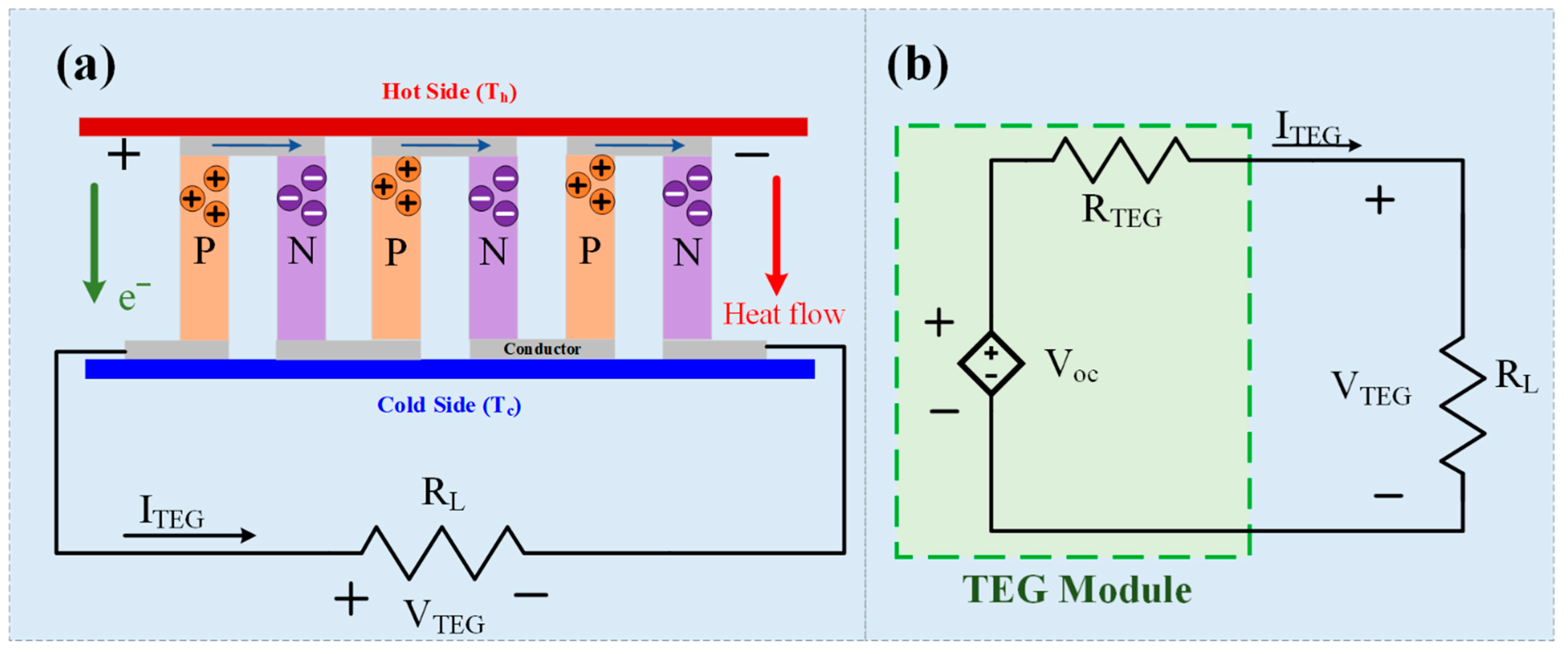
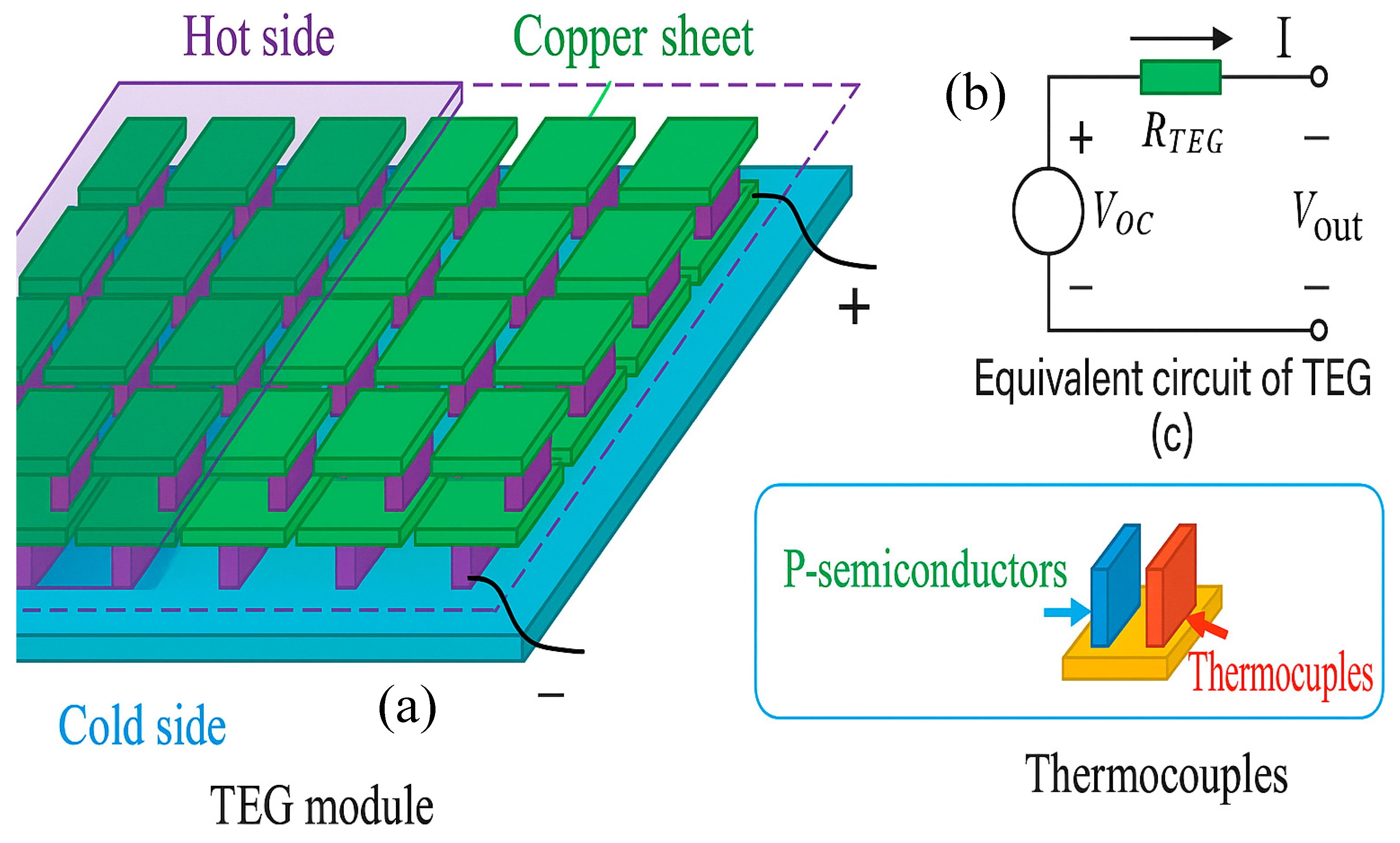


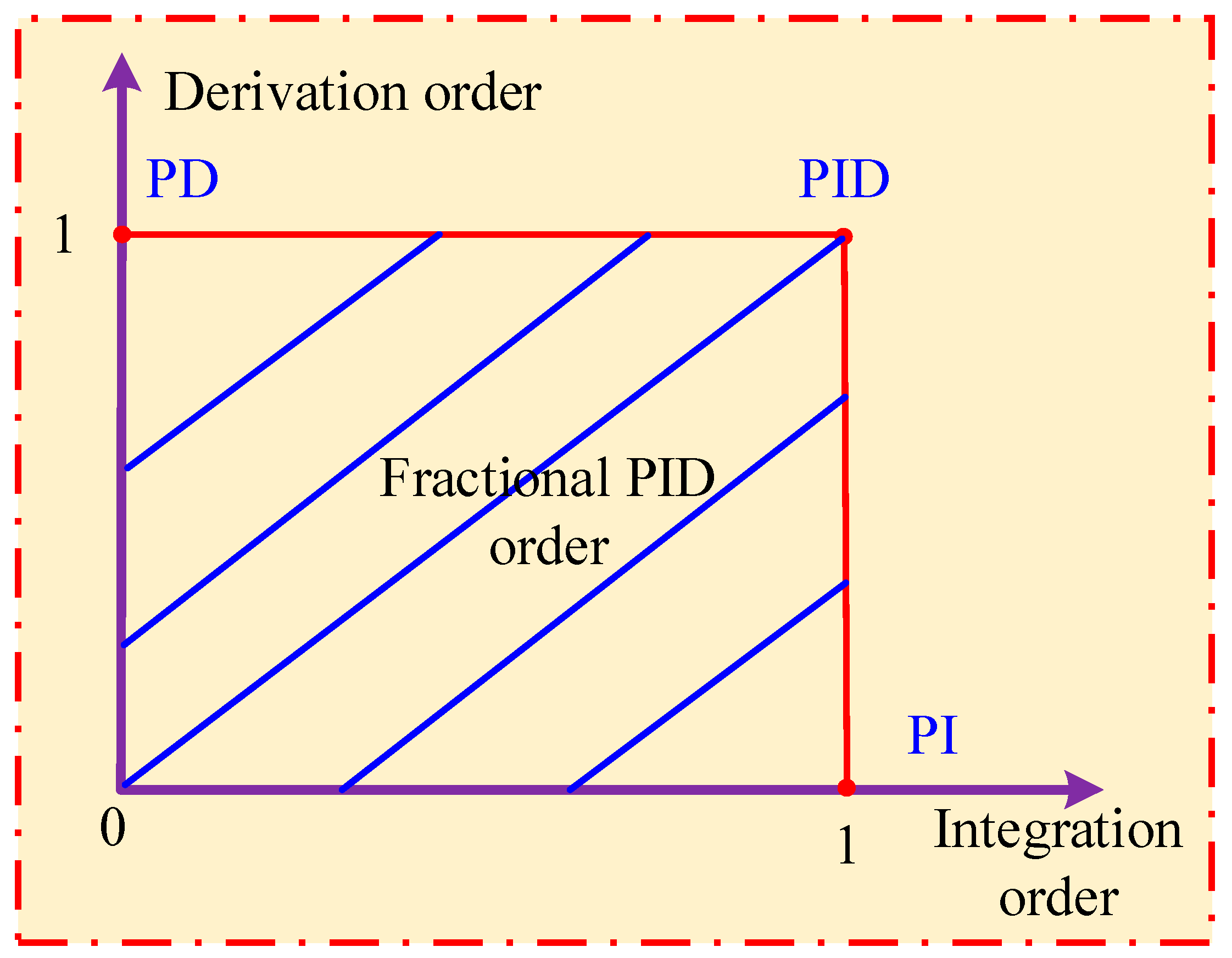
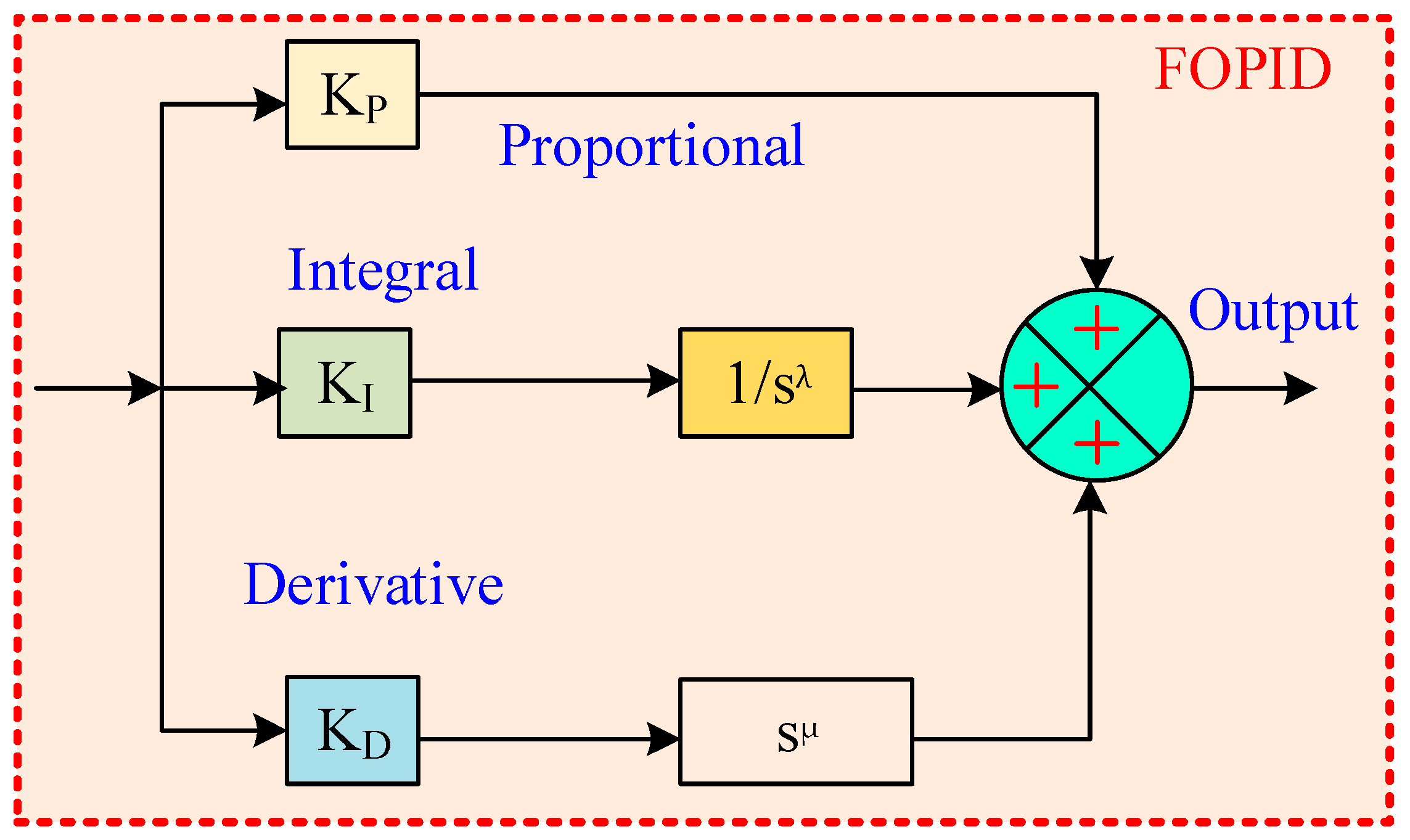


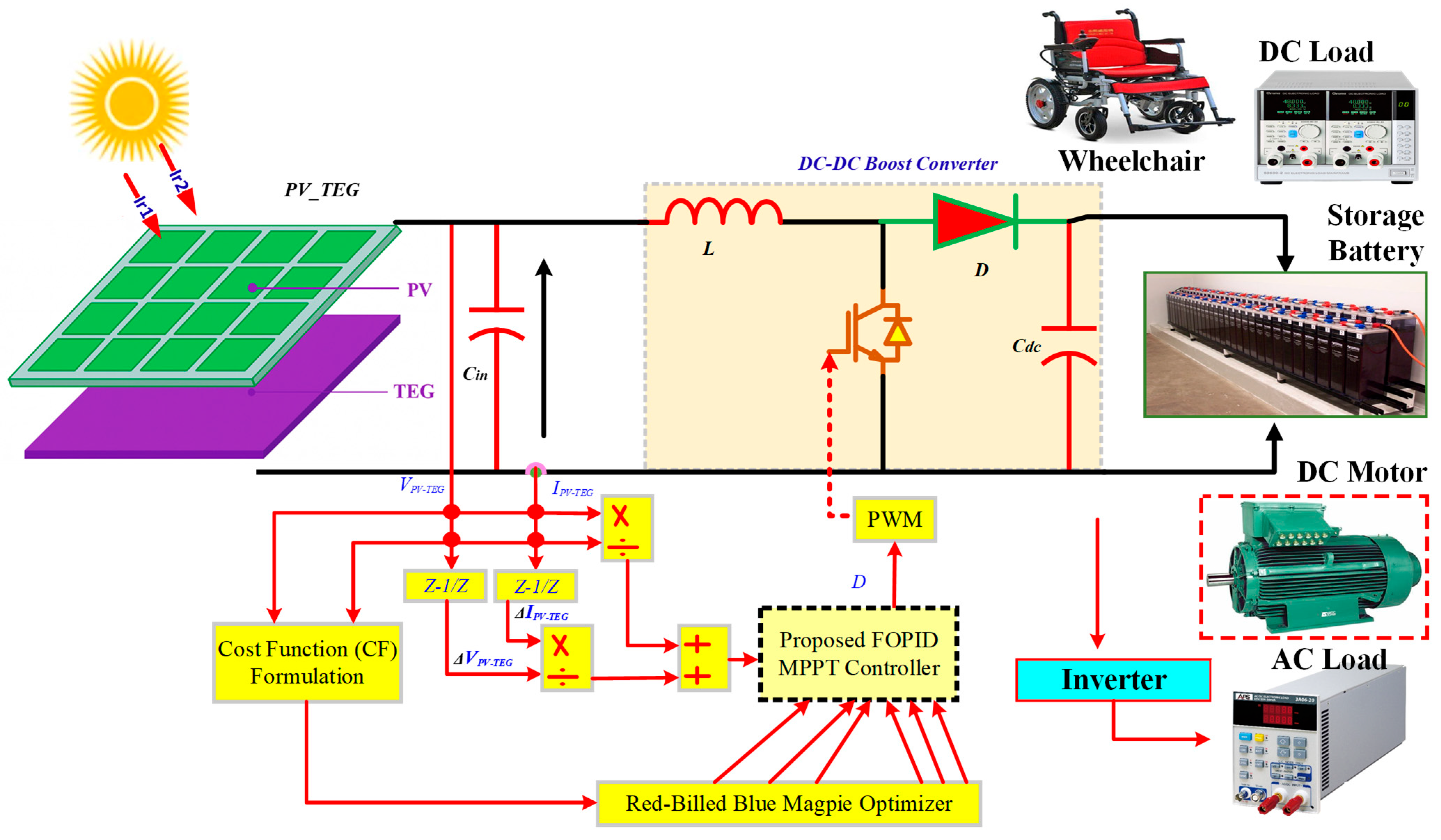


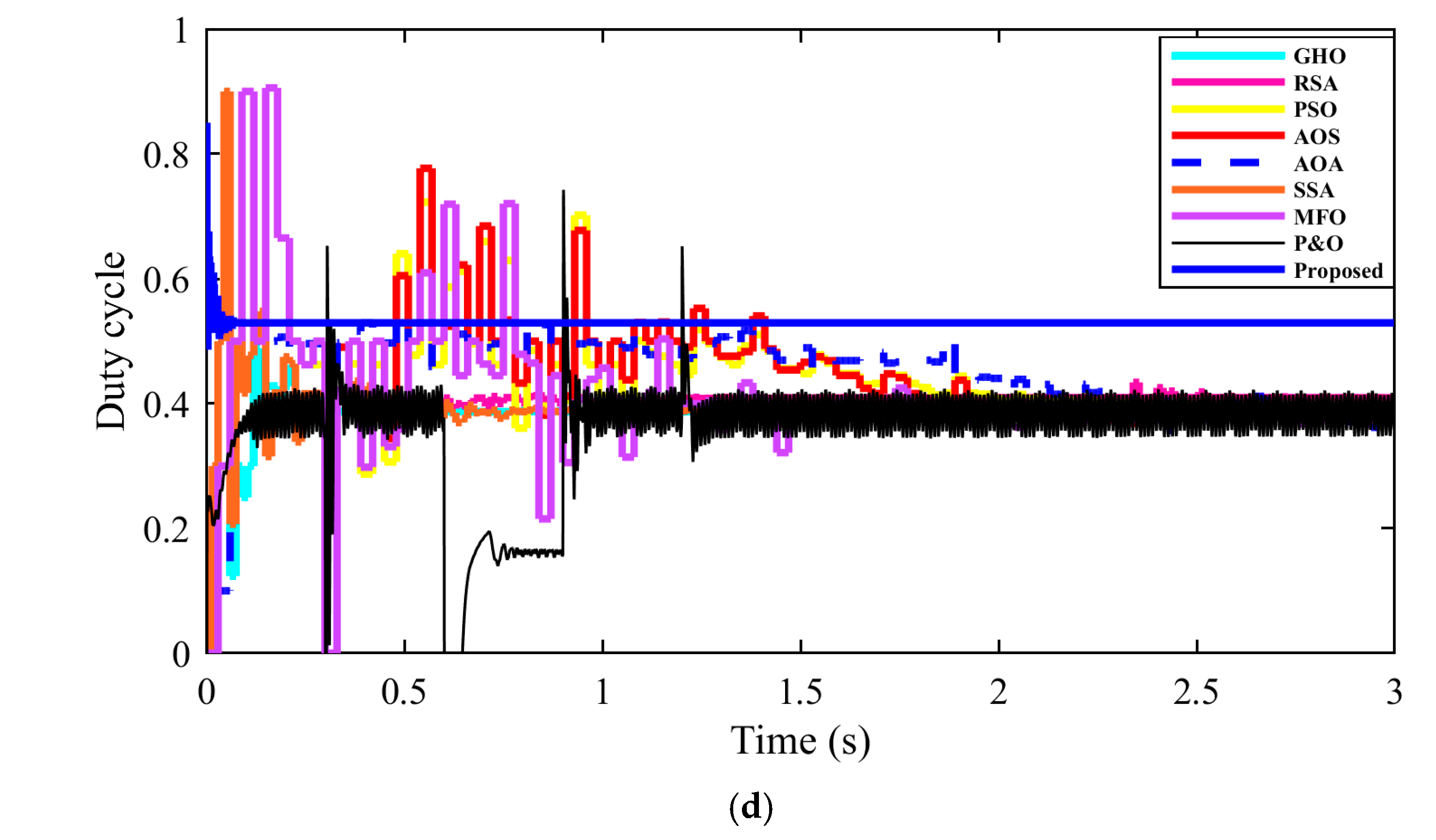
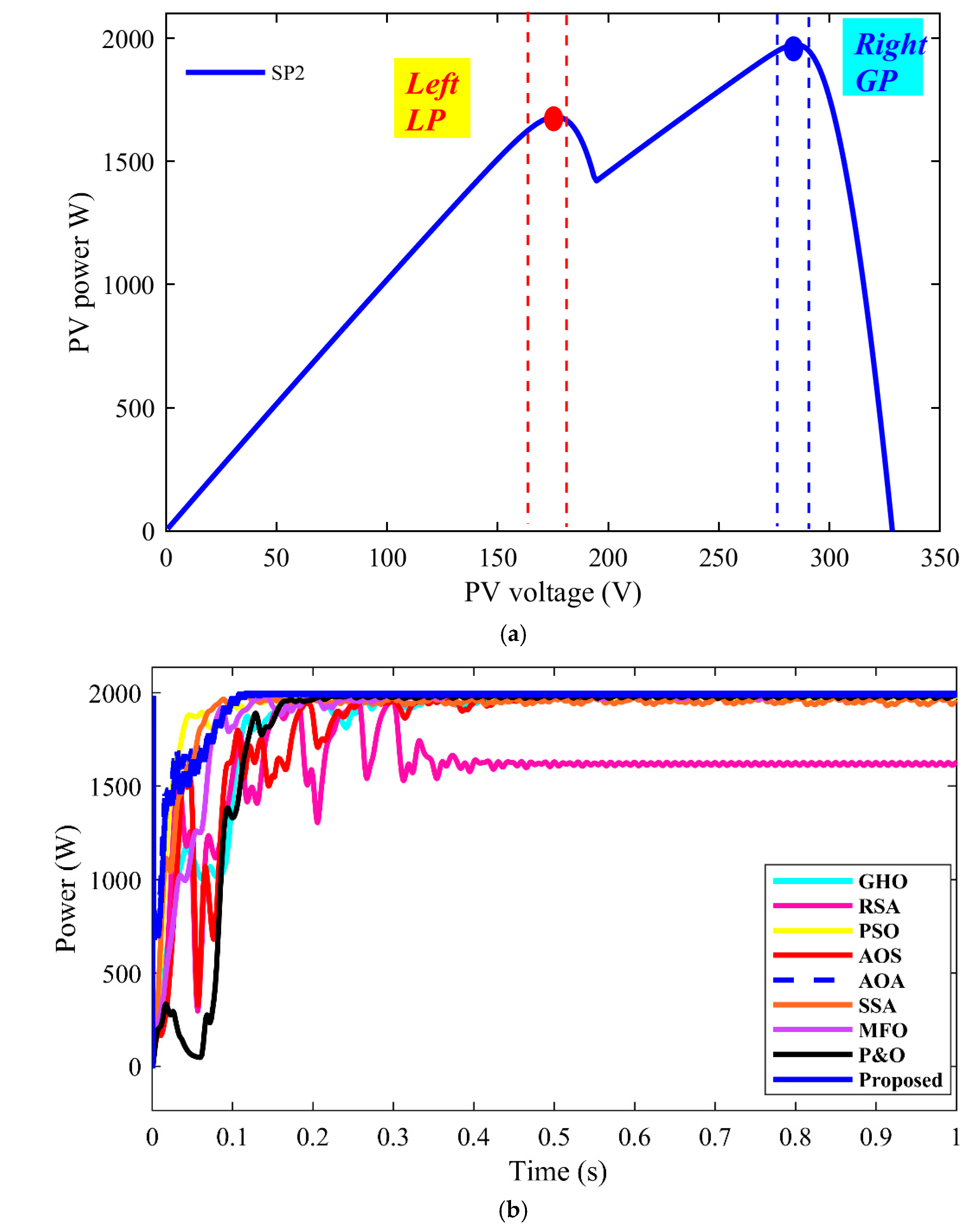
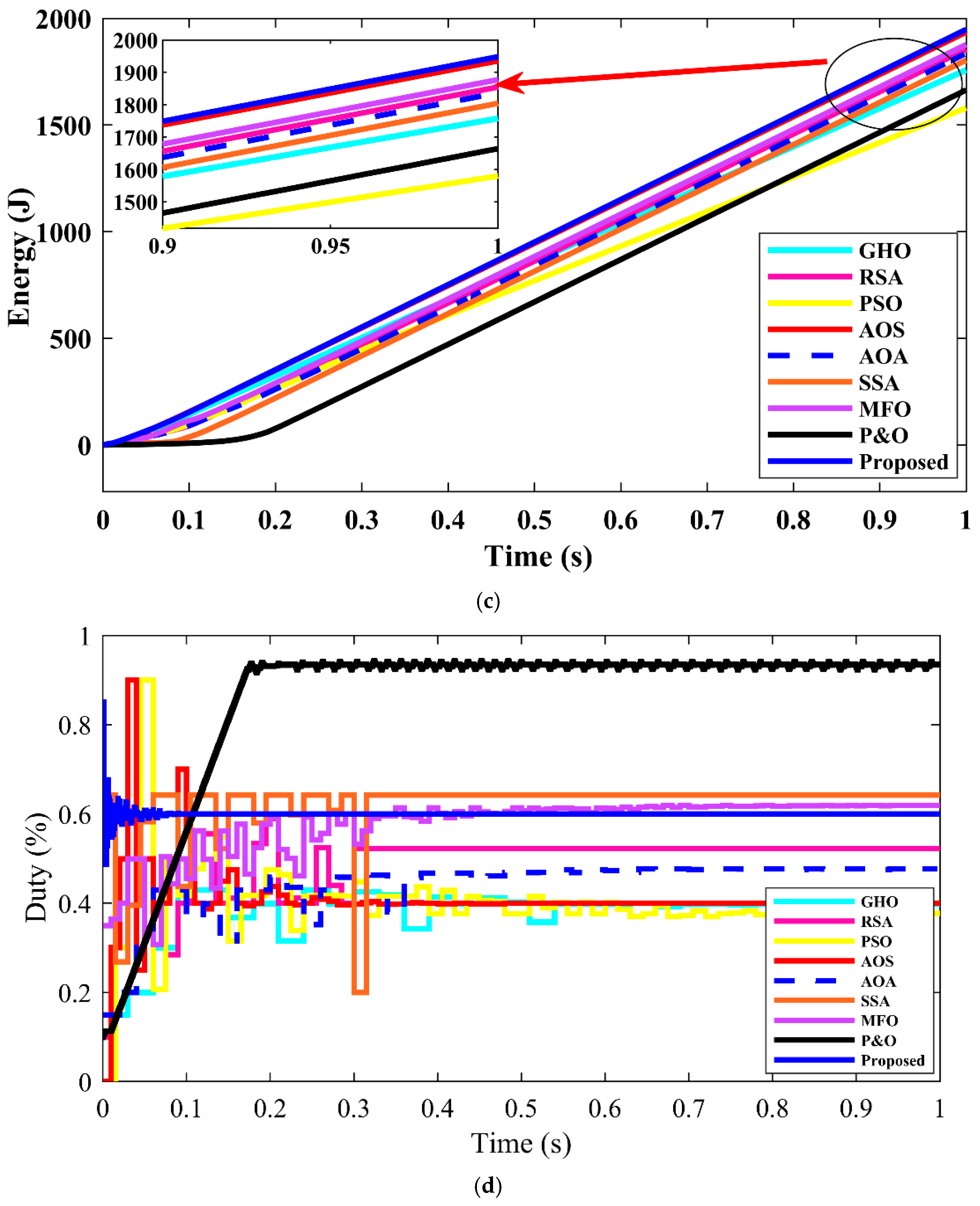
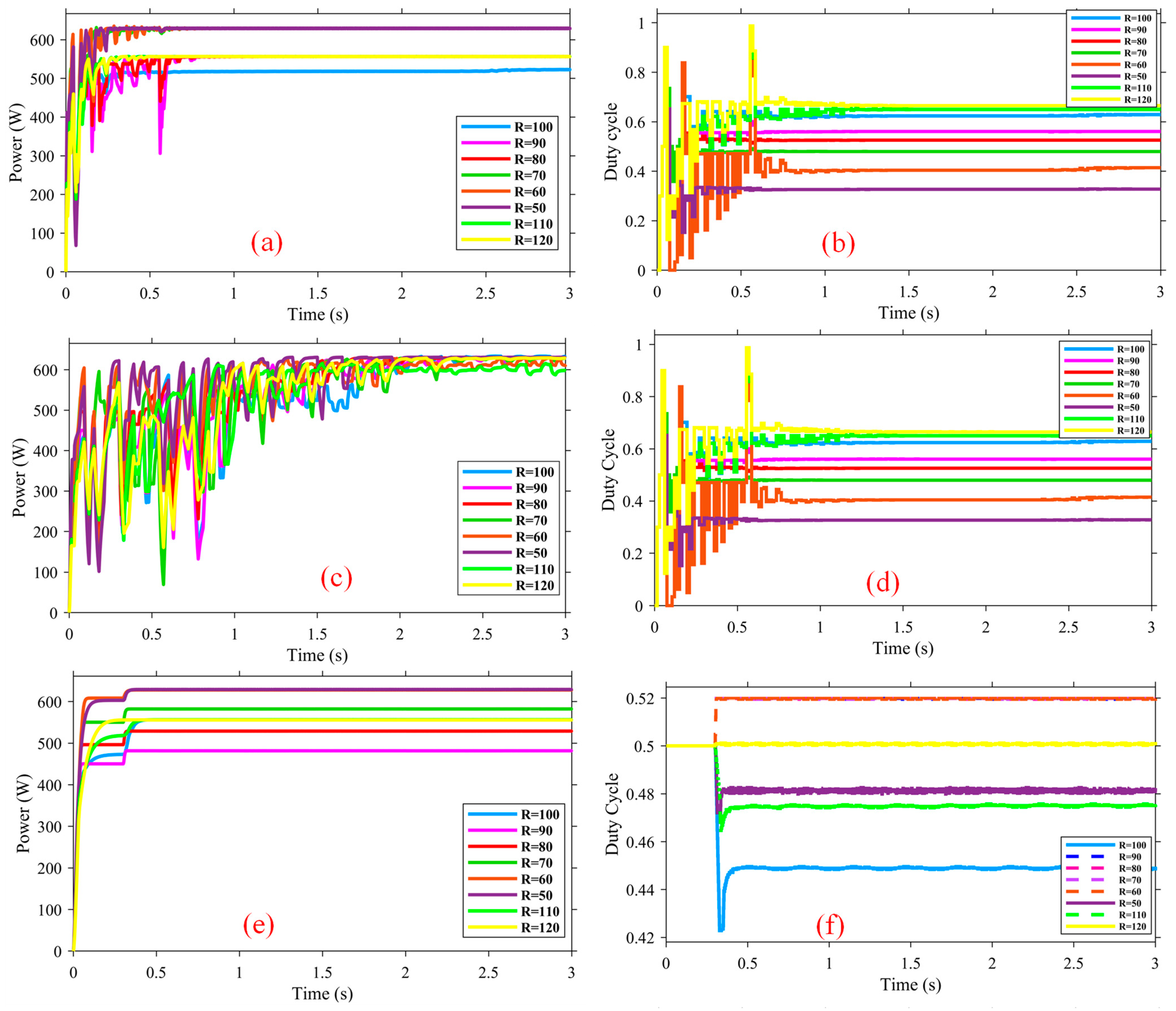


| Method Family | Typical Advantages | Typical Disadvantages (PV-TEG Context) |
|---|---|---|
| P&O [43] | Simple, low-cost; fast on single-peak curves; easy to implement on MCU. | Prone to local-peak lock-in under partial shading/multi-peak; steady-state oscillation; sensitive to step size and noise. |
| IncCond [15,44] | Better slope awareness than P&O; moderate speed; modest compute. | Still local method; accuracy depends on noisy (dI/dV); tuning trade-off between speed and ripple. |
| FLC [45] | Nonlinear rule base can handle uncertainties; no exact model required. | Rule design/tuning is expert-heavy; scaling issues; behavior can drift outside trained envelope. |
| Integer-order PID [40] | Familiar design; decent transient shaping; easy to deploy. | Fixed structure; performance degrades across wide irradiance/temperature/load changes; requires re-tuning; limited GMPP ability. |
| FOPID (Fractional-order PID) [46] | Extra orders (λ, µ) improve speed–robustness trade-off; can reduce ripple and overshoot. | Realization details (band/order, discretization, anti-windup) are nontrivial; still needs global search help for GMPP. |
| Meta-heuristics (PSO/SSA/MRFO/AOA/HGSO/ASA, etc.) [1] | Global search capability; flexible objective design; robust to nonconvex (P)–(V). | Often slower convergence; duty oscillation risk without damping; results depend on bounds/seeds; reproducibility varies. |
| Data-driven (NN/ANFIS/NNCGA, etc.) [47] | Can capture complex, time-varying relations; potential for adaptive/global behavior. | Data-hungry; generalization and stability concerns; training cost; opaque tuning; reproducibility often limited. |
| Dual-MPPT (separate PV & TEG) [30] | Independent optimization of each source; simple modularity. | Coordination/coupling can cause cross-oscillation; higher component count; harder to guarantee bus stability. |
| Centralized PV-TEG MPPT [22] | System-level optimum on a common DC bus; avoids source conflicts. | More complex controller; requires accurate sensing and well-defined search/constraints to prevent chatter. |
| Adaptive FOPID (Our approach) | Combines fast local control (FOPID) with global meta-tuning; good GMPP tracking with low ripple; parameters bounded and reproducible. | Needs careful specification of fractional realization and meta-tuning settings; modest compute overhead vs. fixed PID. |
| Block | Parameter | Value/Setting | Notes |
|---|---|---|---|
| Sampling and Discretization | Sampling time (Ts) | 1 ms (1 kHz) | Common to control and differentiation |
| Discretization | Tustin (bilinear) | Pre-warp at 2π·10 Hz for FOPID band center | |
| FOPID Structure | Control law | (Δd[k] = Kp e[k] + Ki(-λI){e}[k] + KdµD{e}[k]) | (-λI) and µD are fractional ops |
| Fractional orders | λ, µ ϵ [0.8, 1.2]) | See bounds below | |
| Derivative roll-off | (Gd(s) = N/(1 + N/s) with N = 20 · 2π rad/s | Limits noise amplification | |
| Output limits | d ϵ {dmin,dmax} = [0.05, 0.90] | Duty cycle clamp | |
| Anti-windup | Back-calculation with (Kaw = 1/Ti); tracking limiter | (Ti = 1/Ki (effective) | |
| Oustaloup Approx. | Order | 5 (per frac. operator) | Balanced accuracy/complexity |
| Freq. band | 0.1–100 Hz (0.628–628 rad/s) | Matches MPPT dynamics band | |
| (dP/dV) Estimation | Raw power | (P[k] = V[k], I[k]) at DC bus | Includes converter losses upstream |
| Differentiator | Savitzky–Golay, window 15, poly 2 | On (P(V)) stream sampled at 1 kHz | |
| Regularization | EMA on derivative, (α = 0.2) | (xf[k] = αx[k] + (1 − α)xf[k − 1]) | |
| Outlier filter | Hampel, window 11, 3σ | Optional; default on | |
| Decimation | 200 Hz for controller after filtering | Reduces chatter | |
| RBBMO (Meta-Tuning) | Population size | 25 | Agents |
| Iterations | 60 | Early stop if no best update in 10 iters | |
| Coefficients | (w = 0.7) (inertia), (c1 = 1.4), (c2 = 1.2), (ps = 0.2) | Standardized RBBMO params | |
| Seeds | {2024, 2025, 2026} | Report median over seeds | |
| Fitness | Maximize (E1s) (1-s energy)—β.ripple—γ.satCount | (β = 0.5,Wh), (γ = 0.01) | |
| Bounds | (Kp ϵ [0.00, 1.50], Ki ϵ [0, 400], Kd ϵ [0.00, 0.20], λ, µ ϵ [0.80, 1.20]) | Box constraints | |
| Constraint handling | Clamp to bounds; penalty if at bound >10% of time | Prevents edge-seeking | |
| Deployment | Final gains | Best-seed gains (median) | Logged in Supplement YAML |
| Runtime adapts. | Small-gain online adaptation (±10%/s cap) | From (Δe) sign and magnitude |
| PV Parameters Value | TEG Parameters Value | ||
|---|---|---|---|
| Parameters | Value | Parameters | Value |
| PV output voltage | 240 V | Measurement conditions Tc, Th (°C) | 30 and 200 |
| PV converter inductance | 116.4 mH | Component dimensions (mm × mm × mm) | 40 × 40 × 4.4 |
| PV converter capacitance (Cin) and (Co) | 48.25 μF | Typical peak power (W) | 7.5 |
| Battery capacity | 48 Ah | Isc | 2.65 A |
| Initial SoC of BESS | 50% | Voc | 11 V |
| Battery inductance | 116.4 mH | Number of thermoelectric units | 200 |
| Algorithm | Time to 95% MPP, t95 (s) | Settling Time (±1%) (s) | Overshoot (%) | Steady Ripple (±%) | Energy @ 1 s (J) | Notes/Rank |
|---|---|---|---|---|---|---|
| Proposed | 0.06 | 0.12 | <0.5 | 1 | 1950 | Best energy and fastest; smooth duty |
| AOS | 0.14 | 0.30 | 1–2 | 2–3 | 1910 | 2nd; close to proposed |
| PSO | 0.18 | 0.35 | 2–3 | 2–3 | 1880 | 3rd |
| MFO | 0.22 | 0.40 | 4–6 | 3–5 | 1780 | 4th |
| SSA | 0.24 | 0.45 | 6–8 | 4–6 | 1650 | 5th; pronounced transients |
| GHO | 0.20 | 0.35 | 3–5 | 3–4 | 1600 | 6th |
| RSA | 0.28 | >0.50 | 5–8 | 5–7 | 1050 | 7th; slow and noisy |
| AOA | —(low plateau) | — | — | large | 420 | 8th; fails to reach high plateau |
| P&O | 0.22–0.25 | 0.40–0.45 | 5 | 2–3 | 200 | Slow ramp; lowest energy among baselines |
| Algorithm | Step t95 (s) | Step Settle (s) | Ripple (±%) | Energy @1 s (kJ) | Notes/Rank |
|---|---|---|---|---|---|
| Proposed | 0.06–0.08 | 0.12–0.15 | ≈1 | 0.95–0.98 | Fastest reacquisition; smallest ripple |
| AOS | 0.18–0.25 | 0.30–0.35 | 2–3 | 0.90 | 2nd |
| GHO | 0.18–0.30 | 0.30–0.35 | 3–4 | 0.88 | 3rd |
| RSA | 0.25–0.35 | 0.35–0.45 | 4–5 | 0.83 | 4th |
| AOA | 0.25–0.35 | 0.40–0.50 | 5–7 | 0.78–0.80 | 5th |
| MFO | 0.30–0.40 | 0.45–0.55 | 3–5 | ~0.74 | moderate oscillations |
| SSA | 0.30–0.45 | 0.50–0.60 | 4–6 | 0.57 | large dips |
| P&O | slow | slow | 2–3 | 0.68–0.70 | sluggish recovery |
| PSO | 0.25–0.35 | 0.35–0.45 | 2–3 | 0.40–0.42 | weakest energy |
| Algorithm | Time to 95% of GP (s) | Settle (±1%) (s) | Ripple (±%) | Energy @1 s (kJ) | Notes/Rank |
|---|---|---|---|---|---|
| Proposed | 0.06–0.08 | 0.12–0.15 | ≈1 | 1.95–2.00 | Locks GP on first attempt |
| AOS | 0.15–0.22 | 0.25–0.35 | 2–3 | 1.90–1.96 | 2nd |
| GHO | 0.18–0.25 | 0.30–0.40 | 3–4 | 1.78–1.86 | 3rd–4th |
| MFO | 0.18–0.25 | 0.30–0.40 | 3–5 | 1.80–1.86 | 3rd–4th |
| RSA | —(LP trap) | — | 4–6 | 1.60–1.70 | converges near LP |
| PSO | 0.20–0.30 | 0.35–0.45 | 2–3 | ~1.70 | slower, undershoot |
| AOA | — | — | large | <1.6 | unstable |
| P&O | slow | slow | 2–3 | ~1.45 | pronounced dips |
| Testing Scenarios | Indicators | Proposed | AOS | PSO | MFO | SSA | GHO | RSA | AOA | P&O |
|---|---|---|---|---|---|---|---|---|---|---|
| Start-up test (search phase) | Energy (J) | 1950 | 1910 | 1880 | 1780 | 1650 | 1600 | 1050 | 420 | 200 |
| Δvmax (%) | 13.0 | 26.0 | 32.0 | 36.0 | 39.0 | 33.0 | 45.0 | 58.0 | 8.0 | |
| Δvavg (%) | 0.15 | 0.30 | 0.41 | 0.45 | 0.49 | 0.42 | 0.58 | 0.60 | 0.08 | |
| Stepwise variations in irradiance | Energy (J) | 965 | 900 | 410 | 740 | 570 | 880 | 830 | 790 | 690 |
| Δvmax (%) | 20.3 | 33.1 | 33.5 | 26.7 | 26.4 | 28.9 | 23.5 | 30.0 | 12.0 | |
| Δvavg (%) | 0.32 | 0.59 | 0.62 | 0.48 | 0.49 | 0.46 | 0.34 | 0.56 | 0.15 | |
| Partial shading | Energy (J) | 1950–2000 | 1900–1960 | ~1700 | 1800–1860 | 1600–1700 | 1780–1860 | 1600–1700 | <1600 | 1450 |
| Δvmax (%) | 18.0 | 25.0 | 30.0 | 28.0 | 32.0 | 27.0 | 34.0 | 38.0 | 15.0 | |
| Δvavg (%) | 0.28 | 0.40 | 0.50 | 0.46 | 0.55 | 0.44 | 0.58 | 0.60 | 0.12 | |
| Field—Spring | Energy (kWh) | 0.00088 | 0.00085 | 0.00082 | 0.00084 | 0.00081 | 0.00084 | 0.00080 | 0.00083 | 0.00072 |
| Δvmax (%) | 8.432 | 6.654 | 6.1209 | 5.6754 | 10.768 | 8.1127 | 6.2709 | 10.5627 | 10.877 | |
| Δvavg (%) | 0.0254 | 0.0265 | 0.0676 | 0.0678 | 0.0427 | 0.0397 | 0.0214 | 0.0735 | 0.0635 | |
| Field—Summer | Energy (kWh) | 0.00295 | 0.00285 | 0.00276 | 0.00280 | 0.00278 | 0.00278 | 0.00270 | 0.00275 | 0.00210 |
| Δvmax (%) | 9.43 | 6.6742 | 4.4675 | 5.6708 | 6.7083 | 6.435 | 4.8425 | 9.3071 | 10.709 | |
| Δvavg (%) | 0.0342 | 0.0435 | 0.0345 | 0.0451 | 0.054 | 0.0421 | 0.0370 | 0.078 | 0.0236 | |
| Field—Autumn | Energy (kWh) | 0.00290 | 0.00280 | 0.00268 | 0.00274 | 0.00272 | 0.00272 | 0.00265 | 0.00270 | 0.002235 |
| Δvmax (%) | 7.9982 | 9.8092 | 6.4321 | 7.123 | 8.6540 | 9.109 | 5.0981 | 7.6190 | 9.5098 | |
| Δvavg (%) | 0.0269 | 0.0367 | 0.0717 | 0.0673 | 0.0542 | 0.0324 | 0.0443 | 0.0459 | 0.0397 | |
| Field—Winter | Energy (kWh) | 0.00155 | 0.00149–0.00150 | 0.00147 | 0.00147 | 0.00146 | 0.00147 | 0.00148–0.00150 | 0.00147 | 0.00120 |
| Δvmax (%) | 8.1496 | 11.546 | 6.7650 | 8.2109 | 10.299 | 8.2309 | 6.4509 | 12.709 | 12.345 | |
| Δvavg (%) | 0.0240 | 0.0412 | 0.0809 | 0.0670 | 0.0570 | 0.0389 | 0.0345 | 0.0972 | 0.0908 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, A.-W.; Al-Shamma’a, A.A.; Xu, J.; Li, D.; Farh, H.M.H.; Alwesabi, K. A Novel Red-Billed Blue Magpie Optimizer Tuned Adaptive Fractional-Order for Hybrid PV-TEG Systems Green Energy Harvesting-Based MPPT Algorithms. Fractal Fract. 2025, 9, 704. https://doi.org/10.3390/fractalfract9110704
Ibrahim A-W, Al-Shamma’a AA, Xu J, Li D, Farh HMH, Alwesabi K. A Novel Red-Billed Blue Magpie Optimizer Tuned Adaptive Fractional-Order for Hybrid PV-TEG Systems Green Energy Harvesting-Based MPPT Algorithms. Fractal and Fractional. 2025; 9(11):704. https://doi.org/10.3390/fractalfract9110704
Chicago/Turabian StyleIbrahim, Al-Wesabi, Abdullrahman A. Al-Shamma’a, Jiazhu Xu, Danhu Li, Hassan M. Hussein Farh, and Khaled Alwesabi. 2025. "A Novel Red-Billed Blue Magpie Optimizer Tuned Adaptive Fractional-Order for Hybrid PV-TEG Systems Green Energy Harvesting-Based MPPT Algorithms" Fractal and Fractional 9, no. 11: 704. https://doi.org/10.3390/fractalfract9110704
APA StyleIbrahim, A.-W., Al-Shamma’a, A. A., Xu, J., Li, D., Farh, H. M. H., & Alwesabi, K. (2025). A Novel Red-Billed Blue Magpie Optimizer Tuned Adaptive Fractional-Order for Hybrid PV-TEG Systems Green Energy Harvesting-Based MPPT Algorithms. Fractal and Fractional, 9(11), 704. https://doi.org/10.3390/fractalfract9110704







