Perfect Projective Synchronization of a Class of Fractional-Order Chaotic Systems Through Stabilization near the Origin via Fractional-Order Backstepping Control
Abstract
1. Introduction
- A novel FOBC framework is developed for perfectly projective synchronization of IFOCS.
- Mittag-Leffler stability theory is effectively employed to rigorously prove global asymptotic stability of the synchronization errors.
- A practical synchronization example is provided using the Van-der Pol and Rayleigh systems, showcasing the method’s robustness and applicability.
- Simulation studies validate the effectiveness and reliability of the proposed control strategy across different initial conditions and non-identical fractional-order derivatives that are not close to 1.
2. Overview of Fractional-Order Operators
2.1. Fractional-Order Derivative
2.2. Stability Analysis of IFOCS
2.2.1. Stability in Lyapunov Creterion
2.2.2. Stability in Mittag-Leffler Sense
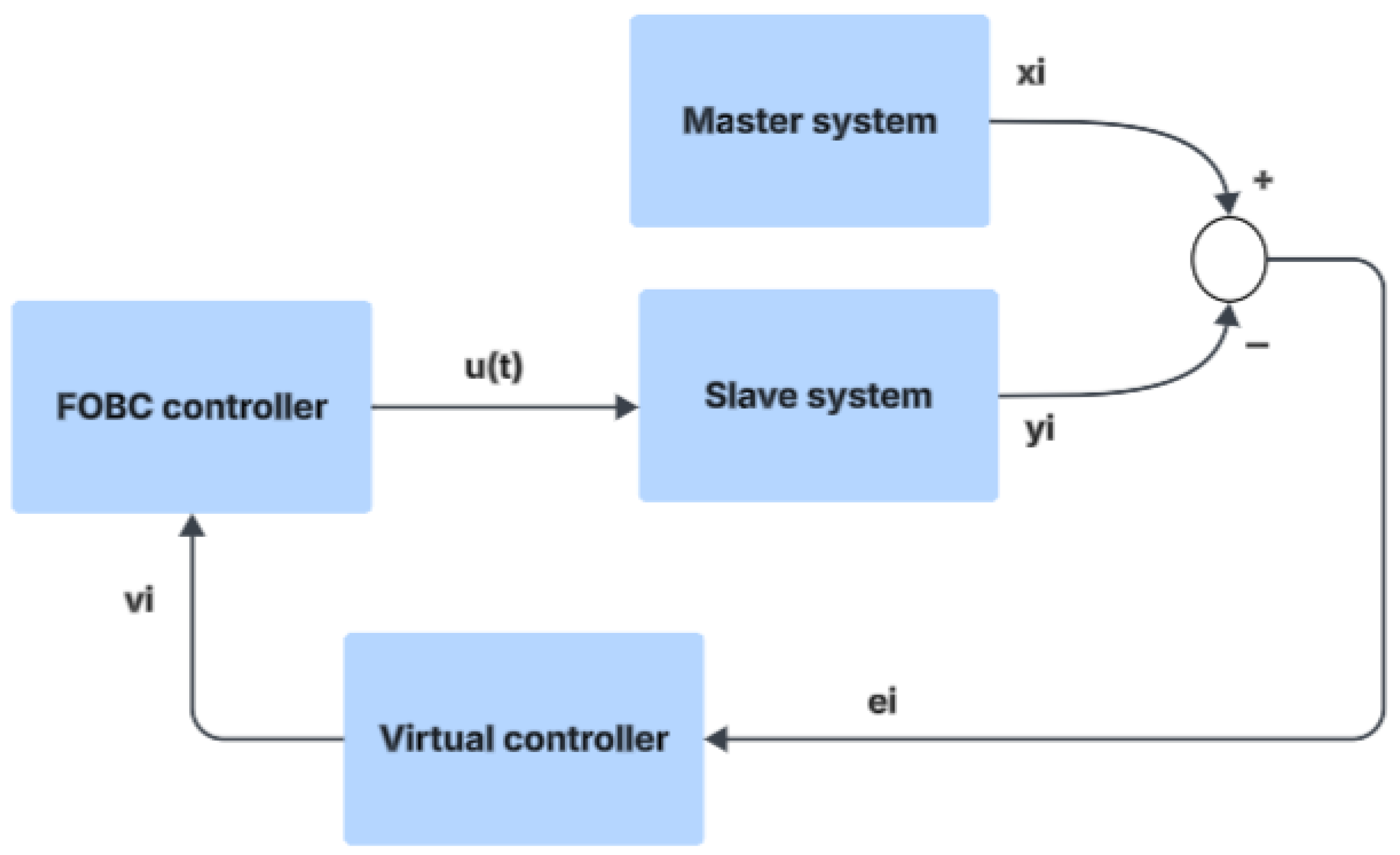
3. System Summary and Problem Definition
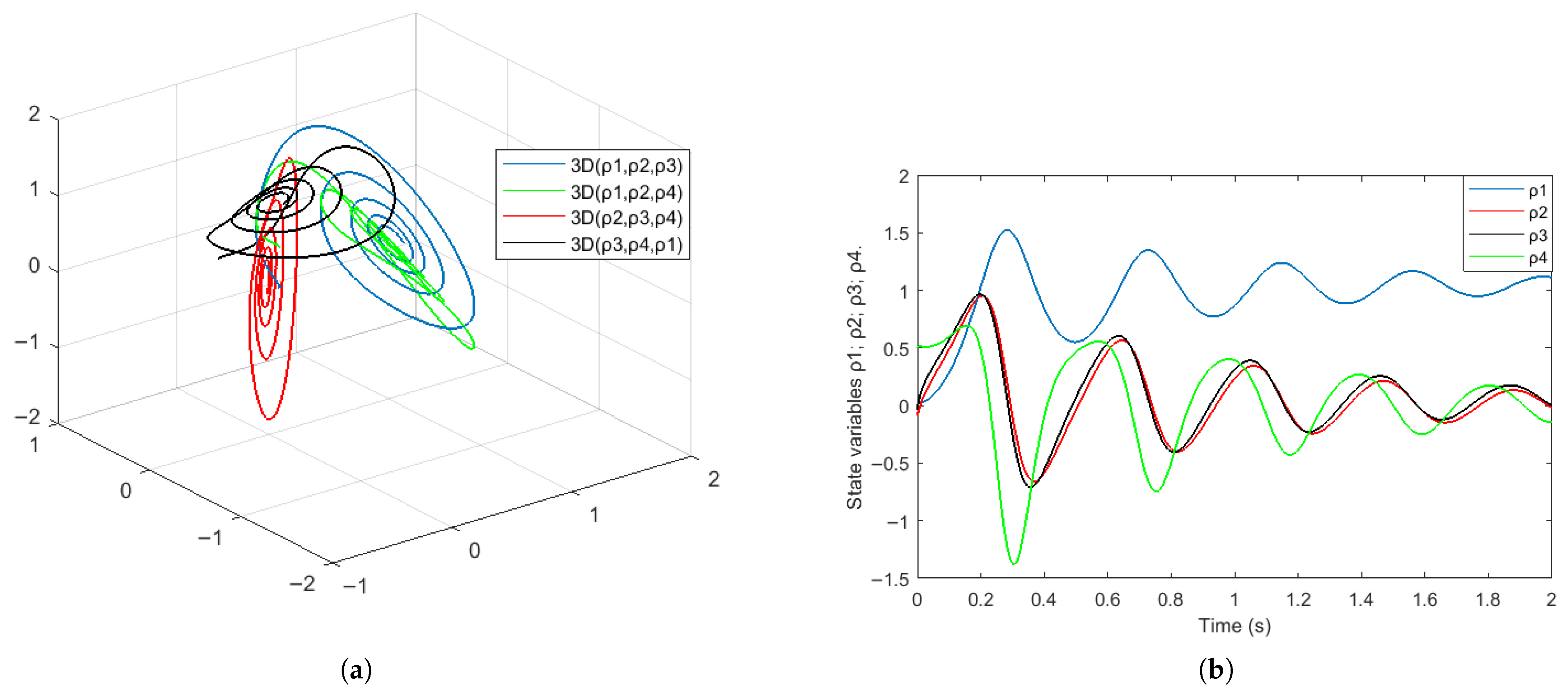
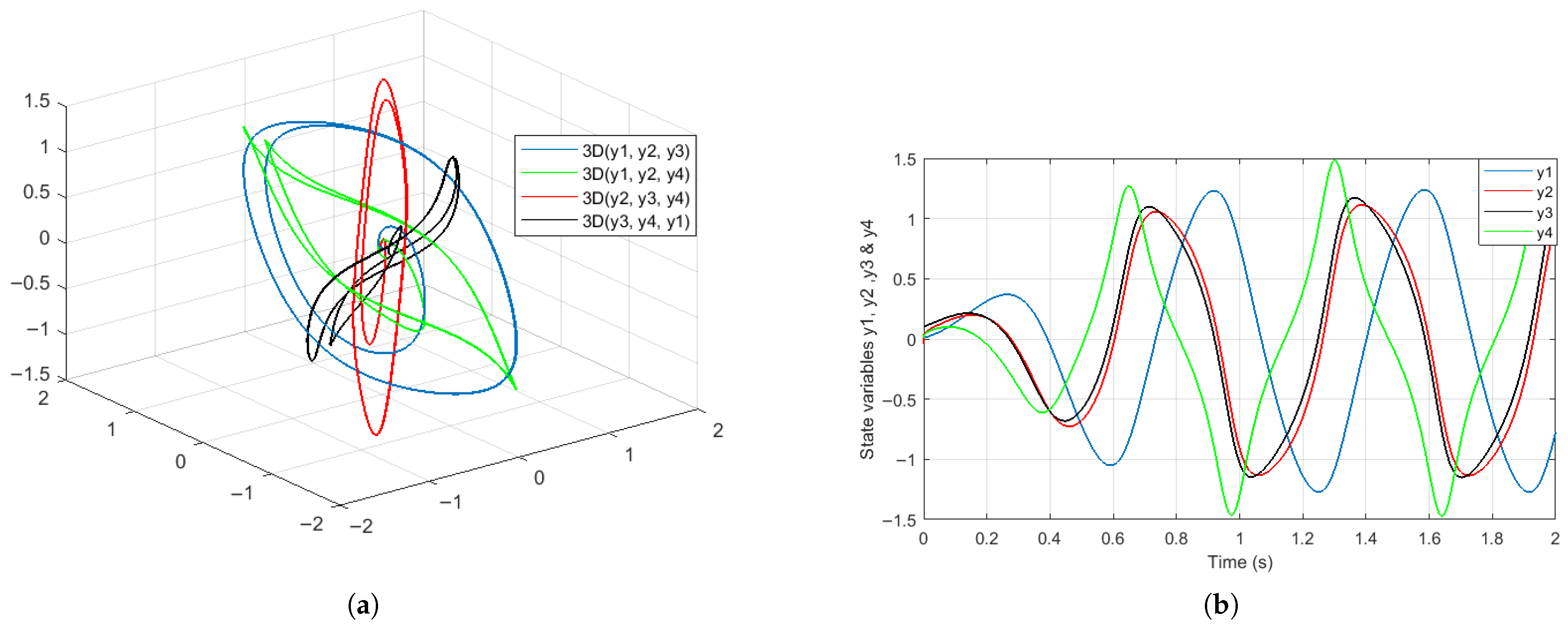
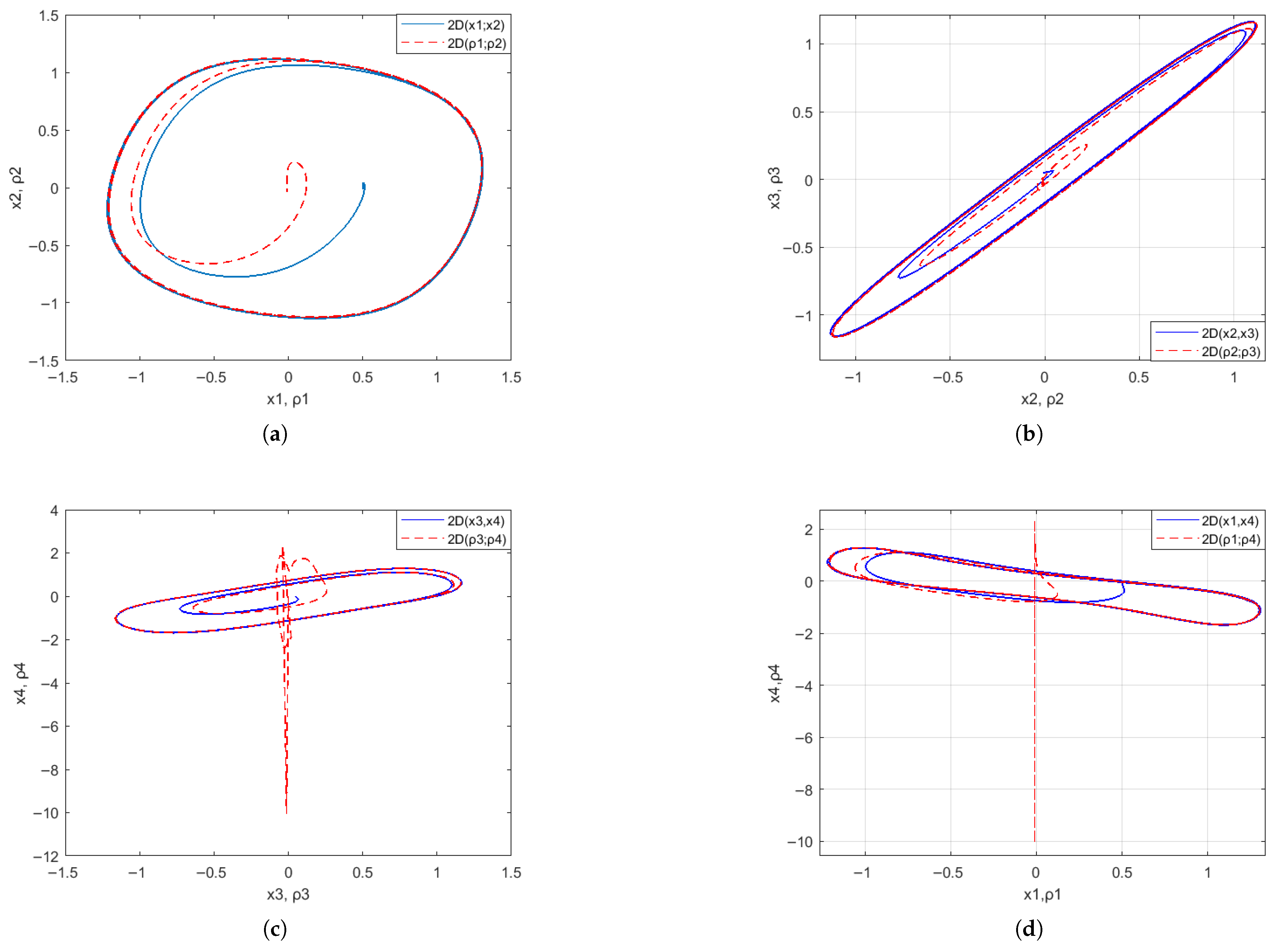
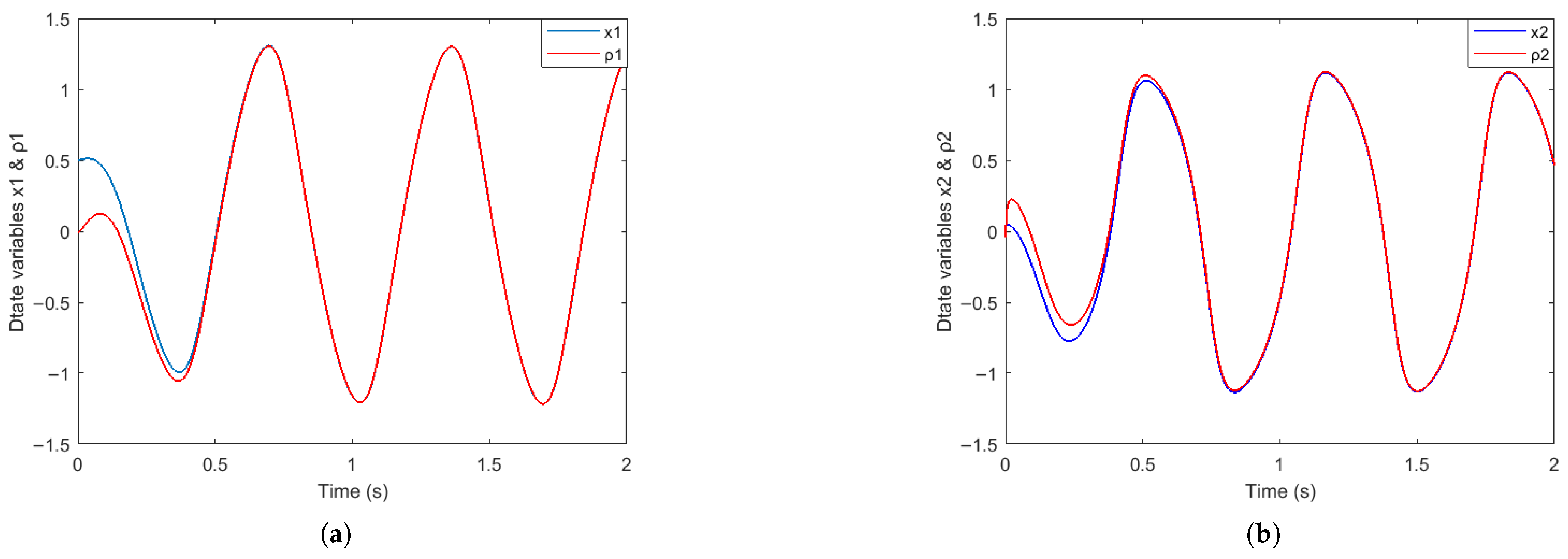
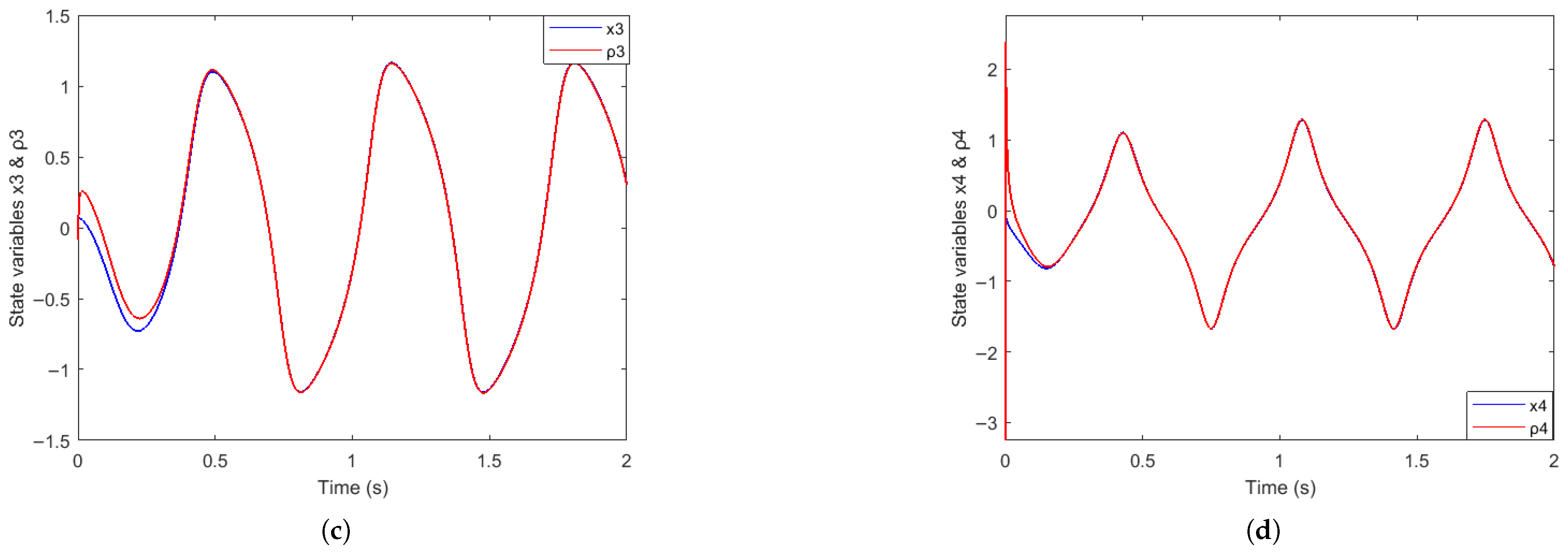
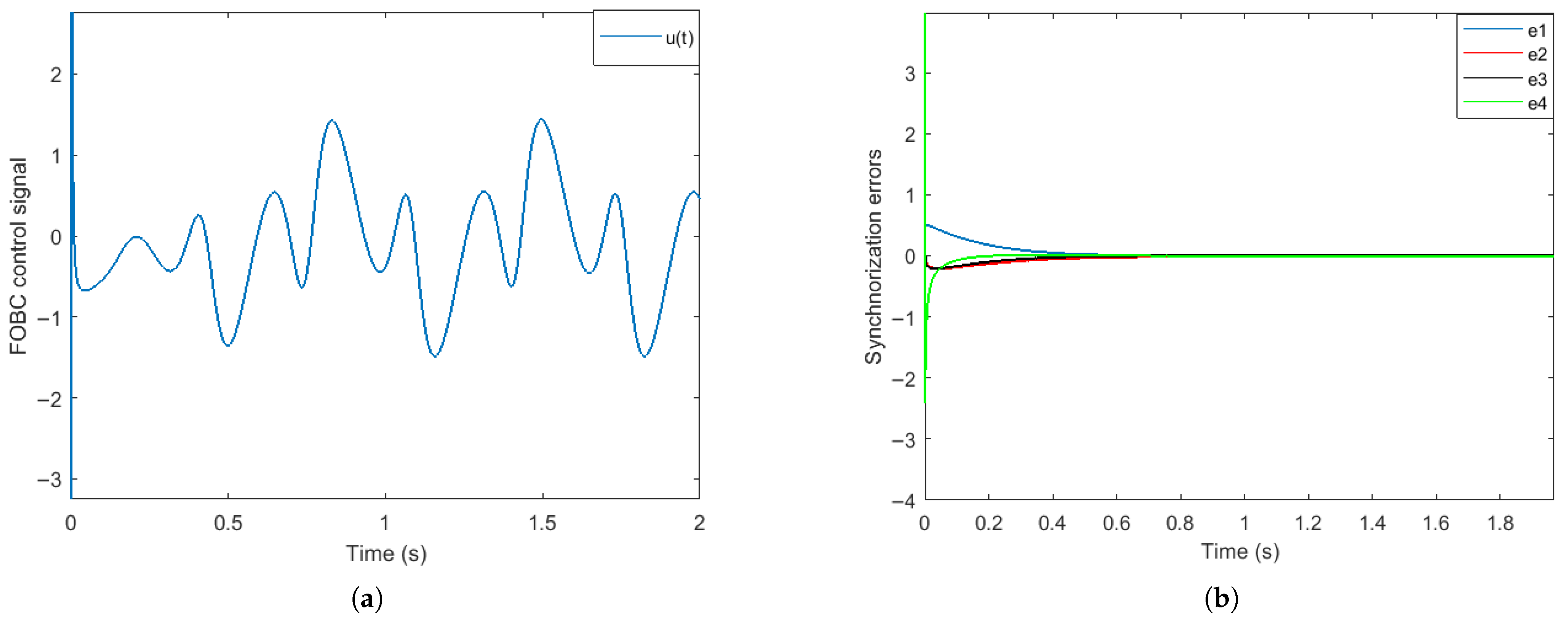
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef] [PubMed]
- Djari, A. Optimal Projective Synchronization of Non-identical Fractional-Order Chaotic Systems with Uncertainties and Disturbances Using Fractional Sliding Mode Control with GA and PSO Algorithms. Arab. J. Sci. Eng. 2020, 45, 10147–10161. [Google Scholar] [CrossRef]
- Yao, X.; Shi, J.; Zhong, S.; Du, Y. Synchronization for Delayed Fractional-Order Memristive Neural Networks Based on Intermittent-Hold Control with Application in Secure Communication. Fractal. Fract. 2024, 8, 519. [Google Scholar] [CrossRef]
- Nail, B.; Atoussi, M.A.; Saadi, S.; Tibermacine, I.E.; Napoli, C. Real-Time Synchronisation of Multiple Fractional-Order Chaotic Systems: An Application Study in Secure Communication. Fractal. Fract. 2024, 8, 104. [Google Scholar] [CrossRef]
- Zourmba, K.; Wamba, J.; Fortuna, L. Multi-Level Synchronization of Chaotic Systems for Highly-Secured Communication. Electronics 2025, 14, 2592. [Google Scholar] [CrossRef]
- Hu, G.-H.; Ho, C.-W.; Yan, J.-J. Robust Angular Frequency Control of Incommensurate Fractional-Order Permanent Magnet Synchronous Motors via State-Sequential Sliding Mode Control. Mathematics 2025, 13, 2669. [Google Scholar] [CrossRef]
- Zhang, R.; Choi, H.-S.; Jung, D.; Cho, H.; Anh, P.H.N.; Vu, M.T. Fixed-Time Control with an Improved Sparrow Search Algorithm for Robotic Arm Performance Optimization. Appl. Sci. 2024, 14, 10096. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, L.; He, D. Application of Variable Universe Fuzzy PID Controller Based on ISSA in Bridge Crane Control. Electronics 2024, 13, 3534. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, X.; Yin, Y. Duality Revelation and Operator-Based Method in Viscoelastic Problems. Fractal. Fract. 2025, 9, 274. [Google Scholar] [CrossRef]
- Busarello Wolff, J.G.; Kingeski, R.; Santos, W.P.d.; Cristani, J.; Traverso, S.D.; Paterno, A.S. Multifrequency Electrical Impedance Tomography Images for Swine Pneumonia Detection Using Conductivity Differences. Electronics 2024, 13, 1463. [Google Scholar] [CrossRef]
- Sagi, Y.; Brook, M.; Almog, I.; Davidson, N. Observation of Anomalous Diffusion and Fractional Self-Similarity in One Dimension. Phys. Rev. Lett. 2012, 108, 093002. [Google Scholar] [CrossRef]
- Favela, L.H.; Amon, M.J. Enhancing Bayesian Approaches in the Cognitive and Neural Sciences via Complex Dynamical Systems Theory. Dynamics 2023, 3, 115–136. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Dang, S. Dynamic Behavior and Fixed-Time Synchronization Control of Incommensurate Fractional-Order Chaotic System. Fractal. Fract. 2025, 9, 18. [Google Scholar] [CrossRef]
- Abualhomos, M.; Abbes, A.; Gharib, G.M.; Shihadeh, A.; Al Soudi, M.S.; Alsaraireh, A.A.; Ouannas, A. Bifurcation, Hidden Chaos, Entropy and Control in Hénon-Based Fractional Memristor Map with Commensurate and Incommensurate Orders. Mathematics 2023, 11, 4166. [Google Scholar] [CrossRef]
- Boulkroune, A.; Bouzeriba, A.; Bouden, T. Fuzzy generalized projective synchronization of incommensurate fractional-order chaotic systems. Neurocomputing 2016, 173, 606–614. [Google Scholar] [CrossRef]
- Ahcene, H.; Nadia, D.; Maamar, B. Fixed-time synergetic ADRC for nonlinear fractional-order systems with uncertainties and external disturbance. Int. J. Dyn. Control 2025, 13, 62. [Google Scholar] [CrossRef]
- Eshaghi, S.; Ordokhani, Y.; Bayram, M.; Inc, M. Synchronization and control of fractional laser chaotic systems defined based on the regularized Prabhakar derivative with incommensurate parameters. Nonlinear Dyn. 2025, 113, 5643–5669. [Google Scholar] [CrossRef]
- Derakhshannia, M.; Moosapour, S.S. Adaptive arbitrary time synchronisation control for fractional order chaotic systems with external disturbances. Int. J. Syst. Sci. 2024, 56, 1540–1560. [Google Scholar] [CrossRef]
- Taheri, M.; Chen, Y.; Zhang, C.; Berardehi, Z.R.; Roohi, M.; Khooban, M.H. A finite-time sliding mode control technique for synchronization chaotic fractional-order laser systems with application on encryption of color images. Optik 2023, 285, 170948. [Google Scholar]
- Zhang,, Y.; Li, Y. Improved fixed-time sliding mode synchronization control of a new 4-cell memristive CNN chaotic system with the offset boosting via certain self-parameters. Chaos Solitons Fractals 2025, 199, 116800. [Google Scholar]
- Khettab, K.; Ladaci, S.; Bensafia, Y. Fuzzy adaptive control of fractional order chaotic systems with unknown control gain sign using a fractional order Nussbaum gain. IEEE/CAA Autom. Sin. 2019, 6, 816–823. [Google Scholar] [CrossRef]
- Bai, Z.; Li, S.; Liu, H.; Zhang, X. Adaptive Fuzzy Backstepping Control of Fractional-Order Chaotic System Synchronization Using Event-Triggered Mechanism and Disturbance Observer. Fractal Fract. 2022, 6, 714. [Google Scholar] [CrossRef]
- Das, K.; Srinivas, M.N.; Madhusudanan, V.; Pinelas, S. Mathematical Analysis of a Prey–Predator System: An Adaptive Back-Stepping Control and Stochastic Approach. Math. Comput. Appl. 2019, 24, 22. [Google Scholar] [CrossRef]
- Noshad, E.; Nozari, H.A.; Castaldi, P. A novel fractional-order integral backstepping control approach: An application to integer-order nonlinear glucose-insulin system dynamics. J. Control Decis. 2025, 1–13. [Google Scholar] [CrossRef]
- Fatemeh, D.; Hamed, M. An ADRC-based backstepping control design for a class of fractional-order systems. ISA Trans. 2022, 121, 140–146. [Google Scholar]
- Lavín-Delgado, J.E.; Soto-Mendiola, R.M.; Gómez-Aguilar, J.F.; Gallardo-Bernal, I.; Hernández-Castillo, E.; Pérez-Careta, E. Controlling a quadrotor UAV flight using a fractional Caputo–Fabrizio backstepping control for trajectory tracking tasks. Int. J. Dyn. Control 2025, 13, 286. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Kui, Q.; Yao, W.; Sun, G. Fractional-Order Lyapunov-Based Backstepping-Like Feedback Control of N-DOF Mechanical Systems. IEEE Trans. Autom. Sci. Eng. 2025, 22, 12949–12959. [Google Scholar] [CrossRef]
- Michał, G. A comment on the “Robust stability analysis of fractional order interval polynomials”, by Nusret Tan et al. ISA Trans. 2011, 50, 11. [Google Scholar] [PubMed]
- Zhang, D.; Wei, B. Learning Control: Applications in Robotics and Complex Dynamical Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 93–102. [Google Scholar]
- Ding, D.; Qi, D.; Wang, Q. Non-linear Mittag–Leffler stabilisation of commensurate fractional-order non-linear systems. IET Control Theor. Appl. 2015, 9, 681–690. [Google Scholar] [CrossRef]
- Sun, Z.; Xue, Q.; Zhao, N. Chimera states in fractional-order coupled Rayleigh oscillators. Commun. Nonlinear Sci. Numer. Simul. 2024, 135, 108083. [Google Scholar] [CrossRef]
- Solis, C.U.; Clempner, J.B.; Poznyak, A.S. Fast Terminal Sliding-Mode Control with an Integral Filter Applied to a Van Der Pol Oscillator. IEEE Trans. Ind. Electron. 2017, 64, 5622–5628. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djari, A.; Djabri, R.; Aouiche, A.; Bouarroudj, N.; Houam, Y.; Bettayeb, M.; Alawad, M.A.; Alkhrijah, Y. Perfect Projective Synchronization of a Class of Fractional-Order Chaotic Systems Through Stabilization near the Origin via Fractional-Order Backstepping Control. Fractal Fract. 2025, 9, 687. https://doi.org/10.3390/fractalfract9110687
Djari A, Djabri R, Aouiche A, Bouarroudj N, Houam Y, Bettayeb M, Alawad MA, Alkhrijah Y. Perfect Projective Synchronization of a Class of Fractional-Order Chaotic Systems Through Stabilization near the Origin via Fractional-Order Backstepping Control. Fractal and Fractional. 2025; 9(11):687. https://doi.org/10.3390/fractalfract9110687
Chicago/Turabian StyleDjari, Abdelhamid, Riadh Djabri, Abdelaziz Aouiche, Noureddine Bouarroudj, Yehya Houam, Maamar Bettayeb, Mohamad A. Alawad, and Yazeed Alkhrijah. 2025. "Perfect Projective Synchronization of a Class of Fractional-Order Chaotic Systems Through Stabilization near the Origin via Fractional-Order Backstepping Control" Fractal and Fractional 9, no. 11: 687. https://doi.org/10.3390/fractalfract9110687
APA StyleDjari, A., Djabri, R., Aouiche, A., Bouarroudj, N., Houam, Y., Bettayeb, M., Alawad, M. A., & Alkhrijah, Y. (2025). Perfect Projective Synchronization of a Class of Fractional-Order Chaotic Systems Through Stabilization near the Origin via Fractional-Order Backstepping Control. Fractal and Fractional, 9(11), 687. https://doi.org/10.3390/fractalfract9110687




