On Generalized Wirtinger Inequalities for (k,ψ)-Caputo Fractional Derivatives and Applications

Abstract

The primary aim of this study is to establish new Wirtinger-type inequalities involving fractional derivatives, which are essential tools in analysis and applied mathematics. We derive generalized Wirtinger-type inequalities incorporating the $(k,\psi )$-Caputo fractional derivatives using Taylor’s expansion. The inequalities are derived in $L_p$ spaces $(p>1)$ through Hölder’s inequality. A detailed analytical discussion is provided to further examine the derived inequalities. The theoretical findings are validated through numerical examples and graphical representations. Furthermore, the novelty and applicability of the proposed technique are demonstrated through the applications of the resulting inequalities to derive new results related to the arithmetic–geometric mean inequality.

1. Introduction

Fractional calculus is a crucial branch of mathematics that extends the concept of integrals and derivatives to non-integer orders. The study of fractional derivatives and integrals gained significance in the 20th century, as researchers explored their applications in diverse fields, including bioengineering [1], electrical and mechanical engineering [2], atmospheric and statistical physics [3], optimization, viscoelasticity [4], machine learning [5], robotics [6], and control theory [7]. In the literature, several definitions of fractional integrals and derivatives have been proposed. Among these are the Riemann–Liouville and Caputo [8], the Hadamard [9], the Caputo–Hadamard [10], and the Hilfer [11] fractional operators are widely used in both theoretical studies and real-world applications. Fractional derivatives such as the $\psi$-Riemann–Liouville operator in [8] and the $\psi$-Caputo operator in [12], introduced by Almeida, have been developed to offer further analytical flexibility beyond classical operators.

In several domains, particularly optimization, special means and integral estimates frequently rely on the analysis of mathematical inequalities. This field of inequalities employing fractional integrals has advanced significantly in the last few decades. Applications of these fractional inequalities can be found in numerous areas such as probability theory, image and signal processing, quantitative quadrature, and optimization problems. In recent decades, many researchers have extended classical inequalities into the framework of fractional calculus. The most well-known inequality in the literature is the Wirtinger inequality, named after Wilhelm Wirtinger. The Wirtinger inequality was an essential tool in the proof of the isoperimetric inequality when it appeared in 1904. Its importance is due to its ability to relate the integral of the square of a function with the integral of the square of its derivative.

According to [13], if $\mathrm{\Omega }\in {\mathit{C}}^1[\mu ,\upsilon ]$ satisfies the condition $\mathrm{\Omega }\left(\mu \right)=\mathrm{\Omega }\left(\upsilon \right)=0$, then the following is obtained:

$$\begin{array}{c}\hfill {\int }_{\mu }^{\upsilon }{\mathrm{\Omega }}^2\left(\phi \right)d\phi \le {\int }_{\mu }^{\upsilon }{\left({\mathrm{\Omega }}^{\prime }\left(\phi \right)\right)}^{2}d\phi .\end{array}$$

(1)

Beesack extended (1) in [14]. In particular, if the function $\mathrm{\Omega }\in {\mathit{C}}^2[\mu ,\upsilon ]$ satisfies the conditions $\mathrm{\Omega }\left(\mu \right)=\mathrm{\Omega }\left(\upsilon \right)=0$, then the following holds:

$$\begin{array}{c}\hfill {\int }_{\mu }^{\upsilon }{\mathrm{\Omega }}^4\left(\phi \right)d\phi \le {\displaystyle \frac{4}{3}}{\int }_{\mu }^{\upsilon }{\left({\mathrm{\Omega }}^{\prime }\left(\phi \right)\right)}^{4}d\phi ,\end{array}$$

(2)

In [15], Beesack examined the relationship between a function and its derivative in the context of inequalities. Several important problems rely on Beesack’s conclusions and on related contributions by other researchers, including integral estimation, series convergence, and the determination of the least eigenvalues of the differential operators. For example, the Poincare inequality, which is a generalization of the Wirtinger inequality, attains its best constant as the first eigenvalue of the Laplace operator, as shown in [16]. Furthermore, C.A. Swanson extended the Wirtinger inequality to n-dimensional context in [17]. Alzer investigated modifications of the Wirtinger inequality in both discrete and continuous settings in [18]. Additionally, Böttcher and Widom in [19] evaluated sequences of constants that emerged in specific situations. They highlighted the identification of the best constant in the Wirtinger–Sobolev inequality, which characterizes the relationship between the integral of the square of a function and the square of its higher-order derivatives. Alomari in [20] established Beesack-Wirtinger-type inequalities for absolutely continuous functions having derivatives in $L_p$ spaces where $p>1$. Moreover, Erden in [21] presented Wirtinger-type inequalities concerning higher-order differential functions. In [22], Sarikaya proposed several modified versions of Wirtinger-type inequalities.

Theorem 1. 

Suppose $\mathrm{\Omega }\in {\mathit{C}}^1[\mu ,\upsilon ]$ is a function satisfying $\mathrm{\Omega }\left(\mu \right)=\mathrm{\Omega }\left(\upsilon \right)=0$, and let ${\mathrm{\Omega }}^{\prime }\in L_2[\mu ,\upsilon ]$. Then, we have the following inequality

$$\begin{array}{c}\hfill {\int }_{\mu }^{\upsilon }{\left[\mathrm{\Omega }\left(\phi \right)\right]}^{2}d\phi \le {\displaystyle \frac{{(\upsilon -\mu )}^2}{6}}{\int }_{\mu }^{\upsilon }{\left[{\mathrm{\Omega }}^{\prime }\left(\phi \right)\right]}^{2}d\phi .\end{array}$$

(3)

We begin by presenting a few definitions and basic results that are essential for our main findings.

In [23], Diaz et al. introduced the k–gamma function, which is defined as follows:

Definition 1. 

Let $z\in \mathbb{C}$ such that $Re\left(z\right)>0$ and $k\in {\mathbb{R}}_{+}\setminus 0$. Then, the k-gamma function ${\mathrm{\Gamma }}_k(.)$ is defined as follows:

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_k\left(z\right)={\int }_0^{\infty }{e}^{{\displaystyle \frac{-r^k}{k}}}{r}^{z-1}dr.\end{array}$$

By placing $k=1$ in Definition 1, the k-gamma function reduces to the classical gamma function.

Studying a fractional operator with a kernel that depends on another function, the definitions of $\psi$-Riemann–Liouville fractional integrals and derivatives are given below, as introduced in [8].

Definition 2. 

Let Ω be an integrable function defined over $I=[\mu ,\upsilon ]$. If $\psi \in {\mathit{C}}^1\left(I\right)$ is increasing with ${\psi }^{\prime }\left(\varsigma \right)\ne 0$ for all $\varsigma \in I$. Then the ψ-Riemann–Liouville fractional integrals of order $\gamma >0$ are expressed as follows:

$$\begin{array}{c}\hfill {}^{Rl}\mathit{I}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\gamma \right)}}{\int }_{\mu }^{\varsigma }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\varsigma \right)-\psi \left(\vartheta \right))}^{\gamma -1}\mathrm{\Omega }\left(\vartheta \right)d\vartheta ,\\ \hfill {}^{Rl}\mathit{I}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\gamma \right)}}{\int }_{\varsigma }^{\upsilon }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\vartheta \right)-\psi \left(\varsigma \right))}^{\gamma -1}\mathrm{\Omega }\left(\vartheta \right)d\vartheta .\end{array}$$

Definition 3. 

The ψ-Riemann–Liouville fractional derivatives of order $\gamma >0$ are formulated as follows:

$$\begin{array}{cc}\hfill {}^{Rl}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)=& {\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i{}^{Rl}\mathit{I}_{\mu +}^{i-\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathrm{\Gamma }(i-\gamma )}}{\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i{\int }_{\mu }^{\varsigma }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\varsigma \right)-\psi \left(\vartheta \right))}^{i-\gamma -1}\mathrm{\Omega }\left(\vartheta \right)d\vartheta ,\hfill \\ \hfill {}^{Rl}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)=& {(-1)}^i{\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i{}^{Rl}\mathit{I}_{\upsilon -}^{i-\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\hfill \\ \hfill & ={\displaystyle \frac{{(-1)}^i}{\mathrm{\Gamma }(i-\gamma )}}{\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i{\int }_{\mu }^{\varsigma }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\vartheta \right)-\psi \left(\varsigma \right))}^{i-\gamma -1}\mathrm{\Omega }\left(\vartheta \right)d\vartheta .\hfill \end{array}$$

For specific choices of $\psi$, the definition simplifies to well-known fractional derivatives. Particularly, placing $\psi \left(\varsigma \right)=\varsigma$ yields the classical Riemann–Liouville fractional derivative introduced in [8], while choosing $\psi \left(\varsigma \right)=log\varsigma$ leads to the Hadamard fractional derivative given in [9].

According to [12], the definitions of $\psi$-Caputo fractional derivatives are defined as follows:

Definition 4. 

Let $\gamma >0$ and $i\in \mathbb{N}$. Consider the interval $I=[\mu ,\upsilon ]$, and let $\mathrm{\Omega },\psi \in C^i\left(I\right)$ be two functions where ψ is increasing and ${\psi }^{\prime }\left(\vartheta \right)\ne 0$ for all $\vartheta \in I$. Then, the left- and right-sided ψ–Caputo fractional derivatives of order γ are given as follows:

$$\begin{array}{cc}\hfill {}^c\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)=& {}^{Rl}\mathit{I}_{\mu +}^{i-\gamma ,\psi }{\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i\mathrm{\Omega }\left(\varsigma \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathrm{\Gamma }(i-\gamma )}}{\int }_{\mu }^{\varsigma }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\varsigma \right)-\psi \left(\vartheta \right))}^{i-\gamma -1}{\mathrm{\Omega }}_{\psi }^{\left[i\right]}\left(\vartheta \right)d\vartheta ,\hfill \\ \hfill {}^c\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)=& {}^{Rl}\mathit{I}_{\upsilon -}^{i-\gamma ,\psi }{\left(-{\displaystyle \frac{1}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i\mathrm{\Omega }\left(\varsigma \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathrm{\Gamma }(i-\gamma )}}{\int }_{\varsigma }^{\upsilon }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\vartheta \right)-\psi \left(\varsigma \right))}^{i-\gamma -1}{(-1)}^i{\mathrm{\Omega }}_{\psi }^{\left[i\right]}\left(\vartheta \right)d\vartheta .\hfill \end{array}$$

For simplicity, we use the following abbreviation:

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_{\psi }^{\left[i\right]}\left(\varsigma \right)={\left({\displaystyle \frac{1}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i\mathrm{\Omega }\left(\varsigma \right).\end{array}$$

For specific choices of $\psi$, the definition coincides with the Caputo fractional derivative presented in [8], when $\psi \left(\varsigma \right)=\varsigma$, while choosing $\psi \left(\varsigma \right)=log\varsigma$ leads to the Caputo–Hadamard fractional derivative defined in [10].

The $(k,\psi )$-Riemann–Liouville fractional integrals defined in [24] is given by the following definition:

Definition 5. 

Let $\mathrm{\Omega }\in L_1[\mu ,\upsilon ]$ and $k\in {\mathbb{R}}_{+}$. Then, the left- and right-sided $(k,\psi )$-Riemann–Liouville fractional integrals of order $\gamma >0$$(\gamma \in \mathbb{R})$ of the function Ω are defined as follows:

$$\begin{array}{c}\hfill {}^{kRl}\mathit{I}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\mu }^{\varsigma }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\varsigma \right)-\psi \left(\vartheta \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\mathrm{\Omega }\left(\vartheta \right)d\vartheta ,\\ \hfill {}^{kRl}\mathit{I}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\varsigma }^{\upsilon }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\vartheta \right)-\psi \left(\varsigma \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\mathrm{\Omega }\left(\vartheta \right)d\vartheta .\end{array}$$

By setting $k=1$ in Definition 5, the expression reduces to the $\psi$-Riemann–Liouville integral.

As in [24], the left-sided and right-sided $(k,\psi )$-Riemann–Liouville fractional derivatives are defined as follows:

Definition 6. 

Let $\gamma ,k\in {\mathbb{R}}_{+}$. Consider the functions $\psi ,\mathrm{\Omega }\in C^i[\mu ,\upsilon ]$ with $(m\in \mathbb{N})$ and such that ${\psi }^{\prime }\left(\varsigma \right)\ne 0$ for all $\varsigma \in [\mu ,\upsilon ]$. Then the $(k,\psi )$-Riemann–Liouville fractional derivatives of order $\gamma >0$ are given by the following:

$$\begin{array}{cc}\hfill {}^{kRl}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)& ={\left({\displaystyle \frac{k}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i{}^{kRl}\mathit{I}_{\mu +}^{ik-\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\hfill \\ \hfill & ={\left({\displaystyle \frac{k}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k(ik-\gamma )}}{\int }_{\mu }^{\varsigma }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\varsigma \right)-\psi \left(\vartheta \right))}^{{\displaystyle \frac{ik-\gamma }{k}}-1}\mathrm{\Omega }\left(\vartheta \right)d\vartheta ,\hfill \\ \hfill {}^{kRl}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)& ={\left(-{\displaystyle \frac{k}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i{}^{kRl}\mathit{I}_{\upsilon -}^{ik-\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\hfill \\ \hfill & ={\left(-{\displaystyle \frac{k}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k(ik-\gamma )}}{\int }_{\varsigma }^{\upsilon }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\vartheta \right)-\psi \left(\varsigma \right))}^{{\displaystyle \frac{ik-\gamma }{k}}-1}\mathrm{\Omega }\left(\vartheta \right)d\vartheta .\hfill \end{array}$$

By placing $k=1$ in Definition 6, the definition reduces to $\psi$-Riemann– Liouville derivative.

The definitions of $(k,\psi )$-Caputo fractional derivatives presented in [24], are given below.

Definition 7. 

Let $\gamma ,k\in {\mathbb{R}}_{+}$, and $\psi ,\mathrm{\Omega }\in C^i[\mu ,\upsilon ]$ with $i\in \mathbb{N}$. Assume that ${\psi }^{\prime }\left(\varsigma \right)\ne 0$ for all $\varsigma \in [\mu ,\upsilon ]$. Then the $(k,\psi )$-Caputo fractional derivatives of order $\gamma >0$ are expressed as follows:

$$\begin{array}{cc}\hfill {}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)& ={}^{kc}\mathit{I}_{\mu +}^{ik-\gamma ,\psi }{\left({\displaystyle \frac{k}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i\mathrm{\Omega }\left(\varsigma \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k(ik-\gamma )}}{\int }_{\mu }^{\varsigma }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\varsigma \right)-\psi \left(\vartheta \right))}^{{\displaystyle \frac{ik-\gamma }{k}}-1}{}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\vartheta \right)d\vartheta ,\hfill \\ \hfill {}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)& ={}^{kc}\mathit{I}_{\upsilon -}^{ik-\gamma ,\psi }{\left(-{\displaystyle \frac{k}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i\mathrm{\Omega }\left(\varsigma \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k(ik-\gamma )}}{\int }_{\varsigma }^{\upsilon }{\psi }^{\prime }\left(\vartheta \right){(\psi \left(\vartheta \right)-\psi \left(\varsigma \right))}^{{\displaystyle \frac{ik-\gamma }{k}}-1}{(-1)}^i{}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\varsigma \right)d\vartheta .\hfill \end{array}$$

For simplicity, we use the following abbreviation:

$$\begin{array}{c}\hfill {}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\varsigma \right)={\left({\displaystyle \frac{k}{{\psi }^{\prime }\left(\varsigma \right)}}{\displaystyle \frac{d}{d\varsigma }}\right)}^i\mathrm{\Omega }\left(\varsigma \right).\end{array}$$

By setting $k=1$ in Definition 7, the expression reduces to the $\psi$-Caputo fractional derivative.

In the analysis of the existence and uniqueness of solutions to fractional differential equations, several types of fractional derivatives have been introduced. Among them, the $(k,\psi )$-Caputo fractional derivative has emerged as a powerful and highly adaptable tool. By incorporating a real parameter k and a monotonic function $\psi$, this operator generalizes the classical Caputo derivative, offering greater flexibility in capturing memory effects and nonlocal behavior. In this paper, we employ this operator to establish new Wirtinger-type inequalities. These inequalities have found diverse applications across various areas of mathematical analysis. For instance, Samir H. Saker in [25] utilized Wirtinger-type inequalities to identify large gaps between the zeros of the Riemann zeta function. In [26], Seuret et al. applied these inequalities in the study of time-delay systems. Furthermore, Bo Du employed the Wirtinger inequality to examine the existence of antiperiodic solutions for an inertial competitive neutral-type network in [27].

Many scholars have investigated Wirtinger-type inequalities in the contexts of both fractional calculus and classical calculus. Erden presented results for classical derivatives in [21], and Erden et al. further extended these results to the Caputo and Riemann–Liouville fractional derivatives in [28]. Moreover, Samraiz et al. broadened these results for Caputo–Hadamard and Hadamard fractional derivatives in [29], while Wu et al. modified the theory by considering tempered $\psi$-fractional derivatives in [30].

Inspired by these prior findings and their diverse applications, the main objective of this research is to develop a new class of inequalities incorporating the $(k,\psi )$-Caputo and $(k,\psi )$-Riemann–Liouville fractional derivatives with a particular focus on the Wirtinger inequality. We derive significant results by applying Hölder’s inequality, which are relevant to different fields such as statistical modeling, mathematical analysis, engineering, and computational sciences. Additionally, the results of this study may stimulate further research into inequalities related to the $(k,\psi )$-Caputo operator.

Although Wirtinger-type inequalities have been established by several researchers for various fractional derivatives, such as the Caputo, Riemann–Liouville, Caputo–Hadamard, and Hadamard fractional derivatives, these results remain limited to specific operator forms and lack a unified generalized structure. Moreover, there has been little investigation into a comprehensive framework that involves both the kernel function $\psi$ and another parameter k, which could extend the existing findings to a broader class of fractional derivatives. To address this gap, the present research introduces new Wirtinger-type inequalities involving the $(k,\psi )$-Caputo fractional derivatives. These inequalities enhance the analytical significance of various prior findings while generalizing and extending them.

In this work, we introduce Wirtinger-type inequalities for the $(k,\psi )$-Caputo and $(k,\psi )$-Riemann–Liouville fractional derivatives, contributing to the growing field of fractional calculus. These modified operators generalize classical fractional operators by incorporating a kernel function $\psi$ and an additional parameter k, offering greater flexibility in memory-dependent and nonlocal phenomena. The main objective of this paper is to establish novel inequalities within the $(k,\psi )$-Caputo framework, owing to its analytical capabilities and effectiveness for initial value problems. Moreover, we extend our results to the $(k,\psi )$-Riemann–Liouville case to enhance the applicability of the proposed inequalities.

The key objective of this work is to construct new generalized Wirtinger-type inequalities involving the $(k,\psi )$-Caputo fractional derivatives, which are useful tools in mathematical analysis. The work aims to expand the classical Wirtinger framework to fractional settings in both $L_2$ and in general $L_p$$(p>1)$ spaces. The presented inequalities provide a more unified and flexible analytical method by generalizing a number of well-known results as special cases. Numerical examples, graphical illustrations, and an application to the arithmetic–geometric mean inequality are also provided to demonstrate the effectiveness and significance of the obtained results.

The organization of the paper is as follows: Section 1 provides an introduction, highlighting the background, purpose, and significance of the study. Section 2 derives Wirtinger-type inequalities for the $(k,\psi )$-Caputo and $(k,\psi )$-Riemann–Liouville fractional operators. Section 3 explores applications of these results in relation to the arithmetic–geometric mean. Finally, Section 4 concludes the paper by summarizing the key findings.

2. Inequalities Involving $(\mathit{k},\mathit{\psi })$-Caputo and $(\mathit{k},\mathit{\psi })$-Riemann–Liouville Fractional Derivatives

In this section, we present Wirtinger-type inequalities involving the $(k,\psi )$-Caputo and the $(k,\psi )$-Riemann–Liouville fractional derivatives. By examining the relationships among fractional operators, specifically between the $\psi$-Riemann–Liouville and $\psi$-Caputo, we derive several special cases. Here, we analyze the connection between two types of fractional derivatives.

Lemma 1. 

Suppose that $\mathrm{\Omega }\in {AC}^i[\mu ,\upsilon ]$, $i-1<\gamma <i$ with $i\in \mathbb{N}$, and $k\in {\mathbb{R}}_{+}$. Then, the following results hold:

$$\begin{array}{cc}\hfill & {}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={}^{kRl}\mathit{D}_{\mu +}^{\gamma ,\psi }\left[\mathrm{\Omega }\left(\vartheta \right)-\sum _{j=0}^{i-1}{\displaystyle \frac{{(\psi \left(\vartheta \right)-\psi \left(\mu \right))}^j}{{\mathrm{\Gamma }}_k(jk+k)}}{}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right)\right]\left(\varsigma \right),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & {}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={}^{kRl}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\left[\mathrm{\Omega }\left(\vartheta \right)-\sum _{j=0}^{i-1}{\displaystyle \frac{{(\psi \left(\upsilon \right)-\psi \left(\vartheta \right))}^j}{{\mathrm{\Gamma }}_k(jk+k)}}{}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right)\right]\left(\varsigma \right).\hfill \end{array}$$

(5)

The following can be obtained from the above relation:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={}^{kRl}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right),\hfill & \mathrm{if}\mathrm{we}\mathrm{set}{}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right)=0;\hfill \\ {}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={}^{kRl}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right),\hfill & \mathrm{if}\mathrm{we}\mathrm{set}{}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right)=0.\hfill \end{array}\right.\end{array}$$

(6)

Remark 1. 

(i)

By setting $k=0$ in (4) and (5), we recover Theorem 3 in [12].

(ii)

By setting $k=0$ and $\psi \left(\varsigma \right)=log\varsigma$ in (4) and (5), we obtain equations (16) and (17) in [10].

(iii)

By setting $k=0$ and $\psi \left(\varsigma \right)=\varsigma$ in (4) and (5), we obtain equations (2.4.1) and (2.4.2) in [8].

All findings in this section are obtained by utilizing the fundamental identities given in (7) and (8).

Lemma 2. 

Let $\mathrm{\Omega }\in A{C}^i[\mu ,\upsilon ]$ or $C^i[\mu ,\upsilon ]$ with $i-1<{\displaystyle \frac{\gamma }{k}}<i$, $k\in {\mathbb{R}}_{+}$. Then the following identities hold:

$$\begin{array}{c}\hfill \mathrm{\Omega }\left(\varsigma \right)={}^{kRl}\mathit{I}_{\mu +}^{\gamma ,\psi }\left[{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right]+\sum _{j=0}^{i-1}{\displaystyle \frac{{(\psi \left(\varsigma \right)-\psi \left(\mu \right))}^j}{{\mathrm{\Gamma }}_k(jk+k)}}{}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right),\end{array}$$

(7)

$$\begin{array}{c}\hfill \mathrm{\Omega }\left(\varsigma \right)={}^{kRl}\mathit{I}_{\upsilon -}^{\gamma ,\psi }\left[{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right]+\sum _{j=0}^{i-1}{\displaystyle \frac{{(\psi \left(\varsigma \right)-\psi \left(\mu \right))}^j}{{\mathrm{\Gamma }}_k(jk+k)}}{}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right).\end{array}$$

(8)

Proof. 

By applying the left-sided and right-sided $(k,\psi )$-Riemann–Liouville integral to (4) and (5), respectively, and by applying [24] (Theorem 5.4), we obtain (7) and (8). □

Theorem 2. 

Consider the functions $\mathrm{\Omega },\psi \in C^i[\mu ,\upsilon ]$ where $i\in \mathbb{N}\setminus \left\{0\right\}$ and $i=\lceil {\displaystyle \frac{\gamma }{k}}\rceil$. Assume that ${}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)$, ${}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\in L_2[\mu ,\upsilon ]$. Under the conditions that ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right)={}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right)=0$ and $\gamma \ge k$, the following inequality holds:

$$\begin{array}{cc}\hfill {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma & \le {\displaystyle \frac{U^2}{6k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^2}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2{\displaystyle (\frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^2+{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^2\right]d\tau .\hfill \end{array}$$

(9)

Proof. 

Supposing ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right){=}^k{\mathrm{\Omega }}_{\psi }^{\left[i\right]}\left(\upsilon \right)=0$, we take the absolute values of (7) and (8). Then, by applying Cauchy–Schwarz inequality to the resulting terms, we obtain the following:

$$\begin{array}{cc}\hfill {\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^2& ={\left[{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\mu }^{\varsigma }{\psi }^{\prime }\left(\eta \right){(\psi \left(\varsigma \right)-\psi \left(\eta \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|d\eta \right]}^2\hfill \\ \hfill & \le {\left[{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\mu }^{\varsigma }U{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|d\eta \right]}^2\hfill \\ \hfill & \le {\displaystyle \frac{1}{k^2{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{U}^2{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\left(\varsigma -\mu \right){\int }_{\mu }^{\varsigma }{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^{2}d\eta ,\hfill \end{array}$$

(10)

and

$$\begin{array}{cc}\hfill {\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^2& ={\left[{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\varsigma }^{\upsilon }{\psi }^{\prime }\left(\eta \right){(\psi \left(\eta \right)-\psi \left(\varsigma \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|d\eta \right]}^2\hfill \\ \hfill & \le {\left[{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\varsigma }^{\upsilon }U{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|d\eta \right]}^2\hfill \\ \hfill & \le {\displaystyle \frac{1}{k^2{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{U}^2{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\left(\upsilon -\varsigma \right){\int }_{\varsigma }^{\upsilon }{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^{2}d\eta .\hfill \end{array}$$

(11)

By integrating (10) over the interval $[\mu ,\omega \mu +(1-\omega \left)\upsilon \right]$ with respect to $\varsigma$, where $\omega \in [0,1]$, and using Dirichlet’s integral formula, we arrive at the following result:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^2}{k^2{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }(\varsigma -\mu ){\int }_{\mu }^{\varsigma }{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^{2}d\eta d\varsigma \hfill \\ \hfill & ={\displaystyle \frac{U^2}{k^2{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^2{\int }_{\eta }^{\omega \mu +(1-\omega )\upsilon }(\varsigma -\mu )d\varsigma d\eta \hfill \\ \hfill & ={\displaystyle \frac{U^2}{2k^2{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^2\left({(\upsilon -\mu )}^2{(1-\omega )}^2-{(\eta -\mu )}^2\right)d\eta .\hfill \end{array}$$

(12)

Integrating (11) over the interval $[\omega \mu +(1-\omega )\upsilon ,\upsilon ]$, and employing Dirichlet’s integral formula, we obtain the following result:

$$\begin{array}{cc}\hfill & {\int }_{\omega \mu +(1-\omega )\upsilon }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^2}{k^2{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\omega \mu +(1-\omega )\upsilon }^{\upsilon }(\upsilon -\varsigma ){\int }_{\varsigma }^{\upsilon }{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^{2}d\eta d\varsigma \hfill \\ \hfill & ={\displaystyle \frac{U^2}{k^2{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\upsilon }^{\omega \mu +(1-\omega )\upsilon }{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma }\mathrm{\Omega }\left(\eta \right)\right|}^2{\int }_{\eta }^{\omega \mu +(1-\omega )\upsilon }(\upsilon -\varsigma )d\varsigma d\eta \hfill \\ \hfill & ={\displaystyle \frac{U^2}{2k^2{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{U}^2{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\omega \mu +(1-\omega )\upsilon }^{\upsilon }{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^2\left({(\upsilon -\mu )}^2{\omega }^2-{(\upsilon -\eta )}^2\right)d\eta .\hfill \end{array}$$

(13)

To further refine the expressions, we apply the substitution $\eta =\sigma \mu +(1-\sigma )\upsilon$ to (12) and (13). We obtain the following:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^2}{2k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^3}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\omega }^1\left({(1-\omega )}^2-{(1-\sigma )}^2\right){\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{2}d\sigma ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\int }_{\omega \mu +(1-\omega )\upsilon }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^2}{2k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^3}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_0^{\omega }\left({\omega }^2-{\sigma }^2\right){\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{2}d\sigma .\hfill \end{array}$$

By adding the two inequalities above and integrating over the interval [0, 1], with respect to $\omega$, results in the following expression:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^2}{2k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^3}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times [{\int }_0^1{\int }_{\omega }^1\left({(1-\omega )}^2-{(1-\sigma )}^2\right){\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{2}d\sigma d\omega \hfill \\ \hfill & +{\int }_0^1{\int }_0^{\omega }\left({\omega }^2-{\sigma }^2\right){\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{2}d\sigma d\omega ].\hfill \end{array}$$

(14)

By rearranging the order of integration, we obtain the following:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^2}{2k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^3}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times [{\int }_0^1{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^2{\int }_0^{\sigma }\left({(1-\omega )}^2-{(1-\sigma )}^2\right)d\omega d\sigma \hfill \\ \hfill & +{\int }_0^1{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^2{\int }_{\sigma }^1\left({\omega }^2-{\sigma }^2\right)d\omega d\sigma ].\hfill \end{array}$$

Moreover, we obtain the following:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^2}{2k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^3}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times [{\int }_0^1{Z}_1\left(\sigma \right){\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{2}d\sigma \hfill \\ \hfill & +{\int }_0^1{Z}_2\left(\sigma \right){\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{2}d\sigma ],\hfill \end{array}$$

(15)

where

$$\begin{array}{c}\hfill Z_1\left(\sigma \right)={\displaystyle \frac{1}{3}}-{\displaystyle \frac{{(1-\sigma )}^3}{3}}-\sigma {(1-\sigma )}^2,\end{array}$$

and

$$\begin{array}{c}\hfill Z_2\left(\sigma \right)={\displaystyle \frac{1}{3}}-{\displaystyle \frac{{\sigma }^3}{3}}-{\sigma }^2(1-\sigma ).\end{array}$$

Applying the change of variables $\tau =\sigma \mu +(1-\sigma )\upsilon$ to (15), and observing that both functions $Z_1\left(\sigma \right)$ and $Z_2\left(\sigma \right)$ attain their maximum value ${\displaystyle \frac{1}{3}}$ for $\sigma \in [0,1]$, we deduce (9). □

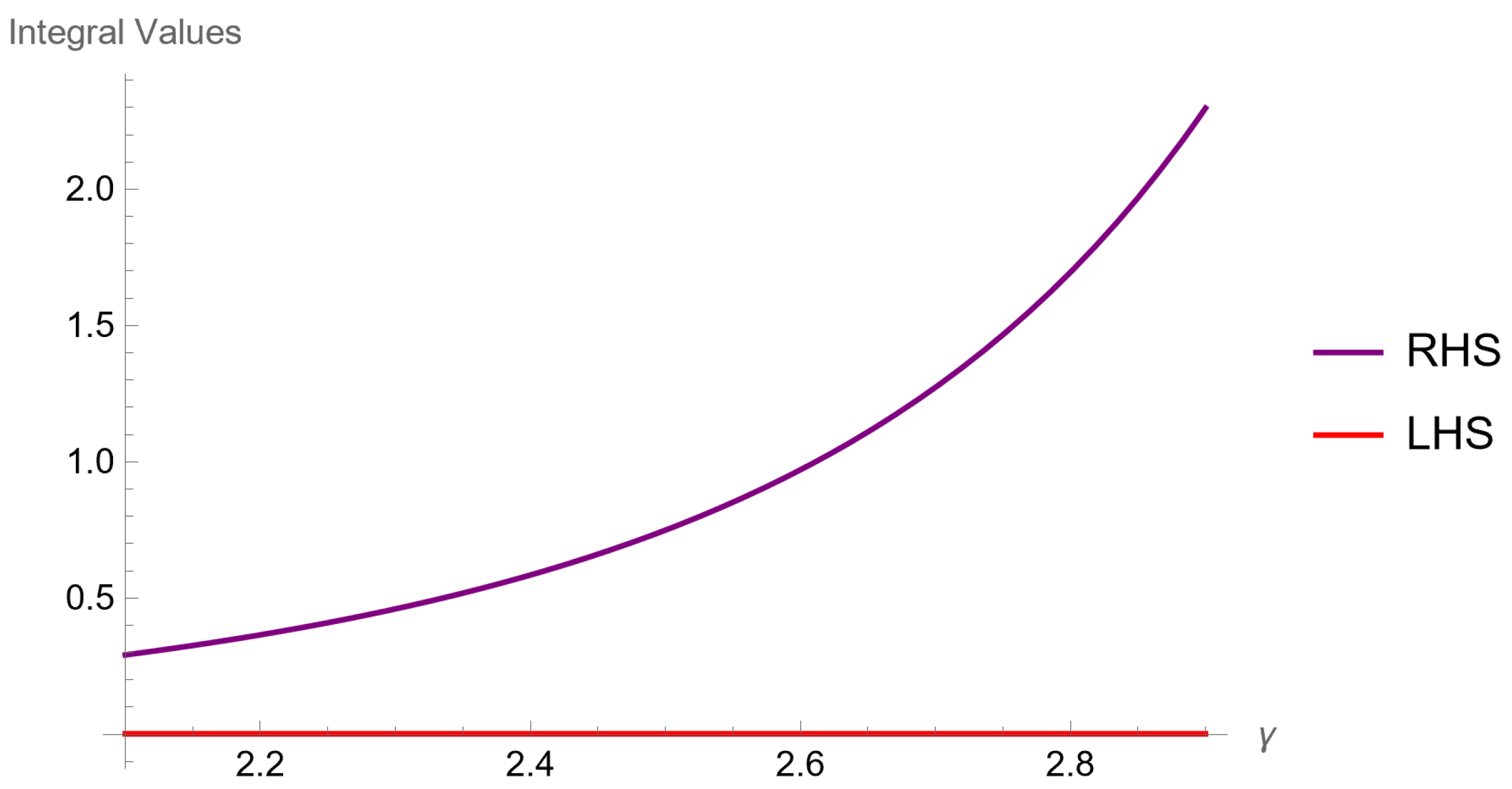
Example 1. 

Consider the functions $\mathrm{\Omega }\left(\varsigma \right)={\varsigma }^i{(\varsigma -1)}^i$ and $\psi \left(\varsigma \right)=\varsigma$ defined over $[0,1]$ and fulfilling the requirements of the theorem ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(0\right)={}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(1\right)=0$. Let $i=2$, $\gamma =2.2$, $k=2$ and $U=1$. Then, we obtain the following result:

$$\begin{array}{c}\hfill {\int }_0^1{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma =0.0015873.\end{array}$$

To evaluate the right-hand side of (9), we proceed as follows:

$$\begin{array}{cc}\hfill {}^{kc}\mathit{D}_{0+}^{2.2}\mathrm{\Omega }\left(\varsigma \right)& =1.54582\left[8.88889{\varsigma }^{0.9}-28.0702{\varsigma }^{1.9}+19.3587{\varsigma }^{2.9}\right],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {}^{kc}\mathit{D}_{1-}^{2.2}\mathrm{\Omega }\left(\varsigma \right)& =1.54582\left[8.88889{(1-\varsigma )}^{0.9}+{(1-\varsigma )}^{0.9}\left(-8.71143+\varsigma (-10.6473+19.3587\varsigma )\right)\right].\hfill \end{array}$$

Applying the Theorem 2 leads to the following result:

$$\begin{array}{c}\hfill {\int }_0^1\left[{|}^{kc}{\mathit{D}}_{0+}^{2.2}{\mathrm{\Omega }\left(\varsigma \right)|}^2+{{|}^{kc}{\mathit{D}}_{1-}^{2.2}\mathrm{\Omega }\left(\varsigma \right)|}^2\right]d\varsigma =2.29306.\end{array}$$

We also calculate the coefficients using the assumed parameters.

$$\begin{array}{c}\hfill {\displaystyle \frac{U^2}{6k^2{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(1\right)-\psi \left(0\right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}=0.159083,\end{array}$$

for $\gamma =2.2$, $U=1$ and $k=2$. Substituting these values into the right-hand side of (9) yields the following:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{U^2}{6k^2}}{\displaystyle \frac{{(1-0)}^2}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(1\right)-\psi \left(0\right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}{\int }_0^1\left[{|}^{kc}{\mathit{D}}_{0+}^{2.2}{\mathrm{\Omega }\left(\varsigma \right)|}^2+{{|}^{kc}{\mathit{D}}_{1-}^{2.2}\mathrm{\Omega }\left(\varsigma \right)|}^2\right]d\upsilon \hfill \\ \hfill & =0.159083\ast 2.29306\hfill \\ \hfill & =0.364787.\hfill \end{array}$$

Our numerical calculations for (9) yields the following result:

$$\begin{array}{c}\hfill 0.0015873\le 0.364787,\end{array}$$

confirming the validity of the inequality.

Table 1. The following table presents the left-hand and right-hand side values of (9) for $\gamma \in [2.1,2.4]$.

$\mathit{\gamma }$	$2.1$	$2.2$	$2.3$	$2.4$
Left side	$0.0015873$	$0.0015873$	$0.0015873$	$0.0015873$
Right side	$0.291172$	$0.364787$	$0.459924$	$0.584262$

and

Table 2. Comparison of the left-hand and right-hand side values of (9) for $\gamma \in [2.5,2.8]$.

$\mathit{\gamma }$	$2.6$	$2.7$	$2.8$	$2.9$
Left side	$0.0015873$	$0.0015873$	$0.0015873$	$0.0015873$
Right side	$0.748903$	$0.970218$	$1.27289$	$1.69509$

show the numerical values, while Figure 1 illustrates the corresponding graphs of (9) for the function $\psi \left(\varsigma \right)=\varsigma$ over the interval $[0,1]$, with $\gamma$ varying from $2.1$ to $2.9$.

Discussion The above example confirms the validity of (9) by employing a function that satisfies the essential conditions of the theorem. The numerical results and the corresponding graphical representations were obtained using Wolfram Mathematica 13.2. As $\gamma$ increases, the right-hand side values increase correspondingly.

The following remarks clearly show that the proposed inequalities provide a unified and generalized framework encompassing several well-known fractional operators, including $\psi$-Caputo, Caputo–Hadamard, and Caputo cases as particular instances. In contrast to previous formulations, the inclusion of the parameter k and the kernel function $\psi$ enhances the adaptability and flexibility of the inequalities. This extension enables them to cover a wider class of fractional derivatives within a single framework.

Remark 2. 

Setting $k=1$ in Theorem 2 leads to the corresponding result for ψ-Caputo fractional derivatives.

$$\begin{array}{cc}\hfill {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma & \le {\displaystyle \frac{U^2}{6}}{\displaystyle \frac{{(\upsilon -\mu )}^2}{{\left[\mathrm{\Gamma }\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2\left(\gamma -1\right)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^c\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^2+{\left|{}^c\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^2\right]d\tau .\hfill \end{array}$$

Remark 3. 

By substituting $k=1$ and $\psi \left(\varsigma \right)=\varsigma$ into Theorem 2, we derive the corresponding result for Caputo fractional derivatives established by Erden et al. in [28].

Remark 4. 

Setting $k=1$ and $\psi \left(\varsigma \right)=log\left(\varsigma \right)$ in Theorem 2 yields the corresponding result for Caputo–Hadamard fractional derivatives as presented by Samraiz et al. in [29].

We further derive Wirtinger-type inequalities within the framework of $(k,\psi )$-Riemann–Liouville fractional derivatives.

Theorem 3. 

Let $\mathrm{\Omega },\psi \in C^i[\mu ,\upsilon ]$ with $i\in \mathbb{N}\setminus \left\{0\right\}$. Assume that ${}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)$ and ${}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)$ belong to $L_2[\mu ,\upsilon ]$, with the conditions ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right)={}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right)=0$, where $\gamma \ge k$ and $i=\lceil {\displaystyle \frac{\gamma }{k}}\rceil$. Thus, we have the following inequality:

$$\begin{array}{cc}\hfill {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma & \le {\displaystyle \frac{U^2}{6k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^2}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^{kRl}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^2+{\left|{}^{kRl}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^2\right]d\tau .\hfill \end{array}$$

(16)

Proof. 

From the condition ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right)={}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right)=0$ and by applying (6), we arrive at (16). □

Theorem 4. 

Assume that $\mathrm{\Omega },\psi \in C^i[\mu ,\upsilon ]$, where $i\in \mathbb{N}\setminus \left\{0\right\}$ and $i=\lceil \gamma \rceil$. Suppose that ${}^c\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)$, ${}^c\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\in L_p[\mu ,\upsilon ]$ for $p>1$. If ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right)={}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right)=0$ and $\gamma \ge k$, then the following inequality holds:

$$\begin{array}{cc}\hfill {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma & \le {\displaystyle \frac{U^p}{p(p+1)k^p}}{\displaystyle \frac{{(\upsilon -\mu )}^p}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^p+{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^p\right]d\tau .\hfill \end{array}$$

(17)

Proof. 

Assuming ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right)={}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right)=0$, taking the absolute values (7) and (8) and employing Hölder’s inequality with the exponents p and ${\displaystyle \frac{p}{p-1}}$ to the resulting expressions yield the following inequalities:

$$\begin{array}{cc}\hfill {\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^p& ={\left[{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\mu }^{\varsigma }{\psi }^{\prime }\left(\eta \right){(\psi \left(\varsigma \right)-\psi \left(\eta \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|d\eta \right]}^p\hfill \\ \hfill & \le {\left[{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\mu }^{\varsigma }U{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|d\eta \right]}^p\hfill \\ \hfill & \le {\displaystyle \frac{1}{k^p{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{U}^p{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}{\left(\varsigma -\mu \right)}^{p-1}{\int }_{\mu }^{\varsigma }{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^{p}d\eta ,\hfill \end{array}$$

(18)

and

$$\begin{array}{cc}\hfill {\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^p& ={\left[{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\varsigma }^{\upsilon }{\psi }^{\prime }\left(\eta \right){(\psi \left(\eta \right)-\psi \left(\varsigma \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|d\eta \right]}^p\hfill \\ \hfill & \le {\left[{\displaystyle \frac{1}{k{\mathrm{\Gamma }}_k\left(\gamma \right)}}{\int }_{\varsigma }^{\upsilon }U{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{{\displaystyle \frac{\gamma }{k}}-1}\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|d\eta \right]}^p\hfill \\ \hfill & \le {\displaystyle \frac{1}{k^p{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{U}^p{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}{\left(\upsilon -\varsigma \right)}^{p-1}{\int }_{\varsigma }^{\upsilon }{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^{p}d\eta .\hfill \end{array}$$

(19)

Integrating (18) and (19) over the intervals $[\mu ,\mu \omega +(1-\omega \left)\upsilon \right]$ and $[\mu \omega +(1-\omega )\upsilon ,\upsilon ]$, respectively, with respect to $\varsigma$ for $\omega \in [0,1]$ and applying Dirichlet’s integral formula to the resulting expressions, we obtain the following:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^p}{k^p{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }{(\varsigma -\mu )}^{p-1}{\int }_{\mu }^{\varsigma }{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^{p}d\eta d\varsigma \hfill \\ \hfill & ={\displaystyle \frac{U^p}{k^p{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^p{\int }_{\eta }^{\omega \mu +(1-\omega )\upsilon }{(\varsigma -\mu )}^{p-1}d\varsigma d\eta \hfill \\ \hfill & ={\displaystyle \frac{U^p}{p{k}^p{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^p\left({(\upsilon -\mu )}^p{(1-\omega )}^p-{(\eta -\mu )}^p\right)d\eta .\hfill \end{array}$$

(20)

Similarly, we obtain the following:

$$\begin{array}{cc}\hfill & {\int }_{\omega \mu +(1-\omega )\upsilon }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^p}{k^p{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\omega \mu +(1-\omega )\upsilon }^{\upsilon }(\upsilon -\varsigma ){\int }_{\varsigma }^{\upsilon }{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^{p}d\eta d\varsigma \hfill \\ \hfill & ={\displaystyle \frac{U^p}{k^p{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\upsilon }^{\omega \mu +(1-\omega )\upsilon }{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma }\mathrm{\Omega }\left(\eta \right)\right|}^p{\int }_{\eta }^{\omega \mu +(1-\omega )\upsilon }{(\upsilon -\varsigma )}^{p-1}d\varsigma d\eta \hfill \\ \hfill & ={\displaystyle \frac{U^p}{p{k}^p{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\omega \mu +(1-\omega )\upsilon }^{\upsilon }{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\eta \right)\right|}^p\left({(\upsilon -\mu )}^p{\omega }^p-{(\upsilon -\eta )}^p\right)d\eta .\hfill \end{array}$$

(21)

After substituting $\varsigma =\sigma \mu +(1-\sigma )\upsilon$ into (20) and (21), we obtain the following results:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\omega \mu +(1-\omega )\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^p}{p{k}^p}}{\displaystyle \frac{{(\upsilon -\mu )}^{p+1}}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\omega }^1\left({(1-\omega )}^p-{(1-\sigma )}^p\right){\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{p}d\sigma ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\int }_{\omega \mu +(1-\omega )\upsilon }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^p}{p{k}^p}}{\displaystyle \frac{{(\upsilon -\mu )}^{p+1}}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_0^{\omega }\left({\omega }^p-{\sigma }^p\right){\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{p}d\sigma .\hfill \end{array}$$

Aligning the resulting inequalities and taking the integral with respect to $\omega$ over [0, 1], we obtain the following:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^p}{p{k}^p}}{\displaystyle \frac{{(\upsilon -\mu )}^{p+1}}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times [{\int }_0^1{\int }_{\omega }^1\left({(1-\omega )}^p-{(1-\sigma )}^p\right){\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{p}d\sigma d\omega \hfill \\ \hfill & +{\int }_0^1{\int }_0^{\omega }\left({\omega }^p-{\sigma }^p\right){\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{p}d\sigma d\omega ].\hfill \end{array}$$

Changing the order of integration yields the following:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^p}{p{k}^p}}{\displaystyle \frac{{(\upsilon -\mu )}^{p+1}}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times [{\int }_0^1{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^p{\int }_0^{\sigma }\left({(1-\omega )}^p-{(1-\sigma )}^p\right)d\omega d\sigma \hfill \\ \hfill & +{\int }_0^1{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^p{\int }_{\sigma }^1\left({\omega }^p-{\sigma }^p\right)d\omega d\sigma ].\hfill \end{array}$$

Furthermore, we obtain the following:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^p}{p{k}^p}}{\displaystyle \frac{{(\upsilon -\mu )}^{p+1}}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times [{\int }_0^1{Z}_3\left(\sigma \right){\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{p}d\sigma \hfill \\ \hfill & +{\int }_0^1{Z}_4\left(\sigma \right){\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }(\sigma \mu +(1-\sigma )\upsilon )\right|}^{p}d\sigma ],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & Z_3\left(\sigma \right)={\displaystyle \frac{1}{p+1}}-{\displaystyle \frac{{(1-\sigma )}^{p+1}}{p+1}}-\sigma {(1-\sigma )}^p,\hfill \\ \hfill & Z_4\left(\sigma \right)={\displaystyle \frac{1}{p+1}}-{\displaystyle \frac{{\sigma }^{p+1}}{p+1}}-{\sigma }^p(1-\sigma ).\hfill \end{array}$$

Observing that $max[Z_3\left(\sigma \right),Z_4\left(\sigma \right)]={\displaystyle \frac{1}{p+1}}$ and making the substitution $\tau =\sigma \mu +(1-\sigma )\upsilon$ in the above inequality, we obtain (17). □

Example 2. 

Let $\mathrm{\Omega }\left(\varsigma \right)={\varsigma }^i{(\varsigma -1)}^i$ and $\psi \left(\varsigma \right)=\varsigma$ be a functions defined on $[0,1]$, fulfilling the conditions ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(0\right)={}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(1\right)=0$. For the choice of parameters $i=2$, $p=4$, $k=2$, $\gamma =2.2$ and $U=1$, we obtain the following:

$$\begin{array}{c}\hfill {\int }_0^1{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{4}d\varsigma =0.00000457059.\end{array}$$

To evaluate the right-hand side of (17), we proceed as follows:

$$\begin{array}{cc}\hfill {}^{kc}\mathit{D}_{0+}^{2.2}\mathrm{\Omega }\left(\varsigma \right)& =1.54582\left[8.88889{\varsigma }^{0.9}-28.0702{\varsigma }^{1.9}+19.3587{\varsigma }^{2.9}\right],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {}^{kc}\mathit{D}_{1-}^{2.2}\mathrm{\Omega }\left(\varsigma \right)& =1.54582\left[8.88889{(1-\varsigma )}^{0.9}+{(1-\varsigma )}^{0.9}\left(-8.71143+\varsigma (-10.6473+19.3587\varsigma )\right)\right].\hfill \end{array}$$

Applying Theorem 4, we obtain the following:

$$\begin{array}{c}\hfill {\int }_0^1\left[{|}^{kc}{\mathit{D}}_{0+}^{2.2}{\mathrm{\Omega }\left(\varsigma \right)|}^4+{{|}^{kc}{\mathit{D}}_{1-}^{2.2}\mathrm{\Omega }\left(\varsigma \right)|}^4\right]d\varsigma =3.91181.\end{array}$$

For the assumed parameters, we compute the following:

$$\begin{array}{c}\hfill {\displaystyle \frac{U^4}{20k^4}}{\displaystyle \frac{{(1-0)}^4}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^4}}{(\psi \left(1\right)-\psi \left(0\right))}^{4\left({\displaystyle \frac{\gamma }{k}}-1\right)}=0.182214.\end{array}$$

Hence, the right-hand side of (17) becomes the following:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{U^4}{20k^4}}{\displaystyle \frac{{(1-0)}^4}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^4}}{(\psi \left(1\right)-\psi \left(0\right))}^{4\left({\displaystyle \frac{\gamma }{k}}-1\right)}{\int }_0^1\left[{|}^{kc}{\mathit{D}}_{0+}^{2.2}{\mathrm{\Omega }\left(\varsigma \right)|}^4+{{|}^{kc}{\mathit{D}}_{1-}^{2.2}\mathrm{\Omega }\left(\varsigma \right)|}^4\right]d\varsigma \hfill \\ \hfill & =0.182214\ast 3.91181\hfill \\ \hfill & =0.712785.\hfill \end{array}$$

Thus, the numerical evaluation of (17) yields the following:

$$\begin{array}{c}\hfill 0.00000457059\le 0.712785,\end{array}$$

which confirms the validity of the inequality.

Table 3. Comparison of the numerical values of the left-hand and right-hand sides of (17) for $\gamma \in [2.1,2.4]$.

$\mathit{\gamma }$	$2.1$	$2.2$	$2.3$	$2.4$
Left side	$0.00000457$	$0.00000457$	$0.00000457$	$0.00000457$
Right side	$0.451062$	$0.712785$	$1.14016$	$1.84898$

and

Table 4. Numerical values of the left-hand and right-hand sides of (17) over the interval $\gamma \in [2.5,2.8]$.

$\mathit{\gamma }$	$2.5$	$2.6$	$2.7$	$2.8$
Left side	$0.00000457$	$0.00000457$	$0.00000457$	$0.00000457$
Right side	$3.04669$	$5.11661$	$8.79332$	$15.5461$

provide the values of (17), while Figure 2 illustrates the corresponding graphical representations for $\psi \left(\varsigma \right)=\varsigma$ over the interval $[0,1]$, with $\gamma$ ranging from $2.1$ to $2.9$.

Remark 5. 

By setting $k=1$ in Theorem 4, we obtain the corresponding result for ψ-Caputo fractional derivatives:

$$\begin{array}{cc}\hfill {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma & \le {\displaystyle \frac{U^p}{p(p+1)}}{\displaystyle \frac{{(\upsilon -\mu )}^p}{{\left[\mathrm{\Gamma }\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p\left(\gamma -1\right)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^c\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^p+{\left|{}^c\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^p\right]d\tau .\hfill \end{array}$$

Remark 6. 

Taking $k=1$ and $\psi \left(\varsigma \right)=\varsigma$ in Theorem 4 leads to the corresponding results for Caputo fractional derivatives established by Erden et al. in [28] (Theorem 8).

Remark 7. 

By setting $k=1$ and $\psi \left(\varsigma \right)=log\left(\varsigma \right)$ in Theorem 4, we recover the result for Caputo–Hadamard fractional derivatives given by Samraiz et al. in [29].

Remark 8. 

Substituting $k=1$, $\psi \left(\varsigma \right)=log\left(\varsigma \right)$ and $p=4$ into Theorem 4, we obtain Remark 2.2 in [29].

Remark 9. 

By setting $p=2$ in Theorem 4, we obtain (9).

Furthermore, we establish a result related to $(k,\psi )$-Riemann–Liouville fractional derivatives.

Theorem 5. 

Let $\mathrm{\Omega },\psi \in C^i[\mu ,\upsilon ]$ where $i\in \mathbb{N}\setminus \left\{0\right\}$. Assume that ${}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)$, ${}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\in L_p[\mu ,\upsilon ]$ for $p>1$. If $\gamma \ge k$ and ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right)={}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right)=0$, then the following inequality holds:

$$\begin{array}{cc}\hfill {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Omega }\left(\varsigma \right)\right|}^{p}d\varsigma & \le {\displaystyle \frac{U^p}{p(p+1)k^p}}{\displaystyle \frac{{(\upsilon -\mu )}^p}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^p}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{p({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^{kRl}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^p+{\left|{}^{kRl}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^p\right]d\tau .\hfill \end{array}$$

(22)

Proof. 

Using the condition ${}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\mu \right)={}^k\mathrm{\Omega }_{\psi }^{\left[i\right]}\left(\upsilon \right)=0$ along with (6), we arrive at (22). □

3. Applications of Wirtinger-Type Inequalities Involving $(\mathit{k},\mathit{\psi })$-Caputo Fractional Operator in Arithmetic–Geometric Means

In this section, we analyze Wirtinger-type inequalities associated with $(k,\psi )$-Caputo fractional derivatives. After suitable simplification, these inequalities reveal an explicit link to the well-known arithmetic mean–geometric mean-type inequalities. Such inequalities play a fundamental role in various mathematical domains, such as optimization, functional analysis, and number theory, as they connect arithmetic and geometric quantities and provide sharp bounds. We begin by reviewing several key inequalities stated in [31], which will be used in establishing the results of this portion. For real numbers $X_1,X_2,\dots ,X_m\ge 0(m\ge 1)$, the following inequalities are valid:

$$\begin{array}{c}\hfill {\left(\prod _{v=1}^m{X}_v\right)}^{{\displaystyle \frac{1}{m}}}\le {\displaystyle \frac{1}{m}}\sum _{v=1}^m{X}_v,\end{array}$$

(23)

$$\begin{array}{c}\hfill {\left(\sum _{v=1}^m{X}_v\right)}^2\le m\sum _{v=1}^m{X}_v^2,\end{array}$$

(24)

where $X_1,\dots ,X_v$ are real. In the theorems below, left-hand side involves geometric-type expressions, while right-hand side contains arithmetic-type terms.

Theorem 6. 

Let $\mathrm{\Lambda }\left(\varsigma \right)$ be a continuous, non-negative and real-valued function defined on the interval $I=[\mu ,\upsilon ]$. Assume that the function $\mathrm{\Omega }\left(\varsigma \right)$ satisfies ${}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right){,}^{kc}{\mathit{D}}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\in C^{n-1}\left(I\right)$ and for $u=1,2,\dots ,n$, the functions $D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)$ and $D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)$ are absolutely continuous on I. If the condition $\mathrm{\Omega }\left(\mu \right)=\mathrm{\Omega }\left(\upsilon \right)=0$ is satisfied, then the following inequality holds:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Lambda }\left(\varsigma \right)\right|}^2[{\left(\prod _{u=1}^n\left|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|\right)}^{{\displaystyle \frac{2}{n}}}\hfill \\ \hfill & +{\left(\prod _{u=1}^n\left|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|\right)}^{{\displaystyle \frac{2}{n}}}]d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^2}{6k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^3}{4n{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Lambda }\left(\tau \right)\right|}^2+{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Lambda }\left(\tau \right)\right|}^2\right]d\tau \hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[\sum _{u=1}^n\left({\left|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2+{\left|D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right)\right]d\varsigma .\hfill \end{array}$$

(25)

Proof. 

It can be easily confirmed that the following identities hold:

$$\begin{array}{cc}\hfill & D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={\int }_{\mu }^{\varsigma }{D}^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)d\vartheta ,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)=-{\int }_{\varsigma }^{\upsilon }{D}^u{}^C\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)d\vartheta ,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)={\int }_{\mu }^{\varsigma }{D}^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)d\vartheta ,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)=-{\int }_{\varsigma }^{\upsilon }{D}^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)d\vartheta ,\hfill \end{array}$$

(29)

for $\varsigma \in I$ and $u=1,2,\dots ,n$. From (26)–(29), we obtain the following:

$$\begin{array}{c}\hfill \left|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|\le {\displaystyle \frac{1}{2}}{\int }_{\mu }^{\upsilon }\left|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|d\varsigma ,\end{array}$$

(30)

and

$$\begin{array}{c}\hfill \left|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|\le {\displaystyle \frac{1}{2}}{\int }_{\mu }^{\upsilon }\left|D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|d\varsigma .\end{array}$$

(31)

Taking (30) into account and utilizing the Cauchy–Schwarz inequality along with (23) and (24), we arrive at the following result:

$$\begin{array}{cc}\hfill & {\left(\prod _{u=1}^n\left|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|\right)}^{{\displaystyle \frac{2}{n}}}\hfill \\ \hfill & \le {\left[\prod _{u=1}^n\left({\displaystyle \frac{1}{2}}{\int }_{\mu }^{\upsilon }\left|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|d\varsigma \right)\right]}^{{\displaystyle \frac{2}{n}}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{4}}{\left[{\displaystyle \frac{1}{n}}\sum _{u=1}^n\left({\int }_{\mu }^{\upsilon }\left|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|d\varsigma \right)\right]}^2\hfill \\ \hfill & \le {\displaystyle \frac{\upsilon -\mu }{4n}}\sum _{u=1}^n\left({\int }_{\mu }^{\upsilon }{\left|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \right)\hfill \\ \hfill & ={\displaystyle \frac{\upsilon -\mu }{4n}}{\int }_{\mu }^{\upsilon }\left(\sum _{u=1}^n{\left|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right)d\varsigma .\hfill \end{array}$$

(32)

Applying the same approach to (31), we obtain the following:

$$\begin{array}{cc}\hfill & {\left(\prod _{u=1}^n\left|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|\right)}^{{\displaystyle \frac{2}{n}}}\hfill \\ \hfill & \le {\displaystyle \frac{\upsilon -\mu }{4n}}{\int }_{\mu }^{\upsilon }\left(\sum _{u=1}^n{\left|D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right)d\varsigma .\hfill \end{array}$$

(33)

By combining (32) and (33), we acquire the following:

$$\begin{array}{cc}\hfill & {\left(\prod _{u=1}^n\left|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|\right)}^{{\displaystyle \frac{2}{n}}}+{\left(\prod _{u=1}^n\left|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|\right)}^{{\displaystyle \frac{2}{n}}}\hfill \\ \hfill & \le {\displaystyle \frac{\upsilon -\mu }{4n}}{\int }_{\mu }^{\upsilon }\left[\sum _{u=1}^n\left({\left|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2+{\left|D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right)\right]d\varsigma .\hfill \end{array}$$

(34)

Multiplying both sides of (34) by ${\left|\mathrm{\Lambda }\left(\varsigma \right)\right|}^2$, integrating over the interval $[\mu ,\upsilon ]$ and using Theorem 2, we obtain the desired result. □

Remark 10. 

By placing $n=1$ into (25), we obtain the following Wirtinger-type inequality:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }{\left|\mathrm{\Lambda }\left(\varsigma \right)\right|}^2\left[{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2+{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right]d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{\upsilon -\mu }{4}}{\displaystyle \frac{U^2}{6k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^2}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Lambda }\left(\tau \right)\right|}^2+{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Lambda }\left(\tau \right)\right|}^2\right]d\tau \hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[\left({\left|D{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2+{\left|D{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right)\right]d\varsigma .\hfill \end{array}$$

Theorem 7. 

The following inequality is derived under the conditions of Theorem 6:

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }\mathrm{\Lambda }\left(\varsigma \right)\left[{\left(\prod _{u=1}^n{\left|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right)}^{{\displaystyle \frac{2}{m}}}+{\left(\prod _{u=1}^n{\left|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right)}^{{\displaystyle \frac{2}{n}}}\right]d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{1}{m}}{\displaystyle \frac{U^2}{6k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^2}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Lambda }\left(\tau \right)\right|}^2+{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Lambda }\left(\tau \right)\right|}^2\right]d\tau \hfill \\ \hfill & \times \left[\sum _{u=1}^n\right({\int }_{\mu }^{\upsilon }|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }{\mathrm{\Omega }\left(\varsigma \right)|}^{2}d\varsigma {\int }_{\mu }^{\upsilon }{\left|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \hfill \\ \hfill & +{\int }_{\mu }^{\upsilon }|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }{\mathrm{\Omega }\left(\varsigma \right)|}^{2}d\varsigma {\int }_{\mu }^{\upsilon }{|D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|}^{2}d\varsigma \left)\right].\hfill \end{array}$$

(35)

Proof. 

We start the proof by considering the following identities:

$$\begin{array}{cc}\hfill & {\left[D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right]}^2=2{\int }_{\mu }^{\varsigma }\left[D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)\right]\left[D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)\right]ds,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & {\left[D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right]}^2=-2{\int }_{\varsigma }^{\upsilon }\left[D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)\right]\left[D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)\right]ds,\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & {\left[D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right]}^2=2{\int }_{\mu }^{\varsigma }\left[D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)\right]\left[D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)\right]ds,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & {\left[D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right]}^2=-2{\int }_{\varsigma }^{\upsilon }\left[D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)\right]\left[D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\vartheta \right)\right]ds,\hfill \end{array}$$

(39)

for $\varsigma \in I$ and $u=1,2,\dots ,n$. By adding (36) and (37), we obtain following inequality:

$$\begin{array}{c}\hfill |D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }{\mathrm{\Omega }\left(\varsigma \right)|}^2\le {\int }_{\mu }^{\upsilon }|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }{\mathrm{\Omega }\left(\varsigma \right)|}^2{|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|}^{2}d\varsigma .\end{array}$$

(40)

Similarly, by adding (38) and (39), we obtain the following:

$$\begin{array}{c}\hfill |D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }{\mathrm{\Omega }\left(\varsigma \right)|}^2\le {\int }_{\mu }^{\upsilon }|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }{\mathrm{\Omega }\left(\varsigma \right)|}^2{|D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|}^{2}d\varsigma .\end{array}$$

(41)

Using the Cauchy–Schwarz inequality together with inequalities (23) and (24) to (40), we obtain the following:

$$\begin{array}{cc}\hfill & {\left[\prod _{u=1}^n{\left|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right]}^{{\displaystyle \frac{2}{n}}}\hfill \\ \hfill & \le {\left[\prod _{u=1}^n\left({\int }_{\mu }^{\upsilon }|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\left|\right|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|d\varsigma \right)\right]}^{{\displaystyle \frac{2}{n}}}\hfill \\ \hfill & \le {\left[{\displaystyle \frac{1}{n}}\sum _{u=1}^n\left({\int }_{\mu }^{\upsilon }|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\left|\right|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|d\varsigma \right)\right]}^2\hfill \\ \hfill & \le {\displaystyle \frac{1}{n^2}}\left[n\sum _{u=1}^n{\left({\int }_{\mu }^{\upsilon }|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\left|\right|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|d\varsigma \right)}^2\right]\hfill \\ \hfill & \le {\displaystyle \frac{1}{n}}\left[\sum _{u=1}^n\right(\left({\int }_{\mu }^{\upsilon }{|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|}^{2}d\varsigma \right)\hfill \\ \hfill & \times \left({\int }_{\mu }^{\upsilon }{|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|}^{2}d\varsigma \right)\left)\right].\hfill \end{array}$$

(42)

Applying the same steps to (41), we obtain the following:

$$\begin{array}{cc}\hfill & {\left[\prod _{u=1}^n{\left|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right]}^{{\displaystyle \frac{2}{n}}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{n}}\left[\sum _{u=1}^n\right(\left({\int }_{\mu }^{\upsilon }{\left|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \right)\hfill \\ \hfill & \times \left({\int }_{\mu }^{\upsilon }{\left|D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \right)\left)\right].\hfill \end{array}$$

(43)

By combining (42) and (43), we obtain the following:

$$\begin{array}{cc}\hfill & {\left[\prod _{u=1}^n{\left|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right]}^{{\displaystyle \frac{2}{n}}}+{\left[\prod _{u=1}^n{\left|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^2\right]}^{{\displaystyle \frac{2}{n}}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{n}}\left[\sum _{u=1}^n\right(\left({\int }_{\mu }^{\upsilon }{\left|D^{u-1}{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \right)\left({\int }_{\mu }^{\upsilon }{\left|D^u{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \right)\hfill \\ \hfill & +\left({\int }_{\mu }^{\upsilon }{\left|D^{u-1}{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \right)\left({\int }_{\mu }^{\upsilon }{\left|D^u{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)\right|}^{2}d\varsigma \right)\left)\right].\hfill \end{array}$$

(44)

By multiplying both sides of (44) by ${\left|\mathrm{\Lambda }\left(\varsigma \right)\right|}^2$, integrating over $[\mu ,\upsilon ]$ and using Theorem 2 yields (35). □

Remark 11. 

Substituting $n=1$ into (35) yields the following Wirtinger-type inequality.

$$\begin{array}{cc}\hfill & {\int }_{\mu }^{\upsilon }\mathrm{\Lambda }\left(\varsigma \right)\left[|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }{\mathrm{\Omega }\left(\varsigma \right)|}^4+{|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|}^4\right]d\varsigma \hfill \\ \hfill & \le {\displaystyle \frac{U^2}{6k^2}}{\displaystyle \frac{{(\upsilon -\mu )}^2}{{\left[{\mathrm{\Gamma }}_k\left(\gamma \right)\right]}^2}}{(\psi \left(\upsilon \right)-\psi \left(\mu \right))}^{2({\displaystyle \frac{\gamma }{k}}-1)}\hfill \\ \hfill & \times {\int }_{\mu }^{\upsilon }\left[{\left|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^2+{\left|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\tau \right)\right|}^2\right]d\tau \hfill \\ \hfill & \times [\left({\int }_{\mu }^{\upsilon }|{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }{\mathrm{\Lambda }\left(\varsigma \right)|}^{2}d\varsigma {\int }_{\mu }^{\upsilon }{|D{}^{kc}\mathit{D}_{\mu +}^{\gamma ,\psi }\mathrm{\Lambda }\left(\varsigma \right)|}^{2}d\varsigma \right)\hfill \\ \hfill & +\left({\int }_{\mu }^{\upsilon }|{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }{\mathrm{\Omega }\left(\varsigma \right)|}^{2}d\varsigma {\int }_{\mu }^{\upsilon }{|D{}^{kc}\mathit{D}_{\upsilon -}^{\gamma ,\psi }\mathrm{\Omega }\left(\varsigma \right)|}^{2}d\varsigma \right)].\hfill \end{array}$$

4. Conclusions

Fractional derivatives provide powerful tools for describing systems with hereditary effects and nonlocal interactions, enabling accurate representations of intricate real-world phenomena compared to classical integer-order derivatives. In the study of fractional differential equations, inequalities play a key role, offering valuable methods for establishing convergence properties, stability criteria, and solution bounds. Fractional inequalities present a systematic analytical framework to examine the existence, uniqueness, and consistency of solutions while exploring the fundamental properties of fractional differential systems. This study formulated Wirtinger-type inequalities for $(k,\psi )$-Caputo fractional derivatives in $L_p$ spaces $(p>1)$ and extended them to the $(k,\psi )$-Riemann–Liouville fractional derivatives. The proposed results also generalize several existing Wirtinger-type inequalities associated with other fractional operators as special cases, highlighting their broader applicability. The validity and applicability of the theoretical results are verified through numerical examples accompanied by graphical and tabular representations. The findings provide a framework for exploring applications in classical inequalities, such as the arithmetic–geometric mean. The strategies and observations presented in this study aim to encourage novel ideas and inspire further research.