Modeling Fractional Dust-Acoustic Shock Waves in a Complex Plasma Using Novel Techniques
Abstract
1. Introduction
- Model (I):
- For a collisionless unmagnetized complex plasma having dust kinematic viscosity [34], the fluid model equations that are governed the dynamics of nonlinear dust-acoustic (DA) shock waves can be reduced to the following one-dimensional integer Burgers equation (BE) using the reductive perturbation method (RPM)where the coefficients on the nonlinear term A and the dissipative term B are functions of various relevant plasma model parameters. Equation (1) supports a hierarchy of multi-shock wave solutions, including the following single-shock wave solution:where and represent the peak amplitude and width of shock waves, whereas denotes the shock wave speed.To investigate the memory impact on the profile of shock waves described by Equation (1), we follow El-Wakil’s investigations, as illustrated in detail in Refs. [2,3]. Consequently, the one-dimensional integer BE (1) can be converted to the following homogenous one-dimensional fractional BE (FBE)with the IC
- Model (II):
- If the perturbations are considered in two dimensions, in this case, the fluid model equations that govern a physical model can be reduced to a two-dimensional BE [35]where .The exact one-shock wave solution for Equation (5) reads
2. Basic Definitions
- (I)
- (II)
3. Physical Plasma Model and Fractional Burgers-Type Equations
3.1. Analyzing One-Dimensional FBE
3.1.1. The TT for Analyzing One-Dimensional FBE
- Step (1)
- Assume that the approximate solution to Equation (21) is expressed in the following infinite convergence series form:where denotes the IC and are unknown functions that will be determined later.
- Step (2)
- Step (3)
- Collecting all terms that have the same power of , the following equation is obtained:withand
- Step (4)
- Since Equation (25) must hold for all values of t, therefore, each coefficient must equal zero. Consequently, we have the subsequent system of equations
- Step (5)
- By solving Equation (26) in , we ultimately obtain the value of the function as a function of as follows:Here, ∀, is used only for simplicity.
- Then, move to Equation (27), which includes , and use the obtained value of given in Equation (29), and we finally get the value of the function as a function of as follows:
where the coefficients , , and are given in Appendix A.1. - Step (6)
- Now, by inserting the value of the IC given in Equation (22) into Equations (29)–(31), the following explicit values of , , and are obtained:where the coefficients , , are given in Appendix A.2.
- Step (7)
- Substituting the values obtained of , , …, into Equation (23), we ultimately obtain the subsequent approximation of the 3rd-order.
3.1.2. NIM for Analyzing One-Dimensional FBE
- Step (1)
- Rearrange Equation (21) in the following form:
- Step (2)
- Applying LT to Equation (36), we get
- Step (3)
- Step (4)
- The application of the inverse LT to Equation (39) produces
- Step (5)
- The estimated approximation based on the NIM up to the -order approximations is given by
- Step (6)
- Accordingly, both linear and nonlinear terms can be decomposed as follows:and
- Step (7)
- The zeroth-order approximation can be obtained by using in Equation (40),
- Step (8)
- Step (9)
- From Equation (44), we get the following approximationswhere the coefficients , , , and are given in Appendix A.3.
- Step (10)
- By collecting the obtained values of , , … and adding them to Equation (43), ultimately we obtain the second-order approximation in the following manner:
3.2. Analyzing Two-Dimensional FBE
3.2.1. The TT for Analyzing Two-Dimensional FBE
- Step (1)
- Assume that the approximate solution to Equation (48) is expressed in the following infinite convergence series form:where denotes the IC and are unknown functions that will be determined later.
- Step (2)
- Step (3)
- Collecting all terms that have the same power of , the following equation is obtained:withand
- Step (4)
- Since Equation (53) must hold for all values of t, therefore, each coefficient must equal zero. Therefore, we get the following system of equations:
- Step (5)
- By solving Equations (54)–(56) in , , , we ultimately obtain the explicit values of , , and as follows:
- Step (6)
- Substituting the values obtained of , , …, into Equation (51), ultimately, we obtain the approximation of the third-order in the following manner:
3.2.2. NIM for Analyzing 2D-FBE
- Step (1)
- Rearrange Equation (48) in the following form:
- Step (2)
- Applying the LT to both sides of Equation (61), we obtain the following result:
- Step (3)
- Step (4)
- Applying the inverse LT to Equation (64) yields
- Step (5)
- The estimated approximation based on the NIM up to the -order approximations is given by
- Step (6)
- Accordingly, both linear and nonlinear terms can be decomposed as follows:and
- Step (7)
- The zeroth-order approximation can be determined using in Equation (65),
- Step (8)
- Step (9)
- From Equation (71), we get the following approximations:andwhere the coefficients and are given in the Appendix A.
- Step (10)
- By collecting the obtained values of , , … and adding them to Equation (70), ultimately we obtain the approximation of the third order in the following manner:
4. Conclusions
- (I)
- Using the TT, the one-dimensional FBE has been analyzed, and some analytical approximations up to the third order have been derived. Given the fast computation of this technique and its ability to overcome many complexities, as well as the small size of the derived approximations, this approach can quickly generate high-order approximations with low computational cost. However, the one-dimensional FBE was also analyzed using the NIM, and an approximation up to the second order was produced. It is worth noting that higher-order approximations are possible, but they require significantly higher computational costs, unlike the TT. Additionally, the obtained approximations using the NIM are very large and may not be possible to insert into the text.
- (II)
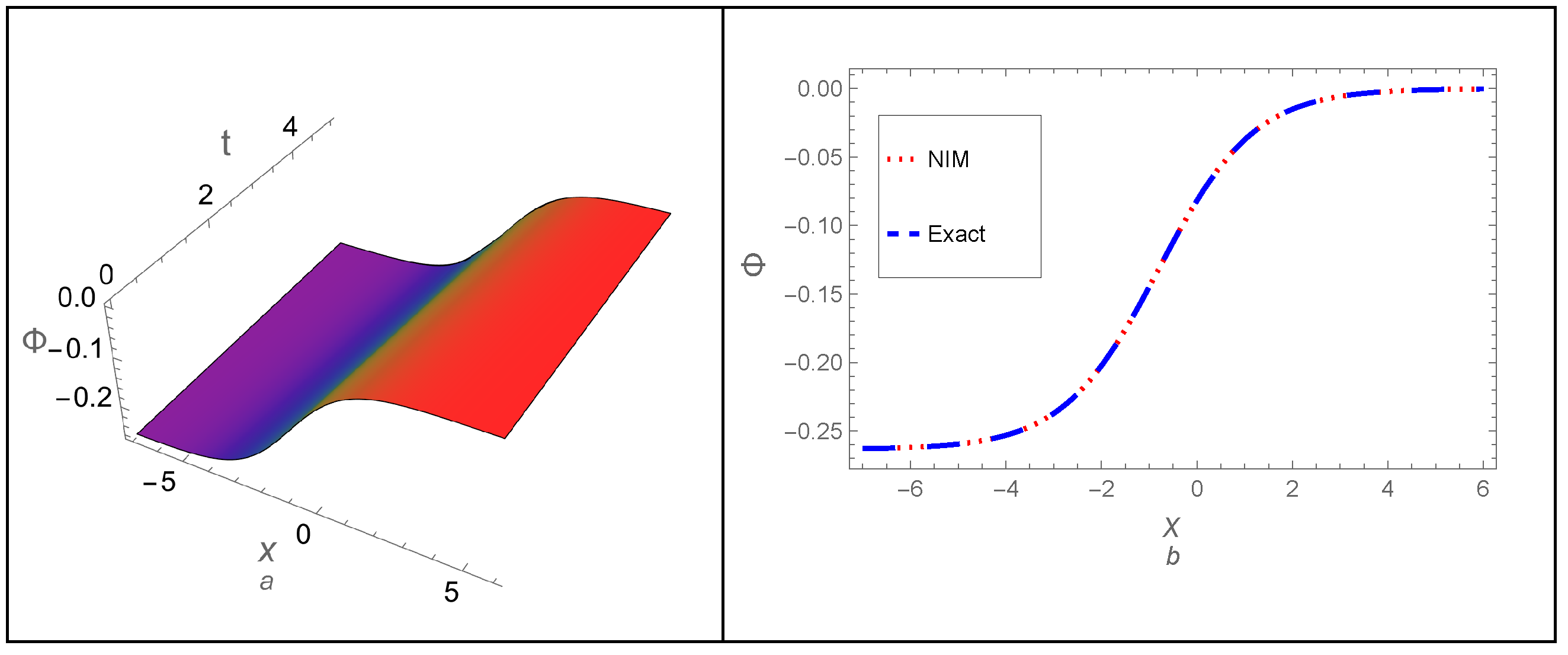
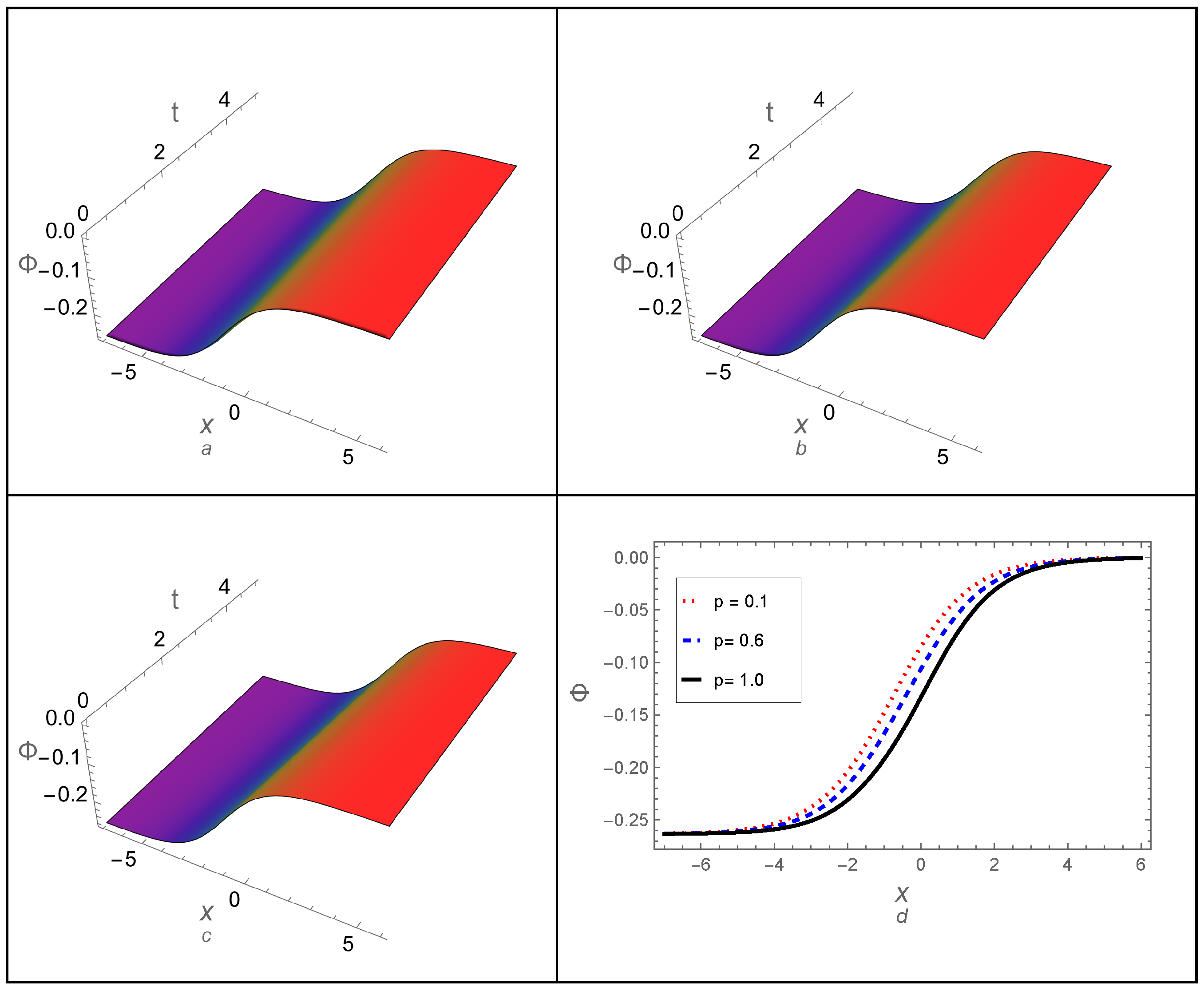
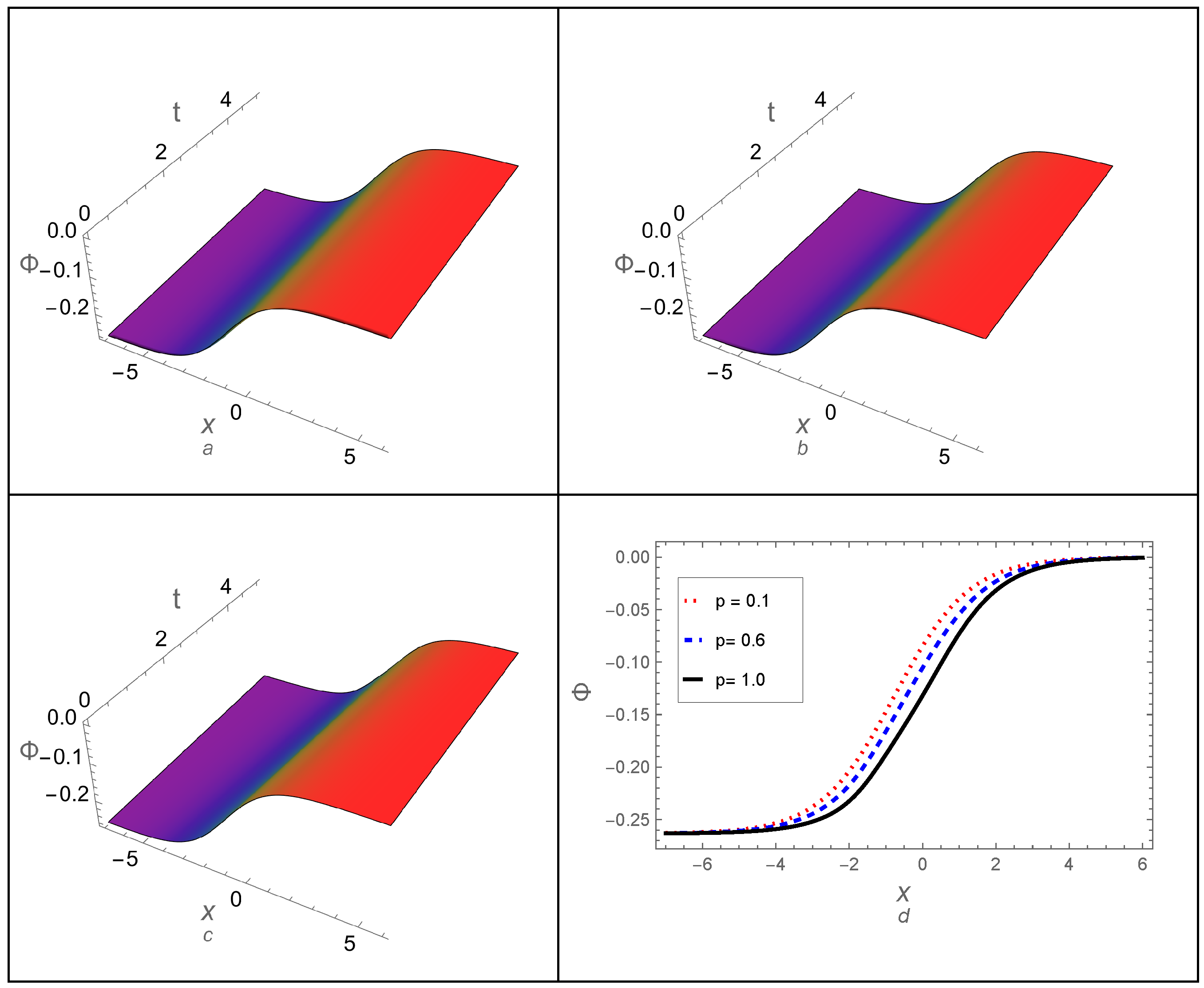
- The memory effect, represented by the fractional-order parameter p, has been studied on the dynamical behavior of the DA shock wave profile. Additionally, an analytical comparison between the derived approximations and the exact solution for the non-fractional case () confirmed the high precision of all the derived approximations. The residual error across the whole study domain and the absolute error of the approximations have also been computed. Both methods were found to demonstrate high accuracy and stability throughout the study, even over long periods.
- (III)
- Additionally, the two-dimensional FBE has been analyzed using both proposed approaches, and some third-order approximations have been generated. Furthermore, the effect of fractionality p on the DA shock wave profile has been examined, revealing that the shock wave profile is sensitive to changes in the fractional-order parameter, exposing behaviors that the integer form of the two-dimensional BE cannot detect. To verify the accuracy and stability of the generated approximations, a graphical comparison has been performed between all derived approximations and the exact solution to the two-dimensional BE, i.e., for . The comparison showed complete agreement among all generated approximations and the exact solution. Furthermore, the residual and absolute errors have also been calculated for each approximation, demonstrating that all approximations exhibit high accuracy and confirming the effectiveness of both approaches in analyzing more complex fractional EWEs.
- (IV)
- Advantages of the TT
- Does not need linearization, discretization, or perturbation.
- Does not require writing the linear or nonlinear terms in a complicated manner, such as other methods.
- Fast and low-cost computations.
- Works easily for more complicated nonlinear FDEs.
- Easy to implement computations.
- Provides accurate and stable solutions.
- Higher-order approximations are easy to generate.
- Does not require applying any transform to facilitate the calculation process, unlike other methods.
- All generated approximations are characterized by being short expressions compared to other methods.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
Appendix A.3
Appendix A.4
References
- Abdou, M.A. An analytical method for space–time fractional nonlinear differential equations arising in plasma physics. J. Ocean. Sci. 2017, 2, 288–292. [Google Scholar] [CrossRef]
- El-Wakil, S.A.; Abulwafa, E.M.; Zahran, M.A.; Mahmoud, A.A. Time-Fractional KdV Equation: Formulation and Solution using Variational Methods. Nonlinear Dyn. 2011, 65, 55–63. [Google Scholar] [CrossRef]
- El-Wakil, S.A.; Abulwafa, E.M.; El-Shewy, E.K.; Mahmoud, A.A. Time-fractional KdV equation for electron-acoustic waves in plasma of cold electron and two different temperature isothermal ions. Astrophys. Space Sci. 2011, 333, 269–276. [Google Scholar] [CrossRef]
- Shiri, B.; Baleanu, D. All linear fractional derivatives with power functions’ convolution kernel and interpolation properties. Chaos Solitons Fractals 2023, 170, 113399. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Kulish, V.V.; Lage, J.L. Application of fractional calculus to fluid mechanics. J. Fluids Eng. 2002, 124, 803–806. [Google Scholar] [CrossRef]
- Szymanek, E. Use of fractional calculus in modeling of heat transfer process through external building partitions. Acta Innov. 2018, 27, 61–70. [Google Scholar] [CrossRef]
- Blaszczyk, T.; Leszczynski, J.; Szymanek, E. Numerical solution of composite left and right fractional Caputo derivative models for granular heat flow. Mech. Res. Commun. 2013, 48, 42–45. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J.H. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Ali, M.F.; Sharma, M.; Jain, R. An application of fractional calculus in electrical engineering. Adv. Eng. Technol. Appl. 2016, 5, 41–45. [Google Scholar] [CrossRef]
- Das, S. Application of Generalized Fractional Calculus in Electrical Circuit Analysis and Electromagnetics. In Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Engheia, N. On the role of fractional calculus in electromagnetic theory. IEEE Antennas Propag. Mag. 1997, 39, 35–46. [Google Scholar] [CrossRef]
- Atangana, A.; Bildik, N. The use of fractional order derivative to predict the groundwater flow. Math. Probl. Eng. 2013, 2013, 543026. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Integrations and Differentiations of Arbitrary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Debnath, L. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003, 2003, 3413–3442. [Google Scholar] [CrossRef]
- Vargas, A.M. Finite difference method for solving fractional differential equations at irregular meshes. Math. Comput. Simul. 2022, 193, 204–216. [Google Scholar] [CrossRef]
- Appadu, A.R.; Kelil, A.S. Some finite difference methods for solving linear fractional KdV equation. Front. Appl. Math. Statistics 2023, 9, 1261270. [Google Scholar] [CrossRef]
- Deng, W.H. Finite element method for the space and time fractional Fokker-Planck equation. SIAM J. Numer. Anal. 2008, 47, 204–226. [Google Scholar] [CrossRef]
- Gu, Y. High-order numerical method for the fractional Korteweg-de Vries equation using the discontinuous Galerkin method. AIMS Math. 2025, 10, 1367–1383. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method a kind of non-linear analytical technique: Some examples. Int. J. Nonlin. Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Modified Adomian polynomials. Math. Comput. Model. 1996, 24, 39–46. [Google Scholar] [CrossRef]
- El-Borai, M.M.; El-Sayed, W.G.; Jawad, A.M. Adomian decomposition method for solving fractional differential equations. Int. Res. J. Eng. Technol. 2015, 2, 295–306. [Google Scholar]
- Javeed, S.; Baleanu, D.; Waheed, A.; Khan, M.S.; Affan, H. Analysis of homotopy perturbation method for solving fractional order differential equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef]
- Wang, Q. Homotopy perturbation method for fractional KdV-Burgers equation. Chaos Solitons Fractals 2008, 35, 843–850. [Google Scholar] [CrossRef]
- Zurigat, M.; Momani, S.; Odibat, Z.; Alawneh, A. The homotopy analysis method for handling systems of fractional differential equations. Appl. Math. Model. 2010, 34, 24–35. [Google Scholar] [CrossRef]
- Mesloub, S.; Obaidat, S. Homotopy Analysis Method for a Fractional Order Equation with Dirichlet and Non-Local Integral Conditions. Mathematics 2019, 7, 1167. [Google Scholar] [CrossRef]
- Saad, K.M.; Atangana, A.; Baleanu, D. New fractional derivatives with non-singular kernel applied to the Burgers equation. Chaos 2018, 28, 063109. [Google Scholar] [CrossRef]
- Abu Arqub, O. Application of residual power series method for the solution of time-fractional Schrödinger equations in one-dimensional space. Fundam. Inform. 2019, 166, 87–110. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, X. Laplace-residual power series method for solving fractional generalized long wave equations. Ocean. Eng. 2024, 310, 118693. [Google Scholar] [CrossRef]
- Wu, G.C.; Shiri, B.; Fan, Q.; Feng, H.-R. Terminal Value Problems of Non-homogeneous Fractional Linear Systems with General Memory Kernels. J. Nonlinear Math. Phys. 2023, 30, 303–314. [Google Scholar] [CrossRef]
- Prakash, A.; Kumar, M.; Baleanu, D. A new iterative technique for a fractional model of nonlinear Zakharov–Kuznetsov equations via Sumudu transform. Appl. Math. Comput. 2018, 334, 30–40. [Google Scholar] [CrossRef]
- Ferdousi, M.; Miah, M.R.; Sultana, S.; Mamun, A.A. Dust-acoustic shock waves in an electron depleted nonextensive dusty plasma. Astrophys. Space Sci. 2015, 360, 43. [Google Scholar] [CrossRef]
- Mohamed, N.A. Solving one- and two-dimensional unsteady Burgers’ equation using fully implicit finite difference schemes. Arab. J. Basic Appl. Sci. 2019, 26, 254–268. [Google Scholar] [CrossRef]
- Debnath, L. Partial Differential Equations for Scientists and Engineers; Birkhäuser: Boston, MA, USA, 1997. [Google Scholar]
- Ozis, T.; Ozdes, A. A direct variational methods applied to Burgers’ equation. J. Comput. Appl. Math. 1996, 71, 163–175. [Google Scholar] [CrossRef]
- Pospelov, L.A. Propagation of finite amplitude elastic waves (Longitudinal elastic wave of finite amplitude propagation in isotropic solid). Sov. Phys.-Acoust. 1966, 11, 302–304. [Google Scholar]
- Debnath, L.; Debnath, L. Nonlinear Partial Differential Equations for Scientists and Engineers; Birkhäuser: Boston, MA, USA, 2005; Volume 2. [Google Scholar]
- Blackstock, D.T. Thermoviscous attenuation of plane, periodic, finite-amplitude sound waves. J. Acoust. Soc. Am. 1964, 36, 534–542. [Google Scholar] [CrossRef]
- Emamuddin, M.; Mamun, A.A. Dust-acoustic shock waves for multi-temperature electrons and ions. J. Korean Phys. Soc. 2019, 74, 959–966. [Google Scholar] [CrossRef]
- Esen, A.; Tasbozan, O. Numerical solution of time fractional Burgers equation by cubic B-spline finite elements. Mediterr. J. Math. 2016, 13, 1325–1337. [Google Scholar] [CrossRef]
- Jain, S.; Leung, H.H.; Kamalov, F. A computational numerical study of burger equation with fractal fractional derivative. Prog. Frac. Appl. 2022, 1, 1–15. [Google Scholar]
- Esen, A.; Yagmurlu, N.M.; Tasbozan, O. Approximate analytical solution to time-fractional damped Burger and Cahn-Allen equations. Appl. Math. Inf. Sci. 2013, 7, 1951–1956. [Google Scholar] [CrossRef]
- Abdel-Salam, E.B.; Yousif, E.A.; Arko, Y.A.; Gumma, E.A. Solution of Moving Boundary Space-Time Fractional Burger’s Equation. J. Appl. Math. 2014, 2014, 218092. [Google Scholar] [CrossRef]
- Inc, M. The approximate and exact solutions of the space-and time-fractional Burgers equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 2008, 345, 476–484. [Google Scholar] [CrossRef]
- Li, D.; Zhang, C.; Ran, M. A linear finite difference scheme for generalized time fractional burgers equation. Appl. Math. Model. 2016, 40, 6069–6081. [Google Scholar] [CrossRef]
- Almuqrin, A.H.; Tiofack, C.G.L.; Mohamadou, A.; Alim, A.; Ismaeel, S.M.E.; Alhejaili, W.; El-Tantawy, S.A. On the “Tantawy Technique” and other methods for analyzing the family of fractional Burgers’ equations: Applications to plasma physics. J. Low Freq. Noise Vib. Act. Control 2025, 44, 1323–1352. [Google Scholar] [CrossRef]
- Almuqrin, A.H.; Tiofack, C.G.L.; Douanla, D.V.; Mohamadou, A.; Alhejaili, W.; Ismaeel, S.M.E.; El-Tantawy, S.A. On the “Tantawy Technique” and other methods for analyzing Fractional Fokker Plank-type Equations. J. Low Freq. Noise Vib. Act. Control 2025, 44, 1353–1373. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Al-Johani, A.S.; Almuqrin, A.H.; Khan, A.; El-Sherif, L.S. Novel approximations to the fourth-order fractional Cahn–Hillard equations: Application to the Tantawy Technique and other two techniques with Yang transform. J. Low Freq. Noise Vib. Act. Control 2025, 44, 1374–1400. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Bacha, S.I.H.; Khalid, M.; Alhejaili, W. Application of the Tantawy technique for modeling fractional ion-acoustic waves in electronegative plasmas having Cairns distributed-electrons, Part (I): Fractional KdV Solitary Waves. Braz. J. Phys. 2025, 55, 123. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Alhejaili, W.; Khalid, M.; Al-Johani, A.S. Application of the Tantawy Technique for Modeling Fractional Ion-Acoustic Waves in Electronegative nonthermal Plasmas, Part (II): Fractional modifed KdV-Solitary Waves. Braz. J. Phys. 2025, 55, 176. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Khan, D.; Khan, W.; Khalid, M.; Alhejaili, W. A Novel Approximation to the Fractional KdV Equation Using the Tantawy Technique and Modeling Fractional Electron-Acoustic Cnoidal Waves in a Nonthermal. Plasma. Braz. J. Phys. 2025, 55, 163. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Khalid, M.; Bacha, S.I.H.; Alyousef, H.A.; El-Sherif, L. On the Tantawy Technique for Modeling Fractional Ion-Acoustic KdV Solitary Waves in a Nonthermal Plasma Having Electron Beams. Braz. J. Phys. 2025, 55, 191. [Google Scholar] [CrossRef]
- Alhejaili, W.; Khan, A.; Al-Johani, A.S.; El-Tantawy, S.A. Novel Approximations to the Multi-Dimensional Fractional Diffusion Models Using the Tantawy Technique and Two Other Transformed Methods. Fractal Fract. 2025, 9, 423. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Alhejaili, W.; Al-Johani, A.S. On the Tantawy technique for analyzing (in) homogeneous fractional physical wave equations. J. Supercomput. 2025, 81, 1377. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Rahman, A.; Alyousef, H.A.; Al-Johani, A.S. On the Tantawy technique for modeling fractional dissipative dust-acoustic solitons in a polarized complex plasma, part (I): Fractional damped KdV equation. J. Low Freq. Noise Vib. Act. Control 2025. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Bhalekar, S. Solving fractional diffusion-wave equations using a new iterative method. Fract. Calc. Appl. Anal. 2008, 11, 193–202. [Google Scholar]
- Bhalekar, S.; Daftardar-Gejji, V. New iterative method: Application to partial differential equations. Appl. Math. Comput. 2008, 203, 778–783. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. Solving Fractional-Order Logistic Equation Using a New Iterative Method. Int. J. Differ. Equ. 2012, 2012, 975829. [Google Scholar] [CrossRef]
- Falade, K.I.; Tiamiyu, A.T. Numerical solution of partial differential equations with fractional variable coefficients using new iterative method (NIM). Math. Sci. Comput. 2020, 3, 12–21. [Google Scholar] [CrossRef]
- Hemeda, A.A. New Iterative Method: An Application for Solving Fractional Physical Differential Equations. Abstr. Appl. Anal. 2013, 2013, 617010. [Google Scholar] [CrossRef]
- Zada, L.; Nawaz, R.; Ahsan, S.; Nisar, K.S.; Baleanu, D. New iterative approach for the solutions of fractional order inhomogeneous partial differential equations. AIMS Math. 2021, 6, 1348–1365. [Google Scholar] [CrossRef]
- Šmarda, Z. Laplace adomian decomposition method for solving fractional delay differential equations with variable coefficients. AIP Conf. Proc. 2023, 2849, 370009. [Google Scholar]
- Jafari, H.; Khalique, C.M.; Nazari, M. Application of the Laplace decomposition method for solving linear and nonlinear fractional diffusion–wave equations. Appl. Math. Lett. 2011, 24, 1799–1805. [Google Scholar] [CrossRef]
- Shiri, B.; Shi, Y.; Baleanu, D. Ulam–Hyers stability of incommensurate systems for weakly singular integral equations. J. Comput. Appl. Math. 2026, 474, 116920. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alyousef, H.A.; Alharthi, M.R. Novel approximations to a nonplanar nonlinear Schrödinger equation and modeling nonplanar rogue waves/breathers in a complex plasma. Chaos Solitons Fractals 2022, 1635, 112612. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Salas, A.H.; Matoog, R.T.; El-Tantawy, S.A. On the analytical and numerical approximations to the forced damped Gardner Kawahara equation and modeling the nonlinear structures in a collisional plasma. Phys. Fluids 2022, 34, 103105. [Google Scholar] [CrossRef]
- Büyükaşık, Ş.A.; Pashaev, O.K. Exact solutions of forced Burgers equations with time variable coefficients. Commun. Nonlinear Sci. Numer. Simulat. 2013, 18, 1635–1651. [Google Scholar] [CrossRef]
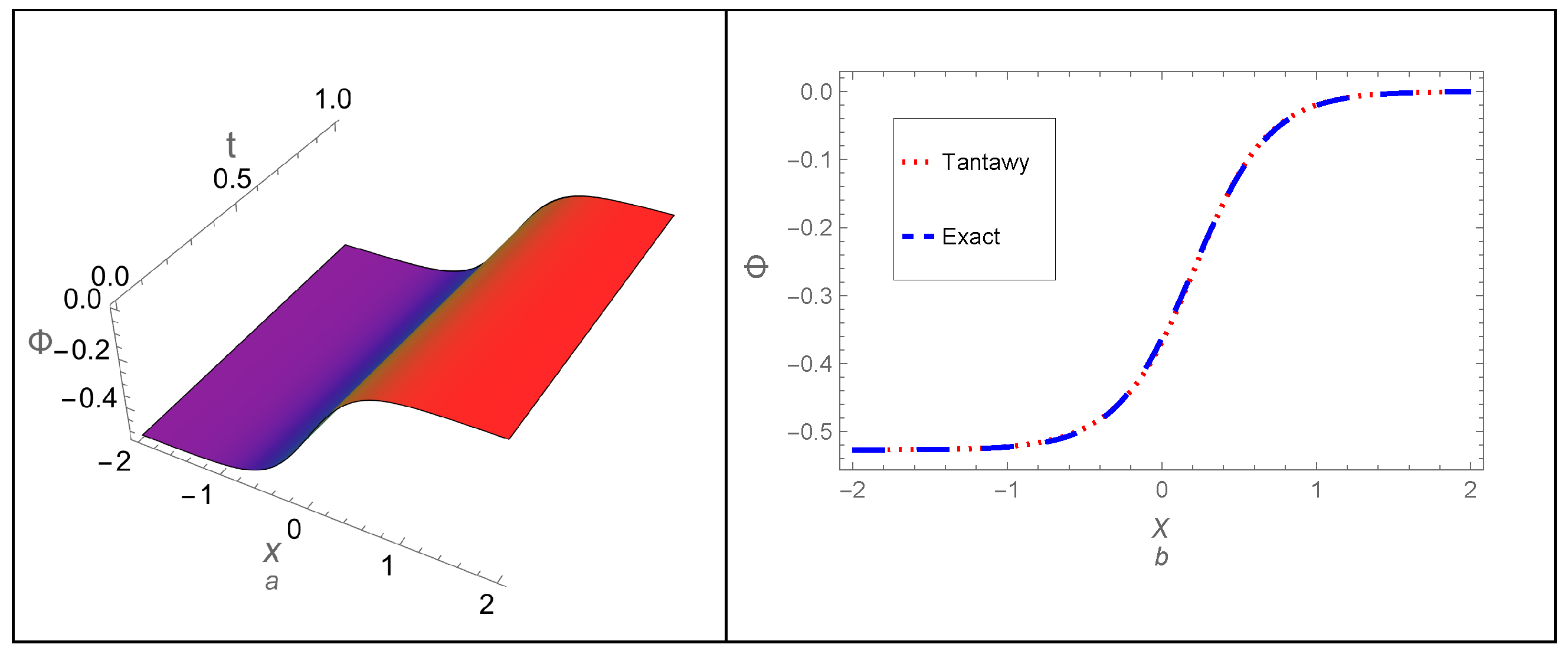
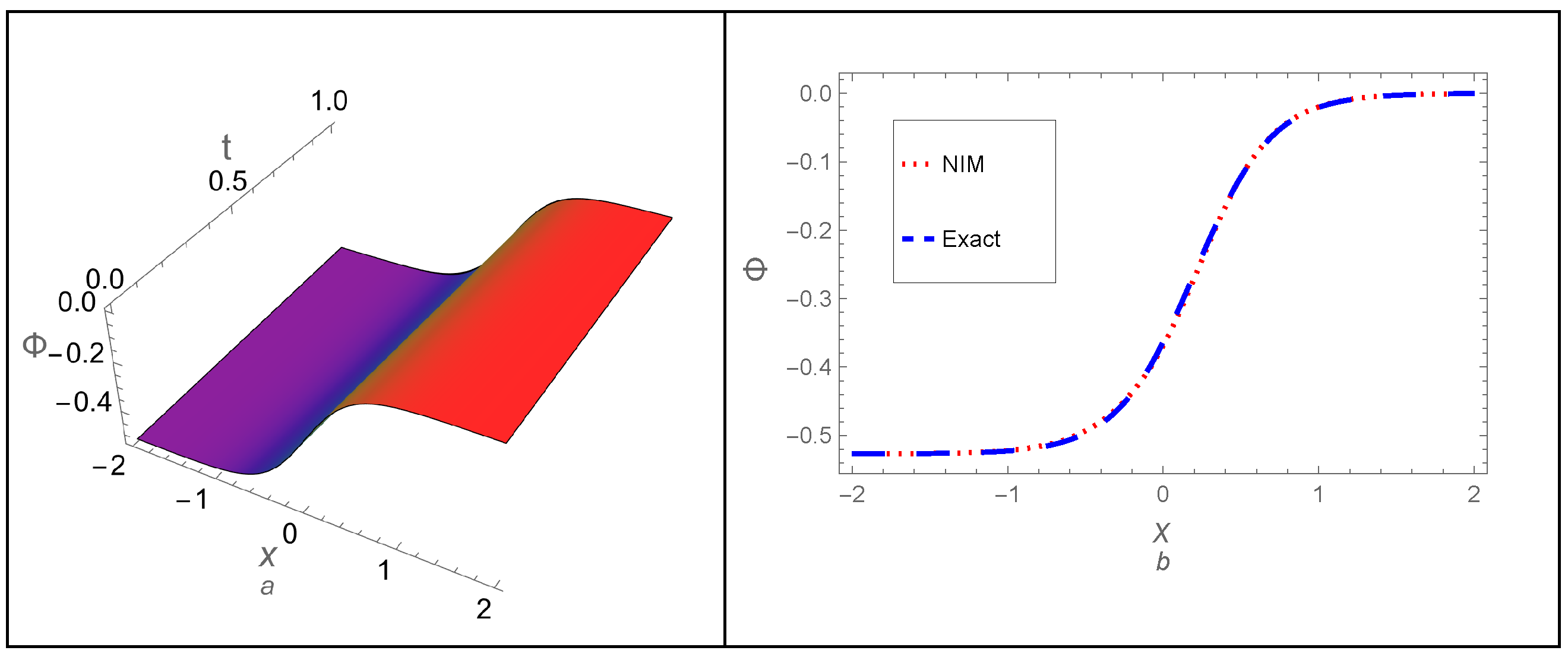
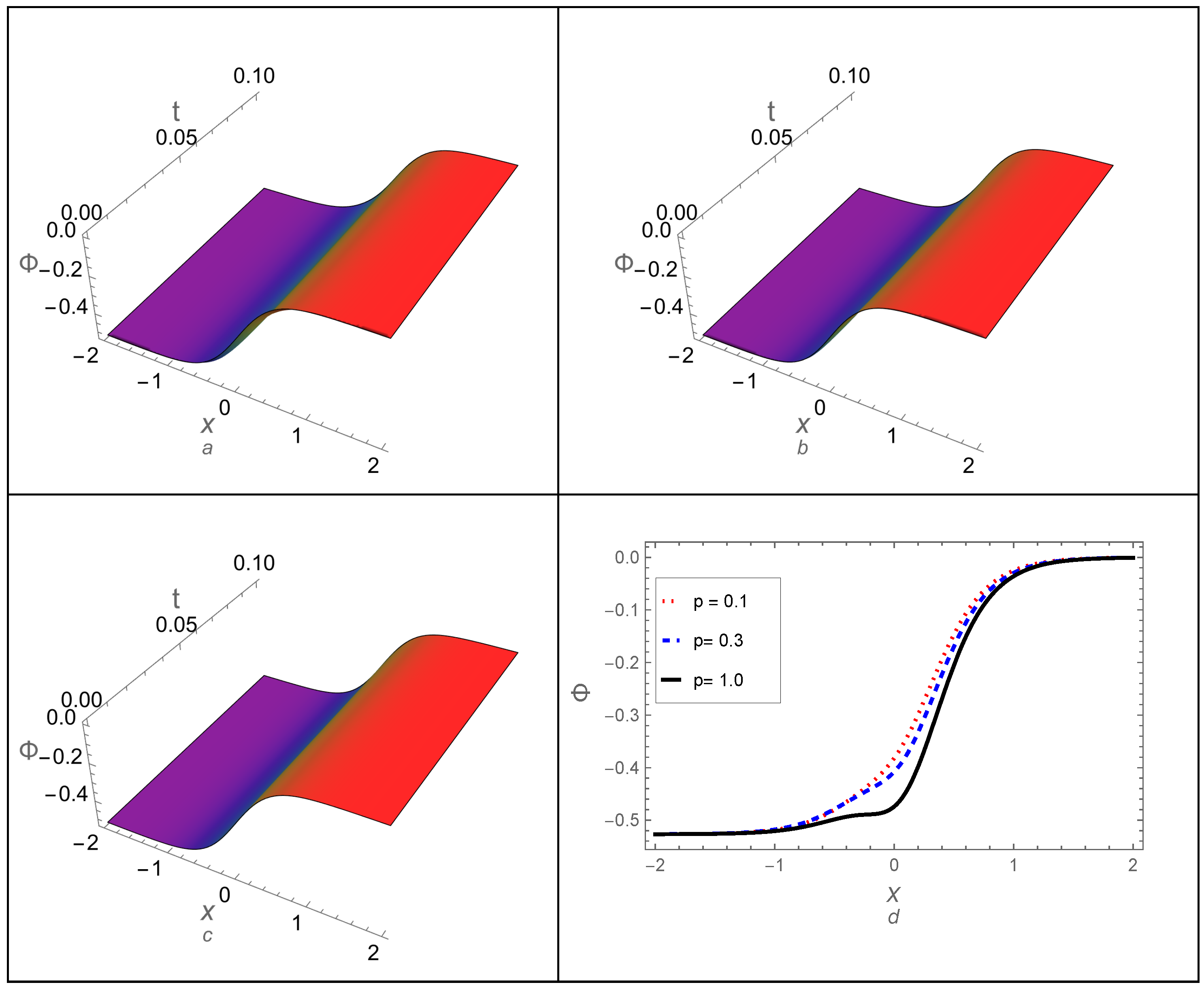
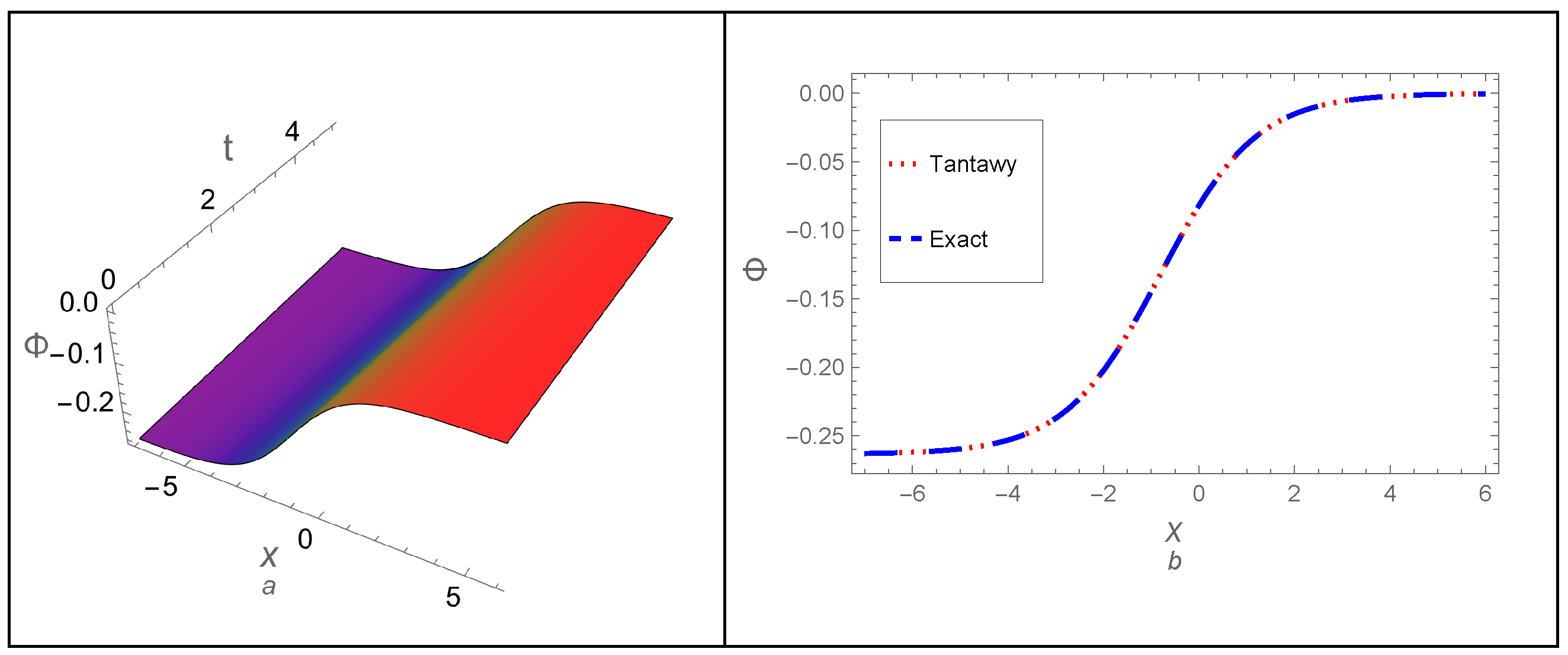
| x | |||||||
|---|---|---|---|---|---|---|---|
| −2 | −0.526668 | −0.526668 | −0.526668 | −0.526668 | 0.0147656 | 0.0147454 | 0.0295294 |
| −1.5 | −0.525628 | −0.525628 | −0.525628 | −0.525628 | 0.108224 | 0.107135 | 0.210893 |
| −1 | −0.518071 | −0.518071 | −0.518072 | −0.518072 | 0.752045 | 0.697962 | 1.1936 |
| −0.5 | −0.46832 | −0.468321 | −0.468323 | −0.468323 | 3.27381 | 1.76408 | 1.74589 |
| 0 | −0.273952 | −0.273952 | −0.273946 | −0.273946 | 5.61593 | 5.61593 | 0.359417 |
| 0.5 | −0.0673612 | −0.0673597 | −0.0673614 | −0.0673614 | 0.216939 | 1.72667 | 1.99569 |
| 1 | −0.0102489 | −0.0102488 | −0.0102495 | −0.0102495 | 0.66801 | 0.722092 | 1.21939 |
| 1.5 | −0.00141075 | −0.00141075 | −0.00141086 | −0.00141086 | 0.11033 | 0.111419 | 0.217471 |
| 2 | −0.000191367 | −0.000191367 | −0.000191382 | −0.000191382 | 0.0153254 | 0.0153456 | 0.0304844 |
| x | NIM | Tantawy | Exact | ||
|---|---|---|---|---|---|
| −8 | −0.263219 | −0.263219 | −0.263219 | 0.153462 | 0.151786 |
| −6 | −0.26197 | −0.26197 | −0.26197 | 1.11237 | 1.02325 |
| −4 | −0.253099 | −0.253099 | −0.253099 | 7.25512 | 3.31422 |
| −2 | −0.202441 | −0.202439 | −0.202441 | 1.04658 | 21.268 |
| 0 | −0.081666 | −0.0816677 | −0.0816655 | 5.10837 | 21.9776 |
| 2 | −0.0151005 | −0.0150997 | −0.0151001 | 4.01212 | 3.24312 |
| 4 | −0.00215006 | −0.00215004 | −0.00215015 | 0.887141 | 1.09854 |
| 6 | −0.000293043 | −0.000293043 | −0.000293059 | 0.160118 | 0.164237 |
| 8 | −0.0000396972 | −0.0000396972 | −0.0000396994 | 0.0224462 | 0.0225222 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhejaili, W.; Alzaben, L.; El-Tantawy, S.A. Modeling Fractional Dust-Acoustic Shock Waves in a Complex Plasma Using Novel Techniques. Fractal Fract. 2025, 9, 674. https://doi.org/10.3390/fractalfract9100674
Alhejaili W, Alzaben L, El-Tantawy SA. Modeling Fractional Dust-Acoustic Shock Waves in a Complex Plasma Using Novel Techniques. Fractal and Fractional. 2025; 9(10):674. https://doi.org/10.3390/fractalfract9100674
Chicago/Turabian StyleAlhejaili, Weaam, Linda Alzaben, and Samir A. El-Tantawy. 2025. "Modeling Fractional Dust-Acoustic Shock Waves in a Complex Plasma Using Novel Techniques" Fractal and Fractional 9, no. 10: 674. https://doi.org/10.3390/fractalfract9100674
APA StyleAlhejaili, W., Alzaben, L., & El-Tantawy, S. A. (2025). Modeling Fractional Dust-Acoustic Shock Waves in a Complex Plasma Using Novel Techniques. Fractal and Fractional, 9(10), 674. https://doi.org/10.3390/fractalfract9100674








