Stabilization of DC Microgrids Using Frequency-Decomposed Fractional-Order Control and Hybrid Energy Storage
Abstract
1. Introduction
- •
- Renewable energy intermittency: Weather and irradiance-related variations in solar photovoltaics lead to instability in standalone DC microgrids.
- •
- Dynamic and pulsed loads: High-power, rapidly fluctuating loads, such as those found in aerospace and marine applications, cause voltage fluctuations and strain on storage devices.
- •
- Stress on batteries and their short lifespan: Deep cycling, overshoots, and increased battery degradation are the results of traditional PI-based control.
- •
- The drawbacks of classical control include the inability of integer-order PI controllers to handle nonlinearities, disturbances, and fast dynamics in an optimal manner, despite their simplicity.
- •
- Fractional-order controller complexity: Better adaptability is provided by fractional-order control, but its implementation and tuning are mathematically challenging.
- Offers a FOPI controller that is optimized for regulating DC bus voltage in solar-powered DC microgrids with hybrid energy storage (battery + ultracapacitor).
- Introduces frequency-decomposed control, which improves transient stability by dividing power demand between a battery (slow dynamics) and an ultracapacitor (rapid dynamics) via filter-based energy management.
- Uses GWO optimizer: This eliminates the need for human trial-and-error tweaking by automatically and optimally adjusting FOPI settings.
- Improves performance over PI: Simulation findings indicate a decrease of around 80% in DC bus voltage error, a 40% improvement in settling time, and a 50% reduction in overshoot.
- offers a verified simulation framework: a MATLAB/Simulink model shows resilience to various load and solar perturbations.
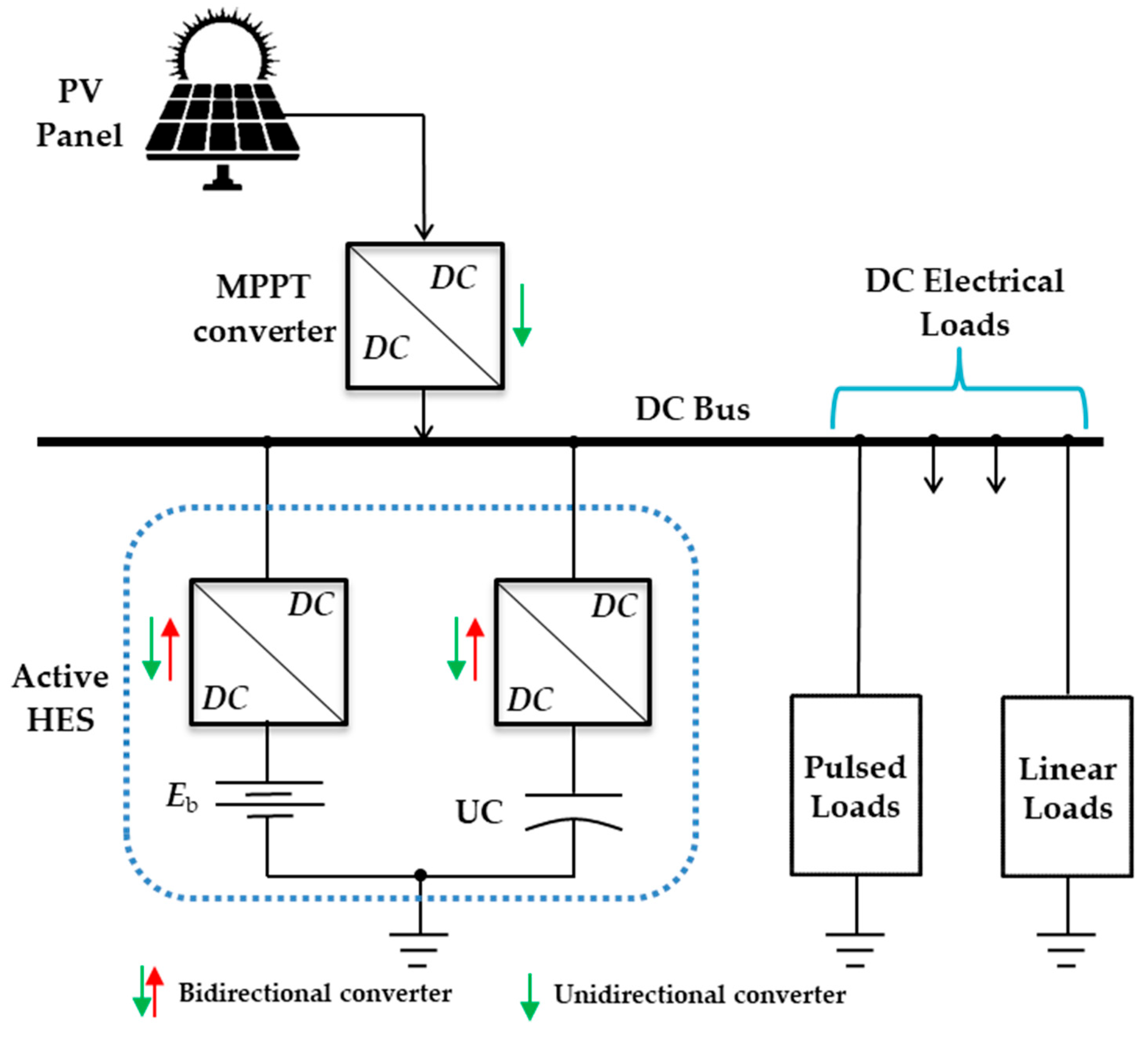
2. Suggested DC Microgrid Assembly & Modeling
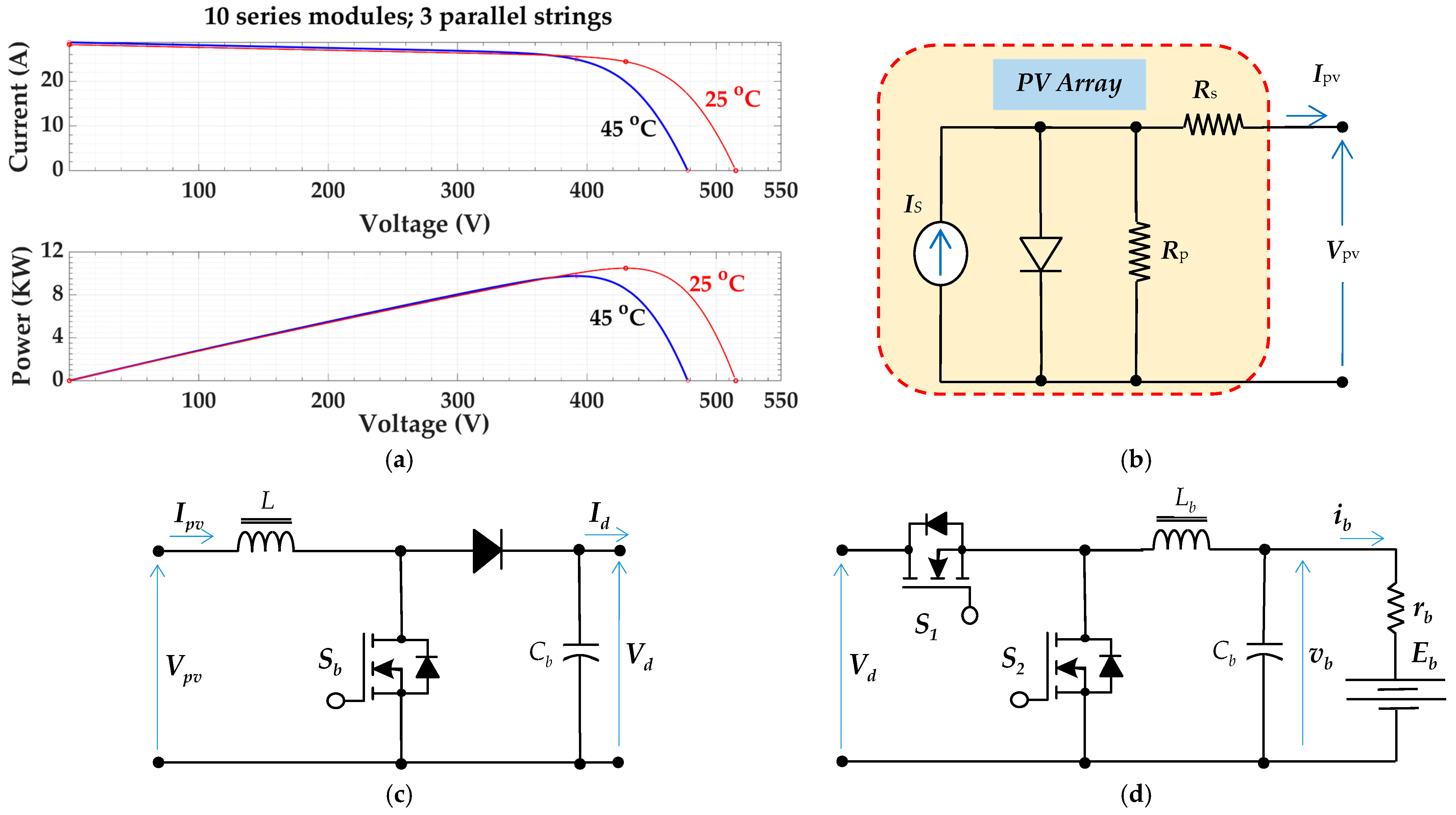
2.1. Photovoltaic (PV) Array with MPPT
2.2. Battery Bank Storage System
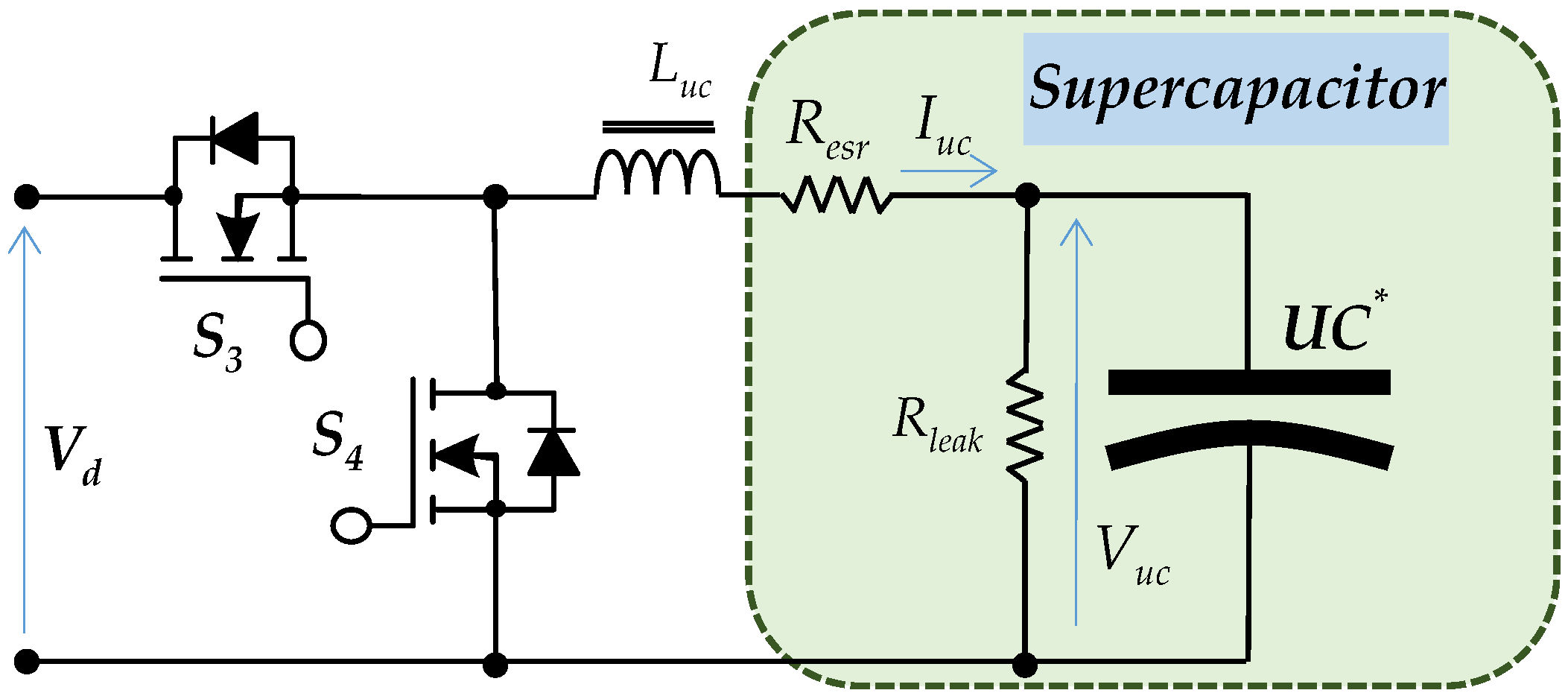
2.3. Supercapacitor Energy Storage System
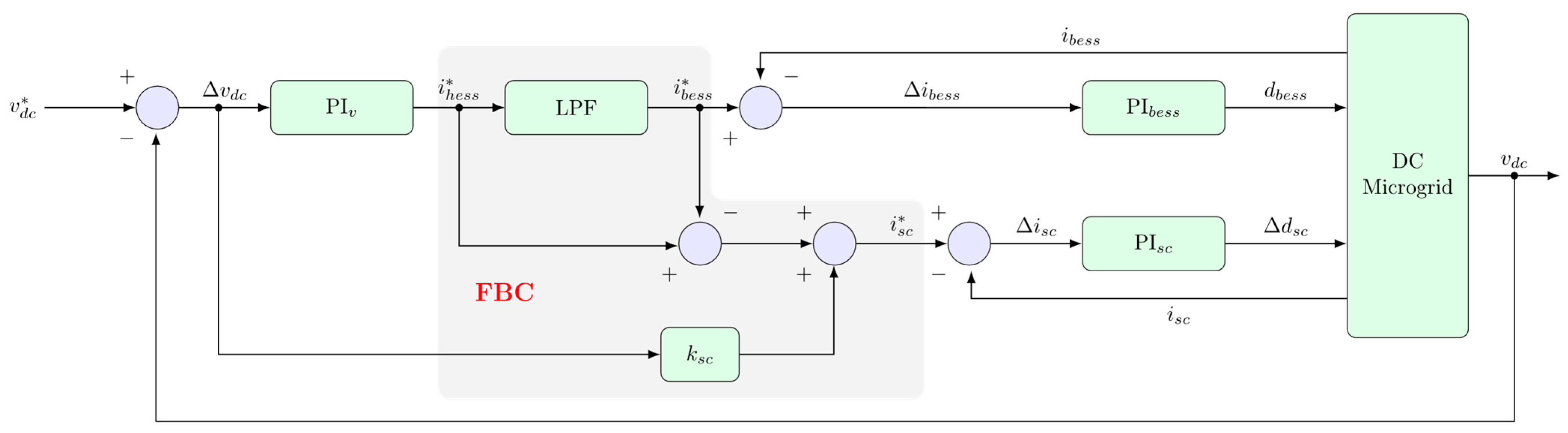
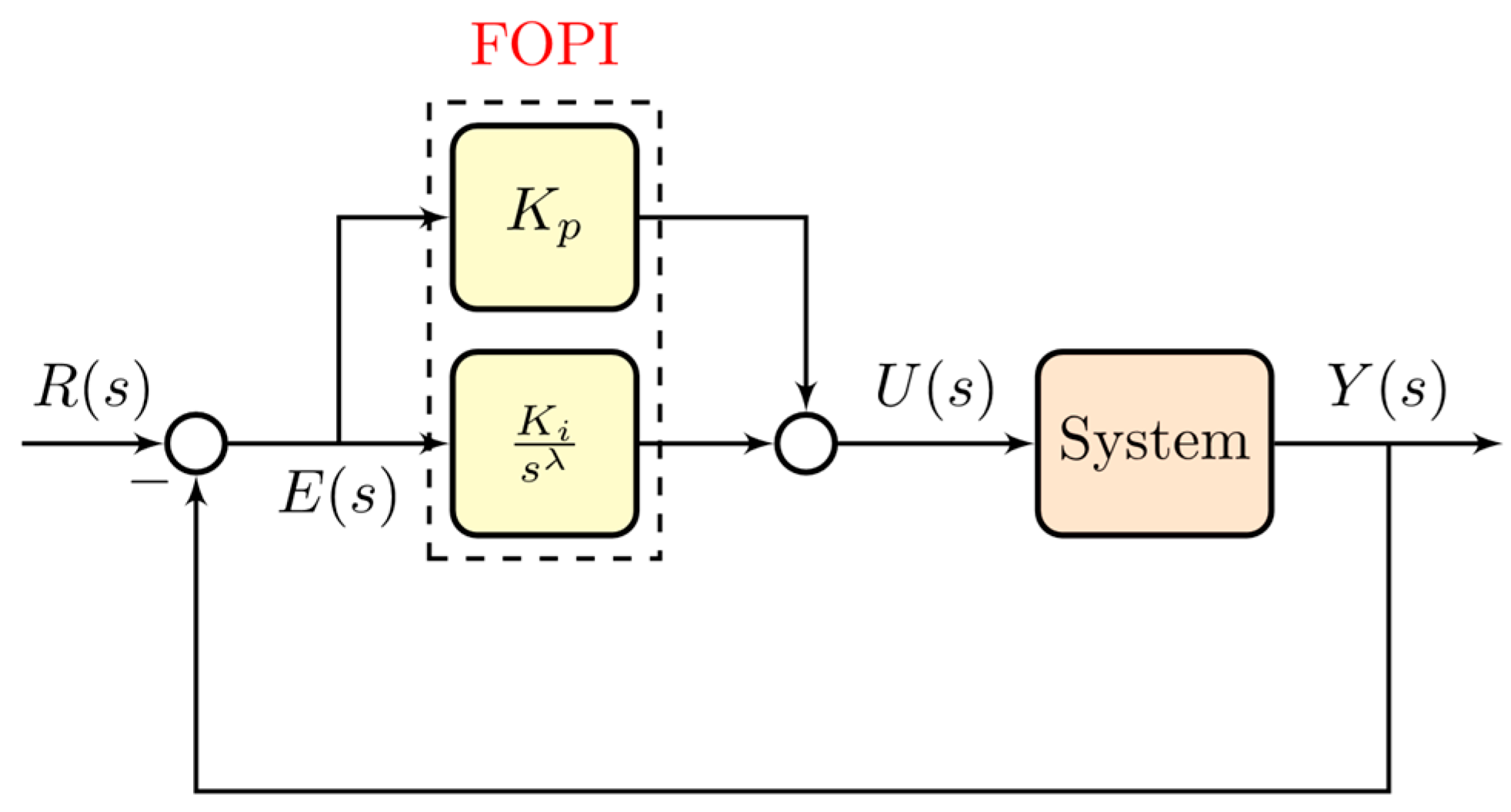
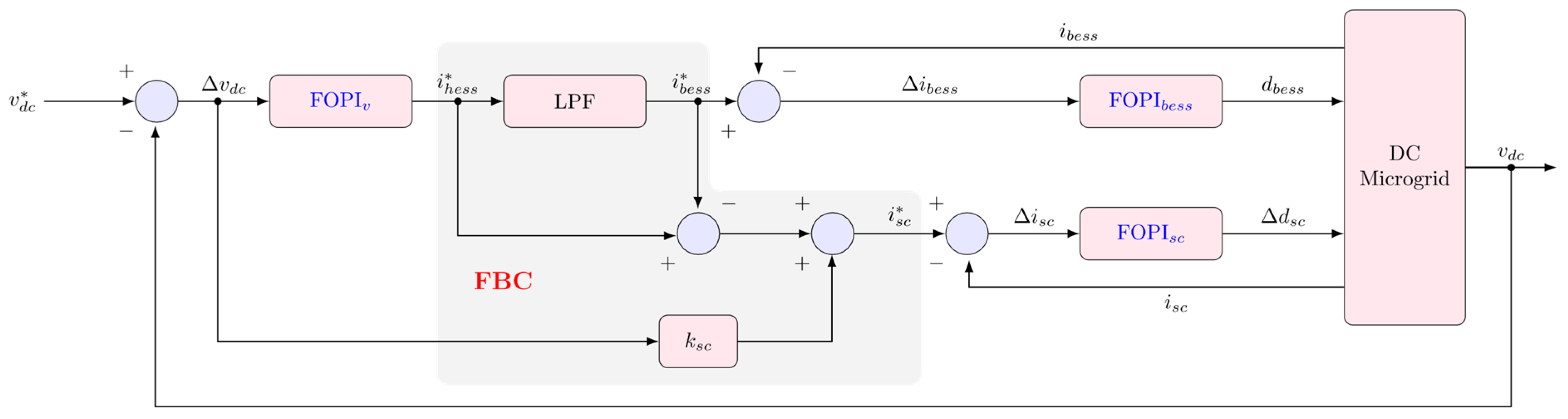
3. Proposed Fractional-Order Frequency-Decomposed Control for DC Microgrids
3.1. Conventional FBC Using the PI Controller
3.2. Proposed FBC Using the Fractional-Order PI Controller
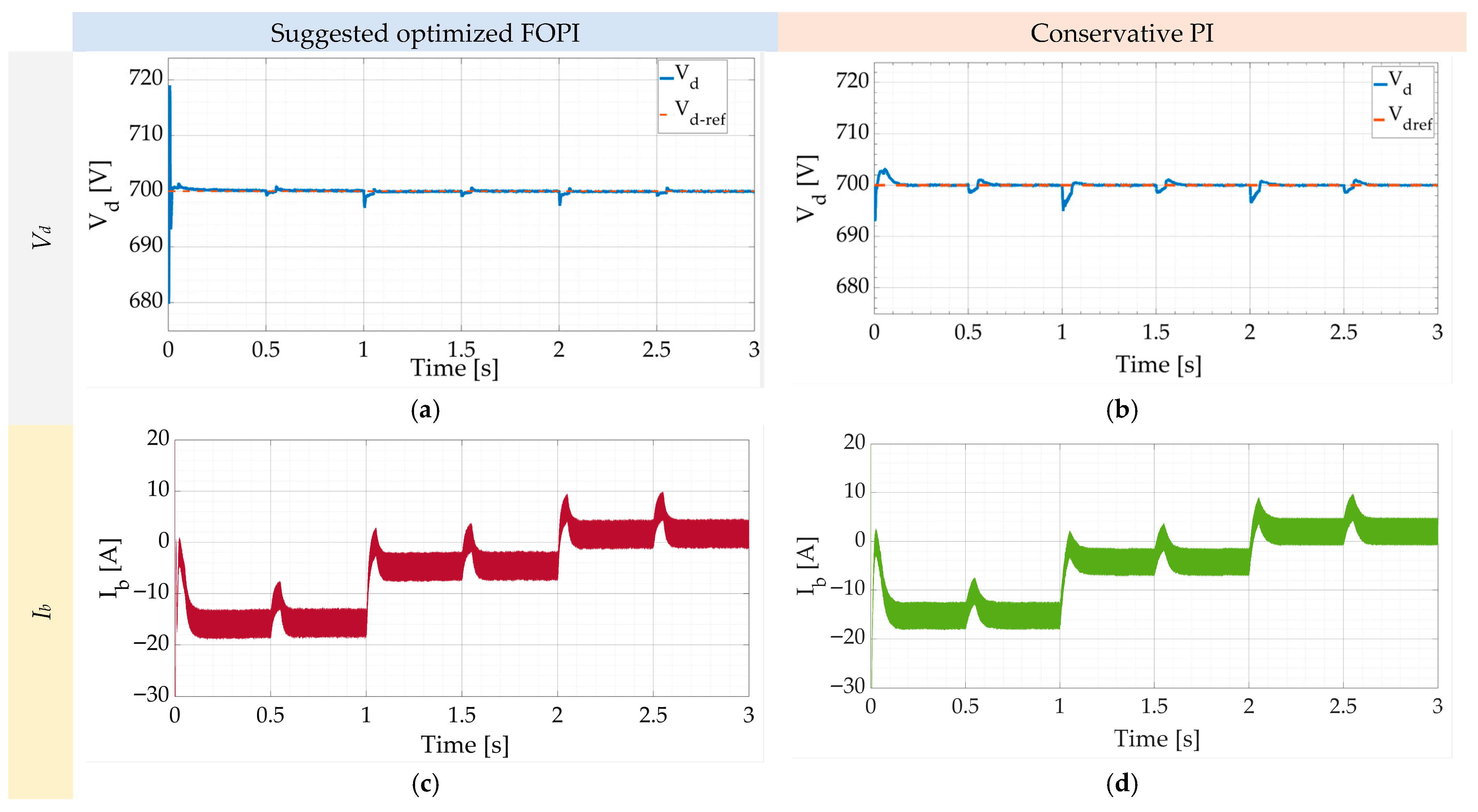
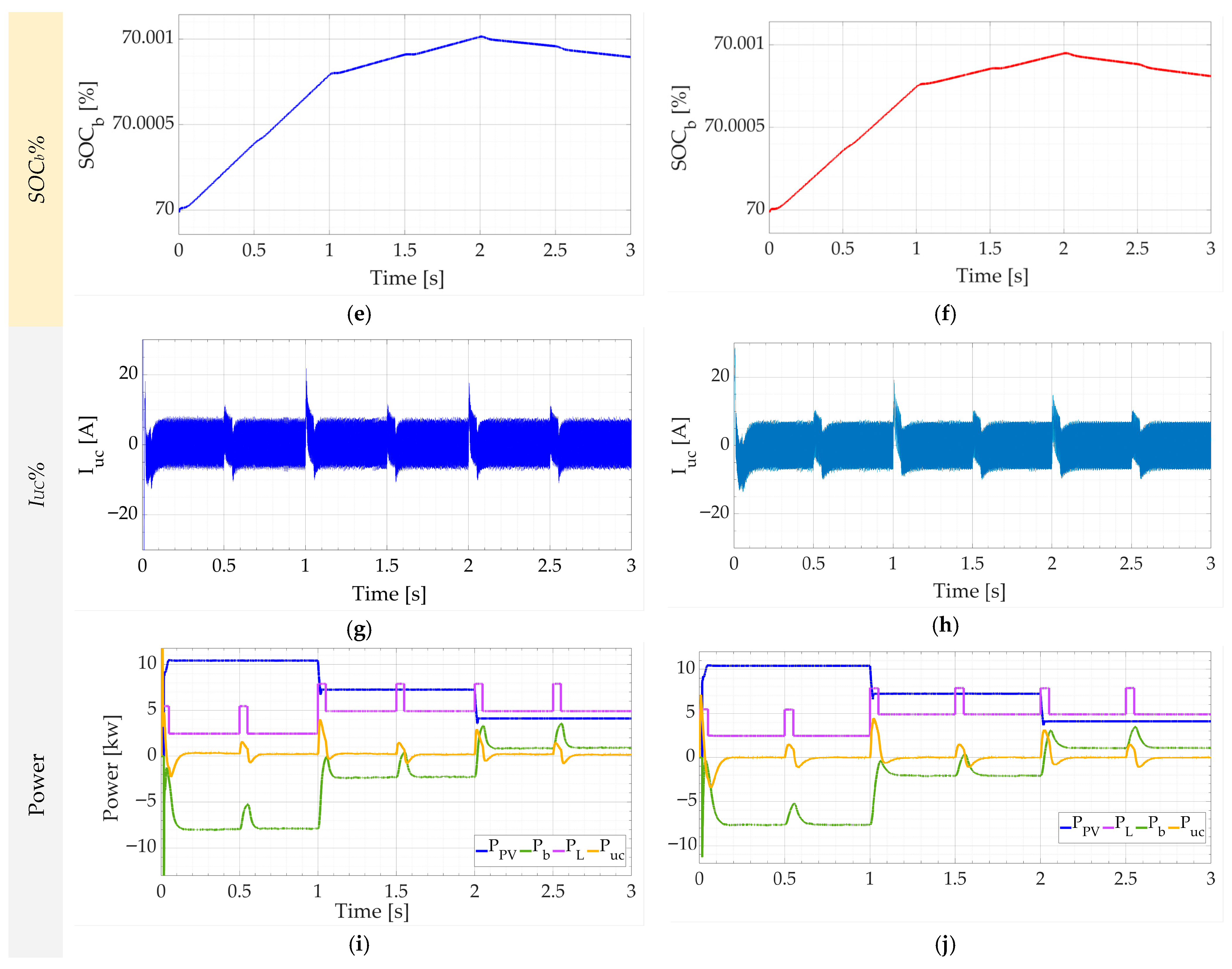
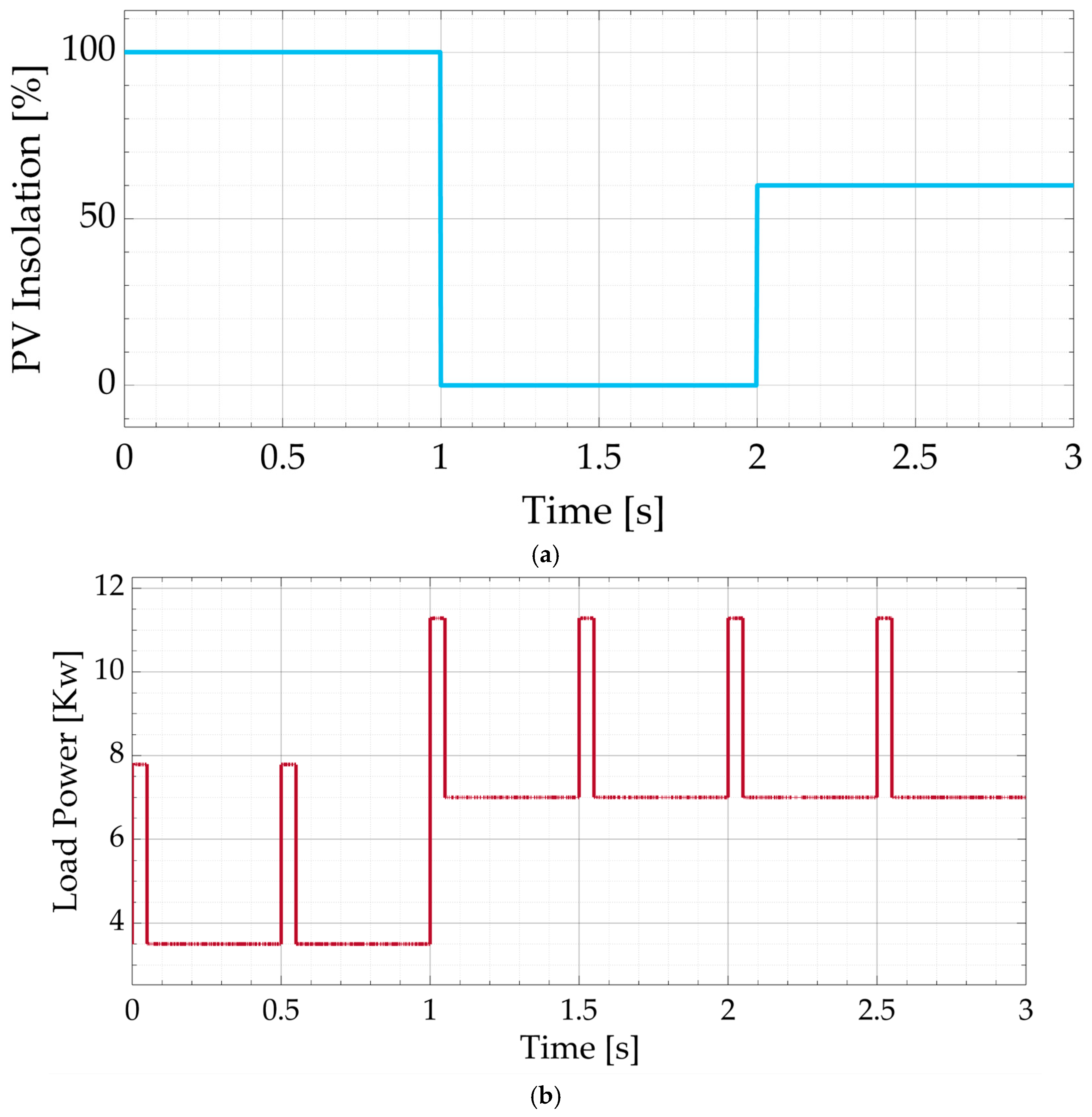
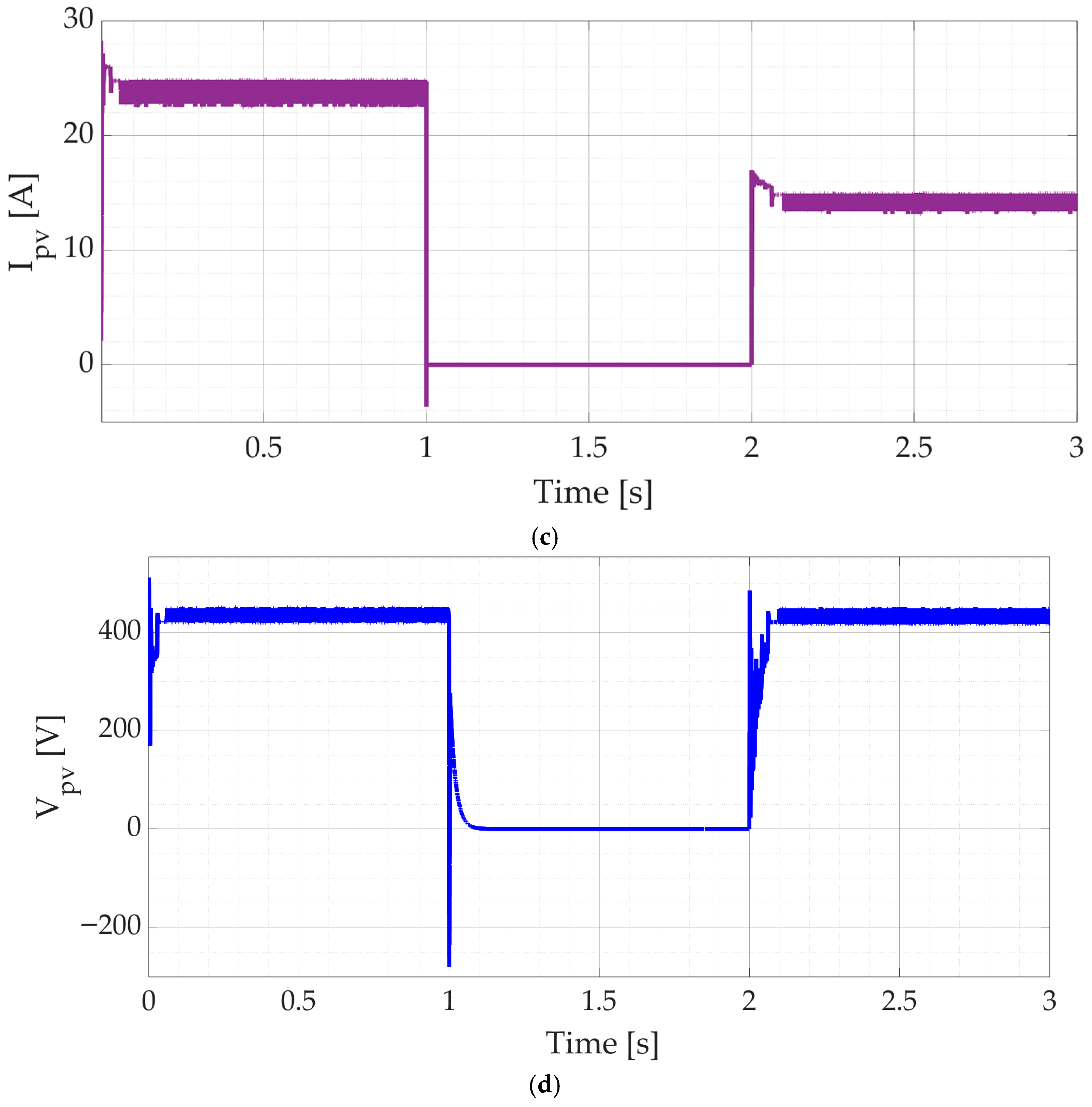
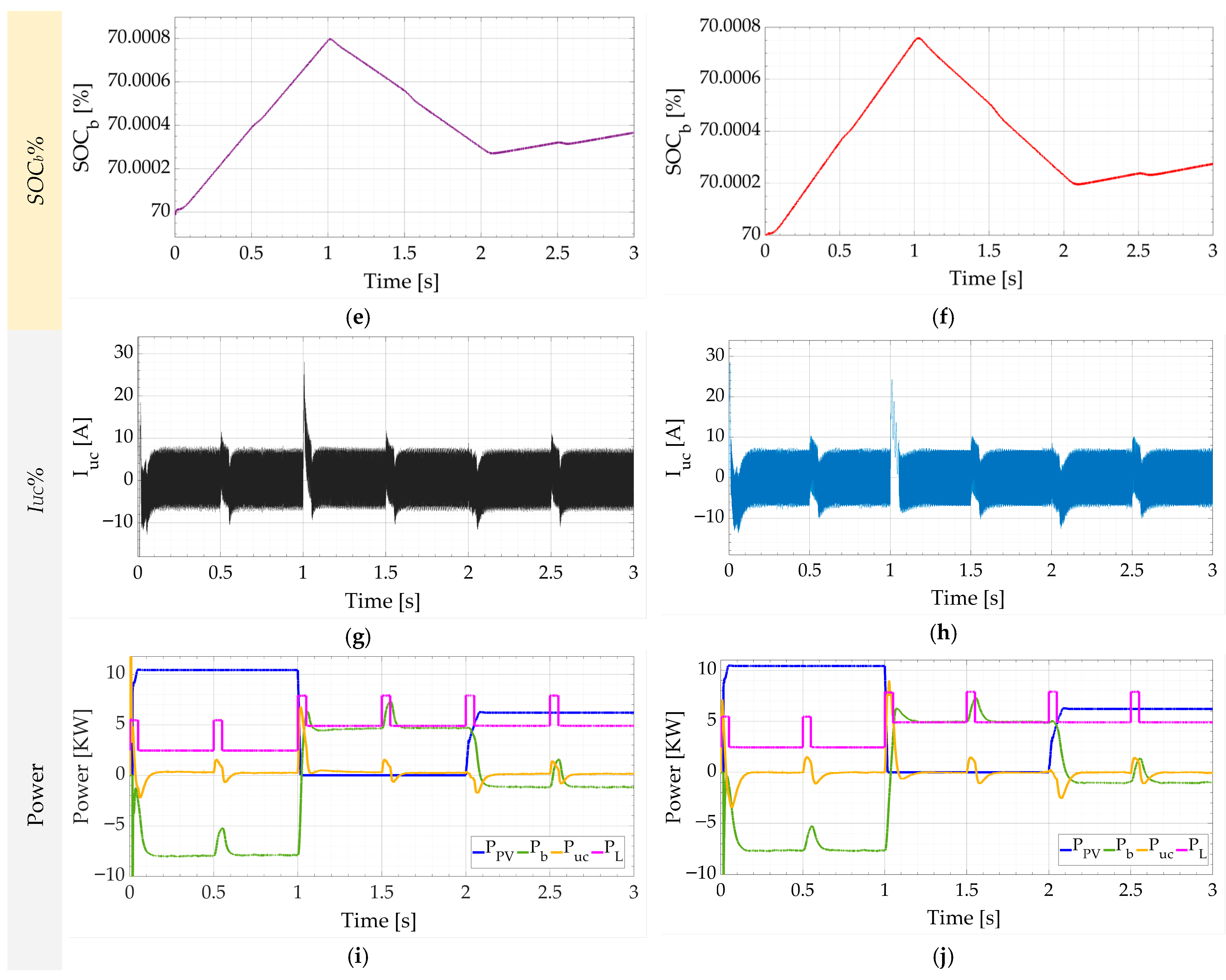
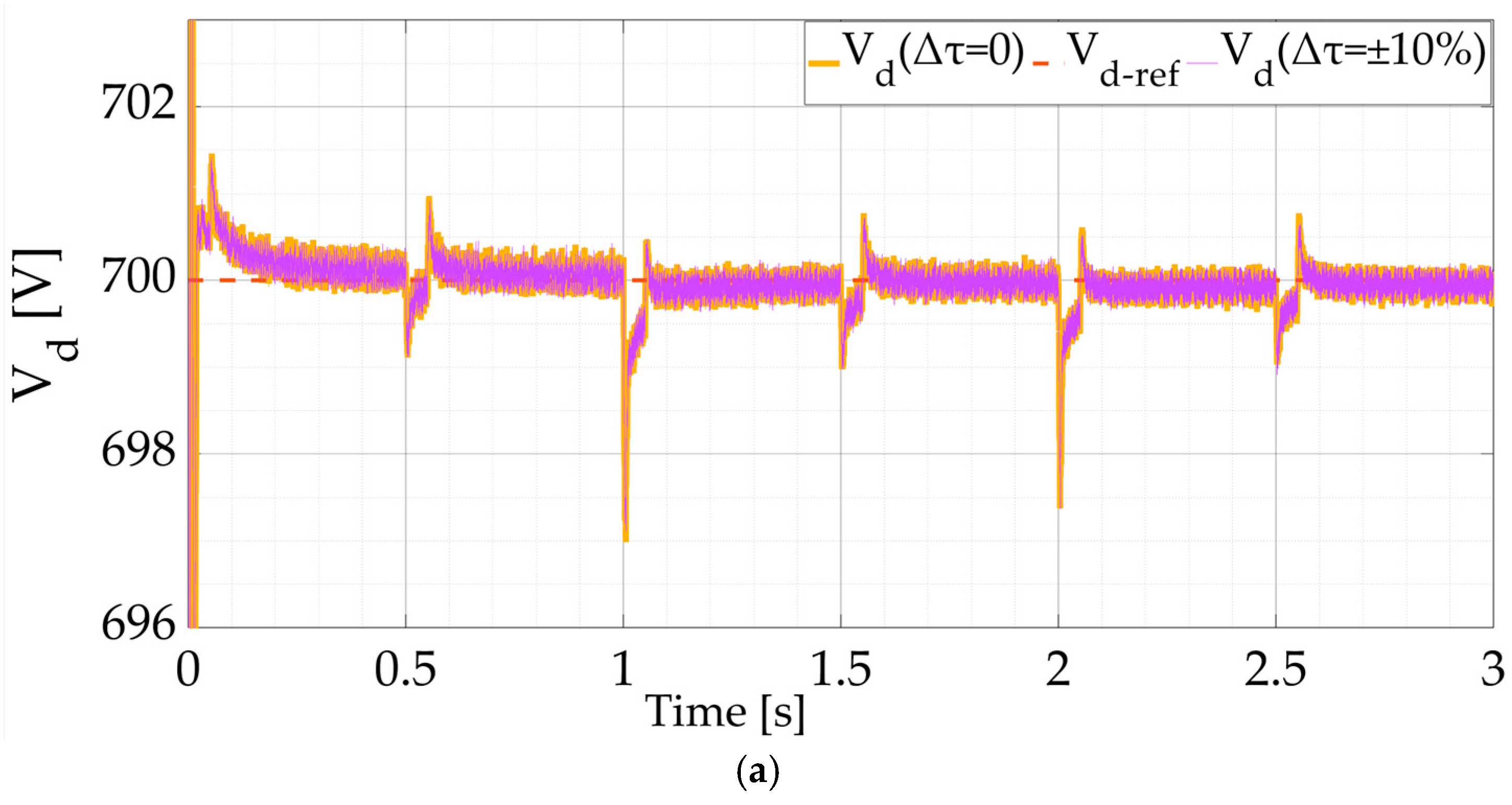
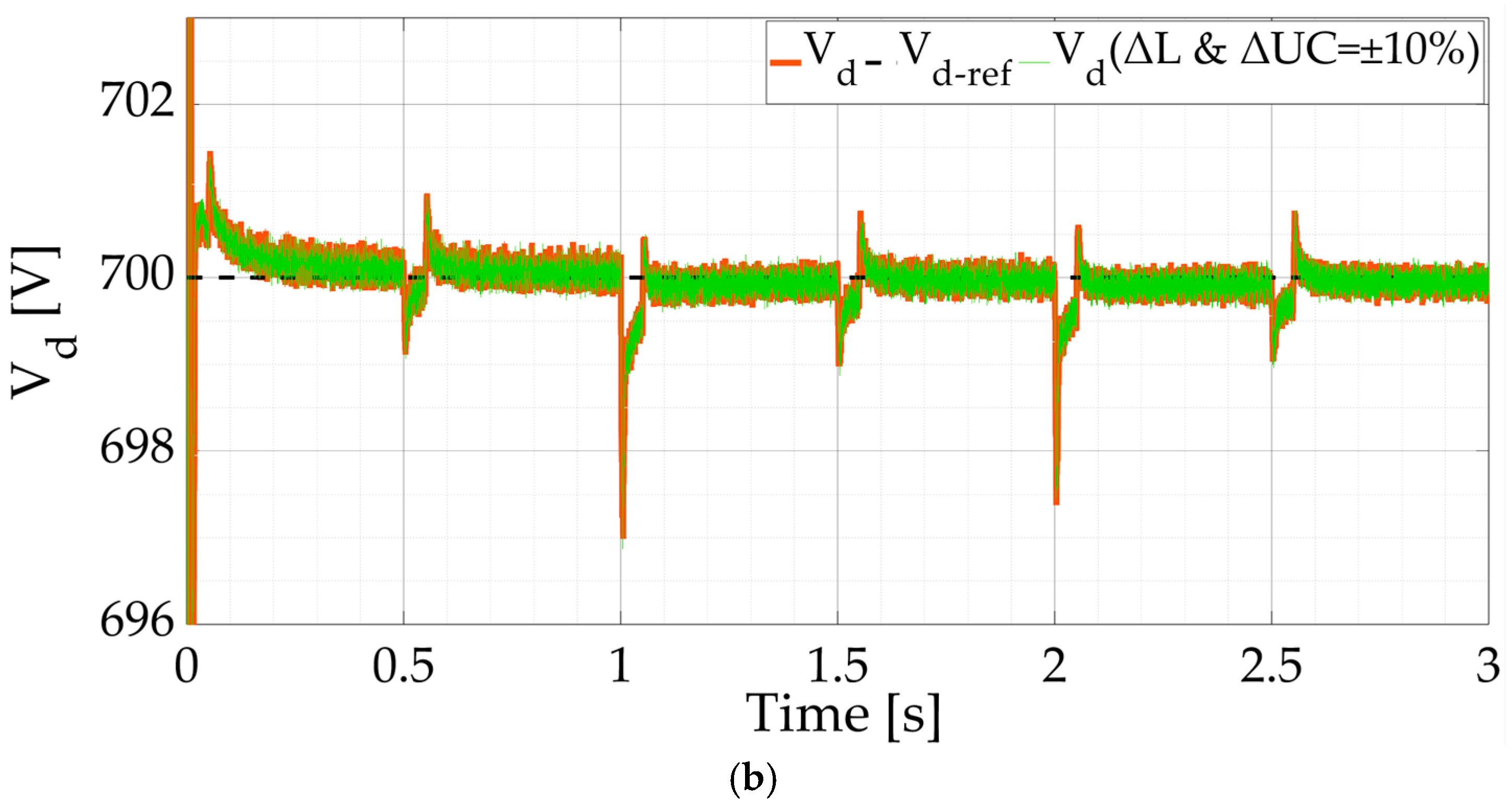
4. Simulation Results and Discussion
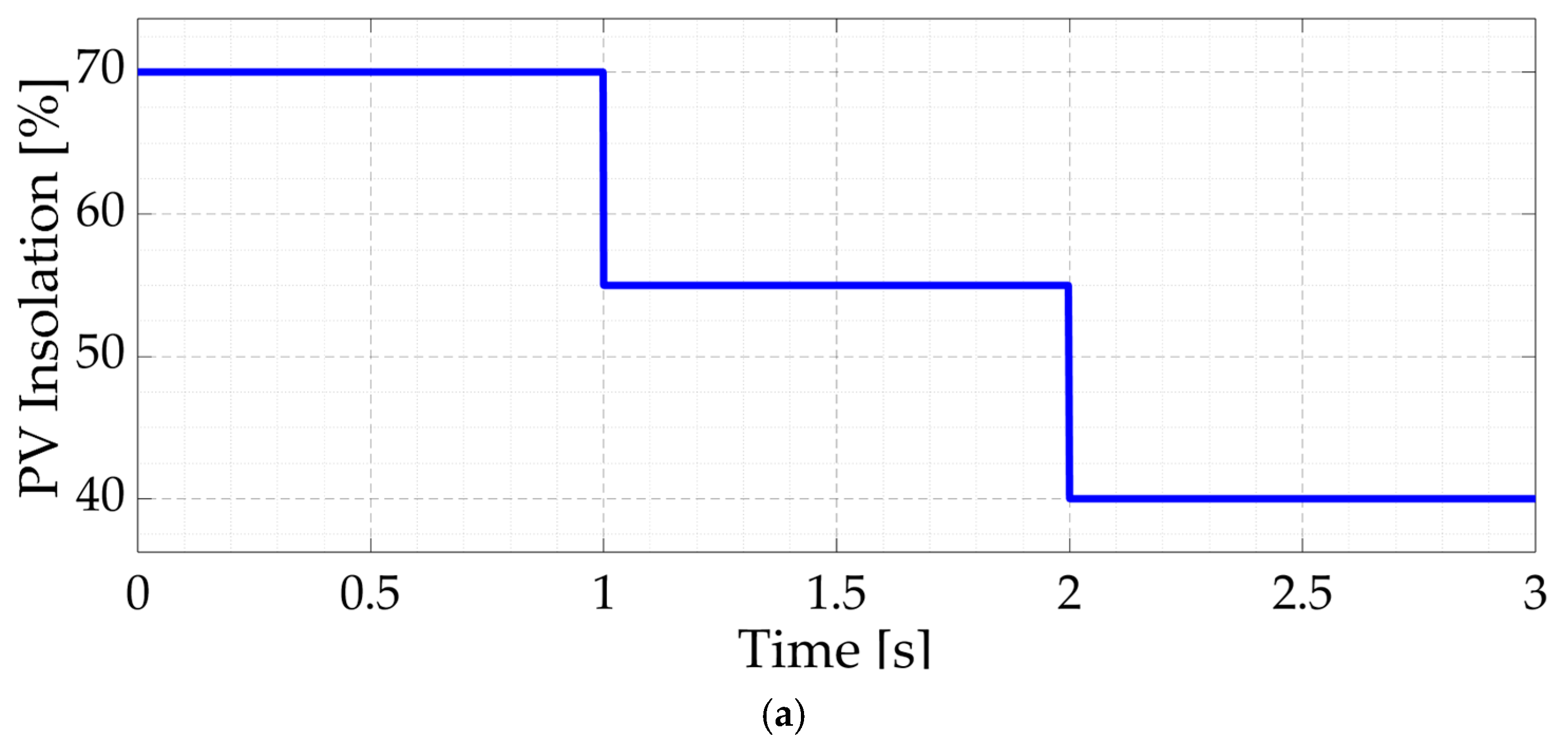
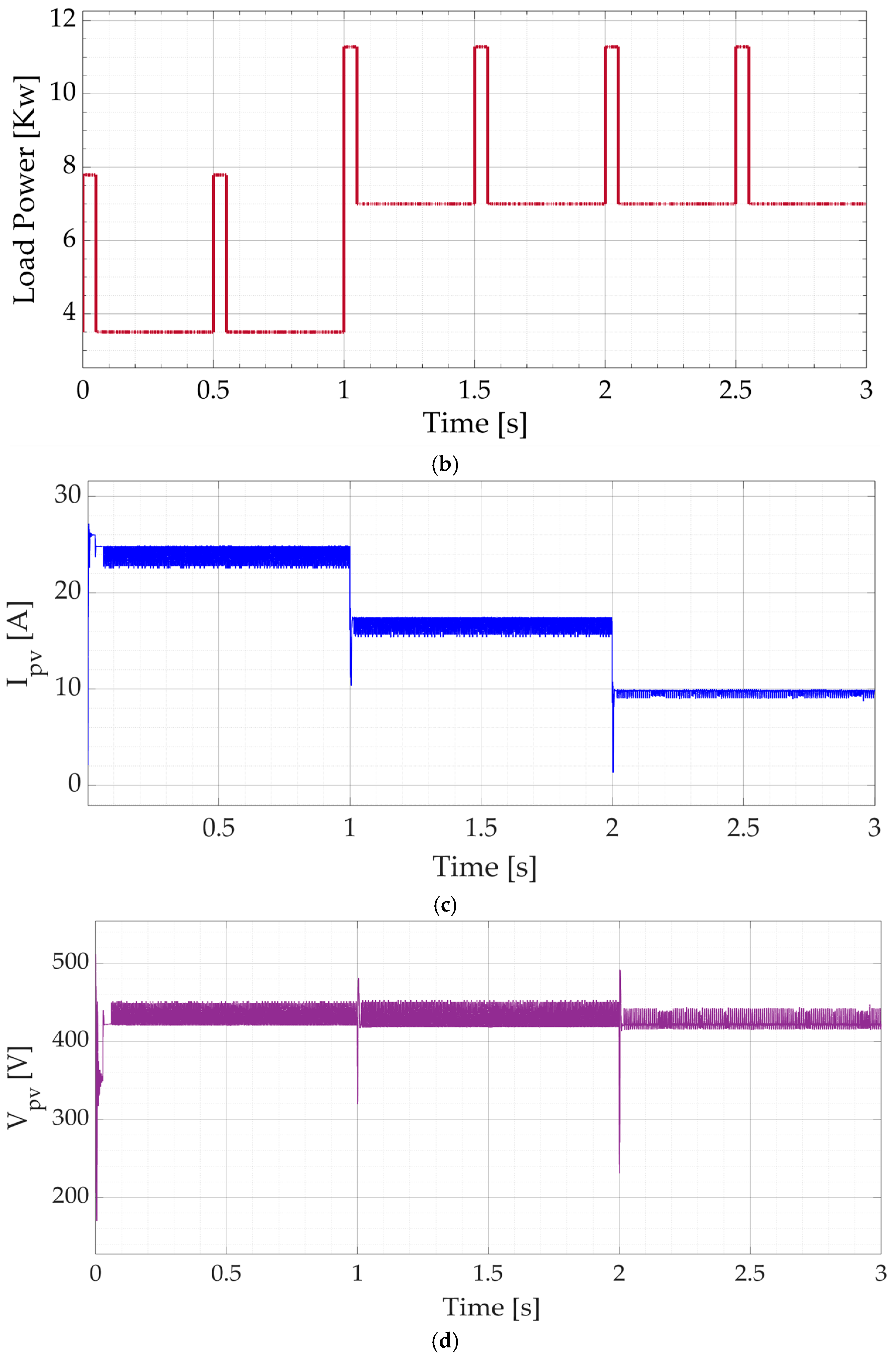
4.1. Scenario #1 (Sufficient but Variable PV Energy with Dynamic Load)
4.2. Scenario #2 (Fault in the PV with Dynamic Load)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Is | the short circuit current of the PV panel |
| d1 | the duty cycle of the step-up DC/DC |
| (Vd, Id) | the DC-bus voltage and current |
| (Vpv, Ipv) | the PV output’s average current and voltage. |
| (Rs, Rp) | the panel equivalent series and parallel resistances |
| Eb | the battery’s open circuit voltage |
| rb | the battery’s internal resistance |
| (SOCb, SOC0) | the battery’s state of charge and its initial value |
| η | the coulombic efficiency |
| vb | the battery terminal voltage |
| m | the mode factor |
| (Cb, Lb) | the filter capacitance and filter inductance |
| (Vuc, Iuc) | the supercapacitor terminal voltage and current, and are |
| (Resr, Rleak) | the electrical circuit parameters of the supercapacitor |
| C* | the effective capacitance of the supercapacitor |
| Euc | the energy of the supercapacitor |
| Cdc | the equivalent DC bus capacitance |
| the current provided by the hybrid ESS and its reference | |
| iPV | the PV current |
| iload | the load current drawn by the DC loads across the DC bus |
| the supercapacitor current and its reference | |
| the BESS current and its reference | |
| LPF | the low-pass filter |
| τ | the LPF’s time constant |
| Kp and Ki | the proportional and integral gains of the PI controller |
| the DC link voltage and its reference | |
| N | the approximation order of the Oustaloup method |
| λ | the fractional integral order coefficient |
| Vdc_ref | Reference DC bus voltage (V) |
| D | Duty ratio of the DC/DC converter |
| fc | Cut-off frequency of the filter (Hz) |
| FOPI | Fractional-Order Proportional–Integral controller |
| GWO | Grey Wolf Optimizer |
| HPF | High-Pass Filter |
| ib | Battery current (A) |
| iuc | Ultracapacitor current (A) |
| LSE | Least Square Error (performance index) |
| Pb | Battery power (W) |
| Pload | Load demand power (W) |
| Puc | Ultracapacitor power (W) |
| Qₙ | Nominal capacity of the battery (Ah) |
| s | Laplace operator |
| SOC | State of charge of the battery |
| SOC0 | Initial state of charge |
| Vdc | DC bus voltage (V) |
| FOPI | the fractional-order proportional-integral |
| FO | the fractional-order |
| Kpv, Kiv, and λv | the proportional gain, integral gain, and the FO’s outer voltage loop control |
| Kpi, Kii, and λi | the proportional gain, integral gain, and the FO’s inner current loop control |
References
- Peters, R.; Berlekamp, J.; Kabiri, C.; Kaplin, B.A.; Tockner, K.; Zarfl, C. Sustainable Pathways towards Universal Renewable Electricity Access in Africa. Nat. Rev. Earth Environ. 2024, 5, 137–151. [Google Scholar] [CrossRef]
- Kartal, M.T.; Pata, U.K.; Alola, A.A. Renewable Electricity Generation and Carbon Emissions in Leading European Countries: Daily-Based Disaggregate Evidence by Nonlinear Approaches. Energy Strategy Rev. 2024, 51, 101300. [Google Scholar] [CrossRef]
- Wang, P.; Huang, R.; Zaery, M.; Wang, W.; Xu, D. A Fully Distributed Fixed-Time Secondary Controller for DC Microgrids. IEEE Trans. Ind. Appl. 2020, 56, 6586–6597. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Fulwani, D. Adaptive Voltage Tuning Based Load Sharing in DC Microgrid. IEEE Trans. Ind. Appl. 2020, 57, 977–986. [Google Scholar] [CrossRef]
- Behera, M.K.; Saikia, L.C. A Novel Resilient Control of Grid-Integrated Solar PV-Hybrid Energy Storage Microgrid for Power Smoothing and Pulse Power Load Accommodation. IEEE Trans. Power Electron. 2022, 38, 3965–3980. [Google Scholar] [CrossRef]
- Dhar, R.K.; Merabet, A.; Bakir, H.; Ghias, A.M. Implementation of Water Cycle Optimization for Parametric Tuning of PI Controllers in Solar PV and Battery Storage Microgrid System. IEEE Syst. J. 2021, 16, 1751–1762. [Google Scholar] [CrossRef]
- Lazard’s Levelized Cost of Energy Analysis—Version 16. Available online: https://www.lazard.com/research-insights/2023-levelized-cost-of-energyplus/ (accessed on 1 April 2023).
- Soudagar, M.E.M.; Ramesh, S.; Khan, T.Y.; Almakayeel, N.; Ramesh, R.; Ghazali, N.N.N.; Cuce, E.; Shelare, S. An Overview of the Existing and Future State of the Art Advancement of Hybrid Energy Systems Based on PV-Solar and Wind. Int. J. Low-Carbon Technol. 2024, 19, 207–216. [Google Scholar] [CrossRef]
- Shi, X.; Shi, X.; Dong, W.; Zang, P.; Jia, H.; Wu, J.; Wang, Y. Research on Energy Storage Configuration Method Based on Wind and Solar Volatility. In Proceedings of the 2020 10th International Conference on Power and Energy Systems (ICPES), Chengdu, China, 25–27 December 2020; IEEE: New York, NY, USA, 2020; pp. 464–468. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. Development of Hybrid Battery–Supercapacitor Energy Storage for Remote Area Renewable Energy Systems. Appl. Energy 2015, 153, 56–62. [Google Scholar] [CrossRef]
- Jarrahi, M.A.; Abolghasemi, V. A Power Control and Management Framework for Integration of PV-Based DC Microgrids with Battery Storages and Supercapacitors. IEEE Open Access J. Power Energy 2025. [Google Scholar] [CrossRef]
- Sinha, S.; Bajpai, P. Power Management of Hybrid Energy Storage System in a Standalone DC Microgrid. J. Energy Storage 2020, 30, 101523. [Google Scholar] [CrossRef]
- Faisal, M.; Hannan, M.A.; Ker, P.J.; Hussain, A.; Mansor, M.B.; Blaabjerg, F. Review of Energy Storage System Technologies in Microgrid Applications: Issues and Challenges. IEEE Access 2018, 6, 35143–35164. [Google Scholar] [CrossRef]
- Jing, W.; Hung Lai, C.; Wong, S.H.W.; Wong, M.L.D. Battery-Supercapacitor Hybrid Energy Storage System in Standalone DC Microgrids: A Review. IET Renew. Power Gener. 2017, 11, 461–469. [Google Scholar] [CrossRef]
- Gee, A.M.; Robinson, F.V.P.; Dunn, R.W. Analysis of Battery Lifetime Extension in a Small-Scale Wind-Energy System Using Supercapacitors. IEEE Trans. Energy Convers. 2013, 28, 24–33. [Google Scholar] [CrossRef]
- Xu, G.; Shang, C.; Fan, S.; Hu, X.; Cheng, H. A Hierarchical Energy Scheduling Framework of Microgrids with Hybrid Energy Storage Systems. IEEE Access 2018, 6, 2472–2483. [Google Scholar] [CrossRef]
- Xu, Q.; Hu, X.; Wang, P.; Xiao, J.; Tu, P.; Wen, C.; Lee, M.Y. A Decentralized Dynamic Power Sharing Strategy for Hybrid Energy Storage System in Autonomous DC Microgrid. IEEE Trans. Ind. Electron. 2017, 64, 5930–5941. [Google Scholar] [CrossRef]
- Chia, Y.Y.; Lee, L.H.; Shafiabady, N.; Isa, D. A Load Predictive Energy Management System for Supercapacitor-Battery Hybrid Energy Storage System in Solar Application Using the Support Vector Machine. Appl. Energy 2015, 137, 588–602. [Google Scholar] [CrossRef]
- Mohanty, S.; Sahoo, B.; Rout, P.K. Advanced Fractional Filter-Based Control Strategy for Smart City Microgrid Operations. In Proceedings of the 2025 International Conference on Intelligent and Cloud Computing (ICoICC), Bhubaneswar, India, 2–3 May 2025; IEEE: New York, NY, USA, 2025; pp. 1–6. [Google Scholar]
- Taye, B.A.; Choudhury, N.B.D. Adaptive Filter Based Control Method for Performance Improvement of Hybrid Energy Storage System in DC Microgrid. In Proceedings of the 2023 IEEE Guwahati Subsection Conference (GCON), Guwahati, Assam, 23–25 June 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Liao, H.; Peng, J.; Wu, Y.; Li, H.; Zhou, Y.; Zhang, X.; Huang, Z. Adaptive Split-Frequency Quantitative Power Allocation for Hybrid Energy Storage Systems. IEEE Trans. Transp. Electrif. 2021, 7, 2306–2317. [Google Scholar] [CrossRef]
- Ramos, G.A.; Costa-Castelló, R. Energy Management Strategies for Hybrid Energy Storage Systems Based on Filter Control: Analysis and Comparison. Electronics 2022, 11, 1631. [Google Scholar] [CrossRef]
- Nair, U.R.; Costa-Castelló, R. A Model Predictive Control Based Energy Management Scheme for Hybrid Storage System in Islanded Microgrids. IEEE Access 2020, 8, 97809–97822. [Google Scholar] [CrossRef]
- Cui, J.; Tian, G.; Liu, G.; Wu, Y.; Guo, Z. Research on Coordinated Control Strategy of Isolated DC Microgrid with PV/Hybrid Energy Storage. Energy Rep. 2022, 8, 893–899. [Google Scholar] [CrossRef]
- Almasoudi, F.M.; Magdy, G.; Bakeer, A.; Alatawi, K.S.S.; Rihan, M. A New Load Frequency Control Technique for Hybrid Maritime Microgrids: Sophisticated Structure of Fractional-Order PIDA Controller. Fractal Fract. 2023, 7, 435. [Google Scholar] [CrossRef]
- Wahidujjaman, M.; Bari, T.U.; Alam, M.S.; Islam, M.R.; Hossain, M.A.; Hossain, M.A.; Sheikh, M.R.I. Enhanced Stability and Performance of Islanded DC Microgrid Systems Using Optimized Fractional Order Controller and Advanced Energy Management. Eng. Rep. 2025, 7, e70122. [Google Scholar] [CrossRef]
- Asmy, N.A.; Ramprabhakar, J.; Anand, R.; Meena, V.P.; Jadoun, V.K. A Relative Analysis to Cascaded Fractional-Order Controllers in Microgrid Non-Minimum Phase Converters Using EHO. Sci. Rep. 2025, 15, 10333. [Google Scholar] [CrossRef]
- Muresan, C.I.; Birs, I.; Ionescu, C.; Dulf, E.H.; De Keyser, R. A Review of Recent Developments in Autotuning Methods for Fractional-Order Controllers. Fractal Fract. 2022, 6, 37. [Google Scholar] [CrossRef]
- Saleem, O.; Ali, S.; Iqbal, J. Robust MPPT Control of Stand-Alone Photovoltaic Systems via Adaptive Self-Adjusting Fractional Order PID Controller. Energies 2023, 16, 5039. [Google Scholar] [CrossRef]
- Albalawi, H.; Zaid, S.A.; Alatwi, A.M.; Moustafa, M.A. Application of an Optimal Fractional-Order Controller for a Standalone (Wind/Photovoltaic) Microgrid Utilizing Hybrid Storage (Battery/Ultracapacitor) System. Fractal Fract. 2024, 8, 629. [Google Scholar] [CrossRef]
- Manandhar, U.; Ukil, A.; Gooi, H.B.; Tummuru, N.R.; Kollimalla, S.K.; Wang, B.; Chaudhari, K. Energy Management and Control for Grid Connected Hybrid Energy Storage System under Different Operating Modes. IEEE Trans. Smart Grid 2019, 10, 1626–1636. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Kriging Based Surrogate Modeling for Fractional Order Control of Microgrids. IEEE Trans. Smart Grid 2014, 6, 36–44. [Google Scholar] [CrossRef]
- Şahin, M.E.; Blaabjerg, F. A Hybrid PV-Battery/Supercapacitor System and a Basic Active Power Control Proposal in MATLAB/Simulink. Electronics 2020, 9, 129. [Google Scholar] [CrossRef]
- Rashid, M. Power Electronics Handbook, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Awad, M.; Ibrahim, A.M.; Alaas, Z.M.; El-Shahat, A.; Omar, A.I. Design and Analysis of an Efficient Photovoltaic Energy-Powered Electric Vehicle Charging Station Using Perturb and Observe MPPT Algorithm. Front. Energy Res. 2022, 10, 969482. [Google Scholar] [CrossRef]
- Rasool, S.; Muttaqi, K.M.; Sutanto, D. A Multi-Filter Based Dynamic Power Sharing Control for a Hybrid Energy Storage System Integrated to a Wave Energy Converter for Output Power Smoothing. IEEE Trans. Sustain. Energy 2022, 13, 1693–1706. [Google Scholar] [CrossRef]
- Roja, P.; Venkatramanan, D.; John, V. A Nonlinear Model Based Analysis and Accurate Design of Ultracapacitor Stack for Energy Storage Systems. IEEE Trans. Energy Convers. 2022, 37, 403–412. [Google Scholar] [CrossRef]
- Tummuru, N.R.; Mishra, M.K.; Srinivas, S. Dynamic Energy Management of Renewable Grid Integrated Hybrid Energy Storage System. IEEE Trans. Ind. Electron. 2015, 62, 7728–7737. [Google Scholar] [CrossRef]
- Albalawi, H.; Bakeer, A.; Zaid, S.A.; Aggoune, E.-H.; Ayaz, M.; Bensenouci, A.; Eisa, A. Fractional-Order Model-Free Predictive Control for Voltage Source Inverters. Fractal Fract. 2023, 7, 433. [Google Scholar] [CrossRef]
- Zaid, S.A.; Bakeer, A.; Magdy, G.; Albalawi, H.; Kassem, A.M.; El-Shimy, M.E.; AbdelMeguid, H.; Manqarah, B. A New Intelligent Fractional-Order Load Frequency Control for Interconnected Modern Power Systems with Virtual Inertia Control. Fractal Fract. 2023, 7, 62. [Google Scholar] [CrossRef]
- Bingi, K.; Prusty, R.; Singh, A. A Review on Fractional-Order Modelling and Control of Robotic Manipulators. Fractal Fract. 2023, 7, 77. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-Band Complex Noninteger Differentiator: Characterization and Synthesis. IEEE Trans. Circuits Syst. I 2000, 47, 25–39. [Google Scholar] [CrossRef]

| Control Loop | Parameter | Value |
|---|---|---|
| Outer loop (common with BESS and UC) | Kpv | 1.477 |
| Kiv | 100 | |
| λv | 0.6 | |
| Inner loop (for BESS) | Kpi | 0.043 |
| Kii | 5 | |
| λi | 0.6 | |
| Inner loop (for UC) | Kpi | 0.45 |
| Kii | 5 | |
| λi | 0.5 |
| Scenario | Controller | Overshoot (%) | Settling Time (s) | LSE of DC Bus Voltage | Improvement vs. PI | |
|---|---|---|---|---|---|---|
| 1 | Pulsed load + PV variation | PI | ~10% | 0.5 s | 1.0 | – |
| 1 | Pulsed load + PV variation | Optimized FOPI | ~5% | 0.3 s | 0.2 | 80% lower LSE, 50% lower overshoot, 40% faster settling |
| 2 | PV fault + dynamic load | PI | ~12% | 0.55 s | 1.2 | – |
| 2 | PV fault + dynamic load | Optimized FOPI | ~6% | 0.33 s | 0.25 | 80% lower LSE, 50% lower overshoot, 40% faster settling |
| Control Method | Overshoot | Settling Time | Battery Stress | Complexity | Notes |
|---|---|---|---|---|---|
| PI/PID | High | Slow | High | Low | Simple, but weak under fast dynamics |
| SMC | Low | Fast | Medium | Medium | Robust but suffers chattering |
| MPC | Very Low | Very Fast | Low | High | Excellent but computationally heavy |
| Droop/Filter-based [22] | Medium | Medium | Medium | Low | Works well for power sharing |
| Proposed FOPI (opt.) | Low (~50% less) | Fast (~40% faster) | Low (reduced) | Medium | Balanced trade-off, optimized via GWO |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaid, S.A.; Albalawi, H.; El-Hageen, H.M.; Wadood, A.; Bakeer, A. Stabilization of DC Microgrids Using Frequency-Decomposed Fractional-Order Control and Hybrid Energy Storage. Fractal Fract. 2025, 9, 670. https://doi.org/10.3390/fractalfract9100670
Zaid SA, Albalawi H, El-Hageen HM, Wadood A, Bakeer A. Stabilization of DC Microgrids Using Frequency-Decomposed Fractional-Order Control and Hybrid Energy Storage. Fractal and Fractional. 2025; 9(10):670. https://doi.org/10.3390/fractalfract9100670
Chicago/Turabian StyleZaid, Sherif A., Hani Albalawi, Hazem M. El-Hageen, Abdul Wadood, and Abualkasim Bakeer. 2025. "Stabilization of DC Microgrids Using Frequency-Decomposed Fractional-Order Control and Hybrid Energy Storage" Fractal and Fractional 9, no. 10: 670. https://doi.org/10.3390/fractalfract9100670
APA StyleZaid, S. A., Albalawi, H., El-Hageen, H. M., Wadood, A., & Bakeer, A. (2025). Stabilization of DC Microgrids Using Frequency-Decomposed Fractional-Order Control and Hybrid Energy Storage. Fractal and Fractional, 9(10), 670. https://doi.org/10.3390/fractalfract9100670






