Time-Fractional Differential Operator Modeling of Contaminant Transport with Adsorption and Decay
Abstract
1. Introduction
2. Advection-Dispersion Models with Atangana–Baleanu Differential Operator
2.1. Advection-Dispersion Model
2.2. Atangana-Baleanu Differential Operator
2.3. Advection–Dispersion Models with AB Differential Operator
3. The AB-ADM with Linear Adsorption
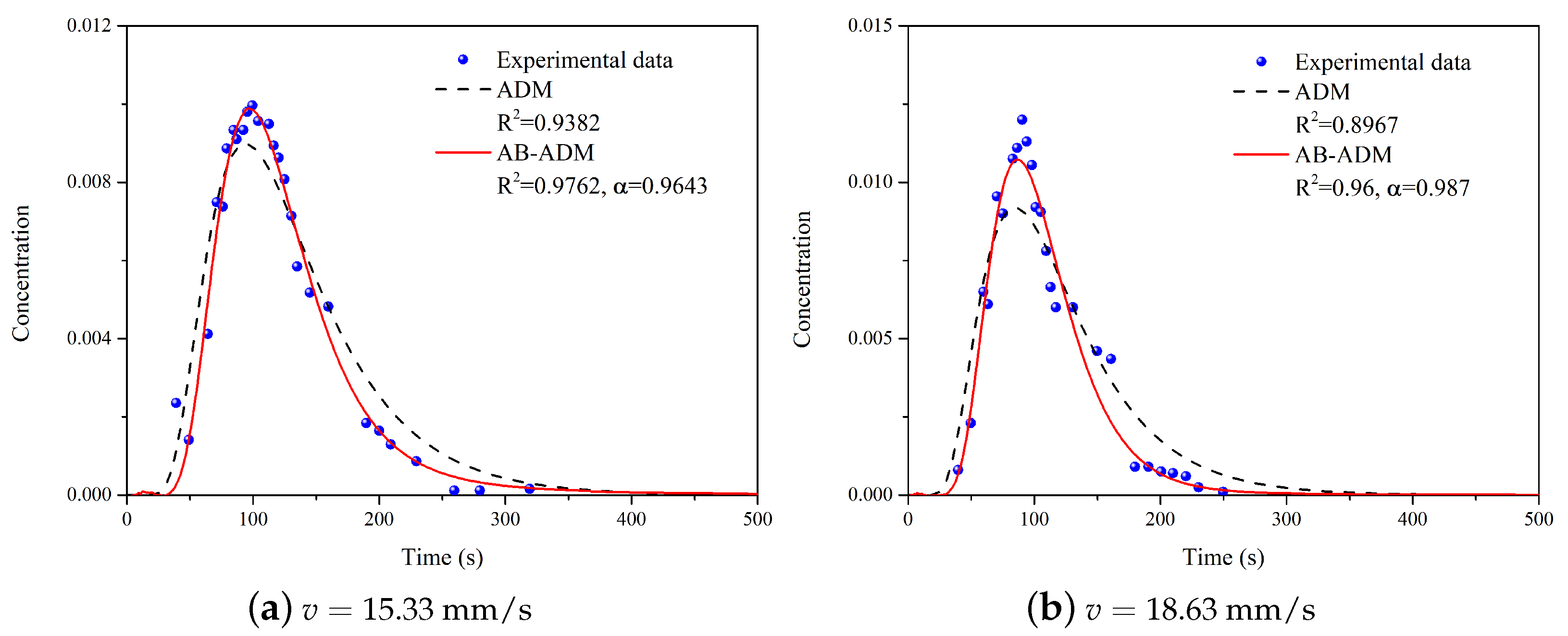
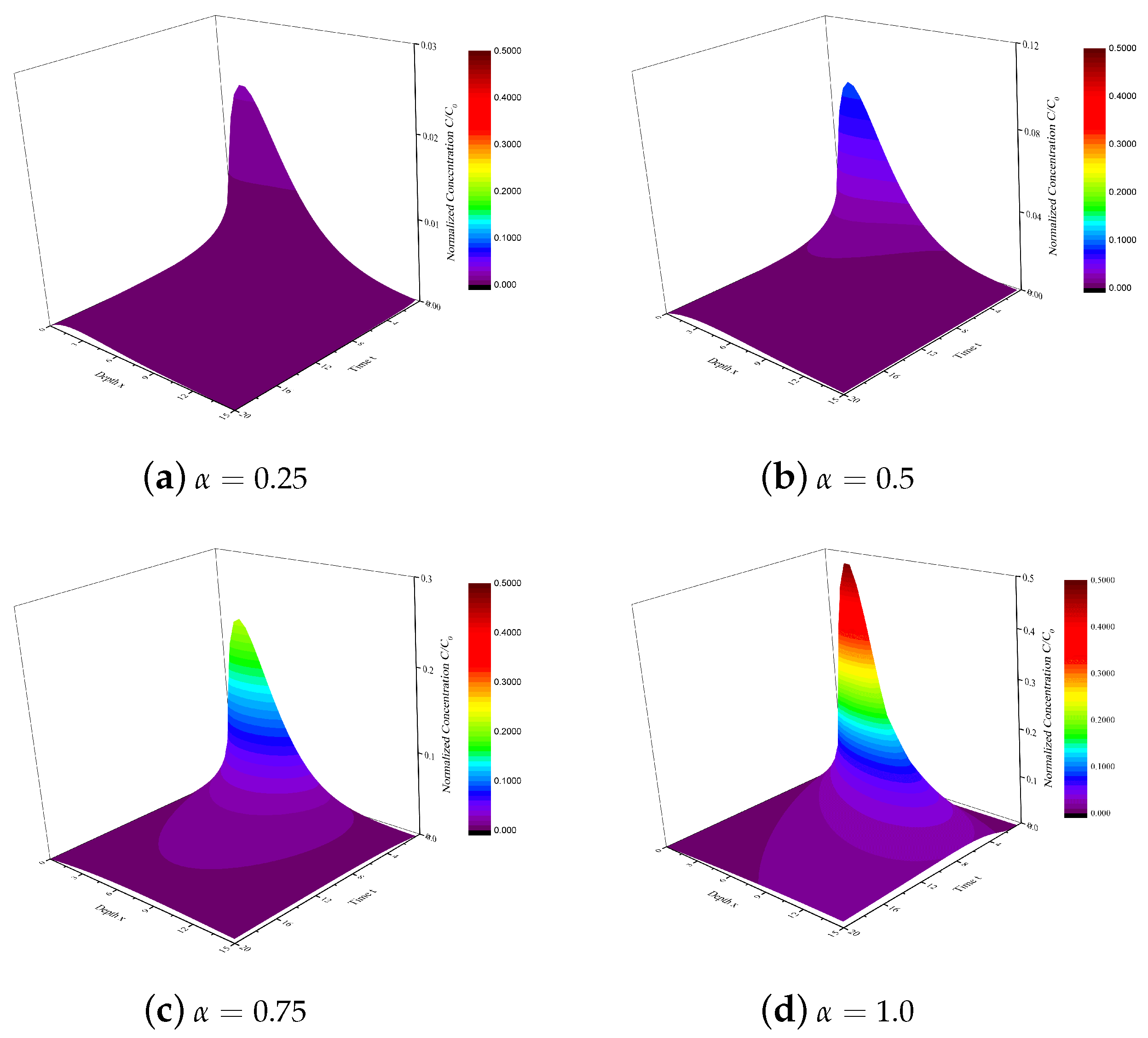
3.1. AB-ADM with Linear Adsorption for Pulse-like Input Source
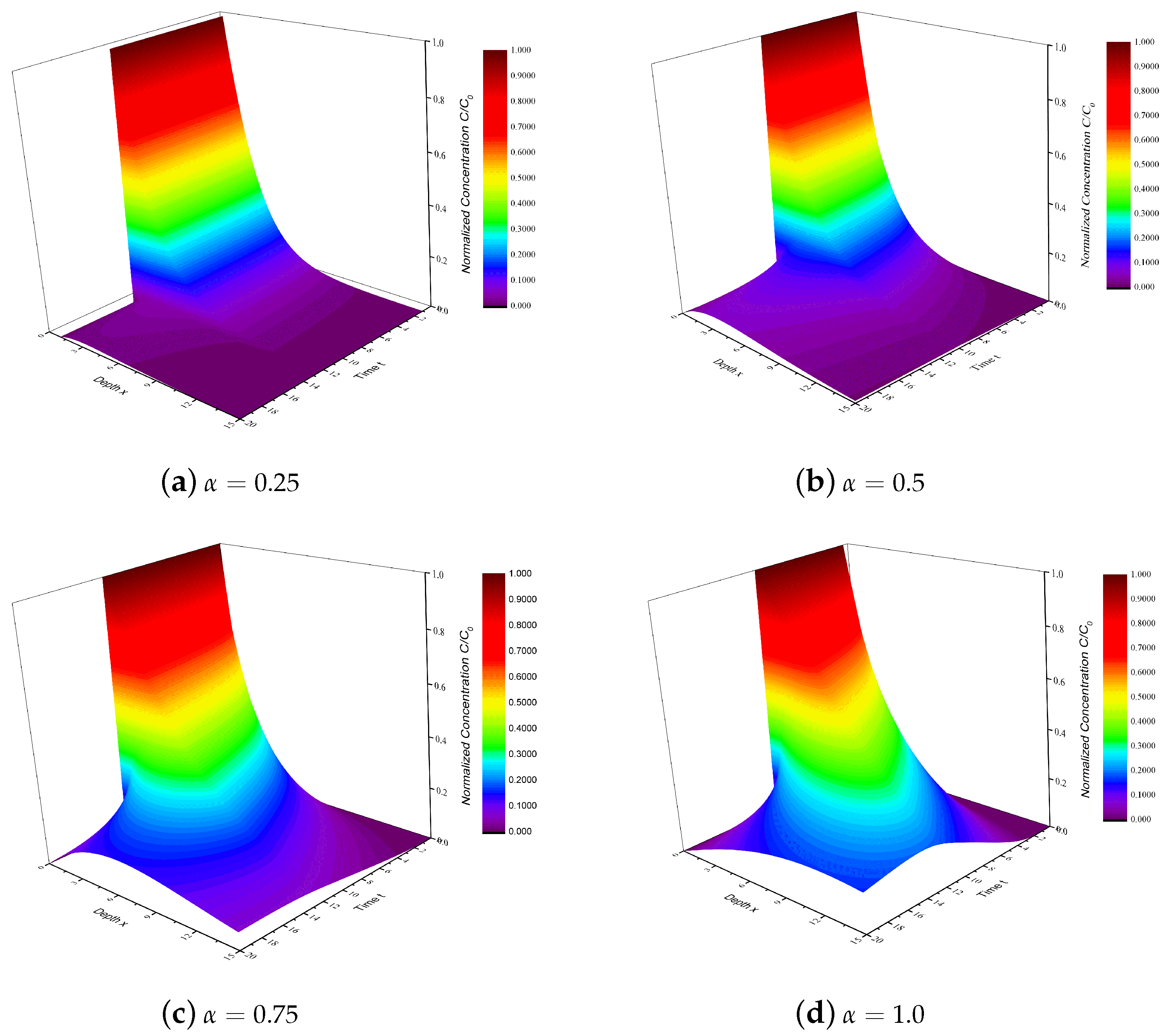
3.2. AB-ADM with Linear Adsorption for Constant Concentration Source
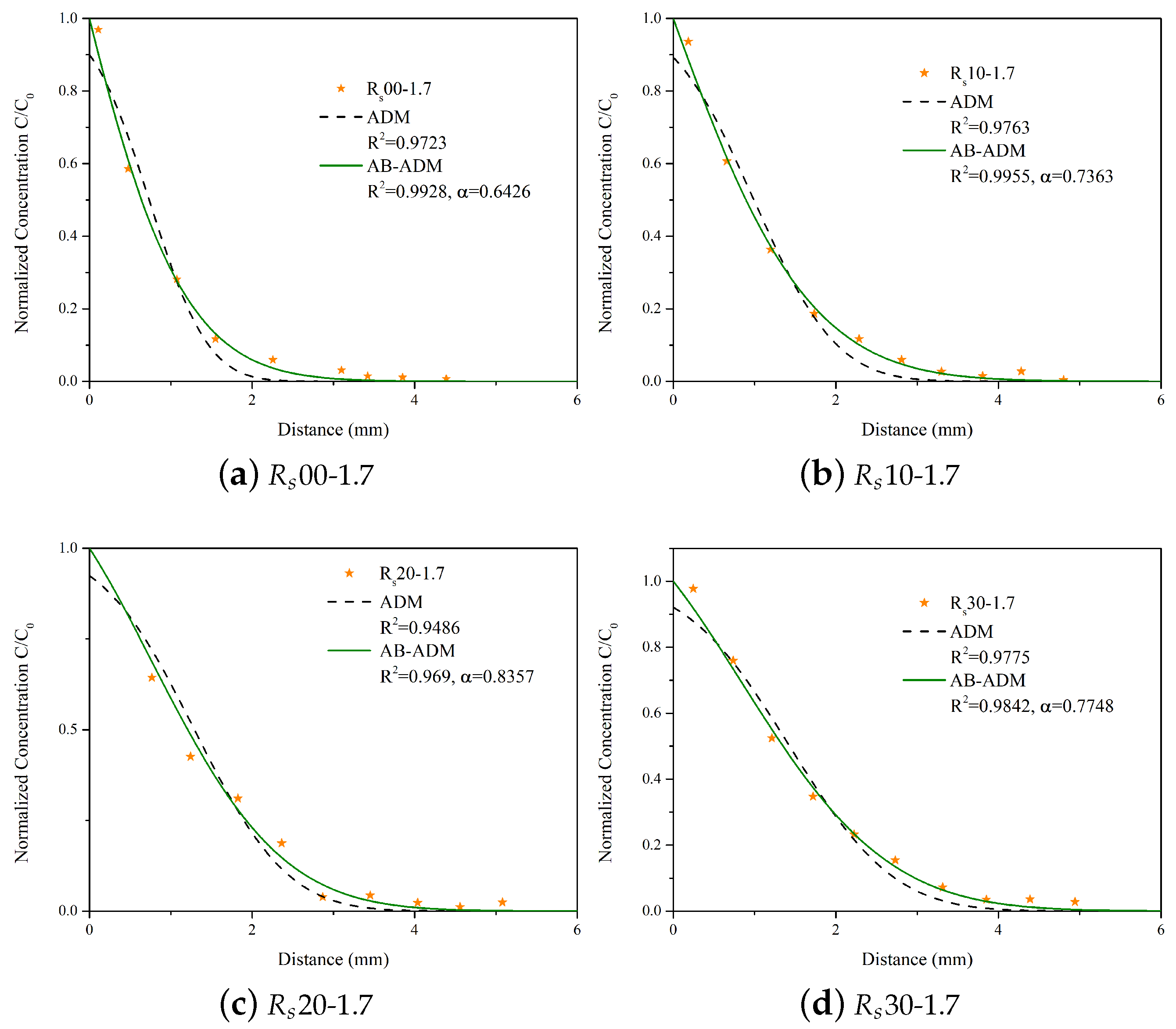
4. The AB-ADM with First-Order Decay
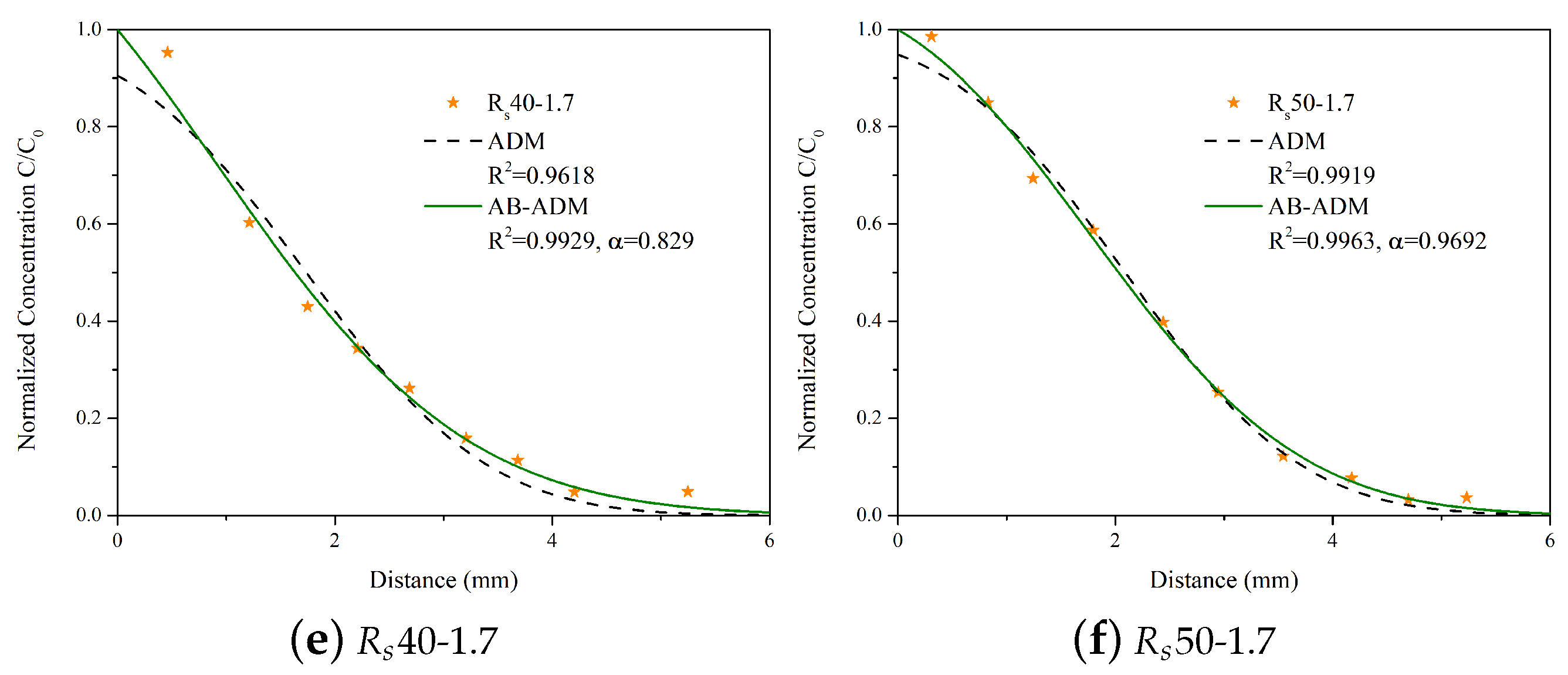
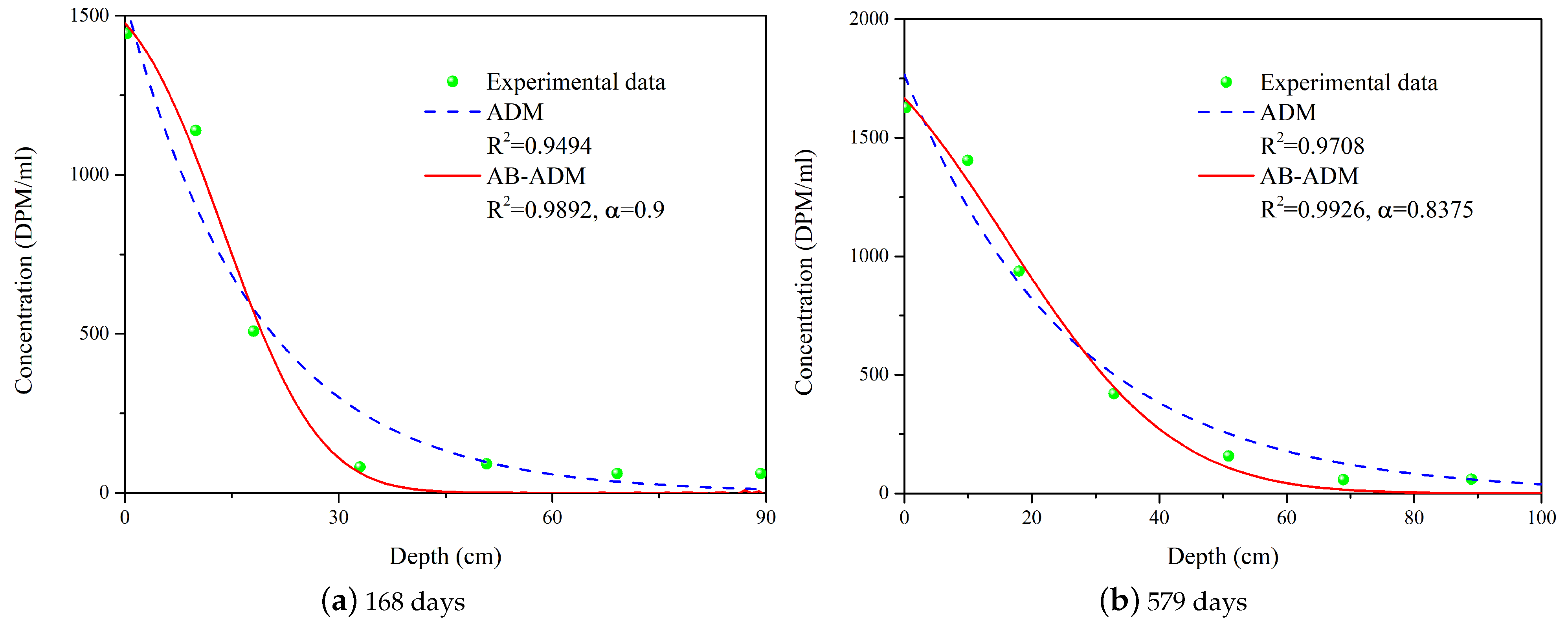
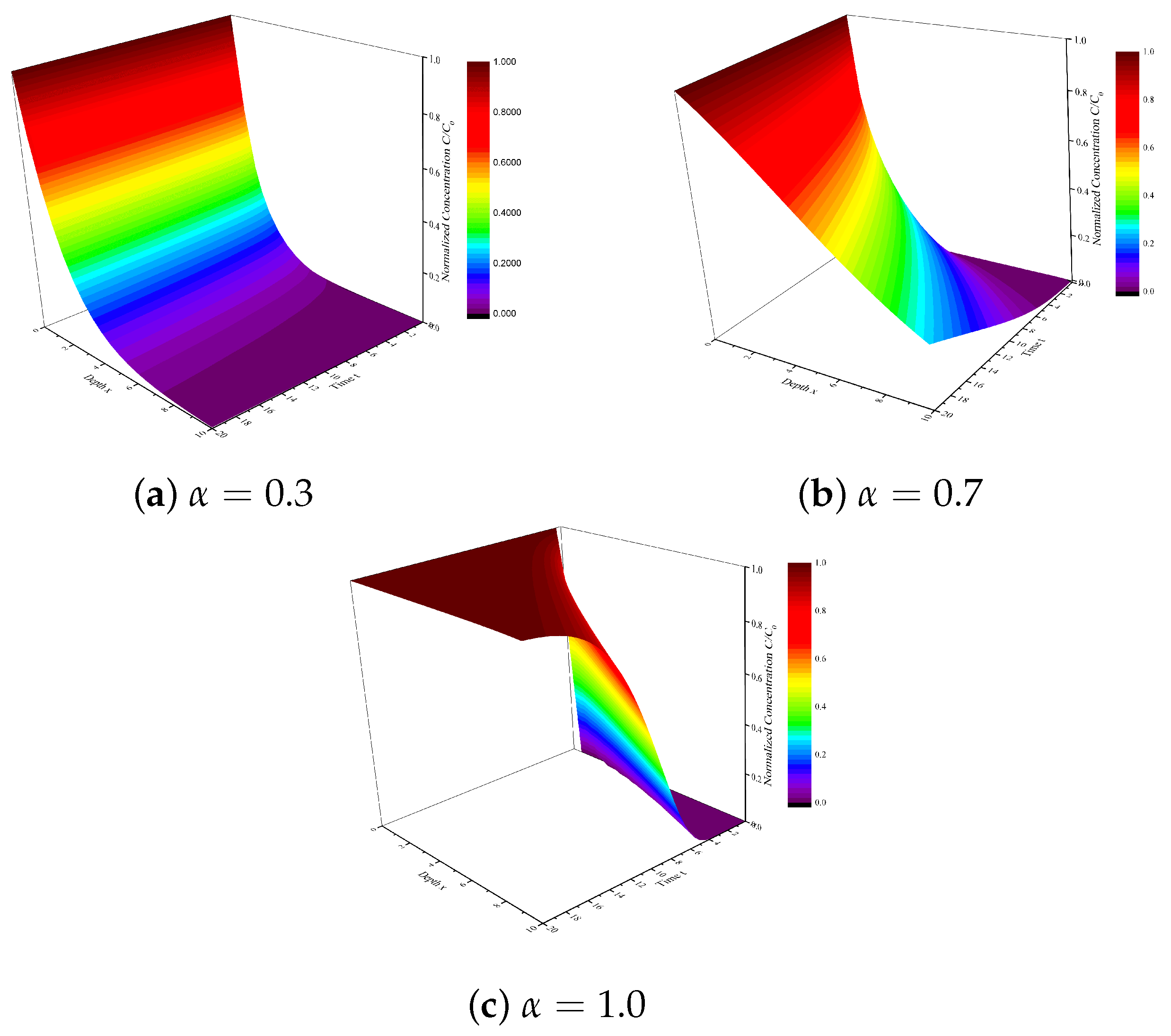
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADM | Advection–dispersion model |
| AB | Atangana–Baleanu |
| AB-ADMs | Atangana–Baleanu advection-dispersion models |
| L.T. | Laplace transform |
| I.L.T. | Inverse Laplace transform |
| F.S.T. | Fourier sine transform |
| I.F.S.T. | Inverse Fourier sine transform |
Appendix A. Integral Transforms
References
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Zheng, C.M.; Bennett, G. Applied Contaminant Transport Modeling; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Medved’, I.; Černý, R. Modeling of radionuclide transport in porous media: A review of recent studies. J. Nucl. Mater. 2019, 526, 151765. [Google Scholar] [CrossRef]
- Ajayi, I.R.; Fischer, H.W.; Burak, A.; Qwasmeh, A.; Tabot, B. Concentration and vertical distribution of 137Cs in the undisturbed soil of southwestern Nigeria. Health Phys. 2007, 92, 73. [Google Scholar] [CrossRef]
- Krsti, D.; Nikezi, D.; Stevanovi, N.; Jeli, M. Vertical profile of 137Cs in soil. Appl. Radiat. Isot. 2004, 61, 1487–1492. [Google Scholar] [CrossRef]
- Pang, L.; Goltz, M.; Close, M. Application of the method of temporal moments to interpret solute transport with sorption and degradation. J. Contam. Hydrol. 2003, 60, 123–134. [Google Scholar] [CrossRef]
- Casey, F.; Ong, S.K.; Horton, R. Degradation and transformation of trichloroethylene in miscible-displacement experiments through zerovalent metals. Environ. Sci. Technol. 2000, 34, 5023–5029. [Google Scholar] [CrossRef]
- Chen, T.; Sun, M.; Li, C.; Tian, W.; Liu, X.; Wang, L.; Wang, X.; Liu, C. The influence of temperature on the diffusion of 125I in Beishan granite. Int. J. Chem. Asp. Nucl. Sci. Technol. 2010, 98, 301–305. [Google Scholar] [CrossRef]
- Chen, T.; Li, C.; Liu, X.Y.; Wang, L. Migration study of iodine in Beishan granite by a column method. J. Radioanal. Nucl. Chem. 2013, 298, 219–225. [Google Scholar] [CrossRef]
- Zhang, X.X.; Crawford, J.W.; Deeks, L.K.; Stutter, M.I.; Bengough, A.G.; Young, I.M. A mass balance based numerical method for the fractional advection-dispersion equation: Theory and application. Water Resour. Res. 2005, 41, 62–75. [Google Scholar] [CrossRef]
- Hatano, Y.; Hatano, N. Dispersive transport of ions in column experiments: An explanation of long-tailed profiles. Water Resour. Res. 1998, 34, 1027–1034. [Google Scholar] [CrossRef]
- Raveh-Rubin, S.; Edery, Y.; Dror, I.; Berkowitz, B. Nickel migration and retention dynamics in natural soil columns. Water Resour. Res. 2015, 51, 7702–7722. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2010. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Chen, K.W.; Zhan, H.B.; Yang, Q. Fractional models simulating non-Fickian behavior in four stage single well push pull tests. Water Resour. Res. 2017, 53, 9528–9545. [Google Scholar] [CrossRef]
- Yang, S.; Song, H.C.; Zhou, H.W.; Xie, S.L.; Zhang, L.; Zhou, W.T. A fractional derivative insight into full-stage creep behavior in deep coal. Fractal Fract. 2025, 9, 473. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.G.; Li, X. Fractional Derivative Modeling in Mechanics and Engineering; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Yang, S.; Jia, W.H.; Xie, S.L.; Wang, H.C.; An, L. Fractional modeling of deep coal rock creep considering strong time-dependent behavior. Mathematics 2025, 13, 3247. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. Ann. Geophys. 1966, 19, 383–393. [Google Scholar] [CrossRef]
- Zhou, H.W.; Yang, S. Fractional derivative approach to non-Darcian flow in porous media. J. Hydrol. 2018, 566, 910–918. [Google Scholar] [CrossRef]
- Benson, D.A.; Meerschaert, M.M.; Revielle, J. Fractional calculus in hydrologic modeling: A numerical perspective. Adv. Water Resour. 2013, 51, 479–497. [Google Scholar] [CrossRef]
- Caputo, M.; Plastino, W. Diffusion in porous layers with memory. Geophys. J. Int. 2004, 158, 385–396. [Google Scholar] [CrossRef]
- Caputo, M. Diffusion of fluids in porous media with memory. Geothermics 1999, 28, 113–130. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Sheikh, N.A.; Ali, F.; Khan, I.; Saqib, M. A modern approach of Caputo–Fabrizio time-fractional derivative to MHD free convection flow of generalized second-grade fluid in a porous medium. Neural Comput. Appl. 2018, 30, 1865–1875. [Google Scholar] [CrossRef]
- Wei, Q.; Zhou, H.W.; Yang, S. Non-Darcy flow models in porous media via Atangana-Baleanu derivative. Chaos Solitons Fractals 2020, 141, 110335. [Google Scholar] [CrossRef]
- Khan, M.A.; Hammouch, Z.; Baleanu, D. Modeling the dynamics of hepatitis E via the Caputo–Fabrizio derivative. Math. Model. Nat. Phenom. 2019, 14, 311. [Google Scholar] [CrossRef]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. A fractional differential equation model for the COVID-19 transmission by using the Caputo–Fabrizio derivative. Adv. Differ. Equ. 2020, 2020, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Yu, Y.J.; Deng, Z.C. Fractional order theory of cattaneo-type thermoelasticity using new fractional derivatives. Appl. Math. Model. 2020, 87, 731–751. [Google Scholar] [CrossRef]
- Wei, Q.; Yang, S.; Zhou, H.W.; Zhang, S.Q.; Li, X.N.; Hou, W. Fractional diffusion models for radionuclide anomalous transport in geological repository systems. Chaos Solitons Fractals 2021, 146, 110863. [Google Scholar] [CrossRef]
- Sin, C.S.; Zheng, L.C.; Sin, J.S.; Liu, F.W.; Liu, L. Unsteady flow of viscoelastic fluid with the fractional K-BKZ model between two parallel plates. Appl. Math. Model. 2017, 47, 114–127. [Google Scholar] [CrossRef]
- Kundu, S.; Ghoshal, K. Effects of non-locality on unsteady nonequilibrium sediment transport in turbulent flows: A study using space fractional ADE with fractional divergence. Appl. Math. Model. 2021, 96, 617–644. [Google Scholar] [CrossRef]
- Mirza, I.A.; Akram, M.S.; Shah, N.A.; Imtiaz, W.; Chung, J.D. Analytical solutions to the advection-diffusion equation with Atangana-Baleanu time-fractional derivative and a concentrated loading. Alex. Eng. J. 2021, 60, 1199–1208. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling non-Fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44, RG2003. [Google Scholar] [CrossRef]
- Haggerty, R.; Gorelick, S.M. Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Water Resour. Res. 1995, 31, 2383–2400. [Google Scholar] [CrossRef]
- Schumer, R.; Benson, D.A.; Meerschaert, M.M.; Baeumer, B. Fractal mobile/immobile solute transport. Water Resour. Res. 2003, 39, 1296. [Google Scholar] [CrossRef]
- Jury, W.A.; Roth, K. Transfer Functions and Solute Movement Through Soil: Theory and Applications; Birkhauser Verlag: Basel, Switzerland, 1990. [Google Scholar]
- Marino, M.A. Distribution of contaminants in porous media flow. Water Resour. Res. 1974, 10, 1013–1018. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publication: New York, NY, USA, 1972. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and applications of fractional differential equations. In North-Holland Mathematics Studies; Elsevier Science: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Legua, M.P.; Morales, I.; Ruiz, L.M.S. The heaviside step function and matlab. In Computational Science and Its Applications—ICCSA 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1212–1221. [Google Scholar]
- Qian, J.Z.; Chen, Z.; Zhan, H.B.; Luo, S.H. Solute transport in a filled single fracture under non-darcian flow. Int. J. Rock Mech. & Min. Sci. 2011, 48, 132–140. [Google Scholar] [CrossRef]
- Ogata, A.; Banks, R. A Solution of the Differential Equation of Longitudinal Dispersion in Porous Media; Geological Survey Professional Paper 411 (A); U.S. Geological Survey: Reston, VA, USA, 1961. [Google Scholar] [CrossRef]
- Lang, Z.; Zhang, H.; Ming, Y.; Hang, C.; Ming, Z. Laboratory determination of migration of Eu(III) in compacted bentonite-sand mixtures as buffer/backfill material for high-level waste disposal. Appl. Radiat. Isot. 2013, 82, 139–144. [Google Scholar] [CrossRef]
- Genuchten, M.T.V.; Alves, W.J. Analytical Solutions of the One-Dimensional Convective-Dispersive Solute Transport Equation; Technical Bulletin No. 1661; US Department of Agriculture, Agricultural Research Service: Beltsville, MA, USA, 1982. [CrossRef]
- Toupiol, C.; Willingham, T.W.; Valocchi, A.J.; Werth, C.J.; Krapac, I.G.; Stark, T.D.; Daniel, D.E. Long-term tritium transport through field-scale compacted soil liner. J. Geotech. Geoenviron. Eng. 2002, 128, 640–650. [Google Scholar] [CrossRef][Green Version]
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications, 3rd ed.; Taylor & Francis Group: Abingdon, UK, 2015. [Google Scholar][Green Version]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Wei, Q.; Xie, S.; Zhou, H.; An, L. Time-Fractional Differential Operator Modeling of Contaminant Transport with Adsorption and Decay. Fractal Fract. 2025, 9, 671. https://doi.org/10.3390/fractalfract9100671
Yang S, Wei Q, Xie S, Zhou H, An L. Time-Fractional Differential Operator Modeling of Contaminant Transport with Adsorption and Decay. Fractal and Fractional. 2025; 9(10):671. https://doi.org/10.3390/fractalfract9100671
Chicago/Turabian StyleYang, Shuai, Qing Wei, Senlin Xie, Hongwei Zhou, and Lu An. 2025. "Time-Fractional Differential Operator Modeling of Contaminant Transport with Adsorption and Decay" Fractal and Fractional 9, no. 10: 671. https://doi.org/10.3390/fractalfract9100671
APA StyleYang, S., Wei, Q., Xie, S., Zhou, H., & An, L. (2025). Time-Fractional Differential Operator Modeling of Contaminant Transport with Adsorption and Decay. Fractal and Fractional, 9(10), 671. https://doi.org/10.3390/fractalfract9100671






