Quantitative Characterization of Fractals and Curvatures in Complex Geological Structures of Wugou Coal Mine, Huaibei Coalfield
Abstract
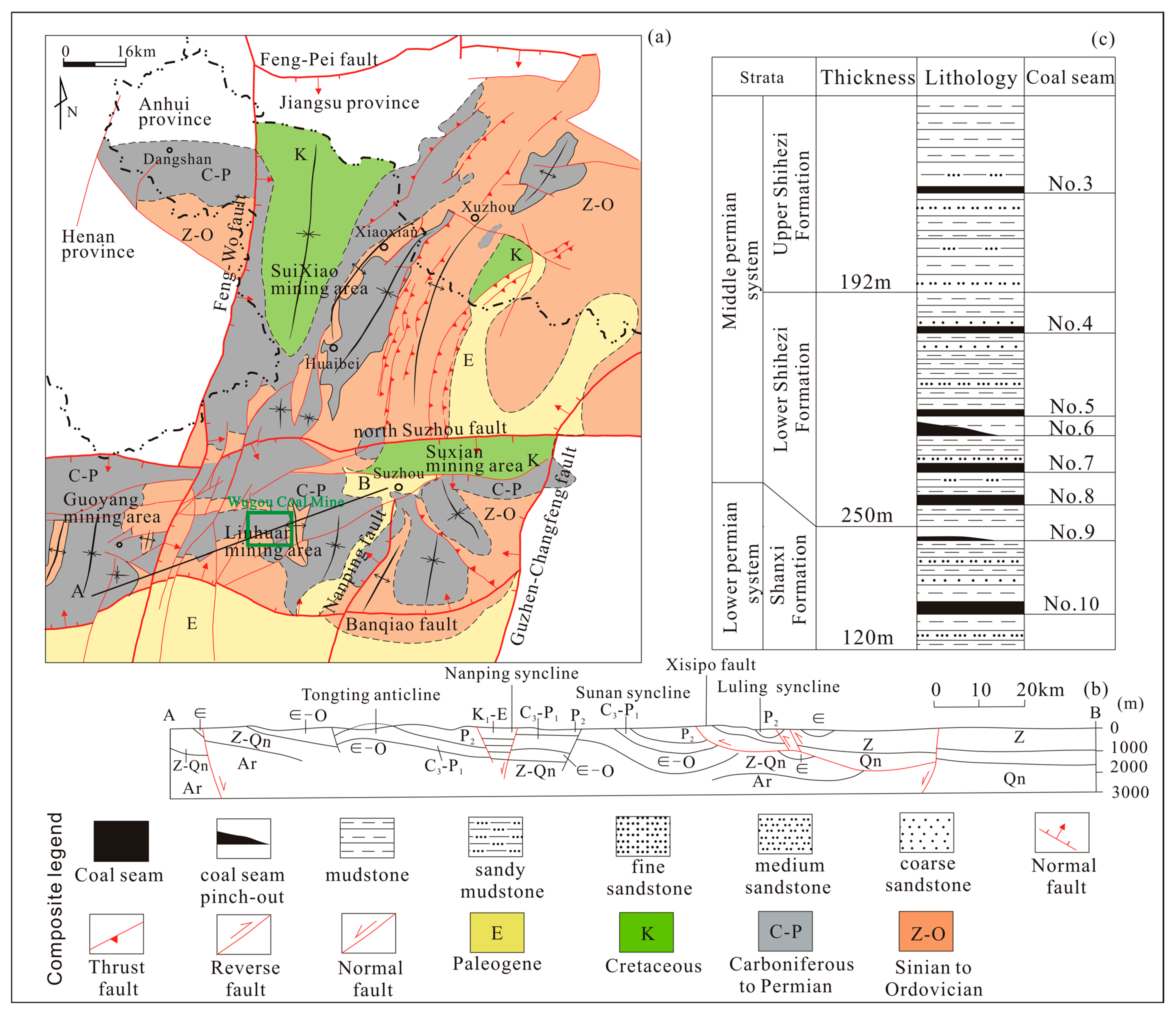
1. Introduction
2. Research and Computational Methods
2.1. Fractal Dimension and Calculation
- (1)
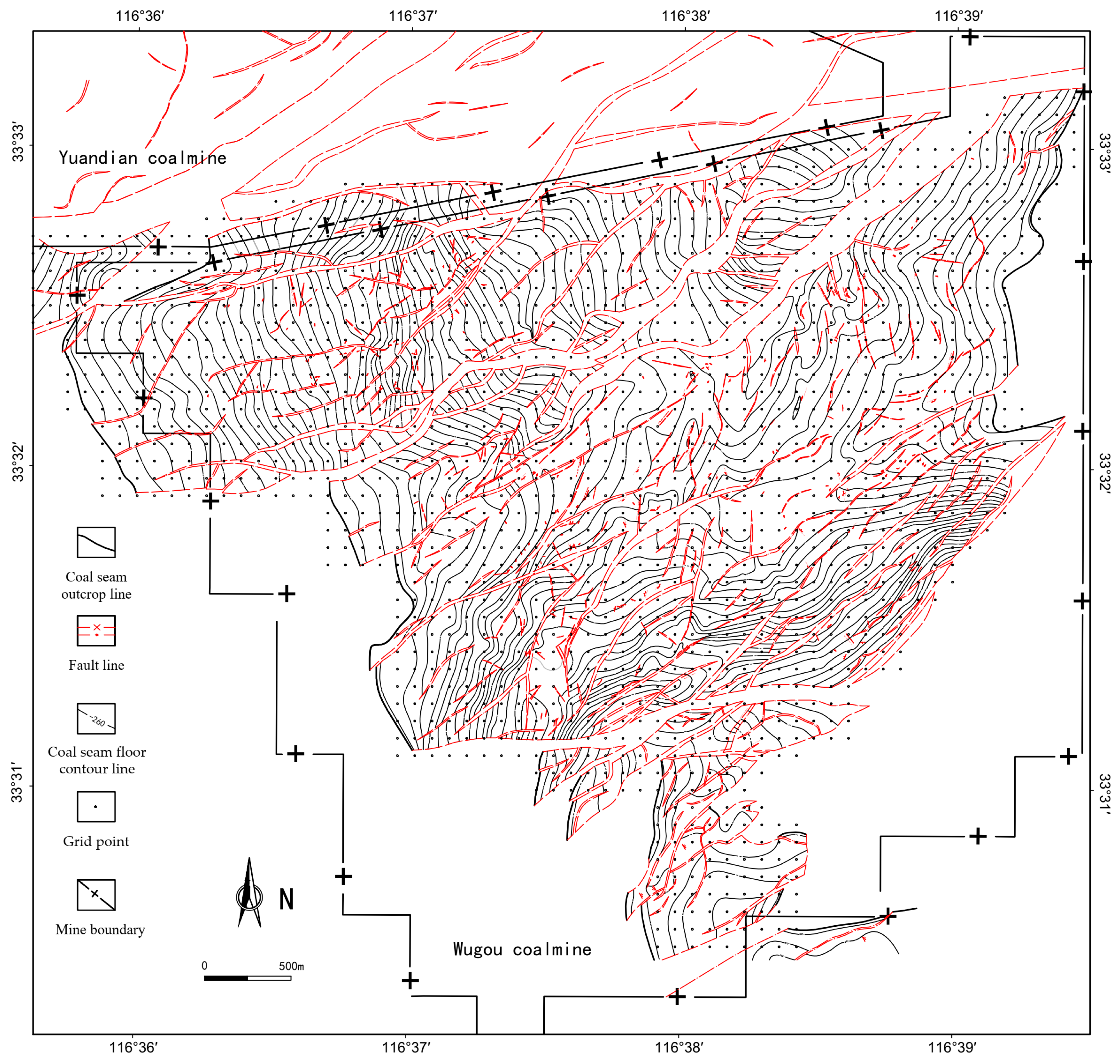
- Define the study object: Based on the contour map of the No. 10 coal seam floor, update the fault-coal intersection lines and fault trace maps using the latest exploration research results to clarify the fault development range for calculating the fractal capacity dimension.
- (2)
- Set the initial scale: Select an appropriate initial grid size ε (i.e., the side length of each grid cell) as the starting point. This scale should be chosen according to the size and complexity of the study object to ensure full coverage and capture of detailed features. The analysis target in this study exhibits a highly complex fractal structure, requiring finer grid sizes to ensure sufficient resolution and evaluation accuracy. However, finer grids significantly increase computational workload exponentially.
- (3)
- Overlay the grid: Cover the fault–coal intersection lines and fault traces with a square grid of side length ε. Ensure the grid fully covers the study object and that its boundaries align appropriately with the extent of the structures.
- (4)
- Count the number of boxes: Count the number of grid cells (boxes) N(ε) that contain any part of the fractal pattern.
- (5)
- Change the scale and repeat: Gradually reduce the grid size (i.e., increase the grid density) and repeat the steps above (re-cover the object and count the number of boxes). By varying the scale multiple times and collecting data, a series of N(ε) values corresponding to different scales can be obtained.
- (6)
- Calculate the fractal dimension: Finally, use Formula (1) to calculate the fractal dimension Dk, which is the target capacity dimension. Since it is practically impossible to take ε to zero, Dk is typically estimated by observing four gradually reduced values of ε and their corresponding N(ε) values, plotting lnN(ε) against lnε, and estimating the slope of the linear fit. The negative of this slope provides an approximate value of Dk.
- (7)
- Validate the results: The calculated results must be verified and evaluated. Reliability can be assessed by examining whether data points at different scales closely align with the fitted straight line. Comparison with results from other methods can also help confirm the accuracy of the fractal dimension.
2.2. Calculation Method of Structural Curvature
3. Results and Discussion
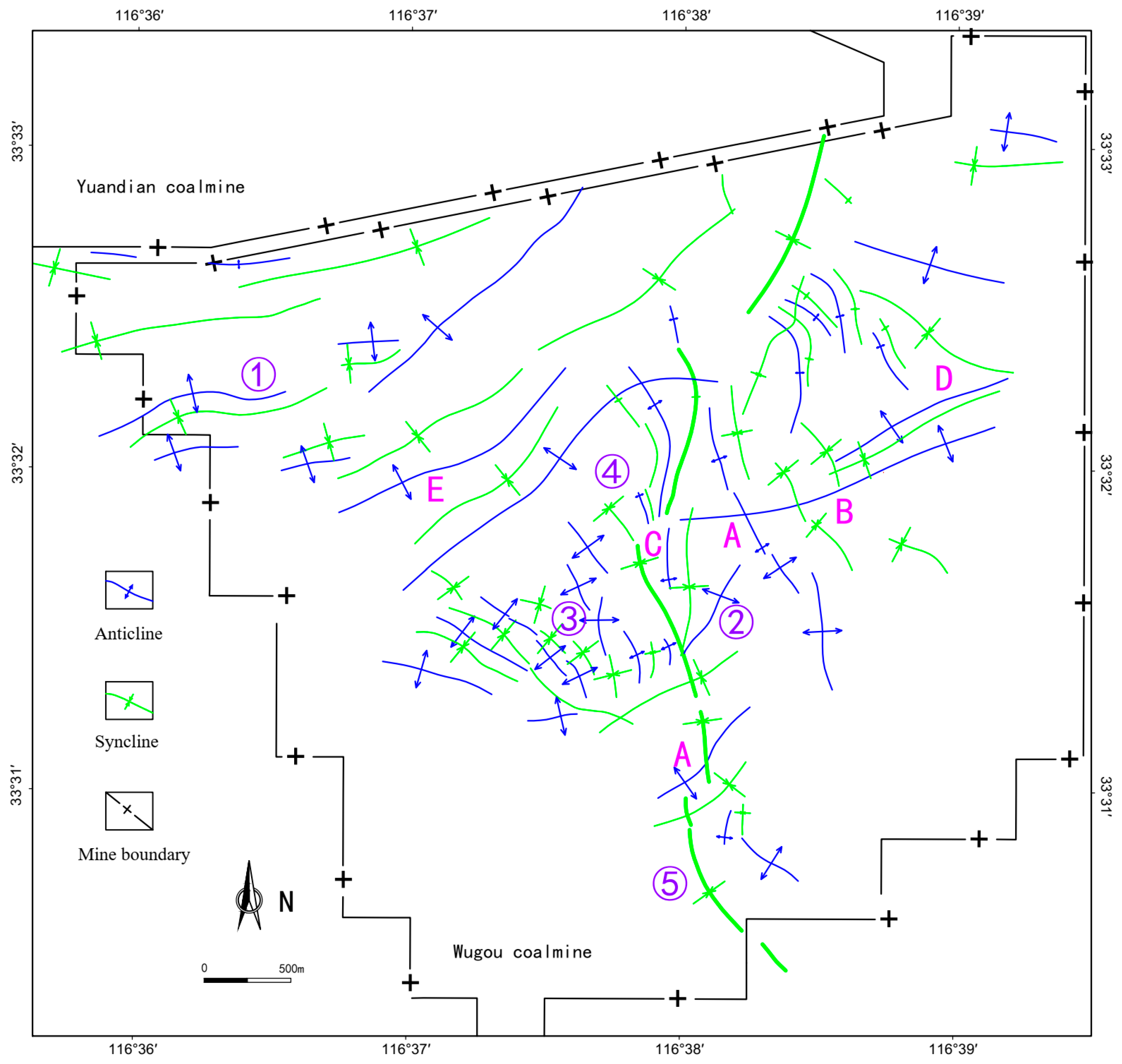
3.1. Characteristics of Structural Development
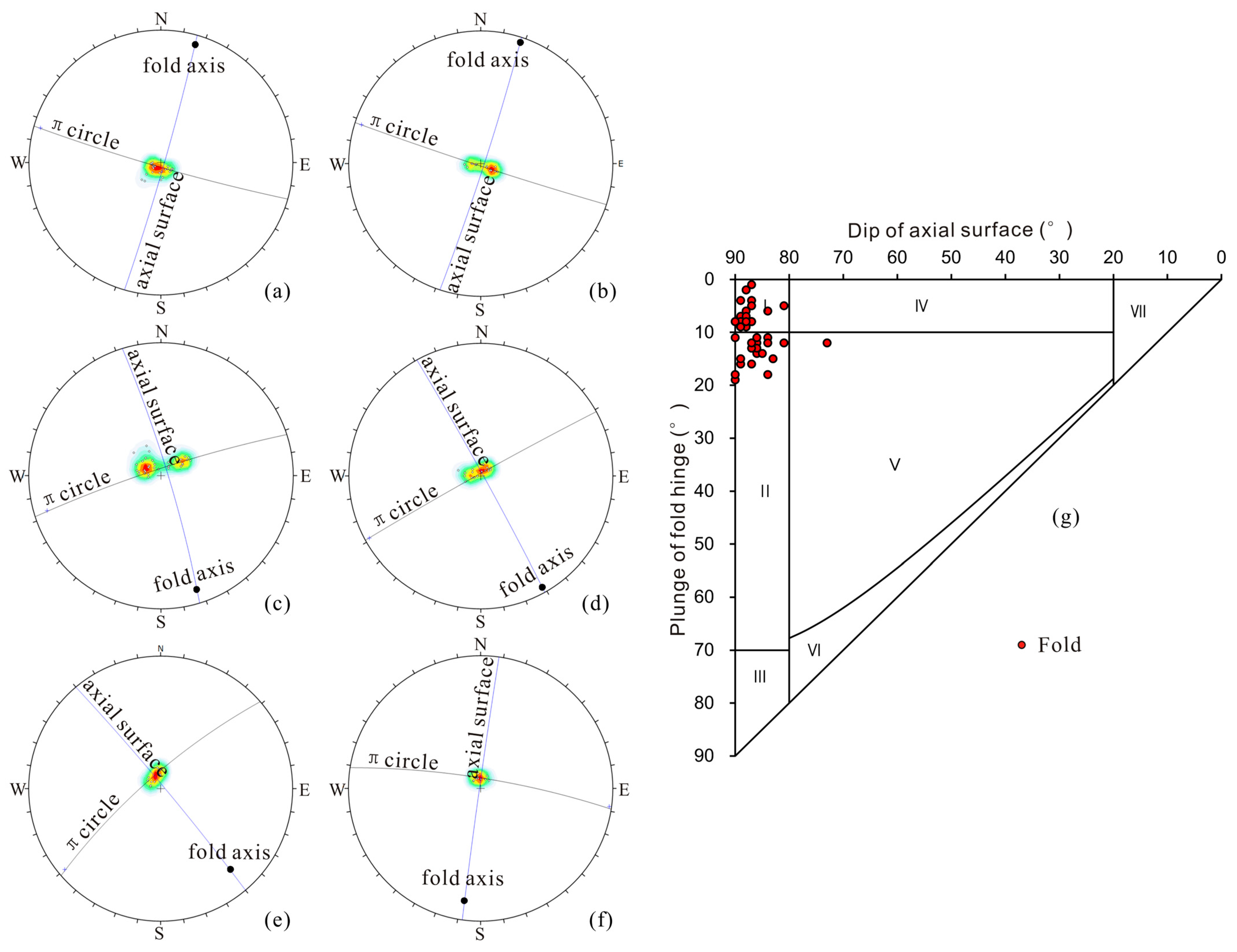
3.1.1. Fold Morphology and Combination
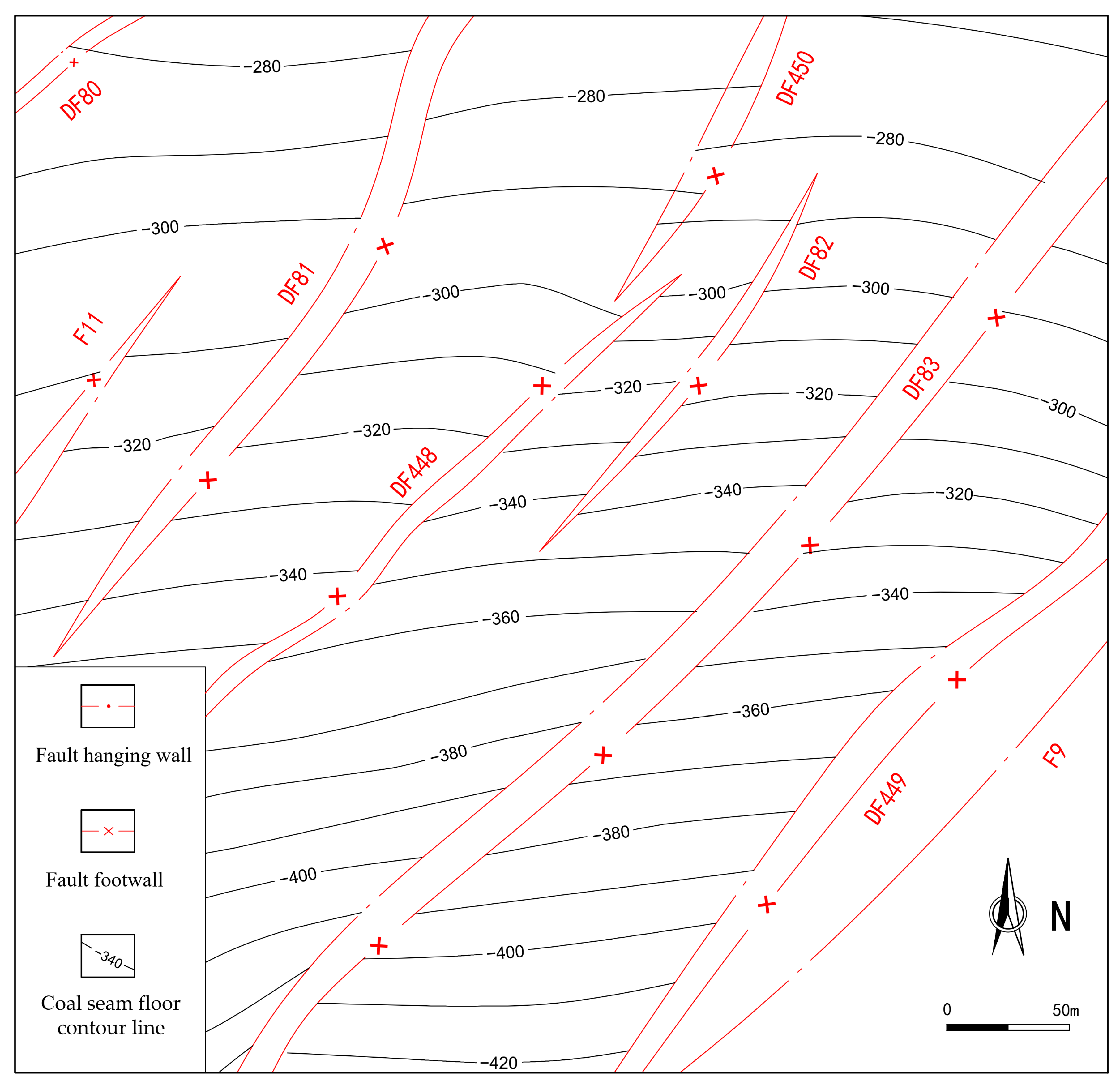
3.1.2. Characteristics of Fault Development
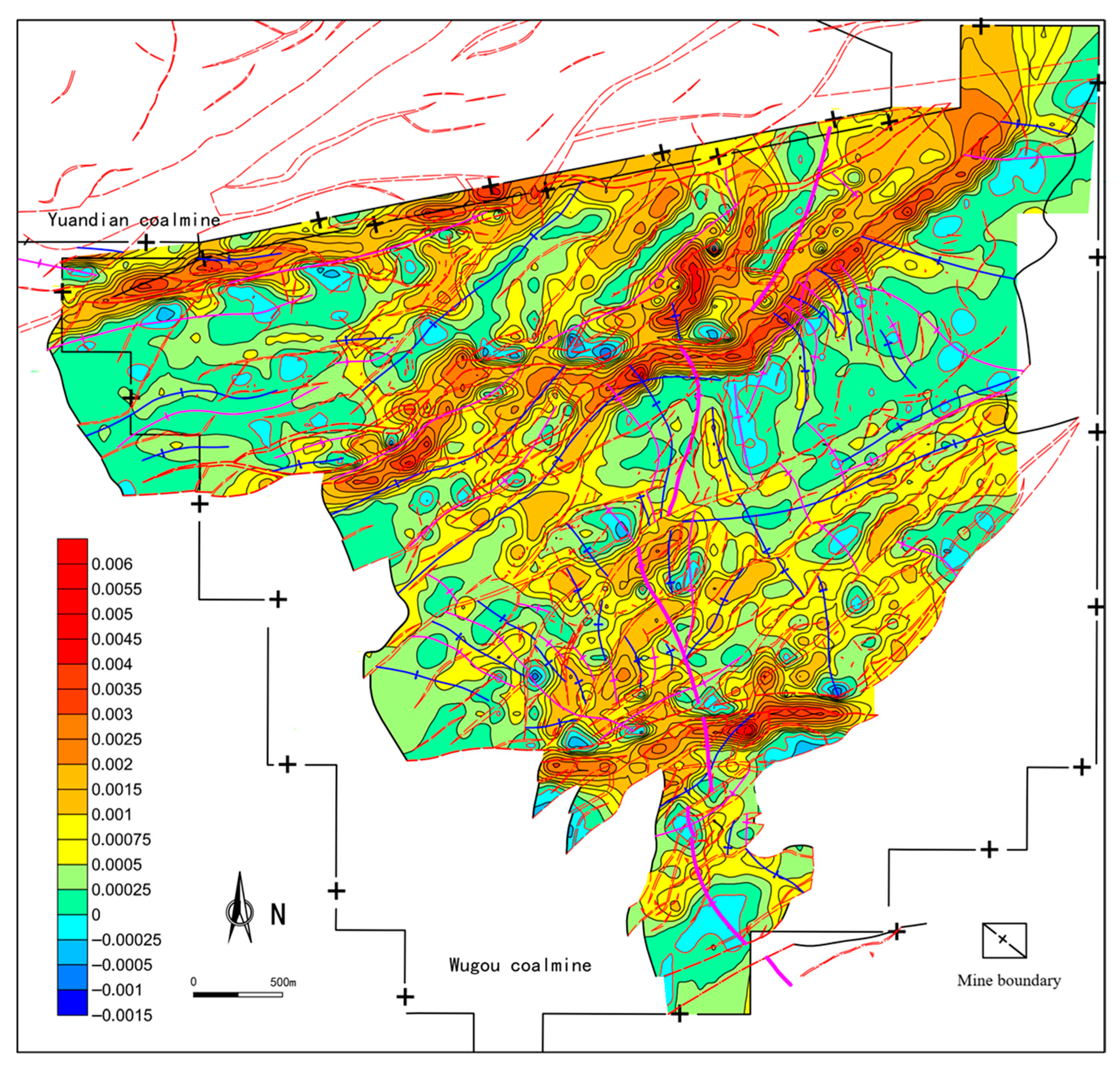
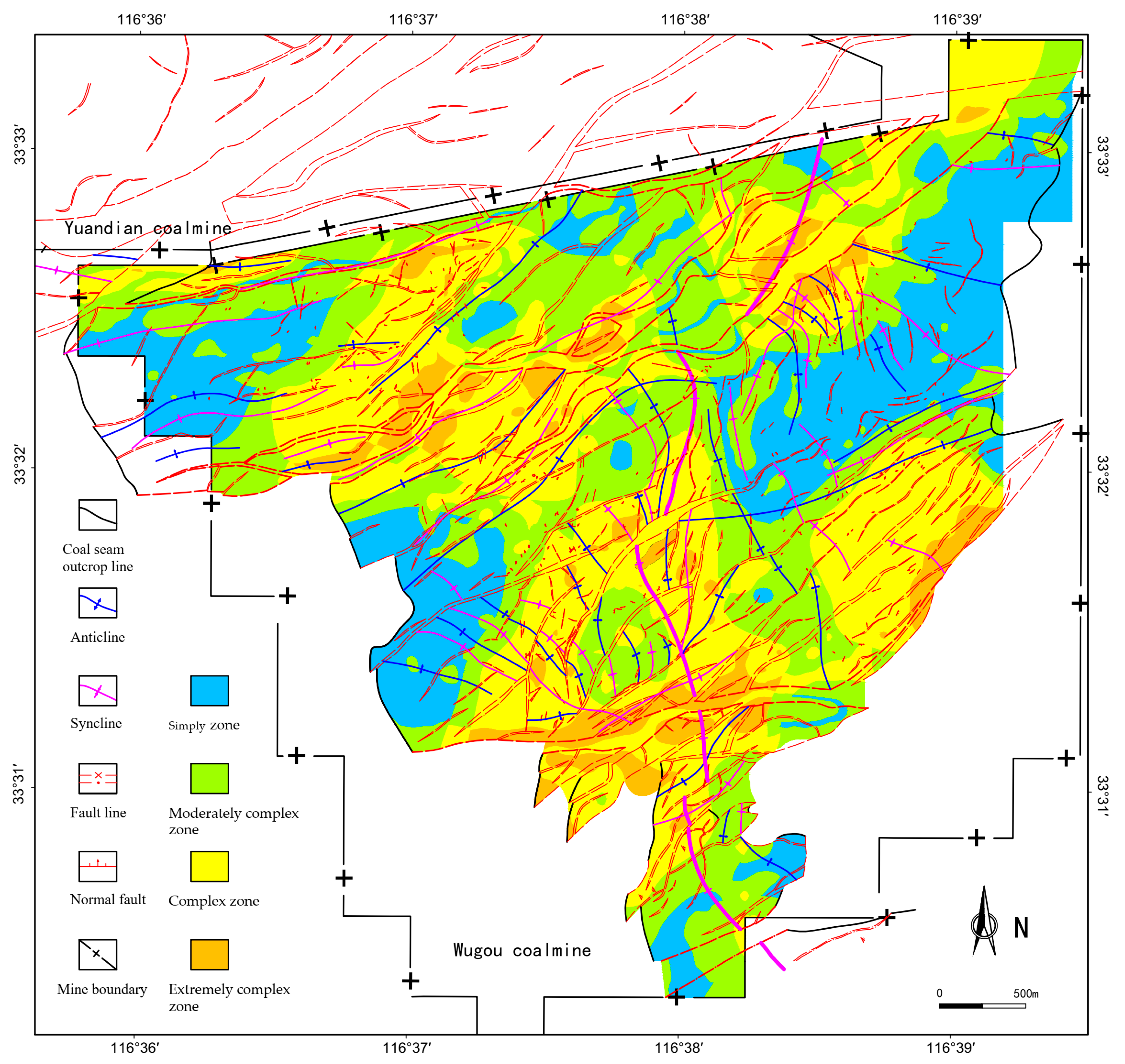
3.2. Fractal Quantitative Evaluation
3.3. Quantitative Evaluation of Structural Curvature
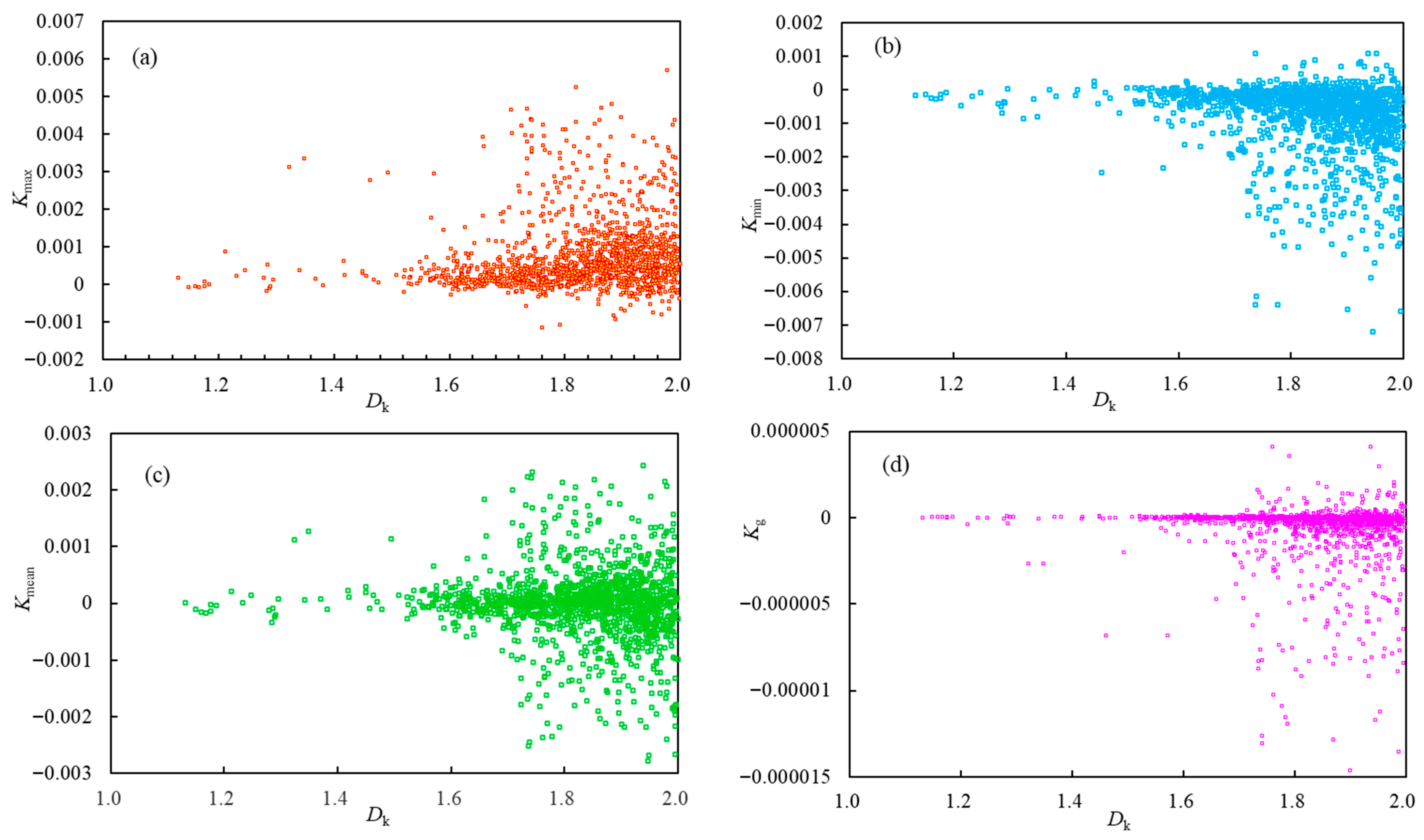
3.3.1. Evaluation of Maximum and Minimum Curvature
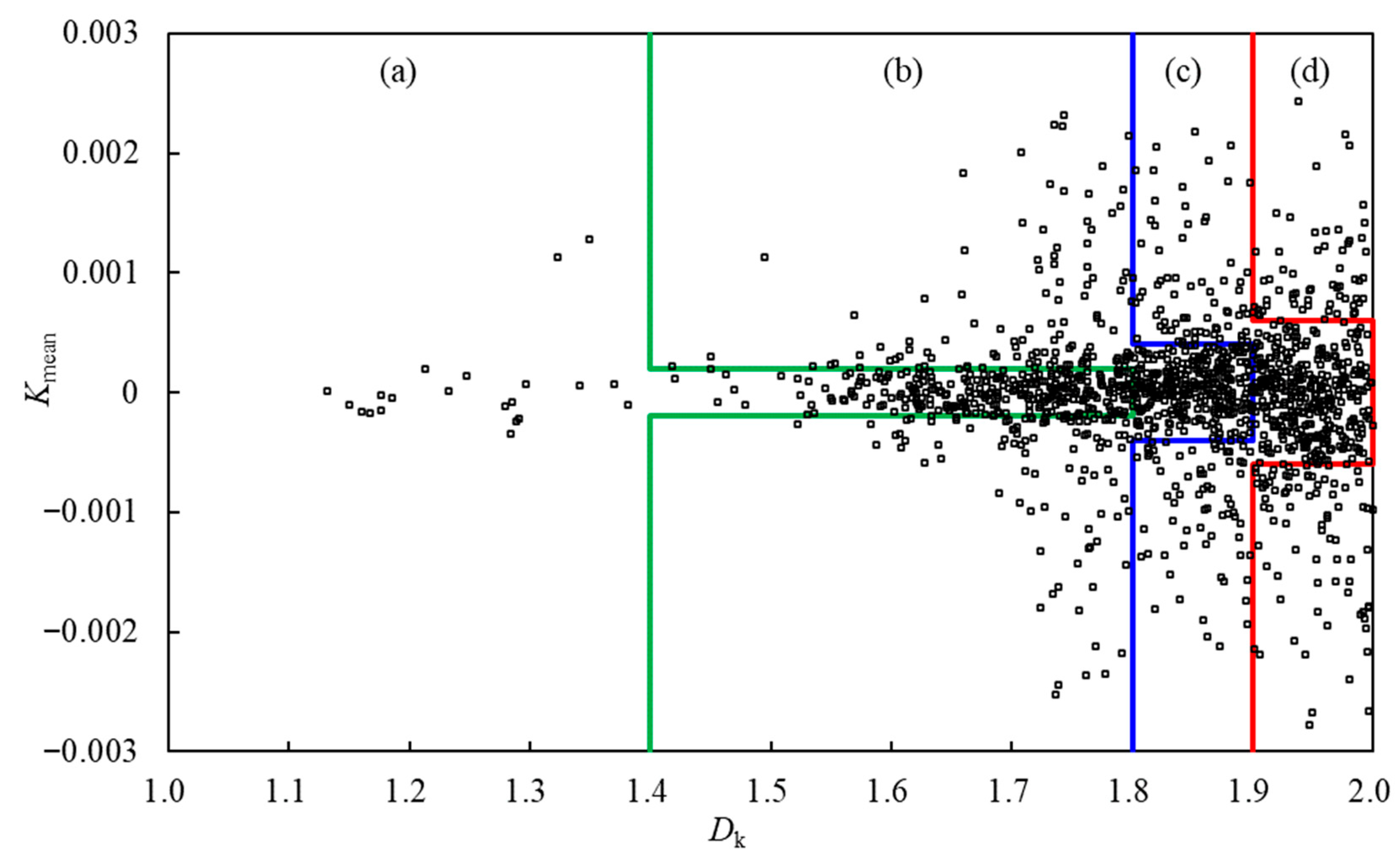
3.3.2. Evaluation of Mean Curvature
3.3.3. Evaluation of Gaussian Curvature
3.4. Comprehensive Evaluation of Structural Complexity
4. Conclusions
- (1)
- The geological structure of Wugou Coal Mine is complex and highly deformed. It is a composite superimposed fold structure combination with dense faults. The fold structure has a complex morphology and weak deformation. The parallel, branching, en echelon, brush-like, and arc-shaped folds combination types are observed. Superimposed folds are mainly classified into oblique-crossing, crossing, deflection, oblique-limiting, and enhancement types. The fold structures are products of four phases of tectonic deformation. Fault structures are exceptionally well-developed, dominated by normal faults that generally exhibit a step-like assemblage pattern. Parallel fault combinations are the most common planar fault type in the mine.
- (2)
- The fractal dimension effectively characterizes the development degree and distribution density of faults, but demonstrates limited capability in quantitatively characterizing fault scale, throw, and fold structures. The planar distribution of the capacity dimension (Dk) exhibits significant variation and distinct zonation. According to the fault capacity dimension values, the structural complexity of the study area is classified into four zones: an Extremely Complex Fault Zone (1.9 ≤ Dk < 2.0), a Complex Fault Zone (1.8 ≤ Dk < 1.9), a Moderately Developed Fault Zone (1.4 ≤ Dk < 1.8), and a Simply Developed Fault Zone (0 ≤ Dk < 1.4).
- (3)
- Different types of curvature parameters exhibit varying sensitivities to different structural types or structural positions. Maximum curvature and minimum curvature serve as effective indicators for characterizing anticlines, the footwalls of normal faults, synclines, and the hanging walls of normal faults, respectively. Their magnitudes are determined by fault throw and the degree of fold bending deformation, reflecting the influence scope and intensity of fold and fault structures. Mean curvature provides a comprehensive characterization of various structural types and positions. Gaussian curvature proves to be an effective indicator for quantifying coal seam deformation intensity and identifying superposed fold structures.
- (4)
- Based on the planar distribution and structural responses of curvature and fractal dimension, by combining the strengths of fractal analysis and curvature characterization, a fractal-curvature integrated evaluation model was developed to assess structural complexity. This model facilitates a high-resolution quantitative evaluation, delineating the geological structures of the Wugou Coal Mine into zones of extremely complex, complex, moderately complex, and simple structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bates, B.; McIntosh, J.; Lohse, K.; Brooks, P. Influence of groundwater flow paths, residence times and nutrients on the extent of microbial methanogenesis in coal beds: Powder River Basin, USA. Chem. Geol. 2011, 284, 45–61. [Google Scholar] [CrossRef]
- Ma, T.; Liu, J.; Fu, J.; Wu, B. Drilling and completion technologies of coalbed methane exploitation: An overview. Int. J. Coal Sci. Technol. 2022, 9, 1–31. [Google Scholar] [CrossRef]
- Bachu, S.; Michael, K. Possible controls of hydrogeological and stress regimes on the producibility of coalbed methane in Upper Cretaceous-Tertiary strata of the Alberta Basin, Canada. AAPG Bull. 2003, 87, 1729–1754. [Google Scholar] [CrossRef]
- Karacan, C.; Goodman, G. Analyses of geological and hydrodynamic controls on methane emissions experienced in a Lower Kittanning coal mine. Int. J. Coal Geol. 2012, 98, 110–127. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Liu, D.; Yao, Y.; Li, J.; Qiu, Y. Geological controls on prediction of coalbed methane of No.3 coal seam in Southern Basin, North China. Int. J. Geol. 2011, 88, 101–112. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, S.; Hu, Z.; Shen, B.; Feng, D.; Zhang, J.; Ye, J.; Ma, C.; Dong, Z. Characteristics and controlling factors of coal-measure unconventional reservoirs—A case study of the Carboniferous-Permian in the Ordos Basin. Unconvent. Resour. 2025, 6, 100153. [Google Scholar]
- Jiang, B.; Qin, Y.; Ju, Y.; Wang, J. Research on tectonic stress field of generate and reservoir of coalbed methane. J. China Univ. Min. Technol. 2005, 34, 565–569, (In Chinese with English abstract). [Google Scholar]
- Wang, J.; Jiang, B. Using Fuzzy Artificial Neural Network to Evaluate the Mine Structure. J. China Univ. Min. Technol. 2005, 34, 609–612, (In Chinese with English abstract). [Google Scholar]
- Ju, Y.; Wang, G.; Jiang, B.; Hou, Q. Microcosmic analysis of ductile shearing zones of coal seams of brittle deformation domain in superficial lithosphere. Sci. China Earth Sci. 2004, 47, 393–404. [Google Scholar] [CrossRef]
- Ju, Y.; Wei, M.; Xue, C. Control of basin-mountain evolution on the occurrence of deep coal and coalbed methane in North China. J. China Univ. Min. Technol. 2011, 40, 390–398, (In Chinese with English abstract). [Google Scholar]
- Fan, C.; Li, S.; Luo, M.; Du, W.; Yang, Z. Coal and gas outburst dynamic system. Int. J. Min. Sci. Technol. 2017, 27, 49–55. [Google Scholar] [CrossRef]
- Li, H.; Ogawa, Y. Pore structure of sheared coals and related coalbed methane. Environ. Geol. 2001, 40, 1455–1461. [Google Scholar] [CrossRef]
- Li, M.; Jiang, B.; Lin, S.; Wang, J.; Ji, M.; Qu, Z. Tectonically deformed coal types and pore structures in Puhe and Shanchahe coal mines in western Guizhou. Int. J. Min. Sci. Technol. 2011, 21, 353–357. [Google Scholar] [CrossRef]
- Li, M.; Jiang, B.; Lin, S.; Lan, F.; Wang, J. Structural controls on coalbed methane reservoirs in Faer coal mine, Southwest China. J. Earth Sci. 2013, 24, 437–448. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, B.; Li, M.; Qu, Z.; Wang, L.; Li, L. Structural control on pore-fracture characteristics of coals from Xinjing coal mine, northeastern Qinshui basin, China. Arab. J. Geosci. 2015, 8, 4421–4431. [Google Scholar] [CrossRef]
- Li, J.; Min, Z.; Chen, X.; Li, D.; Wang, S.; Song, T. Connotation analyses, source-reservoir assemblage types and development potential of unconventional hydrocarbon in China. Acta. Pet. Sin. 2016, 2, 135–148. [Google Scholar]
- Keshavarz, A.; Sakurovs, R.; Grigore, M.; Sayyafzadeh, M. Effect of maceral composition and coal rank on gas diffusion in Australian coals. Int. J. Coal Geol. 2017, 173, 65–75. [Google Scholar] [CrossRef]
- Li, R.; Wang, Q.; Wang, X.; Liu, X.; Li, J.; Zhang, Y. Relationship analysis of the degree of fault complexity and the water irruption rate, based on fractal theory. Mine Water Environ. 2017, 36, 18–23. [Google Scholar] [CrossRef]
- Zhang, G.; Guo, J.; Xu, B.; Xu, L.; Dai, Z.; Yin, S.; Mohamad, R.S. Quantitative analysis and evaluation of coal mine geological structures based on fractal theory. Energies 2021, 14, 1925. [Google Scholar] [CrossRef]
- Guarnieri, P. Regional strain derived from fractal analysis applied to strike slip fault systems in NW Sicily. Chaos Solitons Fractals 2002, 14, 71–76. [Google Scholar] [CrossRef]
- Carpinteri, A.; Paggi, M. Size scale effects on strength, friction and fracture energy of faults: A unified interpretation according to fractal geometry. Rock Mech. Rock Eng. 2008, 41, 735–746. [Google Scholar] [CrossRef]
- Sengupta, P.; Nath, S.K.; Thingbaijam, K.K.S.; Mistri, S. Fractal analysis of major faults in India on a regional scale. J. Geol. Soc. India 2011, 78, 226. [Google Scholar] [CrossRef]
- Yang, B.; Yuan, J.; Duan, L.; Liu, Q. Using GIS and fractal theory to evaluate degree of fault complexity and water yield. Mine Water Environ. 2018, 38, 261–267. [Google Scholar] [CrossRef]
- Aviles, C.A.; Scholz, C.H.; Boatwright, J. Fractal analysis applied to characteristic segments of the San Andreas fault. J. Geophys. Res. Solid Earth 1987, 92, 331–344. [Google Scholar] [CrossRef]
- Hirata, T. Fractal dimension of fault systems in Japan: Fractal structure in rock fracture geometry at various scales. Pure Appl. Geophys. 1989, 131, 157–170. [Google Scholar] [CrossRef]
- Sukmono, S.; Zen, M.T.; Kadir, W.G.A.; Hendrajaya, L.; Santoso, D.; Dubois, J. Fractal geometry of the Sumatra active fault system and its geodynamical implications. J. Geodyn. 1996, 22, 1–9. [Google Scholar] [CrossRef]
- Pérez, L.R.; Paredes, C.; Muñoz, M.A. Relationship between the fractal dimension anisotropy of the spatial faults distribution and the paleostress fields on a Variscan granitic massif (Central Spain): The F parameter. J. Struct. Geol. 2005, 27, 663–677. [Google Scholar] [CrossRef]
- Carpinteri, A.; Paggi, M. A fractal interpretation of size scale effects on strength, friction and fracture energy of faults. Chaos Soliton Fractals 2009, 39, 540–546. [Google Scholar] [CrossRef]
- Babanouri, N.; Nasab, S.K.; Sarafrazi, S. A hybrid particle swarm optimization and multi-layer perceptron algorithm for bivariate fractal analysis of rock fractures roughness. Int. J. Rock Mech. Min. Sci. 2013, 60, 66–74. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, X.; Wang, J.; Lin, W.; Han, D.; Wang, C.; Li, Y.; Xiong, Y.; Zhang, X. Pore structure and fractal characteristics of coal-bearing Cretaceous Nenjiang shales from Songliao Basin, Northeast China. J. Nat. Gas Geosci. 2024, 9, 197–208. [Google Scholar] [CrossRef]
- Liu, Z.; Han, J.; Yang, H.; Lv, J.; Dong, S. A new model for coal gas seepage based on fracture-pore fractal structure characteristics. Int. J. Rock Mech. Min. Sci. 2024, 173, 105626. [Google Scholar] [CrossRef]
- Lisle, R.J. Detection of zones of abnormal strains in structures using Gaussian curvature analysis. AAPG Bull. 1994, 78, 1811–1819. [Google Scholar] [CrossRef]
- Ozkaya, S.I. QUADRO—A program to estimate principal curvatures of folds. Comput. Geosci. 2002, 28, 467–472. [Google Scholar] [CrossRef]
- Shen, J.; Fu, X.; Qin, Y.; Liu, Z. Control actions of structural curvature of coal-seam floor on coalbed gas in the NO.8 coal mine of Pingdingshan. J. China Coal Soc. 2010, 35, 586–589, (In Chinese with English abstract). [Google Scholar]
- Guo, C.; Xia, Y.; Wei, Z.; Sun, X.; Dai, G.; Wang, S.; Shen, J.; Ren, Y. Coalbed methane accumulation characteristics and type classification in Hancheng mining area. J. China Coal Soc. 2018, 43 (Suppl. S1), 192–202, (In Chinese with English abstract). [Google Scholar]
- Zhou, P.; Liang, L.; Bai, L.; Zeng, J. Study on the structural complexity of the yangmeishu syncline based on fractal theory. Nat. Gas Technol. Econ. 2019, 13, 25–27+80, (In Chinese with English abstract). [Google Scholar]
- Liu, J.; Yang, S.; Chen, N.; Zhao, X. Forecasting method of tectoclase in the igneous reservoirs using a curvature of the microtectonics. J. China Univ. Min. Technol. 2009, 38, 815–819, (In Chinese with English abstract). [Google Scholar]
- Jiang, B.; Qu, Z.; Wang, G.G.X.; Li, M. Effects of structural deformation on formation of coalbed methane reservoirs in Huaibei Coalfield, China. Int. J. Coal Geol. 2010, 82, 175–183. [Google Scholar] [CrossRef]
- Roberts, A. Curvature attributes and their application to 3D interpreted horizons. First Break 2001, 19, 85–100. [Google Scholar] [CrossRef]
- Anderson, J.G.C. Superposition of Caledonoid Folds on an older fold-system in the Dalradians of Malin Head. Geol. Mag. 1955, 92, 83–84. [Google Scholar] [CrossRef]
- Ramsay, G.J. Geology of Folds. Nature 1968, 217, 293. [Google Scholar] [CrossRef]
- Bühn, B.; Stanistreet, L.G.; Charlesworth, E.G. Fold shape variation controlling interference mechanisms and patterns during oblique fold superpositions in the Damara Orogen, eastern Namibia. Ann. Tectonol. 1993, 7, 113–128. [Google Scholar]
- Mazzoli, S.; Carnemolla, S. Effects of the superposition of compaction and tectonic strain during folding of a multilayer sequence-model and observations. J. Struct. Geol. 1993, 15, 277–291. [Google Scholar] [CrossRef]
- Zhou, P.; Chen, X.; Zhang, Y.; Shao, Z.; Li, B.; Jiang, T.; Xu, D. Obstacle leads to local stress reorientation: Insights from the formation mechanism of the Maiduoshan superimposed fold in the Weiningbeishan fold-thrust belt, NW China. J. Asian Earth Sci. 2024, 276, 103361. [Google Scholar] [CrossRef]

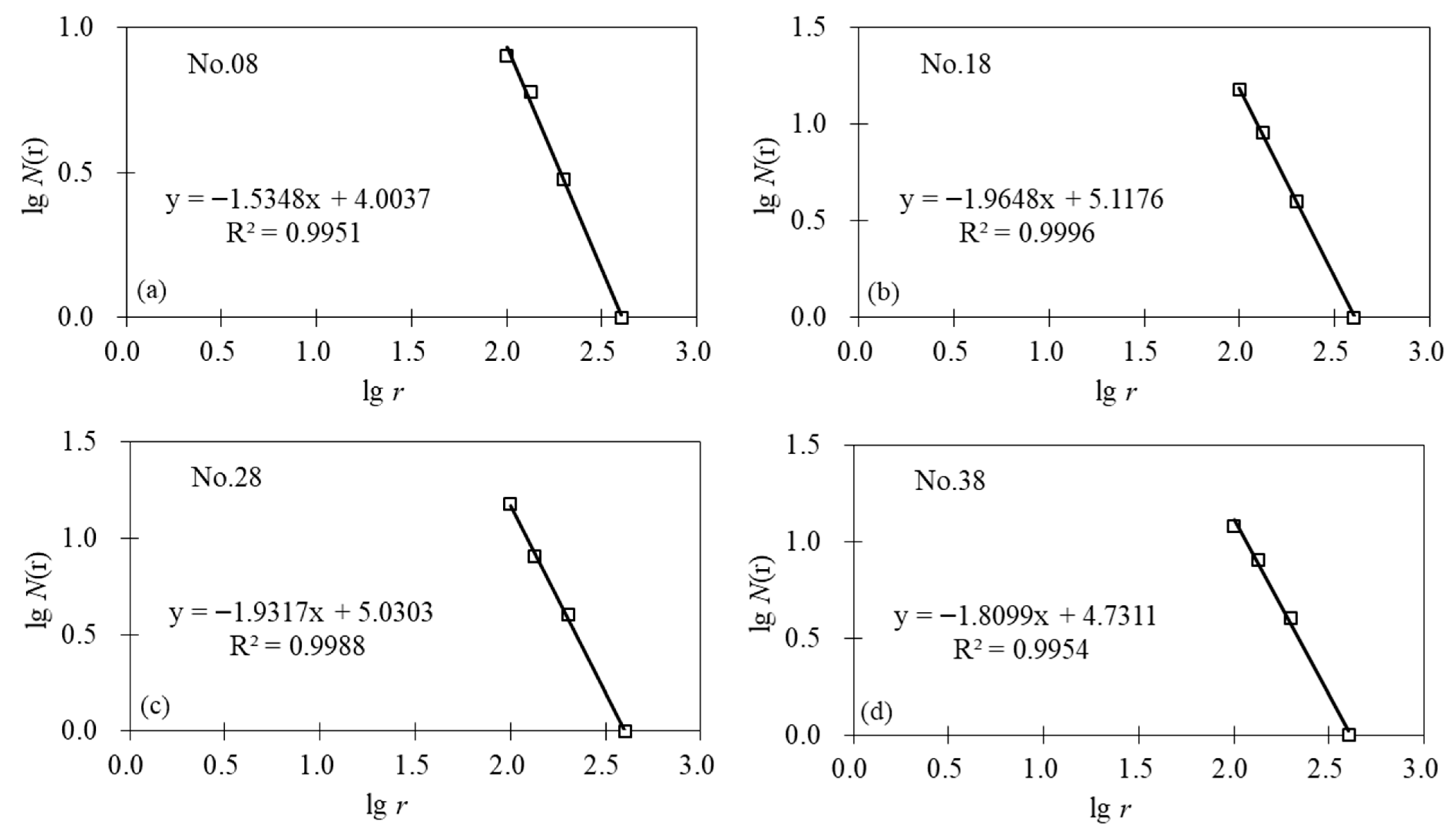


| No. | Dk | R2 | No. | Dk | R2 | No. | Dk | R2 | No. | Dk | R2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.00 | 1.00 | 33 | 2.00 | 1.00 | 65 | 2.00 | 1.00 | 97 | 1.85 | 1.00 |
| 2 | 1.20 | 0.99 | 34 | 1.85 | 1.00 | 66 | 1.77 | 1.00 | 98 | 1.96 | 1.00 |
| 3 | 1.38 | 0.96 | 35 | 1.71 | 0.98 | 67 | 1.89 | 1.00 | 99 | 1.77 | 1.00 |
| 4 | 1.89 | 1.00 | 36 | 2.00 | 1.00 | 68 | 1.65 | 0.97 | 100 | 1.89 | 1.00 |
| 5 | 1.96 | 1.00 | 37 | 1.96 | 1.00 | 69 | 1.57 | 0.98 | 101 | 2.00 | 1.00 |
| 6 | 1.65 | 0.97 | 38 | 1.81 | 1.00 | 70 | 1.73 | 0.99 | 102 | 1.51 | 0.96 |
| 7 | 1.57 | 0.98 | 39 | 1.81 | 1.00 | 71 | 1.73 | 0.99 | 103 | 1.93 | 1.00 |
| 8 | 1.53 | 1.00 | 40 | 1.73 | 0.99 | 72 | 1.73 | 0.99 | 104 | 1.96 | 1.00 |
| 9 | 1.77 | 1.00 | 41 | 2.00 | 1.00 | 73 | 1.85 | 1.00 | 105 | 1.73 | 0.99 |
| 10 | 1.67 | 0.99 | 42 | 2.00 | 1.00 | 74 | 1.89 | 1.00 | 106 | 1.96 | 1.00 |
| 11 | 1.66 | 1.00 | 43 | 1.81 | 1.00 | 75 | 1.93 | 1.00 | 107 | 2.00 | 1.00 |
| 12 | 1.84 | 0.99 | 44 | 1.65 | 0.97 | 76 | 1.85 | 1.00 | 108 | 1.86 | 0.99 |
| 13 | 2.00 | 1.00 | 45 | 1.89 | 1.00 | 77 | 2.00 | 1.00 | 109 | 1.71 | 1.00 |
| 14 | 1.96 | 1.00 | 46 | 1.57 | 0.98 | 78 | 1.96 | 1.00 | 110 | 1.96 | 1.00 |
| 15 | 1.81 | 1.00 | 47 | 1.64 | 0.99 | 79 | 1.76 | 0.99 | 111 | 2.00 | 1.00 |
| 16 | 1.46 | 0.98 | 48 | 1.57 | 0.98 | 80 | 2.00 | 1.00 | 112 | 2.00 | 1.00 |
| 17 | 1.77 | 1.00 | 49 | 1.89 | 1.00 | 81 | 1.60 | 1.00 | 113 | 2.00 | 1.00 |
| 18 | 1.96 | 1.00 | 50 | 1.93 | 1.00 | 82 | 1.76 | 0.99 | 114 | 1.96 | 1.00 |
| 19 | 2.00 | 1.00 | 51 | 1.68 | 0.99 | 83 | 2.00 | 1.00 | 115 | 2.00 | 1.00 |
| 20 | 1.62 | 0.98 | 52 | 1.85 | 1.00 | 84 | 1.96 | 1.00 | 116 | 1.85 | 1.00 |
| 21 | 1.46 | 0.96 | 53 | 1.96 | 1.00 | 85 | 1.75 | 1.00 | 117 | 1.73 | 0.99 |
| 22 | 1.63 | 0.98 | 54 | 1.65 | 0.97 | 86 | 1.76 | 0.99 | 118 | 1.16 | 0.96 |
| 23 | 1.73 | 0.99 | 55 | 1.89 | 1.00 | 87 | 1.85 | 1.00 | 119 | 1.89 | 1.00 |
| 24 | 1.52 | 0.97 | 56 | 1.96 | 1.00 | 88 | 2.00 | 1.00 | 120 | 1.89 | 1.00 |
| 25 | 1.85 | 1.00 | 57 | 1.73 | 0.99 | 89 | 1.96 | 1.00 | 121 | 1.52 | 0.97 |
| 26 | 1.89 | 1.00 | 58 | 1.70 | 1.00 | 90 | 1.81 | 1.00 | 122 | 1.93 | 1.00 |
| 27 | 1.76 | 0.99 | 59 | 1.51 | 0.97 | 91 | 1.96 | 1.00 | 123 | 1.89 | 1.00 |
| 28 | 1.93 | 1.00 | 60 | 1.57 | 0.96 | 92 | 1.96 | 1.00 | 124 | 1.65 | 0.97 |
| 29 | 1.08 | 0.96 | 61 | 1.93 | 1.00 | 93 | 2.00 | 1.00 | 125 | 1.85 | 1.00 |
| 30 | 1.12 | 0.98 | 62 | 1.96 | 1.00 | 94 | 1.63 | 0.98 | 126 | 1.93 | 1.00 |
| 31 | 1.85 | 1.00 | 63 | 1.96 | 1.00 | 95 | 1.73 | 0.99 | 127 | 1.64 | 0.99 |
| 32 | 1.96 | 1.00 | 64 | 2.00 | 1.00 | 96 | 2.00 | 1.00 | 128 | 2.00 | 1.00 |
| Evaluation Area | Dk | Kmean | Structural Characteristics |
|---|---|---|---|
| Simplyzone | 1.0 ~ 1.4 | −0.003 ~ 0.003 | Fault structures are poorly developed |
| 1.4 ~ 1.8 | −0.0002 ~ 0.0002 | Sparsely distributed small-scale faults | |
| Moderately complex zone | 1.4 ~ 1.8 | 0.0002 ~ 0.003 −0.003 ~ −0.0002 | Poorly developed secondary structures along major faults |
| 1.8 ~ 1.9 | −0.0004 ~ 0.0004 | Sparsely distributed large faults and folds, accompanied by the development of small-scale faults | |
| Complex zone | 1.8 ~ 1.9 | 0.0004 ~ 0.003 −0.003 ~ −0.0004 | Sparsely developed secondary structures adjacent to major faults |
| 1.9 ~ 2.0 | −0.0006 ~ 0.0006 | Densely developed large faults, secondary faults, and folds | |
| Extremely complex zone | 1.9 ~ 2.0 | 0.0006 ~ 0.003 | Hanging walls of major faults with extensively developed secondary faults and folds |
| 1.9 ~ 2.0 | −0.003 ~ −0.0006 | Footwalls of major faults with extensively developed secondary faults and folds |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Jiang, B.; Lan, F. Quantitative Characterization of Fractals and Curvatures in Complex Geological Structures of Wugou Coal Mine, Huaibei Coalfield. Fractal Fract. 2025, 9, 669. https://doi.org/10.3390/fractalfract9100669
Li M, Jiang B, Lan F. Quantitative Characterization of Fractals and Curvatures in Complex Geological Structures of Wugou Coal Mine, Huaibei Coalfield. Fractal and Fractional. 2025; 9(10):669. https://doi.org/10.3390/fractalfract9100669
Chicago/Turabian StyleLi, Ming, Bo Jiang, and Fengjuan Lan. 2025. "Quantitative Characterization of Fractals and Curvatures in Complex Geological Structures of Wugou Coal Mine, Huaibei Coalfield" Fractal and Fractional 9, no. 10: 669. https://doi.org/10.3390/fractalfract9100669
APA StyleLi, M., Jiang, B., & Lan, F. (2025). Quantitative Characterization of Fractals and Curvatures in Complex Geological Structures of Wugou Coal Mine, Huaibei Coalfield. Fractal and Fractional, 9(10), 669. https://doi.org/10.3390/fractalfract9100669






