On the Qualitative Stability Analysis of Fractional-Order Corruption Dynamics via Equilibrium Points
Abstract
1. Introduction
2. Preliminaries
3. Model Formulation
4. Fundamental Procedure for Suggested Method
5. Existence of the Equilibrium Points and Their Stability
6. Solution of the Projected Model Using q-HATM
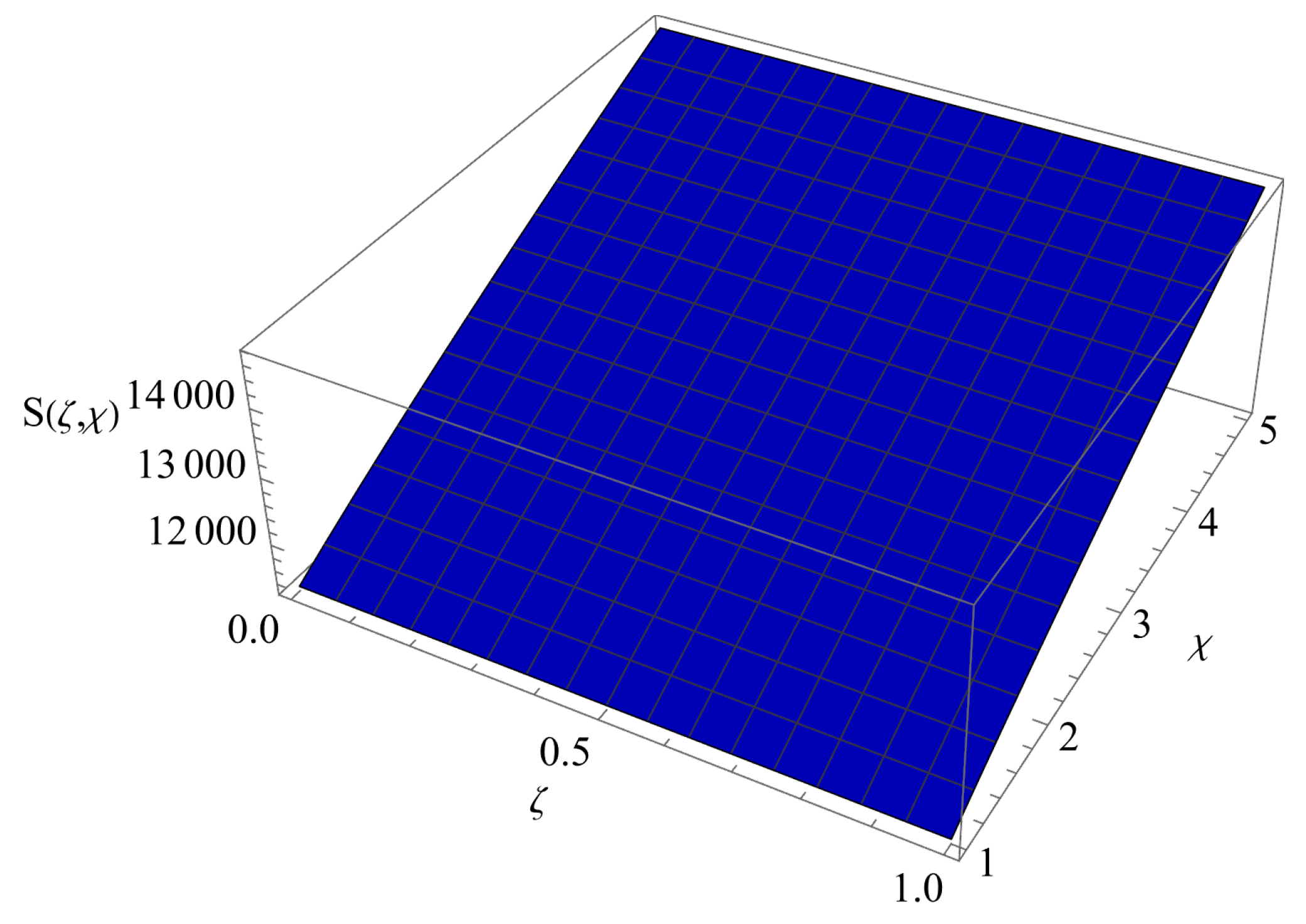
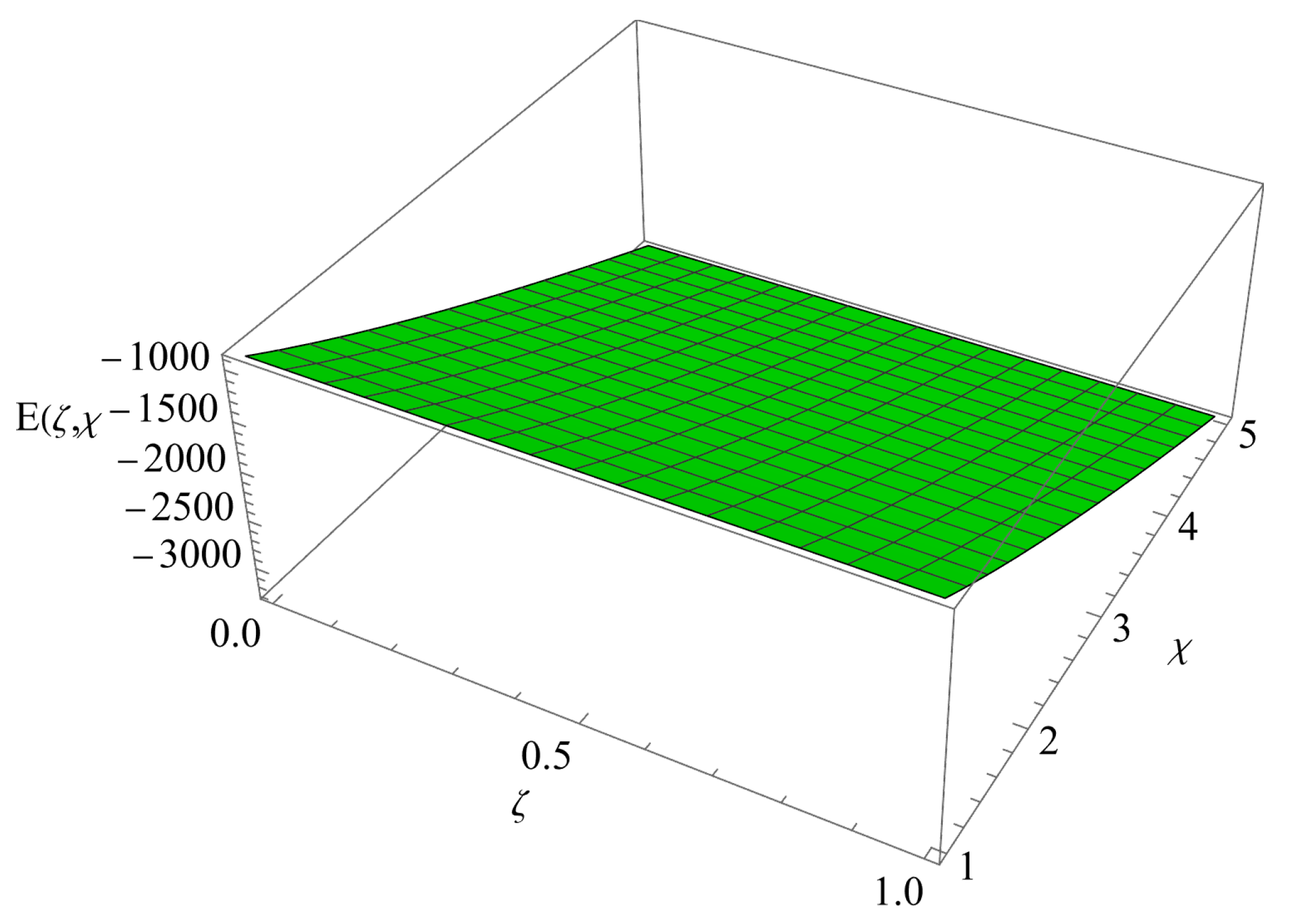
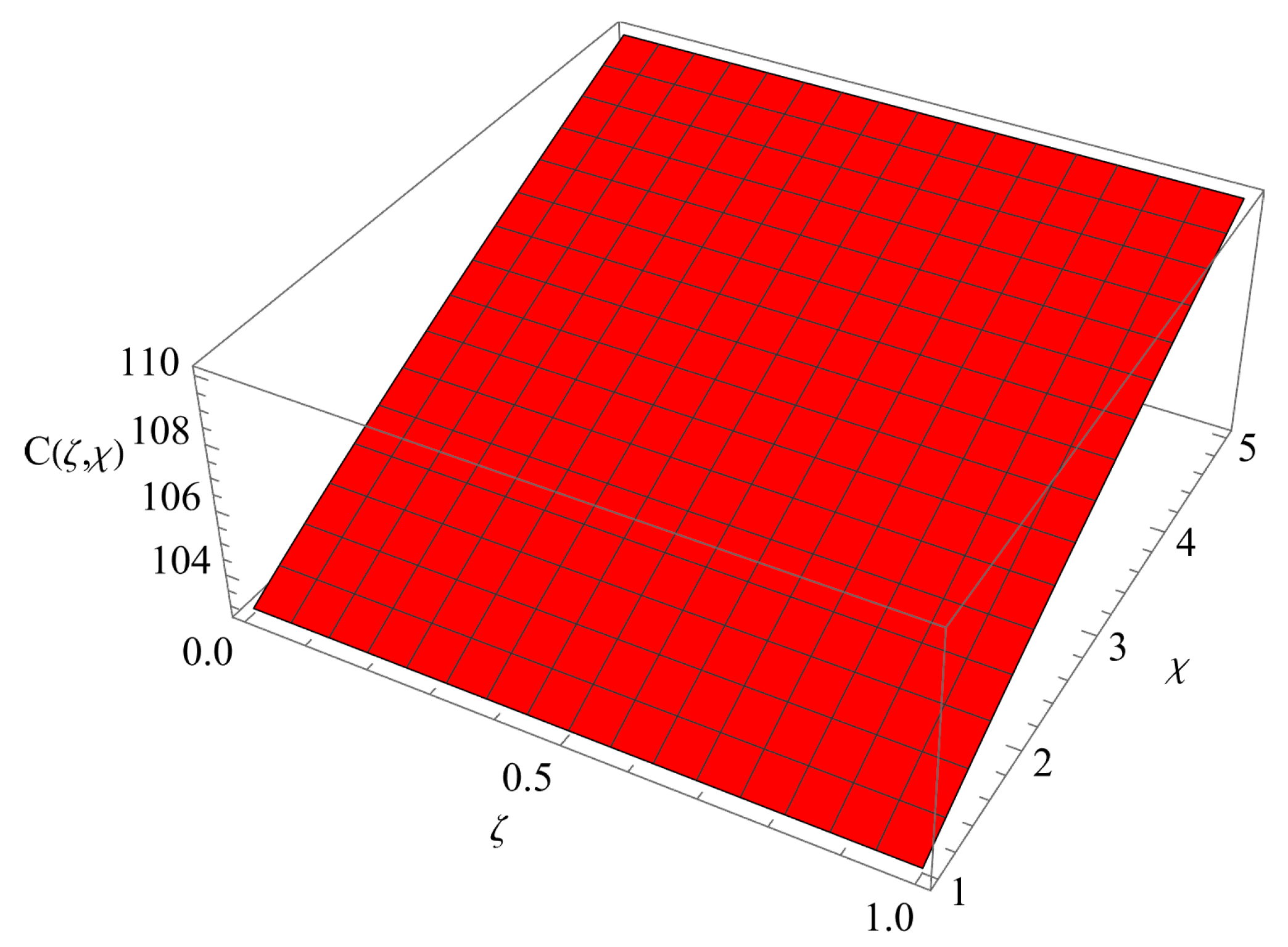
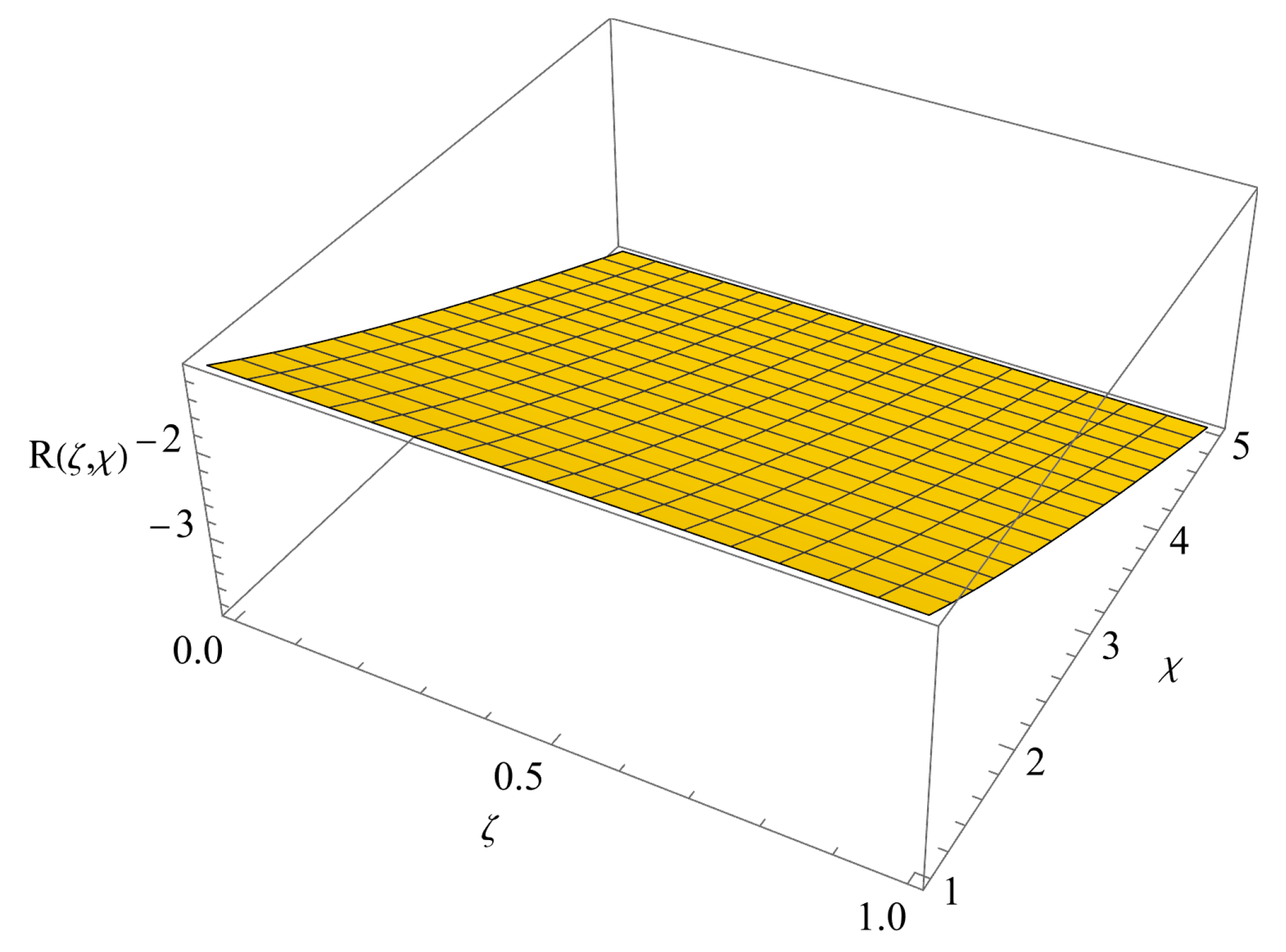
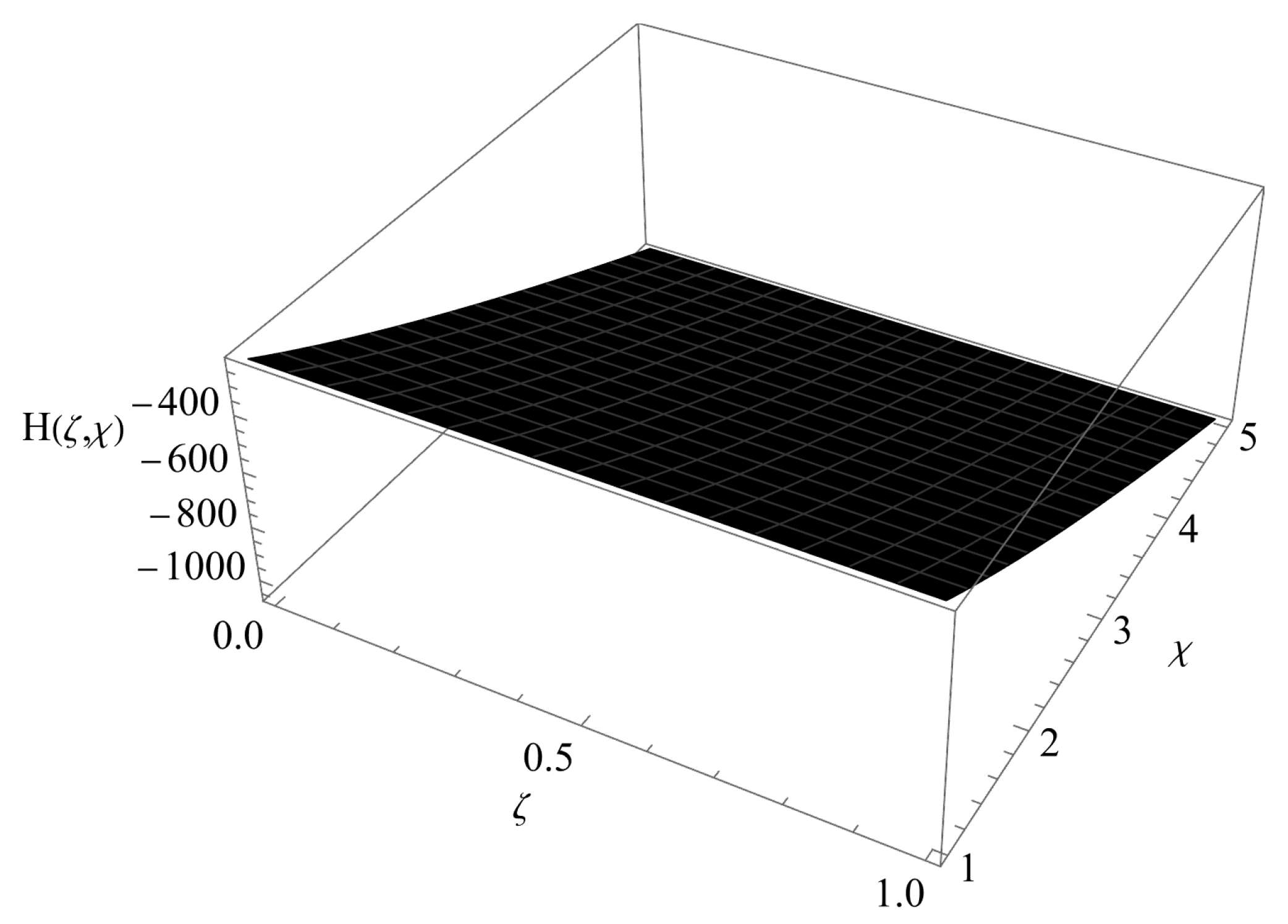
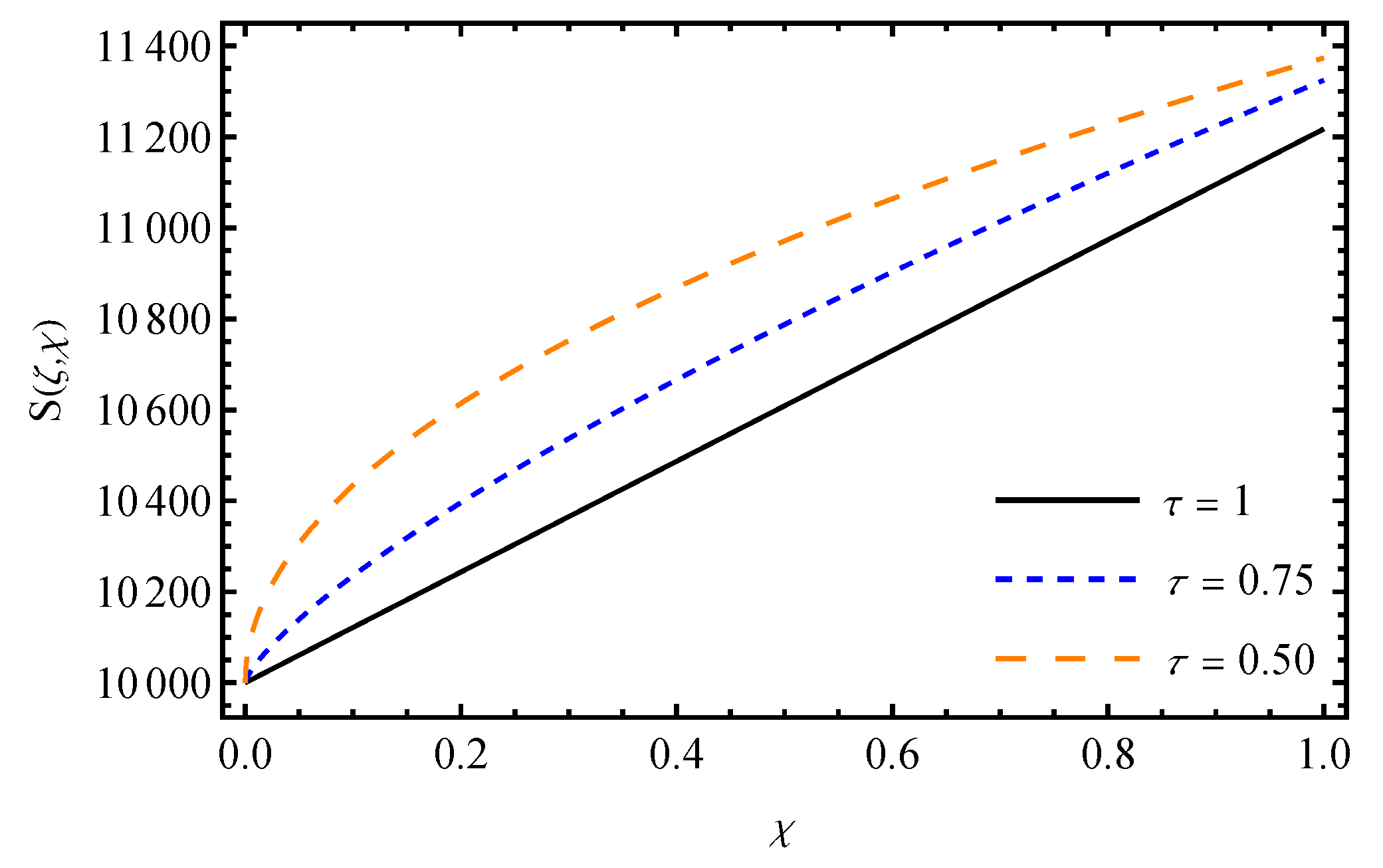
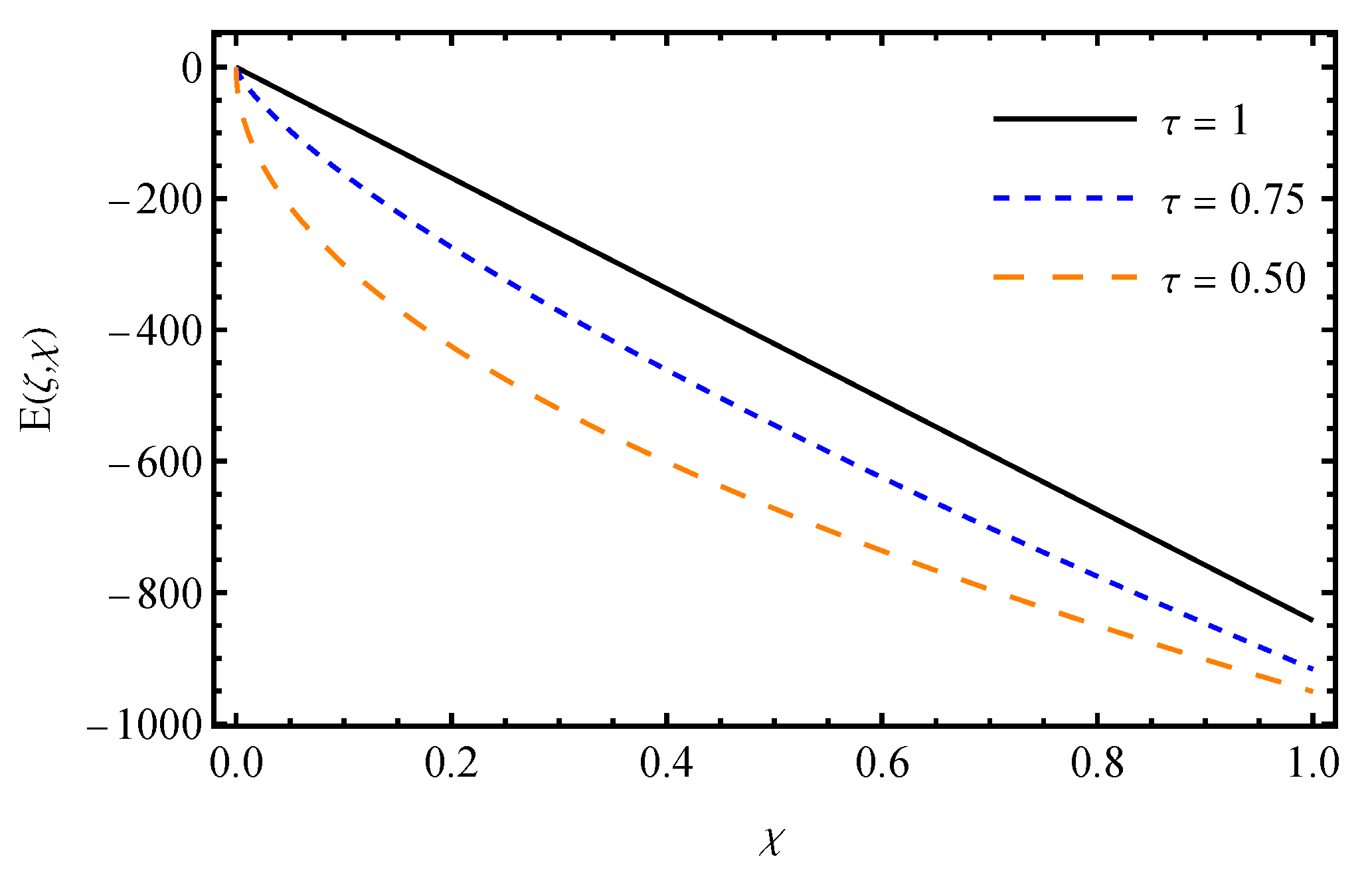
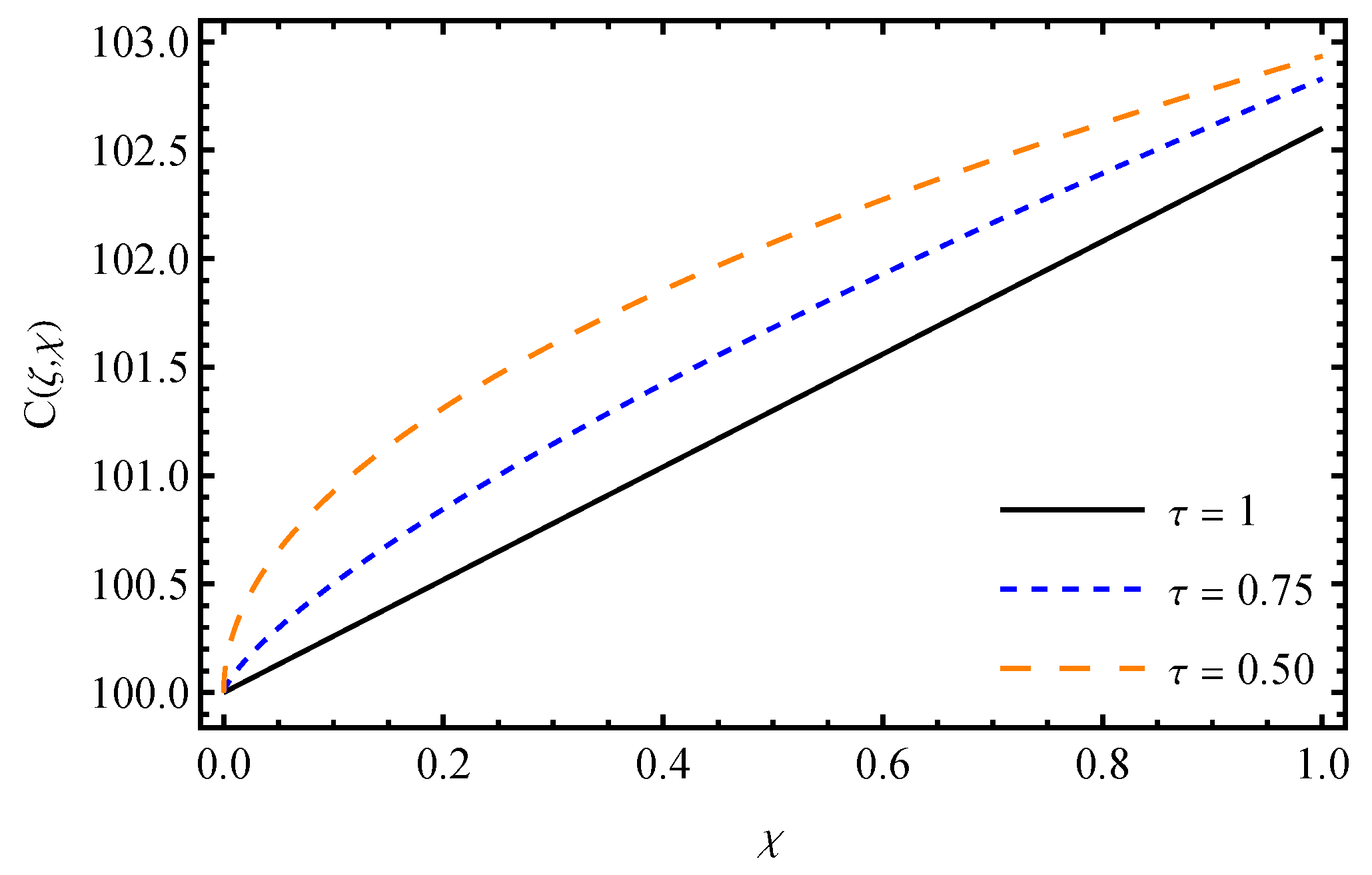
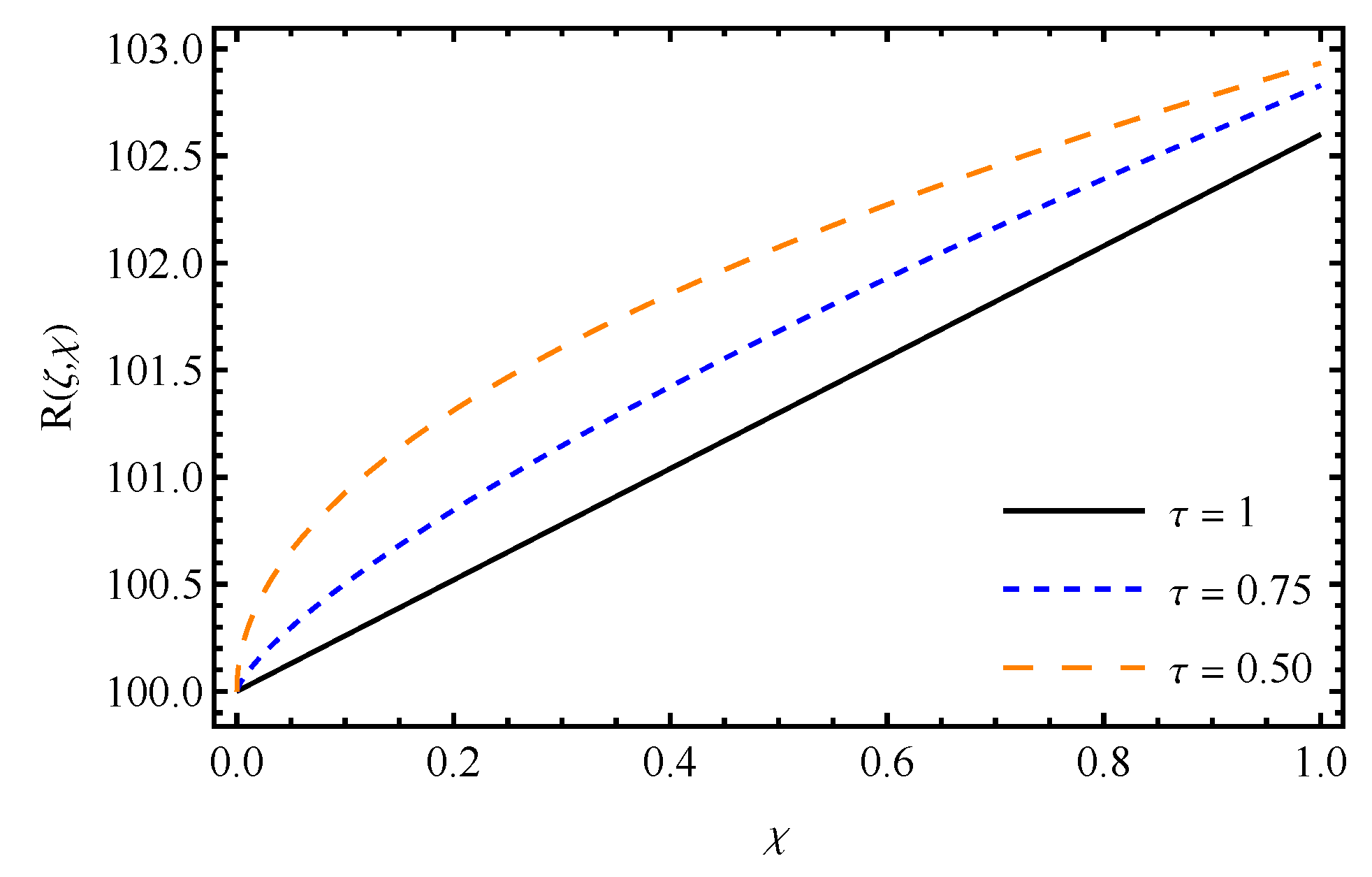
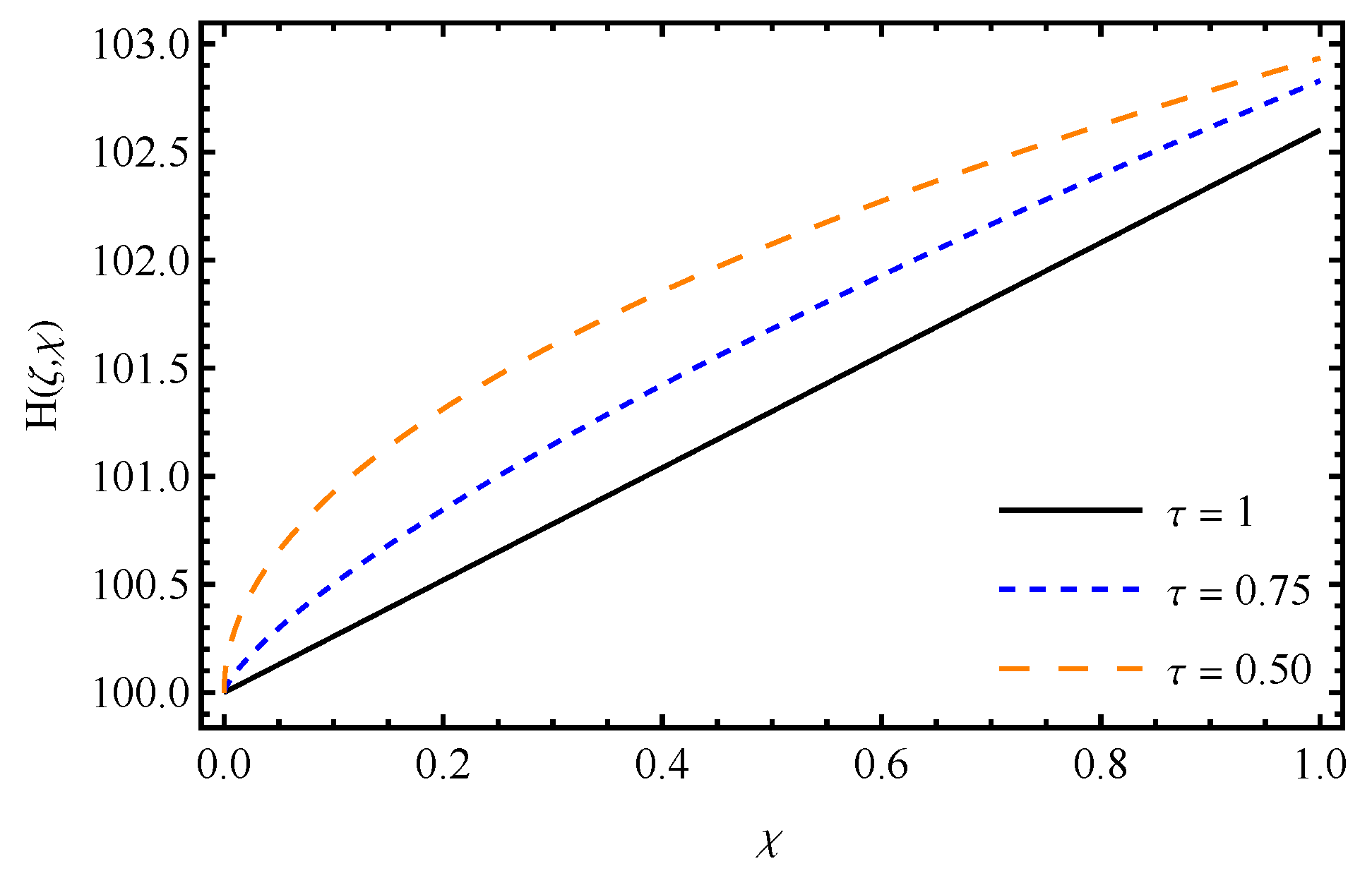
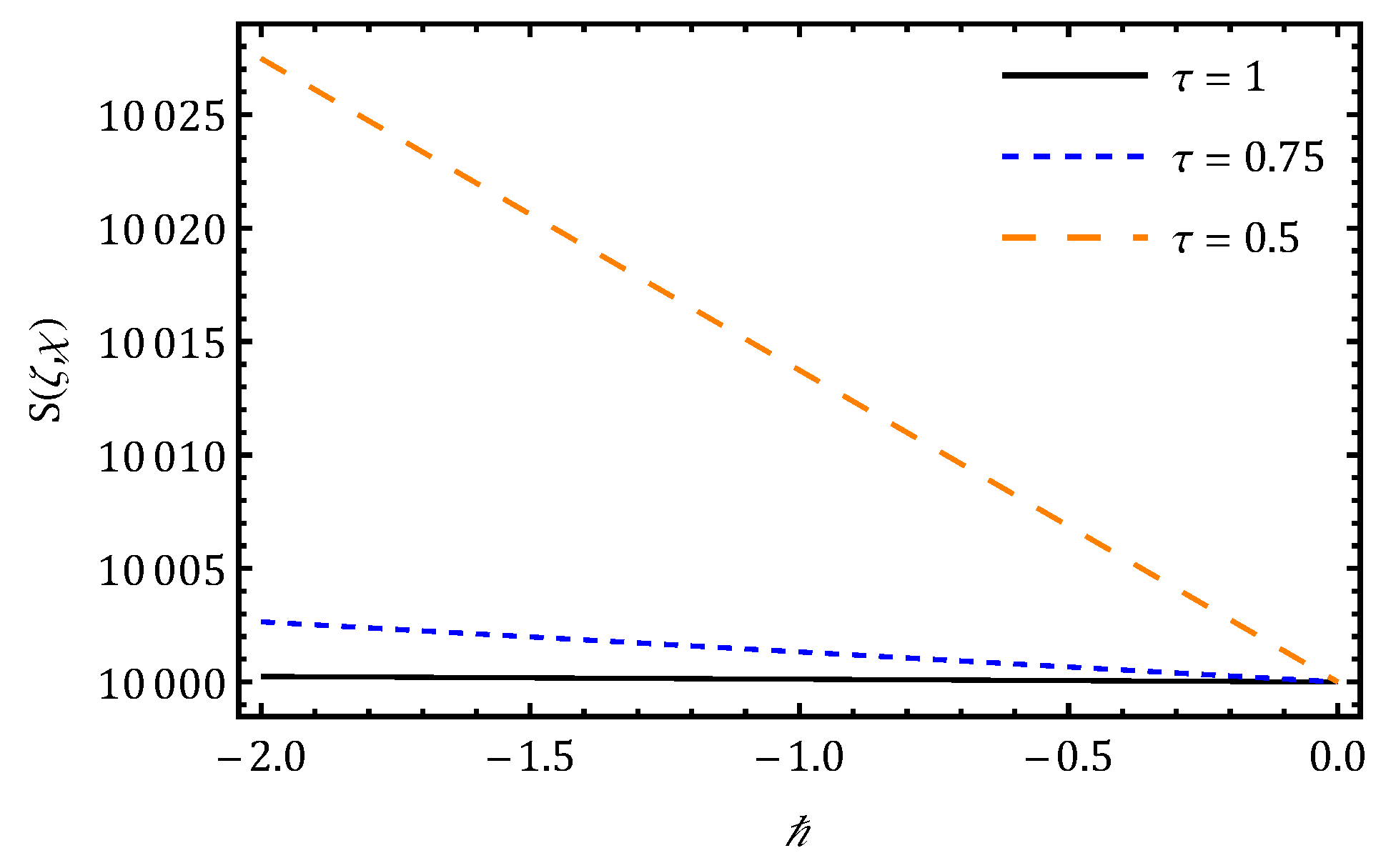
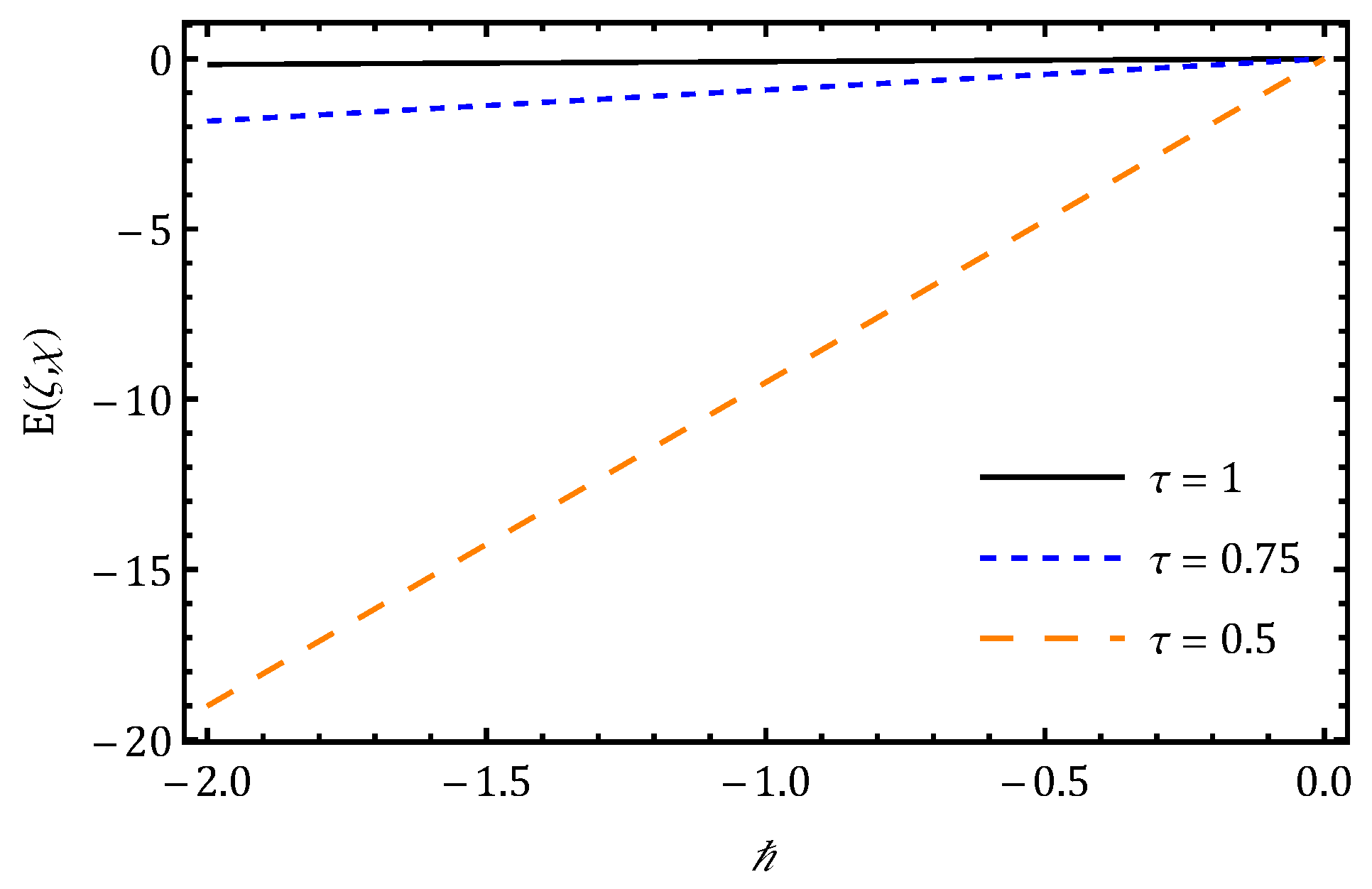
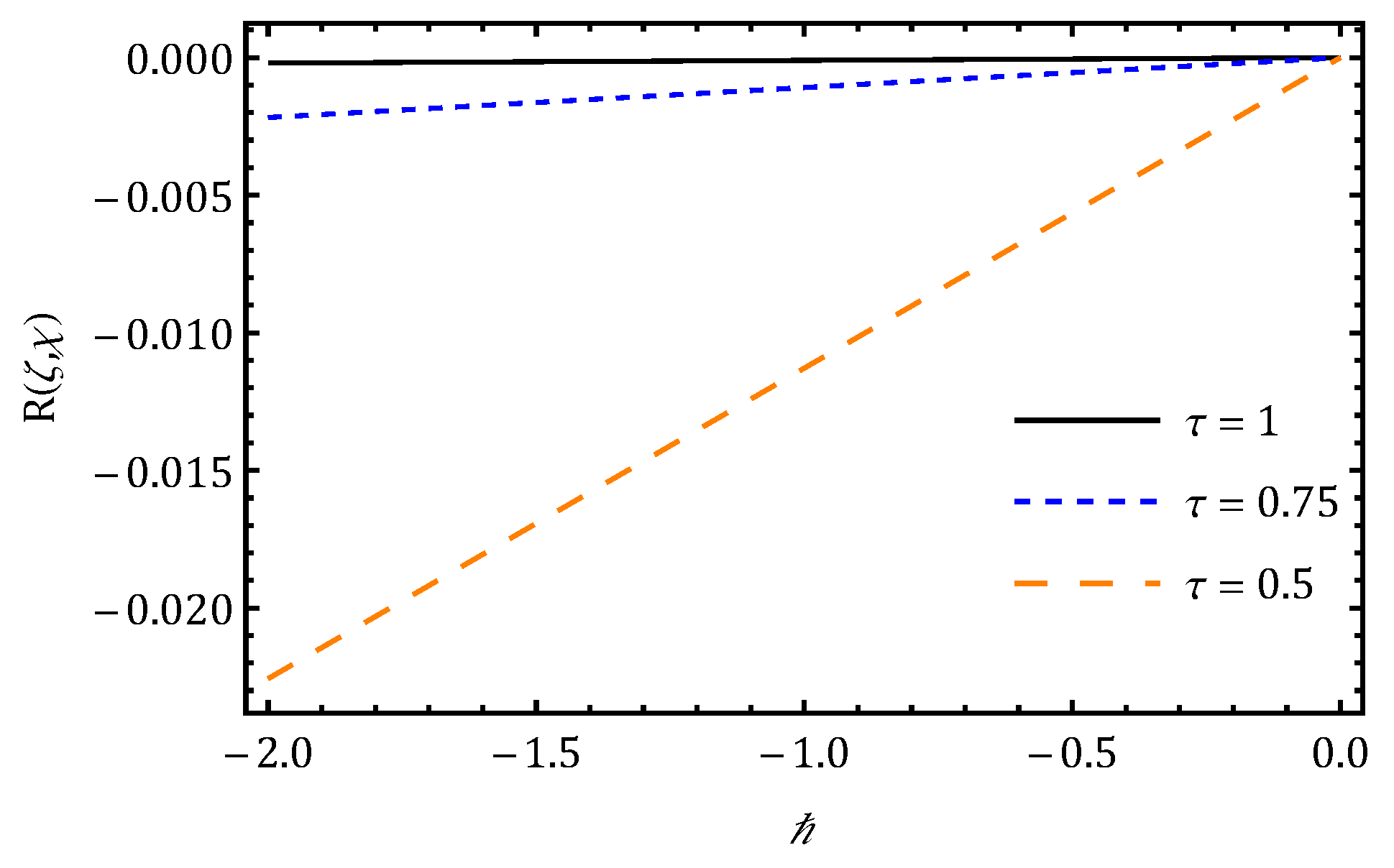
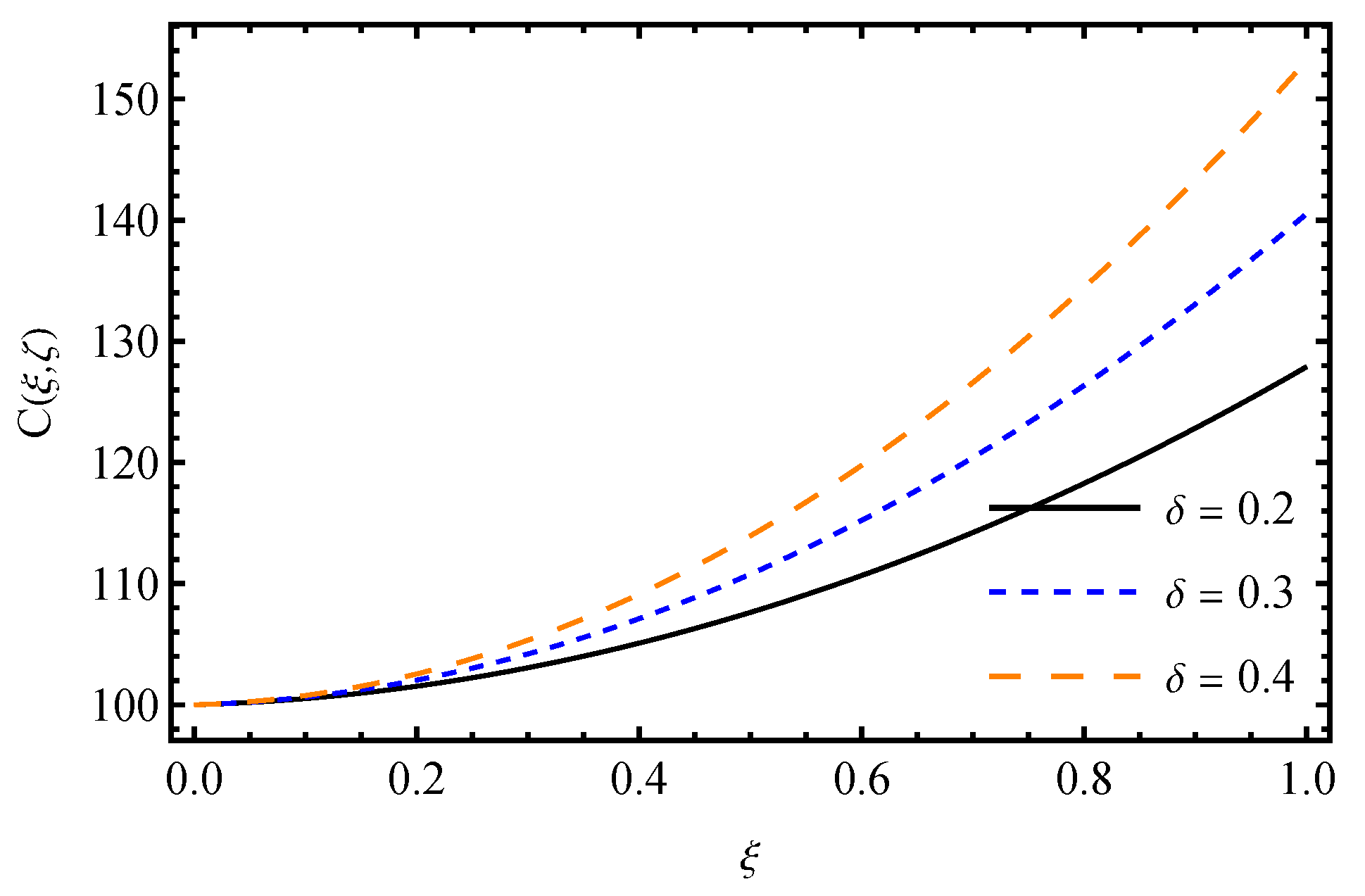
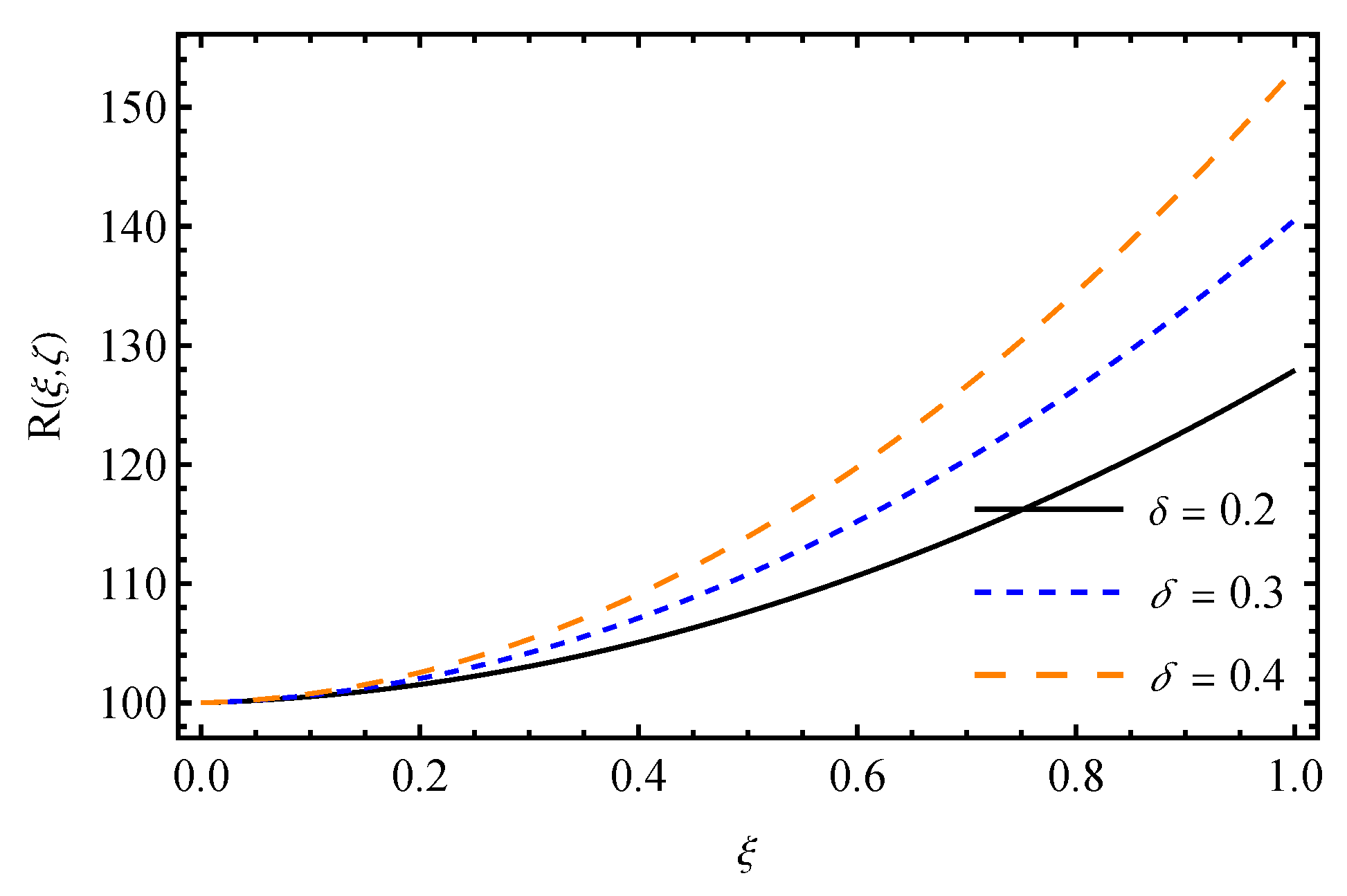
7. Results and Discussion
| Parameter | |||||||||
| Value | 85 |
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gweryina, R.I.; Kura, M.Y.; Okwu, E. An epidemiological model of corruption with immunity clause in Nigeria. World J. Model. Simul. 2019, 15, 262–275. [Google Scholar]
- World Bank. Helping Countries Combat Corruption: The Role of the World Bank; World Bank: Washington, DC, USA, 2020. [Google Scholar]
- Kaufmann, D. Myths and realities of governance and corruption. SSRN Electron. J. 2005, 829244. [Google Scholar] [CrossRef]
- Lehtinen, J.; Locatelli, G.; Sainati, T.; Artto, K.; Evans, B. The grand challenge: Effective anti-corruption measures in projects. Int. J. Proj. Manag. 2022, 40, 347–361. [Google Scholar] [CrossRef]
- Gibbon, E. Decline and Fall of the Roman Empire; BoD–Books on Demand; Strahan & Cadell: London, UK, 2024; Volume V. [Google Scholar]
- Corruption Transparency International. The Global Coalition Against Corruption. 2022. Available online: www.transparency.org/cpi (accessed on 1 January 2022).
- Ijewereme, O.B. Anatomy of corruption in the Nigerian public sector: Theoretical perspectives and some empirical explanations. Sage Open 2015, 5, 2158244015581188. [Google Scholar]
- Goel, R.K.; Nelson, M.A. Economic freedom versus political freedom: Cross–country influences on corruption. Aust. Econ. Perspect. 2005, 19, 19–42. [Google Scholar] [CrossRef]
- Dimant, E. The Antecedents and Effects of Corruption-A Reassessment of Current (Empirical) Findings; University Library of Munich: Munich, Germany, 2014. [Google Scholar]
- Fantaye, A.K.; Birhanu, Z.K. Mathematical Model and Analysis of Corruption Dynamics with Optimal Control. J. Appl. Math. 2022, 2022, 8073877. [Google Scholar] [CrossRef]
- Anjam, Y.N.; Aslam, M.I.; Cheema, S.A.; Munawar, S.; Saleem, N.; Rahman, M.U. Stability analysis of the corruption dynamics under fractional-order interventions. Nonlinear Eng. 2024, 13, 20220363. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 206. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Cruz–Duarte, J.M.; Rosales-Garcia, J.; Correa-Cely, C.R.; Garcia–Perez, A.; Avina–Cervantes, J.G. A closed form expression for the Gaussian–based Caputo–Fabrizio fractional derivative for signal processing applications. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 138–148. [Google Scholar]
- Tarasov, V.E. General non-local electrodynamics: Equations and non-local effects. Ann. Phys. 2022, 445, 169082. [Google Scholar] [CrossRef]
- Zhang, Y.; Meerschaert, M.M. Particle tracking solutions of vector fractional differential equations: A review. HFCA 2019, 3, 275–285. [Google Scholar]
- Waheed, W.; Deng, G.; Liu, B. Discrete Laplacian operator and its applications in signal processing. IEEE Access 2020, 8, 89692–89707. [Google Scholar] [CrossRef]
- Naveen, K.; Mukhtar, S.; Mahnashi, A.M.; Shah, R.; Prakasha, D.G.; Archana, D.K. A robust technique to study fractional model describing economic and environmental mathematical system. Eng. Comput. 2025, 42, 1205–1224. [Google Scholar] [CrossRef]
- Kumar, C.V.D.; Prakasha, D.G.; Turki, N.B. Exploring the dynamics of fractional-order nonlinear dispersive wave system through homotopy technique. Open Phys. 2025, 23, 20250128. [Google Scholar] [CrossRef]
- Chethan, H.B.; Turki, N.B.; Prakasha, D.G. High performance computational approach to study model describing reversible two-step enzymatic reaction with time fractional derivative. Sci. Rep. 2024, 14, 21114. [Google Scholar] [CrossRef] [PubMed]
- Liao, S. Homotopy analysis method: A new analytical technique for nonlinear problems. Commun. Nonlinear Sci. Numer. Simul. 1997, 2, 95–100. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Swaroop, R. Numerical solution of time-and space-fractional coupled Burgers’ equations via homotopy algorithm. Alex. Eng. J. 2016, 55, 1753–1763. [Google Scholar] [CrossRef]
- Veeresha, P.; Malagi, N.S.; Prakasha, D.G.; Baskonus, H.M. An efficient technique to analyze the fractional model of vector-borne diseases. Phys Scr. 2022, 97, 054004. [Google Scholar] [CrossRef]
- Naveen, K.; Prakasha, D.G.; Mofarreh, F.; Haseeb, A. A study on solutions of fractional order equal-width equation using novel approach. Mod. Phys. Lett. B 2025, 39, 2550058. [Google Scholar] [CrossRef]
- Qi, X.; Xu, C. An efficient numerical method to the stochastic fractional heat equation with random coefficients and fractionally integrated multiplicative noise. Fract. Calc. Appl. Anal. 2024, 27, 2754–2780. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. A modified Laplace transform for certain generalized fractional operators. Results Nonlinear Anal. 2018, 1, 88–98. [Google Scholar]
- Magrenan, A.A. A new tool to study real dynamics: The convergence plane. Appl. Math. Comput. 2014, 248, 215–224. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Naveen, K.; Prakasha, D.G.; Baskonus, H.M. On the Qualitative Stability Analysis of Fractional-Order Corruption Dynamics via Equilibrium Points. Fractal Fract. 2025, 9, 666. https://doi.org/10.3390/fractalfract9100666
Chen Q, Naveen K, Prakasha DG, Baskonus HM. On the Qualitative Stability Analysis of Fractional-Order Corruption Dynamics via Equilibrium Points. Fractal and Fractional. 2025; 9(10):666. https://doi.org/10.3390/fractalfract9100666
Chicago/Turabian StyleChen, Qiliang, Kariyanna Naveen, Doddabhadrappla Gowda Prakasha, and Haci Mehmet Baskonus. 2025. "On the Qualitative Stability Analysis of Fractional-Order Corruption Dynamics via Equilibrium Points" Fractal and Fractional 9, no. 10: 666. https://doi.org/10.3390/fractalfract9100666
APA StyleChen, Q., Naveen, K., Prakasha, D. G., & Baskonus, H. M. (2025). On the Qualitative Stability Analysis of Fractional-Order Corruption Dynamics via Equilibrium Points. Fractal and Fractional, 9(10), 666. https://doi.org/10.3390/fractalfract9100666






