Regularity and Qualitative Study of Parabolic Physical Ginzburg–Landau Equations in Variable Exponent Herz Spaces via Fractional Bessel–Riesz Operators

Abstract

In this article, we investigate the regularization and qualitative properties of parabolic Ginzburg–Landau equations in variable exponent Herz spaces. These spaces capture both local and global behavior, providing a natural framework for our analysis. We establish boundedness results for fractional Bessel–Riesz operators, construct examples highlighting their advantage over classical Riesz potentials, and recover several known theorems as special cases. As an application, we analyze a parabolic Ginzburg–Landau operator with VMO coefficients, showing that our estimates ensure the boundedness and continuity of solutions.

1. Introduction

Over recent decades, singular and fractional integral operators have become central to modern harmonic analysis, with profound applications in the theory of partial differential equations (PDEs). These operators such as the classical Riesz potentials and their variants are intimately linked to fundamental questions of smoothness, decay, and regularity. Among them, the Bessel–Riesz operator stands out for its ability to simultaneously capture local and nonlocal behaviors, making it particularly effective in addressing delicate regularity issues in nonlinear evolution equations. By blending the singular features of Riesz operators with the structural flexibility of Bessel potentials, its kernel provides a powerful analytic framework with applications ranging from fluid dynamics and potential theory to dispersive equations and geometric flows.

Integral operators occupy a central role in harmonic analysis, serving as indispensable tools for understanding the structural and qualitative behavior of functions. Classical examples include the Hardy–Littlewood maximal operator [1], as well as a wide family of fractional integrals such as the Riesz [2], Bessel–Riesz [3], and Bochner–Riesz potentials [4]. Collectively, these operators provide the analytical foundation for much of the modern theory of partial differential equations (PDEs), particularly in the study of regularity, decay, and stability phenomena. Within this framework, the Bessel–Riesz operator plays a distinguished role: it generalizes the classical Riesz potential by introducing an additional decay parameter $\mathrm{\gamma }\ge 0$, which enhances its ability to capture both local and nonlocal effects. Its explicit form is given by

$${\mathfrak{I}}_{\alpha ,\mathrm{\gamma }}\varphi \left(\mathfrak{y}\right)={\int }_{{\mathfrak{R}}^{\mathtt{n}}}{\mathrm{K}}_{\alpha ,\mathrm{\gamma }}(\mathfrak{y}-\mathfrak{z})\varphi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}={\int }_{{\mathfrak{R}}^{\mathtt{n}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\alpha -\mathtt{n}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\varphi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z},$$

where $\varphi \in {\mathrm{L}}_{\mathrm{loc}}^p\left({\mathfrak{R}}^{\mathtt{n}}\right)$, with $p\ge 1$, $\mathrm{\gamma }\ge 0$, and $0<\alpha <\mathtt{n}$. The kernel

$${\mathrm{K}}_{\alpha ,\mathrm{\gamma }}\left(\mathfrak{y}\right)={\displaystyle \frac{{\left|\mathfrak{y}\right|}^{\alpha -\mathtt{n}}}{{(1+|\mathfrak{y}\left|\right)}^{\mathrm{\gamma }}}}$$

is called the Bessel–Riesz kernel. When $\mathrm{\gamma }=0$, the operator reduces to the classical fractional integral operator (Riesz potential) ${\mathfrak{I}}_{\alpha }$.

The boundedness properties of Bessel–Riesz operators have been the subject of significant recent attention in harmonic analysis. For instance, Mehmood et al. [5] carried out a detailed study of these operators on measure metric spaces, establishing their boundedness in both classical Lebesgue and Morrey spaces. Their work was subsequently expanded by Nasir et al. [6], who moved beyond the classical setting and developed a comprehensive framework in the variable exponent Lebesgue spaces, thereby broadening the applicability of the theory. Further progress was made in [7], where the boundedness of Bessel–Riesz operators was demonstrated under more general structural assumptions, and the scope of the analysis was extended from the classical Morrey framework to generalized Morrey spaces. More recently, Adhikari and Parui [8] advanced this line of research by introducing Dunkl-type analogues, proving bounded mapping properties of Dunkl Bessel–Riesz operators within the setting of Dunkl-type Morrey spaces. Collectively, these contributions highlight the growing importance of Bessel–Riesz operators across diverse functional frameworks and underline their adaptability in both classical and non-standard analytical contexts.

In the classical framework, Shen [9] obtained fundamental bounds for Riesz transforms on ${\mathrm{L}}^{\mathfrak{r}}$ spaces associated with second-order elliptic operators, while Duong and McIntosh [10] investigated their boundedness on ${\mathrm{L}}^{\mathfrak{r}}$ spaces for operators in divergence form. These foundational results were subsequently broadened by Assaad and Ouhabaz [11], who extended the theory to Schrödinger operators on manifolds, thereby enriching the geometrical dimension of the subject. In a different direction, Maas and van Neerven [12] addressed the boundedness of Riesz transforms linked to elliptic operators in the setting of abstract Wiener spaces, opening new avenues for analysis in infinite-dimensional contexts. Further contributions include the work of Huang [13], who analyzed the boundedness of Riesz transforms associated with Hermite expansions in weighted Hardy spaces, and Betancor et al. [14], who deepened the interplay between special functions theory and harmonic analysis by examining Riesz and fractional integral operators in the Bessel framework. Parallel to these advances, Burenkov [15] provided a comprehensive overview of the boundedness of classical operators in generalized Morrey spaces, while Guliyev and Hasanov [16] furnished characterizations for the boundedness of Bessel–Riesz potentials in B-Morrey spaces through necessary and sufficient conditions. More recently, Sultan et al. [17] extended this line of inquiry to the setting of grand Herz–Morrey spaces, establishing refined boundedness results under variable exponent assumptions.

The Ginzburg–Landau equation, first proposed in the 1950s by V.L. Ginzburg and L.D. Landau [18] in the realm of superconductivity theory, has developed into a comprehensive framework for characterizing various pattern-formation and phase transition phenomena. In its diverse manifestations that are elliptic, parabolic, or complex-valued, it constitutes a fundamental framework for the examination of the emergence of coherent structures in nonlinear systems.

Numerous applications of the Ginzburg–Landau equation are found across various domains, particularly in quantum fluid mechanics, as it describes superfluidity and Bose–Einstein condensates by illustrating the properties of the macroscopic wave function close to the critical temperature [19]. In nonlinear optics, the equation describes the progression of optical pulses in nonlinear materials and accounts for the formation of patterns in laser cavities [20]. In fluid dynamics, it acts as a simplified model for instabilities and the shift to turbulence, along with vortex filament behavior in superfluids and rotating flows [21]. The equation is also crucial in phase transition theory and materials science, illustrating pattern development in crystal growth, phase separation, and the progress of domain structures in liquid crystals [22]. In chemical and biological systems, it has been utilized to simulate oscillatory reactions like the Belousov–Zhabotinsky reaction [23] and biological pattern development during growth processes [24]. Additionally, in plasma physics, the Ginzburg–Landau model explains wave instabilities, envelope behaviors, and energy localization in plasma waves [25]. This wide relevance highlights its significance as a cohesive framework for exploring interactions between diffusion and nonlinearity in intricate systems.

Regularity theory and well-posedness of partial differential equations (PDEs) is central to understanding the qualitative behavior of solutions, especially when dealing with degenerate, fractional, or stochastic structures. Regularity is the smoothness and differentiability of solutions. It describes the multiplicity of the derivatives that solutions of the solution have and the smoothness of those derivatives in the domain and near its boundary. In the absence of well-posedness, solutions may not even exist, may fail to be unique, and may exhibit chaotic behavior in response to small perturbations; it is then hopeless to use the model in practice.

The study of the well-posedness and regularity of partial differential equations (PDEs) and stochastic differential equations (SDEs) has received a lot of attention in the recent past, from numerous authors in diverse scenarios. Ambrosio et al. [26] derived well-posedeness theorems of ordinary differential equations and continuity equations whose vector fields are nonsmooth using applications in the fluid dynamics and transport theory. Weinan and his colleagues [27] studied renormalized powers of Ornstein–Uhlenbeck processes and proved that stochastic Ginzburg–Landau equations were well-posed through this, thus gaining an interesting insight into nonlinear stochastic PDEs. In a parallel manner, Marino et al. [28] investigated the well-posedness of degenerate Levy-driven SDEs with Hölder continuous coefficients, and they dealt with some problems associated with irregular noise and coefficients. More recently, Wu et al. [29] studied the stochastic high-order modified Zakharov–Kuznetsov equation, paving the way to well-posedness results with very low regularity assumptions. Agresti et al. [30] made contributions to the global well-posedness theory of 2D Navier–Stokes equations perturbed by a fractional boundary noise, and Kunze et al. [31] studied perturbations of strong Feller semigroups and the well-posedness of semilinear stochastic equations on Banach spaces. Furthermore, Wang et al. [32] considered Gaussian fluctuations of systems of interacting particles having singular kernels with an interplay between the stochastic analysis and regularity of PDEs. Cruzeiro et al. [33] conducted a study of the well-posedness and the existence of quasi-invariant measures to a non-periodic modified Euler equation with a transition of deterministic to probabilistic methods.

M.A. Ragusa [34,35] used Calderón–Zygmund operator estimates to analyze the regularity of elliptic PDEs within Morrey and Herz spaces. In particular, she proved the following:

Theorem 1 

(Regularity Estimate in Morrey Spaces). Let $\Omega \subset {\mathfrak{R}}^{\mathrm{n}}$ be a bounded open set and $\mathrm{K}⋐\Omega$ be a compact subset. Consider an operator $\mathcal{L}$ of the form $\mathcal{L}\mathrm{u}=div(a\nabla \mathrm{u})$, where the coefficient function a is in the space $\mathit{VMO}\cap {\mathrm{L}}^{\infty }\left({\mathfrak{R}}^{\mathrm{n}}\right)$ and satisfies the uniform ellipticity condition; i.e., there exists a constant $\sigma >0$ such that, for almost every $\mathrm{x}\in \Omega$ and all $\mathit{\xi }\in {\mathfrak{R}}^{\mathrm{n}}$, we have

$$a\left(\mathrm{x}\right)·\mathit{\xi }·\mathit{\xi }\ge {\sigma \left|\mathit{\xi }\right|}^2.$$

Suppose that we have a solution $\mathrm{u}\in W^{1,\mathfrak{r}}(\Omega )$ to the equation

$$\mathcal{L}\mathrm{u}=div\varphi \mathit{in}\Omega ,$$

where $\varphi \in {\left[{\mathrm{L}}^{\mathfrak{r},\mathrm{\lambda }}(\Omega )\right]}^{\mathrm{n}}$ for some $1<\mathfrak{r}<\infty$ and $0<\mathrm{\lambda }<\mathrm{n}$.

Then, the gradient of the solution, $\nabla \mathrm{u}$, is locally in the Morrey space ${\mathrm{L}}^{\mathfrak{r},\mathrm{\lambda }}\left(\mathrm{K}\right)$. More specifically, there exists a constant $c>0$, depending on $\mathrm{n},\mathfrak{r},\mathrm{\lambda },\sigma$, and the sets $\mathrm{K}$ and Ω, such that the following estimate holds for all $2<\mathfrak{r}<\infty$:

$${\parallel \nabla \mathrm{u}\parallel }_{{\mathrm{L}}^{\mathfrak{r},\mathrm{\lambda }}\left(\mathrm{K}\right)}\le c\left({\parallel \mathrm{u}\parallel }_{{\mathrm{L}}^2(\Omega )}+{\parallel \varphi \parallel }_{{\mathrm{L}}^{\mathfrak{r},\mathrm{\lambda }}(\Omega )}\right).$$

Andrea Scapellato [36] employed BMO-type Calderón–Zygmund operators to study regularity estimates for elliptic PDEs in Herz spaces, utilizing the following crucial results:

Theorem 2. 

Let $\mathrm{b}\in \mathrm{BMO}\left({\mathfrak{R}}^{\mathrm{n}}\right)$ and let ${\mathfrak{r}}_1(·)\in \mathcal{B}\left({\mathfrak{R}}^{\mathrm{n}}\right)$, ${\mathfrak{s}}_1(·),{\mathfrak{s}}_2(·)\in \mathbf{P}\left({\mathfrak{R}}^{\mathrm{n}}\right)$ satisfy

$$inf{\mathfrak{s}}_2\ge sup{\mathfrak{s}}_1.$$

If the parameter $\mathrm{\alpha }$ lies within the interval

$$-\mathrm{n}{\mathrm{t}}_{12}<\mathrm{\alpha }<\mathrm{n}{\mathrm{t}}_{11},$$

where ${\mathrm{t}}_{11},{\mathrm{t}}_{12}$ are constants from Lemma 7 in [36], then the commutator $[\mathrm{b},\mathrm{T}]$ acts boundedly as an operator

$$[\mathrm{b},\mathrm{T}]:{\dot{\mathbf{K}}}_{{\mathfrak{r}}_1(·)}^{\mathrm{\alpha },{\mathfrak{s}}_2(·)}\left({\mathfrak{R}}^{\mathrm{n}}\right)\to {\dot{\mathbf{K}}}_{{\mathfrak{r}}_1(·)}^{\mathrm{\alpha },{\mathfrak{s}}_1(·)}\left({\mathfrak{R}}^{\mathrm{n}}\right).$$

Recently, Afzal et al. [37] introduced for the first time a novel exponentially damped Riesz potential and investigated the regularity of elliptic PDEs in variable Lebesgue spaces. Their main result can be stated as follows:

Theorem 3. 

Let $0<\varkappa <\mathfrak{n}$, $0<\delta <\infty$ with $\varkappa <\delta$, and suppose that the variable exponent function $\mathfrak{p}(·)$ belongs to the class ${\mathbf{P}}_0^{log}(\Omega )\left({\mathfrak{R}}^{+}\right)$, satisfying the log-Hölder continuity condition. Define the fractional integral operator with an exponential-type kernel by

$${\mathfrak{I}}_{\varkappa ,\delta }\phi \left(\mathit{\xi }\right):={\int }_{{\mathbf{R}}^{\mathfrak{n}}}{\displaystyle \frac{\phi \left(\zeta \right)}{{|\mathit{\xi }-\zeta |}^{\mathfrak{n}-\varkappa }}}{e}^{-\delta |\mathit{\xi }-\zeta |}d\zeta .$$

Then, ${\mathfrak{I}}_{\varkappa ,\delta }$ is a bounded linear operator on the variable exponent Lebesgue space ${\mathrm{L}}^{\mathfrak{p}(·)}\left({\mathfrak{R}}^{+}\right)$; i.e.,

$${\mathfrak{I}}_{\varkappa ,\delta }:{\mathrm{L}}^{\mathfrak{p}(·)}\left({\mathfrak{R}}^{+}\right)\to {\mathrm{L}}^{\mathfrak{p}(·)}\left({\mathfrak{R}}^{+}\right)$$

is bounded.

For further results concerning the regularity, well-posedness, and boundedness of solutions to classical operators, we refer the interested reader to [38,39,40,41,42] and the references therein.

Motivation for the Study:

• The primary motivation of this study, and the associated research gap in the literature, lies in the observation that recent work has investigated the boundedness of the Bessel–Riesz operator primarily in Morrey spaces [5] and Lebesgue spaces [6], both of which predominantly capture local behavior. In contrast, the present study establishes the boundedness in variable Herz spaces, which are capable of describing both local and global behaviors. This approach not only refines but also generalizes several related results available in the current literature.
• Moreover, this study generalizes and refines the results of [43,44,45], in which the authors examined the boundedness properties of classical Riesz operators within the settings of classical Lebesgue spaces and Herz spaces. In contrast, we investigate the Bessel–Riesz operator, which possesses enhanced analytical properties compared to the classical Riesz operator. For clarity, a comparative analysis of the two operators is presented in

  Table 1. Comparison between Riesz and Bessel–Riesz operators in variable Herz spaces, showing that the classical Riesz potential does not ensure boundedness, while the Bessel–Riesz potential does.

  Setting	Classical Riesz Potential	Bessel–Riesz Potential
  Function Space	Variable Herz space ${\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathrm{\alpha }(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)$	Same as left
  Exponent Settings	$\mathfrak{r}\left(\mathrm{\mu }\right)=2.3+0.4cos\left(\right|\mathrm{\mu }\left|\right)$,   $\mathfrak{s}=4$,   $\mathrm{\alpha }\left(\mathrm{\mu }\right)=0.8+0.3{\mathrm{e}}^{-\left|\mathrm{\mu }\right|}$	Same as left
  Kernel Parameters	$\alpha =1$, $\gamma =0$ (no extra decay)	$\alpha =1$, $\gamma =2$ (polynomial decay factor)
  Additional Decay	None	${(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{-\gamma }$
  Result	Insufficient decay at infinity and limited singularity control	Satisfies boundedness owing to improved decay and integrability

  . Furthermore, we work within the framework of variable Herz spaces, where all parameters are allowed to vary, providing a natural and more comprehensive generalization of the aforementioned studies.
• Furthermore, motivated by the regularity results established in [35,36,37,38], we aimed to investigate the regularity of Ginzburg–Landau-type parabolic initial–boundary value problems. The main distinction lies in the fact that their work focuses on elliptic problems using Calderón–Zygmund operators, whereas our study addresses parabolic problems employing Bessel–Riesz operators.

The structure of this article is as follows. Section 1 provides an introduction that highlights the main motivation of the study and places it within the broader context of harmonic analysis and nonlinear Ginzburg–Landau equations. In Section 2, we establish the theoretical groundwork by recalling essential definitions and auxiliary results, with particular emphasis on variable exponent Lebesgue spaces and Herz-type spaces, which serve as the analytical framework for our investigation. Section 3 presents the core analytical contributions: we introduce a new class of fractional potential operators, examine their structural and regularity properties, and derive precise boundedness estimates for these operators as well as their classical counterparts under a wide range of integrability and structural conditions. The applicability of these results is demonstrated in Section 4, where we study a nonlinear parabolic system and show that its solutions remain bounded under the action of the newly constructed operators. Finally, Section 5 summarizes the principal findings and suggests several promising directions for future research.

2. Preliminary Framework

This section reviews essential definitions and preliminary results, with emphasis on operator boundedness and the structural features of variable exponent Lebesgue and Herz-type spaces. For further background, we refer to the monograph of Cruz-Uribe and Fiorenza and related work [45,46]. We also fix the notation and conventions used throughout the paper.

• Notation and Conventions

Unless stated otherwise, the following notation will be used consistently throughout the article. We denote by ${\mathfrak{R}}^n$ the n-dimensional Euclidean space, ${\mathbf{R}}^{+}$ the set of positive real numbers, and $\mathfrak{B}(\mathfrak{y},r)$ the open ball centered at $\mathfrak{y}$ with radius $r>0$. The support of a function $\varphi$ is written $supp\varphi$, while $|\Omega |$ stands for the Lebesgue measure of a measurable set $\Omega \subset {\mathfrak{R}}^n$, and ${\mathrm{\chi }}_E$ denotes the characteristic function of E. Throughout, “a.e.” refers to almost everywhere with respect to the Lebesgue measure. For variable exponent spaces, $\mathbf{P}(\Omega )$ denotes measurable exponents $\mathfrak{s}(·)$ with $1<{\mathfrak{s}}_{-}\le \mathfrak{s}\left(\mathfrak{y}\right)\le {\mathfrak{s}}_{+}<\infty$, and ${\mathbf{P}}_0^{log}(\Omega )$ consists of exponents that are log-Hölder continuous. We write ${\mathrm{L}}_{\mathrm{loc}}^{\mathfrak{s}(·)}(\Omega )$ for the space of locally integrable functions with respect to $\mathfrak{s}(·)$, and ${\mathrm{W}}^{1,\mathfrak{r}}\left({\mathfrak{R}}^n\right)$ for the usual Sobolev space. For operators, we use $\varphi \lesssim \mathrm{\psi }$ to indicate $\varphi \left(\mathfrak{y}\right)\le c\mathrm{\psi }\left(\mathfrak{y}\right)$ for some constant $c>0$, and ${\Omega }_1\hookrightarrow {\Omega }_2$ to denote continuous embedding. Convolution is defined by $(\varphi \ast \mathrm{\psi })\left(\mathfrak{y}\right)={\int }_{{\mathfrak{R}}^n}\varphi (\mathfrak{y}-\nu )\mathrm{\psi }\left(\nu \right)d\nu$. Finally, dyadic decompositions are given by ${\mathfrak{B}}_k=\mathfrak{B}(0,2^k)$, ${\mathbf{R}}_k={\mathfrak{B}}_k\setminus {\mathfrak{B}}_{k-1}$, and ${\mathrm{\chi }}_k={\mathrm{\chi }}_{{\mathbf{R}}_k}$ for $k\in \mathbf{Z}$.

2.1. Modular Function Spaces

Semi-modular spaces generalize normed linear spaces by replacing norms with modular functionals. Before discussing their structure and applications, we recall the essential definitions and main properties of modular and semi-modular formulations.

Definition 1 

([46]). Let $\mathbf{X}$ be a linear space over $\mathbf{K}\in \{\mathbf{R},\mathbf{C}\}$. A mapping $\mathrm{\sigma }:\mathbf{X}\to [0,\infty )$ is semi-modular if, for all $\mathrm{\chi }\in \mathbf{X}$:

1. 

Zero at origin: $\mathrm{\sigma }\left(0\right)=0.$

2. 

Unitary invariance: $\mathrm{\sigma }\left(\mathrm{\alpha }\mathrm{\chi }\right)=\mathrm{\sigma }\left(\mathrm{\chi }\right)$ for all $\mathrm{\alpha }\in \mathbf{K}$ with $\left|\mathrm{\alpha }\right|=1.$

3. 

Definiteness: If $\mathrm{\sigma }\left(\mathrm{\upsilon }\mathrm{\chi }\right)=0$ for every $\mathrm{\upsilon }>0$, then $\mathrm{\chi }=0.$

4. 

Monotonicity in scale: For $0\le {\mathrm{\upsilon }}_1<{\mathrm{\upsilon }}_2$,

$$\mathrm{\sigma }\left({\mathrm{\upsilon }}_1\mathrm{\chi }\right)\le \mathrm{\sigma }\left({\mathrm{\upsilon }}_2\mathrm{\chi }\right).$$

5. 

Left-continuity in scale: For each fixed $\mathrm{\chi }$, the map $\mathrm{\upsilon }\mapsto \mathrm{\sigma }\left(\mathrm{\upsilon }\mathrm{\chi }\right)$ is left-continuous on $(0,\infty )$.

The collection of vectors where the semi-modular function attains finite values under some positive scaling forms the corresponding modular space, denoted by

$${\mathbf{X}}_{\mathrm{\sigma }}:=\left\{\mathrm{\chi }\in \mathbf{X}\mid \exists \mathrm{\upsilon }>0\mathrm{such}\mathrm{that}\mathrm{\sigma }\left(\mathrm{\upsilon }\mathrm{\chi }\right)<\infty \right\}.$$

This class of elements serves as the fundamental basis for investigating the central analytic features of semi-modular function spaces, including various notions of convergence, conditions ensuring modular completeness, and the criteria under which such spaces become normable.

2.2. Variable Exponent Spaces

We recall the notion of variable exponent Lebesgue spaces, a generalization of the classical case where the integrability exponent is permitted to vary across the domain.

Let $\Theta \subset {\mathfrak{R}}^{\mathtt{n}}$ be measurable, and let $\delta :\Theta \to (0,\infty )$ be a measurable variable exponent function. Its essential bounds are

$${\delta }^{-}:=\underset{\omega \in \Theta }{ess\; inf}\delta (\omega ),{\delta }^{+}:=\underset{\omega \in \Theta }{ess\; sup}\delta (\omega ).$$

We define the sets

$${\Theta }_{\mathrm{reg}}:=\{1<\delta (\omega )<\infty \},{\Theta }_{\min }:=\{\delta (\omega )=1\},{\Theta }_{\max }:=\{\delta (\omega )=\infty \}.$$

The pointwise Hölder conjugate ${\delta }^{\prime }:\Theta \to [1,\infty ]$ is

$${\delta }^{\prime }(\omega ):=\left\{\begin{array}{cc}\infty ,\hfill & \omega \in {\Theta }_{\min },\hfill \\ {\displaystyle \frac{\delta (\omega )}{\delta (\omega )-1}},\hfill & \omega \in {\Theta }_{\mathrm{reg}},\hfill \\ 1,\hfill & \omega \in {\Theta }_{\max },\hfill \end{array}\right.\mathrm{satisfying}{\displaystyle \frac{1}{\delta (\omega )}}+{\displaystyle \frac{1}{{\delta }^{\prime }(\omega )}}=1\mathrm{a}.\mathrm{e}.\mathrm{in}\Theta .$$

For constant $\delta$, this reduces to ${\delta }^{\prime }={\displaystyle \frac{\delta }{\delta -1}}$.

Let

$${\mathbf{P}}_0(\Theta ):=\{\delta :{\delta }^{-}>0\},\mathbf{P}(\Theta ):=\{\delta \in {\mathbf{P}}_0(\Theta ):{\delta }^{-}\ge 1\}.$$

For $\delta \in {\mathbf{P}}_0(\Theta )$ and $\mathrm{\phi }\in {\mathrm{L}}_{\mathrm{loc}}^0(\Theta )$, define the modular

$${\mathrm{\vartheta }}_{\delta (·)}\left(\mathrm{\phi }\right):={\int }_{\Theta }{\Phi }_{\delta (\theta )}\left(\right|\mathrm{\phi }(\theta )\left|\right)\mathrm{d}\theta ,$$

where

$${\Phi }_{\delta }\left(\mathrm{\tau }\right):=\left\{\begin{array}{cc}{\mathrm{\tau }}^{\delta },\hfill & 0<\delta <\infty ,\hfill \\ 0,\hfill & \mathrm{\tau }\le 1,\delta =\infty ,\hfill \\ \infty ,\hfill & \mathrm{\tau }>1,\delta =\infty .\hfill \end{array}\right.$$

This modular generates the space ${\mathrm{L}}^{\delta (·)}(\Theta )$, capturing spatial variability in integrability.

Definition 2 

([46]). For a measurable $\delta :{\mathfrak{R}}^{\mathtt{n}}\to (0,\infty )$, the variable exponent Lebesgue space is

$${\mathrm{L}}^{\delta (·)}\left({\mathfrak{R}}^{\mathtt{n}}\right):=\left\{\varphi :{\mathfrak{R}}^{\mathtt{n}}\to \mathbf{C}\mathit{measurable}|\exists \mathrm{\upsilon }>0:{\mathrm{\vartheta }}_{\delta (·)}\left({\displaystyle \frac{\varphi }{\mathrm{\upsilon }}}\right)<\infty \right\},$$

where ${\mathrm{\vartheta }}_{\delta (·)}$ is the associated modular.

It is equipped with the Luxemburg norm

$${\parallel \varphi \parallel }_{\delta (·)}:=inf\left\{\mathrm{\upsilon }>0:{\mathrm{\vartheta }}_{\delta (·)}\left({\displaystyle \frac{\varphi }{\mathrm{\upsilon }}}\right)\le 1\right\},$$

making ${\mathrm{L}}^{\delta (·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)$ a Banach space when ${\delta }^{-}>1$.

If ${\delta }^{+}:{=}_{\mathfrak{y}\in \Omega }\delta \left(\mathfrak{y}\right)<\infty$, then $\mathrm{\phi }\in {\mathrm{L}}^{\delta (·)}(\Omega )$ iff

$${\int }_{\Omega }{\left|\mathrm{\phi }\left(\mathfrak{y}\right)\right|}^{\delta \left(\mathfrak{y}\right)}\mathrm{d}\mathfrak{y}<\infty .$$

Example 1. 

Let

$$\delta \left(\mathfrak{z}\right):=\left\{\begin{array}{cc}2,\hfill & \left|\mathfrak{z}\right|\le 1,\hfill \\ 3,\hfill & \left|\mathfrak{z}\right|>1,\hfill \end{array}\right.\varphi \left(\mathfrak{z}\right):=(1-|\mathfrak{z}\left|\right){\chi }_{[-1,1]}\left(\mathfrak{z}\right).$$

Then,

$${\mathrm{\vartheta }}_{\delta (·)}(\varphi )={\int }_{-1}^1{(1-|\mathfrak{z}\left|\right)}^2\mathrm{d}\mathfrak{z}=\frac{2}{3}<\infty ,$$

so $\varphi \in {\mathrm{L}}^{\delta (·)}\left(\mathbf{R}\right)$ with ${\parallel \varphi \parallel }_{\delta (·)}\le {\left(\frac{2}{3}\right)}^{1/2}$.

To guarantee the analytic stability and boundedness of key operators, the exponent function $\delta :\Omega \to {\mathbf{R}}^{+}$ is assumed to satisfy the following:

• Local log-Hölder continuity: There exists $c_{log}(\delta )>0$ such that, for all $\mathfrak{y},\mathfrak{z}\in \Omega$,

  $$|\delta \left(\mathfrak{y}\right)-\delta \left(\mathfrak{z}\right)|\le {\displaystyle \frac{c_{log}(\delta )}{log\left(\mathrm{e}+\frac{1}{|\mathfrak{y}-\mathfrak{z}|}\right)}}.$$
• Log-Hölder continuity at infinity: There exist ${\delta }_{\infty }\in \mathbf{R}$ and $c_{log}(\delta )>0$ such that, for all $\mathfrak{y}\in \Omega$,

  $$|\delta \left(\mathfrak{y}\right)-{\delta }_{\infty }|\le {\displaystyle \frac{c_{log}(\delta )}{log\left(\mathrm{e}+\left|\mathfrak{y}\right|\right)}}.$$

If both hold, $\delta$ is globally log-Hölder continuous, written $\delta \in {\mathbf{C}}_{log}(\delta )$. The class of globally regular exponents is

$${\mathbf{P}}_0^{log}(\Omega ):=\left\{\delta \in {\mathbf{P}}_0(\Omega ):{\displaystyle \frac{1}{\delta }}\in {\mathbf{C}}_{log}(\delta )\right\}.$$

In what follows, we use the modular ${\mathrm{\vartheta }}_{\delta (·)}$ and Luxemburg norm ${\parallel ·\parallel }_{{\mathrm{L}}^{\delta (·)}(\Omega )}$, which are equivalent under standard bounds on $\delta$.

Theorem 4 

([46]). Let Θ be a measurable domain and $\mathfrak{r}(·)\in \mathbf{P}(\Theta )$. For all $\varphi \in {\mathrm{L}}^{\mathfrak{r}(·)}(\Theta )$ and $\mathrm{\psi }\in {\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}(\Theta )$,

$$\varphi \mathrm{\psi }\in {\mathrm{L}}^1(\Theta )$$

and the generalized Hölder inequality holds:

$${\int }_{\Theta }|\varphi \left(\mathrm{\zeta }\right)\mathrm{\psi }\left(\mathrm{\zeta }\right)|\mathrm{d}\mathrm{\zeta }\le {\mathbf{K}}_{\mathfrak{r}(·)}{\parallel \varphi \parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}(\Theta )}{\parallel \mathrm{\psi }\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}(\Theta )},$$

where

$${\mathbf{K}}_{\mathfrak{r}(·)}:={\displaystyle \frac{1}{{\mathfrak{r}}_{-}}}-{\displaystyle \frac{1}{{\mathfrak{r}}_{+}}}+\parallel {\mathrm{\chi }}_{{\Theta }_{\infty }}{\parallel }_{\infty }+\parallel {\mathrm{\chi }}_{{\Theta }_1}{\parallel }_{\infty }+{\parallel {\mathrm{\chi }}_{{\Theta }_0}\parallel }_{\infty }.$$

We now introduce Herz spaces with variable smoothness and integrability, first formulated and systematically studied in [47]. They extend the classical Herz spaces by permitting the integrability and smoothness parameters to vary with position, offering a flexible framework for capturing local regularity and scaling behavior.

Definition 3 

([47]). Let $\mathfrak{r},\mathfrak{s}\in {\mathbf{P}}_0\left({\mathbf{R}}^{\mathrm{n}}\right)$ be variable exponents and let $\mathrm{\alpha }\in {\mathrm{L}}^{\infty }\left({\mathbf{R}}^{\mathrm{n}}\right)$ be a bounded measurable function, called the smoothness parameter.

We use the dyadic decomposition of ${\mathbf{R}}^{\mathrm{n}}$:

$${\mathfrak{B}}_{\mathrm{k}}=\mathfrak{B}(0,2^{\mathrm{k}}),{\mathbf{R}}_{\mathrm{k}}={\mathfrak{B}}_{\mathrm{k}}\setminus {\mathfrak{B}}_{\mathrm{k}-1},{\mathrm{\chi }}_{\mathrm{k}}={\mathrm{\chi }}_{{\mathbf{R}}_{\mathrm{k}}},\mathrm{k}\in \mathbf{Z}.$$

The inhomogeneous Herz space with variable exponents is defined as

$${\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}\left({\mathbf{R}}^{\mathrm{n}}\right):=\left\{\varphi \in {\mathrm{L}}_{\mathrm{loc}}^{\mathfrak{r}(·)}\left({\mathbf{R}}^{\mathrm{n}}\right):{\parallel \varphi \parallel }_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}<\infty \right\},$$

with quasi-norm

$${\parallel \varphi \parallel }_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}:={\parallel \varphi {\mathrm{\chi }}_{{\mathfrak{B}}_0}\parallel }_{\mathfrak{r}(·)}+\parallel {\left(2^{\mathrm{k}\mathrm{\alpha }(·)}\varphi {\mathrm{\chi }}_{\mathrm{k}}\right)}_{\mathrm{k}\ge 1}{\parallel }_{{\ell }^{\mathfrak{s}(·)}\left({\mathrm{L}}^{\mathfrak{r}(·)}\right)}.$$

Here, the first term controls the local integrability inside ${\mathfrak{B}}_0$, while the second term describes weighted integrability on the dyadic shells ${\mathbf{R}}_{\mathrm{k}}$ ($\mathrm{k}\ge 1$).

The homogeneous Herz space with variable exponents is

$${\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}\left({\mathbf{R}}^{\mathrm{n}}\right):=\left\{\varphi \in {\mathrm{L}}_{\mathrm{loc}}^{\mathfrak{r}(·)}({\mathbf{R}}^{\mathrm{n}}\setminus \left\{0\right\}):{\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}<\infty \right\},$$

with quasi-norm

$${\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}:=\parallel {\left(2^{\mathrm{k}\mathrm{\alpha }(·)}\varphi {\mathrm{\chi }}_{\mathrm{k}}\right)}_{\mathrm{k}\in \mathbf{Z}}{\parallel }_{{\ell }^{\mathfrak{s}(·)}\left({\mathrm{L}}^{\mathfrak{r}(·)}\right)}.$$

In this case, the decomposition runs over all shells ${\mathbf{R}}_{\mathrm{k}},\mathrm{k}\in \mathbf{Z}$, without a separate contribution from ${\mathfrak{B}}_0$.

Remark 1. 

Definition 3 recovers several known Herz-type spaces under specific choices of the exponent functions:

• If $\mathrm{\alpha }(·)=\mathrm{\alpha }$, $\mathfrak{r}(·)=\mathfrak{r}$, and $\mathfrak{s}(·)=\mathfrak{s}$, then we recover the classical Herz spaces (Herz [48]).
• If $\mathrm{\alpha }(·)=\mathrm{\alpha }$, $\mathfrak{r}(·)$ is variable, and $\mathfrak{s}(·)=\mathfrak{s}$, then we obtain Herz-type spaces with variable $\mathfrak{r}(·)$ (Izuki [49]).
• If $\mathrm{\alpha }(·)=\mathrm{\alpha }$, $\mathfrak{r}(·)=\mathfrak{r}$, and $\mathfrak{s}(·)=\mathfrak{s}$, we again recover the classical Herz spaces (Lu and Yang [50]).

Example 2. 

Taking the same assumptions on the exponent functions as in Definition 3, we consider the real line domain $\mathbf{R}$ and define

$$\mathrm{\psi }\left(\mathfrak{y}\right)={\displaystyle \frac{{\mathrm{\chi }}_{[4,\infty )}\left(\mathfrak{y}\right)}{{\mathfrak{y}}^{5/4}}},\mathfrak{p}\left(\mathfrak{y}\right)=5{\mathrm{\chi }}_{{\mathbf{R}}_{-}^{*}}\left(\mathfrak{y}\right)+4{\mathrm{\chi }}_{{\mathbf{R}}_{+}}\left(\mathfrak{y}\right),\mathfrak{q}\left(\mathfrak{y}\right)=4{\mathrm{\chi }}_{{\mathbf{R}}_{-}^{*}}\left(\mathfrak{y}\right)+3{\mathrm{\chi }}_{{\mathbf{R}}_{+}}\left(\mathfrak{y}\right),\mathrm{\beta }\left(\mathfrak{y}\right)=-\frac{1}{2},$$

where ${\mathrm{\chi }}_E$ denotes the characteristic function of a set E. Here, we denote

$${\mathbf{R}}_{+}=(0,\infty ),{\mathbf{R}}_{-}^{*}=(-\infty ,0).$$

Since $supp\mathrm{\psi }\subset [4,\infty )\subset {\mathbf{R}}_{\mathrm{k}}$ for $\mathrm{k}\ge 2$, it follows from Definition 3 that

$${\parallel \mathrm{\psi }\parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{p}(·),\mathfrak{q}(·)}^{\mathrm{\beta }(·)}\left(\mathbf{R}\right)}=\parallel {\left(2^{-\mathrm{k}/2}\mathrm{\psi }{\mathrm{\chi }}_{\mathrm{k}}\right)}_{\mathrm{k}\ge 2}{\parallel }_{{\ell }^2\left(L^2\right)}.$$

The corresponding modular is

$${\varrho }_{{\ell }^2\left(L^2\right)}\left({\displaystyle \frac{2^{-\mathrm{k}/2}\mathrm{\psi }{\mathrm{\chi }}_{\mathrm{k}}}{\mathrm{\tau }}}\right)={\displaystyle \frac{1}{{\mathrm{\tau }}^2}}\sum _{\mathrm{k}=2}^{\infty }{2}^{-\mathrm{k}}{\int }_{2^{\mathrm{k}}}^{2^{\mathrm{k}+1}}{\mathfrak{y}}^{-5/2}\mathrm{d}\mathfrak{y}.$$

Evaluating the integral yields

$${\int }_{2^{\mathrm{k}}}^{2^{\mathrm{k}+1}}{\mathfrak{y}}^{-5/2}\mathrm{d}\mathfrak{y}={\displaystyle \frac{2}{3}}{2}^{-3\mathrm{k}/2}\left(1-2^{-3/2}\right),$$

and hence

$$\varrho \lesssim {\displaystyle \frac{1}{{\mathrm{\tau }}^2}}\sum _{\mathrm{k}=2}^{\infty }{2}^{-5\mathrm{k}/2}={\displaystyle \frac{1}{{\mathrm{\tau }}^2}}·{\displaystyle \frac{2^{-5}}{1-2^{-5/2}}}.$$

By choosing

$$\mathrm{\tau }={\left(\sum _{\mathrm{k}=2}^{\infty }{2}^{-5\mathrm{k}/2}\right)}^{-1/2},$$

we obtain

$${\parallel \mathrm{\psi }\parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{p}(·),\mathfrak{q}(·)}^{\mathrm{\beta }(·)}\left(\mathbf{R}\right)}<\infty .$$

Therefore,

$$\mathrm{\psi }\in {\dot{\mathbf{K}}}_{\mathfrak{p}(·),\mathfrak{q}(·)}^{\mathrm{\beta }(·)}\left(\mathbf{R}\right).$$

Lemma 1 

([45]). Let $\mathrm{\alpha }\in {\mathrm{L}}^{\infty }\left({\mathbf{R}}^{\mathrm{n}}\right)$ and assume ${\mathrm{s}}_1>0$. If $\mathrm{\alpha }$ satisfies the log-Hölder continuity condition near the origin and at infinity, then

$${\mathrm{s}}_1^{\mathrm{\alpha }\left(\mathfrak{y}\right)}\lesssim {\mathrm{s}}_2^{\mathrm{\alpha }\left(\mathfrak{z}\right)}\times \left\{\begin{array}{cc}{\left({\displaystyle \frac{{\mathrm{s}}_1}{{\mathrm{s}}_2}}\right)}^{{\mathrm{\alpha }}^{+}},\hfill & 0<{\mathrm{s}}_2\le {\displaystyle \frac{{\mathrm{s}}_1}{2}},\hfill \\ 1,\hfill & {\displaystyle \frac{{\mathrm{s}}_1}{2}}<{\mathrm{s}}_2\le 2{\mathrm{s}}_1,\hfill \\ {\left({\displaystyle \frac{{\mathrm{s}}_1}{{\mathrm{s}}_2}}\right)}^{{\mathrm{\alpha }}^{-}},\hfill & {\mathrm{s}}_2>2{\mathrm{s}}_1,\hfill \end{array}\right.$$

for any $\mathfrak{y}\in \mathfrak{B}(0,{\mathrm{s}}_1)\setminus \mathfrak{B}\left(0,{\displaystyle \frac{{\mathrm{s}}_1}{2}}\right)$ and $\mathfrak{z}\in \mathfrak{B}(0,{\mathrm{s}}_2)\setminus \mathfrak{B}\left(0,{\displaystyle \frac{{\mathrm{s}}_2}{2}}\right)$, with constants independent of $\mathfrak{y}$, $\mathfrak{z}$, ${\mathrm{s}}_1$, and ${\mathrm{s}}_2$.

Lemma 2 

([45]). Let $\mathfrak{r}\in {\mathbf{P}}^{log}\left({\mathbf{R}}^{\mathrm{n}}\right)$. For any cubes (or balls) $\mathbf{M}\subset \mathbf{N}$,

$$\mathrm{C}{\left({\displaystyle \frac{\left|\mathbf{N}\right|}{\left|\mathbf{M}\right|}}\right)}^{1/{\mathfrak{r}}^{+}}⩽{\displaystyle \frac{\parallel {\mathrm{\chi }}_{\mathbf{N}}{\parallel }_{\mathfrak{r}(·)}}{\parallel {\mathrm{\chi }}_{\mathbf{M}}{\parallel }_{\mathfrak{r}(·)}}}⩽\mathrm{c}{\left({\displaystyle \frac{\left|\mathbf{N}\right|}{\left|\mathbf{M}\right|}}\right)}^{1/{\mathfrak{r}}^{-}},$$

where $\mathrm{c},\mathrm{C}>0$ are independent of $\left|\mathbf{N}\right|$ and $\left|\mathbf{M}\right|$.

Proposition 1 

([45]). Let $\mathrm{\alpha }\in {\mathrm{L}}^{\infty }\left({\mathfrak{R}}^{\mathtt{n}}\right)$, $\mathfrak{r}\in \mathbf{P}\left({\mathfrak{R}}^{\mathtt{n}}\right)$, and $\mathfrak{s}\in (0,\infty ]$. If $\mathrm{\alpha }(·)$ is log-Hölder continuous as $\left|\mathfrak{y}\right|\to \infty$, then

$${\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathrm{\alpha }(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)={\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{{\mathrm{\alpha }}_{\infty }}\left({\mathfrak{R}}^{\mathtt{n}}\right).$$

If $\mathrm{\alpha }(·)$ also has logarithmic decay near the origin, then

$${\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathrm{\alpha }(·)}}\approx {∥\left\{2^{\mathrm{k}\mathrm{\alpha }\left(0\right)}\varphi {\mathrm{\chi }}_{\mathrm{k}}\right\}∥}_{{\ell }_{<}^{\mathfrak{s}}\left({\mathrm{L}}^{\mathfrak{r}(·)}\right)}+{∥\left\{2^{\mathrm{k}{\mathrm{\alpha }}_{\infty }}\varphi {\mathrm{\chi }}_{\mathrm{k}}\right\}∥}_{{\ell }_{>}^{\mathfrak{s}}\left({\mathrm{L}}^{\mathfrak{r}(·)}\right)}.$$

Remark 2. 

Let $\mathrm{\alpha }\in \mathbb{R}$, $0<\mathfrak{r}\le \infty$, and $0<\mathfrak{s}<\infty$. It is worth noting that the homogeneous Herz space ${\dot{\mathbf{K}}}_{\mathfrak{s}}^{\mathrm{\alpha },\mathfrak{r}}(\Omega )$ admits a continuous embedding into each space ${\dot{\mathbf{K}}}_{{\mathfrak{s}}^{\prime }}^{\mathrm{\alpha },\mathfrak{r}}(\Omega )$ whenever ${\mathfrak{s}}^{\prime }\le \mathfrak{s}$. In other words, fixing $\mathrm{\alpha }$ and $\mathfrak{r}$, a decrease in the parameter $\mathfrak{s}$ preserves the inclusion relation between the corresponding Herz spaces, and the embedding operator acts continuously under these assumptions.

Lemma 3 

([51]). Let $0<\mathtt{a}<1$, $0<\mathfrak{s}⩽\infty$, and $\left\{{\mathrm{ϵ}}_{\mathrm{k}}\right\}\subset {\mathbf{R}}^{+}$ satisfy $\parallel \left\{{\mathrm{ϵ}}_{\mathrm{k}}\right\}{\parallel }_{{\ell }^{\mathfrak{s}}}=\mathbf{I}<\infty$. Then,

$${\delta }_{\mathrm{k}}=\sum _{\mathrm{j}⩽\mathrm{k}}{\mathtt{a}}^{\mathrm{k}-\mathrm{j}}{\mathrm{ϵ}}_{\mathrm{j}},{\mathrm{\sigma }}_{\mathrm{k}}=\sum _{\mathrm{j}⩾\mathrm{k}}{\mathtt{a}}^{\mathrm{j}-\mathrm{k}}{\mathrm{ϵ}}_{\mathrm{j}}$$

belong to ${\ell }^{\mathfrak{s}}$, and

$$\parallel \left\{{\delta }_{\mathrm{k}}\right\}{\parallel }_{{\ell }^{\mathfrak{s}}}+{\parallel \left\{{\mathrm{\sigma }}_{\mathrm{k}}\right\}\parallel }_{{\ell }^{\mathfrak{s}}}⩽\mathtt{c}\mathbf{I}.$$

Lemma 4 

([51]). Let $\mathfrak{r}\in {\mathbf{P}}_{\infty }^{log}\left({\mathbf{R}}^{\mathrm{n}}\right)$ and $\mathbf{R}:=\mathfrak{B}(0,\mathrm{r})\setminus \mathfrak{B}(0,r/2)$. If $\left|\mathbf{R}\right|⩾2^{-\mathtt{n}}$; then,

$$\parallel {\mathrm{\chi }}_{\mathbf{R}}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}\approx {\left|\mathbf{R}\right|}^{{\displaystyle \frac{1}{\mathfrak{r}\left(\mathfrak{y}\right)}}}\approx {\left|\mathbf{R}\right|}^{{\displaystyle \frac{1}{{\mathfrak{r}}_{\infty }}}},$$

with constants independent of $\mathrm{r}$ and $\mathfrak{y}\in \mathbf{R}$.

Definition 4 

([34]). $\mathrm{BMO}\left({\mathfrak{R}}^{\mathtt{n}}\right):=\{\mathrm{b}\in {\mathrm{L}}_{\mathrm{loc}}^1\left({\mathfrak{R}}^{\mathtt{n}}\right){:\parallel \mathrm{b}\parallel }_{\mathrm{BMO}}<\infty \}$, where

$${\parallel \mathrm{b}\parallel }_{\mathrm{BMO}}:=\underset{\mathrm{B}\subseteq {\mathfrak{R}}^{\mathtt{n}}}{sup}{\displaystyle \frac{1}{\left|\mathrm{B}\right|}}{\int }_{\mathrm{B}}\left|\mathrm{b}\left(\mathfrak{y}\right)-{\mathrm{b}}_{\mathrm{B}}\right|\mathtt{d}\mathfrak{y}.$$

Definition 5 

([34]). $\mathrm{VMO}\left({\mathfrak{R}}^{\mathtt{n}}\right):=\{\mathrm{b}\in \mathrm{BMO}\left({\mathfrak{R}}^{\mathtt{n}}\right):{lim}_{\mathfrak{z}\to 0^{+}}{\mathrm{\gamma }}_{\mathrm{b}}\left(\mathfrak{z}\right)=0\}$, with

$${\mathrm{\gamma }}_{\mathrm{b}}\left(\mathfrak{z}\right):=\underset{\mathrm{\rho }\le \mathfrak{z}}{sup}\underset{{\mathrm{B}}_{\mathrm{\rho }}}{sup}{\displaystyle \frac{1}{|{\mathrm{B}}_{\mathrm{\rho }}|}}{\int }_{{\mathrm{B}}_{\mathrm{\rho }}}\left|\mathrm{b}\left(\mathfrak{y}\right)-{\mathrm{b}}_{{\mathrm{B}}_{\mathrm{\rho }}}\right|d\mathfrak{y}.$$

3. The Major Results

The objective of this section is to examine the boundedness properties of a classical Bessel–Riesz-type operator denoted as ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$, which generalizes several known operators and recovers them as special cases under suitable choices of parameters. This formulation enhances analytical flexibility and is particularly effective for addressing complex integral estimates.

To highlight its structure and motivation, we consider the following classical Bessel–Riesz-type potential operator:

$${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\varphi \left(\mathfrak{y}\right):={\int }_{{\mathfrak{R}}^{\mathfrak{m}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\varphi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z},$$

where $\mathrm{\alpha }\in (0,\mathfrak{m})$ governs the singularity order and $\mathrm{\gamma }\ge 0$ controls polynomial decay at large distances.

For $\mathfrak{y}\notin supp\varphi$, the operator satisfies the following pointwise estimate:

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}(\varphi )\left(\mathfrak{y}\right)\right|\le {\int }_{{\mathfrak{R}}^{\mathfrak{m}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.$$

(1)

This inequality (1) captures the kernel’s refined structure: a fractional-type singularity governed by $\mathrm{\alpha }$ and a polynomial decay controlled by $\mathrm{\gamma }$. Such a structure provides a robust framework for the boundedness analysis of singular and potential-type operators, particularly in the setting of Herz spaces and other related function spaces.

Remark 3 

(Recovery of Classical Operators). The classical Bessel–Riesz-type operator is defined as follows (see Figure 1)

$${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\varphi \left(\mathfrak{y}\right):={\int }_{{\mathfrak{R}}^{\mathfrak{m}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\varphi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z},$$

which generalizes several well-known integral operators depending on the choice of parameters $\mathrm{\alpha },\mathrm{\gamma }\in \mathbb{R}$:

(i) 

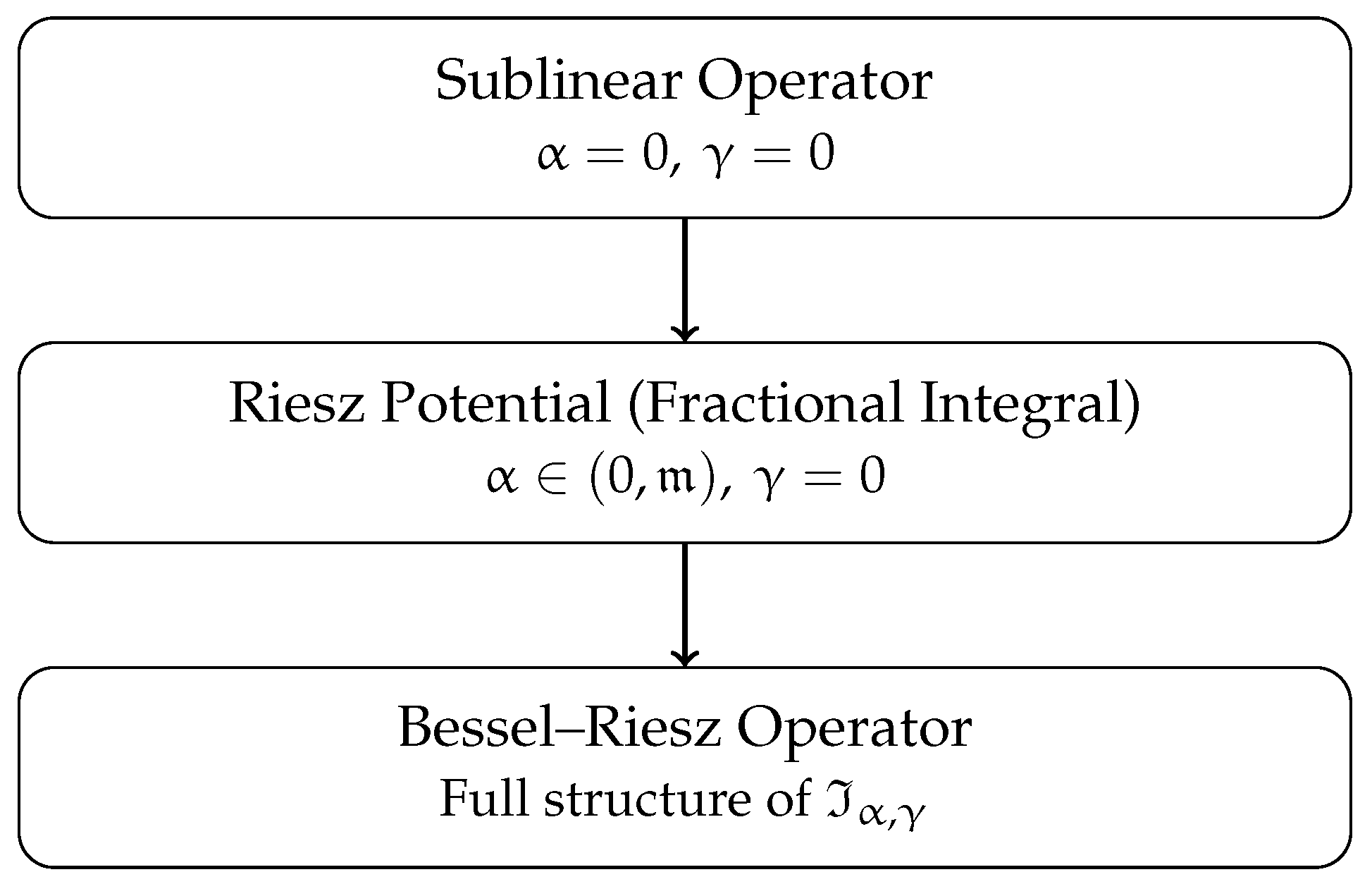
Classical fractional integral operator (Riesz potential):

If $\mathrm{\gamma }=0$, then ${\mathfrak{I}}_{\mathrm{\alpha },0}$ reduces to the Riesz potential of order $\mathrm{\alpha }\in (0,\mathfrak{m})$:

$$\mathfrak{I}\varphi \left(\mathfrak{y}\right)={\int }_{{\mathfrak{R}}^{\mathfrak{m}}}{\displaystyle \frac{\varphi \left(\mathfrak{z}\right)}{{|\mathfrak{y}-\mathfrak{z}|}^{\mathfrak{m}-\mathrm{\alpha }}}}\mathrm{d}\mathfrak{z},$$

as classically studied in [52,53].

(ii) 

Bessel–Riesz operator:

When $\mathrm{\gamma }>0$, the operator becomes the classical Bessel–Riesz potential:

$$\mathfrak{I}\varphi \left(\mathfrak{y}\right)={\int }_{{\mathfrak{R}}^{\mathfrak{m}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\varphi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z},$$

which improves the decay at infinity and appears in various potential-theoretic contexts [54].

(iii) 

Sublinear-type singular integral:

If $\mathrm{\alpha }=0$ and $\mathrm{\gamma }=0$, then

$$\mathfrak{I}\varphi \left(\mathfrak{y}\right)={\int }_{{\mathfrak{R}}^{\mathfrak{m}}}{\displaystyle \frac{\varphi \left(\mathfrak{z}\right)}{{|\mathfrak{y}-\mathfrak{z}|}^{\mathfrak{m}}}}\mathrm{d}\mathfrak{z},$$

which represents a highly singular kernel and arises in limiting cases of classical potential operators [53].

Novelty and Significance of the Operator: The classical Riesz potential does not provide sufficient decay at infinity and therefore fails to map $\varphi \in {\mathbf{K}}_2^{-1,1}\left({\mathfrak{R}}^3\right)$ into the same space. In contrast, the Bessel–Riesz operator ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ incorporates an additional decay factor ${(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{-\mathrm{\gamma }}$, which improves both the behavior at infinity and the integrability near the origin, allowing boundedness for the same $\varphi$.

Boundedness of Bessel–Riesz-Type Operators in Herz-Type Spaces

We have the following results.

Theorem 5. 

Let $\mathtt{n}\in \mathbb{N}$ and $0<\mathfrak{s}\le \infty$. Assume that $\mathfrak{r}\in {\mathcal{P}}_{\infty }^{log}\left({\mathbb{R}}^{\mathtt{n}}\right)$ is a variable exponent such that

$$1<{\mathfrak{r}}^{-}\le {\mathfrak{r}}^{+}<\infty .$$

Let $\mathfrak{a}(·)\in {\mathrm{L}}^{\infty }\left({\mathbb{R}}^{\mathtt{n}}\right)$ be log-Hölder continuous at infinity, with its value at infinity ${\mathfrak{a}}_{\infty }$ satisfying

$$-{\displaystyle \frac{\mathtt{n}}{{\mathfrak{r}}_{\infty }}}<{\mathfrak{a}}_{\infty }<{\displaystyle \frac{\mathtt{n}}{{\mathfrak{r}}_{\infty }^{\prime }}}.$$

Consider the Bessel–Riesz-type operator defined by

$${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\varphi \left(\mathfrak{y}\right):={\int }_{{\mathfrak{R}}^{\mathtt{n}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathtt{n}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\varphi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z},$$

where $\mathrm{\alpha }\in (0,\mathtt{n})$ is the singularity order and $\mathrm{\gamma }\ge 0$ is the decay parameter. Assume that ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ is bounded on the variable Lebesgue space ${\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)$. Then, ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ extends to a bounded operator on the homogeneous variable exponent Herz space ${\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)$, meaning that

$${∥{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}(\varphi )∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)}\le \mathrm{C}{∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)},$$

for all $\varphi \in {\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)\cap {\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)$, where the constant $\mathrm{C}>0$ depends only on the parameters of the operator and the function spaces.

Proof. 

Let ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ be the classical Bessel–Riesz-type operator defined by

$${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}(\varphi )\left(\mathfrak{y}\right):={\int }_{{\mathfrak{R}}^{\mathtt{n}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathtt{n}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\varphi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z},$$

where $\mathrm{\alpha }\in (0,\mathtt{n})$ and $\mathrm{\gamma }\ge 0$.

Suppose that ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ is bounded on the variable Lebesgue space ${\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)$, and let $\mathrm{\alpha }(·)\in {\mathrm{L}}^{\infty }\left({\mathfrak{R}}^{\mathtt{n}}\right)$ be log-Hölder continuous at infinity. Then, ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ is also a bounded operator on the variable exponent Herz space ${\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathrm{\alpha }(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)$.

To prove this, we estimate the Herz quasi-norm of ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}(\varphi )$ by using a dyadic decomposition of the domain. For a fixed $\mathrm{k}\in \mathbb{Z}$, we can decompose the function $\varphi$ as

$$\varphi =\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-1}}+\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}+1}\setminus {\mathfrak{B}}_{\mathrm{k}-1}}+\varphi ·{\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathrm{k}+1}}.$$

This leads to a decomposition of the operator:

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\varphi \left(\mathfrak{y}\right)\right|\le \left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-1}}\right)\left(\mathfrak{y}\right)\right|+\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}+1}\setminus {\mathfrak{B}}_{\mathrm{k}-1}}\right)\left(\mathfrak{y}\right)\right|+\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathrm{k}+1}}\right)\left(\mathfrak{y}\right)\right|.$$

We now estimate the contribution of the first term, ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-1}}\right)$, for $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{k}}:={\mathfrak{B}}_{\mathrm{k}}\setminus {\mathfrak{B}}_{\mathrm{k}-1}$. For all $\mathfrak{z}\in {\mathfrak{B}}_{\mathrm{k}-1}$, we have $\left|\mathfrak{z}\right|<2^{\mathrm{k}-1}$, and for $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{k}}$, we have $\left|\mathfrak{y}\right|\ge 2^{\mathrm{k}-1}$. This gives the pointwise estimate for the kernel:

$$|\mathfrak{y}-\mathfrak{z}|\gtrsim \left|\mathfrak{y}\right|\approx 2^{\mathrm{k}}.$$

Therefore, the kernel can be estimated as

$${\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathtt{n}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\lesssim {\left(2^{\mathrm{k}}\right)}^{\mathrm{\alpha }-\mathtt{n}}·{\left(2^{\mathrm{k}}\right)}^{-\mathrm{\gamma }}=2^{-\mathrm{k}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}.$$

This leads to the pointwise estimate for the operator:

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-1}}\right)\left(\mathfrak{y}\right)\right|\lesssim 2^{-\mathrm{k}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}{\int }_{{\mathfrak{B}}_{\mathrm{k}-1}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.$$

Applying Hölder’s inequality for the variable exponent space, we have

$${\int }_{{\mathfrak{B}}_{\mathrm{k}-1}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}\le {∥\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-1}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)}·{∥{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-1}}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)}.$$

Since ${\mathfrak{B}}_{\mathrm{k}-1}$ is a ball, ${∥{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-1}}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}}$ is equivalent to $|{\mathfrak{B}}_{\mathrm{k}-1}{|}^{{\displaystyle \frac{1}{{\mathfrak{r}}_{*}}}}$ for a suitable average ${\mathfrak{r}}_{*}$ of ${\mathfrak{r}}^{\prime }$ on the ball. Thus,

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-1}}\right)\left(\mathfrak{y}\right)\right|\lesssim 2^{-\mathrm{k}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}{∥\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-1}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)}.$$

The remaining two terms can be estimated similarly.

We now estimate the term involving the classical Bessel–Riesz operator applied to the “inner part” of the function,

$${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-2}\setminus {\mathfrak{B}}_{-2}}\right)\left(\mathfrak{y}\right).$$

Let $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{k}}:={\mathfrak{B}}_{\mathrm{k}}\setminus {\mathfrak{B}}_{\mathrm{k}-1}$, and let $\mathfrak{z}\in {\mathfrak{B}}_{\mathrm{k}-2}\setminus {\mathfrak{B}}_{-2}$. Then,

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-2}\setminus {\mathfrak{B}}_{-2}}\right)\left(\mathfrak{y}\right)\right|\le \sum _{\mathrm{j}=-1}^{\mathrm{k}-2}{\int }_{{\mathcal{A}}_{\mathrm{j}}}{\displaystyle \frac{1}{{|\mathfrak{y}-\mathfrak{z}|}^{\mathtt{n}-\mathrm{\alpha }}}}·{\displaystyle \frac{1}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.$$

For $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{k}}$ and $\mathfrak{z}\in {\mathcal{A}}_{\mathrm{j}}$ with $\mathrm{j}\le \mathrm{k}-2$, we have $|\mathfrak{y}-\mathfrak{z}|\gtrsim \left|\mathfrak{y}\right|\approx 2^{\mathrm{k}};$ hence,

$${\displaystyle \frac{1}{{|\mathfrak{y}-\mathfrak{z}|}^{\mathtt{n}-\mathrm{\alpha }}}}·{\displaystyle \frac{1}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\lesssim 2^{-\mathrm{k}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}.$$

Therefore,

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-2}\setminus {\mathfrak{B}}_{-2}}\right)\left(\mathfrak{y}\right)\right|\lesssim 2^{-\mathrm{k}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}\sum _{\mathrm{j}=-1}^{\mathrm{k}-2}{\int }_{{\mathcal{A}}_{\mathrm{j}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.$$

Applying Hölder inequality on each annulus and using the standard estimate for the characteristic function yields

$${\int }_{{\mathcal{A}}_{\mathrm{j}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}\le {∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{j}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)}·{∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{j}}}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)},$$

and consequently

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-2}\setminus {\mathfrak{B}}_{-2}}\right)\left(\mathfrak{y}\right)\right|\lesssim 2^{-\mathrm{k}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}\sum _{\mathrm{j}=-1}^{\mathrm{k}-2}{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{j}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)}{∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{j}}}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)}.$$

Using the norm estimates ${∥{\mathrm{\chi }}_{\mathrm{j}}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}}\approx 2^{{\displaystyle \frac{\mathrm{j}\mathtt{n}}{{\mathfrak{r}}_{\infty }^{\prime }}}}$ and ${∥{\mathrm{\chi }}_{\mathrm{k}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}\approx 2^{{\displaystyle \frac{\mathrm{k}\mathtt{n}}{{\mathfrak{r}}_{\infty }}}}$, the ${\mathrm{L}}^{\mathfrak{r}(·)}$-norm of the term is bounded by

$${∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}}}{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-2}\setminus {\mathfrak{B}}_{-2}}\right)∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}\lesssim \sum _{\mathrm{j}=-1}^{\mathrm{k}-2}{2}^{-\mathrm{k}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}{∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{j}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}{∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{j}}}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}}.$$

Substituting the norm estimates, we get

$${∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}}}{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{k}-2}\setminus {\mathfrak{B}}_{-2}}\right)∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}\lesssim 2^{-\mathrm{k}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}{2}^{{\displaystyle \frac{\mathrm{k}\mathtt{n}}{{\mathfrak{r}}_{\infty }}}}\sum _{\mathrm{j}=-1}^{\mathrm{k}-2}{2}^{{\displaystyle \frac{\mathrm{j}\mathtt{n}}{{\mathfrak{r}}_{\infty }^{\prime }}}}{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{j}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}.$$

Using the quasi-triangle inequality for ${\mathrm{L}}^{\mathfrak{r}(·)}$ norms, we have

$${∥\varphi {\mathrm{\chi }}_{{\overline{\mathbf{A}}}_{\mathrm{k}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}\lesssim \sum _{\mathrm{j}=-1}^1{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}+\mathrm{j}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}.$$

Hence,

$${∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}}}{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}^{\mathrm{\beta }}\left(\varphi {\mathrm{\chi }}_{{\overline{\mathbf{A}}}_{\mathrm{k}}}\right)∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}\lesssim \sum _{\mathrm{j}=-1}^1{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}+\mathrm{j}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}.$$

Taking the ${\ell }^{\mathfrak{s}}$-quasinorm over $\mathrm{k}\in \mathbb{Z}$, we obtain

$$\begin{array}{cc}& {\left\{\sum _{\mathrm{k}\in \mathbb{Z}}{2}^{\mathrm{k}{\mathrm{\alpha }}_{\infty }\mathfrak{s}}{∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}}}{\mathfrak{I}}_{\mathrm{\alpha },\gamma }^{\mathrm{\beta }}\left(\varphi {\mathrm{\chi }}_{{\overline{\mathbf{A}}}_{\mathrm{k}}}\right)∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}^{\mathfrak{s}}\right\}}^{{\displaystyle \frac{1}{\mathfrak{s}}}}\hfill \\ & \lesssim {\left\{\sum _{\mathrm{k}\in \mathbb{Z}}{2}^{\mathrm{k}{\mathrm{\alpha }}_{\infty }\mathfrak{s}}{\left(\sum _{\mathrm{j}=-1}^1{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}+\mathrm{j}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}\right)}^{\mathfrak{s}}\right\}}^{{\displaystyle \frac{1}{\mathfrak{s}}}}\hfill \\ & \lesssim {\left\{\sum _{\mathrm{j}=-1}^1\sum _{\mathrm{k}\in \mathbb{Z}}{2}^{\mathrm{k}{\mathrm{\alpha }}_{\infty }\mathfrak{s}}{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}+\mathrm{j}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}^{\mathfrak{s}}\right\}}^{{\displaystyle \frac{1}{\mathfrak{s}}}}\hfill \\ & ={\left\{\sum _{\mathrm{j}=-1}^1{2}^{-\mathrm{j}{\mathrm{\alpha }}_{\infty }\mathfrak{s}}\sum _{\ell \in \mathbb{Z}}{2}^{\ell {\mathrm{\alpha }}_{\infty }\mathfrak{s}}{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\ell }}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}^{\mathfrak{s}}\right\}}^{{\displaystyle \frac{1}{\mathfrak{s}}}}\hfill \\ & \lesssim {\left\{\sum _{\ell \in \mathbb{Z}}{2}^{\ell {\mathrm{\alpha }}_{\infty }\mathfrak{s}}{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\ell }}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}^{\mathfrak{s}}\right\}}^{{\displaystyle \frac{1}{\mathfrak{s}}}}\hfill \\ & ={∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{{\mathrm{\alpha }}_{\infty }}\left({\mathfrak{R}}^{\mathtt{n}}\right)}.\hfill \end{array}$$

The final step is to show that ‘${∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{{\mathrm{\alpha }}_{\infty }}}\le \mathrm{C}{∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathrm{\alpha }(·)}}$’ by leveraging the log-Hölder continuity of the exponent ‘$\mathrm{\alpha }(·)$’ and the properties of the Herz space norm.

• Estimation of ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathrm{k}+\mathbf{2}}}\right)\left(\mathfrak{y}\right)$:

We now consider the term where the support of the function is far from the point of evaluation. Let $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{k}}$, and let $\mathfrak{z}\in {\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathrm{k}+\mathbf{2}}$. The latter implies that $\mathfrak{z}\in {\mathcal{A}}_{\mathrm{j}}$ for some $\mathrm{j}\ge \mathbf{k}+\mathbf{2}$. The operator action satisfies

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathrm{k}+\mathbf{2}}}\right)\left(\mathfrak{y}\right)\right|\le \sum _{\mathrm{j}⩾\mathrm{k}+\mathbf{2}}{\int }_{{\mathcal{A}}_{\mathrm{j}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathtt{n}}}{{(\mathbf{1}+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.$$

For $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{k}}$ and $\mathfrak{z}\in {\mathcal{A}}_{\mathrm{j}}$ with $\mathrm{j}\ge \mathbf{k}+\mathbf{2}$, we have the pointwise estimate:

$$|\mathfrak{y}-\mathfrak{z}|\ge \left|\mathfrak{z}\right|-\left|\mathfrak{y}\right|\gtrsim {\mathbf{2}}^{\mathrm{j}}.$$

Combining this with the decay of the kernel, we obtain

$${\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathtt{n}}}{{(\mathbf{1}+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\lesssim {\mathbf{2}}^{-\mathrm{j}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}.$$

Therefore, the far-field contribution satisfies

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathrm{k}+\mathbf{2}}}\right)\left(\mathfrak{y}\right)\right|\lesssim \sum _{\mathrm{j}⩾\mathrm{k}+\mathbf{2}}{\mathbf{2}}^{-\mathrm{j}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}{\int }_{{\mathcal{A}}_{\mathrm{j}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.$$

Applying the variable exponent Hölder’s inequality and the norm estimates from Lemma 4, we have

$${\int }_{{\mathcal{A}}_{\mathrm{j}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}\lesssim {∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{j}}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}·{\mathbf{2}}^{{\displaystyle \frac{\mathrm{j}\mathtt{n}}{{\mathfrak{r}}_{\infty }^{\prime }}}}.$$

This gives the ${\mathbf{L}}^{\mathfrak{r}(·)}$-norm estimate for the term on ${\mathcal{A}}_{\mathbf{k}}$:

$$\begin{array}{cc}\hfill {\mathbf{2}}^{\mathbf{k}{\mathrm{\alpha }}_{\infty }}& {∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{k}}}{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathrm{k}+\mathbf{2}}}\right)∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}\hfill \\ & \lesssim {\mathbf{2}}^{\mathbf{k}{\mathrm{\alpha }}_{\infty }}{∥{\mathrm{\chi }}_{{\mathcal{A}}_{\mathbf{k}}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}\sum _{\mathbf{j}⩾\mathbf{k}+\mathbf{2}}{\mathbf{2}}^{-\mathrm{j}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}·{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathbf{j}}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}·{\mathbf{2}}^{{\displaystyle \frac{\mathbf{j}\mathtt{n}}{{\mathfrak{r}}_{\infty }^{\prime }}}}\hfill \\ & \lesssim {\mathbf{2}}^{\mathrm{k}{\mathrm{\alpha }}_{\infty }}·{\mathbf{2}}^{{\displaystyle \frac{\mathrm{k}\mathtt{n}}{{\mathfrak{r}}_{\infty }}}}\sum _{\mathbf{j}⩾\mathbf{k}+\mathbf{2}}{\mathbf{2}}^{\mathrm{j}\left(-\mathtt{n}+\mathrm{\alpha }-\mathrm{\gamma }+{\displaystyle \frac{\mathtt{n}}{{\mathfrak{r}}_{\infty }^{\prime }}}\right)}{∥\varphi {\mathrm{\chi }}_{{\mathcal{A}}_{\mathrm{j}}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}.\hfill \end{array}$$

To conclude, we first decompose $\varphi$ as follows:

$$\varphi =\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathbf{0}}}+\varphi {\mathrm{\chi }}_{{\mathbf{R}}_{\mathbf{1}}}+\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathbf{1}}}.$$

Then, for $\mathfrak{y}\in {\mathfrak{B}}_{\mathbf{0}}$, we use the triangle inequality to estimate the operator pointwise:

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\varphi \left(\mathfrak{y}\right)\right|\le \left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathbf{0}}}\right)\left(\mathfrak{y}\right)\right|+\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathbf{R}}_{\mathbf{1}}}\right)\left(\mathfrak{y}\right)\right|+\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathbf{1}}}\right)\left(\mathfrak{y}\right)\right|.$$

We treat each term in turn.

• Local part: Using the boundedness of ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ on ${\mathbf{L}}^{\mathfrak{r}(·)}$, we have

$${∥{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathbf{0}}}\right){\mathrm{\chi }}_{{\mathfrak{B}}_{\mathbf{0}}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}\lesssim {∥\varphi {\mathrm{\chi }}_{{\mathfrak{B}}_{\mathbf{0}}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}\le {∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{{\mathrm{\alpha }}_{\infty }}}.$$

Near shell: Similarly, for the near-shell region, the boundedness of the operator yields

$${∥{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathbf{R}}_{\mathbf{1}}}\right){\mathrm{\chi }}_{{\mathfrak{B}}_{\mathbf{0}}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}\lesssim {∥\varphi {\mathrm{\chi }}_{{\mathbf{R}}_{\mathbf{1}}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}\le {∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{{\mathrm{\alpha }}_{\infty }}}.$$

Tail part: For $\mathfrak{y}\in {\mathfrak{B}}_{\mathbf{0}}$ and $\mathfrak{z}\in {\mathbf{R}}_{\mathrm{k}}\subset {\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathbf{1}}$, $\mathbf{k}\ge \mathbf{2}$, we have $|\mathfrak{y}-\mathfrak{z}|\gtrsim {\mathbf{2}}^{\mathrm{k}}$, and $\parallel \mathfrak{z}\parallel \gtrsim {\mathbf{2}}^{\mathrm{k}}$. Hence,

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathbf{1}}}\right)\left(\mathfrak{y}\right)\right|\lesssim \sum _{\mathrm{k}\ge \mathbf{2}}{\mathbf{2}}^{-\mathrm{k}(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma })}{\int }_{{\mathbf{R}}_{\mathrm{k}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.$$

Applying Hölder’s inequality and Lemma 4, we have

$${\int }_{{\mathbf{R}}_{\mathrm{k}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}\lesssim {∥\varphi {\mathrm{\chi }}_{\mathrm{k}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}{\mathbf{2}}^{{\displaystyle \frac{\mathrm{k}\mathtt{n}}{{\mathfrak{r}}_{\infty }^{\prime }}}},$$

so we conclude that

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathbf{1}}}\right)\left(\mathfrak{y}\right)\right|\lesssim \sum _{\mathbf{k}\ge \mathbf{2}}{\mathbf{2}}^{-\mathbf{k}\left(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma }-{\displaystyle \frac{\mathtt{n}}{{\mathfrak{r}}_{\infty }^{\prime }}}\right)}{∥\varphi {\mathrm{\chi }}_{\mathbf{k}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}.$$

Taking the ${\mathbf{L}}^{\mathfrak{r}(·)}$-norm over ${\mathfrak{B}}_{\mathbf{0}}$ yields

$${∥{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi {\mathrm{\chi }}_{{\mathfrak{R}}^{\mathtt{n}}\setminus {\mathfrak{B}}_{\mathbf{1}}}\right){\mathrm{\chi }}_{{\mathfrak{B}}_{\mathbf{0}}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}\lesssim \sum _{\mathrm{k}\ge \mathbf{2}}{\mathbf{2}}^{-\mathrm{k}\left(\mathtt{n}-\mathrm{\alpha }+\mathrm{\gamma }-{\displaystyle \frac{\mathtt{n}}{{\mathfrak{r}}_{\infty }^{\prime }}}\right)}{∥\varphi {\mathrm{\chi }}_{\mathrm{k}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}\lesssim {∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{{\mathrm{\alpha }}_{\infty }}}.$$

Combining all parts yields the final estimate:

$${∥\left({\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\varphi \right){\mathrm{\chi }}_{{\mathfrak{B}}_{\mathbf{0}}}∥}_{{\mathbf{L}}^{\mathfrak{r}(·)}}\lesssim {∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{{\mathrm{\alpha }}_{\infty }}}\le \mathbf{C}{∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathrm{\alpha }(·)}\left({\mathfrak{R}}^{\mathtt{n}}\right)}.$$

This completes the proof. □

Remark 4. 

This remark emphasizes that Theorem 5 extends several existing results in the literature.

In particular,

• For $\mathrm{\alpha }(·)=\mathrm{\alpha }$ and $\mathrm{\gamma }=0$, the result reduces to Theorem 3.3 in [43].
• For $\mathfrak{r}(·)=\mathfrak{r}$, $\mathrm{\alpha }(·)=\mathrm{\alpha }$, and $\mathrm{\gamma }=0$, the result reduces to Theorem 2.1 in [44].
• For $\mathrm{\gamma }=0$, the result refines Theorem 4.2 and recovers the corresponding results in [45].

Theorem 6. 

Let $0<\mathrm{\alpha }<\mathrm{m}$ and $\mathrm{\gamma }\ge 0$. Let $\mathfrak{r}(·)$ be a variable exponent such that

$$\mathfrak{r}\in {\mathbf{P}}_0^{log}\left({\mathfrak{R}}^{\mathrm{m}}\right)\cap {\mathbf{P}}_{\infty }^{log}\left({\mathfrak{R}}^{\mathrm{m}}\right)$$

and

$$1<{\mathfrak{r}}^{-}\le {\mathfrak{r}}^{+}<{\displaystyle \frac{\mathrm{m}}{\mathrm{\alpha }}}.$$

Let $\mathfrak{s}(·)\in {\mathbf{P}}_0\left({\mathfrak{R}}^{\mathrm{m}}\right)$. Let $\mathfrak{a}(·)\in {\mathrm{L}}^{\infty }\left({\mathfrak{R}}^{\mathrm{m}}\right)$ be log-Hölder continuous both at the origin and at infinity, with

$$\mathrm{\alpha }-{\displaystyle \frac{\mathrm{m}}{{\mathfrak{r}}^{-}}}<{\mathfrak{a}}^{-}\le {\mathfrak{a}}^{+}<{\displaystyle \frac{\mathrm{m}}{{\mathfrak{r}}^{\prime +}}}.$$

Define the unweighted Bessel–Riesz-type operator by

$${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\varphi (\omega ):={\int }_{{\mathfrak{R}}^{\mathrm{m}}}{\displaystyle \frac{{|\omega -\mathfrak{z}|}^{\mathrm{\alpha }-\mathrm{m}}}{{(1+|\omega -\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\varphi \left(\mathfrak{z}\right)d\mathfrak{z}.$$

If ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ is bounded from

$${\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathrm{m}}\right)\mathit{into}{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}\left({\mathfrak{R}}^{\mathrm{m}}\right),$$

where the Sobolev conjugate exponent ${\mathfrak{r}}^{*}(·)$ is defined by

$${\displaystyle \frac{1}{{\mathfrak{r}}^{*}\left(\mathfrak{y}\right)}}={\displaystyle \frac{1}{\mathfrak{r}\left(\mathfrak{y}\right)}}-{\displaystyle \frac{\mathrm{\alpha }}{\mathrm{m}}},$$

then it is also bounded between the homogeneous variable-exponent Herz spaces:

$${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}:{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathrm{m}}\right)⟶{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathrm{m}}\right).$$

Proof. 

In light of Proposition 1, let $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{\kappa }}$ for some $\mathrm{\kappa }\in \mathbb{Z}$. We decompose the domain of integration as

$${\mathfrak{R}}^{\mathfrak{m}}={\mathfrak{B}}_{\mathrm{\kappa }-2}\cup {\tilde{\mathfrak{B}}}_{\mathrm{\kappa }}\cup \left({\mathfrak{R}}^{\mathfrak{m}}\setminus {\mathfrak{B}}_{\mathrm{\kappa }+2}\right),$$

where

$${\mathfrak{B}}_r=\left\{\right|\mathfrak{z}|<2^r\},{\tilde{\mathfrak{B}}}_{\mathrm{\kappa }}=\{2^{\mathrm{\kappa }-2}\le \left|\mathfrak{z}\right|<2^{\mathrm{\kappa }+2}\}.$$

Hence, by linearity and the quasi-triangle inequality,

$$\begin{array}{cc}\hfill \left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\varphi \left(\mathfrak{y}\right)\right|& \le \left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)\left(\mathfrak{y}\right)\right|+\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\overline{\mathfrak{B}}}_{\mathrm{\kappa }}}\right)\left(\mathfrak{y}\right)\right|\hfill \\ & +\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{R}}^{\mathfrak{m}}\setminus {\mathfrak{B}}_{\mathrm{\kappa }+2}}\right)\left(\mathfrak{y}\right)\right|.\hfill \end{array}$$

Here, the operator is defined by

$${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\varphi \left(\mathfrak{y}\right):={\int }_{{\mathfrak{R}}^{\mathfrak{m}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\varphi \left(\mathfrak{z}\right)\mathrm{d}\mathfrak{z}.$$

We now focus on the first term, the inner part. We decompose the ball ${\mathfrak{B}}_{\mathrm{\kappa }-2}$ dyadically:

$${\mathfrak{B}}_{\mathrm{\kappa }-2}=\bigcup _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{\mathcal{A}}_{\mathrm{\sigma }},{\mathcal{A}}_{\mathrm{\sigma }}=\{2^{\mathrm{\sigma }}\le \left|\mathfrak{z}\right|<2^{\mathrm{\sigma }+1}\}.$$

Using this decomposition and the quasi-triangle inequality, we have

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)\left(\mathfrak{y}\right)\right|\le \sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{\int }_{{\mathcal{A}}_{\mathrm{\sigma }}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.$$

Since $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{\kappa }}$ and $\mathfrak{z}\in {\mathcal{A}}_{\mathrm{\sigma }}$ with $\mathrm{\sigma }\le \mathrm{\kappa }-2$, we have $|\mathfrak{y}-\mathfrak{z}|\approx \left|\mathfrak{y}\right|\approx 2^{\mathrm{\kappa }}$. The kernel can then be estimated as

$${\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\lesssim 2^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}.$$

Therefore,

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)\left(\mathfrak{y}\right)\right|\lesssim \sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}{\int }_{{\mathcal{A}}_{\mathrm{\sigma }}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.$$

Applying the variable exponent Hölder inequality and the norm estimate

$$\parallel {\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}}\approx 2^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}$$

from Lemma 4, we obtain for each $\mathrm{\sigma }$:

$${\int }_{{\mathcal{A}}_{\mathrm{\sigma }}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}\lesssim \parallel \varphi {\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}{2}^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}.$$

Substituting this back, we have

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)\left(\mathfrak{y}\right)\right|\lesssim 2^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}\sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}\parallel \varphi {\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}.$$

Taking the ${\mathrm{L}}^{\mathfrak{r}(·)}$-norm in $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{\kappa }}$ and using the estimate

$$\parallel {\mathrm{\chi }}_{\mathrm{\kappa }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}\approx 2^{{\displaystyle \frac{\mathrm{\kappa }\mathfrak{m}}{{\mathfrak{r}}_{\infty }}}}$$

from Lemma 4, we obtain

$$\begin{array}{cc}& 2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}\parallel {\mathrm{\chi }}_{\mathrm{\kappa }}{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right){\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}\hfill \\ & \lesssim 2^{\mathrm{\kappa }({\mathfrak{a}}_{\infty }+{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}_{\infty }}})}{2}^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}\sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}\parallel \varphi {\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}\hfill \\ & =2^{\mathrm{\kappa }\overline{\delta }}\sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}\parallel \varphi {\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}},\hfill \end{array}$$

where

$$\tilde{\delta }:={\mathfrak{a}}_{\infty }+{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}_{\infty }}}-(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma }).$$

Under the restriction

$$0<{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}^{\prime +}}}$$

the geometric factor $2^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}$ is summable as $\mathrm{\sigma }\to -\infty$. After taking the ${\ell }^{\mathfrak{s}}$-quasinorm in $\mathrm{\kappa }$, the inner contribution is controlled by the Herz quasi-norm:

$${\left\{\sum _{\mathrm{\kappa }<0}{2}^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }\mathfrak{s}}\parallel {\mathrm{\chi }}_{\mathrm{\kappa }}{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right){\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}^{\mathfrak{s}}\right\}}^{1/\mathfrak{s}}\lesssim {\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathfrak{a}(·)}}.$$

From the previous inner-region estimate and using the log-Hölder property of $\mathfrak{a}$, we multiply both sides by $2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}$. For the (unweighted) Bessel–Riesz operator ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ we get

$$\begin{array}{cc}\hfill 2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)\left(\mathfrak{y}\right)\right|& \lesssim 2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}\sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{\int }_{{\mathbf{R}}_{\mathrm{\sigma }}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

Since $\mathfrak{y}\in {\mathbf{R}}_{\mathrm{\kappa }}$ and $\mathfrak{z}\in {\mathbf{R}}_{\mathrm{\sigma }}\subset {\mathfrak{B}}_{\mathrm{\kappa }-2}$, we have $|\mathfrak{y}-\mathfrak{z}|\gtrsim 2^{\mathrm{\kappa }}$ and $\left|\mathfrak{z}\right|\lesssim 2^{\mathrm{\sigma }+1}$, $\left|\mathfrak{y}\right|\approx 2^{\mathrm{\kappa }}$. Hence,

$${\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\lesssim 2^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}.$$

Using this in the previous display and the log–Hölder relation

$$2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}\le C{2}^{(\mathrm{\kappa }-\mathrm{\sigma }){\mathfrak{a}}^{+}}{2}^{\mathrm{\sigma }\mathfrak{a}\left(\mathfrak{z}\right)},$$

we obtain

$$\begin{array}{cc}\hfill 2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)\left(\mathfrak{y}\right)\right|& \lesssim \sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{(\mathrm{\kappa }-\mathrm{\sigma }){\mathfrak{a}}^{+}}{2}^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}\hfill \\ & ·{\int }_{{\mathbf{R}}_{\mathrm{\sigma }}}{2}^{\mathrm{\sigma }\mathfrak{a}\left(\mathfrak{z}\right)}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

Now take the ${\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}$-norm in $\mathfrak{y}$ over ${\mathbf{R}}_{\mathrm{\kappa }}$. By generalized Minkowski and Hölder,

$$\begin{array}{cc}& \parallel 2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}){\mathrm{\chi }}_{\mathrm{\kappa }}{\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}}\hfill \\ & \lesssim \parallel {\mathrm{\chi }}_{\mathrm{\kappa }}{\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}}\sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{(\mathrm{\kappa }-\mathrm{\sigma }){\mathfrak{a}}^{+}}{2}^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}{\int }_{{\mathbf{R}}_{\mathrm{\sigma }}}{2}^{\mathrm{\sigma }\mathfrak{a}\left(\mathfrak{z}\right)}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

Apply Hölder on the inner integral and Lemma 4 (norms of characteristic functions):

$${\int }_{{\mathbf{R}}_{\mathrm{\sigma }}}{2}^{\mathrm{\sigma }\mathfrak{a}\left(\mathfrak{z}\right)}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}\lesssim \parallel 2^{\mathrm{\sigma }\mathfrak{a}(·)}\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}\parallel {\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}}\approx \parallel 2^{\mathrm{\sigma }\mathfrak{a}(·)}\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}{2}^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}.$$

Substituting and simplifying the powers of 2 gives

$$\begin{array}{cc}& \parallel 2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}){\mathrm{\chi }}_{\mathrm{\kappa }}{\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}}\hfill \\ & \lesssim \parallel {\mathrm{\chi }}_{\mathrm{\kappa }}{\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}}{2}^{\mathrm{\kappa }\left({\mathfrak{a}}^{+}-(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })\right)}\sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{-\mathrm{\sigma }\left({\mathfrak{a}}^{+}-{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}\right)}\parallel 2^{\mathrm{\sigma }\mathfrak{a}(·)}\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}.\hfill \end{array}$$

Set

$$\tilde{\delta }:={\mathfrak{a}}^{+}-(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })+{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{*}}},$$

so the prefactor becomes $2^{\mathrm{\kappa }\overline{\delta }}$ (using $\parallel {\mathrm{\chi }}_{\mathrm{\kappa }}{\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}}\approx 2^{{\displaystyle \frac{\mathrm{\kappa }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{*}}}}$). To guarantee the summability of the inner geometric factor as $\mathrm{\sigma }\to -\infty$, we impose the condition

$${\mathfrak{a}}^{+}-{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}>0.$$

Under this restriction, summing the geometric series and then taking the ${\ell }^{\mathfrak{s}}$-quasinorm in $\mathrm{\kappa }<0$ yields the control

$${\left\{\sum _{\mathrm{\kappa }<0}{2}^{\mathrm{\kappa }\mathfrak{a}\left(0\right)\mathfrak{s}}\parallel {\mathrm{\chi }}_{\mathrm{\kappa }}{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}){\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}}^{\mathfrak{s}}\right\}}^{1/\mathfrak{s}}\lesssim {\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}}^{\mathfrak{a}(·)}}.$$

We now estimate the local contribution to the norm of the Bessel–Riesz operator. We first recall the properties of variable exponents. For any ${\mathfrak{y}}_{\mathrm{\sigma }}\in {\mathcal{A}}_{\mathrm{\sigma }}$ and ${\mathfrak{y}}_{\mathrm{\kappa }}\in {\mathcal{A}}_{\mathrm{\kappa }}$, where $\mathrm{\sigma }\le \mathrm{\kappa }-2$, the log-Hölder continuity of $\mathfrak{r}(·)$ implies

$${\displaystyle \frac{{\left|{\mathcal{A}}_{\mathrm{\kappa }}\right|}^{\frac{1}{\mathfrak{r}\left({\mathfrak{y}}_{\mathrm{\kappa }}\right)}}}{{\left|{\mathcal{A}}_{\mathrm{\sigma }}\right|}^{\frac{1}{\mathfrak{r}\left({\mathfrak{y}}_{\mathrm{\sigma }}\right)}}}}\le \mathrm{C}·2^{(\mathrm{\kappa }-\mathrm{\sigma }){\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}^{-}}}}.$$

We estimate the local contribution where the function $\varphi$ is supported on the inner ball ${\mathfrak{B}}_{\mathrm{\kappa }-2}$. For $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{\kappa }}$, we have

$$\begin{array}{cc}\hfill \left|{\mathfrak{I}}_{\mathrm{\alpha },\gamma }\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)\left(\mathfrak{y}\right)\right|& \le \sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{\int }_{{\mathcal{A}}_{\mathrm{\sigma }}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}|\varphi \left(\mathfrak{z}\right)|\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

Since $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{\kappa }}$ and $\mathfrak{z}\in {\mathcal{A}}_{\mathrm{\sigma }}$ with $\mathrm{\sigma }\le \mathrm{\kappa }-2$, we have $|\mathfrak{y}-\mathfrak{z}|\approx \left|\mathfrak{y}\right|\approx 2^{\mathrm{\kappa }}$. The kernel can thus be bounded as follows:

$${\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\lesssim 2^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}.$$

Applying the variable exponent Hölder’s inequality and the norm estimate $\parallel {\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}}\lesssim 2^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}$, we obtain the pointwise bound

$$\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)\left(\mathfrak{y}\right)\right|\lesssim \sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}{2}^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}\parallel \varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}.$$

Taking the ${\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}$-norm on ${\mathcal{A}}_{\mathrm{\kappa }}$, we have

$$\begin{array}{cc}& {∥{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right){\mathrm{\chi }}_{\mathrm{\kappa }}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}}\hfill \\ & \lesssim \sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}·2^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}\parallel \varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}·{\parallel {\mathrm{\chi }}_{\mathrm{\kappa }}\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}}\hfill \\ & \lesssim 2^{\mathrm{\kappa }\left({\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{*}}}\right)}\sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}·2^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}{\parallel \varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}\parallel }_{{\mathrm{L}}^{\mathfrak{r}(·)}}.\hfill \end{array}$$

The final bound is then obtained by a change in variable and summation over $\mathrm{\kappa }$, under the condition

$$\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma }>0$$

to ensure that the series converges.

To estimate $2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}·{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)$ in the ${\ell }_{>}^{{\mathfrak{s}}_{\infty }}$-norm, we argue analogously, now with $2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}$ in place of $2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}$. Then,

$$\begin{array}{cc}& {∥2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}·{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)·{\mathrm{\chi }}_{\mathrm{\kappa }}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}\hfill \\ & \lesssim \sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{(\mathrm{\kappa }-\mathrm{\sigma }){\mathfrak{a}}^{+}}·2^{-\mathrm{\kappa }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}·{∥2^{\mathrm{\sigma }\mathfrak{a}(·)}\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}·{\left|{\mathcal{A}}_{\mathrm{\sigma }}\right|}^{-{\displaystyle \frac{1}{\mathfrak{r}\left({\mathfrak{y}}_{\mathrm{\sigma }}\right)}}}·{\left|{\mathcal{A}}_{\mathrm{\kappa }}\right|}^{{\displaystyle \frac{1}{\mathfrak{r}\left({\mathfrak{y}}_{\mathrm{\kappa }}\right)}}}\hfill \\ & \lesssim \sum _{\mathrm{\sigma }=-\infty }^{\mathrm{\kappa }-2}{2}^{(\mathrm{\kappa }-\mathrm{\sigma })\left({\mathfrak{a}}^{+}-(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })+{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}^{-}}}\right)}·{∥2^{\mathrm{\sigma }\mathfrak{a}(·)}\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}.\hfill \end{array}$$

For any $\mathrm{\kappa }\ge 0$, we once again apply Lemma 3 to obtain

$$\begin{array}{cc}\hfill & {\left\{\sum _{\mathrm{\kappa }=0}^{\infty }{∥2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}·{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)·{\mathrm{\chi }}_{\mathrm{\kappa }}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}^{{\mathfrak{s}}_{\infty }}\right\}}^{{\displaystyle \frac{1}{{\mathfrak{s}}_{\infty }}}}\hfill \\ \hfill & \le \mathrm{C}\left\{\sum _{\mathrm{\kappa }=0}^{\infty }\left[2^{\mathrm{\kappa }\left({\mathfrak{a}}^{+}-(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })+{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}^{-}}}\right)}·\sum _{\mathrm{\sigma }=-\infty }^0{2}^{-\mathrm{\sigma }\left({\mathfrak{a}}^{+}-(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })+{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}^{-}}}\right)}\right.\right.\hfill \\ \hfill & {\left.{\left.·\underset{\mathrm{\sigma }\le 0}{sup}{2}^{\mathrm{\sigma }\mathfrak{a}\left(0\right)}{∥\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}\right]}^{{\mathfrak{s}}_{\infty }}\right\}}^{{\displaystyle \frac{1}{{\mathfrak{s}}_{\infty }}}}\hfill \\ \hfill & +\mathrm{C}{\left\{\sum _{\mathrm{\kappa }=0}^{\infty }{\left[\sum _{\mathrm{\sigma }=1}^{\mathrm{\kappa }-2}{2}^{(\mathrm{\kappa }-\mathrm{\sigma })\left({\mathfrak{a}}^{+}-(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })+{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}^{-}}}\right)}·{∥2^{\mathrm{\sigma }\mathfrak{a}(·)}\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}\right]}^{{\mathfrak{s}}_{\infty }}\right\}}^{{\displaystyle \frac{1}{{\mathfrak{s}}_{\infty }}}}.\hfill \end{array}$$

Since ${\mathfrak{a}}^{+}-(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })+{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}^{-}}}<0,$ we conclude that

$${\left\{\sum _{\mathrm{\kappa }=0}^{\infty }{∥2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}·{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{B}}_{\mathrm{\kappa }-2}}\right)·{\mathrm{\chi }}_{\mathrm{\kappa }}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}^{{\mathfrak{s}}_{\infty }}\right\}}^{{\displaystyle \frac{1}{{\mathfrak{s}}_{\infty }}}}\le \mathrm{C}{∥\varphi ∥}_{{\mathbf{K}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}.$$

For the middle part ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\overline{\mathbf{A}}}_{\mathrm{\kappa }}}\right),$ by using the boundedness of ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$ from ${\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)$ to ${\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)$, we obtain

$$\begin{array}{cc}& {∥{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\overline{\mathbf{A}}}_{\mathrm{\kappa }}}\right)∥}_{{\overline{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}\hfill \\ & \le {∥\left\{2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}·{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\overline{\mathbf{A}}}_{\mathrm{\kappa }}}\right)·{\mathrm{\chi }}_{\mathrm{\kappa }}\right\}∥}_{{\ell }_{<}^{\mathfrak{s}\left(0\right)}\left({\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)\right)}+{∥\left\{2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}·{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\overline{\mathbf{A}}}_{\mathrm{\kappa }}}\right)·{\mathrm{\chi }}_{\mathrm{\kappa }}\right\}∥}_{{\ell }_{>}^{{\mathfrak{s}}_{\infty }}\left({\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)\right)}\hfill \\ & \le \mathrm{C}·{∥\left\{2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}·{∥\varphi ·{\mathrm{\chi }}_{{\overline{\mathbf{A}}}_{\mathrm{\kappa }}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}\right\}∥}_{{\ell }_{<}^{\mathfrak{s}\left(0\right)}}+\mathrm{C}·{∥\left\{2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}·{∥\varphi ·{\mathrm{\chi }}_{{\overline{\mathbf{A}}}_{\mathrm{\kappa }}}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}\right\}∥}_{{\ell }_{>}^{{\mathfrak{s}}_{\infty }}}\hfill \\ & \le \mathrm{C}·{∥\varphi ∥}_{{\overline{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}.\hfill \end{array}$$

We now estimate the far-field part of the operator ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$. We consider $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{\kappa }}$ for $\mathrm{\kappa }<0$ and the contribution from the outer region ${\mathfrak{R}}^{\mathfrak{m}}\setminus {\mathfrak{B}}_{\mathrm{\kappa }+2}$:

$${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{R}}^{\mathfrak{m}}\setminus {\mathfrak{B}}_{\mathrm{\kappa }+2}}\right).$$

By the definition of ${\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}$, we write the pointwise estimate:

$$\begin{array}{cc}\hfill & 2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{R}}^{\mathfrak{m}}\setminus {\mathfrak{B}}_{\mathrm{\kappa }+2}}\right)\left(\mathfrak{y}\right)\right|\hfill \\ \hfill & \le 2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}\sum _{\mathrm{\sigma }=\mathrm{\kappa }+3}^{\infty }{\int }_{{\mathcal{A}}_{\mathrm{\sigma }}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}·\left|\varphi \left(\mathfrak{z}\right)\right|\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

Since $\mathfrak{y}\in {\mathcal{A}}_{\mathrm{\kappa }}$ and $\mathfrak{z}\in {\mathcal{A}}_{\mathrm{\sigma }}$ with $\mathrm{\sigma }\ge \mathrm{\kappa }+3$, we have the distance estimate

$$|\mathfrak{y}-\mathfrak{z}|\gtrsim \left|\mathfrak{z}\right|\approx 2^{\mathrm{\sigma }}.$$

Hence, the kernel can be estimated as

$${\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\mathrm{\gamma }}}}\lesssim 2^{-\mathrm{\sigma }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}.$$

Applying the log-Hölder continuity of $\mathfrak{a}$, we use the relation

$$2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}\approx 2^{(\mathrm{\kappa }-\mathrm{\sigma }){\mathfrak{a}}^{-}}·2^{\mathrm{\sigma }\mathfrak{a}\left(\mathfrak{z}\right)}.$$

Substituting these estimates, we obtain

$$\begin{array}{cc}\hfill & 2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}\left|{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}^{\mathrm{\beta }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{R}}^{\mathfrak{m}}\setminus {\mathfrak{B}}_{\mathrm{\kappa }+2}}\right)\left(\mathfrak{y}\right)\right|\hfill \\ \hfill & \lesssim \sum _{\mathrm{\sigma }=\mathrm{\kappa }+3}^{\infty }{2}^{(\mathrm{\kappa }-\mathrm{\sigma }){\mathfrak{a}}^{-}}·2^{-\mathrm{\sigma }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}·2^{(\mathrm{\sigma }-\mathrm{\kappa }){\mathrm{\beta }}_{\mp }}{\int }_{{\mathcal{A}}_{\mathrm{\sigma }}}{2}^{\mathrm{\sigma }\mathfrak{a}\left(\mathfrak{z}\right)}\left|\varphi \left(\mathfrak{z}\right)\right|\mathrm{d}\mathfrak{z}.\hfill \end{array}$$

Applying Hölder’s inequality to the integral term and using the estimate

$$\parallel {\mathrm{\chi }}_{\mathrm{\sigma }}{\parallel }_{{\mathrm{L}}^{{\mathfrak{r}}^{\prime }(·)}}\lesssim 2^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}},$$

we find

$${\int }_{{\mathcal{A}}_{\mathrm{\sigma }}}{2}^{\mathrm{\sigma }\mathfrak{a}\left(\mathfrak{z}\right)}\left|\varphi \left(\mathfrak{z}\right)\right|\mathrm{d}\mathfrak{z}\lesssim {∥2^{\mathrm{\sigma }\mathfrak{a}(·)}\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}·2^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}.$$

Therefore, we deduce the bound

$$\begin{array}{cc}& {∥2^{\mathrm{\kappa }\mathfrak{a}\left(0\right)}·{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}^{\mathrm{\beta }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{R}}^{\mathfrak{m}}\setminus {\mathfrak{B}}_{\mathrm{\kappa }+2}}\right)·{\mathrm{\chi }}_{\mathrm{\kappa }}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}\hfill \\ & \le \mathrm{C}\sum _{\mathrm{\sigma }=\mathrm{\kappa }+3}^{\infty }{2}^{(\mathrm{\kappa }-\mathrm{\sigma })\left({\mathfrak{a}}_{-}+{\mathrm{\beta }}_{\mp }\right)}·2^{-\mathrm{\sigma }(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma })}·2^{{\displaystyle \frac{\mathrm{\sigma }\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}}{∥2^{\mathrm{\sigma }\mathfrak{a}(·)}\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}.\hfill \end{array}$$

The summation is not reducible to a simple geometric series and imposes conditions on $\mathrm{\beta }$ for convergence.

For $\mathrm{\kappa }\ge 0$, we estimate the ${\ell }_{>}^{{\mathfrak{s}}_{\infty }}$-norm using the weight $2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}$:

$$\begin{array}{cc}& {\left\{\sum _{\mathrm{\kappa }=0}^{\infty }{∥2^{\mathrm{\kappa }{\mathfrak{a}}_{\infty }}·{\mathfrak{I}}_{\mathrm{\alpha },\mathrm{\gamma }}^{\mathrm{\beta }}\left(\varphi ·{\mathrm{\chi }}_{{\mathfrak{R}}^{\mathfrak{m}}\setminus {\mathfrak{B}}_{\mathrm{\kappa }+2}}\right)·{\mathrm{\chi }}_{\mathrm{\kappa }}∥}_{{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}^{{\mathfrak{s}}_{\infty }}\right\}}^{1/{\mathfrak{s}}_{\infty }}\hfill \\ & \le \mathrm{C}{\left\{\sum _{\mathrm{\kappa }=0}^{\infty }{\left(\sum _{\mathrm{\sigma }=\mathrm{\kappa }+3}^{\infty }{2}^{(\mathrm{\kappa }-\mathrm{\sigma })\left[{\mathfrak{a}}_{\infty }-(\mathfrak{m}-\mathrm{\alpha }+\mathrm{\gamma }-{\mathrm{\beta }}_{\mp })+{\displaystyle \frac{\mathfrak{m}}{{\mathfrak{r}}_{\infty }^{\prime }}}-{\mathrm{\beta }}_{\mp }\right]}·{∥2^{\mathrm{\sigma }\mathfrak{a}(·)}\varphi ·{\mathrm{\chi }}_{\mathrm{\sigma }}∥}_{{\mathrm{L}}^{\mathfrak{r}(·)}}\right)}^{{\mathfrak{s}}_{\infty }}\right\}}^{1/{\mathfrak{s}}_{\infty }}\hfill \\ & \le \mathrm{C}·{∥\varphi ∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathfrak{m}}\right)}.\hfill \end{array}$$

This completes the proof. □

Remark 5. 

This remark illustrates how Theorem 6 both recovers and refines several existing results. Specifically,

• When $\mathfrak{a}(·)=\mathfrak{a},\mathrm{\gamma }=0,\mathfrak{r}(·)=\mathfrak{r},\mathfrak{s}(·)=\mathfrak{s}$, our result refines Theorem 2.3 in [45].
• When $\mathrm{\alpha }(·)=0$ and $\mathfrak{r}(·)=\mathfrak{s}(·)$, our result both refines and recovers Theorem 6 in [55].

4. Regularity Framework for Nonlinear Parabolic PDEs in Variable Exponent Herz Spaces

In this section, we employ the boundedness properties of a newly introduced fractional potential operator of Bessel–Riesz type with exponential damping to investigate the existence and regularity of solutions for a specific class of partial differential equations. These applications are particularly relevant within the broader framework of regularity theory for elliptic and parabolic PDEs. Our approach is primarily inspired by the seminal work of Ragusa [34], which emphasized the pivotal role of homogeneous Herz spaces in analyzing regularity properties. Furthermore, the framework developed by Scapellato [36], concerning elliptic equations in Herz spaces with variable exponents, and the substantial contributions by Makharadze et al. [38] on grand variable exponent Morrey spaces, serve as essential foundations for our study. Collectively, these investigations provide a refined analytical setting for examining the behavior and mapping properties of a broad class of differential and integral operators, particularly in generalized and non-standard function space contexts.

Ginzburg–Landau-Type Parabolic Model and Linearization Framework

The Ginzburg–Landau equation is a prototypical model arising in superconductivity, superfluidity, and nonlinear wave phenomena. The variable $\mathrm{\mu }\in {\mathbf{R}}^{\mathrm{n}}$ represents the spatial position, while $\mathrm{t}\in [0,\mathrm{T})$ denotes time. The unknown function $u(\mathrm{\mu },\mathrm{t})$ may represent, for example, a complex order parameter describing the macroscopic quantum state. The nonlinear term $\left({\left|u\right|}^2-1\right)u$ models self-interaction with a saturation effect.

Let $\Omega \subset {\mathbf{R}}^{\mathrm{n}}$ be a bounded spatial domain and consider a finite time interval $\mathfrak{I}:=(0,\mathrm{T})\subset \mathbf{R}$. We introduce the space–time cylinder

$${\Omega }_{\mathfrak{I}}:=\Omega \times \mathfrak{I},$$

with parabolic boundary ${\partial }_{\mathfrak{r}}{\Omega }_{\mathfrak{I}}$.

• The Nonlinear Problem

The Ginzburg–Landau-type parabolic initial–boundary value problem is formulated as

$$\left\{\begin{array}{cc}{\partial }_{\mathrm{t}}u-\mathbf{L}u+\left({\left|u\right|}^2-1\right)u=\varphi ,\hfill & \mathrm{in}{\Omega }_{\mathfrak{I}},\hfill \\ u=0,\hfill & \mathrm{on}{\partial }_{\mathfrak{r}}{\Omega }_{\mathfrak{I}},\hfill \\ u(0,·)=u_0,\hfill & \mathrm{in}\Omega ,\hfill \end{array}\right.$$

(2)

where the source term satisfies

$$\varphi \in {\mathrm{L}}^{\mathfrak{r}(·)}\left({\Omega }_{\mathfrak{I}}\right),u_0\in {\mathrm{L}}^2(\Omega ).$$

• Diffusion Operator

The diffusion term is represented by

$$\mathbf{L}u:=\sum _{\mathrm{i},\mathrm{j}=1}^{\mathrm{n}}{\partial }_{{\mathrm{\mu }}_{\mathrm{i}}}\left({\mathrm{a}}^{\mathrm{ij}}(\mathrm{\mu },\mathrm{t}){\partial }_{{\mathrm{\mu }}_{\mathrm{j}}}u\right),$$

(3)

with the coefficient matrix $\left({\mathrm{a}}^{\mathrm{ij}}\right)$ describing anisotropic or spatially heterogeneous diffusivity.

• Structural Assumptions

We impose the following conditions on the coefficients:

$${\mathrm{a}}^{\mathrm{ij}}\in {\mathrm{L}}^{\infty }\left({\Omega }_{\mathfrak{I}}\right)\cap \mathrm{VMO}\left({\Omega }_{\mathfrak{I}}\right),\forall \mathrm{i},\mathrm{j}=1,\dots ,\mathrm{n},$$

(4)

$${\mathrm{a}}^{\mathrm{ij}}(\mathrm{\mu },\mathrm{t})={\mathrm{a}}^{\mathrm{ji}}(\mathrm{\mu },\mathrm{t}),\forall \mathrm{i},\mathrm{j},\mathrm{a}.\mathrm{e}.(\mathrm{\mu },\mathrm{t})\in {\Omega }_{\mathfrak{I}},$$

(5)

$${\nu }^{-1}{\left|\mathrm{\xi }\right|}^2\le \sum _{\mathrm{i},\mathrm{j}=1}^{\mathrm{n}}{\mathrm{a}}^{\mathrm{ij}}(\mathrm{\mu },\mathrm{t}){\mathrm{\xi }}_{\mathrm{i}}{\mathrm{\xi }}_{\mathrm{j}}\le \nu {\left|\mathrm{\xi }\right|}^2,\forall \mathrm{\xi }\in {\mathbf{R}}^{\mathrm{n}},$$

(6)

where $\nu >0$ ensures uniform ellipticity.

• Potential Energy

A prototypical choice for the Ginzburg–Landau framework is

$$W\left(u\right)={\displaystyle \frac{1}{4}}{\left({\left|u\right|}^2-1\right)}^2,W^{\prime }\left(u\right)=\left({\left|u\right|}^2-1\right)u,W^{\prime \prime }\left(u\right)=3u^2-1\left(\mathrm{real}\mathrm{scalar}\mathrm{case}\right),$$

(7)

where u may also be taken as complex-valued in physical applications.

• Frozen-Coefficient Approximation

Let $\widetilde{{\Omega }_{\mathfrak{I}}}\subset {\Omega }_{\mathfrak{I}}$ be a set where (4)–(5) hold pointwise. For a fixed reference point $({\mathrm{\mu }}_0,{\theta }_0)\in \widetilde{{\Omega }_{\mathfrak{I}}}$ and state $u_0$, we define the frozen–coefficient linearized operator:

$${\mathbf{L}}_0\mathrm{v}(\mathrm{\mu },\mathrm{t}):={\partial }_{\mathrm{t}}\mathrm{v}-\sum _{\mathrm{i},\mathrm{j}=1}^{\mathrm{n}}{\mathrm{a}}^{\mathrm{ij}}({\mathrm{\mu }}_0,{\mathrm{\theta }}_0){\partial }_{{\mathrm{\mu }}_{\mathrm{i}}{\mathrm{\mu }}_{\mathrm{j}}}\mathrm{v}+\left[\left(|u_0{|}^2-1\right)+2u_0^2\right]\mathrm{v},$$

(8)

where the last term corresponds to the Fréchet derivative of the cubic nonlinearity.

• Fundamental Solution

For the purely diffusive case (no cubic term), the fundamental solution is the anisotropic heat kernel:

$$\begin{array}{cc}\hfill \mathrm{\Gamma }\left(({\mathrm{\mu }}_0,{\theta }_0),(\mathrm{\tau },\theta )\right)& ={\displaystyle \frac{1}{{\left(4\pi ({\theta }_0-\theta )\right)}^{\mathrm{n}/2}\sqrt{det\mathrm{A}({\mathrm{\mu }}_0,{\theta }_0)}}}\hfill \\ \hfill & \times exp\left[-{\displaystyle \frac{1}{4({\theta }_0-\theta )}}\sum _{\mathrm{i},\mathrm{j}=1}^{\mathrm{n}}{\mathrm{A}}^{\mathrm{ij}}({\mathrm{\mu }}_0,{\theta }_0)\left({\mathrm{\mu }}_{\mathrm{i}}-{\mathrm{\tau }}_{\mathrm{i}}\right)\left({\mathrm{\mu }}_{\mathrm{j}}-{\mathrm{\tau }}_{\mathrm{j}}\right)\right],\hfill \end{array}$$

(9)

where ${\mathrm{A}}^{\mathrm{ij}}$ are the entries of ${\left({\mathrm{a}}^{\mathrm{ij}}\right)}^{-1}$. If the linearized cubic term is present, an extra multiplicative factor $exp\left(({\theta }_0-\theta )W^{\prime \prime }\left(u_0\right)\right)$ appears.

• Kernel Derivatives

Spatial derivatives are given by

$${\Gamma }_{\mathrm{i}}:={\displaystyle \frac{\partial }{\partial {\mathrm{\tau }}_{\mathrm{i}}}}\Gamma ,{\Gamma }_{\mathrm{i}\mathrm{j}}:={\displaystyle \frac{{\partial }^2}{\partial {\mathrm{\tau }}_{\mathrm{i}}\partial {\mathrm{\tau }}_{\mathrm{j}}}}\Gamma .$$

• Derivative Bound

For some compact $\mathfrak{z}\subset {\mathbf{R}}^{\mathrm{n}}\times (0,\mathrm{T})$ excluding the singularity $(\mathrm{\mu },\mathrm{t})=(\mathrm{\tau },\theta )$, set

$$\mathbf{M}:=\underset{\mathrm{i},\mathrm{j}=1,\dots ,\mathrm{n}}{max}\underset{\left|\mathrm{\alpha }\right|\le 2\mathrm{n}}{max}{∥{\displaystyle \frac{{\partial }^{\left|\mathrm{\alpha }\right|}{\Gamma }_{\mathrm{i}\mathrm{j}}}{\partial {\mathrm{\tau }}^{\mathrm{\alpha }}}}∥}_{{\mathrm{L}}^{\infty }({\Omega }_{\mathfrak{I}}\times \mathfrak{z})}.$$

This constant will later serve in estimating singular integral terms.

When applied to superconductivity, superfluidity, or phase–field modeling, the above system would describe the time dynamics of an order parameter u that defines the macroscopic state of the system. The parabolic operator $\mathbf{L}$ takes into consideration anisotropic or spatially varying diffusion, and in this case, the coefficients ${\mathrm{a}}^{\mathrm{ij}}$ can be assumed to possess inhomogeneities at the fine scale by satisfying VMO. The nonlinear term $\left({\left|u\right|}^2-1\right)u$ pulls the system to configurations with the minimal Ginzburg–Landau energy, thus simulating self-interaction and saturation effects and regulating the appearance and dynamics of vortices or interfaces. The homogeneous boundary condition, $u=0$, can symbolize a fixed state (e.g., the suppression of the order parameter), but it is applied at the boundary. The tension $\Gamma$ is the Green function of the underlying anisotropic reaction–diffusion operator; otherwise, $\varphi$ may correspond to external forcing, bulk effects, or couplings to other physical fields.

We are now in a position to establish our main result. The argument relies on a representation formula for the second-order derivatives of solutions belonging to the space ${\mathbf{W}}_0^{2,\mathfrak{r}(·)}$.

Theorem 7 

(a priori estimate for a Ginzburg–Landau-type parabolic system). Let ${\mathfrak{B}}_{\mathrm{r}}⋐\Omega$ be a ball of radius $\mathrm{r}<{\mathrm{\rho }}_0$, and $\mathfrak{I}:=(0,\mathrm{T})$ a finite time interval. Suppose that

1. 

The coefficient and structural conditions (4)–(5) hold for the diffusion tensor ${\mathrm{a}}^{\mathrm{ij}}$.

2. 

The variable exponent functions $\mathfrak{r}(·)$, $\mathfrak{s}(·)$, and $\mathrm{\alpha }(·)$ satisfy the hypotheses of Theorem 6.

3. 

$\mathbf{V}\in {\mathbf{W}}_0^{2,\mathfrak{r}(·)}\left({\mathfrak{B}}_{\mathrm{r}}\right)$ is a weak solution of the Ginzburg–Landau initial–boundary value problem

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\partial }_{\mathrm{t}}\mathbf{V}-\mathbf{L}\mathbf{V}+\left({\left|\mathbf{V}\right|}^2-1\right)\mathbf{V}=\varphi ,\hfill & \mathit{in}{\mathfrak{B}}_{\mathrm{r}}\times \mathfrak{I},\hfill \\ \mathbf{V}=0,\hfill & \mathit{on}\partial {\mathfrak{B}}_{\mathrm{r}}\times \mathfrak{I},\hfill \\ \mathbf{V}(0,·)={\mathbf{V}}_0,\hfill & \mathit{in}{\mathfrak{B}}_{\mathrm{r}},\hfill \end{array}\right.\end{array}$$

(10)

where $\mathbf{L}$ is given by (3) and ${\mathbf{V}}_0\in {\mathrm{L}}^2\left({\mathfrak{B}}_{\mathrm{r}}\right)$.

4. 

The cubic restoring term $\left({\left|\mathbf{V}\right|}^2-1\right)\mathbf{V}$ satisfies the local boundedness condition

$${∥\left({\left|\mathbf{V}\right|}^2-1\right)\mathbf{V}∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}\left({\mathfrak{B}}_{\mathrm{r}}\right)}\le C_{\mathrm{NL}}{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}\left({\mathfrak{B}}_{\mathrm{r}}\right)}$$

for some constant $C_{\mathrm{NL}}$ depending on the local energy bounds of $\mathbf{V}$.

Then, there exist constants

$$\mathrm{C}=\mathrm{C}\left(\mathrm{n},\mathfrak{r}(·),\mathfrak{s}(·),\mathrm{\alpha }(·),\mathbf{M},C_{\mathrm{NL}}\right),{\mathrm{\rho }}_0={\mathrm{\rho }}_0(\mathrm{C},\mathrm{n}),$$

such that the second-order a priori estimate

$${∥{\partial }_{{\mathfrak{y}}_i{\mathfrak{y}}_j}\mathbf{V}∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}\left({\mathfrak{B}}_{\mathrm{r}}\right)}\le \mathrm{C}{∥\varphi ∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}\left({\mathfrak{B}}_{\mathrm{r}}\right)},\forall i,j=1,\dots ,n,$$

holds, where the variable Sobolev conjugate exponent ${\mathfrak{r}}^{*}(·)$ is given by

$${\displaystyle \frac{1}{{\mathfrak{r}}^{*}\left(\mathfrak{y}\right)}}={\displaystyle \frac{1}{\mathfrak{r}\left(\mathfrak{y}\right)}}-{\displaystyle \frac{\mathrm{\beta }}{n}}.$$

Proof. 

Fix ${\mathfrak{B}}_{\mathrm{r}}\subset \Omega$ with $\mathrm{r}<{\mathrm{\rho }}_0$. Under the stated assumptions, the weak solution $\mathbf{V}$ to the Ginzburg–Landau-type problem

$${\partial }_{\mathrm{t}}\mathbf{V}-\mathrm{\nu }\Delta \mathbf{V}+\left({\left|\mathbf{V}\right|}^2-1\right)\mathbf{V}=\varphi$$

admits, by standard linearization around a fixed state, a singular integral representation for its second derivatives:

$${\partial }_{{\mathrm{\mu }}_i{\mathrm{\mu }}_j}{\mathrm{V}}^{\ell }(\mathrm{\mu },t)={\mathrm{J}}_1+{\mathrm{J}}_2+{\mathfrak{R}}^{\ell }(\mathrm{\mu },t),$$

where

$$\begin{array}{cc}\hfill {\mathrm{J}}_1& :=\mathrm{P}.\mathrm{V}.{\int }_{{\mathfrak{B}}_{\mathrm{r}}}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau };t,\vartheta ){\varphi }^{\mathfrak{m}}(\mathrm{\tau },\vartheta )\mathrm{d}\mathrm{\tau },\hfill \\ \hfill {\mathrm{J}}_2& :=\mathrm{P}.\mathrm{V}.{\int }_{{\mathfrak{B}}_{\mathrm{r}}}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau };t,\vartheta )\left[\left({\left|\mathbf{V}(\mathrm{\tau },\vartheta )\right|}^2-1\right){\delta }_k^{\mathfrak{m}}\right]{\partial }_{{\mathrm{\tau }}_k}\mathbf{V}\mathrm{d}\mathrm{\tau },\hfill \end{array}$$

with ${\mathbb{L}}_{ij}^{\ell \mathfrak{m}}$ the kernel adapted to the anisotropic parabolic operator, and ${\mathfrak{R}}^{\ell }$ a regular remainder term.

Indeed, although our PDE is parabolic in nature, in the analysis of the singular integral terms, we restrict our attention to the spatial component at a fixed time. In this setting, the associated kernel naturally takes the elliptic Calderón–Zygmund form. Specifically, the kernel ${\mathbb{L}}_{ij}^{\ell \mathfrak{m}}$ satisfies the standard Calderón–Zygmund estimates:

$$\left|{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathfrak{y},\mathrm{\tau })\right|\le {\displaystyle \frac{C}{{|\mathfrak{y}-\mathrm{\tau }|}^{\mathfrak{m}}}}.$$

To control the variation of the kernel, consider its gradient with respect to $\mathfrak{y}$:

$${\nabla }_{\mathfrak{y}}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathfrak{y},\mathrm{\tau })=\left({\displaystyle \frac{\partial }{\partial {\mathfrak{y}}_1}}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}},\dots ,{\displaystyle \frac{\partial }{\partial {\mathfrak{y}}_{\mathfrak{m}}}}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}\right).$$

By explicit differentiation of the singular kernel,

$${\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathfrak{y},\mathrm{\tau })={|\mathfrak{y}-\mathrm{\tau }|}^{-\mathfrak{m}},{\partial }_{{\mathfrak{y}}_k}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathfrak{y},\mathrm{\tau })=-\mathfrak{m}{\displaystyle \frac{{\mathfrak{y}}_k-{\mathrm{\tau }}_k}{{|\mathfrak{y}-\mathrm{\tau }|}^{\mathfrak{m}+2}}},$$

so that

$$\left|{\partial }_{{\mathfrak{y}}_k}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathfrak{y},\mathrm{\tau })\right|\le {\displaystyle \frac{\mathfrak{m}}{{|\mathfrak{y}-\mathrm{\tau }|}^{\mathfrak{m}+1}}}.$$

Hence, the gradient norm satisfies

$$\begin{array}{c}\hfill \left|{\nabla }_{\mathfrak{y}}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathfrak{y},\mathrm{\tau })\right|=\sqrt{\sum _{k=1}^{\mathfrak{m}}{\left|{\partial }_{{\mathfrak{y}}_k}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathfrak{y},\mathrm{\tau })\right|}^2}\le {\displaystyle \frac{C}{{|\mathfrak{y}-\mathrm{\tau }|}^{\mathfrak{m}+1}}}.\end{array}$$

(11)

The gradient estimate guarantees that the kernel satisfies the smoothness condition required for Calderón–Zygmund operators. Consequently, the singular integral defining ${\mathrm{J}}_1$ can be interpreted as a variable-exponent Bessel–Riesz-type operator. In particular, under the setting $\mathrm{\alpha }=\gamma =0$, this operator directly controls the estimate in (11):

$${\mathfrak{I}}_{\mathrm{\alpha },\gamma }\varphi \left(\mathfrak{y}\right):={\int }_{{\mathfrak{R}}^{\mathfrak{m}}}{\displaystyle \frac{{|\mathfrak{y}-\mathfrak{z}|}^{\mathrm{\alpha }-\mathfrak{m}}}{{(1+|\mathfrak{y}-\mathfrak{z}\left|\right)}^{\gamma }}}\varphi \left(\mathfrak{z}\right)d\mathfrak{z}.$$

Therefore, we have the boundedness estimate

$${∥{\mathrm{J}}_1∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\le C{∥\varphi ∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}},$$

showing explicitly that the gradient control of the kernel ensures the boundedness of ${\mathrm{J}}_1$ in the corresponding Herz space.

The cubic term $\left(\right|\mathbf{V}{|}^2-1)\mathbf{V}$ is a lower-order perturbation. Using the a priori local boundedness assumption,

$${∥\left(\right|\mathbf{V}{|}^2-1)\mathbf{V}∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\le C_{\mathrm{NL}}{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}},$$

and applying the Calderón–Zygmund boundedness of the kernel yields

$${∥{\mathrm{J}}_2∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\le C{C}_{\mathrm{NL}}{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}.$$

Recall that

$${\mathrm{J}}_2:=\mathrm{P}.\mathrm{V}.{\int }_{{\mathfrak{B}}_{\mathrm{r}}}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau };t,\vartheta )\left[\left({\left|\mathbf{V}(\mathrm{\tau },\vartheta )\right|}^2-1\right){\delta }_k^{\mathfrak{m}}\right]{\partial }_{{\mathrm{\tau }}_k}\mathbf{V}\mathrm{d}\mathrm{\tau }.$$

By taking the norm in the homogeneous variable-exponent Herz space, we have

$$\begin{array}{cc}\hfill {∥{\mathrm{J}}_2∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}& ={∥\mathrm{P}.\mathrm{V}.{\int }_{{\mathfrak{B}}_{\mathrm{r}}}{\mathbb{L}}_{ij}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau })\left({\left|\mathbf{V}\left(\mathrm{\tau }\right)\right|}^2-1\right){\partial }_{{\mathrm{\tau }}_k}\mathbf{V}\mathrm{d}\mathrm{\tau }∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\hfill \\ & \le {∥{\mathfrak{I}}_{\mathrm{CZ}}\left[\left(\right|\mathbf{V}{|}^2-1)\nabla \mathbf{V}\right]∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}},\hfill \end{array}$$

where ${\mathfrak{I}}_{\mathrm{CZ}}$ is the Calderón–Zygmund operator associated with the kernel ${\mathbb{L}}_{ij}^{\ell \mathfrak{m}}$. Since ${\mathbb{L}}_{ij}^{\ell \mathfrak{m}}$ satisfies the Calderón–Zygmund size and smoothness conditions, the operator ${\mathfrak{I}}_{\mathrm{CZ}}$ can be controlled by the Bessel–Riesz operator ${\mathfrak{I}}_{\mathrm{\alpha },\gamma }$. Consequently, ${\mathfrak{I}}_{\mathrm{CZ}}$ is bounded in the corresponding Herz space, which yields

$${∥{\mathrm{J}}_1∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\le C{∥\varphi ∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}.$$

$${\mathfrak{I}}_{\mathrm{CZ}}:{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}\to {\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}.$$

Hence,

$${∥{\mathrm{J}}_2∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\le C{∥\left(\right|\mathbf{V}{|}^2-1)\nabla \mathbf{V}∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}.$$

By the assumed a priori local boundedness of the solution, we have

$${∥\left(\right|\mathbf{V}{|}^2-1)\mathbf{V}∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\le C_{\mathrm{NL}}{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}.$$

Using standard product estimates in Herz spaces, the derivative factor can be absorbed into the constant $C_{\mathrm{NL}}$, giving

$${∥\left(\right|\mathbf{V}{|}^2-1)\nabla \mathbf{V}∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\le C_{\mathrm{NL}}{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}}.$$

Combining the above, we finally obtain

$${∥{\mathrm{J}}_2∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\le C{C}_{\mathrm{NL}}{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}.$$

This shows that the cubic term, treated as a lower-order perturbation, is controlled by the local a priori norm of $\mathbf{V}$, completing the boundedness estimate for ${\mathrm{J}}_2$.

The remainder term ${\mathfrak{R}}^{\ell }$ arises from regular contributions in the linearization and from localized smooth corrections in the singular integral representation:

$${\partial }_{{\mathrm{\mu }}_i{\mathrm{\mu }}_j}{\mathbf{V}}^{\ell }(\mathrm{\mu },t)={\mathrm{J}}_1+{\mathrm{J}}_2+{\mathfrak{R}}^{\ell }(\mathrm{\mu },t).$$

By construction, ${\mathfrak{R}}^{\ell }$ involves integrals of kernels that are smooth (non-singular) or have compact support:

$${\mathfrak{R}}^{\ell }(\mathrm{\mu },t):={\int }_{{\mathfrak{B}}_{\mathrm{r}}}{\mathbb{K}}_{ij}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau }){\varphi }^{\mathfrak{m}}\left(\mathrm{\tau }\right)\mathrm{d}\mathrm{\tau },$$

where ${\mathbb{K}}_{ij}^{\ell \mathfrak{m}}$ is a smooth, bounded kernel:

$$\left|{\mathbb{K}}_{ij}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau })\right|\le C.$$

Since the kernel is smooth and bounded, the integral is a standard convolution with a bounded kernel. Using the definition of the homogeneous variable-exponent Herz space ${\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}$, we have

$$\begin{array}{cc}\hfill {∥{\mathfrak{R}}^{\ell }∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}& ={∥{\int }_{{\mathfrak{B}}_{\mathrm{r}}}{\mathbb{K}}_{ij}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau }){\varphi }^{\mathfrak{m}}\left(\mathrm{\tau }\right)\mathrm{d}\mathrm{\tau }∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\hfill \\ & \le {\int }_{{\mathfrak{B}}_{\mathrm{r}}}\left|{\mathbb{K}}_{ij}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau })\right|{∥{\varphi }^{\mathfrak{m}}\left(\mathrm{\tau }\right)∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\mathrm{d}\mathrm{\tau }\hfill \\ & \le C{∥\varphi ∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}.\hfill \end{array}$$

Thus, the remainder term is controlled by the same Herz–Sobolev norm of the source term:

$${∥{\mathfrak{R}}^{\ell }∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}\le C{∥\varphi ∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}},$$

where C depends only on the structural parameters and the radius $\mathrm{r}$, but is independent of $\mathbf{V}$ and $\varphi$.

This shows that ${\mathfrak{R}}^{\ell }$ is a lower-order, regular term whose contribution can be absorbed in the overall a priori estimate.

Combining the estimates for ${\mathrm{J}}_1$, ${\mathrm{J}}_2$, and ${\mathfrak{R}}^{\ell }$, we obtain

$${∥{\partial }_{{\mathfrak{y}}_i{\mathfrak{y}}_j}{\mathbf{V}}^{\ell }∥}_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}\left({\mathfrak{B}}_{\mathrm{r}}\right)}\le C\left({∥\varphi ∥}_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}^{\mathrm{\alpha }(·)}}+C_{\mathrm{NL}}{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathfrak{r}(·),\mathfrak{s}(·)}}\right),$$

which yields the desired second-order a priori estimate after absorbing lower-order terms into the constant C. □

Theorem 8. 

Let $\mathrm{n}\ge 3$, and consider the Ginzburg–Landau type parabolic system

$${\partial }_{\mathrm{t}}\mathbf{V}-\mathrm{\nu }\delta \mathbf{V}+\left({\left|\mathbf{V}\right|}^2-1\right)\mathbf{V}=\varphi \mathit{in}{\mathrm{Q}}_{\sigma }:={\mathrm{B}}_{\sigma }\left({\mathrm{\mu }}_0\right)\times ({\theta }_0-{\sigma }^2,{\theta }_0)⋐{\Omega }_{\mathbf{T}}.$$

Assume the following:

• Parameters: $0<\mathrm{\alpha }<\mathrm{n}$, $\gamma \ge 0$, $\mathrm{\beta }\in \mathbb{R}$.
• Exponents:

  $$\mathrm{r}(·)\in {\mathbf{P}}_0^{log}\left({\mathbb{R}}^{\mathrm{n}}\right)\cap {\mathbf{P}}_{\infty }^{log}\left({\mathbb{R}}^{\mathrm{n}}\right),\mathrm{s}(·)\in {\mathbf{P}}_0\left({\mathbb{R}}^{\mathrm{n}}\right),1<{\mathfrak{r}}^{-}\le {\mathfrak{r}}^{+}<\mathrm{n}/\mathrm{\alpha }.$$
• Weight index: $\mathfrak{a}(·)\in {\mathrm{L}}^{\infty }\left({\mathbb{R}}^{\mathrm{n}}\right)$, log–Hölder continuous at 0 and ∞, with

  $$\mathrm{\alpha }-{\displaystyle \frac{\mathrm{n}}{{\mathfrak{r}}^{-}}}<{\mathfrak{a}}^{-}\le {\mathfrak{a}}^{+}<{\displaystyle \frac{\mathrm{n}}{{\mathrm{p}}^{\prime +}}}.$$

Suppose that

$$\mathbf{V},\varphi \in {\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right),{\nabla }_{\mathrm{\mu }}\mathbf{V}\in {\dot{\mathbf{K}}}_{2,\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right).$$

Then, there exists ${\sigma }_0>0$ such that, for all $0<\sigma \le {\sigma }_0$,

$${\nabla }_{\mathrm{\mu }}\mathbf{V}\in {\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma /2}\right),\mathit{with}{\displaystyle \frac{1}{{\mathfrak{r}}^{*}\left(\mathfrak{y}\right)}}={\displaystyle \frac{1}{\mathrm{p}\left(\mathfrak{y}\right)}}-{\displaystyle \frac{\mathrm{\alpha }}{\mathrm{n}}}.$$

Moreover, the following a priori estimate holds:

$$\parallel {\nabla }_{\mathrm{\mu }}{\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma /2}\right)}\le C\left({\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel {\nabla }_{\mathrm{\mu }}\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{2,\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\right),$$

(12)

where $C>0$ depends only on the structural constants, variable exponents, $\mathfrak{a}(·)$, $\mathrm{\alpha },\gamma$, and the VMO modulus, but is independent of $\mathbf{V}$ and ϕ.

In particular, the singular integral representation of ${\nabla }_{\mathrm{\mu }}^2\mathbf{V}$ can be controlled by the Bessel–Riesz operator ${\mathbf{T}}_{\mathrm{\alpha },\gamma }$, ensuring the boundedness of the second-order derivatives in variable-exponent Herz spaces.

Proof. 

We follow a stepwise localization–representation–absorption scheme, keeping all intermediate estimates.

Choose $0<\gamma <1$ and a standard space–time cut-off function $\varphi \in C_0^{\infty }\left({\mathrm{Q}}_{\sigma }\right)$ such that

$$\varphi =\left\{\begin{array}{cc}1,\hfill & \mathrm{in}{\mathrm{Q}}_{\gamma \sigma },\hfill \\ \in (0,1),\hfill & \mathrm{in}{\mathrm{Q}}_{\sigma }\setminus {\mathrm{Q}}_{\gamma \sigma },\hfill \\ 0,\hfill & \mathrm{outside}{\mathrm{Q}}_{\sigma },\hfill \end{array}\right.0\le \varphi \le 1,supp(\nabla \varphi )\subset {\mathrm{Q}}_{\sigma }\setminus {\mathrm{Q}}_{\gamma \sigma }.$$

Set $v:=\varphi \mathbf{V}$ for the Ginzburg–Landau solution $\mathbf{V}$. Then,

$$\mathcal{L}\left(v\right):={\partial }_{{\mathrm{\mu }}_{\mathrm{i}}}\left({\mathrm{a}}_{\mathrm{i}\mathrm{j}}^{\ell \mathfrak{m}}{\partial }_{{\mathrm{\mu }}_{\mathrm{j}}}{v}^{\mathfrak{m}}\right)-{\partial }_{\mathrm{t}}{v}^{\ell }={div}_{\mathrm{\mu }}\mathbf{G}+g,$$

with (componentwise)

$${\mathrm{G}}_{\mathrm{i}}^{\ell }=\varphi {\varphi }_{\mathrm{i}}^{\ell }+({\mathbf{V}}^{\ell }-\overline{{\mathbf{V}}^{\ell }}){\partial }_{{\mathrm{\mu }}_{\mathrm{i}}}\varphi ,g^{\ell }=-{\mathbf{V}}^{\ell }{\partial }_{\mathrm{t}}\varphi -{\mathrm{a}}_{\mathrm{i}\mathrm{j}}^{\ell \mathfrak{m}}{\partial }_{{\mathrm{\mu }}_{\mathrm{j}}}{\mathbf{V}}^{\mathfrak{m}}{\partial }_{{\mathrm{\mu }}_{\mathrm{i}}}\varphi .$$

Freezing the coefficients at a fixed point and integrating by parts (standard parabolic fundamental solution construction) yields, for a Calderón–Zygmund kernel ${\mathbb{L}}_{\mathrm{i}\mathrm{j}}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau };\mathrm{t},\vartheta )$ and ${\Gamma }_{\mathrm{i}}$ (spatial derivatives of the frozen fundamental solution), the representation

$${\partial }_{{\mathrm{\mu }}_{\mathrm{i}}{\mathrm{\mu }}_{\mathrm{j}}}{v}^{\ell }(\mathrm{\mu },\mathrm{t})={\mathrm{J}}_1(\mathrm{\mu },\mathrm{t})+{\mathrm{J}}_2(\mathrm{\mu },\mathrm{t})+{\mathfrak{R}}^{\ell }(\mathrm{\mu },\mathrm{t}),$$

(13)

where

$${\mathrm{J}}_1(\mathrm{\mu },\mathrm{t}):=\mathrm{P}.\mathrm{V}.{\int \int }_{{\mathrm{Q}}_{\sigma }}{\mathbb{L}}_{\mathrm{i}\mathrm{j}}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau };\mathrm{t},\vartheta ){\varphi }^{\mathfrak{m}}(\mathrm{\tau },\vartheta )d\mathrm{\tau }d\vartheta ,$$

$${\mathrm{J}}_2(\mathrm{\mu },\mathrm{t}):=\mathrm{P}.\mathrm{V}.{\int \int }_{{\mathrm{Q}}_{\sigma }}{\mathbb{L}}_{\mathrm{i}\mathrm{j}}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau };\mathrm{t},\vartheta )\left[{\mathrm{a}}^{\mathfrak{m}\mathrm{k}}(\mathrm{\mu },\mathrm{t})-{\mathrm{a}}^{\mathfrak{m}\mathrm{k}}(\mathrm{\tau },\vartheta )\right]{\partial }_{{\mathrm{\tau }}_{\mathrm{k}}}{V}^{\mathfrak{m}}(\mathrm{\tau },\vartheta )d\mathrm{\tau }d\vartheta ,$$

$${\mathfrak{R}}^{\ell }(\mathrm{\mu },\mathrm{t}):=-{\int \int }_{{\mathrm{Q}}_{\sigma }}{\Gamma }_{\mathrm{i}}(\mathrm{\mu },\mathrm{t};\mathrm{\tau },\vartheta )g^{\ell }(\mathrm{\tau },\vartheta )d\mathrm{\tau }d\vartheta +c_{\mathrm{i}\mathrm{j}}{\mathrm{G}}_{\mathrm{j}}^{\ell }(\mathrm{\mu },\mathrm{t}),c_{\mathrm{i}\mathrm{j}}:={\int }_{\left|\mathit{\xi }\right|=1}{\Gamma }_{\mathrm{i}}(\mathrm{\mu },\mathrm{t};\mathit{\xi },0){\mathit{\xi }}_{\mathrm{j}}d{\sigma }_{\mathit{\xi }}.$$

The kernels ${\mathbb{L}}_{\mathrm{i}\mathrm{j}}$ and ${\Gamma }_{\mathrm{i}}$ satisfy standard spatial Calderón–Zygmund estimates uniformly in time. This allows the use of variable-exponent Bessel–Riesz operators to control the singular integrals ${\mathrm{J}}_1$ and ${\mathrm{J}}_2$, while ${\mathfrak{R}}^{\ell }$ is absorbed via the support of $\nabla \varphi$ and the a priori bounds on $\mathbf{V}$.

Apply the space–time Herz norm to both sides of (13) and use the triangle inequality:

$$\begin{array}{cc}\hfill \parallel {\nabla }_{\mathrm{\mu }}{\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}& \lesssim \parallel \mathrm{P}.\mathrm{V}.{\int \int }_{{\mathrm{Q}}_{\sigma }}{\mathbb{L}}_{\mathrm{i}\mathrm{j}}^{\ell \mathfrak{m}}(·,\mathrm{\tau };·,\vartheta ){\varphi }^{\mathfrak{m}}(\mathrm{\tau },\vartheta )d\mathrm{\tau }d\vartheta {\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\hfill \\ \hfill & +\parallel \mathrm{P}.\mathrm{V}.{\int \int }_{{\mathrm{Q}}_{\sigma }}{\mathbb{L}}_{\mathrm{i}\mathrm{j}}^{\ell \mathfrak{m}}(·,\mathrm{\tau };·,\vartheta )\left[{\mathrm{a}}^{\mathfrak{m}\mathrm{k}}(·,·)-{\mathrm{a}}^{\mathfrak{m}\mathrm{k}}(\mathrm{\tau },\vartheta )\right]\hfill \\ \hfill & \times {\partial }_{{\mathrm{\tau }}_{\mathrm{k}}}{V}^{\mathfrak{m}}(\mathrm{\tau },\vartheta )d\mathrm{\tau }d\vartheta {\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\hfill \\ \hfill & +\parallel \mathbb{R}{\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}.\hfill \end{array}$$

where each norm is taken in

$${\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right),$$

and we estimate the three terms on the right separately.

Fix $\mathrm{t}\in ({\theta }_0-{\sigma }^2,{\theta }_0)$. Define the spatial singular operator

$${\mathcal{T}}_{\mathrm{t}}[\varphi ]\left(\mathrm{\mu }\right):=\mathrm{P}.\mathrm{V}.{\int }_{{\mathrm{B}}_{\sigma }}{\mathbb{L}}_{\mathrm{i}\mathrm{j}}^{\ell \mathfrak{m}}(\mathrm{\mu },\mathrm{\tau };\mathrm{t},\vartheta )\varphi \left(\mathrm{\tau }\right)d\mathrm{\tau }.$$

By employing the kernel estimates and the boundedness of the Bessel–Riesz operator ${\mathfrak{I}}_{\mathrm{\alpha },\gamma }$ in variable Lebesgue spaces (see [54]), we obtain

$${\mathrm{L}}^{\mathrm{r}(·)}⟶{\mathrm{L}}^{{\mathfrak{r}}^{*}(·)},$$

and the operator ${\mathcal{T}}_{\mathrm{t}}$ is pointwise controlled by ${\mathfrak{I}}_{\mathrm{\alpha },\gamma }$ and thus maps

$${\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathrm{n}}\right)⟶{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathrm{n}}\right)$$

uniformly in $\mathrm{t}$.

Therefore, by Fubini’s theorem (integrating over the time interval),

$$\parallel {\mathrm{J}}_1{\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\le C_1{\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)},$$

(14)

with $C_1$ independent of $\mathbf{V}$ and $\varphi$. This provides the first term estimate in the Ginzburg–Landau type parabolic system within variable-exponent Herz spaces.

Write

$${\mathrm{J}}_2(·,\mathrm{t})={\mathcal{T}}_{\mathrm{t}}\left([\mathrm{a}(·,\vartheta )-\mathrm{a}(·,\mathrm{t})]{\partial }_{\mathrm{\tau }}\mathbf{V}(·,\vartheta )\right).$$

Using the mapping property of ${\mathcal{T}}_{\mathrm{t}}$ and variable-exponent multiplication/Hölder estimates in Herz spaces (with the difference factor acting as a bounded multiplier on compact sets), for each fixed $\mathrm{t}$, we have

$$\parallel {\mathrm{J}}_2{(·,\mathrm{t})\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathrm{n}}\right)}\le C_2{\parallel \mathrm{a}(·,\vartheta )-\mathrm{a}(·,\mathrm{t})\parallel }_{L^{\infty }\left({\mathrm{B}}_{\sigma }\right)}{\parallel {\nabla }_{\mathrm{\mu }}\mathbf{V}(·,\mathrm{t})\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathfrak{R}}^{\mathrm{n}}\right)}.$$

Taking the supremum over $(\mathrm{\mu },\mathrm{t})\in {\mathrm{Q}}_{\sigma }$ and using the VMO modulus ${\parallel \mathrm{a}\parallel }_{*,{\mathrm{Q}}_{\sigma }}$ gives

$$\parallel {\mathrm{J}}_2{\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\le C_2{\parallel \mathrm{a}\parallel }_{*,{\mathrm{Q}}_{\sigma }}{\parallel {\nabla }_{\mathrm{\mu }}\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}.$$

(15)

By choosing $\sigma$ small enough, ${\parallel \mathrm{a}\parallel }_{*,{\mathrm{Q}}_{\sigma }}$ can be made arbitrarily small.

Decompose $\mathbb{R}=c_{ij}{\mathbf{G}}_j-\mathcal{R}\left[g\right]$, where

$$\mathcal{R}\left[g\right](\mathrm{\mu },\mathrm{t}):={\int \int }_{{\mathrm{Q}}_{\sigma }}{\Gamma }_i(\mathrm{\mu },\mathrm{t};\mathrm{\tau },\vartheta )g(\mathrm{\tau },\vartheta )d\mathrm{\tau }d\vartheta .$$

(1) The multiplicative term $c_{ij}{\mathbf{G}}_j$ satisfies

$$\parallel c_{ij}{\mathbf{G}}_j{\parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\le C_3{\parallel \mathbf{G}\parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}.$$

(2) $\mathcal{R}$ is a spatial Calderón–Zygmund operator uniform in time; using the same operator-boundedness machinery as before (with effective $\mathrm{\alpha }=1$ for ${\Gamma }_i$), we obtain

$${\parallel \mathcal{R}\left[g\right]\parallel }_{{\dot{\mathbf{K}}}_{{\mathrm{p}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\le C_4{\parallel g\parallel }_{{\dot{\mathbf{K}}}_{{\mathrm{p}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)},$$

where ${\mathfrak{r}}_{*}(·)$ arises from the kernel mapping: $1/{\mathfrak{r}}_{*}(·)=1/\mathrm{r}(·)-1/n$.

Combining the estimates gives

$${\parallel \mathbb{R}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\le C_3{\parallel \mathbf{G}\parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+C_4{\parallel g\parallel }_{{\dot{\mathbf{K}}}_{{\mathrm{p}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}.$$

(16)

Using the cut-off function $\varphi$ (with $supp(\nabla \varphi )\subset {\mathrm{Q}}_{\sigma }\setminus {\mathrm{Q}}_{\gamma \sigma }$ and ${\parallel \nabla \varphi \parallel }_{\infty }\lesssim 1/\left[\sigma (1-\gamma )\right]$), standard multiplication estimates in Herz spaces yield

$$\begin{array}{cc}\hfill {\parallel \mathbf{G}\parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}& \le C_5\left({\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\right),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\parallel g\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}& \le C_6\left(\parallel {\nabla }_{\mathrm{\mu }}{\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\right).\hfill \end{array}$$

(18)

Combining (14)–(18) gives

$$\begin{array}{cc}\hfill \parallel {\nabla }_{\mathrm{\mu }}{\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}& \le {C(\parallel \mathrm{a}\parallel }_{*,{\mathrm{Q}}_{\sigma }}{\parallel {\nabla }_{\mathrm{\mu }}\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\hfill \\ & +{\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel {\nabla }_{\mathrm{\mu }}\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}).\hfill \end{array}$$

Choosing $\sigma$ sufficiently small so that ${C\parallel \mathrm{a}\parallel }_{*,{\mathrm{Q}}_{\sigma }}\le 1/2$ and absorbing the left-hand term yields

$$\parallel {\nabla }_{\mathrm{\mu }}{\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\le C^{\prime }\left({\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel {\nabla }_{\mathrm{\mu }}\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\right).$$

Since $\varphi \equiv 1$ on ${\mathrm{Q}}_{\gamma \sigma }$, we have ${\nabla }_{\mathrm{\mu }}\mathbf{V}={\nabla }_{\mathrm{\mu }}\mathbf{V}$ there; hence,

$$\parallel {\nabla }_{\mathrm{\mu }}{\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}^{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\Gamma \sigma }\right)}\le C^{\prime }\left({\parallel \varphi \parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel \mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{\mathrm{r}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}+{\parallel {\nabla }_{\mathrm{\mu }}\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}\left({\mathrm{Q}}_{\sigma }\right)}\right).$$

If ${\mathfrak{r}}_{*}(·)\le 2$, apply the embedding in the second index to estimate

$$\parallel {\nabla }_{\mathrm{\mu }}{\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{{\mathfrak{r}}_{*}(·),\mathrm{s}(·)}^{\mathfrak{a}(·)}}\le {\parallel {\nabla }_{\mathrm{\mu }}\mathbf{V}\parallel }_{{\dot{\mathbf{K}}}_{2,\mathrm{s}(·)}^{\mathfrak{a}(·)}},$$

and obtain the desired estimate on ${\mathrm{Q}}_{\sigma /2}$. If ${\mathfrak{r}}_{*}(·)>2$, iterate with

$${\mathfrak{r}}^{\left(0\right)}(·)=2,{\mathfrak{r}}^{(\mathrm{k}+1)}(·):={\left({\mathfrak{r}}^{\left(\mathrm{k}\right)}\right)}^{*}(·),{\displaystyle \frac{1}{{\mathfrak{r}}^{(\mathrm{k}+1)}(·)}}={\displaystyle \frac{1}{{\mathfrak{r}}^{\left(\mathrm{k}\right)}(·)}}-{\displaystyle \frac{\mathrm{\alpha }}{\mathrm{n}}},$$

using nested cylinders. After finitely many steps, this produces the final estimate on ${\mathrm{Q}}_{\sigma /2}$.

This completes the proof. □

5. Conclusions and Future Perspectives

In this work, we have extended and improved a number of existing theorems in the literature by establishing new boundedness results for the fractional Bessel–Riesz operator in the framework of variable exponent Herz spaces. The variable Herz spaces used here simultaneously capture both local and global characteristics, providing a more flexible analytical setting than the classical Lebesgue and Morrey spaces, which mainly capture local behavior. Our findings show the sharpness of the derived inequalities, recover previous boundedness theorems as special cases under fixed exponents, and provide a nontrivial comparative example of the superiority of the Bessel–Riesz operator over its classical Riesz counterpart for specific exponent configurations. We have demonstrated the use of these operator estimates as an application to investigate the regularization and qualitative behavior of parabolic Ginzburg–Landau equations with VMO coefficients. We demonstrated that the boundedness of solutions implies their continuity, which naturally leads to regularity, by incorporating our boundedness results into the analysis of the linearized system. This link between PDE regularity theory and harmonic analysis methods demonstrates the strength and promise of our methodology. A number of directions are still open for further research. Investigating similar boundedness and regularity results for nonlinear PDE systems involving more general pseudo-differential or nonlocal operators in variable Besov–Herz or variable Herz–Morrey spaces is one encouraging avenue. Another is to apply the current analysis to weighted or anisotropic environments, where the interaction between local and global behaviors is more complex. Regularity theory in irregular environments may also be improved by applying these methods to systems with rougher coefficients or stochastic PDEs. The qualitative theory of parabolic equations and harmonic analysis may have deeper structural connections if the time–frequency localization properties of Bessel–Riesz operators in variable exponent frameworks are examined.