The Fractional Soliton Solutions for the Three-Component Fractional Nonlinear Schrödinger Equation Under the Zero Background

Abstract

Fractional differential equations have emerged as a prominent focus of modern scientific research due to their advantages in describing the complexity and nonlinear behavior of many physical phenomena. In particular, when considering problems with initial-boundary value conditions, the solution of nonlinear fractional differential equations becomes particularly important. This paper aims to explore the fractional soliton solutions for the three-component fractional nonlinear Schrödinger (TFNLS) equation under the zero background. According to the Lax pair and fractional recursion operator, we obtain fractional nonlinear equations with Riesz fractional derivatives, which ensure the integrability of these equations. In particular, by the completeness relation of squared eigenfunctions, we derive the explicit form of the TFNLS equation. Subsequently, in the reflectionless case, we construct the fractional N-soliton solutions via the Riemann–Hilbert (RH) method. The analysis results indicate that as the order of the Riesz fractional derivative increases, the widths of both one-soliton and two-soliton solutions gradually decrease. However, the absolute values of wave velocity, phase velocity, and group velocity of one component of the vector soliton exhibit an increasing trend, and show power-law relationships with the amplitude.

1. Introduction

Fractional calculus is a mathematical structure used to study the application of integrals and derivatives of arbitrary order, which first originated in some of Leibniz and Euler’s conjectures [1,2,3,4]. Fractional calculus has a broad physical background and becomes an essential tool for simulating many physical processes in multiscale media and physical systems with power-law behavior. For instance, in anomalous diffusion, the square of the displacement is proportional to $t^{\alpha }$ with $\alpha >0$ [5,6,7,8], and this transport phenomenon is prevalent in biology [9,10,11,12], amorphous materials [13,14,15], porous media [16,17,18], and climate science [19]. During the research process, several anomalous physical phenomena do not satisfy the requirements of classical mechanics of integer-order differentiability. For example, the turbulent velocity field of the atmosphere changes its vibration and direction randomly and violently. As a result, the integer-order differentiability classical mechanics cannot accurately describe the changing law of the velocity of the turbulent velocity field [20]. The proposal of fractional order differential theory is more favorable to explore similar strange physical phenomena, which challenges the development of integer-order differential theory. In particular, when considering problems with initial-boundary value conditions, the solution of nonlinear fractional differential equations becomes particularly important.

Currently, according to different definitions of fractional derivative, fractional differential equations are classified into multiple categories. There are various fractional forms for the nonlinear Schrödinger (NLS) equation [21,22], the Korteweg-de Vries (KdV) equation [23,24] and the modified Korteweg-de Vries (mKdV) equation [25,26]. Integrable evolution equations are important for the study of nonlinear dynamics because they are exactly solvable models. In addition, they are essential elements of the Kolmogorov–Arnold–Moser (KAM) theory, which facilitates a deep understanding of the concept of chaos. It is noteworthy that solitons are the fundamental solutions of such equations and of stable local nonlinear waves that propagate without divergence and interact elastically with other solitons [27].

In 2022, Ablowitz, Been, and Carr defined the fractional operator based on the Riesz fractional derivative ${\left|-{\partial }_x^2\right|}^{ϵ}$, $ϵ\in [0,1)$ [28]. The introduction of the Riesz fractional derivative established a connection between fractional calculus and Fourier transforms [29]. It is a fractional generalization of the negative second derivative. For any sufficiently regular function $f\left(x\right)$, ${\left|-{\partial }_x^2\right|}^{ϵ}f\left(x\right)={\mathcal{F}}^{-1}\left({\left|k\right|}^{2ϵ}\mathcal{F}f\left(x\right)\right)$, where $\mathcal{F}$ is the Fourier transform, ${\mathcal{F}}^{-1}$ is the inverse Fourier transform, and ${\left|k\right|}^{2ϵ}$ for $k\in \mathbb{R}$ represents the spectrum of the operator. Then, from the Lax pairs and fractional recursive operators, the new forms of the fractional NLS equation, the fractional KdV equation, the fractional mKdV equation, and the fractional Sine-Gordon equation were obtained [28,30]. These fractional soliton equations are integrable in the sense of inverse scattering transform (IST). Afterwards, forms of the discrete fractional equations and higher order fractional equations are received. In [27], the fractional integrable discrete NLS equation was given, and the peak velocity of its soliton solution showed a more complex behavior than previously obtained. In [31], the anomalous dispersion relation and fractional N-soliton solutions of the fractional integrable higher order NLS equation were investigated through using the IST. In terms of the Riesz fractional derivative, the explicit expression of the fractional coupled Hirota equation was given from the $3\times 3$ spectral equation, and its fractional N-soliton solutions were obtained by the IST in the absence of reflectionlessness [20].

Compared to one-component systems, multi-component systems exhibit richer dynamic behaviors and can describe more complex physical phenomena, such as Bose–Einstein condensates [32], nonlinear optical fibers [33], and so on. The three-component nonlinear Schrödinger (TNLS) equation typically takes the following form:

$$\begin{array}{cc}\hfill & \mathrm{i}{u}_{1t}+{\displaystyle \frac{1}{2}}{u}_{1xx}+\left({\sigma }_1{\left|u_1\right|}^2+{\sigma }_2{\left|u_2\right|}^2+{\sigma }_3{\left|u_3\right|}^2\right)u_1=0,\hfill \\ \hfill & \mathrm{i}{u}_{2t}+{\displaystyle \frac{1}{2}}{u}_{2xx}+\left({\sigma }_1{\left|u_1\right|}^2+{\sigma }_2{\left|u_2\right|}^2+{\sigma }_3{\left|u_3\right|}^2\right)u_2=0,\hfill \\ \hfill & \mathrm{i}{u}_{3t}+{\displaystyle \frac{1}{2}}{u}_{3xx}+\left({\sigma }_1{\left|u_1\right|}^2+{\sigma }_2{\left|u_2\right|}^2+{\sigma }_3{\left|u_3\right|}^2\right)u_3=0,\hfill \end{array}$$

(1)

where $u_j$$(j=1,2,3)$ is a complex function dependent on space variable x and time variable t. Based on the signs of the nonlinear coefficients ${\sigma }_n$$(n=1,2,3)$, the TNLS equation can be classified into three distinct types: (i) the focusing TNLS equation, where ${\sigma }_1={\sigma }_2={\sigma }_3=1$ supports bright–bright soliton solutions [34] and rogue wave solutions [35,36]; (ii) the defocusing TNLS equation for ${\sigma }_1={\sigma }_2={\sigma }_3=-1$, which possesses either dark soliton solutions in all the components [37] or bright–dark soliton solutions [38,39]; and (iii) when ${\sigma }_1={\sigma }_2=1$, ${\sigma }_3=-1$ and ${\sigma }_1=1$, ${\sigma }_2={\sigma }_3=-1$, the TNLS equation for a mixture of focusing and defocusing admits both bright–dark soliton solutions [40,41] and dark–dark soliton solutions [37]. This paper focuses on the fractional form of the focusing TNLS equation (${\sigma }_1={\sigma }_2={\sigma }_3=1$), namely the TFNLS equation. We extend the Riesz fractional derivative to the $4\times 4$ matrix spectral problem and construct an explicit form of the TFNLS equation by employing the completeness relation of squared eigenfunctions. Subsequently, by applying the RH method, we derive the fractional N-soliton solutions in the reflectionless case. The core theoretical value of this work lies in the introduction of the fractional order $ϵ$, which provides a key tunable dimension for soliton dynamics, enabling precise control over properties such as propagation velocity, collision behavior, and wave width. This characteristic makes the TFNLS equation particularly suitable for describing nonlinear wave propagation in complex media with anomalous dispersion or memory effects [42,43], thereby granting it direct application potential in fields such as fractional nonlinear optics [44] and fractional Bose–Einstein condensates [45].

The organization of this work is as follows: In Section 2, the TFNLS equation is obtained in terms of fractional recursion operator ${\mathcal{M}}_{frac.}\left(\mathbf{L}\right)$. Section 3 constructs the RH problem. When scattering data $s_{11}\ne 0$ and ${\tilde{s}}_{11}\ne 0$, the integral expression of the solution of a regular RH problem is provided through using the Plemelj formula. In addition, for the nonregular RH problem with scattering data $s_{11}={\tilde{s}}_{11}=0$, the solution can be obtained using Theorem 1. Then, based on the completeness relation of the squared eigenfunctions, the explicit form of the TFNLS equation is provided in Section 4. In Section 5, the fractional N-soliton solutions of the TFNLS equation are explored. Section 6 is our conclusions.

2. Three-Component Fractional Nonlinear Schrödinger Equation

In this section, based on the Ablowitz–Kaup–Newell–Segur (AKNS) equation and zero curvature equation, we derive the recursion operator for the focusing TNLS equation. Subsequently, we make appropriate change to this recursive operator and find the fractional recursion operator function of the TFNLS equation [20,27].

The $4\times 4$ AKNS spectral problem is as follows

$${\mathbf{Y}}_x(k;x,t)=\mathbf{X}(k;x,t)\mathbf{Y}(k;x,t),$$

(2)

$${\mathbf{Y}}_t(k;x,t)=\mathbf{T}(k;x,t)\mathbf{Y}(k;x,t),$$

(3)

where

$$\begin{array}{cc}& \mathbf{X}(k;x,t)=\mathrm{i}k\sigma +\mathbf{U}(x,t),\sigma =diag(-1,1,1,1),\hfill \\ & \mathbf{U}(x,t)=\left[\begin{array}{cc}0& \mathbf{u}(x,t)\\ \mathbf{w}(x,t)& \mathbf{0}\end{array}\right],\mathbf{T}(k;x,t)=\left[\begin{array}{cc}A(k;x,t)& \mathbf{B}(k;x,t)\\ \mathbf{C}(k;x,t)& \mathbf{D}(k;x,t)\end{array}\right],\hfill \\ & \mathbf{u}(x,t)=\left[\begin{array}{ccc}{u}_1(x,t)& u_2(x,t)& u_3(x,t)\end{array}\right],\mathbf{w}(x,t)={\left[\begin{array}{ccc}{w}_1(x,t)& w_2(x,t)& w_3(x,t)\end{array}\right]}^{\top },\hfill \end{array}$$

where $k\in \mathbb{C}$ is a spectral parameter, $u_j(x,t)$ and $w_j(x,t)$$(j=1,2,3)$ are potential functions, $\mathbf{Y}(k;x,t)={\left[\begin{array}{cccc}{\mathbf{Y}}_1(k;x,t)& {\mathbf{Y}}_2(k;x,t)& {\mathbf{Y}}_3(k;x,t)& {\mathbf{Y}}_4(k;x,t)\end{array}\right]}^{\top }$ are the wave functions, $A(k;x,t)$ is a scalar, ${\mathbf{B}}^{\top }(k;x,t)$ and $\mathbf{C}(k;x,t)$ are three-dimensional column vectors, and $\mathbf{D}(k;x,t)$ is a $3\times 3$ matrix. In the following, to simplify the computation, we take $\mathbf{X}(k;x,t):=\mathbf{X}$ and $\mathbf{T}(k;x,t):=\mathbf{T}$. Then, by calculating the zero curvature equation

$${\mathbf{X}}_t-{\mathbf{T}}_x+\left[\begin{array}{c}\mathbf{X},\mathbf{T}\end{array}\right]=\mathbf{0},$$

(4)

where the commutator is defined by $\left[\begin{array}{c}\mathbf{X},\mathbf{T}\end{array}\right]\equiv \mathbf{X}\mathbf{T}-\mathbf{T}\mathbf{X}$, so we get

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & -A_x-\mathbf{B}\mathbf{w}+\mathbf{u}\mathbf{C}=0,\hfill \\ \hfill & {\mathbf{u}}_t-{\mathbf{B}}_x-2\mathrm{i}k\mathbf{B}-A\mathbf{u}+\mathbf{u}\mathbf{D}=\mathbf{0},\hfill \\ \hfill & {\mathbf{w}}_t-{\mathbf{C}}_x+2\mathrm{i}k\mathbf{C}+\mathbf{w}A-\mathbf{D}\mathbf{w}=\mathbf{0},\hfill \\ \hfill & -{\mathbf{D}}_x+\mathbf{w}\mathbf{B}-\mathbf{C}\mathbf{u}=\mathbf{0},\hfill \end{array}\right.\end{array}$$

(5)

and

$$A=-{\partial }_{-}^{-1}\left(\mathbf{B}\mathbf{w}-\mathbf{u}\mathbf{C}\right)+A_0,$$

(6)

$$\mathbf{D}={\partial }_{-}^{-1}\left(\mathbf{w}\mathbf{B}-\mathbf{C}\mathbf{u}\right)+{\mathbf{D}}_0,$$

(7)

where ${\partial }_{-}^{-1}$ represents an antiderivative with respect to x, defined as ${\partial }_{-}^{-1}=\underset{-\infty }{\overset{x}{\int }}\mathrm{d}y$, and $A_0,{\mathbf{D}}_0$ are constants. Inserting Equations (6) and (7) into Equation (5), we get

$${\left[\begin{array}{c}{\mathbf{u}}^{\top }\\ -\mathbf{w}\end{array}\right]}_t=\mathrm{i}(2k-\mathbf{L})\left[\begin{array}{c}{\mathbf{B}}^{\top }\\ \mathbf{C}\end{array}\right]+\left[\begin{array}{c}{A}_0{\mathbf{u}}^{\top }-{\mathbf{D}}_0^{\top }{\mathbf{u}}^{\top }\\ A_0\mathbf{w}-{\mathbf{D}}_0\mathbf{w}\end{array}\right],$$

(8)

where the recursion operator $\mathbf{L}$ is

$$\mathbf{L}=\mathrm{i}\left[\begin{array}{cc}{\mathbb{I}}_3\left\{{\partial }_x\right\}-{\mathbf{u}}^{\top }{\partial }_{-}^{-1}{\mathbf{w}}^{\top }-{\mathbb{I}}_3\left\{{\partial }_{-}^{-1}{\mathbf{w}}^{\top }{\mathbf{u}}^{\top }\right\}& {\mathbf{u}}^{\top }{\partial }_{-}^{-1}\mathbf{u}-{\partial }_{-}^{-1}{\mathbf{u}}^{\top }\mathbf{u}\\ -\mathbf{w}{\partial }_{-}^{-1}{\mathbf{w}}^{\top }-{\partial }_{-}^{-1}\mathbf{w}{\mathbf{w}}^{\top }& -{\mathbb{I}}_3\left\{{\partial }_x\right\}+\mathbf{w}{\partial }_{-}^{-1}\mathbf{u}+{\mathbb{I}}_3\left\{{\partial }_{-}^{-1}\mathbf{u}\mathbf{w}\right\}\end{array}\right],$$

(9)

where ${\mathbb{I}}_3$ is the unit matrix of rank three. The adjoint operator of $\mathbf{L}$ is defined as

$${\mathbf{L}}^A=\mathrm{i}\left[\begin{array}{cc}-{\mathbb{I}}_3\left\{{\partial }_x\right\}-\mathbf{w}{\partial }_{+}^{-1}\mathbf{u}-{\mathbb{I}}_3\left\{{\partial }_{+}^{-1}\mathbf{u}\mathbf{w}\right\}& -\mathbf{w}{\partial }_{+}^{-1}{\mathbf{w}}^{\top }-{\partial }_{+}^{-1}\mathbf{w}{\mathbf{w}}^{\top }\\ {\mathbf{u}}^{\top }{\partial }_{+}^{-1}\mathbf{u}-{\partial }_{+}^{-1}{\mathbf{u}}^{\top }\mathbf{u}& {\mathbb{I}}_3\left\{{\partial }_x\right\}+{\mathbf{u}}^{\top }{\partial }_{+}^{-1}{\mathbf{w}}^{\top }+{\mathbb{I}}_3\left\{{\partial }_{+}^{-1}{\mathbf{w}}^{\top }{\mathbf{u}}^{\top }\right\}\end{array}\right],$$

(10)

where

$${\partial }_{+}^{-1}=\underset{x}{\overset{+\infty }{\int }}\mathrm{d}y,{\mathbb{I}}_3\left\{·\right\}=\mathrm{diag}\left(·,·,·\right).$$

We assume that

$$\left[\begin{array}{c}{\mathbf{B}}^{\top }\\ \mathbf{C}\end{array}\right]=\sum _{j=1}^n\left[\begin{array}{c}{\mathbf{b}}_j^{\top }\\ {\mathbf{c}}_j\end{array}\right]k^{n-j},A_0=-\mathrm{i}{k}^n,{\mathbf{D}}_0=\mathrm{i}{k}^n{\mathbb{I}}_3.$$

Then, substituting these equations into Equation (8) and matching the coefficients of the same powers of k, we can obtain

$${\left[\begin{array}{c}{\mathbf{u}}^{\top }\\ -\mathbf{w}\end{array}\right]}_t=-\mathrm{i}\mathbf{L}\left[\begin{array}{c}{\mathbf{b}}_n^{\top }\\ {\mathbf{c}}_n\end{array}\right],\left[\begin{array}{c}{\mathbf{b}}_1^{\top }\\ {\mathbf{c}}_1\end{array}\right]=\left[\begin{array}{c}{\mathbf{u}}^{\top }\\ \mathbf{w}\end{array}\right],\left[\begin{array}{c}{\mathbf{b}}_j^{\top }\\ {\mathbf{c}}_j\end{array}\right]={\displaystyle \frac{1}{2}}\mathbf{L}\left[\begin{array}{c}{\mathbf{b}}_{j-1}^{\top }\\ {\mathbf{c}}_{j-1}\end{array}\right],j=2,\dots ,n,$$

and the integrable hierarchy associated with a $4\times 4$ spectral problem

$${\left[\begin{array}{c}{\mathbf{u}}^{\top }\\ -\mathbf{w}\end{array}\right]}_t=-\mathrm{i}\mathcal{M}\left(\mathbf{L}\right)\left[\begin{array}{c}{\mathbf{u}}^{\top }\\ \mathbf{w}\end{array}\right],$$

(11)

where $\mathcal{M}\left(\mathbf{L}\right)={\displaystyle \frac{1}{2^{n-1}}}{\mathbf{L}}^n$, $n=1,2,\dots$. When $n=2$, the function with respect to the recursive operator $\mathbf{L}$ is $\mathcal{M}\left(\mathbf{L}\right)={\displaystyle \frac{1}{2}}{\mathbf{L}}^2$, and the TNLS integrable hierarchy is given by

$${\left[\begin{array}{c}{\mathbf{u}}^{\top }\\ -\mathbf{w}\end{array}\right]}_t=-{\displaystyle \frac{1}{2}}\mathrm{i}{\mathbf{L}}^2\left[\begin{array}{c}{\mathbf{u}}^{\top }\\ \mathbf{w}\end{array}\right],\mathbf{w}=-{\mathbf{u}}^{†}.$$

(12)

In the following, we will derive the TFNLS equation that includes the Riesz fractional derivative ${\left|-{\partial }_x^2\right|}^{ϵ}$, $ϵ\in [0,1)$. The Riesz fractional derivative is characterized by its Fourier multiplier ${\left|k\right|}^{2ϵ}$ and can be understood as the fractional power of $\left|-{\partial }_x^2\right|$ [30]. To introduce the Riesz fractional derivative into the function $\mathcal{M}\left(\mathbf{L}\right)={\displaystyle \frac{1}{2}}{\mathbf{L}}^2$, we define the fractional function ${\mathcal{M}}_{frac.}\left(\mathbf{L}\right)={\displaystyle \frac{1}{2}}{\mathbf{L}}^2{\left|{\mathbf{L}}^2\right|}^{ϵ}$ with respect to the recursive operator $\mathbf{L}$, where ${\left|{\mathbf{L}}^2\right|}^{ϵ}$ includes ${\left|-{\partial }_x^2\right|}^{ϵ}$. Inserting ${\mathcal{M}}_{frac.}\left(\mathbf{L}\right)$ into Equation (11), the TFNLS equation is obtained

$${\left[\begin{array}{c}{\mathbf{u}}^{\top }\\ -\mathbf{w}\end{array}\right]}_t={\displaystyle \frac{1}{2}}\mathrm{i}{\left|{\mathbf{L}}^2\right|}^{ϵ}\left[\begin{array}{c}{\mathbf{u}}_{xx}^{\top }-2{\mathbf{u}}^{\top }{\mathbf{w}}^{\top }{\mathbf{u}}^{\top }\\ {\mathbf{w}}_{xx}-2\mathbf{w}\mathbf{u}\mathbf{w}\end{array}\right],\mathbf{w}=-{\mathbf{u}}^{†}.$$

(13)

Next, by defining the fundamental solution

$$\mathbf{u}=\left[\begin{array}{ccc}{u}_1& u_2& u_3\end{array}\right]\sim \left[\begin{array}{ccc}{e}^{\mathrm{i}\left(z_{1}x-{\omega }_1\left(z_1\right)t\right)}& e^{\mathrm{i}\left(z_{2}x-{\omega }_2\left(z_2\right)t\right)}& e^{\mathrm{i}\left(z_{3}x-{\omega }_3\left(z_3\right)t\right)}\end{array}\right]$$

and substituting it into the linearized equation of TFNLS equation

$$\mathrm{i}{\mathbf{u}}_t+{\displaystyle \frac{1}{2}}{\left|-{\partial }_x^2\right|}^{ϵ}{\mathbf{u}}_{xx}=\mathbf{0},$$

(14)

we derive the anomalous dispersion relation

$${\mathcal{M}}_{frac.}\left(z_m\right)={\omega }_m\left(-z_m\right)={\displaystyle \frac{1}{2}}{z}_m^2{\left|z_m^2\right|}^{ϵ},ϵ\in [0,1),m=1,2,3.$$

(15)

3. Riemann–Hilbert Problem of the TFNLS Equation

In this section, we construct the reconstruction formula for the potential function $u_j(x,t)(j=1,2,3)$ via the Riemann–Hilbert method.

3.1. Jost Solutions and Scattering Matrix

First, we assume that the potential function $\mathbf{u}$ is sufficiently smooth and rapidly tends to zero as $x\to \pm \infty$. As the matrix $\mathbf{T}$ usually cannot be precisely expressed in the fractional integrable equations, we need to impose constraints on it [20].

$$\mathbf{T}\to \left[\begin{array}{cc}-{\displaystyle \frac{\mathrm{i}}{2}}{\mathcal{M}}_{frac.}\left(2k\right)& \mathbf{0}\\ \mathbf{0}& {\displaystyle \frac{\mathrm{i}}{2}}{\mathcal{M}}_{frac.}\left(2k\right){\mathbb{I}}_3\end{array}\right],x\to \pm \infty .$$

(16)

Then, under the constraint of Equation (16), we obtain the common solutions of the Lax pair Equations (2) and (3), known as the Jost solutions

$${\mathbf{Y}}_{\pm }(k;x,t)\to {\mathrm{e}}^{\mathrm{i}kx\sigma },x\to \pm \infty ,$$

(17)

where subscripts ± indicates the cases $x\to \pm \infty$. Thus, the modified Jost solutions ${\mathbf{J}}_{\pm }(k;x,t)$ can be denoted as

$${\mathbf{J}}_{\pm }(k;x,t):={\mathbf{J}}_{\pm }={\mathbf{Y}}_{\pm }(k;x,t){\mathrm{e}}^{-\mathrm{i}kx\sigma },$$

(18)

and the boundary conditions are

$${\mathbf{J}}_{\pm }\to {\mathbb{I}}_4,x\to \pm \infty .$$

Inserting Equation (18) into spectral problem Equation (2), we find that the modified Jost solutions ${\mathbf{J}}_{\pm }$ satisfy

$${\left({\mathbf{J}}_{\pm }\right)}_x=\mathrm{i}k[\sigma ,{\mathbf{J}}_{\pm }]+\mathbf{U}{\mathbf{J}}_{\pm }.$$

(19)

According to a generalized Liouville’s formula [46], we get

$$det{\mathbf{J}}_{\pm }=1$$

due to $tr\mathbf{U}=0$.

To simplify the calculation process, we replace the Jost solutions ${\mathbf{Y}}_{+}$ and ${\mathbf{Y}}_{-}$ with $\mathbf{\Psi }$ and $\mathbf{\Phi }$, respectively

$$\begin{array}{cc}\hfill & {\mathbf{Y}}_{+}:=\mathbf{\Psi }={\mathbf{J}}_{+}{\mathrm{e}}^{\mathrm{i}kx\sigma },\hfill \\ \hfill & {\mathbf{Y}}_{-}:=\mathbf{\Phi }={\mathbf{J}}_{-}{\mathrm{e}}^{\mathrm{i}kx\sigma },\hfill \end{array}$$

(20)

which are regarded as both fundamental solutions of Equations (2) and (3) and are linearly related by a scattering matrix $\mathbf{S}(k;t):=\mathbf{S}={\left(s_{ij}(k;t)\right)}_{4\times 4}$

$$\mathbf{\Phi }=\mathbf{\Psi }\mathbf{S},k\in \mathbb{R},$$

where $det\mathbf{S}=1$ due to $det{\mathbf{J}}_{\pm }=1$. Then, combining Equation (20), the following relation is obtained

$${\mathbf{J}}_{-}={\mathbf{J}}_{+}{\mathrm{e}}^{\mathrm{i}kx\sigma }\mathbf{S}{\mathrm{e}}^{-\mathrm{i}kx\sigma },k\in \mathbb{R}.$$

(21)

Subsequently, applying the method of variation in parameters and the boundary conditions of Equation (18), we present the Volterra integral equation [47] for ${\mathbf{J}}_{\pm }(k;x,t)$

$${\mathbf{J}}_{-}(k;x,t)={\mathbb{I}}_4+\underset{-\infty }{\overset{x}{\int }}{\mathrm{e}}^{\mathrm{i}k(x-y)\sigma }\mathbf{U}(y;t){\mathbf{J}}_{-}(k;y,t){\mathrm{e}}^{\mathrm{i}k(y-x)\sigma }\mathrm{d}y,$$

(22)

$${\mathbf{J}}_{+}(k;x,t)={\mathbb{I}}_4-\underset{x}{\overset{+\infty }{\int }}{\mathrm{e}}^{\mathrm{i}k(x-y)\sigma }\mathbf{U}(y;t){\mathbf{J}}_{+}(k;y,t){\mathrm{e}}^{\mathrm{i}k(y-x)\sigma }\mathrm{d}y,$$

(23)

where ${\mathbf{J}}_{\pm }=\left[\begin{array}{cccc}{{\mathbf{J}}_1}_{\pm }& {{\mathbf{J}}_2}_{\pm }& {{\mathbf{J}}_3}_{\pm }& {{\mathbf{J}}_4}_{\pm }\end{array}\right]$. Thus ${\mathbf{J}}_{\pm }$ can be analytically continued off the real axis $k\in \mathbb{R}$, provided that the integrals on the right-hand sides of the above Volterra equations converge. The integral in ${{\mathbf{J}}_1}_{+}$ converges since it only contains the exponential factor ${\mathrm{e}}^{2\mathrm{i}k(x-y)}$ which is bounded when $k\in {\mathbb{C}}^{-}$ and the potential function $\mathbf{u}$ is sufficiently smooth and rapidly tends to zero as $x\to \pm \infty$. Carrying out similar analysis on other quantities in ${\mathbf{J}}_{\pm }$, we can easily find that $\left[\begin{array}{cccc}{{\mathbf{J}}_1}_{+}& {{\mathbf{J}}_2}_{-}& {{\mathbf{J}}_3}_{-}& {{\mathbf{J}}_4}_{-}\end{array}\right]$ are analytical for the lower half-plane $k\in {\mathbb{C}}^{-}$. Meanwhile, $\left[\begin{array}{cccc}{{\mathbf{J}}_1}_{-}& {{\mathbf{J}}_2}_{+}& {{\mathbf{J}}_3}_{+}& {{\mathbf{J}}_4}_{+}\end{array}\right]$ are analytical for the upper half-plane $k\in {\mathbb{C}}^{+}$, with ${\mathbb{C}}^{\pm }$ depicted in Figure 1.

In the following, based on the analytic properties of ${\mathbf{J}}_{\pm }$, we introduce two new matrix functions ${\mathbf{K}}^{\pm }={\mathbf{K}}^{\pm }(k;x,t):={lim}_{\kappa \downarrow 0}\mathbf{K}(k;x,t)(k\pm \mathrm{i}\kappa ;x,t)$, which are analytic for $k\in {\mathbb{C}}^{\pm }$, respectively.

Firstly, if we take $\mathbf{\Psi }$, $\mathbf{\Phi }$ to be a collection of columns

$$\begin{array}{cc}\hfill & \mathbf{\Psi }=\left[\begin{array}{cccc}{\mathit{\psi }}_1& {\mathit{\psi }}_2& {\mathit{\psi }}_3& {\mathit{\psi }}_4\end{array}\right],\hfill \\ \hfill & \mathbf{\Phi }=\left[\begin{array}{cccc}{\mathit{\varphi }}_1& {\mathit{\varphi }}_2& {\mathit{\varphi }}_3& {\mathit{\varphi }}_4\end{array}\right],\hfill \end{array}$$

(24)

then the matrix Jost solution [47]

$${\mathbf{K}}^{+}=\left[\begin{array}{cccc}{\mathit{\varphi }}_1& {\mathit{\psi }}_2& {\mathit{\psi }}_3& {\mathit{\psi }}_4\end{array}\right]{\mathrm{e}}^{-\mathrm{i}kx\sigma }={\mathbf{J}}_{-}{\mathbf{P}}_1+{\mathbf{J}}_{+}{\mathbf{P}}_2$$

(25)

is analytic in $k\in {\mathbb{C}}^{+}$ and $det{\mathbf{K}}^{+}=s_{11}$, where ${\mathbf{P}}_1$, ${\mathbf{P}}_2$ are defined by

$${\mathbf{P}}_1=diag(1,0,0,0),{\mathbf{P}}_2=diag(0,1,1,1).$$

Similarly, the matrix Jost solution

$$\left[\begin{array}{cccc}{\mathit{\psi }}_1& {\mathit{\varphi }}_2& {\mathit{\varphi }}_3& {\mathit{\varphi }}_4\end{array}\right]{\mathrm{e}}^{-\mathrm{i}kx\sigma }={\mathbf{J}}_{+}{\mathbf{P}}_1+{\mathbf{J}}_{-}{\mathbf{P}}_2$$

(26)

is analytic in $k\in {\mathbb{C}}^{-}$.

Furthermore, based on the Volterra integral equation in Equations (22) and (23), we obtain the asymptotic properties

$${\mathbf{K}}^{+}\to {\mathbb{I}}_4,k\in {\mathbb{C}}^{+}\to \infty ,$$

(27)

and

$$\left[\begin{array}{cccc}{\mathit{\psi }}_1& {\mathit{\varphi }}_2& {\mathit{\varphi }}_3& {\mathit{\varphi }}_4\end{array}\right]{\mathrm{e}}^{-\mathrm{i}kx\sigma }\to {\mathbb{I}}_4,k\in {\mathbb{C}}^{-}\to \infty .$$

(28)

Secondly, in order to obtain the analytic counterpart of ${\mathbf{K}}^{+}$ on ${\mathbb{C}}^{-}$, the adjoint scattering equation of Equation (19) is considered

$${\left({\mathbf{J}}_{\pm }^{-1}\right)}_x=\mathrm{i}k\left[\begin{array}{c}\sigma ,{\mathbf{J}}_{\pm }^{-1}\end{array}\right]-{\mathbf{J}}_{\pm }^{-1}\mathbf{U},$$

(29)

where ${\mathbf{J}}_{\pm }^{-1}={\left[\begin{array}{cccc}{\tilde{\mathbf{J}}}_{1\pm }& {\tilde{\mathbf{J}}}_{2\pm }& {\tilde{\mathbf{J}}}_{3\pm }& {\tilde{\mathbf{J}}}_{4\pm }\end{array}\right]}^{\top }.$

By an analogous analytical approach to Jost solution ${\mathbf{K}}^{+}$, taking ${\mathbf{\Psi }}^{-1}$, ${\mathbf{\Phi }}^{-1}$ to be a collection of rows,

$$\begin{array}{cc}\hfill {\mathbf{\Psi }}^{-1}& ={\left[\begin{array}{cccc}{\tilde{\mathit{\psi }}}_1& {\tilde{\mathit{\psi }}}_2& {\tilde{\mathit{\psi }}}_3& {\tilde{\mathit{\psi }}}_4\end{array}\right]}^{\top },\hfill \\ \hfill {\mathbf{\Phi }}^{-1}& ={\left[\begin{array}{cccc}{\tilde{\mathit{\varphi }}}_1& {\tilde{\mathit{\varphi }}}_2& {\tilde{\mathit{\varphi }}}_3& {\tilde{\mathit{\varphi }}}_4\end{array}\right]}^{\top },\hfill \end{array}$$

(30)

we find that the adjoint Jost solution

$${\mathbf{K}}^{-}={\mathrm{e}}^{-\mathrm{i}kx\sigma }{\left[\begin{array}{cccc}{\tilde{\mathit{\varphi }}}_1& {\tilde{\mathit{\psi }}}_2& {\tilde{\mathit{\psi }}}_3& {\tilde{\mathit{\psi }}}_4\end{array}\right]}^{\top }={\mathbf{P}}_1{\mathbf{J}}_{-}^{-1}+{\mathbf{P}}_2{\mathbf{J}}_{+}^{-1}$$

(31)

is analytic in $k\in {\mathbb{C}}^{-}$ as well as $det{\mathbf{K}}^{-}={\tilde{s}}_{11}$, where ${\mathbf{S}}^{-1}(k;t)={\left({\tilde{s}}_{ij}(k;t)\right)}_{4\times 4}$. In addition,

$${\mathrm{e}}^{-\mathrm{i}kx\sigma }{\left[\begin{array}{cccc}{\tilde{\mathit{\psi }}}_1& {\tilde{\mathit{\varphi }}}_2& {\tilde{\mathit{\varphi }}}_3& {\tilde{\mathit{\varphi }}}_4\end{array}\right]}^{\top }={\mathbf{P}}_1{\mathbf{J}}_{+}^{-1}+{\mathbf{P}}_2{\mathbf{J}}_{-}^{-1}$$

(32)

is analytic in $k\in {\mathbb{C}}^{+}$. Similarly, we can obtain

$${\mathbf{K}}^{-}\to {\mathbb{I}}_4,k\in {\mathbb{C}}^{-}\to \infty ,$$

(33)

and

$${\mathrm{e}}^{-\mathrm{i}kx\sigma }{\left[\begin{array}{cccc}{\tilde{\mathit{\psi }}}_1& {\tilde{\mathit{\varphi }}}_2& {\tilde{\mathit{\varphi }}}_3& {\tilde{\mathit{\varphi }}}_4\end{array}\right]}^{\top }\to {\mathbb{I}}_4,k\in {\mathbb{C}}^{+}\to \infty .$$

(34)

Consequently, the analytic properties of the Jost solutions can be summarized as follows

$$\mathbf{\Psi }=\left[\begin{array}{cccc}{\mathit{\psi }}_1^{-}& {\mathit{\psi }}_2^{+}& {\mathit{\psi }}_3^{+}& {\mathit{\psi }}_4^{+}\end{array}\right],\mathbf{\Phi }=\left[\begin{array}{cccc}{\mathit{\varphi }}_1^{+}& {\mathit{\varphi }}_2^{-}& {\mathit{\varphi }}_3^{-}& {\mathit{\varphi }}_4^{-}\end{array}\right],$$

$${\mathbf{\Psi }}^{-1}={\left[\begin{array}{cccc}{\tilde{\mathit{\psi }}}_1^{+}& {\tilde{\mathit{\psi }}}_2^{-}& {\tilde{\mathit{\psi }}}_3^{-}& {\tilde{\mathit{\psi }}}_4^{-}\end{array}\right]}^{\top },{\mathbf{\Phi }}^{-1}={\left[\begin{array}{cccc}{\tilde{\mathit{\varphi }}}_1^{-}& {\tilde{\mathit{\varphi }}}_2^{+}& {\tilde{\mathit{\varphi }}}_3^{+}& {\tilde{\mathit{\varphi }}}_4^{+}\end{array}\right]}^{\top },$$

where the superscripts ± indicate that the Jost solutions are analytic in the half-plane ${\mathbb{C}}^{\pm }$.

Based on the scattering relation $\mathbf{\Phi }=\mathbf{\Psi }\mathbf{S}$ and $\det \mathbf{\Phi }=\det \mathbf{\Psi }=1$, we have

$$\begin{array}{cc}\hfill s_{1j}& =|{\mathit{\varphi }}_j,{\mathit{\psi }}_2,{\mathit{\psi }}_3,{\mathit{\psi }}_4|,\hfill \\ \hfill s_{2j}& =|{\mathit{\psi }}_1,{\mathit{\varphi }}_j,{\mathit{\psi }}_3,{\mathit{\psi }}_4|,\hfill \\ \hfill s_{3j}& =|{\mathit{\psi }}_1,{\mathit{\psi }}_2,{\mathit{\varphi }}_j,{\mathit{\psi }}_4|,\hfill \\ \hfill s_{4j}& =|{\mathit{\psi }}_1,{\mathit{\psi }}_2,{\mathit{\psi }}_3,{\mathit{\varphi }}_j|,\hfill \end{array}\begin{array}{cc}\hfill {\tilde{s}}_{j1}& =|{\tilde{\mathit{\varphi }}}_j,{\tilde{\mathit{\psi }}}_2,{\tilde{\mathit{\psi }}}_3,{\tilde{\mathit{\psi }}}_4|,\hfill \\ \hfill {\tilde{s}}_{j2}& =|{\tilde{\mathit{\psi }}}_1,{\tilde{\mathit{\varphi }}}_j,{\tilde{\mathit{\psi }}}_3,{\tilde{\mathit{\psi }}}_4|,\hfill \\ \hfill {\tilde{s}}_{j3}& =|{\tilde{\mathit{\psi }}}_1,{\tilde{\mathit{\psi }}}_2,{\tilde{\mathit{\varphi }}}_j,{\tilde{\mathit{\psi }}}_4|,\hfill \\ \hfill {\tilde{s}}_{j4}& =|{\tilde{\mathit{\psi }}}_1,{\tilde{\mathit{\psi }}}_2,{\tilde{\mathit{\psi }}}_3,{\tilde{\mathit{\varphi }}}_j|,j=1,2,3,4,\hfill \end{array}$$

where $|·,·|$ denotes the determinant. Thus, by combining the analytical properties of the Jost solutions, we can derive the analytical properties of the scattering matrixes $\mathbf{S}$ and ${\mathbf{S}}^{-1}$, which are denoted as

$$\mathbf{S}=\left[\begin{array}{cccc}{s}_{11}^{+}& s_{12}& s_{13}& s_{14}\\ s_{21}& s_{22}^{-}& s_{23}^{-}& s_{24}^{-}\\ s_{31}& s_{32}^{-}& s_{33}^{-}& s_{34}^{-}\\ s_{41}& s_{42}^{-}& s_{43}^{-}& s_{44}^{-}\end{array}\right],{\mathbf{S}}^{-1}=\left[\begin{array}{cccc}{\tilde{s}}_{11}^{-}& {\tilde{s}}_{12}& {\tilde{s}}_{13}& {\tilde{s}}_{14}\\ {\tilde{s}}_{21}& {\tilde{s}}_{22}^{+}& {\tilde{s}}_{23}^{+}& {\tilde{s}}_{24}^{+}\\ {\tilde{s}}_{31}& {\tilde{s}}_{32}^{+}& {\tilde{s}}_{33}^{+}& {\tilde{s}}_{34}^{+}\\ {\tilde{s}}_{41}& {\tilde{s}}_{42}^{+}& {\tilde{s}}_{43}^{+}& {\tilde{s}}_{44}^{+}\end{array}\right],$$

(35)

where the superscript “±” indicates that the scattering data are analytic in the half-plane ${\mathbb{C}}^{\pm }$, while $s_{1j},s_{j1},{\tilde{s}}_{1j}$, and ${\tilde{s}}_{j1}$$(j=2,3,4)$ generally do not allow analytical extensions to ${\mathbb{C}}^{\pm }$ in general. Moreover, according to the constraints of $\mathbf{T}$ Equation (16), the time evolution of the scattering data can be determined

$$\begin{array}{cc}\hfill s_{11}& =s_{11}(k;t)=s_{11}(k;0),{\tilde{s}}_{11}={\tilde{s}}_{11}(k;t)={\tilde{s}}_{11}(k;0),\hfill \\ \hfill s_{1j}& =s_{1j}(k;t)=s_{1j}(k;0){\mathrm{e}}^{-\mathrm{i}{\mathcal{M}}_{frac.}\left(2k\right)t},\hfill \\ \hfill {\tilde{s}}_{1j}& ={\tilde{s}}_{1j}(k;t)={\tilde{s}}_{1j}(k;0){\mathrm{e}}^{-\mathrm{i}{\mathcal{M}}_{frac.}\left(2k\right)t},\hfill \\ \hfill s_{j1}& =s_{j1}(k;t)=s_{j1}(k;0){\mathrm{e}}^{\mathrm{i}{\mathcal{M}}_{frac.}\left(2k\right)t},\hfill \\ \hfill {\tilde{s}}_{j1}& ={\tilde{s}}_{j1}(k;t)={\tilde{s}}_{j1}(k;0){\mathrm{e}}^{\mathrm{i}{\mathcal{M}}_{frac.}\left(2k\right)t},j=2,3,4.\hfill \end{array}$$

3.2. Riemann–Hilbert Problem

In what follows, we will construct the RH problem using the matrix functions ${\mathbf{K}}^{+}(k;x,t)$ and ${\mathbf{K}}^{-}(k;x,t)$, which are analytic for k in ${\mathbb{C}}^{+}$ and k in ${\mathbb{C}}^{-}$, respectively.

First of all, we discuss the regular RH problem, i.e., $\det {\mathbf{K}}^{+}=s_{11}\ne 0$ and $\det {\mathbf{K}}^{-}={\tilde{s}}_{11}\ne 0$, in their domain of analyticity. We introduce the following jump conditions

$${\mathbf{K}}^{-}(k;x,t){\mathbf{K}}^{+}(k;x,t)=\mathbf{G}(k;x,t),k\in \mathbb{R},$$

(36)

where the jump matrix $\mathbf{G}(k;x,t)=\mathbf{G}$ is

$$\mathbf{G}={\mathrm{e}}^{\mathrm{i}kx\sigma }\left[\left({\mathbf{P}}_1{\mathbf{S}}^{-1}+{\mathbf{P}}_2\right)\left(\mathbf{S}{\mathbf{P}}_1+{\mathbf{P}}_2\right)\right]{\mathrm{e}}^{-\mathrm{i}kx\sigma },k\in \mathbb{R}.$$

In order to obtain the solution of the regular RH problem by the Plemelj formula [47], we rewrite Equation (36) as

$${\left({\mathbf{K}}^{+}\right)}^{-1}-{\mathbf{K}}^{-}=\widehat{\mathbf{G}}{\left({\mathbf{K}}^{+}\right)}^{-1},k\in \mathbb{R},$$

(37)

then the formal solution of this problem can be given in terms of the Fredholm integral equation [47]

$${\left({\mathbf{K}}^{+}\right)}^{-1}={\mathbb{I}}_4+{\displaystyle \frac{1}{2\pi \mathrm{i}}}\underset{-\infty }{\overset{+\infty }{\int }}{\displaystyle \frac{\widehat{\mathbf{G}}\left(\xi \right){\left({\mathbf{K}}^{+}\right)}^{-1}\left(\xi \right)}{\xi -k}}\mathrm{d}\xi ,k\in {\mathbb{C}}^{+}.$$

(38)

where $\widehat{\mathbf{G}}={\mathbb{I}}_4-\mathbf{G}$.

Assuming that ${\mathbf{K}}^{\pm }$ and ${\tilde{\mathbf{K}}}^{\pm }$ are two sets of solutions to the RH problem, i.e.,

$${\mathbf{K}}^{-}{\mathbf{K}}^{+}={\tilde{\mathbf{K}}}^{+}{\tilde{\mathbf{K}}}^{-}.$$

(39)

Then, using its canonical normalization condition

$${\mathbf{K}}^{\pm }\to {\mathbb{I}}_4,k\to \infty ,$$

(40)

and Liouville’s theorem in complex analysis, we can obtain

$${\mathbf{K}}^{\pm }={\tilde{\mathbf{K}}}^{\pm },$$

(41)

which suggests that the solution for the regular RH problem is unique.

Afterwards, we consider the nonregular RH problem, i.e., $det{\mathbf{K}}^{+}=s_{11}=0$ and $det{\mathbf{K}}^{-}={\tilde{s}}_{11}=0$ in their plane of analyticity, respectively. The solution of the RH problem is unique if and only if the zeros of $det{\mathbf{K}}^{+}$ and $det{\mathbf{K}}^{-}$ in ${\mathbb{C}}^{\pm }$ are specified along with the kernel structures of ${\mathbf{K}}^{\pm }$ at these zeros.

According to the symmetry relation

$${\mathbf{U}}^{†}(x,t)=-\mathbf{U}(x,t),{\mathbf{J}}^{†}\left(k^{*};x,t\right)={\mathbf{J}}^{-1}\left(k;x,t\right)$$

and the scattering relation Equation (21), the symmetry relation of $\mathbf{S}(k;t)$ can be gained by

$${\mathbf{S}}^{†}\left(k^{*};t\right)={\mathbf{S}}^{-1}(k;t)$$

which implies $s_{11}^{*}\left(k^{*};t\right)={\tilde{s}}_{11}(k;t)$, $k\in {\mathbb{C}}^{-}$. We can suppose that $s_{11}\left(k;t\right)$ has N simple zeros $k_l\in {\mathbb{C}}^{+}$$(l=1,\dots ,N)$, and ${\tilde{s}}_{11}(k;t)$ has N simple zeros $k_l^{*}\in {\mathbb{C}}^{-}$$(l=1,\dots ,N)$. Therefore, $k_l$, $k_l^{*}$$(l=1,\dots ,N)$ are also the discrete spectra of the spectral problem. Based on this assumption, the kernel of ${\mathbf{K}}^{+}(k_l;x,t)$ contains a single column vector ${\mathit{\mu }}_l\equiv {\mathit{\mu }}_l(k_l;x,t)={\left[\begin{array}{cccc}{\mu }_l^1& {\mu }_l^2& {\mu }_l^3& {\mu }_l^4\end{array}\right]}^{\top }$ and the kernel of ${\mathbf{K}}^{-}(k_l^{*};x,t)$ contains a single row vector ${\tilde{\mathit{\mu }}}_l\equiv {\mathit{\mu }}_l(k_l^{*};x,t)=\left[\begin{array}{cccc}{\tilde{\mu }}_l^1& {\tilde{\mu }}_l^2& {\tilde{\mu }}_l^3& {\tilde{\mu }}_l^4\end{array}\right]$, i.e.,

$${\mathbf{K}}^{+}(k_l;x,t){\mathit{\mu }}_l(k_l;x,t)=0,{\tilde{\mathit{\mu }}}_l({\tilde{k}}_l;x,t){\mathbf{K}}^{-}({\tilde{k}}_l;x,t)=0,l=1,\dots ,N.$$

As a result of the above analysis, the following theorem can be presented to obtain the solution of a nonregular RH problem by transforming it into a regular one.

Theorem 1. 

The solution to the nonregular RH problem from Equation (36) with simple zeros under the canonical normalized condition of Equation (40) is

$${\widehat{\mathbf{K}}}^{+}={\mathbf{K}}^{+}{\mathbf{D}}^{-1},{\widehat{\mathbf{K}}}^{-}=\mathbf{D}{\mathbf{K}}^{-}.$$

It should be pointed out that

$$\mathbf{D}={\mathbb{I}}_4-\sum _{j,l=1}^N{\displaystyle \frac{{\mathit{\mu }}_j{\left({\mathbf{V}}^{-1}\right)}_{jl}{\tilde{\mathit{\mu }}}_l}{k-{\tilde{k}}_l}},{\mathbf{D}}^{-1}={\mathbb{I}}_4+\sum _{j,l=1}^N{\displaystyle \frac{{\mathit{\mu }}_j{\left({\mathbf{V}}^{-1}\right)}_{jl}{\tilde{\mathit{\mu }}}_l}{k-k_j}},$$

where the $(j,k)$-th element of matrix ${\left({\mathbf{V}}_{jl}\right)}_{N\times N}$ is defined as

$$\begin{array}{cc}& {\mathbf{V}}_{jl}={\displaystyle \frac{{\tilde{\mathit{\mu }}}_j{\mathit{\mu }}_l}{k_l-{\tilde{k}}_j}},1\le j,l\le N,\hfill \\ & det\mathbf{D}=\prod _{l=1}^N{\displaystyle \frac{k-k_l}{k-{\tilde{k}}_l}}.\hfill \end{array}$$

Thus, ${\widehat{\mathbf{K}}}^{\pm }$ represents the unique solution to the following regular RH problem:

$${\widehat{\mathbf{K}}}^{-}{\widehat{\mathbf{K}}}^{+}=\mathbf{D}\mathbf{G}{\mathbf{D}}^{-1},k\in \mathbb{R},$$

(42)

where ${\widehat{\mathbf{K}}}^{\pm }$ are analytic in ${\mathbb{C}}^{\pm }$, respectively.

The solution for the regular RH problem in Equation (42) can be provided through using the Plemelj formula,

$${\widehat{\mathbf{K}}}^{+}={\mathbb{I}}_4+{\displaystyle \frac{1}{2\pi \mathrm{i}}}\underset{-\infty }{\overset{+\infty }{\int }}{\displaystyle \frac{{\widehat{\mathbf{K}}}^{-}\left(\xi \right)\mathbf{D}\left(\xi \right)(\mathbf{G}\left(\xi \right)-{\mathbb{I}}_4){\mathbf{D}}^{-1}\left(\xi \right)}{\xi -k}}\mathrm{d}\xi ,k\in {\mathbb{C}}^{+}.$$

(43)

Let $k\to \infty$,

$${\widehat{\mathbf{K}}}^{+}={\mathbb{I}}_4-{\displaystyle \frac{1}{2\pi \mathrm{i}k}}\underset{-\infty }{\overset{+\infty }{\int }}{\widehat{\mathbf{K}}}^{-}\left(\xi \right)\mathbf{D}\left(\xi \right)(\mathbf{G}\left(\xi \right)-{\mathbb{I}}_4){\mathbf{D}}^{-1}\left(\xi \right)\mathrm{d}\xi ,k\in {\mathbb{C}}^{+}.$$

(44)

Similarly, $\mathbf{D}$ admits the following asymptotic behaviour as $k\to \infty$,

$$\mathbf{D}\to {\mathbb{I}}_4-{\displaystyle \frac{1}{k}}\sum _{j,l=1}^N{\mathit{\mu }}_j{\left({\mathbf{V}}^{-1}\right)}_{jl}{\tilde{\mathit{\mu }}}_l.$$

(45)

Therefore, by combining the two asymptotic behavior Equations (44) and (45) as $k\to \infty$, we obtain

$$\begin{array}{cc}\hfill {\mathbf{K}}^{+}={\mathbb{I}}_4-{\displaystyle \frac{1}{k}}\left({\displaystyle \frac{1}{2\pi \mathrm{i}}}\right.& \underset{-\infty }{\overset{+\infty }{\int }}{\widehat{\mathbf{K}}}^{-}\left(\xi \right)\mathbf{D}\left(\xi \right)(\mathbf{G}\left(\xi \right)-{\mathbb{I}}_4){\mathbf{D}}^{-1}\left(\xi \right)\mathrm{d}\xi \hfill \\ \hfill & \left.+\sum _{j,l=1}^N{\mathit{\mu }}_j{\left({\mathbf{V}}^{-1}\right)}_{jl}{\tilde{\mathit{\mu }}}_l\right)+\mathcal{O}\left(k^{-2}\right).\hfill \end{array}$$

(46)

Subsequently, we propose the expansion of ${\mathbf{K}}^{+}$ as $k\to \infty$,

$${\mathbf{K}}^{+}={\mathbb{I}}_4+{\displaystyle \frac{1}{k}}{{\mathbf{K}}_1}^{+}(x,t)+{\displaystyle \frac{1}{k^2}}{{\mathbf{K}}_2}^{+}(x,t)+\dots .$$

(47)

Inserting Equation (47) into Equation (19) and matching the highest power of k, we get

$$\mathbf{U}=\mathrm{i}\left[\begin{array}{c}\sigma ,{{\mathbf{K}}_1}^{+}\end{array}\right],$$

(48)

and the potential functions can be reformulated as

$$u_j=2\mathrm{i}{\left({{\mathbf{K}}_1}^{+}\right)}_{1,(j+1)},j=1,2,3,$$

(49)

where

$${{\mathbf{K}}_1}^{+}=-{\displaystyle \frac{1}{2\pi \mathrm{i}}}\underset{-\infty }{\overset{+\infty }{\int }}{\widehat{\mathbf{K}}}^{-}\left(\xi \right)\mathbf{D}\left(\xi \right)(\mathbf{G}\left(\xi \right)-{\mathbb{I}}_4){\mathbf{D}}^{-1}\left(\xi \right)\mathrm{d}\xi +\sum _{j,l=1}^N{\mathit{\mu }}_j{\left({\mathbf{V}}^{-1}\right)}_{jl}{\tilde{\mathit{\mu }}}_l.$$

(50)

4. The Explicit Form of the TFNLS Equation

To derive the explicit form of the TFNLS equation, it is essential to address two fundamental aspects:

• The relationship between the fractional recursion operator function ${\mathcal{M}}_{frac.}\left(\mathbf{L}\right)$ and the squared eigenfunctions;
• The relationship between squared eigenfunctions and potential functions.

Regarding the first question, it is worth noting that squared eigenfunctions are eigenfunctions of the recursion operator for integrable equations. Therefore, the recursion operator $\mathbf{L}$ can act on squared eigenfunctions and be extended to the fractional recursion operator function ${\mathcal{M}}_{frac.}\left(\mathbf{L}\right)$. For the second question, we know that this can be achieved through the completeness of the squared eigenfunctions of the TFNLS equation. The completeness of squared eigenfunctions is closely related to perturbation theory (or variational relations) [47,48,49].

Thus, we first consider a perturbation to the spectral problem (2)

$$\delta {\mathbf{\Phi }}_x=\mathbf{X}\delta \mathbf{\Phi }+\delta \mathbf{U}\mathbf{\Phi }.$$

(51)

From the asymptotic of ${\mathbf{J}}_{\pm }$ at large distances, the asymptotic behaviour of the Jost solution $\mathbf{\Phi }$ is $\mathbf{\Phi }\to {\mathrm{e}}^{\mathrm{i}kx\sigma }$, as $x\to -\infty$; thus $\delta \mathbf{\Phi }\to 0$, as $x\to -\infty$. With this boundary condition, the solution of the inhomogeneous Equation (51) can be found by the method of varying the parameters as follows

$$\delta \mathbf{\Phi }(k;x,t)=\mathbf{\Phi }(k;x,t)\underset{-\infty }{\overset{x}{\int }}{\mathbf{\Phi }}^{-1}(k;y,t)\delta \mathbf{U}(y,t)\mathbf{\Phi }(k;y,t)\mathrm{d}y,$$

(52)

where

$$\delta \mathbf{U}=\left[\begin{array}{cc}0& \delta \mathbf{u}\\ \delta \mathbf{w}& 0\end{array}\right]$$

is a variation in the potential.

Then, considering the asymptotics of $\mathbf{\Psi }\to {\mathrm{e}}^{\mathrm{i}kx\sigma }$ as $x\to +\infty$ and the scattering relation Equation (21), we can derive

$$\delta \mathbf{S}(k;t)=\underset{-\infty }{\overset{+\infty }{\int }}{\mathbf{\Psi }}^{-1}(k;x,t)\delta \mathbf{U}(x,t)\mathbf{\Phi }(k;x,t)\mathrm{d}x,$$

(53)

i.e.,

$$\delta s_{ij}(k;t)=\underset{-\infty }{\overset{+\infty }{\int }}{\tilde{\mathit{\psi }}}_i(k;x,t)\delta \mathbf{U}(x,t){\mathit{\varphi }}_j(k;x,t)\mathrm{d}x.$$

(54)

In a similar way, using the spectral problem (2) for Jost solution $\mathbf{\Psi }$, we can find

$$\delta \left({\mathbf{S}}^{-1}\right)(k;t)=-\underset{-\infty }{\overset{+\infty }{\int }}{\mathbf{\Phi }}^{-1}(k;x,t)\delta \mathbf{U}(x,t)\mathbf{\Psi }(k;x,t)\mathrm{d}x$$

(55)

i.e.,

$$\delta {\tilde{s}}_{ij}(k;t)=-\underset{-\infty }{\overset{+\infty }{\int }}{\tilde{\mathit{\varphi }}}_i(k;x,t)\delta \mathbf{U}(x,t){\mathit{\psi }}_j(k;x,t)\mathrm{d}x.$$

(56)

Nevertheless, $\delta s_{1j},\delta s_{j1},\delta {\tilde{s}}_{1j}$, and $\delta {\tilde{s}}_{j1}$ $(j=2,3,4)$ are also not analytic in ${\mathbb{C}}^{\pm }$. In order to avoid this undesirable non-analytical behaviour, we define the reflection coefficients as

$$\begin{array}{cc}\hfill & {\rho }_1={\displaystyle \frac{s_{21}}{s_{11}}},{\rho }_2={\displaystyle \frac{s_{31}}{s_{11}}},{\rho }_3={\displaystyle \frac{s_{41}}{s_{11}}},\hfill \\ & {\tilde{\rho }}_1={\displaystyle \frac{{\tilde{s}}_{12}}{{\tilde{s}}_{11}}},{\tilde{\rho }}_2={\displaystyle \frac{{\tilde{s}}_{13}}{{\tilde{s}}_{11}}},{\tilde{\rho }}_3={\displaystyle \frac{{\tilde{s}}_{14}}{{\tilde{s}}_{11}}},\hfill \end{array}$$

(57)

and thereby, from the variation relation Equations (54) and (56), we can obtain

$$\begin{array}{cc}\hfill \delta {\rho }_j(k;t)& ={\displaystyle \frac{1}{s_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}{\left({\Pi }_j^{+}(k;x,t)\right)}^{\top }\delta \mathbf{v}(x,t)\mathrm{d}x,\hfill \\ \hfill \delta {\tilde{\rho }}_j(k;t)& ={\displaystyle \frac{1}{{\tilde{s}}_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}{\left({\Pi }_j^{-}(k;x,t)\right)}^{\top }\delta \mathbf{v}(x,t)\mathrm{d}x,\hfill \\ \hfill \mathbf{v}(x,t)& ={\left[\begin{array}{cc}{\mathbf{u}}^{\top }& -\mathbf{w}\end{array}\right]}^{\top },j=1,2,3,\hfill \end{array}$$

(58)

where ${\Pi }_j^{\pm }(j=1,2,3)$ represent the adjoint squared eigenfunctions

$$\begin{array}{cc}\hfill {\Pi }_j^{+}& ={\left[\begin{array}{cccccc}{\tilde{\phi }}_{j1}{\varphi }_{21}& {\tilde{\phi }}_{j1}{\varphi }_{31}& {\tilde{\phi }}_{j1}{\varphi }_{41}& -{\tilde{\phi }}_{j2}{\varphi }_{11}& -{\tilde{\phi }}_{j3}{\varphi }_{11}& -{\tilde{\phi }}_{j4}{\varphi }_{11}\end{array}\right]}^{\top },\hfill \\ \hfill {\Pi }_j^{-}& ={\left[\begin{array}{cccccc}-{\tilde{\varphi }}_{11}{\phi }_{2j}& -{\tilde{\varphi }}_{11}{\phi }_{3j}& -{\tilde{\varphi }}_{11}{\phi }_{4j}& {\tilde{\varphi }}_{12}{\phi }_{1j}& {\tilde{\varphi }}_{13}{\phi }_{1j}& {\tilde{\varphi }}_{14}{\phi }_{1j}\end{array}\right]}^{\top },j=1,2,3,\hfill \end{array}$$

with

$$\begin{array}{cc}& \left[\begin{array}{c}{\tilde{\mathit{\phi }}}_1\\ {\tilde{\mathit{\phi }}}_2\\ {\tilde{\mathit{\phi }}}_3\end{array}\right]=\left[\begin{array}{ccc}{\tilde{s}}_{33}{\tilde{s}}_{44}-{\tilde{s}}_{34}{\tilde{s}}_{43}& {\tilde{s}}_{43}{\tilde{s}}_{34}-{\tilde{s}}_{23}{\tilde{s}}_{44}& {\widehat{s}}_{23}{\tilde{s}}_{34}-{\tilde{s}}_{24}{\tilde{s}}_{33}\\ {\tilde{s}}_{34}{\tilde{s}}_{42}-{\tilde{s}}_{32}{\tilde{s}}_{44}& {\tilde{s}}_{22}{\tilde{s}}_{44}-{\tilde{s}}_{42}{\tilde{s}}_{24}& {\tilde{s}}_{24}{\tilde{s}}_{32}-{\tilde{s}}_{22}{\tilde{s}}_{34}\\ {\tilde{s}}_{32}{\tilde{s}}_{43}-{\tilde{s}}_{33}{\tilde{s}}_{42}& {\tilde{s}}_{23}{\tilde{s}}_{42}-{\tilde{s}}_{22}{\tilde{s}}_{43}& {\tilde{s}}_{22}{\tilde{s}}_{33}-{\tilde{s}}_{23}{\tilde{s}}_{32}\end{array}\right]\left[\begin{array}{c}{\tilde{\mathit{\varphi }}}_2\\ {\tilde{\mathit{\varphi }}}_3\\ {\tilde{\mathit{\varphi }}}_4\end{array}\right],\hfill \\ & {\left[\begin{array}{c}{\mathit{\phi }}_1\\ {\mathit{\phi }}_2\\ {\mathit{\phi }}_3\end{array}\right]}^{\top }={\left[\begin{array}{c}{\mathit{\varphi }}_2\\ {\mathit{\varphi }}_3\\ {\mathit{\varphi }}_4\end{array}\right]}^{\top }\left[\begin{array}{ccc}{s}_{33}{s}_{44}-s_{34}{s}_{43}& s_{43}{s}_{34}-s_{23}{s}_{44}& s_{23}{s}_{34}-s_{24}{s}_{33}\\ s_{34}{s}_{42}-s_{32}{s}_{44}& s_{22}{s}_{44}-s_{42}{s}_{24}& s_{24}{s}_{32}-s_{22}{s}_{34}\\ s_{32}{s}_{43}-s_{33}{s}_{42}& s_{23}{s}_{42}-s_{22}{s}_{43}& s_{22}{s}_{33}-s_{23}{s}_{32}\end{array}\right],\hfill \\ & {\tilde{\mathit{\phi }}}_j=\left[\begin{array}{cccc}{\tilde{\phi }}_{j1}& {\tilde{\phi }}_{j2}& {\tilde{\phi }}_{j3}& {\tilde{\phi }}_{j4}\end{array}\right],{\mathit{\phi }}_j={\left[\begin{array}{cccc}{\phi }_{1j}& {\phi }_{2j}& {\phi }_{3j}& {\phi }_{4j}\end{array}\right]}^{\top },j=1,2,3,\hfill \\ & {\tilde{\mathit{\varphi }}}_2=\left[\begin{array}{cccc}{\tilde{\varphi }}_{j1}& {\tilde{\varphi }}_{j2}& {\tilde{\varphi }}_{j3}& {\tilde{\varphi }}_{j4}\end{array}\right],{\mathit{\varphi }}_j={\left[\begin{array}{cccc}{\varphi }_{1j}& {\varphi }_{2j}& {\varphi }_{3j}& {\varphi }_{4j}\end{array}\right]}^{\top },j=1,2,3,4.\hfill \end{array}$$

At the same time, the variation in the potential by means of variations in the scattering data is as follows

$$\delta \mathbf{v}(x,t)=-{\displaystyle \frac{1}{\pi }}\underset{-\infty }{\overset{+\infty }{\int }}\sum _{j=1}^3\left[{\mathsf{\Xi }}_j^{+}(k;x,t)\delta {\rho }_j(k;t)+{\mathsf{\Xi }}_j^{-}(k;x,t)\delta {\tilde{\rho }}_j(k;t)\right]\mathrm{d}k,$$

(59)

where ${\mathsf{\Xi }}_j^{\pm }(j=1,2,3)$ denote the squared eigenfunctions

$$\begin{array}{cc}& {\mathsf{\Xi }}_j^{+}=\left[\begin{array}{cccccc}{\psi }_{1,j+1}{\tilde{\psi }}_{12}& {\psi }_{1,j+1}{\tilde{\psi }}_{13}& {\psi }_{1,j+1}{\tilde{\psi }}_{14}& {\psi }_{2,j+1}{\tilde{\psi }}_{11}& {\psi }_{3,j+1}{\tilde{\psi }}_{11}& {\psi }_{4,j+1}{\tilde{\psi }}_{11}\end{array}\right],\hfill \\ & {\mathsf{\Xi }}_j^{-}=\left[\begin{array}{cccccc}{\psi }_{11}{\tilde{\psi }}_{j+1,2}& {\psi }_{11}{\tilde{\psi }}_{j+1,3}& {\psi }_{11}{\tilde{\psi }}_{j+1,4}& {\psi }_{21}{\tilde{\psi }}_{j+1,1}& {\psi }_{31}{\tilde{\psi }}_{j+1,1}& {\psi }_{41}{\tilde{\psi }}_{j+1,1}\end{array}\right],j=1,2,3,\hfill \\ & {\tilde{\mathit{\psi }}}_j=\left[\begin{array}{cccc}{\tilde{\psi }}_{j1}& {\tilde{\psi }}_{j2}& {\tilde{\psi }}_{j3}& {\tilde{\psi }}_{j4}\end{array}\right],{\mathit{\psi }}_j={\left[\begin{array}{cccc}{\psi }_{1j}& {\psi }_{2j}& {\psi }_{3j}& {\psi }_{4j}\end{array}\right]}^{\top },j=1,2,3,4.\hfill \end{array}$$

In addition, ${\mathsf{\Xi }}_j^{\pm }$ and ${\Pi }_j^{\pm }$ are also eigenfunctions with eigenvalues of $2k$ for the recursion operator $\mathbf{L}$ and its adjoint operator ${\mathbf{L}}^A$, respectively, which are able to be generalized to the fractional operator ${\mathcal{M}}_{frac.}\left(\mathbf{L}\right)$ and its adjoint operator ${\mathcal{M}}_{frac.}\left({\mathbf{L}}^A\right)$

$$\begin{array}{cc}\hfill {\mathcal{M}}_{frac.}\left(\mathbf{L}\right){\mathsf{\Xi }}_j^{\pm }& ={\mathcal{M}}_{frac.}\left(2k\right){\mathsf{\Xi }}_j^{\pm },\hfill \\ \hfill {\mathcal{M}}_{frac.}\left({\mathbf{L}}^A\right){\Pi }_j^{\pm }& ={\mathcal{M}}_{frac.}\left(2k\right){\Pi }_j^{\pm },j=1,2,3.\hfill \end{array}$$

(60)

Inserting the variation relation Equation (58) into Equation (59), we obtain

$$\begin{array}{cc}\hfill \delta \mathbf{v}(x,t)=-{\displaystyle \frac{1}{\pi }}\left(\underset{{\mathsf{\Gamma }}^{+}}{\int }{\displaystyle \frac{1}{s_{11}^2(k;t)}}\right.& \underset{-\infty }{\overset{+\infty }{\int }}{\mathbf{B}}_1(k;x,y,t)\delta \mathbf{v}(y,t)\mathrm{d}y\mathrm{d}k\hfill \\ \hfill & \left.+\underset{{\mathsf{\Gamma }}^{-}}{\int }{\displaystyle \frac{1}{{\tilde{s}}_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}{\mathbf{B}}_2(k;x,y,t)\delta \mathbf{v}(y,t)\mathrm{d}y\mathrm{d}k\right),\hfill \end{array}$$

(61)

where

$${\mathbf{B}}_1(k;x,y,t)=\sum _{j=1}^3{\mathsf{\Xi }}_j^{+}(k;x,t){\left({\Pi }_j^{+}(k;y,t)\right)}^{\top },{\mathbf{B}}_2(k;x,y,t)=\sum _{j=1}^3{\mathsf{\Xi }}_j^{-}(k;x,t){\left({\Pi }_j^{-}(k;y,t)\right)}^{\top },$$

(62)

and ${\mathsf{\Gamma }}^{\pm }$ are shown in Figure 1. Furthermore, by exchanging the order of integration in Equation (61) and utilizing the properties of the Dirac delta function $\delta \left(x\right)$ [47], the completeness relation is obtained

$$\delta (x-y){\mathbb{I}}_4=-{\displaystyle \frac{1}{\pi }}\left(\underset{{\mathsf{\Gamma }}^{+}}{\int }{\displaystyle \frac{1}{s_{11}^2(k;t)}}{\mathbf{B}}_1(k;x,y,t)\mathrm{d}k+\underset{{\mathsf{\Gamma }}^{-}}{\int }{\displaystyle \frac{1}{{\tilde{s}}_{11}^2(k;t)}}{\mathbf{B}}_2(k;x,y,t)\mathrm{d}k\right).$$

(63)

On the basis of Equation (63), we assume a sufficiently smooth and decaying vector function $\widehat{\mathbf{v}}(x,t)=\left[\begin{array}{c}{\mathbf{u}}^{\top }\\ -{\mathbf{u}}^{†}\end{array}\right]$ which can be extended with respect to eigenfunctions as

$$\begin{array}{cc}\hfill \widehat{\mathbf{v}}(x,t)=-{\displaystyle \frac{1}{\pi }}\left(\underset{{\mathsf{\Gamma }}^{+}}{\int }{\displaystyle \frac{1}{s_{11}^2(k;t)}}\right.& \underset{-\infty }{\overset{+\infty }{\int }}{\mathbf{B}}_1(k;x,y,t)\widehat{\mathbf{v}}(y,t)\mathrm{d}y\mathrm{d}k\hfill \\ & \left.+\underset{{\mathsf{\Gamma }}^{-}}{\int }{\displaystyle \frac{1}{{\tilde{s}}_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}{\mathbf{B}}_2(k;x,y,t)\widehat{\mathbf{v}}(y,t)\mathrm{d}y\mathrm{d}k\right).\hfill \end{array}$$

Subsequently, letting ${\mathcal{M}}_{frac.}\left(\mathbf{L}\right)$ act on it, we can access

$$\begin{array}{cc}\hfill {\mathcal{M}}_{frac.}\left(\mathbf{L}\right)\widehat{\mathbf{v}}(x,t)=-{\displaystyle \frac{1}{\pi }}\left(\underset{{\mathsf{\Gamma }}^{+}}{\int }|4k^2{|}^{ϵ}\right.& {\displaystyle \frac{1}{s_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}{\mathbf{B}}_1(k;x,y,t)\tilde{\kappa }(y,t)\mathrm{d}y\mathrm{d}k\hfill \\ \hfill & \left.+\underset{{\mathsf{\Gamma }}^{-}}{\int }|4k^2{|}^{ϵ}{\displaystyle \frac{1}{{\tilde{s}}_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}{\mathbf{B}}_2(k;x,y,t)\tilde{\kappa }(y,t)\mathrm{d}y\mathrm{d}k\right),\hfill \end{array}$$

(64)

where

$$\begin{array}{cc}\hfill & \tilde{\kappa }(y,t)={\left[\begin{array}{cccccc}{\tilde{\kappa }}_1& {\tilde{\kappa }}_2& {\tilde{\kappa }}_3& {\tilde{\kappa }}_4& {\tilde{\kappa }}_5& {\tilde{\kappa }}_6\end{array}\right]}^{\top },\hfill \\ \hfill & {\tilde{\kappa }}_j=\left\{\begin{array}{c}-{\displaystyle \frac{1}{2}}{u}_{jxx}-u_j\left({\left|u_1\right|}^2+{\left|u_2\right|}^2+{\left|u_3\right|}^2\right),j=1,2,3,\hfill \\ {\displaystyle \frac{1}{2}}{u}_{jxx}^{*}+u_j^{*}\left({\left|u_1\right|}^2+{\left|u_2\right|}^2+{\left|u_3\right|}^2\right),j=4,5,6.\hfill \end{array}\right.\hfill \end{array}$$

(65)

Thus, by combining Equations (11) and (64), we obtain

$$\begin{array}{cc}\hfill \mathrm{i}{\widehat{\mathbf{v}}}_t+{\displaystyle \frac{1}{\pi }}\left(\underset{{\mathsf{\Gamma }}^{+}}{\int }|4k^2{|}^{ϵ}{\displaystyle \frac{1}{s_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}\right.& {\mathbf{B}}_1(k;x,y,t)\tilde{\kappa }(y,t)\mathrm{d}y\mathrm{d}k\hfill \\ \hfill & \left.+\underset{{\mathsf{\Gamma }}^{-}}{\int }|4k^2{|}^{ϵ}{\displaystyle \frac{1}{{\tilde{s}}_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}{\mathbf{B}}_2(k;x,y,t)\tilde{\kappa }(y,t)\mathrm{d}y\mathrm{d}k\right)=\mathbf{0}.\hfill \end{array}$$

(66)

Then, under the assumption

$$\begin{array}{c}\hfill m_{j1}(k;x,y,t)=-{\tilde{\psi }}_{1,j+1}{\varphi }_{11}\left({\tau }_1{\tilde{\kappa }}_4+{\tau }_2{\tilde{\kappa }}_5+{\tau }_3{\tilde{\kappa }}_6\right)+{\tilde{\psi }}_{1,j+1}{\tau }_4\left({\varphi }_{21}{\tilde{\kappa }}_1+{\varphi }_{31}{\tilde{\kappa }}_2+{\varphi }_{41}{\tilde{\kappa }}_3\right),j=1,2,3,\end{array}$$

(67)

$$\begin{array}{c}\hfill m_{j2}(k;x,y,t)=-{\psi }_{11}{\tilde{\varphi }}_{11}\left({\tau }_5{\tilde{\kappa }}_1+{\tau }_6{\tilde{\kappa }}_2+{\tau }_7{\tilde{\kappa }}_3\right)+{\psi }_{11}{\tau }_8\left({\tilde{\varphi }}_{12}{\tilde{\kappa }}_4+{\tilde{\varphi }}_{13}{\tilde{\kappa }}_5+{\tilde{\varphi }}_{14}{\tilde{\kappa }}_6\right),j=1,2,3,\end{array}$$

(68)

with

$$\begin{array}{c}{\tau }_1={\psi }_{12}{\tilde{\phi }}_{12}+{\psi }_{13}{\tilde{\phi }}_{22}+{\psi }_{14}{\tilde{\phi }}_{32},{\tau }_2={\psi }_{12}{\tilde{\phi }}_{13}+{\psi }_{13}{\tilde{\phi }}_{23}+{\psi }_{14}{\tilde{\phi }}_{33},\hfill \\ {\tau }_3={\psi }_{12}{\tilde{\phi }}_{14}+{\psi }_{13}{\tilde{\phi }}_{24}+{\psi }_{14}{\tilde{\phi }}_{34},{\tau }_4={\psi }_{12}{\tilde{\phi }}_{11}+{\psi }_{13}{\tilde{\phi }}_{21}+{\psi }_{14}{\tilde{\phi }}_{31},\hfill \\ {\tau }_5={\tilde{\psi }}_{2,j+1}{\phi }_{21}+{\tilde{\psi }}_{3,j+1}{\phi }_{22}+{\tilde{\psi }}_{4,j+1}{\phi }_{23},{\tau }_6={\tilde{\psi }}_{2,j+1}{\phi }_{31}+{\tilde{\psi }}_{3,j+1}{\phi }_{32}+{\tilde{\psi }}_{4,j+1}{\phi }_{33},\hfill \\ {\tau }_7={\tilde{\psi }}_{2,j+1}{\phi }_{41}+{\tilde{\psi }}_{3,j+1}{\phi }_{42}+{\tilde{\psi }}_{4,j+1}{\phi }_{43},{\tau }_8={\tilde{\psi }}_{2,j+1}{\phi }_{11}+{\tilde{\psi }}_{3,j+1}{\phi }_{12}+{\tilde{\psi }}_{4,j+1}{\phi }_{13},j=1,2,3,\hfill \end{array}$$

the explicit expression of the TFNLS equation can be presented as

$$\begin{array}{cc}\hfill \mathrm{i}{u}_{jt}+{\displaystyle \frac{1}{\pi }}\left(\underset{{\mathsf{\Gamma }}^{+}}{\int }|4k^2{|}^{ϵ}{\displaystyle \frac{1}{s_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}\right.& m_{j1}(k;x,y,t)\mathrm{d}y\mathrm{d}k\hfill \\ \hfill & \left.+\underset{{\mathsf{\Gamma }}^{-}}{\int }|4k^2{|}^{ϵ}{\displaystyle \frac{1}{{\tilde{s}}_{11}^2(k;t)}}\underset{-\infty }{\overset{+\infty }{\int }}{m}_{j2}(k;x,y,t)\mathrm{d}y\mathrm{d}k\right)=0,j=1,2,3.\hfill \end{array}$$

(69)

Notably, when $ϵ=0$, Equation (69) reduces to the classical TNLS Equation (1).

5. Fractional N-Soliton Solutions

This section focuses on the fractional N-soliton solutions of the TFNLS equation. It is widely recognized that the integral term in Equation (50) represents the radiation part of the solution, while the summation term corresponds to its nonradiative part. The nonradiative solution (i.e., reflectionless potential) of the TFNLS equation corresponds to the case $\mathbf{G}={\mathbb{I}}_4$ in its RH problem and is of great significance.

Now, we need to produce the spatial and temporal evolutions for vectors ${\mathit{\mu }}_l$ and ${\tilde{\mathit{\mu }}}_l$. Taking the x-derivative of both sides of the equation ${\mathbf{K}}^{+}{\mathit{\mu }}_l=0$, we can derive

$${\mathbf{K}}^{+}\left({\displaystyle \frac{\mathrm{d}{\mathit{\mu }}_l}{\mathrm{d}x}}-\mathrm{i}{k}_l\mathit{\sigma }{\mathit{\mu }}_l\right)=0.$$

(70)

Analogously, considering the temporal evolutions for vectors ${\mathit{\mu }}_l$, we have

$${\mathbf{K}}^{+}\left({\displaystyle \frac{\mathrm{d}{\mathit{\mu }}_l}{\mathrm{d}t}}-{\displaystyle \frac{\mathrm{i}}{2}}{\mathcal{M}}_{frac.}\left(2k_l\right)\mathit{\sigma }{\mathit{\mu }}_l\right)=0.$$

(71)

Combining these results, the following expressions can be given

$${\mathit{\mu }}_l=\mathbf{E}{\mathrm{e}}^{\underset{x_0}{\overset{x}{\int }}{\mathit{a}}_{1l}\left(y\right)\mathrm{d}y+\underset{t_0}{\overset{t}{\int }}{\mathit{b}}_{1l}\left(s\right)\mathrm{d}s}{\mathit{\zeta }}_l,l=1,\dots ,N,$$

(72)

in addition, the concrete representation of ${\tilde{\mathit{\mu }}}_l$ can be obtained through similar methods

$${\tilde{\mathit{\mu }}}_l={\tilde{\mathit{\zeta }}}_l{\mathbf{E}}^{*}{\mathrm{e}}^{\underset{x_0}{\overset{x}{\int }}{\mathit{a}}_{2l}\left(y\right)\mathrm{d}y+\underset{t_0}{\overset{t}{\int }}{\mathit{b}}_{2l}\left(s\right)\mathrm{d}s},l=1,\dots ,N,$$

(73)

where $\mathbf{E}(k;x,t):=\mathbf{E}={\mathrm{e}}^{\mathrm{i}\theta (k;x,t)\sigma }$, $\theta (k;x,t)=kx+{\displaystyle \frac{1}{2}}{\mathcal{M}}_{frac.}\left(2k\right)t$, ${\mathbf{E}}^{*}$ represents the conjugate of $\mathbf{E}$, ${\mathit{a}}_{1l}\left(x\right),{\mathit{b}}_{1l}\left(t\right),{\mathit{a}}_{2l}\left(x\right),{\mathit{b}}_{2l}\left(t\right)$, which are scalar functions, and ${\mathit{\zeta }}_l={\left[\begin{array}{cccc}{\zeta }_{1l}& {\zeta }_{2l}& {\zeta }_{3l}& {\zeta }_{4l}\end{array}\right]}^{\top }$ and ${\tilde{\mathit{\zeta }}}_l={\mathit{\zeta }}_l^{†}$ which are complex constants. Without losing the generality, let us take ${\mathit{a}}_{1l}={\mathit{b}}_{1l}={\mathit{a}}_{2l}={\mathit{b}}_{2l}=0$, then

$${\mathit{\mu }}_l=\mathbf{E}{\mathit{\zeta }}_l={\left[\begin{array}{cccc}{\mathrm{e}}^{-\theta \left(k_l\right)}{\zeta }_{1l}& {\mathrm{e}}^{\theta \left(k_l\right)}{\zeta }_{2l}& {\mathrm{e}}^{\theta \left(k_l\right)}{\zeta }_{3l}& {\mathrm{e}}^{\theta \left(k_l\right)}{\zeta }_{4l}\end{array}\right]}^{\top },l=1,\dots ,N,$$

(74)

$${\tilde{\mathit{\mu }}}_l={\mathit{\zeta }}_l^{†}{\mathbf{E}}^{*}=\left[\begin{array}{cccc}{\mathrm{e}}^{-{\theta }^{*}\left(k_l\right)}{\zeta }_{1l}^{*}& {\mathrm{e}}^{{\theta }^{*}\left(k_l\right)}{\zeta }_{2l}^{*}& {\mathrm{e}}^{{\theta }^{*}\left(k_l\right)}{\zeta }_{3l}^{*}& {\mathrm{e}}^{{\theta }^{*}\left(k_l\right)}{\zeta }_{4l}^{*}\end{array}\right],l=1,\dots ,N,$$

(75)

where ${\tilde{\mathit{\mu }}}_l={\mathit{\mu }}_l^{†}$, ${\theta }^{*}\left(k_l\right)=k_l^{*}x+k_l^{*2}{\left|4k_l^{*2}\right|}^{ϵ}t$$(l=1,\dots ,N)$.

When $\mathbf{G}={\mathbb{I}}_4$, i.e., the scattering data ${\tilde{s}}_{12}(k;t)={\tilde{s}}_{13}(k;t)={\tilde{s}}_{14}(k;t)=s_{21}(k;t)=s_{31}(k;t)=s_{41}(k;t)=0,k\in {\mathbb{C}}^{\pm }$, Equation (49) is reduced to

$$\begin{array}{c}\hfill u_1=2\mathrm{i}{\left(\sum _{j,l=1}^N{\mathit{\mu }}_j{\left({\mathbf{V}}^{-1}\right)}_{jl}{\tilde{\mathit{\mu }}}_l\right)}_{12},\\ \hfill u_2=2\mathrm{i}{\left(\sum _{j,l=1}^N{\mathit{\mu }}_j{\left({\mathbf{V}}^{-1}\right)}_{jl}{\tilde{\mathit{\mu }}}_l\right)}_{13},\\ \hfill u_3=2\mathrm{i}{\left(\sum _{j,l=1}^N{\mathit{\mu }}_j{\left({\mathbf{V}}^{-1}\right)}_{jl}{\tilde{\mathit{\mu }}}_l\right)}_{14}.\end{array}$$

(76)

Consequently, the fractional N-soliton solutions in Equation (76) of the TFNLS equation can be rewritten in the form of a ratio of determinants

$$\begin{array}{c}\hfill u_1^{\left[N\right]}(x,t)=-2\mathrm{i}{\displaystyle \frac{M_1^{\left[N\right]}}{W^{\left[N\right]}}},u_2^{\left[N\right]}(x,t)=-2\mathrm{i}{\displaystyle \frac{M_2^{\left[N\right]}}{W^{\left[N\right]}}},u_3^{\left[N\right]}(x,t)=-2\mathrm{i}{\displaystyle \frac{M_3^{\left[N\right]}}{W^{\left[N\right]}}},\end{array}$$

(77)

where

$$\begin{array}{cc}\hfill M_j^{\left[N\right]}& =\left|\begin{array}{cccc}{\displaystyle \frac{{\tilde{\mathit{\mu }}}_1{\mathit{\mu }}_1}{k_1-{\tilde{k}}_1}}& \dots & {\displaystyle \frac{{\tilde{\mathit{\mu }}}_N{\mathit{\mu }}_1}{k_1-{\tilde{k}}_N}}& {\mathrm{e}}^{-\theta \left(k_1\right)}{\zeta }_{11}\\ ⋮& \ddots & ⋮& ⋮\\ {\displaystyle \frac{{\tilde{\mathit{\mu }}}_1{\mathit{\mu }}_N}{k_N-{\tilde{k}}_1}}& \dots & {\displaystyle \frac{{\tilde{\mathit{\mu }}}_N{\mathit{\mu }}_N}{k_N-{\tilde{k}}_N}}& {\mathrm{e}}^{-\theta \left(k_N\right)}{\zeta }_{1N}\\ {\mathrm{e}}^{{\theta }^{*}\left(k_1\right)}{\zeta }_{j+1,1}^{*}& \dots & {\mathrm{e}}^{{\theta }^{*}\left(k_3\right)}{\zeta }_{j+1,N}^{*}& 0\end{array}\right|,\hfill \\ \hfill W^{\left[N\right]}& =\left|\begin{array}{ccc}{\displaystyle \frac{{\tilde{\mathit{\mu }}}_1{\mathit{\mu }}_1}{k_1-{\tilde{k}}_1}}& \dots & {\displaystyle \frac{{\tilde{\mathit{\mu }}}_N{\mathit{\mu }}_1}{k_1-{\tilde{k}}_N}}\\ ⋮& \ddots & ⋮\\ {\displaystyle \frac{{\tilde{\mathit{\mu }}}_1{\mathit{\mu }}_N}{k_N-{\tilde{k}}_1}}& \dots & {\displaystyle \frac{{\tilde{\mathit{\mu }}}_N{\mathit{\mu }}_N}{k_N-{\tilde{k}}_N}}\end{array}\right|,j=1,2,3.\hfill \end{array}$$

In what follows, we will examine the fractional one-soliton and two-soliton solutions of the TFNLS equation in terms of the Equation (77) with $N=1,2$.

5.1. Fractional One-Soliton Solutions

By setting $N=1$, the fractional one-soliton solutions of the TFNLS equation can be derived

$$\begin{array}{c}\hfill u_1^{\left[1\right]}={\displaystyle \frac{-2\mathrm{i}{\zeta }_{11}{\zeta }_{21}^{*}(k_1-k_1^{*})e^{{\theta }^{*}\left(k_1\right)-\theta \left(k_1\right)}}{e^{-{\theta }^{*}\left(k_1\right)-\theta \left(k_1\right)}|{\zeta }_{11}{|}^2+e^{{\theta }^{*}\left(k_1\right)+\theta \left(k_1\right)}\left(|{\zeta }_{21}{|}^2+|{\zeta }_{31}{|}^2+|{\zeta }_{41}{|}^2\right)}},\\ \hfill u_2^{\left[1\right]}={\displaystyle \frac{-2\mathrm{i}{\zeta }_{11}{\zeta }_{31}^{*}(k_1-k_1^{*})e^{{\theta }^{*}\left(k_1\right)-\theta \left(k_1\right)}}{e^{-{\theta }^{*}\left(k_1\right)-\theta \left(k_1\right)}|{\zeta }_{11}{|}^2+e^{{\theta }^{*}\left(k_1\right)+\theta \left(k_1\right)}\left(|{\zeta }_{21}{|}^2+|{\zeta }_{31}{|}^2+|{\zeta }_{41}{|}^2\right)}},\\ \hfill u_3^{\left[1\right]}={\displaystyle \frac{-2\mathrm{i}{\zeta }_{11}{\zeta }_{41}^{*}(k_1-k_1^{*})e^{{\theta }^{*}\left(k_1\right)-\theta \left(k_1\right)}}{e^{-{\theta }^{*}\left(k_1\right)-\theta \left(k_1\right)}|{\zeta }_{11}{|}^2+e^{{\theta }^{*}\left(k_1\right)+\theta \left(k_1\right)}\left(|{\zeta }_{21}{|}^2+|{\zeta }_{31}{|}^2+|{\zeta }_{41}{|}^2\right)}}.\end{array}$$

(78)

For brevity, we introduce the following notations. Letting

$$\begin{array}{cc}\hfill k_1& ={\alpha }_1+\mathrm{i}{\beta }_1,{\beta }_1\ne 0,\hfill \end{array}$$

where ${\alpha }_1$ and ${\beta }_1$ are the real and imaginary parts of $k_1$, and defining

$$\begin{array}{cc}\hfill X_1& ={\displaystyle \frac{|{\zeta }_{21}{|}^2+|{\zeta }_{31}{|}^2+|{\zeta }_{41}{|}^2}{|{\zeta }_{11}{|}^2}},\hfill \\ \hfill X_2& =2{\beta }_{1}x+4^{1+ϵ}{\alpha }_1{\beta }_1{({\alpha }_1^2+{\beta }_1^2)}^{ϵ}t,\hfill \end{array}$$

the above solution to Equation (78) can be rewritten as

$$\begin{array}{c}\hfill u_1^{\left[1\right]}=2{\beta }_1{\zeta }_{21}^{*}{\left({\zeta }_{11}^{*}\sqrt{X_1}\right)}^{-1}{e}^{-2\mathrm{i}{\alpha }_{1}x-2^{1+2ϵ}\mathrm{i}({\alpha }_1^2-{\beta }_1^2){({\alpha }_1^2+{\beta }_1^2)}^{ϵ}t}sech(X_2-ln\sqrt{X_1}),\\ \hfill u_2^{\left[1\right]}=2{\beta }_1{\zeta }_{31}^{*}{\left({\zeta }_{11}^{*}\sqrt{X_1}\right)}^{-1}{e}^{-2\mathrm{i}{\alpha }_{1}x-2^{1+2ϵ}\mathrm{i}({\alpha }_1^2-{\beta }_1^2){({\alpha }_1^2+{\beta }_1^2)}^{ϵ}t}sech(X_2-ln\sqrt{X_1}),\\ \hfill u_3^{\left[1\right]}=2{\beta }_1{\zeta }_{41}^{*}{\left({\zeta }_{11}^{*}\sqrt{X_1}\right)}^{-1}{e}^{-2\mathrm{i}{\alpha }_{1}x-2^{1+2ϵ}\mathrm{i}({\alpha }_1^2-{\beta }_1^2){({\alpha }_1^2+{\beta }_1^2)}^{ϵ}t}sech(X_2-ln\sqrt{X_1}).\end{array}$$

(79)

Moreover, it is known that the fractional one-soliton solutions $u_1^{\left[1\right]}$, $u_2^{\left[1\right]}$, and $u_3^{\left[1\right]}$ have the same wave velocity $v_w\left({\alpha }_1,{\beta }_1,ϵ\right)$, phase velocity $v_p\left({\alpha }_1,{\beta }_1,ϵ\right)$, and group velocity $v_g\left({\alpha }_1,{\beta }_1,ϵ\right)$, which can be expressed as follows:

$$\begin{array}{cc}\hfill & v_w\equiv v_w\left({\alpha }_1,{\beta }_1,ϵ\right)=-2^{1+2ϵ}{\alpha }_1{\left({\alpha }_1^2+{\beta }_1^2\right)}^{ϵ},\hfill \\ \hfill & v_p\equiv v_p\left({\alpha }_1,{\beta }_1,ϵ\right)=-4^{ϵ}{\alpha }_1^{-1}\left({\alpha }_1^2-{\beta }_1^2\right){\left({\alpha }_1^2+{\beta }_1^2\right)}^{ϵ},\hfill \\ \hfill & v_g\equiv v_g\left({\alpha }_1,{\beta }_1,ϵ\right)=-2^{1+2ϵ}{\alpha }_1\left(ϵ\left({\alpha }_1^2-{\beta }_1^2\right)+{\alpha }_1^2+{\beta }_1^2\right){\left({\alpha }_1^2+{\beta }_1^2\right)}^{ϵ-1}.\hfill \end{array}$$

(80)

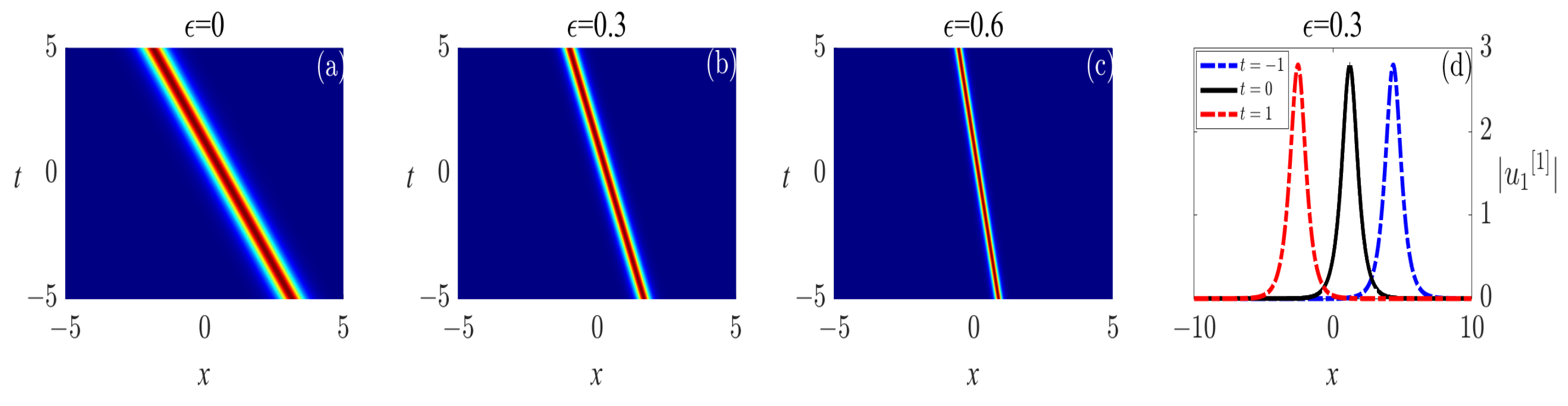
Their images are shown in Figure 2 and Figure 3.

From Equation (79), it is clear that $u_1^{\left[1\right]}$, $u_2^{\left[1\right]}$, and $u_3^{\left[1\right]}$ are essentially identical, differing only in their amplitudes due to the different values of ${\zeta }_{21}$, ${\zeta }_{31}$, and ${\zeta }_{41}$. Therefore, we will exclusively discuss the dynamic behavior of $u_1^{\left[1\right]}$ in Figure 2 and Figure 3. When ${\alpha }_1={\beta }_1=1$, i.e., $k=1+\mathrm{i}$, $u_1^{\left[1\right]}$ is a left-going travelling-wave soliton at $ϵ=0$, $0.3$, $0.6$. Additionally, the width of the wave becomes smaller while its absolute value of wave velocity $v_w$, phase velocity $v_p$, and group velocity $v_g$ become larger as $ϵ$ increases.

5.2. Fractional Two-Soliton Solutions

Taking $N=2$ and the spectral parameters $k_1={\alpha }_1+\mathrm{i}{\beta }_1$, $k_2={\alpha }_2+\mathrm{i}{\beta }_2$ and ${\tilde{k}}_j=k_j^{*}$$(j=1,2)$, the fractional two-soliton solution of the TFNLS equation can be expressed as

$$\begin{array}{c}\hfill u_1^{\left[2\right]}(x,t)=-2\mathrm{i}{\displaystyle \frac{M_1^{\left[2\right]}}{W^{\left[2\right]}}},u_2^{\left[2\right]}(x,t)=-2\mathrm{i}{\displaystyle \frac{M_2^{\left[2\right]}}{W^{\left[2\right]}}},u_3^{\left[2\right]}(x,t)=-2\mathrm{i}{\displaystyle \frac{M_3^{\left[2\right]}}{W^{\left[2\right]}}},\end{array}$$

(81)

where

$$\begin{array}{cc}\hfill M_j^{\left[2\right]}& =\left|\begin{array}{ccc}{\displaystyle \frac{{\tilde{\mathit{\mu }}}_1{\mathit{\mu }}_1}{k_1-{\tilde{k}}_1}}& {\displaystyle \frac{{\tilde{\mathit{\mu }}}_2{\mathit{\mu }}_1}{k_1-{\tilde{k}}_2}}& {\mathrm{e}}^{-\theta \left(k_1\right)}{\zeta }_{11}\\ {\displaystyle \frac{{\tilde{\mathit{\mu }}}_1{\mathit{\mu }}_2}{k_2-{\tilde{k}}_1}}& {\displaystyle \frac{{\tilde{\mathit{\mu }}}_2{\mathit{\mu }}_2}{k_2-{\tilde{k}}_2}}& {\mathrm{e}}^{-\theta \left(k_2\right)}{\zeta }_{12}\\ {\mathrm{e}}^{{\theta }^{*}\left(k_1\right)}{\zeta }_{j+1,1}^{*}& {\mathrm{e}}^{{\theta }^{*}\left(k_2\right)}{\zeta }_{j+1,2}^{*}& 0\end{array}\right|,\hfill \\ \hfill W^{\left[2\right]}& =\left|\begin{array}{cc}{\displaystyle \frac{{\tilde{\mathit{\mu }}}_1{\mathit{\mu }}_1}{k_1-{\tilde{k}}_1}}& {\displaystyle \frac{{\tilde{\mathit{\mu }}}_2{\mathit{\mu }}_1}{k_1-{\tilde{k}}_2}}\\ {\displaystyle \frac{{\tilde{\mathit{\mu }}}_1{\mathit{\mu }}_2}{k_2-{\tilde{k}}_1}}& {\displaystyle \frac{{\tilde{\mathit{\mu }}}_2{\mathit{\mu }}_2}{k_2-{\tilde{k}}_2}}\end{array}\right|,j=1,2,3.\hfill \end{array}$$

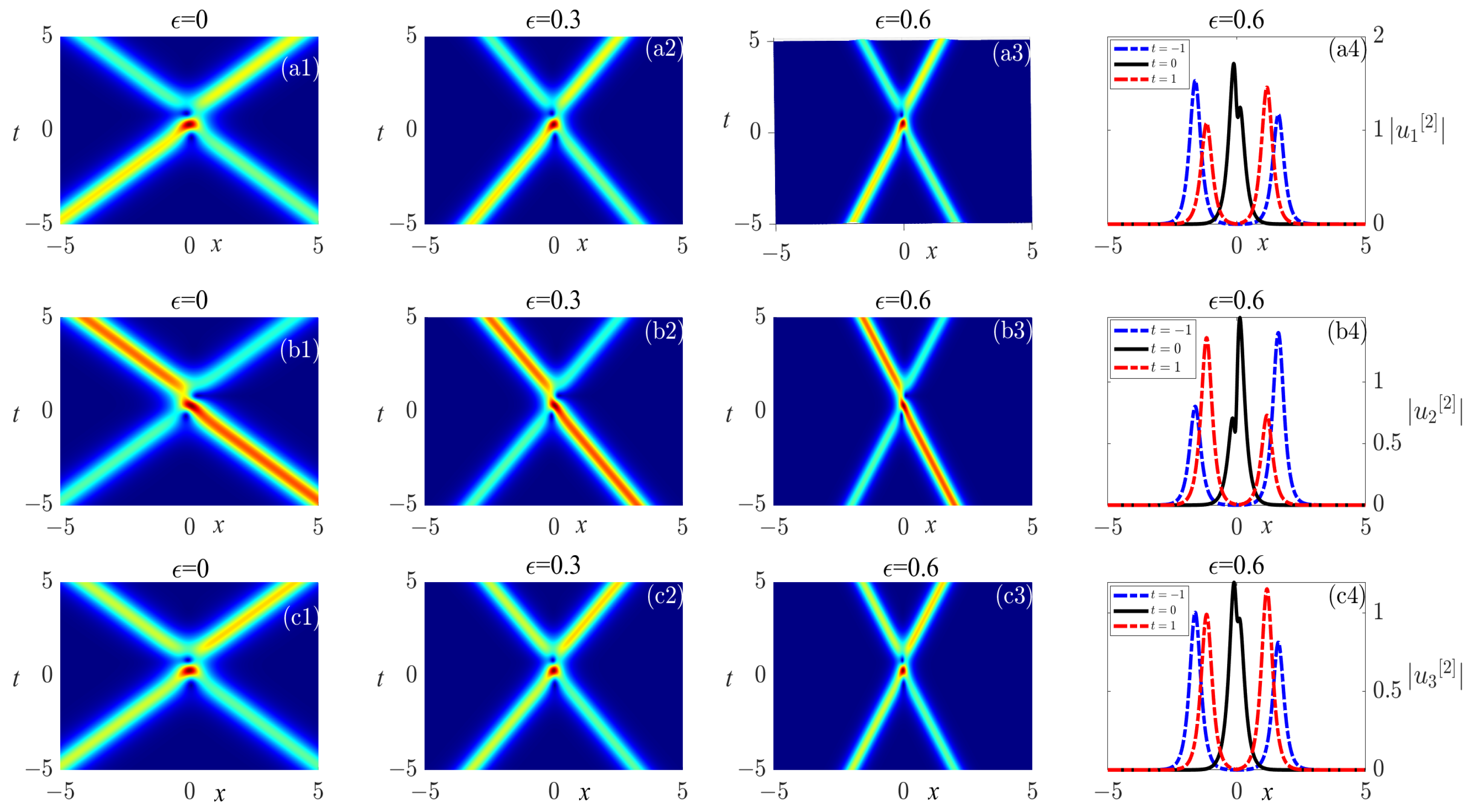
The fractional two-soliton solutions $u_1^{\left[2\right]}$, $u_2^{\left[2\right]}$, and $u_3^{\left[2\right]}$ for $k_1=0.5+\mathrm{i}$ and $k_2=-0.5+\mathrm{i}$ are displayed in Figure 4 and Figure 5. Similar to one-soliton solutions, the three fractional two-soliton solutions $u_1^{\left[2\right]}$, $u_2^{\left[2\right]}$, and $u_3^{\left[2\right]}$ are almost indistinguishable, and as $ϵ$ increases, the width of soliton waves decreases. By observation, we find that Figure 5 shows the soliton transmission. From Figure 5(a1–a4,c1–c4), we notice that after the collision between the right-going wave with a large amplitude (left branch) and the left-going wave with a small amplitude (right branch) of $u_1^{\left[2\right]}$ and $u_3^{\left[2\right]}$, the amplitudes of both remain nearly constant at $ϵ=0$, $0.3$, $0.6$. Similarly, after the collision between the right-going wave with a small amplitude (left branch) and the left-going wave with a large amplitude (right branch) of $u_2^{\left[2\right]}$, the amplitudes of two solitons of $u_2^{\left[2\right]}$ remain nearly unchanged at $ϵ=0$, $0.3$, $0.6$. 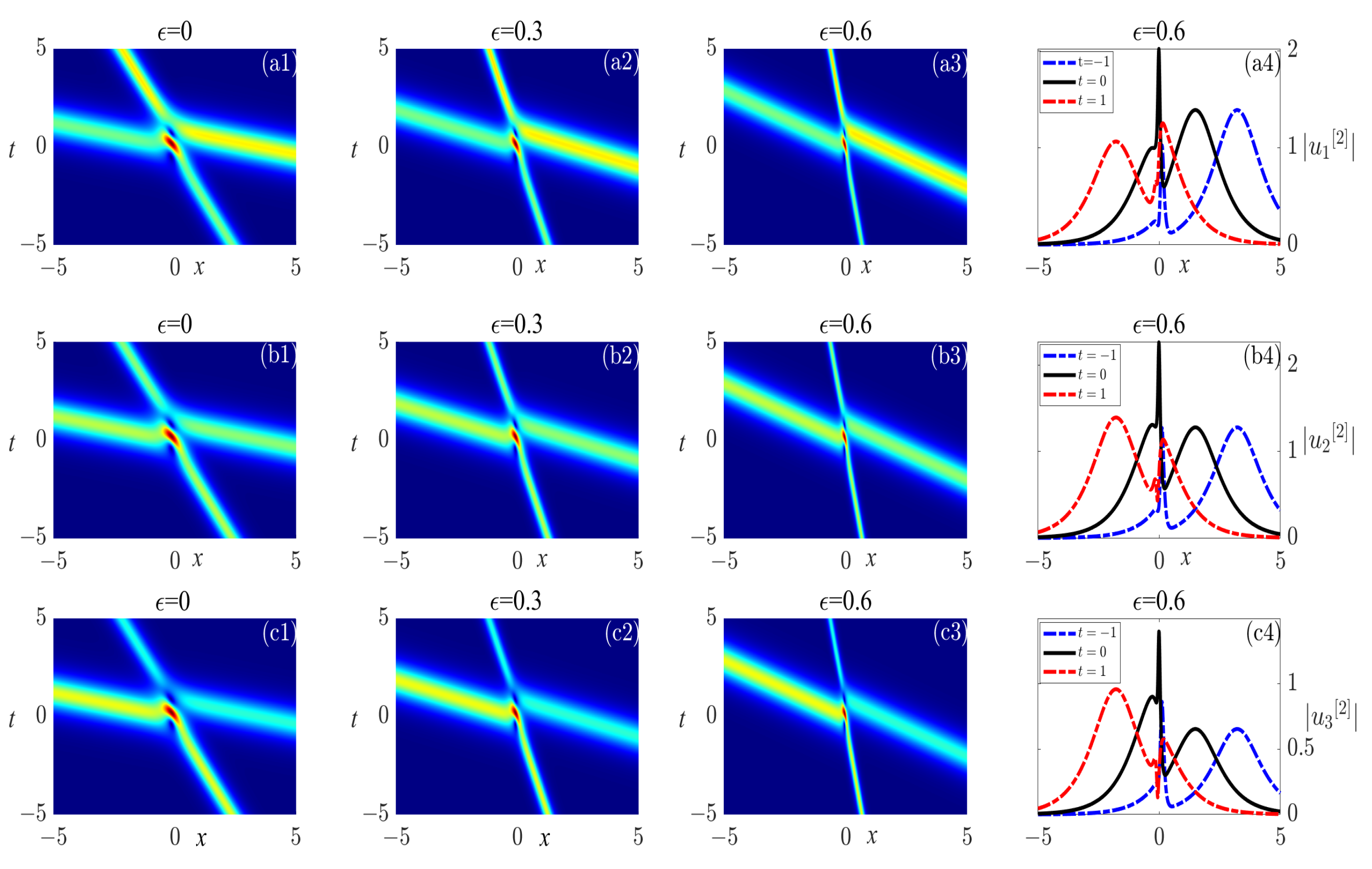However, when $k_1=0.125+\mathrm{i}$ and $k_2=1+\mathrm{i}$, Figure 6 and Figure 7 display the soliton’s reflection. During the collision between two solitons of $u_1^{\left[2\right]}$ and $u_1^{\left[2\right]}$ in Figure 7(a1–b4), the left-going wave with a small width and small amplitude (left branch) experiences an increase in both width and amplitude. Meanwhile, the left-going wave with a large width and large amplitude (right branch) undergoes a decrease in amplitude and width after the collision. This indicates that the energy of the two solitons remains constant during the collision. This kind of collision is not common in integrable systems and can be degenerated into a collision of two solitons in a single NLS equation.

From the analysis of the fractional one- and two-soliton solutions, it is evident that the solitons of the TFNLS equation exhibit significant differences from those of the classical TNLS equation and other fractional models. Compared with the classical TNLS equation, the TFNLS equation incorporates the Riesz fractional operator, allowing the soliton velocity, wave width, and post-collision shifts to be continuously tuned by the fractional order $ϵ$, thus providing additional dynamic flexibility. It is noteworthy that the wave velocity, phase velocity, and group velocity of the fractional one-soliton solution exhibit a power-law relationship with the amplitude. This power-law behavior is a typical mathematical characteristic of the system’s nonlocality, manifesting as anomalous diffusion in diffusion contexts. This unique property is key to why the TFNLS equation can describe complex media with memory effects or anomalous dispersion, thereby surpassing the classical TNLS equation, which is primarily applicable only to ideal dispersive media. Moreover, in contrast to the fNLS equation and the fKdV equation [28,30], the coupled structure of the TFNLS equation enables the description of multi-component soliton interactions, thereby enriching the dynamics of fractional solitons.

6. Conclusions

In this paper, we started with the $4\times 4$ AKNS spectral problem and constructed the integrable hierarchy of the TNLS equation using the recursive operator $\mathbf{L}$. To determine the TFNLS equation, the fractional recursive operator ${\mathcal{M}}_{frac.}\left(\mathbf{L}\right)$ was obtained by adding a fractional power of the operator $\mathbf{L}$ to ${\displaystyle \frac{1}{2}}{\mathbf{L}}^2$. In Section 4, we presented the squared eigenfunctions by making a perturbation to the spectral problem in Equation (2) and the scattering relation in Equation (21). By applying the completeness relation of the squared eigenfunctions, the explicit form of the TFNLS equation was derived. Furthermore, we presented the IST with the RH problem for the TFNLS equation. By utilizing the Plemelj formula, we obtained the solution $\mathbf{K}$ of the regular RH problem Equation (36). When $\mathbf{G}={\mathbb{I}}_4$, we obtained the reflectionless potentials $u_1$, $u_2$, and $u_3$ as given in Equation (76). The N-soliton solutions under zero background were subsequently derived from the spatial and temporal evolution of ${\mathit{\mu }}_j$ and ${\tilde{\mathit{\mu }}}_l$, with specific one- and two-soliton solutions presented for $N=1$ and $N=2$, respectively. Finally, we observed that the soliton widths of $u_1^{\left[1\right]}$, $u_2^{\left[1\right]}$, and $u_3^{\left[1\right]}$ decreased as $ϵ$ increased. The wave velocity, phase velocity, and group velocity exhibited a power-law dependence on amplitude, with their absolute values increasing as $ϵ$ increased. This behavior constitutes a fundamental departure from the linear relationships characterizing the classical TNLS equation, representing a novel dynamic feature introduced by fractional nonlocality. The two-soliton solutions exhibited both soliton transmission and soliton reflection, which are unique and infrequent in integrable systems. It is hoped that our new results will enrich the dynamic properties of integrable nonlinear equations.