Realization of Fractional-Order Current-Mode Multifunction Filter Based on MCFOA for Low-Frequency Applications
Abstract
1. Introduction
Literature Review
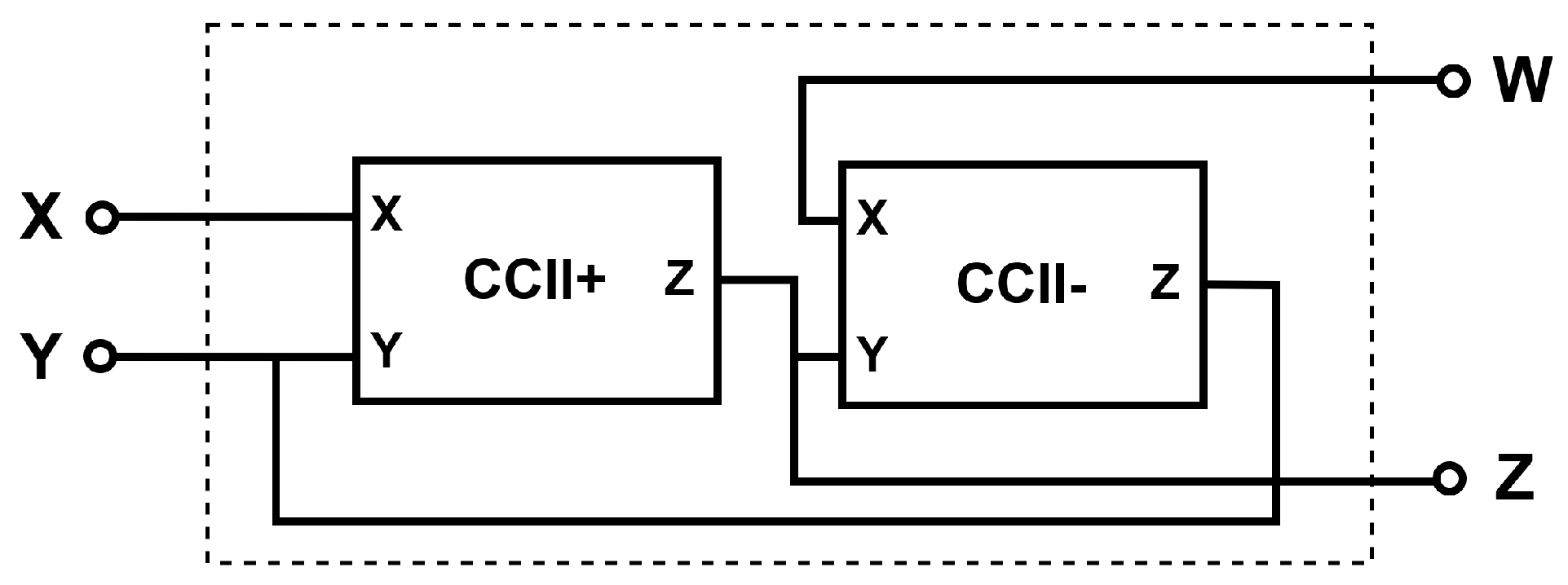
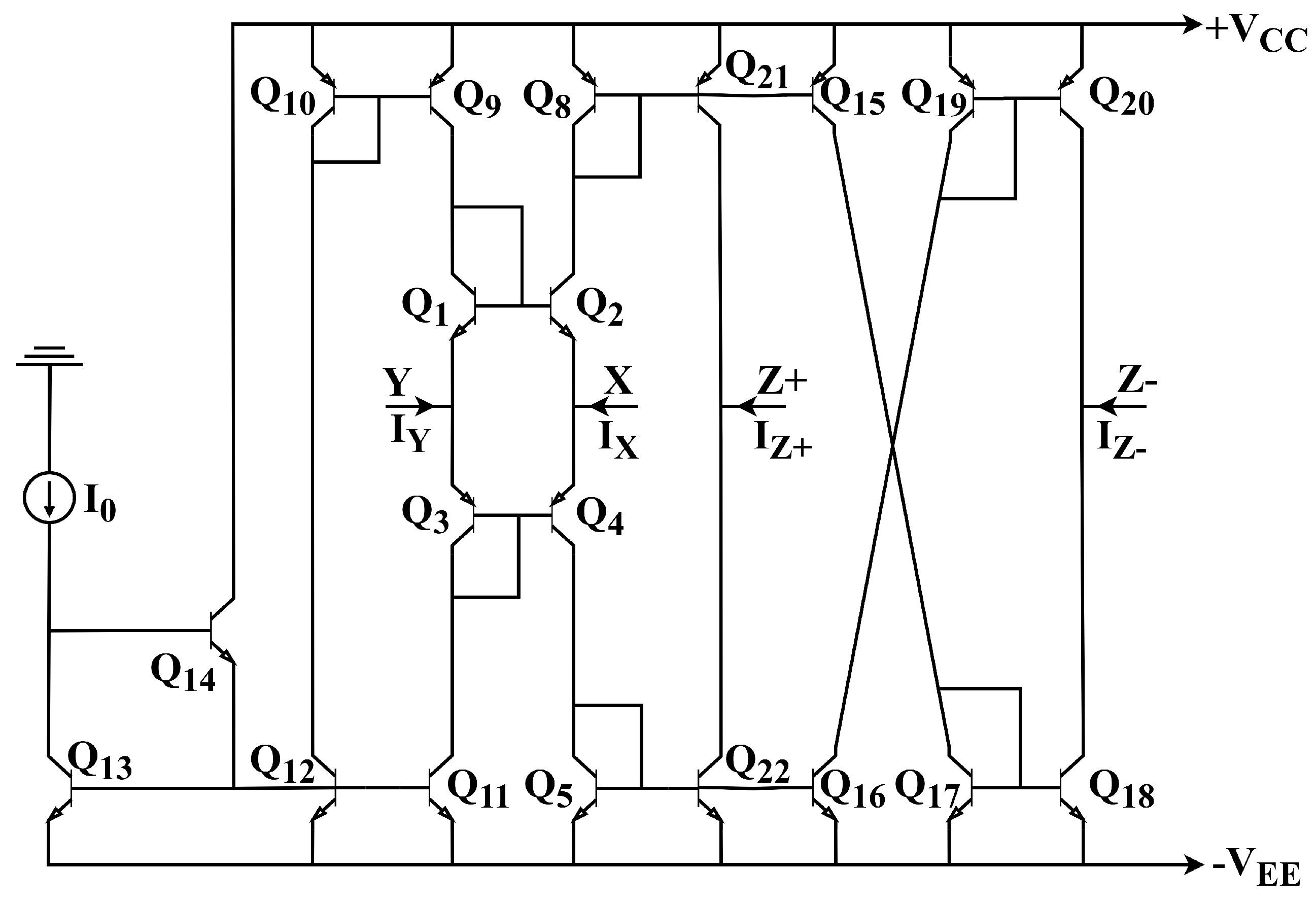
2. Modified Current Feedback Operational Amplifier (MCFOA)
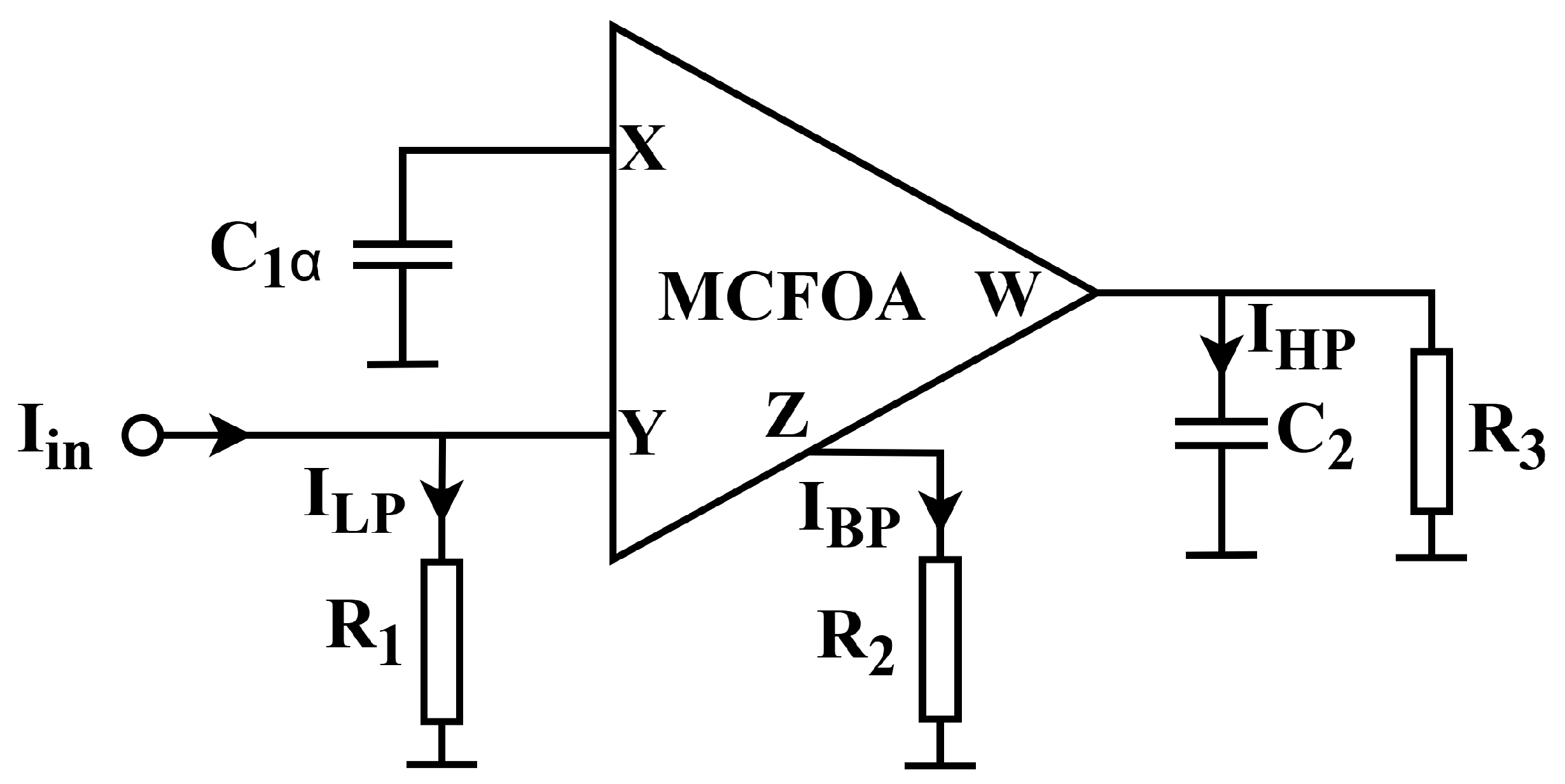
3. MCFOA-Based CM and Fractional-Order Multifunction Filter Circuit
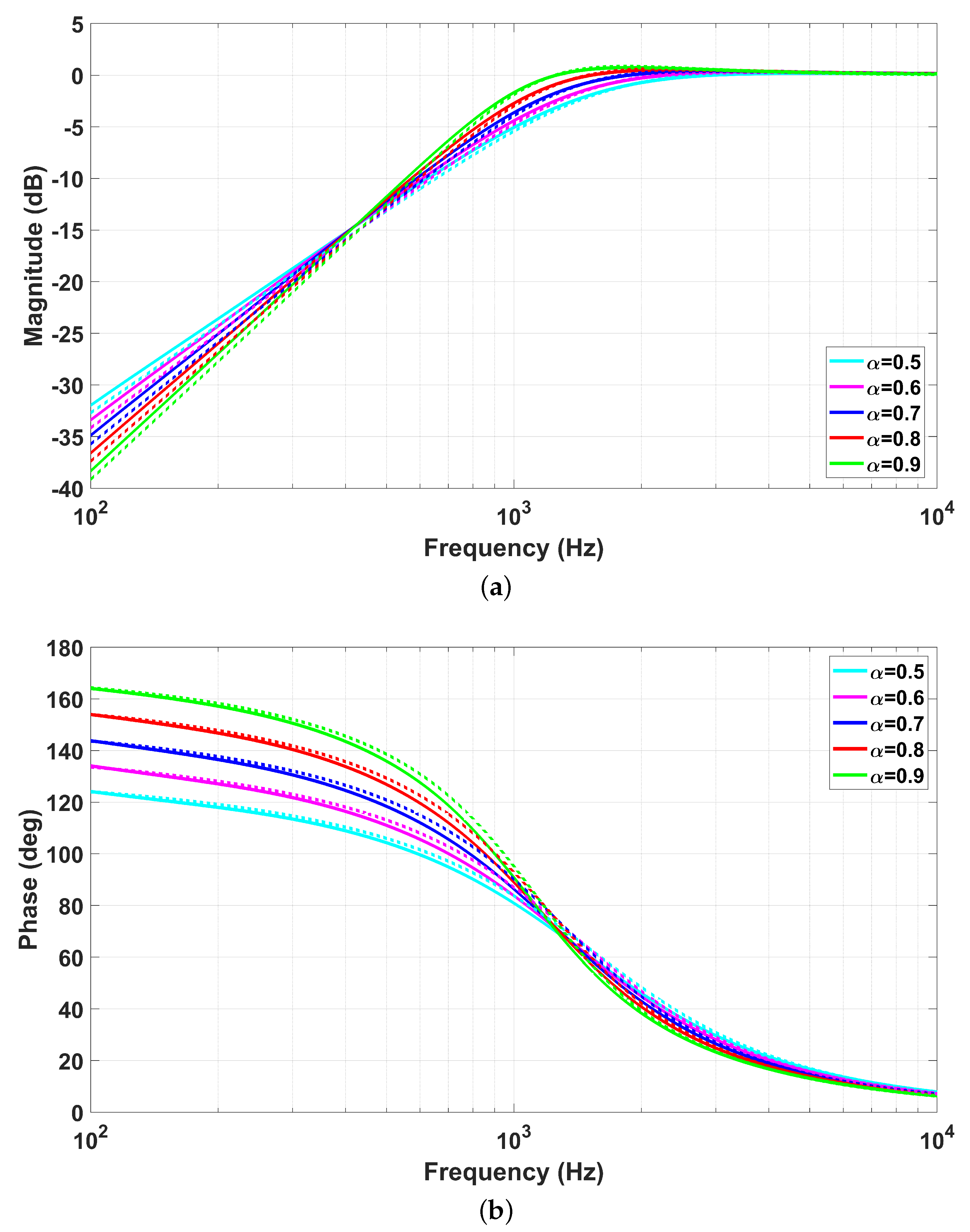
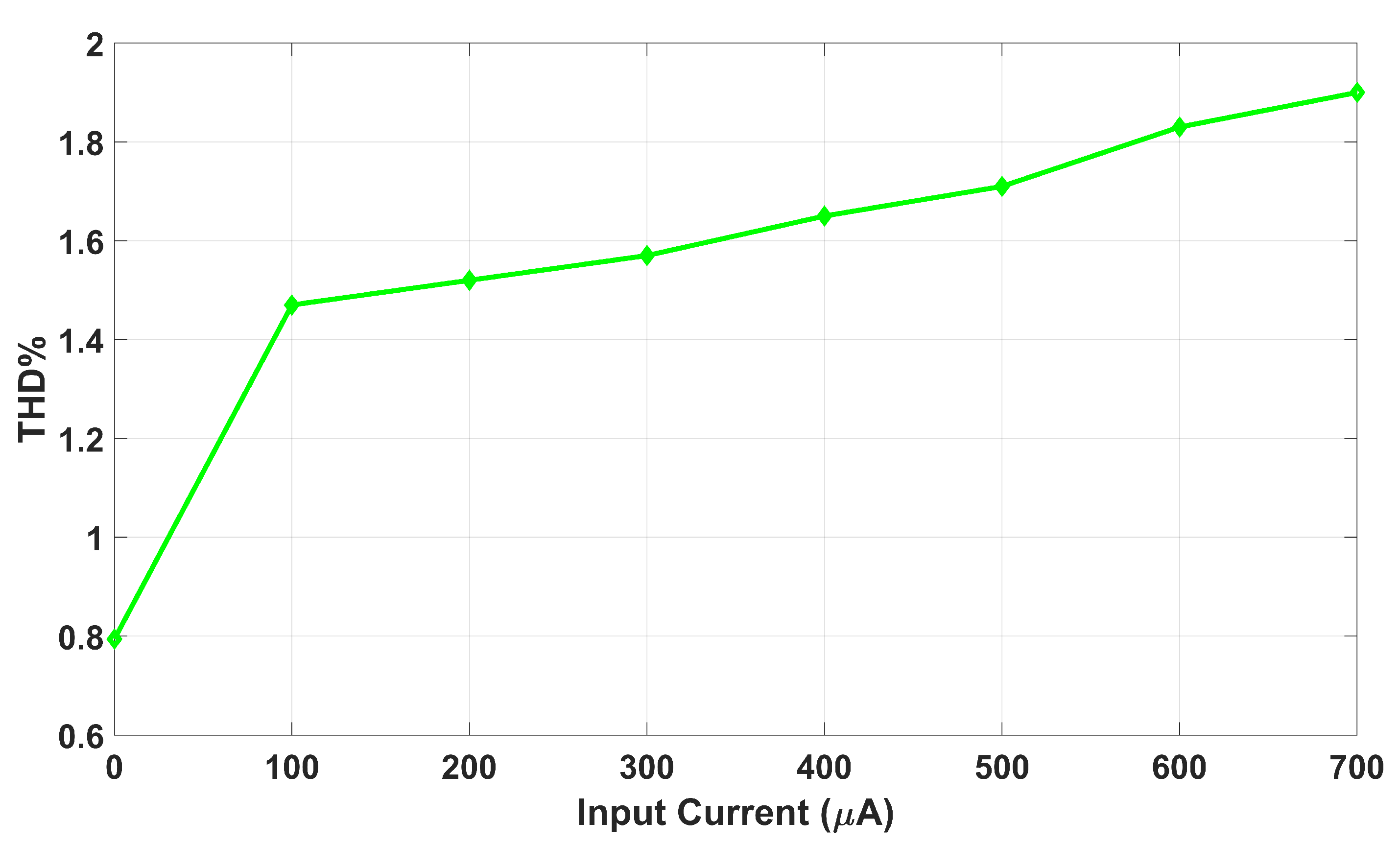
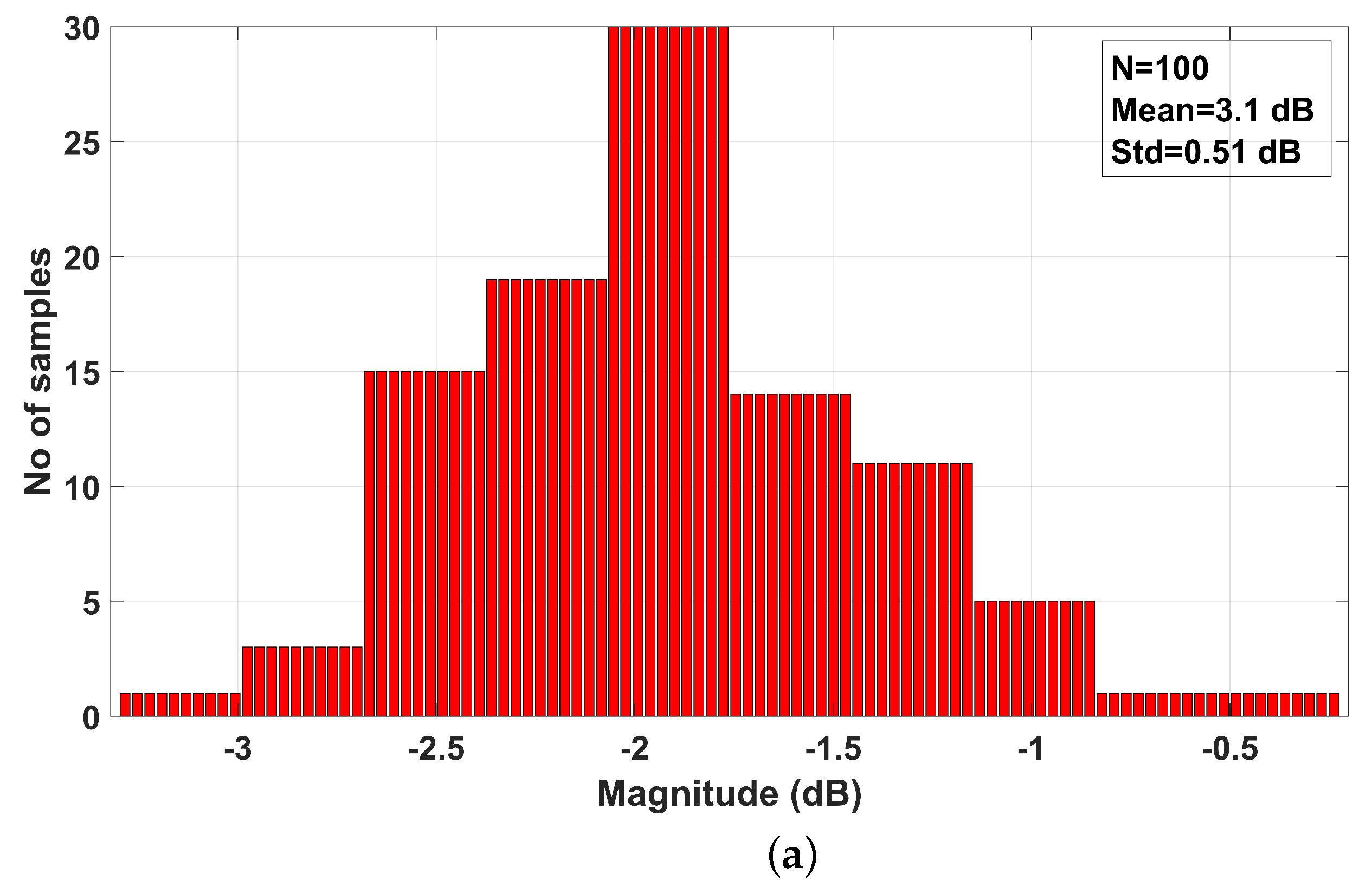
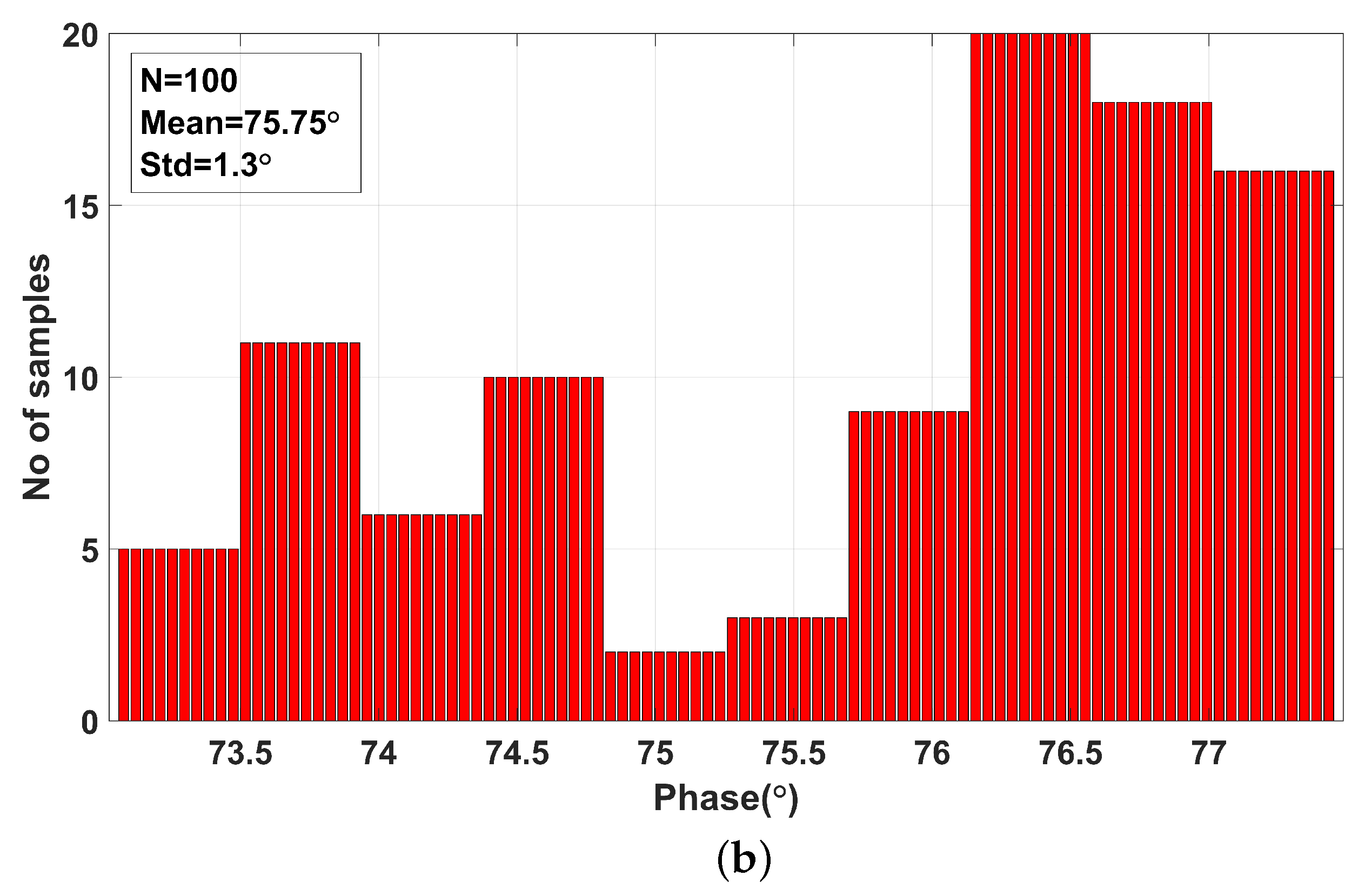
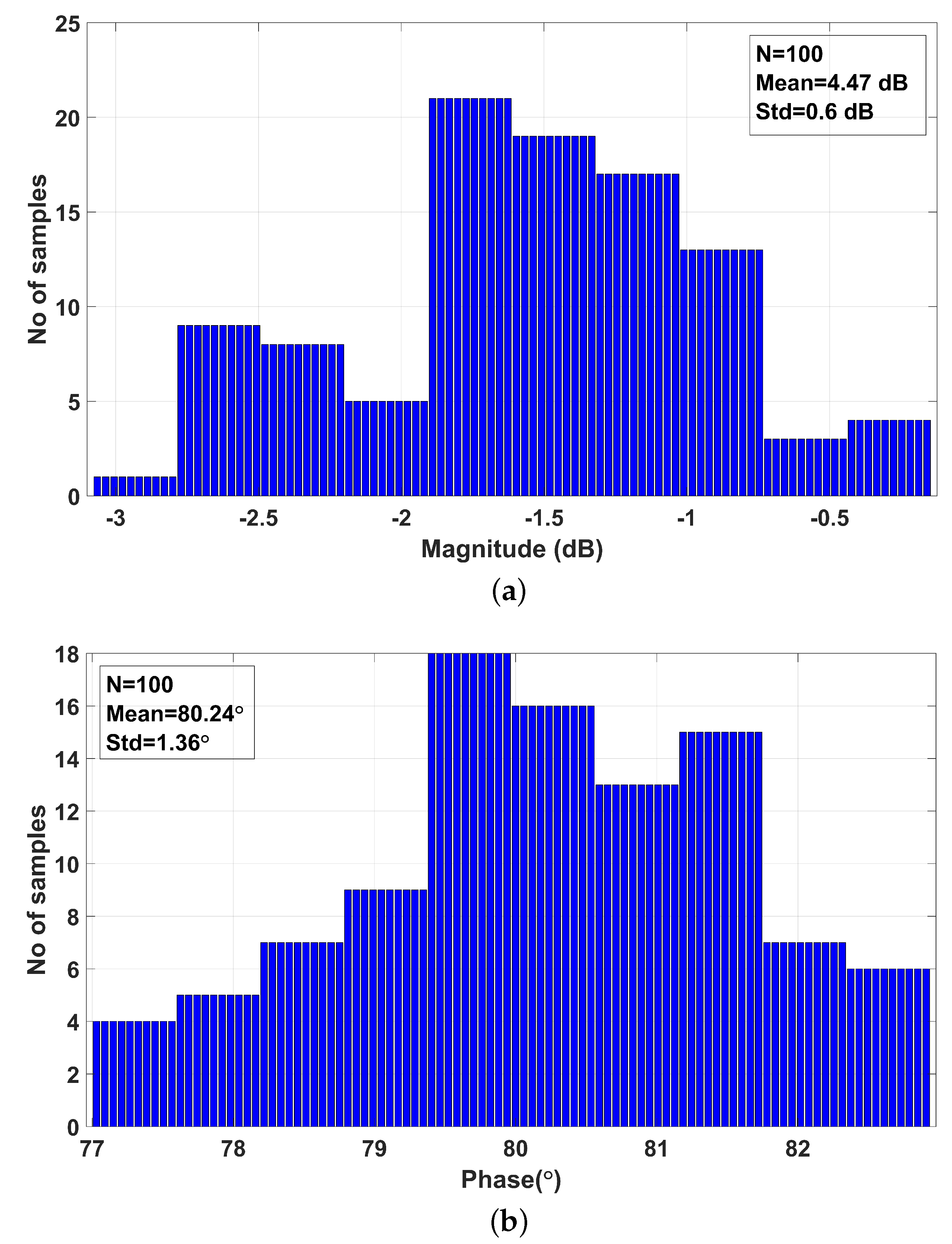
4. Results of the CM Fractional-Order Multifunction Filter Circuit Designed Based on MCFOA
5. Discussion
6. Conclusions
- This proposed design enables the simultaneous generation of FO-LPF, FO-HPF, and FO-BPF outputs within a single circuit structure, thereby providing multifunctional filtering capability.
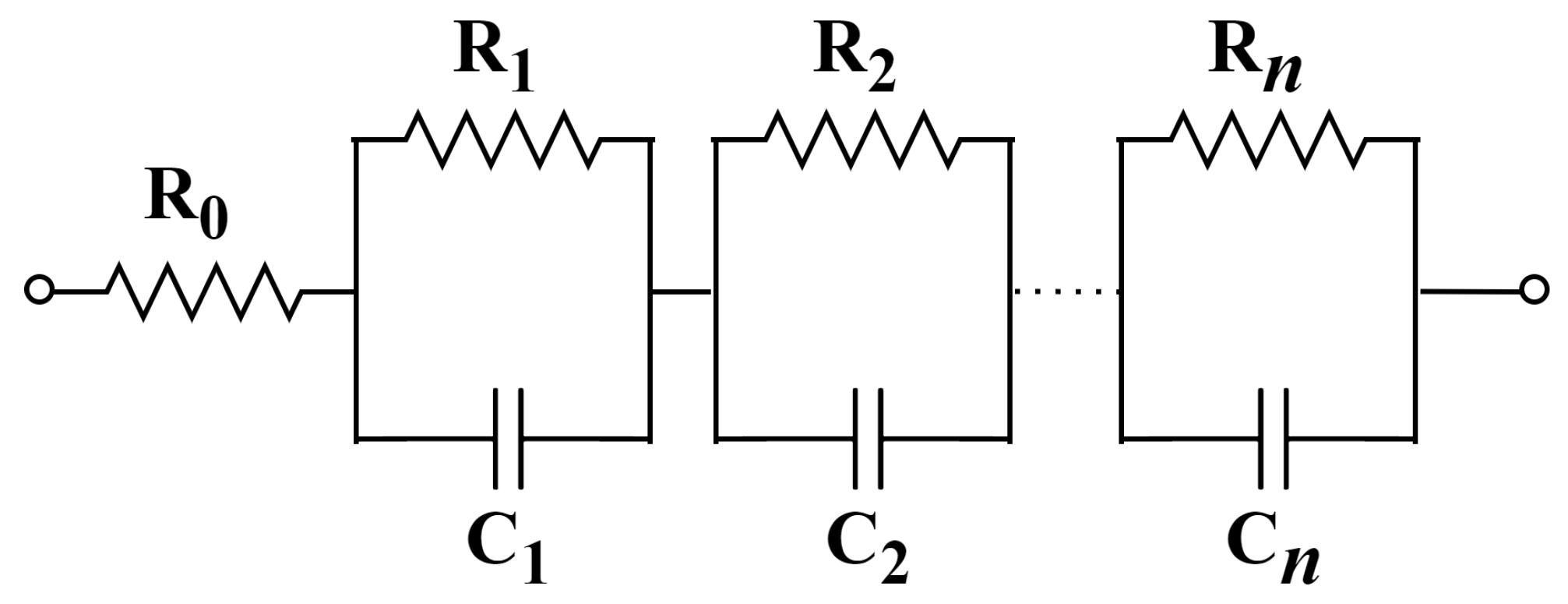
- The filter circuit, rendered fractional-order by incorporating a fractional-order capacitor, was designed using passive component values (including those in Foster type-I RC networks) approximated based on the IEC 60063 E96 standard [31] series, thereby improving its feasibility for real-world application.
- Thanks to its fractional-order design, the transition and stopband slopes can be controlled via the parameter, offering the designer a high degree of flexibility in shaping the frequency response.
- Simulation analyses conducted in the PSpice environment demonstrated that the filter circuit meets key performance criteria such as a low THD, a wide dynamic range, low noise, and low power consumption. Moreover, Monte Carlo analyses confirmed the circuit’s high robustness against variations in both active and passive components.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sen, F.; Kircay, A.; Cobb, B.S.; Akgul, A. MO-CCCII-Based Single-Input Multi-Output (SIMO) Current-Mode Fractional-Order Universal and Shelving Filter. Fractal Fract. 2024, 8, 181. [Google Scholar] [CrossRef]
- He, X.; Hu, Z. Optimization design of fractional-order Chebyshev lowpass filters based on genetic algorithm. Int. J. Circuit Theory Appl. 2022, 50, 1420–1441. [Google Scholar] [CrossRef]
- Sen, F.; Kircay, A.; Cobb, B.S.; Karci, H. Current-mode fractional-order shelving filters using MCFOA for acoustic applications. AEU-Int. J. Electron. Commun. 2023, 163, 154608. [Google Scholar] [CrossRef]
- Kubanek, D.; Freeborn, T.; Koton, J.; Herencsar, N. Evaluation of (1 + α) fractional-order approximated Butterworth high-pass and band-pass filter transfer functions. Elektron. Elektrotechnika 2018, 24, 37–41. [Google Scholar] [CrossRef]
- Yuce, E.; Minaei, S. A modified CFOA and its applications to simulated inductors, capacitance multipliers, and analog filters. IEEE Trans. Circuits Syst. Regul. Pap. 2008, 55, 266–275. [Google Scholar] [CrossRef]
- Said, L.A.; Radwan, A.G.; Madian, A.H.; Soliman, A.M. Fractional-order inverting and non-inverting filters based on CFOA. In Proceedings of the 2016 39th International Conference on Telecommunications and Signal Processing (TSP), Vienna, Austria, 27–29 June 2016; pp. 599–602. [Google Scholar]
- Khateb, F.; Kubánek, D.; Tsirimokou, G.; Psychalinos, C. Fractional-order filters based on low-voltage DDCCs. Microelectron. J. 2016, 50, 50–59. [Google Scholar] [CrossRef]
- Dvorak, J.; Langhammer, L.; Jerabek, J.; Koton, J.; Sotner, R.; Polak, J. Electronically tunable fractional-order low-pass filter with current followers. In Proceedings of the 2016 39th International Conference on Telecommunications and Signal Processing (TSP), Vienna, Austria, 27–29 June 2016; pp. 587–592. [Google Scholar]
- Koton, J.; Jerabek, J.; Herencsar, N.; Kubanek, D. Current conveyors in current-mode circuits approximating fractional-order low-pass filter. In Proceedings of the 2017 European Conference on Circuit Theory and Design (ECCTD), Catania, Italy, 4–6 September 2017; pp. 1–4. [Google Scholar]
- Tsirimokou, G.; Psychalinos, C.; Elwakil, A.S. Fractional-order electronically controlled generalized filters. Int. J. Circuit Theory Appl. 2017, 45, 595–612. [Google Scholar] [CrossRef]
- Verma, R.; Pandey, N.; Pandey, R. Electronically tunable fractional order filter. Arab. J. Sci. Eng. 2017, 42, 3409–3422. [Google Scholar] [CrossRef]
- Hamed, E.M.; AbdelAty, A.M.; Said, L.A.; Radwan, A.G. Effect of different approximation techniques on fractional-order KHN filter design. Circuits Syst. Signal Process. 2017, 37, 5222–5252. [Google Scholar] [CrossRef]
- Kubanek, D.; Freeborn, T.; Koton, J. Fractional-order band-pass filter design using fractional-characteristic specimen functions. Microelectron. J. 2019, 86, 77–86. [Google Scholar] [CrossRef]
- Dvorak, J.; Jerabek, J.; Polesakova, Z.; Kubanek, D.; Blazek, P. Multifunctional electronically reconfigurable and tunable fractional-order filter. Elektron. Elektrotechnika 2019, 25, 26–30. [Google Scholar] [CrossRef]
- Hassanein, A.M.; Soltan, A.; Said, L.A.; Madian, A.H.; Radwan, A.G. Analysis and design of fractional-order low-pass filter with three elements of independent orders. In Proceedings of the 2019 Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 28–30 October 2019; Volume 1, pp. 218–221. [Google Scholar]
- Langhammer, L.; Dvorak, J.; Sotner, R.; Jerabek, J.; Bertsias, P. Reconnection–less reconfigurable low–pass filtering topology suitable for higher–order fractional–order design. J. Adv. Res. 2020, 25, 257–274. [Google Scholar] [CrossRef] [PubMed]
- Swain, S.; Biswal, K.; Tripathy, M.C.; Kar, S.K. Performance analysis of fractional order Sallen-Key high-pass filter using fractional capacitors. In Proceedings of the 2020 International conference on computational intelligence for smart power system and sustainable energy (CISPSSE), Keonjhar, India, 29–31 July 2020; pp. 1–5. [Google Scholar]
- Kaur, G.; Ansari, A.Q.; Hashmi, M.S. Analysis and investigation of CDBA based fractional-order filters. Analog. Integr. Circuits Signal Process. 2020, 105, 111–124. [Google Scholar] [CrossRef]
- Ahmed, O.I.; Yassin, H.M.; Said, L.A.; Psychalinos, C.; Radwan, A.G. Implementation and analysis of tunable fractional-order band-pass filter of order 2α. AEU-Int. J. Electron. Commun. 2020, 124, 153343. [Google Scholar] [CrossRef]
- Sen, F.; Kircay, A. MO-CCCII based current-mode fractional-order universal filter. J. Circuits, Syst. Comput. 2021, 30, 2150132. [Google Scholar] [CrossRef]
- Biswal, K.; Swain, S.; Tripathy, M.C.; Kar, S.K. Re-configurable band-stop and all-pass filter using fractional-order topology. Int. J. Adv. Technol. Eng. Explor. 2022, 9, 1773. [Google Scholar]
- Kaur, G.; Ansari, A.Q.; Hashmi, M.S. Complexity reduced design procedure of a fractional order all-pass filter. Wirel. Pers. Commun. 2022, 125, 2515–2535. [Google Scholar] [CrossRef]
- Krishna, B.T.; Janarthanan, M. Realization of fractional order lowpass filter using different approximation techniques. Bull. Electr. Eng. Inform. 2023, 12, 3552–3561. [Google Scholar] [CrossRef]
- Tasneem, S.; Ranjan, R.K.; Paul, S.K.; Herencsar, N. Power-Efficient Electronically Tunable Fractional-Order Filter. Fractal Fract. 2023, 8, 31. [Google Scholar] [CrossRef]
- Biswal, K.; Swain, S.; Tripathy, M.C.; Kar, S.K. Modeling and performance improvement of fractional-order band-pass filter using fractional elements. IETE J. Res. 2023, 69, 2791–2800. [Google Scholar] [CrossRef]
- Biswal, K.; Swain, S.; Tripathy, M.C.; Kar, S.K. A high-Q fractional-order twin-T notch filter for low-frequency applications. Sādhanā 2023, 48, 38. [Google Scholar] [CrossRef]
- Yokuş, Y.E.; Koton, J.; Sotner, R.; Kartci, A.; Ayten, U.E. A review of the state-of-the-art in fractional-order analog filters. AEU-Int. J. Electron. Commun. 2025, 196, 2791–2800. [Google Scholar] [CrossRef]
- Svoboda, J.A.; McGory, L.; Webb, S. Applications of a commercially available current conveyor. Int. J. Electron. Theor. Exp. 2023, 70, 159–164. [Google Scholar] [CrossRef]
- Cui, X. A Study of Voltage-Mode and Current-Mode Filters Using Modified Current Feedback Operational Amplifier. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2018. [Google Scholar]
- Tsirimokou, G. A systematic procedure for deriving RC networks of fractional-order elements emulators using MATLAB. AEU-Int. J. Electron. Commun. 2017, 78, 7–14. [Google Scholar] [CrossRef]
- IEC 60063; Preferred Number Series for Resistors and Capacitors (Including E96). International Electrotechnical Commission: Geneva, Switzerland, 2015.





| Ref. | Active Block | Configuration | Mode of Opr. | Filter Type | No. of Passive Elements | Using FC | Power Cons. | Dynamic Range | Noise | THD (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| R (Gnd.) | C (Gnd.) | ||||||||||
| [6] | +CFOA (3) +CFOA (3) | NA | +VM +VM | +Inverting FO-LPF, FO-HPF and FO-BPF +Non-Inverting FO-LPF, FO-HPF and FO-BPF | +6 (3) +5 (3) | - | + 2 + 2 | NA | NA | NA | NA |
| [7] | DDCC (5) | MOSFETs | VM | FO-LPF | 7 (7) | 3 (3) | - | 37 A | NA | NA | NA |
| [8] | MO-CF (3) and ACA (5) | NA | CM | FO-LPF | 3 (0) | 3 (3) | - | NA | NA | NA | NA |
| [9] | +CCII (3) and DDCC (1) +CCII (1) and DDCC(3) | NA | CM | FO-LPF | +7 (7) +5 (5) | +3 (3) +3 (3) | - | NA | NA | NA | NA |
| [10] | OTA (11) | MOSFETs | CM | FO-LPF, FO-HPF, FO-BPF and FO-NPF | - | 4 (4) | - | NA | NA | NA | NA |
| [11] | OTA (3) | NA | CM | FO-LPF and FO-BPF | - | - | 2 | NA | NA | NA | NA |
| [12] | CCII (5) | NA | VM | FO-LPF and FO-HPF | 6 (3) | - | 2 | NA | NA | NA | NA |
| [13] | opAmp (3) | NA | VM | Tom-Thomas FO-BPF | 6 (0) | - | 2 | NA | NA | NA | NA |
| [14] | OTA (3) and ACA (3) | NA | CM | FO-LPF, FO-HPF, FO-BPF AND FO-NPF | - | 1 (0) | 1 | NA | NA | NA | NA |
| [15] | opAmp (2) | NA | VM | FO-LPF | 6 (2) | - | 3 | NA | NA | NA | NA |
| [16] | OTA (4) and IOGC-CA (1) | NA | CM | FO-LPF | - | 4 (4) | - | NA | NA | NA | NA |
| [17] | opAmp (1) | NA | VM | Sallen-Key FO-HPF | 2 (1) | - | 2 | NA | NA | NA | NA |
| [18] | +CDBA (5) +CDBA (5) +CDBA (5) | MOSFETs | CM | +FO-LPF and FO-BPF +FO-HPF +FO-NPF and FO-APF | +11 (2) +11 (2) +12 (2) | +3 (3) +3 (3) +3 (3) | - | NA | NA | NA | NA |
| [19] | OTA (11) | MOSFETs | VM | FO-BPF | - | 4 (4) | - | NA | NA | NA | NA |
| [20] | MO-CCII (3) | BJTs | CM | FO-LPF, FO-HPF, FO-BPF, FO-NPF and FO-APF | 2 (2) | 1 (1) | 1 | NA | NA | NA | NA |
| [21] | +opAmp (1) +opAmp (1) | NA | VM | +FO-NPF +FO-APF | +4 (1) +3 (1) | - | +2 +1 and using FI | NA | NA | NA | NA |
| [22] | CDBA (4) | MOSFETs | VM | FO-APF | 11 (1) | 3 (3) | - | NA | NA | NA | NA |
| [23] | opAmp (6) | NA | VM | FO-LPF | 14 (0) | 3 (0) | - | NA | NA | NA | NA |
| [24] | VDDDA (3) | MOSFETs | VM | FO-LPF | Act. Res. (2) | 3 (3) | - | 663 nW | NA | 691 | <4 |
| [25] | opAmp (1) | NA | VM | FO-BPF | 3 (0) | - | 1 and using FI | NA | NA | NA | NA |
| [26] | opAmp (1) | NA | VM | +FO-NPF +FO twin-T NPF | 3 (0) | - | 3 | NA | NA | NA | NA |
| Proposed | MCFOA (1) | BJTs | CM | FO-LPF, FO-HPF and FO-BPF | 3 (3) | 1 (1) | 1 | <2 mW | >80 dB | 67.2 | <2 |
| Parameter | FO-LPF | FO-HPF | FO-BPF |
|---|---|---|---|
| a | |||
| b | |||
| Fractional-Order () | |||||
|---|---|---|---|---|---|
| Pass. Comp. | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| 2.87 | 1.65 | 0.88 | 0.42 | 0.15 | |
| 6.34 | 4.75 | 3.32 | 2 | 0.887 | |
| 8.25 | 7.32 | 5.9 | 4.12 | 2.1 | |
| 14 | 13.7 | 12.7 | 10.2 | 6.04 | |
| 33.2 | 40.2 | 44.2 | 43.2 | 30.9 | |
| 287 | 549 | 1070 | 2320 | 6650 | |
| 2.21 | 3.16 | 4.99 | 9.09 | 22.1 | |
| 8.06 | 9.53 | 12.4 | 19.1 | 39.2 | |
| 15.8 | 16.2 | 18.7 | 24.9 | 45.3 | |
| 22.6 | 20.5 | 20.5 | 23.2 | 35.7 | |
| 26.7 | 18.2 | 13 | 9.31 | 6.81 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sen, F.; Kircay, A. Realization of Fractional-Order Current-Mode Multifunction Filter Based on MCFOA for Low-Frequency Applications. Fractal Fract. 2025, 9, 377. https://doi.org/10.3390/fractalfract9060377
Sen F, Kircay A. Realization of Fractional-Order Current-Mode Multifunction Filter Based on MCFOA for Low-Frequency Applications. Fractal and Fractional. 2025; 9(6):377. https://doi.org/10.3390/fractalfract9060377
Chicago/Turabian StyleSen, Fadile, and Ali Kircay. 2025. "Realization of Fractional-Order Current-Mode Multifunction Filter Based on MCFOA for Low-Frequency Applications" Fractal and Fractional 9, no. 6: 377. https://doi.org/10.3390/fractalfract9060377
APA StyleSen, F., & Kircay, A. (2025). Realization of Fractional-Order Current-Mode Multifunction Filter Based on MCFOA for Low-Frequency Applications. Fractal and Fractional, 9(6), 377. https://doi.org/10.3390/fractalfract9060377







