Hybrid Fuzzy Fractional for Multi-Phasic Epidemics: The Omicron–Malaria Case Study
Abstract
1. Introduction
- Methodological Innovation: We introduce and formally define the Fuzzy Piecewise Fractional Derivative (FPFD) framework. This involves establishing the theoretical underpinnings for a model that can switch its governing mathematical operator in a fuzzy environment, providing a new, powerful tool for applied mathematicians and modelers.
- Rigorous Analytical and Numerical Development: We provide a comprehensive analysis of the proposed FPFD co-infection model, including proofs of the existence, uniqueness, positivity, and boundedness of the solutions. We also design and implement a novel hybrid numerical scheme (combining Fuzzy Runge–Kutta and Fuzzy Adams-Bashforth methods) that can accurately solve such piecewise systems.
- Practical Application and Policy Translation: We demonstrate the framework’s utility by applying it to the Omicron–malaria co-infection scenario. Crucially, we move beyond a purely mathematical discussion by providing a direct interpretation of the model’s fuzzy, interval-valued outputs for public health policy, showcasing how this approach can support more robust and risk-aware strategic planning in the face of complex epidemiological threats.
2. Preliminaries
- 1.
- Continuity: is continuous with respect to both t and .
- 2.
- Lipschitz Condition: is Lipschitz continuous in its second argument, , uniformly in t. That is, there exists a constant such that for any :
3. Model Formulation
- Omicron Transmission: The virus spreads via a direct human-to-human respiratory route. Susceptible humans () become infected upon contact with Omicron-infectious individuals (), governed by the transmission coefficient .
- Malaria Transmission: The model assumes that individuals infected with Omicron () can also be co-infected with malaria and are capable of transmitting the malaria parasite. Susceptible mosquitoes () become infected upon biting these infectious humans (), a process governed by the transmission coefficient .
4. Model Formulation in the Concept of FPFD
Deconstructing the Fuzzy System Function
- Recruitment of Susceptibles: The term represents the recruitment of new individuals into the susceptible class. The uncertainty in both the vaccination proportion and the recruitment rate yields a fuzzy interval for the rate of new, unvaccinated susceptibles.
- Outflow from New Infections (Omicron): The term represents the rate at which susceptible individuals become infected with Omicron through contact with infectious humans. The uncertainty in the transmission rate combines with the fuzzy states of the susceptible () and infectious () human populations to produce a fuzzy rate of new Omicron infections.
- Inflow from Recovery: The term models the inflow of individuals who have recovered from either the infected () or discharged () states and have become susceptible again.
- Inflow from Waning Immunity: The term accounts for vaccinated individuals () whose immunity wanes at an uncertain rate , causing them to re-enter the susceptible population.
- Outflow from Natural Death: The term represents the removal of susceptible individuals from the population due to natural death.
5. Existence and Uniqueness of the Fuzzy Piecewise Solution
Hypotheses and Function Space
6. Positivity and Boundedness of Solution in the Concept of FPFD
7. Equilibrium Points and Basic Reproductive Number
7.1. Disease-Free Equilibrium (DFE)
- From the equation: .
- From the equation: .
- Substituting into the equation: . While this can be solved, the model structure in the paper implies a simpler relationship, likely that decays to and there’s a simpler equilibrium. Given the equations, the most direct solution for the total non-infected population is . Let us adopt the simpler forms derived in many such models.
7.2. Basic Reproductive Number ()
7.3. Disease-Endemic Equilibrium (DEE)
8. Local and Global Stability Analysis
8.1. Local Asymptotic Stability of the Disease-Free Equilibrium (DFE)
8.2. Global Stability Analysis
9. Numerical Scheme
- Initialization: Fuzzify the initial conditions and all model parameters. Discretize the time interval with a uniform step size h, such that . Define the transition index , which marks the end of the classical phase.
- Part 1: Fuzzy Classical Regime (): For the initial memoryless phase, we employ the Fuzzy Runge–Kutta 4th Order (RK4) method. At each step, we solve the system of ODEs for the lower and upper bounds. The derivatives for the bounds are determined by applying interval arithmetic principles:Given the state at time , the state at is computed via the following iterative formulas:
- Step 1 (k1):
- Step 2 (k2):
- Step 3 (k3):
- Step 4 (k4):
- Final Update:
- Handoff: The fuzzy value computed at the final step of the classical regime serves as the initial condition for the subsequent fractional phase. Crucially, the history-dependent sums for the fractional solver are initiated at index . This effectively treats the preceding classical dynamics as having no memory effect on the subsequent phase, aligning the numerical scheme with the model’s theoretical construction where memory begins at .
- Part 2: Fuzzy Fractional Regime (): For the post-intervention phase, we use the Fuzzy Fractional Adams–Bashforth–Moulton (ABM) predictor-corrector algorithm to solve the ABC fractional system. The solution at step is found using the history of derivative values from to . Let be the normalization constant for the ABC derivative.
- Predictor Step: First, we compute the predicted value :whereand the weights are
- Corrector Step: We then correct the predicted value to obtain the final state :whereand the corrector weights are
10. Simulation and Discussion
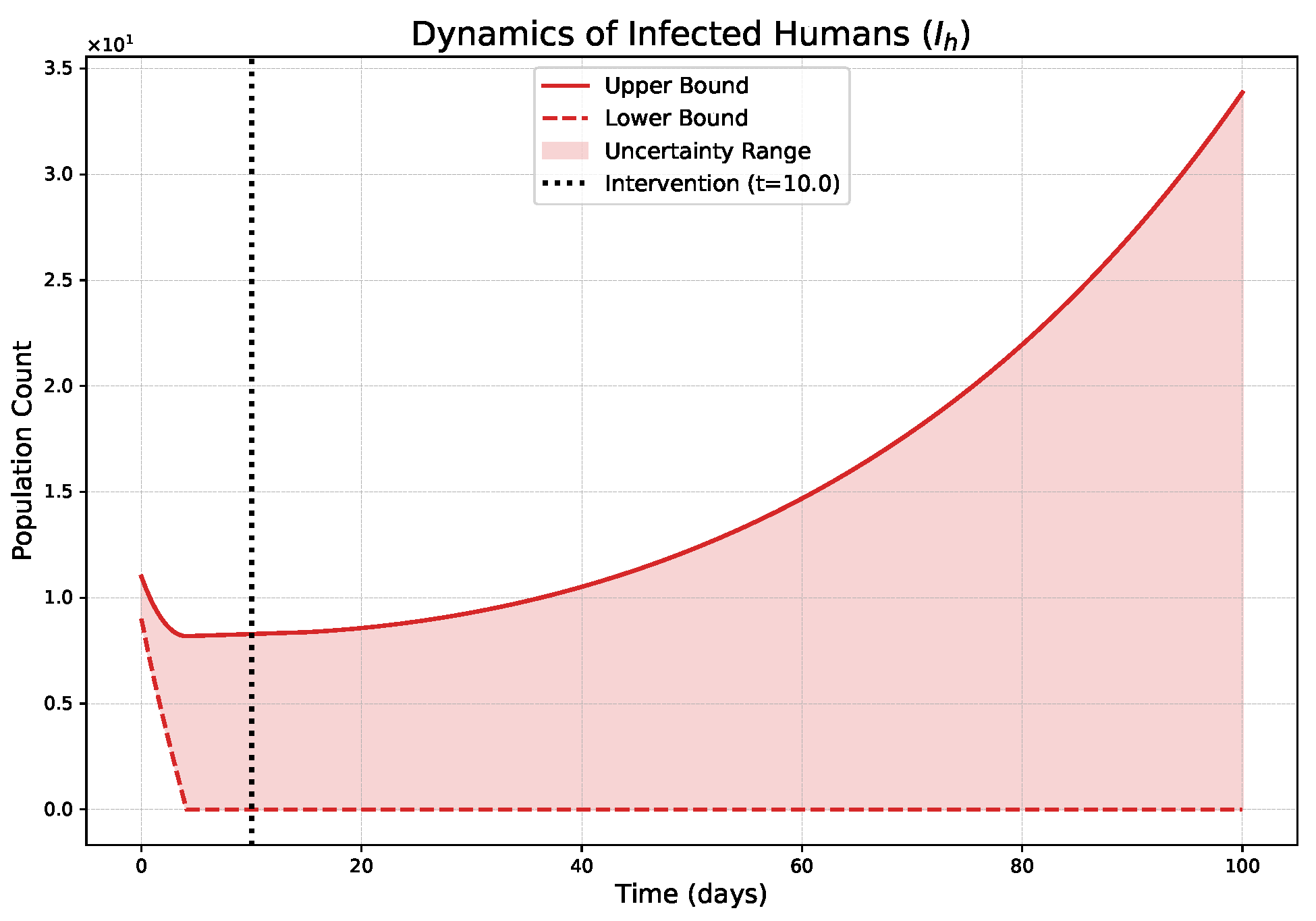
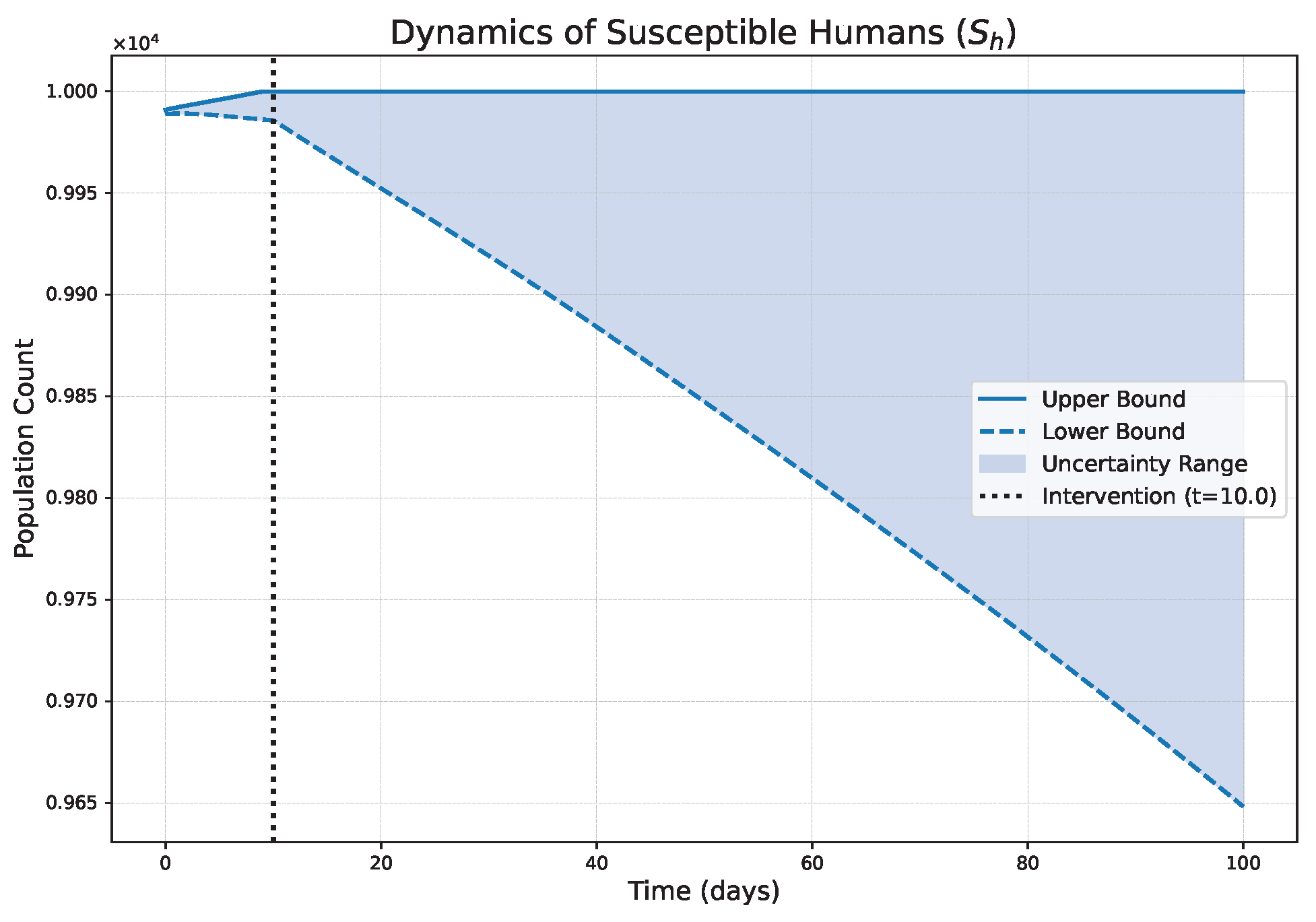
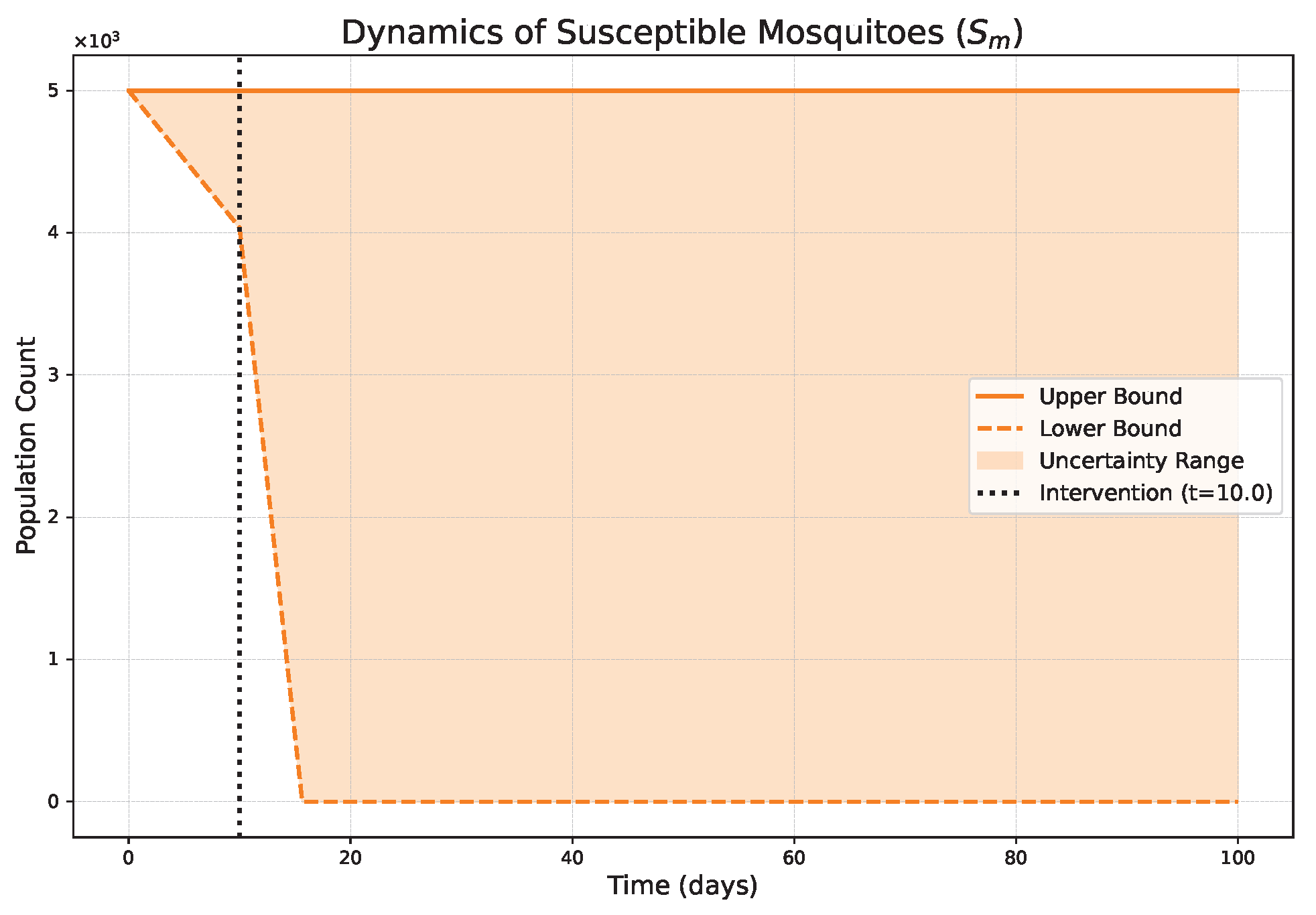
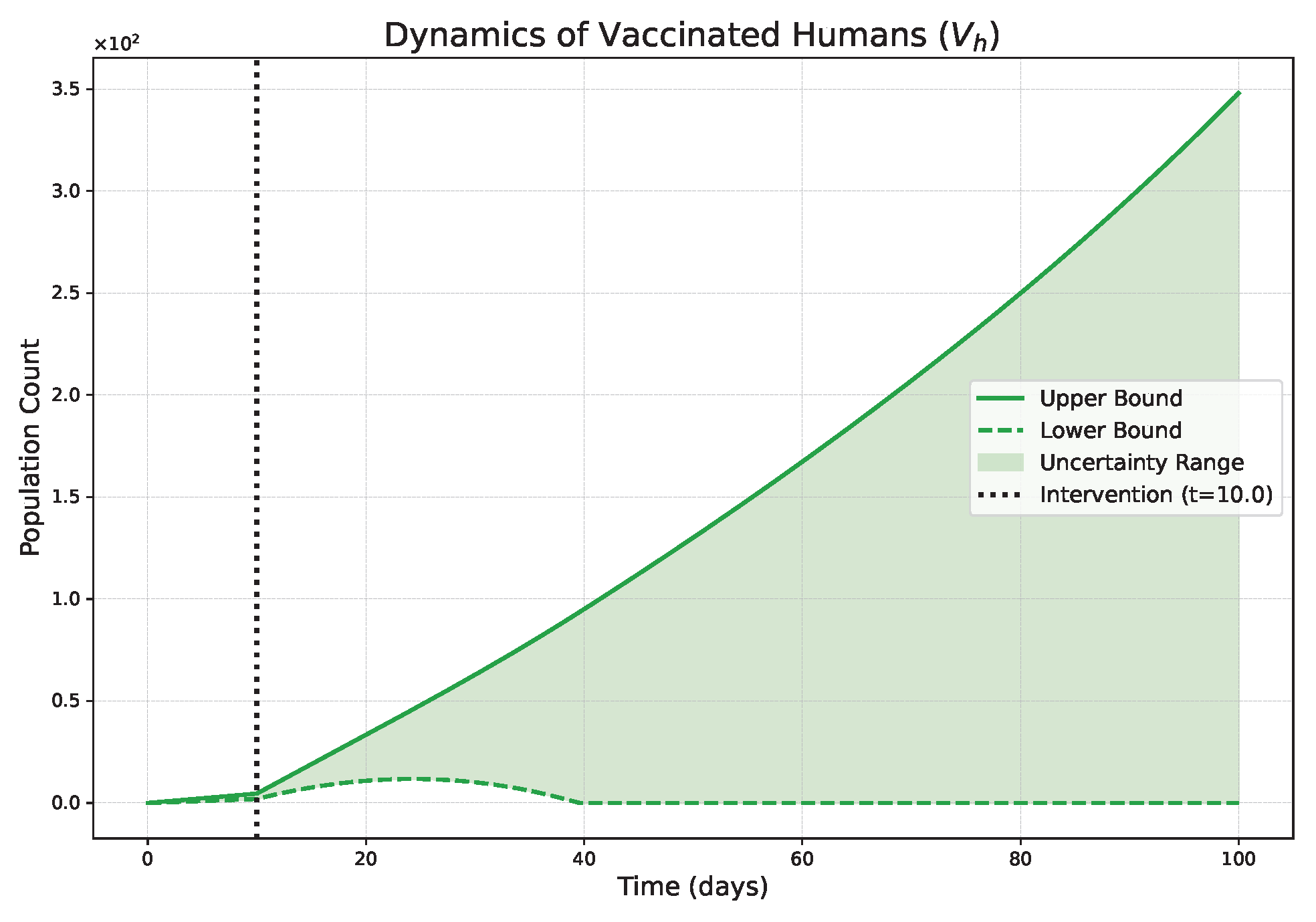
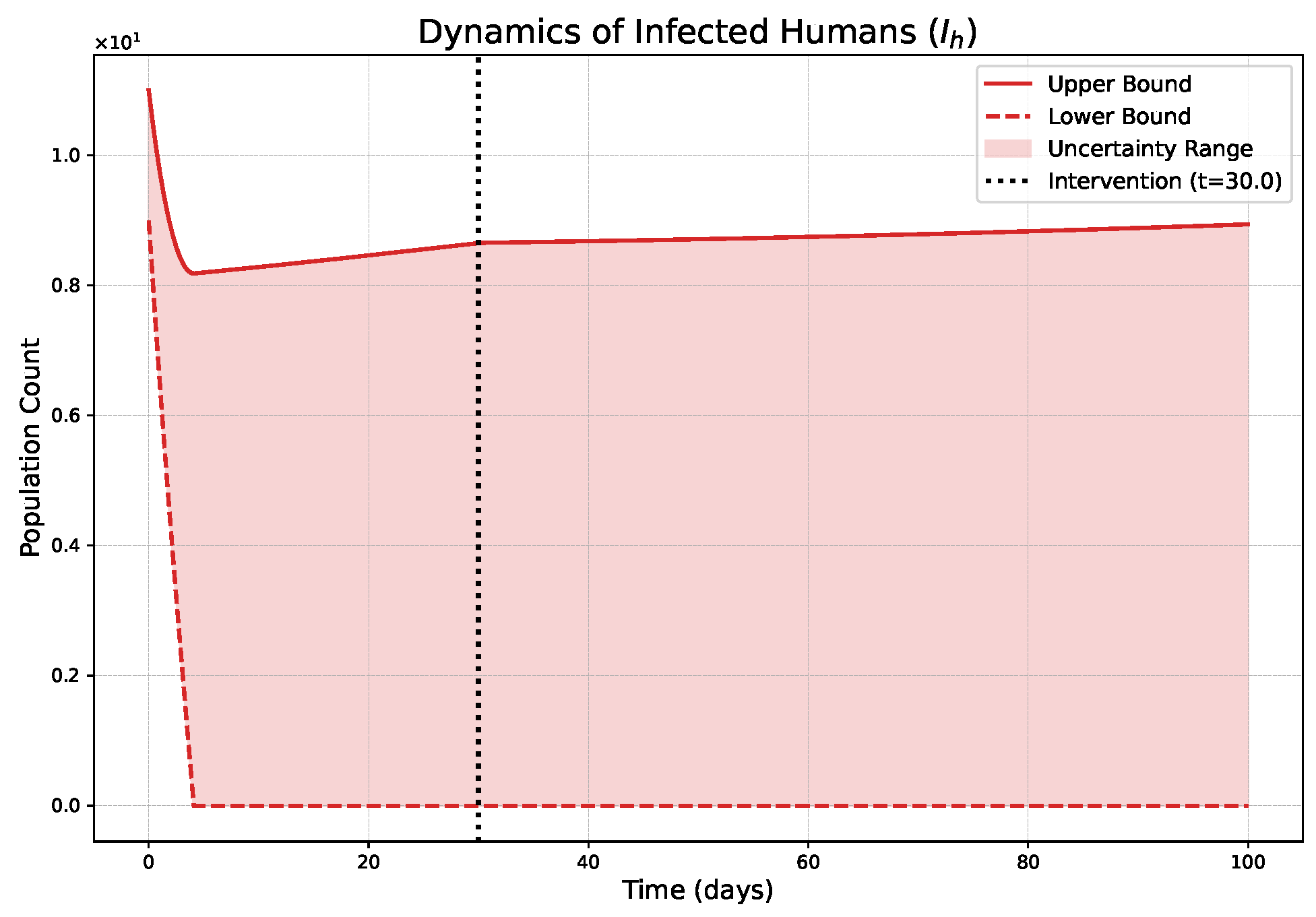
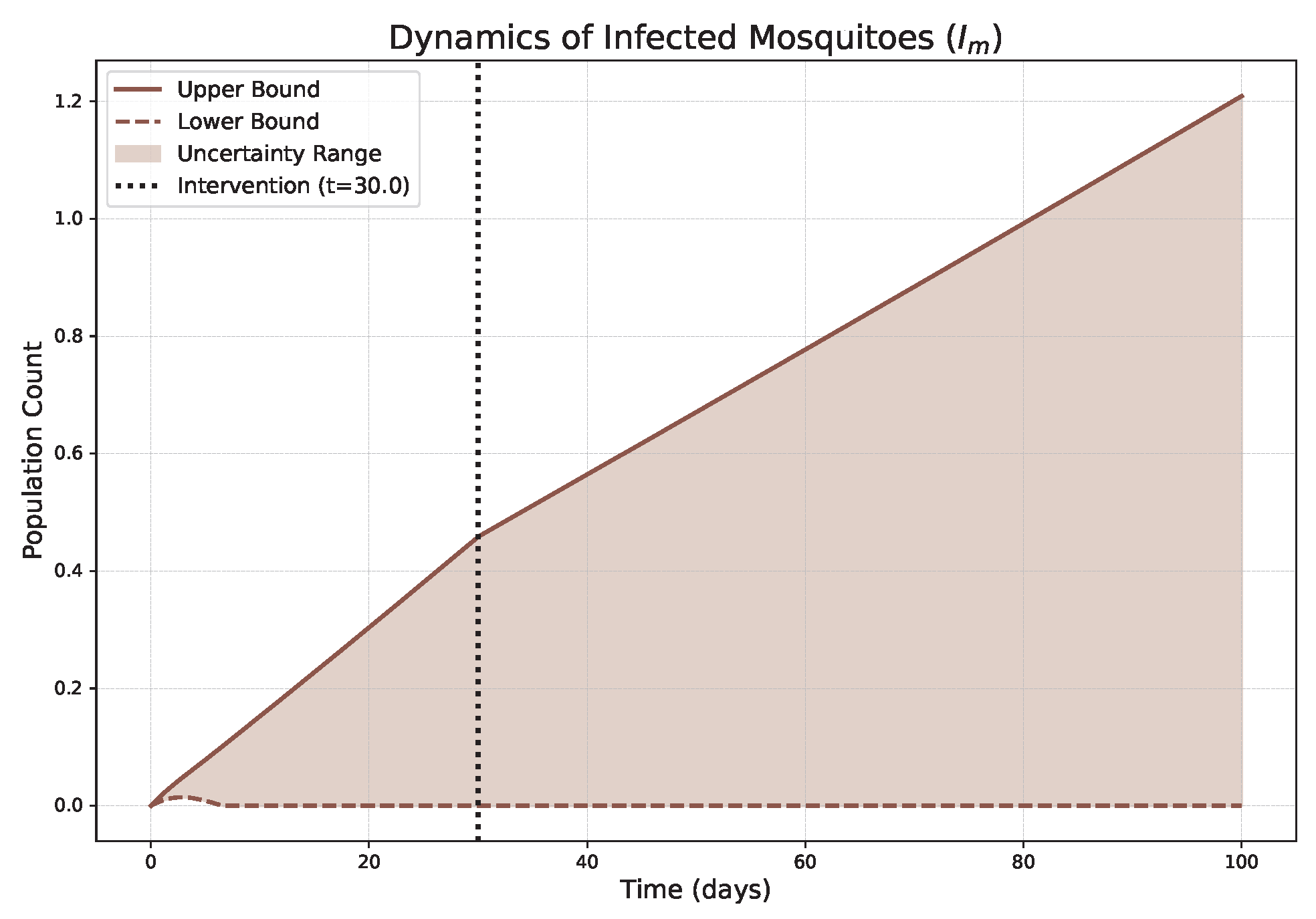
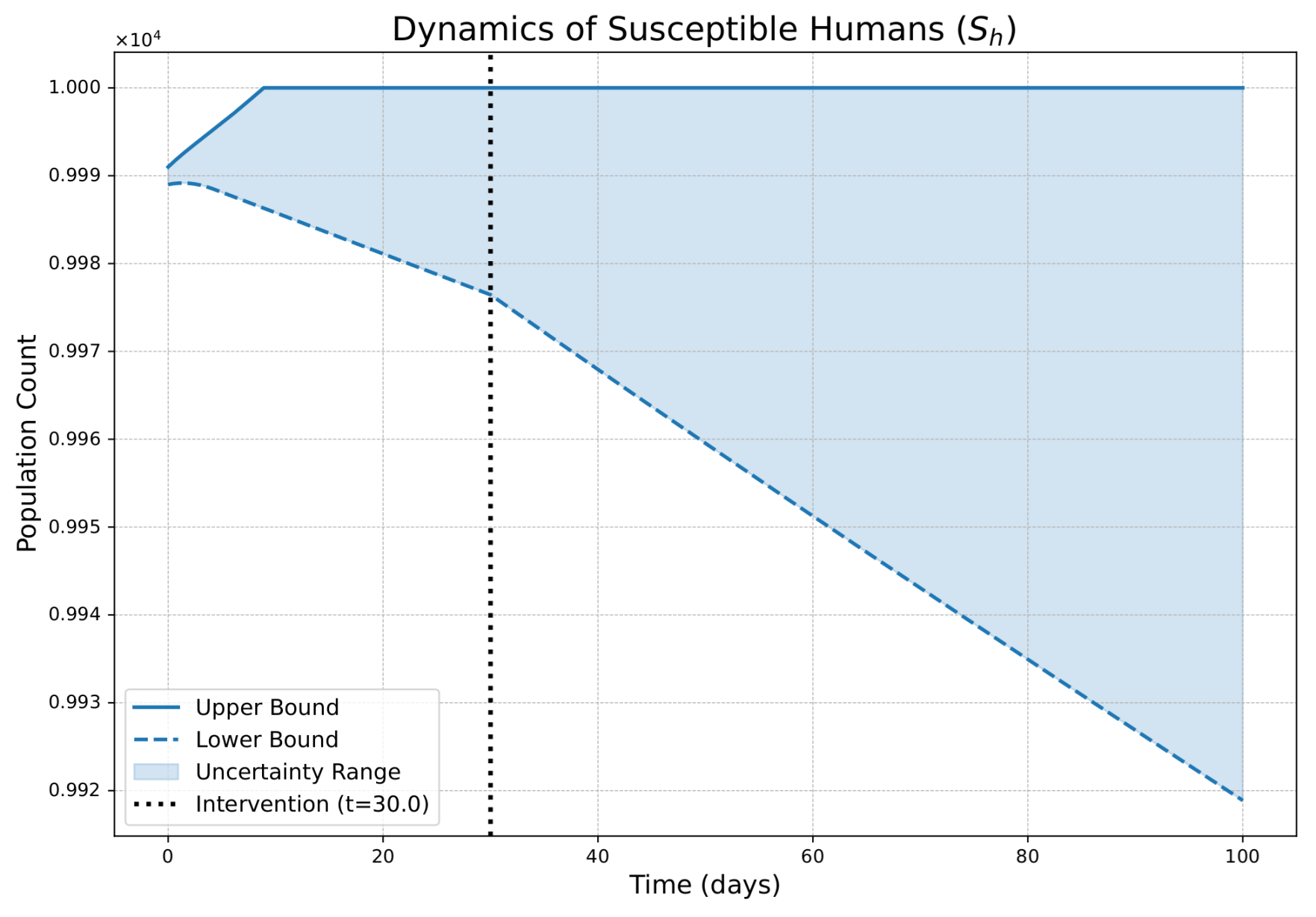
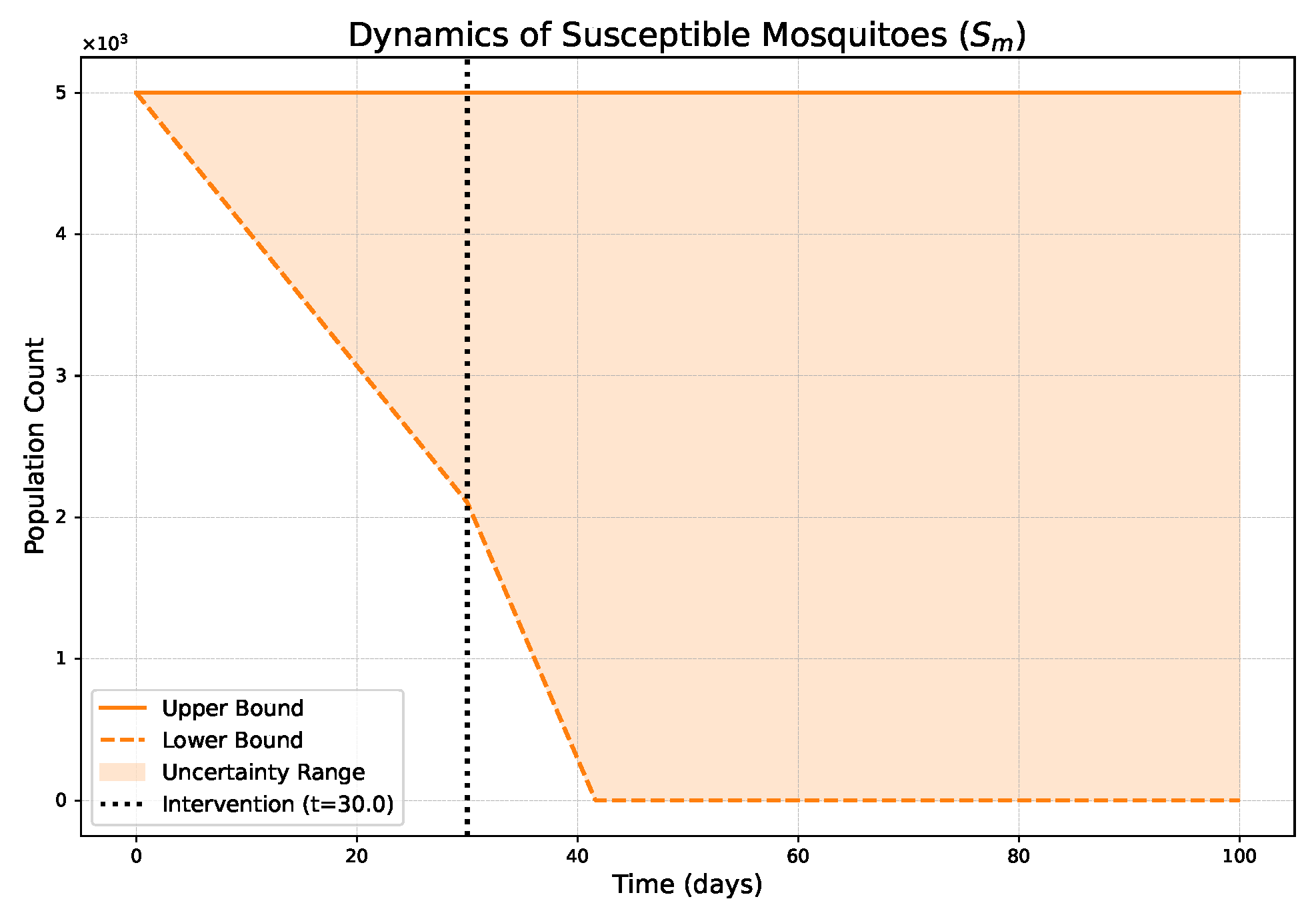
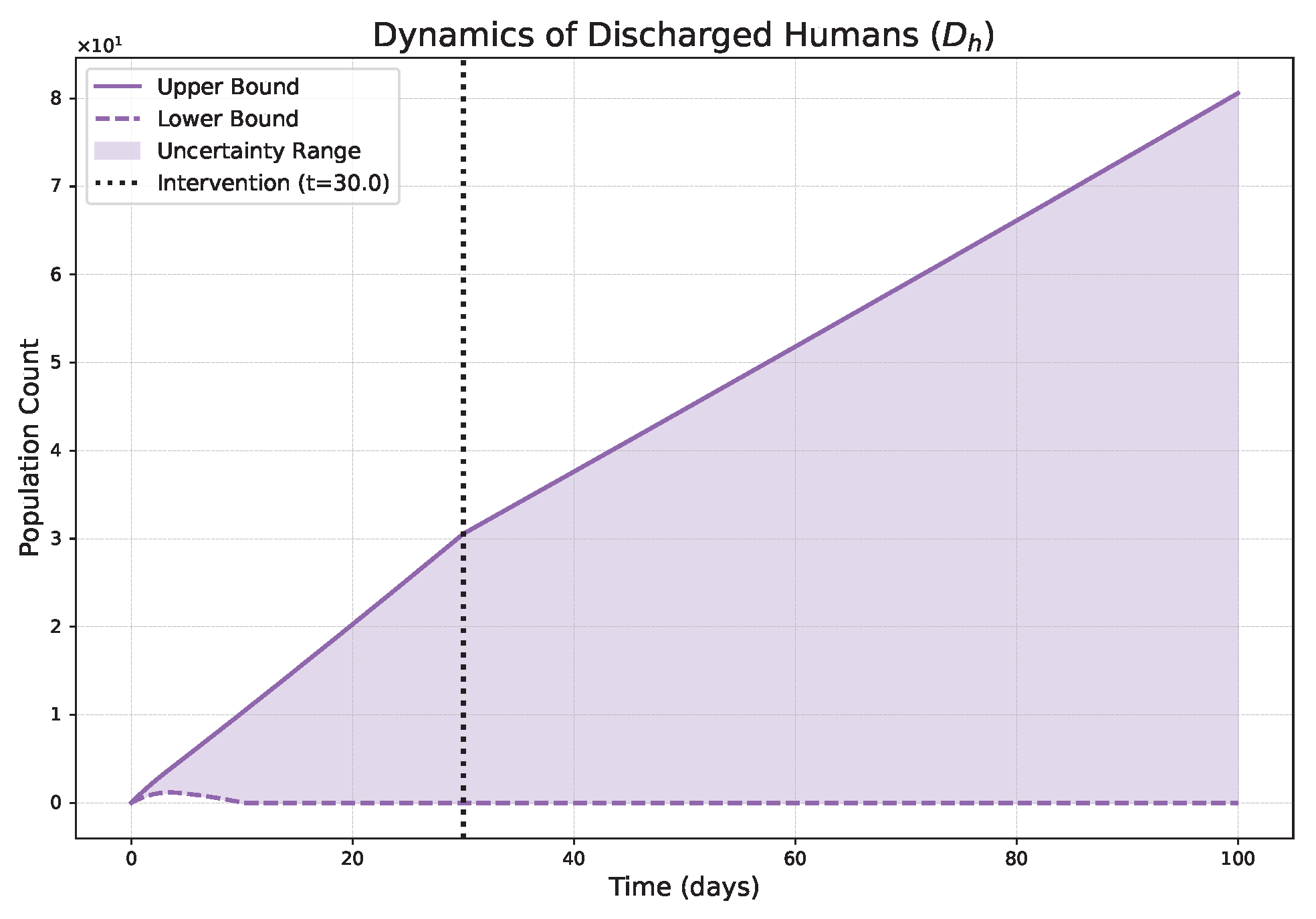
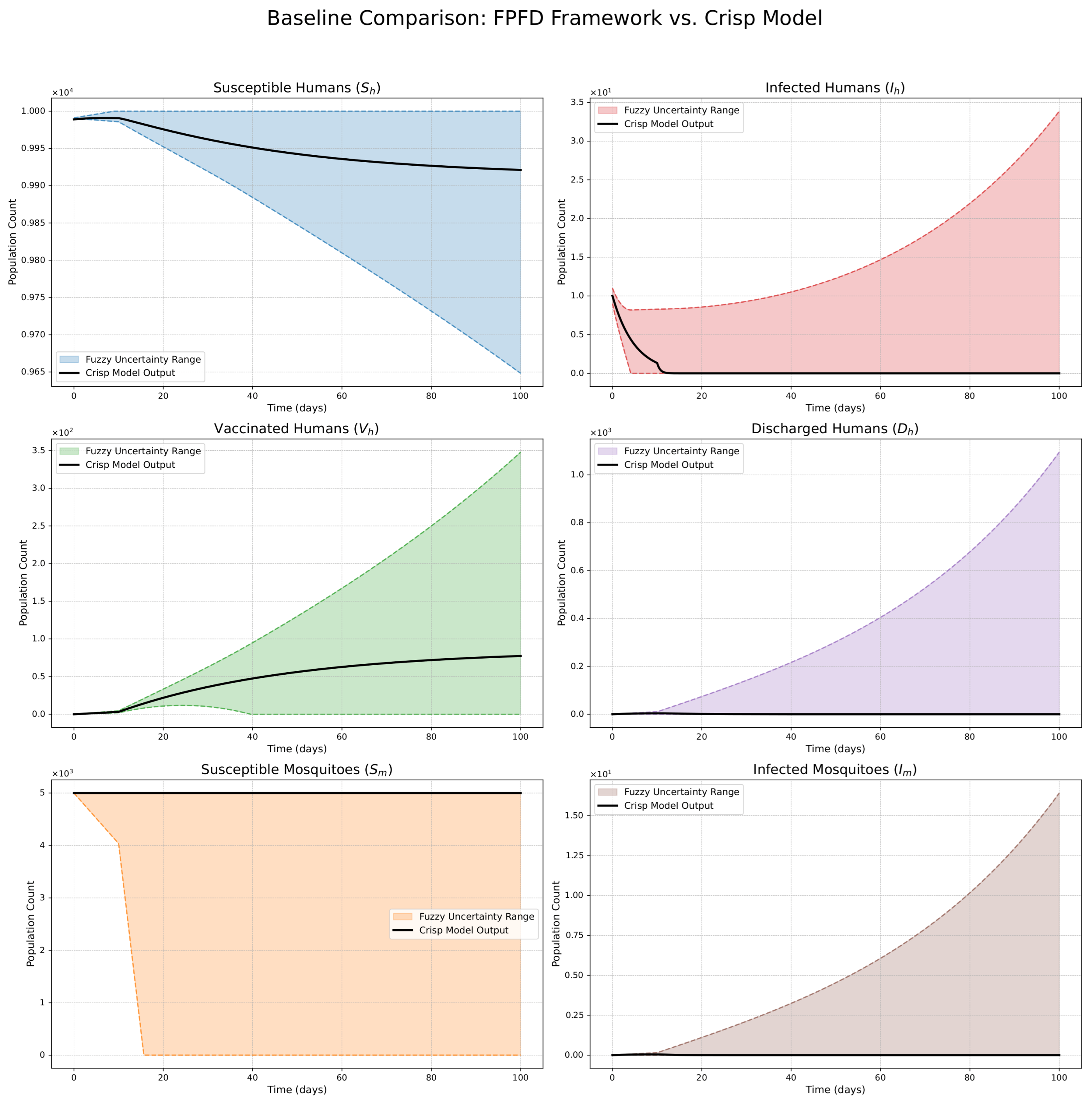
- The FPFD framework effectively models structural shifts in epidemic dynamics. The clear inflection points in the trajectories at the transition time demonstrate the model’s ability to switch from a memoryless (classical fuzzy) regime to a memory-dependent (ABC fuzzy fractional) regime. This allows for a more realistic representation of how interventions can fundamentally alter the course of an outbreak.
- The fractional order is a critical determinant of epidemic “personality”. The simulations conclusively show that acts as a powerful modulator of system memory, with direct biological interpretations:
- Low (strong memory), as shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, results in a protracted, “smoldering” epidemic. The system exhibits high inertia, where interventions are slow to take effect, and the disease persists over a long duration. The associated uncertainty bands consistently widen, signifying that long-term forecasting in such systems is inherently less certain.
- High (weak memory), as shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, produces a fast-moving epidemic characterized by a sharp incidence peak, followed by a rapid response to intervention and convergence to a stable endemic equilibrium. The uncertainty remains bounded and narrow, indicating a more predictable system.
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- 1.
- (Non-negativity).
- 2.
- (Identity).
- 3.
- (Symmetry).
- 4.
- (Property of addition).
- 5.
- (Property of scalar multiplication).
- 6.
- (Triangle inequality for addition).
Appendix B
| Model Feature | Simulation Result (Observed in Figures) | Real-Life Policy Implication |
|---|---|---|
| Piecewise Nature | Dynamics exhibit a clear structural shift at : a gradual trend reversal (Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6) vs. rapid convergence to a new equilibrium (Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12). | Context-Dependent Strategy: Allows for testing how policy timing and type perform in different dynamic contexts (e.g., slow vs. fast-burning outbreaks). |
| Fuzzy Uncertainty Bands | The uncertainty bands quantify outcome variability, widening with strong memory (Figure 1) but stabilizing with weak memory (Figure 7). | Enable Risk-Based Planning: The upper bound informs worst-case scenarios (hospital capacity). The band’s width indicates forecast confidence, guiding the need for adaptive vs. fixed strategies. |
| Strong Memory (Low = 0.20) | High system inertia is shown; an early intervention at fails to halt momentum, leading to a slow, accelerating resurgence post-intervention (Figure 1). | Justify Sustained Policies: Demonstrates that short-term actions are insufficient for diseases with high inertia (e.g., environmental persistence), necessitating long-term, continuous strategies. |
| Weak Memory (High ) | The system shows a rapid response; intervention at halts the outbreak and induces a stable, low-level endemic state (Figure 7). | Support Rapid, Decisive Action: Provides evidence that swift interventions are highly effective for controlling fast-moving epidemics and establishing predictable, long-term outcomes. |
References
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Springer: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Allen, L.J.; Brauer, F.; Van den Driessche, P.; Wu, J. Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008; Volume 1945. [Google Scholar]
- Siettos, C.I.; Russo, L. Mathematical modeling of infectious disease dynamics. Virulence 2013, 4, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, J.A.P. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation; John Wiley Sons: Hoboken, NJ, USA, 2000; Volume 5. [Google Scholar]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: New York, NY, USA, 2015; Volume 61, pp. 9–31. [Google Scholar]
- Ortiz-Barrios, M.; Petrillo, A.; Arias-Fonseca, S.; McClean, S.; de Felice, F.; Nugent, C.; Uribe-López, S.A. An AI-based multiphase framework for improving the mechanical ventilation availability in emergency departments during respiratory disease seasons: A case study. Int. J. Emerg. Med. 2024, 17, 45. [Google Scholar] [CrossRef] [PubMed]
- Barmpounakis, P.; Demiris, N. Multiphasic stochastic epidemic models. J. R. Stat. Soc. Ser. C Appl. Stat. 2025, 74, 491–505. [Google Scholar] [CrossRef]
- Vieira, L.C.; Costa, R.S.; Valério, D. An overview of mathematical modelling in cancer research: Fractional calculus as modelling tool. Fractal Fract. 2023, 7, 595. [Google Scholar] [CrossRef]
- Wang, J. Mathematical models for cholera dynamics—A review. Microorganisms 2022, 10, 2358. [Google Scholar] [CrossRef]
- Bendib, I.; Hammad, M.M.A.; Ouannas, A.; Grassi, G. The Discrete SIR Epidemic Reaction–Diffusion Model: Finite-Time Stability and Numerical Simulations. Comput. Math. Methods 2025, 2025, 9597093. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.İ. New concept in calculus: Piecewise differential and integral operators. Chaos Solitons Fractals 2021, 145, 110638. [Google Scholar] [CrossRef]
- Arık, İ.A.; Araz, S.İ. Crossover behaviors via piecewise concept: A model of tumor growth and its response to radiotherapy. Results Phys. 2022, 41, 105894. [Google Scholar] [CrossRef]
- Naik, P.A.; Farman, M.; Jamil, K.; Nisar, K.S.; Hashmi, M.A.; Huang, Z. Modeling and analysis using piecewise hybrid fractional operator in time scale measure for ebola virus epidemics under Mittag–Leffler kernel. Sci. Rep. 2024, 14, 24963. [Google Scholar] [CrossRef]
- Aldwoah, K.A.; Almalahi, M.A.; Shah, K.; Awadalla, M.; Egami, R.H. Dynamics analysis of dengue fever model with harmonic mean type under fractal-fractional derivative. AIMS Math. 2024, 9, 13894–13926. [Google Scholar] [CrossRef]
- Alraqad, T.; Almalahi, M.A.; Mohammed, N.; Alahmade, A.; Aldwoah, K.A.; Saber, H. Modeling Ebola dynamics with a Φ-piecewise hybrid fractional derivative approach. Fractal Fract. 2024, 8, 596. [Google Scholar] [CrossRef]
- Shah, K.; Khan, A.; Abdalla, B.; Abdeljawad, T.; Khan, K.A. A mathematical model for Nipah virus disease by using piecewise fractional order Caputo derivative. Fractals 2024, 32, 2440013. [Google Scholar] [CrossRef]
- Saleem, M.U.; Farman, M.; Nisar, K.S.; Ahmad, A.; Munir, Z.; Hincal, E. Investigation and application of a classical piecewise hybrid with a fractional derivative for the epidemic model: Dynamical transmission and modeling. PLoS ONE 2024, 19, e0307732. [Google Scholar] [CrossRef]
- Saber, H.; Almalahi, M.A.; Albala, H.; Aldwoah, K.; Alsulami, A.; Shah, K.; Moumen, A. Investigating a nonlinear fractional evolution control model using W-piecewise hybrid derivatives: An application of a breast cancer model. Fractal Fract. 2024, 8, 735. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Vasudevan, A.; Yogeesh, N.; Mohammad, S.I.; Raja, N.; Girija, D.K.; Rashmi, M.; Abu-Shareha, A.A.; Alshurideh, M.T. Unlocking Insights of Fuzzy Mathematics for Enhanced Predictive Modelling. Appl. Math. 2025, 19, 49–60. [Google Scholar]
- Bryniarska, A. Mathematical models of diagnostic information granules generated by scaling intuitionistic fuzzy sets. Appl. Sci. 2022, 12, 2597. [Google Scholar] [CrossRef]
- Bera, S.; Khajanchi, S.; Roy, T.K. Stability analysis of fuzzy HTLV-I infection model: A dynamic approach. J. Appl. Math. Comput. 2023, 69, 171–199. [Google Scholar] [CrossRef]
- Ejegwa, P.A.; Muhiuddin, G.; Algehyne, E.A.; Agbetayo, J.M.; Al-Kadi, D. An Enhanced Fermatean Fuzzy Composition Relation Based on a Maximum-Average Approach and Its Application in Diagnostic Analysis. J. Math. 2022, 2022, 1786221. [Google Scholar]
- Gul, R.; Ayub, S.; Shabir, M.; Hummdi, A.Y.; Aljaedi, A.; Bassfar, Z. A novel approach for fuzzification of rough sets based on fuzzy preference relation: Properties and application to medicine selection problem. IEEE Access 2024, 12, 67681–67703. [Google Scholar] [CrossRef]
- Ayub, S.; Gul, R.; Shabir, M.; Hummdi, A.Y.; Aljaedi, A.; Bassfar, Z. A novel approach to roughness of linear diophantine fuzzy sets by fuzzy relations and its application toward multi-criteria group decision-making. IEEE Access 2024, 12, 53549–53564. [Google Scholar] [CrossRef]
- Areshi, M.; El-Tantawy, S.A.; Alotaibi, B.M.; Zaland, S. Study of Fuzzy Fractional Third-Order Dispersive KdV Equation in a Plasma under Atangana-Baleanu Derivative. J. Funct. Spaces 2022, 2022, 7922001. [Google Scholar] [CrossRef]
- Boulaaras, S.; Rehman, Z.U.; Abdullah, F.A.; Jan, R.; Abdalla, M.; Jan, A. Coronavirus dynamics, infections and preventive interventions using fractional-calculus analysis. AIMS Math. 2023, 8, 8680–8701. [Google Scholar] [CrossRef]
- Aldwoah, K.A.; Almalahi, M.A.; Abdulwasaa, M.A.; Shah, K.; Kawale, S.V.; Awadalla, M.; Alahmadi, J. Mathematical analysis and numerical simulations of the piecewise dynamics model of Malaria transmission: A case study in Yemen. AIMS Math. 2024, 9, 4376–4408. [Google Scholar] [CrossRef]
- Subramanian, S.; Kumaran, A.; Ravichandran, S.; Venugopal, P.; Dhahri, S.; Ramasamy, K. Fuzzy fractional Caputo derivative of susceptible-infectious-removed epidemic model for childhood diseases. Mathematics 2024, 12, 466. [Google Scholar] [CrossRef]
- Qayyum, M.; Fatima, Q.; Akgül, A.; Hassani, M.K. Modeling and analysis of dengue transmission in fuzzy-fractional framework: A hybrid residual power series approach. Sci. Rep. 2024, 14, 30706. [Google Scholar] [CrossRef] [PubMed]
- Gassem, F.; Qurtam, A.A.; Almalahi, M.; Rabih, M.; Aldwoah, K.; El-Sayed, A.; Hassan, E.I. Exploring SEIR Influenza Epidemic Model via Fuzzy ABC Fractional Derivatives with Crowley–Martin Incidence Rate. Fractal Fract. 2025, 9, 402. [Google Scholar] [CrossRef]
- ul Rehman, A.; Singh, R.; Sharma, N.; Singh, J.; Baleanu, D. Optimal solution and sensitivity analysis of fractional-order mathematical modeling of the omicron variant and malaria co-infection. Alex. Eng. J. 2025, 116, 364–373. [Google Scholar] [CrossRef]
- Lefevr, N.; Kanavos, A.; Gerogiannis, V.C.; Iliadis, L.; Pintelas, P. Employing fuzzy logic to analyze the structure of complex biological and epidemic spreading models. Mathematics 2021, 9, 977. [Google Scholar] [CrossRef]
- Thangaraj, C.; Easwaramoorthy, D.; Muhiuddin, G.; Selmi, B.; Kulish, V. Fractal based automatic detection of complexity in COVID-19 X-ray images. Expert Syst. 2025, 42, e13497. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets A Basis A Theory possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Bede, B.; Stefanini, L. Generalized differentiability of fuzzy-valued functions. Fuzzy Sets Syst. 2013, 230, 119–141. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Salahshour, S.; Abbasbandy, S. Explicit solutions of fractional differential equations with uncertainty. Soft Comput. 2012, 16, 297–302. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Ghanbari, B. On the fuzzy fractional differential equation with interval Atangana–Baleanu fractional derivative approach. Chaos Solitons Fractals 2020, 130, 109397. [Google Scholar] [CrossRef]
- Cortez, M.V.; Althobaiti, A.; Aljohani, A.F.; Althobaiti, S. Generalized Fuzzy-Valued Convexity with Ostrowski’s, and Hermite-Hadamard Type Inequalities over Inclusion Relations and Their Applications. Axioms 2024, 13, 471. [Google Scholar] [CrossRef]
- Altaweel, N.H.; Rashid, M.H.; Albalawi, O.; Alshehri, M.G.; Eljaneid, N.H.; Albalawi, R. On the Ideal Convergent Sequences in Fuzzy Normed Space. Symmetry 2023, 15, 936. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Mahboob, A.; Al-Tahan, M.; Muhiuddin, G. Fuzzy (m, n)-filters based on fuzzy points in ordered semigroups. Comput. Appl. Math. 2023, 42, 245. [Google Scholar] [CrossRef]
- Muhiuddin, G.; Abughazalah, N.; Mahboob, A.; Al-Kadi, D. A Novel study of fuzzy bi-ideals in ordered semirings. Axioms 2023, 12, 626. [Google Scholar] [CrossRef]
- Muhiuddin, G.; Mahapatra, T.; Pal, M.; Alshahrani, O.; Mahboob, A. Integrity on m-polar fuzzy graphs and its application. Mathematics 2023, 11, 1398. [Google Scholar] [CrossRef]
- Alanazi, A.M.; Muhiuddin, G.; Alenazi, B.M.; Mahapatra, T.; Pal, M. Utilizing m-Polar Fuzzy Saturation Graphs for Optimized Allocation Problem Solutions. Mathematics 2023, 11, 4136. [Google Scholar] [CrossRef]
- Alanazi, A.M.; Muhiuddin, G.; Mahapatra, T.; Bassfar, Z.; Pal, M. Inverse Graphs in m-Polar Fuzzy Environments and Their Application in Robotics Manufacturing Allocation Problems with New Techniques of Resolvability. Symmetry 2023, 15, 1387. [Google Scholar] [CrossRef]



| Parameter | Biological Meaning | Value/Range | Unit |
|---|---|---|---|
| Human Population Dynamics | |||
| Recruitment rate of the human population. | 0.05 | day−1 | |
| Natural death rate of humans. | 0.039 | day−1 | |
| Disease-induced death rate for Omicron-infected humans. | 0.3 | day−1 | |
| Proportion of new arrivals who are vaccinated against Omicron. | 0.8 | Dimensionless | |
| Disease Transmission Dynamics | |||
| Transmission rate of Omicron from infected humans to susceptible humans. | 0.5 | (person·day)−1 | |
| Transmission rate of Malaria from infected humans to susceptible mosquitoes. | 0.85 | (mosquito·day)−1 | |
| Disease Progression and Recovery (Omicron) | |||
| Recovery rate of Omicron-infected humans. | 0.05 | day−1 | |
| Discharge rate of Omicron-infected humans (moving to the class). | 0.6 | day−1 | |
| Rate of waning immunity from Omicron vaccination. | 0.07 | day−1 | |
| Recovery rate for discharged individuals. | 0.17 | Dimensionless | |
| Disease-induced death rate for discharged individuals. | 0.25 | Dimensionless | |
| Mosquito (Vector) Population Dynamics | |||
| Recruitment rate of the vector population. | 4.0 | day−1 | |
| Natural death rate of mosquitoes. | 0.4 | day−1 | |
| Fuzzy Piecewise Operator Parameters | |||
| Central time of intervention (transition from classical to fractional). | 10, 30 | days | |
| Fractional order of the ABC derivative (controls system memory). | 0.2–0.95 | Dimensionless | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algolam, M.S.; Qurtam, A.A.; Almalahi, M.; Aldwoah, K.; Alqahtani, M.H.; Adam, A.; Ali, S.O. Hybrid Fuzzy Fractional for Multi-Phasic Epidemics: The Omicron–Malaria Case Study. Fractal Fract. 2025, 9, 643. https://doi.org/10.3390/fractalfract9100643
Algolam MS, Qurtam AA, Almalahi M, Aldwoah K, Alqahtani MH, Adam A, Ali SO. Hybrid Fuzzy Fractional for Multi-Phasic Epidemics: The Omicron–Malaria Case Study. Fractal and Fractional. 2025; 9(10):643. https://doi.org/10.3390/fractalfract9100643
Chicago/Turabian StyleAlgolam, Mohamed S., Ashraf A. Qurtam, Mohammed Almalahi, Khaled Aldwoah, Mesfer H. Alqahtani, Alawia Adam, and Salahedden Omer Ali. 2025. "Hybrid Fuzzy Fractional for Multi-Phasic Epidemics: The Omicron–Malaria Case Study" Fractal and Fractional 9, no. 10: 643. https://doi.org/10.3390/fractalfract9100643
APA StyleAlgolam, M. S., Qurtam, A. A., Almalahi, M., Aldwoah, K., Alqahtani, M. H., Adam, A., & Ali, S. O. (2025). Hybrid Fuzzy Fractional for Multi-Phasic Epidemics: The Omicron–Malaria Case Study. Fractal and Fractional, 9(10), 643. https://doi.org/10.3390/fractalfract9100643








