Stylized Facts of High-Frequency Bitcoin Time Series
Abstract
1. Introduction
2. Stylized Facts of Financial Markets
- Fractality: A fractal time series has dimension [35] and scaling of price return x and time t by . Here, x is a stochastic variable with time-dependent probability . Techniques such as DFA and MF-DFA estimate H and multifractal spectra [36,37]. Fractality is documented across many markets [10,37,38,39,40,41].
3. Mathematical Framework
- Definitions and notation: Let be a market index. The simple price return from to isIn predictive models, is the current time and is the time where the price return is estimated. To simplify the notation, we assume . We work with detrended returns. Here, a deterministic trend means a smooth, low-frequency component (e.g., a moving-average) removed before analysis; the remaining stochastic noises are the zero-mean fluctuations captured by the stochastic dynamics introduced below. We therefore do not define separate variables for trend and noise. Define the simple price return aswhere we take in Equation (1).
- Stochastic dynamics and FPE. The model by the Itô SDEwith a Wiener process. The PDF satisfies the Itô FPEFor detrended returns (),
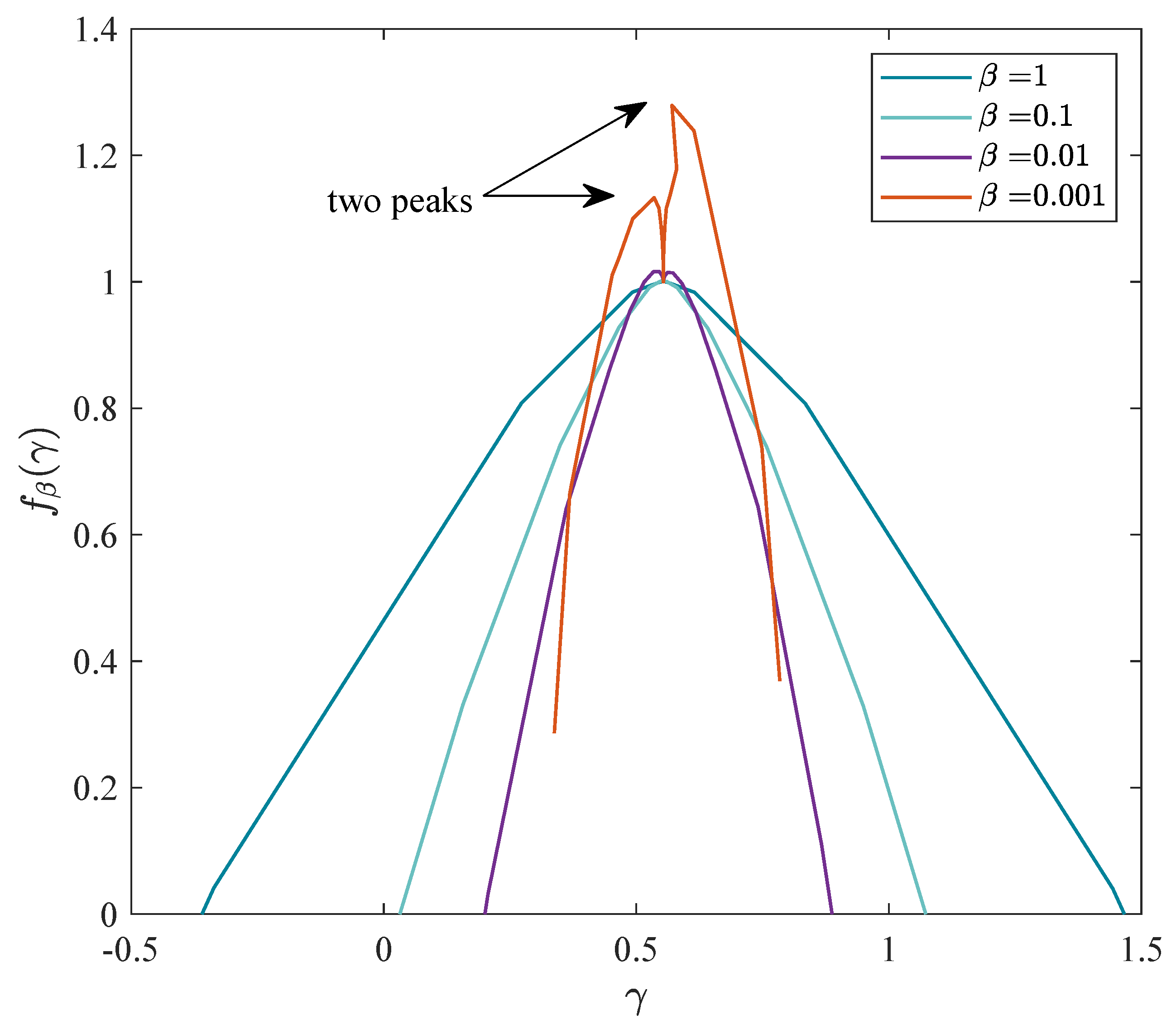
- Nonlinear diffusion (q-Gaussian solution). Empirical evidence suggests volatility depends on P [25]. A convenient closure is the following porous media form:whose solution for is a q-Gaussian (Tsallis distribution) [17,27]:with the q-Gaussian(For , tends to the Gaussian distribution).
- Fractional forms and equivalence: To capture the phenomenology of the stock markets, we must introduce a time stretch with [27]. Sincewe obtain the time-dependent-volatility FPEEquation (6) is equivalent to the local-fractional formwhich results from and (9). Empirical fitting of S&P500 price return shows that price return fluctuations fit well with non-local fractional operators such as Riemann–Liouville or Caputo [3]. The local operator is the first choice for simplicity.
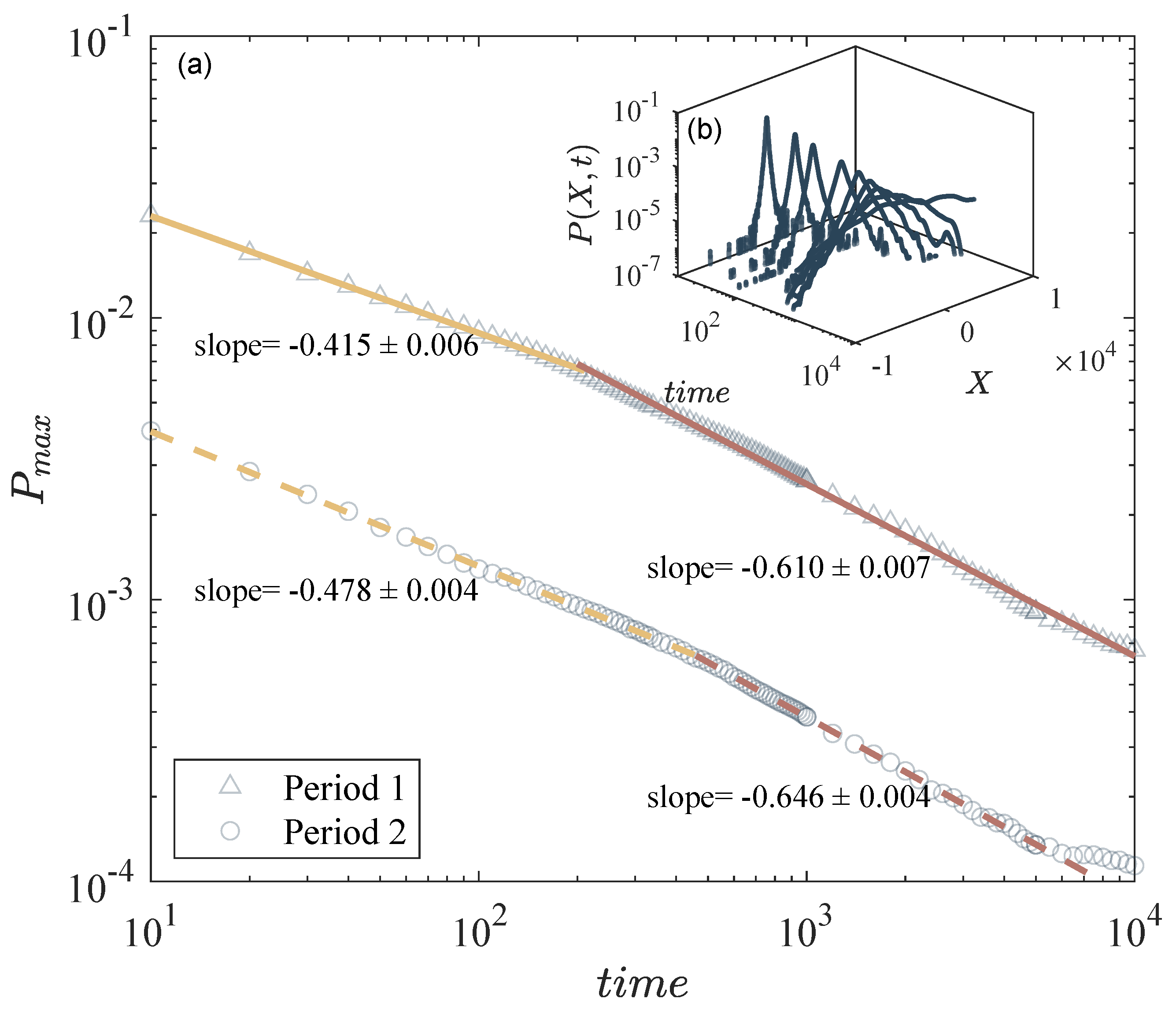
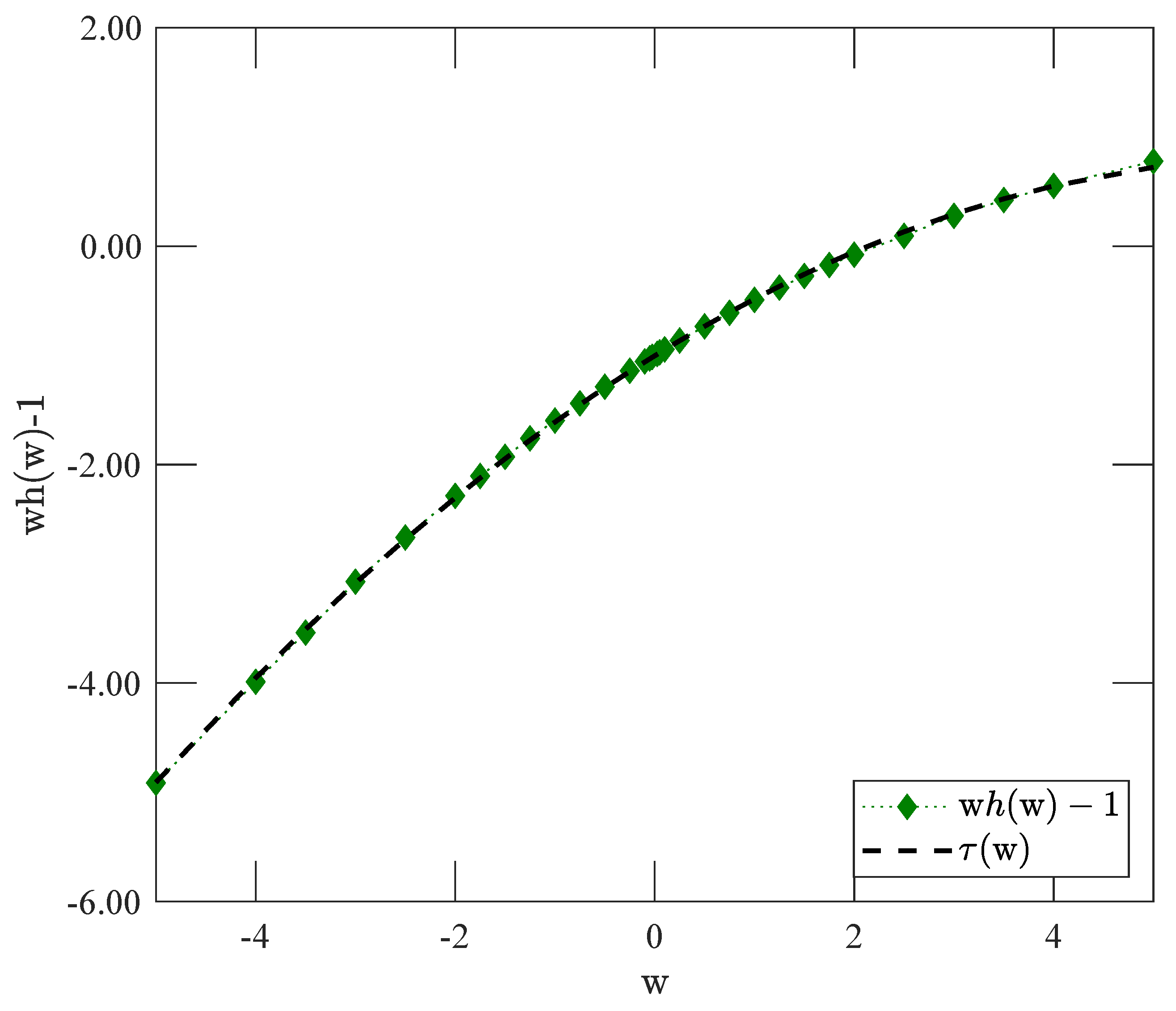
- Anomalous diffusion and PDF peak: If the PDF obeys the scaling ansatz [5]where and are obtained by replacing this anzatz in (13), resulting in . Then, the second moment is , soFor Gaussian diffusion, (). At , , hence with a symmetric peak at 0,The following hyperscaling relation is obtained for local operators [27].More general hyperscaling relations are derived using a non-local operator [3].
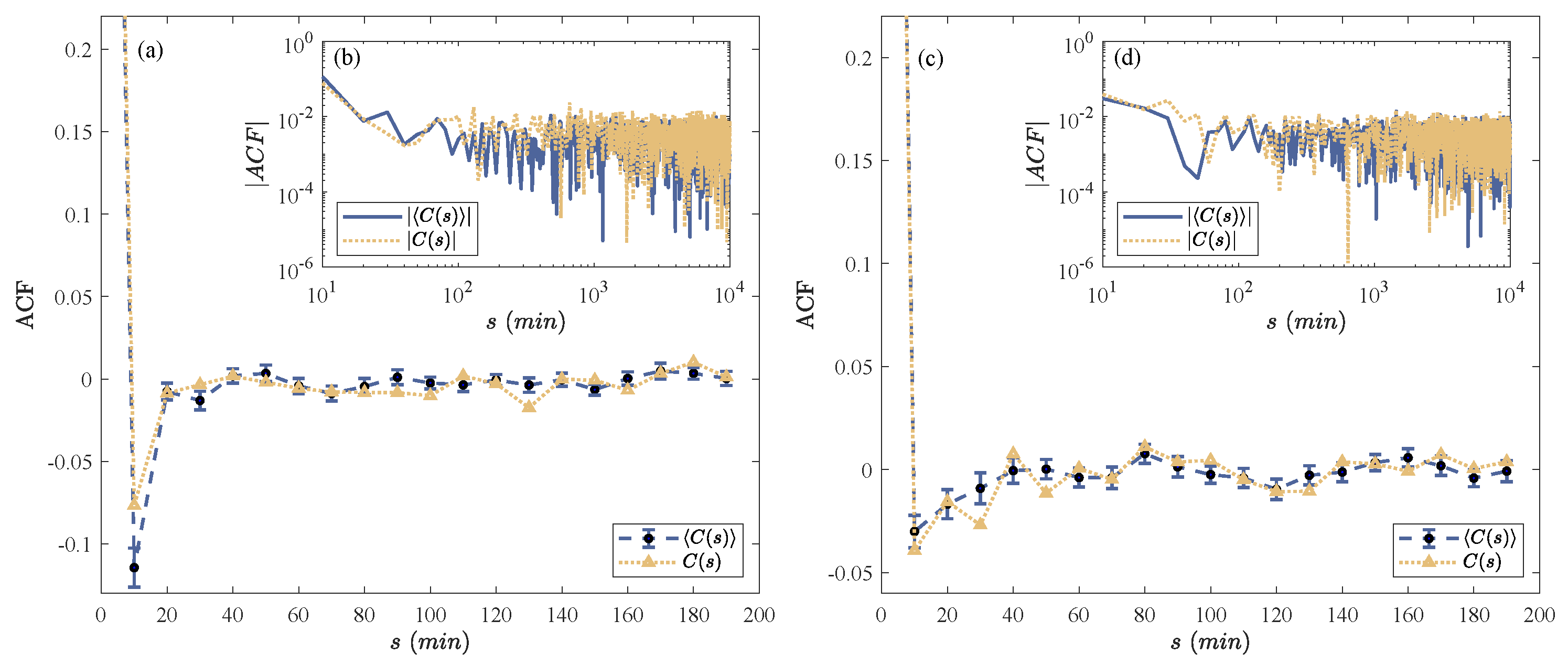
- Autocorrelation Function (ACF)—discrete time. Let be the detrended (zero-mean) return sampled every . If is weakly stationary, the autocovariance and autocorrelation depend only on the lagFor a finite sample , a mean-corrected estimator isIf the stationary marginals of are q-Gaussian, the classical autocorrelation is well-defined only when the variance is finite () [27,45,46,47]. Knowing only the marginals does not determine ; a dynamical model is required. In practice, is computed numerically from data using the estimator above [28].
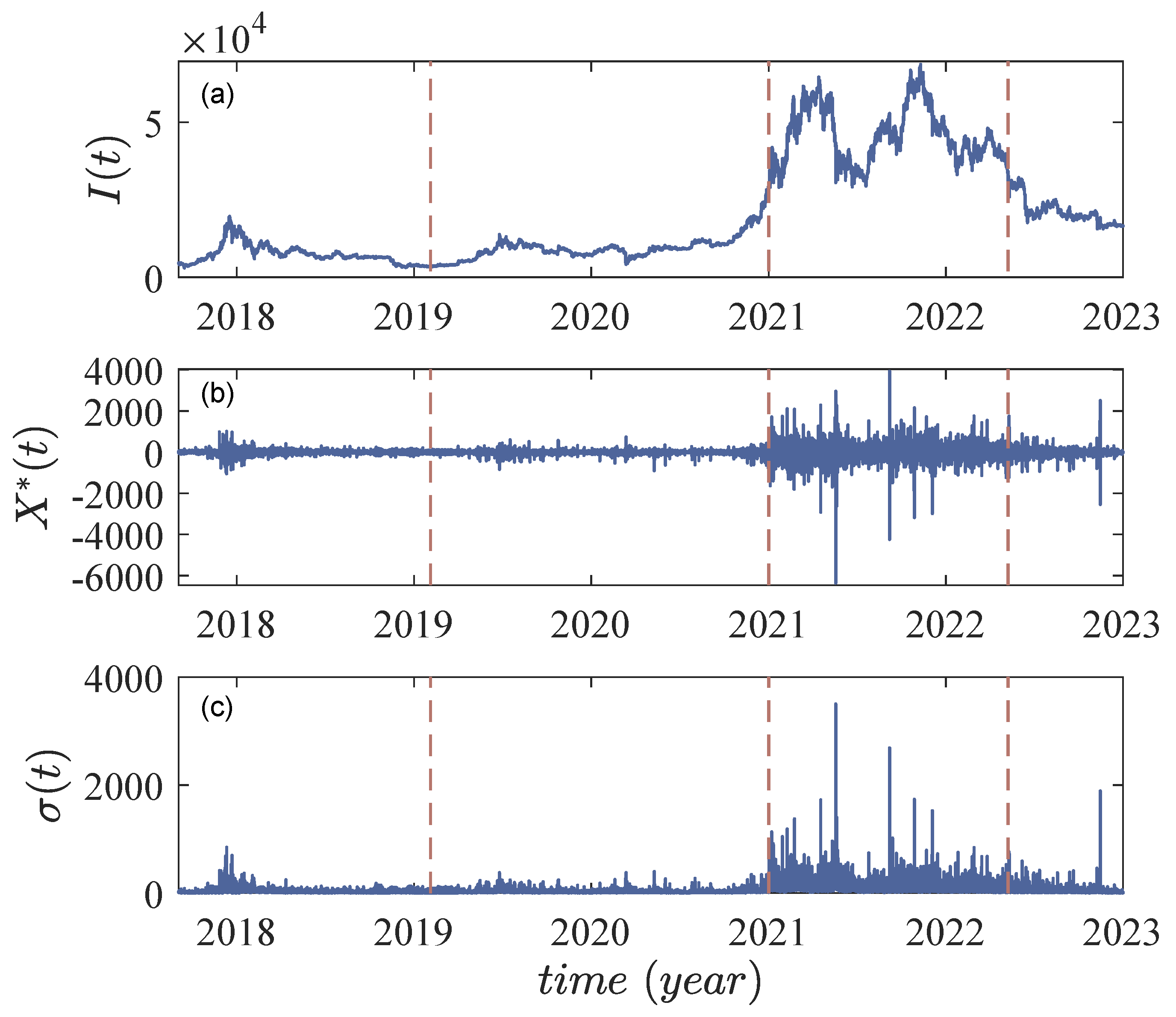
4. Stylized Facts of Bitcoin Market Index
4.1. Anomalous Diffusion and Fat-Tailed Distribution
4.2. Volatility Clustering
4.3. Self-Similarity of Detrended PDF of Price Return
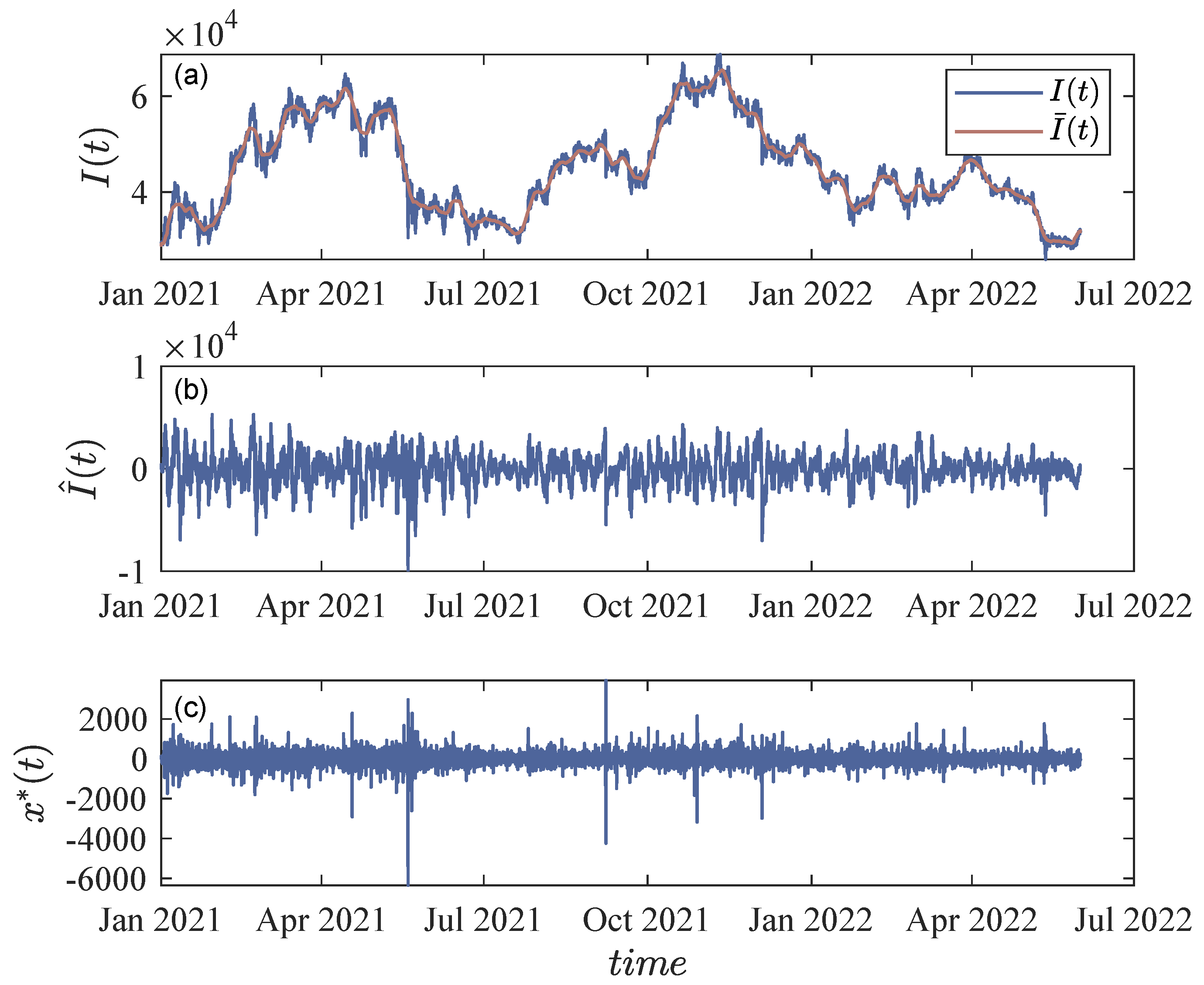
4.3.1. Detrending Time Series
- For
- For
- For
4.3.2. Self-Similarity in PDF of Detrended Price Return
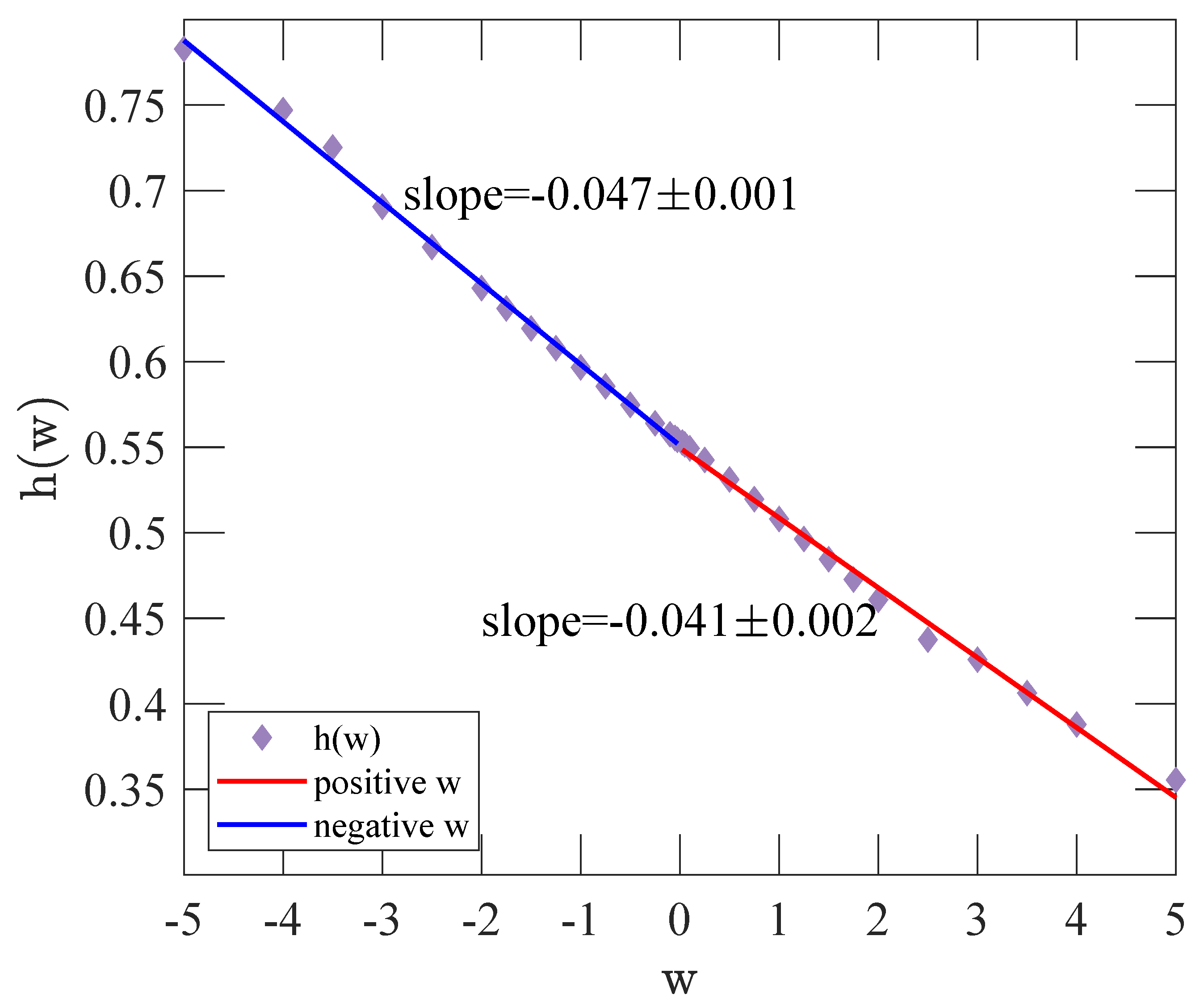
4.4. Scaling Analysis on the Fractality of Price Return
- Step 1: For the trended price return with length N, the process of the DFA starts with defining the ‘profile’ of the time series by calculating the mean-centered cumulative sum of the simple price return (X):where is the mean value of the time series.
- Step 2: Divide the profile into non-overlapping segments with the same length s. The number of segments is calculated as .
- Step 3: Calculate the local trend for each segment by a linear least-square fitting of the time series. Then the variance of each segment v from is calculated using the following equation:where is the mean of each segment of .
- Step 4: The statistical moments are calculated utilizing different values of order w:
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mandelbrot, B.B. Self-affine fractals and fractal dimension. Phys. Scr. 1985, 32, 257. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Gharari, F.; Arias-Calluari, K.; Alonso-Marroquin, F.; Najafi, M.N. Space-time fractional porous media equation: Application on modeling of S&P500 price return. Phys. Rev. E 2021, 104, 054140. [Google Scholar]
- Takaishi, T. Statistical properties and multifractality of Bitcoin. Phys. A Stat. Mech. Its Appl. 2018, 506, 507–519. [Google Scholar] [CrossRef]
- Tang, Y.; Gharari, F.; Arias-Calluari, K.; Alonso-Marroquin, F.; Najafi, M. Variable-order porous media equations: Application on modeling the S&P500 and Bitcoin price return. Phys. Rev. E 2024, 109, 024310. [Google Scholar]
- Corbet, S.; Lucey, B.; Urquhart, A.; Yarovaya, L. Cryptocurrencies as a financial asset: A systematic analysis. Int. Rev. Financ. Anal. 2019, 62, 182–199. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://nakamotoinstitute.org/library/bitcoin/ (accessed on 3 August 2023).
- Global Cryptocurrency Charts. 2023. Available online: https://coinmarketcap.com/charts/ (accessed on 3 August 2023).
- Stoyanov, S.V.; Rachev, S.T.; Racheva-Yotova, B.; Fabozzi, F.J. Fat-Tailed Models for Risk Estimation. J. Portf. Manag. 2011, 37, 107–117. [Google Scholar] [CrossRef]
- Chen, F.; Tian, K.; Ding, X.; Miao, Y.; Lu, C. Finite-size effect and the components of multifractality in transport economics volatility based on multifractal detrending moving average method. Phys. A Stat. Mech. Its Appl. 2016, 462, 1058–1066. [Google Scholar] [CrossRef]
- Scalas, E.; Gorenflo, R.; Luckock, H.; Mainardi, F.; Mantelli, M.; Raberto, M. Anomalous waiting times in high-frequency financial data. Quant. Financ. 2004, 4, 695–702. [Google Scholar] [CrossRef]
- Takaishi, T. Time-varying multifractality in Bitcoin volatility. PLoS ONE 2021, 16, e0261217. [Google Scholar] [CrossRef]
- Kakinaka, S.; Umeno, K. Cryptocurrency market efficiency in short- and long-term horizons during COVID-19: An asymmetric multifractal analysis approach. Financ. Res. Lett. 2022, 46, 102319. [Google Scholar] [CrossRef]
- Shrestha, K. Multifractal detrended fluctuation analysis of return on Bitcoin. Int. Rev. Financ. 2021, 21, 312–323. [Google Scholar] [CrossRef]
- Masoudi, M.; Ito, T. Complexity Analysis of Financial Time Series Using Multifractal and Entropy Measures. arXiv 2025, arXiv:2501.12345. [Google Scholar] [CrossRef]
- Kaldor, N.; Hague, D.C. Capital Accumulation and Economic Growth. In The Theory of Capital; International Economic Association Series; Palgrave Macmillan UK: London, UK, 1961; pp. 177–222. [Google Scholar]
- Arias-Calluari, K.; Alonso-Marroquin, F.; Najafi, M.N.; Harré, M. Methods for forecasting the effect of exogenous risks on stock markets. Phys. A Stat. Mech. Its Appl. 2021, 568, 125587. [Google Scholar] [CrossRef]
- Malmsten, H.; Teräsvirta, T. Stylized facts of financial time series and three popular models of volatility. Eur. J. Pure Appl. Math. 2010, 3, 443–477. [Google Scholar]
- Segnon, M.; Bekiros, S. Forecasting volatility in bitcoin market. Ann. Financ. 2020, 16, 435–462. [Google Scholar] [CrossRef]
- Bariviera, A.F.; Basgall, M.J.; Hasperué, W.; Naiouf, M. Some stylized facts of the Bitcoin market. Phys. A Stat. Mech. Its Appl. 2017, 484, 82–90. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Variation of Certain Speculative Prices. J. Bus. 1963, 36, 394. [Google Scholar] [CrossRef]
- Lèvy, P. Thèorie de lÀddition des Variables Alèatoires; Gauthier–Villars: Paris, France, 1937. [Google Scholar]
- Mantegna, R.N.; Stanley, H.E. Stochastic Process with Ultraslow Convergence to a Gaussian: The Truncated Lévy Flight. Phys. Rev. Lett. 1994, 73, 2946–2949. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Stanley, H.E. Introduction to Econophysics: Correlations and Complexity in Finance; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Borland, L. Microscopic dynamics of the nonlinear Fokker–Planck equation: A phenomenological model. Phys. Rev. E 1998, 57, 6634–6642. [Google Scholar] [CrossRef]
- Malamud, B. Tails of natural hazards. Phys. World 2003, 17, 31–35. [Google Scholar] [CrossRef]
- Alonso-Marroquin, F.; Arias-Calluari, K.; Harré, M.; Najafi, M.N.; Herrmann, H.J. Q-Gaussian diffusion in stock markets. Phys. Rev. E 2019, 99, 062313. [Google Scholar] [CrossRef] [PubMed]
- Beran, J. Statistics for Long-Memory Processes, 1st ed.; Taylor and Francis: London, UK, 2017. [Google Scholar]
- Lo, A.W. Long-Term Memory in Stock Market Prices. Econometrica 1991, 59, 1279–1313. [Google Scholar] [CrossRef]
- Ding, Z.; Granger, C.W.J.; Engle, R.F. A long memory property of stock market returns and a new model. J. Empir. Financ. 1993, 1, 83–106. [Google Scholar] [CrossRef]
- De Sousa Filho, F.N.M.; Silva, J.N.; Bertella, M.A.; Brigatti, E. The Leverage Effect and Other Stylized Facts Displayed by Bitcoin Returns. Braz. J. Phys. 2021, 51, 576–586. [Google Scholar] [CrossRef]
- Kumar, R. 2—Risk and return. In Valuation; Kumar, R., Ed.; Academic Press: San Diego, CA, USA, 2016; pp. 47–72. [Google Scholar] [CrossRef]
- De Silva, H.; McMurran, G.M.; Miller, M.N. 14 - Diversification and the Volatility Risk Premium. In Factor Investing; Jurczenko, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 365–387. [Google Scholar] [CrossRef]
- Ghosh, B.; Bouri, E.; Wee, J.B.; Zulfiqar, N. Return and volatility properties: Stylized facts from the universe of cryptocurrencies and NFTs. Res. Int. Bus. Financ. 2023, 65, 101945. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982; p. 495. [Google Scholar]
- Lahmiri, S.; Bekiros, S. Chaos, randomness and multi-fractality in Bitcoin market. Chaos Solitons Fractals 2018, 106, 28–34. [Google Scholar] [CrossRef]
- Gu, R.; Chen, H.; Wang, Y. Multifractal analysis on international crude oil markets based on the multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2010, 389, 2805–2815. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Park, J.H.; Chang, W. Asymmetric multi-fractality in the U.S. stock indices using index-based model of A-MFDFA. Chaos Solitons Fractals 2017, 97, 28–38. [Google Scholar] [CrossRef]
- Mali, P.; Mukhopadhyay, A. Multifractal characterization of gold market: A multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2014, 413, 361–372. [Google Scholar] [CrossRef]
- Wang, F.; Liao, G.; Li, J.; Li, X.; Zhou, T. Multifractal detrended fluctuation analysis for clustering structures of electricity price periods. Phys. A Stat. Mech. Its Appl. 2013, 392, 5723–5734. [Google Scholar] [CrossRef]
- Önalan, O. Self-similarity and multifractality in financial asset returns. In Proceedings of the 1st International Conference on Computational Finance and its Applications, Bologna, Italy, 21–23 April 2004; pp. 289–295. [Google Scholar]
- Bachelier, L. Théorie de la spéculation. Ann. Sci. De L’École Norm. Supérieure 1900, 17, 21–86. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Sposini, V.; Krapf, D.; Marinari, E.; Sunyer, R.; Ritort, F.; Taheri, F.; Selhuber-Unkel, C.; Benelli, R.; Weiss, M.; Metzler, R.; et al. Towards a robust criterion of anomalous diffusion. Commun. Phys. 2022, 5, 305. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Anteneodo, C.; Borland, L.; Osorio, R. Nonextensive statistical mechanics and economics. Phys. A Stat. Mech. Its Appl. 2003, 324, 89–100. [Google Scholar] [CrossRef]
- Queirós, S.M.D. On non-Gaussianity and dependence in financial time series: A nonextensive approach. Quant. Financ. 2005, 5, 475–487. [Google Scholar] [CrossRef]
- Panyagometh, K. The effect of COVID-19 and US monetary policy on Bitcoin and stock market volatility: An application of DCC-GARCH model. Humanit. Soc. Sci. Commun. 2024, 11, 1735. [Google Scholar] [CrossRef]
- Nguyen, K.Q. The correlation between the stock market and Bitcoin during COVID-19 and other uncertainty periods. Financ. Res. Lett. 2022, 46, 102284. [Google Scholar] [CrossRef] [PubMed]
- Wȩglarczyk, S. Kernel density estimation and its application. ITM Web Conf. 2018, 23, 00037. [Google Scholar] [CrossRef]
- McCauley, J.L. Time vs. ensemble averages for nonstationary time series. Phys. A Stat. Mech. Its Appl. 2008, 387, 5518–5522. [Google Scholar] [CrossRef][Green Version]
- Lahiri, A. Chapter 7—Optical Coherence: Statistical Optics. In Basic Optics; Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 605–696. [Google Scholar][Green Version]
- Bassler, K.E.; McCauley, J.L.; Gunaratne, G.H. Nonstationary increments, scaling distributions, and variable diffusion processes in financial markets. Proc. Natl. Acad. Sci. USA 2007, 104, 17287–17290. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Arias-Calluari, K.; Najafi, M.N.; Harré, M.S.; Tang, Y.; Alonso-Marroquin, F. Testing stationarity of the detrended price return in stock markets. Phys. A Stat. Mech. Its Appl. 2022, 587, 126487. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, P.; Li, X.; Shen, D. Some stylized facts of the cryptocurrency market. Appl. Econ. 2018, 50, 5950–5965. [Google Scholar] [CrossRef]
- Karaa, R.; Slim, S.; Goodell, J.W.; Goyal, A.; Kallinterakis, V. Do investors feedback trade in the Bitcoin—and why? Eur. J. Financ. 2021, 30, 1951–1971. [Google Scholar] [CrossRef]
- Jiang, Y.; Nie, H.; Ruan, W. Time-varying long-term memory in Bitcoin market. Financ. Res. Lett. 2018, 25, 280–284. [Google Scholar] [CrossRef]




| Stylized Fact | Equation | BTC 1 | BTC 2 | S&P500 1 | S&P500 2 |
|---|---|---|---|---|---|
| Fat-tailed Distribution | N/A | ||||
| Anomalous Diffusion (Short time-intervals) | |||||
| q-Gaussian Diffusion | |||||
| Volatility Clustering | N/A | N/A | |||
| Multiscaling Analysis | N/A | ||||
| Fractional derivative |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Arias-Calluari, K.; Najafi, M.N.; Harré, M.S.; Alonso-Marroquin, F. Stylized Facts of High-Frequency Bitcoin Time Series. Fractal Fract. 2025, 9, 635. https://doi.org/10.3390/fractalfract9100635
Tang Y, Arias-Calluari K, Najafi MN, Harré MS, Alonso-Marroquin F. Stylized Facts of High-Frequency Bitcoin Time Series. Fractal and Fractional. 2025; 9(10):635. https://doi.org/10.3390/fractalfract9100635
Chicago/Turabian StyleTang, Yaoyue, Karina Arias-Calluari, Morteza Nattagh Najafi, Michael S. Harré, and Fernando Alonso-Marroquin. 2025. "Stylized Facts of High-Frequency Bitcoin Time Series" Fractal and Fractional 9, no. 10: 635. https://doi.org/10.3390/fractalfract9100635
APA StyleTang, Y., Arias-Calluari, K., Najafi, M. N., Harré, M. S., & Alonso-Marroquin, F. (2025). Stylized Facts of High-Frequency Bitcoin Time Series. Fractal and Fractional, 9(10), 635. https://doi.org/10.3390/fractalfract9100635






