On Computation of Prefactor of Free Boundary in One Dimensional One-Phase Fractional Stefan Problems
Abstract
1. Introduction
2. Modeling the Space and Time Fractional Stefan Problems in a Melting Process
3. The Dimensionless Problems
- 1.
- .
- 2.
- .
- 3.
- .
3.1. The Dimensionless Spacial Fractional Stefan Problem
3.2. The Dimensionless Time Fractional Stefan Problem
4. Computing the Prefactor for the Space Fractional Case
4.1. Closed Solutions
- 1.
- is a non-negative function such that .
- 2.
- The following limits hold:
- 3.
- The function given by is a decreasing function.
4.2. Computing
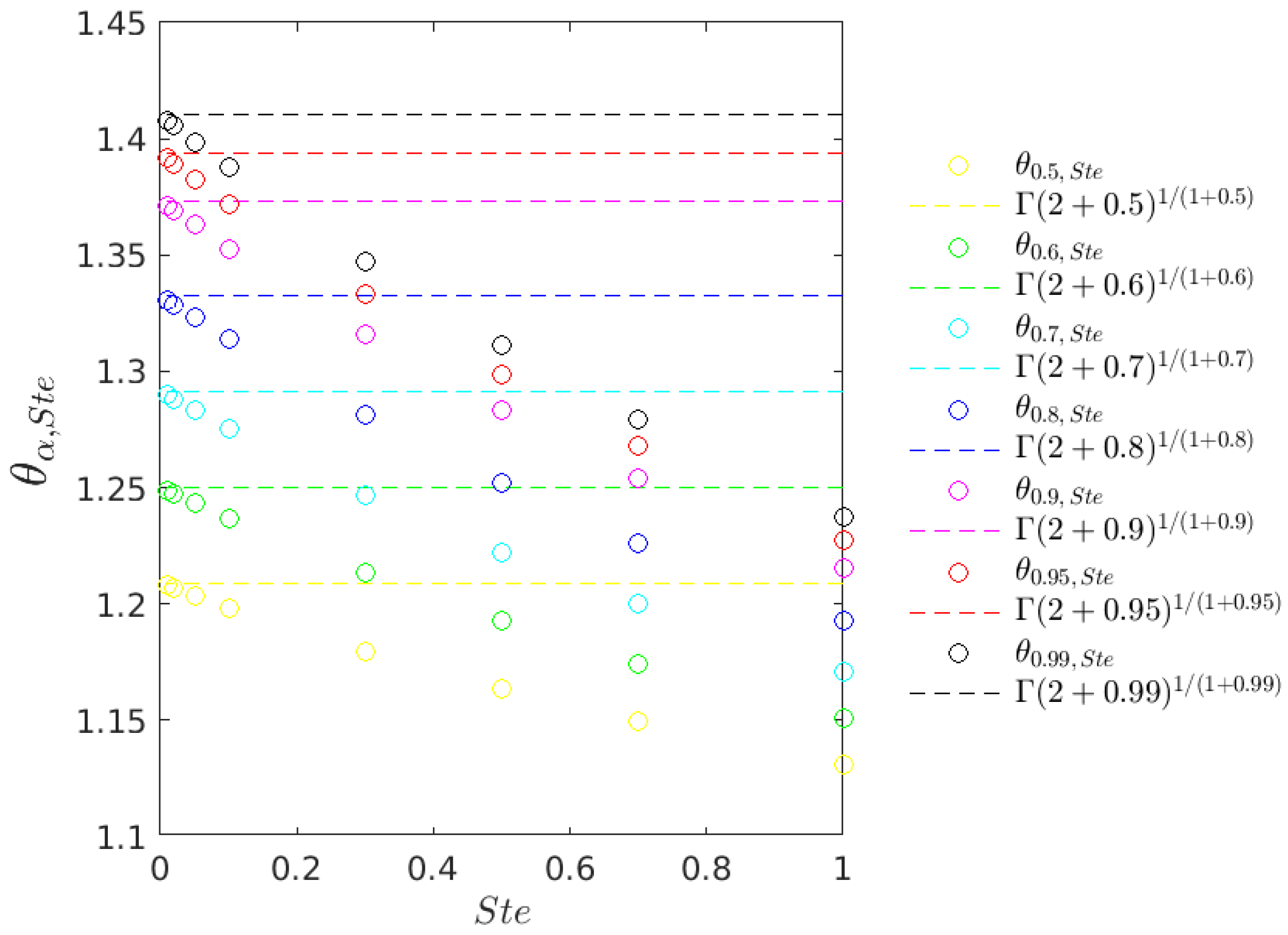
4.3. Analysis of the Convergence to the Quasi-Stationary Case
5. Computing the Parameter for the Time Fractional Case
5.1. Close Solutions
5.2. Computing
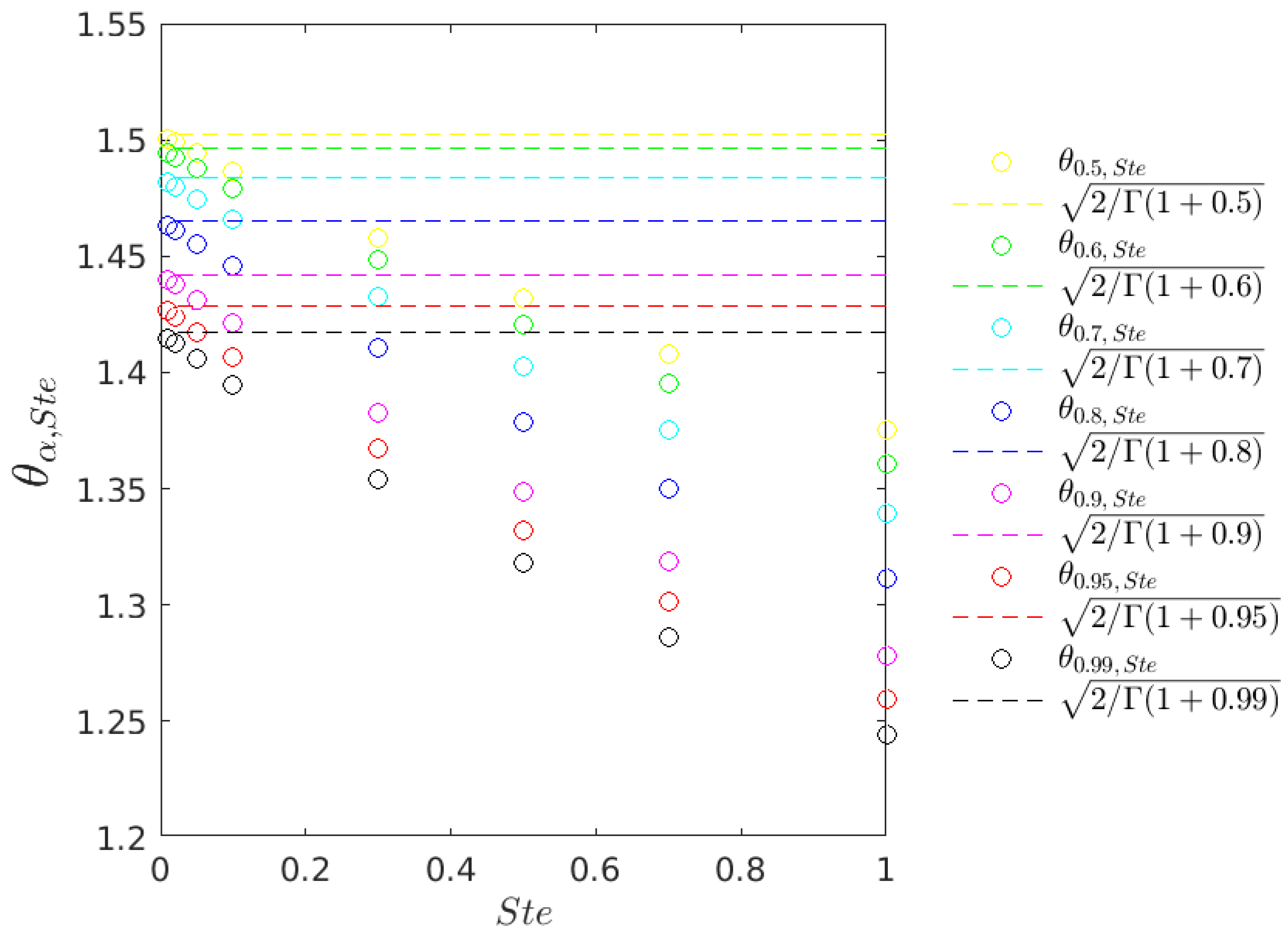
5.3. Analysis of the Convergence to the Quasi-Stationary Case
6. Physical Interpretations
6.1. Integer Case
6.2. Space Fractional Derivative
6.3. Time Fractional Derivative
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tarzia, D.A. A bibliography on moving–free boundary problems for the heat diffusion equation. The Stefan and related problems. MAT—Ser. A 2000, 2, 1–297. [Google Scholar] [CrossRef]
- Alexiades, V.; Solomon, A.D. Mathematical Modelling of Melting and Freezing Processes; Hemisphere: Taylor and Francis: Washington, DC, USA, 1993. [Google Scholar]
- Meirmanov, A. The Stefan Problem; Walter de Gruyter: Berlin, Germany, 1992. [Google Scholar]
- Solomon, A.D. An easily computable solution to a two-phase Stefan problem. J. Sol. Energy 1979, 23, 525–528. [Google Scholar] [CrossRef]
- Zhmakin, A.I. Non-Fourier Heat Conduction. From Phase-Lag Models to Relativistic and Quantum Transport; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Benenti, G.; Donadio, D.; Lepri, S.; Livi, R. Non-Fourier heat transport in nanosystems. Riv. Nuovo Cimento 2023, 46, 105–161. [Google Scholar] [CrossRef]
- Brociek, R.; Słota, D.; Król, M.; Matula, G.; Kwaśny, W. Modeling of Heat Distribution in Porous Aluminum Using Fractional Differential Equation. Fractal Fract. 2017, 1, 17. [Google Scholar] [CrossRef]
- Failla, G.; Zingales, M. Advanced materials modelling via fractional calculus: Challenges and perspectives. Philos. Trans. A Math. Phys. Eng. Sci. 2020, 378, 20200050. [Google Scholar] [CrossRef]
- Feng, Y.; Goree, J.; Liu, B. Identifying anomalous diffusion and melting in dusty plasmas. Phys. Rev. E 2010, 82, 036403. [Google Scholar] [CrossRef]
- Schwarzwälder, M.C.; Myers, T.G.; Hennessy, M.G. The one-dimensional Stefan problem with non-Fourier heat conduction. Int. J. Therm. Sci. 2020, 150, 106210. [Google Scholar] [CrossRef]
- Arya, R.K.; Thapliyal, D.; Sharma, J.; Verros, G.D. Glassy Polymers—Diffusion, Sorption, Ageing and Applications. Coatings 2011, 11, 1049. [Google Scholar] [CrossRef]
- Kukhtetskiy, S.V.; Fomenko, E.V.; Anshits, A.G. Anomalous Diffusion of Helium and Neon in Low-Density Silica Glass. Membranes 2023, 13, 754. [Google Scholar] [CrossRef]
- Eliazar, I.; Klafter, J. Anomalous is ubiquitous. Ann. Phys. 2011, 326, 2517–2531. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rev. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Voller, V.R. Anomalous heat transfer: Examples, fundamentals, and fractional calculus models. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 2018; Volume 50, pp. 333–380. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Company: London, UK, 2000. [Google Scholar]
- Jin, B. Fractional Differential Equations; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Kumar, D.; Singh, J. Fractional Calculus in Medical and Health Science, 1st ed.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Vol. 198 of Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives—Theory and Applications; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Roscani, S.; Voller, V. On an enthalpy formulation for a sharp-interface memory-flux Stefan problem. Chaos Solitons Fractals 2024, 181, 114679. [Google Scholar] [CrossRef]
- Voller, V.R. Fractional Stefan problems. Int. J. Heat Mass Tran. 2014, 74, 269–277. [Google Scholar] [CrossRef]
- Błasik, M.; Klimek, M. Numerical solution of the one phase 1D fractional Stefan problem using the front fixing method. Math. Method Appl. Sci. 2015, 38, 3214–3228. [Google Scholar] [CrossRef]
- Garshasbi, M.; Sanaei, F. Studying a time-fractional moving boundary diffusion model of solvent through a glassy polymer: A computational approach. Int. J. Numer. Model. 2024, 37, e3181. [Google Scholar] [CrossRef]
- Gruber, C.A.; Vogl, C.J.; Miksis, M.J.; Davis, S.H. Anomalous diffusion models in the presence of a moving interface. Interfaces Free Bound 2023, 15, 181–202. [Google Scholar] [CrossRef]
- Kang, J.; Zhou, F.; Xia, T.; Ye, G. Numerical modeling and experimental validation of anomalous time and space subdiffusion for gas transport in porous coal matrix. Int. J. Heat Mass Tran. 2016, 100, 747–757. [Google Scholar] [CrossRef]
- Liu, J.; Xu, M. Some exact solutions to Stefan problems with fractional differential equations. J. Math. Anal. Appl. 2009, 351, 536–542. [Google Scholar] [CrossRef]
- Roscani, S.; Tarzia, D.; Venturato, L. The similarity method and explicit solutions for the fractional space one-phase Stefan problems. Fract. Calc. Appl. Anal. 2022, 25, 995–1021. [Google Scholar] [CrossRef]
- Bertsch, M.; Klaver, M. The Stefan problem with mushy regions: Differentiability of the interfaces. Ann. Mat. Pura Appl. 1994, 166, 27–61. [Google Scholar] [CrossRef]
- Ughi, M. A Melting Problem with a Mushy Region: Qualitative Properties. IMA J. Appl. Math. 1984, 33, 135–152. [Google Scholar] [CrossRef]
- Voller, V.R.; Cross, M.; Markatos, N.C. An enthalpy method for convection/diffusion phase change. Int. J. Numer. Methods Eng. 1987, 24, 271–284. [Google Scholar] [CrossRef]
- Kubica, A.; Ryszewska, K. A self-similar solution to time-fractional Stefan problem. Math. Methods Appl. Sci. 2021, 44, 4245–4275. [Google Scholar] [CrossRef]
- Roscani, S.; Caruso, N.; Tarzia, D. Explicit solutions to fractional Stefan-like problems for Caputo and Riemann–Liouville derivatives. Commun. Nonlinear. Sci. Numer. Simul. 2020, 90, 105361. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M. On Mittag-Leffler type function, fractional calculus operators and solutions of integral equations. Integral Transform. Spec. Funct. 1996, 4, 355–370. [Google Scholar] [CrossRef]
- Caruso, N.; Roscani, S.; Venturato, L. carusonahuel/FractionalStefanProblems_Computing_prefactors: Computing prefactors (v1.0.0). Zenodo 2025. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Choi, J. Zeta and q-Zeta Functions and Associated Series and Integrals; Elsevier: London, UK, 2012. [Google Scholar]
| Symbol | Definition | Dimension |
|---|---|---|
| u | Temperature | [K] |
| x | Spatial position | [L] |
| t | time | [T] |
| k | thermal conductivity | |
| mass density | ||
| c | specific heat | |
| diffusion coefficient | ||
| ℓ | latent heat per unit mass | |
| Stefan number | [-] |
| Ste | 1.00 | 0.70 | 0.50 | 0.30 | 0.10 | 0.05 | 0.02 | 0.01 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| α | ||||||||||
| 0.50 | 1.1311 | 1.1493 | 1.1635 | 1.1797 | 1.1984 | 1.2036 | 1.2068 | 1.2079 | 1.2090 | |
| 0.60 | 1.1508 | 1.1744 | 1.1926 | 1.2132 | 1.2370 | 1.2435 | 1.2475 | 1.2489 | 1.2503 | |
| 0.70 | 1.1711 | 1.2000 | 1.2221 | 1.2470 | 1.2755 | 1.2833 | 1.2882 | 1.2898 | 1.2915 | |
| 0.80 | 1.1926 | 1.2264 | 1.2522 | 1.2811 | 1.3141 | 1.3231 | 1.3287 | 1.3306 | 1.3325 | |
| 0.90 | 1.2155 | 1.2539 | 1.2830 | 1.3157 | 1.3528 | 1.3629 | 1.3692 | 1.3713 | 1.3734 | |
| 0.95 | 1.2276 | 1.2681 | 1.2987 | 1.3331 | 1.3721 | 1.3828 | 1.3894 | 1.3916 | 1.3938 | |
| 0.99 | 1.2376 | 1.2796 | 1.3114 | 1.3471 | 1.3876 | 1.3987 | 1.4055 | 1.4078 | 1.4101 | |
| Ste | 1.00 | 0.70 | 0.50 | 0.30 | 0.10 | 0.05 | 0.02 | 0.01 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| α | ||||||||||
| 0.50 | 1.3751 | 1.4077 | 1.4318 | 1.4580 | 1.4867 | 1.4944 | 1.4991 | 1.5007 | 1.5023 | |
| 0.60 | 1.3606 | 1.3951 | 1.4206 | 1.4485 | 1.4794 | 1.4876 | 1.4927 | 1.4944 | 1.4961 | |
| 0.70 | 1.3391 | 1.3755 | 1.4026 | 1.4324 | 1.4656 | 1.4744 | 1.4799 | 1.4818 | 1.4836 | |
| 0.80 | 1.3114 | 1.3498 | 1.3786 | 1.4103 | 1.4459 | 1.4555 | 1.4614 | 1.4634 | 1.4654 | |
| 0.90 | 1.2782 | 1.3186 | 1.3490 | 1.3829 | 1.4210 | 1.4313 | 1.4377 | 1.4399 | 1.4421 | |
| 0.95 | 1.2598 | 1.3011 | 1.3324 | 1.3673 | 1.4068 | 1.4175 | 1.4242 | 1.4264 | 1.4287 | |
| 0.99 | 1.2441 | 1.2863 | 1.3183 | 1.3540 | 1.3946 | 1.4057 | 1.4125 | 1.4149 | 1.4172 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caruso, N.; Roscani, S.; Venturato, L.; Voller, V. On Computation of Prefactor of Free Boundary in One Dimensional One-Phase Fractional Stefan Problems. Fractal Fract. 2025, 9, 397. https://doi.org/10.3390/fractalfract9070397
Caruso N, Roscani S, Venturato L, Voller V. On Computation of Prefactor of Free Boundary in One Dimensional One-Phase Fractional Stefan Problems. Fractal and Fractional. 2025; 9(7):397. https://doi.org/10.3390/fractalfract9070397
Chicago/Turabian StyleCaruso, Nahuel, Sabrina Roscani, Lucas Venturato, and Vaughan Voller. 2025. "On Computation of Prefactor of Free Boundary in One Dimensional One-Phase Fractional Stefan Problems" Fractal and Fractional 9, no. 7: 397. https://doi.org/10.3390/fractalfract9070397
APA StyleCaruso, N., Roscani, S., Venturato, L., & Voller, V. (2025). On Computation of Prefactor of Free Boundary in One Dimensional One-Phase Fractional Stefan Problems. Fractal and Fractional, 9(7), 397. https://doi.org/10.3390/fractalfract9070397







