Iterated Relation Systems on Riemannian Manifolds
Abstract
1. Introduction
2. Statement of Main Results
- (a)
- There exists an integer such that for any and any ,
- (b)
- For any , if , we require that the following conditions are satisfied:
- (i)
- can be decomposed as a finite family of contractions , where , and can be decomposed as a finite family of contractions , where .
- (ii)
- There exists a good partition on with respect to some finite family of contractions decomposed from (not necessarily the one in ).
- (a)
- , where α is the unique real number such that .
- (b)
- In particular, let be a minimal simplified GIFS associated with G and assume that consists of contractive similitudes . Suppose that . If satisfies (OSC), then is the unique number α satisfyingwhere is the contraction ratio of .
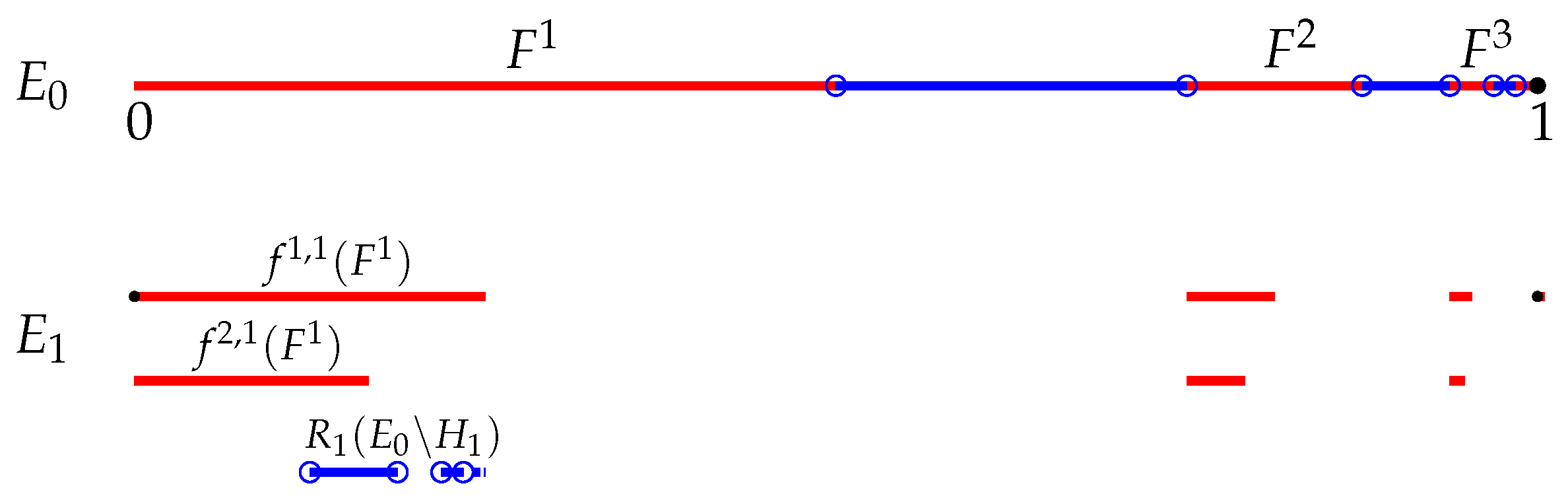
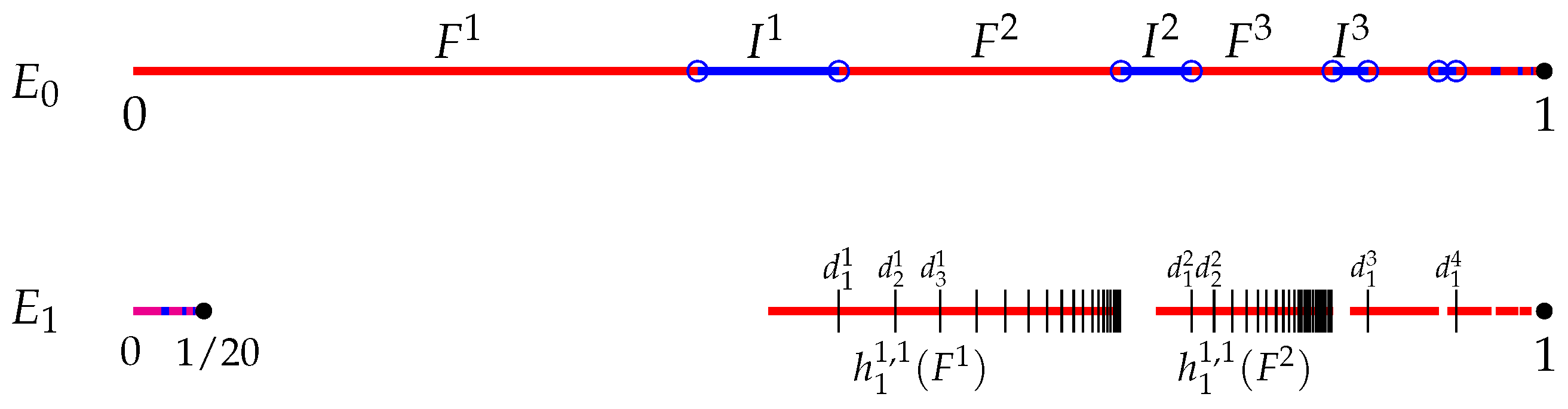
3. Iterated Relation Systems
- (a)
- for any nonempty compact set and , is a nonempty compact set;
- (b)
- for any , .
- (C)
- For any , if there exist some , a subsequence of , and satisfying for all , then there exists a subsequence of converging to some satisfying .
- (a)
- .
- (b)
- If Condition (C) holds, then , and thus (1) holds.
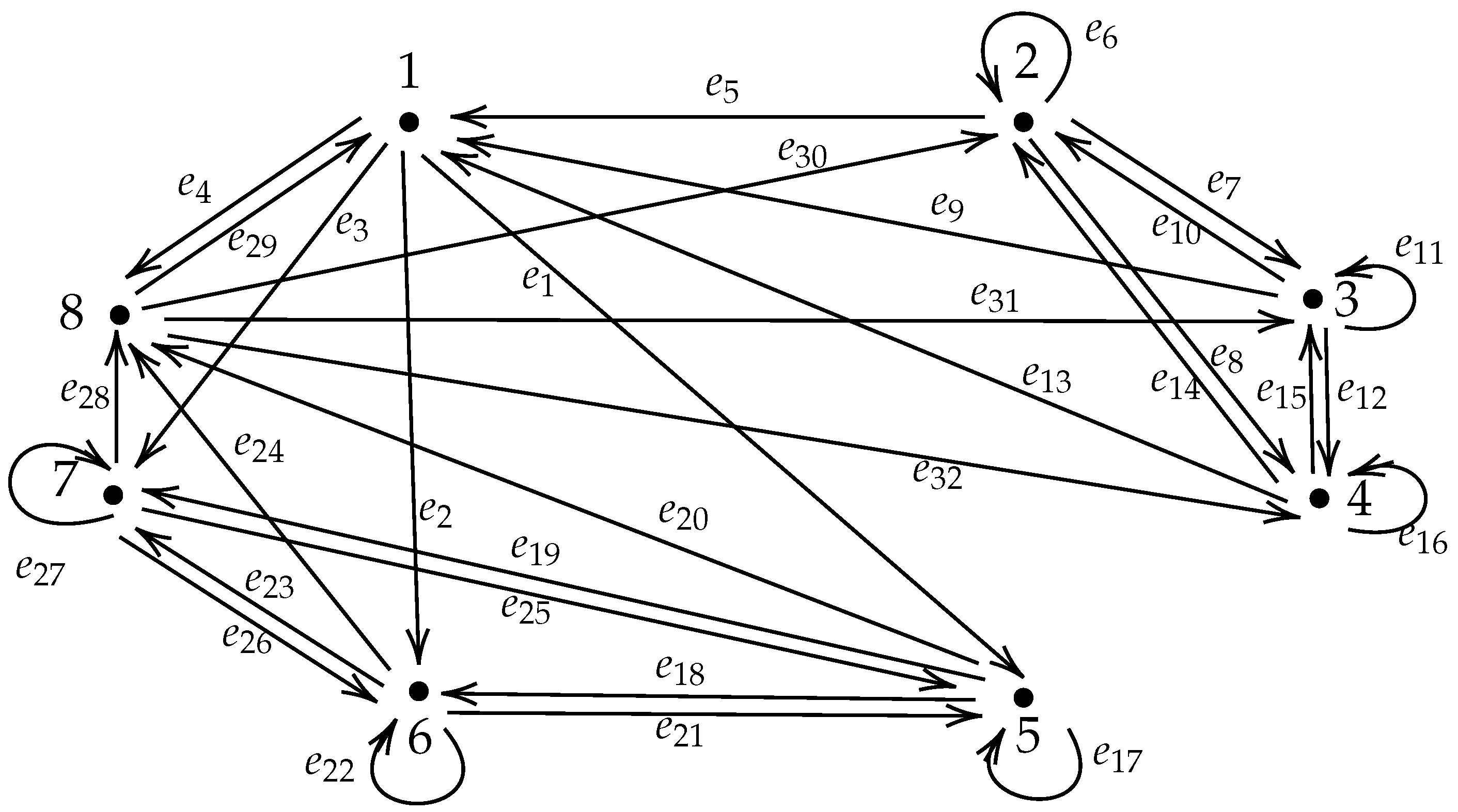
4. Associated Graph-Directed Iterated Function Systems
- (a)
- Assume that conditions (i) and (ii) below hold.
- (i)
- For any and ,
- (ii)
- For any , there exists such that for each and , there exists a contraction , and the following holds
Then we say that is a finite family of contractions decomposed from and that each is a branch of . - (b)
- Let be a collection of compact subsets of satisfyingLet be a finite family of contractions decomposed from and composed of all the branches of . Fix . Assume that for any and , is invariant under for all . Then we call a good partition of with respect to .
- (1)
- , where and .
- (2)
- , where and .
- (3)
- is invariant under , and is invariant under , where .
- (a)
- There exists an integer such that for any and any ,
- (b)
- For any , if , we require that the following conditions are satisfied.
- (i)
- can be decomposed as a finite family of contractions , where , and can be decomposed as a finite family of contractions , where .
- (ii)
- There exist or such that for any and any ,and for any ,
- (a)
- , where and ;
- (b)
- , where and .
- (a)
- and , where .
- (b)
- Let be contractions associated with , and let be an invariant family under . Then for any ,
5. Hausdorff Dimension of Graph Self-Similar Sets Without Overlaps
- (a)
- ;
- (b)
- , for all distinct and .
6. Hausdorff Dimension of Graph Self-Similar Sets with Overlaps
6.1. Graph Finite Type Condition
- (a)
- In (29), .
- (b)
- For and satisfying , and for any integer , a directed path satisfies if and only if it satisfies .
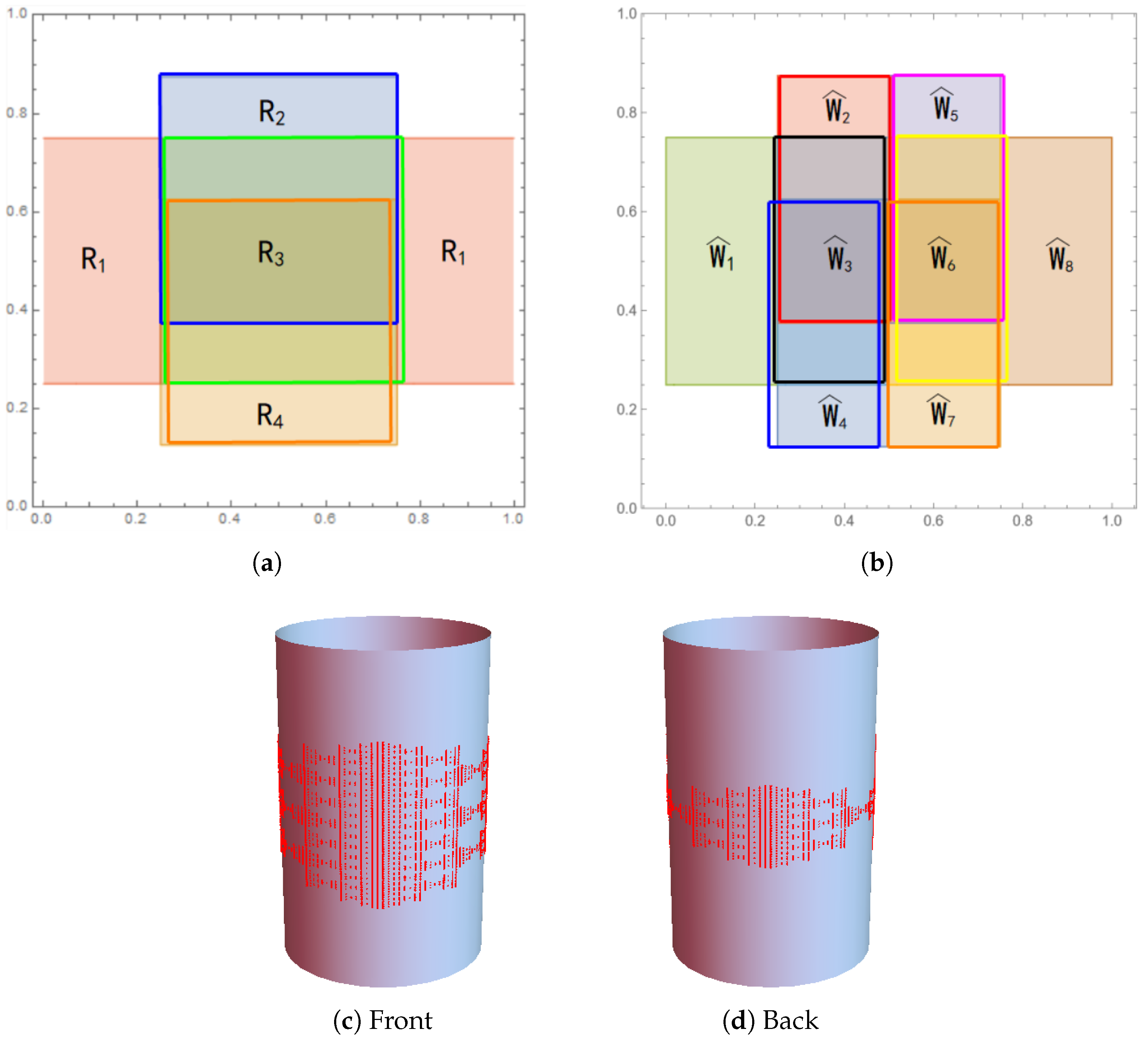
6.2. Examples
- (1)
- There does not exist a global bi-Lipschitz map such that .
- (2)
- Let . One may try to construct a bi-Lipschitz map , where . As might not be a self-similar set, it is not clear how to compute the Hausdorff dimension of .
- (3)
- If K is has a neighborhood on which there exists a local isometry mapping U to , then the problem is much easier; however, this is not the case for Example 2. In fact, although K can be covered by finitely or countably many coordinate charts and then pulled into the Euclidean space by isometries, the image of K in lacks a well-defined structure, and it is not clear how to find an IFS that generates it.
7. IRSs on Riemannian Manifolds That Are Not Locally Euclidean
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
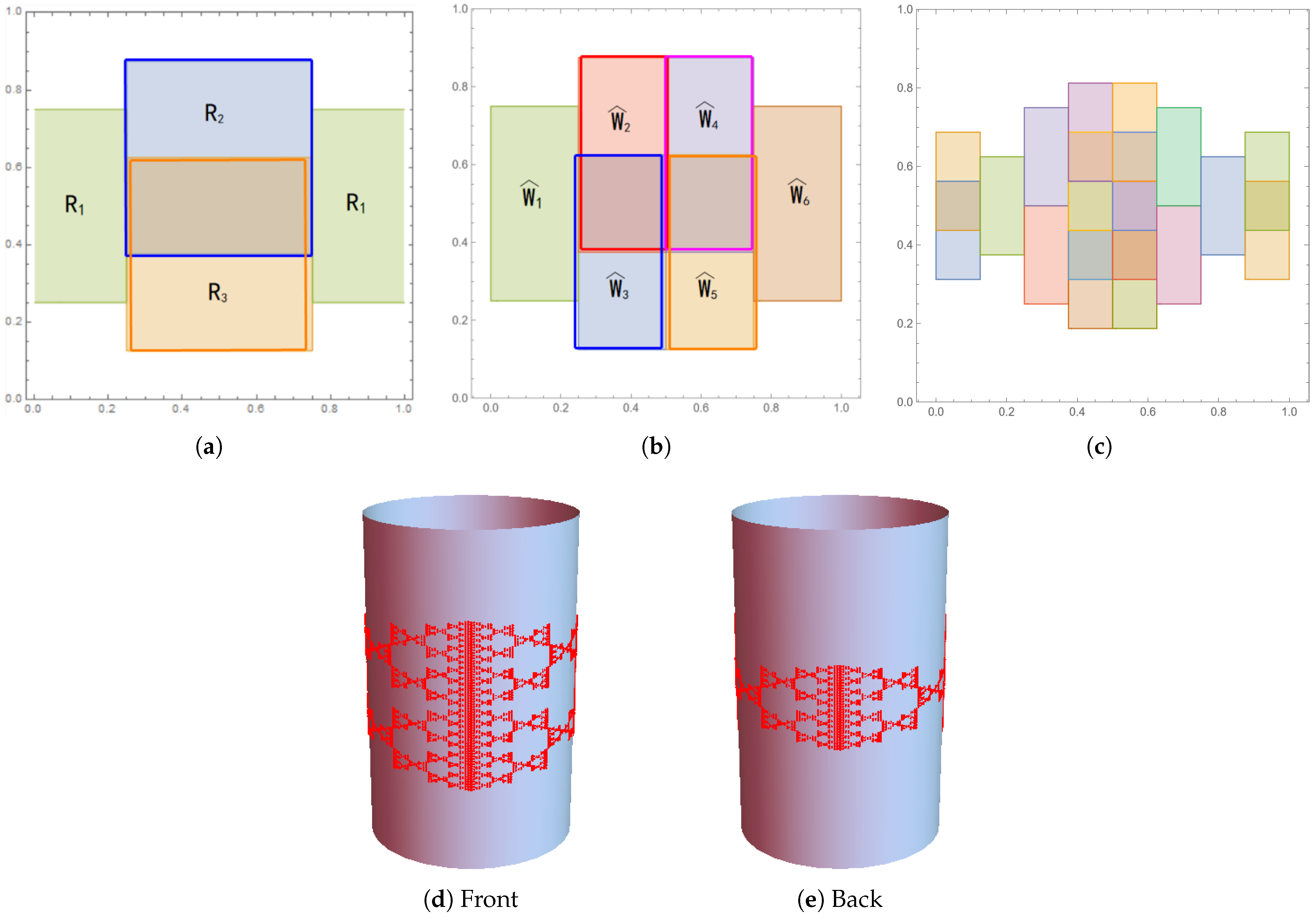
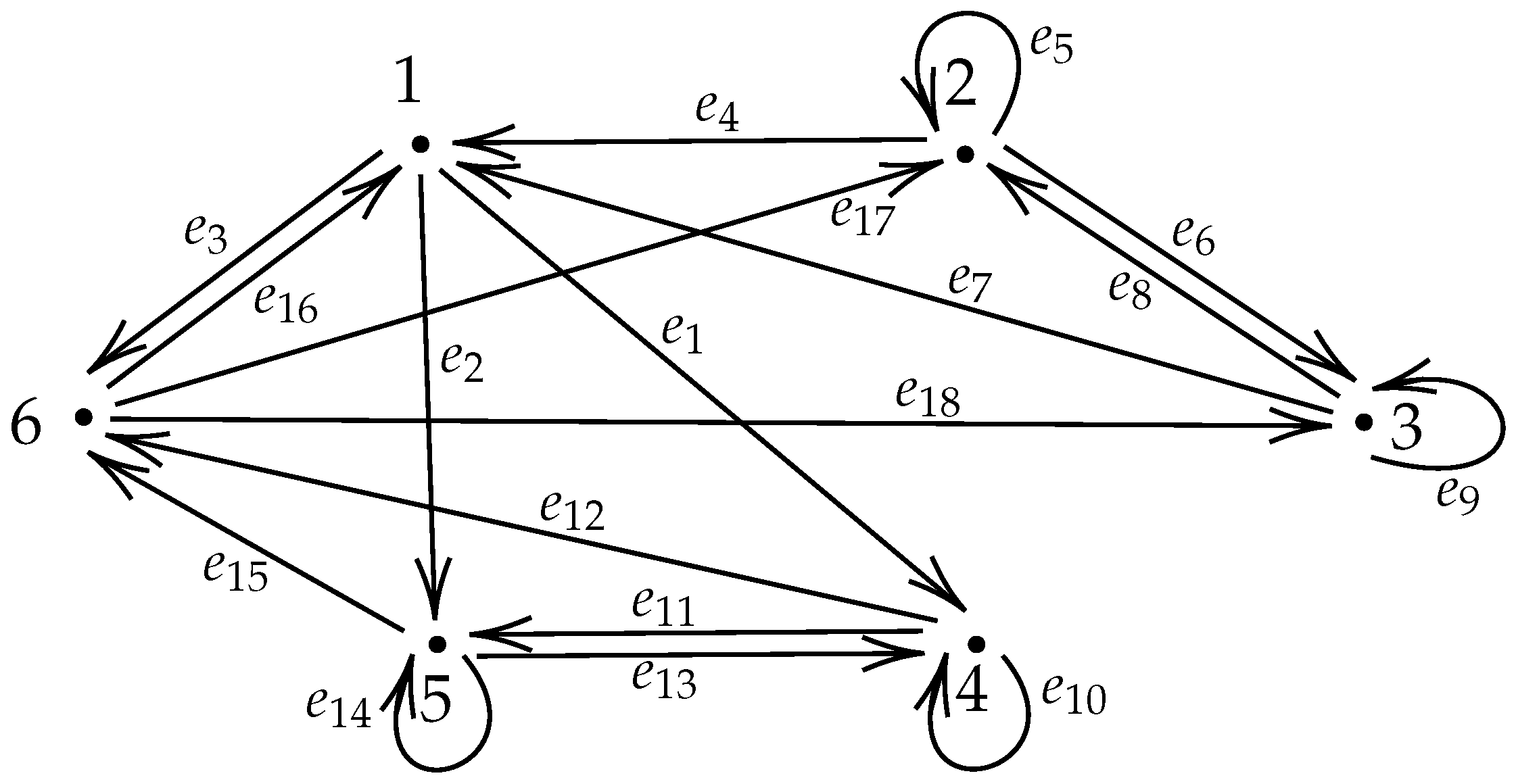
Appendix A. Some Examples
References
- Strichartz, R.S. Self-similarity on nilpotent Lie groups. Contemp. Math. 1992, 140, 123–157. [Google Scholar]
- Balogh, Z.M.; Tyson, J.T. Hausdorff dimensions of self-similar and self-affine fractals in the Heisenberg group. Proc. Lond. Math. Soc. 2005, 91, 153–183. [Google Scholar] [CrossRef]
- Barnsley, M.F.; Vince, A. Real projective iterated function systems. J. Geom. Anal. 2012, 22, 1137–1172. [Google Scholar] [CrossRef]
- Hossain, A.; Akhtar, M.N.; Navascués, M.A. Fractal dimension of fractal functions on the real projective plane. Fractal Fract. 2023, 7, 510. [Google Scholar] [CrossRef]
- Hossain, A.; Akhtar, M.N.; Navascués, M.A. Fractal interpolation on the real projective plane. Numer. Algorithms 2024, 96, 557–582. [Google Scholar] [CrossRef]
- Ngai, S.-M.; Xu, Y.Y. Separation conditions for iterated function systems with overlaps on Riemannian manifolds. J. Geom. Anal. 2023, 33, 262. [Google Scholar] [CrossRef]
- Thangaraj, C.; Easwaramoorthy, D.; Selmi, B.; Chamola, B.P. Generation of fractals via iterated function system of Kannan contractions in controlled metric space. Math. Comput. Simul. 2024, 222, 188–198. [Google Scholar] [CrossRef]
- Cui, M.; Selmi, B.; Li, Z. Expansive measures of nonautonomous iterated function systems. Qual. Theory Dyn. Syst. 2025, 24, 60. [Google Scholar] [CrossRef]
- Balogh, Z.M.; Rohner, H. Self-similar sets in doubling spaces. Ill. J. Math. 2007, 51, 1275–1297. [Google Scholar] [CrossRef]
- Hutchinson, J.E. Fractals and self-similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Wu, D.; Yamaguchi, T. Hausdorff dimension of asymptotic self-similar sets. J. Geom. Anal. 2017, 4, 339–368. [Google Scholar] [CrossRef]
- Ngai, S.-M.; Wang, Y. Hausdorff dimension of self-similar sets with overlaps. J. Lond. Math. Soc. 2001, 2, 655–672. [Google Scholar] [CrossRef]
- Jin, N.; Yau, S.S.T. General finite type IFS and M-matrix. Commun. Anal. Geom. 2005, 13, 821–843. [Google Scholar]
- Lau, K.-S.; Ngai, S.-M. A generalized finite type condition for iterated function systems. Adv. Math. 2007, 208, 647–671. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Hossain, A. Stereographic metric and dimensions of fractals on the sphere. Results Math. 2022, 77, 213. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Prasad, M.G.P.; Navascués, M.A. More general fractal functions on the sphere. Mediterr. J. Math. 2019, 16, 134. [Google Scholar] [CrossRef]
- Navascués, M.A. Fractal functions on the sphere. J. Comput. Anal. Appl. 2007, 9, 257–270. [Google Scholar]
- Vince, A. Möbius iterated function systems. Trans. Amer. Math. Soc. 2013, 365, 491–509. [Google Scholar] [CrossRef]
- Mauldin, R.D.; Williams, S.C. Hausdorff dimension in graph directed constructions. Trans. Amer. Math. Soc. 1988, 309, 811–829. [Google Scholar] [CrossRef]
- Edgar, G.A. Measure, Topology, and Fractal Geometry; Springer: New York, NY, USA, 2008. [Google Scholar]
- Petersen, P. Riemannian Geometry; Graduate Texts in Mathematics; Springer: Cham, Switzerland, 2006; Volume 171. [Google Scholar]
- Jost, J. Riemannian Geometry and Geometric Analysis; Universitext; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Hebey, E. Sobolev Spaces on Riemannian Manifolds; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Chavel, I. Riemannian Geometry: A Modern Introduction; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Falconer, K.J. Fractal Geometry: Mathematical Foundations and Applications, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Das, M.; Ngai, S.-M. Graph-directed iterated function systems with overlaps. Indiana Univ. Math. J. 2004, 53, 109–134. [Google Scholar] [CrossRef]
- Kigami, J. Analysis on Fractals; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]


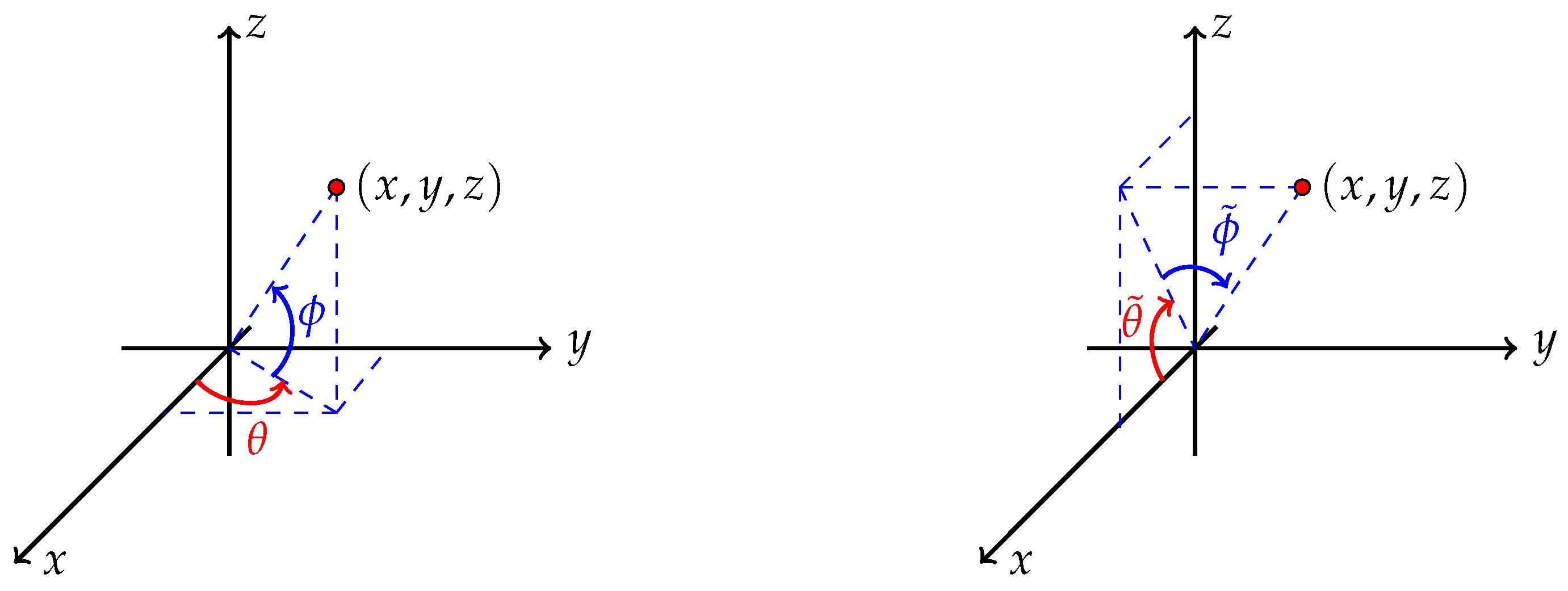

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Ngai, S.-M.; Ouyang, L. Iterated Relation Systems on Riemannian Manifolds. Fractal Fract. 2025, 9, 637. https://doi.org/10.3390/fractalfract9100637
Liu J, Ngai S-M, Ouyang L. Iterated Relation Systems on Riemannian Manifolds. Fractal and Fractional. 2025; 9(10):637. https://doi.org/10.3390/fractalfract9100637
Chicago/Turabian StyleLiu, Jie, Sze-Man Ngai, and Lei Ouyang. 2025. "Iterated Relation Systems on Riemannian Manifolds" Fractal and Fractional 9, no. 10: 637. https://doi.org/10.3390/fractalfract9100637
APA StyleLiu, J., Ngai, S.-M., & Ouyang, L. (2025). Iterated Relation Systems on Riemannian Manifolds. Fractal and Fractional, 9(10), 637. https://doi.org/10.3390/fractalfract9100637





