Analytical Study of Soliton Solutions and Modulation Instability Analysis in the M-Truncated Fractional Coupled Ivancevic Option-Pricing Model
Abstract
1. Introduction
2. The Truncated -Fractional Derivative
- .
- .
- .
- , where is a constant.
- If is differentiable, then
3. Extraction of the Solutions
3.1. Solutions via Newly Created Kumar-Malik Method
- The Jacobi elliptic solutionsSubcase 1.1. If andSubcase 1.2. IfSubcase 1.3. IfSubcase 1.4. IfSubcase 1.5. IfCase-2: For Solving the algebraic system yields
- The explicit dark, singular and periodic wave solutionsSubcase 2.1. If andSubcase 2.2. IfCase-3: For Solving the algebraic system yields
- The hyperbolic and trigonometric solutionsSubcase 3.1. If andSubcase 3.2. IfCase-4: For and Solving the algebraic system yields
- The exponential function solution
3.2. Solutions via Modified Sardar Subequation Method
3.3. Solutions via Generalized Arnous Method
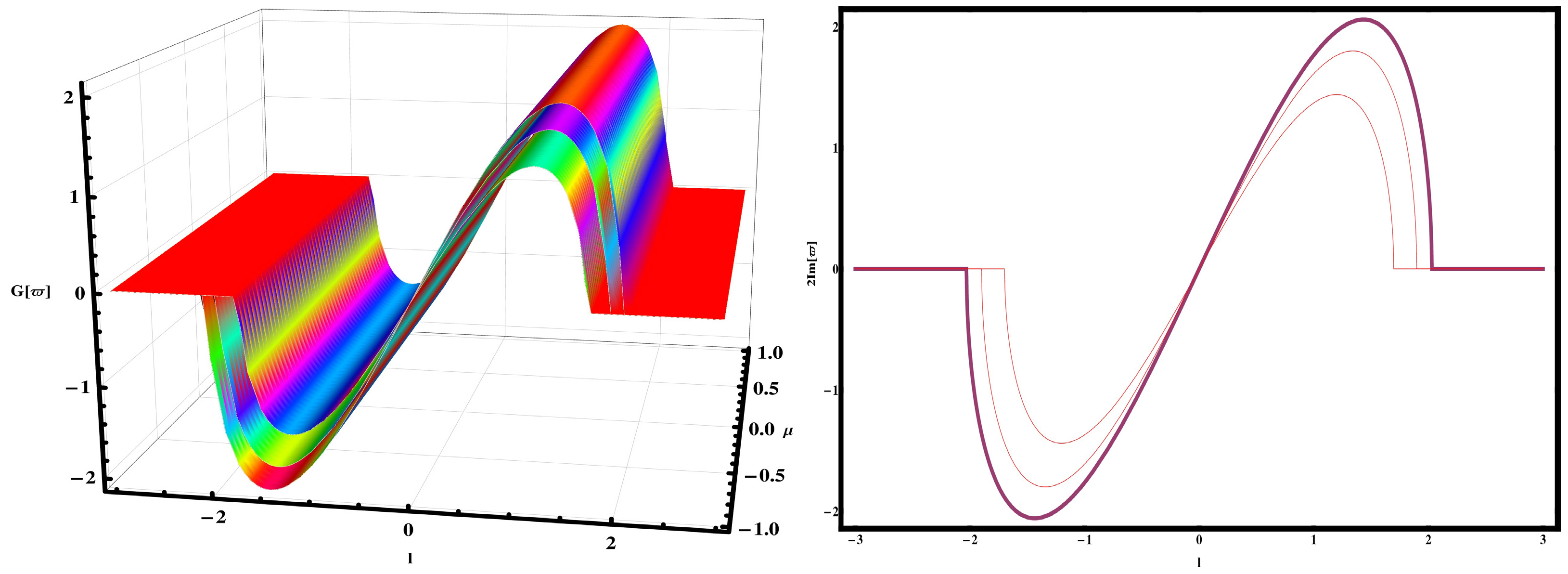
4. Modulation Instability
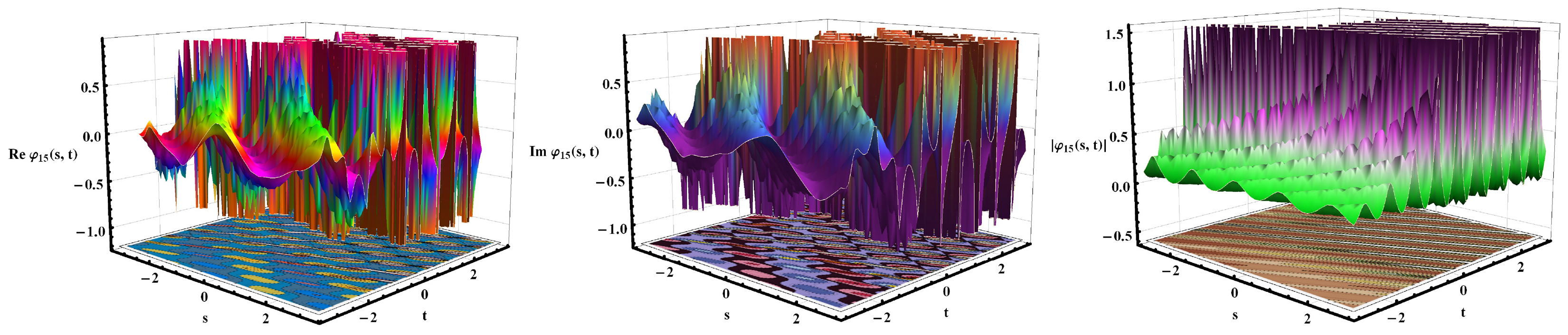
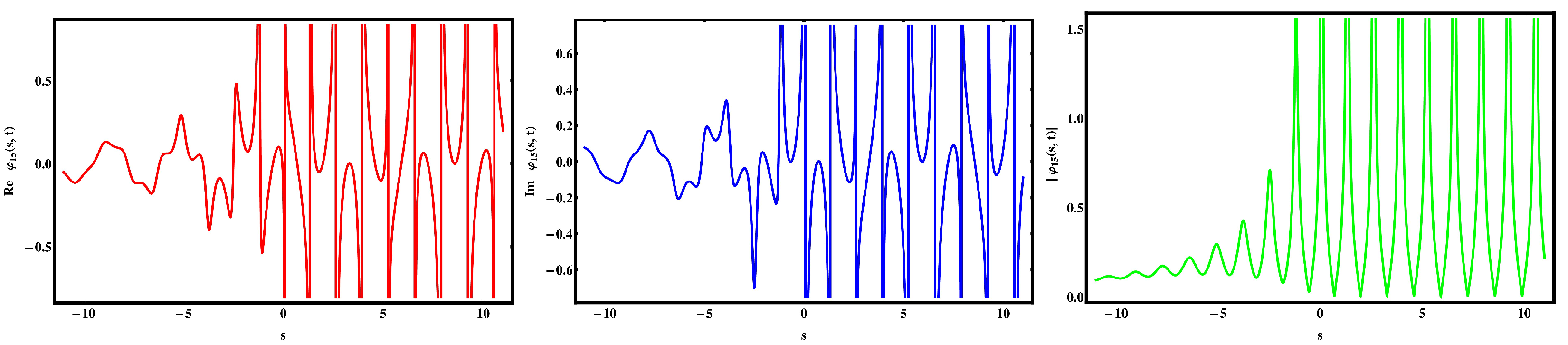
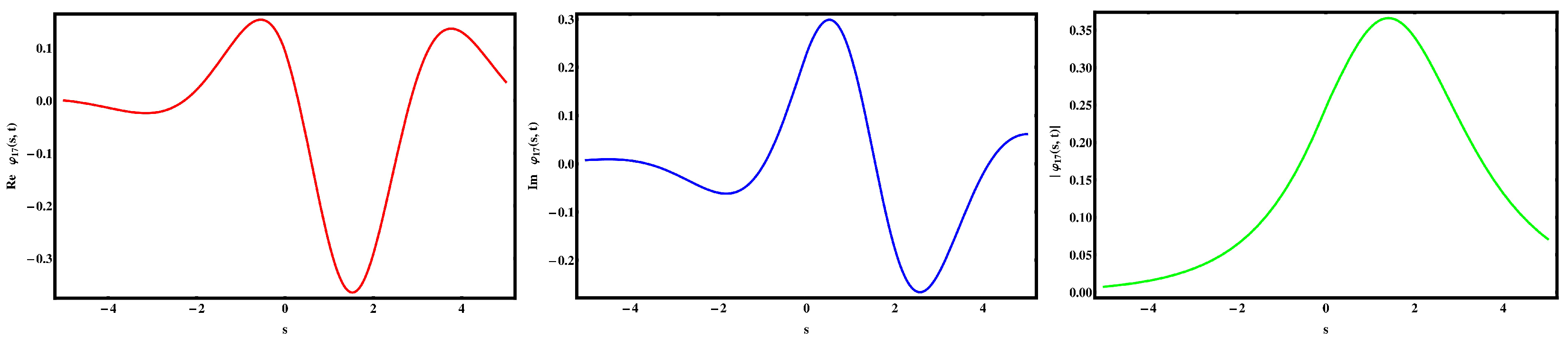
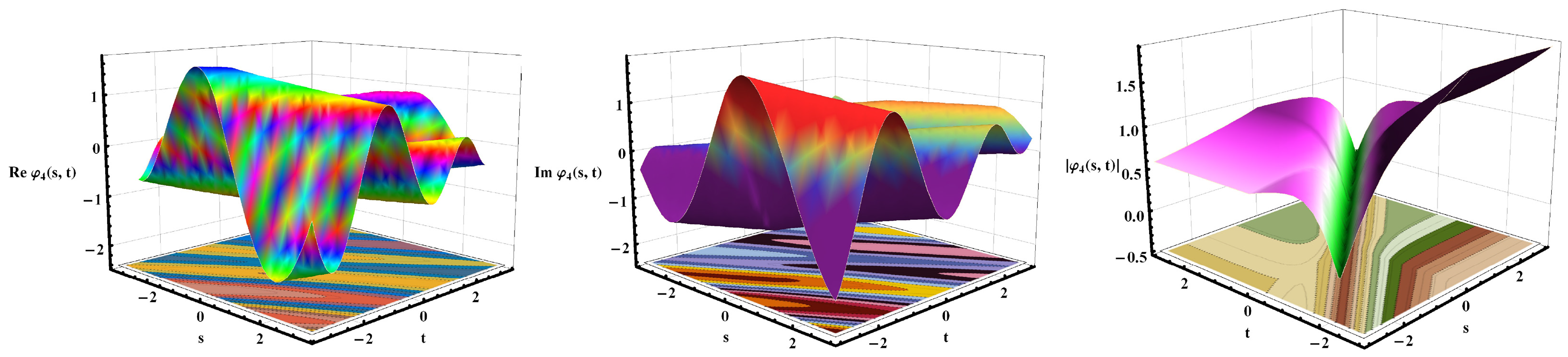
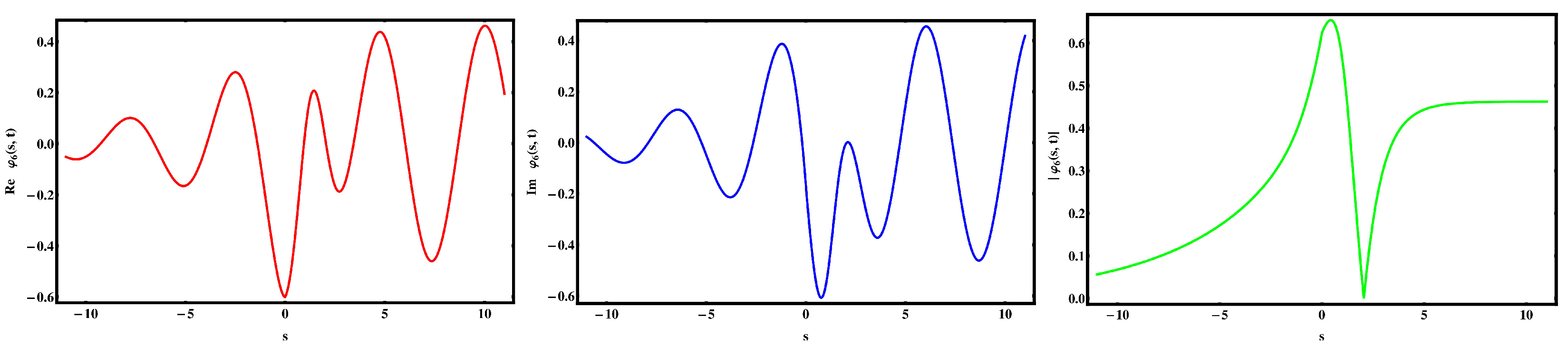
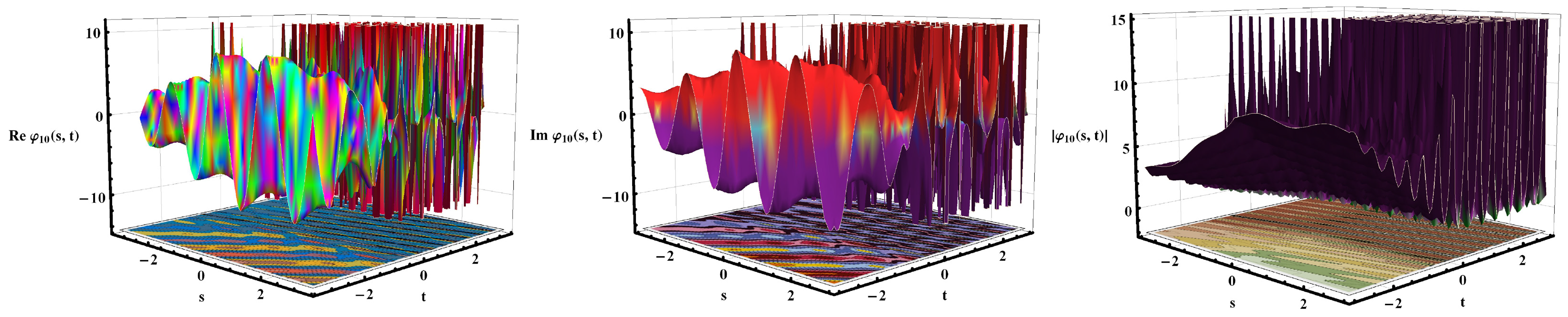
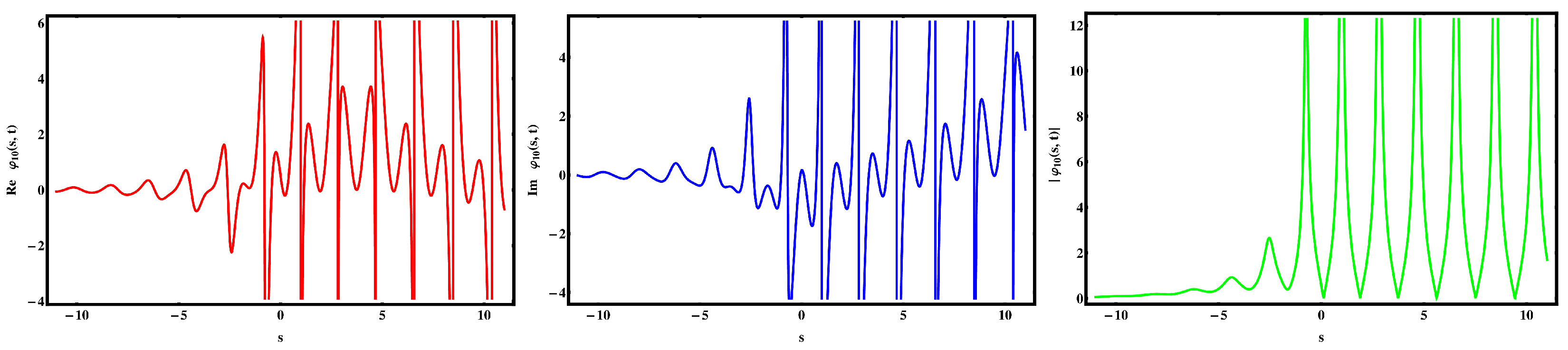
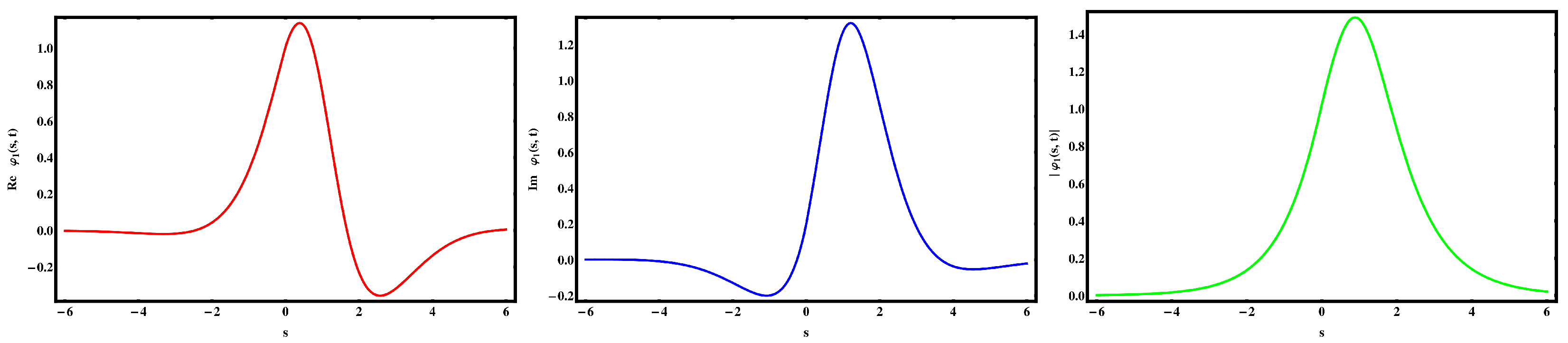
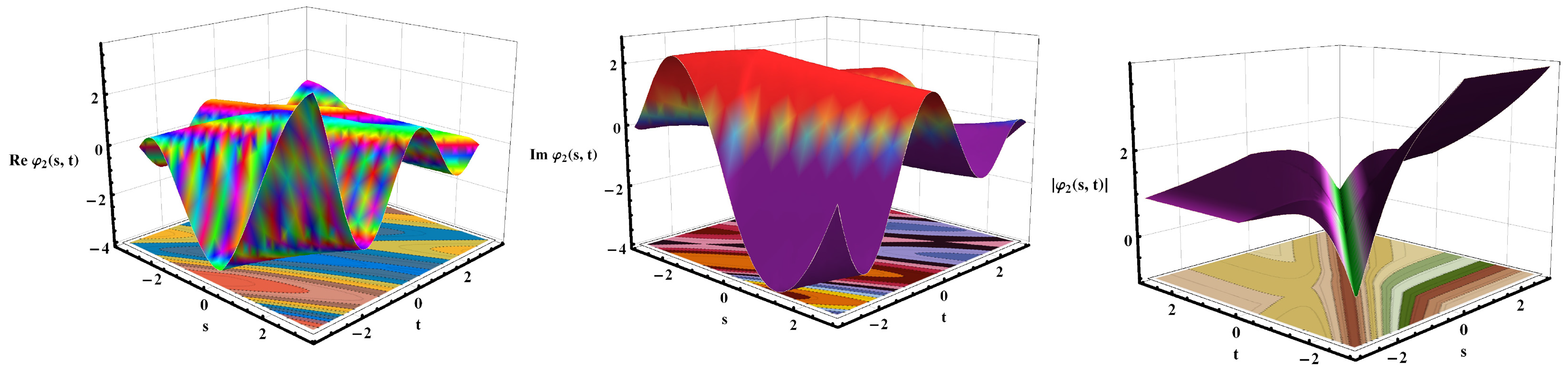
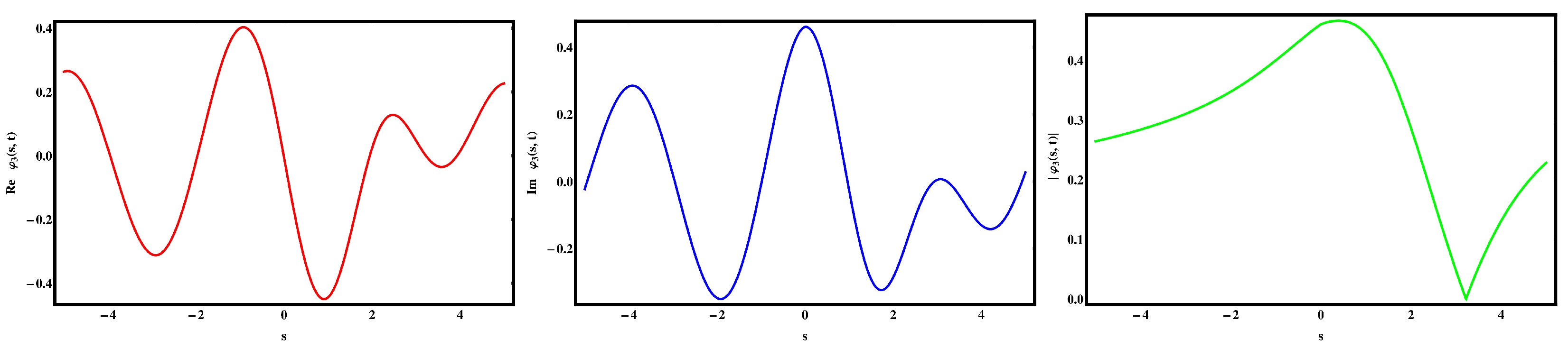
5. Discussion and Visual Illustration
Comparison
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dallago, B.; Casagrande, S. The Routledge Handbook of Comparative Economic Systems; Routledge: London, UK, 2023. [Google Scholar]
- El Karoui, N.; Peng, S.; Quenez, M.C. Backward stochastic differential equations in finance. Math. Fin. 1997, 7, 1–71. [Google Scholar] [CrossRef]
- Sharp, K.P. Stochastic differential equations in finance. Appl. Math. Comput. 1990, 39, 207–224. [Google Scholar] [CrossRef]
- Antonelli, F. Stability of backward stochastic differential equations. Stochastic Process. Appl. 1996, 62, 103–114. [Google Scholar] [CrossRef]
- Irving, A.D.; Dewson, T. Determining mixed linear-nonlinear coupled differential equations from multivariate discrete time series sequences. Physica D 1997, 102, 15–36. [Google Scholar] [CrossRef]
- Jin, X.; Deng, S. Existence and uniqueness of optimal consumption and portfolio rules in a continuous-time finance model with habit formation and without short sales. J. Math. Econ. 1997, 28, 187–205. [Google Scholar] [CrossRef]
- Ganesh, B.; Muthukumar, P.P. Controllability study on fractional order impulsive stochastic differential equation. IFAC-PapersOnLine 2016, 4, 516–521. [Google Scholar] [CrossRef]
- Samarskii, A.A. Economical difference schemes for parabolic equations with mixed derivatives. USSR Comput. Math. Math. Phys. 1964, 4, 182–191. [Google Scholar] [CrossRef]
- Decardi-Nelson, B.; Liu, J. Robust economic model predictive control with zone control. IFAC-PapersOnLine 2021, 54, 237–242. [Google Scholar] [CrossRef]
- Adomian, G. On the modeling and analysis of a national economy. IFAC Proc. Vol. 1983, 16, 189–196. [Google Scholar] [CrossRef]
- Maffezoni, C.; Magnani, G.; Marcocci, L. Computer aided modelling of large power plants. IFAC Proc. Vol. 1984, 17, 1–9. [Google Scholar] [CrossRef]
- Bienvenue, D.; Houwe, A.; Rezazadeh, H.; Bekir, A.; Nsangou, M.; Betchewe, G. New explicit and exact traveling waves solutions to the modified complex Ginzburg Landau equation. Opt. Quantum Electron. 2022, 54, 237. [Google Scholar] [CrossRef]
- Zhu, S.D. The generalizing Riccati equation mapping method in non-linear evolution equation: Application to (2 + 1)-dimensional Boiti–Leon–Pempinelle equation. Chaos Solitons Fractals 2008, 37, 1335–1342. [Google Scholar] [CrossRef]
- Akram, S.; Ahmad, J.; Rehman, S.U.; Ali, A. New family of solitary wave solutions to new generalized Bogoyavlensky–Konopelchenko equation in fluid mechanics. Int. J. Appl. Comput. Math 2023, 9, 63. [Google Scholar] [CrossRef]
- Raza, N.; Salman, F.; Butt, A.R.; Gandarias, M.L. Lie symmetry analysis, soliton solutions and qualitative analysis concerning to the generalized q-deformed Sinh-Gordon equation. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106824. [Google Scholar] [CrossRef]
- Noorizadegan, A.; Chen, C.S.; Young, D.L. Effective condition number for the selection of the RBF shape parameter with the fictitious point method. Appl. Numer. Math. 2022, 178, 280–295. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Ibrahim, S.H. Exact solutions of nonlinear evolution equations in mathematical physics using the modified simple equation method. Chin. Phys. Lett. 2012, 29, 060201. [Google Scholar] [CrossRef]
- Nadeem, M.; Cheng, B.; Iambor, L.F. Numerical investigation of the Time-Fractional Black–Scholes problem using the caputo fractional derivative in the financial industry. Fractal Fract. 2025, 9, 490. [Google Scholar] [CrossRef]
- Tripathy, A.; Sahoo, S.; Rezazadeh, H.; Izgi, Z.P.; Osman, M.S. Dynamics of damped and undamped wave natures in ferromagnetic materials. Optik 2023, 281, 170817. [Google Scholar] [CrossRef]
- Rehman, S.U.; Bilal, M.; Ahmad, J. Dynamics of soliton solutions in saturated ferromagnetic materials by a novel mathematical method. J. Magn. Magn. Mater. 2021, 538, 168245. [Google Scholar] [CrossRef]
- Haque, M.M.; Akbar, M.A.; Rezazadeh, H.; Bekir, A. A variety of optical soliton solutions in closed-form of the nonlinear cubic quintic Schrödinger equations with beta derivative. Opt. Quantum Electron. 2023, 55, 1144. [Google Scholar] [CrossRef]
- Younas, U.; Muhammad, J. Wave propagation and multistability analysis to the modified fractional KDV-KP equation in diversity of fields. Model. Earth Syst. Environ. 2025, 11, 262. [Google Scholar] [CrossRef]
- Muhammad, J.; Rehman, S.U.; Nasreen, N.; Bilal, M.; Younas, U. Exploring the fractional effect to the optical wave propagation for the extended Kairat-II equation. Nonlinear Dyn. 2025, 113, 1501–1512. [Google Scholar] [CrossRef]
- Islam, M.T.; Akter, M.A.; Gomez-Aguilar, J.F.; Akbar, M.A.; Pérez-Careta, E. Innovative and diverse soliton solutions of the dual core optical fiber nonlinear models via two competent techniques. J. Nonlinear Opt. Phys. Mater. 2023, 32, 2350037. [Google Scholar] [CrossRef]
- Ozisik, M. Novel (2+1) and (3+1) forms of the Biswas-Milovic equation and optical soliton solutions via two efficient techniques. Optik 2022, 269, 169798. [Google Scholar] [CrossRef]
- Sivasundari, S.A.S.; Jeyabarathi, P.; Rajendran, L. Theoretical analysis of nonlinear equation in reaction-diffusion system: Hyperbolic function method. Eur. J. Math. Stat. 2023, 4, 24–31. [Google Scholar] [CrossRef]
- Wang, S. Novel soliton solutions of CNLSEs with Hirota bilinear method. J. Opt. 2023, 52, 1602–1607. [Google Scholar] [CrossRef]
- Ansari, A.R.; Jhangeer, A.; Imran, M.; Inc, M.; Beenish, A. A study of self-adjointness, Lie analysis, wave structures, and conservation laws of the completely generalized shallow water equation. Eur. Phys. J. Plus 2024, 139, 489. [Google Scholar] [CrossRef]
- Zafar, A.; Shakeel, M.; Ali, A.; Akinyemi, L.; Rezazadeh, H. Optical solitons of nonlinear complex Ginzburg-Landau equation via two modified expansion schemes. Opt. Quantum Electron. 2022, 54, 1–15. [Google Scholar] [CrossRef]
- Chen, Q.; Baskonus, H.M.; Gao, W.; İlhan, E. Soliton theory and modulation instability analysis: The Ivancevic option-pricing model in economy. Alex. Eng. J. 2022, 61, 7843–7851. [Google Scholar] [CrossRef]
- Gaafele, C.; Madimabe, E.B.; Ndebele, K.; Otlaadisa, P.; Mozola, B.; Matabana, T.; Pilane, P. Modulational instability of the time-fractional Ivancevic option-pricing model and the coupled nonlinear volatility and option price model. arXiv 2024, arXiv:2405.19887. [Google Scholar]
- Kosko, B. Bidirectional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18, 49–60. [Google Scholar] [CrossRef]
- Manakov, S. Complete integrability and stochastization of discrete dynamical systems. Zh. Eksp. Teor. Fiz. 1974, 67, 543–555. [Google Scholar]
- Ma, P.C.; Najafi, A.; Gomez-Aguilar, J.F. Sub mixed fractional Brownian motion and its application to finance. Chaos Solitons Fractals 2024, 184, 114968. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Goswami, A.; Singh, J.; Kumar, D.; Sushila. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Physica A 2019, 524, 563–575. [Google Scholar] [CrossRef]
- Goswami, A.; Sushila; Singh, J.; Kumar, D. Numerical computation of fractional Kersten-Krasil’shchik coupled KdV-mKdV system occurring in multi-component plasmas. AIMS Math. 2020, 5, 2346–2368. [Google Scholar]
- Rehman, H.U.; Asjad, M.I.; Iqbal, I.; Akgül, A. Soliton solutions of space-time fractional Zoomeron differential equation. Int. J. Appl. Nonlinear Sci. 2023, 4, 29–46. [Google Scholar] [CrossRef]
- Saglam, F.N.K.; Malik, S. Various traveling wave solutions for (2+1)-dimensional extended Kadomtsev–Petviashvili equation using a newly created methodology. Chaos Solitons Fractals 2024, 186, 115318. [Google Scholar] [CrossRef]
- Onder, I.; Secer, A.; Ozisik, M.; Bayram, M. Investigation of optical soliton solutions for the perturbed Gerdjikov-Ivanov equation with full-nonlinearity. Heliyon 2023, 9, e13519. [Google Scholar] [CrossRef]
- Park, C.; Nuruddeen, R.I.; Ali, K.K.; Muhammad, L.; Osman, M.S.; Baleanu, D. Novel hyperbolic and exponential ansatz methods to the fractional fifth-order Korteweg–de Vries equations. Adv. Differ. Equ. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Rasool, T.; Hussain, R.; Sharif, M.A.A.; Mahmoud, W.; Osman, M.S. A variety of optical soliton solutions for the M-truncated Paraxial wave equation using Sardar-subequation technique. Opt. Quantum Electron. 2023, 55, 396. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Hakami, K.H.; Altalbe, A.; Bayram, M. The discovery of Truncated M-fractional exact solitons and a qualitative analysis of the generalized Bretherton model. Mathematics 2024, 12, 2772. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; de Oliveira, E.C.A. New truncated M-Fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar] [CrossRef]
- Ali, A.; Ahmad, J.; Javed, S. Stability analysis and novel complex solutions to the malaria model utilising conformable derivatives. Eur. Phys. J. Plus 2023, 138, 1–17. [Google Scholar] [CrossRef]
- Rehman, H.U.; Wong, P.J.Y.; Aljohani, A.F.; Iqbal, I.; Saleem, M.S. The fractional soliton solutions: Shaping future finances with innovative wave profiles in option pricing system. AIMS Math. 2024, 9, 24699–24721. [Google Scholar] [CrossRef]
- Jhangeer, A.; Faridi, W.A.; Alshehri, M. Soliton wave profiles and dynamical analysis of fractional Ivancevic option-pricing model. Sci. Rep. 2024, 14, 23804. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilal, M.; Abdullah, A.R.; Rehman, S.U.; Younas, U. Analytical Study of Soliton Solutions and Modulation Instability Analysis in the M-Truncated Fractional Coupled Ivancevic Option-Pricing Model. Fractal Fract. 2025, 9, 630. https://doi.org/10.3390/fractalfract9100630
Bilal M, Abdullah AR, Rehman SU, Younas U. Analytical Study of Soliton Solutions and Modulation Instability Analysis in the M-Truncated Fractional Coupled Ivancevic Option-Pricing Model. Fractal and Fractional. 2025; 9(10):630. https://doi.org/10.3390/fractalfract9100630
Chicago/Turabian StyleBilal, Muhammad, Aljethi Reem Abdullah, Shafqat Ur Rehman, and Usman Younas. 2025. "Analytical Study of Soliton Solutions and Modulation Instability Analysis in the M-Truncated Fractional Coupled Ivancevic Option-Pricing Model" Fractal and Fractional 9, no. 10: 630. https://doi.org/10.3390/fractalfract9100630
APA StyleBilal, M., Abdullah, A. R., Rehman, S. U., & Younas, U. (2025). Analytical Study of Soliton Solutions and Modulation Instability Analysis in the M-Truncated Fractional Coupled Ivancevic Option-Pricing Model. Fractal and Fractional, 9(10), 630. https://doi.org/10.3390/fractalfract9100630





