Super-Quadratic Stochastic Processes with Fractional Inequalities and Their Applications

Abstract

The theory of stochastic processes is the prominent part of advanced probability theory and very influential in various mathematical models having randomness. One of the potential aspects is to investigate the stochastic convex processes. Working in the following direction, this study explores the set-valued super-quadratic processes through a unified approach under the centre-radius order relation, which is a totally ordered relation. First, we discuss some captivating properties and important results, which serve as a criterion. Relying on the newly proposed class of super-quadratic processes, we develop several fundamental inequalities within the fractional framework. Moreover, we present some novel deductions to complement the theoretical results with the existing literature. Also, we have provided the graphical breakdown, applications to the means, information theory, and divergence measures of the main inequalities.

1. Introduction

Over the years, researchers have focused on the theory of inequalities to increase the range of its application in diverse domains of mathematics, including optimization, operational research, differential equations, dynamical systems, machine learning, and information theory. Another aspect to study the inequalities is to reduce the shortcomings of existing results by presenting new generalization involving multiple strategies and frameworks. Also, for the development of bounds of mathematical quantities, inequalities always play an essential role. These factors lay down the foundation to conduct further research in the following direction. Among the potential strategies for the generation of inequalities is convex mapping theory. One can recapture directly and indirectly all the fundamental results of inequalities through the application of convexity. Let us recall the definition of convexity-preserving mapping:

A mapping $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to \mathbb{R}$ is called convex, if

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\ell }_1\right)+\varrho (\tilde{\mathcal{K}}\left({ı}_1\right)-\tilde{\mathcal{K}}\left({\ell }_1\right))-\tilde{\mathcal{K}}((1-\varrho ){\ell }_1+\varrho {ı}_1)\ge 0,\forall \varrho \in [0,1].\end{array}$$

Recently, various generalization of convex mappings have been introduced in the literature. Strong convexity and its related classes are promising to refine the inequalities. Another interesting class of functions defined by a support line and translation of itself instead of quadratic support is known as a super-quadratic function. In [1], Abramovich gave the idea of super-quadratic mappings and related Jensen’s inequalities. Kian [2] proved the operator form of Jensen’s inequalities pertaining to operator super-quadratic mappings. Further inequalities through super-quadratic mappings are explored in [3,4].

One of the specific sub-domains of set-valued is interval analysis to resolve the error analysis of numerical. Moore was the first one who explored the properties of intervals, interval-valued mappings, their derivatives and integrals, and ordering relations in [5]. His contributions are still a pathway to conduct research in the following direction for subsequent advancements. In recent years, researchers have employed the interval-valued techniques to investigate the problems associated with dynamical systems, combinatorics, differential equations, neural networking, and inequalities. Breckner [6] worked on convexity properties of set-valued mappings and proved the Hermite–Hadamard inequality. Budak et al. [7] discussed the fractional interval-valued perspective of trapezoid inequalities. While in [8], approximately interval-valued convexity and its related inequalities have been discussed. Cheng et al. [9] bridged the fuzzy and quantum interval-valued concepts and analyzed various fractional counterparts of fundamental inequalities. Mohsin et al. [10] delivered the set-valued coordinated harmonic convexity and several inequalities. For more detail, see [11,12,13,14].

Fractional operators are useful to study the memory and nonlocal properties in various mathematical models. Although, they provide a more flexible environment to study the various physical models. Additionally, the analytical solution of several complex dynamic systems of differential equations can be obtained. Following the significance of interval-valued calculus and fractional calculus, researchers bridged both frameworks to study the problems through a unified approach. Now we mention the essential results of interval analysis.

Stochastic processes are significant to explore the models having randomness. Convex stochastic processes are useful and provide various tools to tackle an immense amount of problems in stochastic optimization and inequalities. The concept of stochastic convexity was initiated by Nikodem [15], and he proved various fundamental results of it. Kotrys [16] developed the trapezium-like inequalities associated with convex stochastic processes. In [17], Skowronski explored Wright convexity, leveraging stochastic concepts. In [18], Okur et al. constructed the stochastic variants of Hadamard’s type inequalities involving the generalized E-convexity. In [19], Jung et al. discussed the $\eta$-stochastic processes. In [20], Agahi and Babakhani developed the fractional analogues of stochastic Hadamard-like inequalities. Afzal et al. [21,22] presented the Hadamard’s and Jensen’s type inequalities pertaining to centre-radius order generalized Godunova–Levin convexity and ℏ-convex stochastic processes in an interval-valued framework, respectively. Javed et al. [23] introduced the concept of an extended class of stochastic processes based on quasi means and proved various fundamental inequalities. Khan and Butt [24] purported the idea of totally ordered super-quadratic mappings and formulated the fractional inequalities. Mohsen [25] presented the idea of super-quadratic stochastic processes and also derived various integral inequalities.

Super-quadratic mappings are pivotal among the other classes of strong convexity. Recently, researchers have been exploring super-quadratic mappings in different frameworks, including interval-valued, fuzzy-valued, and stochastic analysis. The recent studies motivated us to introduce a generic class of super-quadratic processes along with detailed characterisation. Incorporating with a control mapping, we introduce the idea of a ℏ-super-quadratic process. Based on newly developed concepts of convexity, we prove some fundamental results of inequalities. Additionally, some fractional versions of trapezium-type inequalities are also provided. Information theory and its applications will also be discussed.

2. Preliminaries

First, we give the Definition of super-quadratic mapping.

Definition 1

([1]). A mapping $\tilde{\mathcal{K}}:[0,\infty )\to \mathbb{R}$ is regarded as super-quadratic for $\delta \ge 0$ if there exist a constant $C\left(\delta \right)\in \mathbb{R}$ such that

$$\tilde{\mathcal{K}}\left({\delta }_1\right)\ge \tilde{\mathcal{K}}\left(\delta \right)+C\left(\delta \right)({\delta }_1-\delta )+\tilde{\mathcal{K}}\left(\right|\delta -{\delta }_1\left|\right),{\delta }_1\ge 0.$$

Alternative, it can be read as

Definition 2

([1]). A mapping $\tilde{\mathcal{K}}:[0,\infty )\to \mathbb{R}$ is called super-quadratic if, and only if,

$$\tilde{\mathcal{K}}((1-\varrho )\delta +\varrho {\delta }_1)\le (1-\varrho )\tilde{\mathcal{K}}\left(\delta \right)+\varrho \tilde{\mathcal{K}}\left({\delta }_1\right)-\varrho \tilde{\mathcal{K}}((1-\varrho )|\delta -{\delta }_1\left|\right)-(1-\varrho )\tilde{\mathcal{K}}\left(\varrho \right|\delta -{\delta }_1\left|\right),$$

holds $\forall \delta ,{\delta }_1\ge 0$ and $0\le \varrho \le 1$.

The ℏ-super-quadratic is defined as follows:

Definition 3

([26]). A mapping $\tilde{\mathcal{K}}:[0,\infty )\to \mathbb{R}$ is called ℏ-super-quadratic if, and only if,

$$\tilde{\mathcal{K}}((1-\varrho )\delta +\varrho {\delta }_1)\le \hslash (1-\varrho )\tilde{\mathcal{K}}\left(\delta \right)+\hslash \left(\varrho \right)\tilde{\mathcal{K}}\left({\delta }_1\right)-\hslash \left(\varrho \right)\tilde{\mathcal{K}}((1-\varrho )|\delta -{\delta }_1\left|\right)-\hslash (1-\varrho )\tilde{\mathcal{K}}\left(\varrho \right|\delta -{\delta }_1\left|\right),$$

holds $\forall \delta ,{\delta }_1\ge 0$ and $0\le \varrho \le 1$ and ℏ be a non-negative mapping.

Theorem 1

([26]). Let $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to \mathbb{R}$ be a ℏ-super-quadratic mapping, then

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right)\le \sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\tilde{\mathcal{K}}\left({\widehat{\delta }}_q\right)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|\right).\end{array}$$

They also proved another version of Jensen-Mercer’s inequality via ℏ-super-quadratic.

Theorem 2

([26]). Let $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to \mathbb{R}$ be a ℏ-super-quadratic mapping, then

$$\begin{array}{cc}\hfill \tilde{\mathcal{K}}\left({ı}_1+{\ell }_1-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right)& \le \tilde{\mathcal{K}}\left({ı}_1\right)+\tilde{\mathcal{K}}\left({\ell }_1\right)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\tilde{\mathcal{K}}\left({\widehat{\delta }}_q\right)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)[\tilde{\mathcal{K}}({\widehat{\delta }}_q-{ı}_1)+\tilde{\mathcal{K}}({\ell }_1-{\widehat{\delta }}_q)]\hfill \\ \hfill & -\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|\right).\hfill \end{array}$$

Now let us recall the basic notions and operations of real intervals. Suppose the space of compact intervals, and positive compact intervals are showcased by ${\mathbb{R}}_I^{+}$, and ${\mathbb{R}}_I^{+}$, respectively. For any ${\mathcal{E}}_1,{\mathcal{E}}_2\in {\mathbb{R}}_I$ such that ${\mathcal{E}}_1=[{{\delta }_3}_{★},{{\delta }_3}^{★}]$ and ${\mathcal{E}}_2=[{{\delta }_4}_{★},{{\delta }_4}^{★}]$ and $\lambda \in \mathbb{R}$, then Minkowski addition

$$\begin{array}{c}\hfill {\mathcal{E}}_1+{\mathcal{E}}_2=[{{\delta }_3}_{★},{{\delta }_3}^{★}]+[{{\delta }_4}_{★},{{\delta }_4}^{★}]=[{{\delta }_3}_{★}+{{\delta }_4}_{★},{{\delta }_3}^{★}+{{\delta }_4}^{★}],\end{array}$$

and multiplication is defined as

$$\begin{array}{c}\hfill {\mathcal{E}}_1·{\mathcal{E}}_2=[min\{{{\delta }_3}_{★}{{\delta }_4}_{★},{{\delta }_3}_{★}{{\delta }_4}^{★},{{\delta }_3}^{★}{{\delta }_4}_{★},{{\delta }_3}^{★}{{\delta }_4}^{★}\},max\{{{\delta }_3}_{★}{{\delta }_4}_{★},{{\delta }_3}_{★}{{\delta }_4}^{★},{{\delta }_3}^{★}{{\delta }_4}_{★},{{\delta }_3}^{★}{{\delta }_4}^{★}\}],\end{array}$$

and

$$\begin{array}{c}\hfill \lambda [{{\delta }_3}_{★},{{\delta }_3}^{★}]=\left\{\begin{array}{c}[\lambda {{\delta }_3}_{★},\lambda {{\delta }_3}^{★}],\lambda >0,\hfill \\ [\lambda {{\delta }_3}^{★},\lambda {{\delta }_3}_{★}],\lambda <0,\hfill \\ 0,\lambda =0.\hfill \end{array}\right.\end{array}$$

Now, we give notion of interval-valued Riemann integral. For more brevity, we specify the space of Riemann integrable and interval-valued Riemann integrable mappings by $R_{[{ı}_1,{\ell }_1]}$ and $I{R}_{[{ı}_1,{\ell }_1]}$, respectively. If $\tilde{\mathcal{K}}=[{\tilde{\mathcal{K}}}_{*},{\tilde{\mathcal{K}}}^{*}]$ is an interval-valued mapping, then ${\tilde{\mathcal{K}}}_{*}$ and ${\tilde{\mathcal{K}}}^{*}$ are known as end point mappings such that ${\tilde{\mathcal{K}}}_{*}\le {\tilde{\mathcal{K}}}^{*}$.

Theorem 3

([5]). Presume that $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to \mathbb{R}$ be an $I.V$ mapping such that $\tilde{\mathcal{K}}\in I{R}_{[{ı}_1,{\ell }_1]}\iff {\tilde{\mathcal{K}}}_{*},{\tilde{\mathcal{K}}}^{*}\in R_{[{ı}_1,{\ell }_1]}$ and

$$\begin{array}{c}\hfill \left(IR\right){\int }_{{ı}_1}^{{\ell }_1}\tilde{\mathcal{K}}\left(\widehat{\delta }\right)\mathrm{d}\widehat{\delta }=\left[\left(R\right){\int }_{{ı}_1}^{{\ell }_1}{\tilde{\mathcal{K}}}_{*}\left(\widehat{\delta }\right)\mathrm{d}\widehat{\delta },\left(R\right){\int }_{{ı}_1}^{{\ell }_1}{\tilde{\mathcal{K}}}^{*}\left(\widehat{\delta }\right)\mathrm{d}\widehat{\delta }\right].\end{array}$$

In [27], Bhunia et al. sought out the problem of interval ranking through total order relation and presented the center-radius approach and stated as

$$\begin{array}{c}\hfill \widehat{\mathcal{B}}=〈{\widehat{\mathcal{B}}}_c,{\widehat{\mathcal{B}}}_r〉=〈{\displaystyle \frac{{\widehat{\mathcal{B}}}_{*}+{\widehat{\mathcal{B}}}^{*}}{2}},{\displaystyle \frac{{\widehat{\mathcal{B}}}^{*}-{\widehat{\mathcal{B}}}_{*}}{2}}〉.\end{array}$$

Definition 4

([27]). The center-radius relation between $\widehat{\mathcal{B}}=\left[{\widehat{\mathcal{B}}}_{*},{\widehat{\mathcal{B}}}^{*}\right]=〈{\widehat{\mathcal{B}}}_c,{\widehat{\mathcal{B}}}_r〉$ and $\mathcal{S}=\left[{\mathcal{S}}_{*},{\mathcal{S}}^{*}\right]=〈{\mathcal{S}}_c,{\mathcal{S}}_r〉$ is defined as

$$\begin{array}{c}\hfill \widehat{\mathcal{B}}{⪯}_{cr}\mathcal{S}\iff \left\{\begin{array}{c}{\widehat{\mathcal{B}}}_c<{\mathcal{S}}_c,if{\widehat{\mathcal{B}}}_c\ne {\mathcal{S}}_c\\ {\widehat{\mathcal{B}}}_r\le {\mathcal{S}}_r,if{\widehat{\mathcal{B}}}_c={\mathcal{S}}_c.\end{array}\right.\end{array}$$

The monotonic property of integrals incorporating center-radius was proved by Shi et al. [28].

Theorem 4

([28]). Consider $\tilde{\mathcal{K}},\xi :[{ı}_1,{\ell }_1]\to {\mathbb{R}}_I^{+}$ be two $I.V$. mappings such that $\tilde{\mathcal{K}}\left({\delta }_1\right)=\left[{\tilde{\mathcal{K}}}_{*}\left({\delta }_1\right),{\tilde{\mathcal{K}}}^{*}\left({\delta }_1\right)\right],\xi \left({\delta }_1\right)=\left[{\xi }_{*}\left({\delta }_1\right),{\xi }^{*}\left({\delta }_1\right)\right]$. If $\tilde{\mathcal{K}},\xi \in I{R}_{\left(\left[{ı}_1,{\ell }_1\right]\right)}$ and $\tilde{\mathcal{K}}\left({\delta }_1\right){⪯}_{cr}\xi \left({\delta }_1\right)$, then

$$\begin{array}{c}\hfill \underset{{ı}_1}{\overset{{\ell }_1}{\int }}\tilde{\mathcal{K}}\left({\delta }_1\right)d{\delta }_1{⪯}_{cr}\underset{{ı}_1}{\overset{{\ell }_1}{\int }}\xi \left({\delta }_1\right)d{\delta }_1.\end{array}$$

To visualize the impact of collaborated study of $cr$-convexity and inequalities, reach out the following articles [28,29].

Now, we recall the fractional Riemann–Liouville (R-L) operators:

Definition 5.

Let $\tilde{\mathcal{K}}\left(\widehat{\delta }\right)=[{\tilde{\mathcal{K}}}_{*}\left(\widehat{\delta }\right),{\tilde{\mathcal{K}}}^{*}\left(\widehat{\delta }\right)]$ and ${\tilde{\mathcal{K}}}_{*}\left(\widehat{\delta }\right)$ and ${\tilde{\mathcal{K}}}^{*}\left(\widehat{\delta }\right)$ are Lebesgue integrable on $[{ı}_1,{\ell }_1]$. Then

$$\begin{array}{c}\hfill J_{{\widehat{\delta }}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}\left({\ell }_1\right)={\displaystyle \frac{1}{\Gamma \left({\beta }_1\right)}}{\int }_{\widehat{\delta }}^{{\ell }_1}{({\ell }_1-\widehat{\delta })}^{{\beta }_1-1}\tilde{\mathcal{K}}\left(\widehat{\delta }\right)\mathrm{d}\widehat{\delta },{\ell }_1>\widehat{\delta },\end{array}$$

and

$$\begin{array}{c}\hfill J_{{{\delta }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}\left({ı}_1\right)={\displaystyle \frac{1}{\Gamma \left({\beta }_1\right)}}{\int }_{{ı}_1}^{{\delta }_1}{(\widehat{\delta }-{ı}_1)}^{{\beta }_1-1}\tilde{\mathcal{K}}\left(\widehat{\delta }\right)\mathrm{d}\widehat{\delta },{ı}_1<{\delta }_1,\end{array}$$

with ${\beta }_1\ge 0$. We observe that

$$\begin{array}{c}\hfill J_{{\widehat{\delta }}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}\left({\ell }_1\right)=\left[J_{{\widehat{\delta }}^{+}}^{{\beta }_1}{\tilde{\mathcal{K}}}_{*}\left({\ell }_1\right),J_{{\widehat{\delta }}^{+}}^{{\beta }_1}{\tilde{\mathcal{K}}}^{*}\left({\ell }_1\right)\right],\end{array}$$

and

$$\begin{array}{c}\hfill J_{{{\delta }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}\left({ı}_1\right)=\left[J_{{{\delta }_1}^{-}}^{{\beta }_1}{\tilde{\mathcal{K}}}_{*}\left({ı}_1\right),J_{{{\delta }_1}^{-}}^{{\beta }_1}{\tilde{\mathcal{K}}}^{*}\left({ı}_1\right)\right].\end{array}$$

Suppose that $(\Lambda ,\varphi ,P)$ be a probability space and any measurable mapping $\tilde{\mathcal{K}}:\Lambda \to \mathbb{R}$ is termed as random variable. A mapping $\tilde{\mathcal{K}}:T\times \Lambda \to \mathbb{R}$ is reported as S.P if $\forall \widehat{\delta }\in T\subset \mathbb{R}$ the mapping $\tilde{\mathcal{K}}(\widehat{\delta },·)$ is random variable. A S.P $\tilde{\mathcal{K}}:T\times \Lambda \to \mathbb{R}$ is termed as

• P-bounded from above on $\varphi \subset I$ if, and only, if

  $$\begin{array}{c}\hfill \underset{\sigma \to \infty }{lim}\underset{\widehat{\delta }\in \varphi }{sup}\left\{P\left(\{\widehat{\delta }\in \Lambda :\tilde{\mathcal{K}}(\widehat{\delta },\widehat{\delta })\ge \sigma \}\right)\right\}=0,\end{array}$$
• P-bounded from below on $\varphi \subseteq I$ if, and only, if

  $$\begin{array}{c}\hfill \underset{\sigma \to \infty }{lim}\underset{\widehat{\delta }\in \varphi }{sup}\left\{P\left(\{\widehat{\delta }\in \Lambda :\tilde{\mathcal{K}}(\widehat{\delta },\widehat{\delta })\le -\sigma \}\right)\right\}=0,\end{array}$$
• continuous on I, if $\forall \widehat{\delta }\in I$,

  $$\begin{array}{c}\hfill P-\underset{\widehat{\delta }\to {\widehat{\delta }}_{\circ }}{lim}\tilde{\mathcal{K}}(\widehat{\delta },·)=\tilde{\mathcal{K}}({\widehat{\delta }}_{\circ },·),\end{array}$$

  where the limit in probability space is denoted by P-limit.
• continuous of mean-square (m.s) type on I, if

  $$\begin{array}{c}\hfill \underset{\widehat{\delta }\to {\widehat{\delta }}_{\circ }}{lim}E\left[{(\tilde{\mathcal{K}}(\widehat{\delta },·)-\tilde{\mathcal{K}}({\widehat{\delta }}_{\circ },·))}^2\right]=0,\end{array}$$

  and $E\left[\tilde{\mathcal{K}}(\widehat{\delta },·)\right]$ demonstrates the expected value of $\tilde{\mathcal{K}}(\widehat{\delta },·)$.
• differentiable of m.s type at ${\widehat{\delta }}_{\circ }$, if random variable ${\tilde{\mathcal{K}}}^{\prime }(\widehat{\delta },·):I\times \Lambda :\to \mathbb{R}$ exist, such that

  $$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}^{\prime }({\widehat{\delta }}_{\circ },·)=P-\underset{\widehat{\delta }\to {\widehat{\delta }}_{\circ }}{lim}{\displaystyle \frac{\tilde{\mathcal{K}}(\widehat{\delta },·)-\tilde{\mathcal{K}}({\widehat{\delta }}_{\circ },·)}{\widehat{\delta }-{\widehat{\delta }}_{\circ }}}.\end{array}$$
• The processes $\tilde{\mathcal{K}}(\widehat{\delta },·)$ is called m.s integrable with $E\left[\tilde{\mathcal{K}}(\widehat{\delta },·)\right]<\infty$. The random variable $Z:\Lambda \to \mathbb{R}$ is m.s integral of $\tilde{\mathcal{K}}(\widehat{\delta },·)$ if for each partition of $I=[{ı}_1,{\ell }_1]$ such that ${ı}_1={\delta }_0\le {\delta }_1\le {\delta }_2\le ,\cdots ,\le {\delta }_{\sigma }={\ell }_1$ and for all ${\widehat{\delta }}_k\in [{\delta }_{k-1},{\delta }_k]$, we have

  $$\begin{array}{c}\hfill \underset{\sigma \to \infty }{lim}E\left[{\left(\sum _{k=1}^{\sigma }\tilde{\mathcal{K}}({\widehat{\delta }}_k,·)({\widehat{\delta }}_k-{\widehat{\delta }}_{k-1})-z(.)\right)}^2\right]=0.\end{array}$$

This can be written as

$$\begin{array}{c}\hfill Z(.)={\int }_{{ı}_1}^{{\ell }_1}\tilde{\mathcal{K}}(\widehat{\delta },·)\mathrm{d}\widehat{\delta }(a.e).\end{array}$$

The m.s integral develops when the S.P $\tilde{\mathcal{K}}$ preserves m.s continuity.

Definition 6

([15]). A process $\tilde{\mathcal{K}}:I\times \Lambda \to \mathbb{R}$ is called a convex S.P, if

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}((1-\varrho ){ı}_1+\varrho {\ell }_1,·)\le (1-\varrho )\tilde{\mathcal{K}}({ı}_1,·)+\varrho \tilde{\mathcal{K}}({\ell }_1,·),\end{array}$$

holds $\forall {ı}_1,{\ell }_1\in I,\widehat{\delta }\in [0,1]$.

Kotrys proved the trapezoid inequality for convex stochastic processes in [16]. This inequality is described as

Theorem 5.

Consider $\tilde{\mathcal{K}}:I\times {\beta }_1\to \mathbb{R}$ be a convex stochastic and m.s continuous process in the interval $I\times {\beta }_1$. Then

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)\le {\displaystyle \frac{1}{{\ell }_1+{ı}_1}}\tilde{\mathcal{K}}(\delta ,·)\mathrm{d}\widehat{\delta }\le {\displaystyle \frac{\tilde{\mathcal{K}}({ı}_1,·)+({\ell }_1,·)}{2}},\end{array}$$

(1)

for all ${ı}_1,{\ell }_1\in I$ and ${\ell }_1<{ı}_1$.

Now, we are demonstrating the notion of a center-radius S.P.

Definition 7

(see [21]). Let $\hslash :[0,1]\to {\mathbb{R}}^{+}$. Any interval-valued ($I.V$) S.P $\tilde{\mathcal{K}}(\widehat{\delta },·)=[{\tilde{\mathcal{K}}}_c(\widehat{\delta },·),{\tilde{\mathcal{K}}}_r(\widehat{\delta },·)]$ is said to be $I.V$ cr-ℏ-convex S.P, if

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}((1-\varrho ){ı}_1+\varrho {\ell }_1,·){⪯}_{cr}\hslash (1-\varrho )\tilde{\mathcal{K}}({ı}_1,·)+\hslash \left(\widehat{\delta }\right)\tilde{\mathcal{K}}({\ell }_1,·),\widehat{\delta }\in [0,1].\end{array}$$

Hafiz [30] studied the Stochastic analogue of Riemann-Liouville (RL)-fractional integral operators.

Definition 8.

Let $\tilde{\mathcal{K}}(\widehat{\delta },·)=[{\tilde{\mathcal{K}}}_c\left(\widehat{\delta }\right),{\tilde{\mathcal{K}}}_r\left(\widehat{\delta }\right)]$ and ${\tilde{\mathcal{K}}}_c(\widehat{\delta },·)$ and ${\tilde{\mathcal{K}}}_r(\widehat{\delta },·)$ are m.s Riemann integrable on $[{ı}_1,{\ell }_1]$. Then

$$\begin{array}{c}\hfill J_{{\widehat{\delta }}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)={\displaystyle \frac{1}{\Gamma \left({\beta }_1\right)}}{\int }_{\widehat{\delta }}^{{\ell }_1}{({\ell }_1-\widehat{\delta })}^{{\beta }_1-1}\tilde{\mathcal{K}}(\widehat{\delta },·)\mathrm{d}\widehat{\delta },{\ell }_1>\widehat{\delta },\end{array}$$

and

$$\begin{array}{c}\hfill J_{{{\delta }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)={\displaystyle \frac{1}{\Gamma \left({\beta }_1\right)}}{\int }_{{ı}_1}^{{\delta }_1}{(\widehat{\delta }-{ı}_1)}^{{\beta }_1-1}\tilde{\mathcal{K}}(\widehat{\delta },·)\mathrm{d}\widehat{\delta },{ı}_1<{\delta }_1,\end{array}$$

with ${\beta }_1\ge 0$. We observe that

$$\begin{array}{c}\hfill J_{{\widehat{\delta }}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)=\left[J_{{\widehat{\delta }}^{+}}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({\ell }_1,·),J_{{\widehat{\delta }}^{+}}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({\ell }_1,·)\right],\end{array}$$

and

$$\begin{array}{c}\hfill J_{{{\delta }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)=\left[J_{{{\delta }_1}^{-}}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({ı}_1,·),J_{{{\delta }_1}^{-}}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({ı}_1,·)\right].\end{array}$$

Recently, in [25], authors introduced the concept of super-quadratic stochastic processes.

Definition 9.

Suppose that $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to {\mathbb{R}}_I$ be an $I.V$.S.P such that $\tilde{\mathcal{K}}=[\underset{-}{\tilde{\mathcal{K}}},\stackrel{-}{\tilde{\mathcal{K}}}]=\langle {\tilde{\mathcal{K}}}_c,{\tilde{\mathcal{K}}}_r\rangle$ and $\hslash \ge 0$. Then $\tilde{\mathcal{K}}$ is assumed to be an $I.V$-ℏ-cr super-quadratic S.P, if

$$\begin{array}{cc}\hfill & \tilde{\mathcal{K}}((1-\varrho ){ı}_1+\varrho {\ell }_1,·)\hfill \\ \hfill & {⪯}_{cr}\varrho [\tilde{\mathcal{K}}({\ell }_1,·)-\tilde{\mathcal{K}}((1-\varrho )|{ı}_1-{\ell }_1|,·)]+(1-\varrho )[\tilde{\mathcal{K}}({ı}_1,·)-\tilde{\mathcal{K}}\left(\delta \right|{ı}_1-{\ell }_1|,·)],\hfill \end{array}$$

holds for all $\widehat{\delta }\in [{ı}_1,{\ell }_1]$ and for each $\varrho \in [0,1]$.

First, we investigate a new generalization of Definition 9 and its related inequalities with applications. Next, we prove our main results.

3. Totally Ordered-ℏ-Super-Quadratic Stochastic Processes

Now, we provide the concept of $cr$-super-quadratic S.P., which operates on the centre-radius relations and nonnegative mapping ℏ.

Definition 10.

Suppose that $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to {\mathbb{R}}_I$ be an $I.V$.S.P such that $\tilde{\mathcal{K}}=[\underset{-}{\tilde{\mathcal{K}}},\stackrel{-}{\tilde{\mathcal{K}}}]=\langle {\tilde{\mathcal{K}}}_c,{\tilde{\mathcal{K}}}_r\rangle$ and $\hslash \ge 0$. Then $\tilde{\mathcal{K}}$ is assumed to be an $I.V$-ℏ-cr super-quadratic S.P, if

$$\begin{array}{cc}\hfill & \tilde{\mathcal{K}}((1-\varrho ){ı}_1+\varrho {\ell }_1,·)\hfill \\ \hfill & {⪯}_{cr}\hslash \left(\varrho \right)[\tilde{\mathcal{K}}({\ell }_1,·)-\tilde{\mathcal{K}}((1-\varrho )|{ı}_1-{\ell }_1|,·)]+\hslash (1-\varrho )[\tilde{\mathcal{K}}({ı}_1,·)-\tilde{\mathcal{K}}\left(\delta \right|{ı}_1-{\ell }_1|,·)],\hfill \end{array}$$

holds for all $\widehat{\delta }\in [{ı}_1,{\ell }_1]$ and for each $\varrho \in [0,1]$.

Remark 1.

By taking $\hslash \left(\varrho \right)=\varrho$, $\hslash \left(\varrho \right)={\varrho }^s$, $\hslash \left(\varrho \right)={\varrho }^{-s}$, $\hslash \left(\varrho \right)=\varrho (1-\varrho )$, $\hslash \left(\varrho \right)=1$, and $\hslash \left(\varrho \right)=exp\left(\varrho \right)-1$ in Definition 10, we obtain class of $I.V$-cr [25], $I.V$-cr-s, $I.V$-cr-s-Godunova, $I.V$-cr-$tgs$, $I.V$-cr-P, and $I.V$-cr-exponential super-quadratic S.P, respectively.

Here, we represent the collection of ℏ-super-quadratic S.P and $I.V$-cr-ℏ super-quadratic S.P defined over $[{ı}_1,{\ell }_1]$ by $SSSP([{ı}_1,{\ell }_1],\hslash )$ and $SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$ respectively.

Proposition 1.

Let us consider $\tilde{\mathcal{K}},g:[{ı}_1,{\ell }_1]\to \mathbb{R}$ are two $I.V$ mappings. If $\tilde{\mathcal{K}},g\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$. Then

• $\tilde{\mathcal{K}}+g\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$.
• $m\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$, $m\ge 0$.

Proof. 

From Definition and $(\tilde{\mathcal{K}}+g)\left(\delta \right)=\tilde{\mathcal{K}}\left(\delta \right)+g\left(\delta \right)$, we have

$$\begin{array}{cc}\hfill & (\tilde{\mathcal{K}}+g)((1-\varrho ){ı}_1+\varrho {\ell }_1,·)\hfill \\ \hfill & {⪯}_{cr}\hslash \left(\varrho \right)[(\tilde{\mathcal{K}}+g)({\ell }_1,·)-(\tilde{\mathcal{K}}+g)((1-\varrho )|{ı}_1-{\ell }_1|,·)]+\hslash (1-\varrho )[(\tilde{\mathcal{K}}+g)({ı}_1,·)-(\tilde{\mathcal{K}}+g)\left(\delta \right|{ı}_1-{\ell }_1|,·)]\hfill \\ \hfill & =\hslash \left(\varrho \right)[\tilde{\mathcal{K}}({\ell }_1,·)-\tilde{\mathcal{K}}((1-\varrho )|{ı}_1-{\ell }_1|,·)]+\hslash (1-\varrho )[\tilde{\mathcal{K}}({ı}_1,·)-\tilde{\mathcal{K}}\left(\delta \right|{ı}_1-{\ell }_1|,·)]\hfill \\ \hfill & +\hslash \left(\varrho \right)[g({\ell }_1,·)-g((1-\varrho )|{ı}_1-{\ell }_1|,·)]+\hslash (1-\varrho )[g({ı}_1,·)-g\left(\delta \right|{ı}_1-{\ell }_1|,·)]\hfill \end{array}$$

This completes the proof of first part and similarly, we can prove the second part. □

Proposition 2.

If $\tilde{\mathcal{K}}\in SSSQIF([{ı}_1,{\ell }_1],cr,{\hslash }_1)$ and ${\hslash }_1\left(\varrho \right)\le {\hslash }_2\left(\varrho \right)$. Then $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,{\hslash }_2)$.

Proof. 

One can easily prove that by the Definition 10 of $I.V$-cr-ℏ super-quadratic processes. □

Proposition 3.

Let $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to {\mathbb{R}}_I^{+}$ be an $I.V$.S.P. Then $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$ if ${\tilde{\mathcal{K}}}_c,{\tilde{\mathcal{K}}}_r\in SSSP([{ı}_1,{\ell }_1],\hslash )$.

Proof. 

Let ${\tilde{\mathcal{K}}}_c,{\tilde{\mathcal{K}}}_r\in SSSP([{ı}_1,{\ell }_1],h)$ and $\forall \widehat{\delta }\in [{ı}_1,{\ell }_1]$. Then by incorporating with cr relation, we have

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c((1-\varrho ){\ell }_1+\varrho {ı}_1,·)\le \hslash (1-\varrho ){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c((1-\varrho )|{\ell }_1-{ı}_1|,·)-\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c\left(\varrho \right|{\ell }_1-{ı}_1|,·),\end{array}$$

and

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_r((1-\varrho ){\ell }_1+\varrho {ı}_1,·)\le \hslash (1-\varrho ){\tilde{\mathcal{K}}}_r({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_r({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_r((1-\varrho )|{\ell }_1-{ı}_1|,·)-\hslash (1-\varrho ){\tilde{\mathcal{K}}}_r\left(\varrho \right|{\ell }_1-{ı}_1|,·).\end{array}$$

If

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c((1-\varrho ){\ell }_1+\varrho {ı}_1,·)\ne \hslash (1-\varrho ){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c((1-\varrho )|{\ell }_1-{ı}_1|,·)-\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c\left(\varrho \right|{\ell }_1-{ı}_1|,·),\end{array}$$

then $\forall \varrho \in (0,1)$ and for each $\widehat{\delta }\in [{ı}_1,{\ell }_1]$, we have

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c((1-\varrho ){\ell }_1+\varrho {ı}_1,·)<\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c((1-\varrho )|{\ell }_1-{ı}_1|,·)-\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c\left(\varrho \right|{\ell }_1-{ı}_1|,·).\end{array}$$

This implies that

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}((1-\varrho ){\ell }_1+\varrho {ı}_1,·){⪯}_{cr}\hslash (1-\varrho )\tilde{\mathcal{K}}({\ell }_1,·)+\hslash \left(\varrho \right)\tilde{\mathcal{K}}({ı}_1,·)-\hslash \left(\varrho \right)\tilde{\mathcal{K}}((1-\varrho )|{\ell }_1-{ı}_1|,·)-\hslash (1-\varrho )\tilde{\mathcal{K}}\left(\varrho \right|{\ell }_1-{ı}_1|,·)\end{array}$$

Otherwise, for all $\varrho \in (0,1)$ and for each $\widehat{\delta }\in [{ı}_1,{\ell }_1]$, we have

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_r((1-\varrho ){\ell }_1+\varrho {ı}_1,·)\le \hslash (1-\varrho ){\tilde{\mathcal{K}}}_r({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_r({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_r((1-\varrho )|{\ell }_1-{ı}_1|,·)-\hslash (1-\varrho ){\tilde{\mathcal{K}}}_r\left(\varrho \right|{\ell }_1-{ı}_1|,·),\end{array}$$

The above inequality meets the cr relation. This implies that

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}((1-\varrho ){\ell }_1+\varrho {ı}_1,·){⪯}_{cr}\hslash (1-\varrho )\tilde{\mathcal{K}}({\ell }_1,·)+\hslash \left(\varrho \right)\tilde{\mathcal{K}}({ı}_1,·)-\hslash \left(\varrho \right)\tilde{\mathcal{K}}((1-\varrho )|{\ell }_1-{ı}_1|,·)-\hslash (1-\varrho )\tilde{\mathcal{K}}\left(\varrho \right|{\ell }_1-{ı}_1|,·).\end{array}$$

This completes the proof. □

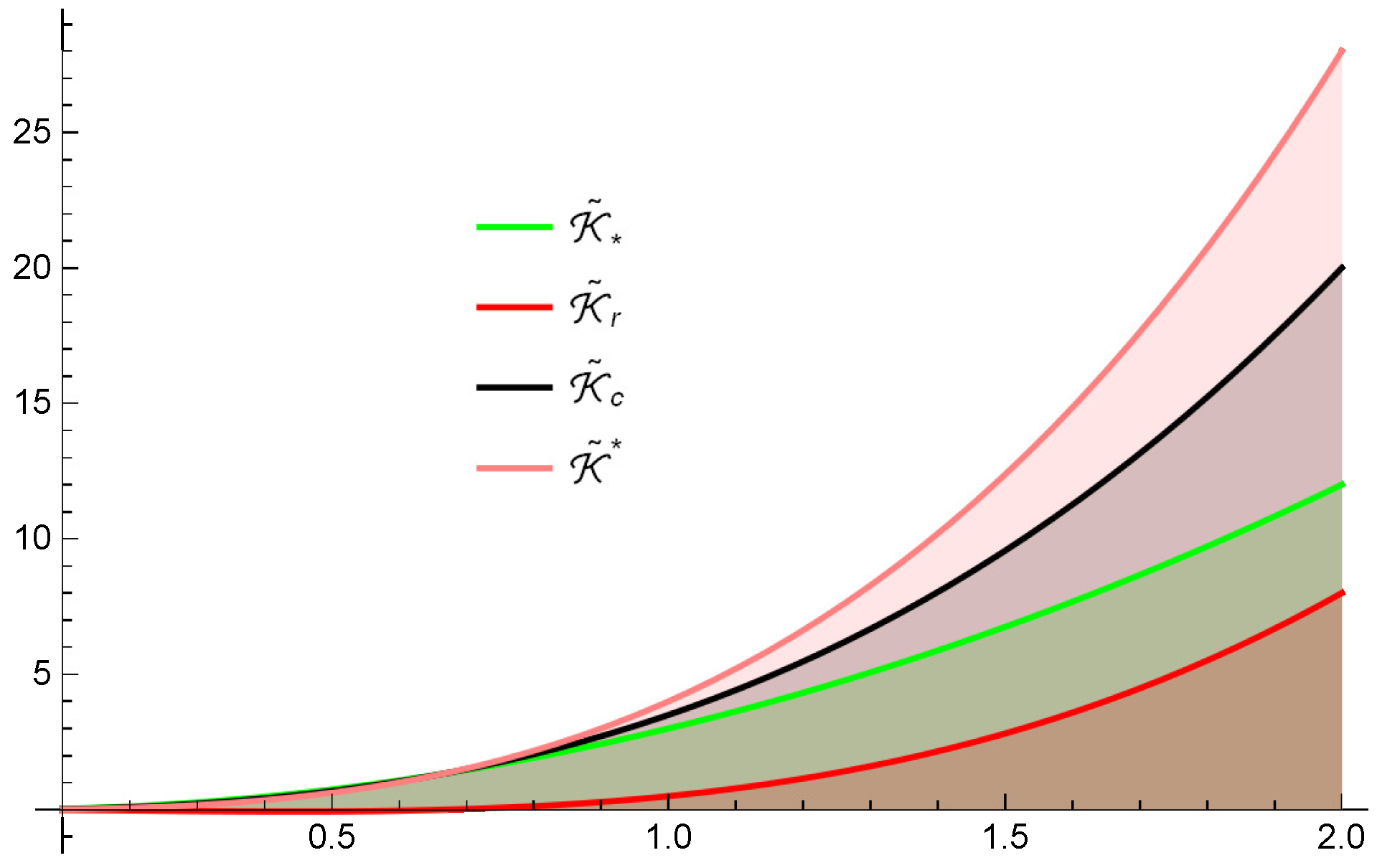
Example 1.

Let $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to {\mathbb{R}}_{\mathbb{I}}^{+}$ be defined as

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left(\widehat{\delta }\right)=[3{\widehat{\delta }}^2,{\widehat{\delta }}^2+3{\widehat{\delta }}^3],\widehat{\delta }\in [0,2]\end{array}$$

where $\underset{-}{\tilde{\mathcal{K}}}\left(\widehat{\delta }\right)=3{\widehat{\delta }}^2$ and $\stackrel{-}{\tilde{\mathcal{K}}}\left(\widehat{\delta }\right)={\widehat{\delta }}^2+3{\widehat{\delta }}^3$. Obviously, $\underset{-}{\tilde{\mathcal{K}}}\left(\widehat{\delta }\right)$ and $\stackrel{-}{\tilde{\mathcal{K}}}\left(\widehat{\delta }\right)$ are ℏ-cr super-quadratic S.P mappings and they are given as

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c\left(\widehat{\delta }\right)={\displaystyle \frac{4{\widehat{\delta }}^2+3{\widehat{\delta }}^3}{2}},{\tilde{\mathcal{K}}}_r\left(\widehat{\delta }\right)={\displaystyle \frac{3{\widehat{\delta }}^3-2{\widehat{\delta }}^2}{2}}.\end{array}$$

By choosing $\widehat{\delta }\in [0,2]$, the visualization of mappings are given below:

In Figure 1, ${\tilde{\mathcal{K}}}_{*}$ and ${\tilde{\mathcal{K}}}^{*}$ demonstrates the both lower and upper mappings respectively.

Theorem 6.

Assume that $\hslash :(0,1]:\to [0,\infty )$ be a non-negative supermultiplicative mapping. If $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$. Then

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right){⪯}_{cr}\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\tilde{\mathcal{K}}({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right),\end{array}$$

(2)

for ${\widehat{\delta }}_q\in [{ı}_1,{\ell }_1]$, ${\varrho }_q\in [0,1]$ such that ${\mathcal{C}}_{\sigma }={\sum }_{q=1}^{\sigma }{\delta }_q$.

Proof. 

If $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$, then

$$\begin{array}{cc}\hfill & 〈{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right),{\tilde{\mathcal{K}}}_r\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)〉\hfill \\ \hfill & {⪯}_{cr}〈{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\delta }_q{\tilde{\mathcal{K}}}_c\left({\widehat{\delta }}_q\right),·\right)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right),\hfill \\ \hfill & \sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_r({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_r\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right)〉\hfill \end{array}$$

Through cr relation, we can split the above inequality into the following form

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)\le \sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right),\end{array}$$

(3)

and

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_r\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)\le \sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_r({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_r\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\end{array}$$

(4)

We prove our result by utilizing the principle of induction. By taking ${\displaystyle \frac{{\delta }_1}{{\mathcal{C}}_2}}={\beta }_1$, ${\displaystyle \frac{{\delta }_2}{{\mathcal{C}}_2}}=1-{\beta }_1$ and $\sigma =2$, the following Inequalities obtained from (3) and (4).

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_c\left({\beta }_1{ı}_1+(1-{\beta }_1){\ell }_1,·\right)& \le \hslash \left({\beta }_1\right){\tilde{\mathcal{K}}}_c({ı}_1,·)+\hslash \left((1-{\beta }_1)\right){\tilde{\mathcal{K}}}_c({\ell }_1,·)-\hslash \left({\beta }_1\right){\tilde{\mathcal{K}}}_c\left((1-{\beta }_1)|{ı}_1-{\ell }_1|,·\right)\hfill \\ \hfill & -\hslash \left((1-{\beta }_1)\right){\tilde{\mathcal{K}}}_c\left({\beta }_1|{ı}_1-{\ell }_1|,·\right),\hfill \end{array}$$

(5)

and

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_r\left({\beta }_1{ı}_1+(1-{\beta }_1){\ell }_1,·\right)& \le \hslash \left({\beta }_1\right){\tilde{\mathcal{K}}}_r({ı}_1,·)+\hslash \left((1-{\beta }_1)\right){\tilde{\mathcal{K}}}_r({\ell }_1,·)-\hslash \left({\beta }_1\right){\tilde{\mathcal{K}}}_r\left((1-{\beta }_1)|{ı}_1-{\ell }_1|,·\right)\hfill \\ \hfill & -\hslash \left((1-{\beta }_1)\right){\tilde{\mathcal{K}}}_r\left({\beta }_1|{ı}_1-{\ell }_1|,·\right).\hfill \end{array}$$

(6)

The definition of $I.V$-cr-ℏ super-quadratic S.P attained by comparing (5) and (6). Moreover, we assume that (2) is satisfied for $\sigma -1$, then

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left(\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right),·\right){⪯}_{cr}\sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right)\tilde{\mathcal{K}}({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right)\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right)\right|,·\right).\end{array}$$

This can be switched as

$$\begin{array}{cc}\hfill & 〈{\tilde{\mathcal{K}}}_c\left(\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right),·\right),{\tilde{\mathcal{K}}}_r\left(\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right),·\right)〉\hfill \\ \hfill & {⪯}_{cr}〈{\tilde{\mathcal{K}}}_c\left(\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}{\tilde{\mathcal{K}}}_c\left({\widehat{\delta }}_q\right),·\right)-\sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right){\tilde{\mathcal{K}}}_c\left(\left|{\widehat{\delta }}_q-\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right)\right|,·\right),\hfill \\ \hfill & \sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right){\tilde{\mathcal{K}}}_r({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right){\tilde{\mathcal{K}}}_r\left(\left|{\widehat{\delta }}_q-\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right)\right|,·\right)〉\hfill \end{array}$$

This implies that

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c\left(\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right),·\right)\le \sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right){\tilde{\mathcal{K}}}_c({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right){\tilde{\mathcal{K}}}_c\left(\left|{\widehat{\delta }}_q-\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right)\right|,·\right),\end{array}$$

(7)

and

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_r\left(\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right),·\right)\le \sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right){\tilde{\mathcal{K}}}_r({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right){\tilde{\mathcal{K}}}_r\left(\left|{\widehat{\delta }}_q-\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right)\right|,·\right).\end{array}$$

(8)

Now, we show that for $q=\sigma$ the relation (2) is valid.

$$\begin{array}{cc}\hfill & {\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)\hfill \\ \hfill & ={\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{\delta }_n{x}_{\sigma }}{{\mathcal{C}}_{\sigma }}}+{\displaystyle \frac{{\mathcal{C}}_{\sigma -1}}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right),·\right)\hfill \\ \hfill & \le \hslash \left({\displaystyle \frac{{\delta }_{\sigma }}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c({\widehat{\delta }}_{\sigma },·)+\hslash \left({\displaystyle \frac{{\mathcal{C}}_{\sigma -1}}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c\left(\sum _{q=1}^{\sigma -1}\left({\displaystyle \frac{{\delta }_q{\widehat{\delta }}_q}{{\mathcal{C}}_{\sigma -1}}}\right),·\right)-\hslash \left({\displaystyle \frac{{\delta }_{\sigma }}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{\mathcal{C}}_{\sigma -1}}{{\mathcal{C}}_{\sigma }}}\left|{\widehat{\delta }}_{\sigma }-\sum _{q=1}^{\sigma -1}\left({\displaystyle \frac{{\delta }_q{\widehat{\delta }}_q}{{\mathcal{C}}_{\sigma -1}}}\right)\right|,·\right)\hfill \\ \hfill & -\hslash \left({\displaystyle \frac{{\mathcal{C}}_{\sigma -1}}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{\delta }_{\sigma }}{{\mathcal{C}}_{\sigma }}}\left|{\widehat{\delta }}_{\sigma }-\sum _{q=1}^{\sigma -1}\left({\displaystyle \frac{{\delta }_q{\widehat{\delta }}_q}{{\mathcal{C}}_{\sigma -1}}}\right)\right|,·\right).\hfill \end{array}$$

(9)

Using (7) in (9) and supermultiplicative property of ℏ, we recapture

$$\begin{array}{cc}\hfill & {\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)\hfill \\ \hfill & \le \hslash \left({\displaystyle \frac{{\delta }_{\sigma }}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c({\widehat{\delta }}_{\sigma },·)+\hslash \left({\displaystyle \frac{{\mathcal{C}}_{\sigma -1}}{{\mathcal{C}}_{\sigma }}}\right)\left[\sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right){\tilde{\mathcal{K}}}_c({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma -1}\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\right){\tilde{\mathcal{K}}}_c\left(\left|{\widehat{\delta }}_q-\sum _{q=1}^{\sigma -1}{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma -1}}}\left({\widehat{\delta }}_q\right)\right|,·\right)\right]\hfill \\ \hfill & -\hslash \left({\displaystyle \frac{{\delta }_{\sigma }}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{\mathcal{C}}_{\sigma -1}}{{\mathcal{C}}_{\sigma }}}\left|{\widehat{\delta }}_{\sigma }-\sum _{q=1}^{\sigma -1}\left({\displaystyle \frac{{\delta }_q{\widehat{\delta }}_q}{{\mathcal{C}}_{\sigma -1}}}\right)\right|,·\right)\hfill \\ \hfill & -\hslash \left({\displaystyle \frac{{\mathcal{C}}_{\sigma -1}}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{\delta }_{\sigma }}{{\mathcal{C}}_{\sigma }}}\left|{\widehat{\delta }}_{\sigma }-\sum _{q=1}^{\sigma -1}\left({\displaystyle \frac{{\delta }_q{\widehat{\delta }}_q}{{\mathcal{C}}_{\sigma -1}}}\right)\right|,·\right).\hfill \end{array}$$

Thus, we have

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)\le \sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right)\end{array}$$

(10)

Similarly,

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_r\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)\le \sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_r({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_r\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\end{array}$$

(11)

Applying the cr relation on (10), and (11) yield the intended result. □

Here, we extract few Jensen’s type inequalities under certain substitutions in Theorem 6.

• Theorem 6 generates the following inequality for $I.V$-cr-P super-quadratic S.P by taking ${\sum }_{q=1}^{\sigma }{\delta }_q={\mathcal{C}}_{\sigma }=1$,

  $$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left(\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right){⪯}_{cr}\sum _{q=1}^{\sigma }\hslash \left({\varrho }_q\right)\tilde{\mathcal{K}}({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\varrho }_q\right)\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\end{array}$$
• Theorem 6 yields the inequality for $I.V$-cr super-quadratic S.P by substituting $\hslash \left(\varrho \right)=\varrho$, which is proved in [25],

  $$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right){⪯}_{cr}\sum _{q=1}^{\sigma }{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\tilde{\mathcal{K}}({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }{\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\end{array}$$
• Theorem 6 results the following inequality for $I.V$-cr-s super-quadratic S.P by substituting $\hslash \left(\varrho \right)={\varrho }^s$,

  $$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right){⪯}_{cr}\sum _{q=1}^{\sigma }{\left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)}^{s}f({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }{\left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)}^s\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\end{array}$$
• Inserting $\hslash \left(\varrho \right)={\varrho }^{-s}$ in Theorem 6, we recover the Jensen’s inequality for $I.V$-cr-s Godunova super-quadratic S.P,

  $$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right){⪯}_{cr}\sum _{q=1}^{\sigma }{\left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)}^{-s}\tilde{\mathcal{K}}({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }{\left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)}^{-s}\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\end{array}$$
• Theorem 6 produces the following inequality for $I.V$-cr-P super-quadratic S.P by substituting $\hslash \left(\varrho \right)=1$,

  $$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right){⪯}_{cr}\sum _{q=1}^{\sigma }{\left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)}^{-s}\tilde{\mathcal{K}}({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }{\left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)}^{-s}\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\end{array}$$
• Theorem 6 yields the Jensen’s like inequality for $I.V$-cr exponential super-quadratic S.P by substituting $\hslash \left(\varrho \right)=exp\left(\varrho \right)-1$,

  $$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right){⪯}_{cr}\sum _{q=1}^{\sigma }\left[exp\left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)-1\right]\tilde{\mathcal{K}}({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\left[exp\left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)-1\right]\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=0}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\end{array}$$

Next, we prove another Jensen’s like inequality.

Theorem 7.

If $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$ and ${\delta }_1,{\delta }_2,{\widehat{\delta }}_3\in [{ı}_1,{\ell }_1]$ with ${\delta }_1<{\delta }_2<{\widehat{\delta }}_3$ such that ${\delta }_2-{\delta }_1,{\widehat{\delta }}_3-{\delta }_2$ and ${\widehat{\delta }}_3-{\delta }_1\in [0,1]$. Then

$$\begin{array}{c}\hfill \hslash ({\widehat{\delta }}_3-{\delta }_1)\tilde{\mathcal{K}}({\delta }_2,·){⪯}_{cr}\hslash ({\widehat{\delta }}_3-{\delta }_2)[\tilde{\mathcal{K}}({\delta }_1,·)-\tilde{\mathcal{K}}({\delta }_2-{\delta }_1,·)]+\hslash ({\delta }_2-{\delta }_1)[\tilde{\mathcal{K}}({\widehat{\delta }}_3,·)-\tilde{\mathcal{K}}({\widehat{\delta }}_3-{\delta }_2,·)].\end{array}$$

Proof. 

Assuming that ${\delta }_1,{\delta }_2,{\widehat{\delta }}_3\in I$ with ${\delta }_1<{\delta }_2<{\widehat{\delta }}_3$ such that ${\delta }_2-{\delta }_1,{\widehat{\delta }}_3-{\delta }_2$ and ${\widehat{\delta }}_3-{\delta }_1\in [0,1]$. Since $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$, and ℏ possess the supermultiplicative, then

$$\begin{array}{cc}\hfill & {\tilde{\mathcal{K}}}_c({\delta }_2,·)={\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{\widehat{\delta }}_3-{\delta }_2}{{\widehat{\delta }}_3-{\delta }_1}}{\delta }_1+{\displaystyle \frac{{\delta }_2-{\delta }_1}{{\widehat{\delta }}_3-{\delta }_1}}{\delta }_2,·\right)\hfill \\ \hfill & \le \hslash \left({\displaystyle \frac{{\widehat{\delta }}_3-{\delta }_2}{{\widehat{\delta }}_3-{\delta }_1}}\right)\left[\tilde{\mathcal{K}}({\delta }_1,·)-\tilde{\mathcal{K}}\left({\displaystyle \frac{{\delta }_2-{\delta }_1}{{\widehat{\delta }}_3-{\delta }_1}}|{\widehat{\delta }}_3-{\delta }_1|,·\right)\right]\hfill \\ \hfill & +\hslash \left({\displaystyle \frac{{\delta }_2-{\delta }_1}{{\widehat{\delta }}_3-{\delta }_1}}\right)\left[\tilde{\mathcal{K}}({\widehat{\delta }}_3,·)-\tilde{\mathcal{K}}\left({\displaystyle \frac{{\widehat{\delta }}_3-{\delta }_2}{{\widehat{\delta }}_3-{\delta }_1}}|{\widehat{\delta }}_3-{\delta }_1|,·\right)\right].\hfill \end{array}$$

The product of $\hslash ({\widehat{\delta }}_3-{\delta }_1)$ and previous inequality and leveraging the supermultiplicative property of ℏ, we have

$$\begin{array}{c}\hfill \hslash ({\widehat{\delta }}_3-{\delta }_1){\tilde{\mathcal{K}}}_c({\delta }_2,·)\le \hslash ({\widehat{\delta }}_3-{\delta }_2)[{\tilde{\mathcal{K}}}_c({\delta }_1,·)-{\tilde{\mathcal{K}}}_c({\delta }_2-{\delta }_1,·)]+\hslash ({\delta }_2-{\delta }_1)[{\tilde{\mathcal{K}}}_c({\widehat{\delta }}_3,·)-{\tilde{\mathcal{K}}}_c({\widehat{\delta }}_3-{\delta }_2,·)].\end{array}$$

(12)

Similarly, we get

$$\begin{array}{c}\hfill \hslash ({\widehat{\delta }}_3-{\delta }_1){\tilde{\mathcal{K}}}_r({\delta }_2,·)\le \hslash ({\widehat{\delta }}_3-{\delta }_2)[{\tilde{\mathcal{K}}}_r({\delta }_1,·)-{\tilde{\mathcal{K}}}_r({\delta }_2-{\delta }_1,·)]+\hslash ({\delta }_2-{\delta }_1)[{\tilde{\mathcal{K}}}_r({\widehat{\delta }}_3,·)-{\tilde{\mathcal{K}}}_r({\widehat{\delta }}_3-{\delta }_2,·)].\end{array}$$

(13)

Coupling the (12) and (13) by cr order relation, we acquire the desired inequality. □

The converse Jensen’s inequality associated with $I.V$-ℏ-cr super-quadratic S.P.

Theorem 8.

For ${\delta }_q\ge 0$ and $(a,\mathcal{W})\subseteq I$. Let $\hslash :(0,1]\to [0,\infty )$ be non negative supermultiplicative mapping and $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$. Then

$$\begin{array}{cc}\hfill \sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\tilde{\mathcal{K}}({\widehat{\delta }}_q,·)& {⪯}_{cr}\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\left[\hslash \left({\displaystyle \frac{\mathcal{W}-{\widehat{\delta }}_q}{\mathcal{W}-a}}\right)\tilde{\mathcal{K}}(a,·)+\hslash \left({\displaystyle \frac{{\widehat{\delta }}_q-a}{\mathcal{W}-a}}\right)\tilde{\mathcal{K}}(\mathcal{W},·)\right]\hfill \\ \hfill & -\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\left[\hslash \left({\displaystyle \frac{\mathcal{W}-{\widehat{\delta }}_q}{\mathcal{W}-a}}\right)\tilde{\mathcal{K}}({\widehat{\delta }}_q-a,·)+\hslash \left({\displaystyle \frac{{\widehat{\delta }}_q-a}{\mathcal{W}-a}}\right)\tilde{\mathcal{K}}(\mathcal{W}-{\widehat{\delta }}_q,·)\right].\hfill \end{array}$$

Proof. 

By inserting ${\widehat{\delta }}_q=a,{\ell }_1={\widehat{\delta }}_q$ and ${\widehat{\delta }}_3=\mathcal{W}$ in Theorem 7 and taking the product of obtained inequality by $\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)$. Finally by applying the sum from $q=1$ to $q=\sigma$, we get our desired outcome. □

The $I.V$-cr Jensen-Mercer Stochastic process inequality is given below.

Theorem 9.

Let $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,{\hslash }_1)$ and ${\widehat{\delta }}_q\in ({ı}_1,{\ell }_1)$ and ${\delta }_q\ge 0$, then

$$\begin{array}{cc}\hfill \tilde{\mathcal{K}}\left({ı}_1+{\ell }_1-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)& {⪯}_{cr}\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\tilde{\mathcal{K}}({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)[\tilde{\mathcal{K}}({\widehat{\delta }}_q-{ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1-{\widehat{\delta }}_q,·)]\hfill \\ \hfill & -\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)\tilde{\mathcal{K}}\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\hfill \end{array}$$

Proof. 

Presume that ${\tilde{\mathcal{K}}}_c$ and ${\tilde{\mathcal{K}}}_r$ are ℏ super-quadratic S.P then from Theorem 2, we have

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_c\left({ı}_1+{\ell }_1-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)& {⪯}_{cr}{\tilde{\mathcal{K}}}_c({ı}_1,·)+{\tilde{\mathcal{K}}}_c({\ell }_1,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)[{\tilde{\mathcal{K}}}_c({\widehat{\delta }}_q-{ı}_1,·)+{\tilde{\mathcal{K}}}_c({\ell }_1-{\widehat{\delta }}_{\varkappa },·)]\hfill \\ \hfill & -\sum _{\varkappa =1}^{\sigma }\hslash \left({\displaystyle \frac{{\delta }_{\varkappa }}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_c\left(\left|{\widehat{\delta }}_{\varkappa }-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{\varkappa =1}^{\sigma }{\delta }_{\varkappa }{\widehat{\delta }}_{\varkappa }\right|,·\right).\hfill \end{array}$$

(14)

and

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_r\left({ı}_1+{\ell }_1-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma }{\varrho }_q{\widehat{\delta }}_q,·\right)& {⪯}_{cr}{\tilde{\mathcal{K}}}_r({ı}_1,·)+{\tilde{\mathcal{K}}}_r({\ell }_1,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_r({\widehat{\delta }}_q,·)-\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right)[{\tilde{\mathcal{K}}}_r({\widehat{\delta }}_q-{ı}_1,·)+{\tilde{\mathcal{K}}}_r({\ell }_1-{\widehat{\delta }}_q,·)]\hfill \\ \hfill & -\sum _{q=1}^{\sigma }\hslash \left({\displaystyle \frac{{\varrho }_q}{{\mathcal{C}}_{\sigma }}}\right){\tilde{\mathcal{K}}}_r\left(\left|{\widehat{\delta }}_q-{\displaystyle \frac{1}{{\mathcal{C}}_{\sigma }}}\sum _{q=1}^{\sigma }{\varrho }_q{\widehat{\delta }}_q\right|,·\right).\hfill \end{array}$$

(15)

Leveraging the concept of cr ordered relation and inequalities (14), and (15), we attain the intended inequality. □

3.1. Fractional Set-Valued Hadamard’s Inequalities

This part presents the set-valued Hermite-Hadamard’s like inequalities pertaining to generalized class of totally ordered super-quadratic stochastic processes.

Lemma 1.

If $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$, then

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){⪯}_{cr}\hslash \left({\displaystyle \frac{1}{2}},·\right)\tilde{\mathcal{K}}(\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{1}{2}}\right)\tilde{\mathcal{K}}({ı}_1+{\ell }_1-\widehat{\vartheta },·)-2\hslash \left({\displaystyle \frac{1}{2}}\right)\tilde{\mathcal{K}}\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right).\end{array}$$

Proof. 

Assume that $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to {\mathbb{R}}_I^{+}$ be $I.V$-ℏ-cr super-quadratic S.P, we have

$$\begin{array}{cc}\hfill & \tilde{\mathcal{K}}((1-\varrho ){\ell }_1+\varrho {ı}_1,·){⪯}_{cr}\hslash (1-\varrho ,·)\tilde{\mathcal{K}}({\ell }_1,·)+\hslash \left(\varrho \right)\tilde{\mathcal{K}}({ı}_1,·)-\hslash \left(\varrho \right)\tilde{\mathcal{K}}((1-\varrho )|{\ell }_1-{ı}_1|,·)\hfill \\ \hfill & -\hslash (1-\varrho )\tilde{\mathcal{K}}\left(\varrho \right|{\ell }_1-{ı}_1|,·).\hfill \end{array}$$

This inequality can also be written as

$$\begin{array}{c}〈{\tilde{\mathcal{K}}}_c((1-\varrho ){\ell }_1+\varrho {ı}_1,·),{\tilde{\mathcal{K}}}_r((1-\varrho ){\ell }_1+\varrho {ı}_1,·)〉\hfill \\ {⪯}_{cr}〈\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c((1-\varrho )|{\ell }_1-{ı}_1|,·)\hfill \\ -\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c\left(\varrho \right|{\ell }_1-{ı}_1|,·),\hslash (1-\varrho ){\tilde{\mathcal{K}}}_r({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_r({ı}_1,·)\hfill \\ -\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_r\left((1-\varrho )\right|{\ell }_1-{ı}_1|,·)-\hslash (1-\varrho ){\tilde{\mathcal{K}}}_r\left(\varrho \right|{\ell }_1-{ı}_1|,·)〉.\hfill \end{array}$$

Through cr relation, we dissolve aforementioned inequality in the following way

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_c((1-\varrho ){\ell }_1+\varrho {ı}_1,·)& <\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c((1-\varrho )|{\ell }_1-{ı}_1|,·)\hfill \\ \hfill & -\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c\left(\varrho \right|{\ell }_1-{ı}_1|,·),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_r((1-\varrho ){\ell }_1+\varrho {ı}_1,·)& <\hslash (1-\varrho ){\tilde{\mathcal{K}}}_r({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_r({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_r((1-\varrho )|{\ell }_1-{ı}_1|,·)\hfill \\ \hfill & -\hslash (1-\varrho ){\tilde{\mathcal{K}}}_r\left(\varrho \right|{\ell }_1-{ı}_1|,·).\hfill \end{array}$$

Firstly, considering the left center inequality

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_c((1-\varrho ){\ell }_1+\varrho {ı}_1,·)& <\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c\left(\right|{\ell }_1-(t{x}_2+(1-\varrho ){ı}_1|),·)\hfill \\ \hfill & -\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c\left(\right|{ı}_1-((1-\varrho ){ı}_1+\varrho {\ell }_1)|,·).\hfill \end{array}$$

Let $\vartheta ={\displaystyle \frac{1}{2}}$

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)& \le \hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c\left(\left|{\ell }_1-\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right)\right|,·\right)\hfill \\ \hfill & -\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c\left(\left|{ı}_1-\left({\displaystyle \frac{{\ell }_1+{ı}_1}{2}}\right)\right|,·\right).\hfill \end{array}$$

Changing ${\ell }_1$ by $\widehat{\vartheta }$ and ${ı}_1$ by ${ı}_1+{\ell }_1-\widehat{\vartheta }$, we get

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)& \le \hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)-\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c\left(\left|\widehat{\vartheta }-\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right)\right|,·\right)\hfill \\ \hfill & -\hslash \left({\displaystyle \frac{1}{2}},·\right){\tilde{\mathcal{K}}}_c\left(\left|{ı}_1+{\ell }_1-\widehat{\vartheta }-\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right)\right|,·\right)\hfill \\ \hfill {\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)& \le \hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)-2\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c\left(\left|\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right)\right|,·\right).\hfill \end{array}$$

(16)

Similarly,

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_r\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)\le \hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_r(\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_r({ı}_1+{\ell }_1-\widehat{\vartheta },·)-2\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_r\left(\left|\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right)\right|,·\right).\end{array}$$

(17)

Considering the inequalities (16) and (17), we have

$$\begin{array}{c}\hfill \tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){⪯}_{cr}\hslash \left({\displaystyle \frac{1}{2}}\right)\tilde{\mathcal{K}}(\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{1}{2}}\right)\tilde{\mathcal{K}}({ı}_1+{\ell }_1-\widehat{\vartheta },·)-2\hslash \left({\displaystyle \frac{1}{2}}\right)\tilde{\mathcal{K}}\left(\left|\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right)\right|,·\right).\end{array}$$

Finally, the proof is accomplished. □

Theorem 10.

If $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$, then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}\tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)+{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\tilde{\mathcal{K}}\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)\right).\hfill \end{array}$$

Proof. 

From $I.V$-cr-ℏ super-quadratic S.P, we have

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)& ={\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\displaystyle \frac{{\beta }_1}{2{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & ={\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Utilizing Lemma 1, we have

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)& \le {\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}\left[\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)\right.\hfill \\ \hfill & \left.-2\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_c\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\right]\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(18)

Similarly,

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_r\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)& \le {\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}\left[\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_r(\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_r({ı}_1+{\ell }_1-\widehat{\vartheta },·)\right.\hfill \\ \hfill & \left.-2\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_r\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\right]\mathrm{d}\widehat{\vartheta }\hfill \end{array}$$

From (18), we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)\hfill \\ \hfill & \le {\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}\left[{\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)+{\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)\right.\hfill \\ \hfill & \left.-2{\tilde{\mathcal{K}}}_c\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\right]\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & ={\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}\left({\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)+{\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\right.\hfill \\ \hfill & \left.-2{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_c\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\right]\hfill \\ \hfill & ={\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}\left({\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\right.\hfill \\ \hfill & +{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & -{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_c\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & \left.-{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_c\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\right]\hfill \\ \hfill & ={\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}\left({\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1},·\right)\mathrm{d}\widehat{\vartheta }\right.\hfill \\ \hfill & +{\int }_{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}^{{\ell }_1}{\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & -{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_c\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & \left.-{\int }_{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}^{{\ell }_1}{\tilde{\mathcal{K}}}_c\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\right]\hfill \\ \hfill & ={\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[{\int }_{{ı}_1}^{{\ell }_1}{\widetilde{\tilde{\mathcal{K}}}}_c(\widehat{\vartheta },·)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\right.\hfill \\ \hfill & \left.-{\int }_{{ı}_1}^{{\ell }_1}{\widetilde{\tilde{\mathcal{K}}}}_c\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\right]\hfill \\ \hfill & ={\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{ı}_1+}^{{\beta }_1}{\widetilde{\tilde{\mathcal{K}}}}_c({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}{\widetilde{\tilde{\mathcal{K}}}}_c({ı}_1,·)\right]\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}{\widetilde{\tilde{\mathcal{K}}}}_c\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(19)

Also, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\hslash \left(\frac{1}{2},·\right)}}{\tilde{\mathcal{K}}}_r\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)\hfill \\ \hfill & \le {\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{ı}_1+}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({ı}_1,·)\right]\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}{\tilde{\mathcal{K}}}_r\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(20)

According to the cr order relation, (19) and (20), we get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}\tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)\hfill \\ \hfill & \le {\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{ı}_1+}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)\right]\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\tilde{\mathcal{K}}\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Hence, the intended result is acquired. □

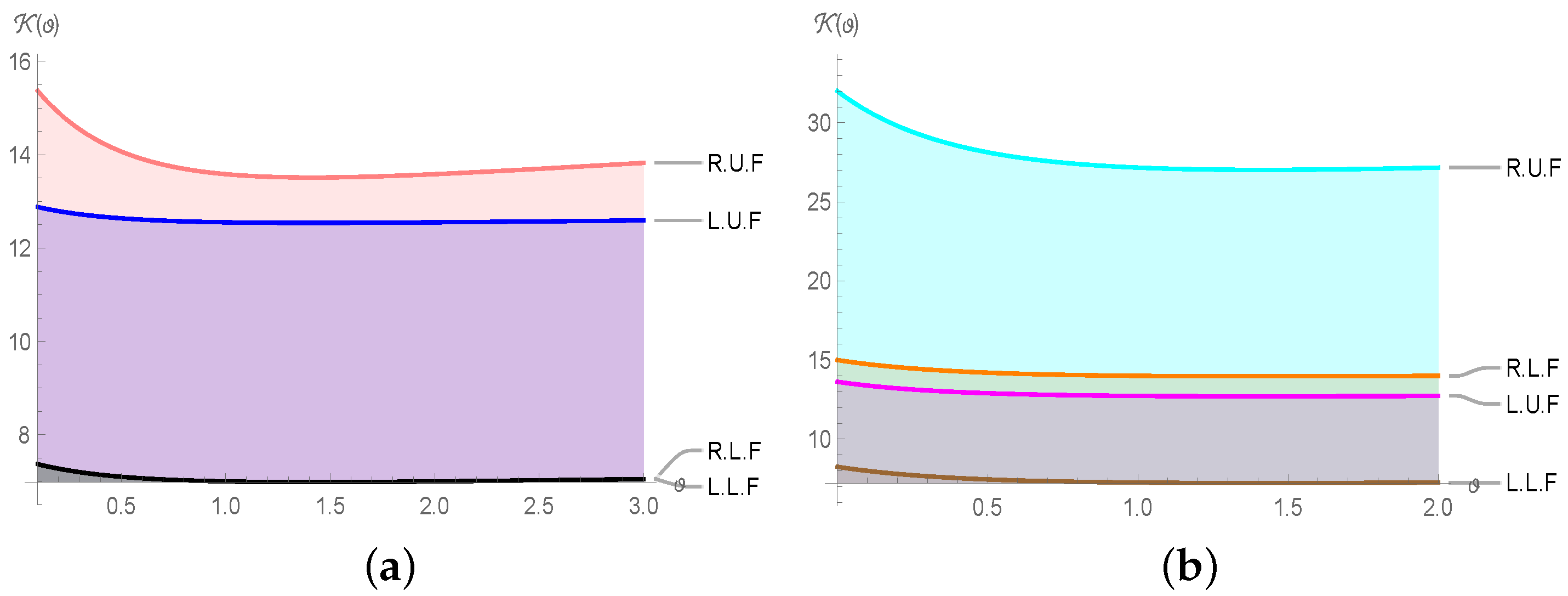
Example 2.

Let $\tilde{\mathcal{K}}\left(\widehat{\vartheta }\right)=[3{\widehat{\vartheta }}^2,{\widehat{\vartheta }}^2+3{\widehat{\vartheta }}^3]$ with $[{ı}_1,{\ell }_1]\to [1,2]$, which satisfies the Theorem 10.

$$\begin{array}{cc}\hfill Leftterm& =\left[{\displaystyle \frac{27}{4}},{\displaystyle \frac{99}{8}}\right]+\hslash \left({\displaystyle \frac{1}{2}}\right){\beta }_1{\int }_1^2\tilde{\mathcal{K}}\left|{\displaystyle \frac{3}{2}}-\widehat{\vartheta }\right|[{(2-\widehat{\vartheta })}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}]\mathrm{d}\widehat{\vartheta }.\hfill \\ \hfill Rightterm& =\hslash \left({\displaystyle \frac{1}{2}}\right){\beta }_1{\int }_1^2\tilde{\mathcal{K}}\left(\widehat{\vartheta }\right)[{(2-\widehat{\vartheta })}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}]\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

For graphical visualization, we have ${ı}_1=1$, ${\ell }_1=2$ and $0<{\beta }_1\le 2$. The Figure 2 provides the comparison between left and the right terms of Theorem 10.

Additionally, the numerical comparison for both cases are provided in the below

Table 1. Comparison between the sides of Theorem 10 for $\hslash \left(\varrho \right)=\varrho$.

${\mathit{\beta }}_1$	${\mathit{L}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{L}}^{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}^{*}\left({\mathit{\beta }}_1\right)$
$0.5$	7.1000	12.6377	7.1000	14.0667
$1.0$	7.0000	12.5521	7.0000	13.5833
$1.5$	6.9857	12.5404	6.9857	13.5143
$2.0$	7.0000	12.5521	7.0000	13.5833
$2.5$	7.0238	12.5712	7.0238	13.6984
$3.0$	7.0500	12.5922	7.0500	13.8250

and

Table 2. Comparison between the sides of Theorem 10 for $\hslash \left(\varrho \right)=1$.

${\mathit{\beta }}_1$	${\mathit{L}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{L}}^{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}^{*}\left({\mathit{\beta }}_1\right)$
$0.5$	7.4500	12.9003	14.2000	28.1333
$1.0$	7.2500	12.7292	14.0000	27.1667
$1.5$	7.2214	12.7058	13.9714	27.0286
$2.0$	7.2500	12.7292	14.0000	27.1667
$2.5$	7.2976	12.7675	14.0476	27.3968
$3.0$	7.3500	12.8094	14.1000	27.6500

.

Lemma 2.

If $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$, then

$$\begin{array}{cc}\hfill & \tilde{\mathcal{K}}(\widehat{\vartheta },·)+\tilde{\mathcal{K}}({ı}_1+{\ell }_1-\widehat{\vartheta },·){⪯}_{cr}\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·)-2\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)-2\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·).\hfill \end{array}$$

Proof. 

Presume that $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to {\mathbb{R}}_I^{+}$ be an $I.V$-cr-ℏ superquardatic S.P on $[{ı}_1,{\ell }_1]$, then ${\tilde{\mathcal{K}}}_c$ can be written as

$$\begin{array}{cc}\hfill {\tilde{\mathcal{K}}}_c((1-\varrho ){\ell }_1+\varrho {ı}_1,·)& \le \hslash (1-\varrho ){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c\left((1-\varrho )\right|{ı}_1-(\varrho {ı}_1+(1-\varrho ){\ell }_1|),·)\hfill \\ \hfill & -\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c\left(\varrho \right|{\ell }_1-((1-\varrho ){\ell }_1+\varrho {ı}_1|),·).\hfill \end{array}$$

Now choosing $\widehat{\vartheta }=((1-\varrho ){\ell }_1+\varrho {ı}_1)$ then by solving for $\vartheta$ we get $\vartheta ={\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}$

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)\le \hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c(\widehat{\vartheta }-{ı}_1,·)-\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({\ell }_1-\widehat{\vartheta },·)\end{array}$$

(21)

Replacing $\widehat{\vartheta }$ by ${ı}_1+{\ell }_1-\widehat{\vartheta }$ in (21), we acquire

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)\le \hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({\ell }_1,·)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({ı}_1,·)-\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c(\widehat{\vartheta }-{ı}_1,·)-\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({\ell }_1-\widehat{\vartheta },·)\end{array}$$

(22)

Summing (21) and (22)

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)+{\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)\le {\tilde{\mathcal{K}}}_c({ı}_1,·)+{\tilde{\mathcal{K}}}_c({\ell }_1,·)-2\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({\ell }_1-\widehat{\vartheta },·)-2\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c(\widehat{\vartheta }-{ı}_1,·).\end{array}$$

(23)

Similarly

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_r(\widehat{\vartheta },·)+{\tilde{\mathcal{K}}}_r({ı}_1+{\ell }_1-\widehat{\vartheta },·)\le {\tilde{\mathcal{K}}}_r({ı}_1,·)+{\tilde{\mathcal{K}}}_r({\ell }_1,·)-2\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_r({\ell }_1-\widehat{\vartheta },·)-2\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_r(\widehat{\vartheta }-{ı}_1,·).\end{array}$$

(24)

To get the final inequality, we compare (23) and (24) via cr ordering relation. □

Theorem 11.

If $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$, then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)\right)\hfill \\ \hfill & {⪯}_{cr}\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·)-{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left(\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)\right)\hfill \\ \hfill & \times \left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Proof. 

Considering the left inequality of Theorem 11, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)\right)\hfill \\ \hfill & =〈{\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({ı}_1,·)\right),{\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({ı}_1,·)\right)〉\hfill \\ \hfill & =〈{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}{\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta },\hfill \\ \hfill & {\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}{\tilde{\mathcal{K}}}_r(\widehat{\vartheta },·)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }〉\hfill \\ \hfill & =〈{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta },\hfill \\ \hfill & {\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_r(\widehat{\vartheta },·)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}{\tilde{\mathcal{K}}}_r({ı}_1+{\ell }_1-\widehat{\vartheta },·)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }〉\hfill \end{array}$$

From the inequality for center of S.P and utilising the Lemma 2, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({ı}_1,·)\right)\hfill \\ \hfill & ={\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}[{\tilde{\mathcal{K}}}_c(\widehat{\vartheta },·)+{\tilde{\mathcal{K}}}_c({ı}_1+{\ell }_1-\widehat{\vartheta },·)]\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & \le {\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}}\left({\tilde{\mathcal{K}}}_c({ı}_1,·)+{\tilde{\mathcal{K}}}_c({\ell }_1,·)-2\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({\ell }_1-\widehat{\vartheta },·)-2\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c(\widehat{\vartheta }-{ı}_1,·)\right)\hfill \\ \hfill & \times \left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & ={\tilde{\mathcal{K}}}_c({ı}_1,·)+{\tilde{\mathcal{K}}}_c({\ell }_1,·)-{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left(\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({\ell }_1-\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c(\widehat{\vartheta }-{ı}_1,·)\right)\hfill \\ \hfill & \times \left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(25)

likewise,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({ı}_1,·)\right)\hfill \\ \hfill & \le {\tilde{\mathcal{K}}}_r({ı}_1,·)+{\tilde{\mathcal{K}}}_r({\ell }_1,·)-{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left(\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_r({\ell }_1-\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_r(\widehat{\vartheta }-{ı}_1,·)\right)\hfill \\ \hfill & \times \left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(26)

To attain our final result, we bridge the inequalities (25) and (26) via $cr$-ordered relation. □

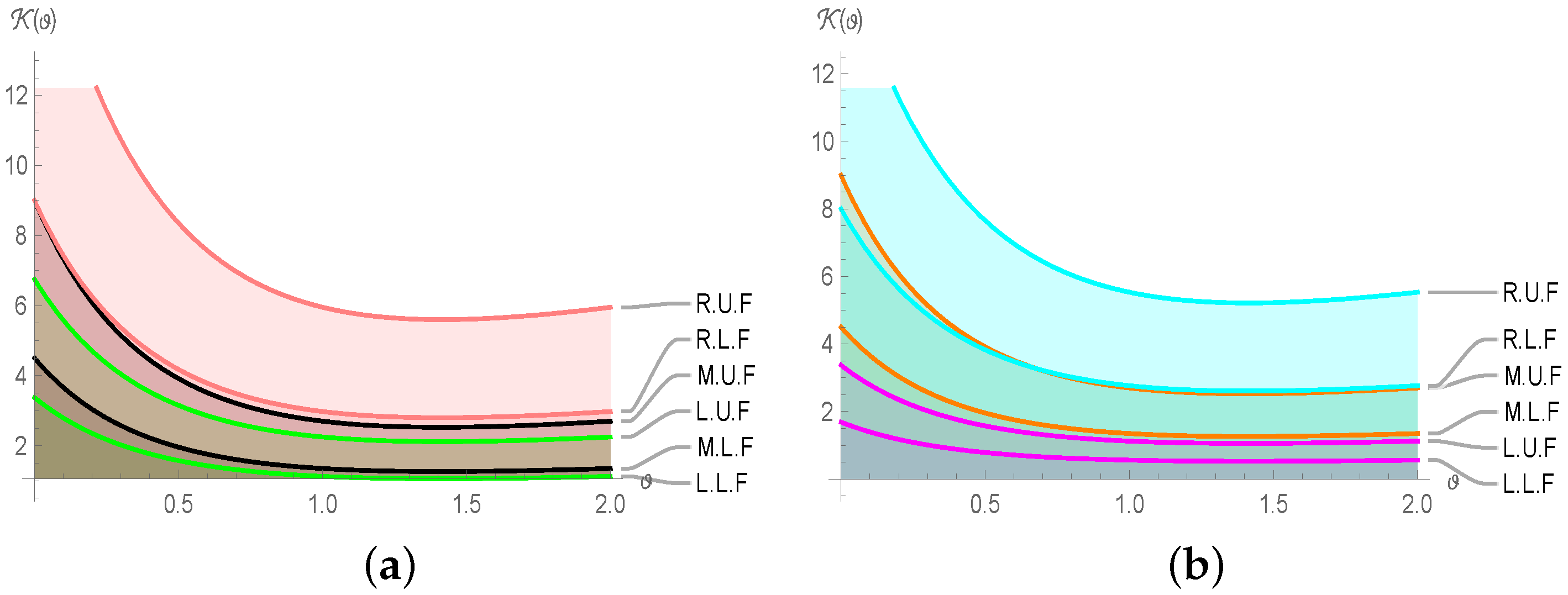
Example 3.

Let $\tilde{\mathcal{K}}\left(\widehat{\vartheta }\right)=[3{\widehat{\vartheta }}^2,{\widehat{\vartheta }}^2+3{\widehat{\vartheta }}^3]$ with $[{ı}_1,{\ell }_1]\to [1,2]$ which satisfies the Theorem 11.

$$\begin{array}{cc}\hfill Leftterm& ={\beta }_1{\int }_1^2\tilde{\mathcal{K}}\left(\widehat{\vartheta }\right)[{(2-\widehat{\vartheta })}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}]\mathrm{d}\widehat{\vartheta }.\hfill \\ \hfill Rightterm& =[15,32]-{\beta }_1{\int }_1^2[\hslash \left({\displaystyle \frac{\widehat{\vartheta }}{2}}\right)\tilde{\mathcal{K}}(2-\widehat{\vartheta })+\hslash \left({\displaystyle \frac{2-\widehat{\vartheta }}{2}}\right)\tilde{\mathcal{K}}\left(\widehat{\vartheta }\right)][{(2-\widehat{\vartheta })}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}]\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

To visualize the pictorial way, we vary ${ı}_1=1$, ${\ell }_1=2$ and $0<{\beta }_1\le 2$.

The graphical and numerical comparison for both cases of Theorem 11 are provided in the below

Table 3. Comparison between the sides of Theorem 11 for $\hslash \left(\varrho \right)=\varrho$.

${\mathit{\beta }}_1$	${\mathit{L}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{L}}^{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}^{*}\left({\mathit{\beta }}_1\right)$
$0.5$	14.2000	28.1333	18.8000	37.7143
$1.0$	14.0000	27.1667	19.0000	38.1333
$1.5$	13.9714	27.0286	19.0286	38.1922
$2.0$	14.0000	27.1667	19.0000	38.1333
$2.5$	14.0476	27.3968	18.9524	38.0357
$3.0$	14.1000	27.6500	18.9000	37.9286

and

Table 4. Comparison between the sides of Theorem 11 for $\hslash \left(\varrho \right)=1$.

${\mathit{\beta }}_1$	${\mathit{L}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{L}}^{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}^{*}\left({\mathit{\beta }}_1\right)$
$0.5$	14.2000	28.1333	31.4000	62.6667
$1.0$	14.0000	27.1667	31.0000	61.3333
$1.5$	13.9714	27.0286	30.9429	61.1429
$2.0$	14.0000	27.1667	31.0000	61.3333
$2.5$	14.0476	27.3968	31.0952	61.6508
$3.0$	14.1000	27.6500	31.2000	62.0000

; and Figure 3.

Theorem 12.

If $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],cr,\hslash )$, then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}\tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)+{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\tilde{\mathcal{K}}\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)\right)\hfill \\ \hfill & {⪯}_{cr}\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·)-{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left(\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)\right)\hfill \\ \hfill & \times \left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Proof. 

From Theorem 10, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}\tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)+{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\tilde{\mathcal{K}}\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)\right).\hfill \end{array}$$

(27)

From Theorem 11, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)\right)\hfill \\ \hfill & {⪯}_{cr}\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·)-{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left(\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)+\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)\right)\hfill \\ \hfill & \times \left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(28)

To conclude the proof, we compare (27) and (28). □

Remark 2.

For $\hslash \left(\vartheta \right)=\vartheta$ in Theorem 12, we obtain the result proved in [25].

Corollary 1.

For $\hslash \left(\vartheta \right)=1$ in Theorem 12, we obtain

$$\begin{array}{cc}\hfill & \tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)+{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\tilde{\mathcal{K}}\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)\right)\hfill \\ \hfill & {⪯}_{cr}\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·)-{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left(\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)+\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)\right)\hfill \\ \hfill & \times \left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Corollary 2.

For $\hslash \left(\vartheta \right)={\vartheta }^s$ in Theorem 12, we obtain

$$\begin{array}{cc}\hfill & 2^{-s}\tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)+{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\tilde{\mathcal{K}}\left(\left|{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}-\widehat{\vartheta }\right|,·\right)\left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & {⪯}_{cr}{\displaystyle \frac{\Gamma (1+{\beta }_1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left(J_{{ı}_1+}^{{\beta }_1}\tilde{\mathcal{K}}({\ell }_1,·)+J_{{\ell }_1-}^{{\beta }_1}\tilde{\mathcal{K}}({ı}_1,·)\right)\hfill \\ \hfill & {⪯}_{cr}\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·)-{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left({\left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)}^s\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)+{\left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)}^s\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)\right)\hfill \\ \hfill & \times \left({({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

3.2. Fractional Hadamard-Fejer’s Inequality

Theorem 13.

If $\tilde{\mathcal{K}}\in SSSIP([{ı}_1,{\ell }_1],\hslash )$ and $g:[{ı}_1,{\ell }_1]\to \mathbb{R}$ be a non negative integrable symmetric S.P about ${\displaystyle \frac{{ı}_1+{\ell }_1}{2}}$. Then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2\hslash \left(\frac{1}{2}\right)}}\tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}g({ı}_1,·)\right]\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\tilde{\mathcal{K}}\left(\left|\widehat{\vartheta }-{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right|,·\right)g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & ⪯{\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}g({ı}_1,·)\right]\hfill \\ \hfill & ⪯(\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·))·{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\left[\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}]\left[\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Proof. 

Since $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to {\mathbb{R}}_I^{+}$ be an $I.V$-ℏcr super-quadratic S.P, then

$$\begin{array}{c}\hfill {\tilde{\mathcal{K}}}_{*}\left({\displaystyle \frac{\widehat{\vartheta }+y}{2}},·\right)\le \hslash \left({\displaystyle \frac{1}{2}}\right)[{\tilde{\mathcal{K}}}_{*}(\widehat{\vartheta },·)+{\tilde{\mathcal{K}}}_{*}(y,·)]-2\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_{*}\left({\displaystyle \frac{1}{2}}|y-\widehat{\vartheta }|,·\right).\end{array}$$

the aforementioned inequality can be interpreted as

$$\begin{array}{cc}\hfill & {\tilde{\mathcal{K}}}_{*}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right)\hfill \\ \hfill & \le \hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_{*}\left(\varrho {\ell }_1+(1-\varrho ){ı}_1,·\right)+\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_{*}\left(\varrho {ı}_1+(1-\varrho ){\ell }_1,·\right)-2\hslash \left({\displaystyle \frac{1}{2}}\right){\tilde{\mathcal{K}}}_{*}\left({\displaystyle \frac{{\ell }_1-{ı}_1}{2}}|1-2\varrho |,·\right).\hfill \end{array}$$

(29)

As $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to {\mathbb{R}}^{+}I$ be a fuzzy interval-valued ℏ-super-quadratic S.P. Then multiplying (29) by ${\varrho }^{{\beta }_1-1}g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)$ and applying integration with respect to $"\varrho "$ on $[0,1]$, we get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\int }_0^1{\varrho }^{{\beta }_1-1}g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho \hfill \\ \hfill & \le {\int }_0^1{\varrho }^{{\beta }_1-1}{\tilde{\mathcal{K}}}_c(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho +{\int }_0^1{\varrho }^{{\beta }_1-1}{\tilde{\mathcal{K}}}_c(\varrho {ı}_1+(1-\varrho ){\ell }_1,·)g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho \hfill \\ \hfill & -2{\int }_0^1{\varrho }^{{\beta }_1-1}{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{\ell }_1-{ı}_1}{2}}\left|1-2\varrho \right|,·\right)g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho .\hfill \end{array}$$

Since g is symmetric S.P about ${\displaystyle \frac{{ı}_1+{\ell }_1}{2}}$, then $g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)=g((1-\varrho ){\ell }_1+\varrho {ı}_1,·)$. Using this fact in above equation, we get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2\hslash \left(\frac{1}{2}\right)}}{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\int }_0^1{\varrho }^{{\beta }_1-1}[g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)+g(\varrho {ı}_1+(1-\varrho ){\ell }_1,·)]\mathrm{d}\varrho \hfill \\ \hfill & \le {\int }_0^1{\varrho }^{{\beta }_1-1}{\tilde{\mathcal{K}}}_c(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho +{\int }_0^1{\varrho }^{{\beta }_1-1}{\tilde{\mathcal{K}}}_c(\varrho {ı}_1+(1-\varrho ){\ell }_1,·)g(\varrho {ı}_1+(1-\varrho ){\ell }_1,·)\mathrm{d}\varrho \hfill \\ \hfill & -{\int }_0^1{\varrho }^{{\beta }_1-1}{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{\ell }_1-{ı}_1}{2}}\left|1-2\varrho \right|,·\right)[g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)+g(\varrho {ı}_1+(1-\varrho ){\ell }_1,·)]\mathrm{d}\varrho .\hfill \end{array}$$

After some simple computations, we have following inequality

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2\hslash \left(\frac{1}{2}\right)}}{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}g({ı}_1,·)\right]\hfill \\ \hfill & \le {\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({\ell }_1,·)g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({ı}_1,·)g({ı}_1,·)\right]\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]{\tilde{\mathcal{K}}}_c\left(\left|\widehat{\vartheta }-{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right|,·\right)g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(30)

By following similar procedure, we get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2\hslash \left(\frac{1}{2}\right)}}{\tilde{\mathcal{K}}}_r\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}g({ı}_1,·)\right]\hfill \\ \hfill & \le {\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({\ell }_1,·)g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({ı}_1,·)g({ı}_1,·)\right]\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]{\tilde{\mathcal{K}}}_r\left(\left|\widehat{\vartheta }-{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right|,·\right)g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(31)

Implementing the pseudo ordering relation on (30) and (31) results in the following relation:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2\hslash \left(\frac{1}{2}\right)}}\tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}g({ı}_1,·)\right]\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\tilde{\mathcal{K}}\left(\left|\widehat{\vartheta }-{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right|,·\right)g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & ⪯{\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}g({ı}_1,·)\right].\hfill \end{array}$$

(32)

To prove our secondary inequality, we utilize the definition of super-Quadratic processes, and we get

$$\begin{array}{cc}\hfill & {\tilde{\mathcal{K}}}_c(\varrho {ı}_1+(1-\varrho ){\ell }_1,·)g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho +{\int }_0^1{\varrho }^{{\beta }_1-1}{\tilde{\mathcal{K}}}_c(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\hfill \\ \hfill & \le [{\tilde{\mathcal{K}}}_c({\ell }_1,·)+{\tilde{\mathcal{K}}}_c({ı}_1,·)][\hslash \left(\varrho \right)+\hslash (1-\varrho )]\hfill \\ \hfill & -2\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c\left((1-\varrho )\right|{\ell }_1-{ı}_1|,·)-2\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c\left(\varrho \right|{\ell }_1-{ı}_1|,·).\hfill \end{array}$$

(33)

Multiplying (33) by ${\varrho }^{{\beta }_1-1}g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)$ and applying integrating with respect to $“\varrho ”$ on $[0,1]$, we get

$$\begin{array}{cc}\hfill & {\int }_0^1{\varrho }^{{\beta }_1-1}{\tilde{\mathcal{K}}}_c(\varrho {ı}_1+(1-\varrho ){\ell }_1,·)g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho +{\int }_0^1{\varrho }^{{\beta }_1-1}{\tilde{\mathcal{K}}}_c(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho \hfill \\ \hfill & \le [{\tilde{\mathcal{K}}}_c({\ell }_1,·)+{\tilde{\mathcal{K}}}_c({ı}_1,·)]{\int }_0^1{\varrho }^{{\beta }_1-1}[\hslash \left(\varrho \right)+\hslash (1-\varrho )]g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho \hfill \\ \hfill & -2{\int }_0^1{\varrho }^{{\beta }_1-1}\hslash \left(\varrho \right){\tilde{\mathcal{K}}}_c\left((1-\varrho )\right|{\ell }_1-{ı}_1|,·)g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho \hfill \\ \hfill & -2{\int }_0^1{\varrho }^{{\beta }_1-1}\hslash (1-\varrho ){\tilde{\mathcal{K}}}_c\left(\varrho \right|{\ell }_1-{ı}_1|,·)g(\varrho {\ell }_1+(1-\varrho ){ı}_1,·)\mathrm{d}\varrho .\hfill \end{array}$$

After performing some computations, we get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({\ell }_1,·)g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}{\tilde{\mathcal{K}}}_c({ı}_1,·)g({ı}_1,·)\right]\hfill \\ \hfill & \le \left({\tilde{\mathcal{K}}}_c({ı}_1,·)+{\tilde{\mathcal{K}}}_c({\ell }_1,·)\right)·{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\left[\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}]\left[\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c(\widehat{\vartheta }-{ı}_1,·)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right){\tilde{\mathcal{K}}}_c({\ell }_1-\widehat{\vartheta },·)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(34)

Similarly, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({\ell }_1,·)g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}{\tilde{\mathcal{K}}}_r({ı}_1,·)g({ı}_1,·)\right]\hfill \\ \hfill & \le (\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·))·{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\left[\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}]\left[\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(35)

Inequalities (34) and (35) produce the following relation

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}g({ı}_1,·)\right]\hfill \\ \hfill & ⪯(\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·))·{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\left[\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}]\left[\hslash \left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)+\hslash \left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

(36)

Finally, bridging inequalities (32) and (36), we achieve Hermite–Hadmard–Fejer inequality. □

Corollary 3.

For $\hslash \left(\vartheta \right)=\vartheta$ in Theorem 13, we obtain

$$\begin{array}{cc}\hfill & \tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}g({ı}_1,·)\right]\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\tilde{\mathcal{K}}\left(\left|\widehat{\vartheta }-{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right|,·\right)g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & ⪯{\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}g({ı}_1,·)\right]\hfill \\ \hfill & ⪯(\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·))·{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}]\left[{\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)+{\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Corollary 4.

For $\hslash \left(\vartheta \right)=1$ in Theorem 13, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}\tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}g({ı}_1,·)\right]\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\tilde{\mathcal{K}}\left(\left|\widehat{\vartheta }-{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right|,·\right)g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & ⪯{\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}g({ı}_1,·)\right]\hfill \\ \hfill & ⪯2(\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·))·{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}]\left[\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Corollary 5.

For $\hslash \left(\vartheta \right)={\vartheta }^s$ in Theorem 13, we obtain

$$\begin{array}{cc}\hfill & 2^{s-1}\tilde{\mathcal{K}}\left({\displaystyle \frac{{ı}_1+{\ell }_1}{2}},·\right){\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}g({ı}_1,·)\right]\hfill \\ \hfill & +{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\tilde{\mathcal{K}}\left(\left|\widehat{\vartheta }-{\displaystyle \frac{{ı}_1+{\ell }_1}{2}}\right|,·\right)g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & ⪯{\displaystyle \frac{\Gamma ({\beta }_1+1)}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}\left[J_{{{ı}_1}^{+}}^{{\beta }_1}\tilde{\mathcal{K}}g({\ell }_1,·)+J_{{{\ell }_1}^{-}}^{{\beta }_1}\tilde{\mathcal{K}}g({ı}_1,·)\right]\hfill \\ \hfill & ⪯(\tilde{\mathcal{K}}({ı}_1,·)+\tilde{\mathcal{K}}({\ell }_1,·))·{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}\left[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}\right]\left[{\left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)}^s+{\left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)}^s\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_1}{{({\ell }_1-{ı}_1)}^{{\beta }_1}}}{\int }_{{ı}_1}^{{\ell }_1}[{({\ell }_1-\widehat{\vartheta })}^{{\beta }_1-1}+{(\widehat{\vartheta }-{ı}_1)}^{{\beta }_1-1}]\left[{\left({\displaystyle \frac{{\ell }_1-\widehat{\vartheta }}{{\ell }_1-{ı}_1}}\right)}^s\tilde{\mathcal{K}}(\widehat{\vartheta }-{ı}_1,·)+{\left({\displaystyle \frac{\widehat{\vartheta }-{ı}_1}{{\ell }_1-{ı}_1}}\right)}^s\tilde{\mathcal{K}}({\ell }_1-\widehat{\vartheta },·)\right]g(\widehat{\vartheta },·)\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Example 4.

Let $g:[1,2]\to \mathbb{R}$ be a symmetric integrable mappings, and $\tilde{\mathcal{K}}\left(\widehat{\vartheta }\right)=[2{\widehat{\vartheta }}^3,4{\widehat{\vartheta }}^3]$, with $\tilde{\mathcal{K}}:[{ı}_1,{\ell }_1]\to [1,2]$. Both mapping satisfies the hypothesis of Theorem 13. Then

$$\begin{array}{cc}\hfill LeftTerm& ={\displaystyle \frac{1}{2\hslash \left(\frac{1}{2}\right)}}\left[{\displaystyle \frac{27}{4}},{\displaystyle \frac{27}{2}}\right]+{\beta }_1{\int }_1^2\left[{(2-\widehat{\vartheta })}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}\right]{\left(\widehat{\vartheta }-{\displaystyle \frac{3}{2}}\right)}^2\mathrm{d}\widehat{\vartheta }\hfill \\ & +{\beta }_1{\int }_1^2\tilde{\mathcal{K}}\left|{\displaystyle \frac{3}{2}}-\widehat{\vartheta }\right|[{(2-\widehat{\vartheta })}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}]{\left(\widehat{\vartheta }-{\displaystyle \frac{3}{2}}\right)}^2\mathrm{d}\widehat{\vartheta },\hfill \\ \hfill MiddleTerm& ={\beta }_1{\int }_1^2[{(2-\widehat{\vartheta })}^{{\beta }_1-1}\tilde{\mathcal{K}}\left(\vartheta \right)+{(\vartheta -1)}^{{\beta }_1-1}\tilde{\mathcal{K}}\left(\vartheta \right)]{\left(\widehat{\vartheta }-{\displaystyle \frac{3}{2}}\right)}^2\mathrm{d}\widehat{\vartheta },\hfill \\ \hfill RightTerm& =\left[18,36\right]+{\beta }_1{\int }_1^2\left[{(2-\widehat{\vartheta })}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}\right]\left[\hslash (2-\vartheta )+\hslash (\vartheta -1)\right]{\left(\widehat{\vartheta }-{\displaystyle \frac{3}{2}}\right)}^2\mathrm{d}\widehat{\vartheta }\hfill \\ & +{\beta }_1{\int }_1^2[{(2-\widehat{\vartheta })}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}]\left[\hslash (2-\vartheta )\tilde{\mathcal{K}}(\vartheta -1)+\hslash (\vartheta -1)\tilde{\mathcal{K}}(2-\vartheta )\right]{\left(\widehat{\vartheta }-{\displaystyle \frac{3}{2}}\right)}^2\mathrm{d}\widehat{\vartheta }.\hfill \end{array}$$

Figure 4 illustrates the comparison between the sides of Theorem 13.

Additionally, the numerical comparison for both cases are provided in the below

Table 5. Comparison between the sides of Theorem 13 for $\hslash \left(\varrho \right)=\varrho$.

$\left({\mathit{\beta }}_1\right)$	${\mathit{L}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{L}}^{*}\left({\mathit{\beta }}_1\right)$	${\mathit{M}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{M}}^{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}^{*}\left({\mathit{\beta }}_1\right)$
$0.5$	0.7875	1.5750	1.9571	3.9143	3.8286	7.65714
$1.0$	0.5625	1.1250	1.3500	2.7000	2.7667	5.53333
$1.5$	0.5304	1.0607	1.2662	2.5325	2.6130	5.22597
$2.0$	0.5625	1.1250	1.3500	2.7000	2.7667	5.53333
$2.5$	0.6161	1.2321	1.4880	2.9760	3.0239	6.04773
$3.0$	0.6750	1.3500	1.6393	3.2786	3.3071	6.61429

and

Table 6. Comparison between the sides of Theorem 13 for $\hslash \left(\varrho \right)=1$.

$\left({\mathit{\beta }}_1\right)$	${\mathit{L}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{L}}^{*}\left({\mathit{\beta }}_1\right)$	${\mathit{M}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{M}}^{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}_{*}\left({\mathit{\beta }}_1\right)$	${\mathit{R}}^{*}\left({\mathit{\beta }}_1\right)$
$0.5$	1.5750	3.1500	1.9571	3.9143	4.1764	8.3529
$1.0$	1.1250	2.2500	1.3500	2.7000	2.9762	5.9524
$1.5$	1.0607	2.1214	1.2662	2.5325	2.8053	5.6105
$2.0$	1.1250	2.2500	1.3500	2.7000	2.9762	5.9524
$2.5$	1.2321	2.4643	1.4880	2.9760	3.2608	6.5216
$3.0$	1.3500	2.7000	1.6393	3.2786	3.5738	7.1476

.

4. Applications

4.1. Application to Shanon Entropy

It is known that uncertainty is approximated in a collection of possible outcomes through entropy. It is regarded as a principle of information sciences. This theory was studied by Claude Shannon in his paper A Mathematical Theory of Communication. He introduced the mathematical strategy to investigate the information, assuming it to be measurable quantities. He developed the concept of entropy to formulate the precise probabilistic measurement of information data, and it is quantified in bits. It is stated as follows:

For a discrete random variable (R.V) $\varphi$ with probability distribution (P.D) ${\mathbf{E}}_0=(E_1,\dots ,E_{\sigma })$, where each $E_q$ represents the probability that $\varphi$ takes its q-th possible value, the Shannon entropy is defined as follows:

$$S\left(\varphi \right)=-\sum _{q=1}^{\sigma }{E}_{q}ln{E}_q.$$

(37)

Now, we developed an interesting inequality based on Jensen–Mercer inequality obtained in the previous section.

Theorem 14.

Let X be a R.V with $E_0=(E_1,\dots ,E_{\sigma })$ as its P.D where $E_q\ge 0$, for each q, $1\le q\le \sigma$ and $H_{\sigma }\left(E_0\right)=\sigma$ then

$$\begin{array}{cc}\hfill & \langle 0,{(a+b-H_{\sigma }\left(E_o\right))}^{2}ln(a+b-H_{\sigma }\left(E_o\right))\rangle \hfill \\ \hfill & {⪯}_c^r〈0,ln\left(a^{a^2}{b}^{b^2}\right)+S\left(X\right)-\sum _{q=0}^{\sigma }{\displaystyle \frac{1}{E_q}}\left[{\left({\displaystyle \frac{1}{E_q}}-a\right)}^{2}ln\left({\displaystyle \frac{1}{E_q}}-a\right)+{\left(b-{\displaystyle \frac{1}{E_q}}\right)}^{2}ln\left(b-{\displaystyle \frac{1}{E_q}}\right)\right]\hfill \\ \hfill & +\sum _{q=0}^{\sigma }{\displaystyle \frac{1}{E_q}}{\left|{\displaystyle \frac{1}{E_q}}-H\left(E_o\right)\right|}^{2}ln\left|{\displaystyle \frac{1}{E_q}}-H_{\sigma }\left(E_o\right)\right|〉.\hfill \end{array}$$

4.2. Applications to Divergence Measures

To differentiate between two probability distributions is an intrinsic aspect of research in statistics, information theory, and machine learning. Divergence measures determine the difference between the distributions. In 1991, Lin [31] utilized the concept of Shannon entropy. His measure provides a framework to compute the difference between distributions following the information-theoretical principles. In 1995, Shioya and Da-te [32] developed the Hadamard $\tilde{\mathcal{K}}$-divergence measure by using Hermite-Hadamard’s inequality. Now, we recall some renowned divergence measures, which are essential to prove our main results.

Definition 11

(Csiszar $\tilde{\mathcal{K}}$-divergence [33]).

$$\begin{array}{c}\hfill D_{\tilde{\mathcal{K}}}\left(E\right|\left|f\right)={\int }_{\Lambda }f\left(\widehat{\vartheta }\right)\tilde{\mathcal{K}}\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}\right)d\vartheta \left(\widehat{\vartheta }\right),E,f\in P,\end{array}$$

(38)

where ϑ represents a σ-finite measure and mapping $\tilde{\mathcal{K}}$ is a convex. Additionally, the collection of all probabilities densities is given as

$$\begin{array}{c}\hfill P=\left\{E|E:\Lambda \to \Re ,E\left(\widehat{\vartheta }\right)\ge 0,{\int }_{\Lambda }E\left(\widehat{\vartheta }\right)d\vartheta \left(\widehat{\vartheta }\right)=1\right\}.an\end{array}$$

(39)

Remark 3.

For strongly convex and super-quadratic mappings, we get the Csiszar $\tilde{\mathcal{K}}$-divergence measures.

Definition 12

(Hermite-Hadamard $\tilde{\mathcal{K}}$-divergence [34]).

$$\begin{array}{c}\hfill D_{HH}^{\tilde{\mathcal{K}}}\left(E\right|\left|f\right)={\int }_{\Lambda }f\left(\widehat{\vartheta }\right){\displaystyle \frac{{\int }_1^{\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}\tilde{\mathcal{K}}\left(\widehat{\vartheta }\right)d\widehat{\vartheta }}{\left(\frac{E\left(\widehat{\vartheta }\right)}{f\left(\varkappa \right)}-1\right)}}d\vartheta \left(\varkappa \right),E,f\in P.\end{array}$$

(40)

Definition 13

(Stochastic divergence [35]). If $\tilde{\mathcal{K}}:I\times \Pi \to \Re$, on $I\subseteq (0,\infty )$ is a convex S.P and satisfy the condition $\tilde{\mathcal{K}}(1,·)=0$. Then stochastic divergence over $E,f\in P$ is stated as

$$\begin{array}{c}\hfill S{D}_{\tilde{\mathcal{K}}}\left(E\right|\left|f\right)={\int }_{\Lambda }f\left(\widehat{\vartheta }\right)\tilde{\mathcal{K}}\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}},·\right)d\vartheta \left(\widehat{\vartheta }\right),E,f\in P.\end{array}$$

(41)

Remark 4.

Stochastic divergence for a $I.V$-cr super-quadratic S.P $\tilde{\mathcal{K}}:I\times \Pi \to {\Re }_I^{+}$ is given by $\tilde{\mathcal{K}}=[\underline{\tilde{\mathcal{K}}},\overline{\tilde{\mathcal{K}}}]=\langle {\tilde{\mathcal{K}}}_c,{\tilde{\mathcal{K}}}_r\rangle$ such that ${\tilde{\mathcal{K}}}_c(1,·)={\tilde{\mathcal{K}}}_r(1,·)=0$ and $E,f\in P$ is stated as

$$\begin{array}{c}\hfill S{D}_{\tilde{\mathcal{K}}}\left(E\right|\left|f\right)=\langle S{D}_{{\tilde{\mathcal{K}}}_c}\left(E\right|\left|f\right),S{D}_{{\tilde{\mathcal{K}}}_r}\left(E\right|\left|f\right)\rangle ,\end{array}$$

(42)

where

$$\begin{array}{c}\hfill S{D}_{{\tilde{\mathcal{K}}}_c}\left(E\right|\left|f\right)={\int }_{\Lambda }f\left(\widehat{\vartheta }\right){\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}},·\right)d\vartheta \left(\widehat{\vartheta }\right),E,f\in P\end{array}$$

(43)

and

$$\begin{array}{c}\hfill S{D}_{{\tilde{\mathcal{K}}}_r}\left(E\right|\left|f\right)={\int }_{\Lambda }f\left(\widehat{\vartheta }\right){\tilde{\mathcal{K}}}_r\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}},·\right)d\vartheta \left(\widehat{\vartheta }\right),E,f\in P.\end{array}$$

(44)

Definition 14

(Stochastic Hadamard divergence [35]). The stochastic Hadamard divergence for $E,f\in P$ based on convex S.P $\tilde{\mathcal{K}}:I\times \Pi \to \Re$, on $I\subseteq (0,\infty )$ is stated as

$$\begin{array}{c}\hfill S{D}_{HH}^{\tilde{\mathcal{K}}}\left(E\right|\left|f\right)={\int }_{\Lambda }f\left(\widehat{\vartheta }\right){\displaystyle \frac{{\int }_1^{\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}\tilde{\mathcal{K}}(\widehat{\vartheta },·)d\widehat{\vartheta }}{\left(\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}-1\right)}}d\vartheta \left(\widehat{\vartheta }\right),E,f\in P.\end{array}$$

(45)

Definition 15

(Riemann-Liouville fractional stochastic Hadamard-divergence [35]). The RL fractional Hadamard-divergence for $E,f\in P$ based on convex S.P $\tilde{\mathcal{K}}:I\times \Pi \to \Re$, on $I\subseteq (0,\infty )$ of order ${\beta }_1>0$ is stated as

$$\begin{array}{c}\hfill {}_1{}^{\beta }\mathit{SD}_{\mathit{HH}}^{\tilde{\mathcal{K}}}\left(E\right|\left|f\right)=\Gamma ({\beta }_1+1){\int }_{\Lambda }f\left(\widehat{\vartheta }\right){\displaystyle \frac{\left[{\mathfrak{J}}_{1+}^{{\beta }_1}\left[\tilde{\mathcal{K}}\right]\left(\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}\right)+{\mathfrak{J}}_{\left(\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}\right)-}^{{\beta }_1}\left[\tilde{\mathcal{K}}\right]\left(1\right)\right]}{2{\left(\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}-1\right)}^{{\beta }_1}}}d\vartheta \left(\widehat{\vartheta }\right),E,f\in P,\end{array}$$

(46)

where the Definition of operators used in (46) are provided in Definition 8.

Remark 5.

For a super-quadratic S.P the divergence measure (46) transform into RL fractional stochastic Hadamard-divergence.

Theorem 15.

If $\tilde{\mathcal{K}}:I\times \Pi \to {\mathbb{R}}_I^{+}$ is an $I.V$-ℏ-cr super-quadratic S.P, such that $\tilde{\mathcal{K}}(\vartheta ,·)=[\underline{\tilde{\mathcal{K}}}(\vartheta ,·),\overline{\tilde{\mathcal{K}}}(\vartheta ,·)]=\langle {\tilde{\mathcal{K}}}_c(\vartheta ,·),{\tilde{\mathcal{K}}}_r(\vartheta ,·)\rangle$ and ${\tilde{\mathcal{K}}}_c(1,·)={\tilde{\mathcal{K}}}_r(1,·)=0$. Then

$$\begin{array}{c}\hfill {\displaystyle \frac{S{D}_{\tilde{\mathcal{K}}}\left(\frac{1}{2}f+\frac{1}{2}E\left|\right|f\right)}{\Gamma (1+{\beta }_1)}}+{\displaystyle \frac{{\beta }_1{\tau }_1}{\Gamma (1+{\beta }_1)}}{⪯}_c^r{\beta }_{1}2S{D}_{HH}^{\tilde{\mathcal{K}}}\left(E\right|\left|f\right){⪯}_c^r{\displaystyle \frac{S{D}_{\tilde{\mathcal{K}}}\left(E\right|\left|f\right)}{\Gamma (1+{\beta }_1)}}-{\displaystyle \frac{{\beta }_1{\tau }_2}{\Gamma (1+{\beta }_1)}},\end{array}$$

$\forall E,f\in P$, and ${\beta }_1>0$.

$$\begin{array}{cc}\hfill {\tau }_{1c}& ={\int }_{\Lambda }{\displaystyle \frac{f\left(\widehat{\vartheta }\right)}{{\left(\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}-1\right)}^{{\beta }_1}}}{\int }_1^{{\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}}\left({\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}-\vartheta \right)}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}\right){\tilde{\mathcal{K}}}_c\left(\left|{\displaystyle \frac{f\left(\widehat{\vartheta }\right)+E\left(\widehat{\vartheta }\right)}{2f\left(\widehat{\vartheta }\right)}}-\vartheta \right|,·\right)d\vartheta d\vartheta \left(\widehat{\vartheta }\right),\hfill \\ \hfill {\tau }_{2c}& ={\int }_{\Lambda }{\displaystyle \frac{f\left(\widehat{\vartheta }\right)}{{\left(\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}-1\right)}^{{\beta }_1+1}}}{\int }_1^{{\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}}\left[{\tilde{\mathcal{K}}}_c\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}-\vartheta ,·\right)+{\tilde{\mathcal{K}}}_c(\vartheta -1,·)\right]\left({\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}-\vartheta \right)}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}\right)d\vartheta d\vartheta \left(\widehat{\vartheta }\right),\hfill \\ \hfill {\tau }_{1r}& ={\int }_{\Lambda }{\displaystyle \frac{f\left(\widehat{\vartheta }\right)}{{\left(\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}-1\right)}^{{\beta }_1}}}{\int }_1^{{\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}}\left({\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}-\vartheta \right)}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}\right){\tilde{\mathcal{K}}}_r\left(\left|{\displaystyle \frac{f\left(\widehat{\vartheta }\right)+E\left(\widehat{\vartheta }\right)}{2f\left(\widehat{\vartheta }\right)}}-\vartheta \right|,·\right)d\vartheta d\vartheta \left(\widehat{\vartheta }\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\tau }_{2r}& ={\int }_{\Lambda }{\displaystyle \frac{f\left(\widehat{\vartheta }\right)}{{\left(\frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}-1\right)}^{{\beta }_1+1}}}{\int }_1^{{\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}}\left[{\tilde{\mathcal{K}}}_r\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}-\vartheta ,·\right)+{\tilde{\mathcal{K}}}_r(\vartheta -1,·)\right]\left({\left({\displaystyle \frac{E\left(\widehat{\vartheta }\right)}{f\left(\widehat{\vartheta }\right)}}-\vartheta \right)}^{{\beta }_1-1}+{(\vartheta -1)}^{{\beta }_1-1}\right)d\vartheta d\vartheta \left(\widehat{\vartheta }\right).\hfill \end{array}$$

Proof. 

The proof is a simple consequence of Theorem 3. □

5. Conclusions

Stochastic analysis is the consistently followed and researched domain of mathematics, which covers every aspect, including modelling, analysis, and computation. Over the years, researchers focused on convex stochastic processes to explore the hidden aspects of optimization and inequalities. In this following study, we have purported the idea of ℏ-super-quadratic stochastic processes. Also, we have discussed various characterisations of the proposed class of super-quadratic processes from an inequality point of view, and we have conducted an exploration of super-quadraticity within the stochastic processes through a unified approach and various fundamental inequalities leveraging the fractional concepts. In the future, we will investigate the coordinated super-quadraticity and its implications. Furthermore, we will establish some applications of the proposed class, like strong convexity in optimization theory through different strategies. The results proved in [36] can be explored using stochastic convexity.