Phase-Based Fractional-Order Repetitive Control for Single-Phase Grid-Tied Inverters
Abstract
1. Introduction
- (1)
- The output frequency of the second-order generalized integrator (SOGI)-based PLL naturally fluctuates, resulting in an inaccurate order of RC in a single-phase inverter, and then affecting the performance of RC. To solve this challenge, a novel phase-based fractional-order repetitive control (PFORC) scheme is developed in this paper.
- (2)
- Based on the linear interpolation method, the different weights are employed for the phase angles from PLL to determine the order of RC, which enhances the frequency adaptability of the PFORC scheme by mitigating the impact of fluctuations in the estimated grid frequency.
- (3)
- A detailed PFORC design procedure and the real-time comparative experimental validation on the single-phase LCL-type grid-tied inverters are presented, in which both performance and robustness are considered.
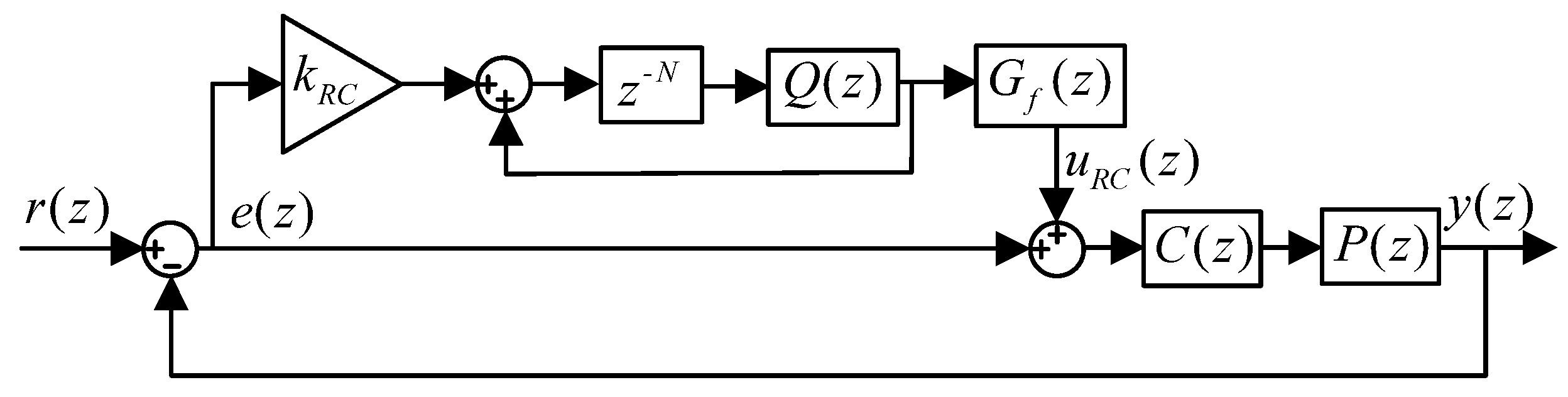
2. Conventional Frequency-Based Fractional-Order Repetitive Control
- The closed-loop transfer function without RC, , is stable;
- .
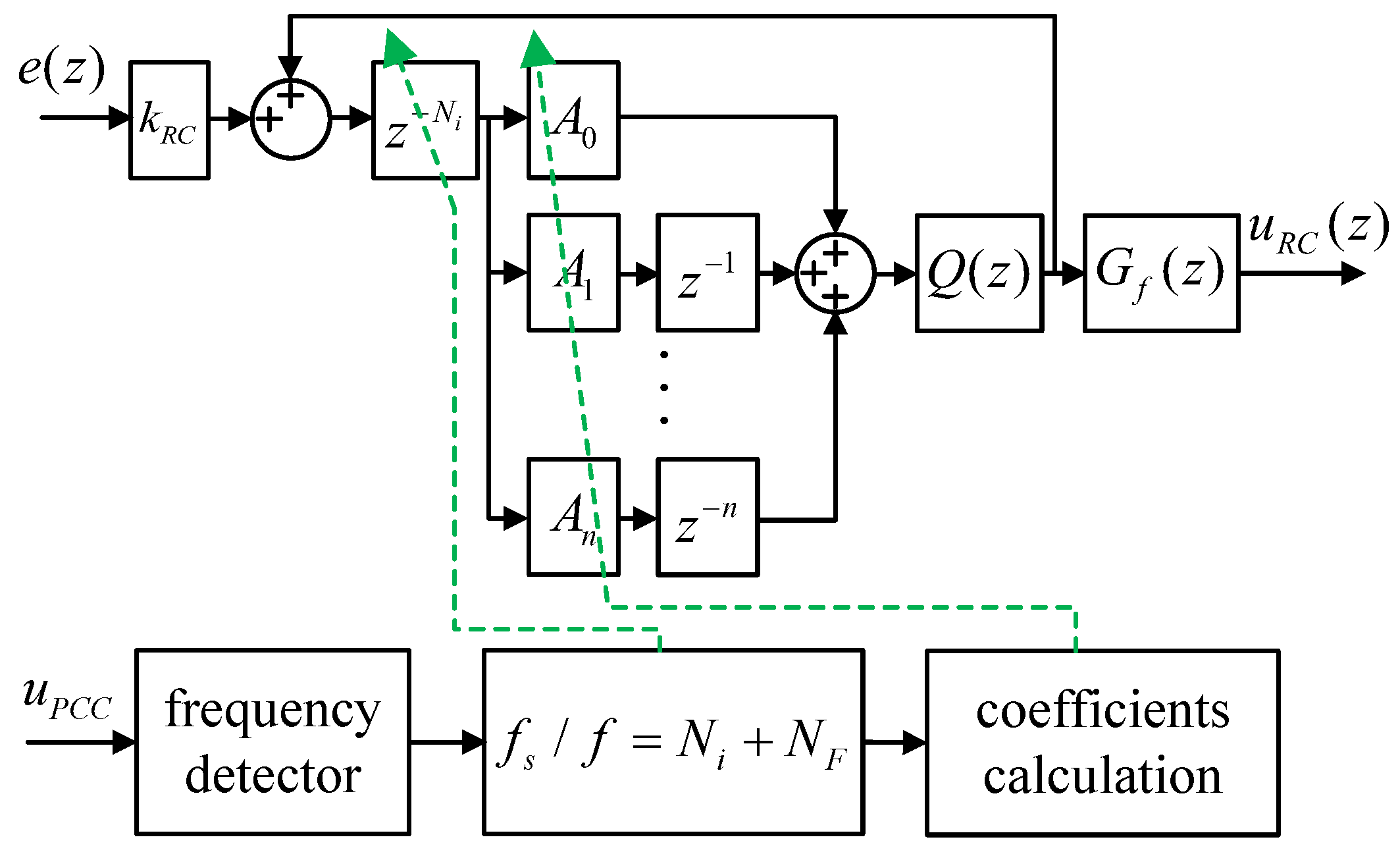
3. Proposed Phase-Based Fractional-Order Repetitive Control
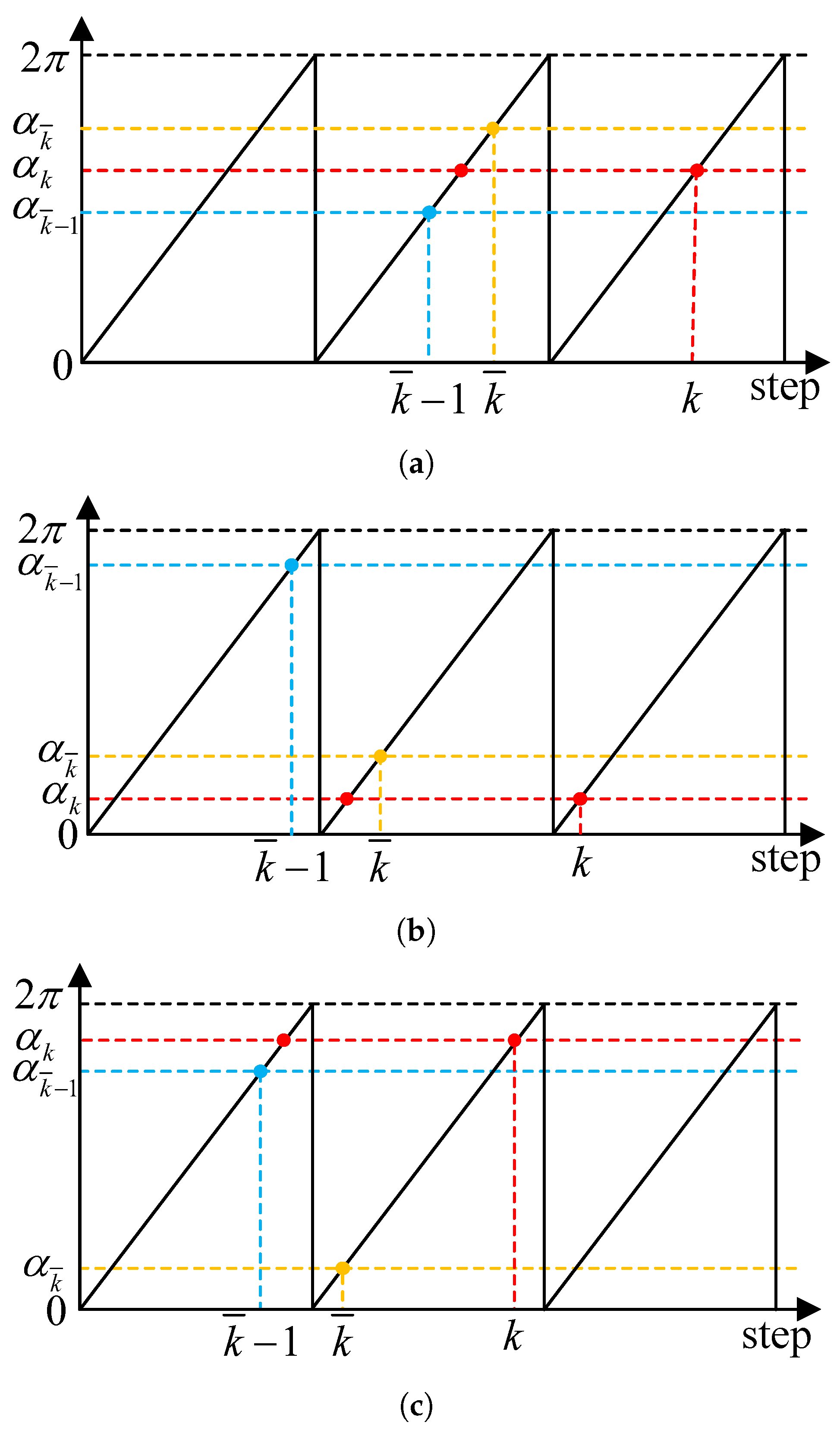
3.1. Principle
3.2. Implementation
3.3. Stability Conditions
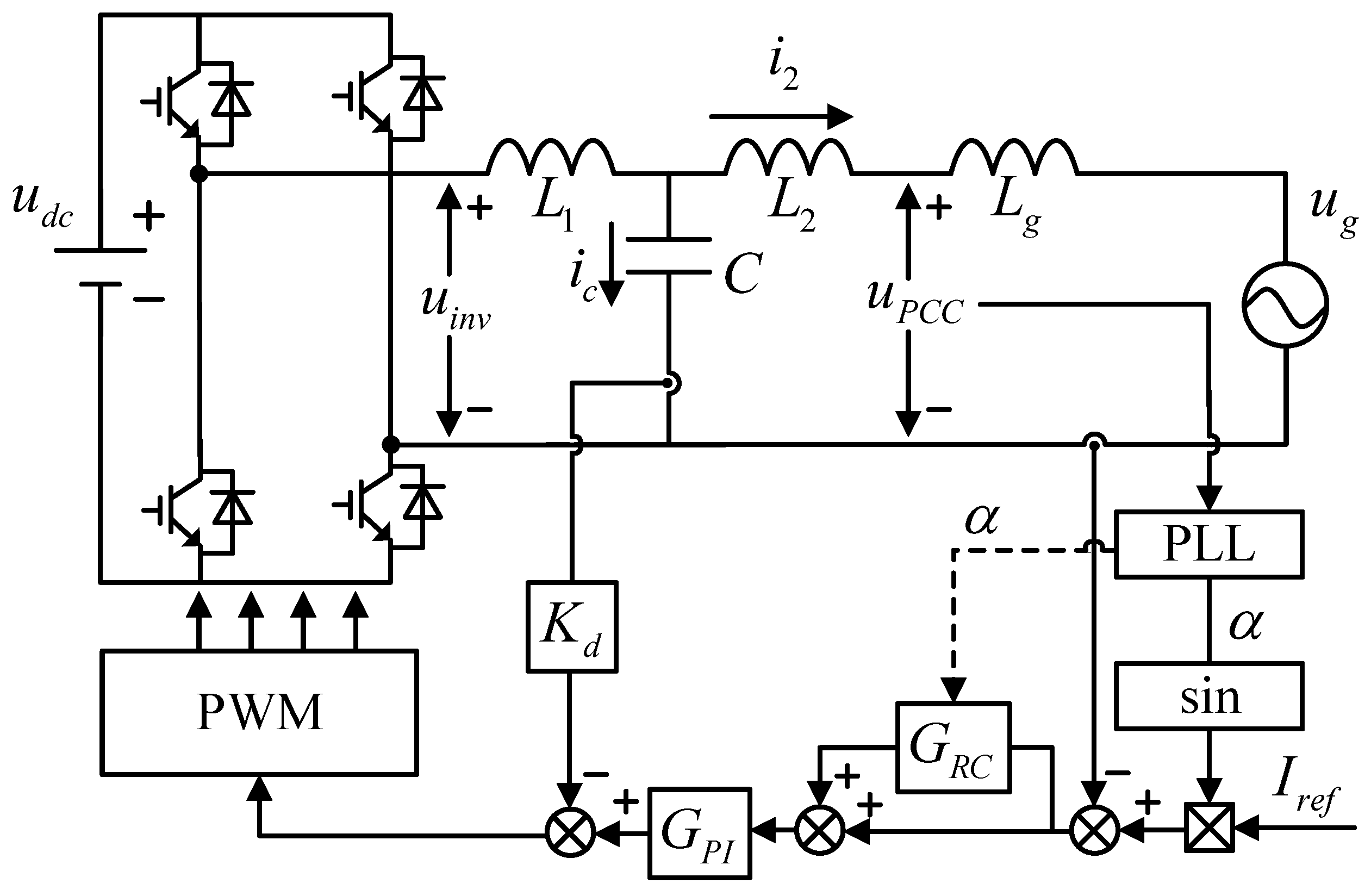
4. Application to a Single-Phase LCL-Type Grid-Tied Inverter
4.1. Modeling of the Single-Phase LCL-Type Grid-Tied Inverter
4.2. Controller Design
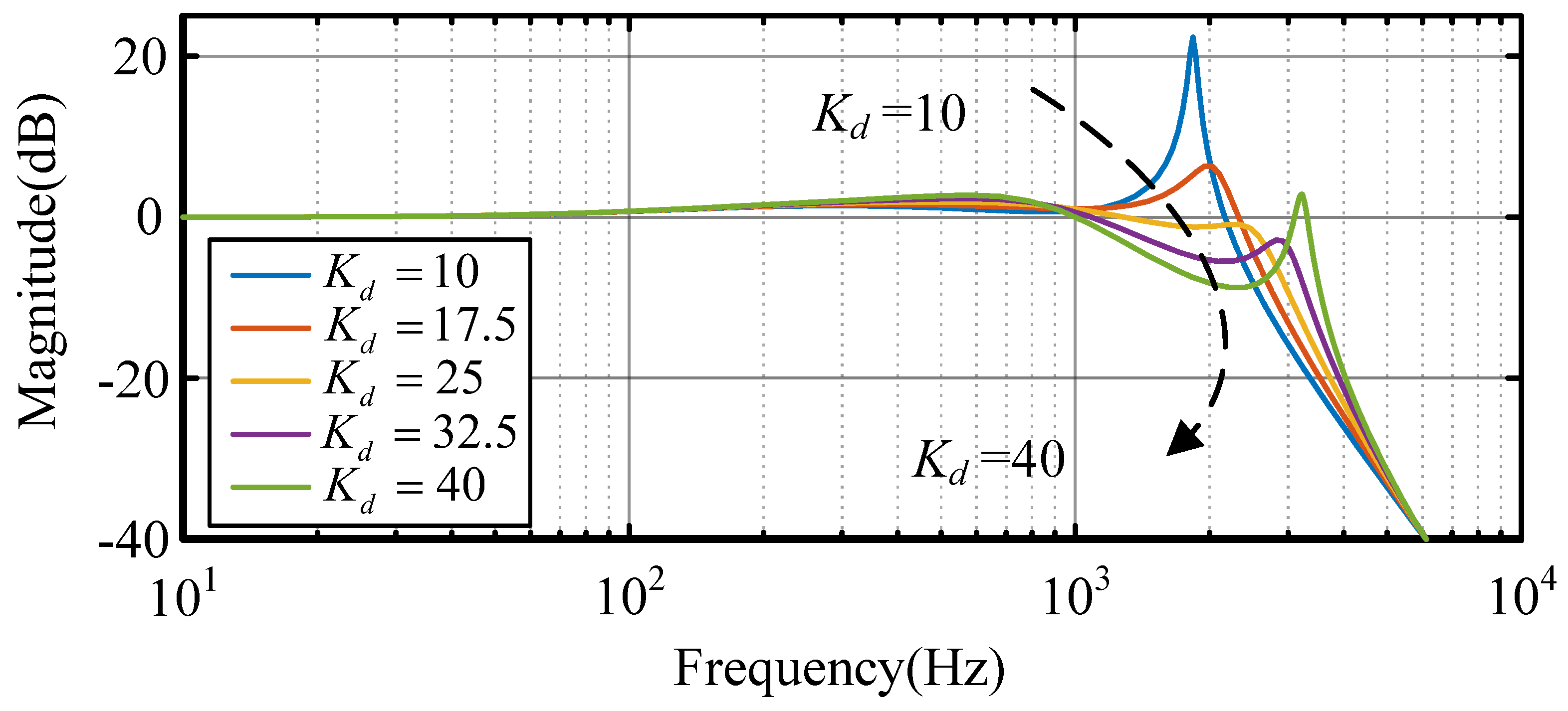
4.2.1. PI Controller and Active Damping Gain
4.2.2.
4.2.3.
4.2.4.
5. Experimental Verification
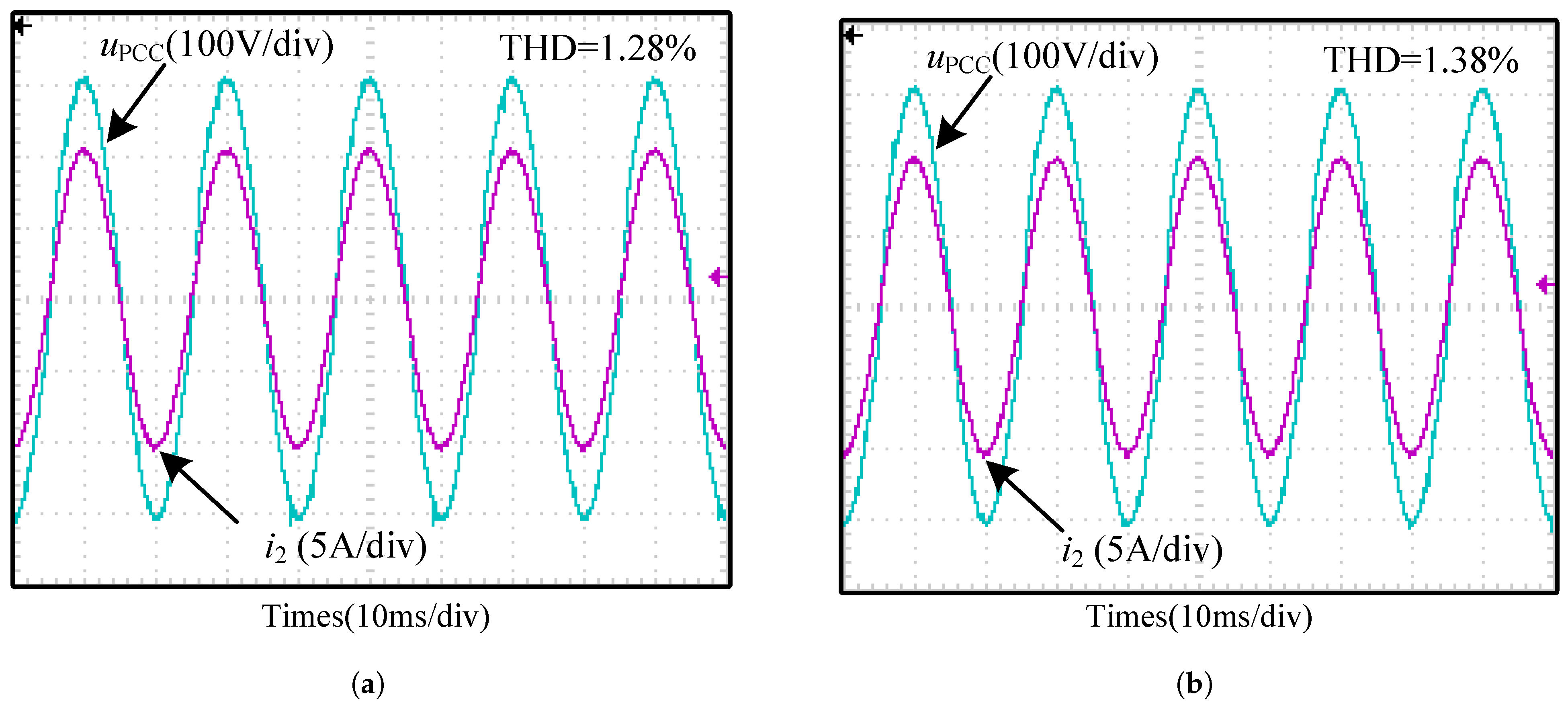
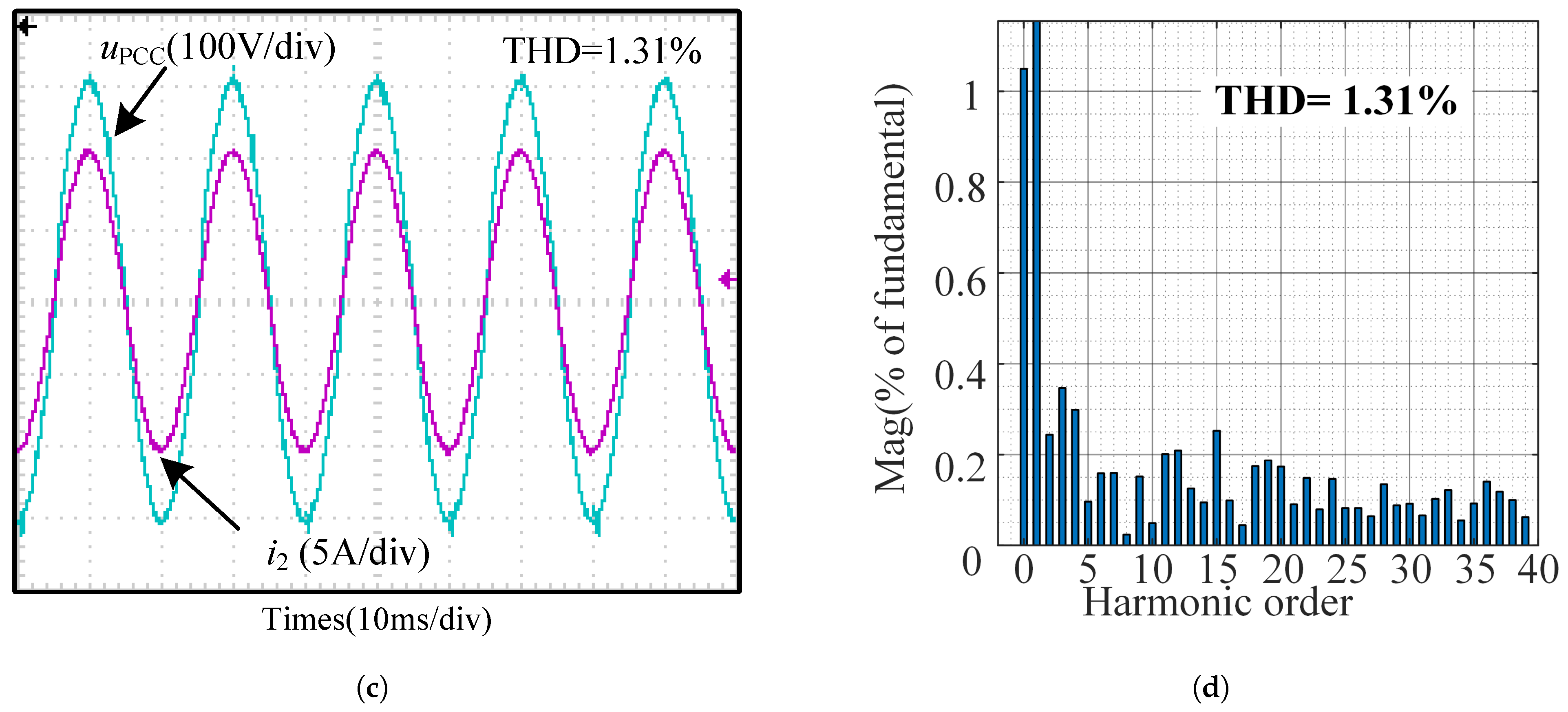
5.1. Steady State Response
5.2. Transient Response
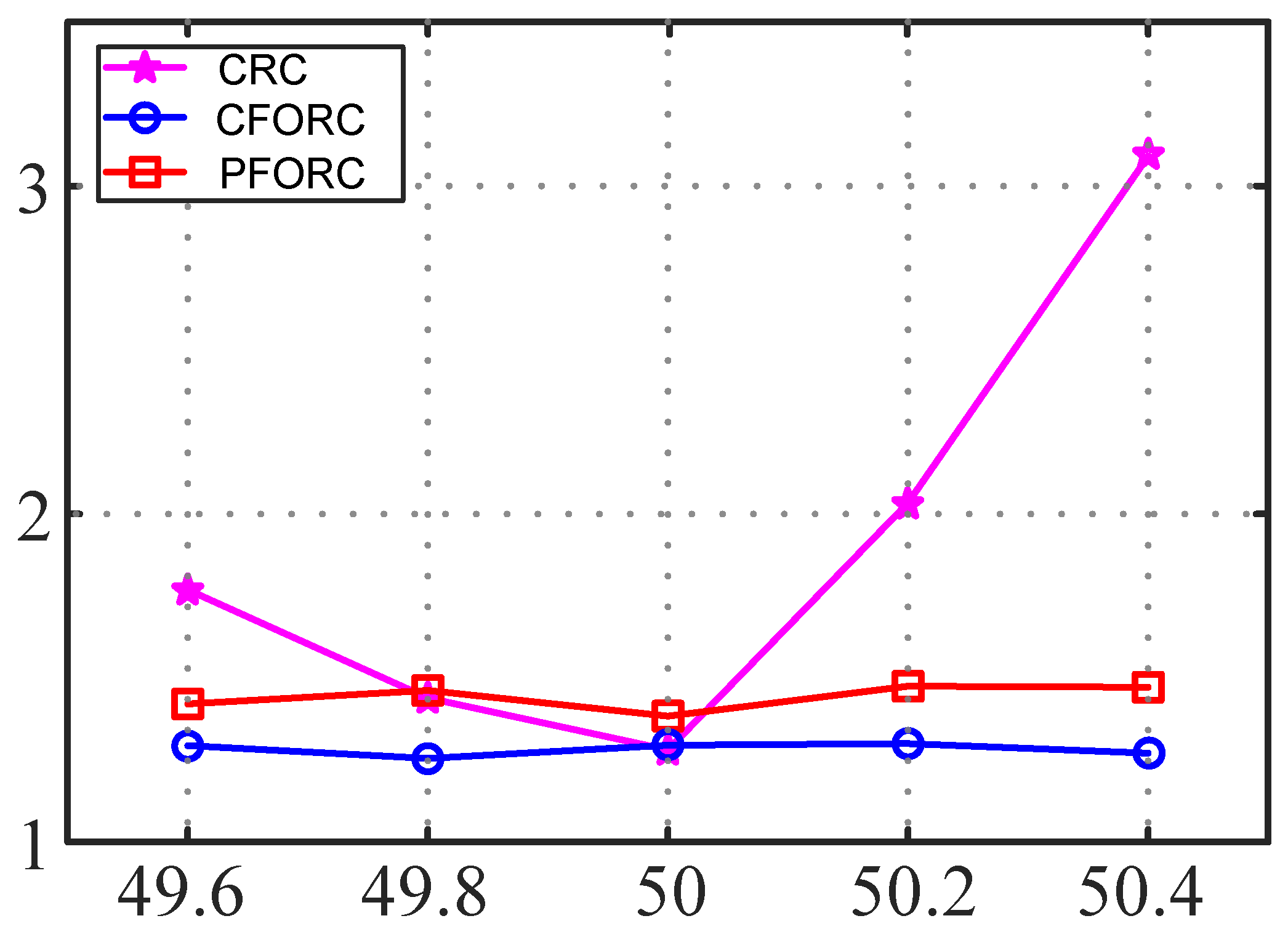
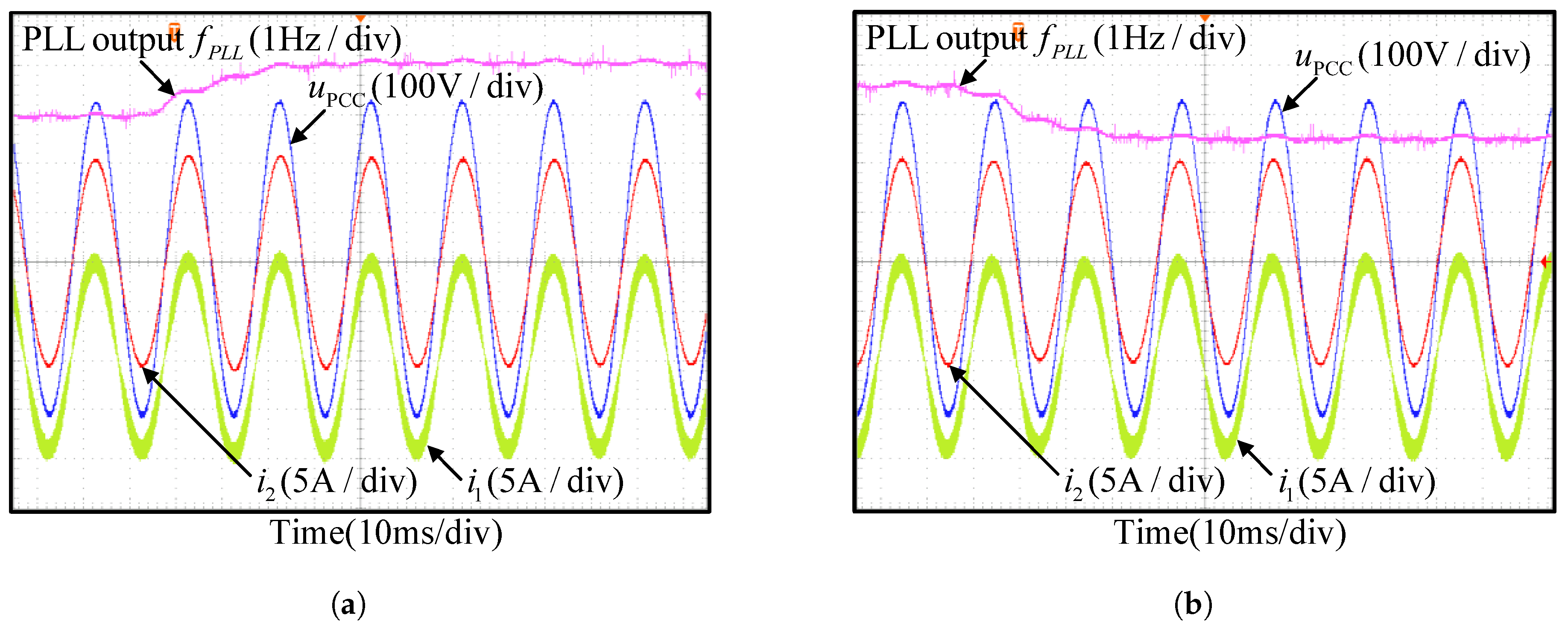
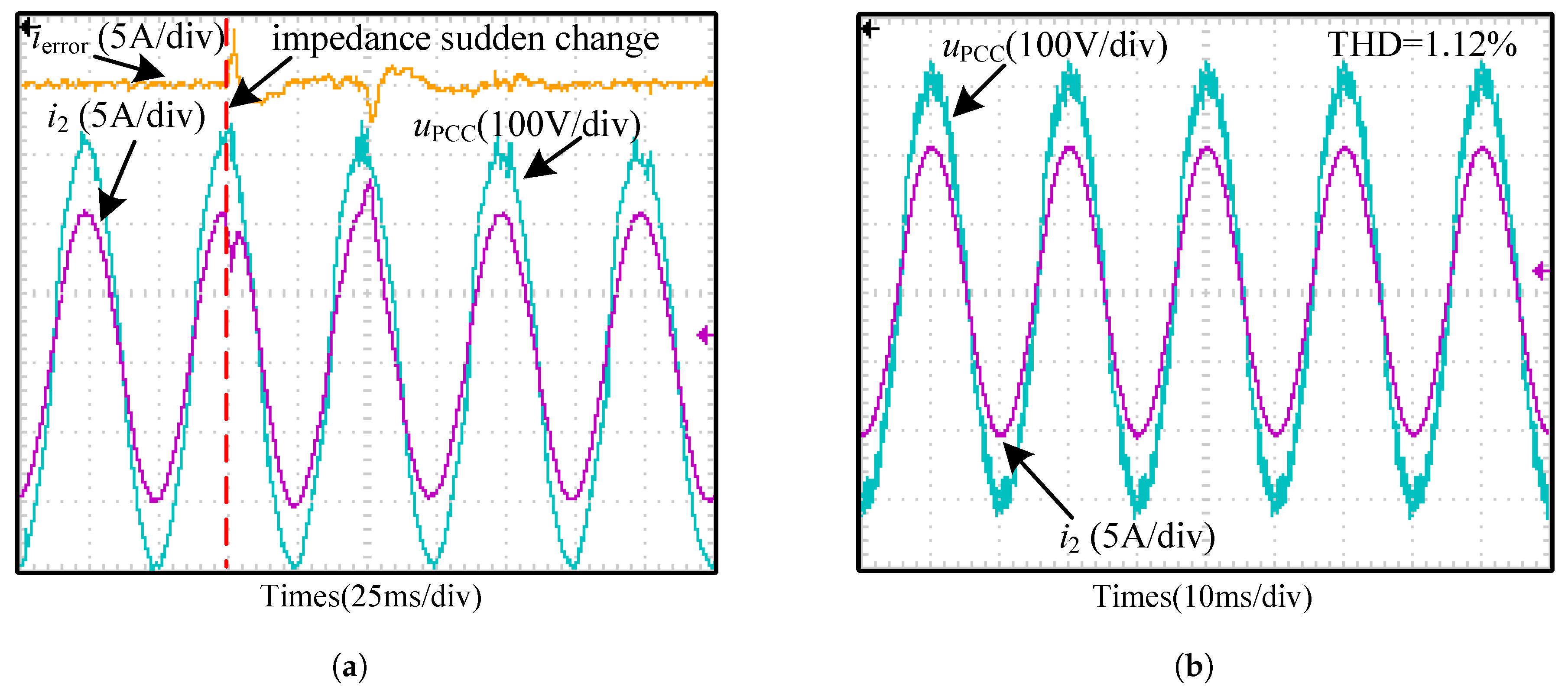
5.3. Robustness Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Chen, J.; Zhang, L.; Li, H.; Zhang, X. Static and dynamic event-triggered mechanisms for distributed sec-ondary control of inverters in low-voltage islanded microgrids. IEEE Trans. Cybern. 2022, 52, 6925–6938. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, F.; Wang, G.; Li, S.; Yu, L. Generalized proportional integral observer based robust finite control set predictive current control for induction motor systems with time-varying disturbances. IEEE Trans. Ind. Inform. 2018, 14, 4159–4168. [Google Scholar] [CrossRef]
- Shubhra, S.; Singh, B. Three-phase grid-interactive solar PV-battery microgrid control based on normalized gradient adaptive regularization factor neural filter. IEEE Trans. Ind. Inform. 2020, 16, 2301–2314. [Google Scholar] [CrossRef]
- Kurniawan, E.; Burrohman, A.M.; Purwowibowo, P.; Wijonarko, S.; Maftukhah, T.; Prakosa, J.A.; Rustandi, D.; Pratiwi, E.B.; Az-Zukhruf, A. Discrete-time design of fractional delay-based repetitive controller with sliding mode approach for uncertain linear systems with multiple periodic signals. Fractal Fract. 2025, 9, 41. [Google Scholar] [CrossRef]
- Chigane, K.; Ouassaid, M. Experimental assessment of integral-type terminal sliding mode control designed for a single-phase grid-interlinked PV system. Control Eng. Pract. 2024, 147, 105903. [Google Scholar] [CrossRef]
- Liu, E.; Han, Y.; Zalhaf, A.S.; Yang, P.; Wang, C. Performance evaluation of isolated three-phase voltage source inverter with LC filter adopting different MPC methods under various types of load. Control Eng. Pract. 2023, 135, 105520. [Google Scholar]
- Zhao, Q.; Zhang, H.; Xia, Y.; Chen, Q.; Ye, Y. Equivalence relation analysis and design of repetitive con-trollers and multiple quasi-resonant controllers for single-phase inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 3338–3349. [Google Scholar] [CrossRef]
- Liang, F.; Lee, H.-J.; Zhang, H. Fractional-order phase lead compensation multirate repetitive control for grid-tied inverters. Fractal Fractals 2023, 7, 848. [Google Scholar] [CrossRef]
- Huang, P.; Li, Z.; Zhou, M.; Kan, Z. Divergent component of motion planning and adaptive repetitive control for wearable walking exoskeletons. IEEE Trans. Cybern. 2024, 54, 2244–2256. [Google Scholar] [CrossRef] [PubMed]
- Pandove, G.; Singh, M. Robust repetitive control design for a three-phase four-wire shunt active power filter. IEEE Trans. Ind. Informat. 2019, 15, 2810–2818. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, Q.; Zhang, H.; Xia, Y.; Ye, Y. A novel RC-ESO-ADRC for harmonics suppression and robustness improvement of grid-tied inverters in a weak and distorted grid. IEEE Trans. Power Electron. 2025, 40, 12581–12593. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, D.; Zhou, K.; Wang, Y. Linear phase lead compensation repetitive control of a CVCF PWM inverter. IEEE Trans. Ind. Electron. 2008, 55, 1595–1602. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhou, G.; Xia, Y.; Zhu, Y.; Yu, D.; Zhang, H. Feedforward dual-mode repetitive control for sin-gle-phase V2G inverters in residential grids. IEEE Trans. Transp. Electrific. 2025, 11, 10927–10937. [Google Scholar] [CrossRef]
- Kurniawan, E.; Wang, H.; Septanto, H.; Adinanta, H.; Suryadi, S.; Pratomo, H.; Hanto, D. Design and analysis of higher-order repetitive sliding mode controller for uncertain linear systems with time-varying periodic disturbances. Trans. Inst. Meas. Control. 2023, 45, 2219–2234. [Google Scholar] [CrossRef]
- Herrán, M.A.; Fischer, J.R.; González, S.A.; Judewicz, M.G.; Carugati, I.; Carrica, D.O. Repetitive control with adaptive sampling frequency for wind power generation systems. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 58–69. [Google Scholar] [CrossRef]
- Cao, Z.; Ledwich, G. Adaptive repetitive control to track variable periodic signals with fixed sampling rate. IEEE/ASME Trans. Mechatron. 2002, 7, 378–384. [Google Scholar]
- Kolluri, S.; Gorla, N.B.Y.; Sapkota, R.; Panda, S.K. A new control architecture with spatial comb filter and spatial repetitive controller for circulating current harmonics elimination in a droop-regulated modular multilevel converter for wind farm application. IEEE Trans. Power Electron. 2019, 34, 10509–10523. [Google Scholar] [CrossRef]
- Mooren, N.; Witvoet, G.; Oomen, T. Gaussian process repetitive control with application to an industrial substrate carrier system with spatial disturbances. IEEE Trans. Control Syst. Technol. 2023, 31, 344–358. [Google Scholar] [CrossRef]
- Escobar, G.; Mattavelli, P.; Hernandez-Gomez, M.; Martinez-Rodriguez, P.R. Filters with linear-phase properties for repetitive feedback. IEEE Trans. Ind. Electron. 2014, 61, 405–413. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, K.; Tang, C.; Shu, Y.; Yang, Y. Fractional-order multiperiodic odd-harmonic repetitive control of programmable AC power sources. IEEE Trans. Power Electron. 2022, 37, 7751–7758. [Google Scholar] [CrossRef]
- Liu, P.; Wang, C.; Zhang, Y.; Liang, Y.; Cui, Y.; Fang, J. Frequency adaptive repetitive control of new energy grid-connected inverter based on improved IIR. IEEE Trans. Power Electron. 2023, 38, 9539–9551. [Google Scholar] [CrossRef]
- Valdez-Fernández, A.A.; Escobar, G.; Catzin-Contreras, G.A.; Hernández-Ruíz, M.E.; Morales-Caporal, R. A 6h±1 repetitive scheme for the three-phase CHB seven-level converter used in an APF application. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 1641–1653. [Google Scholar] [CrossRef]
- Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. A new single-phase PLL structure based on second order generalized integrator. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006; pp. 1–6. [Google Scholar]
- Yang, Y.; Zhou, K.; Blaabjerg, F. Enhancing the frequency adaptability of periodic current controllers with a fixed sampling rate for grid-connected power converters. IEEE Trans. Power Electron. 2016, 31, 7273–7285. [Google Scholar] [CrossRef]
- Zou, Z.-X.; Zhou, K.; Wang, Z.; Cheng, M. Frequency-adaptive fractional-order repetitive control of shunt active power filters. IEEE Trans. Ind. Electron. 2015, 62, 1659–1668. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, D. Digital repetitive learning controller for three-phase CVCF PWM inverter. IEEE Trans. Ind. Electron. 2001, 48, 820–830. [Google Scholar] [CrossRef]
- Xu, J.; Qian, H.; Hu, Y.; Bian, S.; Xie, S. Overview of SOGI-based single-phase phase-locked loops for grid synchronization under complex grid conditions. IEEE Access 2021, 9, 39275–39291. [Google Scholar] [CrossRef]
- Hu, B.; Nian, H.; Li, M.; Liao, Y.; Yang, J.; Tong, H. Impedance characteristic analysis and stability improvement method for DFIG system within PLL bandwidth based on different reference frames. IEEE Trans. Ind. Electron. 2023, 70, 532–543. [Google Scholar] [CrossRef]
- Merry, R.; Kessels, D.; Heemels, W.; Molengraft, M.v.; Steinbuch, M. Delay-varying repetitive control with application to a walking piezo actuator. Automatica 2011, 47, 1737–1743. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, Q.; Ye, Y.; Qu, B. Using IIR filter in fractional order phase lead compensation PIMR-RC for grid-tied inverters. IEEE Trans. Ind. Electron. 2023, 70, 9399–9409. [Google Scholar] [CrossRef]
- Pan, D.; Ruan, X.; Bao, C.; Li, W.; Wang, X. Optimized controller design for LCL-type grid-connected inverter to achieve high robustness against grid-impedance variation. IEEE Trans. Ind. Electron. 2015, 62, 1537–1547. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, X.; Chen, Y.; Lv, Z.; He, Z.; Wu, W.; Yang, L.; Yan, K.; Luo, A.; Guerrero, J.M. Invert-er-current-feedback resonance-suppression method for LCL-type DG system to reduce resonance-frequency offset and grid-inductance effect. IEEE Trans. Ind. Electron. 2018, 65, 7036–7048. [Google Scholar] [CrossRef]











| Symbol | Quantity | Nominal Value |
|---|---|---|
| DC-link voltage | 380 V | |
| Grid voltage (RMS) | 220 V | |
| Output power | 2 kW | |
| DC bus capacitor | 1360 uF | |
| Inverter side inductance | 2.9 mH | |
| C | Filter Capacitor | 6 µF |
| Grid side inductance | 2 mH | |
| Switching frequency | 10 kHz | |
| Sampling frequency | 20 kHz | |
| PLL bandwidth | 15 Hz | |
| PLL damping ratio | 0.707 | |
| PWM Gain | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Dong, H.; Zhou, G.; Ye, Y. Phase-Based Fractional-Order Repetitive Control for Single-Phase Grid-Tied Inverters. Fractal Fract. 2025, 9, 626. https://doi.org/10.3390/fractalfract9100626
Zhao Q, Dong H, Zhou G, Ye Y. Phase-Based Fractional-Order Repetitive Control for Single-Phase Grid-Tied Inverters. Fractal and Fractional. 2025; 9(10):626. https://doi.org/10.3390/fractalfract9100626
Chicago/Turabian StyleZhao, Qiangsong, Hao Dong, Guohui Zhou, and Yongqiang Ye. 2025. "Phase-Based Fractional-Order Repetitive Control for Single-Phase Grid-Tied Inverters" Fractal and Fractional 9, no. 10: 626. https://doi.org/10.3390/fractalfract9100626
APA StyleZhao, Q., Dong, H., Zhou, G., & Ye, Y. (2025). Phase-Based Fractional-Order Repetitive Control for Single-Phase Grid-Tied Inverters. Fractal and Fractional, 9(10), 626. https://doi.org/10.3390/fractalfract9100626





