New Solitary Wave Solutions of the Lakshamanan–Porsezian–Daniel Model with the Application of the Φ⁶ Method in Fractional Sense

Abstract

This paper explores a significant fractional model, which is the fractional Lakshamanan–Porsezian–Daniel ($\mathcal{FLPD}$) model, widely used in various fields like nonlinear optics and plasma physics. An advanced analytical solution for it is attained by the ${\mathsf{\Phi }}^6$ technique. According to this methodology, effective and accurate solutions for wave structures within various types can be produced in the $\mathcal{FLPD}$ model framework. Solutions such as dark, bright, singular, periodic, and plane waves are studied in detail to identify their stability and behavior. Validations are also brought forward to assess the precision and flexibility of the ${\mathsf{\Phi }}^6$ technique in modeling fractional models. Therefore, it is established in this study that the ${\mathsf{\Phi }}^6$ technique represents a powerful tool for examining wave patterns in differential fractional order models.

1. Introduction

Nonlinear systems are very important in modeling complex phenomena across different scientific and engineering disciplines. Unlike linear systems, they do not obey the superposition principle, making their analysis and solution more complex for nonlinear systems in different scientific fields and fluids [1,2,3]. Fractional models are of utmost importance in modeling complex physical systems because integer-order differential equations cannot provide the accuracy of modeling memory effects and non-local behaviors that fractional models can. They deal with fractional derivatives, where the order of differentiation is not an integer; therefore, more flexible and accurate modeling of reality appears, like anomalous diffusion, viscoelasticity, and fluid dynamics [4,5,6]. Fractional derivatives introduce concepts of models, so they can even improve describing phenomena with history path dependences. Therefore, those are precious for theoretical understanding along with their practical use, first, in the sectors of physics and finance and in all of engineering [7,8]. One objective is to model this typical nonlinear wave propagation by presenting the fractional variant of a standard $\mathcal{FLPD}$ model [9]. The $\mathcal{FLPD}$ model is one of the most important generalizations of the nonlinear Schrödinger equation, which plays a critical role in understanding complex phenomena in nonlinear optics, for example, the propagation of optical solitons in birefringent fibers and Heisenberg spin chains [10].

When using a conformable derivative approach [11], fractional derivatives are simplified to maintain many useful properties of classical derivatives while accommodating fractional orders [12]. This approach to the $\mathcal{FLPD}$ model captures complex wave dynamics like dark and bright solitons and plane and singular waves and can model variations in the propagation medium [13,14,15,16].

To solve these fractional models [17,18], sophisticated analytical methods are necessary. Due to their ability to solve nonlinear and fractional models with flexibility and convergence, techniques including the Sardar sub-equation method [19], the Adomian Decomposition technique [20], the q-Homotopy Analysis technique [21], Hirota bilinear method [22], F-expansion technique [23], symmetry reduction technique [24], and many more [25,26,27] are frequently used. These approaches’ dependability and efficiency in capturing the complex behaviors of fractional systems are confirmed by comparing the findings produced with conventional numerical approaches [28,29,30]. This offers a greater understanding of the physical phenomena at play.

The current research work explores the novel results of the $\mathcal{FLPD}$ model by using the ${\mathsf{\Phi }}^6$ technique to extract and validate the results through stability analysis. The $\mathcal{FLPD}$ model [31] with a conformable derivative is as follows:

$$\begin{array}{cc}\hfill & i{D}_t^{\alpha }\mathcal{R}(x,t)+q_1{D}_x^{2\alpha }\mathcal{R}(x,t)+q_2{D}_{xt}^{2\alpha }\mathcal{R}(x,t)+q_3{\left|\mathcal{R}(x,t)\right|}^2\mathcal{R}(x,t)=q_4{D}_x^{4\alpha }\mathcal{R}(x,t)+q_5{\left(D_x^{\alpha }\mathcal{R}(x,t)\right)}^2{\mathcal{R}}^{*}(x,t)\hfill \\ & +q_6|D_x^{\alpha }{\mathcal{R}(x,t)|}^2\mathcal{R}(x,t)+q_7\left|\mathcal{R}(x,t)\right|D_x^{2\alpha }\mathcal{R}(x,t)+q_8{\mathcal{R}}^2(x,t)D_{xx}^{2\alpha }{\mathcal{R}}^{*}(x,t)+q_9{\left|\mathcal{R}(x,t)\right|}^4\mathcal{R}(x,t),\hfill \end{array}$$

(1)

where x represents the spatial term, t represents temporal term, $\mathcal{R}(x,t)$ is a dependent function of complex terms, $q_1$ is the group velocity, $q_2$ represents spatial-temporal dispersions, $q_3$ is the modulation of the self phase, $q_4$ and $q_9$ are fourth orders of photon dispersions, and $q_5,q_6,q_7,$ and $q_8$ are perturb parameters. There are several uses for the $\mathcal{FLPD}$ model in physics, especially in domains where the study of intricate wave propagation and non-local interactions is necessary. This model, which is an extension of the nonlinear Schrödinger model, is very useful for explaining wave dynamics in fluid dynamics, plasma, and optical fibers because it uses fractional derivatives to account for memory and hereditary characteristics. To better understand the behavior of the soliton under the nonlinearity of the Kerr law [32,33], the $\mathcal{FLPD}$ model is frequently used to simulate wave propagation in optical fibers. In recent years, fractional calculus has emerged as an even more powerful tool in modeling systems with memory and hereditary properties, providing a far more comprehensive framework than traditional integer-order models. Applying fractional derivatives to the $\mathcal{FLPD}$ model allows for a greater ability to explore the dynamics of optical solitons under the complexities inherent in materials and interactions in reality. This study aims to obtain new solitary wave solutions of the $\mathcal{FLPD}$ model using the ${\mathsf{\Phi }}^6$ technique. Therefore, the research will deepen understanding of how nonlinear waves behave in the media of optical fibers, possibly aiding in the designing of more advanced optical communication systems and furthering studies in nonlinear dynamics.

Controlling signal stability and dispersion over long distances is essential for enhancing the design of optical communication systems. The $\mathcal{FLPD}$ model in plasma physics [34] improves our comprehension of energy transfer and wave stability in plasma environments by capturing the propagation of solitary waves as well as the impacts of weak nonlinearity and nonlocality. The model offers insights into intricate magnetic and wave interference phenomena by describing dynamics in birefringent fibers and Heisenberg spin chains. Applications for this include materials with spin orbit coupling and magnetic resonance imaging. These uses highlight the value of the $\mathcal{FLPD}$ model in the development of technologies that depend on steady and regulated wave propagation. The novelty of the paper is to computationally solve the $\mathcal{FLPD}$ model with an analytical technique of ${\mathsf{\Phi }}^6$ [35] to extract novel results and validate these results through stability analysis.

The layout of the paper is as follows. In Section 2, we discuss the fractional derivatives of conformables. Section 3 covers the mathematical analysis of the technique ${\mathsf{\Phi }}^6$. In Section 4, we implement in detail the analytical technique for the governing model with validation of the acquired results. Section 5 covers the results and discussion with physical structures. In Section 6, we conclude with the acquired results.

2. Fractional Conformable Derivative

As contemporary method of fractional calculus [36], the conformable fractional derivative seeks to enhance and simplify the characteristics of conventional fractional derivatives. The conformable derivative was introduced as a substitute for traditional definitions and is particularly regarded for upholding several crucial calculus rules, including linearity, the product rule, and the chain rule, which facilitates its application in differential equations and engineering difficulties. Conformable fractional derivatives provide a well-behaved and simple definition of a derivative by enabling fractional differentiation that complies with normal calculus standards. It is frequently referred to as a limit and maintains well-known mathematics characteristics that are not necessarily found in conventional fractional derivatives [37].

In disciplines like physics, biology, and finance [38,39,40], this derivative has been used to solve ordinary and partial differential equations, offering answers to practical issues involving memory effects and inherited characteristics. The primary benefit of the conformable derivative is that it follows the principles of classical derivatives, making analytical solutions easier to understand and enabling applications that call for fractional calculus, such as signal processing and modeling anomalous diffusion. The conformable derivative is linear, as with the deformed derivative previously mentioned, which limits it to the capture of nonlinear effects. Nonlinear derivatives, such as the Nobre derivative [41], Caputo–Fabrizio, and Atangana–Baleanu fractional derivatives, describe complex phenomena better because of their nonlinearity and nonlocality. Incorporation of these nonlinear derivatives may give a more holistic description of the $\mathcal{FLPD}$ model.

Definition 1.

Suppose that a function $f\left(t\right):(0,+\infty )\to R.$ Then, the fractional order of conformable α to f is defined as

$$D_t^{\alpha }f\left(t\right)=\underset{\delta \to 0}{lim}{\displaystyle \frac{f(t+\delta t^{1-\alpha })-f\left(t\right)}{\delta }},$$

(2)

where $t>0$ and $\alpha \in (0,1].$ The $f\left(t\right)$ function is differentiable conformably at point t.

Theorem 1.

Suppose that $f_1\left(t\right)$ and $f_2\left(t\right)$ are two conformable derivatives for all $t>0$. The following define the properties of conformable derivatives.

properties:

• $D_t^{\alpha }(m_1{f}_1+m_2{f}_2)=m_1{D}_t^{\alpha }{f}_1+m_2{D}_t^{\alpha }{f}_2$.
• $D_t^{\alpha }(t^{m_1})=m_1{t}^{m_1-\alpha }$.
• $D_t^{\alpha }\left(c\right)=0$.
• $D_t^{\alpha }\left(f_1{f}_2\right)=f_1{D}_t^{\alpha }{f}_2+f_2{D}_t^{\alpha }{f}_1.$
• $D_t^{\alpha }\left({\displaystyle \frac{f_1}{f_2}}\right)={\displaystyle \frac{f_2{D}_t^{\alpha }{f}_1-f_1{D}_t^{\alpha }{f}_2}{f_2^2}}$.
• $f_1$ is differentiable $D_t^{\alpha }\left(f_1\right)\left(t\right)=t^{1-\alpha }{\displaystyle \frac{d{f}_1}{dt}}.$

Theorem 2.

Suppose that $f_1\left(t\right)$ represents conformable derivatives, and $f_2\left(t\right)$ is differentiable in the range of $f_1\left(t\right)$ for all $t>0$. Then,

$$D_t^{\alpha }(f_1\left(t\right)\circ f_2\left(t\right))=t^{1-\alpha }{\displaystyle \frac{d{f}_2}{dt}}{\displaystyle \frac{d}{dt}}\left(f_1\left(f_2\left(t\right)\right)\right).$$

(3)

3. Description of Analytical Technique

This section briefly describes the ${\mathsf{\Phi }}^6$ analytical technique. The fractional derivatives allow us to propose novel solutions for the $\mathcal{FLPD}$ model. For this, we consider the following complex wave equation

$$\begin{array}{c}\hfill \mathcal{R}(x,t)=e^{i\delta }M\left(\zeta \right),\end{array}$$

(4)

where

$$\begin{array}{c}\hfill M\left(\zeta \right)=L\left(M\left(\zeta \right)\right),\zeta ={\displaystyle \frac{x^{\alpha }}{\alpha }}-\eta {\displaystyle \frac{t^{\alpha }}{\alpha }},\delta (x,t)=-a{\displaystyle \frac{x^{\alpha }}{\alpha }}+b{\displaystyle \frac{t^{\alpha }}{\alpha }}+\mathsf{\Gamma },\end{array}$$

(5)

where $L\left(M\right(\zeta \left)\right)$ represents the functional complex wave of transformation of $M\left(\zeta \right).$ Then, $\delta (x,t)$ represents the phase factors. The parameters $a,b,\mathsf{\Gamma }$, and $\eta$ are proposed solutions that indicate the numbers of solitons, phase constants, velocity parameters, and frequency numbers. L in Equation (6) illustrates the variable transformation, and $M\left(\zeta \right)$ satisfies the ${\mathsf{\Phi }}^6$ technique in the form as

$$\begin{array}{c}\hfill {\left(M{\left(\zeta \right)}^{\prime }\right)}^2={\displaystyle \frac{1}{3}}{s}_{5}M{\left(\zeta \right)}^6+{\displaystyle \frac{1}{2}}{s}_{3}M{\left(\zeta \right)}^4+s_{1}M{\left(\zeta \right)}^2+s_0,\\ \hfill M{\left(\zeta \right)}^{″}=s_{5}M{\left(\zeta \right)}^5+s_{3}M{\left(\zeta \right)}^3+s_{1}M\left(\zeta \right),\end{array}$$

(6)

as $s_j$ for all $j=0,1,2,...$ are real constants.

The solutions to Equation (6) are as follows:

$$\begin{array}{c}\hfill M\left(\zeta \right)={\displaystyle \frac{G\left(\zeta \right)}{\sqrt{pG{\left(\zeta \right)}^2+k}}}.\end{array}$$

(7)

Since $pG{\left(\zeta \right)}^2+k>0$, the solution for Jacobi methods is

$$\begin{array}{c}\hfill {\left(G{\left(\zeta \right)}^{\prime }\right)}^2=e_{4}G{\left(\zeta \right)}^4+e_{2}G{\left(\zeta \right)}^2+e_0,\end{array}$$

(8)

where

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(e_2-s_1\right)}{2(e_2-s_1{)}^2-4e_2\left(e_2-s_1\right)+6e_0{e}_4}},\end{array}$$

(9)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3e_0{s}_3}{2(e_2-s_1{)}^2-4e_2\left(e_2-s_1\right)+6e_0{e}_4}},\end{array}$$

(10)

under constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9e_0{e}_4}{e_2-s_1}}-\left(2e_2+s_1\right){)}^2+s_3^2\left({\displaystyle \frac{9e_0{e}_4}{e_2-s_1}}-\left(2e_2+s_1\right)\right)=0.\end{array}$$

(11)

The following cases are solutions to satisfy the governing model using the ${\mathsf{\Phi }}^6$ technique.

4. Implementation

In this section, we solve Equation (1) using the ${\mathsf{\Phi }}^6$ technique combined with the conformable derivative. Firstly, we convert $\mathcal{FLPD}$ model into an ordinary differential equation; for this, we insert Equation (4) into Equation (1), using the conformable derivatives of Equations (2) and (3), to acquire the following equations in the form of real and imaginary parts.

$$\begin{array}{c}\hfill q_4{\displaystyle \frac{d^{4}M}{d{\zeta }^4}}-(q_1-q_2\eta +6q_4{a}^2){\displaystyle \frac{d^{2}M}{d{\zeta }^2}}-(q_{2}ab-b-q_1{a}^2-q_4{a}^4)M-(q_5+q_6+q_7+q_8)a^2{M}^3\\ \hfill +q_9{M}^5-q_3{M}^3+(q_5+q_6)M{\left({\displaystyle \frac{dM}{d\zeta }}\right)}^2+(q_7+q_8)M^2{\displaystyle \frac{d^{2}M}{d{\zeta }^2}}=0,\end{array}$$

(12)

$$\begin{array}{c}\hfill (1-q_2\alpha )\left(\eta +\left(2q_{1}a+4q_4{a}^3-q_{2}b\right)\right){\displaystyle \frac{dM}{d\zeta }}-2\left(q_5+q_6+q_7+q_8\right)a{M}^2{\displaystyle \frac{dM}{d\zeta }}-4q_{4}a{\displaystyle \frac{d^{3}M}{d{\zeta }^3}}=0.\end{array}$$

(13)

The coefficients of the linear function $q_4=0,q_5+q_6=0$, and $q_7+q_8=0$ are set to be zero in Equations (12) and (13) such that Equation (13) becomes the following equation.

$$\begin{array}{c}\hfill ((1-q_{2}a)\eta +(2q_{1}a-q_{2}b)){\displaystyle \frac{dM}{d\zeta }}=0.\end{array}$$

(14)

We simplify the above equation to obtain the value of the speed function $\eta$.

$$\eta ={\displaystyle \frac{q_{2}b-2q_{1}a}{1-q_{2}a}}.$$

(15)

Now, we solve the perturb parameters $q_5$ and $q_7$, in Equations (12) and (13) using the elimination technique of Gaussian:

$$\left[\begin{array}{c}{q}_4\\ q_5\\ q_6\\ q_7\\ q_8\end{array}\right]=\left[\begin{array}{c}0\\ 1\\ -1\\ 0\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 0\\ 1\\ -1\end{array}\right]q_7.$$

(16)

Thus, Equation (12) becomes

$$(q_1-q_2\eta ){\displaystyle \frac{d^{2}M}{d{\zeta }^2}}-(b+q_1{a}^2-q_{2}ba)M\left(\zeta \right)-q_9{M}^5\left(\zeta \right)+q_3{M}^3\left(\zeta \right)=0.$$

(17)

We simplify the above equation to acquire the required

$$-M\left(\zeta \right)\left(a^2{q}_1+ab\left(-q_2\right)+b\right)+\left(q_1-\eta q_2\right)M{\left(\zeta \right)}^{″}-q_{9}M{\left(\zeta \right)}^5+q_{3}M{\left(\zeta \right)}^3=0.$$

(18)

Inserting the required derivatives of $M\left(\zeta \right)$, given in Equation (6), into Equation (18), putting all the acquired equations into the general solutions to Equation (7), and collecting all the coefficients of $M\left(\zeta \right)$, we extract soliton solutions. After solving these equations in Mathematica, we obtain the following family-1.

Family-1

$$\left\{b\to {\displaystyle \frac{q_1\left(a^2-s_1\right)+\eta q_2{s}_1}{a{q}_2-1}},q_3\to s_3\left(\eta q_2-q_1\right),q_9\to s_5\left(q_1-\eta q_2\right)\right\}.$$

(19)

According to above Family-1, we use all the cases given Table 1 and reinsert all the values in Equation (18); then, the general solutions given in Equations (7) and (8) are put into Equation (1) to obtain the required soliton solutions. Additionally, the cases summarized in Table 2 are applied to describe the transition behaviors under the ${\mathsf{\Phi }}^6$ technique.

Table 1. Jacobi elliptic functions solutions according to $h\to 0$ and $h\to 1$.

Cases	${\mathit{e}}_0$	${\mathit{e}}_2$	${\mathit{e}}_4$	$\mathit{G}\left(\mathit{\zeta }\right)$
1	1	$-(1+h^2)$	$h^2$	$\mathrm{sn}\left(\zeta \right)$ or $\mathrm{cd}\left(\zeta \right)$
2	$1-h^2$	$2h^2-1$	$-h^2$	$\mathrm{cn}\left(\zeta \right)$
3	$h^2-1$	$2-h^2$	$-1$	$\mathrm{dn}\left(\zeta \right)$
4	$h^2$	$-(1+h^2)$	1	$\mathrm{ns}\left(\zeta \right)$ or $\mathrm{dc}\left(\zeta \right)$
5	$-h^2$	$2h^2-1$	$1-h^2$	$\mathrm{nc}\left(\zeta \right)$
6	$-1$	$2-h^2$	$-(1-h^2)$	$\mathrm{nd}\left(\zeta \right)$
7	1	$2-h^2$	$1-h^2$	$\mathrm{sc}\left(\zeta \right)$
8	1	$2h^2-1$	$-h^2(1-h^2)$	$\mathrm{sd}\left(\zeta \right)$
9	$1-h^2$	$2-h^2$	1	$\mathrm{cs}\left(\zeta \right)$
10	$-h^2(1-h^2)$	$2h^2-1$	1	$\mathrm{ds}\left(\zeta \right)$
11	${\displaystyle \frac{1-h^2}{4}}$	${\displaystyle \frac{1+h^2}{2}}$	${\displaystyle \frac{1-h^2}{4}}$	$\mathrm{nc}\left(\zeta \right)\pm \mathrm{sc}\left(\zeta \right)$ or ${\displaystyle \frac{\mathrm{cn}\left(\zeta \right)}{1\pm \mathrm{sn}\left(\zeta \right)}}$
12	$-{\displaystyle \frac{{(1-h^2)}^2}{4}}$	${\displaystyle \frac{1+h^2}{2}}$	${\displaystyle \frac{1}{4}}$	$h\mathrm{cn}\left(\zeta \right)\pm \mathrm{dn}\left(\zeta \right)$
13	${\displaystyle \frac{1}{4}}$	${\displaystyle \frac{1-2h^2}{2}}$	${\displaystyle \frac{1}{4}}$	${\displaystyle \frac{\mathrm{sn}\left(\zeta \right)}{1\pm \mathrm{cn}\left(\zeta \right)}}$
14	${\displaystyle \frac{1}{4}}$	${\displaystyle \frac{1+h^2}{2}}$	${\displaystyle \frac{{(1-h^2)}^2}{4}}$	${\displaystyle \frac{\mathrm{sn}\left(\zeta \right)}{\mathrm{cn}\left(\zeta \right)\pm \mathrm{dn}\left(\zeta \right)}}$

Table 2. Cases of ${\mathsf{\Phi }}^6$ technique.

$\mathit{h}\to 0$	$\mathit{h}\to 1$
sn$(\zeta ,0)$ = $\sin \left(\zeta \right)$	sn$(\zeta ,1)$ = $\tanh \left(\zeta \right)$
cd$(\zeta ,0)$ = $\tan \left(\zeta \right)$	cn$(\zeta ,1)$ = $\mathrm{sech}\left(\zeta \right)$
cn$(\zeta ,0)$ = $\cos \left(\zeta \right)$	dn$(\zeta ,1)$ = $\mathrm{sech}\left(\zeta \right)$
ns$(\zeta ,0)$ = $\csc \left(\zeta \right)$	cs$(\zeta ,1)$ = $\cot \left(\zeta \right)$
ds$(\zeta ,0)$ = $\csc \left(\zeta \right)$	cs$(\zeta ,1)$ = $\mathrm{csch}\left(\zeta \right)$
sc$(\zeta ,0)$ = $\tan \left(\zeta \right)$	ds$(\zeta ,1)$ = $\mathrm{csch}\left(\zeta \right)$
sd$(\zeta ,0)$ = $\sin \left(\zeta \right)$	sc$(\zeta ,1)$ = $\sinh \left(\zeta \right)$
nc$(\zeta ,0)$ = $\sec \left(\zeta \right)$	sd$(\zeta ,1)$ = $\sinh \left(\zeta \right)$
dn$(\zeta ,0)$ = 1	nc$(\zeta ,1)$ = $\cosh \left(\zeta \right)$

Case-1: When $e_0=1,e_2=-(1+h^2)$, and $e_4=h^2$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{1,1}={\displaystyle \frac{\mathrm{sn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(-h^2-s_1-1\right)\mathrm{sn}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}+\frac{3s_3}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}}}},\end{array}$$

(20)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(-h^2-s_1-1\right)}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}},\end{array}$$

(21)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}},\end{array}$$

(22)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9h^2}{-h^2-s_1-1}}-2\left(-h^2-1\right)-s_1{)}^2+s_3^2\left({\displaystyle \frac{9h^2}{-h^2-s_1-1}}-2\left(-h^2-1\right)-s_1\right)=0,\end{array}$$

(23)

when $h\to 1$, we acquire the dark solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{1,1}={\displaystyle \frac{\tanh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-2\right)s_3\tanh {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}+\frac{3s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}}}},\end{array}$$

(24)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(-s_1-2\right)s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}},\end{array}$$

(25)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}},\end{array}$$

(26)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{-s_1-2}}+4{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{-s_1-2}}+4\right)=0,\end{array}$$

(27)

when $h\to 0$, we acquire the periodic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{1,1}{\displaystyle \frac{\sin \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-1\right)s_3\sin {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}+\frac{3s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}}}},\end{array}$$

(28)

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(-s_1-1\right)s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\end{array}$$

(29)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\end{array}$$

(30)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(2-s_1{)}^2+s_3^2\left(2-s_1\right)=0,\end{array}$$

(31)

or

$$\begin{array}{c}\hfill {\mathcal{R}}_{1,2}={\displaystyle \frac{\mathrm{cd}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(-h^2-s_1-1\right)\mathrm{cd}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}+\frac{3s_3}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}}}},\end{array}$$

(32)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(-h^2-s_1-1\right)}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}},\end{array}$$

(33)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}},\end{array}$$

(34)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9h^2}{-h^2-s_1-1}}-2\left(-h^2-1\right)-s_1{)}^2+s_3^2\left({\displaystyle \frac{9h^2}{-h^2-s_1-1}}-2\left(-h^2-1\right)-s_1\right)=0.\end{array}$$

(35)

When $h\to 1$, we acquire the rational solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{1,2}={\displaystyle \frac{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-2\right)s_3{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}+\frac{3s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}}}},\end{array}$$

(36)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(-s_1-2\right)s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}},\end{array}$$

(37)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}},\end{array}$$

(38)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{-s_1-2}}+4{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{-s_1-2}}+4\right)=0,\end{array}$$

(39)

when $h\to 0$, we acquire the periodic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{1,2}={\displaystyle \frac{\cos \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-1\right)s_3\cos {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}+\frac{3s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}}}},\end{array}$$

(40)

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(-s_1-1\right)s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\end{array}$$

(41)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\end{array}$$

(42)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(2-s_1{)}^2+s_3^2\left(2-s_1\right)=0.\end{array}$$

(43)

Case-2: When $e_0=1-h^2,e_2=2h^2-1\&e_4=-h^2$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{2,1}={\displaystyle \frac{\mathrm{cn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(2h^2-s_1-1\right)\mathrm{cn}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}+\frac{3\left(1-h^2\right)s_3}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}}}},\end{array}$$

(44)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(2h^2-s_1-1\right)}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}},\end{array}$$

(45)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3\left(1-h^2\right)s_3}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}},\end{array}$$

(46)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-{\displaystyle \frac{9\left(1-h^2\right)h^2}{2h^2-s_1-1}}-2\left(2h^2-1\right)-s_1{)}^2+s_3^2\left(-{\displaystyle \frac{9\left(1-h^2\right)h^2}{2h^2-s_1-1}}-2\left(2h^2-1\right)-s_1\right)=0,\end{array}$$

(47)

when $h\to 1$, we acquire the bright solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{2,1}={\displaystyle \frac{\mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3\mathrm{sech}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(48)

as

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(49)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(50)

when $h\to 0$, we acquire the periodic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{2,1}={\displaystyle \frac{\cos \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-1\right)s_3\cos {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}+\frac{3s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}}}},\end{array}$$

(51)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(-s_1-1\right)s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\end{array}$$

(52)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\end{array}$$

(53)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(2-s_1{)}^2+s_3^2\left(2-s_1\right)=0.\end{array}$$

(54)

Case-3: When $e_0=h^2-1,e_2=-2-h^2$, and $e_4=-1$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{3,1}={\displaystyle \frac{\mathrm{dn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(-h^2-s_1+2\right)\mathrm{dn}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)-6\left(h^2-1\right)}+\frac{3\left(h^2-1\right)s_3}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)-6\left(h^2-1\right)}}}},\end{array}$$

(55)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(-h^2-s_1+2\right)}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)-6\left(h^2-1\right)}},\end{array}$$

(56)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3\left(h^2-1\right)s_3}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)-6\left(h^2-1\right)}},\end{array}$$

(57)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-{\displaystyle \frac{9\left(h^2-1\right)}{-h^2-s_1+2}}-2\left(2-h^2\right)-s_1{)}^2+s_3^2\left(-{\displaystyle \frac{9\left(h^2-1\right)}{-h^2-s_1+2}}-2\left(2-h^2\right)-s_1\right)=0,\end{array}$$

(58)

when $h\to 1$, we acquire the bright solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{3,1}={\displaystyle \frac{\mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3\mathrm{sech}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(59)

as

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(60)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(61)

when $h\to 0$, we acquire the plane wave solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{3,1}={\displaystyle \frac{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(2-s_1\right)s_3{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}-\frac{3s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}}}},\end{array}$$

(62)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(2-s_1\right)s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}},\end{array}$$

(63)

$$\begin{array}{c}\hfill k=-{\displaystyle \frac{3s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}},\end{array}$$

(64)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{2-s_1}}-4{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{2-s_1}}-4\right)=0.\end{array}$$

(65)

Case-4: When $e_0=h^2,e_2=-(1+h^2)$, and $e_4=1$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{4,1}={\displaystyle \frac{\mathrm{ns}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(-h^2-s_1-1\right)\mathrm{ns}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}+\frac{3h^2{s}_3}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}}}},\end{array}$$

(66)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(-h^2-s_1-1\right)}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}},\end{array}$$

(67)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3h^2{s}_3}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}},\end{array}$$

(68)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9h^2}{-h^2-s_1-1}}-2\left(-h^2-1\right)-s_1{)}^2+s_3^2\left({\displaystyle \frac{9h^2}{-h^2-s_1-1}}-2\left(-h^2-1\right)-s_1\right)=0,\end{array}$$

(69)

when $h\to 1$, we acquire the singular solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{4,1}={\displaystyle \frac{\coth \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-2\right)s_3\coth {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}+\frac{3s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}}}},\end{array}$$

(70)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(-s_1-2\right)s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}},\end{array}$$

(71)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}},\end{array}$$

(72)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{-s_1-2}}+4{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{-s_1-2}}+4\right)=0,\end{array}$$

(73)

when $h\to 0$, we acquire the trigonometric solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{4,1}={\displaystyle \frac{\csc \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-1\right)s_3\csc {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}}}},\end{array}$$

(74)

as

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(-s_1-1\right)s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(75)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(2-s_1{)}^2+s_3^2\left(2-s_1\right)=0,\end{array}$$

(76)

or

$$\begin{array}{c}\hfill {\mathcal{R}}_{4,2}={\displaystyle \frac{\mathrm{dc}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(-h^2-s_1-1\right)\mathrm{dc}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}+\frac{3h^2{s}_3}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}}}},\end{array}$$

(77)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(-h^2-s_1-1\right)}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}},\end{array}$$

(78)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3h^2{s}_3}{2(-h^2-s_1-1{)}^2-4\left(-h^2-1\right)\left(-h^2-s_1-1\right)+6h^2}},\end{array}$$

(79)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9h^2}{-h^2-s_1-1}}-2\left(-h^2-1\right)-s_1{)}^2+s_3^2\left({\displaystyle \frac{9h^2}{-h^2-s_1-1}}-2\left(-h^2-1\right)-s_1\right)=0,\end{array}$$

(80)

when $h\to 1$, we acquire the hyperbolic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{4,2}={\displaystyle \frac{\cosh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{p\mathrm{dc}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2+k}}},\end{array}$$

(81)

where

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(-s_1-2\right)s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}},\end{array}$$

(82)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-s_1-2{)}^2+8\left(-s_1-2\right)+6}},\end{array}$$

(83)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{-s_1-2}}+4{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{-s_1-2}}+4\right)=0,\end{array}$$

(84)

when $h\to 0$, we acquire the periodic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{4,2}={\displaystyle \frac{\sec \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{p\sec {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2+k}}},\end{array}$$

(85)

where

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(-s_1-1\right)s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(86)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(2-s_1{)}^2+s_3^2\left(2-s_1\right)=0.\end{array}$$

(87)

Case-5: When $e_0=-h^2,e_2=2h^2-1$, and $e_4=1$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{5,1}={\displaystyle \frac{\mathrm{nc}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(2h^2-s_1-1\right)\mathrm{nc}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}-\frac{3h^2{s}_3}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}}}},\end{array}$$

(88)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(2h^2-s_1-1\right)}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}},\end{array}$$

(89)

$$\begin{array}{c}\hfill k=-{\displaystyle \frac{3h^2{s}_3}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}},\end{array}$$

(90)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-{\displaystyle \frac{9\left(1-h^2\right)h^2}{2h^2-s_1-1}}-2\left(2h^2-1\right)-s_1{)}^2+s_3^2\left(-{\displaystyle \frac{9\left(1-h^2\right)h^2}{2h^2-s_1-1}}-2\left(2h^2-1\right)-s_1\right)=0,\end{array}$$

(91)

when $h\to 1$, we acquire the hyperbolic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{5,1}={\displaystyle \frac{\cosh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3\cosh {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}-\frac{3s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(92)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\end{array}$$

(93)

$$\begin{array}{c}\hfill k=-{\displaystyle \frac{3s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\end{array}$$

(94)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(95)

when $h\to 0$, we acquire the periodic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{5,1}={\displaystyle \frac{\sec \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-1\right)s_3\sec {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}}}},\end{array}$$

(96)

as

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(-s_1-1\right)s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(97)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(2-s_1{)}^2+s_3^2\left(2-s_1\right)=0.\end{array}$$

(98)

Case-6: When $e_0=-1,e_2=2-h^2$, and $e_4=-(1-h^2)$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{6,1}={\displaystyle \frac{\mathrm{nd}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(-h^2-s_1+2\right)\mathrm{nd}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)-6\left(h^2-1\right)}-\frac{3s_3}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)-6\left(h^2-1\right)}}}},\end{array}$$

(99)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(-h^2-s_1+2\right)}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)-6\left(h^2-1\right)}},\end{array}$$

(100)

$$\begin{array}{c}\hfill k=-{\displaystyle \frac{3s_3}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)-6\left(h^2-1\right)}},\end{array}$$

(101)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-{\displaystyle \frac{9\left(h^2-1\right)}{-h^2-s_1+2}}-2\left(2-h^2\right)-s_1{)}^2+s_3^2\left(-{\displaystyle \frac{9\left(h^2-1\right)}{-h^2-s_1+2}}-2\left(2-h^2\right)-s_1\right)=0,\end{array}$$

(102)

when $h\to 1$, we acquire the hyperbolic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{6,1}={\displaystyle \frac{\coth \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3\coth {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}-\frac{3s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(103)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\end{array}$$

(104)

$$\begin{array}{c}\hfill k=-{\displaystyle \frac{3s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\end{array}$$

(105)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(106)

when $h\to 0$, we acquire the trigonometric solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{6,1}={\displaystyle \frac{\csc \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(2-s_1\right)s_3\csc {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}-\frac{3s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}}}},\end{array}$$

(107)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(2-s_1\right)s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}},\end{array}$$

(108)

$$\begin{array}{c}\hfill k=-{\displaystyle \frac{3s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}},\end{array}$$

(109)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{2-s_1}}-4{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{2-s_1}}-4\right)=0.\end{array}$$

(110)

Case-7: When $e_0=1,e_2=2-h^2$, and $e_4=1-h^2$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{7,1}={\displaystyle \frac{\mathrm{sc}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(-h^2-s_1+2\right)\mathrm{sc}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)+6\left(1-h^2\right)}+\frac{3s_3}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)+6\left(1-h^2\right)}}}},\end{array}$$

(111)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(-h^2-s_1+2\right)}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)+6\left(1-h^2\right)}},\end{array}$$

(112)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)+6\left(1-h^2\right)}},\end{array}$$

(113)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9\left(1-h^2\right)}{-h^2-s_1+2}}-2\left(2-h^2\right)-s_1{)}^2+s_3^2\left({\displaystyle \frac{9\left(1-h^2\right)}{-h^2-s_1+2}}-2\left(2-h^2\right)-s_1\right)=0,\end{array}$$

(114)

when $h\to 1$, we acquire the hyperbolic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{7,1}={\displaystyle \frac{\sinh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3\sinh {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}+\frac{3s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(115)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\end{array}$$

(116)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\end{array}$$

(117)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(118)

when $h\to 0$, we acquire the periodic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{7,1}={\displaystyle \frac{\tan \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(2-s_1\right)s_3\tan {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}+\frac{3s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}}}},\end{array}$$

(119)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(2-s_1\right)s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}},\end{array}$$

(120)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}},\end{array}$$

(121)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{2-s_1}}-4{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{2-s_1}}-4\right)=0.\end{array}$$

(122)

Case-8: When $e_0=1,e_2=2h^2-1$, and $e_4=-h^2(1-h^2)$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{8,1}={\displaystyle \frac{\mathrm{sd}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(2h^2-s_1-1\right)\mathrm{sd}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}+\frac{3s_3}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}}}},\end{array}$$

(123)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(2h^2-s_1-1\right)}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}},\end{array}$$

(124)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}},\end{array}$$

(125)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-{\displaystyle \frac{9\left(1-h^2\right)h^2}{2h^2-s_1-1}}-2\left(2h^2-1\right)-s_1{)}^2+s_3^2\left(-{\displaystyle \frac{9\left(1-h^2\right)h^2}{2h^2-s_1-1}}-2\left(2h^2-1\right)-s_1\right)=0,\end{array}$$

(126)

when $h\to 1$, we acquire the hyperbolic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{8,1}={\displaystyle \frac{\sinh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3\sinh {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}+\frac{3s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(127)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\end{array}$$

(128)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\end{array}$$

(129)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(130)

when $h\to 0$, we acquire the periodic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{8,1}={\displaystyle \frac{\sin \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-1\right)s_3\sin {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}+\frac{3s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}}}},\end{array}$$

(131)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(-s_1-1\right)s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\end{array}$$

(132)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\end{array}$$

(133)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(2-s_1{)}^2+s_3^2\left(2-s_1\right)=0.\end{array}$$

(134)

Case-9: When $e_0=1-h^2,e_2=2-h^2$, and $e_4=1$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{9,1}={\displaystyle \frac{\mathrm{cs}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(-h^2-s_1+2\right)\mathrm{cs}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)+6\left(1-h^2\right)}+\frac{3\left(1-h^2\right)s_3}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)+6\left(1-h^2\right)}}}},\end{array}$$

(135)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(-h^2-s_1+2\right)}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)+6\left(1-h^2\right)}},\end{array}$$

(136)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3\left(1-h^2\right)s_3}{2(-h^2-s_1+2{)}^2-4\left(2-h^2\right)\left(-h^2-s_1+2\right)+6\left(1-h^2\right)}},\end{array}$$

(137)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9\left(1-h^2\right)}{-h^2-s_1+2}}-2\left(2-h^2\right)-s_1{)}^2+s_3^2\left({\displaystyle \frac{9\left(1-h^2\right)}{-h^2-s_1+2}}-2\left(2-h^2\right)-s_1\right)=0,\end{array}$$

(138)

when $h\to 1$, we acquire the hyperbolic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{9,1}={\displaystyle \frac{\mathrm{csch}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3\mathrm{csch}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(139)

as

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(140)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(141)

when $h\to 0$, we acquire the periodic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{9,1}={\displaystyle \frac{\cot \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(2-s_1\right)s_3\cot {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}+\frac{3s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}}}},\end{array}$$

(142)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(2-s_1\right)s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}},\end{array}$$

(143)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{2(2-s_1{)}^2-8\left(2-s_1\right)+6}},\end{array}$$

(144)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{2-s_1}}-4{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{2-s_1}}-4\right)=0.\end{array}$$

(145)

Case-10: When $e_0=-h^2(1-h^2),e_2=2h^2-1$, and $e_4=1$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{10,1}={\displaystyle \frac{\mathrm{ds}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(2h^2-s_1-1\right)\mathrm{ds}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}-\frac{3h^2\left(1-h^2\right)s_3}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}}}},\end{array}$$

(146)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(2h^2-s_1-1\right)}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}},\end{array}$$

(147)

$$\begin{array}{c}\hfill k=-{\displaystyle \frac{3h^2\left(1-h^2\right)s_3}{2(2h^2-s_1-1{)}^2-4\left(2h^2-1\right)\left(2h^2-s_1-1\right)-6\left(1-h^2\right)h^2}},\end{array}$$

(148)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-{\displaystyle \frac{9\left(1-h^2\right)h^2}{2h^2-s_1-1}}-2\left(2h^2-1\right)-s_1{)}^2+s_3^2\left(-{\displaystyle \frac{9\left(1-h^2\right)h^2}{2h^2-s_1-1}}-2\left(2h^2-1\right)-s_1\right)=0,\end{array}$$

(149)

when $h\to 1$, we acquire the hyperbolic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{10,1}={\displaystyle \frac{\mathrm{csch}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3\mathrm{csch}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(150)

as

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(151)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(152)

when $h\to 0$, we acquire the periodic solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{10,1}={\displaystyle \frac{\csc \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(-s_1-1\right)s_3\csc {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}}}},\end{array}$$

(153)

as

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(-s_1-1\right)s_3}{2(-s_1-1{)}^2+4\left(-s_1-1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(154)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(2-s_1{)}^2+s_3^2\left(2-s_1\right)=0.\end{array}$$

(155)

Case-11: When $e_0={\displaystyle \frac{1-h^2}{4}},e_2={\displaystyle \frac{1+h^2}{2}}$, and $e_4={\displaystyle \frac{1-h^2}{4}}$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{11,1}={\displaystyle \frac{\left(\mathrm{nc}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \mathrm{sc}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(\frac{1}{2}\left(h^2+1\right)-s_1\right){\left(\mathrm{nc}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \mathrm{sc}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}{2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2}+\frac{3\left(1-h^2\right)s_3}{4\left(2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2\right)}}}},\end{array}$$

(156)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)}{2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2}},\end{array}$$

(157)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3\left(1-h^2\right)s_3}{4\left(2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2\right)}},\end{array}$$

(158)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9{\left(1-h^2\right)}^2}{16\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)}}-h^2-s_1-1{)}^2+s_3^2\left({\displaystyle \frac{9{\left(1-h^2\right)}^2}{16\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)}}-h^2-s_1-1\right)=0,\end{array}$$

(159)

when $h\to 1$, we acquire the combination of hyperbolic solutions.

$$\begin{array}{c}\hfill {\mathcal{R}}_{11,1}={\displaystyle \frac{\left(\cosh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \sinh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3{\left(\cosh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \sinh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(160)

as

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(161)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(162)

when $h\to 0$, we acquire the combination of periodic solutions.

$$\begin{array}{c}\hfill {\mathcal{R}}_{11,1}={\displaystyle \frac{\left(\sec \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \tan \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(\frac{1}{2}-s_1\right)s_3{\left(\sec \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \tan \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}{2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}}+\frac{3s_3}{4\left(2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}\right)}}}},\end{array}$$

(163)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(\frac{1}{2}-s_1\right)s_3}{2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}}},\end{array}$$

(164)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{4\left(2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}\right)}},\end{array}$$

(165)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{16\left(\frac{1}{2}-s_1\right)}}-1{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{16\left(\frac{1}{2}-s_1\right)}}-1\right)=0.\end{array}$$

(166)

Case-12: When $e_0=-{\displaystyle \frac{{(1-h^2)}^2}{4}},e_2={\displaystyle \frac{1+h^2}{2}}$, and $e_4={\displaystyle \frac{1}{4}}$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{12,1}={\displaystyle \frac{\left(h\mathrm{cn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \mathrm{dn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{s_3\left(\frac{1}{2}\left(h^2+1\right)-s_1\right){\left(h\mathrm{cn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \mathrm{dn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}{2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2}-\frac{3{\left(1-h^2\right)}^2{s}_3}{4\left(2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2\right)}}}},\end{array}$$

(167)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)}{2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2}},\end{array}$$

(168)

$$\begin{array}{c}\hfill k=-{\displaystyle \frac{3{\left(1-h^2\right)}^2{s}_3}{4\left(2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2\right)}},\end{array}$$

(169)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9{\left(1-h^2\right)}^2}{16\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)}}-h^2-s_1-1{)}^2+s_3^2\left({\displaystyle \frac{9{\left(1-h^2\right)}^2}{16\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)}}-h^2-s_1-1\right)=0,\end{array}$$

(170)

when $h\to 1$, we acquire the bright solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{12,1}={\displaystyle \frac{\left(\mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \tanh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3{\left(\mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \tanh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}},\end{array}$$

(171)

as

$$\begin{array}{cc}\hfill & p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\hfill \\ \hfill & k=0,\hfill \end{array}$$

(172)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(173)

when $h\to 0$, we acquire the dark solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{12,1}={\displaystyle \frac{\left(0\pm \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(\frac{1}{2}-s_1\right)s_3{\left(0\pm \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}{2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}}-\frac{3s_3}{4\left(2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}\right)}}}},\end{array}$$

(174)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(\frac{1}{2}-s_1\right)s_3}{2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}}},\end{array}$$

(175)

$$\begin{array}{c}\hfill k=-{\displaystyle \frac{3s_3}{4\left(2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}\right)}},\end{array}$$

(176)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{16\left(\frac{1}{2}-s_1\right)}}-1{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{16\left(\frac{1}{2}-s_1\right)}}-1\right)=0.\end{array}$$

(177)

Case-13: When $e_0={\displaystyle \frac{1}{4}},e_2={\displaystyle \frac{1-2h^2}{2}}$, and $e_4={\displaystyle \frac{1}{4}}$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{13,1}={\displaystyle \frac{\mathrm{sn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\left(1\pm \mathrm{cn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\sqrt{\frac{s_3\left(\frac{1}{2}\left(1-2h^2\right)-s_1\right)\mathrm{sn}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{\left(2(\frac{1}{2}\left(1-2h^2\right)-s_1{)}^2-2\left(1-2h^2\right)\left(\frac{1}{2}\left(1-2h^2\right)-s_1\right)+\frac{3}{8}\right){\left(1\pm \mathrm{cn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}+k}}},\end{array}$$

(178)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(\frac{1}{2}\left(1-2h^2\right)-s_1\right)}{2(\frac{1}{2}\left(1-2h^2\right)-s_1{)}^2-2\left(1-2h^2\right)\left(\frac{1}{2}\left(1-2h^2\right)-s_1\right)+\frac{3}{8}}},\end{array}$$

(179)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{4\left(2(\frac{1}{2}\left(1-2h^2\right)-s_1{)}^2-2\left(1-2h^2\right)\left(\frac{1}{2}\left(1-2h^2\right)-s_1\right)+\frac{3}{8}\right)}},\end{array}$$

(180)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9}{16\left(\frac{1}{2}\left(1-2h^2\right)-s_1\right)}}+2h^2-s_1-1{)}^2+s_3^2\left({\displaystyle \frac{9}{16\left(\frac{1}{2}\left(1-2h^2\right)-s_1\right)}}+2h^2-s_1-1\right)=0,\end{array}$$

(181)

when $h\to 1$, we acquire the combination of dark and bright solitons.

$$\begin{array}{c}\hfill {\mathcal{R}}_{13,1}={\displaystyle \frac{\tanh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\left(1\pm \mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\sqrt{\frac{\left(-s_1-\frac{1}{2}\right)s_3\tanh {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{\left(2(-s_1-\frac{1}{2}{)}^2+2\left(-s_1-\frac{1}{2}\right)+\frac{3}{8}\right){\left(1\pm \mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}+\frac{3s_3}{4\left(2(-s_1-\frac{1}{2}{)}^2+2\left(-s_1-\frac{1}{2}\right)+\frac{3}{8}\right)}}}},\end{array}$$

(182)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(-s_1-\frac{1}{2}\right)s_3}{2(-s_1-\frac{1}{2}{)}^2+2\left(-s_1-\frac{1}{2}\right)+\frac{3}{8}}},\end{array}$$

(183)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{4\left(2(-s_1-\frac{1}{2}{)}^2+2\left(-s_1-\frac{1}{2}\right)+\frac{3}{8}\right)}},\end{array}$$

(184)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{16\left(-s_1-\frac{1}{2}\right)}}+1{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{16\left(-s_1-\frac{1}{2}\right)}}+1\right)=0,\end{array}$$

(185)

when $h\to 0$, we acquire the combination of periodic solitons.

$$\begin{array}{c}\hfill {\mathcal{R}}_{13,1}={\displaystyle \frac{\sin \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\left(1\pm \cos \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\sqrt{\frac{\left(\frac{1}{2}-s_1\right)s_3\sin {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{\left(2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}\right){\left(1\pm \cos \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}+\frac{3s_3}{4\left(2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}\right)}}}},\end{array}$$

(186)

as

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(\frac{1}{2}-s_1\right)s_3}{2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}}},\end{array}$$

(187)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{4\left(2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}\right)}},\end{array}$$

(188)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{16\left(\frac{1}{2}-s_1\right)}}-1{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{16\left(\frac{1}{2}-s_1\right)}}-1\right)=0.\end{array}$$

(189)

Case-14: When $e_0={\displaystyle \frac{1}{4}},e_2={\displaystyle \frac{1+h^2}{2}}$, and $e_4={\displaystyle \frac{{(1-h^2)}^2}{4}}$, we acquire the following solution.

$$\begin{array}{c}\hfill {\mathcal{R}}_{14,1}={\displaystyle \frac{\mathrm{sn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\left(\mathrm{cn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \mathrm{dn}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\sqrt{p\mathrm{sn}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2+k}}},\end{array}$$

(190)

where

$$\begin{array}{c}\hfill p={\displaystyle \frac{s_3\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)}{2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2}},\end{array}$$

(191)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{4\left(2(\frac{1}{2}\left(h^2+1\right)-s_1{)}^2-2\left(h^2+1\right)\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)+\frac{3}{8}{\left(1-h^2\right)}^2\right)}},\end{array}$$

(192)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5({\displaystyle \frac{9{\left(1-h^2\right)}^2}{16\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)}}-h^2-s_1-1{)}^2+s_3^2\left({\displaystyle \frac{9{\left(1-h^2\right)}^2}{16\left(\frac{1}{2}\left(h^2+1\right)-s_1\right)}}-h^2-s_1-1\right)=0,\end{array}$$

(193)

when $h\to 1$, we acquire the combination of dark and bright solitons.

$$\begin{array}{c}\hfill {\mathcal{R}}_{14,1}={\displaystyle \frac{\tanh \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\left(\mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\sqrt{\frac{p\tanh {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{{\left(\mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}+k}}},\end{array}$$

(194)

where

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(1-s_1\right)s_3}{2(1-s_1{)}^2-4\left(1-s_1\right)}},\end{array}$$

(195)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{4\left(2(1-s_1{)}^2-4\left(1-s_1\right)\right)}},\end{array}$$

(196)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1-2{)}^2+s_3^2\left(-s_1-2\right)=0,\end{array}$$

(197)

when $h\to 0$, we acquire the combination of periodic and plane wave solutions’ solitons.

$$\begin{array}{c}\hfill {\mathcal{R}}_{14,1}={\displaystyle \frac{\sin \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\left(\cos \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)\sqrt{\frac{p\sin {\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{{\left(\cos \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\pm \left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\right)}^2}+k}}},\end{array}$$

(198)

where

$$\begin{array}{c}\hfill p={\displaystyle \frac{\left(\frac{1}{2}-s_1\right)s_3}{2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}}},\end{array}$$

(199)

$$\begin{array}{c}\hfill k={\displaystyle \frac{3s_3}{4\left(2(\frac{1}{2}-s_1{)}^2-2\left(\frac{1}{2}-s_1\right)+\frac{3}{8}\right)}},\end{array}$$

(200)

with constraint conditions.

$$\begin{array}{c}\hfill 4s_5(-s_1+{\displaystyle \frac{9}{16\left(\frac{1}{2}-s_1\right)}}-1{)}^2+s_3^2\left(-s_1+{\displaystyle \frac{9}{16\left(\frac{1}{2}-s_1\right)}}-1\right)=0.\end{array}$$

(201)

5. Simulations and Discussions

In this section, we compare our results with the available work and also present the new work. In [31], the authors studied model (1) and extracted dynamical results. In the current research work, we explore novel results using the ${\mathsf{\Phi }}^6$ technique on model (1). Solitons are special stable waves that may travel great distances without losing their structure in the intriguing fields of wave theory and nonlinear dynamics. Each of these forms of solutions, whether dark, bright, kink, periodic, single, hyperbolic, and even combinations, has unique properties and uses. We examine the various soliton types, their characteristics, and their applications in science and technology in this section. Primarily, the motivation to understand the phenomenon of complex nonlinear events in the system of optical fibers and relevant media arises from a case-by-case basis using the ${\mathsf{\Phi }}^6$ technique within the context of the fractional calculus framework for $\mathcal{FLPD}$ models. This type of $\mathcal{FLPD}$ model develops the nonlinear Schrödinger equation and thus is useful in detailing the dynamics of an optical soliton, an appropriate stable localized wave packet that keeps its form on traveling. By applying the ${\mathsf{\Phi }}^6$ technique in a fractional sense, researchers can obtain new solitary wave solutions that account for memory effects and hereditary properties inherent in real-world materials, which are often not captured by integer-order models. This approach will allow for a more accurate representation of wave propagation in media with fractal or anomalous diffusion characteristics, thus improving the design and optimization of optical communication systems and other technologies reliant on precise wave dynamics. A self-reinforcing solitary wave that keeps its shape while moving at a steady speed is called a soliton. Solitons, which are frequently modeled in domains such as quantum physics, fluid dynamics, and optics, result from a delicate balance between nonlinear and dispersive processes inside a material. For many years, physicists have been fascinated by solitons. They are essential for comprehending and simulating a wide range of scientific processes, from quantum field theories to wave propagation in optical fibers. Solitons are perfect for applications requiring accurate and persistent wave behaviors because of their stability and robustness. When it comes to solitons, there is no one-size-fits-all solution. Because of their distinct qualities, each type can be used in a variety of situations.

Let us take a closer look at each. Dark solitons show up as “dips” or isolated areas of reduced intensity in a continuous larger wave. In contrast to other solitons, they exhibit a distinct “dark” or lower-energy state in fluid and optical systems. In nonlinear optical systems, such fiber optics, dark solitons are frequently used to control signal pulses with the least amount of interference. They are useful in communications technology because of their stability, particularly for long-distance data transfer.

Concentrated “packets” of energy or intensity are represented as bright solitons. They are frequently observed in settings where the soliton is able to preserve its compact form because of a focusing or attracting nonlinearity in the medium. Bose–Einstein condensates, optical fibers, and other quantum systems are characterized by bright solitons. These solitons are employed in particle interaction experiments and are particularly helpful in applications requiring localized high-intensity waveforms.

Kink solitons, which frequently manifest as a “step” that moves from one stable state to another, create a transition between two distinct states within a medium. Kink solitons, in contrast to other solitons, are often non-localized, yet retain their shape as they move. These solitons are important in field theories and condensed matter physics because they show phase transitions and domain boundaries in a variety of materials, including liquid crystals and magnets. The distinctive feature of periodic solitons is their regular recurrence.

They are perfect for circumstances that call for rhythmic or cyclic patterns since they act similarly to waves but have the extra stability of soliton solutions. In photonics and fluid mechanics, periodic solitons are employed to examine wave patterns and oscillations in regulated settings. These solitons provide a foundation for researching resonance phenomena and the behavior of rhythmic waves. In contrast to the smoother forms of other solitons, singular solitons have abrupt peaks or points of infinite amplitude inside their structure. Certain boundary conditions are frequently necessary for these solitons to exist. When analyzing extremely high- or low-energy or pressure values, singular solitons are used in high-energy physics and fluid dynamics. They simulate processes involving abrupt drastic energy shifts, such as shock waves. Hyperbolic solitons are solutions to hyperbolic partial differential equations that frequently have a pronounced exponential character. They work effectively for characterizing waves in media where the direction of the signal affects its speed. These solitons are used in signal processing to help control wave directions and speeds and in general relativity to represent the transmission of gravitational waves. Features from several soliton kinds, such as dark–bright or hyperbolic–kink pairings, are combined in combined solitons. The dynamics of solitons were demonstrated using graphical representations and the FLPD model with fractional coefficient, which clarifies the stability and propagation of the solitons. Another study analyzed the LPD model and found evidence of the dynamics the model displayed via graphical representation. Including such graphical features in a paper highlights its originality and importance by enabling readers to comprehend the smallest intricacies of the study findings.

Complex behaviors and customized applications in engineering and physics are made possible by these hybrid systems. Scientists can investigate more intricate and accurate models of wave phenomena by combining several soliton kinds, particularly useful for simulations that need a variety of wave behavious in a single scenario is this fusion strategy. Solitons in fiber optics stop signals from dispersing, allowing for long-distance fast communication without compromising data integrity. For preserving signal clarity, dark and bright solitons are especially useful. Since stable isolated wave packets can encode and send quantum information via safe long-distance networks, soliton technology may find use in quantum computing. Solitons may open up new uses as technology develops in areas like energy transfer systems, environmental monitoring, and biomedical imaging, where precise regulated wave behaviors are crucial. Because of their exceptional stability and adaptability, solitons can be used in a wide range of applications, including quantum mechanics and optics. Scientists and engineers can use the distinct qualities that each form of soliton offers to create novel solutions in computing, communications, and other fields. (See Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8).

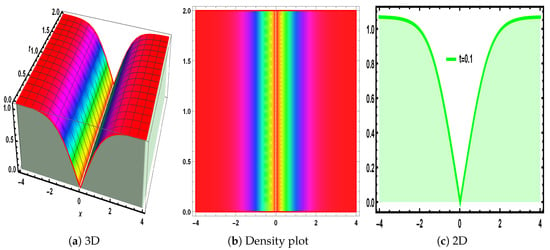
Figure 1. The visualization of Equation (24), under the parametric values $\alpha =0.9999,\eta =-1.1,a=1.2,s_1=0.6,\mathsf{\Gamma }=1.2,q_1=0.2,q_2=0.7$, and $s_3=0.8$.

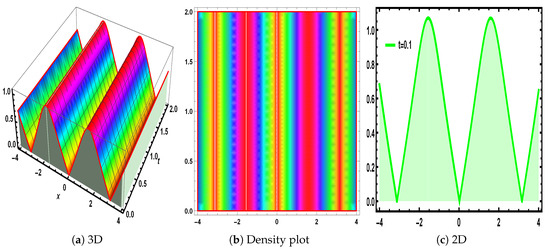
Figure 2. The visualization of Equation (28), under the parametric values $\alpha =0.9999,\eta =-1.1,a=1.2,s_1=0.6,\mathsf{\Gamma }=1.2,q_1=0.2,q_2=0.7$, and $s_3=0.8$.

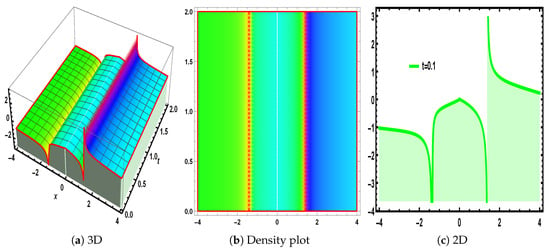
Figure 3. The visualization of Equation (36), under the parametric values $\alpha =0.9999,\eta =-1.1,a=1.2,s_1=0.6,\mathsf{\Gamma }=1.2,q_1=0.2,q_2=0.7$, and $s_3=0.8$.

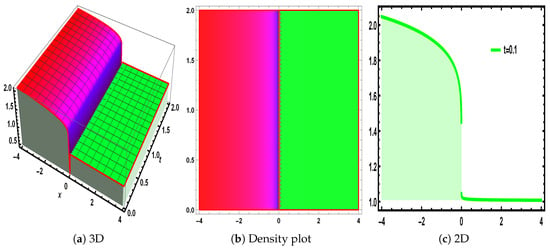
Figure 4. The visualization of Equation (40), under the parametric values $\alpha =0.9999,\eta =-1.1,a=1.2,s_1=0.6,\mathsf{\Gamma }=1.2,q_1=0.2,q_2=0.7$, and $s_3=0.8$.

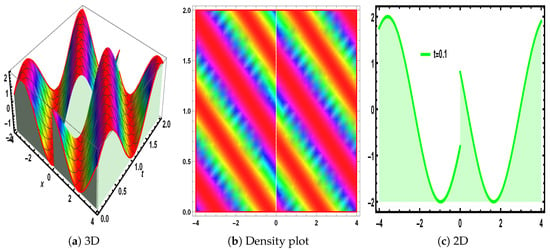
Figure 5. The visualization of Equation (48), under the parametric values $\alpha =0.9999,\eta =-1.1,a=1.2,s_1=0.6,\mathsf{\Gamma }=1.2,q_1=0.2,q_2=0.7$, and $s_3=0.8$.

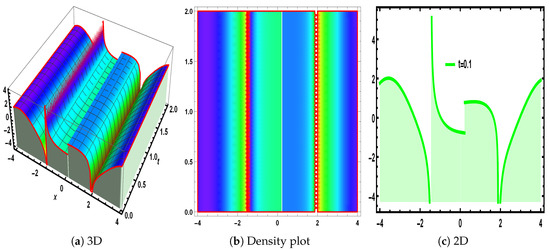
Figure 6. The visualization of Equation (70), under the parametric values $\alpha =0.9999,\eta =-1.1,a=1.2,s_1=0.6,\mathsf{\Gamma }=1.2,q_1=0.2,q_2=0.7$, and $s_3=0.8$.

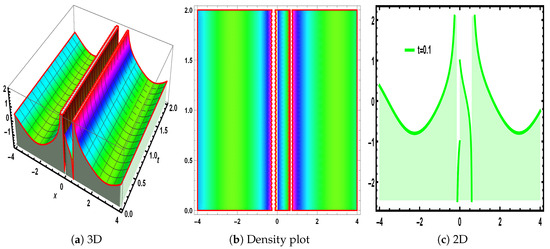
Figure 7. The visualization of Equation (160), under the parametric values $\alpha =0.9999,\eta =-1.1,a=1.2,s_1=0.6,\mathsf{\Gamma }=1.2,q_1=0.2,q_2=0.7$, and $s_3=0.8$.

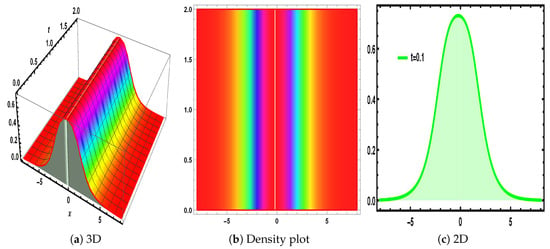
Figure 8. The visualization of Equation (171), under the parametric values $\alpha =0.9999,\eta =-1.1,a=1.2,s_1=0.6,\mathsf{\Gamma }=1.2,q_1=0.2,q_2=0.7$, and $s_3=0.8$.

5.1. Stability Analysis

The momentum and Hamiltonian for the considered equation are defined here. The process in this type of system is expressed as

$$\begin{array}{c}\hfill \mathfrak{F}={\displaystyle \frac{1}{2}}{\int }_{-\infty }^{+\infty }{\mathcal{R}}^{2}d\zeta .\end{array}$$

(202)

$\mathfrak{F}$ represents the system’s velocity, while $\mathcal{F}$ represents its electric potential. One of the most important elements of steady single pulses is

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \mathfrak{F}}{\partial \zeta }}>0,\end{array}$$

(203)

given that $\zeta$ is the frequency.

5.2. Validation of Soliton Solutions

The following result is obtained by combining Equation (202) with the moving pulse solution to Equation (59).

$$\begin{array}{c}\hfill \mathfrak{R}={\displaystyle \frac{1}{2}}{\int }_{-10}^{10}{\left({\displaystyle \frac{\mathrm{sech}\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)\exp \left(i\left(\frac{t^{\alpha }\left(q_1\left(a^2-s_1\right)+\eta q_2{s}_1\right)}{\alpha \left(a{q}_2-1\right)}-\frac{a{x}^{\alpha }}{\alpha }+\mathsf{\Gamma }\right)\right)}{\sqrt{\frac{\left(1-s_1\right)s_3\mathrm{sech}{\left(\frac{x^{\alpha }}{\alpha }-\frac{\eta t^{\alpha }}{\alpha }\right)}^2}{2(1-s_1{)}^2-4\left(1-s_1\right)}}}}\right)}^{2}dx.\end{array}$$

(204)

Following our simplifications, we obtain the intended outcome.

$$\begin{array}{c}\hfill 1.785>0,\end{array}$$

(205)

where $\alpha =0.1,\eta =1.2,q_1=2.2,a=1.1,b=1,s_1=1.8,\mathsf{\Gamma }=1.1,x=2.1,s_2=0.3,s_3=0.7,q_2=1.1$, and $t=1$. The obtained solutions are stable according to Equation (205).

6. Conclusions

To summarize our research on the $\mathcal{FLPD}$ model, we found that the addition of fractional derivatives offers a more accurate and comprehensive depiction of dynamic behaviors, especially in nonlinear systems. This model accurately captures memory effects and nonlocal interactions by using the ${\mathsf{\Phi }}^6$ technique. These elements are crucial for simulating real-world phenomena with hereditary features to derive soliton solutions. The investigation showed that the fractional order has a substantial impact on the stability and solution behavior of the system, providing a further level of control and flexibility when modeling complicated dynamical systems. The $\mathcal{FLPD}$ model may find use in a variety of domains where these dynamics are common, including biology, engineering, and physics. The results of this study not only broaden our theoretical knowledge of fractional systems but also pave the way for future investigations into the model’s possible uses and effective numerical and analytical techniques for solving fractional differential equations. Future studies could examine numerical methods, optimal control schemes, and useful applications that further capitalize on the model’s special qualities for accurate real-world uses.