Fractional Fourier Series on the Torus and Applications

Abstract

This paper introduces the fractional Fourier series on the fractional torus and proceeds to investigate several fundamental aspects. Our study includes topics such as fractional convolution, fractional approximation, fractional Fourier inversion, and the Poisson summation formula. We also explore the relationship between the decay of its fractional Fourier coefficients and the smoothness of a function. Additionally, we establish the convergence of the fractional Féjer means and Bochner–Riesz means. Finally, we demonstrate the practical applications of the fractional Fourier series, particularly in the context of solving fractional partial differential equations with periodic boundary conditions, and showcase the utility of approximation methods on the fractional torus for recovering non-stationary signals.

1. Introduction

It is well known that the Fourier series plays a crucial role in studying boundary value problems, like vibrating strings and the heat equation. Fourier’s approach to solving the problem of heat distribution in the cube ${\mathbf{T}}^3$ involves a triple sine series of three-variable functions. Dirichlet [1] studied the convergence of the Fourier series for piecewise and monotonic functions under a certain kernel on a circle. Inspired by the periodicity observed in astronomical and geophysical phenomena, many scholars have dedicated their efforts to studying expansions of periodic functions, as mentioned in [2]. The relevance of these expansions in both theoretical frameworks and practical applications underscores the importance of analyzing Fourier series properties on the torus.

The n-torus ${\mathbf{T}}^n$ is defined as the cube ${[0,1]}^n$ with opposite sides identified. It is important to note that functions on ${\mathbf{T}}^n$ exhibit periodicity with a period of 1 in every coordinate. The m-th Fourier coefficient can be defined using the Fourier transform as follows:

$$\begin{array}{c}\hfill \mathcal{F}(f)(m)={\int }_{{\mathbf{T}}^n}f(x)e^{-2\pi im·x}dx,\end{array}$$

where $f\in L^1({\mathbf{T}}^n)$, $m\in {\mathbf{Z}}^n$. The Fourier series of f is the series

$$\begin{array}{c}\hfill \sum _{m\in {\mathbf{Z}}^n}\mathcal{F}(f)(m)e^{2\pi im·x}.\end{array}$$

(1)

Kolmogorov [3,4] demonstrated the existence of a function $f\in L^1({\mathbf{T}}^1)$ whose Fourier series diverges almost everywhere. For $1<p<\infty$, Carleson and Hunt [5,6] observed that the Fourier series of an $L^p({\mathbf{T}}^1)$ function converges almost everywhere. Fefferman [7] presented an alternative proof for this result. Lacey and Thiele [8], by combining ideas from [5,7], introduced a third approach to Carleson’s theorem on the pointwise convergence of the Fourier series, providing valuable insights into the subject. For a comprehensive understanding of the essential properties and applications of the Fourier series on the torus, one can refer to [9,10,11,12] and references therein.

With the development of signal processing, the Fourier transform has revealed limitations in its ability to handle non-stationary signals. To address this challenge, the fractional Fourier transform (FRFT) was introduced. In this situation, the fractional Fourier transform was proposed to overcome this problem. Additionally, when a signal f exhibits t-periodicity with $t<1$, it is not well defined on ${\mathbf{T}}^n$. In such cases, we cannot obtain its frequency components. Therefore, we need to introduce the matched fractional torus to study such a kind of signal (or function).

Definition 1.

Let $\alpha \in \mathbb{R}$, $\alpha \notin \pi \mathbf{Z}$. The fractional torus of order α, denoted by ${\mathbf{T}}_{\alpha }^n$, is the cube ${[0,|\sin \alpha |]}^n$ with opposite sides identified.

Clearly, ${\mathbf{T}}_{\alpha }^n={\mathbf{T}}^n$ for $\alpha =\pi /2+2\pi \mathbf{Z}$; see Figure 1a for a two-dimensional torus. The graphs of the fractional torus ${\mathbf{T}}_{\alpha }^2$ for $\alpha =\pi /2,\pi /3,\pi /6$ are shown in Figure 1b. We say that function f is $|\sin \alpha |$-periodic in every coordinate for fixed $\alpha$ if f on ${\mathbb{R}}^n$ satisfies $f(x+|\sin \alpha |m)=f(x)$ for any $x\in {\mathbb{R}}^n$ and $m\in {\mathbf{Z}}^n$.

The idea of the fractional power of the Fourier operator first appeared in the work of Wiener [13]. Namias [14] introduced the FRFT to address specific types of ordinary and partial differential equations encountered in quantum mechanics. McBride and Kerr [15] provided a rigorous definition of the FRFT in integral form on the Schwartz space $S(\mathbb{R})$ based on a modification of Namias’ fractional operators. Subsequently, Kerr [16] discussed the $L^2(\mathbb{R})$ theory of FRFT. Zayed [17] introduced a novel convolution structure for the FRFT that preserves the convolution theorem for the Fourier transform. In [18], Zayed presented a new class of fractional integral transforms, encompassing the fractional Fourier and Hankel transforms. Additionally, Zayed [19] explored the two-dimensional FRFT and investigated its properties, including the inversion theorem, convolution theorem, and Poisson summation formula. Kamalakkannan and Roopkumar [20] established the convolution theorem and product theorem for the multidimensional fractional Fourier transform. The $L^p(\mathbb{R})$ theory of FRFT for $1\le p<2$ was established in [21]. Fu et al. [22,23] introduced the Riesz transform associated with the FRFT and explored its applications in image edge detection. The FRFT also has various applications in many fields, such as optics [24], signal processing [25,26], image processing [27,28,29,30], and so on. In this paper, our focus centers on studying the convergence and applications of the fractional Fourier series on ${\mathbf{T}}_{\alpha }^n$.

This paper is organized as follows. In Section 2, we introduce fractional Fourier coefficients and give some basic properties including fractional convolution on ${\mathbf{T}}_{\alpha }^n$. In Section 3, we establish the fractional Fourier inversion and Poisson summation formula. Section 4 is devoted to the relationship between the decay of fractional Fourier coefficients and the smoothness of a function. The pointwise convergences of fractional Fejér means are given in Section 5. In Section 6, using fractional Fourier series on ${\mathbf{T}}_{\alpha }^n$, we obtain the solutions of the fractional heat equation and fractional Dirichlet problem. Finally, we present a non-stationary signal on ${\mathbf{T}}_{\alpha }^n$, which can be recovered by an approximating method.

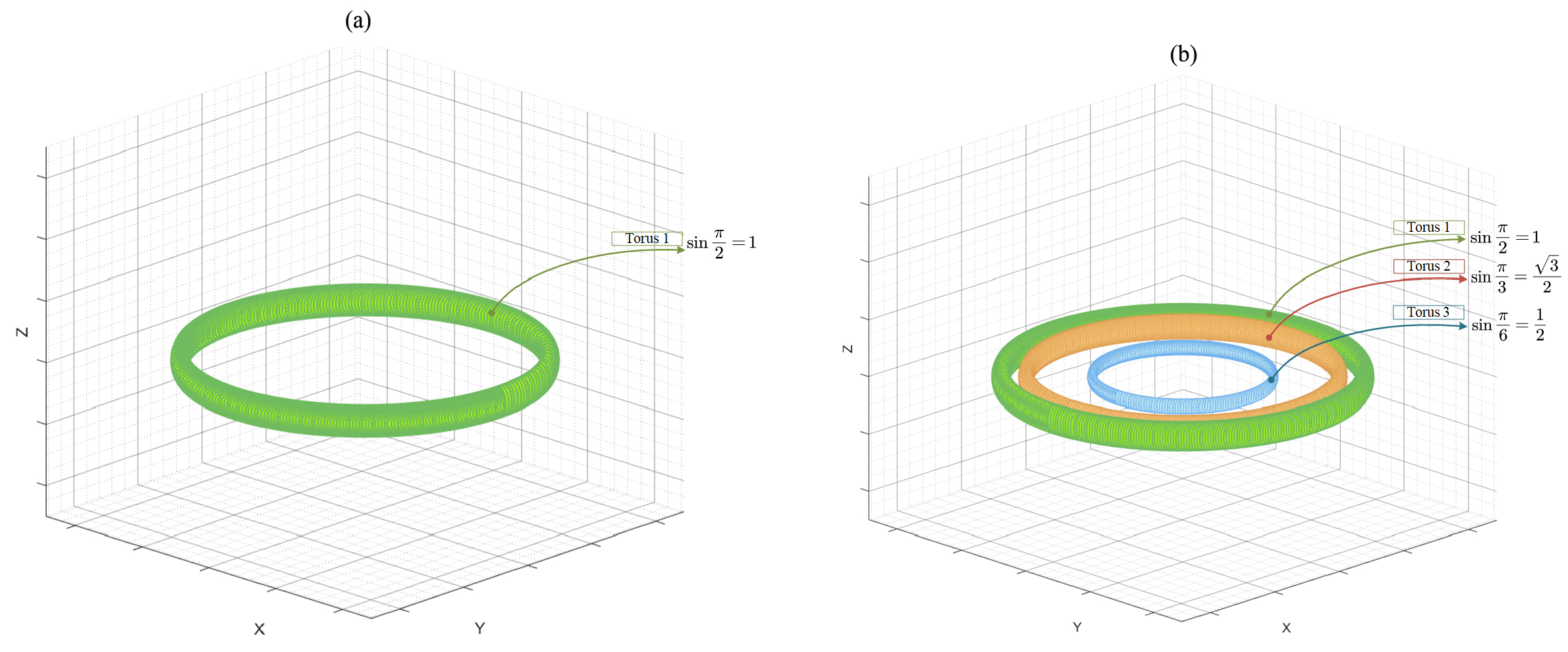
2. Fractional Fourier Series on the Torus

In this section, we begin by introducing the definition of fractional Fourier series in the setting ${\mathbf{T}}_{\alpha }^n$. Subsequently, we establish some basic facts of fractional Fourier analysis. Additionally, we give the fractional convolution and obtain a fractional approximation in $L^p({\mathbf{T}}_{\alpha }^n)$, $1\le p\le \infty$.

Let $\alpha \in \mathbb{R}$, $\alpha \notin \pi \mathbf{Z}$. Set $e_{\alpha }(x):=e^{{\pi i|x|}^2\cot \alpha }$ and $e_{\alpha }f(x):=e_{\alpha }(x)f(x)$ for a function f on ${\mathbf{T}}_{\alpha }^n$. For $1\le p<\infty$, ${\parallel f\parallel }_p:={\parallel f\parallel }_{L^p({\mathbf{T}}_{\alpha }^n)}:={\left({\int }_{{\mathbf{T}}_{\alpha }^n}{|f(x)|}^p\right)}^{1/p}$. For $p=\infty$, ${\parallel f\parallel }_{\infty }:={\parallel f\parallel }_{L^{\infty }({\mathbf{T}}_{\alpha }^n)}:=ess.\sup |f|$.

Definition 2.

Let $1\le p\le \infty$. We say that a function f on ${\mathbf{T}}_{\alpha }^n$ lies in the space $e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$ if

$$\begin{array}{c}\hfill f(x)=e_{-\alpha }g(x),g\in L^p({\mathbf{T}}_{\alpha }^n)\end{array}$$

and satisfies ${\parallel f\parallel }_{L^p({\mathbf{T}}_{\alpha }^n)}<\infty$.

Definition 3.

For a complex-valued function $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$, $\alpha \in \mathbb{R}$ and $m\in {\mathbf{Z}}^n$, we define

$${\displaystyle {\mathcal{F}}_{\alpha }(f)(m)=\left\{\begin{array}{cc}{\displaystyle {\int }_{{\mathbf{T}}_{\alpha }^n}f(x)K_{\alpha }(m,x)dx,}\hfill & \alpha \notin \pi \mathbf{Z},\hfill \\ f(m),\hfill & \alpha =2\pi \mathbf{Z},\hfill \\ f(-m),\hfill & \alpha =2\pi \mathbf{Z}+\pi ,\hfill \end{array}\right.}$$

where

$$\begin{array}{c}\hfill K_{\alpha }(m,x):=A_{\alpha }^n{e}_{\alpha }(x)e_{\alpha }(m,x)e_{\alpha }(m),\end{array}$$

here, $A_{\alpha }=\sqrt{1-i\cot \alpha }$ and $e_{\alpha }(m,x)=e^{-2\pi i(m·x)\csc \alpha }$. We call ${\mathcal{F}}_{\alpha }(f)(m)$ the m-th fractional Fourier coefficient of order α of f.

In order to state our results, we recall some notation. For $k\in \mathbf{Z}$, we say functions $\varphi \in C^k({\mathbf{T}}_{\alpha }^n)$ if ${\partial }^{\beta }\varphi$ exist and are continuous for all $|\beta |\le k$. Denote $C^0({\mathbf{T}}_{\alpha }^n)$ by $C({\mathbf{T}}_{\alpha }^n)$, and $C({\mathbf{T}}_{\alpha }^n)$ is the space of continuous functions.

$$\begin{array}{c}\hfill C^{\infty }({\mathbf{T}}_{\alpha }^n):=\bigcap _{k=0}^{\infty }{C}^k({\mathbf{T}}_{\alpha }^n).\end{array}$$

Definition 4.

For $0\le k\le \infty$, the space $e_{-\alpha }{C}^k({\mathbf{T}}_{\alpha }^n)$ is defined to be the space of functions f on ${\mathbf{T}}_{\alpha }^n$ such that

$$\begin{array}{c}\hfill f(x)=e_{-\alpha }g(x),g\in C^k({\mathbf{T}}_{\alpha }^n).\end{array}$$

Notice that the spaces $e_{-\alpha }{C}^k({\mathbf{T}}_{\alpha }^n)$ are contained in $e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$ for all $1\le p\le \infty$.

We denote by $\overline{f}$ the complex conjugate of the function f, by $\tilde{f}$ the function $\tilde{f}(x)=f(-x)$, and by ${\tau }_y(f)(x)$ the function ${\tau }_y(f)(x)=f(x-y)$ for all $y\in {\mathbf{T}}_{\alpha }^n$. If $\alpha =\pi \mathbf{Z}$, we obtain ${\mathbf{T}}_{\alpha }^n=\left\{0\right\}$. Hence, throughout this paper, for $\alpha \notin \pi \mathbf{Z}$, we always assume ${\mathbf{T}}_{\alpha }^n={[-|\sin \alpha |/2,|\sin \alpha |/2]}^n$. Next, we give some elementary properties of fractional Fourier coefficients.

Proposition 1.

Let $f,g\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$. Then, for ∀$m,k\in {\mathbf{Z}}^n$, $\lambda \in \mathbb{C}$, $y\in {\mathbf{T}}_{\alpha }^n$, we obtain:

1. 

${\mathcal{F}}_{\alpha }(f+g)(m)={\mathcal{F}}_{\alpha }(f)(m)+{\mathcal{F}}_{\alpha }(g)(m)$;

2. 

${\mathcal{F}}_{\alpha }(\lambda f)(m)=\lambda {\mathcal{F}}_{\alpha }(f)(m)$;

3. 

${\mathcal{F}}_{\alpha }(\overline{f})(m)=\overline{{\mathcal{F}}_{-\alpha }(f)(m)}$;

4. 

${\mathcal{F}}_{\alpha }(\tilde{f})(m)={\mathcal{F}}_{\alpha }(f)(-m)$;

5. 

${\mathcal{F}}_{\alpha }[e_{-\alpha }{\tau }_y(e_{\alpha }f)](m)={\mathcal{F}}_{\alpha }(f)(m)e_{\alpha }(m,y)$;

6. 

${\mathcal{F}}_{\alpha }[e_{-\alpha }(k,·)f](m)e^{-2\pi i(m·k)\cot \alpha }{e}_{\alpha }(k)={\mathcal{F}}_{\alpha }(f)(m-k)$;

7. 

${\displaystyle {\mathcal{F}}_{\alpha }(f)(0)=A_{\alpha }^n{\int }_{{\mathbf{T}}_{\alpha }^n}{e}_{-\alpha }f(x)dx}$;

8. 

${\sup }_{m\in {\mathbf{Z}}^n}|{\mathcal{F}}_{\alpha }{(f)(m)|\le |\csc \alpha |}^{n/2}{\parallel f\parallel }_{L^1({\mathbf{T}}_{\alpha }^n)}$;

9. 

${\mathcal{F}}_{\alpha }[e_{-\alpha }{\partial }^{\beta }(e_{\alpha }f)](m)={(2\pi im\csc \alpha )}^{\beta }{\mathcal{F}}_{\alpha }(f)(m),$ whenever $f\in e_{-\alpha }{C}^{\beta }({\mathbf{T}}_{\alpha }^n)$.

Proof. 

It is obvious that properties (1)–(4) and (7) hold. We now pay attention to (5). Note that

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\alpha }[e_{-\alpha }{\tau }_y\left(e_{\alpha }f\right)](m)=& A_{\alpha }^n{e}_{\alpha }(m){\int }_{{\mathbf{T}}_{\alpha }^n}(e_{\alpha }f)(x-y)e_{\alpha }(m,x)dx\hfill \\ \hfill =& A_{\alpha }^n{e}_{\alpha }(m){\int }_{{\mathbf{T}}_{\alpha }^n-y}(e_{\alpha }f)(x^{\prime })e_{\alpha }(m,x^{\prime }+y)d{x}^{\prime }\hfill \\ \hfill =& {\mathcal{F}}_{\alpha }(f)(m)e_{\alpha }(m,y),\hfill \end{array}$$

where we make the variable change $x^{\prime }=x-y$ in the second equality, and the third equality follows from the periodicity of function.

Next, we deal with (6).

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\alpha }(f)(m-k)=& A_{\alpha }^n{\int }_{{\mathbf{T}}_{\alpha }^n}f(x)e_{\alpha }(x)e_{\alpha }(m-k)e_{\alpha }(m-k,x)dx\hfill \\ \hfill =& e_{\alpha }(k)e^{-2\pi i(m·k)\cot \alpha }{\int }_{{\mathbf{T}}_{\alpha }^n}{e}_{-\alpha }(k,x)f(x)K_{\alpha }(m,x)dx\hfill \\ \hfill =& {\mathcal{F}}_{\alpha }[e_{-\alpha }(k,·)f](m)e^{-2\pi i(m·k)\cot \alpha }{e}_{\alpha }(k).\hfill \end{array}$$

It follows from the fact $|K_{\alpha }{(m,x)|\le |\csc \alpha |}^{n/2}$ that (8) holds.

Now, we turn to (9). By the periodicity and integration by parts, we have

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\alpha }[e_{-\alpha }{\partial }^{\beta }(e_{\alpha }f)](m)=& A_{\alpha }^n{e}_{\alpha }(m){\int }_{{\mathbf{T}}_{\alpha }^n}{\partial }^{\beta }(e_{\alpha }f)(x)e^{-2\pi i(m·x)\csc \alpha }dx\hfill \\ \hfill =& {(2\pi im\csc \alpha )}^{\beta }{A}_{\alpha }^n{e}_{\alpha }(m){\int }_{{\mathbf{T}}_{\alpha }^n}{e}_{\alpha }f(x)e^{-2\pi i(m·x)\csc \alpha }dx\hfill \\ \hfill =& {(2\pi im\csc \alpha )}^{\beta }{\mathcal{F}}_{\alpha }(f)(m).\hfill \end{array}$$

This completes the proof. □

Remark 1.

Suppose $f_1\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^{n_1})$ and $f_2\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^{n_2})$. We obtain that the tensor function

$$(f_1\otimes f_2)(x_1,x_2)=f_1(x_1)f_2(x_2)$$

is in $e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^{n_1+n_2})$. Moreover, it is easy to check

$$\begin{array}{c}\hfill {\mathcal{F}}_{\alpha }\left(f_1\otimes f_2\right)(m_1,m_2)={\mathcal{F}}_{\alpha }(f_1)(m_1){\mathcal{F}}_{\alpha }(f_2)(m_2),\end{array}$$

(2)

where $m_1\in {\mathbf{Z}}^{n_1}$ and $m_2\in {\mathbf{Z}}^{n_2}$.

Definition 5.

For $\alpha \notin \pi \mathbf{Z}$, a trigonometric polynomial of order α on ${\mathbf{T}}_{\alpha }^n$ is defined by

$$\begin{array}{c}\hfill P_{\alpha }(x)=\sum _{m\in {\mathbf{Z}}^n}{c}_{m,\alpha }{K}_{-\alpha }(m,x),\end{array}$$

where $m=(m_1,\dots ,m_n)$ and $c_{m,\alpha }$ is a constant depending on m and α. The degree of $P_{\alpha }$ is the largest number $|m_1| +\cdots + |m_n|$ such that $c_{m,\alpha }\ne 0$.

For $x\in {\mathbf{T}}_{\alpha }^n$, $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$, the fractional Fourier series of order $\alpha$ of f is the series

$$\begin{array}{c}\hfill \sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x).\end{array}$$

(3)

Now, we wonder in which sense (3) converges. The convergence of the fractional Fourier series is the main topic in this paper. Next, we introduce a kind of fractional convolution of order $\alpha$ to study the convergence of fractional Fourier series.

Definition 6.

Let $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$ and $g\in L^1({\mathbf{T}}^n)$. Define the fractional convolution of order α as follows:

$$\begin{array}{c}\hfill (f\stackrel{\alpha }{\ast }g)(x)={|\csc \alpha |}^n{e}_{-\alpha }(x){\int }_{{\mathbf{T}}_{\alpha }^n}{e}_{\alpha }(y)f(y)({\delta }^{\alpha }g)(x-y)dy,\end{array}$$

where $({\delta }^{\alpha }g)(x)=g(x\csc \alpha )$.

Let $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$. We have

$$\begin{array}{cc}\hfill \sum _{|m|\le N}{\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x)& =\sum _{|m|\le N}{\int }_{{\mathbf{T}}_{\alpha }^n}f(y)K_{\alpha }(m,y)dy{K}_{-\alpha }(m,x)\hfill \\ \hfill & ={|\csc \alpha |}^n{e}_{-\alpha }(x)\sum _{|m|\le N}{\int }_{{\mathbf{T}}_{\alpha }^n}{e}_{\alpha }(y)f(y)e^{2\pi im·(x-y)\csc \alpha }dy\hfill \\ \hfill & ={|\csc \alpha |}^n{e}_{-\alpha }(x){\int }_{{\mathbf{T}}_{\alpha }^n}{e}_{\alpha }(y)f(y)\sum _{|m|\le N}{e}^{2\pi im·(x-y)\csc \alpha }dy\hfill \\ \hfill & =:\left(f\stackrel{\alpha }{\ast }{D}_N^n\right)(x),\hfill \end{array}$$

where $D_N^n(x)$ is the classical multidimensional Dirichlet kernel.

Noting that the one-dimensional Dirichlet kernel $D_N^1$ is not an approximate identity, in dimension 1, Cesàro and Fejér independently study the arithmetic means of the Dirichlet kernel. Specifically,

$$\begin{array}{c}\hfill F_N^1(x):={\displaystyle \frac{1}{N+1}}\left[D_0^1(x)+D_1^1(x)+\cdots +D_N^1(x)\right].\end{array}$$

By proposition 3.1.7 in [10], we have the following equivalent way to write the kernel $F_N^1$:

$$\begin{array}{c}\hfill F_N^1(x)=\sum _{j=-N}^N\left(1-{\displaystyle \frac{|j|}{N+1}}\right)e^{2\pi ijx}={\displaystyle \frac{1}{N+1}}{\left({\displaystyle \frac{\sin \left((N+1)\pi x\right)}{\sin (\pi x)}}\right)}^2.\end{array}$$

(4)

The function $F_N^1$ given by (4) is called the Fejér kernel. Let

$$F_N^{1,\alpha }(x):=|\csc \alpha |F_N^1(x\csc \alpha ).$$

Proposition 2.

For all $N\in \mathbf{Z}$, $N\ge 0$ and ∀$x\in {\mathbf{T}}_{\alpha }^1$, the identity

$$\begin{array}{c}\hfill F_N^{1,\alpha }(x)=|\csc \alpha |\sum _{j=-N}^N\left(1-{\displaystyle \frac{|j|}{N+1}}\right)e^{2\pi ijx\csc \alpha }={\displaystyle \frac{|\csc \alpha |}{N+1}}{\left({\displaystyle \frac{\sin \left((N+1)\pi x\csc \alpha \right)}{\sin (\pi x\csc \alpha )}}\right)}^2\end{array}$$

(5)

holds. Hence,

$${\mathcal{F}}_{\alpha }\left(e_{-\alpha }{F}_N^{1,\alpha }\right)(m)=A_{\alpha }{e}_{\alpha }(m)\left(1-{\displaystyle \frac{|m|}{N+1}}\right)$$

if $|m|\le N$ and zero otherwise.

Proof. 

Obviously, $F_N^{1,\alpha }\in L^1({\mathbf{T}}_{\alpha }^1)$. We have

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\alpha }\left(e_{-\alpha }{F}_N^{1,\alpha }\right)(m)=& {\int }_{{\mathbf{T}}_{\alpha }^1}{e}_{-\alpha }(x)F_N^{1,\alpha }(x)K_{\alpha }(m,x)dx\hfill \\ \hfill =& A_{\alpha }|\csc \alpha |e_{\alpha }(m)\sum _{j=-N}^N\left(1-{\displaystyle \frac{|j|}{N+1}}\right){\int }_{{\mathbf{T}}_{\alpha }^1}{e}_{\alpha }(m,x)e_{-\alpha }(j,x)dx\hfill \\ \hfill =& A_{\alpha }{e}_{\alpha }(m)\left(1-{\displaystyle \frac{|m|}{N+1}}\right),\hfill \end{array}$$

(6)

where

$$\begin{array}{c}\hfill |\csc \alpha |\sum _{j=-N}^N\left(1-{\displaystyle \frac{|j|}{N+1}}\right){\int }_{{\mathbf{T}}_{\alpha }^1}{e}_{\alpha }(m,x)e_{-\alpha }(j,x)dx=0,m\notin j,\end{array}$$

$$\begin{array}{c}\hfill |\csc \alpha |\sum _{j=-N}^N\left(1-{\displaystyle \frac{|j|}{N+1}}\right){\int }_{{\mathbf{T}}_{\alpha }^1}{e}_{\alpha }(m,x)e_{-\alpha }(j,x)dx=1-{\displaystyle \frac{|m|}{N+1}},m=j.\end{array}$$

This completes the proof. □

Definition 7.

Let $N\in \mathbf{Z}$ and $N\ge 0$. The function $F_N^{1,\alpha }$, which we call the fractional Fejér kernel of order α, is given by (5).

The classical Fejér kernel $F_N^n$ on ${\mathbf{T}}^n$ is defined by $F_N^n(x_1,\dots ,x_n):={\prod }_{j=1}^n{F}_N^1(x_j)$. Similarly, we define the fractional Fejér kernel $F_N^{n,\alpha }$ as follows:

$$\begin{array}{cc}\hfill F_N^{n,\alpha }(x_1,\dots ,x_n):=& \prod _{j=1}^n{F}_N^{1,\alpha }(x_j).\hfill \end{array}$$

For all $N\in \mathbf{Z}$ with $N\ge 0$ and $m=(m_1,m_2,\cdots ,m_n)\in {\mathbf{Z}}^n$, let

$$\begin{array}{c}\hfill \sum _{m\in {\mathbf{Z}}^n,|m_j|\le N}=\sum _{|m_1|\le N}\sum _{|m_2|\le N}\cdots \sum _{|m_n|\le N}.\end{array}$$

Remark 2.

For all $N\ge 0$, by (5), we obtain

$$\begin{array}{cc}\hfill F_N^{n,\alpha }(x_1,\dots ,x_n)=& {|\csc \alpha |}^n\sum _{m\in {\mathbf{Z}}^n,|m_j|\le N}\prod _{j=1}^n\left(1-{\displaystyle \frac{|m_j|}{N+1}}\right)e^{2\pi i(m·x)\csc \alpha }\hfill \\ \hfill =& {\displaystyle \frac{{|\csc \alpha |}^n}{{(N+1)}^n}}\prod _{j=1}^n{\left({\displaystyle \frac{\sin \left((N+1)\pi x_j\csc \alpha \right)}{\sin (\pi x_j\csc \alpha )}}\right)}^2.\hfill \end{array}$$

Thus, $F_N^{n,\alpha }\ge 0$. Note that $F_0^{n,\alpha }(x)={|\csc \alpha |}^n$ and $F_N^{n,\alpha }(0)={|\csc \alpha |}^n{(N+1)}^n$.

Proposition 3.

The sequence ${\left\{F_N^{n,\alpha }\right\}}_{N=0}^{\infty }$ is an approximate identity on ${\mathbf{T}}_{\alpha }^n$.

Proof. 

It is easy to see that

$$\begin{array}{c}\hfill \parallel F_N^{n,\alpha }{\parallel }_{L^1({\mathbf{T}}_{\alpha }^n)}={\int }_{{\mathbf{T}}_{\alpha }^n}{F}_N^{n,\alpha }(x)dx=\prod _{j=1}^n{\int }_{{\mathbf{T}}_{\alpha }^1}{F}_N^{1,\alpha }(x_j)d{x}_j=1.\end{array}$$

By noting that $1\le |t|/|\sin t|\le \pi /2$ when $|t|\le \pi /2$, we obtain

$$\begin{array}{cc}\hfill F_N^{1,\alpha }(x)\le & {\displaystyle \frac{|\csc \alpha |}{N+1}}\min {\left({\displaystyle \frac{(N+1)|\pi x\csc \alpha |}{|\sin (\pi x\csc \alpha )|}},{\displaystyle \frac{1}{|\sin (\pi x\csc \alpha )|}}\right)}^2\hfill \\ \hfill \le & {\displaystyle \frac{|\csc \alpha |}{N+1}}{\displaystyle \frac{{\pi }^2}{4}}\min {\left(N+1,{\displaystyle \frac{1}{|\pi x\csc \alpha |}}\right)}^2,\hfill \end{array}$$

where $|x|\le {\displaystyle \frac{1}{2|\csc \alpha |}}$. For $\delta >0$, we obtain

$$\begin{array}{c}\hfill {\int }_{\delta \le |x|\le {\displaystyle \frac{1}{2|\csc \alpha |}}}{F}_N^{1,\alpha }(x)dx\le {\displaystyle \frac{|\csc \alpha |}{N+1}}{\displaystyle \frac{{\pi }^2}{4}}{\int }_{\delta \le |x|\le {\displaystyle \frac{1}{2|\csc \alpha |}}}{\displaystyle \frac{1}{{|\pi \delta \csc \alpha |}^2}}dx\le {\displaystyle \frac{1}{4{\delta }^2}}{\displaystyle \frac{1}{N+1}}\to 0\end{array}$$

as $N\to \infty$.

In higher dimensions, given $x=(x_1,\dots ,x_n)\in {[-|\sin \alpha |/2,|\sin \alpha |/2]}^n$ with $|x|\ge \delta ,$ we can find a $j\in \{1,\dots ,n\}$ such that $|x_j|\ge \delta /\sqrt{n}$, and thus,

$$\begin{array}{cc}\hfill {\int }_{|x|\ge \delta }{F}_N^{n,\alpha }(x)dx\le & {\int }_{|x_j|\ge {\displaystyle \frac{\delta }{\sqrt{n}}}}{F}_N^{1,\alpha }(x_j)d{x}_j\prod _{k\notin j}{\int }_{{\mathbf{T}}_{\alpha }^1}{F}_N^{1,\alpha }(x_k)d{x}_k\le {\displaystyle \frac{n}{4{\delta }^2}}{\displaystyle \frac{1}{N+1}}\to 0,\hfill \end{array}$$

(7)

which completes the proof. □

Theorem 1.

Let $\alpha \in \mathbb{R}$ and $\alpha \notin \pi \mathbf{Z}$.

(1) 

If $f\in e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$, $1\le p<\infty$, then

$$\begin{array}{c}\hfill \underset{N\to \infty }{\lim }\parallel f\stackrel{\alpha }{\ast }{F}_N^n-f{\parallel }_{L^p({\mathbf{T}}_{\alpha }^n)}=0.\end{array}$$

(2) 

If $f\in e_{-\alpha }{L}^{\infty }({\mathbf{T}}_{\alpha }^n)$ is uniformly continuous on a subset K of ${\mathbf{T}}_{\alpha }^n$, then

$$\begin{array}{c}\hfill \underset{N\to \infty }{\lim }\parallel f\stackrel{\alpha }{\ast }{F}_N^n-f{\parallel }_{L^{\infty }(K)}=0.\end{array}$$

Proof. 

We first deal with the case $1\le p<\infty$. It is easy to check that

$$\begin{array}{cc}\hfill (f\stackrel{\alpha }{\ast }{F}_N^n)(x)-f(x)=& e_{-\alpha }(x){\int }_{{\mathbf{T}}_{\alpha }^n}{e}_{\alpha }f(t)F_N^{n,\alpha }(x-t)\mathrm{d}t-{\int }_{{\mathbf{T}}_{\alpha }^n}f(x)F_N^{n,\alpha }(t)\mathrm{d}t\hfill \\ \hfill =& e_{-\alpha }(x){\int }_{{\mathbf{T}}_{\alpha }^n}\left((e_{\alpha }f)(x-t)-(e_{\alpha }f)(x)\right)F_N^{n,\alpha }(t)\mathrm{d}t.\hfill \end{array}$$

By approximation, we have

$$\begin{array}{c}\hfill {\int }_{{\mathbf{T}}_{\alpha }^n}|(e_{\alpha }f)(x-h)-(e_{\alpha }f)(x){|}^{p}dx\to 0ash\to 0.\end{array}$$

For a given $\epsilon >0$, there exists $\delta >0$ such that

$$\begin{array}{c}\hfill {\int }_{{\mathbf{T}}_{\alpha }^n}|(e_{\alpha }f)(x-h)-(e_{\alpha }f)(x){|}^{p}dx<{\displaystyle \frac{{\epsilon }^p}{2^p}},h\in [-\delta ,\delta ].\end{array}$$

(8)

Then,

$$\begin{array}{cc}\hfill (f\stackrel{\alpha }{\ast }{F}_N^n)(x)-f(x)& =e_{\alpha }(x){\int }_{|t|\le \delta }\left((e_{\alpha }f)(x-t)-(e_{\alpha }f)(x)\right)F_N^{n,\alpha }(t)\mathrm{d}t\hfill \\ \hfill & +e_{\alpha }(x){\int }_{|t|>\delta }\left((e_{\alpha }f)(x-t)-(e_{\alpha }f)(x)\right)F_N^{n,\alpha }(t)dt\hfill \\ \hfill & =:I_1+I_2.\hfill \end{array}$$

By Minkowski’s integral inequality and (7), we obtain

$$\begin{array}{cc}\hfill \parallel I_2{\parallel }_p& \le {\int }_{|t|>\delta }{\left({\int }_{{\mathbf{T}}_{\alpha }^n}|\left(e_{\alpha }f\right)(x-t)-\left(e_{\alpha }f\right)(x){|}^{p}dx\right)}^{1/p}{F}_N^{n,\alpha }(t)dt\hfill \\ & \le {2\parallel f\parallel }_p{\int }_{|t|>\delta }{F}_N^{n,\alpha }(t)dt\to 0asN\to \infty .\hfill \end{array}$$

(9)

In addition, by (8), we obtain

$$\begin{array}{cc}\hfill \parallel I_1{\parallel }_p& \le {\int }_{|t|\le \delta }{\left({\int }_{{\mathbf{T}}_{\alpha }^n}|\left(e_{\alpha }f\right)(x-t)-\left(e_{\alpha }f\right)(x){|}^{p}dx\right)}^{1/p}{F}_N^{n,\alpha }(t)dt<{\displaystyle \frac{\epsilon }{2}}.\hfill \end{array}$$

This, together with (9), implies the required conclusion.

Now, we turn to conclusion $(2)$. Let $e_{\alpha }f$ be a bounded function on ${\mathbf{T}}_{\alpha }^n$ that is uniformly continuous on K. Given $\epsilon >0$, there exists a neighborhood V of 0 such that

$$\begin{array}{c}\hfill |(e_{\alpha }f)(x-h)-(e_{\alpha }f)(x)|<{\displaystyle \frac{\epsilon }{2}}\mathrm{for}\mathrm{all}h\in V\mathrm{and}x\in K.\end{array}$$

Applying this along with (7), we obtain that as $N\to \infty$

$$\begin{array}{cc}\hfill & \underset{x\in K}{\sup }|(f\stackrel{\alpha }{\ast }{F}_N^{n,\alpha })(x)-f(x)|\hfill \\ \hfill & \le {\int }_{|t|\le \delta }\underset{x\in K}{\sup }|(e_{\alpha }f)(x-t)-(e_{\alpha }f)(x)|F_N^{n,\alpha }(t)\mathrm{d}t\hfill \\ \hfill & +{\int }_{|t|>\delta }\underset{x\in K}{\sup }|(e_{\alpha }f)(x-t)-(e_{\alpha }f)(x)|F_N^{n,\alpha }(t)dt\hfill \\ \hfill & \le {\displaystyle \frac{\epsilon }{2}},\hfill \end{array}$$

which completes the proof. □

Proposition 4.

For $1\le p<\infty$, the set of trigonometric polynomials of order α is dense in $e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$.

Proof. 

For $1\le p<\infty$, we claim that $f\stackrel{\alpha }{\ast }{F}_N^n$ is also a trigonometric polynomial of order α. In fact,

$$\begin{array}{cc}\hfill (f\stackrel{\alpha }{\ast }{F}_N^n)(x)=& \underset{|m_j|\le N}{\sum _{m\in {\mathbf{Z}}^n}}\prod _{j=1}^n\left(1-{\displaystyle \frac{|m_j|}{N+1}}\right){\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x).\hfill \end{array}$$

It follows from Theorem 1 that $f\stackrel{\alpha }{\ast }{\mathcal{F}}_N^n$ converges to f as $N\to \infty$. This finishes the proof. □

Corollary 1.

Every continuous function on ${\mathbf{T}}_{\alpha }^n$ is a uniform limit of trigonometric polynomials with order α.

Proof. 

Note that ${\mathbf{T}}_{\alpha }^n$ is a compact set. By Theorem 1(2), we know that $f\stackrel{\alpha }{\ast }{\mathcal{F}}_N^n$ converges uniformly to f as $N\to \infty$. Since $f\stackrel{\alpha }{\ast }{\mathcal{F}}_N^n$ is a trigonometric polynomial of order $\alpha$, we obtain that every continuous function on ${\mathbf{T}}_{\alpha }^n$ can be uniformly approximated by trigonometric polynomials of order $\alpha$. □

3. Reproduction of Functions from Their Fractional Fourier Coefficients

In this section, we establish the fractional Fourier inversion on $e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$ and study the basic properties of $e_{-\alpha }{L}^2({\mathbf{T}}_{\alpha }^n)$. Moreover, to explore the connections between fractional Fourier analysis on ${\mathbf{T}}_{\alpha }^n$ and fractional Fourier analysis on ${\mathbb{R}}^n$, we give the fractional Poisson summation formula.

3.1. Fractional Fourier Inversion

We now define the partial sums of fractional Fourier series.

Definition 8.

Let $N\in \mathbb{N}$, $\alpha \in \mathbb{R}$ and $\alpha \notin \pi \mathbf{Z}$. The fractional Fejér means (or fractional Cesàro means) of f are defined by

$$\begin{array}{cc}\hfill (f\stackrel{\alpha }{\ast }{F}_N^n)(x)=& \underset{|m_j|\le N}{\sum _{m\in {\mathbf{Z}}^n}}\prod _{j=1}^n\left(1-{\displaystyle \frac{|m_j|}{N+1}}\right){\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x).\hfill \end{array}$$

(10)

In the following propositions, we obtain that the fractional Fourier series uniquely determine the function.

Proposition 5.

If $f, g$ belong to $e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$ and satisfy ${\mathcal{F}}_{\alpha }(f)(m)={\mathcal{F}}_{\alpha }(g)(m)$ for all $m\in {\mathbf{Z}}^n$, we obtain $f=g$ almost everywhere.

Proof. 

By linearity of ${\mathcal{F}}_{\alpha }$, we can set $g=0$. If ${\mathcal{F}}_{\alpha }(f)(m)=0$ for all $m\in {\mathbf{Z}}^n$, we know from (10) that $f\stackrel{\alpha }{\ast }{F}_N^n=0$ for all $N\in {\mathbf{Z}}^{+}$. By Theorem 1, we have

$$\begin{array}{c}\hfill \parallel f\stackrel{\alpha }{\ast }{F}_N^n-f{\parallel }_{L^1({\mathbf{T}}_{\alpha }^n)}\to 0\end{array}$$

as $N\to \infty$. Then,

$$\begin{array}{c}\hfill {\parallel f\parallel }_{L^1({\mathbf{T}}_{\alpha }^n)}\le \parallel f\stackrel{\alpha }{\ast }{F}_N^n-f{\parallel }_{L^1({\mathbf{T}}_{\alpha }^n)}+\parallel f\stackrel{\alpha }{\ast }{F}_N^n{\parallel }_{L^1({\mathbf{T}}_{\alpha }^n)}\to 0,\end{array}$$

from which we conclude that $f=0$ almost everywhere. □

Does ${\sum }_{|m|\le N}|{\mathcal{F}}_{\alpha }(f)(m)|\to f$ as $N\to \infty$? We give a firm answer to this question.

Corollary 2

(Fractional Fourier inversion). Suppose $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$ and

$$\sum _{m\in {\mathbf{Z}}^n}|{\mathcal{F}}_{\alpha }(f)(m)|<\infty .$$

Then,

$$\begin{array}{c}\hfill f(x)=\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x)a.e.,\end{array}$$

(11)

and therefore, f is almost everywhere equal to a continuous function.

Proof. 

For $m,u\in {\mathbf{Z}}^n$, it is easy to see that

$$\begin{array}{c}\hfill K_{-\alpha }(m,x)K_{\alpha }(u,x)={|\csc \alpha |}^n{e}_{-\alpha }(m)e_{\alpha }(u)e_{\alpha }(u-m,x),m\ne u.\end{array}$$

This implies

$$\begin{array}{c}\hfill {\int }_{{\mathbf{T}}_{\alpha }^n}{K}_{-\alpha }(m,x)K_{\alpha }(u,x)dx=0,m\ne u.\end{array}$$

Meanwhile,

$$\begin{array}{cc}\hfill {\int }_{{\mathbf{T}}_{\alpha }^n}{K}_{-\alpha }(m,x)K_{\alpha }(m,x)dx=& {|\csc \alpha |}^n{\int }_{{\mathbf{T}}_{\alpha }^n}dx=1.\hfill \end{array}$$

Set

$$G(x):=\sum _{u\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(u)K_{-\alpha }(u,x).$$

It is obvious that $G\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$. Consequently,

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\alpha }(G)(m)=& {\int }_{{\mathbf{T}}_{\alpha }^n}\left(\sum _{u\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(u)K_{-\alpha }(u,x)\right)K_{\alpha }(m,x)dx={\mathcal{F}}_{\alpha }(f)(m).\hfill \end{array}$$

By Proposition 5, we have

$$\begin{array}{c}\hfill f(x)=\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x)a.e.\end{array}$$

This completes the proof. □

3.2. Fractional Fourier Series of Square Summable Functions

Now, consider the space $e_{-\alpha }{L}^2({\mathbf{T}}_{\alpha }^n)$ with inner product

$$\begin{array}{c}\hfill \langle f|g\rangle ={\int }_{{\mathbf{T}}_{\alpha }^n}f(t)\overline{g(t)}dt.\end{array}$$

It is easy to check that

$${\int }_{{\mathbf{T}}_{\alpha }^n}{K}_{-\alpha }(m,x)\overline{K_{-\alpha }(u,x)}dx=\left\{\begin{array}{cc}1,\hfill & whenm=u,\hfill \\ 0,\hfill & whenm\ne u.\hfill \end{array}\right.$$

This implies that the sequence $\left\{K_{-\alpha }(m,·)\right\}$ is orthonormal. Meanwhile, for all $f\in e_{-\alpha }{L}^2({\mathbf{T}}_{\alpha }^n)$, we have

$$\begin{array}{cc}\hfill \langle f|K_{-\alpha }(m,·)\rangle =& {\int }_{{\mathbf{T}}_{\alpha }^n}f(y)\overline{K_{-\alpha }(m,y)}dy={\mathcal{F}}_{\alpha }(f)(m).\hfill \end{array}$$

If $\langle f|K_{-\alpha }(m,·)\rangle =0$ for all $m\in {\mathbf{Z}}^n$, we know from Proposition 5 that $f=0$ almost everywhere. Therefore, the completeness of the sequence $\left\{K_{-\alpha }(m,·)\right\}$ holds.

Proposition 6.

The following are valid for $f,g\in e_{-\alpha }{L}^2({\mathbf{T}}_{\alpha }^n)$ and

(1) 

(Plancherel’s identity)

$$\begin{array}{c}\hfill {\parallel f\parallel }_2^2=\sum _{m\in {\mathbf{Z}}^n}{|{\mathcal{F}}_{\alpha }(f)(m)|}^2.\end{array}$$

(2) 

The function $f(x)$ is almost everywhere equal to the $e_{-\alpha }{L}^2({\mathbf{T}}_{\alpha }^n)$ limit of the sequence

$$\begin{array}{c}\hfill \sum _{|m|\le M}{\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x).\end{array}$$

(3) 

(Parseval’s relation)

$$\begin{array}{c}\hfill {\int }_{{\mathbf{T}}_{\alpha }^n}f(t)\overline{g(t)}dt=\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)\overline{{\mathcal{F}}_{\alpha }(g)(m)}.\end{array}$$

(4) 

The map $f\mapsto \left\{{\mathcal{F}}_{\alpha }(f)(m)\right\}$ is an isometry from $e_{-\alpha }{L}^2({\mathbf{T}}_{\alpha }^n)$ onto $l^2$.

(5) 

For all $m\in {\mathbf{Z}}^n$, we have

$$\begin{array}{c}\hfill {\mathcal{F}}_{\alpha }\left[e_{\alpha }(·)fg\right](m)=A_{\alpha }^n{e}_{\alpha }^2(m)\sum _{j\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(j)e^{-2\pi i(j·m)\cot \alpha }{\mathcal{F}}_{-\alpha }(e_{\alpha }^2(·)g)(j-m).\end{array}$$

Proof. 

The proofs of (1), (2), (3), and (4) are quite similar to those in the case of Fourier series, so we omit them. Now, we turn to (5). Let $\overline{G(x)}=e_{\alpha }(x)g(x)K_{\alpha }(m,x)$. From (3), we have

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\alpha }\left[e_{\alpha }(fg)\right](m)=& {\int }_{{\mathbf{T}}_{\alpha }^n}{e}_{\alpha }(x)f(x)g(x)K_{\alpha }(m,x)dx\hfill \\ \hfill =& {\int }_{{\mathbf{T}}_{\alpha }^n}f(x)\overline{G(x)}dx\hfill \\ \hfill =& \sum _{j\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(j)\overline{{\mathcal{F}}_{\alpha }(G)(j)}.\hfill \end{array}$$

In view of Proposition 1(6), we obtain

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\alpha }(G)(j)=& {\int }_{{\mathbf{T}}_{\alpha }^n}\overline{e_{\alpha }(x)g(x)K_{\alpha }(m,x)}{K}_{\alpha }(j,x)dx\hfill \\ \hfill =& \overline{A_{\alpha }^n}{e}_{-\alpha }(m){\int }_{{\mathbf{T}}_{\alpha }^n}\left[\overline{e_{\alpha }^2(x)g(x)}{e}^{2\pi imx\csc \alpha }\right]K_{\alpha }(j,x)dx\hfill \\ \hfill =& \overline{A_{\alpha }^n}{e}_{-\alpha }(m){\mathcal{F}}_{\alpha }\left(\overline{e_{\alpha }^{2}g}{e}_{-\alpha }(m,·)\right)(j)\hfill \\ \hfill =& \overline{A_{\alpha }^n}{e}_{-\alpha }^2(m)e^{2\pi i(j·m)\cot \alpha }{\mathcal{F}}_{\alpha }\left(\overline{e_{\alpha }^{2}g}\right)(j-m).\hfill \end{array}$$

By Proposition 1(3), we have

$$\begin{array}{cc}\hfill \overline{{\mathcal{F}}_{\alpha }(G)(j)}=& A_{\alpha }^n{e}_{\alpha }^2(m)e^{-2\pi i(j·m)\cot \alpha }\overline{{\mathcal{F}}_{\alpha }\left(\overline{e_{\alpha }^{2}g}\right)(j-m)}\hfill \\ \hfill =& A_{\alpha }^n{e}_{\alpha }^2(m)e^{-2\pi i(j·m)\cot \alpha }{\mathcal{F}}_{-\alpha }\left(e_{\alpha }^{2}g\right)(j-m).\hfill \end{array}$$

This completes the proof. □

3.3. The Fractional Poisson Summation Formula

In this subsection, we establish an important connection between fractional Fourier analysis on ${\mathbf{T}}_{\alpha }^n$ and Fourier analysis on ${\mathbb{R}}^n$.

Theorem 2

(Fractional Poisson summation formula). Suppose that f is a continuous function on ${\mathbb{R}}^n$. If there exists $C,\delta >0$ such that

$$\begin{array}{c}\hfill |f(x)|\le {\displaystyle \frac{C}{{(1+|x|)}^{n+\delta }}},\forall x\in {\mathbb{R}}^n\end{array}$$

(12)

and the fractional Fourier transform ${\mathcal{F}}_{\alpha }(e_{-\alpha }f)$ restricted on ${\mathbf{Z}}^n$ satisfies

$$\begin{array}{c}\hfill \sum _{m\in {\mathbf{Z}}^n}|{\mathcal{F}}_{\alpha }\left(e_{-\alpha }f\right)(m)|<\infty .\end{array}$$

(13)

Then, for all $x\in {\mathbb{R}}^n$ we have

$$\begin{array}{c}\hfill \sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }\left(e_{-\alpha }f\right)(m)K_{-\alpha }(m,x)=e_{-\alpha }(x)\sum _{k\in {\mathbf{Z}}^n}f(x+k|\sin \alpha |),\end{array}$$

(14)

and, in particular,

$$\begin{array}{c}\hfill A_{-\alpha }^n\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }\left(e_{-\alpha }f\right)(m)e_{-\alpha }(m)=\sum _{k\in {\mathbf{Z}}^n}f(k|\sin \alpha |).\end{array}$$

Proof. 

Suppose

$$F(x)=e_{-\alpha }(x)\sum _{k\in {\mathbf{Z}}^n}f(x+k|\sin \alpha |).$$

It is easy to check that $F\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$. We show that ${\mathcal{F}}_{\alpha }(F)(m)={\mathcal{F}}_{\alpha }(e_{-\alpha }f)(m)$ for all $m\in {\mathbf{Z}}^n$. In fact, for any $k\in {\mathbf{Z}}^n$, we obtain

$$\begin{array}{c}\hfill |k|\sin \alpha |+x|\ge |k\sin \alpha |-|x|\ge |k\sin \alpha | - {\displaystyle \frac{|\sin \alpha |}{2}}\sqrt{n}\end{array}$$

for all $x\in {[-|\sin \alpha |/2,|\sin \alpha |/2]}^n$. This, together with (12), implies

$$\begin{array}{cc}\hfill \sum _{k\in {\mathbf{Z}}^n}|f(x+k|\sin \alpha |)|\le & \sum _{k\in {\mathbf{Z}}^n}{\displaystyle \frac{C_{n,\delta }}{{(1+|k\sin \alpha |)}^{n+\delta }}}<\infty .\hfill \end{array}$$

(15)

Therefore,

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\alpha }(F)(m)=& A_{\alpha }^n{e}_{\alpha }(m){\int }_{{\mathbf{T}}_{\alpha }^n}{e}^{-2\pi i(m·x)\csc \alpha }\sum _{k\in {\mathbf{Z}}^n}f(x+k|\sin \alpha |)dx\hfill \\ \hfill =& A_{\alpha }^n{e}_{\alpha }(m)\sum _{k\in {\mathbf{Z}}^n}{\int }_{{\mathbf{T}}_{\alpha }^n}{e}^{-2\pi i(m·x)\csc \alpha }f(x+k|\sin \alpha |)dx\hfill \\ \hfill =& A_{\alpha }^n{e}_{\alpha }(m)\sum _{k\in {\mathbf{Z}}^n}{\int }_{{\mathbf{T}}_{\alpha }^n+k|\sin \alpha |}{e}^{-2\pi i(m·x)\csc \alpha }f(x)dx\hfill \\ \hfill =& A_{\alpha }^n{e}_{\alpha }(m){\int }_{{\mathbb{R}}^n}{e}^{-2\pi i(m·x)\csc \alpha }f(x)dx\hfill \\ \hfill =& {\mathcal{F}}_{\alpha }(e_{-\alpha }f)(m),\hfill \end{array}$$

where the second equality follows from (15). Meanwhile, we also obtain that F is continuous. The fact that ${\mathcal{F}}_{\alpha }(F)(m)={\mathcal{F}}_{\alpha }(e_{-\alpha }f)(m)$ for all $m\in {\mathbf{Z}}^n$ implies (13) holds. By Corollary 2, we obtain that (14) holds for $x\in {\mathbf{T}}_{\alpha }^n$, and then, by periodicity, for all $x\in {\mathbb{R}}^n$. □

4. Decay of Fractional Fourier Coefficient

This section is devoted to studying the decay of the fractional Fourier coefficients.

4.1. Decay of Fractional Fourier Coefficients of Integrable Function

Proposition 7

(Riemann–Lebesgue lemma). Suppose $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$. We have

$$\begin{array}{c}\hfill |{\mathcal{F}}_{\alpha }(f)(m)|\to 0as|m|\to \infty .\end{array}$$

Proof. 

For all $\epsilon >0$, there exists a trigonometric polynomial $P_{\alpha }$ such that $\parallel f - P_{\alpha }{\parallel }_{L^1} < \epsilon$. If $|m|>\mathrm{degree}(P_{\alpha })$, then we have ${\mathcal{F}}_{\alpha }(P_{\alpha })(m)=0$. Hence,

$$\begin{array}{c}\hfill |{\mathcal{F}}_{\alpha }(f)(m)| = |{\mathcal{F}}_{\alpha }(f)(m)-{\mathcal{F}}_{\alpha }(P_{\alpha })(m)| \le \parallel f-P_{\alpha }{\parallel }_{L^1} < \epsilon .\end{array}$$

This implies that $|{\mathcal{F}}_{\alpha }(f)(m)|\to 0$ as $|m|\to \infty$. □

For $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$, we claim that $|{\mathcal{F}}_{\alpha }(f)(m)|$ may tend to zero arbitrarily slowly. More precisely, we have the following theorem.

Theorem 3.

Suppose that a sequence of positive real numbers ${(d_m)}_{m\in {\mathbf{Z}}^n}$ satisfies $d_m\to 0$ as $|m|\to \infty$. Then, there exists a function $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$ such that $|{\mathcal{F}}_{\alpha }(f)(m)|\ge d_m$ for ∀$m\in {\mathbf{Z}}^n$. Namely, given any rate of decay, there exists an integrable function on ${\mathbf{T}}_{\alpha }^n$ whose absolute values of fractional Fourier coefficients have slower rates of decay.

Proof. 

We first deal with $n=1$. Let ${\left\{a_m\right\}}_{m\in \mathbf{Z}}$ be a sequence of positive numbers and ${\left\{a_m\right\}}_{m\in \mathbf{Z}}\to 0$ as $|m|\to \infty$. Apply Lemma 3.3.2 in [10] to the sequence ${\{a_m+a_{-m}\}}_{m\ge 0}$ to find a convex sequence ${\left\{c_m\right\}}_{m\ge 0}$ that dominates ${\{a_m+a_{-m}\}}_{m\ge 0}$ and decreases to zero as $|m|\to \infty$. Extend $c_m$ for $m<0$ by taking $c_m=c_{|m|}$. Set

$$\begin{array}{c}\hfill f(x)=e_{-\alpha }(x)\sum _{j=0}^{\infty }(j+1)(c_j+c_{j+2}-2c_{j+1})F_j^{1,\alpha }(x).\end{array}$$

(16)

Using Lemma 3.3.3 in [10] with $s=0$, we have

$$\begin{array}{c}\hfill \sum _{j=0}^{\infty }(j+1)(c_j+c_{j+2}-2c_{j+1}){\parallel F_j^{1,\alpha }\parallel }_{L^1({\mathbf{T}}_{\alpha }^1)}=c_0<\infty ,\end{array}$$

(17)

since $\parallel F_j^{1,\alpha }{\parallel }_{L^1({\mathbf{T}}_{\alpha }^1)}=1$ for all j. Therefore, we obtain that $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^1)$ by noting that the series in (16) converges in $L^1({\mathbf{T}}_{\alpha }^1)$. For $m\in \mathbf{Z}$, we obtain

$$\begin{array}{cc}\hfill |{\mathcal{F}}_{\alpha }(f)(m)|=& \sum _{j=0}^{\infty }(j+1)(c_j+c_{j+2}-2c_{j+1})|{\mathcal{F}}_{\alpha }(e_{-\alpha }{F}_j^{1,\alpha })(m)|\hfill \\ \hfill =& \sum _{j=|m|}^{\infty }(j+1)(c_j+c_{j+2}-2c_{j+1})|A_{\alpha }{e}_{\alpha }(m)\left(1-{\displaystyle \frac{|m|}{j+1}}\right)|\hfill \\ \hfill =& {|\csc \alpha |}^{1/2}\sum _{r=0}^{\infty }(r+1)(c_{r+|m|}+c_{r+|m|+2}-2c_{r+|m|+1})\hfill \\ \hfill =& {|\csc \alpha |}^{1/2}{c}_{|m|}={|\csc \alpha |}^{1/2}{c}_m,\hfill \end{array}$$

(18)

where the second equality follows from Proposition 2 and the third equality is due to Lemma 3.3.3 in [10] with $s=|m|$.

Next, we turn to $n\ge 2$. Let ${(d_m)}_{m\in {\mathbf{Z}}^n}$ be a sequence of positive real numbers with $d_m\to 0$ as $|m|\to \infty$. There exists a positive sequence ${\left\{a_j\right\}}_{j\in \mathbf{Z}}$ such that $a_{m_1}\cdots a_{m_n}\ge d_{(m_1,\dots ,m_n)}$ and $a_j\to 0$ as $|j|\to \infty$. Set

$$\mathbf{f}(x_1,\dots ,x_n)=f(x_1)\cdots f(x_n),$$

where f is defined as in (16) such that $|{\mathcal{F}}_{\alpha }(f)(m)|\ge a_m$. This, together with (2), implies $|{\mathcal{F}}_{\alpha }(\mathbf{f})(m)|\ge d_m$. □

4.2. Decay of Fractional Fourier Coefficients of Smooth Functions

In this subsection, we are devoted to studying the relationship between the decay of fractional Fourier coefficients and the smoothness of a function.

Definition 9.

For $0<\gamma <1$, the homogeneous Lipschitz space of order γ on ${\mathbf{T}}_{\alpha }^n$ is defined by

$${\dot{\Lambda }}_{\gamma }({\mathbf{T}}_{\alpha }^n)=\{f:{\mathbf{T}}_{\alpha }^n\to {Cwith\parallel f\parallel }_{{\dot{\Lambda }}_{\gamma }}<\infty \},$$

where

$${\parallel f\parallel }_{{\dot{\Lambda }}_{\gamma }}:=\underset{h\notin 0}{\underset{x,h\in {\mathbf{T}}_{\alpha }^n}{\sup }}{\displaystyle \frac{|f(x+h)-f(x)|}{{|h|}^{\gamma }}}.$$

Next, we discuss the decay of fractional Fourier coefficients of Lipschitz functions.

Theorem 4.

Suppose $s\in \mathbf{Z}$ and $s\ge 0$.

(a) 

Let $f\in e_{-\alpha }{C}^s({\mathbf{T}}_{\alpha }^n)$. Then,

$$\begin{array}{c}\hfill |{\mathcal{F}}_{\alpha }(f)(m)|\le {\left({\displaystyle \frac{\sqrt{n}}{2\pi |\csc \alpha |}}\right)}^s{\displaystyle \frac{\underset{|\beta |=s}{\max }|{\mathcal{F}}_{\alpha }[e_{-\alpha }{\partial }^{\beta }(e_{\alpha }f)](m)|}{{|m|}^s}}\end{array}$$

(19)

and thus,

$$\begin{array}{c}\hfill |{\mathcal{F}}_{\alpha }(f)(m)|(1+{|m|}^s)\to 0\end{array}$$

as $|m|\to \infty$.

(b) 

Suppose that $f\in e_{-\alpha }{C}^s({\mathbf{T}}_{\alpha }^n)$ and whenever $|\beta |=s$, ${\partial }^{\beta }(e_{\alpha }f)$ are in ${\dot{\Lambda }}_{\gamma }({\mathbf{T}}_{\alpha }^n)$ for some $0<\gamma <1$. Then,

$$\begin{array}{c}\hfill |{\mathcal{F}}_{\alpha }(f)(m)|\le {\displaystyle \frac{{(\sqrt{n})}^{s+\gamma }}{{(2\pi )}^s{|\csc \alpha |}^{s+\gamma +n-1}{2}^{\gamma +1}}}{\displaystyle \frac{\underset{|\beta |=s}{\max }\parallel {\partial }^{\beta }(e_{\alpha }f){\parallel }_{{\dot{\Lambda }}_{\gamma }}}{{|m|}^{s+\gamma }}},m\notin 0.\end{array}$$

(20)

Proof. 

For fixed $m\in {\mathbf{Z}}^n\setminus \left\{0\right\}$, there exists a j such that $|m_j| ={\sup }_{1\le k\le n}|m_k|$. Therefore, $|m|\le \sqrt{n}|m_j|$. For $f\in e_{-\alpha }{C}^s({\mathbf{T}}_{\alpha }^n)$, we obtain

$$\begin{array}{cc}\hfill {\mathcal{F}}_{\alpha }(f)(m)=& A_{\alpha }^n{e}_{\alpha }(m){\int }_{{\mathbf{T}}_{\alpha }^n}(e_{\alpha }f)(x)e^{-2\pi i(m·x)\csc \alpha }dx\hfill \\ \hfill =& A_{\alpha }^n{e}_{\alpha }(m){\int }_{{\mathbf{T}}_{\alpha }^n}{\partial }_j^s(e_{\alpha }f)(x){\displaystyle \frac{e^{-2\pi i(m·x)\csc \alpha }}{{(2\pi i{m}_j\csc \alpha )}^s}}dx\hfill \\ \hfill =& {\displaystyle \frac{1}{{(2\pi i{m}_j\csc \alpha )}^s}}{\int }_{{\mathbf{T}}_{\alpha }^n}{e}_{-\alpha }(x){\partial }_j^s(e_{\alpha }f)(x)K_{\alpha }(m,x)dx\hfill \\ \hfill =& {\displaystyle \frac{1}{{(2\pi i{m}_j\csc \alpha )}^s}}{\mathcal{F}}_{\alpha }[e_{-\alpha }{\partial }_j^s(e_{\alpha }f)](m).\hfill \end{array}$$

(21)

Then,

$$|{\mathcal{F}}_{\alpha }(f)(m)|\le {\left({\displaystyle \frac{\sqrt{n}}{2\pi |\csc \alpha |}}\right)}^s{\displaystyle \frac{\underset{|\beta |=s}{\max }|{\mathcal{F}}_{\alpha }[e_{-\alpha }{\partial }^{\beta }(e_{\alpha }f)](m)|}{{|m|}^s}}.$$

We now turn to conclusion (b). Let $e_j=(0,\cdots ,|\sin \alpha |,\cdots ,0)$ be the element of the torus ${\mathbf{T}}_{\alpha }^n$ whose j-th coordinate is $|\sin \alpha |$ and all the others are zero. By noting that $e^{\pi i}=e^{-\pi i}=-1$, we have

$$\begin{array}{c}\hfill {\int }_{{\mathbf{T}}_{\alpha }^n}{\partial }_j^s(e_{\alpha }f)(x)e^{-2\pi i(m·x)\csc \alpha }dx=-{\int }_{{\mathbf{T}}_{\alpha }^n}{\partial }_j^s(e_{\alpha }f)\left(x-{\displaystyle \frac{e_j}{2m_j}}\right)e^{-2\pi i(m·x)\csc \alpha }dx.\end{array}$$

Therefore,

$$\begin{array}{cc}\hfill & {\int }_{{\mathbf{T}}_{\alpha }^n}{\partial }_j^s\left(e_{\alpha }f\right)(x)e^{-2\pi i(m·x)\csc \alpha }dx\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\int }_{{\mathbf{T}}_{\alpha }^n}\left[{\partial }_j^s\left(e_{\alpha }f\right)(x)-{\partial }_j^s\left(e_{\alpha }f\right)\left(x-{\displaystyle \frac{e_j}{2m_j}}\right)\right]e^{-2\pi i(m·x)\csc \alpha }dx.\hfill \end{array}$$

Notice that

$$\begin{array}{c}\hfill |{\partial }_j^s(e_{\alpha }f)(t)-{\partial }_j^s(e_{\alpha }f)\left(t-{\displaystyle \frac{e_j}{2m_j}}\right)|\le {\displaystyle \frac{\parallel {\partial }_j^s(e_{\alpha }f){\parallel }_{{\dot{\Lambda }}_{\gamma }}}{(2|m_j\csc \alpha {|)}^{\gamma }}}.\end{array}$$

This, combined with (21), leads to

$$\begin{array}{cc}\hfill |{\mathcal{F}}_{\alpha }(f)(m)|=& |{\displaystyle \frac{A_{\alpha }^n{e}_{\alpha }(m)}{{(2\pi i{m}_j\csc \alpha )}^s}}{\int }_{{\mathbf{T}}_{\alpha }^n}{\partial }_j^s\left(e_{\alpha }f\right)(x)e^{-2\pi im·x\csc \alpha }dx|\hfill \\ \hfill \le & {\left({\displaystyle \frac{\sqrt{n}}{2\pi |\csc \alpha ||m|}}\right)}^s{\displaystyle \frac{|A_{\alpha }^n|}{{2|\csc \alpha |}^n}}{\displaystyle \frac{\parallel {\partial }_j^s(e_{\alpha }f){\parallel }_{{\dot{\Lambda }}_{\gamma }}}{(2|m_j\csc \alpha {|)}^{\gamma }}}\hfill \\ \hfill \le & {\left({\displaystyle \frac{\sqrt{n}}{2\pi |\csc \alpha ||m|}}\right)}^s{\displaystyle \frac{1}{{2|\csc \alpha |}^{n/2}}}{\left({\displaystyle \frac{\sqrt{n}}{2|\csc \alpha ||m|}}\right)}^{\gamma }\parallel {\partial }_j^s\left(e_{\alpha }f\right){\parallel }_{{\dot{\Lambda }}_{\gamma }}\hfill \\ \hfill \le & {\displaystyle \frac{{(\sqrt{n})}^{s+\gamma }}{{(2\pi )}^s{|\csc \alpha |}^{s+\gamma +n/2}{2}^{\gamma +1}}}{\displaystyle \frac{\underset{|\beta |=s}{\max }\parallel {\partial }_j^s(e_{\alpha }f){\parallel }_{{\dot{\Lambda }}_{\gamma }}}{{|m|}^{s+\gamma }}},\hfill \end{array}$$

which completes the proof. □

The following corollary is a consequence of Theorem 4.

Corollary 3.

Suppose $s\in \mathbf{Z}$ with $s\ge 0$.

(a) 

Let $f\in e_{-\alpha }{C}^s({\mathbf{T}}_{\alpha }^n)$. Then,

$$\begin{array}{c}\hfill |{\mathcal{F}}_{\alpha }(f)(m)|\le c_{n,s,\alpha }{\displaystyle \frac{\max (\parallel f{\parallel }_1,{\max }_{|\beta |=s}\parallel {\partial }^{\beta }(e_{\alpha }f){\parallel }_1)}{{(1+|m|)}^s}}\end{array}$$

(b) 

Suppose that $f\in e_{-\alpha }{C}^s({\mathbf{T}}_{\alpha }^n)$ and whenever $|\beta |=s$, ${\partial }^{\beta }(e_{\alpha }f)$ are in ${\dot{\Lambda }}_{\gamma }({\mathbf{T}}_{\alpha }^n)$ for some $0<\gamma <1$. Then,

$$\begin{array}{cc}\hfill |{\mathcal{F}}_{\alpha }(f)(m)|\le & c_{n,s,\alpha }{\displaystyle \frac{\max (\parallel f{\parallel }_1,{\max }_{|\beta |=s}\parallel {\partial }_j^s(e_{\alpha }f){\parallel }_{{\dot{\Lambda }}_{\gamma }})}{{(1+|m|)}^{s+\gamma }}}.\hfill \end{array}$$

Next, we establish the following result, which is a partial converse to Theorem 4. Denote $[[s]]$ to be the largest integer strictly less than a given real number s.

Proposition 8.

Suppose $s>0$. If $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$ and satisfies

$$\begin{array}{c}\hfill |{\mathcal{F}}_{\alpha }{(f)(m)|\le C(1+|m|)}^{-s-n}\end{array}$$

(22)

for all $m\in {\mathbf{Z}}^n$, then $e_{\alpha }f$ has partial derivatives of all orders $|\beta |\le [[s]]$. Moreover, ${\partial }^{\beta }(e_{\alpha }f)\in {\dot{\Lambda }}_{\gamma }$ for all multi-indices β satisfying $|\beta |=[[s]]$ with $0<\gamma <s-[[s]]$.

Proof. 

Using (22) and Corollary 2, we have

$$\begin{array}{c}\hfill f(x)=\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x)\end{array}$$

(23)

for almost all $x\in {\mathbf{T}}_{\alpha }^n$. Let $f_m(x)={\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x)$. If a series $g={\sum }_m{g}_m$ satisfies ${\sum }_m{\parallel {\partial }^{\beta }{g}_m\parallel }_{\infty }<\infty$ for all $|\beta |\le M$, we obtain $g\in C^M$ and ${\partial }^{\beta }g={\sum }_m{\partial }^{\beta }{g}_m$. Then, we need to check

$$\sum _{m\in {\mathbf{Z}}^n}|{\partial }^{\beta }(e_{\alpha }{f}_m)(x)|<\infty .$$

Notice that

$$\begin{array}{cc}\hfill {\partial }^{\beta }(e_{\alpha }{f}_m)(x)=& A_{-\alpha }^n{e}_{-\alpha }(m){\mathcal{F}}_{\alpha }(f)(m){(2\pi im\csc \alpha )}^{\beta }{e}^{2\pi i(m·x)\csc \alpha }.\hfill \end{array}$$

For $|\beta |\le [[s]]$, by (22), we obtain

$$\begin{array}{cc}\hfill \sum _{m\in {\mathbf{Z}}^n}|{\partial }^{\beta }(e_{\alpha }{f}_m)(x)|\le & |A_{-\alpha }^n|\sum _{m\in {\mathbf{Z}}^n}|{\mathcal{F}}_{\alpha }(f)(m)|\underset{x\in {\mathbf{T}}_{\alpha }^n}{\sup }|{(2\pi im\csc \alpha )}^{\beta }{e}_{-\alpha }(m,x)|<\infty .\hfill \end{array}$$

Hence, $e_{\alpha }f\in C^{[[s]]}({\mathbf{T}}_{\alpha }^n)$, and

$$\begin{array}{cc}\hfill {\partial }^{\beta }(e_{\alpha }f)(x)=& e_{\alpha }(x)\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m){(2\pi im\csc \alpha )}^{\beta }{K}_{-\alpha }(m,x).\hfill \end{array}$$

For $|\beta |=[[s]]$ and $0<\gamma <s-[[s]]$, we obtain

$$\begin{array}{c}\hfill |e^{2\pi i(m·h)\csc \alpha }-1|\le \min (2,2\pi |m||h||\csc \alpha |)\le 2^{1-\gamma }{(2\pi )}^{\gamma }{|m|}^{\gamma }{|h|}^{\gamma }{|\csc \alpha |}^{\gamma }.\end{array}$$

This, together with (22), implies

$$\begin{array}{cc}\hfill & |{\partial }^{\beta }(e_{\alpha }f)(x+h)-{\partial }^{\beta }(e_{\alpha }f)(x)|\hfill \\ \hfill =& |A_{-\alpha }^n\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)e_{-\alpha }(m)e_{-\alpha }(m,x)\left(e^{2\pi i(m·h)\csc \alpha }-1\right){(2\pi im\csc \alpha )}^{\beta }|\hfill \\ \hfill \le & \sum _{m\in Z^n}|{\mathcal{F}}_{\alpha }({\mathcal{M}}_{-\alpha }f)(m)||A_{\alpha }{e}^{-\pi i{m}^2\cot \alpha }||{(2\pi im\csc \alpha )}^{\beta }||e^{2\pi imx\csc \alpha }||e^{2\pi imh\csc \alpha }-1|\hfill \\ \hfill \le & \sum _{m\in {\mathbf{Z}}^n}{\displaystyle \frac{{C|\csc \alpha |}^{n/2}}{{(1+|m|)}^{s+n}}}{(2\pi )}^{[[s]]}{|m|}^{[[s]]}{|\csc \alpha |}^{[[s]]}|e^{2\pi i(m·h)\csc \alpha }-1|\hfill \\ \hfill \le & \sum _{m\in {\mathbf{Z}}^n}{\displaystyle \frac{{C|\csc \alpha |}^{n/2}}{{(1+|m|)}^{s+n}}}{(2\pi )}^{[[s]]}{|m|}^{[[s]]}{|\csc \alpha |}^{[[s]]}{2}^{1-\gamma }{(2\pi )}^{\gamma }{|m|}^{\gamma }{|h|}^{\gamma }{|\csc \alpha |}^{\gamma }\hfill \\ \hfill \le & 2^{1-\gamma }{|h|}^{\gamma }{(2\pi )}^{[[s]]+\gamma }{|\csc \alpha |}^{[[s]]+n/2+\gamma }\sum _{m\in {\mathbf{Z}}^n}{\displaystyle \frac{{C|m|}^{[[s]]+\gamma }}{{(1+|m|)}^{s+n}}}\hfill \\ \hfill \le & 2^{1-\gamma }{|h|}^{\gamma }{(2\pi )}^s{|\csc \alpha |}^{[[s]]+n/2+\gamma }\sum _{m\in {\mathbf{Z}}^n}{\displaystyle \frac{{C|m|}^{[[s]]+\gamma }}{{(1+|m|)}^{s+n}}}\hfill \\ \hfill \le & C{2}^{1-\gamma }{(2\pi )}^s{|\csc \alpha |}^{[[s]]+n/2+\gamma }{|h|}^{\gamma }.\hfill \end{array}$$

Therefore, ${\partial }^{\beta }(e_{\alpha }f)\in {\dot{\Lambda }}_{\gamma }$, and the proof is complete. □

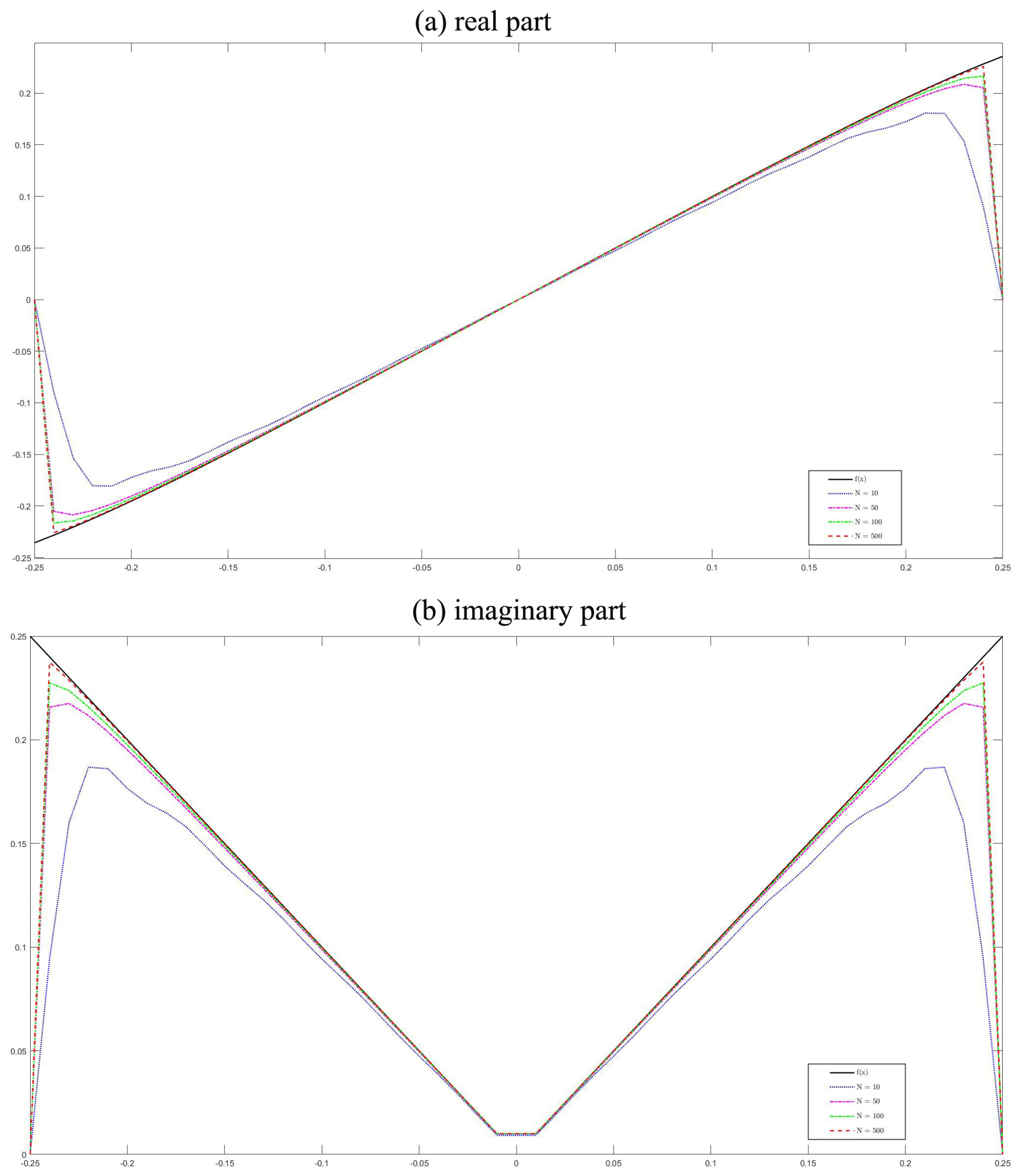
5. Convergence of Fractional Fourier Series

As we know, the convergence of Fourier series and the boundedness of singular integral and related operators have always been the core subjects of harmonic analysis; see [31,32,33] and references therein. In this section, we discuss the convergence of fractional means. For the convergence of other means, such as Bochner–Riesz means, one can refer to [34,35] and references therein.

5.1. Almost Everywhere Convergence of Fractional Fejér Means

Theorem 5.

Suppose $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$.

(a) 

Let

$${\mathcal{H}}_{\alpha }f:=\underset{N\in {\mathbf{Z}}^{+}}{\sup }|f\stackrel{\alpha }{\ast }{F}_N^n|.$$

Then, ${\mathcal{H}}_{\alpha }$ maps $e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$ to $L^{1,\infty }({\mathbf{T}}_{\alpha }^n)$ and $e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$ to $L^p({\mathbf{T}}_{\alpha }^n)$ for $1<p\le \infty$, where ${\parallel f\parallel }_{L^{1,\infty }(T_{\alpha }^n)}:={\sup }_{\lambda >0}\lambda |\{x\in T_{\alpha }^n:|f(x)|>\lambda \}|.$

(b) 

For any function $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$, we obtain that as $N\to \infty$

$$\begin{array}{c}\hfill f\stackrel{\alpha }{\ast }{F}_N^n\to fa.e.\end{array}$$

Proof. 

Recall that $1\le {\displaystyle \frac{|t|}{|\sin t|}}\le {\displaystyle \frac{\pi }{2}}$ with $|t|\le {\displaystyle \frac{\pi }{2}}$. Then,

$$\begin{array}{cc}\hfill |F_N^{1,\alpha }(x)|=& {\displaystyle \frac{|\csc \alpha |}{N+1}}|{\displaystyle \frac{\sin \left((N+1)\pi x\csc \alpha \right)}{\sin (\pi x\csc \alpha )}}{|}^2\hfill \\ \hfill \le & {\displaystyle \frac{(N+1)|\csc \alpha |}{4}}|{\displaystyle \frac{\sin \left((N+1)\pi x\csc \alpha \right)}{(N+1)x\csc \alpha }}{|}^2\hfill \\ \hfill \le & {\displaystyle \frac{(N+1)|\csc \alpha |}{4}}\min \left\{{\pi }^2,{\displaystyle \frac{1}{{(N+1)}^2{|x\csc \alpha |}^2}}\right\}\hfill \\ \hfill \le & {\displaystyle \frac{{\pi }^2}{2}}{\displaystyle \frac{(N+1)|\csc \alpha |}{1+{(N+1)}^2{|x|}^2}}.\hfill \end{array}$$

where $|x|\le {\displaystyle \frac{1}{2|\csc \alpha |}}$. For $t\in \mathbb{R}$, set $\phi (t)={(1+t^2)}^{-1}$ and ${\phi }_{\epsilon }(t)={\epsilon }^{-1}\phi (t/\epsilon )$ for $\epsilon >0$. For $x\in$${\mathbf{T}}_{\alpha }^n$, let $\Phi (x)=\phi (x_1)\cdots \phi (x_n)$ and ${\Phi }_{\epsilon }(t)={\epsilon }^{-n}\Phi (t/\epsilon )$. Hence, for $|x|\le |\sin \alpha |/2$ we obtain $|F_N^{1,\alpha }(x)|\le {\pi }^2|\csc \alpha |{\phi }_{\epsilon }(x)$ with $\epsilon ={(N+1)}^{-1}$. In addition, for $y\in {[-|\sin \alpha |/2,|\sin \alpha |/2]}^n$, we obtain

$$|F_N^{n,\alpha }(y)|\le {\pi }^{2n}{|\csc \alpha |}^n{\Phi }_{\epsilon }(y),$$

where $\epsilon ={(N+1)}^{-1}$.

Now, let $e_{\alpha }f$ be an integrable function on ${\mathbf{T}}_{\alpha }^n$ and let $f_0$ denote its periodic extension on ${\mathbb{R}}^n$. For $x\in {[-|\sin \alpha |/2,|\sin \alpha |/2]}^n$, we obtain

$$\begin{array}{cc}\hfill {\mathcal{H}}_{\alpha }f(x)=& \underset{N\in {\mathbf{Z}}^{+}}{\sup }|e_{-\alpha }(x){\int }_{{\mathbf{T}}_{\alpha }^n}(e_{\alpha }f)(x-t)F_N^{n,\alpha }(t)\mathrm{d}t|\hfill \\ \hfill \le & {\pi }^{2n}{|\csc \alpha |}^n\underset{\epsilon >0}{\sup }{\int }_{{\mathbf{T}}_{\alpha }^n}|(e_{\alpha }f)(x-t)|{\Phi }_{\epsilon }(t)\mathrm{d}t\hfill \\ \hfill \le & {10}^n{|\csc \alpha |}^n\underset{\epsilon >0}{\sup }{\int }_{{\mathbf{T}}_{\alpha }^n}|f_0(x-t)|{\Phi }_{\epsilon }(t)\mathrm{d}t\hfill \\ \hfill \le & {10}^n{|\csc \alpha |}^n\underset{\epsilon >0}{\sup }{\int }_{{\mathbb{R}}^n}|(f_0{\chi }_Q)(x-t)|{\Phi }_{\epsilon }(t)\mathrm{d}t\hfill \\ \hfill =:& {10}^n{|\csc \alpha |}^n\mathfrak{F}(f_0{\chi }_Q)(x),\hfill \end{array}$$

where Q is the cube ${[-|\sin \alpha |,|\sin \alpha |]}^n$ and operator $\mathfrak{F}$ is defined by

$$\mathfrak{F}(h)=\underset{\epsilon >0}{\sup }|h|\ast {\Phi }_{\epsilon }.$$

By Lemma 3.4.5 in [10], we have

$$\begin{array}{c}\hfill \parallel {\mathcal{H}}_{\alpha }{f\parallel }_{L^{1,\infty }({\mathbf{T}}_{\alpha }^n)}\le {10}^n{|\csc \alpha |}^n\parallel \mathfrak{F}(f_0{\chi }_Q){\parallel }_{L^{1,\infty }({\mathbb{R}}^n)}\le C_{n,\alpha }\parallel f_0{\chi }_Q{\parallel }_{L^1({\mathbb{R}}^n)}\le C_{n,\alpha }{\parallel f\parallel }_{L^1({\mathbf{T}}_{\alpha }^n)}.\end{array}$$

Meanwhile, it is easy to see

$$\begin{array}{c}\hfill \parallel {\mathcal{H}}_{\alpha }{f\parallel }_{L^{\infty }({\mathbf{T}}_{\alpha }^n)}\le C_{n,\alpha }{\parallel f\parallel }_{L^{\infty }({\mathbf{T}}_{\alpha }^n)}.\end{array}$$

By the Marcinkiewicz interpolation theorem, we obtain the $L^p$ conclusion.

Now, we turn to conclusion (b). Since the sequence ${\left\{F_N^{n,\alpha }\right\}}_{N=0}^{\infty }$ is an approximate identity and $e_{-\alpha }{C}^{\infty }({\mathbf{T}}_{\alpha }^n)$ is dense in $e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$, we have

$$f\stackrel{\alpha }{\ast }{F}_N^n\to f,f\in e_{-\alpha }{C}^{\infty }({\mathbf{T}}_{\alpha }^n),$$

uniformly on ${\mathbf{T}}_{\alpha }^n$ as $N\to \infty$. Since ${\mathcal{H}}_{\alpha }$ maps $e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$ to $L^{1,\infty }({\mathbf{T}}_{\alpha }^n)$ and using Theorem 2.1.14 in [10], we obtain that for $f\in e_{-\alpha }{L}^1({\mathbf{T}}_{\alpha }^n)$, $f\stackrel{\alpha }{\ast }{F}_N^n\to f$ almost everywhere. □

5.2. Norm Convergence of the Fractional Bochner–Riesz Means

Theorem 6.

Let $R>0$ and $m\in {\mathbf{Z}}^n$. Suppose that $a(m,R)$ are complex numbers satisfying the following conditions:

(1) 

For every $R>0$, there exists constant $q_R$ such that $a(m,R)=0$ when $|m|>q_R$;

(2) 

There exists constant $M_0<\infty$ such that $|a(m,R)|\le M_0$, ∀$m\in {\mathbf{Z}}^n$ and $R>0$;

(3) 

$li{m}_{R\to \infty }a(m,R)=a_m<\infty$ for all $m\in {\mathbf{Z}}^n$.

Let $1\le p<\infty$. For $f\in e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$ and $x\in {\mathbf{T}}_{\alpha }^n$, define

$$\begin{array}{c}\hfill S_{R}f(x)=\sum _{m\in {\mathbf{Z}}^n}a(m,R){\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x).\end{array}$$

For $h\in e_{-\alpha }{C}^{\infty }({\mathbf{T}}_{\alpha }^n)$, define

$$\begin{array}{c}\hfill Ah(x)=\sum _{m\in {\mathbf{Z}}^n}{a}_m{\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x).\end{array}$$

Then, for all $f\in e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$ the sequence $S_{R}f$ converges in $L^p({\mathbf{T}}_{\alpha }^n)$ as $R\to \infty$ if and only if there exists a constant $K<\infty$ such that

$$\begin{array}{c}\hfill \underset{R>0}{\sup }{\parallel S_R\parallel }_{L^p\to L^p}\le K.\end{array}$$

(24)

Furthermore, if (24) holds, then for the same constant K and $h\in e_{-\alpha }{C}^{\infty }({\mathbf{T}}_{\alpha }^n)$, we have

$$\begin{array}{c}\hfill \underset{h\notin 0}{\sup }{\parallel Ah\parallel }_{L^p\to L^p}\le K,\end{array}$$

(25)

and the A extends to a bounded operator $\tilde{A}$ from $e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$ to $L^p({\mathbf{T}}_{\alpha }^n)$; moreover, for every $f\in e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$ we have $S_{R}f\to \tilde{A}f$ in $L^p$ as $R\to \infty$.

Proof. 

If $S_{R}f$ converges in $L^p({\mathbf{T}}_{\alpha }^n)$, then $\parallel S_R{f\parallel }_{L^p}\le C_f$, where constant $C_f$ depends on f. Moreover, $\parallel S_R{f\parallel }_{L^p}\le C^{*}{\parallel f\parallel }_{L^p}$, where $C^{*}=\#\{m\in {\mathbf{Z}}^n:|m|\le q_R\}{M}_0$. Therefore, by the uniform boundedness theorem, we obtain that the operator norms of $S_R$ are bounded uniformly in R. (24) holds.

Conversely, assume (24). For $h\in e_{-\alpha }{C}^{\infty }({\mathbf{T}}_{\alpha }^n)$, by condition (2) and Lebesgue’s dominated convergence theorem, we obtain

$$\begin{array}{c}\hfill \underset{R\to \infty }{\lim }\sum _{m\in {\mathbf{Z}}^n}a(m,R){\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x)=\sum _{m\in {\mathbf{Z}}^n}{a}_m{\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x).\end{array}$$

Fatou’s lemma gives

$$\begin{array}{c}\hfill {\parallel Ah\parallel }_{L^p}=\parallel \underset{R\to \infty }{\lim }{S}_R{h\parallel }_{L^p}\le K{\parallel h\parallel }_{L^p},\end{array}$$

hence (25) holds. Thus, A extends to a bounded operator $\tilde{A}$ on $e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$ by density.

For $f\in e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$, we need to prove $S_{R}f\to \tilde{A}f$ in $L^p$ as $R\to \infty$. For all $\epsilon >0$, there exists a trigonometric polynomial $P_{\alpha }$ such that $\parallel f - P_{\alpha }{\parallel }_{L^p} \le \epsilon$. Notice that ${\mathcal{F}}_{\alpha }(P_{\alpha })(m)=0$ for $|m|>\mathrm{degree}(P_{\alpha })$. For some $R_0>0$, by condition (2), we obtain

$$\begin{array}{c}\hfill \sum _{|m_1|+\cdots +|m_n|\le \mathrm{degree}(P_{\alpha })}|a(m,R)-a_m|{\mathcal{F}}_{\alpha }(P_{\alpha })(m)\le \epsilon ,\forall R>R_0.\end{array}$$

For $R>R_0$, we deduce that

$$\begin{array}{cc}\hfill \parallel S_R{P}_{\alpha }-A{P}_{\alpha }{\parallel }_{L^p}& \le \parallel S_R{P}_{\alpha }-A{P}_{\alpha }{\parallel }_{L^{\infty }}\hfill \\ \hfill & \lesssim \sum _{|m_1|+\cdots +|m_n|\le \mathrm{degree}(P_{\alpha })}|a(m,R)-a_m|{\mathcal{F}}_{\alpha }(P_{\alpha })(m)\lesssim \epsilon .\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill \parallel S_{R}f-\tilde{A}{f\parallel }_{L^p}& \le \parallel S_{R}f-S_R{P}_{\alpha }{\parallel }_{L^p}+\parallel S_R{P}_{\alpha }-\tilde{A}{P}_{\alpha }{\parallel }_{L^p}+{\parallel \tilde{A}{P}_{\alpha }-\tilde{A}f\parallel }_{L^p}\hfill \\ \hfill & \lesssim (2K+1)\epsilon \hfill \end{array}$$

for $R>R_0$. This completes the proof. □

Definition 10.

For $\gamma \ge 0$, define the Bochner–Riesz means as follows:

$$\begin{array}{c}\hfill B_R^{\gamma }(f)(x)=\sum _{m\in {\mathbf{Z}}^n,|m|\le R}{\left(1-{\displaystyle \frac{{|m|}^2}{R^2}}\right)}^{\gamma }{\mathcal{F}}_{\alpha }(f)(m)K_{-\alpha }(m,x).\end{array}$$

In fact, suppose $a(m,R)={\left(1-{\displaystyle \frac{{|m|}^2}{R^2}}\right)}^{\gamma }$ for $|m|\le R$ in Theorem 6. It is easy to check that the sequence ${\left(1-{\displaystyle \frac{{|m|}^2}{R^2}}\right)}^{\gamma }$ satisfies properties (1)–(3) in Theorem 6. Hence, we have the following corollary.

Corollary 4.

Set $1\le p<\infty$ and $\gamma \ge 0$. For $f\in e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$, then

$$\begin{array}{c}\hfill \underset{R\to \infty }{\lim }\parallel B_R^{\gamma }{(f)-f\parallel }_{L^p}=0⟺\underset{R>0}{\sup }{\parallel B_R^{\gamma }\parallel }_{L^p\to L^p}<\infty .\end{array}$$

Furthermore, using Theorem 6, taking $a(m,R)=1$ for $|m_j| \le R$ and zero otherwise, we also have the following corollary.

Corollary 5.

Suppose $1\le p<\infty$ and $f\in e_{-\alpha }{L}^p({\mathbf{T}}_{\alpha }^n)$. Then,

$$\begin{array}{c}\hfill \underset{R\to \infty }{\lim }\parallel f\stackrel{\alpha }{\ast }{D}_R^n{-f\parallel }_{L^p}=0⟺\underset{R>0}{\sup }{\parallel S_R\parallel }_{L^p\to L^p}<\infty .\end{array}$$

6. Applications to Partial Differential Equations

It is well known that Fourier theory plays a key role in the solution of differential equations; see [36,37,38] and references therein for more details. In this section, we apply fractional Fourier series to obtain solutions of the fractional heat equation and fractional Dirichlet problem.

Definition 11.

For fixed $k>0$, define the fractional heat kernel of order α:

$$H_t^{\alpha }(x)=\sum _{m\in {\mathbf{Z}}^n}{e}^{-4{\pi }^2{|m|}^2{|\csc \alpha |}^{2}kt}{e}^{2\pi im·x},$$

where $t>0$. Note that $H_t^{\alpha }$ is absolutely convergent for any $t>0$.

When $\alpha =\pi /2+k\pi$, $k\in \mathbb{Z}$ in Definition 11, the fractional heat kernel of order $H_t^{\alpha }(x)$ is the classical heat kernel. For a fixed $k>0$, the classical heat equation is defined by

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial t}F(x,t)=k{▵}_{x}F(x,t),t\in (0,\infty ),x\in {\mathbb{R}}^n.}\end{array}$$

Similarly, we introduce the following fractional heat equation.

Definition 12.

Let $k>0$ be fixed. The fractional heat equation of order α is defined as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial t}\left(e_{\alpha }(x)F_{\alpha }(x,t)\right)=k{▵}_x\left(e_{\alpha }(x)F_{\alpha }(x,t)\right),t\in (0,\infty ),x\in {\mathbf{T}}_{\alpha }^n.}\end{array}$$

Proposition 9.

Let $k>0$ be fixed and $f\in e_{-\alpha }{C}^{\infty }({\mathbf{T}}_{\alpha }^n)$. Then, the fractional heat equation of order α

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial t}\left(e_{\alpha }(x)F_{\alpha }(x,t)\right)=k{▵}_x\left(e_{\alpha }(x)F_{\alpha }(x,t)\right),t\in (0,\infty ),x\in {\mathbf{T}}_{\alpha }^n,}\end{array}$$

(26)

under the initial condition

$$\begin{array}{c}\hfill F_{\alpha }(x,0)=f(x),x\in {\mathbf{T}}_{\alpha }^n,\end{array}$$

(27)

has a unique solution, which is $C^{\infty }$ on $[0,\infty )\times {\mathbf{T}}_{\alpha }^n$, given by

$$\begin{array}{c}\hfill F_{\alpha }(x,t)=(f\stackrel{\alpha }{\ast }{H}_t^{\alpha })(x)=\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)e^{-4{\pi }^2{|m|}^2{|\csc \alpha |}^{2}kt}{K}_{-\alpha }(m,x).\end{array}$$

(28)

Proof. 

For $f\in e_{-\alpha }{C}^{\infty }({\mathbf{T}}_{\alpha }^n)$, it is easy to check that the series in (28) is rapidly convergent in m and $C^{\infty }$ function on $[0,\infty )\times {\mathbf{T}}_{\alpha }^n$. According to Corollary 2, $F_{\alpha }$ satisfies (27). Next, it remains to check (26).

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial }{\partial t}}\left(e_{\alpha }(x)F_{\alpha }(x,t)\right)=& {\displaystyle \frac{\partial }{\partial t}}\left[\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)e^{-4{\pi }^2{|m|}^2{|\csc \alpha |}^{2}kt}{A}_{-\alpha }^n{e}_{-\alpha }(m)e_{-\alpha }(m,x)\right]\hfill \\ \hfill =& k\left[\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)e^{-4{\pi }^2{m}^2{|\csc \alpha |}^{2}kt}{A}_{-\alpha }^n{e}_{-\alpha }(m)\sum _{j=1}^n{\displaystyle \frac{{\partial }^2}{\partial x_j^2}}{e}_{-\alpha }(m,x)\right]\hfill \\ \hfill =& k\sum _{j=1}^n{\displaystyle \frac{{\partial }^2}{\partial x_j^2}}\left[\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)e^{-4{\pi }^2{m}^2{|\csc \alpha |}^{2}kt}{A}_{-\alpha }^n{e}_{-\alpha }(m)e_{-\alpha }(m,x)\right]\hfill \\ \hfill =& k{▵}_x\left(e_{\alpha }(x)F_{\alpha }(x,t)\right),\hfill \end{array}$$

where the last equality follows from the convergence of the series.

Finally, let $G_{\alpha }(x,t)$ be another solution. We write

$$G_{\alpha }(x,t):=\sum _{m\in {\mathbf{Z}}^n}{c}_m^{\alpha }(t)K_{-\alpha }(m,x),$$

where

$$c_m^{\alpha }(t)={\int }_{{\mathbf{T}}_{\alpha }^n}{G}_{\alpha }(y,t)K_{\alpha }(m,y)dy.$$

Then, $c_m^{\alpha }(t)$ is a smooth function on $(0,\infty )$ since $G_{\alpha }$ is $C^{\infty }$ on $[0,\infty )\times {\mathbf{T}}_{\alpha }^n$. By Equation (26), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}{c}_m^{\alpha }(t)=& {\int }_{{\mathbf{T}}_{\alpha }^n}{\displaystyle \frac{\partial }{\partial t}}\left(e_{\alpha }(x)G_{\alpha }(x,t)\right)e_{-\alpha }(x)K_{\alpha }(m,x)dx\hfill \\ \hfill =& k{A}_{\alpha }^n{e}_{\alpha }(m)\sum _{j=1}^n{\int }_{{\mathbf{T}}_{\alpha }^n}{\displaystyle \frac{{\partial }^2}{\partial x_j^2}}\left(e_{\alpha }(x)G_{\alpha }(x,t)\right)e^{-2\pi i(m·x)\csc \alpha }dx\hfill \\ \hfill =& -4{\pi }^2{|m|}^2{|\csc \alpha |}^{2}k{c}_m^{\alpha }(t),\hfill \end{array}$$

where the last equality follows from the periodicity. In addition, $c_m^{\alpha }(0)={\mathcal{F}}_{\alpha }(f)(m)$. Therefore, we obtain

$$c_m^{\alpha }(t)={\mathcal{F}}_{\alpha }(f)(m)e^{-4{\pi }^2{|m|}^2{|\csc \alpha |}^{2}kt}.$$

This implies $G_{\alpha }=F_{\alpha }$ on $[0,\infty )\times {\mathbf{T}}_{\alpha }^n$. □

Remark 3.

Let ${\mathbb{H}}_t^{\alpha }(x)={|\csc \alpha |}^n{H}_t^{\alpha }(x\csc \alpha )$. The family ${\left\{{\mathbb{H}}_t^{\alpha }\right\}}_{t>0}$ is an approximate identity on ${\mathbf{T}}_{\alpha }^n$.

Definition 13.

Define the fractional Poisson kernel of order α

$$P_t^{\alpha }(x)=\sum _{m\in {\mathbf{Z}}^n}{e}^{-2\pi |m||\csc \alpha |t}{e}^{2\pi im·x},$$

where $t>0$. Note that $P_t^{\alpha }$ is absolutely convergent for any $t>0$.

Proposition 10.

Let $f\in e_{-\alpha }{C}^{\infty }({\mathbf{T}}_{\alpha }^n)$. Then, the fractional Dirichlet problem of order α

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{{\partial }^2}{\partial t^2}\left(e_{\alpha }(x)F_{\alpha }(x,t)\right)+\sum _{j=1}^n\frac{{\partial }^2}{\partial {x_j}^2}\left(e_{\alpha }(x)F_{\alpha }(x,t)\right)=0;t\in (0,\infty ),x\in {\mathbf{T}}_{\alpha }^n,}\hfill \\ F_{\alpha }(x,0)=f(x);x\in {\mathbf{T}}_{\alpha }^n,\hfill \end{array}\right.\end{array}$$

(29)

has a solution which is $C^{\infty }$ on $[0,\infty )\times {\mathbf{T}}_{\alpha }^n$ given by

$$\begin{array}{c}\hfill F_{\alpha }(x,t)=(f\stackrel{\alpha }{\ast }{P}_t^{\alpha })(x)=\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)e^{-2\pi |m||\csc \alpha |t}{K}_{-\alpha }(m,x).\end{array}$$

Proof. 

It is easy to check $F_{\alpha }(x,t)$ is $C^{\infty }$ on $[0,\infty )\times {\mathbf{T}}_{\alpha }^n$. By Corollary 2, $F_{\alpha }$ satisfies the initial condition. It suffices to verify (29). Notice that

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2}{\partial t^2}}\left(e_{\alpha }(x)F_{\alpha }(x,t)\right)=& -\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)e^{-2\pi |m||\csc \alpha |t}{A}_{-\alpha }^n{e}_{-\alpha }(m)\sum _{j=1}^n{\displaystyle \frac{{\partial }^2}{\partial x_j^2}}{e}_{\alpha }(m,x)\hfill \\ \hfill =& -\sum _{j=1}^n{\displaystyle \frac{{\partial }^2}{\partial x_j^2}}\left[e_{\alpha }(x)\sum _{m\in {\mathbf{Z}}^n}{\mathcal{F}}_{\alpha }(f)(m)e^{-2\pi |m||\csc \alpha |t}{K}_{-\alpha }(m,x)\right]\hfill \\ \hfill =& -{▵}_x\left(e_{\alpha }(x)F_{\alpha }(x,t)\right).\hfill \end{array}$$

This completes the proof. □

Remark 4.

Let ${\mathbb{P}}_t^{\alpha }(x)={|\csc \alpha |}^n{P}_t^{\alpha }(x\csc \alpha )$. The family ${\left\{{\mathbb{P}}_t^{\alpha }\right\}}_{t>0}$ is an approximate identity on ${\mathbf{T}}_{\alpha }^n$.

7. Applications to Non-Stationary Signals

In this section, we will demonstrate the use of Corollary 2 and Theorem 5 in the recovery of non-stationary signals. For example, suppose

$${\displaystyle g(x)=\left\{\begin{array}{cc}x,\hfill & -\frac{1}{4}<x\le \frac{1}{4},\hfill \\ \frac{1}{4},\hfill & x=-\frac{1}{4},\hfill \end{array}\right.}$$

and $g(x+1/4)=g(x)$ for all $x\in \mathbb{R}$. By taking $\alpha =\pi /6$, we have

$$f(x)=e^{-\pi i{x}^2\cot \pi /6}g(x)=\left\{\begin{array}{cc}x{e}^{-\sqrt{3}\pi i{x}^2},\hfill & -{\displaystyle \frac{1}{4}}<x\le {\displaystyle \frac{1}{4}},\hfill \\ {\displaystyle \frac{1}{4}}{e}^{-{\displaystyle \frac{\sqrt{3}}{16}}\pi i},\hfill & x=-{\displaystyle \frac{1}{4}}.\hfill \end{array}\right.$$

It is easy to see that $f\in e_{-\pi /6}{L}^1({\mathbf{T}}_{-\pi /6}^1)$. Note that

$${\mathcal{F}}_{\alpha }(f)(m)=\left\{\begin{array}{cc}{\displaystyle i{A}_{\alpha }^1{e}^{\sqrt{3}\pi i{m}^2}\frac{{(-1)}^m}{8\pi m},}& m\notin 0,\\ {\displaystyle 0,}& m=0.\end{array}\right.$$

Therefore, the series ${\sum }_{m\in \mathbf{Z}}|{\mathcal{F}}_{\alpha }(f)(m)|$ is not convergent and we cannot recover the signal $f(x)$ by fractional Fourier inversion. Meanwhile, the approximating method (Theorem 5) can give another way to recover the non-stationary signal $f(x)$. In fact, for $N\ge 0$ we obtain

$$\begin{array}{cc}\hfill (f\stackrel{\pi /6}{\ast }{F}_N^1)(x)=& i{e}^{-\sqrt{3}\pi i{x}^2}\sum _{m=-N}^N\left(1-{\displaystyle \frac{|m|}{N+1}}\right){\displaystyle \frac{{(-1)}^m}{4\pi m}}{e}^{4\pi imx}.\hfill \end{array}$$

Figure 2 shows the rea- and imaginary-part graphs of the fractional convolution $f\stackrel{\pi /6}{\ast }{F}_N^1$ with $N=10, 50, 100, 500$.

By Theorem 5, we obtain that $(f\stackrel{\pi /6}{\ast }{F}_N^1)(x)\to f$ for almost every $x\in {\mathbf{T}}_{-\pi /6}^1$ as $N\to \infty$.