Influence of Local Thermodynamic Non-Equilibrium to Photothermally Induced Acoustic Response of Complex Systems
Abstract
1. Introduction
2. Theory of Heat Conduction including the Non-Equilibrium Relaxation
3. Model of PA Signal including Local Thermal Non-Equilibrium in the Sample
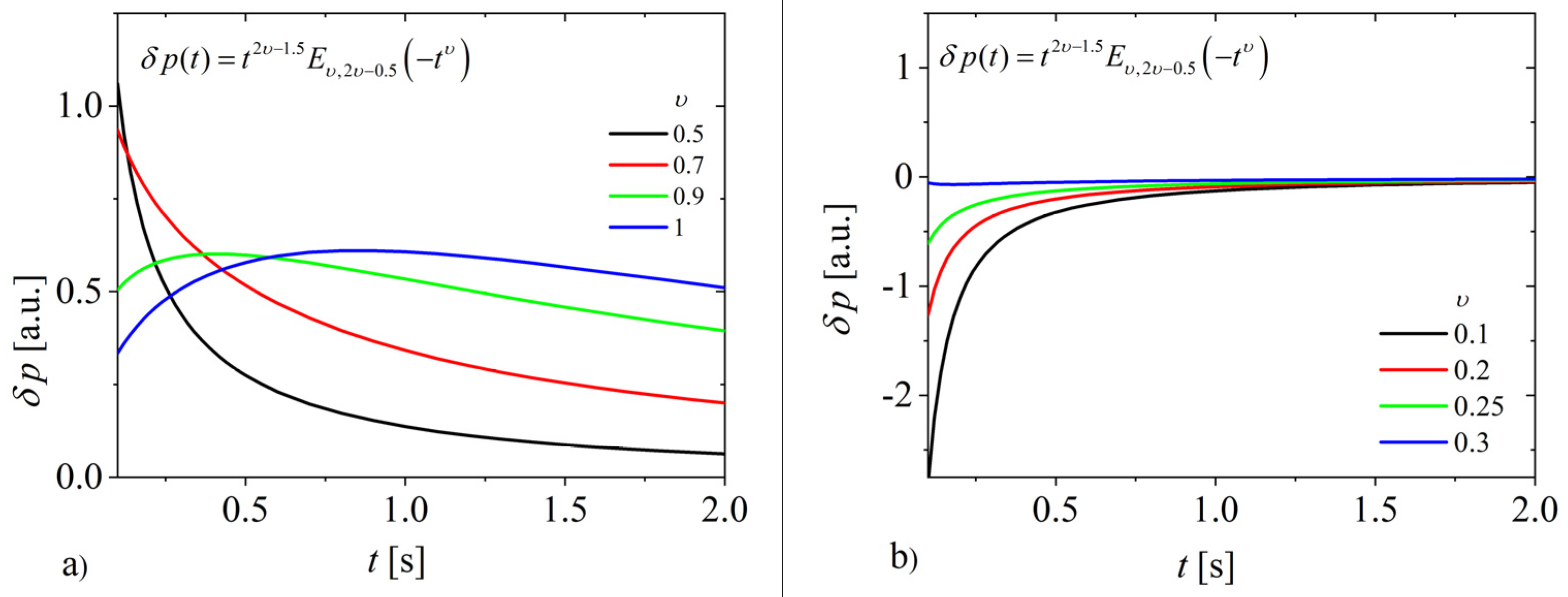
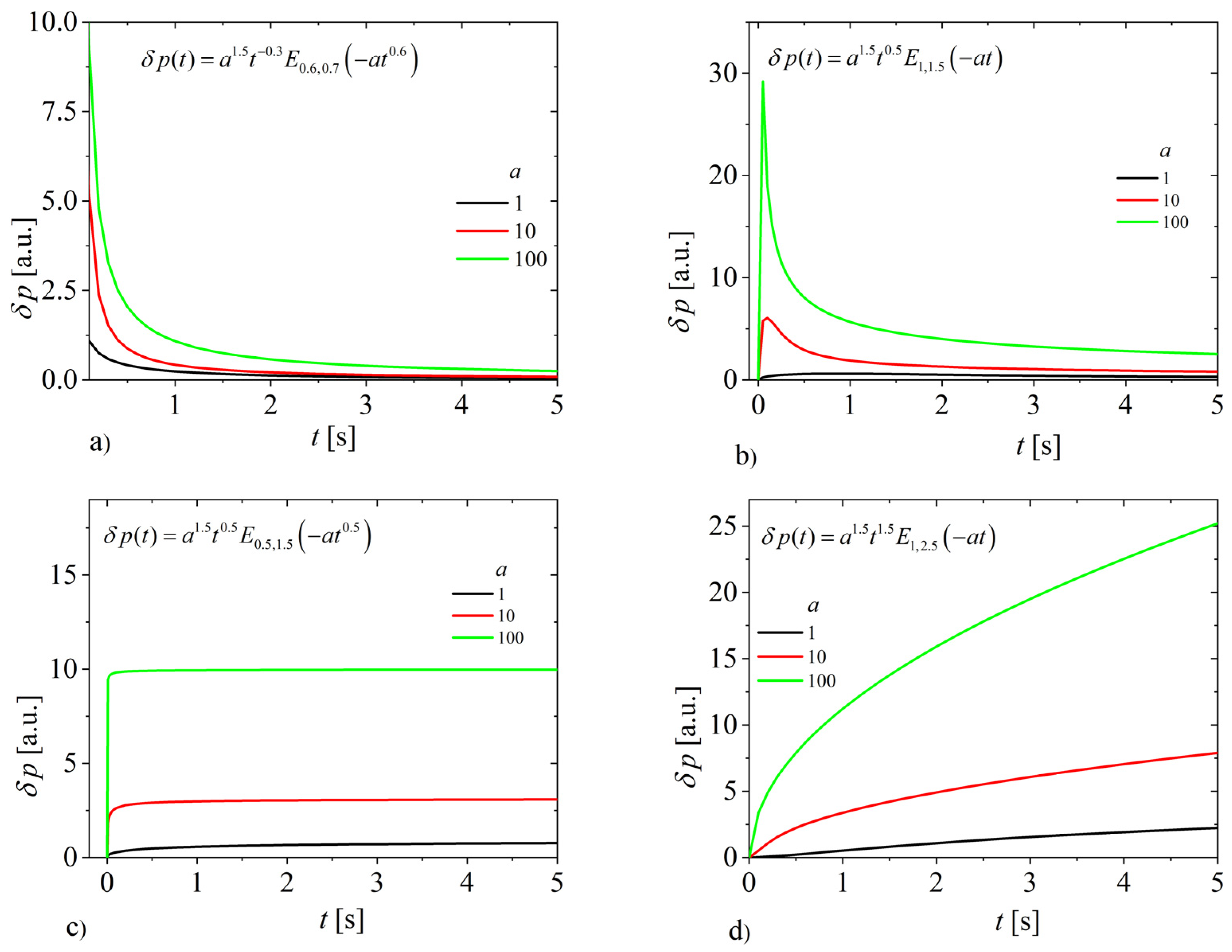
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosencwaig, A.; Gersho, A. Theory of the photoacoustic effect with solids. J. Appl. Phys. 1976, 47, 64–69. [Google Scholar] [CrossRef]
- Tam, A.C. Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 1986, 58, 381–431. [Google Scholar] [CrossRef]
- Park, H.K.; Grigoropoulos, C.P.; Tam, A.C. Optical measurements of thermal diffusivity of a material. Int. J. Thermophys. 1995, 16, 973–995. [Google Scholar] [CrossRef]
- Vargas, H.; Miranda, L.C.M. Photoacoustic and related photothermal techniques. Phys. Rep. 1988, 161, 43–101. [Google Scholar] [CrossRef]
- Bialkowski, S. Photothermal Spectroscopy Methods for Chemical Analysis; John Wiley: New York, NY, USA, 1996; ISBN 978-1-119-27907-5. [Google Scholar]
- Sarode, A.P.; Mahajan, O.H. Theoretical Aspects of Photoacoustic Effect with Solids: A Review. Int. J. Sci. Adv. Res. Technol. 2018, 4, 1237–1242. [Google Scholar] [CrossRef]
- Isaiev, M.; Mussabek, G.; Lishchuk, P.; Dubyk, K.; Zhylkybayeva, N.; Yar-Mukhamedova, G.; Lacroix, D.; Lysenko, V. Application of the Photoacoustic Approach in the Characterization of Nanostructured Materials. Nanomaterials 2022, 12, 708. [Google Scholar] [CrossRef] [PubMed]
- Mandelis, A.; Royce, B.S.H. Time-domain photoacoustic spectroscopy of solids. J. Appl. Phys. 1979, 50, 4330–4338. [Google Scholar] [CrossRef]
- Mandelis, A.; Hess, P. Semiconductors and Electronic Materials; SPIE Opt. Eng. Press: Belingham, WA, USA, 2000; ISBN 0819435066. [Google Scholar]
- Olenka, L.; Nogueiran, E.S.; Medina, A.N.; Baesso, M.L.; Bento, A.C.; Muniz, E.C.; Rubira, A.F. Photoacoustic study of PET films and fibers dyed in supercritical CO2 reactor. Rev. Sci. Instrum. 2003, 74, 328–330. [Google Scholar] [CrossRef]
- Pichardo-Molina, J.L.; Gutiérrez-Juárez, G.; Huerta-Franco, R.; Vargas-Luna, M.; Cholico, P.; Alvarado-Gil, J.J. Open Photoacoustic Cell Technique as a Tool for Thermal and Thermo-Mechanical Characterization of Teeth and Their Restorative Materials. Int. J. Thermophys. 2005, 26, 243–253. [Google Scholar] [CrossRef]
- Lishchuk, P.; Isaiev, M.; Osminkina, L.; Burbelo, R.; Nychyporuk, T.; Timoshenko, V. Photoacoustic characterization of nanowire arrays formed by metal-assisted chemical etching of crystalline silicon substrates with different doping level. Phys. E Low-Dimens. Syst. Nanostructures 2019, 107, 131–136. [Google Scholar] [CrossRef]
- Lishchuk, P.; Andrusenko, D.; Isaiev, M.; Lysenko, V.; Burbelo, R. Investigation of Thermal Transport Properties of Porous Silicon by Photoacoustic Technique. Int. J. Thermophys. 2015, 36, 2428–2433. [Google Scholar] [CrossRef]
- Dubyk, K.; Borisova, T.; Paliienko, K.; Krisanova, N.; Isaiev, M.; Alekseev, S.; Skryshevsky, V.; Lysenko, V.; Geloen, A. Bio-distribution of Carbon Nanoparticles Studied by Photoacoustic Measurements. Nanoscale Res. Lett. 2022, 17, 127. [Google Scholar] [CrossRef]
- Li, C.; Wang, L.V. Photoacoustic tomography and sensing in biomedicine. Phys. Med. Biol. 2009, 54, 59–97. [Google Scholar] [CrossRef]
- Somer, A.; Camilotti, F.; Costa, G.F.; Bonardi, C.; Novatski, A.; Andrade, A.V.C.; Kozlowski, V.A.; Cruz, G.K. The thermoelastic bending and thermal diffusion processes influence on photoacoustic signal generation using open photoacoustic cell technique. J. Appl. Phys. 2013, 114, 063503. [Google Scholar] [CrossRef]
- Bein, B.; Pelzl, J. Theory of signal generation in a photoacoustic cell. J. Phys. Colloq. 1983, 44, 6–27. Available online: https://hal.science/jpa-00223163 (accessed on 27 June 2024). [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959; ISBN 0198533683. [Google Scholar]
- Sobolev, S.L. Local non-equilibrium transport models. Phys. Uspekhi 1997, 167, 1095–1106. [Google Scholar] [CrossRef]
- Sobolev, S.L.; Dai, W. Heat Transport on Ultrashort Time and Space Scales in Nanosized Systems: Diffusive or Wave-like? Materials 2022, 15, 4287. [Google Scholar] [CrossRef] [PubMed]
- Sobolev, S.L. Hyperbolic heat conduction, effective temperature, and third law for nonequilibrium systems with heat flux. Phys. Rev. E 2018, 97, 022122. [Google Scholar] [CrossRef]
- Sobolev, S.L. Effective temperature in nonequilibrium state with heat flux using discrete variable model. Phys. Lett. A 2017, 381, 2893–2897. [Google Scholar] [CrossRef]
- Garden, J.L. Macroscopic non-equilibrium thermodynamics in dynamic calorimetry. Thermochim. Acta 2007, 452, 85–105. [Google Scholar] [CrossRef]
- Garden, J.L.; Richard, J.; Saruyama, Y. Entropy production in TMDSC. J. Therm. Anal. Calorim. 2008, 94, 585–590. Available online: https://hal.science/hal-00311748 (accessed on 27 June 2024). [CrossRef]
- Birge, N.O. Specific-heat spectroscopy of glycerol and propylene glycol near the glass transition. Phys. Rev. B 1986, 34, 1631–1642. [Google Scholar] [CrossRef] [PubMed]
- Birge, N.O.; Nagel, S.R. Specific-heat spectroscopy of the glass transition. Phys. Rev. Lett. 1985, 54, 2674–2677. [Google Scholar] [CrossRef]
- Novikov, I.A.; Kolpashchikov, V.L.; Shnip, A.I. Rheophysics and Heat Physics of Nonequilibrium Systems; Izd. Akad. Nauk Belorus. SSR: Minsk, Belarus, 1991. (In Russian) [Google Scholar]
- Novikov, I.A. Harmonic thermal waves in materials with thermal memory. J. Appl. Phys. 1997, 81, 1067–1072. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro-to-Microscale Heat Transfer: The Lagging Behavior; Taylor and Francis: Washington, DC, USA, 1996; pp. 323–332. Available online: https://lib.ugent.be/catalog/rug01:001873084 (accessed on 27 June 2024).
- Wunderlih, B. Thermal Analysis of Polymeric Materials; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005. [Google Scholar]
- Roetzel, W.; Putra, N.; Das, S.K. Experiment and analysis for non-Fourier conduction in materials with non-homogeneous inner structure. Int. J. Therm. Sci. 2003, 42, 541–552. [Google Scholar] [CrossRef]
- Dixon, P.K. Specific-heat spectroscopy and dielectric susceptibility measurements of salol at the glass transition. Phys. Rev. B 1990, 42, 8179–8186. [Google Scholar] [CrossRef] [PubMed]
- Scherrenberg, R.; Mathot, V.; Steeman, P. The Applicability of TMDSC to Polymeric Systems General theoretical description based on the full heat capacity formulation. J. Therm. Anal. Calorim. 1998, 54, 477–499. [Google Scholar] [CrossRef]
- Saiter, A.; Couderc, H.; Grenet, J. Characterisation of structural relaxation phenomena in polymeric materials from thermal analysis investigations. J. Therm. Anal. Calorim. 2007, 88, 483–488. [Google Scholar] [CrossRef]
- Saruyama, Y. AC calorimetry at the first order phase transition point. J. Therm. Anal. 1992, 38, 1827–1833. [Google Scholar] [CrossRef]
- Liu, K.C.; Wang, Y.; Chen, Y. Investigation of the bioheat transfer with dual phase lag effect. Int. J. Therm. Sci. 2012, 58, 29–35. [Google Scholar] [CrossRef]
- Mitra, K.; Kumar, S.; Vedavarez, A.; Moallemi, M.K. Experimental Evidence of Hyperbolic Heat Conduction in Processed Meat. J. Heat Transf. 1995, 117, 568–573. [Google Scholar] [CrossRef]
- Djordjevic, K.L.; Milicevic, D.; Galovic, S.P.; Suljovrujic, E.; Jacimovski, S.K.; Furundzic, D.; Popovic, M. Photothermal Response of Polymeric Materials Including Complex Heat Capacity. Int. J. Thermophys. 2022, 43, 68. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended irreversible thermodynamics. Rep. Prog. Phys. 1988, 51, 1105–1179. [Google Scholar] [CrossRef]
- Davies, R.O. The Macroscopic Theory of Irreversibility. Rep. Prog. Phys. 1956, 19, 326–367. [Google Scholar] [CrossRef]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland Publishing Company: Amsterdam, The Netherands, 1962; ISBN 0486153509. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; John Wiley and Sons: New York, NY, USA, 1968; ISBN 0470699280. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Korabel, N.; Klages, R.; Chechkin, A.V.; Sokolov, I.M.; Gonchar, V.Y. Fractal properties of anomalous diffusion in intermittent maps. Phys. Rev. E 2007, 75, 036213. [Google Scholar] [CrossRef] [PubMed]
- Bouchaud, J.-P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, W.; Metzler, R. Anomalous diffusion, non-Gaussianity, and nonergodicity for subordinated fractional Brownian motion with a drift. arXiv 2023, arXiv:2302.04872v1. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Rajyaguru, A.; Berkowitz, B. Modelling anomalous diffusion in semi-infinite disordered systems and porous media. New J. Phys. 2022, 24, 123004. [Google Scholar] [CrossRef]
- Sposini, V.; Krapf, D.; Marinari, E.; Sunyer, R.; Ritort, F.; Taheri, F.; Selhuber-Unkel, C.; Benelli, R.; Weiss, M.; Metzler, R.; et al. Towards a robust criterion of anomalous diffusion. Commun. Phys. 2022, 5, 305. [Google Scholar] [CrossRef]
- Comptey, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A Math. Gen. 1997, 30, 7277–7289. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-662-43930-2. (eBook). [Google Scholar] [CrossRef]
- Kiryakova, V.S. Generalized Fractional Calculus and Applications; Longman Scientific and Technical: Harlow, UK, 1994. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Tateishi, A.A.; Lenzi, E.K.; Da Silva, L.R.; Ribeiro, H.V.; Picoli, S.; Mendes, R.S. Different diffusive regimes, generalized Langevin and diffusion equations. Phys. Rev. E 2012, 85, 011147. [Google Scholar] [CrossRef] [PubMed]
- Dzielinski, A.; Sierociuk, D.; Sarwas, G. Some applications of fractional order calculus. Bull. Pol. Acad. Sci. Tech. Sci. 2010, 58, 583–592. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Somer, A.; Zola, R.S.; Da Silva, R.S.; Lenzi, M.K.A. Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids 2003, 8, 34. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. Admissible frequency domain response functions of dielectrics. Math. Method Appl. Sci. 2014, 38, 930–936. [Google Scholar] [CrossRef]
- Saxena, R.K.; Saxena, R.; Kalla, S.L. Solution of space time fractional schroedinger equation occurring in quantum mechanics. Fract. Calc. Appl. 2010, 13, 190–201. Available online: http://hdl.handle.net/10525/1648 (accessed on 27 June 2024).
- Del Castillo Negrete, D.; Carreras, B.A.; Lynch, V.E. Fractional diffusion in plasma turbulence. Phys. Plasmas 2004, 11, 3854–3864. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: New York, NY, USA, 2006. [Google Scholar]
- Djordjević, K.L.; Stoisavljević, Z.Z.; Dragaš, M.A.; Stanimirović, I.; Stanimirović, Z.; Suljovrujic, E.; Galović, S.P. Application of neural network to study of frequency range effect to photoacoustic measurement of thermoelastic properties of thin aluminum samples. Measurement 2024, 236, 115043. [Google Scholar] [CrossRef]
- Miletic, V.V.; Popovic, M.N.; Galovic, S.P.; Markushev, D.D.; Nesic, M.V. Photothermally induced temperature variations in a low-absorption sample via backside absorption. J. Appl. Phys. 2023, 133, 075101. [Google Scholar] [CrossRef]
- Galovic, S.P.; Stanimirovic, Z.; Stanimirovic, I.; Djordjevic, K.L.; Milicevic, D.; Suljovrujic, E. Time-resolved photoacoustic response of thin solids measured using minimal volume cell. Int. Commun. Heat Mass Transf. 2024, 155, 107574. [Google Scholar] [CrossRef]
- Sablikov, V.A.; Sandomirskii, V.B. The Photoacoustic effect in semiconductors. Phys. Stat. Solidi (a) 1983, 120, 471–480. [Google Scholar] [CrossRef]
- Galović, S.; Šoškić, Z.; Popović, M.; Čevizović, D.; Stojanović, Z. Theory of photoacoustic effect in media with thermal memory. J. Appl. Phys. 2014, 116, 024901. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Sorokin, V.G.; Zhurov, A.I. Delay Ordinary and Partial Differential Equation; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar] [CrossRef]
- Galović, S.; Kostoski, D. Photothermal wave propagation in media with thermal memory. J. Appl. Phys. 2003, 93, 3063–3070. [Google Scholar] [CrossRef]
- Somer, A.; Galovic, S.; Lenzi, E.K.; Novatski, A.; Djordjevic, K. Temperature profile and thermal piston component of photoacoustic response calculated by the fractional dual-phase-lag heat conduction theory. Int. J. Heat Mass Transf. 2023, 203, 123801. [Google Scholar] [CrossRef]
- Galovic, S.P.; Djordjevic, K.L.; Nesic, M.V.; Popovic, M.N.; Markushev, D.D.; Markushev, D.K.; Todorovic, D.M. Time-domain minimum-volume cell photoacoustic of thin semiconductor layer. I. Theory. J. Appl. Phys. 2023, 133, 245701. [Google Scholar] [CrossRef]
- Galovic, S.; Soskic, Z.; Popovic, M. Analysis of photothermal response of thin solid films by analogy with passive linear electric networks. Therm. Sci. 2009, 13, 129–142. [Google Scholar] [CrossRef]
- Roberts, G.E.; Kaufman, H. Table of Laplace Transform; W.B. Saunders Company: Philadelphia, PA, USA; London, UK, 1966. [Google Scholar]
- Saenko, V.V. Integral Representation of the Mittag-Leffler Function. Russ. Math. 2022, 66, 43–58. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler Functions and Their Applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef]
- Baumann, G. Sinc Based Inverse Laplace Transforms, Mittag-Leffler Functions and Their Approximation for Fractional Calculus. Fractal Fract. 2021, 5, 43. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Petras, I.; Vinagre, B.M. A list of Laplace and Inverse Laplace Transforms Related to Fractional Order Calculus. 2007. Available online: http://www.tuke.sk/petras/foc_laplace.pdf (accessed on 27 June 2024).
- Hilfer, R. Fractional Diffusion Based on Riemann-Liouville Fractional Derivatives. J. Phys. Chem. B 2000, 104, 3914–3917. [Google Scholar] [CrossRef]
- Abdon, A.; Gómez-Aguilar, J.F. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 166. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of the fractional time-derivative operators in anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef]


| Laplace Transform G(s) | Inverse Laplace Transform L−1 [G(s)] |
|---|---|
| Laplace Transform F(s) | Inverse Laplace Transform L−1 [F(s)] |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galovic, S.; Djordjevic, A.I.; Kovacevic, B.Z.; Djordjevic, K.L.; Chevizovich, D. Influence of Local Thermodynamic Non-Equilibrium to Photothermally Induced Acoustic Response of Complex Systems. Fractal Fract. 2024, 8, 399. https://doi.org/10.3390/fractalfract8070399
Galovic S, Djordjevic AI, Kovacevic BZ, Djordjevic KL, Chevizovich D. Influence of Local Thermodynamic Non-Equilibrium to Photothermally Induced Acoustic Response of Complex Systems. Fractal and Fractional. 2024; 8(7):399. https://doi.org/10.3390/fractalfract8070399
Chicago/Turabian StyleGalovic, Slobodanka, Aleksa I. Djordjevic, Bojan Z. Kovacevic, Katarina Lj. Djordjevic, and Dalibor Chevizovich. 2024. "Influence of Local Thermodynamic Non-Equilibrium to Photothermally Induced Acoustic Response of Complex Systems" Fractal and Fractional 8, no. 7: 399. https://doi.org/10.3390/fractalfract8070399
APA StyleGalovic, S., Djordjevic, A. I., Kovacevic, B. Z., Djordjevic, K. L., & Chevizovich, D. (2024). Influence of Local Thermodynamic Non-Equilibrium to Photothermally Induced Acoustic Response of Complex Systems. Fractal and Fractional, 8(7), 399. https://doi.org/10.3390/fractalfract8070399









