A New Fractional Boundary Element Model for Anomalous Thermal Stress Effects on Cement-Based Materials
Abstract
1. Introduction
2. Formulation of the Problem
3. BEM for Anomalous Fractional Heat Diffusion Equation
4. BEM for Displacement of Cement-Based Materials
5. Thermal Stress Intensity Factor of Cement-Based Materials
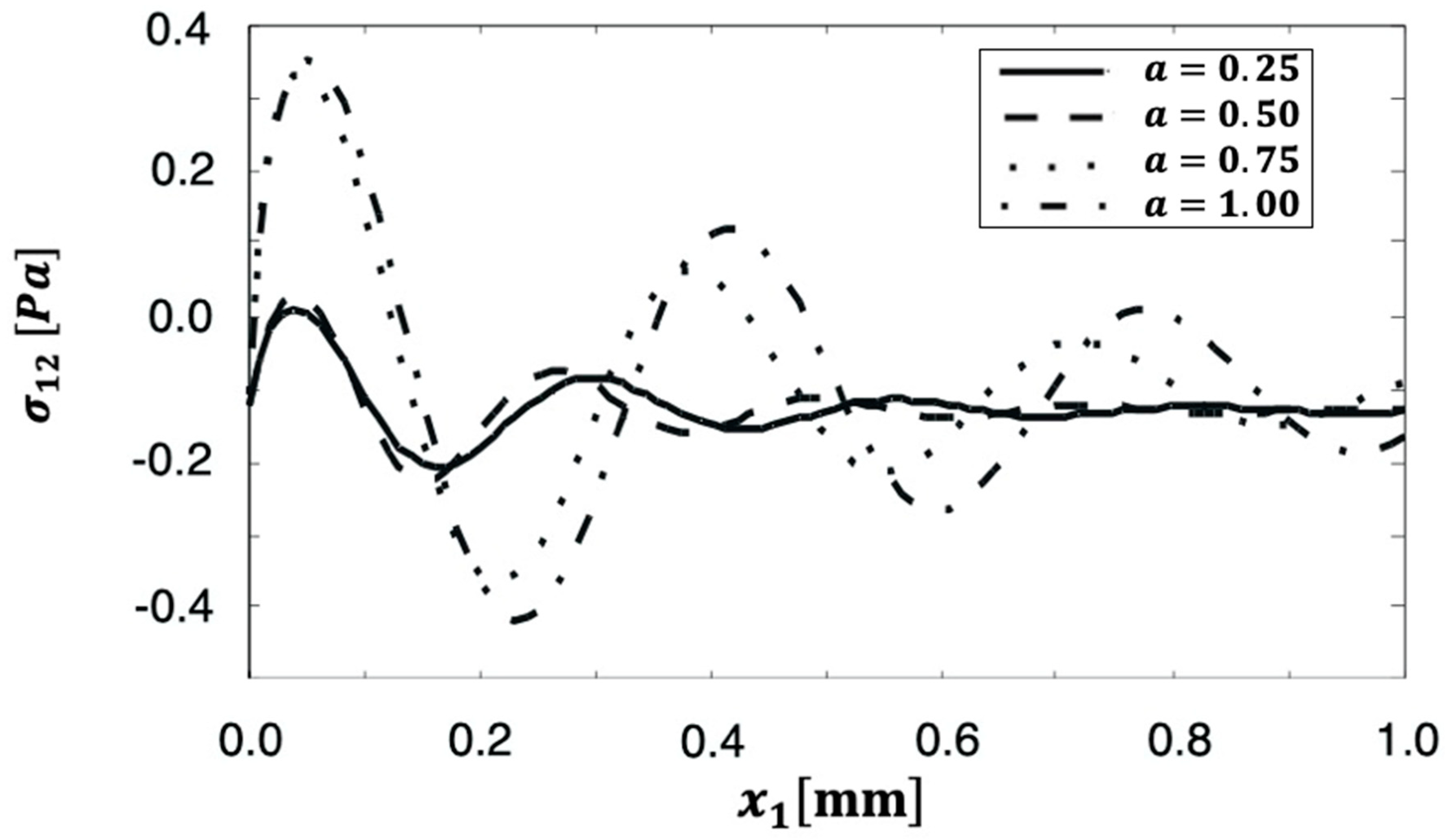
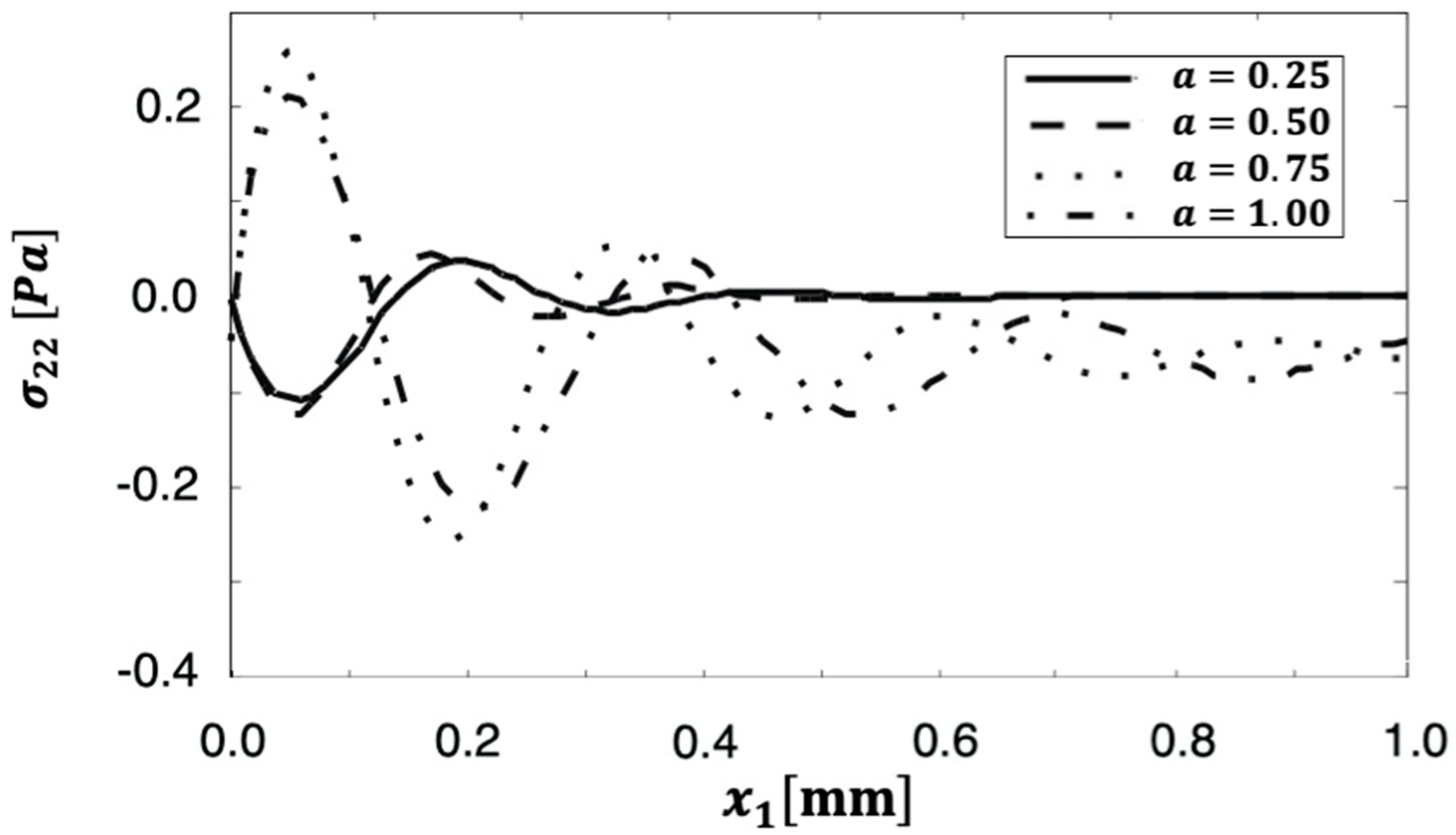
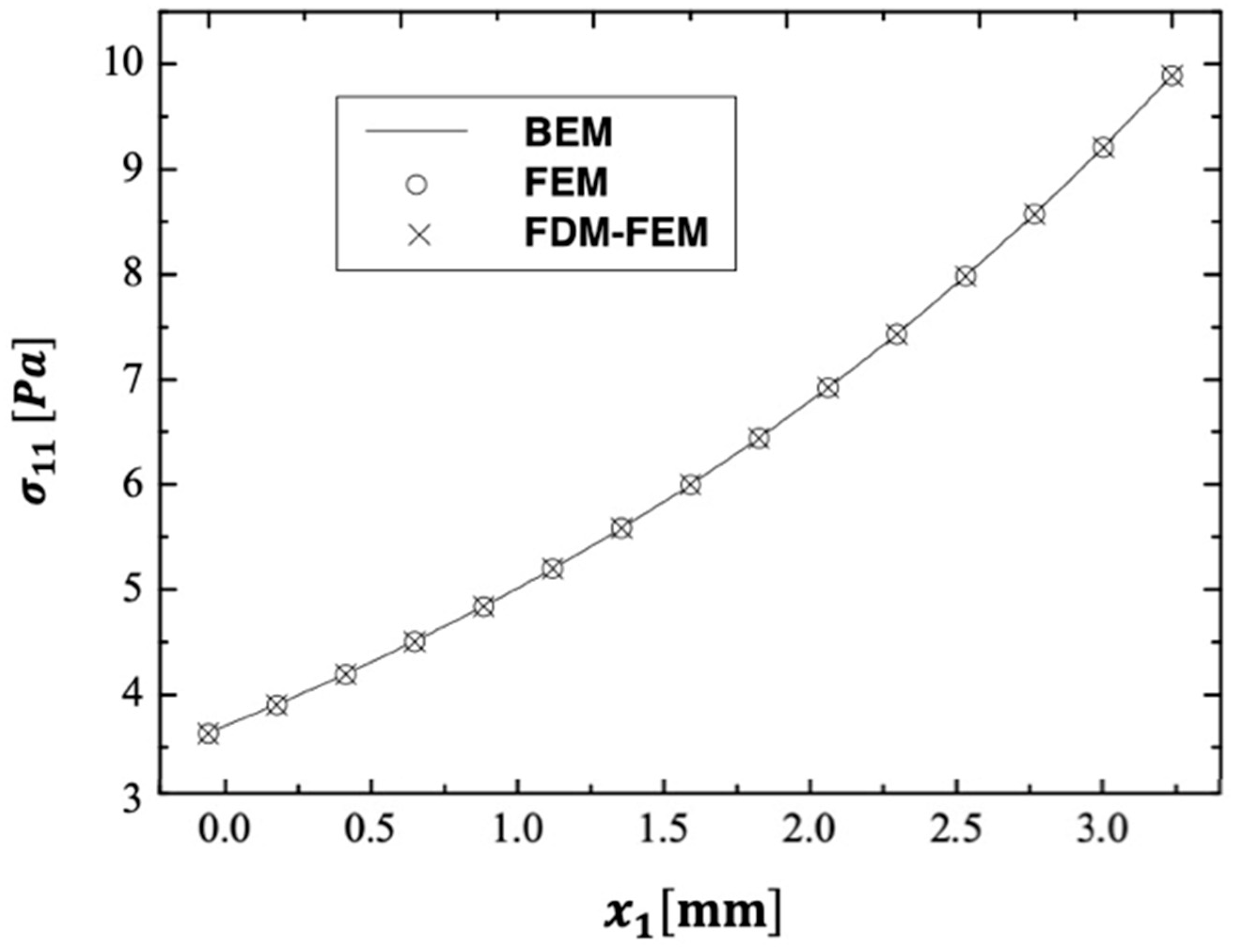
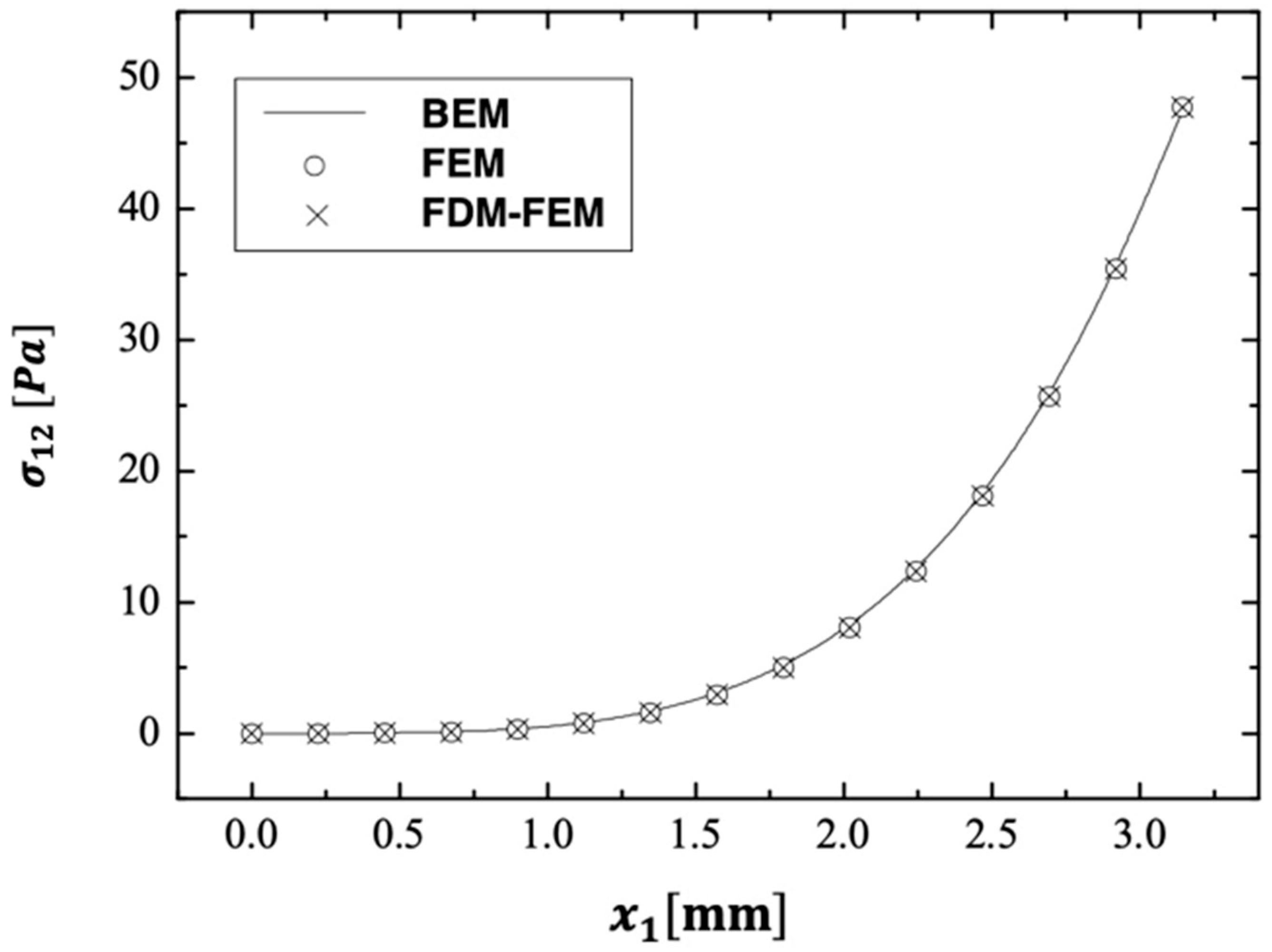
6. Numerical Results and Discussion
7. Conclusions
- A novel fractional BEM has been developed to address anomalous thermal stress issues in cement-based materials.
- The suggested formulation determines the unknown values of temperature and heat flux at time using their current values and all preceding temperature data.
- The proposed formulation can overcome the non-locality of the fractional operators.
- The proposed fractional BEM formulation produces precise and dependable findings; even a modest value of the fractional time derivative, , resulted in good agreement with previously reported results. This led us to believe that the fractional BEM formulation can cover the entire range
- The equality sign in is permitted because the conventional thermal stress problem is a specific case of an anomalous thermal stress problem.
- The proposed Caputo derivative BEM shows that the boundary element technique is a valuable tool for solving fractional and fracture problems in cement-based materials.
- BEM solves problems more efficiently and accurately than domain techniques, minimizing the processing costs.
- BEM emerges as the most appropriate solution for the situation under consideration.
- The versatility of cement-based materials has led to their extensive use throughout human society. Hydraulic binders were adjusted to meet functional requirements in various settings. To safeguard the environment from contamination, cement-based compounds have been used in several sectors, including water and soil. To improve these materials’ functionality in a variety of applications,
- Consider investigating the effects of incorporating industrial waste into cements, such as ordinary Portland cement (OPC), to increase productivity.
- Create models, such as the proposed model, that forecast materials’ long-term behavior.
- Cement-based products have been widely employed in numerous applications, such as bridges, walkways, slabs, pavements, floors, and walls and are among the structural and prefabricated components constructed with cement-based materials. Concrete is also utilized to construct storage tanks, swimming pools, subterranean parking lots, and other structures.
- Future work on the numerical model will focus on anomalous moisture transport, thermal stress sensitivity assessment, and optimization calculations of elastic and elastic-plastic formulations in cement-based materials, all while lowering operation and maintenance costs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Fractional-order parameter | & | Diffusion coefficients | |
| Time interval | Height of three-point beam | ||
| Stress–temperature coefficients | Dilatation | ||
| Kronecker delta | |||
| Strain tensor | Crack length | ||
| Fluid volume variation | Basis functions of order o | ||
| Tractions, | & | Unit outward normal components | |
| Pore pressure, | |||
| Heat flux | |||
| Bulk density | Fluid specific flux | ||
| Fluid density | Solid–fluid coupling parameter | ||
| Solid density | Domain | ||
| Total stress tensor, | Splitting tensile strength of concrete | ||
| Break point stress | Temperature functions, | ||
| Cohesive stress | Crack opening displacement | ||
| Time, | Stress-free crack width | ||
| Porosity | Solid displacements, | ||
| Break point displacement | |||
| & | Weighting functions | ||
| Biot’s effective stress coefficient | |||
| Constant elastic moduli, | |||
| Boundary | Fluid–solid displacements | ||
| Source term |
References
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley-Interscience: Hoboken, NJ, USA, 1993. [Google Scholar]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Lectures Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2011; Volume 84. [Google Scholar]
- Küntz, M.; Lavallée, P. Experimental evidence and theoretical analysis of anomalous diffusion during water infiltration in porous building materials. J. Phys. D Appl. Phys. 2001, 34, 2547–2554. [Google Scholar] [CrossRef]
- Li, Q.; Xu, S.; Zeng, Q. A fractional kinetic model for drying of cement-based porous materials. Dry. Technol. 2015, 34, 1231–1242. [Google Scholar] [CrossRef]
- Alderete, N.; Zaccardi, Y.V.; De Belie, N. Physical evidence of swelling as the cause of anomalous capillary water uptake by cementitious materials. Cem. Concr. Res. 2019, 120, 256–266. [Google Scholar] [CrossRef]
- Srimook, P.; Maruyama, I. Anomalous moisture transport in dried cementitious material: A numerical analysis. Constr. Build. Mater. 2024, 449, 138365. [Google Scholar] [CrossRef]
- Zhang, L.; Ren, Q.; Li, Z.; Zhang, G. Predicting the Drying of Concrete by an Anomalous Diffusion Model. J. Mater. Civ. Eng. 2019, 31, 04019010. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Zhang, X.; Korošak, D. Anomalous diffusion modeling by fractal and fractional derivatives. Comput. Math. Appl. 2010, 59, 1754–1758. [Google Scholar] [CrossRef]
- A. Lockington, D.; Parlange, J.-Y. Anomalous water absorption in porous materials. J. Phys. D Appl. Phys. 2003, 36, 760–767. [Google Scholar] [CrossRef]
- Taylor, S.C.; Hoff, W.D.; Wilson, M.A.; Green, K.M. Anomalous water transport properties of Portland and blended cement-based materials. J. Mater. Sci. Lett. 1999, 18, 1925–1927. [Google Scholar] [CrossRef]
- Saeidpour, M.; Wadsö, L. Evidence for anomalous water vapor sorption kinetics in cement based materials. Cem. Concr. Res. 2015, 70, 60–66. [Google Scholar] [CrossRef]
- Zhang, Z.; Angst, U. Modelling Anomalous Moisture Transport in Cement-Based Materials by the Dual-Permeability Concept. Int. J. Mol. Sci. 2020, 21, 837. [Google Scholar] [CrossRef]
- Coussy, O. Mechanics of Porous Continua; John Wiley and Sons Ltd.: Chichester, UK, 1995. [Google Scholar]
- Mainguy, M.; Coussy, O.; Baroghel-Bouny, V. Role of Air Pressure in Drying of Weakly Permeable Materials. J. Eng. Mech. 2001, 127, 582–592. [Google Scholar] [CrossRef]
- Philip, J.R.; De Vries, D.A. Moisture movement in porous materials under temperature gradients. Trans. Am. Geophys. Union 1957, 38, 222–232. [Google Scholar] [CrossRef]
- Zhang, Z.; Thiery, M.; Baroghel-Bouny, V. An equation of drying kinetics for cementitious materials. Dry. Technol. 2017, 36, 1446–1459. [Google Scholar] [CrossRef]
- Lockington, D.; Parlange, J.-Y.; Dux, P. Sorptivity and the estimation of water penetration into unsaturated concrete. Mater. Struct. 1999, 32, 342–347. [Google Scholar] [CrossRef]
- Mindess, S.; Young, J.F. Concrete; Prentice-Hall: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Zeng, Q.; Xu, S. A two-parameter stretched exponential function for dynamic water vapor sorption of cement-based porous materials. Mater. Struct. 2017, 50, 128. [Google Scholar] [CrossRef]
- Scherer, G.W. Drying, Shrinkage, and Cracking of Cementitious Materials. Transp. Porous Media 2015, 110, 311–331. [Google Scholar] [CrossRef]
- Zhou, C.; Ren, F.; Wang, Z.; Chen, W.; Wang, W. Why Permeability to Water Is Anomalously Lower than That to Many Other Fluids for Cement-Based Material? Cem. Concr. Res. 2017, 100, 373–384. [Google Scholar] [CrossRef]
- Wang, L.; Hoyos, L.R.; Wang, J.; Voyiadjis, G.; Abadie, C. Anisotropic Properties of Asphalt Concrete: Characterization and Implications for Pavement Design and Analysis. J. Mater. Civ. Eng. 2005, 17, 535–543. [Google Scholar] [CrossRef]
- Maruyama, I.; Rymeš, J.; Vandamme, M.; Coasne, B. Cavitation of water in hardened cement paste under short-term desorption measurements. Mater. Struct. 2018, 51, 159. [Google Scholar] [CrossRef]
- Zhang, Z.; Thiery, M.; Baroghel-Bouny, V. Investigation of moisture transport properties of cementitious materials. Cem. Concr. Res. 2016, 89, 257–268. [Google Scholar] [CrossRef]
- Xi, Y.; Bažant, Z.P.; Molina, L.; Jennings, H.M. Moisture diffusion in cementitious materials Moisture capacity and diffusivity. Adv. Cem. Based Mater. 1994, 1, 258–266. [Google Scholar] [CrossRef]
- Baroghel-Bouny, V. Water vapour sorption experiments on hardened cementitious materials. Part II: Essential tool for assessment of transport properties and for durability prediction. Cem. Concr. Res. 2007, 37, 438–454. [Google Scholar] [CrossRef]
- Savage, B.M.; Janssen, D.J. Soil Physics Principles Validated for Use in Predicting Unsaturated Moisture Movement in Portland Cement Concrete. ACI Mater. J. 1997, 94, 63–70. [Google Scholar]
- Monlouis-Bonnaire, J.; Verdier, J.; Perrin, B. Prediction of the relative permeability to gas flow of cement-based materials. Cem. Concr. Res. 2004, 34, 737–744. [Google Scholar] [CrossRef]
- Zhou, C. Predicting water permeability and relative gas permeability of unsaturated cement-based material from hydraulic diffusivity. Cem. Concr. Res. 2014, 58, 143–151. [Google Scholar] [CrossRef]
- Carlier, J.-P.; Burlion, N. Experimental and Numerical Assessment of the Hydrodynamical Properties of Cementitious Materials. Transp. Porous Media 2010, 86, 87–102. [Google Scholar] [CrossRef]
- Zhang, Z.; Thiery, M.; Baroghel-Bouny, V. Numerical modelling of moisture transfers with hysteresis within cementitious materials: Verification and investigation of the effects of repeated wetting–drying boundary conditions. Cem. Concr. Res. 2015, 68, 10–23. [Google Scholar] [CrossRef]
- Zhang, Z.; Thiéry, M.; Baroghel-Bouny, V. A review and statistical study of existing hysteresis models for cementitious materials. Cem. Concr. Res. 2014, 57, 44–60. [Google Scholar] [CrossRef]
- Carlier, J.-P.; Rougelot, T.; Burlion, N. Performance evaluation of models describing sorption isotherm in cementitious materials between saturation and oven dryness. Constr. Build. Mater. 2012, 37, 58–66. [Google Scholar] [CrossRef]
- Jonasson, J.E.; Growth, P.; Hedlund, H. Modelling of temperature and moisture field in concrete to study early ages movements as a basis for stress analysis. In Thermal Cracking in Concrete at Early Ages, Proceedings RILEM Symposium, Munich; CRC Press: Boca Raton, FL, USA, 1994; pp. 45–52. [Google Scholar]
- Honorio, T.; Bary, B.; Benboudjema, F. Thermal properties of cement-based materials: Multiscale estimations at early-age. Cement and Concrete Composites 2018, 87, 205–219. [Google Scholar] [CrossRef]
- Lee, S.L.; Tam, C.T.; Swaddiwudhipong, S.; Mani, A.C. Temperature distribution and thermal stresses in thick concrete pours. In Proceedings of the 3rd International Conference on Structural Failure, Singapore, 23–26 July 1991; pp. 17–33. [Google Scholar]
- Ceretani, A.N. A Note on Models for Anomalous Phase-Change Processes. Fract. Calc. Appl. Anal. 2020, 23, 167–182. [Google Scholar] [CrossRef]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. A Ritz-based finite element method for a fractional-order boundary value problem of nonlocal elasticity. Int. J. Solids Struct. 2020, 202, 398–417. [Google Scholar] [CrossRef]
- Fahmy, M.A. BEM Modeling for Stress Sensitivity of Nonlocal Thermo-Elasto-Plastic Damage Problems. Computation 2024, 12, 87. [Google Scholar] [CrossRef]
- Brebbia, C.A.; Telles, J.C.F.; Wrobel, L.C.; Mukherjee, S. Boundary Element Techniques. Theory and Applications in Engineering. J. Appl. Mech. 1985, 52, 241. [Google Scholar] [CrossRef]
- Katsikadelis, J.T. The BEM for numerical solution of partial fractional differential equations. Comput. Math. Appl. 2011, 62, 891–901. [Google Scholar] [CrossRef]
- Dehghan, M.; Safarpoor, M. The dual reciprocity boundary elements method for the linear and nonlinear two-dimensional time-fractional partial differential equations. Math. Methods Appl. Sci. 2016, 39, 3979–3995. [Google Scholar] [CrossRef]
- Carrer, J.A.M.; Seaid, M.; Trevelyan, J.; Solheid, B.d.S. The boundary element method applied to the solution of the anomalous diffusion problem. Eng. Anal. Bound. Elements 2019, 109, 129–142. [Google Scholar] [CrossRef]
- Fahmy, M.A. Fractional Temperature-Dependent BEM for Laser Ultrasonic Thermoelastic Propagation Problems of Smart Nanomaterials. Fractal Fract. 2023, 7, 536. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Alsulami, M.O.; Abouelregal, A.E. Three-Temperature Boundary Element Modeling of Ultrasound Wave Propagation in Anisotropic Viscoelastic Porous Media. Axioms 2023, 12, 473. [Google Scholar] [CrossRef]
- Fahmy, M.A. Boundary Element Algorithm for Modeling and Simulation of Dual-Phase Lag Bioheat Transfer and Biomechanics of Anisotropic Soft Tissues. Int. J. Appl. Mech. 2018, 10, 1850108. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Alsulami, M.O.; Abouelregal, A.E. Sensitivity analysis and design optimization of 3T rotating thermoelastic structures using IGBEM. AIMS Math. 2022, 7, 19902–19921. [Google Scholar] [CrossRef]
- Fahmy, M.A. Boundary Element Algorithm for Nonlinear Modeling and Simulation of Three-Temperature Anisotropic Generalized Micropolar Piezothermoelasticity with Memory-Dependent Derivative. Int. J. Appl. Mech. 2020, 12, 2050027. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Alzubaidi, M.H.M. A boundary element analysis of quasi-potential inviscid incompressible flow in multiply connected airfoil wing. J. Umm Al-Qura Univ. Eng. Arch. 2024, 15, 398–402. [Google Scholar] [CrossRef]
- Fahmy, M.A. A time-stepping DRBEM for nonlinear fractional sub-diffusion bio-heat ultrasonic wave propagation problems during electromagnetic radiation. J. Umm Al-Qura Univ. Appl. Sci. 2024. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Toujani, M. Fractional Boundary Element Solution for Nonlinear Nonlocal Thermoelastic Problems of Anisotropic Fibrous Polymer Nanomaterials. Computation 2024, 12, 117. [Google Scholar] [CrossRef]
- Fahmy, M.A. Design optimization for a simulation of rotating anisotropic viscoelastic porous structures using time-domain OQBEM. Math. Comput. Simul. 2019, 166, 193–205. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Shaw, S.; Mondal, S.; Abouelregal, A.E.; Lotfy, K.; Kudinov, I.A.; Soliman, A.H. Boundary Element Modeling for Simulation and Optimization of Three-Temperature Anisotropic Micropolar Magneto-thermoviscoelastic Problems in Porous Smart Structures Using NURBS and Genetic Algorithm. Int. J. Thermophys. 2021, 42, 29. [Google Scholar] [CrossRef]
- Brebbia, C.A.; Dominguez, J. Boundary Elements: An Introductory Course; WIT Press & Computational Mechanics Publication: Boston, MA, USA; Southampton, UK, 1998. [Google Scholar]
- Zienkiewicz, O.C.; Morgan, K. Finite Elements & Approximation; John Wiley & Sons, Inc.: New York, NY, USA, 1983. [Google Scholar]
- Carrer, J.A.M.; Cunha, C.L.N.; Mansur, W.J. The boundary element method applied to the solution of two-dimensional diffusion–advection problems for non-isotropic materials. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4533–4545. [Google Scholar] [CrossRef]
- Berger, J.R.; Karageorghis, A. The Method of Fundamental Solutions for Heat Conduction in Layered Materials. Int. J. Numer. Methods Eng. 1999, 45, 1681–1694. [Google Scholar] [CrossRef]
- Carrer, J.; Solheid, B.; Trevelyan, J.; Seaid, M. A boundary element method formulation based on the Caputo derivative for the solution of the anomalous diffusion problem. Eng. Anal. Bound. Elements 2021, 122, 132–144. [Google Scholar] [CrossRef]
- Huang, F.-Y.; Liang, K.-Z. Boundary element method for micropolar thermoelasticity. Eng. Anal. Bound. Elements 1996, 17, 19–26. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of Micropolar Elasticity. In Fracture; Liebowitz, H., Ed.; Academic Press: New York, NY, USA, 1968; pp. 621–729. [Google Scholar]
- Dragos, L. Fundamental solutions in micropolar elasticity. Int. J. Eng. Sci. 1984, 22, 265–275. [Google Scholar] [CrossRef]
- Salama, F.M.; Hamid, N.N.A.; Ali, N.H.M.; Ali, U. An efficient modified hybrid explicit group iterative method for the time-fractional diffusion equation in two space dimensions. AIMS Math. 2022, 7, 2370–2392. [Google Scholar] [CrossRef]
- Dong, W.; Wu, Z.; Zhou, X.; Wang, C. A comparative study on two stress intensity factor-based criteria for prediction of mode-I crack propagation in concrete. Eng. Fract. Mech. 2016, 158, 39–58. [Google Scholar] [CrossRef]
- Petersson, P.E. Crack Growth and Development of Fracture Zones in Plain Concrete and Similar Materials; Division of Building Materials, LTH, Lund University: Lund, Sweden, 1981; Volume 1006. [Google Scholar]
- Jenq, Y.; Shah, S. A Fracture toughness criterion for concrete. Eng. Fract. Mech. 1985, 21, 1055–1069. [Google Scholar] [CrossRef]
- Cifuentes, H.; Montero-Chacón, F.; Galán, J.; Cabezas, J.; la Concha, A.M.-D. A Finite Element-Based Methodology for the Thermo-mechanical Analysis of Early Age Behavior in Concrete Structures. Int. J. Concr. Struct. Mater. 2019, 13, 41. [Google Scholar] [CrossRef]
- RILEM TCS. Determination of the fracture energy of mortar and concrete by means of three-point bend tests on notched beams. Mater. Struct. 1985, 18, 287–290. [Google Scholar] [CrossRef]
- Do, T.A. A Combination of Finite Difference and Finite Element Methods for Temperature and Stress Predictions of Early-Age Concrete Members. In Finite Element Methods and Their Applications; Baccouch, M., Ed.; IntechOpen: London, UK. [CrossRef]
- Lin, Y.; Chen, H.-L. Thermal analysis, and adiabatic calorimetry for early-age concrete members. J. Therm. Anal. Calorim. 2016, 124, 227–239. [Google Scholar] [CrossRef]
- Darvishi, M.; Hessari, P. A modified symmetric successive overrelaxation method for augmented systems. Comput. Math. Appl. 2011, 61, 3128–3135. [Google Scholar] [CrossRef]
- Hadjidirnos, A.; Psimarni, A.; Saridakis, Y.G.; Yeyios, A.K. The Block Modified Accelerated Overrelaxation (MAOR) Method for Generalized Consistently Ordered Matrices; Department of Computer Science Technical Reports; Paper 23; Purdue University: West Lafayette, IN, USA, 1990; Available online: https://docs.lib.purdue.edu/cstech/23 (accessed on 18 December 2024).


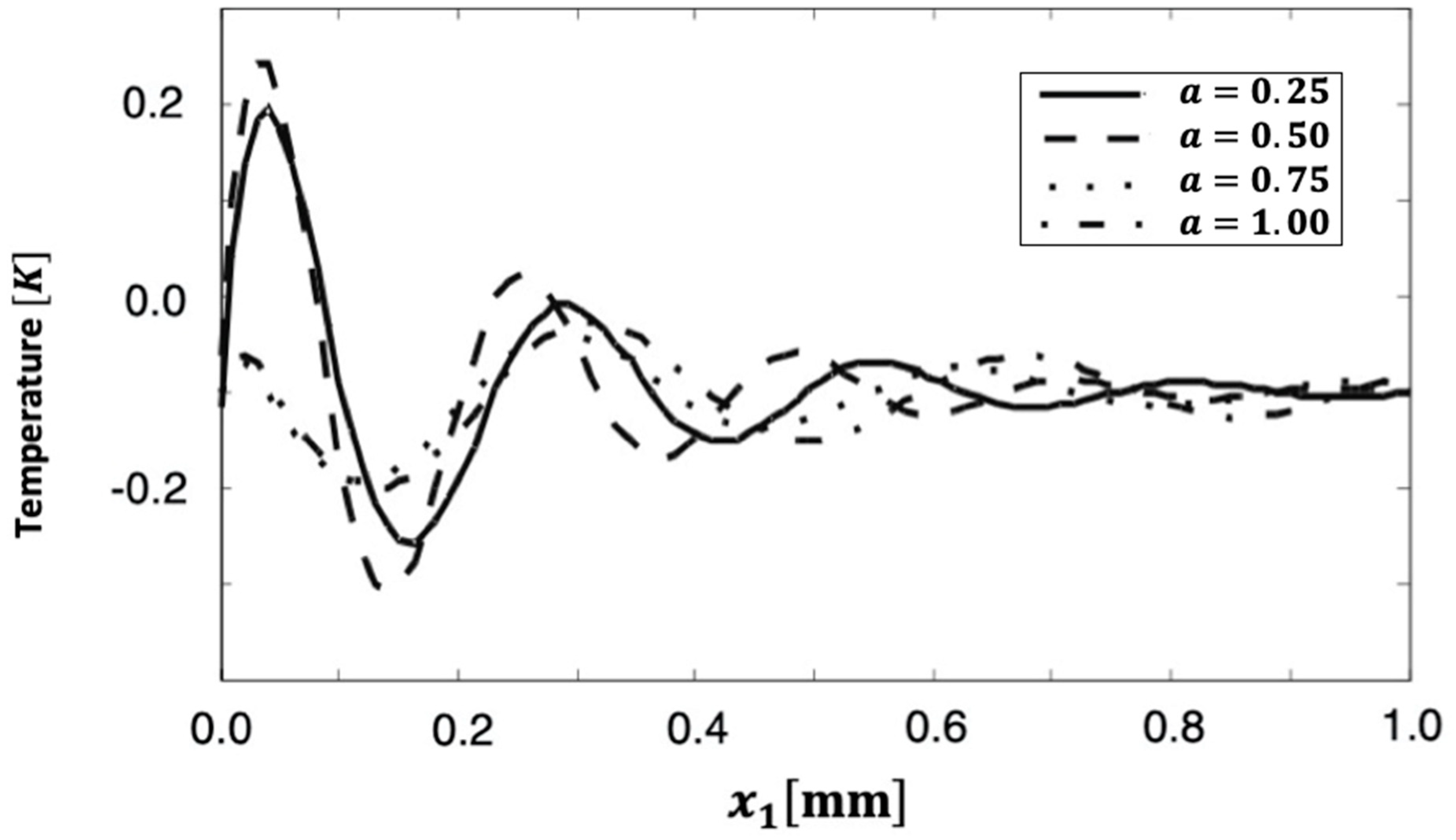
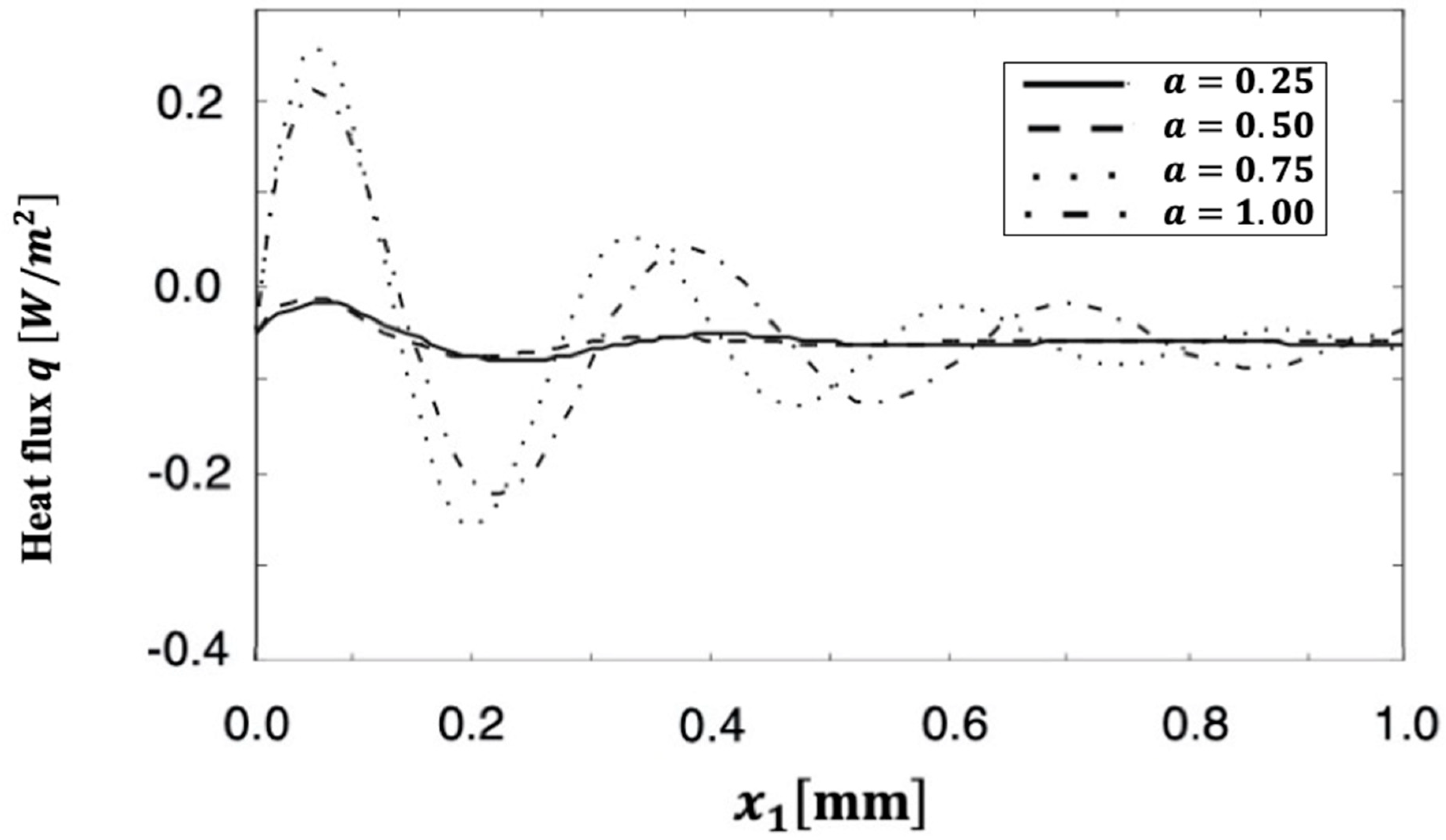
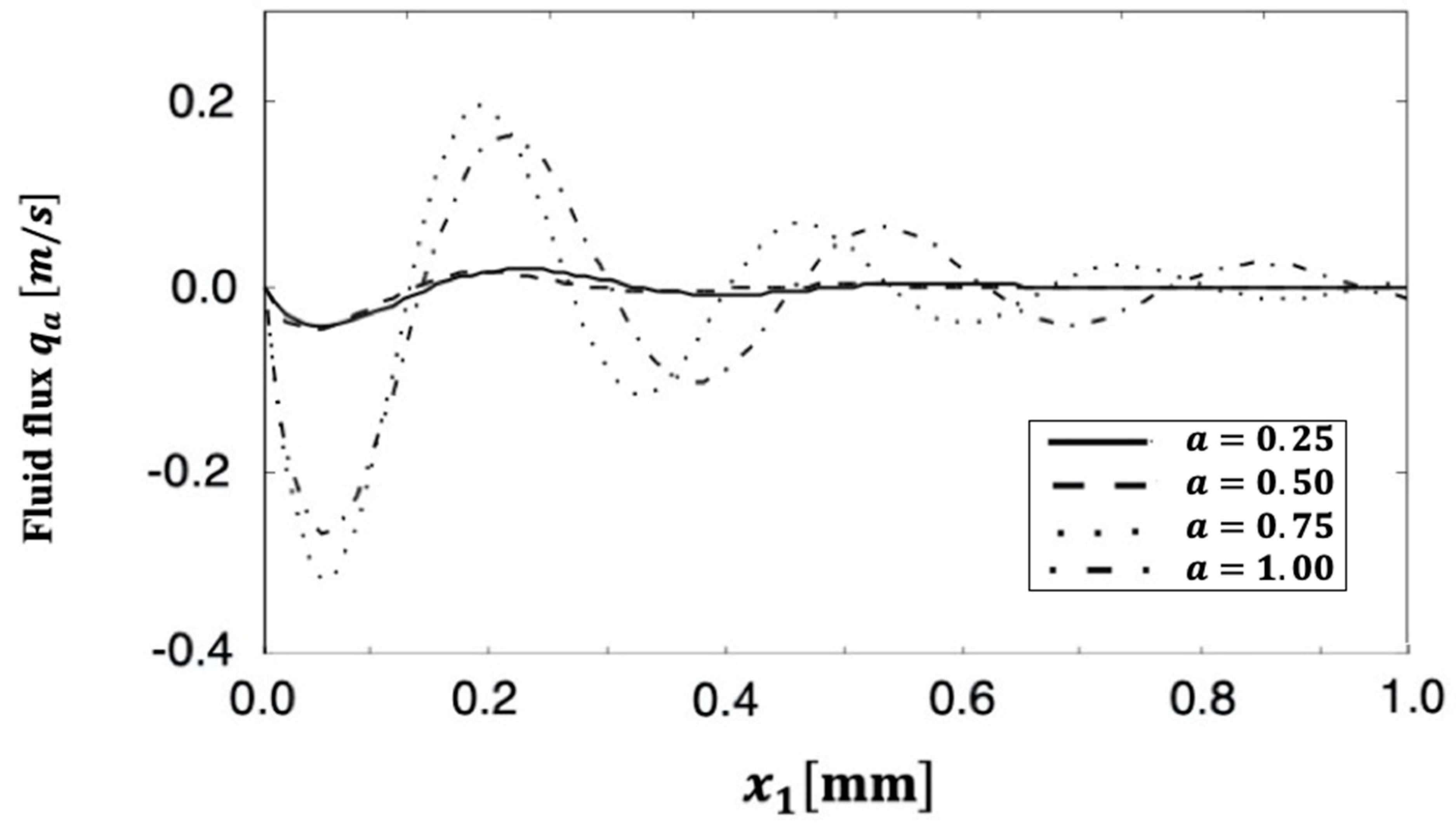
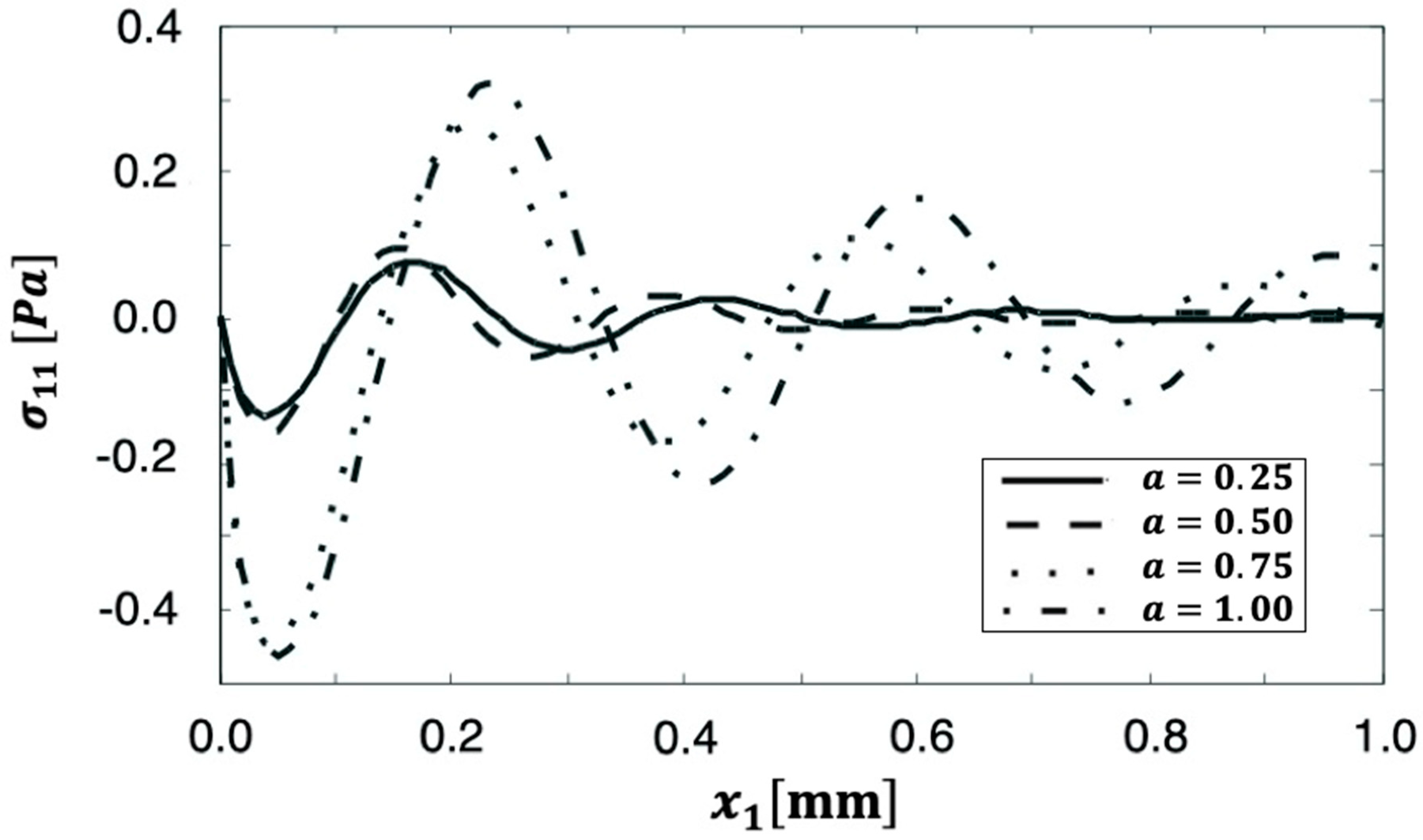
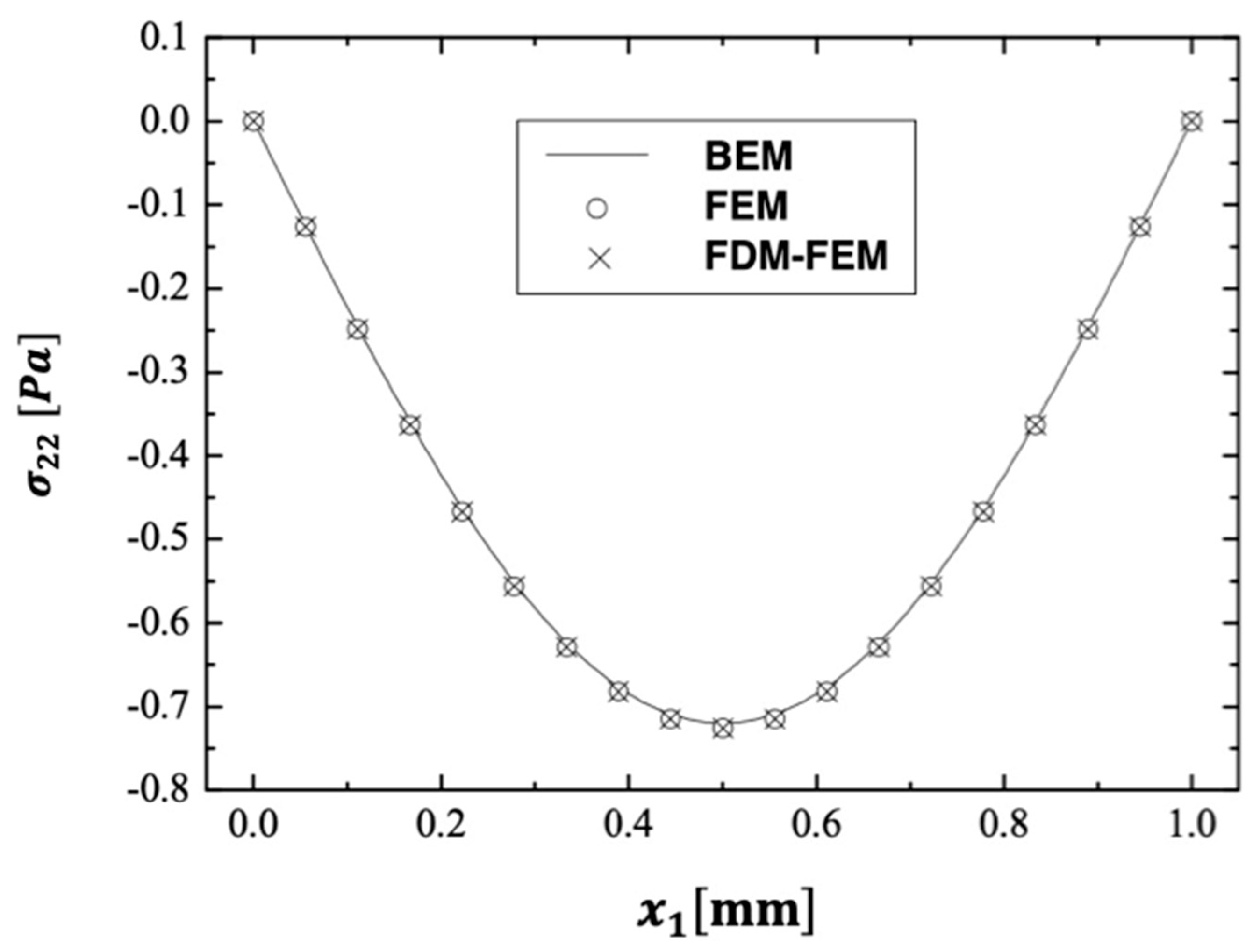
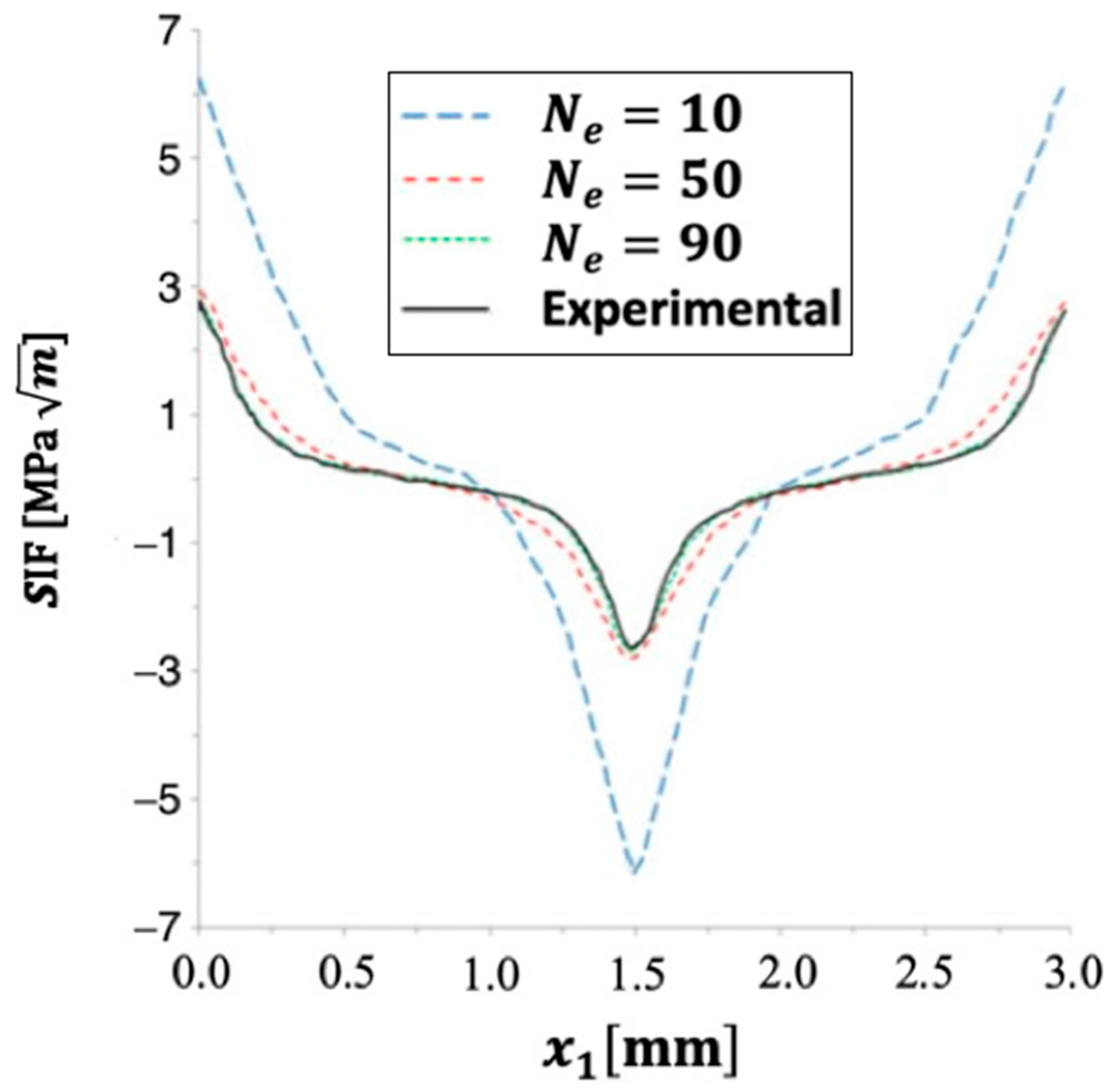
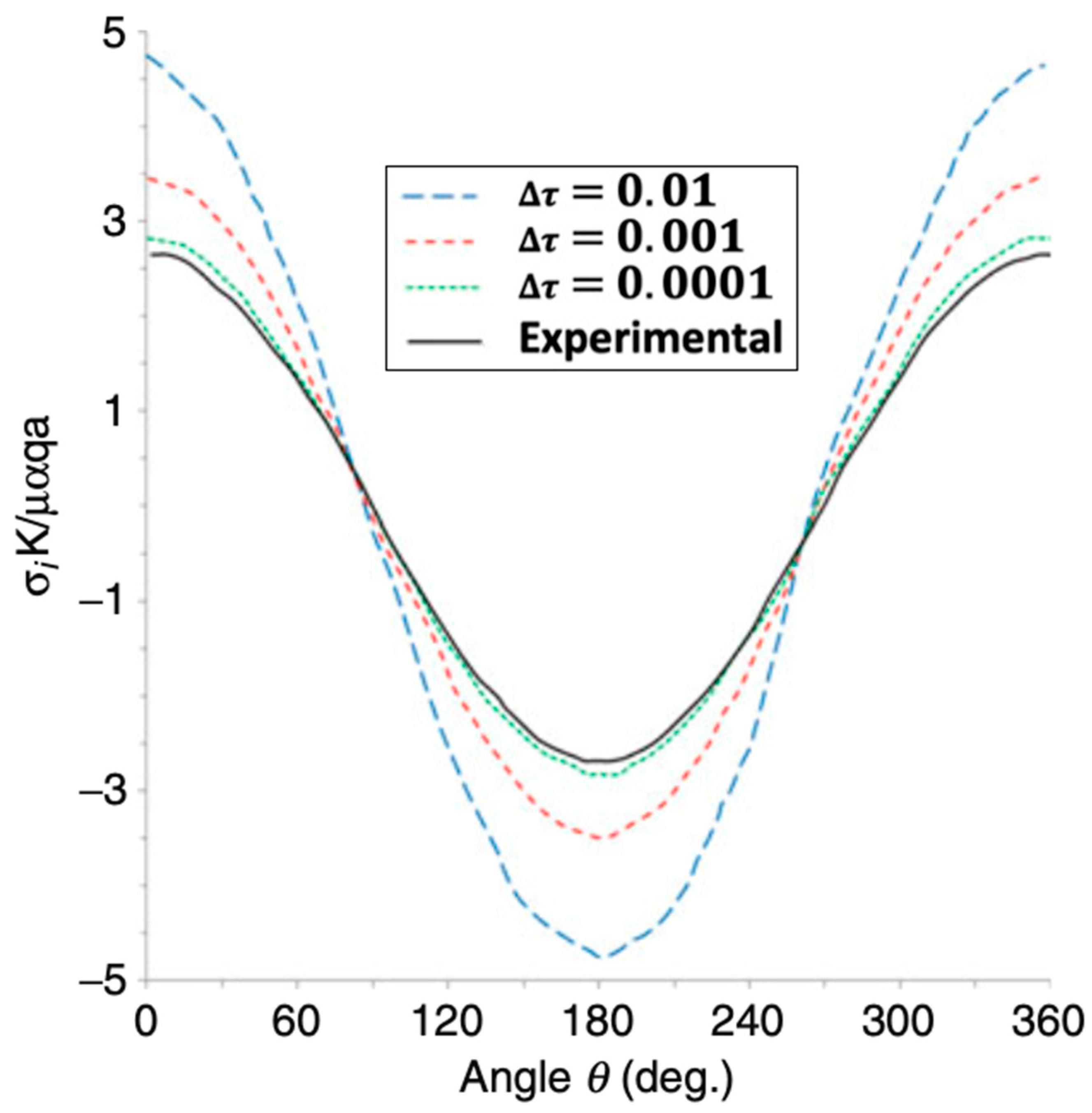
| Discretization Level | Preconditioning Level | MSSOR | MAOR | MHEG | |||
|---|---|---|---|---|---|---|---|
| Processor Timings | Execution Counts | Processor Timings | Execution Counts | Processor Timings | Execution Counts | ||
| 1 (28) | 0 | 0.07 | 7 | 0.09 | 7 | 0.06 | 7 |
| 2 (56) | 0 | 0.19 | 9 | 0.24 | 9 | 0.17 | 8 |
| 1 | 0.16 | 7 | 0.2 | 7 | 0.12 | 7 | |
| 3 (112) | 0 | 0.48 | 11 | 0.64 | 12 | 0.42 | 10 |
| 1 | 0.44 | 9 | 0.56 | 10 | 0.34 | 7 | |
| 2 | 0.38 | 7 | 0.5 | 8 | 0.3 | 5 | |
| 4 (224) | 0 | 2.42 | 14 | 2.52 | 18 | 1.88 | 12 |
| 1 | 1.86 | 12 | 2.1 | 16 | 1.58 | 8 | |
| 2 | 1.58 | 8 | 1.84 | 12 | 1.42 | 6 | |
| 3 | 1.44 | 6 | 1.58 | 8 | 1.38 | 4 | |
| 5 (448) | 0 | 10.86 | 16 | 13.01 | 20 | 8.78 | 14 |
| 1 | 9.2 | 14 | 11.12 | 18 | 7.79 | 10 | |
| 2 | 9.28 | 12 | 10.28 | 16 | 7.08 | 8 | |
| 3 | 8.26 | 10 | 9.42 | 12 | 6.69 | 6 | |
| 4 | 8.1 | 6 | 8.98 | 8 | 6.12 | 4 | |
| 6 (896) | 0 | 42.3 | 22 | 48.6 | 24 | 36 | 16 |
| 1 | 38.6 | 20 | 46.7 | 22 | 34.2 | 14 | |
| 2 | 37.5 | 18 | 44.4 | 20 | 32.5 | 12 | |
| 3 | 35.4 | 14 | 40.7 | 16 | 30.7 | 10 | |
| 4 | 28.5 | 12 | 30.6 | 14 | 26.6 | 8 | |
| 5 | 24.8 | 10 | 28.8 | 12 | 20.8 | 4 | |
| BEM | FEM [64] | FDM-FEM [66] | |
|---|---|---|---|
| Number of nodes | 56 | 60,000 | 58,000 |
| Number of elements | 20 | 11,000 | 10,000 |
| CPU time [min] | 2 | 200 | 220 |
| Memory [Mbyte] | 1 | 160 | 150 |
| Disk space [Mbyte] | 0 | 270 | 290 |
| Accuracy of results [%] | 1.0 | 2.6 | 2.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fahmy, M.A.; Jeli, R.A.A. A New Fractional Boundary Element Model for Anomalous Thermal Stress Effects on Cement-Based Materials. Fractal Fract. 2024, 8, 753. https://doi.org/10.3390/fractalfract8120753
Fahmy MA, Jeli RAA. A New Fractional Boundary Element Model for Anomalous Thermal Stress Effects on Cement-Based Materials. Fractal and Fractional. 2024; 8(12):753. https://doi.org/10.3390/fractalfract8120753
Chicago/Turabian StyleFahmy, Mohamed Abdelsabour, and Roqia Abdullah A. Jeli. 2024. "A New Fractional Boundary Element Model for Anomalous Thermal Stress Effects on Cement-Based Materials" Fractal and Fractional 8, no. 12: 753. https://doi.org/10.3390/fractalfract8120753
APA StyleFahmy, M. A., & Jeli, R. A. A. (2024). A New Fractional Boundary Element Model for Anomalous Thermal Stress Effects on Cement-Based Materials. Fractal and Fractional, 8(12), 753. https://doi.org/10.3390/fractalfract8120753







