Analytical Scheme for Time Fractional Kawahara and Modified Kawahara Problems in Shallow Water Waves
Abstract
1. Introduction
2. Preliminaries
- 1.
- , .
- 2.
- ,
- 3.
- 4.
- ,
3. Algorithm of SHTM
4. Sufficient Condition, Uniqueness, and Convergence Analysis of Shehu Transform
4.1. Sufficient Condition for the Existence of Shehu Transform
4.2. Existence and Uniqueness for SHTM
4.3. Convergence Analysis of SHTM
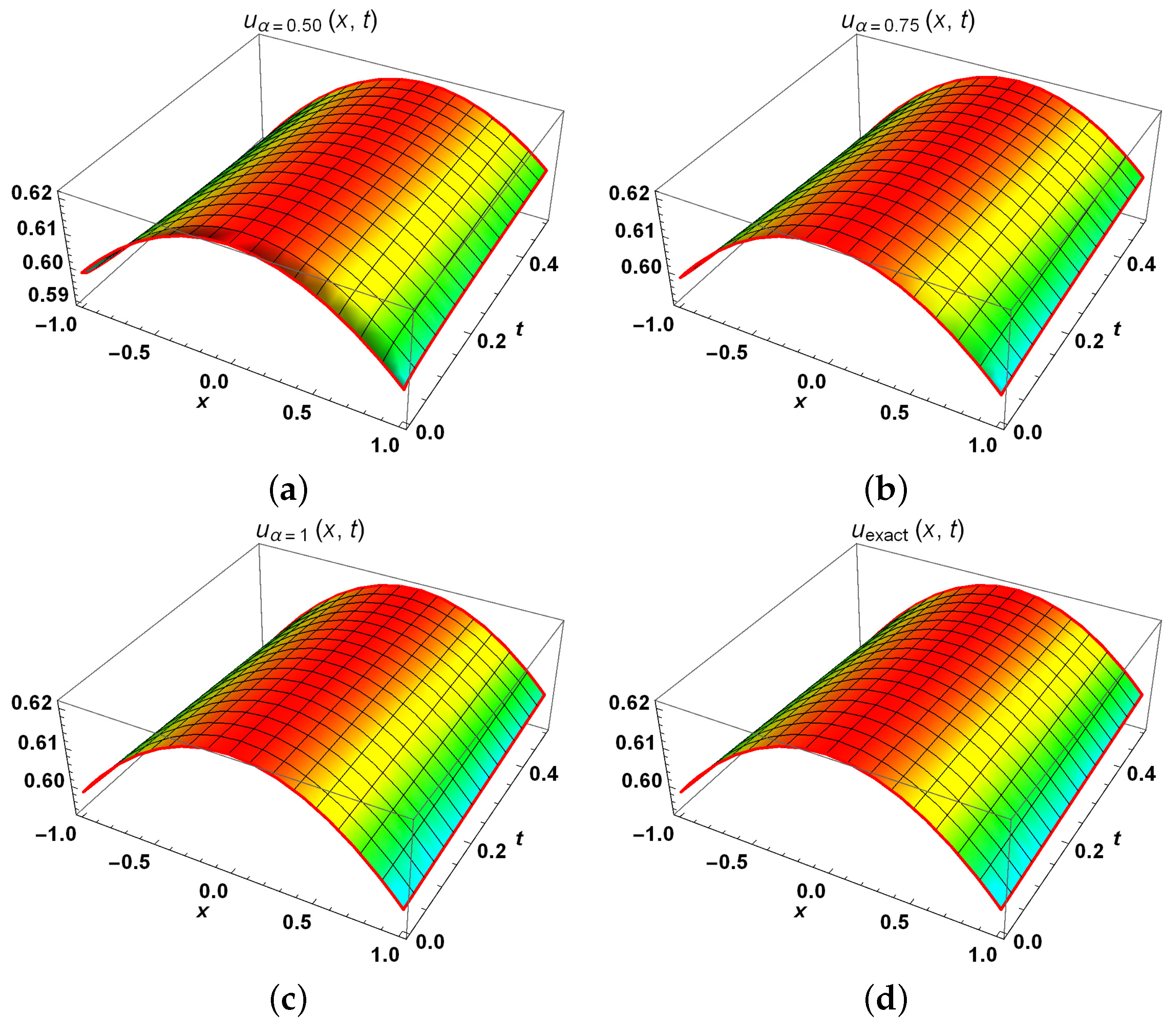
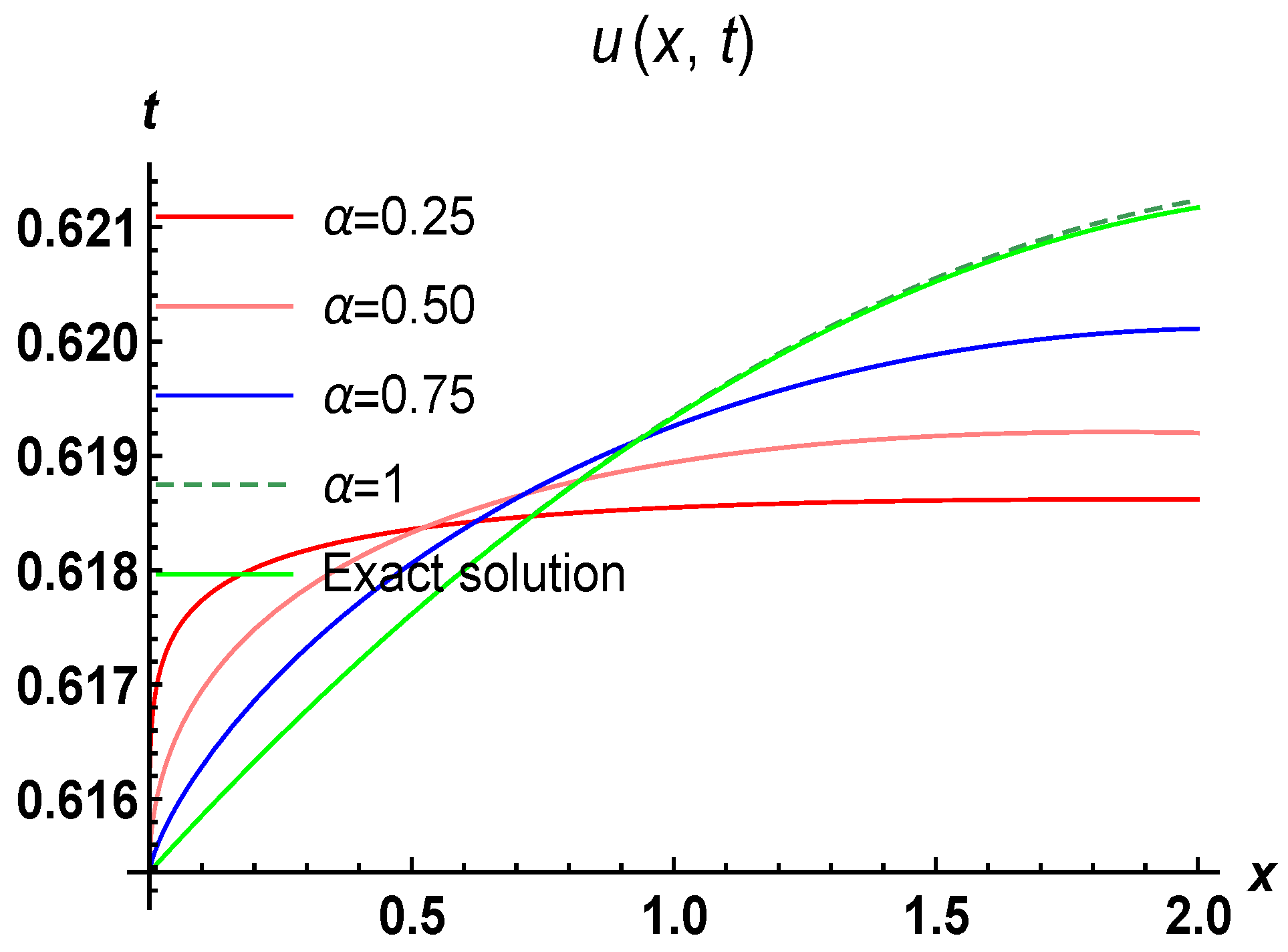
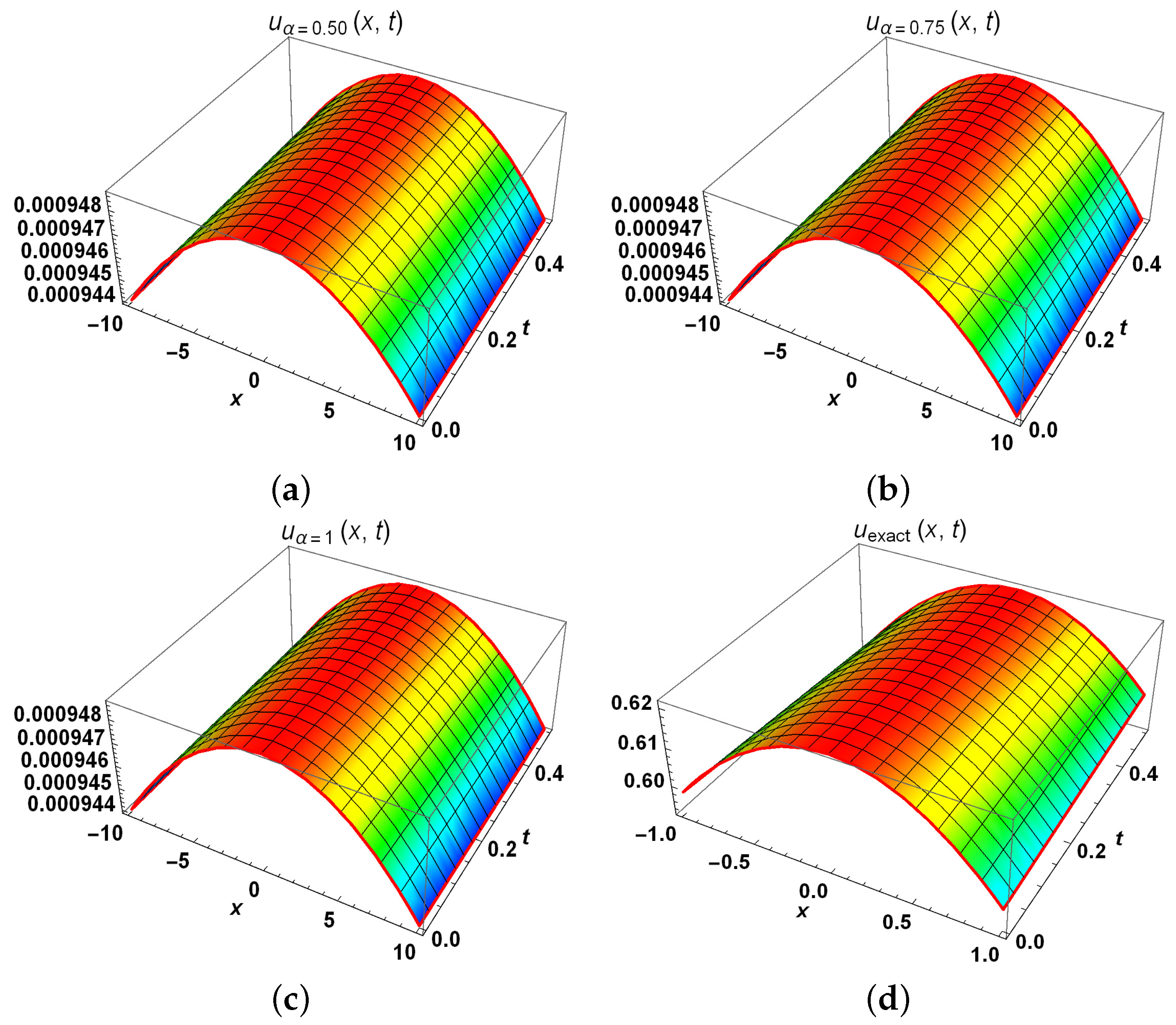
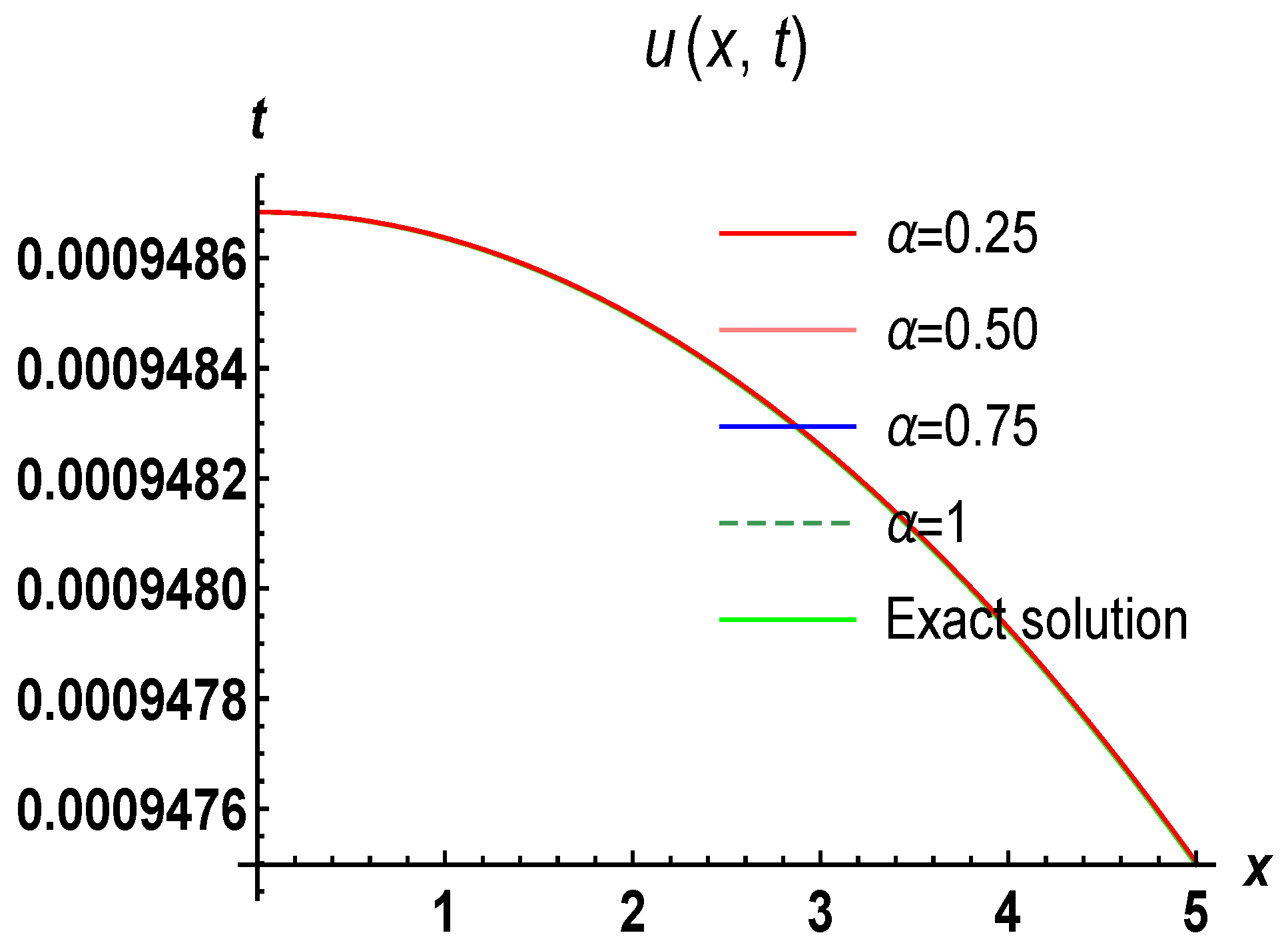
5. Numerical Applications
5.1. Problem 1
5.2. Problem 2
6. Results And Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uchaikin, V.V. Fractional derivatives for physicists and engineers. In Nonlinear Physical Science; Higher Education Press: Beijing, China, 2013; Volume I. [Google Scholar]
- Pang, G.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional physics-informed neural networks. SIAM J. Sci. Comput. 2019, 41, A2603–A2626. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Samet, B.; Gómez-Aguilar, J.; Osman, M. A chaos study of tumor and effector cells in fractional tumor-immune model for cancer treatment. Chaos Solit. Fractals 2020, 141, 110321. [Google Scholar] [CrossRef]
- Cuesta, E.; Kirane, M.; Malik, S.A. Image structure preserving denoising using generalized fractional time integrals. Signal Process. 2012, 92, 553–563. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2011. [Google Scholar]
- Jafari, H.; Nazari, M.; Baleanu, D.; Khalique, C.M. A new approach for solving a system of fractional partial differential equations. Comput. Math. Appl. 2013, 66, 838–843. [Google Scholar] [CrossRef]
- Alquran, M.; Ali, M.; Alsukhour, M.; Jaradat, I. Promoted residual power series technique with Laplace transform to solve some time-fractional problems arising in physics. Results Phys. 2020, 19, 103667. [Google Scholar] [CrossRef]
- Zhang, Y. A finite difference method for fractional partial differential equation. Appl. Math. Comput. 2009, 215, 524–529. [Google Scholar] [CrossRef]
- Gaber, A.; Aljohani, A.; Ebaid, A.; Machado, J.T. The generalized Kudryashov method for nonlinear space–time fractional partial differential equations of Burgers type. Nonlinear Dyn. 2019, 95, 361–368. [Google Scholar] [CrossRef]
- Zheng, B.; Wen, C. Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Korkmaz, A.; Eslami, M.; Vahidi, J.; Asghari, R. Traveling wave solution of conformable fractional generalized reaction Duffing model by generalized projective Riccati equation method. Opt. Quantum Electron. 2018, 50, 1–13. [Google Scholar] [CrossRef]
- Aksoy, E.; Kaplan, M.; Bekir, A. Exponential rational function method for space–time fractional differential equations. Waves Random Complex Media 2016, 26, 142–151. [Google Scholar] [CrossRef]
- Tariq, H.; Akram, G. New approach for exact solutions of time fractional Cahn–Allen equation and time fractional Phi-4 equation. Phys. A Stat. Mech. Its Appl. 2017, 473, 352–362. [Google Scholar] [CrossRef]
- Mishra, N.K.; AlBaidani, M.M.; Khan, A.; Ganie, A.H. Two novel computational techniques for solving nonlinear time-fractional laxs korteweg-de vries equation. Axioms 2023, 12, 400. [Google Scholar] [CrossRef]
- Aniqa, A.; Ahmad, J. Soliton solution of fractional sharma-tasso-olever equation via an efficient (G’/G)-expansion method. Ain Shams Eng. J. 2022, 13, 101528. [Google Scholar] [CrossRef]
- Kaya, D.; Al-Khaled, K. A numerical comparison of a Kawahara equation. Phys. Lett. A 2007, 363, 433–439. [Google Scholar] [CrossRef]
- Daşcıoğlu, A.; Ünal, S.Ç. New exact solutions for the space-time fractional Kawahara equation. Appl. Math. Model. 2021, 89, 952–965. [Google Scholar] [CrossRef]
- Başhan, A. An efficient approximation to numerical solutions for the Kawahara equation via modified cubic B-spline differential quadrature method. Mediterr. J. Math. 2019, 16, 14. [Google Scholar] [CrossRef]
- Kawahara, T. Oscillatory solitary waves in dispersive media. J. Phys. Soc. Jpn. 1972, 33, 260–264. [Google Scholar] [CrossRef]
- Wazwaz, A.M. New solitary wave solutions to the modified Kawahara equation. Phys. Lett. A 2007, 360, 588–592. [Google Scholar] [CrossRef]
- Sirendaoreji. New exact travelling wave solutions for the Kawahara and modified Kawahara equations. Chaos Solit. Fractals 2004, 19, 147–150. [Google Scholar] [CrossRef]
- Jin, L. Application of variational iteration method and homotopy perturbation method to the modified Kawahara equation. Math. Comput. Model. 2009, 49, 573–578. [Google Scholar] [CrossRef]
- AlBaidani, M.A.M.; Ganie, A.H.; Aljuaydi, F.; Khan, A. Application of analytical techniques for solving fractional physical models arising in applied sciences. Fract. Fract. 2023, 7, 584. [Google Scholar] [CrossRef]
- Koppala, P.; Kondooru, R. An efficient technique to solve time-fractional Kawahara and modified Kawahara equations. Symmetry 2022, 14, 1777. [Google Scholar] [CrossRef]
- Çulha Ünal, S. Approximate solutions of time fractional kawahara equation by utilizing the residual power series method. Int. J. Appl. Comput. Math. 2022, 8, 78. [Google Scholar] [CrossRef]
- Odibat, Z.Z.; Momani, S.; Xu, H. A reliable algorithm of homotopy analysis method for solving nonlinear fractional differential equations. Appl. Math. Model. 2010, 34, 593–600. [Google Scholar] [CrossRef]
- He, J.H.; Latifizadeh, H. A general numerical algorithm for nonlinear differential equations by the variational iteration method. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 4797–4810. [Google Scholar] [CrossRef]
- Rani, D.; Mishra, V.; Cattani, C. Numerical inverse laplace transform for solving a class of fractional differential equations. Int. Symmetry 2019, 11, 530. [Google Scholar] [CrossRef]
- Qureshi, S.; Kumar, P. Using Shehu integral transform to solve fractional order Caputo type initial value problems. J. Appl. Math. Comput. Mech. 2019, 18, 75–83. [Google Scholar] [CrossRef]
- Jena, S.R.; Sahu, I. A novel approach for numerical treatment of traveling wave solution of ion acoustic waves as a fractional nonlinear evolution equation on Shehu transform environment. Phys. Scr. 2023, 98, 085231. [Google Scholar] [CrossRef]
- Shah, R.; Saad Alshehry, A.; Weera, W. A semi-analytical method to investigate fractional-order gas dynamics equations by Shehu transform. Symmetry 2022, 14, 1458. [Google Scholar] [CrossRef]
- Areshi, M.; Zidan, A.; Shah, R.; Nonlaopon, K. A modified techniques of fractional-order Cauchy-reaction diffusion equation via Shehu transform. J. Funct. Spaces 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- Yıldırım, A.; Koçak, H. Homotopy perturbation method for solving the space–time fractional advection–dispersion equation. Adv. Water Resour. 2009, 32, 1711–1716. [Google Scholar] [CrossRef]
- Farhood, A.K.; Mohammed, O.H. Homotopy perturbation method for solving time-fractional nonlinear variable-order delay partial differential equations. Partial Differ. Equ. Appl. Math. 2023, 7, 100513. [Google Scholar] [CrossRef]
| x | t | SHTM Results | SHTM Results | SHTM Results | Precise Results |
|---|---|---|---|---|---|
| 0.25 | 0.1 | 0.620501 | 0.62025 | 0.620053 | 0.620053 |
| 0.3 | 0.620734 | 0.620664 | 0.620475 | 0.620475 | |
| 0.5 | 0.620760 | 0.62088 | 0.620811 | 0.620810 | |
| 0.50 | 0.1 | 0.616948 | 0.616285 | 0.615854 | 0.615854 |
| 0.3 | 0.617843 | 0.617322 | 0.616777 | 0.616777 | |
| 0.5 | 0.618329 | 0.618060 | 0.617616 | 0.617615 | |
| 0.75 | 0.1 | 0.610484 | 0.609421 | 0.608763 | 0.608763 |
| 0.3 | 0.612027 | 0.611064 | 0.610171 | 0.610171 | |
| 0.5 | 0.612965 | 0.612311 | 0.611500 | 0.611498 | |
| 1 | 0.1 | 0.601218 | 0.599771 | 0.598897 | 0.598897 |
| 0.3 | 0.603383 | 0.601993 | 0.600768 | 0.600768 | |
| 0.5 | 0.604756 | 0.601993 | 0.602564 | 0.602562 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadeem, M.; Khan, A.; Javeed, M.A.; Yubin, Z. Analytical Scheme for Time Fractional Kawahara and Modified Kawahara Problems in Shallow Water Waves. Fractal Fract. 2024, 8, 395. https://doi.org/10.3390/fractalfract8070395
Nadeem M, Khan A, Javeed MA, Yubin Z. Analytical Scheme for Time Fractional Kawahara and Modified Kawahara Problems in Shallow Water Waves. Fractal and Fractional. 2024; 8(7):395. https://doi.org/10.3390/fractalfract8070395
Chicago/Turabian StyleNadeem, Muhammad, Asad Khan, Muhammad Awais Javeed, and Zhong Yubin. 2024. "Analytical Scheme for Time Fractional Kawahara and Modified Kawahara Problems in Shallow Water Waves" Fractal and Fractional 8, no. 7: 395. https://doi.org/10.3390/fractalfract8070395
APA StyleNadeem, M., Khan, A., Javeed, M. A., & Yubin, Z. (2024). Analytical Scheme for Time Fractional Kawahara and Modified Kawahara Problems in Shallow Water Waves. Fractal and Fractional, 8(7), 395. https://doi.org/10.3390/fractalfract8070395






