Unveiling Temporal Cyclicities in Seismic b-Values and Major Earthquake Events in Japan by Local Singularity Analysis and Wavelet Methods
Abstract
1. Introduction
2. Data and Methods
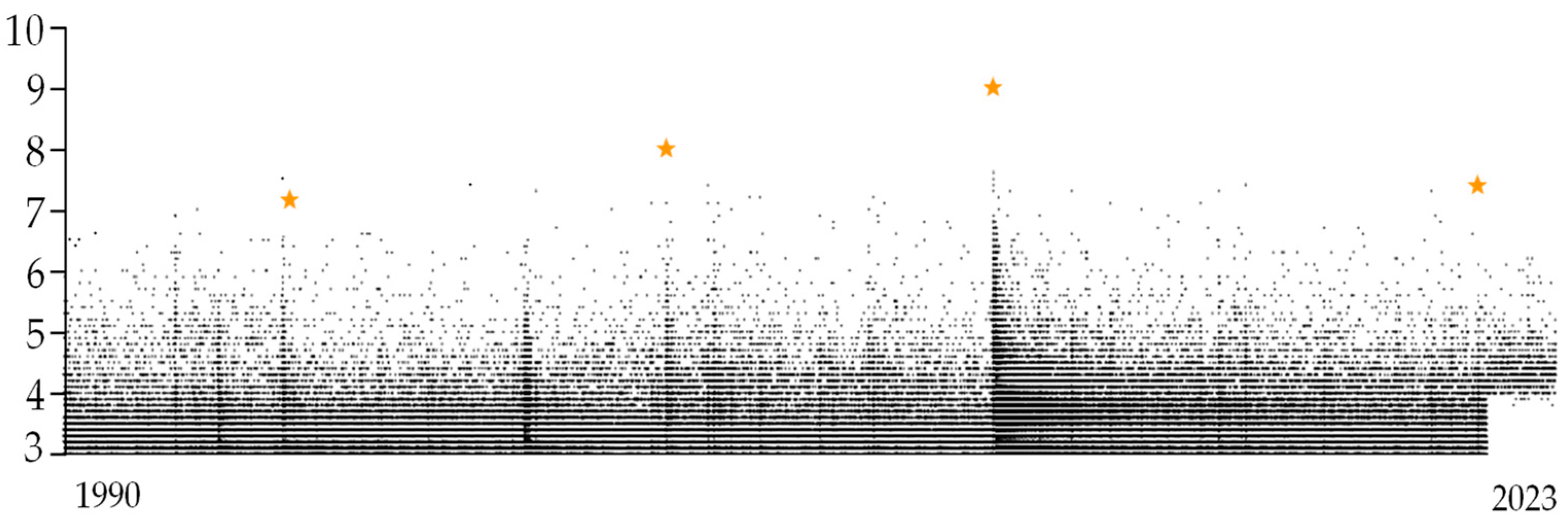
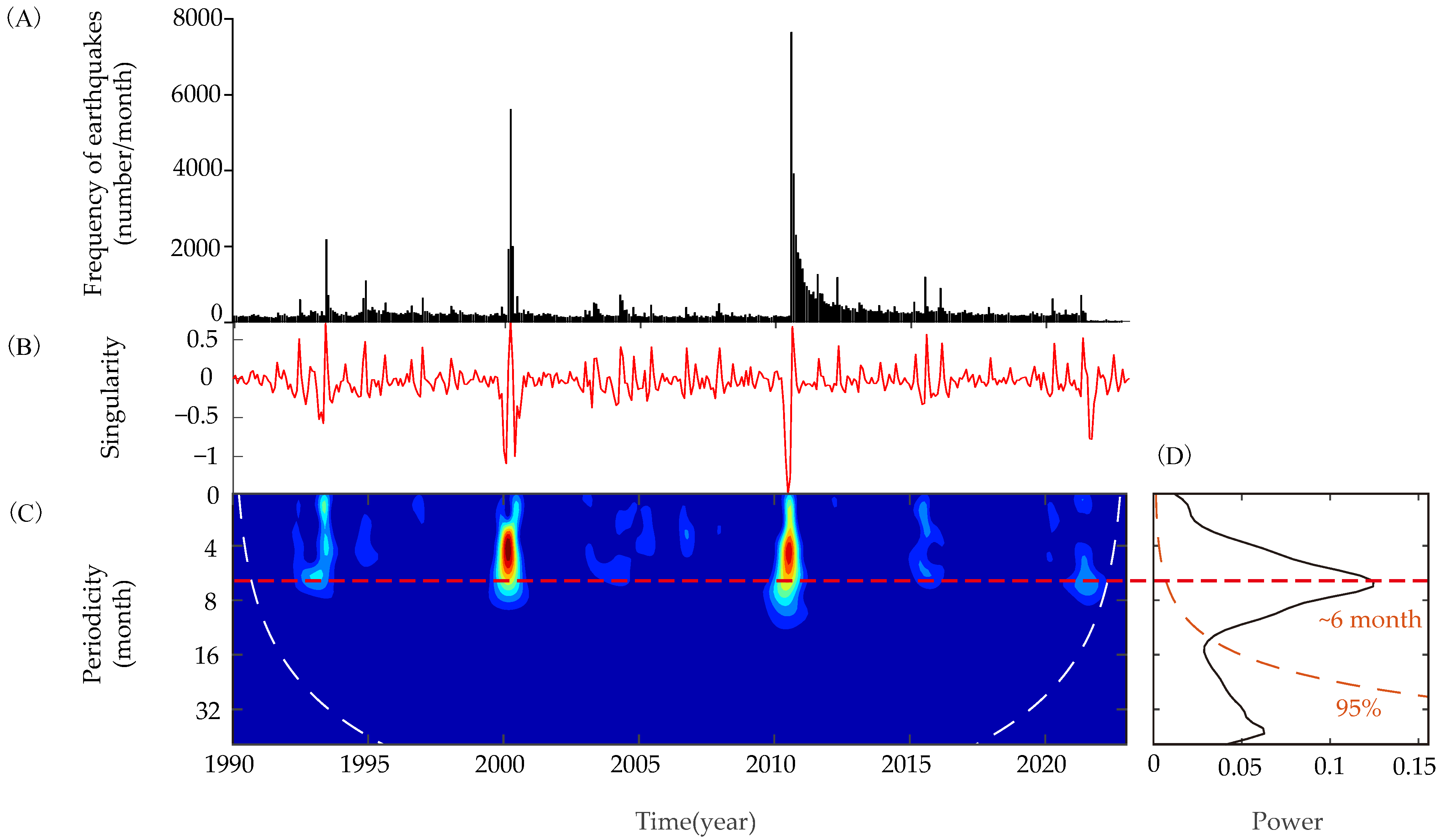
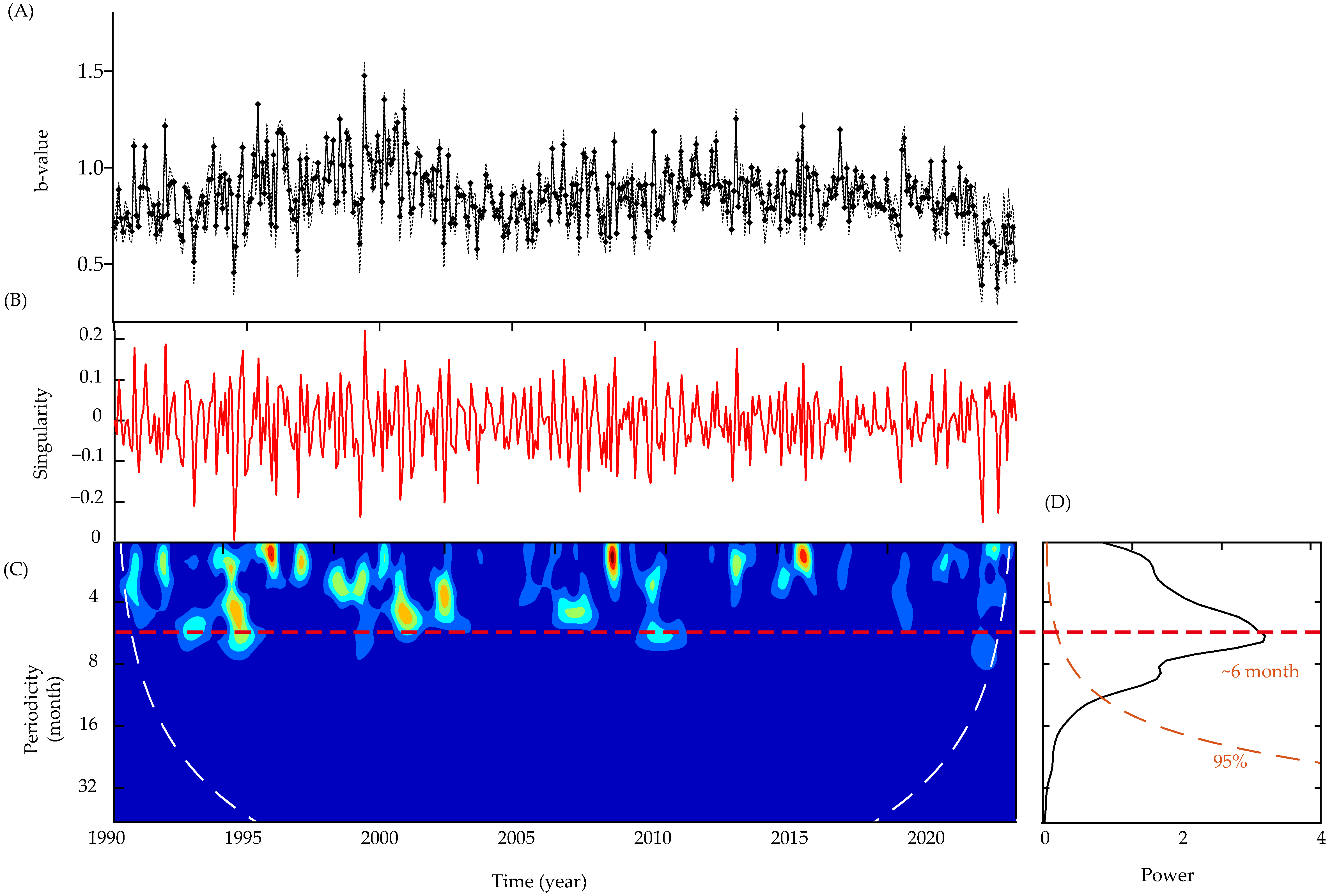
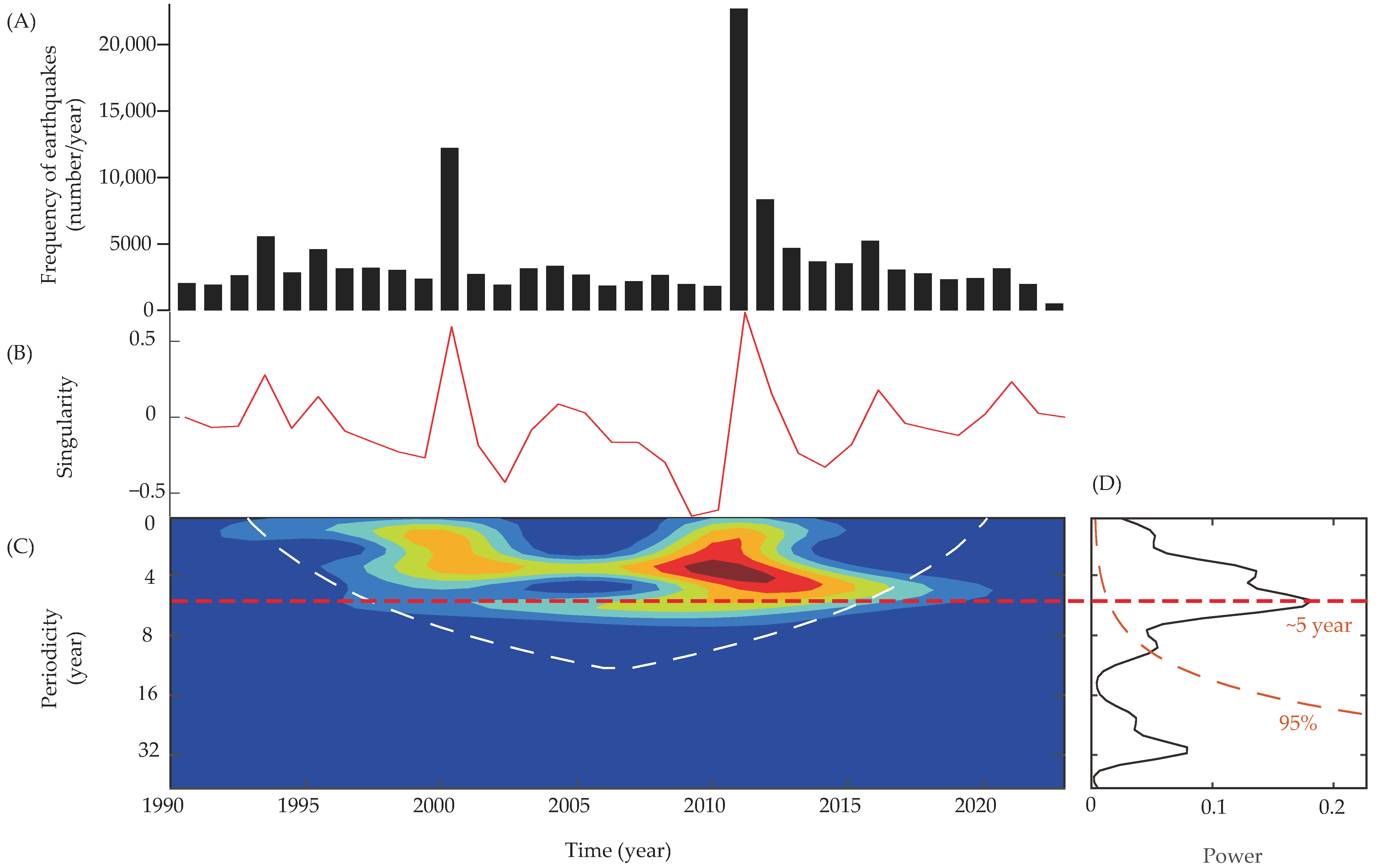
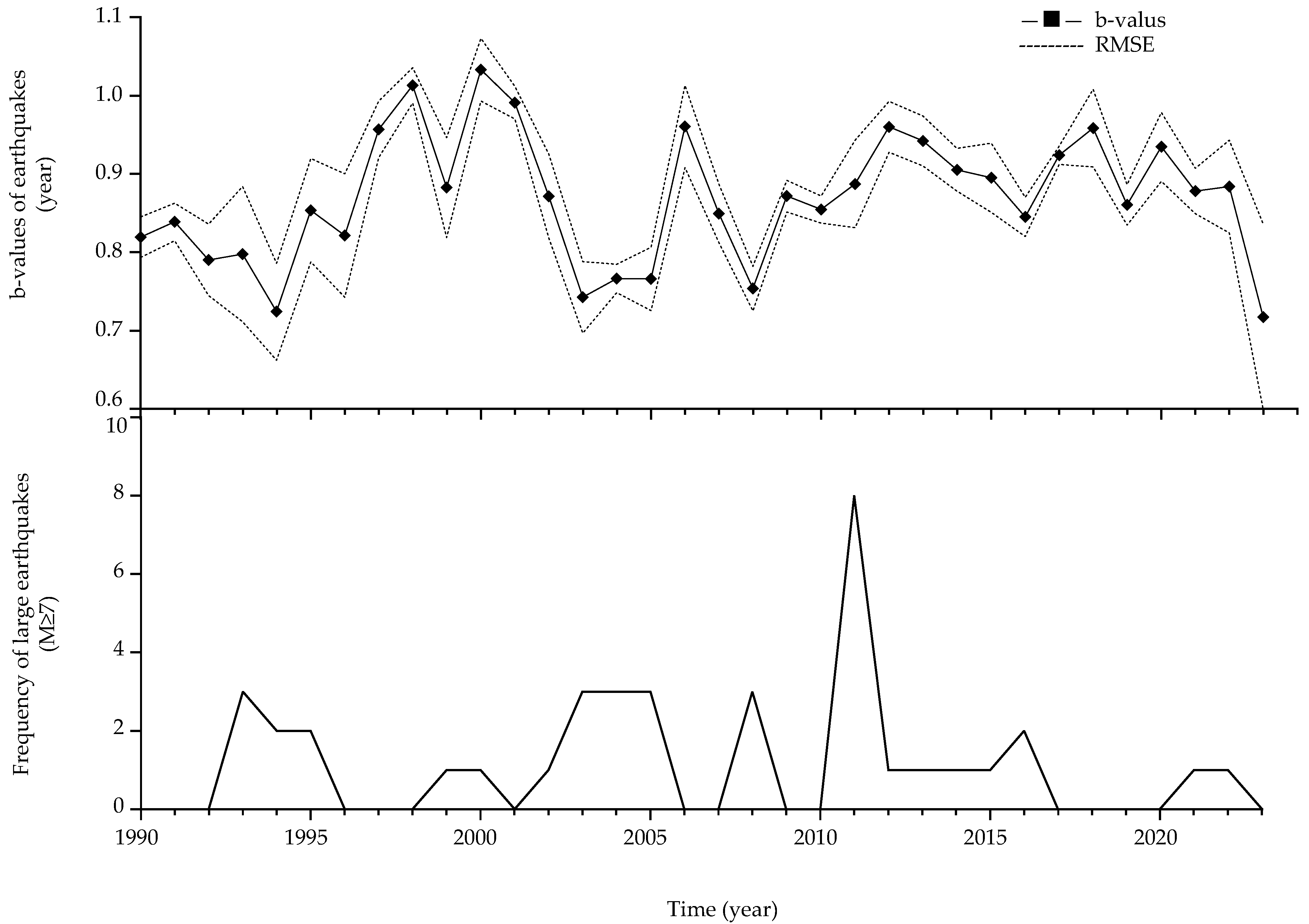
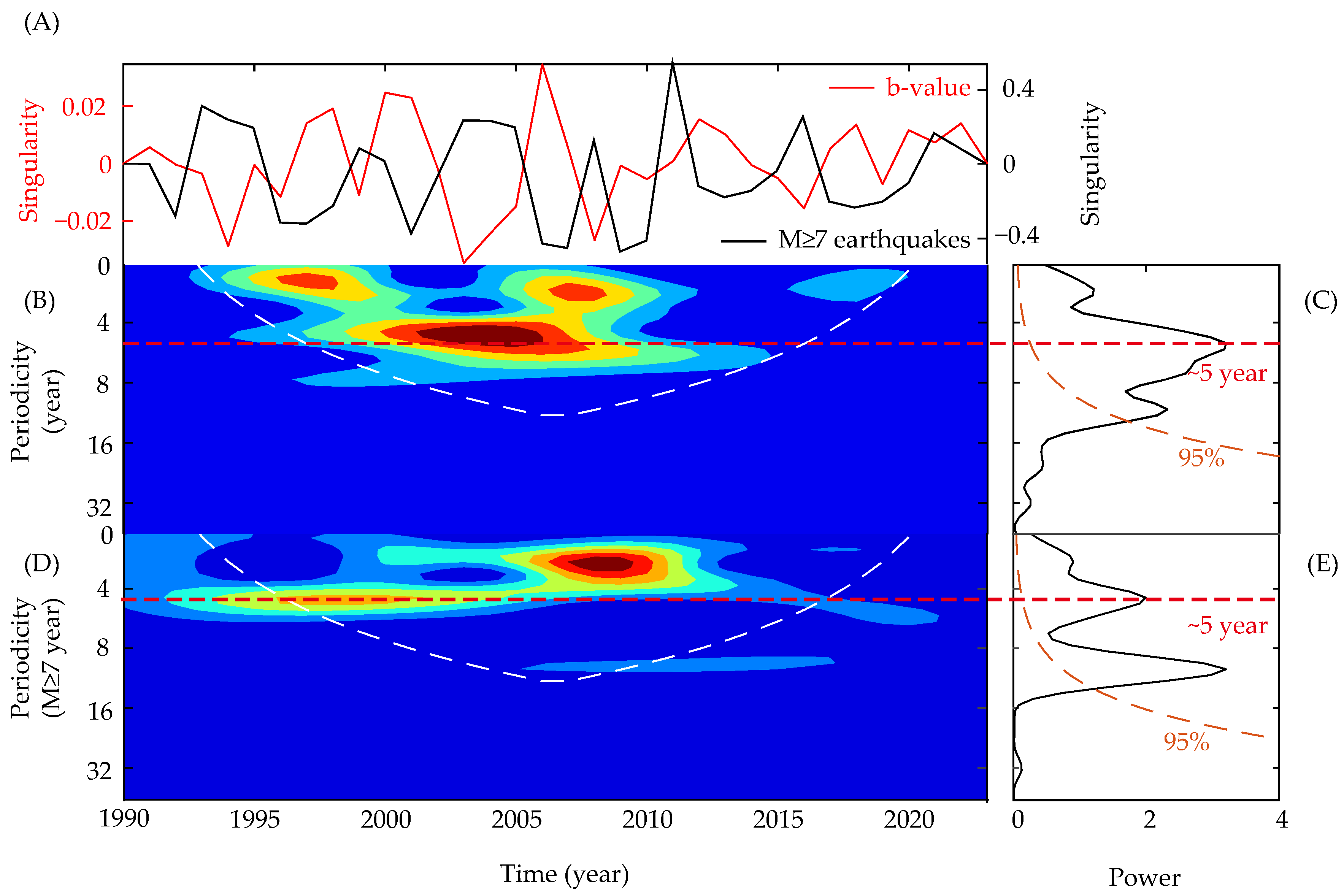
3. Results
4. Discussion
4.1. Time Series Analysis of Earthquake Frequency
4.2. Time Series Analysis of Earthquake Frequency-Magnitude Relationship (b-Values)
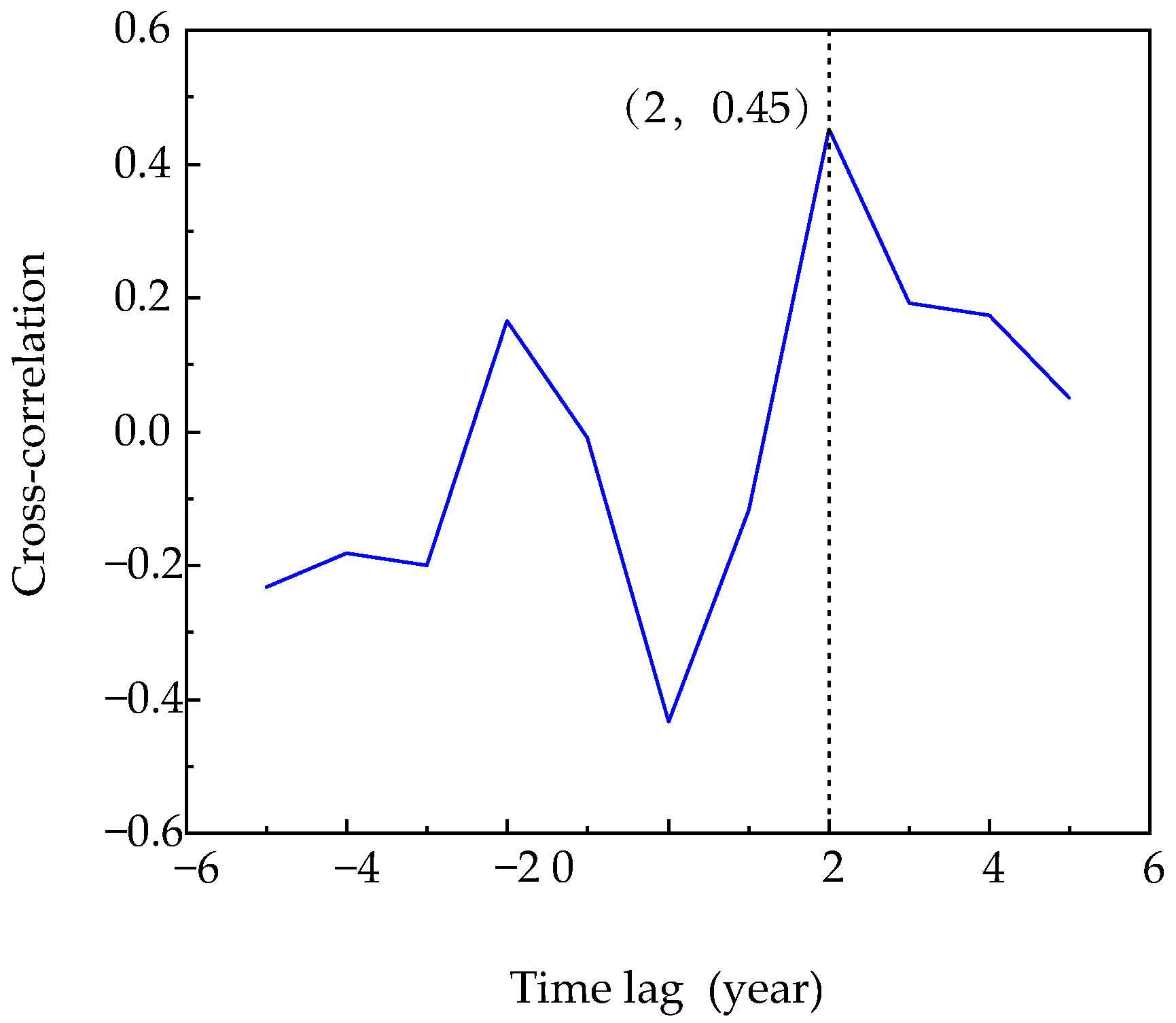
4.3. Analysis of Major Earthquake Temporal Characteristics
5. Conclusions and Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Mogi, K. Study of the elastic shocks caused by the fracture of heterogeneous materials and its relation to earthquake phenomena. Bull. Earthq. Res. Inst. 1962, 40, 831–853. [Google Scholar]
- Mogi, K. Magnitude-frequency relation for elastic shocks accompanying fractures of various materials and some related problems in earthquakes (2nd Paper). Bull. Earthq. Res. Univ. Tokyo 1963, 40, 831–853. [Google Scholar]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar] [CrossRef]
- Wyss, M.; Schorlemmer, D.; Wiemer, S. Mapping asperities by minima of local recurrence time: San Jacinto-Elsinore fault zones. J. Geophys. Res. Solid Earth 2000, 105, 7829–7844. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Gui, Z.; Bai, Y.L.; Wang, Z.J.; Li, T.F. Seismic b-value anomalies in the Sumatran region: Seismotectonic implications. J. Asian Earth Sci. 2019, 173, 29–41. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Chen, L. The characteristics of the b-value anomalies preceding the 2004 Mw9.0 Sumatra earthquake. Geomat. Nat. Hazards Risk 2022, 13, 390–399. [Google Scholar] [CrossRef]
- Fiedler, B.; Hainzl, S.; Zöller, G.; Holschneider, M. Detection of Gutenberg-Richter b-value changes in earthquake time series. Bull. Seismol. Soc. Am. 2018, 108, 2778–2787. [Google Scholar] [CrossRef]
- Lacidogna, G.; Borla, O.; De Marchi, V. Statistical Seismic Analysis by b-Value and Occurrence Time of the Latest Earthquakes in Italy. Remote Sens. 2023, 15, 5236. [Google Scholar] [CrossRef]
- Suyehiro, S. Difference between aftershocks and foreshocks in the relationship of magnitude to frequency of occurrence for the great Chilean earthquake of 1960. Bull. Seismol. Soc. Am. 1966, 56, 185–200. [Google Scholar] [CrossRef]
- Gorgun, E. Analysis of the b-values before and after the 23 October 2011 Mw7.2VanErci, Turkeyearthquake. Tectonophysics 2013, 603, 213–221. [Google Scholar] [CrossRef]
- Sharma, V.; Biswas, R. Spatio-temporal variation in b-value prior to the 26 November 2021 Mizoram earthquake of northeastIndia. Geol. J. 2022, 57, 5361–5373. [Google Scholar] [CrossRef]
- Sidorin, A.Y. Features of the diurnal periodicity of earthquakes in Japan. Seism. Instrum. 2014, 50, 246–267. [Google Scholar] [CrossRef]
- Lyubushin, A.A. Cyclic properties of seismic noise and the problem of predictability of the strongest earthquakes in Japanese Islands. Atmos. Ocean. Phys. 2018, 54, 1460–1469. [Google Scholar] [CrossRef]
- Tanaka, Y. An approximately 9-yr-period variation in seismicity and crustal deformation near the Japan Trench and a consideration of its origin. Geophys. J. Int. 2014, 196, 760–787. [Google Scholar] [CrossRef][Green Version]
- Hutton, K.; Woessner, J.; Hauksson, E. Earthquake Monitoring in Southern California for Seventy-Seven Years (1932–2008). Bull. Seismol. Soc. Am. 2010, 100, 423–446. [Google Scholar] [CrossRef]
- Cheng, Q. Singularity analysis of global zircon U-Pb age series and implication of continental crust evolution. Gondwana Res. 2017, 51, 51–63. [Google Scholar] [CrossRef]
- Chen, G.; Cheng, Q. Cyclicity and Persistence of Earth’s Evolution Over Time Wavelet and Fractal Analysis. Geophys. Res. Lett. 2018, 45, 8223–8230. [Google Scholar] [CrossRef]
- Cheng, Q.M. Mathematical Geosciences: Local Singularity Analysis of Nonlinear Earth Processes and Extreme Geo-Events. In Handbook of Mathematical Geosciences; Springer: Berlin/Heidelberg, Germany, 2018; pp. 179–208. [Google Scholar]
- Chen, Z.; Cheng, Q.; Chen, J.; Xie, S. A novel iterative approach for mappingocal singularities from geochemical data. Nonlinear Process. Geophys. 2007, 14, 317–324. [Google Scholar] [CrossRef][Green Version]
- Chen, G.; Zhang, H. Wavelets in Geosciences. In Encyclopedia of Mathematical Geosciences; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–11. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing. Comput. Music. J. 2007, 31, 83–85. [Google Scholar]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1997, 79, 61. [Google Scholar] [CrossRef]
- Cheng, Q.; Sun, H. Variation of singularity of earthquake-size distribution with respect to tectonic regime. Geosci. Front. 2018, 9, 453–458. [Google Scholar] [CrossRef]
- Ozawa, S.; Nishimura, T.; Suito, H.; Kobayashi, T.; Tobita, M.; Imakiire, T. Coseismic and postseismic slip of the 2011 magnitude-9 Tohoku-Oki earthquake. Nature 2011, 475, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.Y.; Zhao, L.; Liu, Y.J.; Ning, J.Y.; Chen, Q.F.; Lin, J. Stress adjustment revealed by seismicity and earthquake focal mechanisms in northeast China before and after the 2011 Tohoku-Oki earthquake. Tectonophysics 2016, 666, 23–32. [Google Scholar] [CrossRef]
- Shao, Z.G.; Zhan, W.; Zhang, L.P.; Xu, J. Analysis of the Far-Field Co-seismic and Post-seismic Responses Caused by the 2011 MW 9.0 Tohoku-Oki Earthquake. Pure Appl. Geophys. 2016, 173, 411–424. [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.K. Present-Day Crustal Deformation of Continental China Derived From GPS and Its Tectonic Implications. J. Geophys. Res.-Solid Earth 2020, 125, e2019JB018774. [Google Scholar] [CrossRef]
- Zhao, Q.; Fu, G.Y.; Wu, W.W.; Liu, T.; Su, L.N.; Su, X.N.; Shestakov, N.V. Spatial-temporal evolution and corresponding mechanism of the far-field post-seismic displacements following the 2011 M w 9.0 Tohoku earthquake. Geophys. J. Int. 2018, 214, 1774–1782. [Google Scholar] [CrossRef]
- Gong, W.; Chen, H.; Gao, Y.; Li, Q.; Sun, Y. A test on methods for Mc estimation and spatial-temporal distribution of b-value in the eastern Tibetan Plateau. Front. Earth Sci. 2024, 12, 1335938. [Google Scholar] [CrossRef]
- Prasad, S.; Singh, C. Evolution of b-values before large earthquakes of mb ≥6.0 in the Andaman region. Geol. Acta 2015, 13, 205–210. [Google Scholar]
- Wu, W.; Long, F.; Liang, M.; Wei, Y.; Sun, W.; Chen, X.; Zhao, J. Spatial and Temporal Variations in Earthquake Stress Drops between the 2008 Wenchuan and 2013 Lushan Earthquakes. Acta Geol. Sin. (Engl. Ed.) 2020, 94, 1635–1650. [Google Scholar] [CrossRef]
- Zhao, G.M.; Wu, Z.H.; Liu, Y.H. Fault interaction, stress triggering and differential response of active faults in the southeastern margin of Qinghai-Tibet Plateau. Geol. Bull. 2014, 4, 470–484. [Google Scholar]
- Li, C.L. Re-estimate of Major Earthquake Activity in Surrounding Areas after the M-S 6.6 Jinghe Earthquake in Xinjiang, 2017. Pure Appl. Geophys. 2019, 176, 563–576. [Google Scholar] [CrossRef]
- Wyss, M.; Wiemer, S. Change in the probability for earthquakes in southern California due to the Landers magnitude 7.3 earthquake. Science 2000, 290, 1334–1338. [Google Scholar] [CrossRef]
- David, B.; Julia, M.; Yannick, C. Geometrically controlled slow slip enhanced by seismic waves: A mechanism for delayed triggering. Earth Planet. Sci. Lett. 2021, 554, 116695. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhou, Y.; Cheng, Q. Unveiling Temporal Cyclicities in Seismic b-Values and Major Earthquake Events in Japan by Local Singularity Analysis and Wavelet Methods. Fractal Fract. 2024, 8, 359. https://doi.org/10.3390/fractalfract8060359
Li S, Zhou Y, Cheng Q. Unveiling Temporal Cyclicities in Seismic b-Values and Major Earthquake Events in Japan by Local Singularity Analysis and Wavelet Methods. Fractal and Fractional. 2024; 8(6):359. https://doi.org/10.3390/fractalfract8060359
Chicago/Turabian StyleLi, Siyuan, Yuanzhi Zhou, and Qiuming Cheng. 2024. "Unveiling Temporal Cyclicities in Seismic b-Values and Major Earthquake Events in Japan by Local Singularity Analysis and Wavelet Methods" Fractal and Fractional 8, no. 6: 359. https://doi.org/10.3390/fractalfract8060359
APA StyleLi, S., Zhou, Y., & Cheng, Q. (2024). Unveiling Temporal Cyclicities in Seismic b-Values and Major Earthquake Events in Japan by Local Singularity Analysis and Wavelet Methods. Fractal and Fractional, 8(6), 359. https://doi.org/10.3390/fractalfract8060359






